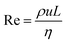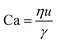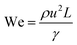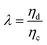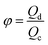Passive and active droplet generation with microfluidics: a review
Pingan
Zhu
 ab and
Liqiu
Wang
*ab
ab and
Liqiu
Wang
*ab
aDepartment of Mechanical Engineering, The University of Hong Kong, Hong Kong, China. E-mail: lqwang@hku.hk
bHKU-Zhejiang Institute of Research and Innovation (HKU-ZIRI), 311300, Hangzhou, Zhejiang, China
First published on 1st November 2016
Abstract
Precise and effective control of droplet generation is critical for applications of droplet microfluidics ranging from materials synthesis to lab-on-a-chip systems. Methods for droplet generation can be either passive or active, where the former generates droplets without external actuation, and the latter makes use of additional energy input in promoting interfacial instabilities for droplet generation. A unified physical understanding of both passive and active droplet generation is beneficial for effectively developing new techniques meeting various demands arising from applications. Our review of passive approaches focuses on the characteristics and mechanisms of breakup modes of droplet generation occurring in microfluidic cross-flow, co-flow, flow-focusing, and step emulsification configurations. The review of active approaches covers the state-of-the-art techniques employing either external forces from electrical, magnetic and centrifugal fields or methods of modifying intrinsic properties of flows or fluids such as velocity, viscosity, interfacial tension, channel wettability, and fluid density, with a focus on their implementations and actuation mechanisms. Also included in this review is the contrast among different approaches of either passive or active nature.
1. Introduction
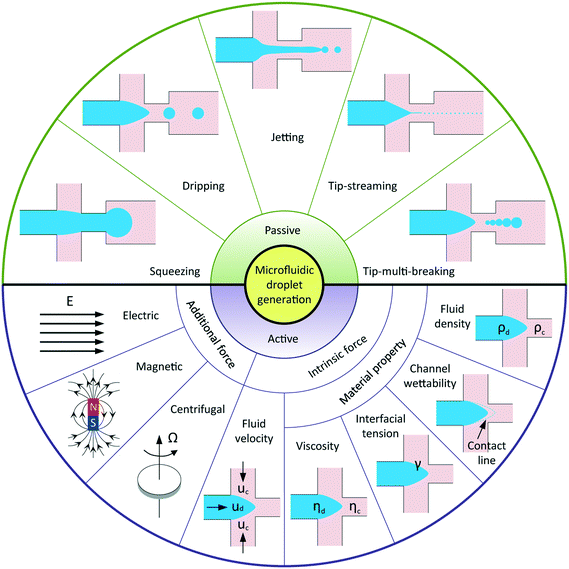
Droplet-based microfluidics has emerged as a versatile tool for widespread applications, attributed to the following advantages: a small volume of reagents consumed, massive production of monodisperse droplets, high surface-area-to-volume ratio that facilitates fast reaction, and independent control of each droplet.1 In general, applications of microfluidic droplets arise from two distinct but complementary aspects.2 One exploits droplets with well-defined components and structures as templates in materials science, for example, synthesis of microcapsules,3–5 microparticles,6–9 and microfibers10 applicable to pharmaceuticals, cosmetics, and foods; another involves lab-on-a-chip applications where droplets are used as microreactors to perform chemical and biochemical reactions. In most of these applications, highly uniform droplets are desired to ensure constant, controlled and predictable outcomes. In addition, a wide range of tunable droplet volumes, typically from femtolitres to nanolitres, is preferable. Some applications require even smaller droplets, such as several hundred nanometers in diameter, for the production of nanodroplets and nanoparticles.11,12 Moreover, instead of utilizing uniform droplets, some applications favor well-controlled sequences of droplets with different volumes, for example, multi-volume droplet digital polymerase-chain-reaction (PCR) for precise and quantitative detection of genetic targets.13 Aside from commonly used passive methods, more sophisticated techniques have been adopted to actively control droplet generation. Reliable generation of droplets with accurate control over their size and size distribution is therefore of vital importance to meet the increasingly high demands in various applications. To this end, it is critical to have a deep and systematic understanding of microfluidic droplet formation, including both passive and active techniques.Droplet generation originates from fluid instabilities. In passive microfluidic devices, introduction of one immiscible fluid (dispersed fluid) into another (continuous fluid) typically leads to the formation of droplets in one of the five modes (Fig. 1): squeezing,14 dripping,15 jetting,15 tip-streaming16 and tip-multi-breaking.17 The squeezing arises from a quite different mechanism from the capillary (Rayleigh–Plateau) instability that is responsible for the other four modes. Channel confinement plays a dominant role in the squeezing regime and inhibits capillary instability so that breakup exhibits quasi-static mechanisms until the last stage of thread pinch-off. The other four modes of breakup come from the capillary instability as interfacial tension forces seek to minimize the interfacial area according to the thermodynamic principle of minimum interfacial energy. In these cases, viscous and inertial forces that act to deform the liquid interface counteract interfacial tension forces that resist the deformation. It is the competition of these forces that determines the specific breakup mode of droplet generation for a given set of parameters.
In comparison with passive methods, active techniques add another level of controllability in modulating droplet formation with the aid of additional energy input by external elements. Apart from the advantage of fast response time, active controls are essential in some extreme situations and applications, such as breaking fluid threads in aqueous two-phase systems (ATPS) with ultra-low interfacial tension,18 producing droplets from highly viscous liquids,19 and on-demand droplet generation, for example, to encapsulate cells with deterministic cell numbers.20 According to the nature of the external energy input, active techniques are categorized into electrical, magnetic, centrifugal, optical, thermal, and mechanical controls. The additional energy input modifies the force balance on the interface and thus manipulates interfacial instabilities. In principle, the interfacial force balance can be modified by two basic strategies in active controls: (i) introducing additional forces like electrical, magnetic, and centrifugal force; (ii) modifying viscous, inertial, and capillary force by varying intrinsic parameters like flow velocity and material properties (Fig. 1).
Previous reviews of droplet formation have concentrated mainly on passive approaches1,2,21–24 with an exception of a very recent one exclusively on active droplet generation.25 Rather than focusing on either passive or active approach in those reviews, we aim to present a unified review of both in a systematic manner from the point of view of physical mechanisms. Our focus is on droplet generation in liquid–liquid biphasic flows, though some examples of gas–liquid14 and liquid–gas26 flows are cited for the sake of elucidating breakup mechanisms. We also limit our discussion to cases where continuous phase fluids preferentially wet the channel walls, so that dispersed droplets are completely surrounded by continuous fluids. In what follows, we outline the governing equations and fundamental dimensionless parameters for droplet generation in section 2. We summarize the commonly used devices in producing microfluidic droplets in section 3. In section 4, we discuss breakup modes of passive droplet generation, especially, the generation process, mechanism, condition of occurrence, characteristics, and nature of fluid instabilities for each mode. Finally, we highlight, in section 5, the state-of-the-art techniques for active droplet generation, organized according to their mechanisms of manipulation: techniques utilizing additional forces followed by those via modulating intrinsic parameters.
2. Dimensionless numbers
Fluid motions with various characteristics could occur in microflows, which are normally determined by competing physical effects, such as force balance. Dimensionless numbers characterize the relative predominance of different effects and are capable of contrasting flows in parameter space, thereby unifying flowing features between different systems. To explore the key dimensionless numbers characterizing the droplet generation (Table 1), we start from the governing equations that determine microfluidic two-phase flows.Liquid–liquid two-phase microflows are well described with the continuum hypothesis.27 The incompressible continuity equation reads, for both dispersed and continuous phase fluids:
| ∇·us = 0, | (1) |
The momentum equation is the well-known Navier–Stokes equation of incompressible Newtonian fluids:
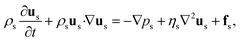 | (2) |
Droplet formation in microfluidic devices involves the deformation and breaking of the liquid–liquid interface. As such, several interfacial boundary conditions should be specified. Among them, the first comes from the continuity of normal velocity at the immiscible interface:29
| ud·n = uc·n, | (3) |
| σd·t = σc·t, | (4) |
| Td·n − Tc·n = − γκ, | (5) |
The above-mentioned governing equations indicate four types of forces that govern the droplet generation: inertial force, viscous force, gravity (for the case without other external force fields) and capillary force. To compare the relative importance of various forces, we unify them in the form of stress (forces per unit area) based on which simple scaling arguments are derived. Considering a volume of fluid flowing at velocity us in a microfluidic device of characteristic length L, inertial stress scales as fi ∼ ρsus2, viscous stress fv ∼ ηsus/L, gravity fg ∼ ρsgL, and capillary pressure fγ ∼ γ/L. Based on this scaling, we can develop several dimensionless numbers useful in studying droplet generation.
In principle, the ratio of any two stresses of the four defines a dimensionless number. The Reynolds number Re represents the relative importance of inertia to viscous force, and thus Re = fi/fv:
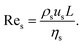 | (6) |
For interfacial flows that are relevant to droplet generation, Reynolds number is rarely used. During the process of the droplet generation, three major steps are normally involved:23 initially, the dispersed and continuous phase fluids meeting at the junction to form an immiscible interface, followed by the large deformation of the interface to an unstable state, and finally the unstable interface fragmenting spontaneously and decaying into disconnected droplets. Interfacial tension thereby plays a key role in droplet generation. Consequently, we focus on examining the following three dimensionless numbers that characterize the relative importance of interfacial tension to the other three forces. Among them, the most commonly used one is the capillary number Ca, which is the ratio of viscous stress to capillary pressure fv/fγ:
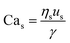 | (7) |
The inertial stress fi does not depend on the device length-scale L directly. Shrinking of device length-scale L would, however, enhance both viscous stress fv and capillary pressure fγ and weaken the gravitational effect via reducing fg. Therefore, viscous and capillary forces would become dominant over the other two if L is sufficiently small. This attributes Ca to be the most frequently used dimensionless number in characterizing microfluidic droplet generation. In microflows, Ca is usually in the range of 10−3 to 10.
Although fluid inertia is negligible for most microfluidic flows, it can be important for the cases such as jet15 and nonlinear bubble30 formation at high flow velocity, or in the vicinity of droplet and bubble pinch-off.31,32 The competition between inertia and capillary pressure, fi/fγ, yields the Weber number We in the form of,
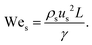 | (8) |
The relative importance of gravity to capillary pressure, fg/fγ, yields the Bond number Bo,
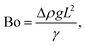 | (9) |
Another two dimensionless numbers are also relevant: the viscosity ratio λ and the flow rate ratio φ of dispersed to continuous phase fluids defined by,
| λ = ηd/ηc, | (10) |
| φ = Qd/Qc. | (11) |
3. Device geometry
The microfluidic channel provides the boundary of microflow and thus its geometry would impact the droplet generation as well. Typical microfluidic geometries used in generating droplets are shown in Fig. 2. Among them, some use viscous shear forces to break off droplets with three types of most frequently used structures being cross-flow, co-flow and flow-focusing geometries. The others employ variations of channel confinement to facilitate or drive droplet generation, such as step emulsification, microchannel emulsification, and membrane emulsification. Herein, we discuss these droplet generators in terms of their features, developments, and variations and compare the fabrication technique, typical droplet generation frequency, droplet size and monodispersity for each droplet generator in Table 2.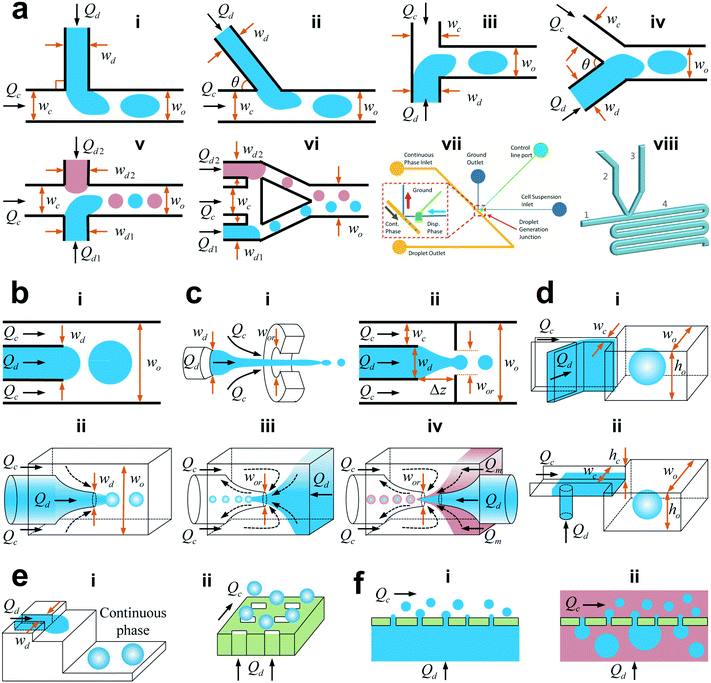 | ||
| Fig. 2 Schematic of various microfluidic device geometries (not to scale). (a) Cross-flow. (i) “T-junction” where the continuous and dispersed phase fluids meet perpendicularly (θ = 90°). (ii) “T-junction” in which the two fluids intersect at an angle θ (0° < θ < 90°). (iii) “Head-on” geometry (θ = 180°). (iv) Y-shaped junction with intersection angle of θ (0° < θ < 180°). (v) Double T-junction with droplet pairs generated at the same location. (vi) Double T-junction that produces droplet pairs at separated parallel T-junctions. (vii) “K-junction”. (viii) “V-junction”. (b) Co-flow. (i) Quasi-2D planner co-flow. (ii) 3D co-flow. (c) Flow-focusing. (i) Axisymmetric flow-focusing geometry. (ii) Planner flow-focusing geometry. (iii) Microcapillary flow-focusing device. (iv) Microcapillary device combining co-flow and flow-focusing geometries. (d) Step emulsification. (i) Horizontal step. (ii) Vertical step. The inlet channel has a high aspect ratio, and the reservoir is wider and deeper, with an abrupt topographic step in between the inlet channel and the reservoir. (e) Microchannel emulsification. (i) Grooved-type microchannel. (ii) Straight-through microchannel. (f) Membrane emulsification. (i) Direct membrane emulsification. (ii) Premix membrane emulsification. Q, w, h, and Δz denote the volumetric flow rate, channel width, channel height, and horizontal distance from the end of the dispersed microchannel to the orifice entrance, respectively. For planar devices, the channel height h is uniform. In the case of the geometry with a circular cross section, w represents the channel diameter. The subscripts “c”, “d”, “o”, and “or” stand for the continuous phase, dispersed phase, outlet channel, and orifice, respectively. (a,vii) is reprinted with permission from ref. 48. Copyright 2012, American Institute of Physics. (a,viii) is reprinted with permission from ref. 50. Copyright 2015, Royal Society of Chemistry. | ||
| Droplet generator | Fabrication technique | Droplet production rate | Minimum droplet size | Monodispersity |
|---|---|---|---|---|
| Cross-flow | For cross-flow, co-flow, and flow-focusing geometries, 2D devices can be fabricated with silicon and glass by etching and with polymers, such as poly(dimethylsiloxane) (PDMS), poly(methyl methacrylate) (PMMA), and poly(urethane), by soft lithography, hot embossing, injection molding, and laser ablation;87 3D devices can be fabricated by assembly of glass capillaries, and with polymers by soft lithography and 3D printing. However, 3D devices are more complicated in fabrication: assembly of glass capillaries requires careful alignment; soft lithography of PDMS usually demands multi-layer fabrication;323 3D printing is limited in the resolution.324 | Up to 7.4 kHz in air-bubble-triggered droplet formation38 | Limited by channel dimension, usually larger than 10 μm33 | CV <2% (ref. 34) |
| Co-flow | Several hundred Hz to tens of kHz (ref. 54) | Several hundred nanometers169 | CV <3% (ref. 54) | |
| Flow-focusing | Up to tens of kHz (ref. 62) | Several hundred nanometers166 | CV <5% (ref. 61) | |
| Step emulsification | Step emulsification devices are made with PMMA by micromachining,67 and with SU-8 (ref. 75) and PDMS70 by photolithography. | Up to 15 kHz (ref. 70) | Several hundred nanometers70 | CV <1% (ref. 70) |
| Microchannel emulsification | Microchannel array devices are fabricated with silicon by photolithography and wet etching.86 | Up to 44 Hz per microchannel88 | 1 μm (ref. 86) | CV <5% (ref. 86) |
| Membrane emulsification | Shirasu porous glass (SPG) membrane is fabricated by phase separation; microsieve membranes are fabricated with nickel by LIGA process, aluminium and stainless steel by laser drilling, and silicon nitride by reactive ion etching.86 | Several tons of dispersed phase per hour (ref. 86) | ∼0.1 μm (ref. 86) | CV ∼20% (ref. 114) |
3.1 Cross-flow
The cross-flow geometry refers to the one where dispersed and continuous phase fluids meet at an angle θ (0° < θ ≤ 180°; Fig. 2a).24 In microfluidics, the cross-flow structure is frequently implemented as a T-junction, where the dispersed and continuous fluids are fed orthogonally (Fig. 2a,i). The T-junction device was first reported by Thorsen et al.33 to produce monodisperse water droplets in oil surroundings for generating ordered dynamic patterns in pressure controlled laminar flows. This geometry is widely used because of its simplicity and ability to produce monodisperse droplets. The coefficient of variation (CV, defined as the ratio of standard deviation to the mean of the droplet radius) of droplets is usually less than 2% in T-junctions.34 Contrary to the typical operation conditions shown in Fig. 2a,i where the continuous phase is introduced from the main channel and the dispersed phase is fed from the side channel, the opposite was also proposed in T-junctions by controlling the wetting properties of channel walls.22,35 Besides functioning as a droplet generator, T-junctions have recently been applied in designing microvalves36 and microactuators37 as well.Variations in T-junction have been studied. A slightly different T-junction with arbitrary angle θ (Fig. 2a,ii)38 was found to influence the process of droplet breakup39 and resultant droplets.40 Another variation from the typical T-junction is the “head-on device”,41 where the dispersed and continuous fluids are fed into the two straight channels from opposite directions, as shown in Fig. 2a,iii. Droplet formation in head-on devices, rich as the flow behaviour was found to be,42 has similar features to that in typical T-junctions. Furthermore, if the two fluids are not injected oppositely but at a crossing angle θ, the head-on device reduces into a Y-shaped junction43 (Fig. 2a,iv).
A single T-junction with the above-mentioned simple structure cannot meet special requirements in some pragmatic applications. In performing chemical reactions via merging two droplet microreactors that contain different reagents,44 or indexing the targeted droplet by the addition of a droplet marker,45 for example, it is desired to generate droplet pairs in microchannels. A double T-junction (Fig. 2a,v) was designed to create stable alternating droplet pairs by Zheng et al.,45 where two dispersed streams pinch off at the same junction alternately. Droplets can also be generated separately at different locations in the main channel and then flushed into a wider channel to initiate fusion.46 In addition, a parallel dual T-junction that produces droplet pairs in two parallelized T-junctions (Fig. 2a,vi) was proposed to tune the size ratio of droplet pairs.47 In biological and chemical assays, on-demand droplet generation with prescribed size, composition and frequency is usually required. To achieve this goal, modified T-junctions such as K-junction48,49 (Fig. 2a,vii) and V-junction50,51 (Fig. 2a,viii) were introduced. For mass production of droplets, the proposed strategies include the integration of parallel T-junction droplet generators52 and splitting primary droplets subsequently into daughter droplets.46,53
3.2 Co-flow
In co-flow geometry, the dispersed and continuous phase fluids meet in parallel streams24 (Fig. 2b). In liquid–liquid systems, the co-flow microfluidic device was first introduced by Umbanhowar et al.54 Co-flow configurations can either be quasi-two-dimensional (2D) planar24 (Fig. 2b,i) or three-dimensional (3D) coaxial55 (Fig. 2b,ii). The former can be fabricated by standard soft lithographic methods,56 while the latter is often made by inserting a tapered cylindrical glass capillary54,55,57 into a rectangular microchannel or a square glass capillary. The polydispersity of the resulting droplets in co-flow geometries depends on the flow conditions: droplets generated in dripping mode are highly monodisperse with CV <3%,54 while those generated in jetting mode are polydisperse.15 Usually, droplet sizes are larger than the dimension of dispersed microchannel wd (Fig. 2b) when droplets are produced in dripping or widening jetting mode.15 Exceptions include the continuous phase flows at very high speeds so that a narrowing jet15 and even tip-streaming regime58,59 occur.3.3 Flow-focusing
To produce smaller droplets, it is recommended to use flow-focusing devices, where the two immiscible fluids are hydrodynamically focused and thereafter in elongating flows when passing through a contraction (Fig. 2c). Similar to co-flow geometries, flow-focusing microfluidic devices can also be categorized into two types: 3D axisymmetric26,60–62 (Fig. 2c,i) and quasi-2D planar24,63 (Fig. 2c,ii). Gañán-Calvo was the first to produce monodisperse micron-sized droplets in a surrounding gas stream26 and mono-sized microbubbles in a focused liquid stream60 using the axisymmetric flow-focusing configuration as shown in Fig. 2c,i. Later in 2003, Anna et al.,63 for the first time, translated the planar flow-focusing geometry (Fig. 2c,ii) into a liquid–liquid microfluidic system. Compared to planar flow-focusing devices, 3D axisymmetric flow-focusing devices avoid issues like wetting of channel walls by the dispersed phase,61 therefore producing monodisperse droplets (CV <5%) with higher throughputs.62 A branch of 3D flow-focusing microfluidic devices is the microcapillary device55 (Fig. 2c,iii), where the continuous and dispersed fluids are supplied into the device in opposite directions and meet at the entrance of the narrow orifice, then focusing downstream through the orifice and generating uniform droplets. In combination with co-flow geometry, the microcapillary device (Fig. 2c,iv) is able to generate monodisperse multiple emulsions in a single step.55,643.4 Step emulsification
In contrast to the aforementioned microfluidic devices that use shear forces to break off fluids in generating droplets, other geometries generate uniform droplets by variations of channel confinement through which a sharp change in capillary pressure occurs and droplet pinch-off is driven by interfacial tension. Among them, a generic structure is the step emulsification geometry where the stabilized co-flow in the high aspect ratio inlet channel gives its way into droplets upon reaching an abrupt geometric step towards the released channel confinement in the reservoir23 (Fig. 2d). Two groups of step emulsification are identified based on the geometric feature of the step:65 horizontal step (Fig. 2d,i) and vertical step (Fig. 2d,ii). To the best of our knowledge, Chan et al.66 were the first to use a vertical step change in a microfluidic device to generate nanoliter droplets for the synthesis of CdSe nanocrystals. Then the geometry of step emulsification was carefully characterized by Priest et al.,67 who produced highly monodisperse droplets (CV <1.5%) and gel emulsions with high volume fraction of the dispersed phase. More recently, femtolitre droplets produced by step emulsification were used to perform PCR68 or solidified to design colloidal building blocks.69 In vertical step emulsification (Fig. 2d,ii), the resultant smallest droplet has its diameter about two to three times the height of the inlet channel hc, such that submicron droplets could be generated via scaling hc down to several hundred nanometers.70,71Step emulsification has several advantages. Firstly, droplet generation in step emulsification is less sensitive to flow rate or pressure fluctuations, resulting in probably the highest monodispersity of droplets (CV <1.5% reported by Priest et al.,67 and CV ∼1% reported by Malloggi et al.70). Secondly, droplets with unaffected size can be generated in a wide range of flow rates by keeping flow rate ratio φ constant, while the production rate can be tuned over two orders of magnitude.67 Thirdly, taking advantage of producing foam-like emulsions in situ, step emulsification has been employed to study the assembly of microdroplets into 3D clusters.72,73 Finally, step emulsification is easier to be parallelized into multiple channels for high-throughput droplet production, because only the flow of the dispersed phase needs to be precisely controlled.74 For example, pairs of droplets with different contents can be produced by duplicating the dispersed inlet channels,75 and numbering the dispersed channels up to 16 (ref. 76) and 252 (ref. 77) was also achieved.
Variations in step emulsification have been proposed. One is using a gradual transition of channel height78 instead of a sudden change from the inlet channel to the reservoir. The generated monodisperse droplet (CV ∼0.1%) is forced away by the gradient of surface energy. The size of droplets mainly depends on the channel geometry and is weakly influenced by flow rates and fluid properties. On-demand chemical reactions can be achieved by guiding droplets with local variations in channel height. In addition, high-throughput generation of droplets was demonstrated by parallelizing 256 parallel nozzles. Another variation is the emulsification method of edge-based droplet generation (EDGE) proposed by van Dijke et al.74,79,80 In this device, the dispersed phase is introduced into a shallow but rather wide quasi-2D plateau and then breaks into droplets at the edge of the plateau adjacent to which a deeper channel feeds the continuous cross flow to flush away the produced droplets. In a regular and organized manner, many sites of droplet generation can occur at the edge of the same plateau.74 Both experiments and simulations showed that the distance between droplet generation sites depends on the height of the plateau and applied pressure.80 A parallelization of up to 196 EDGE units on a single chip was presented to generate quasi-monodisperse droplets (CV <10%) at large production frequency (around 300 kHz).79 In addition, Dutka et al.81 recently incorporated a constriction and bypasses into the dispersed inlet channel of step emulsification geometry. In this geometry, monodisperse droplets were produced by injecting only the dispersed phase fluid into the device. The size of droplets depended weakly on the injection rate, therefore increasing the stability of droplet generation against flow rate fluctuations. Furthermore, pump-free step emulsification configurations that incorporate centrifugal82–84 and magnetic85 controls have been exploited, which will be detailed in section 5 (Active droplet generation).
3.5 Microchannel emulsification
In microchannel emulsification, the dispersed phase is forced through the inlet channel and then fragments into droplets at the end of the channel. Microchannel emulsification can be divided into two groups:86,87 grooved-type microchannel (Fig. 2e, i) and straight-through microchannel (Fig. 2e,ii). To achieve high throughput, microchannel arrays are usually implemented.88 The grooved-type microchannel arrays were first fabricated by Kikuchi et al.89 in 1989, in which the continuous fluid can be either static (dead-end)90 or cross-flow.91,92 For the sake of higher rate of droplet production, cross-flow modules are better than dead-end ones because the former enables more microchannels incorporated on one chip and the continuous flow sweeps away the generated droplets, leaving more space for latter droplets. Compared with grooved-type microchannel arrays, straight-through modules possess higher throughput because of the better utilization of chip surface.86 In straight-through microchannel arrays, the rectangular microchannel (Fig. 2e,ii) is better than the circular shape and can be either symmetric93 or asymmetric.94–96 However, the monodispersity of droplets is seriously constrained by channel dimensions. To produce uniform droplets (CV <2%), an aspect ratio of channel height to width must be larger than three.973.6 Membrane emulsification
To produce fine emulsions at industrial scales, membrane emulsification was proposed in the early 1990s.98 With this technique, the dispersed phase is forced through a porous membrane after which droplets detach into the continuous phase (Fig. 2f). Apart from directly injecting a pure dispersed phase into the membrane, the so-called direct membrane emulsification99 (Fig. 2f,i), pre-emulsions containing coarse droplets are homogenized by pressing the premix through a membrane100 or a packed bed of uniform particles,101 named premix membrane emulsification (Fig. 2f,ii). There are many operation modes of applying shear stress on the membrane surface to facilitate uniform droplet formation with high throughputs, such as cross-flow,98 stirring,102,103 rotating104,105 and vibrating.106,107 The most commonly used membranes are Shirasu porous glass membrane98 and micro-engineered membranes.108 Others include ceramic,109 metallic110,111 and polymeric112,113 membranes. Membrane emulsification enables quasi-monodisperse droplet formation (CV ∼20%).114 The droplet size is affected by characteristics of the membrane (pore morphology, pore size distribution, porosity, spatial arrangement of the pores, surface wettability and charge, to name a few), material properties (viscosity of the two fluids, surfactant type and concentration), and dynamic parameters (transmembrane flux and pressure, shear stress at the membrane surface).115 Both analytical116,117 and computational118–120 models have been developed to predict droplet size in membrane emulsification.In addition to the above geometries, some other structures have been introduced. For example, Amstad et al.121 proposed a microfluidic post-array device to process the crude emulsion into a fine one, which is potentially beneficial for industrial applications due to its high throughput. Other devices enable on-site formation of droplets with predetermined volume by using micro-patterned channels,122,123 where a long microchannel connects large numbers of pre-defined microchambers, either in series122 or in parallel,123 as sites for droplet generation.
4. Passive droplet generation
Droplet generation is of prime importance for various microfluidic applications. In the passive method, microfluidic two-phase flow is controlled by either syringe pumps that supply constant flow rates Qd and Qc or pressure regulators124,125 and gravity-based pressure units81 that set stable source pressures Pd and Pc without additional energy input. During droplet formation, energy introduced from the syringe pumps or pressure controllers is partially converted into interfacial energy and thus facilitates the destabilization of the liquid–liquid interface, whereby discrete droplet shedding from the dispersed phase occurs.23 Despite the complexity of channel geometry, droplet generation can be categorized into several groups due to the similar physical processes and underlying mechanisms involved. In the following subsection 4.1, we identify and characterize five fundamental modes and one transitional mode of droplet generation in most commonly used microfluidic cross-flow, co-flow, and flow-focusing configurations as well as droplet generation in step emulsification structures. The influence of surfactants on droplet generation is also included. Then, in subsection 4.2, we discuss the fluid instabilities of two-phase microflows and relate each of the breakup modes to these instabilities.4.1 Breakup modes
Five fundamental modes of droplet generation have been observed in shear-based droplet generators: squeezing,126 dripping,54 jetting,57 tip-streaming127 and tip-multi-breaking.17 The first three have been observed in cross-flow, co-flow, and flow-focusing geometries; the last two have not been reported in cross-flow yet (Fig. 3a–e). In principle, droplets generated with squeezing mode is larger than the channel dimension and highly monodisperse (Fig. 3a), with dripping is somehow smaller than channel dimension and monodisperse (Fig. 3b), with jetting is polydisperse (Fig. 3c), with tip-streaming can be as small as submicrometer-scale and monodisperse (Fig. 3d), and with tip-multi-breaking are in droplet sequences with polydisperse but geometric-progression size distribution (Fig. 3e). Transitions between different modes can be achieved by changing dispersed and/or continuous phase capillary numbers (Fig. 3f).10 For example, the squeezing–dripping transitional regime occurs at an intermediate continuous-phase capillary number between squeezing and dripping. Similarly, different modes of droplet generation are identified in step emulsification: shear-induced generation, step-regime and jet-regime. In this sub-section, our focus is mainly on the process of droplet generation, mechanism, the condition of occurrence and characteristics of each mode (Table 3) as well as effects of surfactants.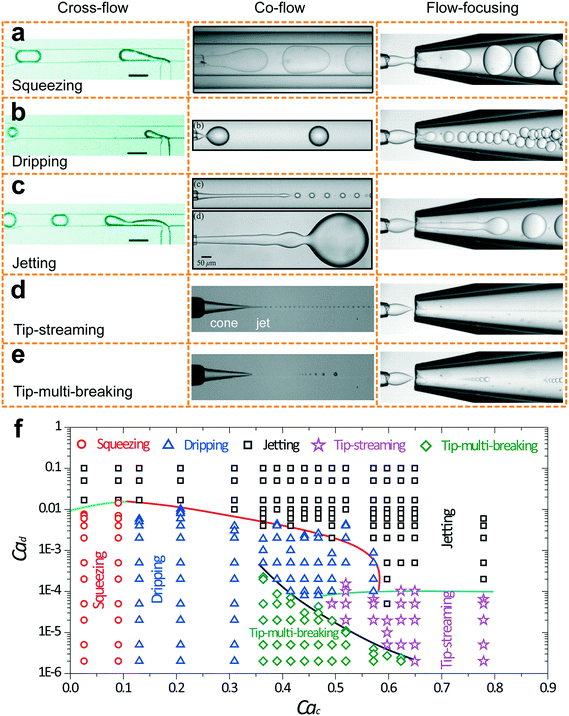 | ||
| Fig. 3 Images of droplet generation with different modes in cross-flow, co-flow and microcapillary flow-focusing geometries. (a) Squeezing mode. (b) Dripping mode. (c) Jetting mode. The upper image in co-flow is a narrowing jet while the lower one is a widening jet. (d) Tip-streaming mode. (e) Tip-multi-breaking mode. Neither tip-streaming nor tip-multi-breaking modes has been reported in cross-flow geometry yet. (f) Phase diagram in (Cac, Cad) plane for various modes observed in microcapillary flow-focusing devices.17 Cross-flows of (a)–(c) are reprinted with permission from ref. 131. Copyright 2010, American Chemical Society. Co-flow of (a) is reprinted with permission from ref. 133. Copyright 2007, American Physical Society. Co-flows of (b) and (c) are reprinted with permission from ref. 15. Copyright 2007, American Physical Society. Co-flows of (d) and (e) are reprinted with permission from ref. 58. Copyright 2013, Cambridge University Press. | ||
| Breakup mode | Condition for occurrence | Characteristics | Specification | Ref. |
|---|---|---|---|---|
| Squeezing | Cac <O(10−2) | L p/wc = ε + δφ | Eqn (12). Plug length is only determined by flow rate ratio and channel dimension. ε and δ are of order unity. | 129 |
| V/(hwc2) = Vfill/(hwc2) + ζφ | Eqn (13). Expression for predicting droplet volume in T-junctions by taking leakage into account. | 146 | ||
| V/(hwc2) = αf + ζfφ | Eqn (14). Prediction of droplet volume in flow-focusing geometries. | 147 | ||
| Squeezing–dripping transition | Cac ≈ O(10−2) |
|
Eqn (20) and (21). Prediction of droplet volume in transitional regime. | 152 |
| V/(hwc2) = αlag + αfill + ζneckφ | Eqn (23). Prediction of droplet volume based on lagging, filling, and necking stages of droplet formation. | 159 | ||
| fre*drop = φ/(αlag + αfill + ζneckφ) | Eqn (24). Prediction of droplet generation frequency based on lagging, filling, and necking stages of droplet formation. | 159 | ||
| Dripping | O(10−2) < Cac < O(1), and Wed < O(1) |
|
Eqn (15). In co-flow geometry, droplet size is the solution of the third-order polynomial. Only shear forces and interfacial tension are considered. | 54 |

|
Solution of eqn (15) when φ ≪ 1. a and b are fitting parameters. Eqn (16) is recovered when a = b = 1. | 54 | ||
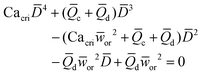
|
Eqn (17). In flow-focusing geometry, droplet size is the solution of the fourth-order polynomial. | 153 | ||
|
Eqn (18). Solution of eqn (17) when φ ≪ 1. | 153 | ||
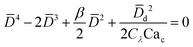
|
Eqn (19). In cross-flow geometry, droplet size is the solution of the fourth-order polynomial. | 155 | ||
| Jetting | Cac + Wed≥ O(1) |
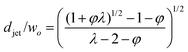
|
Eqn (25), jet diameter in narrowing jetting regime. | 161 |
| d jet/wo = (φ/2)1/2 | Eqn (26), jet diameter in narrowing jetting regime when φ ≪ 1. | 161 | ||
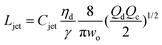
|
Eqn (27), jet length in narrowing jetting regime. | 162 | ||
| D/djet = [3π/(2k*)]1/3 | Ratio of droplet diameter and jet diameter in narrowing jetting regime. | 59 | ||
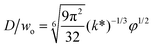
|
Eqn (28), expression for dimensionless droplet diameter in narrowing jetting regime. | 59 | ||
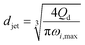
|
Eqn (29), jet diameter in widening jetting regime. | 59 | ||
| D ∼ (Qd/uc)1/2 | Eqn (30), scaling of droplet diameter in widening jetting regime. | 15 | ||
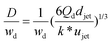
|
Eqn (31), unified expression for dimensionless droplet diameter in both narrowing and widening jetting regimes. | 59 | ||
| Tip-streaming | Rec ≪ 1, Red ≪ 1, Cac > Cacri, and φ ≪ 1 |
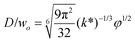
|
Eqn (28), expression for dimensionless droplet size. Tip-streaming can be regarded as narrowing jetting with φ ≪ 1. | 59 |
| Tip-multi-breaking | φ < φmin ≪ 1, and Cac < Cacri | R i = R1χi−1, i = 1, 2,…, n | Eqn (32), geometrical progression of droplet size distribution in a decreasing manner. | 17 |
| Step-regime | Cadwc/hc ≲ 0.38 |
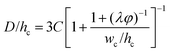
|
Eqn (33). Prediction of droplet size in step emulsification geometry. | 197 |
The pressure rise in the continuous fluid is responsible for the dispersed fluid breakup in squeezing mode. During the breakup, the pressure profile in the dispersed phase fluctuates rather than remains constant. This mechanism was first unveiled by Sivasamy et al.135 in a numerical study and later confirmed experimentally by using Laplace sensors to measure pressures in T-junction136 and flow-focusing137 microfluidic devices. As the emerging droplet blocks the junction region and then necks, the continuous-phase pressure fluctuates in the way of first increasing and then decreasing, in anti-phase with the dispersed-fluid pressure variation.136,137 The amplitude of pressure fluctuations diminishes with the increasing of capillary number Cac.
In a plug-like shape, the droplet generated with squeezing mode has its size characterized by the ratio of the plug length Lp to the continuous phase channel width wc (such as in T-junctions, Fig. 2a,i), Lp/wc. To preliminarily determine the dimensionless length Lp/wc, the process of droplet generation is usually divided into two stages in T-junctions.129,138,139 First, the dispersed-liquid tip fills and blocks the junction region with its length estimated as L1 = εwc; then the dispersed droplet is squeezed by the continuous fluid and has the neck thinning rate proportional to the continuous fluid velocity uc = Qc/(hwc), with h being the channel height. During the second “squeezing” stage, the dispersed plug elongates due to the inflation of dispersed fluid at the rate: ud = Qd/(hwd) (wd is the dispersed channel width, Fig. 2a,i). Accordingly, the length contribution from the second stage is about L2 = ud(d/uc) = dwcQd/(wdQc) = dφwc/wd, where d is the initial neck diameter. Finally, the droplet length Lp = L1 + L2= εwc + dφwc/wd. Therefore, Lp/wc is approximated as,
| Lp/wc = ε + δφ, | (12) |
The continuous phase is not utterly blocked during droplet formation. This has been confirmed by the microscopic particle image velocimetry (μ-PIV) measurements of 3D flow fields around the emerging interface,144,145 especially in rectangular microchannels, where the leakage of continuous fluid from the gutters between liquid interface and channel corners is significant. By considering the leakage, van Steijn et al.146 proposed a closed-form expression to predict droplet and bubble volume V without fitting parameters in T-junctions,
| V/(hwc2) = Vfill/(hwc2) + ζTφ, | (13) |
Similar to eqn (13), Chen et al.147 theoretically predicted the volume of droplet in flow-focusing geometries by accurately reconstructing the 3D shape of the droplet and determining the pressure drop along the droplet via force balance analysis:
| V/(hwc2) = αf + ζfφ, | (14) |
The droplet diameter D can be scaled, by simply balancing the viscous stress of magnitude ηcuc/L and capillary pressure γ/D,15,33 to be D/L ∼Cac−1, where L is the hydraulic length of the nozzle with L = 2hwd/(h + wd) in 2D geometries and L = wd in 3D co-flow and flow-focusing structures. In the squeezing–dripping transitional regime, both shear stress and squeezing pressure play a role in determining the droplet size;130,143,148–150 the scaling power of Cac deviates from −1 to other values such as −0.25 numerically observed by van der Graaf et al.,139 ranging from −0.3 to −0.2 by Liu and Zhang,143,151 −1/3 by Christopher et al.,152 −0.34 by Lan et al.,150 and −0.4 by De Menech et al.130 Here, we focus our attention only on the purely shear-dominant dripping regime.
To predict the absolute droplet size, both the viscous shear and the interfacial tension forces should be analytically determined. In a 3D co-flow geometry, viscous force can be approximated by a modified Stokes formula after considering the shielding effect of the dispersed nozzle: Fv = 3πηc(D − wd)(uc − ud), where ud = Qd/(πD2). Interfacial tension force can be expressed by Fγ = πwdγ. By equating Fv and Fγ, Umbanhowar et al.54 found the dimensionless droplet diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = D/wd as a solution to the third-order polynomial,
= D/wd as a solution to the third-order polynomial,
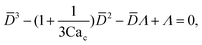 | (15) |
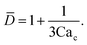 | (16) |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = a + b/(3Cac) takes different fitting values of a and b.
= a + b/(3Cac) takes different fitting values of a and b.
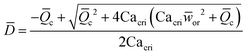
In microcapillary flow-focusing devices (Fig. 3b), a similar deduction was carried out to predict the droplet size. Erb et al.153 defined the same forms of viscous and interfacial tension forces as used by Umbanhowar et al.54 and approximated ud = 4Qd/(πD2) and uc = 4Qc/[π(wor2 − D)2], where wor is the diameter of the focusing orifice. By assuming the condition for droplet rupture to be Fv/Fγ = Cacri, Erb et al.153 pointed out that droplet diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) can be predicted by solving the following polynomial:
can be predicted by solving the following polynomial:
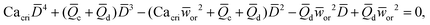 | (17) |
![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) c = Qc/Q0,
c = Qc/Q0, ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) d = Qd/Q0 and
d = Qd/Q0 and ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) or = wor/wd with Q0 = πwd2γ/(12ηc). Similarly, when Qd ≪ Qc, all terms in eqn (17) involving
or = wor/wd with Q0 = πwd2γ/(12ηc). Similarly, when Qd ≪ Qc, all terms in eqn (17) involving ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) d can be neglected. An analytical solution can, therefore, be found by solving the quadratic equation Cacri
d can be neglected. An analytical solution can, therefore, be found by solving the quadratic equation Cacri![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) 2 +
2 + ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) c
c![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) − Cacri
− Cacri![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) or2 −
or2 − ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) c = 0 to determine the physically meaningful root:
c = 0 to determine the physically meaningful root: | (18) |
![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) c = Qc/Q0 = 12ηcQc/(πwd2γ) can be understood as the continuous-phase capillary number Cac at the dispersed nozzle. A single universal value of the fitting parameter Cacri = 0.1 is applicable to a wide range of flow rates, channel dimensions and viscosity ratios.153
c = Qc/Q0 = 12ηcQc/(πwd2γ) can be understood as the continuous-phase capillary number Cac at the dispersed nozzle. A single universal value of the fitting parameter Cacri = 0.1 is applicable to a wide range of flow rates, channel dimensions and viscosity ratios.153
Eqn (18) can be generalized to predict droplet diameter in flow-focusing geometries with an arbitrary shape of the collection microchannel of the cross-sectional area Ar. In this situation, ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) c and
c and ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) or are redefined to be
or are redefined to be ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) c = 3ηcQc/(wd2γ) and
c = 3ηcQc/(wd2γ) and 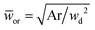 . Liu et al.154 applied the generalized eqn (18) to successfully predict the absolute droplet size in a flow-focusing geometry with a square collection microchannel. Considering the shielding effect in the expression of Fv, the droplet diameter D is assumed to be larger than the nozzle diameter wd in eqn (15)–(18), e.g.
. Liu et al.154 applied the generalized eqn (18) to successfully predict the absolute droplet size in a flow-focusing geometry with a square collection microchannel. Considering the shielding effect in the expression of Fv, the droplet diameter D is assumed to be larger than the nozzle diameter wd in eqn (15)–(18), e.g. ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) > 1. This assumption is however not always valid in flow-focusing configurations when Qc is sufficiently large (see Fig. 3b, flow-focusing). Moreover, the influence of viscosity ratio on droplet diameter is not considered in eqn (15)–(18). Nevertheless, eqn (15)–(18) provide a fast and efficient preliminary determination of the drop size once a two-phase microflow is known.
> 1. This assumption is however not always valid in flow-focusing configurations when Qc is sufficiently large (see Fig. 3b, flow-focusing). Moreover, the influence of viscosity ratio on droplet diameter is not considered in eqn (15)–(18). Nevertheless, eqn (15)–(18) provide a fast and efficient preliminary determination of the drop size once a two-phase microflow is known.
In cross-flow geometries, viscous and interfacial tension force balance is still applicable to the prediction of droplet size. Husny and Cooper-White155 estimated Fγ = πwd2γ/D, and, by taking both dispersed and continuous phase viscosities into account, Fv = CλπηcD{2uc[1 − (Dc − D)2/Dc2] − ud} in a cross-flow geometry, where Cλ = (3 + 2λ)/(1 + λ), uc = Qc/(wch) and ud = βuc, with λ being the viscosity ratio, Dc = 2wch/(wc + h) the hydraulic diameter of the continuous-phase microchannel, and β the ratio of the droplet velocity ud to the average velocity of continuous flow uc (0 < β < 2). By equating Fγ and Fv, a fourth-order polynomial that determines the dimensionless droplet diameter ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = D/Dc reads,21
= D/Dc reads,21
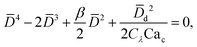 | (19) |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) d = wd/Dc, and Cac = ηcQc/(wchγ). Husny and Cooper-White155 used a fitting value of β = 0.6 to collapse all the experimental data onto the predicted curve, which, within the accuracy of measurements, represented good agreement for all investigated capillary number Cac and viscosity ratio λ. The proposed model (eqn (19)) suggests a decreasing of droplet diameter D as viscosity ratio λ increases at a fixed capillary number Cac, which was however not observed.155 Instead, the measured droplet diameter appears to depend weakly on the viscosity ratio. In all cases, droplet generation frequency fredrop can then be easily obtained based on mass conservation, fredrop = 6Qd/(πD3), provided that droplet diameter D is predicted.
d = wd/Dc, and Cac = ηcQc/(wchγ). Husny and Cooper-White155 used a fitting value of β = 0.6 to collapse all the experimental data onto the predicted curve, which, within the accuracy of measurements, represented good agreement for all investigated capillary number Cac and viscosity ratio λ. The proposed model (eqn (19)) suggests a decreasing of droplet diameter D as viscosity ratio λ increases at a fixed capillary number Cac, which was however not observed.155 Instead, the measured droplet diameter appears to depend weakly on the viscosity ratio. In all cases, droplet generation frequency fredrop can then be easily obtained based on mass conservation, fredrop = 6Qd/(πD3), provided that droplet diameter D is predicted.
Arising from the coexistence of shear stress and squeezing pressure, the droplet size depends on both capillary number Cac and flow rate ratio φ in transitional regime,138,151,156 different from squeezing where droplet size is purely determined by flow rate ratio, and dripping where droplet size solely depends on the capillary number. Semi-empirical models were developed to predict droplet size by fitting experimental and numerical data respectively with the scaling law of Lp/wc = ε + δφnCacm (ref. 138) or Lp/wc = (ε + δφ)Cacm (ref. 151) to determine the empirical parameters ε, δ, n, and m. Applying the balance of capillarity force (Fγ≈ −γh), viscous force (Fv≈ ηcQcb/(wc − b)2 with b being the depth of droplet penetration into the continuous channel) and squeezing pressure (Fp≈ ηcQcb2/(wc − b)3), Christopher et al.152 derived an analytical formula for the prediction of droplet volume in transitional regime,
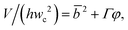 | (20) |
![[b with combining macron]](https://www.rsc.org/images/entities/i_char_0062_0304.gif) = b/wc is expressed as
= b/wc is expressed as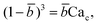 | (21) |
Eqn (20) includes the influence of channel geometry Γ, in addition to flow rate ratio and capillary number, on droplet volume. This approximate model agrees reasonably well with numerical141,157 and experimental158 results, but underpredicts the droplet volume and does not consider the influence of viscosity ratio.152
A more robust model was later developed by Glawdel et al.,159 who experimentally identified three sequential stages of droplet formation in the transitional regime: lagging, filling, and necking.160 The last two stages are similar to those observed in squeezing regime,129 while the initial lagging stage is featured by a receding back of the interface into the injection channel of dispersed fluid after the previous droplet pinch-off. The retraction distance of the interface Llag is evaluated by a balance between the viscocapillary velocity in a two-fluid system31 (uv-c ∼ γλ1/2/ηd) and the injection velocity of dispersed phase (ud ∼ Qd/(hwd)), Llag/wc ∼ uv-c/ud:
| Llag/wc ∼ λ1/2/Cad. | (22) |
The lagging affects not only the downstream droplet spacing but also the droplet volume.160 Taking the three stages into consideration, Glawdel et al.159 developed a predictive model in T-junctions
| V/(hwc2) = αlag + αfill + ζneckφ, | (23) |
| fre*drop = φ/(αlag + αfill + ζneckφ), | (24) |
The characteristics of jetting mode include the jet diameter djet, intact jet length Ljet (the length from the dispersed nozzle to the end of the jet), and droplet diameter D. In narrowing jetting regime, the jet diameter djet can be approximated as the diameter of an unperturbed jet with constant shape governed by Stokes equations for both continuous and dispersed fluids at low Reynolds number: ηs∇2us = ∇ps. By solving Stokes equations, the jet diameter is found to be,161
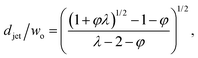 | (25) |
| djet/wo = (φ/2)1/2, | (26) |
The intact jet length Ljet in narrowing jetting is simply estimated as the product of the jet velocity ud = 4Qd/(πdjet2) = 8Qc/(πwo2) (by applying eqn (26)) and the viscous-capillary time tv-c = djetηd/γ.162 Cubaud and Mason,162 therefore, derived the formula for the jet length Ljet to be
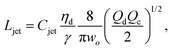 | (27) |
The droplet size in narrowing jetting regime can be determined by mass balance. Subjected to Rayleigh–Plateau instability, the jet breaks up due to the growth of capillary perturbations with the maximum growth rate and wavelength λw. To estimate droplet diameter D, the volume of the droplet is assumed to be equal to the volume of the jet with wavelength λw: πD3/6 = πdjet2λw/4. Since λw = πdjet/k*, with k* being the dimensionless wave number (k* = kdjet/2, with k being the wave number), the droplet diameter D is scaled with djet as D/djet = [3π/(2k*)]1/3. If djet is replaced by wo in eqn (26), then
| D/wo = g(k*)φ1/2, | (28) |
The characteristics of widening jetting differ from those of narrowing jetting as a result of different dominant effects. With a widening shape, the jet velocity is not fully developed prior to droplet pinch-off. Therefore, the steady-state Stokes equations fail to predict the jet diameter djet. Castro-Hernández et al.59 proposed a formula to find djet by using linear stability analysis:
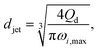 | (29) |
| D ∼ (Qd/uc)1/2. | (30) |
Despite the distinct dominant effects, droplet sizes in both narrowing and widening jetting regimes can be unified,59
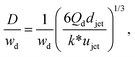 | (31) |
Two distinct mechanisms account for the occurrence of tip-streaming: surfactant-mediated and surfactant-free tip-streaming. The former was proposed by De Bruijn,171 who ascribed tip-streaming phenomenon to the presence of surfactants on the liquid–liquid interface and identified an optimal range of surfactant concentration for tip-streaming to occur. These findings were consistent with later experiments in both simple shear172 and plane hyperbolic173 flows. Subsequent numerical simulations further unveiled the mechanism of surfactant-mediated tip-streaming from free drops174 and bubbles175 in extensional flows. More recently, Anna et al. reported the occurrence of tip-streaming, which was called thread formation by them too, in planar microfluidic flow-focusing devices.24,127,176,177 They argued that the coupling between surfactant transport and bulk flow plays a critical role24 and developed a semi-analytical model to predict the conditions for the occurrence of tip-streaming.177 Tip-streaming phenomenon was also observed in the presence of an interfacial chemical reaction that produces a surfactant.178 On the other hand, no evidence suggested the possibility of surfactant-free tip-streaming until Zhang179 predicted the elegant steady-state solution for the vanishing thin spout ejecting from the perfectly conical tip when the capillary number of external straining fluid is above a critical value. Then more conclusive proof was provided by simulations16 and experiments166 which demonstrated surfactant-free tip-streaming in a double flow-focusing arrangement. In what follows, we focus only on the type of surfactant-free tip-streaming, which is referred to as tip-streaming for short hereafter.
Tip-streaming is featured by the steady cone–jet structure (Fig. 3d) of the dispersed fluid, which very much resembles the Taylor cone in charged liquids during electrospraying.180,181 In the cone region, the continuous viscous stress induces the recirculating flow pattern within the dispersed phase.16 Then a speeding up of the dispersed flow is observed upon approaching the apex of the cone, which is the cone–jet transition region.16 Sufficiently far downstream from the apex, the dispersed flow is nearly plug flow and the jet takes a cylindrical shape with an almost constant diameter of djet.16 The cone–jet transition is affected by both the flow process and the fluid properties. For larger continuous-phase capillary number Cac and smaller viscosity ratio λ, the transition region becomes less slender,168,182 and the local jet slope decreases. Experimental observations reveal that the cone–jet transition is stable for liquid–liquid systems, but not for gas–liquid.168,169,182 This can be qualitatively understood as that the very small viscosity ratio λ for gas–liquid systems requires a quite low jet slope,182 which is, however, difficult to achieve in experiments. The cone–jet geometrical profile has been deduced by Zhang179 in the extreme limit Qd → 0, and by Castro-Hernández et al.168 as a function of Cac, φ, λ and device geometry in co-flow configurations. The resultant droplet size can also be precisely predicted by eqn (28),59,169 because tip-streaming can be regarded as narrowing jetting with extremely thin jet diameter.169,182 However, an accurate prediction for the intact jet length has yet to be developed.
Several conditions should be met for the occurrence of tip-streaming. Note that device geometry has a significant effect. No tip-streaming has been observed yet in cross-flow geometry. According to Tseng and Prosperetti,183 tip-streaming occurs when the local streamlines converge near the interface. This is easy to achieve in co-flow and flow-focusing, but difficult in cross-flow configuration (Fig. 3d). To generate tip-streaming, no flow separation should exist between the continuous flow and the drop interface, which requires creeping flow condition, Rec ≪ 1. Then, to stretch the dispersed fluid into a conical shape, the continuous-fluid viscous stress must overcome the capillary pressure at the injection nozzle, therefore requiring Cac > Cacri (Cacri is a critical constant of the order of unity). For the extremely thin jet to issue from the cone, φ ≪ 1 should also be maintained. The final condition Red ≪ 1 ensures that the average dispersed velocity equals continuous velocity in the thin jet region due to large momentum diffusion, and the fine jet is thus almost a cylinder far downstream from the cone. These four conditions are sufficient to generate the tip-streaming.169
Some effort has been devoted to exploring the value of Cacri. Suryo and Basaran16 found that the critical capillary number Cacri is a function of viscosity ratio λ and flow rate ratio φ. Gañán-Calvo et al.166,182 then theoretically determined Cacri as a function of λ by using a spatiotemporal stability analysis and concluded that once the jet surface velocity ujs is above a critical value, ujs > γ(ηdηc)−1/2Cacri, the jet can be made arbitrarily thin (down to the continuum limit) without transition to dripping as the dispersed flow rate Qd vanishes. More recently, Gordillo et al.58 found that Cacri is less sensitive to flow rate ratio φ than to viscosity ratio λ, who also applied a global stability analysis to obtain the λ-dependent Cacri, below which the cone–jet structure is unsteady and the resultant droplet size is not uniform.58
The unsteady feature of dispersed tip has been widely observed in gas–liquid, liquid–gas and liquid–liquid systems. Garstecki et al.30,126 found that the gas–liquid system destabilized and transitioned from period-1 (dripping, one bubble generation in one period) state to higher-order periodic or chaotic behaviour (as exampled by period-2, period-3 and period-4 behaviour in Fig. 4a,i) when Qc is above some critical value. The transition was ascribed to the inertial-dominated dynamics of the gas–liquid interface.30 Similar phenomena were identified in a multi-orifice system185 and later in a multi-section flow-focusing junction.186 More recently, Evangelio et al.187 observed the unsteady gas meniscus when the continuous liquid velocity uc is lower than the threshold u* (Fig. 4a,ii). In parallel, for a liquid jet focused by a gas, the liquid meniscus is unsteady when the dispersed flow Qd is below the minimum value Qmin (ref. 181, 188–191) (Fig. 4b). These observations suggest that dynamics of both dispersed and continuous fluids plays a role in rendering the meniscus unsteady. In a liquid–liquid co-flow system, Gordillo et al.58 determined the critical continuous-phase capillary number Cacri as a function of viscosity ratio λ, which sets an upper limit for the occurrence of the unsteady conical tip. Zhu et al.17 reported that the number of the droplet in one droplet-train increases with increasing continuous-phase capillary number Cac in a microcapillary flow-focusing device (Fig. 4c). Attributed to the feature that the unsteady dispersed fluid tip breaks off repeatedly into multiple droplets in one cycle, Zhu et al.17 named this mode of droplet breakup as tip-multi-breaking.
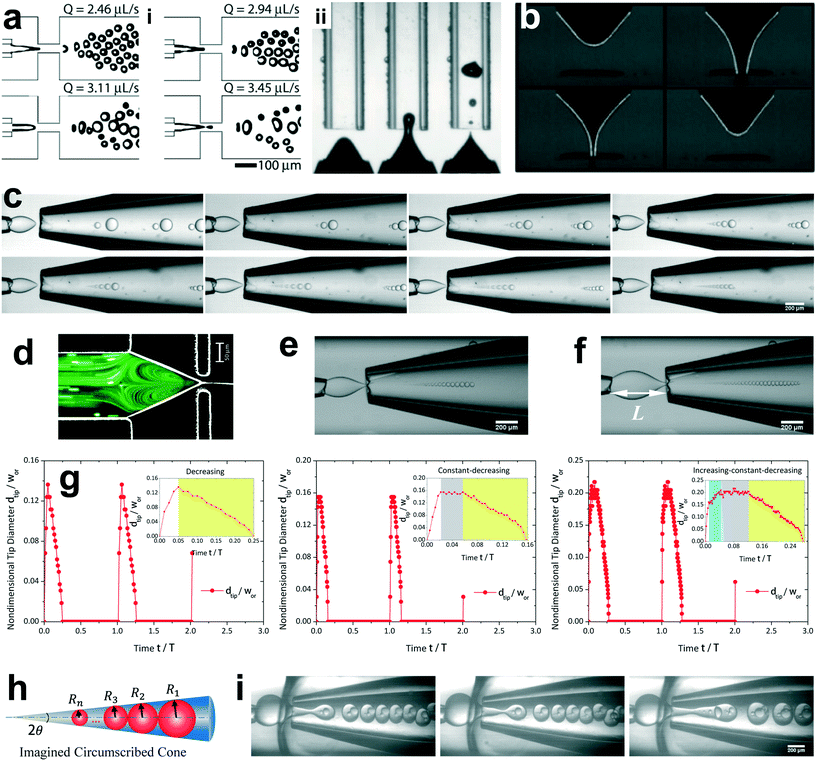 | ||
| Fig. 4 Tip-multi-breaking mode in microfluidic devices. (a) Unsteady gas meniscus during bubble generation in a gas–liquid microsystem. (i) Period-1, period-2, period-4 and period-3 gas thread behaviour with increasing continuous flow rate, respectively (from left to right, top to bottom). (ii) Irregular bubble generation when the continuous-fluid velocity uc is lower than the critical threshold. (b) Unsteady liquid meniscus when a liquid jet is focused by a gas stream. (c) Tip-multi-breaking mode in liquid–liquid microfluidic flows by which droplets of decreasing size are generated in periodic sequences. The number of droplets in one sequence increases as the continuous-phase capillary number increases (from left to right, top to bottom). (d) Recirculation cell in the dispersed meniscus. When Qd is smaller than the minimum flow rate Qmin, the recirculation cell is large and penetrates into the dispersed nozzle, in which case tip-multi-breaking takes place. (e) Droplet size distribution in the form of “constant–decreasing”. (f) Droplet size distribution in the form of “increasing–constant–decreasing”. (g) Temporal evolution of the tip diameter at the focusing orifice in three situations. (h) Schematic of the decreasing droplet size distribution in a geometrical progression. (i) Tip-multi-breaking mode in three-phase microfluidics. Snapshots from left to right are one four-droplet train, one five-droplet train and two droplet trains encapsulated in one middle phase droplet. (a,i) is adapted with permission from ref. 30. Copyright 2005, American Physical Society. (a,ii) is reprinted with permission from ref. 187. Copyright 2015, Cambridge University Press. (b) is reprinted with permission from ref. 189. Copyright 2011, American Physical Society. (d) is adapted with permission from ref. 127. Copyright 2006, American Institute of Physics. | ||
Since the unsteady meniscus gives rise to the generation of a droplet-train, the condition of destabilizing the dispersed meniscus determines the occurrence of tip-multi-breaking mode. While higher-order periodic and chaotic behavior of the gas thread was ascribed to the dominant inertial effects,30 the mechanism responsible for the unsteady liquid meniscus seems to be different. From the perspective of energy balance, once the kinetic energy of the liquid meniscus is overwhelmed by the viscous dissipation and/or free surface energy, the steady emission of continuous droplets is halted.181 Corresponding to the above three energy terms, the dispersed-phase inertial, viscous and capillary forces scale respectively as ∼ρdud2, ∼ηdud/dtip and ∼γ/dtip, where dtip is the liquid tip diameter at the focusing orifice. With the assumption of Qd ∼ uddtip2 and Qd/Qc ≈ (dtip/wor)2 at the focusing orifice (wor is the diameter of the focusing orifice), inertia dominated by viscous forces (ρdud2 < ηdud/dtip) gives (QdQc)1/2 < ηd/(ρdwor), and inertia overwhelmed by capillary forces (ρdud2 < γ/dtip) leads to Qd1/2Qc3/2 < γ/(ρdwor3) for the dispersed meniscus to be unsteady. Both of the criteria suggest a minimum dispersed flow rate Qmin below which a steady liquid tip cannot be formed when Qc is fixed.
In liquid–liquid systems, the Qmin yields the condition that φ < φmin ≪ 1 for the occurrence of tip-multi-breaking.17 Actually, for the dispersed fluid with low viscosity and sufficiently small flow rate, the flow displays a recirculation cell whose size increases as Qd decreases (Fig. 4d). When Qd ≤ Qmin, the recirculation cell is large and penetrates into the injection capillary, consuming a large amount of momentum due to viscous friction between the liquid and the solid wall.181,188,190 Simultaneously, as Qd decreases, the decreasing dtip finally makes the capillary pressure too large to be overcome in generating a new free surface for droplet production, thus destabilizing the dispersed tip.181
Similarly, the continuous fluid also reserves a critical flow rate Qcri lower than which the shear force exerted by the continuous phase is not sufficient to hold a steady liquid meniscus. To have unsteady meniscus at the focusing orifice, the shear stress ∼ηcuc/wor should be dominated by the capillary pressure ∼γ/wor. This criterion then leads to the existence of a critical capillary number Cacri which sets an upper limit for the liquid tip to be unsteady, Cac < Cacri. In liquid–liquid systems, Cacri is a function of viscosity ratio and weakly depends on flow rate ratio φ.58 Apparently, Cac cannot be infinitely small, otherwise, the system would transfer into other modes, such as dripping and squeezing.17 It is worth noting that the two conditions, φ < φmin ≪ 1 and Cac < Cacri, should be met simultaneously for the occurrence of tip-multi-breaking mode in liquid–liquid systems. Experiments revealed that φmin, to some extent, depends on and decreases with Cac.17
The droplet size distribution in tip-multi-breaking mode is highly synchronized with the dynamics of the tip evolution at the focusing orifice. The normalized droplet diameter D/dtip scales as D/dtip ∼ Cac−1 in tip-multi-breaking mode.184 Depending on device geometry, the droplet size distribution can be either monotonically decreasing (Fig. 4c), or first keeping constant and then decreasing (“constant–decreasing” in Fig. 4e), or first increasing followed by keeping constant and finally decreasing (“increasing–constant–decreasing” in Fig. 4f), as the spacing L (Fig. 4f) between the left injection and right focusing orifices increases.184Fig. 4g shows the temporal evolution of dtip/wor for the three cases of droplet size distribution. The very apparent oscillation of the liquid tip is observed with period T. During one cycle of oscillation, dtip can undergo any one of the three evolutional dynamics (insets in Fig. 4g), and simultaneously droplets are ejected from the tip in sequences. This verifies that the non-uniform droplet and unique droplet size distribution is a consequence of the dtip oscillation. It is worth clarifying that an initial very-fast-growing stage of dtip in all three cases (non-shadow areas in insets of Fig. 4g) is due to the penetration of the liquid tip into the focusing orifice, and no droplet is generated at this stage.
The size distribution in one droplet-train is predictable. Since the thinning rate of dtip is nearly linear for all the cases (yellow region in insets of Fig. 4g), the decreasing size of droplet, very interestingly, is in the distribution of geometric progression,17
Ri = R1χi−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ,i = 1, ,i = 1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) …, …,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n, n, | (32) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/(1 + sin
θ)/(1 + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) or dynamically once the linear thinning rate of dtip and material properties are known.17 As a first-order approximation, χ has a correlation with the number of droplets n in the form of 1 – χn−1 ≈ χ, for the droplet train with decreasing size in Fig. 4c.17Eqn (32) is deduced for, but is not limited to, the decreasing size distribution. It can also be applied to the increasing size distribution in Fig. 4f because the increasing rate of dtip is also almost constant (inset in Fig. 4g for “increasing–constant–decreasing”). More effort should be devoted to further characterize the tip-multi-breaking mode, for instance, the condition that distinguishes the three types of droplet size distribution in Fig. 3c, e and f, respectively.
θ) or dynamically once the linear thinning rate of dtip and material properties are known.17 As a first-order approximation, χ has a correlation with the number of droplets n in the form of 1 – χn−1 ≈ χ, for the droplet train with decreasing size in Fig. 4c.17Eqn (32) is deduced for, but is not limited to, the decreasing size distribution. It can also be applied to the increasing size distribution in Fig. 4f because the increasing rate of dtip is also almost constant (inset in Fig. 4g for “increasing–constant–decreasing”). More effort should be devoted to further characterize the tip-multi-breaking mode, for instance, the condition that distinguishes the three types of droplet size distribution in Fig. 3c, e and f, respectively.
To date, studies on the unsteady dispersed meniscus have mainly focused on its hydrodynamic interest but underestimate its potential in applications. This is because droplets generated in tip-multi-breaking mode are non-uniform, while monodisperse droplets are usually in favor for most applications. Nevertheless, some applications prefer non-uniform droplets. For example, in multi-volume droplet digital PCR (MV-dPCR),13 droplets with various volumes provide simultaneous measurements of a sample at different copies per droplet. Compared with single-volume digital PCR, MV-dPCR retains higher detection reproducibility, wider dynamic range, and better resolution while reducing the total number of droplets/wells required for the measurements.13,192,193 Tip-multi-breaking mode can, therefore, fit well in the application of MV-dPCR due to its nature in producing identical droplet trains with a tunable number of droplets and predictable size distribution. Besides, the droplet trains can be successfully encapsulated into middle-phase droplets (Fig. 4i), which would be beneficial for chemical and biomedical applications, for example, in the design of chemically communicating droplet networks.194
Dangla et al.198 investigated the step-regime in a vertical step. They ascribed the breakup to the quasi-static balance between the curvature of the dispersed thread in the inlet channel and that of the droplet protrusion in the reservoir, based on which a lower bound of droplet size is determined. Recently, the closed-form expression for predicting droplet size in step-regime is theoretically derived by Li et al.,197
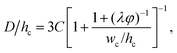 | (33) |
With the increase in dispersed phase flow rate, the step-regime gives its way to the jet-regime at a critical dispersed-phase capillary number.67,199 The condition for such a transition is experimentally determined to be197
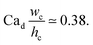 | (34) |
In jet-regime, the dispersed thread shrinks in its width and results in a tongue-like tip upstream near the step, which was ascribed to the capillary focusing effect.70 The quasi-static shape of the tongue has been determined by numerical simulation199 and simplified theoretical modeling,197 both of which were confirmed by experiments. Aside from single step-regime or jet-regime, the coexistence of different regimes on the same dispersed-phase filament was observed recently by Hein et al.,65 which implies a symmetry breaking in filament breakup even under symmetric flow conditions.
Variations of interfacial tension dramatically alter the dynamics of liquid thread pinch-off. During pinch-off, the presence of surfactants lowers the interfacial tension and may induce the depletion of surfactants from the pinch region.208 The reduction in interfacial tension gives rise to a decrease in capillary pressure (∼γ/L) that drives surfactants out of the pinching neck; surfactant depletion induces an interfacial tension gradient and a Marangoni stress counteracting the outflow. Considering the pinch-off of a surfactant-covered fluid thread at a small surfactant Peclet number, Pe (the parameter characterizing the relative strength of the surfactant convection over the diffusion), the interfacial tension starts at the equilibrium value and then increases due to surfactant depletion as pinch-off approaches.209–211 Provided a strong Marangoni stress, a third stage of surface tension reduction can occur,211 which was also observed for a two-fluid thread pinch-off in microchannels.210 The temporal variation of dynamic interfacial tension, therefore, changes the thinning rate of the pinching thread.209,210 Besides, the thread shape near the pinch-off is also altered by surfactants,210–212 which induces variations in pinch-off location211,212 and influences the size of satellite droplets.213
Several models have been developed to predict the dynamic interfacial tension during droplet formation. The experimental measurements of dynamic interfacial tension are carried out by first determining the relationship between interfacial tension and variables such as the droplet generation frequency,214 droplet size,201–206,215 droplet deformation,216 and the pressure drop of the continuous phase217,218 and then measuring these variables. Semi-empirical models are developed by fitting the model with experimental data to determine the empirical parameters, such as those in ref. 201–206, 215, 217 and 218. However, semi-empirical models are highly sensitive to the fluidic system, and the results are normally not transferable. On the other hand, Glawdel and Ren216 developed a theoretical model to predict the dynamic interfacial tension during droplet generation in squeezing–dripping transitional regime in T-junctions, based on which droplet volume is well predicted with surfactants. Nevertheless, no experimental method is available for capturing the spatial distribution of surfactants on the interface, which is usually uneven during droplet formation.219
4.2 Fluid instabilities in microfluidic biphasic flows
The fragmentation of fluid threads into droplets is initiated by fluid instabilities. The currently identified five fundamental modes of droplet formation are related to different types of instabilities, of which droplet pinch-off in squeezing mode is imposed by pressure buildup in the continuous flow, while dripping, jetting, tip-streaming and tip-multi-breaking are associated with capillary instability. Such a difference originates from the distinct degree of channel confinement between squeezing and the other four modes. In this subsection, we briefly summarize the characteristics of hydrodynamic instabilities for each of the five breakup modes in microfluidic biphasic flows (Table 4).| Droplet breakup mode | Interfacial instability | Capillary instability | ||
|---|---|---|---|---|
| Absolute instability | Convective instability | Global instability | ||
| a Fine balance of forces is required to generate absolute instability.225 b Dripping, jetting, and tip-streaming modes are globally stable. | ||||
| Squeezing | √ | |||
| Dripping | √ | |||
| Widening jeta | √ | |||
| Narrowing jet | √ | |||
| Tip-streaming | √ | |||
| Tip-multi-breakingb | √ | |||
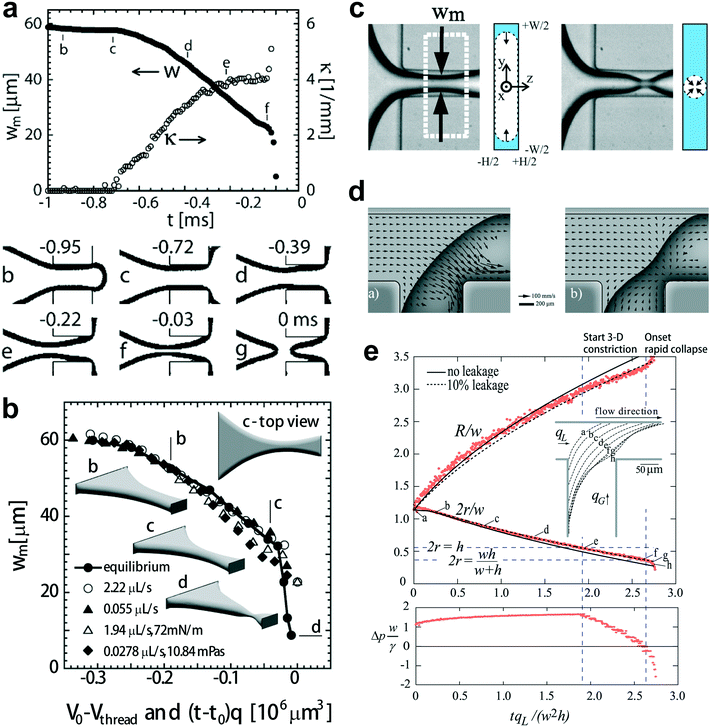 | ||
| Fig. 5 Fluid instability of squeezing mode. (a) Upper diagram: evolution of the minimal width wm, and the axial curvature of the gas–liquid interface in a typical breakup event. Bottom images: optical micrographs of the gas–liquid interface along the breakup trajectory. (b) Comparison of the minimal width wm of the simulated (equilibrium) interface (V0 − Vthread, solid dots connected by solid lines) and the experimentally measured minimal widths wm ((t − t0)q, unconnected symbols). Insets of “b–d” represent the equilibrium shape of the gas–liquid interface along the trajectory leading to final breakup. The interface shown in inset “d” (rapid collapse stage) is also in equilibrium. (c) The gas thread of minimal width wm is first squeezed inwards from the sides by the surrounding liquid (2D collapse, left two graphs). The gas thread experiences finally a fast pinch-off, where it is squeezed radially (3D collapse, right two graphs). (d) In-plane velocity at 0.1h from the top wall. Left: before the rapid collapse, flow in the gutters runs towards the tip end. Right: the thread starting to collapse, liquid now runs from the tip to the neck through all four gutters. (e) Top diagram: evolution of the radii of curvature r and R. Bottom diagram: evolution of the pressure drop over the gutters, indicating that the collapse coincides with reversal of pressure drop in the gutters. (a) and (b) are reprinted with permission from ref. 14. Copyright 2005, American Physical Society. (c) is reprinted with permission from ref. 32. Copyright 2008, American Physical Society. (d) and (e) are reprinted with permission from ref. 144. Copyright 2009, American Physical Society. | ||
The mechanism responsible for the second nonlinear rapid collapsing stage is controversial. Dollet et al.32 argued that the onset of rapid collapse is initiated from capillary instability, coinciding with the detachment of the shrinking thread from the wall (Fig. 5c). Then the shrinkage of the gas thread is driven solely by liquid and gas inertia, with the minimal neck width scaling as wm ∼ (tc − t)1/3, where tc is the critical time for thread breakup. In contrast to the above explanation, comparisons of experimental and simulated static interfaces reveal a quasi-static pinch-off mechanism until the last stage of breakup (Fig. 5b).14 van Steijn et al.144 later demonstrated that the reversal of liquid flow in corner gutters, from the end tip of the gas bubble to the shrinking neck (Fig. 5d), triggers the rapid collapse of gas thread. The flow reversal was attributed to the onset of an adverse liquid pressure drop over the gutters, which determines a critical thread radius rcri for the onset to occur, rcri = hwc/[2(h + wc)], in straight microchannels (Fig. 5e), incompatible with rcri = min[wc/2, h/2] as predicted by capillary instability. Combining all the evidence together, one concludes that the interfacial instability of a squeezing fluid thread does not originate from capillary instability. Consequently, highly monodisperse droplets can be produced in squeezing regime due to the elimination of satellite droplets that are almost inevitable for breakups governed by capillarity instability.
A linear stability analysis221 is usually performed to assess the local instability. In doing this, initial infinitesimal perturbations ψ(z, y, t) that develop in space and time are applied to a given parallel basic flow, where z, y, and t represent streamwise, cross-stream and time coordinates, respectively. Perturbations are then decomposed into elementary solutions ψ(z, y, t) = ξ(y; k)exp[i(kz − ωt)] after linearization around the base state, with complex wavenumber k = kr + iki, complex frequency ω = ωr + iωi and eigenfunction ξ(y; k) that describes the cross-stream distribution of perturbations. In the eigenvalue problem, non-trivial solutions for ξ(y; k) exist if and only if k and ω satisfy a dispersion relation in a manner:
D(k,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω; S) = 0, ω; S) = 0, | (35) |
Typically, a temporal stability analysis is adopted to determine whether a system is stable or not by the following criterion:
 | (36) |
 | (37) |
In general, ω0 are branch-point singularities of k(ω) with two spatial branches k+(ω) and k−(ω). As an additional requirement, the physically relevant complex pair (ω0, k0) must satisfy the Briggs–Bers criterion,220 in which branches k+(ω) and k−(ω) originate respectively from the upper and lower half of the complex k-plane when ωi is decreased from positive values to zero. Convective instability, such as narrowing jetting, displays extrinsic dynamics as a spatial amplifier, where external noises are amplified when advected downstream, while absolute instability, such as dripping, exhibits intrinsic dynamics that induces breakup at a fixed spatial location and at a self-sustained frequency intrinsic to the system. This explains experimental observations that droplets produced by dripping are highly monodisperse, but by jetting are more polydisperse.
Guillot et al.133 performed a linear spatiotemporal stability analysis to parametrically map jetting and dripping regions for confined capillary jets in cylindrical co-flowing microchannels. Consistent with criterion eqn (37), a temporally unstable flow is convectively unstable (jetting) if the front velocity of the trailing edge of the wave packet  is positive (perturbations convected downstream), and is otherwise absolutely unstable (dripping) if
is positive (perturbations convected downstream), and is otherwise absolutely unstable (dripping) if  (upstream propagation of perturbations). Accordingly, a marginal stability criterion was obtained for the jetting–dripping transition:133
(upstream propagation of perturbations). Accordingly, a marginal stability criterion was obtained for the jetting–dripping transition:133
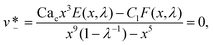 | (38) |
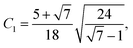 | (39) |
E(x,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ) = −4x + (8 − 4λ−1)x3 + 4(λ−1 − 1)x5, λ) = −4x + (8 − 4λ−1)x3 + 4(λ−1 − 1)x5, | (40) |
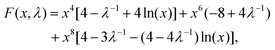 | (41) |
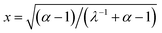 with
with 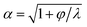 , and capillary number Cac = 8ηcQc[1 + λ(α − 1)]2/(πRc2γ) (Rc, the inner radius of the cylindrical channel wall). Criterion eqn (38) is plotted in the (x, Cac) plane as operational conditions for the jetting–dripping transition with fixed λ (Fig. 6a, where Ka denotes Cac). Guillot et al.222 then extended the analysis to square and rectangular microchannels in which dripping is found to be promoted in comparison to cylindrical channels. Adopting lubrication approximation at low Reynolds numbers (neglecting inertia), eqn (38) is simple and robust in predicting jetting–dripping transition for highly confined jets (Fig. 6a) but fails for the low degree of confinement. Herrada et al.223 proposed axisymmetric models based on the analysis by Guillot et al.133 to improve the accuracy of prediction in low confinement cases. In addition, jetting–dripping transition in an open flow-focusing configuration (Fig. 2c,i) was studied by considering a viscous jet flowing in an unbounded co-flowing viscous liquid domain.224 The transition is mapped in the parametrical space of (Re, We) and shows good agreement with experiments (Fig. 6b).
, and capillary number Cac = 8ηcQc[1 + λ(α − 1)]2/(πRc2γ) (Rc, the inner radius of the cylindrical channel wall). Criterion eqn (38) is plotted in the (x, Cac) plane as operational conditions for the jetting–dripping transition with fixed λ (Fig. 6a, where Ka denotes Cac). Guillot et al.222 then extended the analysis to square and rectangular microchannels in which dripping is found to be promoted in comparison to cylindrical channels. Adopting lubrication approximation at low Reynolds numbers (neglecting inertia), eqn (38) is simple and robust in predicting jetting–dripping transition for highly confined jets (Fig. 6a) but fails for the low degree of confinement. Herrada et al.223 proposed axisymmetric models based on the analysis by Guillot et al.133 to improve the accuracy of prediction in low confinement cases. In addition, jetting–dripping transition in an open flow-focusing configuration (Fig. 2c,i) was studied by considering a viscous jet flowing in an unbounded co-flowing viscous liquid domain.224 The transition is mapped in the parametrical space of (Re, We) and shows good agreement with experiments (Fig. 6b).
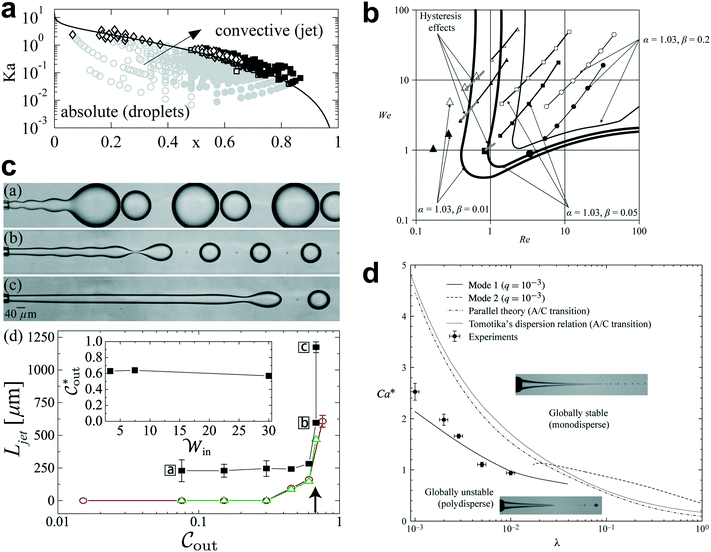 | ||
| Fig. 6 Capillary instability in microfluidic biphasic flows. (a) Flow behaviour in the (x, Ka) plane for a given value of the viscosity ratio λ = 0.23. Symbols of light colour correspond to droplets (absolute instability), and those of dark colour represent jet (convective instability), both of which are experimental data. The line is the theoretical prediction of absolute-to-convective instability transition. (b) Theoretical jetting–dripping transition, for various (α, β, Re, We). α and β stand respectively for density ratio and viscosity ratio of continuous to dispersed phase liquids.224 Re and We are Reynolds number and Weber number of the dispersed liquid, respectively. (c) Top images: jet length increases with increasing continuous capillary number Cout (Cout defined in ref. 225). The oscillations on the jet gradually die out as the length increases at the critical value, C*out. Bottom diagram: plot of the jet length as a function of Cout. The arrow marks C*out obtained from the linear stability analysis. Inset: Linear stability analysis (Win represents the dispersed phase Weber number). Below C*out the jet breaks due to an absolute instability, while above, it breaks due to a convective instability. For these experiments λ = 0.01. (d) The critical capillary number, Ca* (defined in ref. 58) as a function of the viscosity ratio λ, for the transition between globally stable to globally unstable flows. (a) is reprinted with permission from ref. 133. Copyright 2007, American Physical Society. (b) is reprinted with permission from ref. 224. Copyright 2006, Cambridge University Press. (c) is reprinted with permission from ref. 225. Copyright 2008, American Physical Society. (d) is reprinted with permission from ref. 58. Copyright 2013, Cambridge University Press. | ||
Absolute instability is also observed in widening jet breakup (Fig. 6c).225 This is supported by several experimental identifications: (i) the neck diameter oscillates with exponentially growing amplitude until pinch-off occurs, implying a positive temporal growth rate ωi; (ii) the temporal oscillations of the widening jet remain nearly stationary in space, suggesting the zero group velocity at a fixed spatial location; (iii) despite that Wed > O(1) of a widening jet at injection, droplet pinch-off at the end of the jet occurs only when the neck diameter is sufficiently widened such that Wed ≲ O(1), analogous to droplet formation in dripping mode due to absolute instability. Utada et al.225 predicted the critical capillary number Cacri = 0.69 (with λ = 0.01) of the continuous phase by performing a spatial stability analysis. Above Cacri, the absolute instability of widening jets transitions to convective instability together with a significant increase in the jet length (Fig. 6c). The theoretical prediction is in good agreement with the experimental result of Cacri ≈ 0.65 and independent of dispersed Weber number Wed (Fig. 6c).
Spatially developing flows, for example, capillary jets emanating from a nozzle, may exhibit self-sustained global modes when flows have a sufficient region of absolute instability.220,226 In flow-focusing microfluidic devices, the tapering liquid meniscus of the dispersed phase oscillates periodically with time and spatially between the injection and the focusing nozzle, emitting droplets in sequence by tip-multi-braking mode,17,184 which displays global instability.189,190 In comparison, flows in dripping, jetting and tip-streaming modes are globally stable because of their stable menisci (Fig. 3a–d, flow-focusing). Similar to flows in flow-focusing, highly stretched jets in co-flowing streams set off global instability with an unsteady conical meniscus when the continuous-phase capillary number is below the critical value Cacri.58 To determine Cacri that separates tip-streaming from tip-multi-breaking mode, Gordillo et al.58 performed a global stability analysis by taking the real shape of the stretched jets into consideration with no simplification of parallel flows. It was found that Cacri is a decreasing function of viscosity ratio λ but insensitive to flow rate ratio φ provided that λ ≲ 0.1 and φ ≪ 1. The theoretical predictions by global stability analysis are in fair agreement with experiments and more accurate than predictions by local stability analysis of absolute/convective transition (Fig. 6d).
5. Active droplet generation
Modulating droplet generation with the aid of additional energy input by active controls has several advantages over passive droplet generation, for example, (i) active droplet generation offers additional handles and higher flexibility in controlling droplet size and production rate, and in some cases enables on-demand droplet generation (e.g., droplet with prescribed volume produced at a required frequency), therefore largely facilitating practical applications of microfluidic droplets; it is however almost impossible, in passive droplet generation, to independently control droplet size and generation frequency, as they correlate with each other by mass conservation; (ii) system response time, the time needed for stabilized droplet production, is much shorter in active control than in passive method. For example, the response time can be down to several milliseconds in an active approach compared with several seconds or even minutes in a passive method.The energy imbalance modulates the nature of force balance on the interface for droplet generation. According to the nature of force balance variation, the active droplet generation can be categorized into two groups: introducing additional forces and modifying intrinsic forces. As discussed in section 2, microfluidic droplet formation is controlled by external forces and intrinsic ones of inertial, viscous, and capillary effects scaling as fi ∼ ρsus2, fv ∼ ηsus/L, and fγ ∼ γ/L, respectively. An active control is effective in modulating droplet generation if it affects at least one type of the aforementioned four forces. Normally, additional forces are exploited by applying external electric, magnetic and centrifugal fields, and modifying the intrinsic inertial, viscous and capillary forces is realized by manipulating the dynamic velocity u and material properties, including viscosity, interfacial tension, channel wettability, and fluid density. A recent review25 classified active methods according to the energy type: electrical, magnetic, thermal and mechanical. We note that the mechanism of active control could be different even for the same energy input (Table 5). Taking electrical control for example, dielectrophoresis, electrowetting (EW), electrochemical, electrocapillary and electrorheological effects can be utilized. In dielectrophoresis an external dielectric force is applied on the liquid–liquid interface; in EW the wettability of the microchannel substrate is changed; in electrochemical reaction and electrocapillarity, the interfacial tension is modified; by using electrorheological fluids the viscosity is actively controlled (Table 5). As such, we organize this section based on the force-balance argument of active droplet generation.
| Type of control | Mechanism | Implementation | Device geometry | Type of droplet generationa | Ref. |
|---|---|---|---|---|---|
| a Tunable – droplet generation with tunable size and production rate; on-demand – on-demand droplet generation. | |||||
| Electrical | Electric force | Constant DC | Flow-focusing | Tunable | 19, 227, 231 and 232 |
| DC pulse | Step emulsification | On-demand | 229 and 233 | ||
| Low-frequency AC | Flow-focusing | Tunable | 230 | ||
| High-frequency AC | Flow-focusing | Tunable | 228 and 234–236 | ||
| Electrorheology | DC pulse | T-junction | On-demand | 295 | |
| Flow-focusing | On-demand | 295 and 299 | |||
| EW effect | High-frequency AC | Flow-focusing | Tunable | 316–319 | |
| Flow-focusing | On-demand | 320 | |||
| Electrochemical and electrocapillary effects | Constant DC and low-frequency AC | Flow-focusing | Tunable | 313 | |
| Magnetic | Magnetic force | Uniform field, in-plane | Flow-focusing | Tunable | 238–241 and 243 |
| T-junction | Tunable | 240 | |||
| Uniform field, out-of-plane | T-junction | Tunable | 242 | ||
| Non-uniform field | T-junction | Tunable | 237 | ||
| Step emulsification | On-demand | 85 | |||
| Centrifugal | Centrifugal/Coriolis/Euler forces | Rotation | Dispenser nozzle | Tunable | 247–249 |
| Flow-focusing | Tunable | 250 and 251 | |||
| Cross-flow | Tunable | 252 and 253 | |||
| Step emulsification | Tunable | 82–84 | |||
| Optical | Modifying fluid pressure | Laser pulse | T-junction | On-demand | 254 |
| Marangoni effect | Laser heating | T-junction | Tunable | 308 | |
| Flow-focusing | Tunable | 307, 309 and 310 | |||
| Co-flow | Tunable | 311 | |||
| Photosensitive surfactant | UV/blue light | Flow-focusing | Tunable | 315 | |
| Thermal | Temperature dependence of viscosity and interfacial tension | Heating | T-junction | Tunable | 302 and 303 |
| Flow-focusing | Tunable | 297, 300, 301 and 304 | |||
| Marangoni effect | Heating | T-junction | Tunable | 305 and 306 | |
| Phase change | Heating and cooling | Flow-focusing | Tunable | 321 | |
| Mechanical | Modifying fluid pressure | Mechanical vibration | Co-flow | Tunable | 255–260 |
| Off-chip valve | T-junction | On-demand | 261–265 | ||
| Flow-focusing | On-demand | 18 | |||
| Step emulsification | On-demand | 266 | |||
| SAW | T-junction | Tunable | 276 | ||
| On-demand | 273 and 274 | ||||
| Flow-focusing | Tunable | 275 | |||
| Channel deformation/blocking | Piezoelectric actuator | Flow-focusing | Tunable | 269–271 | |
| T-junction | On-demand | 267, 268 and 272 | |||
| Flow-focusing | On-demand | 268 | |||
| On-chip microvalve | T-junction | Tunable | 13, 279, 280, 282, 287 and 291 | ||
| On-demand | 283–286, 289 and 290 | ||||
| Flow-focusing | Tunable | 277, 278, 280, 281, 288 and 292–294 | |||
| On-demand | 284 | ||||
5.1 Additional forces in electrical control
Similar to the cases of electrospray and electrohydrodynamic atomization,180 electric fields can be employed to manipulate droplet generation in microfluidics. To apply an electric field, a microfluidic device is embedded with electrodes, one227 or pairs of228 which are connected to the high voltage and the others are grounded. Taking water–oil systems, for example, high voltage Ue is applied to the water phase, and the grounded oil phase behaves as an insulator (Fig. 7a). Application of electric fields induces the migration and accumulation of charges on the water–oil interface. With appropriate distribution of the electric field, the interaction between the surface charges and the electric field offers an additional handle to control droplet generation. Electrical control is categorized into two groups based on the type of current: direct current (DC)227 and alternating current (AC) control.228 In DC control the voltage is only in one direction, whereas the polarity of voltage reverses periodically in AC control. DC control can be applied at constant227 or pulsatile voltage,229 while AC control is subcategorized into low-frequency (on the order of Hz)230 and high-frequency (on the order of kHz)228 control, depending on whether the frequency of applied voltage is lower (low-frequency) or higher (high-frequency) than that of droplet generation. | ||
| Fig. 7 Electrical control of droplet generation. (a) A high DC voltage Ue is applied to the dispersed phase, and the continuous phase is grounded. Two methods of implementation have been demonstrated: inserting electrodes into the liquids,194 or patterning indium tin oxide (ITO) electrodes on the substrate.190 (b) Droplet generation in a DC electric field. (i) Stable jet. Flow rate ratio φ = 80/350. Voltage Ue = 1200 V. (ii) Electrospray. Flow rate ratio φ = 5/350. Voltage Ue = 2000 V. (c) Top: contour plot of the electric field strength at one time-step during the droplet formation. The black lines indicate the electric field lines. High voltage is applied to the left side inlet. Bottom: contour plot of the volume fraction of the dispersed phase in the regions enclosed by the red dashed curves. The white arrows indicate the vectors of the electric body force induced on the fluid interface. (d) A sequence of images showing the electrogeneration of water droplets with a DC voltage pulse. (i–iii) Images of two droplet formation in one pulse. (i) Advancing of the water jet. (ii) Primary droplet formation. (iii) Secondary droplet formation. (iv) Formation of one droplet per pulse. (e) Droplet series generated using an AC electric field of the triangular waveform. A–I: the first half period. J–R: the second half period. (f) Schematic of a flow-focusing device under an AC electric field. The electrodes are in orange and the dispersed phase is in blue. (b) is adapted with permission from ref. 231. Copyright 2007, American Institute of Physics. (c) is reproduced with permission from ref. 19. Copyright 2015, Royal Society of Chemistry. (d) is adapted with permission from ref. 233. Copyright 2006, American Chemical Society. (e) is adapted with permission from ref. 230. Copyright 2010, American Institute of Physics. | ||
In DC control where constant high voltage is applied to the dispersed phase (Fig. 7a), the electric stress on the water–oil interface scales as227
| fe ∼ εcE2, | (42) |
Variation in DC implementation affects the process of droplet formation. In a flow-focusing geometry where two continuous inlets are connected to high DC power supplier and ground (Fig. 7c), the electric force points from the continuous phase to the dispersed phase due to the smaller εd (εd, the permittivity of dispersed phase) than εc.19 Numerical simulation19 demonstrates three distinct stages of droplet size variation with the increase in voltage: decreasing, increasing and decreasing again. This trend is explained by the counterbalance between the x and y components of electric forces (Fig. 7c). The x component, perpendicular to the flow direction, accelerates the squeezing rate of the viscous droplet, whereas the y component, opposite to the flow direction of dispersed phase, exerts a retardation effect on the fluid interface.
DC pulse is capable of producing droplet on demand.229,233 Initially, the water–oil interface is stabilized by capillary pressure at the orifice. Upon pulse initiation, the interface is forced by electric effects into the narrow orifice channel (Fig. 7d,i) at a nearly constant speed before reaching its equilibrium displacement.229 The maximum equilibrium displacement increases with the pulse amplitude. At high amplitude a droplet is emitted at the end of the protruded jet (Fig. 7d,ii), then the jet either re-protrudes and issues a secondary droplet (Fig. 7d,iii) or directly retracts (Fig. 7d,iv) after the pulse.233 The secondary droplet is only observed in a narrow channel with a high axial aspect ratio (ratio of channel length L to equivalent radius wh/(w + h)). The secondary droplet formation was ascribed to Rayleigh instability, different from the primary one of electrohydrodynamic origin.233
In low-frequency AC control, droplet generation is asynchronous with applied voltage and displays hysteresis.230 The droplet size is independent of the polarity of the electric field, but displays time dependence as electric fields vary with time (Fig. 7e). The irregular size distribution gives rises to uneven charges in individual droplets.230 In addition, the dispersed flow rate Qd issued from the Taylor cone exhibits relaxation oscillation that might be responsible for the hysteresis of droplet size variation.230
In high-frequency AC control, Tan et al.228 designed a microfluidic setup where electrodes are not in contact with fluids (Fig. 7f). This method enables reliable droplet generation and manipulation with response time in the order of milliseconds, based on which a musical interpretation of droplet microfluidics was demonstrated.234 In this design, dripping to jetting transition is observed when the voltage increases.228 At a fixed high voltage, systematic variation of the voltage frequency free and electrical conductivity of the dispersed liquid ke leads to three regimes: dripping, unstable production of droplets, and jetting.228 The dripping and unstable production regimes are separated by the boundary of free/ke ∼ 5 × 105 mF−1, while the transition from jetting to unstable production occurs when free is below a certain value fremess.228,235 In dripping regime, the droplet size is a function of electric field, and can be quantitatively related to an effective capillary number Caeff of the form Caeff = Cac/(1 – Be), where Be is the electric bond number.228 The unstable production of droplets is likely to be induced by nonaxisymmetric instabilities when the electric field at the jet surface is of a critical value.235 In jetting regime,235,236 the jet length Ljet increases with applied voltage and scales as Ljet ∼ (free/ke)−0.5 at a constant voltage. The electrical potential at the tip of jets was found to be about 550 V, which might confirm that jet breakup occurs for a given electric field distribution around the tip.235
5.2 Additional forces in magnetic control
A ferrofluid is a type of nanofluids containing nanometer-sized magnetic particles (≤10 nm), which is magnetized by applying a magnetic field, and demagnetized when the magnetic field is withdrawn. Consequently, ferrofluid is a good candidate for magnetic control of droplet generation in microfluidics. In the presence of a magnetic field, magnetic forces per unit volume fm are expressed as,| fm = μ0M∇H, | (43) |
Implementation of magnetic fields can be adjusted in various aspects: the type of magnet, the location, uniformity, direction, and polarity of the magnetic field. Both permanent magnets85,237,238 and electromagnets239–241 have been used. The magnetic field can either cover the entire microfluidic device85,237–240,242 or be localized,241 and be either uniform238–242 or non-uniform85,237 (Fig. 8a). For the uniform magnetic field, it can be either in-plane238–241 or out-of-plane242 of the microfluidic chip, and either parallel to238–240 or perpendicular to238 the main flow direction (Fig. 8a). Finally, the polarity of the uniform magnetic field can be inverted as well.
 | ||
| Fig. 8 Magnetic control of droplet generation. (a) Schematic of microfluidic devices under magnetic fields, as exampled by flow-focusing (left) and cross-flow (right) geometries. In-plane magnetic field: ①, ②, ④, ⑤. The direction of magnetic field perpendicular (①, ④) to and parallel (②, ⑤) to the main flow direction. Out-of-plane magnetic field with two polarities: ③. Localized magnetic field: ④. The entire device exposed to a magnetic field: ⑤. Uniform magnetic field: ④, ⑤. Non-uniform magnetic field, exampled by a downstream magnet: ⑥. Note that all types of magnetic fields (①–⑥) can be applied to any type of fluidic structures. In addition, ④ and ⑥ can be placed at any locations of microfluidic devices. (b) Formation of ferrofluid droplets by dripping in a flow-focusing device. (i) Magnetic field parallel to the main flow direction. During pinch-off, the droplet is stretched in the main flow direction. (ii) Magnetic field perpendicular to the main flow direction. During pinch-off, the droplet is expanded to block the outlet channel. (c) Alignments of the clustered magnetic nanoparticles in the direction of the magnetic field. (i) Alignment parallel to the dispersed flow direction in a flow-focusing device. (ii) Alignment perpendicular to the dispersed flow direction in a T-junction. (d) Maximum contraction position Cmax (after droplet formation) and droplet size decreasing with magnetic flux density (from left to right). (b) is adapted with permission from ref. 238. Copyright 2013, Royal Society of Chemistry. (c) is adapted with permission from ref. 240. Copyright 2011, American Physical Society. (d) is adapted with permission from ref. 241. Copyright 2015, Springer. | ||
Droplet generation depends on the specific implementation of the magnetic field. First of all, the direction of the magnetic field matters. In T-junctions, the droplet size increases when a permanent magnet is placed upstream of the junction, whereas the size decreases when the magnet is positioned downstream.237 Changing the position of the permanent magnet varies the direction of the non-uniform magnetic field as well as that of the magnetic forces fm. In the upstream case, fm pulls the droplet back and delays the breakup, resulting in larger droplets. In contrast, the downstream case has the opposite effect. In addition, by employing a uniform magnetic field in T-junction, the in-plane application causes a decrease in droplet size,240 while the out-of-plane implementation induces the droplet size increase.242 Moreover, in flow-focusing configuration, magnetic fields parallel to and perpendicular to the main flow mainly affect the breakup (Fig. 8b,i) and expanding (Fig. 8b,ii) process of the dispersed thread, respectively.238 Interestingly, the polarity of the magnetic field has no influence on droplet size.240
Secondly, the device geometry plays a significant role in modulating droplet size. In the case of a uniform magnetic field parallel to the main flow, droplet size increases in flow-focusing but decreases in T-junction geometries as magnetic flux density increases.240 This difference results from the orientation of the magnetic field relative to the dispersed flow direction. When subjected to an external magnetic field, the magnetic nanoparticles align with the magnetic field. In flow-focusing configuration, the alignment is in the same direction as the dispersed flow, elongating the fluid tip and delaying breakup (Fig. 8c,i).240,243 However, in T-junction, the alignment is perpendicular to the dispersed flow direction (Fig. 8c,ii), thereby accelerating breakup.240 In step emulsification, droplet size is not affected by the magnetic field but depends on the channel dimension.85 Kahkeshani and Di Carlo85 recently showed that magnetic body forces, counteracted by interfacial and viscous forces, drive the dispersed fluid into the continuous reservoir. In a device with fixed channel dimension, increasing magnetic forces, or decreasing interfacial and viscous forces enables a larger rate of droplet generation, while droplet size keeps constant.85
Finally, the location of the magnetic field impacts droplet size variation. In flow-focusing geometry with a uniform magnetic field perpendicular to the main flow, the droplet size increases when magnetic field covers the entire device238 but decreases when the field locates at continuous inlet microchannel.241 In the former case, the magnetic field accelerates the expanding velocity of the dispersed tip and results in larger expanding tips as well as larger droplets (Fig. 8b,ii).238 In comparison, the latter observation is interpreted as a result of the magnetic drag.241 The drag drives the dispersed tip to move downstream and block the outlet channel (Fig. 8d), leading to an increased continuous-fluid pressure buildup that accelerates droplet breakup.241
In general, the effectiveness of magnetic control is attenuated by the increase in flow rate237,238,240 because magnetic forces (eqn (43)) are counteracted by the elevated viscous and/or inertial forces. To the best of our knowledge, a closed-form expression or scaling law for predicting the droplet size under external magnetic fields has yet to be developed.
5.3 Additional forces in centrifugal control
Centrifugal microfluidics has been developed to fulfill many unit fluidic functions, such as mixing, valving, separation, detection, metering and droplet generation, and various applications ranging from nucleic acid analysis, immunoassays, cell lysis, blood plasma separation to water, food and soil analyses.244,245 We herein focus exclusively on the droplet generation in centrifugal microfluidics. To this end, several additional forces due to the presence of rotation are introduced first. In a rotating frame of reference, three pseudo forces may act on a fluid volume: centrifugal force fΩ, Coriolis force fCo and Euler force fE, respectively (Fig. 9a). The centrifugal force is caused by the rotary motion of the microchannel network, always pointing radially outward. The Coriolis force is generated by the relative motion of the object, therefore perpendicular to the direction of the motion. The Euler force is proportional to the rotational acceleration. Considering a fluid plug of density ρ at a radial position r rotating at an angular velocity Ω, the three forces scale as (in the form of forces per unit area):246| fΩ ∼ ρΩ2rL, | (44) |
| fCo ∼ ρ2Ω3rL3/η, | (45) |
fE ∼ ρ![[capital Omega, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e1bf.gif) rL, rL, | (46) |
![[capital Omega, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e1bf.gif) refer to the characteristic length scale of the fluid plug, dynamic viscosity of the fluid, and angular acceleration, respectively. During droplet generation, these forces counteract interfacial tension effects and facilitate the fluid breakup. Accordingly, two Bond numbers BoΩ and BoCo can be defined as the ratios of centrifugal and Coriolis forces to interfacial tension force, respectively:
refer to the characteristic length scale of the fluid plug, dynamic viscosity of the fluid, and angular acceleration, respectively. During droplet generation, these forces counteract interfacial tension effects and facilitate the fluid breakup. Accordingly, two Bond numbers BoΩ and BoCo can be defined as the ratios of centrifugal and Coriolis forces to interfacial tension force, respectively:| BoΩ ∼ ρΩ2rL2/γ, | (47) |
| BoCo ∼ ρ2Ω3rL4/ηγ. | (48) |
 | ||
Fig. 9 Centrifugal control of droplet generation. (a) Three pseudo forces in centrifugal droplet generation. Centrifugal force fΩ is proportional to Ω2, pointing radially outward. Coriolis force fCo ∝ Ω3, perpendicular to both Ω and fluid velocity u. Euler force is proportional to angular acceleration, fE ∝ ![[capital Omega, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e1bf.gif) , perpendicular to both , perpendicular to both ![[capital Omega, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e1bf.gif) and radial coordinate r. (b) Schematic of the experimental setup consisting of a centrifugal platform with a micronozzle and Eppendorf tube in a swinging bucket. (c) Centrifugal flow-focusing configuration. The centrifugal force Fω and viscous drag Fd of the sheath flow ϕo support droplet formation. The emerging droplet is squeezed by the inertia (Fi) induced by the transversal component of the sheath flow. The surface tension counterforce Fσ prevents the droplet break-off until a critical mass is reached.250 (d) Droplet formation in a centrifugal cross-flow configuration. While surface tension Fσ indulges in maintaining the symmetric shape of the droplet, centrifugal force Fω and Coriolis force FC continuously pull the liquid finger until pinch-off.252 (e) Centrifugal step emulsification device. The microfluidic device is located on a spinning disk (inset A) and consists of an inlet chamber (red), a channel (red) which connects the inlet chamber to a step emulsification nozzle (inset C), and a droplet collection chamber (PCR chamber, inset B). (b) is reproduced with permission from ref. 247. Copyright 2009, Elsevier. (c) is reproduced with permission from ref. 250. Copyright 2006, Springer. (d) is reproduced with permission from ref. 252. Copyright 2015, American Institute of Physics. (e) is reproduced from ref. 84. Copyright 2016, Royal Society of Chemistry. and radial coordinate r. (b) Schematic of the experimental setup consisting of a centrifugal platform with a micronozzle and Eppendorf tube in a swinging bucket. (c) Centrifugal flow-focusing configuration. The centrifugal force Fω and viscous drag Fd of the sheath flow ϕo support droplet formation. The emerging droplet is squeezed by the inertia (Fi) induced by the transversal component of the sheath flow. The surface tension counterforce Fσ prevents the droplet break-off until a critical mass is reached.250 (d) Droplet formation in a centrifugal cross-flow configuration. While surface tension Fσ indulges in maintaining the symmetric shape of the droplet, centrifugal force Fω and Coriolis force FC continuously pull the liquid finger until pinch-off.252 (e) Centrifugal step emulsification device. The microfluidic device is located on a spinning disk (inset A) and consists of an inlet chamber (red), a channel (red) which connects the inlet chamber to a step emulsification nozzle (inset C), and a droplet collection chamber (PCR chamber, inset B). (b) is reproduced with permission from ref. 247. Copyright 2009, Elsevier. (c) is reproduced with permission from ref. 250. Copyright 2006, Springer. (d) is reproduced with permission from ref. 252. Copyright 2015, American Institute of Physics. (e) is reproduced from ref. 84. Copyright 2016, Royal Society of Chemistry. | ||
To date, four different structures have been employed in centrifugal droplet generation: dispenser nozzle,247–249 flow-focusing,250,251 cross-flow252,253 and step emulsification.82–84 One scheme to generate droplets is to rotate a dispenser nozzle, by which individual droplets are issued into the intermediate air spacer before they are collected by the receiving liquid (Fig. 9b).247–249 To generate a droplet, the pressure difference (Δp = ρdΩ2r2/2) of the dispersed liquid in the nozzle should exceed the capillary pressure (fγ = 4γ/wd). This gives a minimum rotation velocity:247
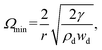 | (49) |
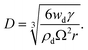 | (50) |
Since flow rate Qd obeys Qd ∝ Δp ∝ Ω2,245 the droplet generation frequency fredrop for Newtonian fluids could be fredrop ∝ Ω4 based on mass conservation. Rotating the dispenser nozzle has been employed to produce alginate/chitosan microparticles after solidification of droplets by cross-linking solutions.247–249 The abilities to tailor the particles into non-spherical shape and with 3D multi-compartment structure have also been demonstrated by varying the distance between the nozzle and the surface of the cross-linking solution and by using a multi-barrelled capillary nozzle, respectively.248
In flow-focusing configuration, the dispersed liquid tip is pulled downstream by centrifugal and viscous drag forces. Once the tip is long enough, thread breakup is stimulated by the junction constriction and inertia coming from the transversal component of continuous flows (Fig. 9c).250 Depending on the channel geometry and Bond number BoΩ, squeezing, dripping and jetting modes of droplet generation are observed. In squeezing and dripping, highly monodisperse droplets (e.g., CV = 0.84% by dripping) are generated with the droplet size decreasing but generation frequency increasing as Ω increases.250 In contrast to this trend, both the bubble length Lp and bubble generation frequency frebubble are proportional to BoΩ (equivalently, Lp ∝ Ω2 and frebubble ∝ Ω2) when BoΩ ≲ 1 in centrifugal bubble generation.251 By programming the rotational speed, it is feasible to tailor the inter-bubble spacing as well as bubble size.251
In cross-flow structure, the force balance depends on the rotation speed Ω. According to eqn (44) and (45), fΩ ∝ Ω2, whereas fCo ∝ Ω3, growing faster with Ω than fΩ. As such, at high Ω, fCo would probably dominate fΩ. In a Y-shaped microchannel with the rotation speed ranging from 104.72 rad s−1 to 167.55 rad s−1, the two Bond numbers are in the range of BoΩ = 0.22–0.2 and BoCo = 12.62–20.90.252 The dominance of fCo over fΩ and fγ indicates that the droplet generation is governed by the effective pulling of Coriolis force until the pinch-off (Fig. 9d). In this circumstance,252 the droplet volume V is ruled by V ∝ Ω−1, and droplet generation frequency fredrop is thus proportional to Ω3. In addition, by executing the rotation speed in alternate clockwise and counterclockwise directions, Kar et al.252 demonstrated the production of long serpentine threads, as a result of the repetitive alterations in the direction of fCo, as well as the impact of Euler force at the momentary time stages of speed turnover.
Centrifugal step emulsification (Fig. 9e) takes the advantage of step emulsification that droplet size is less sensitive to pressure and flow rate fluctuations but only depends on the nozzle geometry and interfacial tension.82 Subsequently, uniform droplet generation (CV of 2–4%) could be achieved, which facilitates the afterward application of digital droplet recombinase polymerase amplification (RPA)82 and digital droplet PCR.84 At high rotation speed (Ω ≈ 125.6 rad s−1),82,83 the setup enables in situ production of gel emulsions with very high internal volume fractions of >97.2%. Parallelization of 72 nozzles improves the droplet production rate up to 3700 Hz.83
5.4 Modifying fluid velocity
Intrinsic forces such as inertial and viscous forces could be modified dynamically by manipulating fluid velocity u. In general, modulating the hydraulic pressure and flow resistance (e.g., changing channel dimension) leads to variations in velocity u, as implemented by off-chip and on-chip actuation. The former implementation includes optical control, mechanical vibration and an off-chip valve, while the latter involves piezoelectric control and an on-chip microvalve. In contrast to on-chip actuation, off-chip modules are simple in assembly and compatible with microfluidic devices.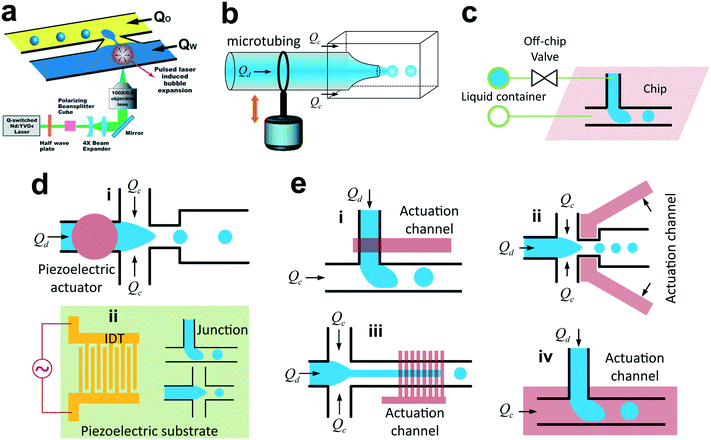 | ||
| Fig. 10 Active control by modulating the dynamic velocity of fluid flows. (a) Schematic of the pulse laser-driven droplet generation device that consists of two microfluidic channels connected by a nozzle-like opening. A highly focused intense laser pulse induces a rapidly expanding cavitation bubble to push the nearby water into the oil channel for droplet formation. (b) Schematic of dispersed fluid pressure perturbed by a mechanical vibrator by shocking the flexible microtubing. (c) Schematic of an off-chip valve regulating the dispersed fluid pressure. In addition, off-chip valves can also be applied to continuous phase fluid. (d) Schematic of piezoelectric actuation. (i) A piezoelectric actuator is incorporated into the dispersed fluid inlet channel. (ii) Droplet generation actuated by SAW. Implementation in both T-junction and flow-focusing devices has been demonstrated. (e) Schematic of on-chip valve actuation. (i) One actuation channel placed upstream of the junction. (ii) Two actuation channels located aside the junction. (iii) Chopping of droplet generation by several actuation channels placed atop the downstream fluidic channel. The actuation channels can also be placed aside the fluidic channel. (iv) Deformable droplet generator with an underneath actuation channel covering the entire fluidic channel with a T-junction. This implementation is also applicable to flow-focusing devices. (a) is reproduced with permission from ref. 254. Copyright 2011, Royal Society of Chemistry. | ||
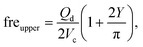 | (51) |
| V ∼ ΔPdton/Rred. | (52) |
Eqn (52) denotes that droplet volume is proportional to the amplitude of pressure pulse ΔPd and valve “on” duration ton, in consistency with experiments.18,261,265 In addition, experiments revealed that in ATPS with a constant continuous-phase flow rate Qc, droplet volume is inversely proportional to the product of Qc and toff.18 As such, V scales as:
| V ∼ ΔPdton/RredQctoff. | (53) |
By programming the on–off cycle, sequences of droplets with various volumes are produced, and independent control over droplet volume and generation frequency is attainable. Moreover, Jung et al.266 demonstrated on-demand control of droplet numbers per pulse by varying ΔPd and ton in a step emulsification device equipped with an outside pressure regulator. Compared with systems actuated by an electromagnetic valve, those by a piezoelectric valve have a higher droplet generation frequency. The frequency is lower than 100 Hz for the former18,261–264 and up to 400 Hz for the latter.265
Different from channel deformation by the pulse of piezoelectric actuator, SAW utilizes acoustic radiation force (ARF) to deform the liquid–liquid interface by advancing one liquid into another.273 In SAW, ARF arises from the gradient in the density of a traveling acoustic wave such as at an interface between two fluids with different acoustic impedances. In the implementation of SAW, a microfluidic device is placed on top of an interdigitated transducer (IDT) that comprises a series of comb-like metal electrodes arrayed on a piezoelectric substrate (Fig. 10d,ii).274 Both on-demand drop generation273,274 and drop size modulation275,276 are achievable by steering SAW. In water–oil systems where the dispersed water phase is pressurized by focused SAW, on-demand emulsification was realized by manipulating the applied power and pulse duration.273,274 Single or a batch of droplets is produced during SAW actuation. The number of droplets is determined by pulse duration, while droplet size is affected by the applied power, pulse duration, continuous-phase flow rate and channel geometry.273,274 As the continuous-phase flow rate increases, squeezing, dripping and jetting regimes are successively observed.273 Meanwhile, by using unfocused SAW, Schmid and Franke demonstrated the decrease in aqueous droplet size in both flow-focusing275 and T-junction.276 The size decrease is explained by a SAW-induced pressure increase in the inlet channel of the continuous phase.275,276
When located upstream of the junction, actuation valves are normally used to perturb the dispersed-fluid velocity. Both blocking and deformation of the dispersed channel have been demonstrated by actuation channels.13,281–286 In the blocking case,283–286 the resultant droplet size can be well predicted by eqn (52), in that underlying mechanisms are the same for both on-chip and off-chip valve-blocked systems. In the case of fluidic channel deformed by an actuation channel (Fig. 10e,i), monodisperse droplets are favored in synchronized regime, and polydisperse droplets are produced in quasiperiodic regime.287 The synchronized regime occurs when the frequency of valve pulse frepulse is close to multiple times the frequency of valve-free droplet generation fre0, such as fredrop/fre0 ≈ 1, 3/2, 2, 3, 4, 5. The under-forcing droplet generation frequency fredrop is synchronized with frepulse in the manner fredrop/frepulse = 1, 2/3, 1/2, 1/4, 1/5.287 Apart from the above normally open valves, a normally closed micro-valve is used where the dispersed channel is initially closed by a PDMS membrane.288 Upon valve actuation, the PDMS membrane is deflected to open the dispersed channel. The degree of membrane deflection maneuvers the dispersed flow velocity so that droplet size is tunable.
Valves located at the junction modulate drop generation by directly affecting the liquid–liquid interface through fluidic channel deformation or blocking. In the deformation case, variations in junction dimension (Fig. 10e,ii) make the continuous-phase shear stress unsteady and the droplet size tunable.277–279 In the case of channel blocking, the volume of the droplet V was found to increase, either linearly289 or nonlinearly,290 with the valve “on” time ton:
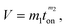 | (54) |
The downstream microvalve (Fig. 10e,iii) can break discrete droplets secondarily into daughter droplets291 and chop the prefocusing stable stream into individual droplets.292–294 In both situations, the resultant droplet sizes decrease with increased pressure that activates the valve. The stable stream is fragmented through a chopping method292–294 where two or more choppers deflect the fluidic channel. The resultant droplets are monodisperse (CV <3%),292 and the size depends on the flow rate ratio and pulse frequency of the chopper. However, the working frequency was relatively low (<17.4 Hz).293,294
Raj et al.280 recently proposed a deformable droplet generator (Fig. 10e,iv) where the actuation channel lay underneath the entire fluidic channel. By characterizing the deformation of fluidic channel in response to the actuation pressure, Raj et al.280 determined the relationship between droplet size and channel deformation, flow rate ratio, and viscosity ratio. The results show that monodisperse droplets are generated in dripping regime for a wider range of capillary number Cac in comparison to the passive method. It is also possible to produce droplets of size slightly smaller than the junction size in this deformable device.
5.5 Modifying material properties
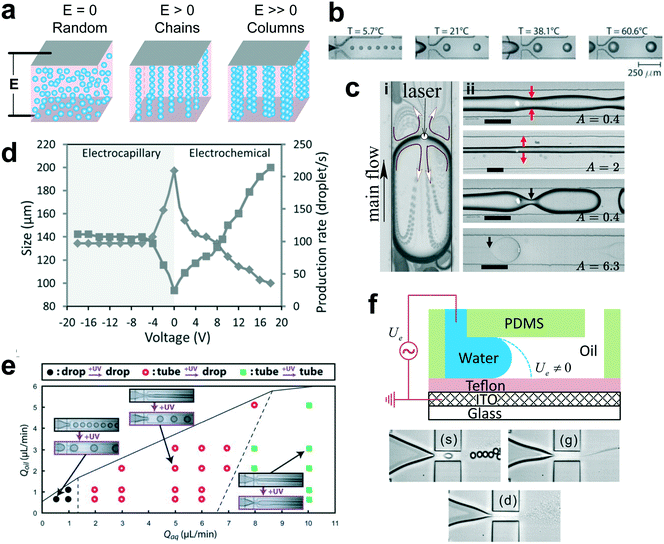 | ||
| Fig. 11 Active droplet generation via modifying material properties. (a) Schematic of chain and column formation with increasing electric field in ER fluid. (b) Images of water drops generated in mineral oil at different temperatures. (c) Laser control of droplet generation. (i) Overlaid images showing the motion of seeding particles near the hot spot. Note that the motion along the interface is directed towards the hot spot. (ii) Optocapillary deformation of the liquid interface by focused laser beam. Top two images: a thick thread (A <1) pinches while a thinner one (A >1) bulges (indicated by red arrows). Bottom two images: for large enough power, the thread eventually breaks in either pinching (A = 0.4) or bulging (A = 6.3) case (indicated by black arrows). (d) Plot of size (diamonds) and production rate (squares) versus DC voltage for both electrochemical and electrocapillary cases. (e) Effect of UV illumination for different flow rates of continuous fluid (Qoil) and AzoTAB solution (Qaq) in a flow-focusing device. (f) EW actuation of droplet generation. Top: schematic of EW implementation. Upon actuation, the contact angle of water on Teflon substrate decreases (dashed curve) and induces a smaller mean curvature of the water meniscus. Bottom: images of dripping, tip-streaming and conical spray regimes (from left to right, top to bottom) under EW actuation. (b) is reproduced with permission from ref. 300. Copyright 2009, American Chemical Society. (c,i) is reproduced with permission from ref. 307. Copyright 2007, American Physical Society. (c,ii) is adapted with permission from ref. 310. Copyright 2015, American Physical Society. (d) is reproduced with permission from ref. 313. Copyright 2015, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim. (e) is reproduced with permission from ref. 315. Copyright 2011, Royal Society of Chemistry. Images in (f) are adapted with permission from ref. 319. Copyright 2008, American Institute of Physics. | ||
MR fluid exhibits tunable rheological characteristics due to the formation of chains/columns under a magnetic field. To display the MR effect, the magnetic particles should be large enough (on the order of 100 nm to 10 μm) to dominate over the effect of Brownian motion, different from those in ferrofluid with size smaller than 10 nm.296 Despite the unique characteristics of MR fluid, few applications of MR fluid to droplet generation were reported in the literature. Although it is weak, the MR effect exists in ferrofluid under certain circumstances. In droplet generation with the dispersed phase being water-based ferrofluid containing Fe3O4 nanoparticles (average size: 100 nm),241 the nanoparticles align to form chain-like structures along the direction of the magnetic field (Fig. 8c). Ferrofluid droplets with magnetically increased viscosity are larger than water droplets with lower viscosity.241 However, the MR effect is limited by the small particle size and counteracted by the magnetic drag that tends to decrease the droplet size.
Thermal control exploits the dependence of fluid viscosity and interfacial tension on temperature. The microfluidic device is heated by microheaters297 or heat exchangers.300 The resultant droplet size D(T) is a function of the combined effect of temperature-dependent viscosity and interfacial tension:297,300
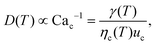 | (55) |
Besides water, water-based nanofluid droplet generation by thermal control has been investigated in both flow-focusing301 and T-junction302,303 configurations. In flow-focusing geometry, water and nanofluid droplet formation exhibit similar characteristics at different temperatures.301 In T-junctions, however, the size of the water droplet can be either larger or smaller than that of the nanofluid droplet depending on the channel dimension and flow rate ratio.302,303 Moreover, the shape of the nanoparticle impacts the dependence of droplet size on temperature. The droplet size increases with increasing temperature for nanofluids with spherical-shaped nanoparticles, but decreases for nanofluids with cylindrical-shaped nanoparticles.302 The underlying mechanism is unclear yet.
Different from the above studies with both continuous and dispersed fluids heated, heating the dispersed phase exclusively can also be able to tune the droplet size. Yeh et al.304 reported the generation of uniform gelatin emulsions (CV <5%) by heating the gelatin phase. When the temperature is over 25 °C by heating, the gelatin transforms from a gel to an aqueous solution with decreased viscosity. The viscosity decrease is responsible for the hastened release of the gelatin droplet, which reduces the continuous phase supply during the formation of each droplet and renders the droplet larger.304
Thermal control can be categorized into uniform and non-uniform heating. In uniform heating, the heating region covers the entire liquid–liquid interface by which the interfacial tension is tuned homogeneously by temperature in the absence of interfacial tension gradient. In this situation, droplet size is controlled by eqn (55), as we have discussed. In contrast, non-uniform heating involves locally heating part of the liquid–liquid interface and producing a thermal gradient. The thermal gradient gives rise to a gradient of interfacial tension that generates Marangoni stress (tangential stress along the liquid–liquid interface. The Marangoni stress, in turn, induces an interfacial flow that affects the droplet formation. In the simulation by Suryo and Basaran,305 heating the liquid–nozzle contact line gave rise to droplet generation owing to the competition between Marangoni stress and capillary pressure. Moreover, in a T-junction configuration, Miralles et al.306 demonstrated the control over droplet size and generation frequency by heating the dispersed entrance of the junction.
In optical control involving laser heating, the laser beam is focused through a microscope objective, locally heating the centerline of the flow downstream of the junction. A dye (a fluorescein for example) is added to the dispersed aqueous phase to mediate laser absorption.307–309 In the presence of Marangoni stress, dispersed bubbles and/or droplets would be forced to migrate with velocity um. Recent experiments suggested that the migration velocity um is proportional to the product of the channel width w and the mean temperature gradient 〈∇T〉 for aqueous droplets in confined rectangular microchannels:309
um![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∝ ∝![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w〈∇T〉, w〈∇T〉, | (56) |
Laser-heating-mediated droplet generation has been demonstrated in both dripping307–309 and jetting310,311 flows, and in both flow-focusing307 and T-junction308 microchannels. In dripping regime, the advancing water–oil interface is blocked at the laser heating spot once the heating power exceeds the threshold, in which case the migration velocity um is larger than the velocity of the droplet imposed by the basic flow.309 The net force exerted on the droplet due to the Marangoni effect is theoretically307 and experimentally312 estimated to be of the order ∼0.1 μN, a sufficiently large force accounting for the blocking. For constant-pressure-driven basic flow, the length of the droplet with laser blocking (Lblock) is shorter than that of the unblocked droplet (L0), while for the constant-flow-rate-driven case, Lblock is larger than L0 and proportional to blocking time τb:309
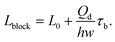 | (57) |
The difference in droplet size variation arises from the different dynamics of neck width evolution. During blocking, the neck width thins exponentially but increases linearly with time at the constant-pressure and constant-flow-rate case, respectively.309
In jetting regime, the interface of the jet is deformed by the Marangoni stress.310 The orientation of the deformation is predicted by the following dimensionless ratio A:310
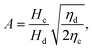 | (58) |
In electrical control employing electrochemical and electrocapillary effects,313 the liquid metal EGaIn (75% gallium, 25% indium) and glycerol–NaOH solution are used as the dispersed and continuous phase, respectively. The voltage is applied by connecting the anode and the cathode to the liquid metal and glycerol–NaOH solution inlet tubes, respectively, or vice versa. Either case can lower the interfacial tension between the two fluids. In the application of a positive (oxidative) bias to the liquid metal phase, electrochemically induced formation of a surface oxide acts as a surfactant and lowers the interfacial tension. In the opposite case where the liquid metal phase is negatively charged, the interfacial tension is decreased due to electrocapillary effect. As such, the droplet size decreases with applied voltage in both cases (Fig. 11d) owing to the increase in capillary number Cac. The size decrease from electrochemical effect is in a larger range than that from electrocapillary effect (Fig. 11d). Different from DC voltage that produces uniform droplets, low-frequency AC control demonstrates its ability to generate sequences of droplets with various sizes. The size variation originates from the varying magnitude of the voltage.
In electrical control using the EW effect, high-frequency AC is applied316 to change the wetting state of the microchannel substrate (Fig. 11f). Under applied voltage Ue, no droplet is generated until the dispersed pressure Pd exceeds an onset value 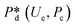 316,317
316,317
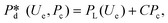 | (59) |
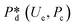 thus decrease with the increase in voltage Ue.316,317 With appropriate design of EW control, it is even possible to have negative values of Rh and PL(Ue).318 Consequently, spontaneous imbibition
thus decrease with the increase in voltage Ue.316,317 With appropriate design of EW control, it is even possible to have negative values of Rh and PL(Ue).318 Consequently, spontaneous imbibition 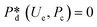 of the dispersed fluid into the microchannel can be achieved.318
of the dispersed fluid into the microchannel can be achieved.318
Three regimes of droplet generation in EW have been identified: dripping, tip-streaming and conical spray (Fig. 11f).319 Dripping occurs when the dispersed pressure Pd is relatively high, while tip-streaming and conical spray occur at intermediate Pd (at low Pd, no droplet generation). Compared with the tip-streaming, the conical spray occurs at a higher voltage where droplets are charged and repulse each other. While the size of generated droplets is comparable to the dimension of the orifice in dripping regime, they can be smaller than 10 μm in diameter in tip-streaming and conical spray regimes. Generally, the droplet size increases monotonically with increasing Pd.319 Nevertheless, the influence of applied voltage is complicated. When the continuous-phase viscous force (∼ηcuc/L) is weak (e.g., low Pc) compared with the electrostatic force (∼εcE2), the droplet size increases with increasing voltage Ue;317 when the viscous force is comparable to electrostatic force, the droplet size is nearly constant as Ue increases,317,319 but the frequency of droplet generation can be varied by one order of magnitude.317 The latter offers possible on-demand generation of droplets.320
6. Concluding remarks
This review is on fundamentals of passive and active generation of microfluidic droplets. Five fundamental modes of droplet generation, squeezing, dripping, jetting, tip-streaming, and tip-multi-breaking, are identified in passive generation. Each of them has its unique characteristics owing to distinct flow instabilities. Suppression of capillary instability by confinement primarily leads to the superior control and monodispersity of droplet size in the squeezing regime. Dripping, from an absolute flow instability that exhibits intrinsic oscillations, prevents external noises, thus producing monodisperse droplets as well. Convectively unstable flows that amplify perturbations of various frequencies render, on the other hand, droplets non-uniform in the jetting regime. Tip-streaming mode enables droplet microfluidics to produce droplets of size (down to submicrometer-scale) unrestricted by the characteristic length scale of devices. The periodic oscillation of the globally unstable tip offers precise control over droplet size distribution in tip-multi-breaking mode. A deep understanding regarding the effects of viscous, inertial and capillary forces and governing dimensionless parameters (e.g., capillary and Weber numbers) is critical for effective production of droplets with the desired outcome.Active droplet generation is achieved by incorporating additional components into microfluidic systems. The state-of-the-art techniques mainly apply electrical, magnetic, centrifugal, optical, thermal and mechanical methods, by which electrical, magnetic and centrifugal forces are introduced, and the flow, viscosity, interfacial tension, channel wettability and fluid density are varied. In principle, any approach that could affect interfacial force balance by applying external forces and/or modifying intrinsic viscous, inertial and capillary forces is capable of actively controlling droplet generation. Based on this speculation, new techniques for active control can be developed, for example using magnetorheological effect296 to tune viscosity, thermo-sensitive surfactant (such as diethylhexyl sodium sulphosuccinate322) to tune interfacial tension, and magnetowetting effect296 to tune channel wettability. Active control, therefore, offers additional flexibility and a tool in manipulating droplet formation.
Several outstanding issues remain to be resolved in order to produce droplets precisely and effectively. In passive generation, it is essential to design a system that enables a stable tip-streaming over a long period of time. As it occurs at quite low flow rate ratio (φ ≪ 1), tip-streaming is stable typically in less than several minutes before being destabilized by the variation in flow rate from syringe pumps. Using constant-pressure-driven flows in 3D devices is beneficial for the stabilization.12 Further studies of tip-multi-breaking dynamics are required to produce digital droplets with precise inter-correlation and thus develop novel applications of droplet microfluidics. For active droplet generation, one of the current challenges is to miniaturize and parallelize the system. In addition, most microfluidic chips with active components suffer from complicity in fabrication. Compared with the on-chip integration (e.g., electrodes, microheaters, piezoelectric actuators), the off-chip-actuated devices are easier to fabricate. Moreover, in the on-demand droplet generation, limited systems are able to produce high-throughput (>kHz) monodisperse (CV <5%) droplets in a wide range of tunable volumes (e.g., from femtolitre-scale to nanolitre-scale). This requires the smart design of microfluidic junctions and development of fast-responding actuation. The pulse laser-driven droplet generation254 and piezoelectric dispenser267 appear promising. The delivery of the promising potential of droplet microfluidics relies on our fundamental understanding of the mechanisms responsible for and the development of effective techniques for droplet generation.
Acknowledgements
The financial support from the Research Grants Council of Hong Kong (GRF 17237316, 17211115, 17207914 and 717613E) and the University of Hong Kong (URC 201511159108, 201411159074 and 201311159187) is gratefully acknowledged. The work is also supported in part by the Zhejiang Provincial, Hangzhou Municipal, and Lin'an County Governments.References
- S. Y. Teh, R. Lin, L. H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 Search PubMed.
- C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045 Search PubMed.
- S. S. Datta, A. Abbaspourrad, E. Amstad, J. Fan, S.-H. Kim, M. Romanowsky, H. C. Shum, B. Sun, A. S. Utada, M. Windbergs, S. Zhou and D. A. Weitz, Adv. Mater., 2014, 26, 2205–2218 Search PubMed.
- T. Y. Lee, T. M. Choi, T. S. Shim, R. A. M. Frijns and S.-H. Kim, Lab Chip, 2016, 16, 3415–3440 Search PubMed.
- T. T. Kong, J. Wu, K. W. K. Yeung, M. K. T. To, H. C. Shum and L. Q. Wang, Biomicrofluidics, 2013, 7, 044128 Search PubMed.
- T. T. Kong, J. Wu, M. To, K. W. K. Yeung, H. C. Shum and L. Q. Wang, Biomicrofluidics, 2012, 6, 034104 Search PubMed.
- T. T. Kong, Z. Liu, Y. Song, L. Q. Wang and H. C. Shum, Soft Matter, 2013, 9, 9780–9784 Search PubMed.
- J. Wu, T. T. Kong, K. W. K. Yeung, H. C. Shum, K. M. C. Cheung, L. Q. Wang and M. K. T. To, Acta Biomater., 2013, 9, 7410–7419 Search PubMed.
- Z. X. Kang, T. T. Kong, L. Y. Lei, P. A. Zhu, X. W. Tian and L. Q. Wang, J. Micromech. Microeng., 2016, 26, 075011 Search PubMed.
- J. Nunes, S. Tsai, J. Wan and H. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002 Search PubMed.
- T. D. Martz, D. Bardin, P. S. Sheeran, A. P. Lee and P. A. Dayton, Small, 2012, 8, 1876–1879 Search PubMed.
- W.-C. Jeong, J.-M. Lim, J.-H. Choi, J.-H. Kim, Y.-J. Lee, S.-H. Kim, G. Lee, J.-D. Kim, G.-R. Yi and S.-M. Yang, Lab Chip, 2012, 12, 1446–1453 Search PubMed.
- Y. Zeng, M. Shin and T. Wang, Lab Chip, 2013, 13, 267–273 Search PubMed.
- P. Garstecki, H. A. Stone and G. M. Whitesides, Phys. Rev. Lett., 2005, 94, 164501 Search PubMed.
- A. S. Utada, A. Fernandez-Nieves, H. A. Stone and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 094502 Search PubMed.
- R. Suryo and O. A. Basaran, Phys. Fluids, 2006, 18, 082102 Search PubMed.
- P. A. Zhu, T. T. Kong, Z. X. Kang, X. W. Tian and L. Q. Wang, Sci. Rep., 2015, 5, 11102 Search PubMed.
- B.-U. Moon, S. G. Jones, D. K. Hwang and S. S. H. Tsai, Lab Chip, 2015, 15, 2437–2444 Search PubMed.
- Y. Li, M. Jain, Y. Ma and K. Nandakumar, Soft Matter, 2015, 11, 3884–3899 Search PubMed.
- D. J. Collins, A. Neild, A. deMello, A.-Q. Liu and Y. Ai, Lab Chip, 2015, 15, 3439–3459 Search PubMed.
- G. Christopher and S. Anna, J. Phys. D: Appl. Phys., 2007, 40, R319–R336 Search PubMed.
- C.-X. Zhao and A. P. J. Middelberg, Chem. Eng. Sci., 2011, 66, 1394–1411 Search PubMed.
- R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2012, 75, 016601 Search PubMed.
- S. L. Anna, Annu. Rev. Fluid Mech., 2016, 48, 285–309 Search PubMed.
- Z. Z. Chong, S. H. Tan, A. M. Gañán-Calvo, S. B. Tor, N. H. Loh and N.-T. Nguyen, Lab Chip, 2016, 16, 35–58 Search PubMed.
- A. M. Gañán-Calvo, Phys. Rev. Lett., 1998, 80, 285 Search PubMed.
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 Search PubMed.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977 Search PubMed.
- G. Batchelor, An Introduction to Fluid Dynamics, Cambridge University Press, Cambridge, 1967 Search PubMed.
- P. Garstecki, M. J. Fuerstman and G. M. Whitesides, Phys. Rev. Lett., 2005, 94, 234502 Search PubMed.
- J. R. Lister and H. A. Stone, Phys. Fluids, 1998, 10, 2758–2764 Search PubMed.
- B. Dollet, W. van Hoeve, J.-P. Raven, P. Marmottant and M. Versluis, Phys. Rev. Lett., 2008, 100, 034504 Search PubMed.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163 Search PubMed.
- J. Xu, S. Li, J. Tan, Y. Wang and G. Luo, AIChE J., 2006, 52, 3005–3010 Search PubMed.
- J. H. Xu, G. S. Luo, S. W. Li and G. G. Chen, Lab Chip, 2006, 6, 131–136 Search PubMed.
- L. Q. Wang, Y. X. Zhang and L. Cheng, Chaos, Solitons Fractals, 2009, 39, 1530–1537 Search PubMed.
- K. Khoshmanesh, A. Almansouri, H. Albloushi, P. Yi, R. Soffe and K. Kalantar-zadeh, Sci. Rep., 2015, 5, 9942 Search PubMed.
- A. R. Abate and D. A. Weitz, Lab Chip, 2011, 11, 1713–1716 Search PubMed.
- L. Ménétrier-Deremble and P. Tabeling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 035303 Search PubMed.
- A. Abate, A. Poitzsch, Y. Hwang, J. Lee, J. Czerwinska and D. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 026310 Search PubMed.
- L. Shui, F. Mugele, A. van den Berg and J. C. T. Eijkel, Appl. Phys. Lett., 2008, 93, 153113 Search PubMed.
- L. Shui, A. van den Berg and J. C. T. Eijkel, J. Appl. Phys., 2009, 106, 124305 Search PubMed.
- M. L. Steegmans, K. G. Schroën and R. M. Boom, Langmuir, 2009, 25, 3396–3401 Search PubMed.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 7336–7356 Search PubMed.
- B. Zheng, J. D. Tice and R. F. Ismagilov, Anal. Chem., 2004, 76, 4977–4982 Search PubMed.
- Y. X. Zhang and L. Q. Wang, in Advances in Transport Phenomena 2010, Springer-Verlag, Berlin Heidelberg, 2011, pp. 171–294 Search PubMed.
- L. Frenz, J. Blouwolff, A. D. Griffiths and J.-C. Baret, Langmuir, 2008, 24, 12073–12076 Search PubMed.
- R. Lin, J. S. Fisher, M. G. Simon and A. P. Lee, Biomicrofluidics, 2012, 6, 024103 Search PubMed.
- M. Rhee, P. Liu, R. J. Meagher, Y. K. Light and A. K. Singh, Biomicrofluidics, 2014, 8, 034112 Search PubMed.
- Y. Ding, X. C. i Solvas and A. deMello, Analyst, 2015, 140, 414–421 Search PubMed.
- U. Tangen, A. Sharma, P. Wagler and J. S. McCaskill, Biomicrofluidics, 2015, 9, 014119 Search PubMed.
- T. Nisisako and T. Torii, Lab Chip, 2008, 8, 287–293 Search PubMed.
- D. Link, S. L. Anna, D. Weitz and H. Stone, Phys. Rev. Lett., 2004, 92, 054503 Search PubMed.
- P. B. Umbanhowar, V. Prasad and D. A. Weitz, Langmuir, 2000, 16, 347–351 Search PubMed.
- A. Utada, L.-Y. Chu, A. Fernandez-Nieves, D. Link, C. Holtze and D. Weitz, MRS Bull., 2007, 32, 702–708 Search PubMed.
- J. R. Anderson, D. T. Chiu, H. Wu, O. Schueller and G. M. Whitesides, Electrophoresis, 2000, 21, 27–40 Search PubMed.
- C. Cramer, P. Fischer and E. J. Windhab, Chem. Eng. Sci., 2004, 59, 3045–3058 Search PubMed.
- J. M. Gordillo, A. Sevilla and F. Campo-Cortés, J. Fluid Mech., 2014, 738, 335–357 Search PubMed.
- E. Castro-Hernández, V. Gundabala, A. Fernández-Nieves and J. M. Gordillo, New J. Phys., 2009, 11, 075021 Search PubMed.
- A. M. Gañán-Calvo and J. M. Gordillo, Phys. Rev. Lett., 2001, 87, 274501 Search PubMed.
- S. Takeuchi, P. Garstecki, D. B. Weibel and G. M. Whitesides, Adv. Mater., 2005, 17, 1067–1072 Search PubMed.
- L. Yobas, S. Martens, W.-L. Ong and N. Ranganathan, Lab Chip, 2006, 6, 1073–1079 RSC.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364 Search PubMed.
- A. Utada, E. Lorenceau, D. Link, P. Kaplan, H. Stone and D. Weitz, Science, 2005, 308, 537–541 Search PubMed.
- M. Hein, J.-B. Fleury and R. Seemann, Soft Matter, 2015, 11, 5246–5252 Search PubMed.
- E. M. Chan, A. P. Alivisatos and R. A. Mathies, J. Am. Chem. Soc., 2005, 127, 13854–13861 Search PubMed.
- C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 88, 024106 Search PubMed.
- M. Leman, F. Abouakil, A. D. Griffiths and P. Tabeling, Lab Chip, 2015, 15, 753–765 Search PubMed.
- B. Shen, J. Ricouvier, F. Malloggi and P. Tabeling, Adv. Sci., 2016, 3, 1600012 Search PubMed.
- F. Malloggi, N. Pannacci, R. Attia, F. Monti, P. Mary, H. Willaime, P. Tabeling, B. Cabane and P. Poncet, Langmuir, 2010, 26, 2369–2373 Search PubMed.
- L. Shui, A. van den Berg and J. C. Eijkel, Microfluid. Nanofluid., 2011, 11, 87–92 Search PubMed.
- L. Shui, E. Stefan Kooij, D. Wijnperle, A. van den Berg and J. C. T. Eijkel, Soft Matter, 2009, 5, 2708–2712 Search PubMed.
- J. Guzowski and P. Garstecki, Phys. Rev. Lett., 2015, 114, 188302 Search PubMed.
- K. C. van Dijke, G. Veldhuis, K. Schroën and R. M. Boom, AIChE J., 2010, 56, 833–836 Search PubMed.
- V. Chokkalingam, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2008, 93, 254101 Search PubMed.
- C. Cohen, R. Giles, V. Sergeyeva, N. Mittal, P. Tabeling, D. Zerrouki, J. Baudry, J. Bibette and N. Bremond, Microfluid. Nanofluid., 2014, 17, 959–966 Search PubMed.
- N. Mittal, C. Cohen, J. Bibette and N. Bremond, Phys. Fluids, 2014, 26, 082109 Search PubMed.
- R. Dangla, S. C. Kayi and C. N. Baroud, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 853–858 Search PubMed.
- K. van Dijke, G. Veldhuis, K. Schroen and R. Boom, Lab Chip, 2009, 9, 2824–2830 Search PubMed.
- K. van Dijke, R. de Ruiter, K. Schroen and R. Boom, Soft Matter, 2010, 6, 321–330 Search PubMed.
- F. Dutka, A. S. Opalski and P. Garstecki, Lab Chip, 2016, 16, 2044–2049 Search PubMed.
- F. Schuler, F. Schwemmer, M. Trotter, S. Wadle, R. Zengerle, F. von Stetten and N. Paust, Lab Chip, 2015, 15, 2759–2766 Search PubMed.
- F. Schuler, N. Paust, R. Zengerle and F. von Stetten, Micromachines, 2015, 6, 1180–1188 Search PubMed.
- F. Schuler, M. Trotter, M. Geltman, F. Schwemmer, S. Wadle, E. Dominguez-Garrido, M. Lopez, C. Cervera-Acedo, P. Santibanez, F. von Stetten, R. Zengerle and N. Paust, Lab Chip, 2016, 16, 208–216 Search PubMed.
- S. Kahkeshani and D. Di Carlo, Lab Chip, 2016, 16, 2474–2480 Search PubMed.
- G. T. Vladisavljević, I. Kobayashi and M. Nakajima, Microfluid. Nanofluid., 2012, 13, 151–178 Search PubMed.
- G. T. Vladisavljević, N. Khalid, M. A. Neves, T. Kuroiwa, M. Nakajima, K. Uemura, S. Ichikawa and I. Kobayashi, Adv. Drug Delivery Rev., 2013, 65, 1626–1663 Search PubMed.
- I. Kobayashi, Y. Wada, K. Uemura and M. Nakajima, Microfluid. Nanofluid., 2010, 8, 255–262 Search PubMed.
- Y. Kikuchi, H. Ohki, T. Kaneko and K. Sato, Biorheology, 1989, 26, 1055 Search PubMed.
- T. Kawakatsu, Y. Kikuchi and M. Nakajima, J. Am. Oil Chem. Soc., 1997, 74, 317–321 Search PubMed.
- T. Kawakatsu, H. Komori, M. Nakajima, Y. Kikuchi and T. Yonemoto, J. Chem. Eng. Jpn., 1999, 32, 241–244 Search PubMed.
- T. Kawakatsu, G. Trägårdh, Y. Kikuchi, M. Nakajima, H. Komori and T. Yonemoto, J. Surfactants Deterg., 2000, 3, 295–302 Search PubMed.
- I. Kobayashi, M. Nakajima, K. Chun, Y. Kikuchi and H. Fujita, AIChE J., 2002, 48, 1639–1644 Search PubMed.
- I. Kobayashi, S. Mukataka and M. Nakajima, Langmuir, 2005, 21, 7629–7632 Search PubMed.
- S. Sugiura, T. Oda, Y. Izumida, Y. Aoyagi, M. Satake, A. Ochiai, N. Ohkohchi and M. Nakajima, Biomaterials, 2005, 26, 3327–3331 Search PubMed.
- I. Kobayashi, Y. Murayama, T. Kuroiwa, K. Uemura and M. Nakajima, Microfluid. Nanofluid., 2009, 7, 107–119 Search PubMed.
- I. Kobayashi, S. Mukataka and M. Nakajima, J. Colloid Interface Sci., 2004, 279, 277–280 Search PubMed.
- T. Nakashima, M. Shimizu and M. Kukizaki, Key Eng. Mater., 1991, 61–62, 513–516 Search PubMed.
- T. Nakashima, M. Shimizu and M. Kukizaki, Adv. Drug Delivery Rev., 2000, 45, 47–56 Search PubMed.
- K. Suzuki, I. Shuto and Y. Hagura, Food Sci. Technol. Int., Tokyo, 1996, 2, 43–47 Search PubMed.
- M. Yasuda, T. Goda, H. Ogino, W. R. Glomm and H. Takayanagi, J. Colloid Interface Sci., 2010, 349, 392–401 Search PubMed.
- S. R. Kosvintsev, G. Gasparini, R. G. Holdich, I. W. Cumming and M. T. Stillwell, Ind. Eng. Chem. Res., 2005, 44, 9323–9330 Search PubMed.
- M. M. Dragosavac, M. N. Sovilj, S. R. Kosvintsev, R. G. Holdich and G. T. Vladisavljević, J. Membr. Sci., 2008, 322, 178–188 Search PubMed.
- G. T. Vladisavljević and R. A. Williams, J. Colloid Interface Sci., 2006, 299, 396–402 Search PubMed.
- M. S. Manga, O. J. Cayre, R. A. Williams, S. Biggs and D. W. York, Soft Matter, 2012, 8, 1532–1538 Search PubMed.
- J. Zhu and D. Barrow, J. Membr. Sci., 2005, 261, 136–144 Search PubMed.
- R. G. Holdich, M. M. Dragosavac, G. T. Vladisavljević and S. R. Kosvintsev, Ind. Eng. Chem. Res., 2010, 49, 3810–3817 Search PubMed.
- N. A. Wagdare, A. T. Marcelis, O. B. Ho, R. M. Boom and C. J. van Rijn, J. Membr. Sci., 2010, 347, 1–7 Search PubMed.
- G. T. Vladisavljević and H. Schubert, J. Dispersion Sci. Technol., 2003, 24, 811–819 Search PubMed.
- P. J. Dowding, J. W. Goodwin and B. Vincent, Colloids Surf., A, 2001, 180, 301–309 Search PubMed.
- X. Liu, D. Bao, W. Xue, Y. Xiong, W. Yu, X. Yu, X. Ma and Q. Yuan, J. Appl. Polym. Sci., 2003, 87, 848–852 Search PubMed.
- I. Kobayashi, M. Yasuno, S. Iwamoto, A. Shono, K. Satoh and M. Nakajima, Colloids Surf., A, 2002, 207, 185–196 Search PubMed.
- L. Giorno, N. Li and E. Drioli, J. Membr. Sci., 2003, 217, 173–180 Search PubMed.
- M. M. Dragosavac, G. T. Vladisavljević, R. G. Holdich and M. T. Stillwell, Langmuir, 2011, 28, 134–143 Search PubMed.
- G. T. Vladisavljević, Adv. Colloid Interface Sci., 2015, 225, 53–87 Search PubMed.
- G. De Luca, F. P. Di Maio, A. Di Renzo and E. Drioli, Chem. Eng. Process., 2008, 47, 1150–1158 Search PubMed.
- N. C. Christov, K. D. Danov, D. K. Danova and P. A. Kralchevsky, Langmuir, 2008, 24, 1397–1410 Search PubMed.
- A. Timgren, G. Trägårdh and C. Trägårdh, Chem. Eng. Res. Des., 2010, 88, 229–238 Search PubMed.
- A. Abrahamse, A. Van der Padt, R. Boom and W. De Heij, AIChE J., 2001, 47, 1285–1291 Search PubMed.
- M. Rayner, G. Trägårdh, C. Trägårdh and P. Dejmek, J. Colloid Interface Sci., 2004, 279, 175–185 Search PubMed.
- E. Amstad, S. Datta and D. Weitz, Lab Chip, 2014, 14, 705–709 RSC.
- L. Wu, G.-P. Li, W. Xu and M. Bachman, Appl. Phys. Lett., 2006, 89, 144106 Search PubMed.
- X. Huang, W. Hui, C. Hao, W. Yue, M. Yang, Y. Cui and Z. Wang, Small, 2014, 10, 758–765 Search PubMed.
- Y. X. Zhang and L. Q. Wang, Nanoscale Microscale Thermophys. Eng., 2009, 13, 228–242 Search PubMed.
- T. Ward, M. Faivre, M. Abkarian and H. A. Stone, Electrophoresis, 2005, 26, 3716–3724 Search PubMed.
- P. Garstecki, I. Gitlin, W. DiLuzio, G. M. Whitesides, E. Kumacheva and H. A. Stone, Appl. Phys. Lett., 2004, 85, 2649–2651 Search PubMed.
- S. L. Anna and H. C. Mayer, Phys. Fluids, 2006, 18, 121512 Search PubMed.
- J. D. Tice, A. D. Lyon and R. F. Ismagilov, Anal. Chim. Acta, 2004, 507, 73–77 Search PubMed.
- P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446 Search PubMed.
- M. De Menech, P. Garstecki, F. Jousse and H. Stone, J. Fluid Mech., 2008, 595, 141–161 Search PubMed.
- M. Zagnoni, J. Anderson and J. M. Cooper, Langmuir, 2010, 26, 9416–9422 Search PubMed.
- J. Fan, Y. X. Zhang and L. Q. Wang, Nano, 2010, 5, 175–184 CrossRef CAS.
- P. Guillot, A. Colin, A. S. Utada and A. Ajdari, Phys. Rev. Lett., 2007, 99, 104502 Search PubMed.
- B. R. Benson, H. A. Stone and R. K. Prud'homme, Lab Chip, 2013, 13, 4507–4511 Search PubMed.
- J. Sivasamy, T.-N. Wong, N.-T. Nguyen and L. T.-H. Kao, Microfluid. Nanofluid., 2011, 11, 1–10 Search PubMed.
- A. R. Abate, P. Mary, V. van Steijn and D. A. Weitz, Lab Chip, 2012, 12, 1516–1521 Search PubMed.
- P. A. Romero and A. R. Abate, Lab Chip, 2012, 12, 5130–5132 Search PubMed.
- J. Xu, S. Li, J. Tan and G. Luo, Microfluid. Nanofluid., 2008, 5, 711–717 Search PubMed.
- S. van der Graaf, T. Nisisako, C. Schroen, R. van der Sman and R. Boom, Langmuir, 2006, 22, 4144–4152 Search PubMed.
- J. D. Tice, H. Song, A. D. Lyon and R. F. Ismagilov, Langmuir, 2003, 19, 9127–9133 Search PubMed.
- A. Gupta and R. Kumar, Microfluid. Nanofluid., 2010, 8, 799–812 Search PubMed.
- Y. Ba, H. Liu, J. Sun and R. Zheng, Int. J. Heat Mass Transfer, 2015, 90, 931–947 Search PubMed.
- H. Liu and Y. Zhang, J. Appl. Phys., 2009, 106, 034906 Search PubMed.
- V. van Steijn, C. R. Kleijn and M. T. Kreutzer, Phys. Rev. Lett., 2009, 103, 214501 Search PubMed.
- V. van Steijn, M. T. Kreutzer and C. R. Kleijn, Chem. Eng. Sci., 2007, 62, 7505–7514 Search PubMed.
- V. van Steijn, C. R. Kleijn and M. T. Kreutzer, Lab Chip, 2010, 10, 2513–2518 Search PubMed.
- X. Chen, T. Glawdel, N. Cui and C. L. Ren, Microfluid. Nanofluid., 2015, 18, 1341–1353 Search PubMed.
- D. Funfschilling, H. Debas, H.-Z. Li and T. Mason, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 015301 Search PubMed.
- K. Xu, C. P. Tostado, J.-H. Xu, Y.-C. Lu and G.-S. Luo, Lab Chip, 2014, 14, 1357–1366 Search PubMed.
- W. Lan, S. Li and G. Luo, Chem. Eng. Sci., 2015, 134, 76–85 Search PubMed.
- H. Liu and Y. Zhang, Phys. Fluids, 2011, 23, 082101 Search PubMed.
- G. F. Christopher, N. N. Noharuddin, J. A. Taylor and S. L. Anna, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036317 Search PubMed.
- R. M. Erb, D. Obrist, P. W. Chen, J. Studer and A. R. Studart, Soft Matter, 2011, 7, 8757–8761 Search PubMed.
- Y. Liu and L. Yobas, Appl. Phys. Lett., 2015, 106, 174101 Search PubMed.
- J. Husny and J. J. Cooper-White, J. Non-Newtonian Fluid Mech., 2006, 137, 121–136 Search PubMed.
- Y. X. Zhang, J. Fan and L. Q. Wang, Curr. Nanosci., 2009, 5, 519–526 Search PubMed.
- A. Gupta, S. M. S. Murshed and R. Kumar, Appl. Phys. Lett., 2009, 94, 164107 Search PubMed.
- T. Fu, Y. Ma, D. Funfschilling, C. Zhu and H. Z. Li, Chem. Eng. Sci., 2010, 65, 3739–3748 Search PubMed.
- T. Glawdel, C. Elbuken and C. L. Ren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016323 Search PubMed.
- T. Glawdel, C. Elbuken and C. L. Ren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 016322 Search PubMed.
- A. Sauret and H. C. Shum, Int. J. Nonlinear Sci. Numer. Simul., 2012, 13, 351–362 Search PubMed.
- T. Cubaud and T. G. Mason, Phys. Fluids, 2008, 20, 053302 Search PubMed.
- S. Tomotika, Proc. R. Soc. London, Ser. A, 1935, 150, 322–337 Search PubMed.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1934, 146, 501–523 Search PubMed.
- H. A. Stone, Annu. Rev. Fluid Mech., 1994, 26, 65–102 Search PubMed.
- A. M. Gañán-Calvo, R. González-Prieto, P. Riesco-Chueca, M. A. Herrada and M. Flores-Mosquera, Nat. Phys., 2007, 3, 737–742 Search PubMed.
- O. A. Basaran and R. Suryo, Nat. Phys., 2007, 3, 679–680 Search PubMed.
- E. Castro-Hernández, F. Campo-Cortés and J. M. Gordillo, J. Fluid Mech., 2012, 698, 423–445 Search PubMed.
- A. G. Marín, F. Campo-Cortés and J. M. Gordillo, Colloids Surf., A, 2009, 344, 2–7 Search PubMed.
- J.-U. Shim, R. T. Ranasinghe, C. A. Smith, S. M. Ibrahim, F. Hollfelder, W. T. Huck, D. Klenerman and C. Abell, ACS Nano, 2013, 7, 5955–5964 Search PubMed.
- R. A. De Bruijn, Chem. Eng. Sci., 1993, 48, 277–284 Search PubMed.
- J. Janssen, A. Boon and W. Agterof, AIChE J., 1994, 40, 1929–1939 Search PubMed.
- J. Janssen, A. Boon and W. Agterof, AIChE J., 1997, 43, 1436–1447 Search PubMed.
- C. D. Eggleton, T.-M. Tsai and K. J. Stebe, Phys. Rev. Lett., 2001, 87, 048302 Search PubMed.
- M. Booty and M. Siegel, J. Fluid Mech., 2005, 544, 243–275 Search PubMed.
- W. Lee, L. M. Walker and S. L. Anna, Phys. Fluids, 2009, 21, 032103 Search PubMed.
- T. M. Moyle, L. M. Walker and S. L. Anna, Phys. Fluids, 2012, 24, 082110 Search PubMed.
- T. Ward, M. Faivre and H. A. Stone, Langmuir, 2010, 26, 9233–9239 Search PubMed.
- W. W. Zhang, Phys. Rev. Lett., 2004, 93, 184502 Search PubMed.
- J. Fernández de la Mora, Annu. Rev. Fluid Mech., 2007, 39, 217–243 Search PubMed.
- A. M. Gañán-Calvo and J. M. Montanero, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 066305 Search PubMed.
- A. M. Gañán-Calvo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 026304 Search PubMed.
- Y.-H. Tseng and A. Prosperetti, J. Fluid Mech., 2015, 776, 5–36 Search PubMed.
- P. A. Zhu, T. T. Kong, L. Y. Lei, X. W. Tian, Z. X. Kang and L. Q. Wang, Sci. Rep., 2016, 6, 21527 Search PubMed.
- P. Garstecki, M. J. Fuerstman and G. M. Whitesides, Nat. Phys., 2005, 1, 168–171 Search PubMed.
- M. Hashimoto and G. M. Whitesides, Small, 2010, 6, 1051–1059 Search PubMed.
- A. Evangelio, F. Campo-Cortes and J. M. Gordillo, J. Fluid Mech., 2015, 778, 653–668 Search PubMed.
- M. A. Herrada, A. M. Gañán-Calvo, A. Ojeda-Monge, B. Bluth and P. Riesco-Chueca, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 036323 Search PubMed.
- J. M. Montanero, N. Rebollo-Muñoz, M. A. Herrada and A. M. Gañán-Calvo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 036309 Search PubMed.
- E. J. Vega, J. M. Montanero, M. A. Herrada and A. M. Gañán-Calvo, Phys. Fluids, 2010, 22, 064105 Search PubMed.
- T. Si, F. Li, X.-Y. Yin and X.-Z. Yin, J. Fluid Mech., 2009, 629, 1–23 Search PubMed.
- J. E. Kreutz, T. Munson, T. Huynh, F. Shen, W. Du and R. F. Ismagilov, Anal. Chem., 2011, 83, 8158–8168 Search PubMed.
- F. Shen, B. Sun, J. E. Kreutz, E. K. Davydova, W. Du, P. L. Reddy, L. J. Joseph and R. F. Ismagilov, J. Am. Chem. Soc., 2011, 133, 17705–17712 Search PubMed.
- J. Guzowski, K. Gizynski, J. Gorecki and P. Garstecki, Lab Chip, 2016, 16, 764–772 Search PubMed.
- K. J. Humphry, A. Ajdari, A. Fernández-Nieves, H. A. Stone and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 056310 Search PubMed.
- D. Saeki, S. Sugiura, T. Kanamori, S. Sato, S. Mukataka and S. Ichikawa, Langmuir, 2008, 24, 13809–13813 Search PubMed.
- Z. Li, A. M. Leshansky, L. M. Pismen and P. Tabeling, Lab Chip, 2015, 15, 1023–1031 Search PubMed.
- R. Dangla, E. Fradet, Y. Lopez and C. N. Baroud, J. Phys. D: Appl. Phys., 2013, 46, 114003 CrossRef.
- M. Hein, S. Afkhami, R. Seemann and L. Kondic, Microfluid. Nanofluid., 2014, 18, 911–917 Search PubMed.
- J.-C. Baret, Lab Chip, 2012, 12, 422–433 Search PubMed.
- M. L. Steegmans, A. Warmerdam, K. G. Schroen and R. M. Boom, Langmuir, 2009, 25, 9751–9758 Search PubMed.
- J. H. Xu, P. F. Dong, H. Zhao, C. P. Tostado and G. S. Luo, Langmuir, 2012, 28, 9250–9258 Search PubMed.
- Y. Chen, G.-T. Liu, J.-H. Xu and G.-S. Luo, Chem. Eng. Sci., 2015, 132, 1–8 Search PubMed.
- Y. Chen, J.-H. Xu and G.-S. Luo, Chem. Eng. Sci., 2015, 138, 655–662 Search PubMed.
- K. Wang, Y. Lu, J. Xu and G. Luo, Langmuir, 2009, 25, 2153–2158 Search PubMed.
- K. Wang, L. Zhang, W. Zhang and G. Luo, Langmuir, 2016, 32, 3174–3185 Search PubMed.
- J.-C. Baret, F. Kleinschmidt, A. El Harrak and A. D. Griffiths, Langmuir, 2009, 25, 6088–6093 Search PubMed.
- Y.-C. Liao, E. I. Franses and O. A. Basaran, Phys. Fluids, 2006, 18, 022101 Search PubMed.
- M. R. de Saint Vincent, J. Petit, M. Aytouna, J.-P. Delville, D. Bonn and H. Kellay, J. Fluid Mech., 2012, 692, 499–510 Search PubMed.
- M. Roché, M. Aytouna, D. Bonn and H. Kellay, Phys. Rev. Lett., 2009, 103, 264501 Search PubMed.
- Q. Xu, Y.-C. Liao and O. A. Basaran, Phys. Rev. Lett., 2007, 98, 054503 Search PubMed.
- F. Jin, N. R. Gupta and K. J. Stebe, Phys. Fluids, 2006, 18, 022103 Search PubMed.
- N. M. Kovalchuk, E. Nowak and M. J. H. Simmons, Langmuir, 2016, 32, 5069–5077 Search PubMed.
- N.-T. Nguyen, S. Lassemono, F. A. Chollet and C. Yang, IEEE Sens. J., 2007, 7, 692–697 Search PubMed.
- K. Muijlwijk, E. Hinderink, D. Ershov, C. Berton-Carabin and K. Schroën, J. Colloid Interface Sci., 2016, 470, 71–79 Search PubMed.
- T. Glawdel and C. L. Ren, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 026308 Search PubMed.
- X. Wang, A. Riaud, K. Wang and G. Luo, Microfluid. Nanofluid., 2015, 18, 503–512 Search PubMed.
- W. Lan, C. Wang, X. Guo, S. Li and G. Luo, AIChE J., 2016, 62, 2542–2549 Search PubMed.
- J. M. Park, M. Hulsen and P. Anderson, Eur. Phys. J.: Spec. Top., 2013, 222, 199–210 Search PubMed.
- P. Huerre and P. A. Monkewitz, Annu. Rev. Fluid Mech., 1990, 22, 473–537 Search PubMed.
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 Search PubMed.
- P. Guillot, A. Colin and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016307 Search PubMed.
- M. A. Herrada, A. M. Gañán-Calvo and P. Guillot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 046312 Search PubMed.
- A. M. Gañán-Calvo and P. Riesco-Chueca, J. Fluid Mech., 2006, 553, 75–84 Search PubMed.
- A. S. Utada, A. Fernandez-Nieves, J. M. Gordillo and D. A. Weitz, Phys. Rev. Lett., 2008, 100, 014502 Search PubMed.
- J. Chomaz, P. Huerre and L. Redekopp, Phys. Rev. Lett., 1988, 60, 25 Search PubMed.
- D. R. Link, E. Grasland-Mongrain, A. Duri, F. Sarrazin, Z. Cheng, G. Cristobal, M. Marquez and D. A. Weitz, Angew. Chem., Int. Ed., 2006, 45, 2556–2560 Search PubMed.
- S. H. Tan, B. Semin and J.-C. Baret, Lab Chip, 2014, 14, 1099–1106 Search PubMed.
- M. He, J. S. Kuo and D. T. Chiu, Appl. Phys. Lett., 2005, 87, 031916 Search PubMed.
- P. He, H. Kim, D. Luo, M. Marquez and Z. Cheng, Appl. Phys. Lett., 2010, 96, 174103 Search PubMed.
- H. Kim, D. Luo, D. Link, D. A. Weitz, M. Marquez and Z. Cheng, Appl. Phys. Lett., 2007, 91, 133106 Search PubMed.
- C.-H. Yeh, M.-H. Lee and Y.-C. Lin, Microfluid. Nanofluid., 2012, 12, 475–484 Search PubMed.
- M. He, J. S. Kuo and D. T. Chiu, Langmuir, 2006, 22, 6408–6413 Search PubMed.
- S. H. Tan, F. Maes, B. Semin, J. Vrignon and J.-C. Baret, Sci. Rep., 2014, 4, 4787 Search PubMed.
- E. Castro-Hernández, P. García-Sánchez, J. Alzaga-Gimeno, S. H. Tan, J.-C. Baret and A. Ramos, Biomicrofluidics, 2016, 10, 043504 Search PubMed.
- E. Castro-Hernández, P. García-Sánchez, S. H. Tan, A. M. Gañán-Calvo, J.-C. Baret and A. Ramos, Microfluid. Nanofluid., 2015, 19, 787–794 Search PubMed.
- S.-H. Tan, N.-T. Nguyen, L. Yobas and T. G. Kang, J. Micromech. Microeng., 2010, 20, 045004 Search PubMed.
- Y. Wu, T. Fu, Y. Ma and H. Z. Li, Soft Matter, 2013, 9, 9792–9798 Search PubMed.
- J. Liu, S.-H. Tan, Y. F. Yap, M. Y. Ng and N.-T. Nguyen, Microfluid. Nanofluid., 2011, 11, 177–187 Search PubMed.
- S. H. Tan and N.-T. Nguyen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 036317 Search PubMed.
- Q. Yan, S. Xuan, X. Ruan, J. Wu and X. Gong, Microfluid. Nanofluid., 2015, 19, 1377–1384 Search PubMed.
- C.-P. Lee, T.-S. Lan and M.-F. Lai, J. Appl. Phys., 2014, 115, 17B527 Search PubMed.
- J. Liu, Y. F. Yap and N.-T. Nguyen, Phys. Fluids, 2011, 23, 072008 Search PubMed.
- O. Strohmeier, M. Keller, F. Schwemmer, S. Zehnle, D. Mark, F. von Stetten, R. Zengerle and N. Paust, Chem. Soc. Rev., 2015, 44, 6187–6229 RSC.
- M. Madou, J. Zoval, G. Jia, H. Kido, J. Kim and N. Kim, Annu. Rev. Biomed. Eng., 2006, 8, 601–628 Search PubMed.
- J. Ducrée, S. Haeberle, S. Lutz, S. Pausch, F. Von Stetten and R. Zengerle, J. Micromech. Microeng., 2007, 17, S103–S115 Search PubMed.
- D. Mark, S. Haeberle, R. Zengerle, J. Ducree and G. T. Vladisavljević, J. Colloid Interface Sci., 2009, 336, 634–641 Search PubMed.
- K. Maeda, H. Onoe, M. Takinoue and S. Takeuchi, Adv. Mater., 2012, 24, 1340–1346 Search PubMed.
- S. Haeberle, L. Naegele, R. Burger, F. v. Stetten, R. Zengerle and J. Ducrée, J. Microencapsulation, 2008, 25, 267–274 Search PubMed.
- S. Haeberle, R. Zengerle and J. Ducrée, Microfluid. Nanofluid., 2007, 3, 65–75 Search PubMed.
- D. Chakraborty and S. Chakraborty, Appl. Phys. Lett., 2010, 97, 234103 Search PubMed.
- S. Kar, S. Joshi, K. Chaudhary, T. K. Maiti and S. Chakraborty, Appl. Phys. Lett., 2015, 107, 244101 Search PubMed.
- Y. Ren and W. W. F. Leung, Micromachines, 2016, 7, 17 Search PubMed.
- S.-Y. Park, T.-H. Wu, Y. Chen, M. A. Teitell and P.-Y. Chiou, Lab Chip, 2011, 11, 1010–1012 Search PubMed.
- A. Sauret, C. Spandagos and H. C. Shum, Lab Chip, 2012, 12, 3380–3386 Search PubMed.
- H. C. Shum, J. Varnell and D. A. Weitz, Biomicrofluidics, 2012, 6, 012808 Search PubMed.
- A. Sauret and H. C. Shum, Appl. Phys. Lett., 2012, 100, 154106 Search PubMed.
- J. Li, N. Mittal, S. Y. Mak, Y. Song and H. C. Shum, J. Micromech. Microeng., 2015, 25, 084009 Search PubMed.
- P. A. Zhu, X. Tang and L. Q. Wang, Microfluid. Nanofluid., 2016, 20, 47 Search PubMed.
- P. A. Zhu, X. Tang, Y. Tian and L. Q. Wang, Sci. Rep., 2016, 6, 31436 Search PubMed.
- H. Zhou and S. Yao, Microfluid. Nanofluid., 2014, 16, 667–675 Search PubMed.
- K. Churski, P. Korczyk and P. Garstecki, Lab Chip, 2010, 10, 816–818 Search PubMed.
- M. E. Dolega, S. Jakiela, M. Razew, A. Rakszewska, O. Cybulski and P. Garstecki, Lab Chip, 2012, 12, 4022–4025 Search PubMed.
- M. Yu, Y. Hou, H. Zhou and S. Yao, Lab Chip, 2015, 15, 1524–1532 Search PubMed.
- S. Jakiela, P. R. Debski, B. Dabrowski and P. Garstecki, Micromachines, 2014, 5, 1002–1011 Search PubMed.
- S.-Y. Jung, S. T. Retterer and C. P. Collier, Lab Chip, 2010, 10, 2688–2694 Search PubMed.
- J. Xu and D. Attinger, J. Micromech. Microeng., 2008, 18, 065020 Search PubMed.
- A. Bransky, N. Korin, M. Khoury and S. Levenberg, Lab Chip, 2009, 9, 516–520 Search PubMed.
- Y. N. Cheung and H. Qiu, J. Micromech. Microeng., 2012, 22, 125003 Search PubMed.
- Y. N. Cheung and H. Qiu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 066310 Search PubMed.
- I. Ziemecka, V. van Steijn, G. J. M. Koper, M. Rosso, A. M. Brizard, J. H. van Esch and M. T. Kreutzer, Lab Chip, 2011, 11, 620–624 Search PubMed.
- J. Shemesh, A. Nir, A. Bransky and S. Levenberg, Lab Chip, 2011, 11, 3225–3230 Search PubMed.
- J. C. Brenker, D. J. Collins, H. Van Phan, T. Alan and A. Neild, Lab Chip, 2016, 16, 1675–1683 Search PubMed.
- D. J. Collins, T. Alan, K. Helmerson and A. Neild, Lab Chip, 2013, 13, 3225–3231 Search PubMed.
- L. Schmid and T. Franke, Lab Chip, 2013, 13, 1691–1694 Search PubMed.
- L. Schmid and T. Franke, Appl. Phys. Lett., 2014, 104, 133501 Search PubMed.
- A. R. Abate, M. B. Romanowsky, J. J. Agresti and D. A. Weitz, Appl. Phys. Lett., 2009, 94, 023503 Search PubMed.
- C.-Y. Lee, Y.-H. Lin and G.-B. Lee, Microfluid. Nanofluid., 2009, 6, 599–610 Search PubMed.
- H.-W. Wu, Y.-C. Huang, C.-L. Wu and G.-B. Lee, Microfluid. Nanofluid., 2009, 7, 45–56 Search PubMed.
- A. Raj, R. Halder, P. Sajeesh and A. K. Sen, Microfluid. Nanofluid., 2016, 20, 102 Search PubMed.
- B. Cai, R. He, X. Yu, L. Rao, Z. He, Q. Huang, W. Liu, S. Guo and X.-Z. Zhao, Microfluid. Nanofluid., 2016, 20, 56 Search PubMed.
- J.-W. Choi, S. Lee, D.-H. Lee, J. Kim and S.-I. Chang, RSC Adv., 2014, 4, 20341–20345 Search PubMed.
- S. Zeng, B. Li, X. o. Su, J. Qin and B. Lin, Lab Chip, 2009, 9, 1340–1343 Search PubMed.
- K. Churski, J. Michalski and P. Garstecki, Lab Chip, 2010, 10, 512–518 Search PubMed.
- F. Guo, K. Liu, X.-H. Ji, H.-J. Ding, M. Zhang, Q. Zeng, W. Liu, S.-S. Guo and X.-Z. Zhao, Appl. Phys. Lett., 2010, 97, 233701 Search PubMed.
- J.-C. Galas, D. Bartolo and V. Studer, New J. Phys., 2009, 11, 075027 Search PubMed.
- H. Willaime, V. Barbier, L. Kloul, S. Maine and P. Tabeling, Phys. Rev. Lett., 2006, 96, 054501 Search PubMed.
- J.-H. Wang and G.-B. Lee, Micromachines, 2013, 4, 306–320 Search PubMed.
- W. S. Lee, S. Jambovane, D. Kim and J. W. Hong, Microfluid. Nanofluid., 2009, 7, 431–438 Search PubMed.
- B.-C. Lin and Y.-C. Su, J. Micromech. Microeng., 2008, 18, 115005 Search PubMed.
- J.-H. Choi, S.-K. Lee, J.-M. Lim, S.-M. Yang and G.-R. Yi, Lab Chip, 2010, 10, 456–461 Search PubMed.
- C.-T. Chen and G.-B. Lee, J. Microelectromech. Syst., 2006, 15, 1492–1498 Search PubMed.
- S.-K. Hsiung, C.-T. Chen and G.-B. Lee, J. Micromech. Microeng., 2006, 16, 2403–2410 Search PubMed.
- C.-H. Lee, S.-K. Hsiung and G.-B. Lee, J. Micromech. Microeng., 2007, 17, 1121–1129 Search PubMed.
- M. Zhang, J. Wu, X. Niu, W. Wen and P. Sheng, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 066305 Search PubMed.
- N.-T. Nguyen, Microfluid. Nanofluid., 2012, 12, 1–16 Search PubMed.
- N.-T. Nguyen, T.-H. Ting, Y.-F. Yap, T.-N. Wong, J. C.-K. Chai, W.-L. Ong, J. Zhou, S.-H. Tan and L. Yobas, Appl. Phys. Lett., 2007, 91, 084102 Search PubMed.
- P. Sheng and W. Wen, Annu. Rev. Fluid Mech., 2012, 44, 143–174 CrossRef.
- X. Niu, M. Zhang, J. Wu, W. Wen and P. Sheng, Soft Matter, 2009, 5, 576–581 Search PubMed.
- C. A. Stan, S. K. Tang and G. M. Whitesides, Anal. Chem., 2009, 81, 2399–2402 Search PubMed.
- S.-H. Tan, S. S. Murshed, N.-T. Nguyen, T. N. Wong and L. Yobas, J. Phys. D: Appl. Phys., 2008, 41, 165501 Search PubMed.
- S. S. Murshed, S. H. Tan, N. T. Nguyen, T. N. Wong and L. Yobas, Microfluid. Nanofluid., 2009, 6, 253–259 Search PubMed.
- S. S. Murshed, S.-H. Tan and N.-T. Nguyen, J. Phys. D: Appl. Phys., 2008, 41, 085502 Search PubMed.
- C.-H. Yeh, K.-R. Chen and Y.-C. Lin, Microfluid. Nanofluid., 2013, 15, 775–784 Search PubMed.
- R. Suryo and O. A. Basaran, Phys. Rev. Lett., 2006, 96, 034504 Search PubMed.
- V. Miralles, A. Huerre, H. Williams, B. Fournie and M.-C. Jullien, Lab Chip, 2015, 15, 2133–2139 Search PubMed.
- C. N. Baroud, J.-P. Delville, F. Gallaire and R. Wunenburger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 046302 Search PubMed.
- C. N. Baroud, M. R. de Saint Vincent and J.-P. Delville, Lab Chip, 2007, 7, 1029–1033 Search PubMed.
- M. R. de Saint Vincent and J.-P. Delville, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 026310 Search PubMed.
- M. R. de Saint Vincent, H. Chraïbi and J.-P. Delville, Phys. Rev. Appl., 2015, 4, 044005 Search PubMed.
- M. L. Cordero, F. Gallaire and C. N. Baroud, Phys. Fluids, 2011, 23, 094111 Search PubMed.
- E. Verneuil, M. a. Cordero, F. Gallaire and C. N. Baroud, Langmuir, 2009, 25, 5127–5134 Search PubMed.
- S.-Y. Tang, I. D. Joshipura, Y. Lin, K. Kalantar-Zadeh, A. Mitchell, K. Khoshmanesh and M. D. Dickey, Adv. Mater., 2016, 28, 604–609 Search PubMed.
- B. Berge, O. Konovalov, J. Lajzerowicz, A. Renault, J. Rieu, M. Vallade, J. Als-Nielsen, G. Grübel and J. Legrand, Phys. Rev. Lett., 1994, 73, 1652 Search PubMed.
- A. Diguet, H. Li, N. Queyriaux, Y. Chen and D. Baigl, Lab Chip, 2011, 11, 2666–2669 Search PubMed.
- F. Malloggi, S. A. Vanapalli, H. Gu, D. van den Ende and F. Mugele, J. Phys.: Condens. Matter, 2007, 19, 462101 Search PubMed.
- F. Malloggi, H. Gu, A. Banpurkar, S. Vanapalli and F. Mugele, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 26, 91–96 Search PubMed.
- H. Gu, M. H. Duits and F. Mugele, Lab Chip, 2010, 10, 1550–1556 Search PubMed.
- H. Gu, F. Malloggi, S. A. Vanapalli and F. Mugele, Appl. Phys. Lett., 2008, 93, 183507 Search PubMed.
- H. Gu, C. U. Murade, M. H. Duits and F. Mugele, Biomicrofluidics, 2011, 5, 011101 Search PubMed.
- K. Wang, L. Xie, Y. Lu and G. Luo, Lab Chip, 2013, 13, 73–76 Search PubMed.
- G. Bolognesi, A. Hargreaves, A. D. Ward, A. K. Kirby, C. D. Bain and O. Ces, RSC Adv., 2015, 5, 8114–8121 Search PubMed.
- M. Zhang, J. Wu, L. Wang, K. Xiao and W. Wen, Lab Chip, 2010, 10, 1199–1203 Search PubMed.
- S. Waheed, J. M. Cabot, N. P. Macdonald, T. Lewis, R. M. Guijt, B. Paull and M. C. Breadmore, Lab Chip, 2016, 16, 1993–2013 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |