DOI:
10.1039/C6JA00282J
(Technical Note)
J. Anal. At. Spectrom., 2017,
32, 415-419
Inter-calibration of a proposed new primary reference standard AA-ETH Zn for zinc isotopic analysis
Received
2nd August 2016
, Accepted 10th November 2016
First published on 10th November 2016
Abstract
We have prepared a large volume of pure, concentrated and homogenous zinc standard solution. This new standard solution is intended to be used as a primary reference standard for the zinc isotope community, and to serve as a replacement for the nearly exhausted current reference standard, the so-called JMC-Lyon Zn. The isotopic composition of this new zinc standard (AA-ETH Zn) has been determined through an inter-laboratory calibration exercise, calibrated against the existing JMC-Lyon standard, as well as the certified Zn reference standard IRMM-3702. The data show that the new standard is isotopically indistinguishable from the IRMM-3702 zinc standard, with a weighted δ66/64Zn value of 0.28 ± 0.02‰ relative to JMC-Lyon. We suggest that this new standard be assigned a δ66/64Zn value of +0.28‰ for reporting of future Zn isotope data, with the rationale that all existing published Zn isotope data are presented relative to the JMC-Lyon standard. Therefore our proposed presentation allows for a direct comparison with all previously published data, and that are directly traceable to a certified reference standard, IRMM-3702 Zn. This standard will be made freely available to all interested labs through contact with the corresponding author.
Introduction
The stable isotopes of Zn have, in recent years, emerged as powerful tracers of natural processes in the Earth sciences. Much of the focus, though by no means exclusively, has been on investigating the role of Zn and its biogeochemical cycling in the modern ocean1–5 and on the understanding of processes occurring during planetary formation.6–9 Common to many of the recently developed non-traditional stable metal isotope systems (e.g. Cu, Mo, Fe, and Li), made analytically feasible due to advances in multiple collector inductively coupled plasma-mass spectrometers (MC-ICPMS), comparative studies of Zn and its isotopes have been complicated by the lack of an internationally certified reference standard. However, where rigorous data comparison for other non-traditional stable metal isotope systems such as Mo has been severely hampered in this regard,10,11 most if not all Zn isotope data to date have been referenced to the same ICP Zn standard, the so-called JMC-Lyon standard, made available by the authors after the initial high-precision Zn isotope study of Maréchal et al.12 Unfortunately the JMC-Lyon standard is nearing exhaustion, and therefore a new reference standard is required.
Recently, efforts have been made to address the problem of a lack of Zn standard, with the creation of a certified reference standard, IRMM-3702 Zn, produced by the Institute for Reference Materials and Measurements (IRMM) in Belgium.13,14 Although the IRMM-3702 Zn standard will prove to be an invaluable reference standard for Zn isotope studies, it suffers from some important limitations which would preclude it from being adopted widespread as a primary reference standard. At the time of writing it only available for purchase in relatively small aliquots (∼3 μmol Zn, or ∼200 μg Zn). Such an amount of Zn would be of use as a primary reference standard to a laboratory routinely measuring Zn isotopes for only a short period of time. This, therefore, would make it expensive for most labs to use in this way. Furthermore, adopting the IRMM-3702 Zn as a primary reference standard would require the IRMM to supply this standard in its current form well into the future, which already seems unlikely given the small quantities in which it is currently distributed. Other potential candidates supplied by international bodies, such as the NIST 3168a Zn standard solution, are also unlikely to be useful to the Zn community as a zero-point reference standard, as data suggest that it is isotopically light with a 66Zn/64Zn ratio, that is the measured atomic ratio of 66Zn relative to 64Zn, that is approximately 1‰ lower than that of the JMC-Lyon reference standard (O. Rouxel, unpbl.). This composition is, therefore, at an extreme end of the natural range thus far reported for Zn isotopes. A second Zn standard from NIST, SRM 682, has an even more extreme composition, which is approximately 2.5‰ lighter than JMC-Lyon Zn.15,16 A third Zn standard supplied by NIST, SRM 683, has a measured composition that falls within the range of natural Zn compositions thus far reported,16,17 and would therefore likely be useful as a reference standard for the Zn isotope community. But as with IRMM 3702, its availability into the future is not guaranteed. Furthermore, although SRM 683 Zn appears to be isotopically homogeneous,17 purified Zn metal standards have long been known to be extremely variable in their isotopic composition.16 This potential for heterogeneity therefore precludes or at the least complicates their adoption as universal zero-point reference standards.
To address this issue, we have prepared a large volume of homogenous Zn solution as a new reference material for the Zn isotope community. Approximately 9 grams of pure Zn metal (Alfa Aesar Zn foil, Product Code 11912, Lot #I17Z058), which we estimate to be enough Zn to serve the Zn isotope community for the next 50 years, was dissolved in twice distilled 15 M nitric acid and diluted to a 5% v/v solution with 18.2 MΩ cm de-ionised water (Milli-Q, Merck Millipore). The isotopic composition of this new Zn standard (AA-ETH Zn) was then determined through an inter-laboratory calibration. Participating labs were chosen to ensure a variety in the Zn isotope methodology and to ensure that any potential biases produced through analytical protocols are resolved.
Analytical methodology
A summary of the analytical protocols used by the participating laboratories is shown in Table 1. Most of the participating labs employ a Zn double spike for correction of mass fractionation. An underlying assumption of using double spike techniques is that mass fractionation occurs according to mass, i.e. all isotopic fractionation processes are mass dependent. This is expected to be the case for elements with Z < 80, such as Zn.18 This expectation is confirmed by the data obtained from the Brest laboratory, using a non-double spike approach to correct for mass fractionation (Table 2). All participating labs performed measurements of the new AA-ETH Zn standard against both the JMC-Lyon and IRMM-3702 Zn standards. Zn isotopic compositions are reported in the usual δ66Zn (‰) notation, and are reported relative to both the JMC-Lyon and IRMM-3702 Zn standards (Table 2), where| | 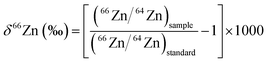 | (1) |
Table 1 Summary of analytical protocols employed by the participating labs
| Lab |
Instrument |
Sample introduction |
Mass bias correctionref |
| ETH Zürich |
Neptune Plus |
Aridus II, Apex-Q |
64Zn–67Zn double spike1 |
| ANU |
Neptune Plus |
Apex-Q |
67Zn–68Zn double spike19 |
| Brest |
Neptune Plus |
Glass spray chamber |
Cu doping20 |
| CPRG – Nancy |
Neptune Plus |
Glass spray chamber |
64Zn–67Zn double spike21 |
| Imperial College London |
NuPlasmaHR |
Aridus II |
64Zn–67Zn double spike22 |
| Indiana |
NuPlasma II |
Aridus II |
64Zn–67Zn double spike21 |
| Kyoto |
Neptune Plus |
Aridus II |
64Zn–67Zn double spike |
Table 2 Zn isotope results of the AA-ETH standard relative to both JMC-Lyon and the IRMM-3702 Zn standards, with the number of analyses in brackets. 2σ is the calculated twice standard deviation for all measurements across all participating labs, with the exception of the weighted mean, where the error reported is the uncertainty of the weighted mean. The weighted mean and its uncertainty were determined by weighting the values produced by each individual lab according to their individual 2σ uncertainties
| Lab |
δ
66ZnJMC |
2σ |
δ
66ZnIRMM |
2σ |
δ
67ZnIRMM |
2σ |
δ
68ZnIRMM |
2σ |
|
Data obtained from the Brest lab was obtained via a non-double spike mass bias correction protocol, which allows for independent determination of additional isotope pairs, which are shown here.
|
| ETH (n = 30) |
0.31 |
0.06 |
−0.01 |
0.07 |
|
|
|
|
| ANU (n = 5) |
|
|
−0.03 |
0.05 |
|
|
|
|
| Bresta (n = 13) |
|
|
−0.02 |
0.04 |
−0.02 |
0.07 |
−0.07 |
0.06 |
| CPRG (n = 20) |
0.33 |
0.12 |
0.02 |
0.08 |
|
|
|
|
| Imperial (n = 18) |
0.28 |
0.05 |
−0.04 |
0.05 |
|
|
|
|
| Indiana (n = 32) |
0.26 |
0.10 |
0.01 |
0.10 |
|
|
|
|
| Kyoto (n = 10) |
0.27 |
0.03 |
−0.01 |
0.02 |
|
|
|
|
| All (JMC: n = 110, IRMM: n = 129) |
0.29 |
0.09 |
0.00 |
0.07 |
|
|
|
|
| All (weighted) |
0.28 |
0.02 |
−0.02 |
0.02 |
|
|
|
|
Similarly, δ67Zn and δ68Zn are described by the above equation, where 66Zn is replaced by 67Zn or 68Zn, respectively. Conversion from δ66Zn to any other Zn isotope pair is achieved by multiplying this value by the factor ln(m2/m1)/ln(m66Zn/m64Zn), where the masses m are the atomic masses, and according to the exponential mass fractionation law. A brief description of the methodology used by each lab is as follows.
ETH Zürich.
All analyses were performed using a Thermo Scientific Neptune Plus MC-ICPMS, using standard sample and skimmer cones. Prior to analysis, each standard was doped with a mixed 64Zn–67Zn double spike to achieve a standard![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) spike ratio of ∼1. Instrumental mass bias correction was performed using the double spike techniques described in the study of Bermin et al.1 Solutions in an ∼0.3 M HNO3 (2% v/v) solution were introduced into the mass spectrometer via a Cetac Aridus II desolvating system or an Elemental Scientific (ESI) Apex-Q desolvating system, both coupled with a PFA nebuliser with a nominal uptake rate of 50 μL min−1. Isobaric interference from 64Ni on 64Zn was monitored using 62Ni, but any correction here was always negligible. For data collected with the Apex, an additional correction for small amounts of hydrides was needed, determined by monitoring the 64ZnH+ hydride produced at mass 65. Typically, hydrides were formed at the 10–20 ppm level. The long term reproducibility of measurements made using both sample introduction systems, as determined by analyses of IRMM-3702 Zn over the course of three years, including those made during each analytical session, is 0.06‰ (2SD).
spike ratio of ∼1. Instrumental mass bias correction was performed using the double spike techniques described in the study of Bermin et al.1 Solutions in an ∼0.3 M HNO3 (2% v/v) solution were introduced into the mass spectrometer via a Cetac Aridus II desolvating system or an Elemental Scientific (ESI) Apex-Q desolvating system, both coupled with a PFA nebuliser with a nominal uptake rate of 50 μL min−1. Isobaric interference from 64Ni on 64Zn was monitored using 62Ni, but any correction here was always negligible. For data collected with the Apex, an additional correction for small amounts of hydrides was needed, determined by monitoring the 64ZnH+ hydride produced at mass 65. Typically, hydrides were formed at the 10–20 ppm level. The long term reproducibility of measurements made using both sample introduction systems, as determined by analyses of IRMM-3702 Zn over the course of three years, including those made during each analytical session, is 0.06‰ (2SD).
Australian National University (ANU).
All analyses were performed using a Thermo Scientific Neptune Plus MC-ICPMS using the procedure described in the study of Samanta et al.19 Prior to analysis, each standard was doped with a mixed 67Zn–68Zn double spike to achieve a standard![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) spike ratio of ∼0.25. Solutions in a 2% v/v HNO3 solution were introduced into the mass spectrometer via an Elemental Scientific (ESI) Apex-Q desolvating system with a PFA nebuliser (ESI) with a nominal uptake rate of 50 μL min−1. A standard Ni sampler cone and a Ni X-skimmer cone were used to enhance instrument sensitivity. At the start of the measurement session, the instrument was optimised for signal intensity on mass 62Ni, 63Cu, 65Cu, 64Zn, 66Zn, 67Zn and 68Zn. All measurements were made in low resolution mode as 1 block of 30 cycles with a 4 second integration time. All measured ratios were corrected for any interference of 64Ni on 64Zn by monitoring the intensity of 62Ni and subtracting the calculated intensity for 64Ni, based on the natural 62Ni/64Ni ratio, from the measured intensity of 64Zn. These corrections were always negligible compared to the standard/spike signal. The interference corrected data were then blank corrected by subtracting the average intensity of the 30 cycle measurement for each isotope from the intensities measured for the 2% v/v HNO3 blank.
spike ratio of ∼0.25. Solutions in a 2% v/v HNO3 solution were introduced into the mass spectrometer via an Elemental Scientific (ESI) Apex-Q desolvating system with a PFA nebuliser (ESI) with a nominal uptake rate of 50 μL min−1. A standard Ni sampler cone and a Ni X-skimmer cone were used to enhance instrument sensitivity. At the start of the measurement session, the instrument was optimised for signal intensity on mass 62Ni, 63Cu, 65Cu, 64Zn, 66Zn, 67Zn and 68Zn. All measurements were made in low resolution mode as 1 block of 30 cycles with a 4 second integration time. All measured ratios were corrected for any interference of 64Ni on 64Zn by monitoring the intensity of 62Ni and subtracting the calculated intensity for 64Ni, based on the natural 62Ni/64Ni ratio, from the measured intensity of 64Zn. These corrections were always negligible compared to the standard/spike signal. The interference corrected data were then blank corrected by subtracting the average intensity of the 30 cycle measurement for each isotope from the intensities measured for the 2% v/v HNO3 blank.
Brest.
All analyses were performed using a Thermo Scientific Neptune MC-ICPMS. The instrument was optimised for signal intensity on mass 62Ni, 63Cu, 65Cu, 64Zn, 66Zn, 67Zn and 68Zn. Instrumental mass bias was corrected for by doping the Zn standard solutions with a pure copper standard solution (NIST SRM 3114) whose isotopic composition has been calibrated against NIST SRM 976. The data reduction scheme is similar to the approach of Maréchal et al.,12 which involves measuring 65Cu/63Cu to determine the instrumental mass bias factor using an exponential mass fractionation law. In addition to Cu normalisation, Zn ratios were further corrected using a standard bracketing approach, where measured Zn isotope ratios of the sample are normalised to the average composition of its bracketing reference standard.20 All measurements were made in low resolution mode as 1 block of 25 cycles with a 4 second integration time. Solutions in 0.28 M HNO3 were introduced into the plasma using a double spray quartz chamber system (cyclonic and double pass) and a microconcentric PFA nebulizer operating at a flow rate of about 60 μL min−1. The MC-ICPMS was equipped with high-efficiency Ni-cones (X-cones) and run in medium resolution mode. Using this instrumental set-up, Zn and Cu isotopes were measured at concentrations of 300 ng g−1 and 200 ng g−1, respectively. The precision of the measurements, determined as the standard deviation values (2SD) of duplicate δ66Zn analysis of the same standard/sample solution over several analytical sessions, generally ranged from 0.02‰ to 0.04‰.
CPRG – Nancy.
Zn standard solutions (i.e. ETH AA Zn, IRMM-3702 and JMC-Lyon supplied by ETH) with known concentration were doped with a 64Zn–67Zn double spike at a sample–spike ratio (m/m ratio) of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.38 for mass bias correction (following the methods described in the study of Bryan et al.21), and then dried and re-dissolved with 0.1 M HNO3 for Zn isotope ratio analysis. The Zn isotope ratios were determined using a Thermo Scientific Neptune Plus MC-ICPMS. The samples were introduced in wet plasma mode using a PTFE nebulizer, at concentrations of 200 ng mL−1. Data were collected as 1 block of 30 measurements (5 s integration time for each measurement). The wash time between samples was 110 seconds using 0.3 M HNO3, followed by a blank measurement of the same 0.1 M HNO3 that the samples were re-dissolved in. Isobaric interference from 64Ni on 64Zn was monitored using intensity measurements of 62Ni and was negligible (typically less than 10 ppm).
1.38 for mass bias correction (following the methods described in the study of Bryan et al.21), and then dried and re-dissolved with 0.1 M HNO3 for Zn isotope ratio analysis. The Zn isotope ratios were determined using a Thermo Scientific Neptune Plus MC-ICPMS. The samples were introduced in wet plasma mode using a PTFE nebulizer, at concentrations of 200 ng mL−1. Data were collected as 1 block of 30 measurements (5 s integration time for each measurement). The wash time between samples was 110 seconds using 0.3 M HNO3, followed by a blank measurement of the same 0.1 M HNO3 that the samples were re-dissolved in. Isobaric interference from 64Ni on 64Zn was monitored using intensity measurements of 62Ni and was negligible (typically less than 10 ppm).
Imperial College London.
The isotopic analyses were carried out with a Nu Plasma HR MC-ICPMS instrument at the MAGIC Laboratories using protocols modified from those reported by Arnold et al.22 Prior to analysis, a 64Zn–67Zn double spike was added to and equilibrated with each standard solution at a ratio of spike-derived to natural Zn of about 1. The spike–sample mixtures were taken up in 0.1 M HNO3 to achieve total Zn concentrations of ∼100 ng mL−1. An Aridus II (CETAC Technologies) desolvation system fitted with a nominal 100 μL min−1 glass nebulizer was used for sample introduction. The analyses involved simultaneous collection of the ion beams of 64Zn+, 66Zn+, 67Zn+, and 68Zn+, and 62Ni+ and 137Ba2+ for interference correction. Data collection was performed in 3 blocks of 20 × 5 s integrations, with a 15 s electronic background measurement preceding each block. The instrumental mass bias encountered during the analyses was corrected using double spike data reduction methods adapted from those reported by Arnold et al.22 For this, the “raw” measured isotope ratios of 64Zn/67Zn, 66Zn/67Zn and 68Zn/67Zn were processed offline with a spreadsheet-based iterative solver. Corrections for spectral interference from 64Ni+ and Ba2+ ions (132Ba2+, 134Ba2+ and 136Ba2+) were also subjected to mass bias correction. The required corrections were very small, however, at less than 1 × 10−5 for both 64Ni+/64Zn+ and 134Ba2+/67Zn+. Additional interspersed analyses of the in-house London Zn standard solution yielded δ66ZnJMC = 0.12 ± 0.06‰ (2SD), in agreement with three previous studies that reported results of 0.08‰ to 0.14‰ for this sample.13,22,23
Indiana University.
Zinc isotopic standards (AA-ETH Zn, IRMM-3702 Zn and JMC-Lyon Zn) were measured relative to an in-house Zn standard (Sesame Zn) on the NuPlasma II MC-ICPMS in the Sesame Lab at Indiana University Bloomington. Solutions were introduced into the mass spectrometer using a Cetac Aridus II desolvating system. Prior to analysis, standards were doped with a mixed 64Zn–67Zn double spike, and instrumental mass bias correction was performed using the double spike techniques described in the study of Bryan et al.21 Additional analyses of an in-house London Zn standard (δ66ZnSesame = 4.37 ± 0.05‰ (2SD)) simultaneously performed are in agreement with previously reported values of this standard.21
Kyoto University.
All isotopic ratios were measured on a Neptune Plus MC-ICPMS with a glass nebuliser (MicroMist 0.1 mL min−1) and an Aridus II desolvating nebulizer system at the Research Institute for Humanity and Nature, Kyoto, Japan. A standard Ni sampler cone and a Ni H-skimmer cone were used. Instrumental mass bias during MC-ICP-MS measurement was corrected using a mixed 64Zn–67Zn double spike, and isotopic ratios were calculated using the iterative method of Siebert et al.24 The double spike comprised 82.9% 64Zn, 0.5% 66Zn, 16.2% 67Zn, and 0.5% 68Zn. The composition of the double spike was calibrated to the AA-ETH Zn standard by measuring AA Zn standard–double spike mixtures in different proportions.25 The standards (JMC Zn or IRMM Zn) were mixed with a double spike in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio, and diluted to 200–400 ppb Zn with 2% HNO3. Data acquisition for each standard consisted of 30 4 s integrations. The intensity of the 66Zn beam was ∼5 V for 100 ppb natural Zn. In order to correct the instrumental background, a pure 2% HNO3 w/w solution was measured every four samples, with data collected in 15 4 s integration cycles. The average signal of the pure 2% HNO3 solutions was then subtracted from the signals of the bracketed standards. Long term reproducibility, estimated by measurement of an in-house Zn standard during the three months surrounding these measurements, is 0.05‰ (2SD).
1 weight ratio, and diluted to 200–400 ppb Zn with 2% HNO3. Data acquisition for each standard consisted of 30 4 s integrations. The intensity of the 66Zn beam was ∼5 V for 100 ppb natural Zn. In order to correct the instrumental background, a pure 2% HNO3 w/w solution was measured every four samples, with data collected in 15 4 s integration cycles. The average signal of the pure 2% HNO3 solutions was then subtracted from the signals of the bracketed standards. Long term reproducibility, estimated by measurement of an in-house Zn standard during the three months surrounding these measurements, is 0.05‰ (2SD).
Results and recommendation
Table 2 and Fig. 1 summarize the data collected by the seven participating inter-calibration labs, representing a total of 126 separate analyses of the AA-ETH standard. Importantly, the results show a clear agreement between participating labs, with the new AA-ETH Zn standard being isotopically indistinguishable from the already calibrated IRMM-3702.13 Furthermore, both the measured (and implied) offset of IRMM-3702 relative to the JMC-Lyon standard in this dataset are in agreement with previously published values of 0.29 ± 0.05‰ (2SD).13,15,16 The data presented in this inter-calibration exercise were collected using a variety of techniques, both analytically and in terms of data reduction and specifically the methods used for correcting instrumental mass bias. We can therefore confidently assign a value to our proposed new standard identical to that of IRMM-3702, that is δ66Zn = 0.28 ± 0.02‰, relative to JMC-Lyon Zn, where the uncertainty is given by the uncertainty on the weighted mean – see Table 2.
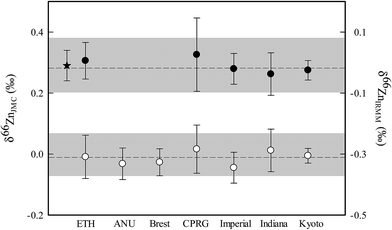 |
| | Fig. 1 Zn isotope results of the AA-ETH standard relative to both JMC-Lyon and the IRMM-3702 Zn. Filled circles show data on the JMC scale and open circles show data on the IRMM scale. The grey bands represent twice the standard deviation of all the measurements made. The dashed line represents the weighted average for each set of measurements. The star shows the value obtained for IRMM-3702, relative to JMC-Lyon from the study of Moeller et al.13 | |
We thus propose that our new AA-ETH Zn standard, which will be made freely available upon request, be adopted as the new “zero-point” reference standard for future Zn isotopic measurements. In common with the approach used for future Mo isotope studies (see the study of Nagler et al.11 and references therein), we suggest that the AA-ETH standard be assigned a specific reference value of 0.28‰, and not “zero”. This approach facilitates the comparison with existing literature data, provides a direct and traceable link to the already existing and universally adopted JMC-Lyon Zn isotope scale, and therefore allows for common reference values such as 0.3‰ for “lithogenic” Zn to be kept for discussion. Converting δ66Zn values to the JMC-Lyon scale, relative to the AA-ETH = 0.28‰, can be done using the standard conversion identity.26 This is expressed here, for the conversion of a δ value determined relative to the AA-ETH standard to the existing JMC scale as follows:
| |  | (2) |
where
δ66Zn
AA-ETH–JMC-Lyon = 0.28 ± 0.02‰. In practice, this conversion can be approximated to:
| | | δ66ZnJMC-Lyon (‰) = δ66ZnAA-ETH + δ66ZnAA-ETH–JMC-Lyon | (3) |
as in many cases any systematic errors introduced by this simplification are smaller than analytical uncertainty. Using the AA-ETH Zn standard with either or both of the IRMM or NIST Zn standards as secondary reference materials will therefore allow for simple and rigorous comparison of results generated in different labs moving into the future.
Acknowledgements
We would like to thank R. Steele and D. Vance for helpful discussions during the writing of this manuscript. We would also like to thank three anonymous reviewers whose comments helped to significantly improve this manuscript.
References
- J. Bermin, D. Vance, C. Archer and P. J. Statham, Chem. Geol., 2006, 226, 280–297 CrossRef CAS.
- D. Vance, C. Archer, J. Bermin, J. Perkins, P. J. Statham, M. C. Lohan, M. J. Ellwood and R. A. Mills, Earth Planet. Sci. Lett., 2008, 274, 204–213 CrossRef CAS.
- T. M. Conway and S. G. John, Global Biogeochem. Cycles, 2014, 28, 1111–1128 CrossRef CAS.
- S. H. Little, D. Vance, C. Walker-Brown and W. M. Landing, Geochim. Cosmochim. Acta, 2014, 125, 673–693 CrossRef CAS.
- C. N. Marechal, E. Nicolas, C. Douchet and F. Albarede, Geochem., Geophys., Geosyst., 2000, 1 DOI:10.1029/1999GC000029.
- C. Kato, F. Moynier, M. C. Valdes, J. K. Dhaliwal and J. M. D. Day, Nat. Commun., 2015, 6 DOI:10.1038/ncomms8617.
- P. S. Savage, M. Boyet and F. Moynier, Meteorit. Planet. Sci., 2014, 49, 353 Search PubMed.
- R. C. Paniello, J. M. D. Day and F. Moynier, Nature, 2012, 490, 376–379 CrossRef CAS PubMed.
- J. M. Luck, D. Ben Othman and F. Albarede, Geochim. Cosmochim. Acta, 2005, 69, 5351–5363 CrossRef CAS.
- T. Goldberg, G. Gordon, G. Izon, C. Archer, C. R. Pearce, J. McManus, A. D. Anbar and M. Rehkamper, J. Anal. At. Spectrom., 2013, 28, 724–735 RSC.
- T. F. Nagler, A. D. Anbar, C. Archer, T. Goldberg, G. W. Gordon, N. D. Greber, C. Siebert, Y. Sohrin and D. Vance, Geostand. Geoanal. Res., 2014, 38, 149–151 Search PubMed.
- C. N. Maréchal, P. Telouk and F. Albarede, Chem. Geol., 1999, 156, 251–273 CrossRef.
- K. Moeller, R. Schoenberg, R.-B. Pedersen, D. Weiss and S. Dong, Geostand. Geoanal. Res., 2012, 36, 177–199 CrossRef CAS.
- E. Ponzevera, C. R. Quetel, M. Berglund, P. D. P. Taylor, P. Evans, R. D. Loss and G. Fortunato, J. Am. Soc. Mass Spectrom., 2006, 17, 1412–1427 CrossRef CAS PubMed.
- T. M. Conway, A. D. Rosenberg, J. F. Adkins and S. G. John, Anal. Chim. Acta, 2013, 793, 44–52 CrossRef CAS PubMed.
- C. Cloquet, J. Carignan, M. F. Lehmann and F. Vanhaecke, Anal. Bioanal. Chem., 2008, 390, 451–463 CrossRef CAS PubMed.
- S. Chen, Y. Liu, J. Hu, Z. Zhang, Z. Hou, F. Huang and H. Yu, Geostand. Geoanal. Res., 2016, 40, 417–432 CrossRef CAS.
-
N. Dauphas and E. A. Schauble, in Annual Review of Earth and Planetary Sciences, ed. R. Jeanloz and K. H. Freeman, 2016, vol. 44, pp. 709–783 Search PubMed.
- M. Samanta, M. J. Ellwood and G. E. Mortimer, Microchem. J., 2016, 126, 530–537 CrossRef CAS.
- S. G. John, O. J. Rouxel, P. R. Craddock, A. M. Engwall and E. A. Boyle, Earth Planet. Sci. Lett., 2008, 269, 17–28 CrossRef CAS.
- A. L. Bryan, S. F. Dong, E. B. Wilkes and L. E. Wasylenki, Geochim. Cosmochim. Acta, 2015, 157, 182–197 CrossRef CAS.
- T. Arnold, M. Schonbachler, M. Rehkamper, S. F. Dong, F. J. Zhao, G. J. D. Kirk, B. J. Coles and D. J. Weiss, Anal. Bioanal. Chem., 2010, 398, 3115–3125 CrossRef CAS PubMed.
- F. Larner and M. Rehkaemper, Environ. Sci. Technol., 2012, 46, 4149–4158 CrossRef CAS PubMed.
- C. Siebert, T. F. Nagler and J. D. Kramers, Geochem., Geophys., Geosyst., 2001, 2, 2000GC000124 CrossRef.
- J. F. Rudge, B. C. Reynolds and B. Bourdon, Chem. Geol., 2009, 265, 420–431 CrossRef CAS.
-
R. E. Criss, Principles of Stable Isotope Distribution, Oxford University Press, Oxford, UK, 1999 Search PubMed.
Footnotes |
| † Now at: School of Earth & Ocean Sciences, Cardiff University, Park Place, CF10 3AT, Cardiff, UK. |
| ‡ Now at: Department of Oceanography, University of Hawaii, Honolulu HI 96822, USA. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article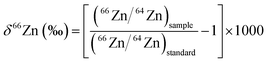
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) spike ratio of ∼1. Instrumental mass bias correction was performed using the double spike techniques described in the study of Bermin et al.1 Solutions in an ∼0.3 M HNO3 (2% v/v) solution were introduced into the mass spectrometer via a Cetac Aridus II desolvating system or an Elemental Scientific (ESI) Apex-Q desolvating system, both coupled with a PFA nebuliser with a nominal uptake rate of 50 μL min−1. Isobaric interference from 64Ni on 64Zn was monitored using 62Ni, but any correction here was always negligible. For data collected with the Apex, an additional correction for small amounts of hydrides was needed, determined by monitoring the 64ZnH+ hydride produced at mass 65. Typically, hydrides were formed at the 10–20 ppm level. The long term reproducibility of measurements made using both sample introduction systems, as determined by analyses of IRMM-3702 Zn over the course of three years, including those made during each analytical session, is 0.06‰ (2SD).
spike ratio of ∼1. Instrumental mass bias correction was performed using the double spike techniques described in the study of Bermin et al.1 Solutions in an ∼0.3 M HNO3 (2% v/v) solution were introduced into the mass spectrometer via a Cetac Aridus II desolvating system or an Elemental Scientific (ESI) Apex-Q desolvating system, both coupled with a PFA nebuliser with a nominal uptake rate of 50 μL min−1. Isobaric interference from 64Ni on 64Zn was monitored using 62Ni, but any correction here was always negligible. For data collected with the Apex, an additional correction for small amounts of hydrides was needed, determined by monitoring the 64ZnH+ hydride produced at mass 65. Typically, hydrides were formed at the 10–20 ppm level. The long term reproducibility of measurements made using both sample introduction systems, as determined by analyses of IRMM-3702 Zn over the course of three years, including those made during each analytical session, is 0.06‰ (2SD).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) spike ratio of ∼0.25. Solutions in a 2% v/v HNO3 solution were introduced into the mass spectrometer via an Elemental Scientific (ESI) Apex-Q desolvating system with a PFA nebuliser (ESI) with a nominal uptake rate of 50 μL min−1. A standard Ni sampler cone and a Ni X-skimmer cone were used to enhance instrument sensitivity. At the start of the measurement session, the instrument was optimised for signal intensity on mass 62Ni, 63Cu, 65Cu, 64Zn, 66Zn, 67Zn and 68Zn. All measurements were made in low resolution mode as 1 block of 30 cycles with a 4 second integration time. All measured ratios were corrected for any interference of 64Ni on 64Zn by monitoring the intensity of 62Ni and subtracting the calculated intensity for 64Ni, based on the natural 62Ni/64Ni ratio, from the measured intensity of 64Zn. These corrections were always negligible compared to the standard/spike signal. The interference corrected data were then blank corrected by subtracting the average intensity of the 30 cycle measurement for each isotope from the intensities measured for the 2% v/v HNO3 blank.
spike ratio of ∼0.25. Solutions in a 2% v/v HNO3 solution were introduced into the mass spectrometer via an Elemental Scientific (ESI) Apex-Q desolvating system with a PFA nebuliser (ESI) with a nominal uptake rate of 50 μL min−1. A standard Ni sampler cone and a Ni X-skimmer cone were used to enhance instrument sensitivity. At the start of the measurement session, the instrument was optimised for signal intensity on mass 62Ni, 63Cu, 65Cu, 64Zn, 66Zn, 67Zn and 68Zn. All measurements were made in low resolution mode as 1 block of 30 cycles with a 4 second integration time. All measured ratios were corrected for any interference of 64Ni on 64Zn by monitoring the intensity of 62Ni and subtracting the calculated intensity for 64Ni, based on the natural 62Ni/64Ni ratio, from the measured intensity of 64Zn. These corrections were always negligible compared to the standard/spike signal. The interference corrected data were then blank corrected by subtracting the average intensity of the 30 cycle measurement for each isotope from the intensities measured for the 2% v/v HNO3 blank.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.38 for mass bias correction (following the methods described in the study of Bryan et al.21), and then dried and re-dissolved with 0.1 M HNO3 for Zn isotope ratio analysis. The Zn isotope ratios were determined using a Thermo Scientific Neptune Plus MC-ICPMS. The samples were introduced in wet plasma mode using a PTFE nebulizer, at concentrations of 200 ng mL−1. Data were collected as 1 block of 30 measurements (5 s integration time for each measurement). The wash time between samples was 110 seconds using 0.3 M HNO3, followed by a blank measurement of the same 0.1 M HNO3 that the samples were re-dissolved in. Isobaric interference from 64Ni on 64Zn was monitored using intensity measurements of 62Ni and was negligible (typically less than 10 ppm).
1.38 for mass bias correction (following the methods described in the study of Bryan et al.21), and then dried and re-dissolved with 0.1 M HNO3 for Zn isotope ratio analysis. The Zn isotope ratios were determined using a Thermo Scientific Neptune Plus MC-ICPMS. The samples were introduced in wet plasma mode using a PTFE nebulizer, at concentrations of 200 ng mL−1. Data were collected as 1 block of 30 measurements (5 s integration time for each measurement). The wash time between samples was 110 seconds using 0.3 M HNO3, followed by a blank measurement of the same 0.1 M HNO3 that the samples were re-dissolved in. Isobaric interference from 64Ni on 64Zn was monitored using intensity measurements of 62Ni and was negligible (typically less than 10 ppm).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio, and diluted to 200–400 ppb Zn with 2% HNO3. Data acquisition for each standard consisted of 30 4 s integrations. The intensity of the 66Zn beam was ∼5 V for 100 ppb natural Zn. In order to correct the instrumental background, a pure 2% HNO3 w/w solution was measured every four samples, with data collected in 15 4 s integration cycles. The average signal of the pure 2% HNO3 solutions was then subtracted from the signals of the bracketed standards. Long term reproducibility, estimated by measurement of an in-house Zn standard during the three months surrounding these measurements, is 0.05‰ (2SD).
1 weight ratio, and diluted to 200–400 ppb Zn with 2% HNO3. Data acquisition for each standard consisted of 30 4 s integrations. The intensity of the 66Zn beam was ∼5 V for 100 ppb natural Zn. In order to correct the instrumental background, a pure 2% HNO3 w/w solution was measured every four samples, with data collected in 15 4 s integration cycles. The average signal of the pure 2% HNO3 solutions was then subtracted from the signals of the bracketed standards. Long term reproducibility, estimated by measurement of an in-house Zn standard during the three months surrounding these measurements, is 0.05‰ (2SD).


