Emerging investigators series: a critical review of decision support systems for water treatment: making the case for incorporating climate change and climate extremes
William J.
Raseman
,
Joseph R.
Kasprzyk
 *,
Fernando L.
Rosario-Ortiz
,
Jenna R.
Stewart
and
Ben
Livneh
*,
Fernando L.
Rosario-Ortiz
,
Jenna R.
Stewart
and
Ben
Livneh
Department of Civil, Environmental and Architectural Engineering, University of Colorado, Boulder, CO 80309, USA. E-mail: joseph.kasprzyk@colorado.edu
First published on 17th November 2016
Abstract
Water treatment plants (WTPs) are tasked with providing safe potable water to consumers. However, WTPs face numerous potential obstacles, including changes in source water quality and quantity, financial burdens related to operations and upgrades, and stringent water quality regulations. Moreover, these challenges may be exacerbated by climate change in the form of long-term climatic perturbations and the increasing frequency and intensity of extreme weather events. To help WTPs overcome these issues, decision support systems (DSSs), which are used to aid and enhance the quality and consistency of decision-making, have been developed. This paper reviews the scientific literature on the development and application of DSSs for water treatment, including physically-based models, statistical models, and artificial intelligence techniques, and suggests future directions in the field. We first set the context of how water quality is impacted by climate change and extreme weather events. We then provide a comprehensive review of DSSs and conclude by offering a series of recommendations for future DSS efforts for WTPs, suggesting that these tools should (1) more accurately reflect the practical needs of WTPs, (2) represent the tradeoffs between the multiple competing objectives inherent to water treatment, (3) explicitly handle uncertainty to better inform decision makers, (4) incorporate nonstationarity, especially with regard to extreme weather events and climate change for long-term planning, and (5) use standardized terminology to accelerate the dissemination of knowledge in the field.
Water impactWater treatment plants (WTPs) must reliably provide clean drinking water to their consumers. To do so, water planners must make decisions about WTP infrastructure and operations despite uncertainties about the future. In this paper, we review tools which can aid in this decision-making process and explore potential impacts of future climate on WTPs. |
1. Introduction
The production of potable water is ranked among the most important developments in public health,1,2 and water treatment plants (WTPs) are responsible for providing this resource to consumers, by treating source water to turn it into potable drinking water (Fig. 1). WTP failures can have devastating impacts on human health and can erode consumer confidence in the safety and reliability of the water supply. To minimize the risk of such failures and promote public health, the United States Environmental Protection Agency (US EPA)3 and similar entities around the world enact strict laws which regulate potable water quality.4 As the impact of contaminants on human health has become more fully understood, additional regulations have been enacted over time. While these laws benefit public health, WTPs must shoulder the fiscal burden to improve their system, if necessary, to remain in compliance.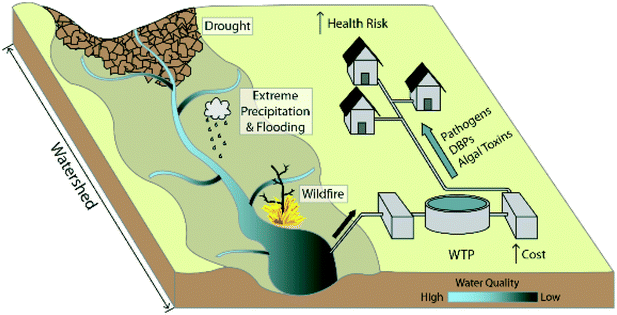 | ||
| Fig. 1 The impact of climate change and extreme weather events on drinking water quality. Degraded source water quality can lead to higher costs for WTPs and elevated health risk for consumers. | ||
In addition to meeting the regulations in the near future, WTP planners must also consider whether the plant will remain in compliance for years to come. Nonstationarity, with regard to a changing climate and the shifting nature of extreme weather events,5–12 makes forecasting future compliance increasingly difficult because these climatic factors (e.g. drought, extreme precipitation, temperature increase) have been linked to source water quality degradation.13–20 Furthermore, the physical, chemical, and biological impacts on source waters may have important design, operating, and cost implications for future drinking water treatment processes (Fig. 1).16–18 In the US, specifically, changes in source water quality could impact compliance with regulations such as Surface Water Treatment Rules and Disinfectants and Disinfection Byproducts Rules (stage 1 and 2). Concerns about climate change amplify the already complex decision-making problem for WTPs, which face regulatory and budgetary constraints, tradeoffs between performance and cost objectives, and high levels of uncertainty.
To deal with system complexity and improve decision-making, WTPs can employ a decision support system (DSS), which is a computer-based aid for decision-making that codifies stakeholder decision variables (possible actions), objectives (measures that quantify performance), and constraints (relationships that maintain desired performance). DSSs have been used in water treatment and throughout related fields to improve the quality, efficiency, and consistency of decision-making.21–24 To date, DSSs in water treatment have aided in operational and infrastructural decision-making on both short- and long-term time horizons.
2. Scope of review
The purpose of this paper is to review existing literature of DSSs regarding WTPs and highlight opportunities for advancement in this field. This review complements other water and wastewater treatment DSS reviews such as Hamouda et al.21 and Zhang et al.24 but differs in that it exclusively focuses on water treatment and addresses climatic impacts on water quality. The paper begins by discussing the effect of climate change and extreme weather on both source and drinking water quality and identifying the types of decisions water managers can choose among to prepare for such events and remain in compliance with regulations. Subsequently, we discuss how DSSs can aid in water treatment decision-making more generally and critically review WTP DSS efforts in the literature. Based on this review, we provide recommendations for the development of future DSSs in the field.Although this paper covers a wide range of topics, there are many important research areas that were beyond the scope of this work. First of all, this review focuses on WTP DSSs rather than the entire “catchment to consumer” potable water system which includes source water management, water treatment, and distribution. For more information regarding source water and drinking water distribution decision-making, we direct the interested reader to the following references on the motivation for source water protection and catchment management (Emelko et al.16 and Honti et al.25), source water DSS (Arabi et al.,26 Borsuk et al.,27 Ferguson et al.,28 Heberling et al.,29 and Rossi et al.30) and water distribution DSS (Kleiner et al.31 and van Zyl et al.32). For a detailed treatment of the impact of climate change and extreme weather events on water quality, the reader should consult Khan et al.,17 Stanford et al.,18 and Delpla et al.,15 since we only cover this topic briefly in this paper.
3. Influence of climate change and extreme weather events on drinking water quality
For WTPs, the physical, chemical, and biological impacts on source waters due to climate change and extreme weather events may have important design, operating, and cost implications for future drinking water treatment processes.16–18 This is evidenced by the results of a recent survey by the Water Research Foundation that covered major water utilities in the United States and Australia. In this survey, utilities expressed concern about the impacts of climatic events on drinking water quality.18 US participants stated that the leading water quality issues from extreme events were related to the formation of disinfection byproducts (DBPs) and changes in source water quality. Other areas of concern for water quality included cyanobacteria and related algae blooms and distribution system water quality degradation. The same survey of Australian utilities produced slightly different results, likely due to differences in DBP regulations between the two countries. In both countries, only a minority of utilities expressed concern for long-term climate trends, such as warming temperatures, rising sea level, and a longer hot season. In general, utilities expressed the greatest interest in extreme events, such as rainfall, flooding, and drought.For utilities looking to mitigate the impact of extreme events, the literature has suggested that planners consider redesigning treatment processes, diversifying water sourcing options, increasing redundancy of plant design, altering long-term operations and maintenance plans, developing effective extreme event response plans, and enhancing water quality monitoring.15,17,18 To aid in this decision-making process, we provide information about the water quality implications of climate change and extreme weather events in the following sections.
Because the magnitude of water quality impacts are highly variable and depend on local conditions,18 we will focus our discussion on general water quality trends. For the sake of illustration, we will discuss the overall water quality implications of climate change and note a few common extremes (i.e. drought, wildfire, extreme precipitation, and floods to inform water planners) that will likely be impacted by climate change in the following sections (Fig. 1). Although it is beyond the scope of this paper, planners should also consider other impacts, such as changing land use, which also contributes to nonstationary source water quality.33–35
3.1 Climate change
As noted by the Intergovernmental Panel on Climate Change (IPCC),10 climate change effects on hydrology show both increasing and decreasing trends in streamflow magnitudes depending on the local geography, precipitation regime and whether the system is snowmelt dominated. However, far fewer studies have assessed the climatic influences on water quality, mostly conducted in isolated studies. Studies from a variety of time periods indicate that in areas with greater precipitation and runoff, pollutant loads tend to increase as more pollutants are continuously transferred from the near surface soil to the channel (e.g. Curriero et al.;14 Tetzlaff et al.36). Temperature also plays a dominant role in water quality, as greater temperatures promote pathogens37 and algal blooms38 to flourish, thereby producing more dissolved organic matter (e.g. Benítez-Gilabert et al.39), and less dissolved oxygen.40 Though trends are mostly statistically significant from local studies, direct relationships between climate and water quality remain largely unknown on a global scale due to the scarcity of climate change water quality studies and the spatial heterogeneity of anthropogenic impacts and land use pollutant sources.3.2 Drought
Reduced rainfall associated with drought decreases runoff within a watershed, altering the transport of materials, such as nutrients and metals, to source waters.41,42 Decreased water volumes also increase the impact of point-sources (e.g. wastewater treatment effluent) on source water quality. Moreover, droughts may encourage algal blooms by increasing nutrient concentrations, water temperatures, and residence times.43,44 Collectively, drought impacts can fundamentally alter nutrient cycling and biota within watersheds and reservoirs for months or even years.42Although droughts tend to degrade water quality among source waters, the impacts on riverine systems and lakes and reservoirs may differ.41 Additionally, the timing of droughts determines the severity of water quality impacts; if droughts are in sequence with other extreme events, their adverse impacts on water quality may compound. For instance, storm events following periods of prolonged drought have been found to markedly increase organic matter concentrations.45
3.3 Wildfires
Water quality impacts due to wildfires are particularly significant because forest catchments are high quality, high quantity source waters. For instance, forest catchments provide one-third of the 105 largest cities in the world with a significant amount of their drinking water and provide two-thirds of all water supplies in western North America, including drinking water for approximately 180 million U.S. citizens.16,46Among several impacts on ecosystems, wildfires are known to affect water quality. Wildfires can increase soil erosion rates by several orders of magnitude due to 1) reduced soil stability and 2) increased exposure to precipitation caused by loss of vegetation, and 3) induced soil water-resistance which increases runoff.47,48 This erosion often leads to increased levels of suspended sediment and sediment-related contaminants (particularly nutrients, organic carbon, and heavy elements) in source water,46,47,49 although better characterization of the mobilization of organic carbon is still being investigated.50 While wildfires can cause erosion, the magnitude is dependent on an area's susceptibility to erosion,51 precipitation patterns, and the severity, spatial extent, and frequency of wildfires.52,53
3.4 Extreme precipitation and floods
Compared to other storm events, floods are responsible for the highest rates of soil erosion in streams.54 Increases in extreme precipitation and flooding due to climate change heighten the likelihood of high erosion and subsequent turbidity events due to increased overland flow30,55,56 and may intensify bacterial and contaminant metal fluxes.57,58 Furthermore, extreme precipitation events are often associated with waterborne disease outbreaks: heavy rainfall can overwhelm WTPs, cross-contaminate sewage and drinking-water pipes (especially for old systems), and lead to sewage overflow into source waters.13,20 In the United States, 51% of waterborne disease outbreaks were preceded by precipitation events above the 90th percentile and 68% by events above the 80th percentile.143.5 Source water quality linked to drinking water quality
In the previous sections, we discussed the potential impacts climate change and extreme events can have on source water quality. In this section, we explore how such source water quality changes can impact drinking water quality. Specifically, we focus on how source water affects three drinking water contaminants of concern: DBPs, pathogens, and algal toxins.DBPs are unintended byproducts formed as a result of adding disinfectants (e.g. chlorine and chloramine) to treat drinking water. They are formed via the reaction between chemical disinfectants and naturally occurring organic matter. Since increased organic matter is often associated with extreme events, this series of events portends a greater potential for DBP formation. DBPs have been associated with cancer risks as well as other acute and chronic effects to human health.59 The concentration and type of DBP in drinking water are dictated by source water quality characteristics, such as pH, temperature, presence of organic matter, and levels of bromide and iodide.60 By law, US WTPs must adhere to the US EPA's maximum contaminant levels for DBPs—including total trihalomethanes, haloacetic acids, bromate, and chlorite—as well as regulations for the DBP precursor, total organic carbon under stages 1 and 2 of the Disinfectants and Disinfection Byproducts Rules.61
As described above, flooding and extreme precipitation can increase the occurrence of pathogens in source waters. In the context of drinking water treatment, if pathogen concentrations exceed the removal capacity of the WTP, disease outbreaks and other human health impacts can occur. Bacterial parameters (e.g. E. coli, coliform, fecal streptococcal, and Clostridium perfringens counts) have been found to increase considerably during extreme runoff events.57 Furthermore, increased turbidity levels, such as those caused by wildfires and floods, can cause a decrease in filtration effectiveness and are often associated with elevated levels of viruses, parasites, and bacteria.62
Most closely linked with droughts, projected temperature increases, changes in water quality, and enhanced stratification promote the growth of harmful algal and cyanobacterial blooms.43,44 These blooms can produce potent neurotoxins of concern in drinking water, including microcystin.60,63 In addition to health risks, algal and cyanobacterial blooms can produce geosmin and 2-methylisoborneol—non-toxic compounds associated with taste and odor issues in water which can lead to distrust among consumers.64 Lastly, algae can release DBP precursors within a drinking water system.65
In summary, the future occurrence of algal toxins, DBPs, and pathogens in drinking water is projected to increase because of changing extreme events due to climate change. Elevated levels of these contaminants pose a risk to consumer health and may increase the treatment costs associated with drinking water. The extent of these impacts, however, is both uncertain and variable from site to site. So what tools can water planners use to make decisions under such uncertain future conditions? Furthermore, do these tools meet the actual needs of water planners? In the following section, we attempt to answer these questions by looking to DSS literature in water treatment.
4. Decision support systems
DSSs are frameworks designed to aid in decision-making. The nature of DSSs can vary greatly in terms of data requirements, time horizon, and purpose. For instance, many quantitative models (e.g. physically-based models or Bayesian networks) can be used to optimize objective functions such as minimizing cost or maximizing the utility (as defined by the stakeholders) of a set of long-term infrastructural decisions. Contrastingly, a rule-based DSS could be used to inform a water treatment operator how to troubleshoot uncommon water quality issues. In general, DSSs comprise a model and a database and are flexible to accommodate changes in the problem formulation and the decision-making approach of stakeholders.66 These types of systems have been successfully used in a range of environmental applications for decision-making, including the development of regional energy strategies,67,68 wastewater treatment,21,24 and remediation of contaminated soils.69,70 In decision-making, there are also tools similar to DSS known as risk assessment tools which quantify or diagnose areas of risk and suggest corrective action to mitigate potential failure (see Schijven et al.,71 Smid et al.,72 Lindhe et al.,73,74 Arvai et al.,67 and Ferguson et al.28) and are popularly used and developed by organizations such as the World Health Organization, the US EPA, and International Organization for Standardization. The term risk assessment tool is often used in public health, microbiology, and risk analysis and management literature but less frequently found in engineering and business management, which use decision support system terminology. Based on its similarities with models commonly used in DSSs (e.g. physically-based and data-driven models), we will include risk assessment tools in this review and frame them with DSS terminology.In the field of water and wastewater treatment DSSs, Zhang et al.24 and Hamouda et al.21 provide comprehensive reviews but dedicate their work predominantly on wastewater rather than water treatment. This emphasis on wastewater DSSs is reflective of the greater body of literature compared to water treatment DSSs. Nonetheless, numerous DSSs for water treatment have been developed in recent decades but they have yet to be compiled into a comprehensive review until this work. In this paper, we will review DSSs for drinking water treatment, specifically.
In the following sections, we provide a brief overview for DSS development in environmental management. An exact framework for the development of DSSs is not widely agreed upon (McIntosh et al.75 and Poch et al.76) but there are common steps found in environmental decision-making literature (see Poch et al.,76 Cortés et al.,77 Hamouda et al.21 for examples). These steps are generally to (1) identify stakeholders, decision makers, and modelers; (2) formulate the problem; (3) collect/analyze data; (4) choose the appropriate DSS; (5) implement and evaluate/verify the DSS. Due to the wide variety of DSSs, we will not attempt to define a general framework for this paper. Instead, we will focus our discussion on steps 1, 2, and 4 listed above, which we feel are widely shared among DSSs and are important to understand for readers interested in DSS development.
4.1 The role of stakeholders, decision makers, and modelers
While DSSs have the potential to improve a project, the amount of information and insight provided from stakeholders and decision makers will ultimately determine the quality and usefulness of the DSS.78–80 All parties that have an interest in the WTP need to be identified, such as operators, water managers, and government officials, so the DSS is representative of the objectives of the entire group, the system is realistically constructed, and practical decisions are considered. In gathering information, modelers should be impartial and attempt to represent the stated preferences of the stakeholders as accurately as possible. This is especially important for a class of applications termed “wicked problems”, in which there are a variety of stakeholders and decision makers with conflicting values and diverging ideas for solutions81—in which public health and welfare is at stake.82–84 To create the DSS, stakeholders must agree on the scope of the DSS in what is known as the problem formulation.4.2 Problem formulation
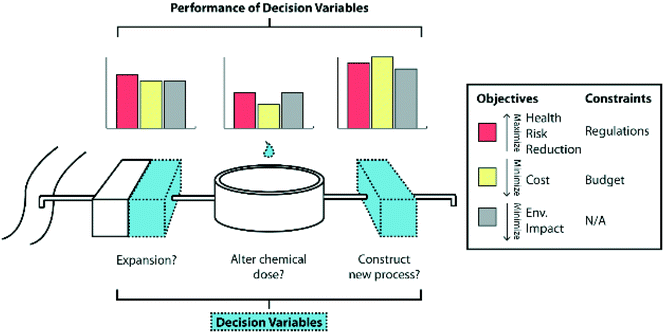
The problem formulation is made up of decision variables, objectives, and constraints. Decision variables (D), also known as decision levers, are parameters a decision maker can realistically change; objectives (O) are metrics that seek to quantify the system's performance (e.g., cost, measurements of water quality, and environmental impact); and constraints (C) are required aspects of the system that must not be violated, such as stakeholders' desired performance. Fig. 2 illustrates these concepts and how they can be applied to water treatment. Depending on the decision context of the problem, various aspects of the problem formulation may be more or less important. For example, a DSS could be constructed to quantitatively evaluate the performance of a given management plan, in which case the decisions could be fixed, but the objective outputs are of paramount importance.22 There could also be a situation in which managers are trying to meet a given regulation, so the set of considered objectives is fixed, but the decisions that could be considered are quite dynamic and need to be found intelligently.Additionally, the stakeholders must determine the time horizon—the frequency at which a decision problem is evaluated—for their formulation. This is because a DSS can be used regularly, perhaps on a daily basis, or it may only be used once to determine a large, infrastructural decision. Determining the correct time horizon for long-term planning, for example, is important so decision-making plans strike the balance between adaptability and efficiency of decision-making. This and other aspects of long-term decision-making are discussed in more detail in section 5. Once stakeholders agree upon the details of the problem formulation, including the time horizon, the appropriate DSS must be selected for the task.
4.3 DSS selection and review
To begin a discussion about the selection of appropriate DSSs, it is important to note that, given the broad definition of DSSs, the terminology used to categorize DSS models is not widely agreed upon within environmental and water management. We invite the interested reader to compare between Cortés et al.,77 Poch et al.,76 Hamouda et al.,21 Kelly (Letcher) et al.,22 Denzer,85 Rizzoli and Young,86 and Zhang et al.24 to explore various classifications. In this paper, we will discuss three categories of DSSs: those based on physically-based models (PBMs), statistical models (SMs), and artificial intelligence (AI). This aligns most closely with the classification found in Cortés et al.,77 Poch et al.,75,76 and Hamouda et al.21 In this section, we discuss both the theory behind DSS selection and review how these have been applied to water treatment literature (Table 1). In Table 1, we review DSSs (or major DSS components) found in WTP literature, provide a brief description of these tools, their objectives, the water quality parameters considered, their treatment of uncertainty, and their intended time horizon for decision-making (e.g. short- or long-term).| Source | DSS or DSS component | Description | Objective(s) | Water quality parameters | Treatment of uncertainty | Decision time horizon |
|---|---|---|---|---|---|---|
| a Denotes DSS which addresses climate change. Definitions. Short-term: time horizon generally less than one year. Long-term: time horizon generally greater than one year. Abbreviations. AOC: assimilable organic carbon. Br-: bromide ion concentration. DO: dissolved oxygen. DOC: dissolved organic carbon. SS: suspended solids. TOC: total organic carbon. TSS: total suspended solids. UV254: ultraviolet absorbance at 254 nm and one cm path length. | ||||||
| Pike120 | BN | Determine likelihood of major violations related to operator decisions and system characteristics | Minimize water quality violations | Total coliform, turbidity, treatment chemicals, inorganic compounds, and synthetic and volatile organic compounds | Inherent to BNs | Short-term |
| Zhu and McBean119 | BN | Select maximum utility design and operations using stakeholder-defined utility functions | Minimize cost, cancer risk, bacterial contamination risk | TOC, pH, alkalinity, DBPs, and treatment chemicals | Inherent to BNs | Short-term |
| Lindhe et al.73 | Fault tree analysis | Perform an integrated, probabilistic risk analysis of drinking water systems from source to tap to identify potential failures in water quality and quantity | Minimize risk | Any water quality regulations | Monte Carlo sampling and Bayesian modeling | Long-term |
| Schijven et al.101 | Statistical analysis | Perform risk assessment for the treatment of surface water to drinking water that aids decision makers in formulating mitigation strategies and preventative measures for water safety | Maximize efficiency and consistency of microbial risk assessment | Concentration of pathogenic organisms | Monte Carlo sampling | Long-term |
| Schijven et al.71 | PBM, statistical analysis, and risk assessment | Predict risk of waterborne and foodborne infectious disease based on climate change scenariosa | Minimize risk and guide climate change adaptation strategies on infectious disease | Temperature, annual precipitation, Campylobacter, Cryptosporidium, and noncholera Vibrio species | Sensitivity analysis, Monte Carlo sampling, | Long-term |
| Collins and Ellis102 | ANN, regression, and expert system | Determine chemical doses from predictive models coupled with expert systems | Maximize efficacy of chemical dose | pH, turbidity, and treatment chemicals | N/A | Short-term |
| Zhu and Simpson106 | Decision and fault trees | Advise operations and diagnose problems using expert systems | Minimize cost | Turbidity and treatment chemicals | N/A | Short-term |
| Chowdhury et al.107,108 | Fuzzy set theory | Evaluate plant design and operations using fuzzy set theory and analytical hierarchy process | Minimize health risk, cost; maximize technical feasibility and disinfectant performance | DBPs, taste/odor, color, and disinfection achieved | Inherent to fuzzy set theory | Long-term |
| Lamrini et al.109 | ANN, expert systems, and fuzzy set theory | Select optimal coagulant dose using artificial neural networks, expert opinion, and fuzzy set theory | Maximize efficiency of coagulant dose | Turbidity, TSS, temperature, pH, conductivity, and DO | Inherent to fuzzy set theory | Short-term |
| Mirsepassi et al.123 | ANN | Predict treated water quality and optimal alum and polymer doses using a supervised learning algorithm | Minimize error in alum and polymer dose prediction | pH, turbidity, apparent color, true color, temperature, polymer dose, and alum dose | N/A | Short-term |
| Baxter et al.122 | ANN | Presents four ANNs for source water quality prediction, water demand forecasting, and process models | Minimize error in water parameter prediction | Flow rate, color, precipitation, air and water temperature, water demand, pH, turbidity, hardness, alkalinity, chemical dose, and overflow rate | N/A | Short-term |
| Maier et al., Van Leeuwen et al., and Zhange and Stanley103,125,126 | ANN, multi-variate regression, and linear regression103 | Predict treated water quality and optimal alum dose to be used in automation | Minimize error in alum dose prediction | Turbidity, pH, color, UV254, alkalinity, alum dose, and alum residual | N/A | Short-term |
| Serodes et al.128 | ANN | Develop methodology to predict optimal chlorine dose or residual concentration at critical locations in the water treatment and distribution system | Minimize error in chlorine dose and residual prediction | Turbidity, color, temperature, flow, chlorine dose, and residual chlorine | N/A | Short-term |
| Kulkarni and Chellam129 | ANN | Predict DBP formation after chlorine disinfection of drinking water | Minimize error in DBP prediction | DOC, UV254, Br-, chlorine dose, pH, contact time, and temperature | N/A | Short-term |
| Wiesner et al.95 | PBM | Determine least-cost design and configuration of unit processes for particle removal using nonlinear optimization program | Minimize cost | Particle size distribution and concentration of suspended solids | N/A | Long-term |
| Wu and Chu97 | PBM | Determine least-cost basin sizes and chemical feed rates for the design and operation of new or existing plant using nonlinear optimization program | Minimize cost | Corrosivity, alum feed rate, turbidity, total coliform, alkalinity, and chlorine disinfection | N/A | Long-term |
| Mhaisalkar and Bassin88 | PBM | Determine least-cost design using dynamic programming considering uncertainty in design | Minimize cost | SS concentration | Sensitivity analysis of optimal design | Long-term |
| Dharmappa et al.96 | PBM | Determine least-cost design and operations which meet regulations using nonlinear programming | Minimize cost | SS parameters and effluent water quality | N/A | Long-term |
| Boccelli et al.89,133 | PBM | Determine least-cost design using dynamic programming while incorporating model parameter uncertainty and influent variability | Minimize cost | Particle size distribution and concentration of suspended solids, and temperature | Sensitivity analysis and Monte Carlo simulations | Long-term |
| Gupta and Shrivastava90 | PBM | Determine least-cost, reliability constrained design using genetic algorithm | Minimize cost | Suspended solids concentration and temperature | Monte Carlo simulations | Long-term |
| Rietveld et al.99 | PBM | Simulate and control of WTP to reduce costs and improve water quality, stability of performance, and understanding of the process for plant operators | Minimize cost and environmental impact | pH, temperature, DOC, calcium, alkalinity, UV254, organic micro-pollutants, AOC, bromide, and treatment chemical doses | Quantify uncertainty in calibration | Short- and long-term |
| Worm et al.98 | PBM | Simulate and control of WTP using a SCADA-like interface and integrated hydraulic, water quality, and process control models | Minimize costs and emissions | Extensive water quality parameters contained in Stimela sub-model | N/A | Short- and long-term |
| Ribera et al.100 | PBM and risk analysis | Perform life cycle and human health risk assessment that serves as a multi-criteria tool for determining percent of water to be treated by nanofiltration | Minimize environmental impact and human health risk | DBPs | N/A | Long-term |
| Delpla et al.110 | PBM, decision tree, and risk analysis | Recommend risk reduction strategies for environmental change, including river basin management, water treatment process design, maintenance, performance, and monitoring considering catchment and treatment characteristics for small to medium plantsa | Minimize health risk | DOC, pH, temperature, micropollutants, and DBPs | Sensitivity analysis | Long-term |
We begin with a discussion of PBMs and SMs because there is overlap between the techniques used in these DSSs. PBMs simulate systems based on equations which represent their fundamental physics and chemistry. SMs, on the other hand, represent systems based on data and are commonly presented as probability distributions. Next, we discuss AI DSS which are used to mimic human reasoning. Within this diverse class of DSS, there are knowledge-based systems (KBSs), Bayesian networks (BNs), and artificial neural networks (ANNs). KBSs, also known as expert systems, consist of a knowledge base and rules or a procedure to make a decision.87 BNs and ANNs are both data-driven models but are distinct in their approach to decision support. BNs represent decision-making using conditional probabilities, while ANNs comprise interconnected neurons capable of predictive modeling of non-linear relationships.
For deterministic models, each set of inputs produces only one set of outputs each time the model is run. This deterministic approach, which is more common for PBMs than SMs (see Table 1), does not accurately reflect the uncertainty of real-world water planning problems. In the case of planning and managing WTPs, for example, the removal efficiency of the plant may be slightly variable over time and deviate from the theoretical conditions in the model. Stochastic models, on the other hand, can incorporate this randomness. While these uncertainties exist in the system, they are not always incorporated into modeling efforts.
To better reflect uncertainties in model parameters, two techniques are typically applied to models: sensitivity analyses, which seek to test the sensitivity of system performance to perturbations of uncertain model parameters,88 and Monte Carlo simulations, which sample from probability distributions of uncertain parameters in order to develop distributions of model outputs.89,90 In addition to the previously mentioned uncertainties, decision makers should be aware of how model structure impacts predictions as it is a primary source of uncertainty. However, for practical reasons, this so-called structural uncertainty is rarely considered in environmental modeling due to its difficulty.91 The interested reader can refer to Boccelli et al.92 for an example on dealing with model structure uncertainty in water treatment simulation, Refsgaard et al.91 regarding a framework for dealing with uncertainty due to model structure, and Refsgaard et al.93 on a general framework for dealing with uncertainty in environmental modeling.
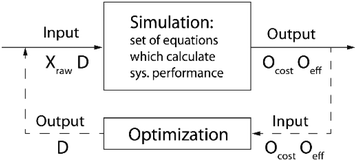
Lastly, techniques coupled with PBMs and SMs, such as scenario analysis and optimization, are necessary to generate and choose between various alternatives. In scenario analysis, a user can explore the system performance for a range of decisions and conditions. For instance, in WTP planning, a stakeholder may want to determine what plant design will perform best, on average, for two different seasons. To approach this problem using scenario analysis, the modeler may specify two influent water quality conditions representative of the different seasons and three design alternatives for a total of six scenarios. Based on the cost and effluent water quality for each model run, the user could then decide which of the three alternatives performs the best, on average. Alternatively, optimization techniques can be coupled with models to explore preferred decisions in a more automated fashion (Fig. 3).
When performing optimization using a model, one should refer to the objective (or objectives) defined in the problem formulation. The most common optimization approach in this review is known as least-cost optimization. In this method, cost is minimized and regulations constrain the effluent water quality. Because there is a single objective to optimize, this process yields a single solution. In multi-objective formulations, a concept referred to as Pareto optimality defines a set of multiple solutions for the problem. In a Pareto set, each solution represents one compromise between the multiple objectives; a solution is Pareto optimal if it is not exceeded in any of its objectives by another feasible solution.94
In water treatment DSS literature, PBMs are commonly used for design applications (Table 1). Most PBMs have been developed for individual WTPs and were based off of a least-cost plant design optimization approach outlined in Wiesner et al.95 For least-cost optimization, the performance of the treatment plant is constrained by water quality regulations and the cost is minimized. New optimization techniques, sensitivity analyses, improved model physics, and new treatment technologies advanced this approach,88,96,97 but until Boccelli et al.89 the uncertainty in these models was not comprehensively considered. To choose designs that are robust across a range of uncertainties, Boccelli et al.89 stressed the importance of considering the inherent variability and uncertainty in a decision-making framework. In a shift from least-cost optimization PBMs, recent literature has explored scenario-based modeling for multiple objectives. Both Worm et al.98 and Rietveld et al.99 use scenario-based numerical models to inform operational decision-making. Furthermore, Ribera et al.100 uses a scenario-based approach to perform a life cycle and human health risk assessment on nanofiltration alternatives.
In water treatment DSS literature, SMs have been generally used for risk assessment and as predictive models. For instance, in risk assessment, Schijven et al.101 collected quantitative microbial, source water quality, and water treatment data to analyze microbial risk from drinking water produced from surface water. These data were then fitted to probability distributions and sampled using Monte Carlo techniques to determine exposure and infection risk and inform decision-making. Additionally, both Collins and Ellis102 and Van Leeuwen et al.103 use statistical regression techniques for predictive modeling to inform operational decision-making for WTPs. These regression models are quite similar to ANNs (discussed in section 4.3.2.3) in that they are data-driven, predictive models. While these models could have been discussed alongside one another as “predictive models”, due to their differing roots—ANNs were created by artificial intelligence engineers and computer scientists while statisticians developed statistical models—we have followed convention of considering ANNs AI rather than a statistical technique.104 A similar argument could be made for considering BNs (see section 4.3.2.2) as SMs since they are heavily based on statistical methods.
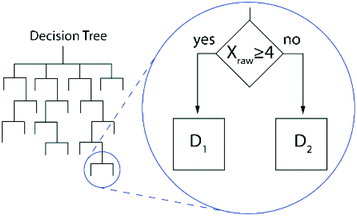
4.3.2.1 Knowledge-based systems. Knowledge-based systems, also known as expert systems, consist of a knowledge base and rules or a procedure to make a decision.87 KBSs include rule-based models, in which “if-then” rules guide the decision maker through possible alternatives; case-based models, in which past events are used to inform decisions regarding similar events; and logic-based models, in which a decision is made based on a series of logical statements. Like many AI tools, these decision-making structures, often conceptualized as decision trees, are relatively intuitive to users because they mimic human reasoning.
While there are many more complex variations, a simplistic decision tree is represented by Fig. 4. The left side of this figure represents the entirety of the tree, with several levels of branches that lead to an ultimate decision. The call out section on the right illustrates one possible pathway. Within the call out, the KBS tests if some numerical data (Xraw), which represents a raw water quality parameter, is greater than 4 units. If it is greater, decision D1 is chosen. If it is less than 4, the alternative is chosen. The other branches in this graphic could be used to classify other aspects of the plant, such as plant size, geographic location, type of disinfectant, whether it has advanced treatment or not, etc. to inform decision-making.
KBSs are advantageous in that, like BNs, they can systematically incorporate expert opinions into decision-making105 and they can also handle both quantitative and qualitative information. Furthermore, the scope of these models can range in detail from the detailed analysis of a small number of specific processes, to the holistic modeling of an entire system. Unlike BNs, which explicitly express uncertainty, KBSs do not commonly incorporate uncertainty into rules or their knowledge base.22
In water treatment DSS literature, the majority of KBSs have been developed to advise operational decision-making in WTPs by incorporating expert opinion. These systems were designed to codify the accumulated knowledge of plant operators about chemical dosages and problem diagnoses.102,106 Over time, more advanced techniques, such as fuzzy set theory and multi-criteria analysis, have been used in decision-making.107–109 Even with improved techniques, KBSs alone cannot be used to represent all types of problems. By coupling KBSs with other types of DSSs, however, authors have been able to look at more complex problems. For instance, Delpla et al.,110 which couples a PBM and a KBS, created a practical decision support tool for small and medium treatment plants planning for climate change. In this two-part DSS, the KBS is used to make catchment management and treatment recommendations based on semi-quantitative data associated with catchment type, climatic conditions, and treatment operations, and the PBM is used to assess the health risk of the plant considering both current and projected water quality levels.
Additionally, a logic-based KBS, known as fault tree analysis, has been used for risk analysis from catchment to consumer in Lindhe et al.73,74 In general, “a fault tree analysis is a risk estimation tool with the ability to model interaction between events… [and] identifies potential causes of system failure.”73 Using primarily expert judgment and some historical data, Lindhe et al. defines hundreds of probability distributions for model variables to describe the system's potential risk due to events that could lead to water quality or quantity failure. Based on this method, users can estimate the probability of failure, mean failure rate, and overall mean downtime of the system and individual sub-systems.
4.3.2.2 Bayesian networks. A BN is a stochastic model which defines causal influences between system variables—such as decisions and objectives—and quantifies the strength of these relationships through conditional probabilities.111–113 BNs are represented by a directed acyclic graph which links nodes (random variables) to represent the relationships between variables; specifically, a node is classified as either a parent or child node.114 A child node is one that is dependent on one or many parent nodes, which is graphically represented by arrows linking related nodes. A node with no parent is an input variable, whereas a node with no child is an output variable.
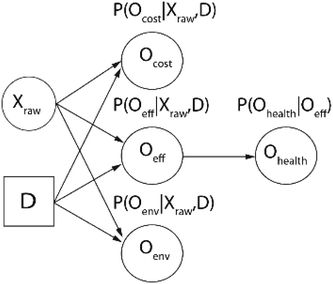
With the exception of input variables, each variable has an associated conditional probability distribution based on observed data or expert judgment.115 For example, if there is a node which represents the cost of a given decision, the probability distribution could be based on an operational cost dataset collected by the WTP. If there are no data available, a WTP expert could estimate this distribution given their accumulated knowledge in the field. These probability distributions are considered conditional because they vary depending on the value of the parent node. Using this information, decision makers can determine the most likely value of their objectives for a given set of decisions and also understand the level of uncertainty involved in their decision. This probabilistic approach to decision-making is what sets BNs apart from most other DSSs. We illustrate this approach for a water treatment application in Fig. 5.
The inputs of the illustrative BN in Fig. 5 are influent raw water quality parameters (Xraw) and a set of operational or infrastructural decision variables (D). Xraw and D are distinct types of input variables. D is deterministic, meaning that users will define a set of their choosing. Contrastingly, Xraw is a random variable which represents uncertain raw water quality characteristics as a probability distribution. Based on these input variables, conditional probability distributions for three objectives—cost (Ocost), effluent water quality (Oeff), and environmental impact (Oenv)—are generated. Furthermore, a conditional probability distribution for a fourth objective, human health risk (Ohealth), is created based on its parent node Oeff. In this example, decision makers can determine the likely performance of various decisions and raw water qualities for the four objectives.
The stochastic nature of these models means that they explicitly handle uncertainties based on assumptions about the system. BNs are also unique in that they can incorporate stakeholder objectives and can be used to optimize the expected utility of these stated objectives. These qualities make BNs successful in fields of water management, such as water resources and environmental management.114,116,117 BNs are relatively simple to construct because although they are capable of representing complex systems, they do not explicitly model each process. On the other hand, if stakeholders were concerned with the detail of a specific process, BNs would not be suited for such an application. For a detailed discussion about evaluating the performance and uncertainty of BNs, see Marcot.118
In water treatment literature, BNs have been used to better represent the uncertainties involved in decision-making and to diagnose treatment issues. Zhu and McBean119 used BNs to represent the tradeoff among uncertainties in a decision maker's belief and the expected utility of infrastructural and operational decisions for multiple objectives. To quantify the benefit of various objective values, the authors created what are known as utility functions. Utility functions (U) represent the expected utility—between 0 and 1—that a stakeholder gains from an objective. For instance, a simple cost utility function could be represented by eqn (1).
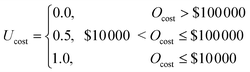 | (1) |
4.3.2.3 Artificial neural networks. An artificial neural network (ANN) is an artificial intelligence method inspired by the biological nervous system.122,123 Constructed from multiple layers of interconnected neurons, ANNs are able to model non-linear relationships between parameters.123 By training ANNs with large amounts of data, the strength of the connection between neurons adapts to minimize error between the neural network prediction value and the known parameter value. Their ability to deal with non-linear relationships makes them well-suited to predict complex water treatment processes.124 To eliminate the need for routine jar testing for coagulation, for example, several papers suggest using ANNs to predict the optimal alum dose for plant operation.103,122,123,125,126Fig. 6 represents a simplistic architecture for an ANN used for such an application.
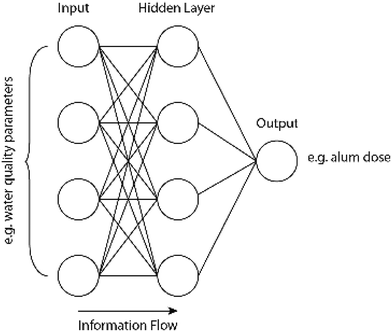 | ||
| Fig. 6 Simplistic architecture of an ANN for the prediction of the optimal alum dose during coagulation. | ||
In Fig. 6, any water quality parameters that are useful indicators of coagulant dose would serve as input nodes (e.g. turbidity, pH, color, UV254, alkalinity, etc.). Any hidden layers—in this example there is only one—then connect the input water quality parameters to the output alum dose prediction. The performance of an ANN is dependent on the architectural parameters chosen by the modeler, such as the number of hidden layers, the number of neurons within each layer, the rate at which the model “learns”, and initial weights on the connections between neurons.127
In addition to their use in coagulant dose prediction, water treatment ANNs been used for optimal chlorine disinfection dosage,128 the prediction of DBPs,129 and modeling nanofiltration127,130 and are generally geared toward the optimization of operations. For guidelines on developing ANNs for water treatment, we direct the interested reader to Baxter et al.,124 Wu et al.,131 and Maier et al.132
ANNs have the advantage of being flexible, able to handle non-linear water quality relationships, and can be used in process automation. For instance, neural networks can be trained using common operational data and can adjust predictions over time based on new data.128 Moreover, when integrated into supervisory control and data acquisition (SCADA) systems, ANNs can inform plant operators about optimal chemical doses and chemical costs in real-time or can automate these processes directly.122 However, ANNs require large quantities of representative historical data to make useful predictions128 in contrast with mechanistic models which require little input data. Furthermore, unlike mechanistic models which are grounded in the fundamental physics and chemistry behind a process, ANNs are criticized for their lack of explanatory power due to the ‘black box’ nature of their hidden layers.
5. Analysis of DSSs and recommendations for future work
The reviewed DSSs consider a wide range of decisions and objectives in water treatment for numerous time horizons. Predictive models, such as ANNs and some SMs, can aid operators in day-to-day decision-making, such as selecting optimal coagulant and disinfectant doses. Optimization using PBMs can inform least-cost designs and do not require large amounts of data to makes accurate predictions. KBSs, such as case-based reasoning, can help operators troubleshoot when a treatment plant experiences conditions beyond their level of expertise. BNs explicitly acknowledge the uncertainty involved in real-world decision-making by representing choices probabilistically. This ensemble of DSSs presents a number of options for water managers or researchers interested in computer-assisted decision-making for water treatment. However, future research in this field should be improved in a number of areas. Based on our review of DSSs for water treatment, we recommend that future work should have the following characteristics:(1) More accurately reflect the practical needs of WTPs.
DSSs are developed, first and foremost, to inform decision makers. For this reason, DSS studies should inherently be application-oriented and include stakeholder input. However, the practical implications of these models are often overlooked in water treatment literature, as noted by Boccelli et al.89 and Dharmappa et al.96 These authors provide context for when DSSs—in their case, least-cost optimization PBMs—are appropriate and discuss their limitations. Moreover, Dharmappa et al. creates a practical framework for integrating data from bench- and pilot-scale studies into DSSs throughout the design process. Worm et al.98 and Rietveld et al.99 also provide good examples of practical DSS research. Their papers include discussions of the graphical user interface, a case study for DSS implementation, and additional features such as operator training support. Other DSS literature which examine practical case studies include Lindhe et al.,73,74 Poch et al.,76 and Kragt.121 These examples of application-based research serve to narrow the gap between DSS theory and application.
(2) Explicitly handle uncertainty in DSSs to better inform decision makers.
There is uncertainty inherent to any DSS but few of these tools accurately express that uncertainty to the decision maker. BNs and fault tree analyses are notable exceptions; however, there are few examples of these types of DSSs that have been developed for WTPs (Table 1). To more accurately consider the uncertainty of WTP decision-making, DSSs should conduct a sensitivity analysis of the parameters, when applicable, and also consider the systematic (epistemic) and inherit variability in a system. Representing such uncertainties can be improved through techniques such as Monte Carlo simulations,89,90 Bayesian methods,119,120 and fuzzy set theory,107,108 but these are not always used in practice. For example, Bayesian techniques have been proposed to represent model uncertainty in ANNs without adding prohibitive computational cost but these have not been widely adopted.134,135
(3) Incorporate nonstationarity in WTP DSSs, especially with regard to extreme weather events and climate change for long-term planning.
Nearly all models reviewed implicitly assume stationarity in their systems—an assumption which is challenged by climate change, population growth, water demand, and land use change. The stationarity assumption can lead to a misrepresentation of the system for long-term decision-making—sometimes in unanticipated ways. For instance, it is important for WTPs to consider changing trends in water use, such as increased uptake water-efficient technologies, because they can cause flows to decrease in the distribution system. Subsequently, low flows increase water age and thus increase the formation of DBPs.136,137 Therefore, in this case, treating water demand as stationary over time would underestimate the actual risks posed to consumers.
Until recently, water treatment planners have assumed stationarity in projecting future climate. Due to the effects of anthropogenic climate change, however, stationarity can no longer be assumed.5–8 To prepare for possible climate futures in long-term planning, DSSs must consider the implications of nonstationary source water quality parameters and estimate their uncertainty. Nonstationarity amplifies the risk and uncertainty in our natural and manmade water systems, especially with respect to extreme weather events (i.e. flooding, drought, heat waves, wildfires, and cyclones).9,56,138–140 Thus far, as noted by Khan et al.,17 the impact of extreme weather events on drinking water treatment decision-making remains largely unstudied. Moreover, we also find few examples of DSS which address climate change in this review.71,110 There needs to be more effort directed toward the development of DSSs which consider these climatic conditions for long-term planning. By using robust decision-making techniques, creating such a DSS for long-term planning is possible.
Long-term planners often face deep uncertainty, in which decision makers do not know or cannot agree on the extents of the system, their objectives and relative weights of each, or the probability distribution for uncertain inputs to the system.141,142 To cope with deep uncertainty, such as when considering a nonstationary climate, decision-making should be robust, i.e. largely insensitive to possible future scenarios.143,144 Robustness can be either static, in which decision makers implement a fixed policy that will perform reasonably well in practically all conceivable situations,142 or adaptive, in which decision makers are prepared to change the policy over time, in case conditions change.142–144 Such strategies for decision-making under deep uncertainty are increasingly being used in the water resources domain for long-term viability of management plans and strategies,82 so it is likely that water treatment DSSs could benefit from these techniques.
(4) Represent the tradeoffs between the multiple competing objectives inherent to water treatment in optimization-based DSSs.
Water treatment is often described as a problem with multiple potentially conflicting goals, including minimizing cost, system failure, health risk, and environmental impact. Nonetheless, for the case of optimization, historically there has been a desire to cast the problem with a singular objective (e.g. minimize cost), especially if a regulation calls for a particular set of requirements that must be made. A growing body of evidence suggests, however, that a multi-objective formulation can provide a more holistic view of a problem.94,144 In fact, multi-objective optimization techniques have been successfully used to explore tradeoffs in related fields, such as wastewater treatment,145,146 water distribution networks,147,148 water resources management,149–151 and groundwater remediation.152,153
Consider the problem of designing WTPs facing extreme events. Although it would be ideal to be able to design a plant to meet regulations under all plausible conditions, doing so would make them prohibitively expensive. Therefore, it may be less advantageous to use the traditional least-cost, regulation-constrained optimization, which dictates that the system must not fail even for extreme events. In reality, a WTP that faces extreme conditions may fail in some manner, which leads to consideration of frequency-based performance objectives that have been shown to be popular in the area of water resources planning and other fields. In this case, the decision maker may care about how likely the system is to fail (reliability), how quickly it recovers from failure (resiliency), and how severe the consequences of failure may be (vulnerability).154 By adding one or more of these failure metrics, the decision maker can better understand the tradeoff between cost and potential failure and make an informed decision accordingly—similar failure metrics were used in fault tree analysis of water systems in Lindhe et al.73 While failure could also be represented as a constraint (e.g. 95% reliability) to maintain the single-objective formulation, this would mask the tradeoff between cost and reliability, which could be of interest to the stakeholder. For example, if increasing the reliability from 95% to 97% is cost-effective, the stakeholder may choose a slightly higher cost to the added reduction in risk.
(5) Use standardized terminology to accelerate the dissemination of knowledge in the field.
Lastly, we recommend that standardized terminology be developed in water and environmental management decision support literature. Because drinking water safety is an interdisciplinary field, researchers in public health, environmental and water resources engineering, and risk assessment and management, each have developed decision-making tools which cater to and use the vocabulary of their respective discipline. If a standard terminology cannot be agreed upon, the inconsistencies in wording between these similar decision-making tools, commonly under the names decision support systems or risk assessment tools, should at least be noted in the literature. Even within reviews of DSSs, there is little consistency in terminology regarding DSS architecture and development frameworks. These inconsistencies in language make it difficult for researchers to find relevant literature and slows progress.155 We hope that the interdisciplinary nature of this critical review may improve the connectedness of the literature and begins a discussion toward more uniform terminology in water and environmental management decision support.
6. Conclusions
Climate change and shifting climate extremes have been shown to degrade source water quality. Consequently, these changes are expected to adversely impact the performance of WTPs. In response, WTPs are seeking better approaches for long-term planning and risk management.18 This paper highlighted how DSSs can be improved to tackle these complex issues. In the process, we critically reviewed DSSs in water treatment more generally in an effort to improve the field as a whole. We found that relative to other branches of water and environmental management, water treatment DSSs receive little attention. Given the complexity nonstationarity adds to decision-making, however, DSSs are more relevant to water treatment than ever. Water planners could benefit from increased uptake of, and improvement upon, water treatment DSSs, especially with regard to long-term planning. Advancements in these DSSs can be informed by the literature referenced in this paper and our recommendations for future work.Acknowledgements
This work was supported by the U.S. Environmental Protection Agency “National Priorities: Systems-Based Strategies to Improve the Nation's Ability to Plan and Respond to Water Scarcity and Drought Due to Climate Change”, Grant No. R835865. The contents of this manuscript are solely the responsibility of the grantee and do not necessarily represent the official views of the US EPA. We acknowledge the considerable effort of anonymous reviewers whose comments have greatly improved the manuscript. We also acknowledge the careful proofreading of Joseph Ronald Kasprzyk.References
- A. Gadgil, Drinking Water in Developing Countries, Annu. Rev. Energy Environ., 1998, 23(1), 253–286 CrossRef.
- World Health Organization, W. H. Guidelines for Drinking-water Quality: Recommendations, World Health Organization, 2004 Search PubMed.
- F. W. Pontius, Update on USEPA's Drinking Water Regulations, J. - Am. Water Works Assoc., 2003, 95(3), 57–68 CAS.
- World Health Organization, Guidlines for Drinking-water Quality, World Health Organization, Geneva, 4th edn, 2011 Search PubMed.
- R. K. Craig, “Stationarity is Dead”-Long Live Transformation: Five Principles for Climate Change Adaptation Law, Harvard Environ. Law Rev., 2010, 34(1), 9–75 Search PubMed.
- P. C. D. Milly, J. Betancourt, M. Falkenmark, R. M. Hirsch, Z. W. Kundzewicz, D. P. Lettenmaier and R. J. Stouffer, Stationarity Is Dead: Whither Water Management?, Science, 2008, 319(5863), 573–574 CrossRef CAS PubMed.
- J. A. Wiens, G. D. Hayward, D. Hugh and C. Giffen, Historical environmental variation in conservation and natural resource management, John Wiley & Sons, 2012 Search PubMed.
- E. M. Wolkovich, B. I. Cook, K. K. McLauchlan and T. J. Davies, Temporal ecology in the Anthropocene, Ecol. Lett., 2014, 17(11), 1365–1379 CrossRef CAS PubMed.
- D. R. Easterling, J. L. Evans, P. Y. Groisman, T. R. Karl, K. E. Kunkel and P. Ambenje, Observed Variability and Trends in Extreme Climate Events: A Brief Review*, Bull. Am. Meteorol. Soc., 2000, 81(3), 417–425 CrossRef.
- IPCC, Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 2014 Search PubMed.
- G. A. Meehl, C. Tebaldi, H. Teng and T. C. Peterson, Current and future U.S. weather extremes and El Niño, Geophys. Res. Lett., 2007, 34(20), L20704 CrossRef.
- Climate Change Impacts in the United States: The Third National Climate Assessment, ed. J. M. Melillo, T. C. Richmond and G. W. Yohe, U.S. Global Change Research Program, 2014, DOI:10.7930/J0Z31WJ2.
- K. F. Cann, D. R. Thomas, R. L. Salmon, A. P. Wyn-Jones and D. Kay, Extreme water-related weather events and waterborne disease, Epidemiol. Infect., 2013, 141(4), 671–686 CrossRef CAS PubMed.
- F. C. Curriero, J. A. Patz, J. B. Rose and S. Lele, The Association Between Extreme Precipitation and Waterborne Disease Outbreaks in the United States, 1948–1994, Am. J. Public Health, 2001, 91(8), 1194–1199 CrossRef CAS PubMed.
- I. Delpla, A.-V. Jung, E. Baures, M. Clement and O. Thomas, Impacts of climate change on surface water quality in relation to drinking water production, Environ. Int., 2009, 35(8), 1225–1233 CrossRef CAS PubMed.
- M. B. Emelko, U. Silins, K. D. Bladon and M. Stone, Implications of land disturbance on drinking water treatability in a changing climate: Demonstrating the need for “source water supply and protection” strategies, Water Res., 2011, 45(2), 461–472 CrossRef CAS PubMed.
- S. J. Khan, D. Deere, F. D. L. Leusch, A. Humpage, M. Jenkins and D. Cunliffe, Extreme weather events: Should drinking water quality management systems adapt to changing risk profiles?, Water Res., 2015, 85, 124–136 CrossRef CAS PubMed.
- B. Stanford, B. Wright, J. C. Routt and S. J. Khan, Water Quality Impacts of Extreme Weather-Related Events, Water Research Foundation, Denver, CO, 2014 Search PubMed.
- P. G. Whitehead, R. L. Wilby, R. W. Battarbee, M. Kernan and A. J. Wade, A review of the potential impacts of climate change on surface water quality, Hydrol. Sci. J., 2009, 54(1), 101–123 CrossRef.
- P. R. Hunter, Climate change and waterborne and vector-borne disease, J. Appl. Microbiol., 2003, 94, 37–46 CrossRef.
- M. A. Hamouda, W. B. Anderson and P. M. Huck, Decision support systems in water and wastewater treatment process selection and design: a review, Water Sci. Technol., 2009, 60(7), 1757 CrossRef CAS PubMed.
- R. A. Kelly (Letcher), A. J. Jakeman, O. Barreteau, M. E. Borsuk, S. ElSawah, S. H. Hamilton, H. J. Henriksen, S. Kuikka, H. R. Maier and A. E. Rizzoli, et al., Selecting among five common modelling approaches for integrated environmental assessment and management, Environ. Model. Softw., 2013, 47, 159–181 CrossRef.
- F. A. Ward, Decision support for water policy: a review of economic concepts and tools, Water Policy, 2007, 9(1), 1–31 CrossRef.
- K. Zhang, A. Zargar, G. Achari, M. S. Islam and R. Sadiq, Application of decision support systems in water management, Environ. Rev., 2014, 22(3), 189–205 CrossRef.
- M. Honti, N. Schuwirth, J. Rieckermann and C. Stamm, Can integrative catchment management mitigate future water quality issues caused by climate change and socio-economic development?, Hydrol. Earth Syst. Sci., 2016, 1–28 Search PubMed.
- M. Arabi, R. S. Govindaraju and M. M. Hantush, Cost-effective allocation of watershed management practices using a genetic algorithm, Water Resour. Res., 2006, 42(10), W10429 CrossRef.
- M. E. Borsuk, C. A. Stow and K. H. Reckhow, A Bayesian network of eutrophication models for synthesis, prediction, and uncertainty analysis, Ecol. Modell., 2004, 173(2–3), 219–239 CrossRef.
- C. M. Ferguson, B. F. W. Croke, P. J. Beatson, N. J. Ashbolt and D. A. Deere, Development of a process-based model to predict pathogen budgets for the Sydney drinking water catchment, J. Water Health, 2007, 5(2), 187–208 Search PubMed.
- M. T. Heberling, C. T. Nietch, H. W. Thurston, M. Elovitz, K. H. Birkenhauer, S. Panguluri, B. Ramakrishnan, E. Heiser and T. Neyer, Comparing drinking water treatment costs to source water protection costs using time series analysis, Water Resour. Res., 2015, 51, 8741–8756 CrossRef.
- N. Rossi, Potential Impacts of Changes in Climate on Turbidity in New York City's Ashokan Reservoir, J. Water Resour. Plan. Manage., 2015, 0(0), 4015066 Search PubMed.
- Y. Kleiner, B. J. Adams and J. S. Rogers, Water Distribution Network Renewal Planning, J. Comput. Civ. Eng., 2001, 15(1), 15–26 CrossRef.
- J. E. van Zyl, D. A. Savic and G. A. Walters, Operational Optimization of Water Distribution Systems Using a Hybrid Genetic Algorithm, J. Water Resour. Plan. Manage., 2004, 130(2), 160–170 CrossRef.
- T. Johnson, J. Butcher, D. Deb, M. Faizullabhoy, P. Hummel, J. Kittle, S. McGinnis, L. O. Mearns, D. Nover and A. Parker, et al., Modeling Streamflow and Water Quality Sensitivity to Climate Change and Urban Development in 20 U.S. Watersheds, J. Am. Water Resour. Assoc., 2015, 51(5), 1321–1341 CrossRef.
- M. H. Mehaffey, M. S. Nash, T. G. Wade, D. W. Ebert, K. B. Jones and A. Rager, Linking Land Cover and Water Quality in New York City'S Water Supply Watersheds, Environ. Monit. Assess., 2005, 107(1–3), 29–44 CrossRef CAS PubMed.
- S. T. Y. Tong and W. Chen, Modeling the relationship between land use and surface water quality, J. Environ. Manage., 2002, 66(4), 377–393 CrossRef PubMed.
- D. Tetzlaff, C. Soulsby and C. Birkel, Hydrological connectivity and microbiological fluxes in montane catchments: the role of seasonality and climatic variability, Hydrol. Processes, 2010, 24(9), 1231–1235 CrossRef.
- C. D. Evans, D. T. Monteith and D. M. Cooper, Long-term increases in surface water dissolved organic carbon: Observations, possible causes and environmental impacts, Environ. Pollut., 2005, 137(1), 55–71 CrossRef CAS PubMed.
- M. T. H. van Vliet and J. J. G. Zwolsman, Impact of summer droughts on the water quality of the Meuse river, J. Hydrol., 2008, 353(1–2), 1–17 CrossRef.
- M. Benítez-Gilabert, M. Alvarez-Cobelas and D. G. Angeler, Effects of climatic change on stream water quality in Spain, Clim. Change, 2010, 103(3–4), 339–352 CrossRef.
- G. B. Sahoo, S. G. Schladow, J. E. Reuter and R. Coats, Effects of climate change on thermal properties of lakes and reservoirs, and possible implications, Stochastic Environ. Res. Risk Assess., 2011, 25(4), 445–456 CrossRef.
- L. M. Mosley, Drought impacts on the water quality of freshwater systems, review and integration, Earth-Sci. Rev., 2015, 140, 203–214 CrossRef CAS.
- B. Wright, B. D. Stanford, A. Reinert, J. C. Routt, S. J. Khan and J. F. Debroux, Managing water quality impacts from drought on drinking water supplies, J. Water Supply: Res. Technol.--AQUA, 2014, 63(3), 179 CrossRef.
- J. Heisler, P. M. Glibert, J. M. Burkholder, D. M. Anderson, W. Cochlan, W. C. Dennison, Q. Dortch, C. J. Gobler, C. A. Heil and E. Humphries, et al., Eutrophication and harmful algal blooms: A scientific consensus, Harmful Algae, 2008, 8(1), 3–13 CrossRef CAS.
- H. W. Paerl and J. Huisman, Climate change: a catalyst for global expansion of harmful cyanobacterial blooms, Environ. Microbiol. Rep., 2009, 1(1), 27–37 CrossRef CAS PubMed.
- D. W. Schindler, P. J. Curtis, S. E. Bayley, B. R. Parker, K. G. Beaty and M. P. Stainton, Climate-induced changes in the dissolved organic carbon budgets of boreal lakes, Biogeochemistry, 1997, 36(1), 9–28 CrossRef CAS.
- H. G. Smith, G. J. Sheridan, P. N. J. Lane, P. Nyman and S. Haydon, Wildfire effects on water quality in forest catchments: A review with implications for water supply, J. Hydrol., 2011, 396(1–2), 170–192 CrossRef CAS.
- K. D. Bladon, M. B. Emelko, U. Silins and M. Stone, Wildfire and the Future of Water Supply, Environ. Sci. Technol., 2014, 48(16), 8936–8943 CrossRef CAS PubMed.
- R. A. Shakesby and S. H. Doerr, Wildfire as a hydrological and geomorphological agent, Earth-Sci. Rev., 2006, 74(3–4), 269–307 CrossRef.
- A. K. Hohner, K. Cawley, J. Oropeza, R. S. Summers and F. L. Rosario-Ortiz, Drinking water treatment response following a Colorado wildfire, Water Res., 2016, 105, 187–198 CrossRef CAS PubMed.
- J. H. Writer, A. Hohner, J. Oropeza, A. Schmidt, K. Cawley and F. L. Rosario-Ortiz, Water Treatment Implications after the High Park Wildfire, Colorado, J. - Am. Water Works Assoc., 2014, 106, E189–E199 CrossRef.
- D. Brunsden, Applicable models of longterm landform evolution, Zeitschrift für Geomorphologic NF Supplement Band, 1980 Search PubMed.
- J. A. Moody and D. A. Martin, Initial hydrologic and geomorphic response following a wildfire in the Colorado Front Range, Earth Surf. Processes Landforms, 2001, 26(10), 1049–1070 CrossRef.
- F. J. Swanson, Fire and geomorphic processes, ed. H. A. Mooney, T. M. Bonnicksen, N. L. Christ and J. E. Lotan, 1981, pp. 401–444 Search PubMed.
- M. G. Wolman and J. P. Miller, Magnitude and Frequency of Forces in Geomorphic Processes, J. Geol., 1960, 68(1), 54–74 CrossRef.
- S. N. Lane, V. Tayefi, S. C. Reid, D. Yu and R. J. Hardy, Interactions between sediment delivery, channel change, climate change and flood risk in a temperate upland environment, Earth Surf. Processes Landforms, 2007, 32(3), 429–446 CrossRef.
- E. Towler, B. Rajagopalan, E. Gilleland, R. S. Summers, D. Yates and R. W. Katz, Modeling hydrologic and water quality extremes in a changing climate: A statistical approach based on extreme value theory, Water Resour. Res., 2010, 46(11), W11504 CrossRef.
- T. Kistemann, T. Claßen, C. Koch, F. Dangendorf, R. Fischeder, J. Gebel, V. Vacata and M. Exner, Microbial Load of Drinking Water Reservoir Tributaries during Extreme Rainfall and Runoff, Appl. Environ. Microbiol., 2002, 68(5), 2188–2197 CrossRef CAS PubMed.
- S. A. Longfield and M. G. Macklin, The influence of recent environmental change on flooding and sediment fluxes in the Yorkshire Ouse basin, Hydrol. Processes, 1999, 13(7), 1051–1066 CrossRef.
- S. Chowdhury, P. Champagne and P. J. McLellan, Models for predicting disinfection byproduct (DBP) formation in drinking waters: A chronological review, Sci. Total Environ., 2009, 407(14), 4189–4206 CrossRef CAS PubMed.
- S. D. Richardson, Disinfection by-products and other emerging contaminants in drinking water, TrAC, Trends Anal. Chem., 2003, 22(10), 666–684 CrossRef CAS.
- US EPA, O. Stage 1 and Stage 2 Disinfectants and Disinfection Byproducts Rules http://www.epa.gov/dwreginfo/stage-1-and-stage-2-disinfectants-and-disinfection-byproducts-rules (accessed Feb 2, 2016).
- US EPA, O. Table of Regulated Drinking Water Contaminants http://www.epa.gov/your-drinking-water/table-regulated-drinking-water-contaminants (accessed Feb 26, 2016).
- W. W. Carmichael, The cyanotoxins, Adv. Bot. Res., 1997, 27, 211–257 CAS.
- S. B. Watson, J. Ridal and G. L. Boyer, Taste and odour and cyanobacterial toxins: impairment, prediction, and management in the Great Lakes, Can. J. Fish. Aquat. Sci., 2008, 65(8), 1779–1796 CrossRef CAS.
- E. C. Wert and F. L. Rosario-Ortiz, Intracellular Organic Matter from Cyanobacteria as a Precursor for Carbonaceous and Nitrogenous Disinfection Byproducts, Environ. Sci. Technol., 2013, 47(12), 6332–6340 CAS.
- R. H. Sprague, A Framework for the Development of Decision Support Systems, MIS Q., 1980, 4(4), 1–26 CrossRef.
- J. Arvai, R. Gregory, D. Bessette and V. Campbell-Arvai, Decision Support for Developing Energy Strategies, Issues Environ. Sci. Technol., 2012, 28(4), 43–52 Search PubMed.
- D. L. Bessette, J. Arvai and V. Campbell-Arvai, Decision Support Framework for Developing Regional Energy Strategies, Environ. Sci. Technol., 2014, 48(3), 1401–1408 CrossRef CAS PubMed.
- J. W. N. Smith and G. Kerrison, Water, Air, Soil Pollut., 2013, 224(12), 1706 CrossRef PubMed.
- M. Sparrevik, D. N. Barton, M. E. Bates and I. Linkov, Use of Stochastic Multi-Criteria Decision Analysis to Support Sustainable Management of Contaminated Sediments, Environ. Sci. Technol., 2012, 46(3), 1326–1334 CrossRef CAS PubMed.
- J. Schijven, M. Bouwknegt, A. M. de Roda Husman, S. Rutjes, B. Sudre, J. E. Suk and J. C. Semenza, A Decision Support Tool to Compare Waterborne and Foodborne Infection and/or Illness Risks Associated with Climate Change, Risk Anal., 2013, 33(12), 2154–2167 CrossRef PubMed.
- J. H. Smid, D. Verloo, G. C. Barker and A. H. Havelaar, Strengths and weaknesses of Monte Carlo simulation models and Bayesian belief networks in microbial risk assessment, Int. J. Food Microbiol., 2010, 139(Supplement), S57–S63 CrossRef PubMed.
- A. Lindhe, L. Rosén, T. Norberg and O. Bergstedt, Fault tree analysis for integrated and probabilistic risk analysis of drinking water systems, Water Res., 2009, 43(6), 1641–1653 CrossRef CAS PubMed.
- A. Lindhe, T. Norberg and L. Rosén, Approximate dynamic fault tree calculations for modelling water supply risks, Reliab. Eng. Syst. Saf., 2012, 106, 61–71 CrossRef.
- B. S. McIntosh, J. C. Ascough II, M. Twery, J. Chew, A. Elmahdi, D. Haase, J. J. Harou, D. Hepting, S. Cuddy and A. J. Jakeman, et al., Environmental decision support systems (EDSS) development – Challenges and best practices, Environ. Model. Softw., 2011, 26(12), 1389–1402 CrossRef.
- M. Poch, J. Comas, I. Rodríguez-Roda, M. Sànchez-Marrè and U. Cortés, Designing and building real environmental decision support systems, Environ. Model. Softw., 2004, 19(9), 857–873 CrossRef.
- U. Cortés, M. Sànchez-Marrè, L. Ceccaroni, I. R-Roda and M. Poch, Artificial Intelligence and Environmental Decision Support Systems, Appl. Artif. Intell., 2000, 13(1), 77–91 Search PubMed.
- R. M. Argent, J.-M. Perraud, J. M. Rahman, R. B. Grayson and G. M. Podger, A new approach to water quality modelling and environmental decision support systems, Environ. Model. Softw., 2009, 24(7), 809–818 CrossRef.
- D. M. Oliver, R. D. Fish, M. Winter, C. J. Hodgson, A. L. Heathwaite and D. R. Chadwick, Valuing local knowledge as a source of expert data: Farmer engagement and the design of decision support systems, Environ. Model. Softw., 2012, 36, 76–85 CrossRef.
- J. Papathanasiou and R. Kenward, Design of a data-driven environmental decision support system and testing of stakeholder data-collection, Environ. Model. Softw., 2014, 55, 92–106 CrossRef.
- C. W. Churchman, Guest editorial: Wicked problems, JSTOR, 1967 Search PubMed.
- J. Kwakkel, W. Walker and M. Haasnoot, Coping with the Wickedness of Public Policy Problems: Approaches for Decision Making under Deep Uncertainty, J. Water Resour. Plan. Manag., 2016, 0(0), 1816001 CrossRef.
- J. C. Liebman, Some Simple-Minded Observations on the Role of Optimization in Public Systems Decision-Making, Interfaces, 1976, 6(4), 102–108 CrossRef.
- H. Rittel and M. Webber, Dilemmas in a General Theory of Planning, Policy Sci., 1973, 4, 155–169 CrossRef.
- R. Denzer, Generic integration of environmental decision support systems – state-of-the-art, Environ. Model. Softw., 2005, 20(10), 1217–1223 CrossRef.
- A. E. Rizzoli and W. J. Young, Delivering environmental decision support systems: software tools and techniques, Environ. Model. Softw., 1997, 12(2), 237–249 CrossRef.
- T. Krueger, T. Page, K. Hubacek, L. Smith and K. Hiscock, The role of expert opinion in environmental modelling, Environ. Model. Softw., 2012, 36, 4–18 CrossRef.
- V. A. Mhaisalkar and J. K. Bassin, Dynamic Programming Optimization of Water-Treatment-Plant Design, J. Environ. Eng., 1993, 119(6), 1158–1175 CrossRef CAS.
- D. L. Boccelli, M. J. Small and U. M. Diwekar, Drinking Water Treatment Plant Design Incorporating Variability and Uncertainty, J. Environ. Eng., 2007, 133(3), 303–312 CrossRef CAS.
- A. Gupta and R. Shrivastava, Reliability-Constrained Optimization of Water Treatment Plant Design Using Genetic Algorithm, J. Environ. Eng., 2009, 136(3), 326–334 CrossRef.
- J. C. Refsgaard, J. P. van der Sluijs, J. Brown and P. van der Keur, A framework for dealing with uncertainty due to model structure error, Adv. Water Resour., 2006, 29(11), 1586–1597 CrossRef.
- D. L. Boccelli, M. J. Small and D. A. Dzombak, Effects of Water Quality and Model Structure on Arsenic Removal Simulation: An Optimization Study, Environ. Eng. Sci., 2006, 23(5), 835–850 CrossRef CAS.
- J. C. Refsgaard, J. P. van der Sluijs, A. L. Højberg and P. A. Vanrolleghem, Uncertainty in the environmental modelling process – A framework and guidance, Environ. Model. Softw., 2007, 22(11), 1543–1556 CrossRef.
- P. M. Reed, D. Hadka, J. D. Herman, J. R. Kasprzyk and J. B. Kollat, Evolutionary Multiobjective Optimization in Water Resources: The Past, Present and Future, Adv. Water Resour., 2013, 51, 438–456 CrossRef.
- M. R. Wiesner, C. R. O'Melia and J. L. Cohon, Optimal water treatment plant design, J. Environ. Eng., 1987, 113(3), 567–584 CrossRef CAS.
- H. B. Dharmappa, O. Fujiwara, J. Verink and S. Vigneswaran, Water-Treatment-System Design for Turbidity Removal, J. Environ. Eng., 1994, 120(4), 921–942 CrossRef CAS.
- M.-Y. Wu and W.-S. Chu, System Analysis of Water Treatment Plant in Taiwan, J. Water Resour. Plan. Manag., 1991, 117(5), 536–548 CrossRef.
- G. I. M. Worm, A. W. C. van der Helm, T. Lapikas, K. M. van Schagen and L. C. Rietveld, Integration of models, data management, interfaces and training support in a drinking water treatment plant simulator, Environ. Model. Softw., 2010, 25(5), 677–683 CrossRef.
- L. C. Rietveld, A. W. C. van der Helm, K. M. van Schagen and L. T. J. van der Aa, Good modelling practice in drinking water treatment, applied to Weesperkarspel plant of Waternet, Environ. Model. Softw., 2010, 25(5), 661–669 CrossRef.
- G. Ribera, F. Clarens, X. Martínez-Lladó, I. Jubany, V. Martí and M. Rovira, Life cycle and human health risk assessments as tools for decision making in the design and implementation of nanofiltration in drinking water treatment plants, Sci. Total Environ., 2014, 466–467, 377–386 CrossRef CAS PubMed.
- J. F. Schijven, P. F. M. Teunis, S. A. Rutjes, M. Bouwknegt and A. M. de Roda Husman, QMRAspot: a tool for Quantitative Microbial Risk Assessment from surface water to potable water, Water Res., 2011, 45(17), 5564–5576 CrossRef CAS PubMed.
- A. G. Collins and G. W. Ellis, Information processing coupled with expert systems for water treatment plants, ISA Trans., 1992, 31(1), 61–72 CrossRef CAS.
- J. van Leeuwen, C. W. K. Chow, D. Bursill and M. Drikas, Empirical mathematical models and artificial neural networks for the determination of alum doses for treatment of southern Australian surface waters, Aqua, 1999, 48(3), 115–127 CAS.
- H. R. Maier and G. C. Dandy, Neural networks for the prediction and forecasting of water resources variables: a review of modelling issues and applications, Environ. Model. Softw., 2000, 15(1), 101–124 CrossRef.
- D. Waterman, A guide to expert systems, 1986 Search PubMed.
- X. Zhu and A. Simpson, Expert System for Water Treatment Plant Operation, J. Environ. Eng., 1996, 122(9), 822–829 CrossRef CAS.
- S. Chowdhury, Decision making with uncertainty: an example of water treatment approach selection, Water Qual. Res. J. Can., 2012, 47(2), 153–165 CrossRef CAS.
- S. Chowdhury, P. Champagne and T. Husain, Fuzzy risk-based decision-making approach for selection of drinking water disinfectants, J. Water Supply: Res. Technol.--AQUA, 2007, 56(2), 75 CrossRef CAS.
- B. Lamrini, E. K. Lakhal and M. V. Le Lann, A decision support tool for technical processes optimization in drinking water treatment, Desalin. Water Treat., 2014, 52(22–24), 4079–4088 CrossRef CAS.
- I. Delpla, D. T. Monteith, C. Freeman, J. Haftka, J. Hermens, T. G. Jones, E. Baurès, A.-V. Jung and O. Thomas, A Decision Support System for Drinking Water Production Integrating Health Risks Assessment, Int. J. Environ. Res. Public Health, 2014, 11(7), 7354–7375 CrossRef PubMed.
- E. Pérez-Miñana, P. J. Krause and J. Thornton, Bayesian Networks for the management of greenhouse gas emissions in the British agricultural sector, Environ. Model. Softw., 2012, 35, 132–148 CrossRef.
- J. Pearl, Probabilistic inference in intelligent systems, Morgan Kaufmann San Mateo, CA, 1988 Search PubMed.
- P. Spirtes, C. N. Glymour and R. Scheines, Causation, Prediction, and Search, MIT Press, 2000 Search PubMed.
- A. Castelletti and R. Soncini-Sessa, Bayesian Networks and participatory modelling in water resource management, Environ. Model. Softw., 2007, 22(8), 1075–1088 CrossRef.
- K. H. Reckhow, Water quality prediction and probability network models, Can. J. Fish. Aquat. Sci., 1999, 56(7), 1150–1158 CrossRef.
- E. Baran and T. Jantunen, Stakeholder consultation for bayesian decision support systems in environmental management, in Proceedings of the Regional Conference on Ecological and Environmental Modeling (ECOMOD), September 15–16, Penang, Malaysia, 2004 Search PubMed.
- J. Bromley, N. A. Jackson, O. J. Clymer, A. M. Giacomello and F. V. Jensen, The use of Hugin® to develop Bayesian networks as an aid to integrated water resource planning, Environ. Model. Softw., 2005, 20(2), 231–242 CrossRef.
- B. G. Marcot, Metrics for evaluating performance and uncertainty of Bayesian network models, Ecol. Modell., 2012, 230, 50–62 CrossRef.
- Z. J. Y. Zhu and E. A. McBean, Selection of water treatment processes using Bayesian decision network analyses, J. Environ. Eng. Sci., 2007, 6(1), 95–102 CrossRef CAS.
- W. A. Pike, Modeling drinking water quality violations with Bayesian networks, J. Am. Water Resour. Assoc., 2004, 40(6), 1563–1578 CrossRef.
- M. E. Kragt, A beginners guide to Bayesian network modelling for integrated catchment management, Landscape Logic, 2009 Search PubMed.
- C. W. Baxter, S. J. Stanley and Q. Zhang, Development of a full-scale artificial neural network model for the removal of natural organic matter by enhanced coagulation, Aqua, 1999, 48(4), 129–136 CAS.
- A. Mirsepassi, B. Cathers and H. B. Dharmappa, Application of artificial neural networks to the real time operation of water treatment plants, in Neural Networks, 1995. Proceedings., IEEE International Conference on, IEEE, 1995, vol. 1, pp. 516–521 Search PubMed.
- C. W. Baxter, S. J. Stanley, Q. Zhang and D. W. Smith, Developing artificial neural network models of water treatment processes: a guide for utilities, J. Environ. Eng. Sci., 2002, 1(3), 201–211 CrossRef CAS.
- H. R. Maier, N. Morgan and C. W. K. Chow, Use of artificial neural networks for predicting optimal alum doses and treated water quality parameters, Environ. Model. Softw., 2004, 19(5), 485–494 CrossRef.
- Q. Zhang and S. J. Stanley, Real-Time Water Treatment Process Control with Artificial Neural Networks, J. Environ. Eng., 1999, 125(2), 153–160 CrossRef CAS.
- G. R. Shetty, H. Malki and S. Chellam, Predicting contaminant removal during municipal drinking water nanofiltration using artificial neural networks, J. Membr. Sci., 2003, 212(1–2), 99–112 CrossRef CAS.
- J. B. Serodes, M. J. Rodriguez and A. Ponton, Chlorcast (c): a methodology for developing decision-making tools for chlorine disinfection control, Environ. Model. Softw., 2001, 16(1), 53–62 CrossRef.
- P. Kulkarni and S. Chellam, Disinfection by-product formation following chlorination of drinking water: Artificial neural network models and changes in speciation with treatment, Sci. Total Environ., 2010, 408(19), 4202–4210 CrossRef CAS PubMed.
- G. R. Shetty and S. Chellam, Predicting membrane fouling during municipal drinking water nanofiltration using artificial neural networks, J. Membr. Sci., 2003, 217(1–2), 69–86 CrossRef CAS.
- W. Wu, G. C. Dandy and H. R. Maier, Application of artificial neural networks to forecasting water quality in a chloraminated water distribution system. 19th Int. Congr. Model. Simul. Modsim2011, 2011, pp. 1112–1118 Search PubMed.
- H. R. Maier, A. Jain, G. C. Dandy and K. P. Sudheer, Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions, Environ. Model. Softw., 2010, 25(8), 891–909 CrossRef.
- D. L. Boccelli, M. J. Small and U. M. Diwekar, Treatment plant design for particulate removal: EFFECTS OF FLOW RATE AND PARTICLE CHARACTERISTICS, J. - Am. Water Works Assoc., 2004, 96(11), 77–90 CAS.
- Y. Gal and Z. Ghahramani, Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning, 2015, ArXiv150602142 Cs Stat.
- J. Denker and Y. Lecun, Transforming Neural-Net Output Levels to Probability Distributions, in Advances in Neural Information Processing Systems 3, Morgan Kaufmann, 1991, pp. 853–859 Search PubMed.
- Y. J. Hasit, J. L. Anderson, A. J. Parolari, T. D. Rockaway and M. L. Frenc, Distribution Water Quality Issues Related to New Development Or Low Usage, American Water Works Association, 2007 Search PubMed.
- National Research Council, Drinking Water Distribution Systems: Assessing and Reducing Risks, The National Academies Press, Washington, D.C., 2006, DOI:10.17226/11728.
- F. Dominguez, E. Rivera, D. P. Lettenmaier and C. L. Castro, Changes in winter precipitation extremes for the western United States under a warmer climate as simulated by regional climate models, Geophys. Res. Lett., 2012, 39(5), L05803 CrossRef.
- R. W. Katz and B. G. Brown, Extreme events in a changing climate: Variability is more important than averages, Clim. Change, 1992, 21(3), 289–302 CrossRef.
- R. E. O'Connor, B. Yarnal, R. Neff, R. Bord, N. Wiefek, C. Reenock, R. Shudak, C. L. Jocoy, P. Pascals and C. G. Knight, WEATHER AND CLIMATE EXTREMES, CLIMATE CHANGE, AND PLANNING: Views of Community Water System Managers in Pennsylvania's Susquehanna River Basin1, J. Am. Water Resour. Assoc., 1999, 35(6), 1411–1419 CrossRef.
- R. J. Lempert, S. W. Popper and S. C. Bankes, Shaping the Next One Hundred Years, http://www.rand.org/pubs/monograph_reports/MR1626.html (accessed Jan 7, 2016) Search PubMed.
- W. E. Walker, R. J. Lempert and J. H. Kwakkel, Deep Uncertainty. In Encyclopedia of Operations Research and Management Science, ed. S. I. Gass and M. C. Fu, Springer US, 2013, pp. 395–402 Search PubMed.
- D. G. Groves, Developing robust strategies for climate change and other risks: a water utility framework, Water Research Foundation, Denver, Colo, 2014 Search PubMed.
- J. R. Kasprzyk, S. Nataraj, P. M. Reed and R. J. Lempert, Many objective robust decision making for complex environmental systems undergoing change, Environ. Model. Softw., 2013, 42, 55–71 CrossRef.
- D. Muschalla, Optimization of integrated urban wastewater systems using multi-objective evolution strategies, Urban Water J., 2008, 5(1), 59–67 CrossRef.
- E. Zechman and R. Ranjithan, Generating Alternatives Using Evolutionary Algorithms for Water Resources and Environmental Management Problems, J. Water Resour. Plan. Manag., 2007, 133(2), 156–165 CrossRef.
- R. Farmani, D. A. Savic and G. A. Walters, Evolutionary multi-objective optimization in water distribution network design, Eng. Optim., 2005, 37(2), 167–183 CrossRef.
- Q. Wang, M. Guidolin, D. Savic and Z. Kapelan, Two-Objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-Known Approximation of the True Pareto Front, J. Water Resour. Plan. Manag., 2015, 141(3), 4014060 CrossRef.
- J. R. Kasprzyk, P. M. Reed, B. R. Kirsch and G. W. Characklis, Managing population and drought risks using many-objective water portfolio planning under uncertainty, Water Resour. Res., 2009, 45(12), W12401 CrossRef.
- M. Mortazavi, G. Kuczera and L. Cui, Multiobjective optimization of urban water resources: Moving toward more practical solutions, Water Resour. Res., 2012, 48(3), W03514 CrossRef.
- H. B. Zeff and G. W. Characklis, Managing water utility financial risks through third-party index insurance contracts, Water Resour. Res., 2013, 49(8), 4939–4951 CrossRef.
- A. N. Piscopo, J. R. Kasprzyk and R. M. Neupauer, An iterative approach to multi-objective engineering design: Optimization of engineered injection and extraction for enhanced groundwater remediation, Environ. Model. Softw., 2015, 69, 253–261 CrossRef.
- P. Reed and B. Minsker, Striking the Balance: Long-Term Groundwater Monitoring Design for Conflicting Objectives, J. Water Resour. Plan. Manag., 2004, 130(2), 140–149 CrossRef.
- T. Hashimoto, J. R. Stedinger and D. P. Loucks, Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation, Water Resour. Res., 1982, 18(1), 14–20 CrossRef.
- H. R. Maier, J. H. A. Guillaume, H. van Delden, G. A. Riddell, M. Haasnoot and J. H. Kwakkel, An uncertain future, deep uncertainty, scenarios, robustness and adaptation: How do they fit together?, Environ. Model. Softw., 2016, 81, 154–164 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |