Accurate and fast numerical algorithms for tracking particle size distributions during nanoparticle aggregation and dissolution†
Amy L.
Dale
ab,
Gregory V.
Lowry
 b and
Elizabeth A.
Casman
*a
b and
Elizabeth A.
Casman
*a
aDepartment of Engineering and Public Policy, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA. E-mail: casman@andrew.cmu.edu
bDepartment of Civil and Environmental Engineering, Carnegie Mellon University, Pittsburgh, Pennsylvania, USA
First published on 18th October 2016
Abstract
Particle size affects the toxicity and environmental fate of engineered nanoparticles (NPs). Although size effects have been widely studied in the experimental NP fate and toxicity literature, no numerical models published to date have attempted to identify and compare state-of-the-art particle modeling methods commonly applied in closely related fields. We compare four numerical frameworks for modeling changes in the size distribution of a NP suspension undergoing dissolution and aggregation: the Sectional Method (SM), Direct Simulation Monte Carlo (DSMC), the Direct Quadrature Method of Moments (DQMOM), and the Extended Quadrature Method of Moments (EQMOM). The SM and the DQMOM were faster or more accurate than the EQMOM and DSMC in nearly every trial. For cases simulating aggregation, the DQMOM took seconds to achieve solutions with ≤2% error, while the SM (a rigorous implementation of the most popular population balance method to date for NPs) took up to 1.5 hours. The SM was far more accurate than the DQMOM for dissolution test cases; however, up to 50 size bins were required to achieve ≤10% error. This raises questions about the validity of the current practice of using five or fewer bins in models of NP fate in rivers. Because runtimes become prohibitive as environmental complexity and particle properties are added, the DQMOM is promising for field-scale models and models that describe NPs with complex morphologies or compositions, such as non-spherical NPs, coated NPs, and nanohybrids. MATLAB code for all models is provided in the ESI.
Environmental significanceParticle size can influence nanoparticle (NP) environmental fate and toxicity. There is therefore a need for numerical models that predict mass concentrations of NPs and their reaction by-products in aquatic media while also capturing changes in the particle size distribution over time in response to size-dependent physicochemical transformations such as aggregation and dissolution. This work presents the first attempt in the NP fate and toxicity literature to present and compare alternative solutions to this difficult numerical problem. Our code and our recommendations are applicable at the scale of both laboratory experiments and natural systems. |
1. Introduction
Concern about the unique environmental and human health risks posed by nanoscale pollutants relative to their micro- or macroscale counterparts has motivated extensive research into the size-dependent toxicity and environmental behavior of engineered nanoparticles (NPs). Experiments show that nanoparticles dissolve faster than their larger counterparts and can also exhibit higher toxicity and bioavailability.1,2 For this reason, mathematical models that predict NP fate and/or toxicity in the laboratory or the environment have attempted to capture NP size effects by tracking the changes in the particle size distribution (PSD) as NPs aggregate and dissolve.3–5All NP fate models that track PSDs are either representative of, or are variants upon, existing “population balance” frameworks that have been applied to a diverse array of particle processes including aerosol particle microphysics,6,7 flocculation during water treatment,8 contaminant transport in granular media filters,9 microbe transport in soils,10 crystal growth,11 soot particle formation in flames,12 and droplet formation during spray combustion.13 Although population balance is often defined simply as an implementation of the population balance equation (PBE), a continuity equation that describes the evolution of a PSD over time and/or space during particle aggregation/fragmentation and growth/dissolution,11,14 the term more generally describes the evolution of the distribution of any particle property or combination of properties (so-called “internal coordinates”) over time and space (“external coordinates”).15 As the definitional property of NPs, the size distribution is the major focus of this work.
Analytical solutions to the PBE are only available for a few simple test cases, such as size-independent aggregation in a batch reactor.13,14 Numerical methods are generally needed, but vary widely with respect to formulation, speed, accuracy, and their appropriateness for a particular problem. Different methods may model every particle in a population separately,16 treat PSDs as continuous, or explicitly model every aggregate size that could result from any possible pairwise aggregation event. The last of these approaches has already been applied to problems of NP homoaggregation, heteroaggregation with one natural colloid size and type, and settling.17,18 However, because these alternatives are computationally burdensome, even intractable, most models instead discretize the PSD to reduce computational demands. The three most popular population balance (PB) frameworks are the sectional method, Monte Carlo methods, and moment-based methods.11,19–21
In the sectional method (SM) or the “method of classes,”11,12 the size domain is divided into sections, or bins, and the PSD is represented as a histogram. Therezien et al. (2014) used the SM to model the homoaggregation and heteroaggregation of monodisperse NP suspensions. Simplified variants on classical sectional approaches have also been developed at the river scale in order to assess the environmental fate of NPs. NP and aggregate populations in river models have typically been described by 5 or fewer size bins of unaggregated or homoaggregated particles (resulting in up to 2 × 5 + 52 = 35 size bins in cases where heteroaggregation was modeled)22,23 divided at even intervals across a fixed grid.22–27 Most such models have only described NP transport processes (e.g., advection, heteroaggregation, and settling), but one also included surface-dependent NP dissolution kinetics.28
Monte Carlo (MC) simulation explicitly models a finite population of (e.g., 103–104) particles.11,21,29 Although MC simulation is considered too computationally expensive for incorporation with computational fluid dynamics code or for use in systems with more than one internal coordinate (e.g. size and chemical composition),15,19,30 it is a reasonable alternative for the treatment of particle size in batch reactor-type systems. MC simulations have been used to describe NP synthesis31,32 as well as NP homoaggregation in simple media.29 A MC model of silver NP homoaggregation and dissolution was also recently developed to predict metal ion formation in cellular toxicity studies.33
Relative to MC and the SM, moment-based methods conserve computational resources by tracking the lower-order statistical moments of a PSD instead of tracking the entire distribution.11,34 As described shortly, the moments capture the essential descriptive metrics associated with a PSD and can also, in specific cases, be used to reconstruct it. Moment methods have been used extensively to describe the intentional and incidental synthesis of NPs,12,35,36 but they have not yet been applied to problems of NP fate and behavior in aqueous media.
The primary benefit of moment-based methods is time saved. The runtime demands of PB models are larger than those of classical mass balance models: for example, each size bin in the SM adds another state variable, which is mathematically equivalent to adding a new chemical species to a classical mass balance. Thus a heteroaggregation model with 30 NP and suspended particulate matter (SPM) size classes (a bivariate problem, as described below) will run approximately (2 × 30 + 302)/3 = 320 times more slowly than an alternative with only one size class of each. Formally, the combinatorial nature of aggregation equations makes their solution a problem of order Nm in the parlance of algorithm complexity analysis, where N is the number of size classes and m is the number of internal coordinates. These runtime demands are prohibitive for (e.g.) watershed-scale models with realistic hydrology and sediment routing.37 Notably, high performance computing has a limited ability to reduce these demands because the constant movement of NPs across size classes makes code parallelization difficult.
This work aims to provide the first systematic comparison of alternative PB numerical methods for problems of NP dissolution, aggregation, and simultaneous dissolution and aggregation. Four PB models are tested: two moment-based methods (Direct Quadrature Method of Moments15,38 and the Extended Quadrature Method of Moments13), one Monte Carlo method, and one Sectional Method.14,39Fig. 1 illustrates the different ways that these four methods describe the PSD. In addition to demonstrating the use of these methods and comparing their speed and accuracy, we highlight potential sources of numerical error and promising areas of future research for both experimentalists and modelers. Because of its dominance in NP fate modeling, we investigate the SM in the greatest detail.
Several authors have argued for4,40 and against5 the use of size-dependent NP fate descriptors and PSD-tracking models at the scale of rivers and watersheds. Notably, we have argued in the past that size-unresolved risk models will likely outperform population balance alternatives until more data become available for model calibration and validation.5 However, this opinion is by no means universally held, and our primary concerns may yet be addressed by advances in analytical methods for NP quantification and characterization in complex media. This debate, while timely and relevant, is largely beyond the scope of the numerical methods comparison presented here.
2. Methods
This section provides a brief overview of the PB frameworks for tracking particle transformations (dissolution and aggregation) developed for this work. Interested readers will find more details in the ESI† Methods section.2.1. Population balance equation
The following population balance equation (PBE) describes the time evolution of the PSD, f(m), due to simultaneous dissolution and aggregation.6–8,11,14,34 | (1) |
The second and third terms on the right-hand side, which is the Smoluchowski equation for particle aggregation,44 describe (respectively) the formation of new aggregates of mass m via the aggregation of particles or aggregates of mass (m − m′) with those of mass m′, and the loss of particles of mass m due to the aggregation of particles of that size with those of any other mass. The Smoluchowski equation applies equally to heteroaggregation (see ref. 45) and to homoaggregation, the focus of this work. One advantage of using particle mass as the internal coordinate instead of radius is that the mass of every newly formed aggregate can be calculated exactly from the masses of the colliding species. In contrast, the radius of a new aggregate must be estimated from the assumed geometry of the colliding species and the aggregate itself.45
2.2. The sectional method
We used the binning method and numerical solution proposed by Lister et al. (1995). This method differs from sectional methods used to date in the NP environmental fate literature at the river scale22,24,25 in that the size grid is not broken into evenly spaced bins. Rather, a geometric series is used to create a grid with increasing bin sizes. This approach has two benefits: (1) it allows the modeler to capture a PSD that is spread over many orders of magnitude in size (e.g., aggregates typically occur in the micron size range)2,46,47 with a smaller number of bins, and (2) it places the highest model resolution (and computational burden) on the smallest particles, for which aggregation and dissolution occur more rapidly and numerical error is more likely to arise.6
A ratio, mrat, is chosen such that the representative particle size at the lower boundary of each bin i + 1, mi+1,lo, is related to the size of the lower boundary of next smallest bin, bin i, by the non-negative integer q.
| mrat = mi+1,lo/mi,lo = 21/q q ≥ 1 | (2) |
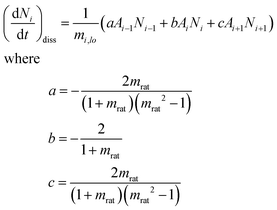 | (3) |
 | (4) |
Eqn (4) is a rigorous alternative to the “weight ratio” heuristic in which volume-conserving ratios are used to apportion newly formed aggregates into the two adjacent bins that most closely approximate the aggregate size.45
2.3. Direct simulation Monte Carlo
In the Monte Carlo approach, a large number of NPs (103–104) are randomly selected from the initial PSD, then evolved in time according to their rates of dissolution and aggregation. For purposes of calculating the statistics of the PSD, the sub-population is treated as a representative sample.For dissolution, each particle in the sample population simply loses mass at the rate specified by the dissolution rate law, A. A fixed time step was used in the “dissolution only” case. Cases that included aggregation had a variable time step.
We employed the Direct simulation Monte Carlo approach of ref. 21. At each time point, the length of the next time step, Δt, was chosen dynamically such that at most one aggregation event would occur during the time step:
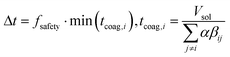 | (5) |
Aggregation is treated probabilistically. Particle i undergoes aggregation during a time step if
 | (6) |
 | (7) |
If the number of particles in the sample drops below half of its original value, the entire population is doubled (by exact replication of the current sample). Doubling prevents errors that would otherwise arise as the number of particles in the sample approached zero. The solution volume is doubled when the sample is doubled, a “stepwise constant-volume” approach.
Because Monte Carlo algorithms vary widely, there may be additional opportunities for improvement of efficiency and accuracy in this method.
2.4. Moment-based methods
 | (8) |
In classical quadrature-based moment methods, eqn (8) is replaced with a discrete approximation using an n-point Gaussian quadrature rule:34
 | (9) |
In effect, the continuous function f(m) is replaced with a discrete approximation defined by its “quadrature points,” or the set of n “abscissas” and “weights” (mi, wi) that exactly predict the lower 2n − 1 moments of the PSD. Quadrature points are calculated from the (known) moments of the PSD using a matrix inversion algorithm such as product-difference or the modified Wheeler algorithm (as described by ref. 11, 34 and 49). Moment-based approaches are generally much faster than the sectional method because they allow the modeler to track the moments of the PSD using a small number (e.g., N < 6) of quadrature points in lieu of many size bins (Fig. 1).
In classical QMOM, the PBE (eqn (1)) is replaced with a continuity equation (the “moment evolution equation”) that balances the moments. For the processes of dissolution and aggregation,34,50
 | (10) |
The quadrature approximation of eqn (10) is34,50
 | (11) |
In classical QMOM, quadrature points are estimated from the moments calculated during the previous time step (or the initial conditions) using matrix inversion. The moments are then updated at each time step according to eqn (11).
| φ = A(0)f(0) | (12) |
In moment methods, only the moments of the PSD are known. Thus we have no way of evaluating f(0). Because the classical QMOM typically tracks six or fewer quadrature points, abscissas rarely lie close enough to the lower boundary to permit an accurate estimate of f(0). We will refer to this as the “dissolution flux problem.” It has only recently gained attention in the population balance literature at large for the case of evaporating droplets (for which it is referred to as the “evaporative flux problem”).13,38,51 In this work, we test three proposed solutions to the generic problem of disappearing particles that arises in the classical QMOM: the DQMOM with and without ratio constraints, and the EQMOM.
2.4.3.1. General principles. The DQMOM approximates the PSD as a sum of i Dirac delta functions with n weights wi at locations (abscissas) mi, i = 1...n.38
 | (13) |
In the univariate case (i.e., for one internal coordinate), this representation is mathematically identical to the quadrature point approximation used in the classical QMOM (Fig. 1).15 In the DQMOM, however, the PBE (eqn (1)) is re-written in terms of the derivatives of the weights and abscissas of the PSD so that the quadrature points may be evolved directly at each time step. This approach is much faster than the classical approach.15
2.4.3.2. Numerical solution of the DQMOM. Let ai and bi describe the evolution of weights and weighted abscissas over time
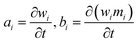 | (14) |
 is a vector of terms describing the evolution of the moments over time (eqn (11)).52
is a vector of terms describing the evolution of the moments over time (eqn (11)).52 | (15) |
Thus the set of quadrature points is evolved directly, and the moments can be calculated ex post facto using eqn (9).
2.4.3.3. Estimating dissolution flux with ratio constraints. As described in 2.4.2, a flux term must be added to eqn (15) when NPs are able to undergo complete dissolution. For a lower size boundary of zero,
 | (16) |
Since moment methods cannot evaluate φ, this system of equations has one too many unknowns. We can solve this problem by adding constraints.38 Fox et al. suggest the following “ratio constraints,” which simply state that the change in the PSD due to dissolution will be smooth.
 | (17) |
Ratio constraints are expected to perform poorly for highly monodisperse particle populations, for which the entire population dissolves completely and instantaneously in a stepwise manner. In such cases, traditional DQMOM (without ratio constraints) may suffice. In this method, the weight associated with an abscissa is simply set to zero when the abscissa crosses the lower size boundary.38
2.4.4.1. General principles. As its name suggests, the EQMOM13 is an extension of the classical QMOM. In both methods, the PSD is approximated by a set of quadrature points calculated from the lower-order moments at each time step using a matrix inversion algorithm, and the moments are transformed directly.
Unlike the classical QMOM and the DQMOM, which treat each abscissa like a discrete node, the EQMOM assumes that each abscissa describes the central tendency of a statistical distribution, δσβ(m, mi). The entire PSD is thus described by a weighted sum of n probability density functions:
 | (18) |
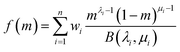 | (19) |
When σβ = 0, the EQMOM is equivalent to the DQMOM. Otherwise, σβ is used to find a set of “secondary” quadrature points distributed around the first (Fig. 1). Thus the EQMOM employs two nested quadrature steps. Unlike the primary quadrature step, which relies on matrix inversion procedures that can estimate fewer than 10 quadrature points with accuracy, the secondary quadrature step is accurate and efficient up to any number of quadrature points. In Beta EQMOM, a simple coordinate transformation recasts the secondary quadrature problem in terms of Jacobi polynomials that are orthogonal with respect to a weight function described by λi and μi. In this special case, any number of quadrature points can be calculated exactly.
2.4.4.2. Numerical solution. The ESI† Methods describe the multi-step algorithm that the EQMOM uses to find σβ and the primary and secondary quadrature points. Once these values are known, a “dual quadrature approximation” of the moment evolution equation is employed.13 Note its similarity to the quadrature approximation used in the classical QMOM and the DQMOM (eqn (11)).
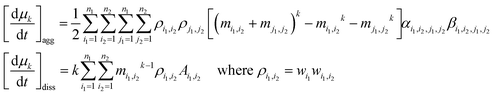 | (20) |
2.4.4.3. Estimation of the dissolution flux. The EQMOM provides two approximations of the PSD: eqn (18) and eqn (S43) (ESI†). In order to estimate the dissolution flux over a given time step, we integrated eqn (18) over the range of particle sizes predicted by Ai1,i2(= dmi1,i2/dt) (eqn (22)), below to dissolve completely within that time step. Once the flux was estimated, the secondary abscissas were advected towards the lower boundary according to Ai1,i2. The weight associated with any abscissa that crossed the lower boundary was set to zero.
2.4.4.4. Choice of moments. The matrix inversion algorithm from the classical QMOM requires the first 2n moments of the distribution.34 The EQMOM requires one additional moment (2n + 1) in order to find σβ.13 The DQMOM and the SM do not rely on the matrix inversion algorithm, so any choice of moments will suffice.
In the DQMOM and the SM, we used the fractional moments (k = 0, 1/3, 2/3, 1). For simplicity, we used integer moments in the EQMOM. The fractional moments were estimated ex post facto from the integral under the reconstructed PSD (eqn (18)) using eqn (8).
2.5. Test cases
We applied the SM, DSMC, the DQMOM with and without ratio constraints, and the EQMOM to problems of NP dissolution, homoaggregation, and simultaneous dissolution and homoaggregation in simple media in a zero-dimensional, no-flow (batch reactor) model such as would be used to describe a static exposure test. This simplified system was chosen for the purpose of contrasting the four PB frameworks. Note that the strengths and weaknesses of numerical frameworks and the details of their implementation are largely indifferent to model scale; thus this comparison is relevant for models of simple test tube experiments as well as “box” and “tanks-in-series” models that describe NP fate in rivers and watersheds.The numerical performance of our four methods should be comparable for both homoaggregation (modeled) and heteroaggregation (not modeled), since both processes are described by the Smolochowski coagulation equation. Particle settling and aggregate break-up were not explicitly included, although their net effect on the hydrodynamic diameter of the particles in suspension was captured in part by the calibration of α as described below. Previous literature suggests that the four numerical methods presented here are similarly accurate with respect to the physical transport processes of aggregation (shown), settling, and break-up (not shown). In contrast, dissolution is subject to unique sources of error including numerical diffusion in the SM6 and error in the flux approximation in moment methods.13
Since most experimental NP studies implicitly assume normality by reporting only the average particle radius and its standard deviation,2,47 we used lognormal distributions with low skews. In particular, we fit our initial lognormal distributions to the following normal distributions: 5 ± 1 nm, 15 ± 3 nm, 50 ± 10 nm, 100 ± 20 nm, and 500 ± 100 nm. We chose these sizes because the standard deviations of newly synthesized NP populations generally increase along with their means.47 We performed a coordinate transformation during the fitting procedure so that PSDs were expressed in terms of our internal coordinate, particle mass, rather than radius. Note that symmetry with respect to radius implies skew with respect to mass (e.g., see Fig. S8†). We also tested model performance for PSDs with high skews and high monodispersity.
 | (21) |
The ESI† Methods compare this model to the oft-cited but rarely used Nernst–Brunner modification2,26,56,57 and describe how it is used to derive the rate law (A) found in eqn (1). Note that the empirical coefficient has changed and the right-hand side is re-expressed in terms of the particle mass by assuming spherical particles.
 | (22) |
We modeled dissolution in two ways. In the first case, the ion concentration in solution was increased until the equilibrium solubility was reached. The size dependence of the equilibrium solubility was estimated from the Ostwald–Freundlich relation (see ESI† Methods) using the initial characteristic diameter of the particles, which is described below.47 In the second case, ions were assumed to be instantaneously removed from the solution (“sink conditions”). We present the results for the second approach in the main body of this work because it maximizes the dissolution rate and dissolution flux, thus maximizing the numerical error; this provides the best basis for a comparison of accuracy in our alternative modeling frameworks.
The second approach may also be most appropriate for environmental systems, in which ions are rapidly sequestered by naturally-occurring ligands. A full treatment of NP dissolution in complex media would require a coupled equilibrium ion speciation model, which is beyond the scope of this paper. However, the two scenarios introduced here (no ion sequestration and complete ion sequestration) do bound the potential influence of free ion activity on NP dissolution rates in the absence of a background metal signal.
We chose a realistic value for the dissolution rate, kS,pb, by calibrating our sectional model to experimental data on the ion release rate for 20 mg L−1 52 ± 9 zinc oxide (ZnO) NPs in 25 °C moderately hard water reaching an equilibrium ion solubility of 2.0 mg L−1 (Fig. S1†).58 We chose ZnO NPs because they are produced in greater volumes than any other reactive NP and their dissolution behavior has been widely studied. Additionally, because ZnO NP dissolution is relatively rapid, models are more likely to exhibit numerical stiffness. ZnO NPs therefore provide a good test case for investigations of the limitations of each framework with respect to numerical instability.
Importantly, reported timescales of ZnO NP dissolution to equilibrium in batch reactor-type experiments vary from minutes to days depending on particle properties (size, morphology, coating) and media properties (pH, organic carbon, phosphate) and experimental methods.2,46,58–60 The simple calibration presented here suffices for a generic introduction to the numerical errors that arise when modeling fast-dissolving particles; a more rigorous procedure would be needed to model a particular laboratory-scale or environmental system.
For all test cases that included dissolution, the characteristic primary (unaggregated) particle size was taken to be the surface-weighted geometric mean diameter, Dgeom,0.61
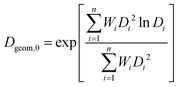 | (23) |
The surface-weighted geometric mean diameter has several advantages over more traditional estimates of particle diameter including the (number-weighted) mean and the geometric mean. The geometric mean of a skewed distribution is a better estimate of its central tendency than its average. For reactive NPs, the surface-weighted diameter is more relevant than the number-weighted diameter because of the controlling influence of surface area on dissolution kinetics. In addition, the surface-weighted diameter does not rely on the zeroth moment (the total number concentration) and is thus robust to numerical errors introduced by approximation of the dissolution flux.
 | (24) |
In order to estimate a realistic constant α, we calibrated our sectional “aggregation and dissolution” test case to the time-resolved dynamic light scattering data corresponding with the ZnO NP samples used to estimate kS,pb.58 Because this example describes only a single set of NP and media properties, and also unrealistically forces α to describe the net effect of aggregation, aggregate break-up, and settling on the hydrodynamic diameter measured in suspension, we do not expect it to apply to a wide range of test conditions. However, it provides a reasonable input for our comparison of numerical model frameworks.
| Di,agg = Dgeom,0(Xgeom,i)1/Df | (25) |
The effect of aggregation on the surface area available for dissolution is poorly understood at present for NPs, and is also an active area of research in the particle modeling community at large.67,68 In order to bound this effect, we considered two extreme cases. We first maximized the dissolution rate by assuming that aggregation has no effect. This approach agrees loosely with experimental results, since small particles have been shown to dissolve faster than large particles even when they form larger or similarly sized aggregates.69 In the second case, which placed a very conservative lower bound on the dissolution rate, we assumed that every aggregation event was followed by complete particle fusion to form a new nonporous sphere with a correspondingly lower surface to volume ratio. This assumption is a common convenience in most models of NP homoaggregation based on the Smoluchowski equation.8
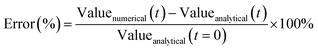 | (26) |
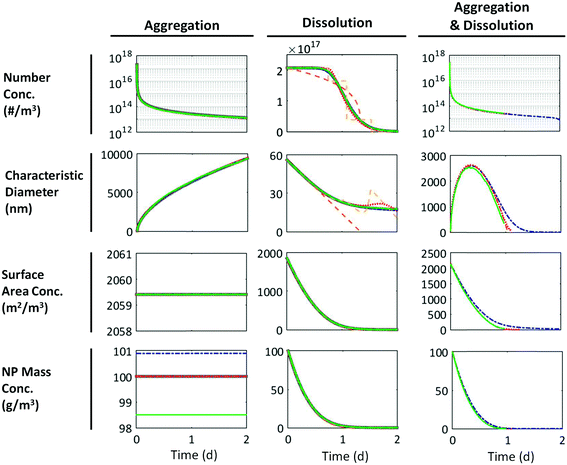 | ||
| Fig. 2 Model results for aggregation, dissolution, and aggregation + dissolution of 100 g m−3 of a lognormal population of 50 ± 10 nm NPs (aggregation, dissolution) or 50 ± 2 nm NPs (aggregation + dissolution). Dissolution and aggregation rates were determined by calibration to data for ZnO NPs Fig. S1 (in the ESI†). Solid grey = analytical solution, dot-dashed blue = SM, dashed orange = DQMOM with ratio constraints, dashed yellow = DQMOM without ratio constraints, dotted red = EQMOM, solid green = DSMC. All methods are accurate for aggregation. Error arises in the DQMOM and the EQMOM for dissolution test cases due to the dissolution flux term. No analytical solution is available for the “aggregation and dissolution” case. | ||
Because values often approached zero during the simulation, relative error approached infinity and could not be used. Error in characteristic diameter estimates was not used in the “aggregation only” case, since normalization by initial conditions in eqn (26) led to high percent errors (e.g., see Fig. S7†) even when absolute error was low. If the model was unable to achieve 2% error or less, the size resolution was simply increased until further increases failed to visibly reduce error.
For each trial, we chose the longest possible time step (within the nearest half order of magnitude) that exhibited numerical stability and maintained error within 2%.
3. Results and discussion
The aggregation and dissolution of engineered NPs affects their PSD and thus affects their number concentration, surface area concentration, and mass concentration: metrics that predict their environmental fate, exposure potential, and toxicity potential. Below, we compare the ability of the four numerical methods presented in Methods to describe these processes accurately and efficiently.Sections 3.1–3.4 present results for the test cases described in section 2.5 and correspond with Table 1 and Fig. 2 and 3, and S2–S5:† section 3.1 describes model resolution, section 3.2 describes the behavior of the NP population over time, and sections 3.3 and 3.4 compare the accuracy and speed of the various PB frameworks, respectively. Sections 3.5 and 3.6, which correspond with Fig. 4 and 5, and S6–S9,† use separate test cases to explore some additional noteworthy features of PB methods.
| Dissolution | Aggregation | Aggregation & dissolution | |
|---|---|---|---|
| a Numbers represent the ratio of the SM runtime to that of the alternative (such that numbers greater than 1 indicate that the alternative is that many times faster than the SM). The ranges represent the effects of different initial ZnO NPs sizes for aggregation and for dissolution to sink conditions and to equilibrium (Fig. 2 and Fig. S2–S4). DQMOM results are for the case with ratio constraints, but runtimes for the case without ratio constraints were comparable. | |||
| SM | 1 | 1 | 1 |
| DSMC | 0.0093–3.9 | 0.028–1.6 | 3.5 |
| DQMOM | 9.0–1900 | 300–530 | 180 |
| EQMOM | 0.067–2.8 | 2.1–5.1 | 21 |
3.1. Resolution of the PSD
The resolution of the PSD for each test case described in section 2.5, which was chosen to balance accuracy and speed, was as follows: for test cases that included dissolution, the SM required values of q (eqn (2)) from 5 to 7. “Aggregation only” required only q = 3. The number of size bins implied by q varied across test cases but always exceeded 100. For the DQMOM, only two quadrature points were needed in all cases; for the EQMOM, we used 2, 2, and 1 primary quadrature points and 20, 20, and 50 secondary quadrature points to describe “aggregation only,” “dissolution only,” and “aggregation and dissolution,” respectively. For dissolution, EQMOM simulations generally failed due to numerical instability if more than three primary quadrature points were used, a result of ill-conditioned or singular matrices in the solution for the secondary quadrature points (see ESI† Methods S1.5.b).3.2. System behavior
Fig. 2 shows the time evolution of a population of 50 ± 10 nm ZnO NPs undergoing aggregation and dissolution (separately) and 50 ± 2 nm ZnO NPs undergoing simultaneous aggregation and dissolution in the SM, DSMC, DQMOM, and EQMOM as calculated from the fractional moments k = 0, 1/3, 2/3, 1. Trends agree with expectations: aggregation caused a rapid decrease in the total particle number concentration (note the log scale) and an increase in the characteristic particle diameter. The total NP mass remained constant. We assumed that the surface area obscured by contact points between particles in each aggregate was negligible such that the surface area concentration (per unit volume of solution) also remained constant. Dissolution decreased the characteristic NP size, NP mass concentration, and surface area concentrations. The particle number concentration only began to decrease once the smallest particles in the system dissolved completely. The behavior in the “aggregation and dissolution” case was a hybrid of the behaviors observed for each process separately. The difference in the initial surface area concentration across test cases reflects a difference in how this value is calculated for unaggregated vs. aggregated particles, as described in ESI† Methods.Fig. S2–S4† present these same results for NP populations of size 5 ± 1 nm, 15 ± 3 nm, 50 ± 10 nm, 100 ± 20 nm, and 500 ± 100 nm. As expected, the smallest particles dissolved faster (minutes) than large particles (days) and aggregated more quickly.
Fig. 3 compares the approximation of the PSD in DSMC, the SM, and the EQMOM to the true analytical solution. The color scale is the same for all figures representing a given test case (e.g., “dissolution only”). Size is expressed in terms of particle or aggregate mass in femtograms (10−15). We truncated the peaks for plotting so that differences in the tails of the distribution could be inspected; the modal (peak) behavior of the PSD was accurately predicted by all methods, as expected given the accurate prediction of the values in Fig. 2 from the moments of the PSD. However, the peaks were tall enough to greatly obscure differences at the tails, so truncation was necessary for clarity.
 | ||
| Fig. 3 Evolution of the PSD expressed as particle or aggregate mass (fg) for the cases shown in Fig. 2. The peaks of the PSDs have been cut off so that behavior at the tails is easier to visualize. In DSMC, the PSD for the randomly sampled sub-population is tracked directly. In the SM, the PSD is tracked directly. In the EQMOM, the PSD is reconstructed from the moments at every time step. DQMOM cannot reproduce the PSD. Results suggest that the SM is the most accurate method for tracking the PSD: the distribution reconstructed from the DSMC sub-population was not smooth for the sub-population size, which was selected to balance speed with accuracy in the prediction of the population moments; the EQMOM over-predicted values at the tails during aggregation and under-predicted them during dissolution. | ||
Trends in Fig. 3 again match expectations: dissolution caused a narrowing of the PSD and a shift towards the lower boundary. Aggregation resulted in the formation of a large and increasingly diffuse peak. The “aggregation and dissolution” case blended the behaviors observed in the dissolution case and the aggregation case. Note that, as expected from Fig. 1, the DSMC reconstruction is choppy, the SM reconstruction is discrete, and the EQMOM reconstruction is smooth.
Since the analytical solution for the “aggregation only” case, which agreed well with our numerical predictions, assumed that the PSD remained lognormal over time, we can safely state that this was the case. In contrast, the analytical solution for the “dissolution only” case does not assume that the PSD remains lognormal, and the evidence suggests that it does not: previous studies with the dissolution rate law presented here suggest the PSD becomes increasingly skewed to the right as dissolution occurs, eventually losing its lognormal character.70 Thus the PSD would not necessarily remain lognormal during dissolution even if the lower portion of the PSD were not “falling off the end” of the size domain as particles fully dissolved.
3.3. Accuracy comparison
The accuracy of each PB method can be observed directly in Fig. 2 and 3 and can also be quantified as the maximum percent error during the simulation (eqn (26)). All four mathematical frameworks were comparably accurate for the case of NP aggregation without dissolution when describing changes in the statistics of the population over time (Fig. 2). The one exception was a small (<2%) error in the SM and DSMC estimates of the initial mass concentration that arose from the discretization of the initial PSD (SM) or non-representativeness in the randomly sampled sub-population (DSMC).For dissolution, the SM agrees well with the “true” (analytical) solution. In contrast, neither the DQMOM flux approximation with ratio constraints (orange dashed line) or without ratio constraints (yellow dashed line) accurately described the changes in the number concentration or average particle size over time (Fig. 2). Because of its stepwise nature, the DQMOM without ratio constraints was also highly unstable. The EQMOM captured the overall shape of the dissolution curve but ultimately under-predicted the dissolution rate at early time steps and over-predicted it later in the simulation. Error in the EQMOM for this case never exceeded 8%. Similar errors are observed for 5 to 500 nm NPs (Fig. S2†). All methods exhibited the highest error at the end of the simulation, when the fewest particles remained. The numerical methods exhibit lower error in the “dissolution to equilibrium” case (Fig. S3†) because little dissolution occurs and the dissolution flux is negligible; the comparative accuracy of these methods clearly depends on the extent of dissolution.
All models were similarly accurate in the case of simultaneous aggregation and dissolution, which suggests that error in estimates of the size of the NPs comprising each aggregate had little impact on the number of aggregates or the characteristic aggregate size. Differences between the SM results and those of the moment methods resulted largely from error in the estimate of the characteristic diameter; error in diameter estimates resulted in turn from a slight overestimation of particle sizes at the upper tail of the distribution due to discretization of the PSD in the SM, which became more influential as small aggregates dissolved.
3.4. Speed comparison
The speed of each approach relative to the SM – a slow but accurate method – is given in Table 1.Although equally accurate, the DQMOM was 300–530 times faster than the SM for the “aggregation only” test cases presented in Fig. 2 and Fig. S4† (Table 1), and the EQMOM was 2–5 times faster. DSMC generally ran more slowly than the SM. Time savings in the moment-based approaches were especially beneficial for the 5 ± 1 nm NP case, since the rapid initial aggregation events undergone by unaggregated particles at early time steps demanded a small simulation time step (<5 milliseconds). Even though we reduced runtimes significantly by increasing the time step later in the simulation, the absolute runtime for our SM simulation of 5 ± 1 nm NP aggregation took over 1.5 hours. The DQMOM solved the same problem in 10 seconds.
Although the EQMOM ran up to 15 times more slowly for dissolution than the SM, runtimes were not restrictive in the absence of aggregation; the SM ran in less than three minutes in all “dissolution only” cases. In spite of their inaccuracies with respect to number concentrations and characteristic particle size, the moment methods accurately predicted changes in the surface area concentration and mass concentration over time. Recall that the dissolution flux, which is the major source of error in moment methods, only affected the zeroth moment (eqn (16)), which was only used to calculate the number concentration.
All models ran in under 10 minutes in the case of simultaneous aggregation and dissolution. However, note that runtimes for a 5 nm test case would have been much longer, as seen for the “aggregation only” case.
3.5. Effect of resolution on accuracy in the SM
Since the SM method has been used exclusively in all PSD-tracking NP environmental fate models to date, we also explored the effect of the choice of the number of size bins on the accuracy of SM model simulations. Most previous models used a small number (≤5) of equally-spaced bins. Our geometrically expanding grid is designed to describe size-dependent processes more accurately than an equally-spaced grid and also requires a large number of bins to achieve coverage of a given size domain, so it is reasonable to assume that the errors in simulations with equally sized bins would be even larger than those reported here.Decreasing the number of bins in the SM degraded model performance gradually. Fig. 4 demonstrates this effect. For this analysis, we narrowed the size domain to ensure that as many bins as possible fell within the 1–100 nm range. PSDs corresponding with each case are shown in Fig. S6.†
 | ||
| Fig. 4 Effect of the number of size bins on error in the SM for dissolution of ∼50 ± 10 nm NPs. Error is reported relative to the analytical solution (solid grey) according to eqn (26). | ||
With only 25 bins, error in the number concentration, characteristic diameter, and NP mass concentration approached or exceeded 10%. Model performance degraded quickly for bin numbers below 25. At 10 bins, error in the characteristic diameter and mass concentration estimates reached 140%. This error had several sources. First, simulations with small bin numbers poorly represented the initial PSD. Error likely also resulted from numerical diffusion. Recall that dissolution in discretized models that perform a particle number balance is described as a loss in the particle number in a given size bin (eqn (3)). In effect, this approach forces complete dissolution of a fraction of the particles to occur in lieu of partial dissolution of all of the particles. The end result is an unrealistic widening and flattening of the PSD over time.71
2.6. An alternative to population balance for dissolution
Well-calibrated population balance models are uniquely well-suited to laboratory research into the complex mechanisms behind NP behaviors and toxicity. Conventional mass balance may be more appropriate, however, when data are limited or only the total NP or ion mass concentration is of interest (e.g., for nanotoxicity assays or environmental exposure models).5 Several authors suggest that ion release curves due to NP dissolution may be predicted by a simple two-parameter first-order linear inhomogeneous differential equation58,72| [Meion]t = [Meion]eq(1 − e−kmbt) | (27) |
Fig. 5(a) compares eqn (27) to benchmark results for PSDs that ranged from roughly exponential to roughly monodisperse, the two extremes of a unimodal distribution, when defined in terms of our internal coordinate, particle mass (see Fig. S8† for PSDs in terms of mass as well as radius). Polydispersity was varied by multiplying the “base case” scale parameter of the initial lognormal distribution by ¼ (most monodisperse), 2, and 4 (most polydisperse). Fig. 5(b) shows model fits for the “aggregation and dissolution” case. The effect of aggregation on dissolution was bounded (blue shaded region) by assuming no fusion (lower bound) or complete fusion (upper bound) during aggregation as described in section 2.5.4. Eqn (27) was fit to the benchmark curves by minimizing root mean squared error over all time steps. The benchmarks for Fig. 5(a) are SM results validated against the analytical solution; the benchmarks for Fig. 5(b) are DQMOM results validated against EQMOM results.
In all cases, this size-independent analytical approximation predicted the dissolution curve within 9% error. For the two-parameter case, which describes NP dissolution to equilibrium (Fig. S9†), fits were exceptional except in the case of complete fusion during aggregation; error remained below 0.9% in all cases. Overlap in Fig. 5(a) and S9(a)† for the most monodisperse PSD (dotted line) and the base case (solid line) indicates that narrowing the PSD had little effect. In contrast, widening it greatly increased the lifetime of the population. Note also the wide uncertainty in the estimate of the particle lifetime in days (Fig. 5(b) and Fig. S9(b),† blue shaded region) that results from the current lack of knowledge about the influence of aggregation on dissolution rates.
4. Conclusions
We implemented four population balance (PB) frameworks with potential applications in NP fate and effects modeling: the Sectional Method,14 Direct Simulation Monte Carlo, the Direct Quadrature Method of Moments,15 and the Extended Quadrature Method of Moments.13For the reasons outlined below, we generally find the DQMOM to be the most accurate and efficient alternative. For PB calculations considering NP dissolution in the absence of aggregation, however, we recommend the SM. Selecting the best framework for a particular NP, system, and model scale will require the modeler to weigh the many aspects of model performance discussed in this work: accuracy in predicting population statistics during NP dissolution or aggregation (and the relative importance of these processes), ability to reconstruct the PSD, runtime, sources of numerical error, and ease of implementation.For almost all cases, our Monte Carlo implementation was either slower or less accurate than the alternatives. The exception was the “dissolution only” case, for which runtimes and accuracy were comparable for DSMC and the SM. The EQMOM was slower and less numerically stable than the DQMOM and was less accurate than the SM in the case of pure dissolution. The EQMOM algorithm was also impractically complex and prone to failure during the search procedure to find σβ. In addition, in the case of simultaneous dissolution and aggregation, the EQMOM and DSMC had to be terminated once the mass concentration dropped below a threshold (1 mg m−3 for EQMOM, 0.05 g m−3 for DSMC) to prevent failure or large errors when only a small number of particles remained in the system. Thus we do not recommend DSMC or the EQMOM. However, DSMC may be appropriate for simple systems if model runtimes are not a concern; it is simple to implement, and its accuracy is easily improved (with an attendant increase in runtimes) by increasing the size of the randomly sampled particle sub-population.
Because the DQMOM was our fastest method by several orders of magnitude, it out-performed the SM in both the “aggregation only” and “simultaneous aggregation and dissolution” cases. It was also simpler to implement than either EQMOM or the SM, and numerical errors (described in ESI† Methods) were easily identified and managed. However, DQMOM was out-performed by the SM in the “dissolution only” case because it was unable to accurately estimate the dissolution flux.
Trial runs of the SM with fewer than 50 bins exhibited significant (>10%) model error. Most size-discretized NP fate models developed to date have used 5 or fewer bins22,24,25 or do not report the number of bins used.28,45 The relevance of this finding to fate modeling efforts at the river or catchment scale is necessarily limited by the simplicity of our test case and the differences between our implementation of the sectional method and those of previous works (described below). Most notably, we intentionally selected a dissolution scenario (sink conditions) that maximizes numerical error by maximizing the NP dissolution rate. In natural systems, processes such as heteroaggregation, the formation of natural surface coatings, and the establishment of local equilibria (particularly in the presence of a non-zero background ion concentration) may greatly reduce the extent or rate of NP dissolution and thus model error. Nonetheless, our results strongly suggest that the number of bins is an important source of error in the SM, and that five or fewer bins may not suffice for soluble NPs. This argument was also recently made by Quik et al. (2015) for heteroaggregation.23We therefore recommend that modelers routinely demonstrate the adequacy of the chosen number of bins by showing that increasing the resolution of the PSD does not improve the accuracy of model results.
Some modelers who are already familiar with the SM and have no preference for faster models may prefer to continue using it. We suggest the following improvements upon current SM modeling frameworks. First, expanding particle size binning schemes (as also employed by ref. 22 and 45) are likely an efficient and accurate alternative to the uniform schemes used to date in NP models at the river scale. Second, we find that the assumption that NPs fuse completely upon aggregation (Fig. 5(b)), which is common in aggregation models,8 can artificially increase particle lifetimes by nearly two orders of magnitude in models that also describe the surface-dependence of NP dissolution. For the case of pure aggregation, we present the numerical solution by Lister et al. (1995) as a robust alternative to the weight ratio approximation used previously.45 We recommend the use of particle mass, rather than radius, as the internal coordinate, and the use of surface-weighted geometric mean diameter as the characteristic particle diameter. Finally, we demonstrated that modeling initial aggregate formation requires a small time step, leading to simulation runtimes over 1 hour for the smallest NPs. We therefore suggest initially seeding SM models with aggregates rather than primary particles when the context justifies such action. This practice is common23–25 (though not universal26,27) in large-scale environmental fate models initialized with realistically transformed NPs, since aggregation is expected to occur in sewage treatment plants prior to environmental release.
If size-resolved data for model calibration or validation are sparse, error tolerance is within 10%, and only information on the ion release rate or NP loss rate is required, assuming a simple first order dissolution rate (eqn (27)) is an attractive alternative to PB methods.58 Quik et al. (2014)17 have similarly observed that first-order rates of NP removal due to aggregation and sedimentation show good agreement with a PB alternative. More generally, Dale et al. (2015)5 argue that models that only balance the total NP mass will probably outperform PSD-tracking alternatives at the river scale until more data become available for model calibration and validation. However, it is important to note that the dissolution rate of the particle population is affected by the distribution's skewness and polydispersity as well as its mean size (the first-order dissolution rates associated with the curves in Fig. 5(a) varied by almost an order of magnitude).
At the lab scale, bivariate or multivariate models (i.e., those that include additional internal coordinates such as surface area or surface charge) are needed to resolve the influence of variation in particle morphology, composition, or charge on the behavior of particle populations with non-spherical morphologies or complex compositions (e.g., heteroaggregates, core–shell structures, natural and engineered surface coatings, nanohybrids).50,73 In fact, we show in this work that is impossible to retain information about the polydispersity of an NP population upon homoaggregation without using a bivariate framework to track the NP size within aggregates of a given size. The literature from related fields suggests that the SM and Monte Carlo simulation will be too computationally demanding for use in bivariate models.74,75 In contrast, moment methods are uniquely well-suited to such computationally demanding problems. In fact, DQMOM has already been used to describe the bivariate problem of NP aggregation and sintering during high-temperature syntheses.12,73
In summary, size-resolved PB frameworks for NPs in aqueous suspension are not only more computationally burdensome than size-unresolved alternatives but are also subject to additional sources of model error. This work presents several numerical frameworks that can be applied directly to problems of NP dissolution and aggregation, coupled with field-scale models, or adapted to describe other particle properties or processes of interest. To facilitate their adoption, and to encourage scrutiny of our approach, we have provided the code for all models as ESI.†
Acknowledgements
We thank Peter Adams at Carnegie Mellon University and Antonia Praetorius at the University of Vienna for their insights during project development, as well as Frédérique Laurent-Nègre at École Centrale Paris for her guidance regarding the EQMOM. This work was supported by the US EPA Science to Achieve Results program; the Transatlantic Initiative for Nanotechnology and the Environment (TINE, R834574); and the National Science Foundation (NSF) and the Environmental Protection Agency (EPA) under NSF Cooperative Agreements EF-0830093 and EF-1266252, Center for the Environmental Implications of Nanotechnology (CEINT). Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF or the EPA. This work has not been subjected to EPA review and no official endorsement should be inferred.References
- S. K. Misra, A. Dybowska, D. Berhanu, S. N. Luoma and E. Valsami-Jones, Sci. Total Environ., 2012, 438, 225–232 CrossRef CAS PubMed.
- S.-W. Bian, I. A. Mudunkotuwa, T. Rupasinghe and V. H. Grassian, Langmuir, 2011, 27, 6059–6068 CrossRef CAS PubMed.
- A. Dale, E. A. Casman, G. V. Lowry, J. R. Lead, E. Viparelli and M. A. Baalousha, Environ. Sci. Technol., 2015, 49, 2587–2593 CrossRef CAS PubMed.
- A. Praetorius, N. Tufenkji, K.-U. Goss, M. Scheringer, F. von der Kammer and M. Elimelech, Environ. Sci.: Nano, 2014, 1, 317–323 RSC.
- A. L. Dale, G. V. Lowry and E. Casman, Environ. Sci.: Nano, 2015, 2, 27–32 RSC.
- M. Z. Jacobson, Fundamentals of atmospheric modeling, Cambridge University Press, Cambridge, England, 2nd edn, 2005 Search PubMed.
- J. H. Seinfeld and S. N. Pandis, Atmospheric chemistry and physics: from air pollution to climate change, John Wiley & Sons, New York, 2nd edn, 2012 Search PubMed.
- M. Elimelech, X. Jia, J. Gregory and R. Williams, Particle deposition and aggregation: measurement, modelling and simulation, Butterworth-Heinemann, Waltham, Massachusetts, 1998 Search PubMed.
- J. E. Tobiason and C. R. O'melia, J. - Am. Water Works Assoc., 1988, 54–64 CAS.
- T. R. Ginn, B. D. Wood, K. E. Nelson, T. D. Scheibe, E. M. Murphy and T. P. Clement, Adv. Water Resour., 2002, 25, 1017–1042 CrossRef CAS.
- D. L. Marchisio, J. T. Pikturna, R. O. Fox, R. D. Vigil and A. A. Barresi, AIChE J., 2003, 49, 1266–1276 CrossRef CAS.
- A. Zucca, D. L. Marchisio, M. Vanni and A. A. Barresi, AIChE J., 2007, 53, 918–931 CrossRef CAS.
- C. Yuan, F. Laurent and R. Fox, J. Aerosol Sci., 2012, 51, 1–23 CrossRef CAS.
- J. Lister, D. Smit and M. Hounslow, AIChE J., 1995, 41, 591–603 CrossRef.
- D. L. Marchisio and R. O. Fox, J. Aerosol Sci., 2005, 36, 43–73 CrossRef CAS.
- N. Riemer, M. West, R. A. Zaveri and R. C. Easter, J. Geophys. Res.: Atmos., 2009, 114(D9), D09202 CrossRef.
- J. T. Quik, D. van De Meent and A. A. Koelmans, Water Res., 2014, 62, 193–201 CrossRef CAS PubMed.
- R. Arvidsson, S. Molander, B. A. Sandén and M. Hassellöv, Hum. Ecol. Risk Assess., 2011, 17, 245–262 CrossRef CAS.
- V. Vikas, C. Hauck, Z. Wang and R. O. Fox, J. Comput. Phys., 2013, 246, 221–241 CrossRef.
- D. E. Rosner, R. McGraw and P. Tandon, Ind. Eng. Chem. Res., 2003, 42, 2699–2711 CrossRef CAS.
- H. Zhao, A. Maisels, T. Matsoukas and C. Zheng, Powder Technol., 2007, 173, 38–50 CrossRef CAS.
- J. de Klein, J. T. Quik, P. Bauerlein and A. A. Koelmans, Environ. Sci.: Nano, 2016, 3, 434–441 RSC.
- J. T. Quik, J. J. de Klein and A. A. Koelmans, Water Res., 2015, 80, 200–208 CrossRef CAS PubMed.
- N. Sani-Kast, M. Scheringer, D. Slomberg, J. Labille, A. Praetorius, P. Ollivier and K. Hungerbühler, Sci. Total Environ., 2015, 535, 150–159 CrossRef CAS PubMed.
- A. Praetorius, M. Scheringer and K. Hungerbühler, Environ. Sci. Technol., 2012, 46, 6705–6713 CrossRef CAS PubMed.
- J. Meesters, A. A. Koelmans, J. T. Quik, A. J. Hendriks and D. Van de Meent, Environ. Sci. Technol., 2014, 48, 5726–5736 CrossRef CAS PubMed.
- A. Markus, J. Parsons, E. Roex, P. de Voogt and R. Laane, Water Res., 2016, 91, 214–224 CrossRef CAS PubMed.
- H. H. Liu and Y. Cohen, Environ. Sci. Technol., 2014, 48, 3281–3292 CrossRef CAS PubMed.
- H. H. Liu, S. Surawanvijit, R. Rallo, G. Orkoulas and Y. Cohen, Environ. Sci. Technol., 2011, 45, 9284–9292 CrossRef CAS PubMed.
- R. Fan, D. L. Marchisio and R. O. Fox, Powder Technol., 2004, 139, 7–20 CrossRef CAS.
- C. Tojo, M. Blanco and M. Lopez-Quintela, Langmuir, 1997, 13, 4527–4534 CrossRef CAS.
- M. Ethayaraja, K. Dutta, D. Muthukumaran and R. Bandyopadhyaya, Langmuir, 2007, 23, 3418–3423 CrossRef CAS PubMed.
- D. Mukherjee, B. F. Leo, S. G. Royce, A. E. Porter, M. P. Ryan, S. Schwander, K. F. Chung, T. D. Tetley, J. Zhang and P. G. Georgopoulos, J. Nanopart. Res., 2014, 16, 1–16 CrossRef CAS PubMed.
- R. McGraw, Aerosol Sci. Technol., 1997, 27, 255–265 CrossRef CAS.
- M. Yu, J. Lin and T. Chan, Powder Technol., 2008, 181, 9–20 CrossRef CAS.
- S. S. Talukdar and M. T. Swihart, J. Aerosol Sci., 2004, 35, 889–908 CrossRef CAS.
- A. L. Dale, G. V. Lowry and E. A. Casman, Environ. Sci. Technol., 2015, 49, 7285–7293 CrossRef CAS PubMed.
- R. O. Fox, F. Laurent and M. Massot, J. Comput. Phys., 2008, 227, 3058–3088 CrossRef.
- M. Hounslow, R. Ryall and V. Marshall, AIChE J., 1988, 34, 1821–1832 CrossRef CAS.
- G. Cornelis, Environ. Sci.: Nano, 2015, 2, 19–26 RSC.
- L. E. Barton, M. Therezien, M. Auffan, J.-Y. Bottero and M. R. Wiesner, Environ. Eng. Sci., 2014, 31, 421–427 CrossRef CAS.
- J. Quik, I. Velzeboer, M. Wouterse, A. Koelmans and D. van de Meent, Water Res., 2014, 48, 269–279 CrossRef CAS PubMed.
- J. Labille, C. Harns, J.-Y. Bottero and J. A. Brant, Environ. Sci. Technol., 2015, 49, 6608–6616 CrossRef CAS PubMed.
- M. V. Smoluchowski, Kolloid-Z., 1917, 21, 98–104 CrossRef.
- M. Therezien, A. Thill and M. R. Wiesner, Sci. Total Environ., 2014, 485, 309–318 CrossRef PubMed.
- N. M. Franklin, N. J. Rogers, S. C. Apte, G. E. Batley, G. E. Gadd and P. S. Casey, Environ. Sci. Technol., 2007, 41, 8484–8490 CrossRef CAS PubMed.
- I. A. Mudunkotuwa, T. Rupasinghe, C.-M. Wu and V. H. Grassian, Langmuir, 2011, 28, 396–403 CrossRef PubMed.
- M. Kostoglou and A. Karabelas, Chem. Eng. Commun., 1995, 136, 177–199 CrossRef CAS.
- C. Yuan and R. O. Fox, J. Comput. Phys., 2011, 230, 8216–8246 CrossRef.
- C. Yoon and R. McGraw, J. Aerosol Sci., 2004, 35, 577–598 CrossRef CAS.
- M. Massot, F. Laurent, D. Kah and S. De Chaisemartin, SIAM J. Appl. Math., 2010, 70, 3203–3234 CrossRef.
- R. Fox, J. Aerosol Sci., 2006, 37, 1562–1580 CrossRef CAS.
- M. Williams, J. Colloid Interface Sci., 1983, 93, 252–263 CrossRef CAS.
- S. Park, R. Xiang and K. Lee, J. Colloid Interface Sci., 2000, 231, 129–135 CrossRef CAS PubMed.
- A. Dokoumetzidis and P. Macheras, Int. J. Pharm., 2006, 321, 1–11 CrossRef CAS PubMed.
- C. A. David, J. Galceran, C. Rey-Castro, J. Puy, E. Companys, J. Salvador, J. Monné, R. Wallace and A. Vakourov, J. Phys. Chem. C, 2012, 116, 11758–11767 CAS.
- P. Borm, F. C. Klaessig, T. D. Landry, B. Moudgil, J. Pauluhn, K. Thomas, R. Trottier and S. Wood, Toxicol. Sci., 2006, 90, 23–32 CrossRef CAS PubMed.
- S. M. Majedi, B. C. Kelly and H. K. Lee, Sci. Total Environ., 2014, 496, 585–593 CrossRef CAS PubMed.
- C. Jiang and H. Hsu-Kim, Environ. Sci.: Processes Impacts, 2014, 16, 2536–2544 CAS.
- R. Ma, C. M. Levard, F. M. Michel, G. E. Brown Jr and G. V. Lowry, Environ. Sci. Technol., 2013, 47, 2527–2534 CrossRef CAS PubMed.
- H. G. Merkus, Particle size measurements: fundamentals, practice, quality, Springer Science & Business Media BV, Dordrecht, The Netherlands, 2009 Search PubMed.
- M. Kostoglou and A. G. Konstandopoulos, J. Aerosol Sci., 2001, 32, 1399–1420 CrossRef CAS.
- R. I. Jeldres, F. Concha and P. G. Toledo, Adv. Colloid Interface Sci., 2015, 224, 62–71 CrossRef CAS PubMed.
- M. U. Bäbler, A. S. Moussa, M. Soos and M. Morbidelli, Langmuir, 2010, 26, 13142–13152 CrossRef PubMed.
- J. C. Flesch, P. T. Spicer and S. E. Pratsinis, AIChE J., 1999, 45, 1114–1124 CrossRef CAS.
- S. Veerapaneni and M. R. Wiesner, J. Colloid Interface Sci., 1996, 177, 45–57 CrossRef CAS PubMed.
- H.-J. Schmid, B. Al-Zaitone, C. Artelt and W. Peukert, Chem. Eng. Sci., 2006, 61, 293–305 CrossRef CAS.
- Z. Peng, E. Doroodchi, M. Sathe, J. B. Joshi, G. M. Evans and B. Moghtaderi, Adv. Powder Technol., 2015, 26, 56–65 CrossRef CAS.
- S. W. Wong, P. T. Leung, A. Djurišić and K. M. Leung, Anal. Bioanal. Chem., 2010, 396, 609–618 CrossRef CAS PubMed.
- Y. Seo and J. Brock, J. Aerosol Sci., 1990, 21, 511–514 CrossRef CAS.
- P. J. Adams and J. H. Seinfeld, J. Geophys. Res.: Atmos., 2002, 107, AAC 4-1–AAC 4-23 CrossRef.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental organic chemistry, Wiley-Interscience, New York, 2005 Search PubMed.
- D. L. Wright, R. McGraw and D. E. Rosner, J. Colloid Interface Sci., 2001, 236, 242–251 CrossRef CAS PubMed.
- A. Buffo, M. Vanni, D. Marchisio and R. O. Fox, Int. J. Multiphase Flow, 2013, 50, 41–57 CrossRef CAS.
- S. Salenbauch, A. Cuoci, A. Frassoldati, C. Saggese, T. Faravelli and C. Hasse, Combust. Flame, 2015, 162, 2529–2543 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6en00330c |
| This journal is © The Royal Society of Chemistry 2017 |


