Comprehensive investigation of novel pore-graded gas diffusion layers for high-performance and cost-effective proton exchange membrane electrolyzers

Abstract

Hydrogen produced by water electrolysis is a promising storage medium for renewable energy. Reducing the capital cost of proton exchange membrane (PEM) electrolyzers without losing efficiency is one of its most pressing challenges. Gas diffusion layers (GDL), such as felts, foams, meshes and sintered plates, are key stack components, but these are either inefficient or expensive. This study presents a new type of GDL produced via vacuum plasma spraying (VPS), which offers a large potential for cost reduction. With this technology, it is possible to introduce a gradient in the pore-size distribution along the thickness of the GDL by varying the plasma parameters and titanium powder particle sizes. This feature was confirmed by cross-section scanning electron microscopy (SEM). X-ray computed tomography (CT) and mercury intrusion porosimetry allowed determining the porosity, pore radii distribution, and pore entry distribution. Pore radii of ca. 10 μm could be achieved in the layers of the GDL close to the bipolar plate, while those in contact with the electrodes were in the range of 5 μm. The thermally sprayed Ti-GDLs allowed achieving PEM electrolyzer performances comparable to those of the state-of-the-art sintered plates and far superior than those of meshes. Moreover, a numerical model showed that the reduced capillary pressure and tortuosity eliminates mass transport limitations at 2 A cm⁻². The results presented herein demonstrate a promising solution to reduce the cost of one of the most expensive components of the stack.

---

Broader context

One of the dominating topics of the 21st century is climate change and indeed, the question of how to reduce greenhouse gases is still unanswered. The rapid increase in the use of renewable energy (RE) sources, such as wind and solar energy, is one promising solution; however, new challenges still emerge. The discrepancy between renewable electricity production and demand still has to be addressed in order to guarantee a stable power-line frequency. This task has to be performed not only during sunny and windy days, but also during those periods of the year with diminished RE sources. Large-scale hydrogen generation via polymer electrolyte membrane (PEM) electrolysis can solve this issue and provide a sustainable conversion of electricity to chemical energy. Moreover, hydrogen can be used as well for seasonal energy storage in the chemical industry and mobility sector, which together are responsible for a large proportion of CO₂ emissions. However, despite all the advantages of hydrogen, PEM electrolysis technology is expensive, with the anode gas diffusion layer (GDL) being one of the most expensive components of the stack. Herein, we present an innovative and cost-effective manufacturing process for the GDL that could potentially change the investment costs of PEM electrolyzers for large-scale energy storage applications.

1. Introduction

The progressive increase in greenhouse gases requires the utilization of sustainable energy carriers.¹ Hydrogen produced by electrolysis can provide the main resource of almost all synthetic fluidic energy carriers by means of renewable energy and water. Proton exchange membrane (PEM) water electrolysis is a very promising technology for sustainable hydrogen production.² One main challenge regarding the large-scale penetration of this technology is the high specific cost of the generated hydrogen compared to that produced by steam reforming and hydrocarbons. The two main cost drivers for sustainable hydrogen production are the electricity and capital expenditure (CAPEX).^3,4 The scientific community and industry are working intensively to decrease the stack cost, which is what predominately governs the CAPEX. The high amount of required noble metals, such as Ir and Pt, are often mentioned as the bottleneck for the commercialization of PEM technology and indeed, the scarcity of these catalysts could limit the expansion of this technology to the gigawatt scale.⁵ Reduction of the precious metal content by improving the activity of the electrocatalytic properties is a high priority and is in the focus of our research efforts as well as several other groups.^6–15 However, the catalysts currently have a relatively small influence on the capital cost.

The most expensive stack components are the interconnectors, chiefly consisting of titanium bipolar plates (BPP) and gas diffusion layers (GDL).^3,16 Two main cell designs are currently used in the industry. In the first design, the BPP is mainly responsible for managing the water distribution and gas collection across the electrode active area.² This task usually requires a complex flow field geometry, which increases the manufacturing cost of the titanium BPPs.^17,18 The BPPs are often combined with very thin GDLs to maintain a uniform electrical connection with the electrode.¹⁹ The second cell design focuses on the GDL, while the BPP is simply regarded as a separator and can be a flat metal sheet without a flow field.^3,20 These separators require more functional GDLs to manage the water distribution and gas collection.^21,22 However, an optimized and highly efficient GDL design is not yet fully envisaged for either the first or second cell design.

In terms of material properties, the GDL needs to be cost effective, highly conductive, and chemically stable under the operating conditions of a PEM electrolyzer. Herein, the use of platinum-group metal (PGM) coatings can guarantee the latter two points but fails in keeping the cost low. Titanium is used as the anode side GDL, which is often coated with precious metals to reduce the contact resistance and reduce oxidation;^23–26 however, the step of coating the anode side GDL with precious metals to reduce the contact resistance is not strictly necessary. Recently, we found that, in fact, the protective PGM coating on Ti is more useful at the cathode, which is in contact with carbon GDL, than in the anode.²⁴ Alternatively, stainless steel interconnectors, coated with Ti only on the anode side, may be used, since austenitic stainless steel is highly resistant to H₂ embrittlement.^27,28 Furthermore, the use of Nb as a protective coating instead of a PGM may be a promising solution²⁹ and also has the benefit that it can be applied by thermal spraying. The complete removal of PGM coatings in the stack interconnectors to decrease the cost of megawatt PEM electrolyzer facilities is still a pressing challenge.

In addition to the material requirements, the GDL must provide optimized water distribution over the electrode and remove the produced gas. Different types of porous titanium structures such as felts,^21,30 meshes,^21,31 foams³⁰ and porous sintered plates^21,30,32,33 are often used as GDLs in the anode side of PEM electrolyzers. While meshes are the cheapest GDLs, the performance of the electrolyzer with this type of GDL is not as high as with the sintered structures or felts. Sintered Ti plates are limited in area and thickness but allow achieving high performances.³⁴ Foams have also been tested in PEM electrolyzers,³⁵ though they may face mechanical stability issues with increasing contact pressure. Zielke and co-workers performed an X-ray tomography-based screening study, reporting the morphological and transport parameters of different felts and sintered plates for their use in a tandem solar cell coupled with a PEM electrolyzer.²²

Unfortunately, the relation of GDL engineering properties, such as thickness, porosity, pore size and surface finishing with phenomena such as the interfacial contact, gas diffusion and mass transport, is hitherto not well understood.¹⁹ Ito et al. reported that high porosity enables the effective transport of the gas and water from the GDL but increases the through-plane electrical resistivity and contact resistance.²¹ Gas transport in porous structures is highly dominated by capillary forces, even at high gas evolution rates (high current density).³⁰ Thus, the optimum pore radii should be between 5 and 6.5 μm to maintain a balance between the contact to the electrode and the mass transport properties.³⁴ Recently, we developed a macro porous layer (MPL) for PEM electrolyzer GDLs that showed improved electrical properties for the contact surface and the mitigation of mass transport issues at high current densities.³² Our findings suggested that the internal distribution of porosity and pore sizes within the GDL as well as the contact area to the electrode play important roles in the effective design of this component. Lee et al. confirmed the positive impact on the water saturation of GDLs having the limiting throat close to the electrode layer, which needs to be breached for the breakthrough to occur.³⁶

The challenge of developing cost-effective PEM electrolyzer GDLs with optimal porosity, pore size, thickness, and surface properties still persists. In this study, we introduce the development of novel freestanding pore-graded titanium layers for their use as GDLs of a PEM electrolyzer. Via extensive physical, electrochemical, and numerical modeling characterizations, we deliver deep insights into the mass transport phenomena of the multifunctional GDLs and discuss the role of the different properties of the contact porous layers for the anode and BPP.

2. Experimental

2.1. Vacuum plasma spraying

Porous titanium layers (PTL) were produced by vacuum plasma spraying on mild steel. The feedstock powders were grade 1 titanium (TLS Technik Spezialpulver) with grain sizes of ca. 45 and 125 μm, which are referred to in this study as Ti45 and Ti125, respectively. Table 1 summarizes the samples that were produced with these powders. The numbers “8”, “16”, and “32” in the sample nomenclature correspond to the iterative number of coating runs or plasma torch sweeps, in which the spraying nozzle moves over the mild steel substrates during the coating process. In general, the labels of the samples are given as follows: “S” and “L” stand for small or large titanium particle size, respectively, samples labeled with “+” contain layers sprayed with different plasma enthalpies; for example, the PTL labeled as 32L + 8S has been produced in two steps: (i) 32 layers of large size (L) Ti particles were sprayed on the substrate with a plasma enthalpy of 21.3 MJ kg⁻¹; (ii) subsequently, 8 layers of small size (S) Ti particles were sprayed on top of the previous ones with a plasma enthalpy of 12.5 MJ kg⁻¹. The gas flow rates of Ar, N₂ and H₂ were carefully chosen to achieve the desired plasma enthalpies. For all the samples, the torch sweep rates were 350 mm s⁻¹. The substrates were pre-heated up to 250 °C before deposition. The chamber pressure was 50 mbar to avoid titanium oxidation during the coating process. Finally, the PTLs were removed from the mild steel substrates by immersing the samples in 0.5 M H₂SO₄ for approx. 1 h to produce the GDLs for testing in PEM electrolyzers.

Table 1 Sample composition of sprayed porous titanium layers (PTL), where “S” and “L” stand for small or large titanium particle size, respectively. The samples labeled with “+” contain layers sprayed with two different plasma enthalpies (fourth column)

PTL	No. of coating runs, Ti (125 μm)	No. of coating runs, Ti (45 μm)	Enthalpy/MJ kg^−1
16S	—	16	12.5
32S	—	32	12.5
16L + 8S	16	8	21.3/12.5
32L + 8S	32	8	21.3/12.5

---

2.2. SEM, porosimetry, and X-ray computer tomography

The morphology of the PTLs was investigated by analyzing the pore variation along the thickness of the samples via SEM and X-ray CT, thereby determining the pore-size distribution, tortuosity, bubble points, and connectivity. The tomography results on the porosity and global pore sizes were compared to the results of mercury intrusion porosimetry (MIP).

Cross-section images were recorded for all the produced samples with an FE-SEM Zeiss ULTRA plus in secondary electrons mode with charge compensation. The working distance and accelerating potential were 8.4 mm and 15 kV, respectively. Porosity measurements of the samples were performed by the mercury intrusion technique (Pascal 140/240, Thermo Scientific) up to a pressure of 200 MPa. The tested sample volume was in the range of 100–200 mm³. Prior to the measurements, the samples were kept in an oven at 100 °C overnight. The pore entry radii were determined by applying Gaussian fittings to the pore-size-distribution profiles.

The X-ray computer tomography (CT) analysis was performed with a Multiscale X-ray nanotomograph (Skyscan 2211, Bruker). The tested sample volume was in the range of 1 mm³. An acceleration potential of 70 kV was used and a voxel size of 1 μm³ was achieved. The reconstructed images were prepared for segmentation by removing artifacts using outlier filters, followed by normalization of the image contrast and applying a 3D median filter. Subsequently, a global threshold was found by visual judgment. Features smaller or equal to 2 × 2 × 2 voxels were considered most likely to be noise and were thus removed using outlier filters. ImageJ was used for analyzing the images of all the steps.³⁷ Finally, the images were cropped to avoid edge effects. For samples 32L + 8S and 16L + 8S, the background on the rough side was masked and removed from all the calculations. The mask was determined by segmenting the pores and applying a broad Gaussian blur filter to the whole dataset, followed by a global threshold in order to mark the background on the rough side. For the tortuosity calculations, the reconstructions were shrunk by a factor of two to decrease the computational time. The calculations were done using the commercial solver GeoDict. The capillary pressure curves were calculated using the pore-morphology method, implemented in GeoDict.³⁸ Both local and global pore-size distributions were made using self-programmed Matlab functions, implementing the method of Delerue et al.³⁹

MIP is a powerful technique for calculating the pore radii of porous structures with throat-like voids. However, the technique allows observing only the size of the pore opening due to the so-called ink-bottle effect.⁴⁰ The measured pore radius can be significantly smaller compared to the one obtained by X-ray CT, which is calculated by tightly fitting spheres into the pore space.³⁹ However, the pore radius from MIP corresponds to the average size of the throat that the generated gas has to overcome for efficient transport out of the electrode. Therefore, both parameters are relevant for our study. In the next sections, the pore size obtained by MIP is termed the pore entry radius, while the pore size calculated by X-ray CT is simply referred to as the pore radius.

2.3. PEM electrolyzer tests

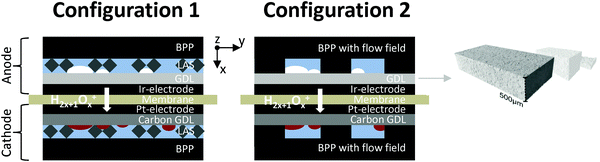
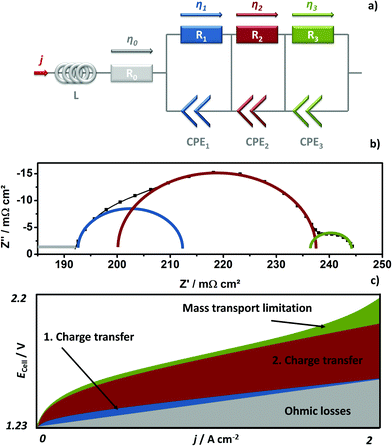
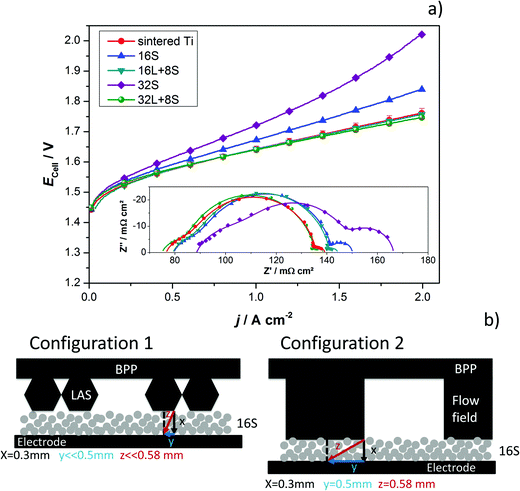
The GDLs were measured in in-house-produced PEM electrolyzers. Fig. 1 shows a scheme of the cell configurations used for the tests. Commercially available MEAs (Greenerity E300) with an Ir-based anode, Pt-based cathode, and Nafion 212 membrane were used for all the measurements. The first electrochemical characterization of the GDLs was performed in configuration 1, which consisted of a 4 cm² active area 2-cell device (Fig. 1, configuration 1) having BPPs without a flow field. The developed GDLs were placed on top of the anode LAS mesh and were in contact with the Ir-electrodes. Small aperture size (SAS) Ti mesh and sintered Ti plates (SIKA-T 10, GKN Sinter Metals), which are state-of-the-art GDLs, were tested as well for comparison purposes. The cells were characterized by recoding polarization curves up to 2 A cm⁻², specifically after one day of MEA activation period at 38 °C and constant 1 A cm⁻². The scan rate was 4 mA cm⁻² s⁻¹, which was sufficiently slow for analyzing the phenomena of interest. Electrochemical impedance spectroscopy (EIS) was performed from 50 kHz to 100 mHz at 0.25 and 1 A cm⁻² with an amplitude of 50 mA and 100 mA, respectively, using a potentiostat/galvanostat (Zahner Elektrik IM6) and booster (Module PP240). All the GDLs were characterized at least three times on new assemblies to ensure reliable data and generate proper error bars.

Fig. 1 Scheme of the PEM electrolyzer cell configurations: configuration 1: cell with bipolar plates (BPP) without a flow field. Configuration 2: cell with BPPs having a flow field. GDL: gas diffusion layer. LAS: large aperture size. The LAS mesh was used to take over the function of a flow field for distributing water and releasing bubbles from the tested GDLs.

The second electrochemical characterization was performed in a 25 cm² active area 2-cell device (Fig. 1, configuration 2) with BPPs having a parallel flow field. The BPPs were manufactured in stainless steel and protected on the anode side with a dense Ti coating, based on a procedure reported elsewhere.^24,25 The cathode side was left uncoated. Straight after the MEA break-in procedure described in the previous paragraph, the polarization curves were recorded up to 2 A cm⁻² with a scanning rate of 4 mA cm⁻² s⁻¹. EIS was performed at 0.5 A cm⁻² with an amplitude of 2 A at frequencies between 100 kHz and 100 mHz at 80 °C. The equivalent circuit shown in Fig. 2a was used to quantify the EIS measurements. An example of the impact of the individual impedances is shown in the Nyquist diagram in Fig. 2b, which can be translated to the corresponding overpotentials for a typical polarization curve (Fig. 2c). The Ohmic resistance is represented by the high frequency (HF) interception of the EIS (gray). The high frequency arc is represented in blue and is attributed to the hydrogen evolution reaction (HER),^41,42 charge transfer resistance accompanied with double layer effects in the electrode,^43–46 or the first charge transfer of the two-electron process of the oxygen evolution reaction (OER).⁴⁷ The red and green arcs in the Nyquist plot in Fig. 2b represent the charge transfer of the rate determining step of the OER and the mass transport phenomena, respectively.^43,45,47

Fig. 2 (a) Equivalent circuit for analysis of the EIS; (b) example of a Nyquist plot with the analyzed arcs (time constants), and (c) the corresponding overpotentials for a typical PEM electrolyzer polarization curve.

3. Results

3.1. Physical properties

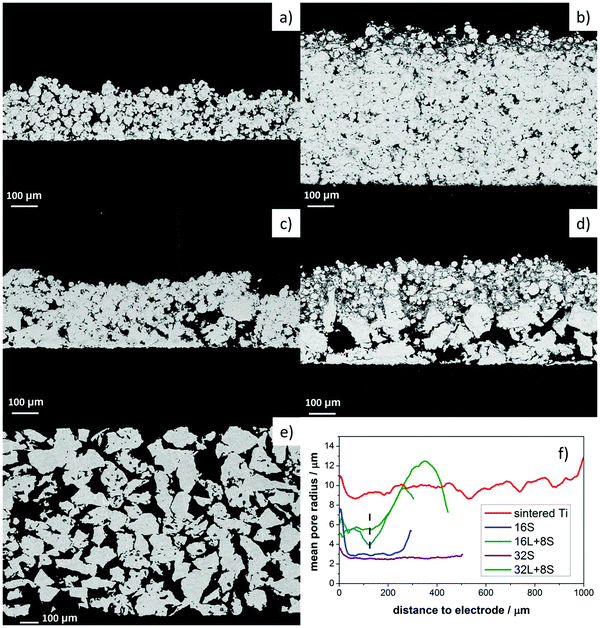
Cross-sectional SEM analysis was performed on the freestanding PTLs to observe the pore variation along the thickness of the samples. The SEM images in Fig. 3a and b depict samples 16S and 32S, respectively, which were produced with small particle size Ti powder (Ti45). Fig. 3c and d show the pore-graded PTLs produced by spraying 8 layers of Ti45 on top of 16 and 32 layers, respectively. The bottom layers were realized with large particle size Ti powder (Ti125). The dual pore size PTLs of Fig. 3c and d were labeled as 16L + 8S and 32L + 8S, respectively.

Fig. 3 (a–e) SEM images of the PTLs: (a) 16S, (b) 32S, (c) 16L + 8S, (d) 32L + 8S, and (e) sintered Ti. The scale bar represents 100 μm. (f) Height-dependent pore diameters of the samples from a–e. When used as GDLs, the MEA electrode would be located on the top of the images and the BPP on the bottom. The boundary between the Ti45 region and the Ti125 region is shown with a dashed line.

The thickness of the Ti45 layers in samples 16S and 32S was approx. 300 and 550 μm, respectively, while the thickness of the Ti45 layers in samples 16L + 8S and 32L + 8S was approx. 120 μm. The differences in thickness were confirmed with the height-dependent pore-size distribution calculated from the X-ray CT reconstructions, see Fig. 3f, where the approximate position of the boundary between the Ti45 region and the Ti125 region are shown with a dashed line. Below the line, the Ti45 structure is located, yielding considerably smaller pore sizes in both cases. Interestingly, the thickness of the Ti125 layer is 180 μm for sample 16L + 8S and 280 μm for sample 32L + 8S. This result indicates that the enthalpy of the plasma is not sufficiently high to form the splat structure of the Ti125 particles, leading to low deposition efficiency. In this regard, the plasma deposition parameters with Ti125 powder are yet to be optimized.

One interesting observation was the fact that the Ti45 layers in samples 16L + 8S and 32L + 8S had larger pore radii than in the 16S and 32S PTLs. The compactness of the Ti45 layers increased with the number of torch sweeps during the plasma spraying process due to a sintering effect. The temperature history during the thermal spray process and subsequent residual stress distribution within the sample also had an impact on the pore properties. The temperature of the sample rose as the number of deposited layers increased.^48,49 The temperature increase, along with the pressure from the impinging hot Ti particles, resulted in a sintering effect, which was more prominent for sample 32S than for 16S. Consequently, the pore entry radius of the former sample was slightly smaller than the latter.

Moreover, the 16S and 32S specimens showed similar sintering morphology as the sintered titanium sample, see Fig. 3e, with the three of them having a homogeneous pore diameter along their thickness. The different nature of the surface on which the Ti45 layers were deposited, dense mild steel for 16S and 32S and porous Ti125 layers for 16L + 8S and 32L + 8S, also played a role in the resulting pore radii of the PTLs. One can clearly observe in the SEM images of Fig. 3c and d that some of the Ti45 particles partially fill the large pores of the 16L and 32L layers, respectively. However, there are still empty pores visible in the 32L layers of sample 32L + 8S, which the Ti45 particles did not fill, resulting in an overall increase in pore entry radii of the 32L region compared to 16L.

Lastly, except for sample 32L + 8S, the pore radii of all the thermally sprayed samples showed a slight increase in pore radius near the electrode, which can be explained by boundary effects and roughness. These boundary effects originate from the symmetric boundary condition, which was chosen for the calculation of the local pore radii. The boundary effects when calculating pore-size distributions is most easily explained with the image shown in Fig. S1 in the ESI,† where a cross-section of the X-ray CT of sample 16S is shown. When quantifying the local sizes of the pore space, the question of the chosen boundary condition rises. There are two options: (i) treat the pores at the border as if they were mirrored (symmetric boundary condition) or (ii) treat the pores to immediately stop at the crop-out border. It makes sense to take option (i), as water will experience pressure originating from the local radius, rather than from a smaller radius resulting from option (ii). However, this results in a tendency to calculate higher local radii at the border of the volume.

Fig. 4a–f present 3D reconstruction images of the free standing PTLs from the X-ray CT analysis of the X-ray CT cross-section images (Fig. S2, ESI†), providing optical impressions of the roughness of the top and bottom surfaces. For comparison, the 3D model of the commercial Ti sintered plate is shown in Fig. 4g. The top area of the PTLs contacts the electrode of the MEA when used as GDLs, as the surface is rougher on the top than on the bottom. The roughness of the contact layer to the electrode may have a positive impact as long as the difference of the peaks and the valleys are not damaging the MEA. Sample 16S PTL had, on an average, an arithmetic absolute roughness (R_a) of 9 ± 1 μm. In contrast, samples 16L + 8S and 32L + 8S had R_a values of 11.8 ± 0.3 μm and 15 ± 2 μm, respectively, due to the high rugosity of the Ti125 bottom layer. The sintered Ti plate on the other hand had a rather even surface with an R_a of 7.7 ± 0.3 μm.

Fig. 4 3D reconstruction of the PTLs from the X-ray CT analysis.

Fig. 5a presents the porosity and pore entry radius of 16S, 16L + 8S, 32S, 32L + 8S, and the sintered Ti plate, obtained from the MIP (Fig. S4, ESI†). Sample 32S had the smallest porosity, pore radius, and pore entry radius among all the samples corresponding to 17%, 2.6 μm and 1.5 μm, respectively. In contrast, the porosity analysis of sample 16S revealed a porosity of 24%, a pore radius of about 3 μm, and a pore entry radius of 2.1 μm. Evidently, on increasing the number of torch sweeps, the incident plasma compresses the layer reducing the porosity. The two pore-graded samples 16L + 8S and 32L + 8S showed two main peaks in the MIP characteristics (Fig. S3, ESI†). The first peak (from left to right) corresponded to the 8S layer, having a pore radii of 5 μm and 5.5 μm for 16L + 8S and 32L + 8S, respectively. The corresponding pore entry radii were 3 and 3.6 μm. The estimated pore entry radii of the 16L and 32L layers were 6.5 μm and 10.5 μm, respectively. These values are comparable to the pore radii observed via the X-ray CT analysis (Fig. 3f). The porosities of the pore-graded samples ranged between 20% and 30%, which were not significantly larger compared to that of sample 16S. The sintered Ti had the highest porosity and the largest pore diameters of all the measured samples.

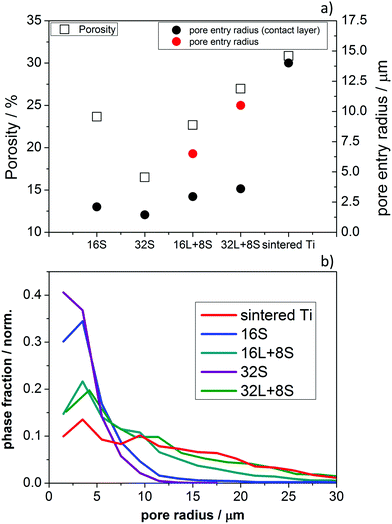Fig. 5 (a) Porosity in % (left y-axis) and pore entry radius in μm (right y-axis) of the PTLs. (b) Complementary pore size distributions calculated from the X-ray CT reconstructions of the samples.

Fig. 5b shows the pore-size distributions calculated by the X-ray CT analysis. One can observe that all the distributions show high phase fractions close to the left end of the x-axis. This suggests that there are numerous pores below the resolution limit of ∼2.5 μm, which cannot be captured by the X-ray tomographic reconstruction, but these can be observed in the SEM images (Fig. 3a–e). Multiscale correlative tomography approaches using FIB coupled with SEM as the imaging method for smaller pores would be needed to complete the picture.⁵⁰ This lack of information due to the resolution limits can be compensated by combining the image-based results with the MIP curves, allowing one to quantify the smaller pores, as can be seen in Fig. 5b.

3.2. Electrochemical characterization

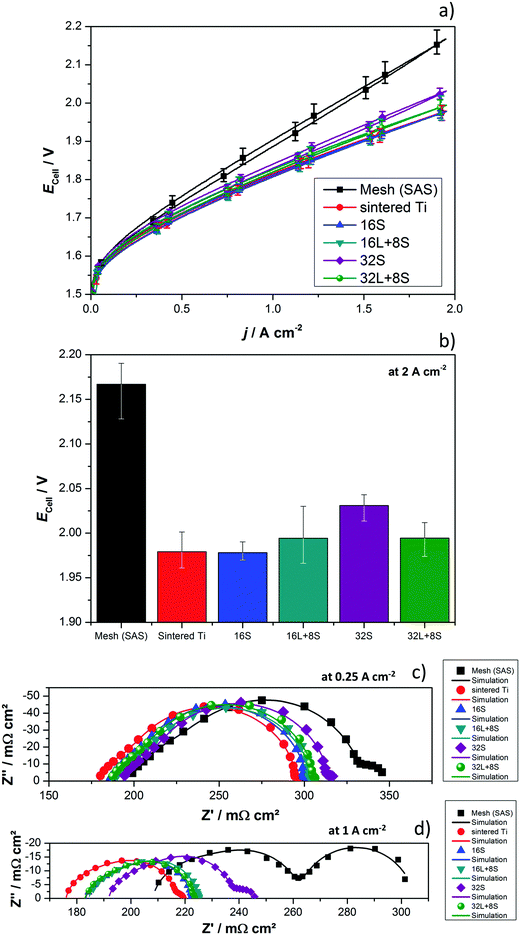
The produced PTLs were used as PEM electrolyzer GDLs and were electrochemically evaluated in the cell designs schematized in Fig. 1. The average current–potential characteristics of the GDLs in a 4 cm² active area 2-cell device without a flow field are presented in Fig. 6a. The LAS mesh was placed between the BPP and the GDL, taking over the function of the flow field for water distribution and gas removal. For clarity, these curves are presented separately in Fig. S4 in the ESI.† The cell voltage (E_cell) measured at 2 A cm⁻² is shown in the histogram of Fig. 6b. One representative EIS, which cannot be related directly to the average polarization curves in Fig. 6a, is shown in Fig. 6c and d. Furthermore, it needs to be mentioned that all the EIS measurements of each individual GDL maintained their shape as well as number and frequency of processes, but showed changes in the absolute values.

Fig. 6 Electrochemical characterization of the PEM electrolyzer GDLs (4 cm² active area): (a) polarization curves; (b) E_cell at 2 A cm⁻². The tests were carried out at 38 °C and ambient pressure. (c and d) Nyquist plots from the EIS measurements (from 50 kHz to 100 mHz) at 0.25 (amplitude 50 mA) and 1 A cm⁻² (amplitude: 100 mA).

As can be seen in Fig. 6a and b, the cell with the SAS mesh in contact with the electrode, which represents the most economic state-of-the-art GDL solution for large-area PEM electrolyzes, shows the highest E_cell. Compared to the cell with the 16S GDL, the E_cell of the electrolyzer with the SAS mesh GDL is 185 mV higher. This increase corresponds to an efficiency drop of approx. 7%, which in Megawatt PEM electrolyzers can have a relevant impact on the operational expenditure (OPEX). Another commercially available GDL is a sintered Ti structure. The E_cell of cells with the 32S, 16L + 8S, 32L + 8S GDLs is higher than the E_cell achieved with the sintered Ti, but considerably lower than the SAS mesh GDL. The performances of the electrolyzers with the 16S and sintered Ti GDLs are comparable. Among all the thermally sprayed GDLs, the 32S GDL produced the worst performance, but it was still higher than the SAS mesh GDL.

It should be noted that the forward and backward polarization curves of the SAS mesh and 32S GDLs in Fig. 6a deviate slightly. This difference between the positive and negative sweeps corresponds to a non-steady state condition like with capacitive currents or mass transport issues. Capacitive currents by means of charging the double layer occur due to high step rates. This argument is correct up to certain extent for all the GDLs but it cannot explain the slight difference of the E_cell at any current density for the 32S and SAS mesh GDLs. Consequently, the hysteresis is attributed to mass transport limitations, which can be confirmed by the Nyquist plots of EIS, as shown in Fig. 6c (at 0.25 A cm⁻²) and 6d (at 1 A cm⁻²). Due to the high impedance, the Ohmic resistance and the behavior of the charge transfer arc can be clearly distinguished from each other at low current densities. However, the mass transport limitations are easily distinguished from the low frequency (LF) arc at high current densities. In both diagrams, the cell with the sintered Ti GDL shows the lowest Ohmic resistance, calculated from the horizontal axis interception at high frequencies (left interception), and this result can explain the high performance of the cell with this GDL.

It can be concluded that, with the exception of the SAS mesh GDL, the charge transfer arc for all the thermally sprayed and sintered Ti GDLs are comparable. In the case of the SAS mesh GDL, the arc appears to be slightly wider, which is most probably due to the low contact area with the electrode, leading to an increased contact resistance and activation overpotential.²¹ Mass transport limitations for the cells with the SAS mesh and 32S GDLs are noticeable in the LF arc of the Nyquist diagram in Fig. 6d. Yet, it is obvious that the mechanisms of mass transport limitations are different for these two GDLs. In the case of the 32S GDLs, water cannot reach the active electrode fast enough since the Ti structure is too packed. The pressure between the electrode and the packed GDL increases since it is not efficiently removed from the electrode. This negative effect can lead to the partial blocking of electrode active centers, inhibiting them from further reactions. Still, water can reach the active surfaces via secondary paths, for example, via thin films or through the ionomer in the catalyst layer, producing efficiency losses. A gas pillow formed between the electrode and the GDL can also explain the increased Ohmic resistance of the cell with the 32S GDL.

On the other hand, in the SAS mesh GDL, the bubbles are not released from the electrode without capillary force until a certain bubble diameter is achieved.^51,52 For the 16S, 16L + 8S and 32L + 8S GDLs, no LF arc can be observed. However, for the sintered Ti, the presence of a small LF arc may indicate that the pore radius in contact with the electrode is already too large for an optimized management of liquid and gas.³² The EIS measurements are in good agreement with the polarization curve in terms of the performance (Δ slope vs. Δ impedance) and mass transport limitations.

To confirm the improved characteristics and benefits of the thermally sprayed GDLs, tests in a cell with an active area of 25 cm² and using BPPs with a flow field were performed. The results obtained with the thermally sprayed GDLs were compared with those generated when using the sintered Ti plate. There were difficulties in assembling the 2-cell device with the SAS mesh as it is quite thin and the flow field deformed its flatness. No further efforts were employed in solving these issues since the performance of the cell in the previous configuration was rather low. The current–potential characteristics of the 25 cm² 2-cell device having the sintered Ti plate and the thermally sprayed GDLs are presented in Fig. 7a. The results are in good agreement with the previous tests, although some differences can be observed. Cells with the 16S and 32S GDLs showed a lower performance than expected. The main reason for this can be elucidated by means of EIS (inset of Fig. 7a) and is attributed to the mass transport limitations, as indicated by the LF arc, which did not appear for the 16S GDL in cell configuration 1. A plausible explanation for this is that the BPP blocks the direct through-plane pathways of water to the electrode, as it covers a significant area of the top of the GDL. An efficient water supply to every point on the electrode thus makes in-plane transport and therefore longer pathways necessary. With the 16S GDL, which is the thinnest GDL, the time for water to distribute effectively in-plane was the shortest. Sample 16S had the second smallest pore radius (∼3 μm), which might be already too small if it is intended to be in contact with a BPP having a flow field. Fig. 7b displays a graphical scheme to illustrate the differences in the through-plane pathways for the two cell configurations with the 16S GDL. The transversal pathway is significantly longer for configuration 2 than for configuration 1. The long transversal pathway of water and gases caused by the use of a flow field may lead to mass transport limitations.

Fig. 7 (a) Polarization curves with 25 cm² active area 2-cell PEM electrolyzer having BPPs with a flow field. Scanning rate: 4 mA cm⁻² s⁻¹. The inset shows the Nyquist diagrams of the corresponding EIS measurements at 0.5 A cm⁻². Amplitude of 2 A at frequencies between 100 kHz and 100 mHz. The measurements were carried out at 80 °C and ambient pressure. (b) Scheme used for explaining the differences in performance of the cells with 16S GDL when tested in cell configurations 1 (left) and 2 (right).

The cell with 32S shows a marked increased cell potential at high current densities, which produces an LF arc in the Nyquist diagram. The low porosity and the small pore size of the 32S GDL prevent efficient removal of the gas from the electrode, thus generating backpressure. The backpressure needs to be overcome by water driven by capillary pressure and this process can lead to mass transport issues. In addition, the interception of the HF arc of the 32S GDL with the x-axis is shifted positively, i.e., higher Ohmic resistance, which can also be related to the increased backpressure, which then reduces the contact between the electrode and the GDL. Clearly, the HF arc is affected by the nature of the GDL, yet further investigations are necessary to clarify the electrochemical processes taking place in this range of frequencies.

Lastly, the multifunctional coatings 16L + 8S and 32L + 8S show an E_cell comparable to the sintered Ti GDL with porosities between 20% and 30% and pore radii contacting the active layer between 5 and 10 μm. The advantages of having a gradient pore size are put in evidence when demonstrating the potential of these multifunctional GDLs for PEM electrolyzers with BPPs with flow fields. The multifunctional GDLs, with pore radii in the range of the recommended size of 5 to 6.5 μm³⁴ in contact with the electrode, decrease contact resistance. Moreover, the large pores and high porosity in contact with the BPP help reduce the mass transport limitations.

3.3. Numerical simulations

Possible explanations for the mass transport behavior of the GDLs may be found in a comparison of the morphology of these through-plane paths. Therefore, the capillary pressure curves and bubble points were calculated. These parameters depend strongly on the pore properties. The “bubble point” refers to the pressure needed to press the wetting phase (water) out of the largest pore along a certain direction. In addition, the tortuosity of the through-plane pore pathways was calculated using the commercial solver GeoDict. Tortuosity can be considered as a measure of the complexity of a pore space in a certain direction and is calculated as τ = εσ_intσ_eff⁻¹, where τ is the tortuosity, ε is the volume fraction of the conducting phase, σ_int is the intrinsic transport parameter, and σ_eff is the effective transport parameter, calculated in the actual microstructure.⁵³ The results of the simulated drainage and imbibition (water uptake) of the GDLs are shown in Fig. 8a and b, respectively. For the sake of clarity, the curves are presented separately in Fig. S5 in the ESI.† The calculated tortuosities and bubble points are presented in Fig. 8c.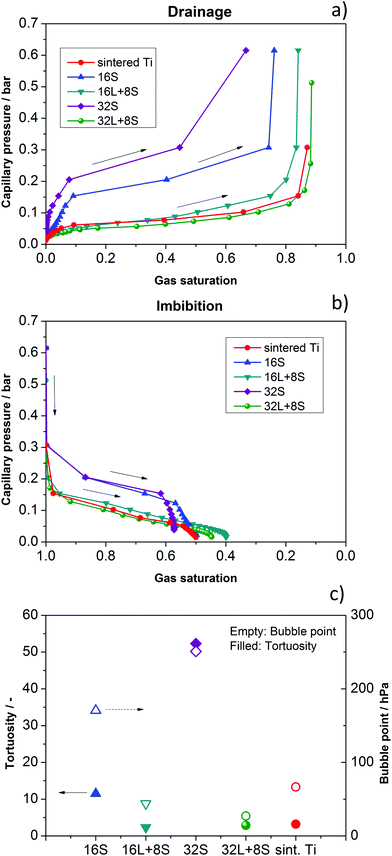

Fig. 8 Simulation of (a) drainage and (b) imbibition for the investigated GDLs: 16S, 32S, 16L + 8S, 32L + 8S, and sintered Ti. (c) Calculated bubble point and tortuosity.

Concerning water extrusion (drainage), one can see that the cells with the 16S and the 32S GDLs show significantly steeper slopes compared to the other GDLs, meaning that more pressure is needed to press water out in the case of gas penetration from the electrode side. These observations explain the lower performance of the cell with 32S GDL, which shows increased Ohmic resistance and mass transport limitation. The later is related to the high pressure necessary for transporting gases through the small pores. Regarding the imbibition, the results also show steeper slopes, meaning that water is more efficiently taken up. However, the capillary pressure is lower than the backpressure produced by blocked pores in the case of drainage. From these results, one can conclude that indeed an optimal pore size and thickness of the GDL exists, as has been reported by Grigoriev et al.³⁴ In the case of the cells with 16L + 8S, 32L + 8S, and sintered Ti GDLs, the flat slopes of the calculated imbibition curves do not seem to play an important role, in contrast to the flat slopes of the drainage curves, which all three samples have in common. These results can explain the high performance of the cells with these GDLs.

Concerning complexity of through-plane pathways, the cells with 16S and the 32S GDLs show exceptionally high tortuosities and capillary pressures, meaning that the pathways that the gas and water have to take are complicated. These findings are in good agreement with the polarization curves in Fig. 7, where both cells show lower performances compared to the cells with other GDLs. Therefore, the low performances of the cells with 16S and 32S GDLs in cell configuration 2 are clearly due to the high tortuosity and capillary pressure, leading to mass transport limitations.

4. Conclusions

Pore-graded gas diffusion layers (GDLs) for proton exchange membrane (PEM) electrolyzers have been developed via vacuum plasma spraying (VPS). The coating technique allowed controlling important functionalities of the GDL design, such as pore size, pore distribution, porosity, roughness, and thickness. Scanning electron microscopy (SEM), mercury intrusion porosimetry (MIP), and X-ray computed tomography (CT) were used to generate the data necessary for calculating the capillary pressure, bubble points, and tortuosity. The produced GDLs were electrochemically tested in two typical PEM electrolyzer cell designs with and without a bipolar plate (BPP) flow field. The polarization curves demonstrated high performance and a significant decrease in mass transport limitations. The optimal pore diameter in contact with the electrode was found to be between 6 and 11 μm, with the porosity higher than 22%. Moreover, depending on the cell design, the complexity of the through-plane pathways and capillary pressure had an impact on the electrolyzer performance. Therefore, it was possible to reduce the tortuosity, capillary pressure, and bubble points by combining different pore sizes in contact with the electrode and BPP. The cost of thermal spraying of GDLs to reach the benchmark in terms of performance and cost for large-scale m²-size production has been estimated as 20–100 USD m⁻².²⁵ Overall, the results suggest the possibility of using thermal spraying for manufacturing the entire stack interconnector on a stainless steel BPP, including for the protective Ti coating,^18,24,25,29 to the large/medium pore-size GDLs (this work) and backing layer.³² All of them could be produced in one manufacturing step, representing a significant cost reduction for the interconnectors, which account for almost 70% of the total stack value.¹⁶

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge Riko Moroni for providing the Matlab code on pore-size distributions. We are also grateful to Ina Plock and Günther Roth for performing the SEM measurements and the production of the PTLs via VPS, respectively. We thank Asif Ansar for the fruitful discussions on plasma spraying.

References

1. U. Nations, United Nations, Adoption of the Paris Agreement, 2015.
2. M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, A comprehensive review on PEM water electrolysis, Int. J. Hydrogen Energy, 2013, 38, 4901–4934,  DOI:10.1016/j.ijhydene.2013.01.151.
3. K. A. Friedrich, PlanDelyKad: Study on Large Scale Water Electrolysis and Hydrogen Storage (in German). German Federal Ministry for Economic Affairs and Energy (BMWi), Berlin, 2015, http://edok01.tib.uni-hannover.de/edoks/e01fb15/824812212.pdf.
4. B. Haubner, B. Pitschak, A. Bayer, A. Gago, P. Lettenmeier, V. Christoph and T. Smolinka, Wie kommen Wind und Sonne ins Gasnetz ?, DVGW, 2017, 12–16.
5. P. C. K. Vesborg and T. F. Jaramillo, Addressing the terawatt challenge: scalability in the supply of chemical elements for renewable energy, RSC Adv., 2012, 2, 7933,  10.1039/c2ra20839c.
6. P. Lettenmeier, L. Wang, U. Golla-Schindler, P. Gazdzicki, N. A. Cañas, M. Handl, R. Hiesgen, S. S. Hosseiny, A. S. Gago and K. A. Friedrich, Nanosized IrO_x-Ir Catalyst with Relevant Activity for Anodes of Proton Exchange Membrane Electrolysis Produced by a Cost-Effective Procedure, Angew. Chem., 2016, 128, 752–756,  DOI:10.1002/ange.201507626.
7. L. Wang, P. Lettenmeier, U. Golla-Schindler, P. Gazdzicki, N. A. Cañas, T. Morawietz, R. Hiesgen, S. S. Hosseiny, A. S. Gago and K. A. Friedrich, Nanostructured Ir-supported on Ti₄O₇ as cost effective anode for proton exchange membrane (PEM) electrolyzers, Phys. Chem. Chem. Phys., 2016, 18, 4487–4495,  10.1039/C5CP05296C.
8. T. Reier, M. Oezaslan and P. Strasser, Electrocatalytic Oxygen Evolution Reaction (OER) on Ru, Ir, and Pt Catalysts: A Comparative Study of Nanoparticles and Bulk Materials, ACS Catal., 2012, 2, 1765–1772,  DOI:10.1021/cs3003098.
9. S. Cherevko, T. Reier, A. R. Zeradjanin, Z. Pawolek, P. Strasser and K. J. J. Mayrhofer, Stability of nanostructured iridium oxide electrocatalysts during oxygen evolution reaction in acidic environment, Electrochem. Commun., 2014, 48, 81–85,  DOI:10.1016/j.elecom.2014.08.027.
10. H. N. Nong, H.-S. Oh, T. Reier, E. Willinger, M. G. Willinger, V. Petkov, D. Teschner and P. Strasser, Oxide-supported IrNiO_x core–shell particles as efficient, cost-effective, and stable catalysts for electrochemical water splitting, Angew. Chem., Int. Ed., 2015, 2, 2975.
11. T. Reier, Z. Pawolek, S. Cherevko, M. Bruns, T. Jones, D. Teschner, S. Selve, A. Bergmann, H. N. Nong, R. Schlögl, K. J. J. Mayrhofer and P. Strasser, Molecular insight in structure and activity of highly efficient, low-Ir Ir–Ni oxide catalysts for electrochemical water splitting (OER), J. Am. Chem. Soc., 2015, 137, 13031–13040,  DOI:10.1021/jacs.5b07788.
12. K. S. Kadakia, P. H. Jampani, O. I. Velikokhatnyi, M. K. Datta, S. K. Park, D. H. Hong, S. J. Chung and P. N. Kumta, Nanostructured F doped IrO₂ electro-catalyst powders for PEM based water electrolysis, J. Power Sources, 2014, 269, 855–865,  DOI:10.1016/j.jpowsour.2014.07.045.
13. V. A. Saveleva, L. Wang, W. Luo, S. Zafeiratos, C. Ulhaq-Bouillet, A. S. Gago, K. A. Friedrich and E. R. Savinova, Uncovering the Stabilization Mechanism in Bimetallic Ruthenium–Iridium Anodes for Proton Exchange Membrane Electrolyzers, J. Phys. Chem. Lett., 2016, 7, 3240–3245,  DOI:10.1021/acs.jpclett.6b01500.
14. L. Wang, F. Song, G. Ozouf, D. Geiger, T. Morawietz, M. Handl, P. Gazdzicki, C. Beauger, U. Kaiser, R. Hiesgen, A. S. Gago and K. A. Friedrich, Improving the activity and stability of Ir catalysts for PEM electrolyzer anodes by SnO₂:Sb aerogel supports: does V addition play an active role in electrocatalysis ?, J. Mater. Chem. A, 2017, 5, 3172–3178,  10.1039/C7TA00679A.
15. L. Wang, V. A. Saveleva, S. Zafeiratos, E. R. Savinova, P. Lettenmeier, P. Gazdzicki, A. S. Gago and K. A. Friedrich, Highly active anode electrocatalysts derived from electrochemical leaching of Ru from metallic Ir 0.7 Ru 0.3 for proton exchange membrane electrolyzers, Nano Energy, 2017, 34, 385–391,  DOI:10.1016/j.nanoen.2017.02.045.
16. L. Bertuccioli, A. Chan, D. Hart, F. Lehner, B. Madden and E. Standen, Development of Water Electrolysis in the European Union, Fuel Cells and Hydrogen Joint Undertaking (FCH JU), 2014, http://www.fch.europa.eu/node/783.
17. C. K. Jin, M. G. Jeong and C. G. Kang, Fabrication of titanium bipolar plates by rubber forming and performance of single cell using TiN-coated titanium bipolar plates, Int. J. Hydrogen Energy, 2014, 1–9,  DOI:10.1016/j.ijhydene.2014.03.013.
18. A. S. Gago, A. S. Ansar, P. Gazdzicki, N. Wagner, J. Arnold and K. A. Friedrich, Low Cost Bipolar Plates for Large Scale PEM Electrolyzers, ECS Trans., 2014, 64, 1039–1048,  DOI:10.1149/06403.1039ecst.
19. Z. Kang, J. Mo, G. Yang, S. T. Retterer, D. A. Cullen, T. J. Toops, J. B. Green Jr, M. M. Mench and F.-Y. Zhang, Investigation of thin/well-tunable liquid/gas diffusion layers exhibiting superior multifunctional performance in low-temperature electrolytic water splitting, Energy Environ. Sci., 2016, 8, 2811–2824,  10.1039/C6EE02368A.
20. O. Emile Tabu, E. Mayousse, T. Smolinka and N. Guillet, Advanced bipolar plates without flow channels, for PEM electrolysers operating at high pressure – TECHNOPORT RERC 2012 Trondheim, April 16–18, 2012, http://www.sintef.no/globalassets/project/stampem/pdf/technoport-rerc-2012-ojong2.pdf.
21. H. Ito, T. Maeda, A. Nakano, A. Kato and T. Yoshida, Influence of pore structural properties of current collectors on the performance of proton exchange membrane electrolyzer, Electrochim. Acta, 2013, 100, 242–248,  DOI:10.1016/j.electacta.2012.05.068.
22. L. Zielke, A. Fallisch, N. Paust, R. Zengerle and S. Thiele, Tomography based screening of flow field / current collector combinations for PEM water electrolysis, RSC Adv., 2014, 4, 58888–58894,  10.1039/C4RA12402B.
23. H.-Y. Jung, S.-Y. Huang and B. N. Popov, High-durability titanium bipolar plate modified by electrochemical deposition of platinum for unitized regenerative fuel cell (URFC), J. Power Sources, 2010, 195, 1950–1956,  DOI:10.1016/j.jpowsour.2009.10.002.
24. P. Lettenmeier, R. Wang, R. Abouatallah, F. Burggraf, A. S. Gago and K. A. Friedrich, Coated Stainless Steel Bipolar Plates for Proton Exchange Membrane Electrolyzers, J. Electrochem. Soc., 2016, 163, F3119–F3124,  DOI:10.1149/2.0141611jes.
25. A. S. Gago, S. A. Ansar, B. Saruhan, U. Schulz, P. Lettenmeier, N. A. Cañas, P. Gazdzicki, T. Morawietz, R. Hiesgen, J. Arnold and K. A. Friedrich, Protective coatings on stainless steel bipolar plates for proton exchange membrane (PEM) electrolysers, J. Power Sources, 2016, 307, 815–825,  DOI:10.1016/j.jpowsour.2015.12.071.
26. C. Rakousky, U. Reimer, K. Wippermann, M. Carmo, W. Lueke and D. Stolten, An analysis of degradation phenomena in polymer electrolyte membrane water electrolysis, J. Power Sources, 2016, 326, 120–128,  DOI:http://dx.doi.org/10.1016/j.jpowsour.2016.06.082.
27. M. B. Whiteman and A. R. Troiano, Hydrogen Embrittlement Of Austenitic Stainless Steel, Corrosion, 1965, 21, 53–56,  DOI:10.5006/0010-9312-21.2.53.
28. E. Herms, J. Olive and M. Puiggali, Hydrogen embrittlement of 316L type stainless steel, Mater. Sci. Eng., A, 1999, 272, 279–283,  DOI:10.1016/S0921-5093(99)00319-6.
29. P. Lettenmeier, R. Wang, R. Abouatallah, B. Saruhan, O. Freitag, P. Gazdzicki, T. Morawietz, R. Hiesgen, A. S. Gago and K. A. Friedrich, Low-Cost and Durable Bipolar Plates for Proton Exchange Membrane Electrolyzers, Sci. Rep., 2017, 7, 44035,  DOI:10.1038/srep44035.
30. F. Arbabi, A. Kalantarian, R. Abouatallah, R. Wang, J. S. Wallace and A. Bazylak, Feasibility study of using microfluidic platforms for visualizing bubble flows in electrolyzer gas diffusion layers, J. Power Sources, 2014, 258, 142–149,  DOI:10.1016/j.jpowsour.2014.02.042.
31. S. Siracusano, A. Di Blasi, V. Baglio, G. Brunaccini, N. Briguglio, A. Stassi, R. Ornelas, E. Trifoni, V. Antonucci and A. S. Aricó, Optimization of components and assembling in a PEM electrolyzer stack, Int. J. Hydrogen Energy, 2011, 36, 3333–3339,  DOI:10.1016/j.ijhydene.2010.12.044.
32. P. Lettenmeier, S. Kolb, F. Burggraf, A. S. Gago and K. A. Friedrich, Towards developing a backing layer for proton exchange membrane electrolyzers, J. Power Sources, 2016, 311, 153–158,  DOI:10.1016/j.jpowsour.2016.01.100.
33. S. A. Grigoriev, K. A. Dzhus, D. G. Bessarabov and P. Millet, Failure of PEM water electrolysis cells: Case study involving anode dissolution and membrane thinning, Int. J. Hydrogen Energy, 2014, 39, 20440–20446,  DOI:http://dx.doi.org/10.1016/j.ijhydene.2014.05.043.
34. S. A. Grigoriev, P. Millet, S. A. Volobuev and V. N. Fateev, Optimization of porous current collectors for PEM water electrolysers, Int. J. Hydrogen Energy, 2009, 34, 4968–4973,  DOI:10.1016/j.ijhydene.2008.11.056.
35. N. Baumann, C. Cremers, K. Pinkwart and J. Tübke, Membrane Electrode Assemblies for Water Electrolysis using WO₃-Supported Ir_xRu_1−xO₂ Catalysts, Energy Technol., 2016, 4, 212–220,  DOI:10.1002/ente.201500258.
36. C. Lee, J. Hinebaugh, R. Banerjee, S. Chevalier, R. Abouatallah, R. Wang and A. Bazylak, Influence of limiting throat and flow regime on oxygen bubble saturation of polymer electrolyte membrane electrolyzer porous transport layers, Int. J. Hydrogen Energy, 2017, 42, 2724–2735,  DOI:10.1016/j.ijhydene.2016.09.114.
37. M. D. Abramoff, P. J. Magalhães and S. J. Ram, Image processing with ImageJ, Biophotonics Int., 2004, 11, 36–42.
38. M. Hilpert and C. T. Miller, Pore-morphology-based simulation of drainage in totally wetting porous media, Adv. Water Resour., 2001, 24, 243–255,  DOI:10.1016/S0309-1708(00)00056-7.
39. J. F. Delerue, E. Perrier, Z. Y. Yu and B. Velde, New algorithms in 3D image analysis and their application to the measurement of a spatialized pore size distribution in soils, Phys. Chem. Earth, Part A Solid Earth Geod., 1999, 24, 639–644,  DOI:10.1016/s1464-1895(99)00093-9.
40. B. Münch and L. Holzer, Contradicting Geometrical Concepts in Pore Size Analysis Attained with Electron Microscopy and Mercury Intrusion, J. Am. Ceram. Soc., 2008, 91, 4059–4067,  DOI:10.1111/j.1551-2916.2008.02736.x.
41. M. A. Travassos, V. V. Lopes, R. A. Silva, A. Q. Novais and C. M. Rangel, Assessing cell polarity reversal degradation phenomena in PEM fuel cells by electrochemical impedance spectroscopy, Int. J. Hydrogen Energy, 2013, 38, 7684–7696,  DOI:10.1016/j.ijhydene.2013.01.132.
42. D. Malevich, E. Halliop, B. A. Peppley, J. G. Pharoah and K. Karan, Investigation of Charge-Transfer and Mass-Transport Resistances in PEMFCs with Microporous Layer Using Electrochemical Impedance Spectroscopy, J. Electrochem. Soc., 2009, 156, B216,  DOI:10.1149/1.3033408.
43. J. T. Mueller and P. M. Urban, Characterization of direct methanol fuel cells by ac impedance spectroscopy, J. Power Sources, 1998, 75, 139–143,  DOI:10.1016/S0378-7753(98)00109-8.
44. P. Lettenmeier, R. Wang, R. Abouatallah, S. Helmly, T. Morawietz, R. Hiesgen, S. Kolb, F. Burggraf, J. Kallo, A. S. Gago and K. A. Friedrich, Durable Membrane Electrode Assemblies for Proton Exchange Membrane Electrolyzer Systems Operating at High Current Densities, Electrochim. Acta, 2016, 210, 502–511,  DOI:10.1016/j.electacta.2016.04.164.
45. O. Antoine, Y. Bultel and R. Durand, Oxygen reduction reaction kinetics and mechanism on platinum nanoparticles inside Nafion®, J. Electroanal. Chem., 2001, 499, 85–94,  DOI:10.1016/S0022-0728(00)00492-7.
46. M. Eikerling and A. A. Kornyshev, Electrochemical impedance of the cathode catalyst layer in polymer electrolyte fuel cells, J. Electroanal. Chem., 1999, 475, 107–123,  DOI:10.1016/S0022-0728(99)00335-6.
47. C. Rozain and P. Millet, Electrochemical characterization of Polymer Electrolyte Membrane Water Electrolysis Cells, Electrochim. Acta, 2014, 131, 160–167,  DOI:10.1016/j.electacta.2014.01.099.
48. J. Liu, R. Bolot and S. Costil, Residual stresses and final deformation of an alumina coating: Modeling and measurement, Surf. Coat. Technol., 2015, 268, 241–246,  DOI:10.1016/j.surfcoat.2014.05.050.
49. R. Bolot, J. Li, R. Bonnet, C. Mateus and C. Coddet, Modeling of the substrate temperature evolution during the APS thermal spray process, in Thermal Spray 2003: Advancing the Science and Applying the Technology, ed. C. Moreau and B. Marple, ASM International, Ohio, 2003, pp. 949–954.
50. R. Moroni, M. Börner, L. Zielke, M. Schroeder, S. Nowak, M. Winter, I. Manke, R. Zengerle and S. Thiele, Multi-Scale Correlative Tomography of a Li-Ion Battery Composite Cathode, Sci. Rep., 2016, 6, 30109,  DOI:10.1038/srep30109.
51. H. Vogt, The problem of the departure diameter of bubbles at gas-evolving electrodes, Electrochim. Acta, 1989, 34, 1429–1432,  DOI:10.1016/0013-4686(89)87183-X.
52. H. Vogt and R. J. Balzer, The bubble coverage of gas-evolving electrodes in stagnant electrolytes, Electrochim. Acta, 2005, 50, 2073–2079,  DOI:10.1016/j.electacta.2004.09.025.
53. M. Doyle, Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells, J. Electrochem. Soc., 1996, 143, 1890,  DOI:10.1149/1.1836921.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee01240c

---