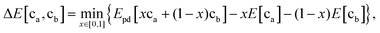Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Compatibility issues between electrodes and electrolytes in solid-state batteries†
Yaosen
Tian‡
 ab,
Tan
Shi‡
ab,
William D.
Richards
c,
Juchuan
Li
ab,
Tan
Shi‡
ab,
William D.
Richards
c,
Juchuan
Li
 b,
Jae Chul
Kim
b,
Jae Chul
Kim
 b,
Shou-Hang
Bo
*b and
Gerbrand
Ceder
*abc
b,
Shou-Hang
Bo
*b and
Gerbrand
Ceder
*abc
aDepartment of Materials Science and Engineering, University of California Berkeley, Berkeley, CA 94720, USA. E-mail: gceder@berkeley.edu
bMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA. E-mail: sbo@lbl.gov
cDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
First published on 26th April 2017
Abstract
Remarkable success has been achieved in the discovery of ceramic alkali superionic conductors as electrolytes in solid-state batteries; however, obtaining a stable interface between these electrolytes and electrodes is difficult. Only limited studies on the compatibility between electrodes and solid electrolytes have been reported, partially because of the need for expensive instrumentation and special cell designs. Without simple yet powerful tools, these compatibility issues cannot be systematically investigated, thus hindering the generalization of design rules for the integration of solid-state battery components. Herein, we present a methodology that combines density functional theory calculations and simple experimental techniques such as X-ray diffraction, simultaneous differential scanning calorimetry and thermal gravimetric analysis, and electrochemistry to efficiently screen the compatibility of numerous electrode/electrolyte pairs. We systemically distinguish between the electrochemical stability of the solid-state conductor, which is relevant wherever the electrolyte contacts an electron pathway, and the electrochemical stability of the electrode/electrolyte interfaces. For the solid electrolyte, we are able to computationally derive an absolute thermodynamic stability voltage window, which is small for Na3PS4 and Na3PSe4, and a larger voltage window which can be kinetically stabilized. The experimental stability, when measured with reliable techniques, falls between these thermodynamic and kinetic limits. Employing a Na solid-state system as an example, we demonstrate the efficiency of our method by finding the most stable system (NaCrO2|Na3PS4|Na–Sn) within a selected chemical space (more than 20 different combinations of electrodes and electrolytes). Important selection criteria for the cathode, electrolyte, and anode in solid-state batteries are also derived from this study. The current method not only provides an essential guide for integrating all-solid-state battery components but can also significantly accelerate the expansion of the electrolyte/electrode compatibility data.
Broader contextAll-solid-state rechargeable batteries have seen a resurgence of interest from researchers in recent years, owing to their potential for enhanced safety and energy density. Many superionic conductors have been discovered and employed as solid state electrolytes with ionic conductivities close to or even higher than those of liquid counterparts. However, the compatibility between electrodes and solid-state electrolytes has not been systematically investigated. In this work, we present a simple yet powerful methodology which combines ab initio modeling and fast characterization tools to investigate the electrochemical stability of the solid-state electrolyte and the chemical stability of the electrode/electrolyte interfaces. Employing Na solid state batteries as an example, our combined theoretical and experimental investigation led us to identify the most stable system (NaCrO2|Na3PS4|Na–Sn) within the selected chemical space (more than 20 different combinations of electrodes and electrolytes). We also provide possible solutions to the interfacial issues and important selection criteria for the cathode, electrolyte, and anode in solid-state batteries. With the focus of solid state battery research shifting toward cell integration, our timely system-level investigations provide a strong foundation. |
Introduction
Pioneered by the study of microbatteries, solid-state batteries have recently attracted significant attention1–9 because of their advantages compared with conventional batteries employing liquid electrolytes. The use of a ceramic solid-state electrolyte not only eliminates the safety hazards associated with flammable organic liquid electrolytes but also opens up the possibility of using novel high-capacity electrodes, such as sulfur cathodes and Na or Li metal anodes. These high-capacity electrodes have proven problematic in liquid systems, partially because of reactivity and/or dissolution with the electrolyte, and poor metal deposition morphology in liquid electrolytes, often leading to dendrite growth.2,10,11 When built with stable interfaces, solid state batteries can also minimize the side reactions that occur in liquid electrolyte batteries, resulting in high Coulombic efficiency and ultra-long cycle life.12,13 Recently, all-solid-state batteries utilizing sulfide-based superionic conductors have even achieved superior performance in terms of power density compared with traditional Li-ion batteries (LIBs) thanks to the discovery of lithium superionic conductors with ionic conductivities of 25 mS cm−1, one magnitude higher than those of state-of-art liquid electrolytes.14–19The main research focus in all-solid-state batteries has been on finding fast ionic conductors, which has resulted in many newly discovered conductors with ionic conductivities close to or even surpassing those of liquid electrolytes. Given that the basic structural and chemical features for high alkali ion conductivity are now reasonably well understood,20,21 it is likely even better conductors will be developed. In Li-ion systems, some NASICON-, perovskite- and garnet-type oxides exhibit room-temperature (RT) conductivities of approximately 1 mS cm−1 or higher but suffer from poor contact with electrodes because of difficulties in pellet pressing and sintering.1,7,22–29 Sulfide-based solid electrolytes such as Li10GeP2S12 and Li2S–P2S5 exhibit conductivities greater than 10 mS cm−1,8,21,30–33 but generally have limited voltage stability windows, which makes electrode selection a difficult task.6,34–36 In some cases, an electrode coating is applied to mitigate this issue; however, the coating process is often imperfect or difficult to scale.8,37–39 In parallel to the developments in solid-state lithium conductors, promising fast Na-ion conductors have also been recently discovered and applied in Na-ion batteries (NIBs).14,16,19,30,32,40–45 However, it is similarly challenging to find a Na conductor with all the desired properties for all-solid-state battery applications, namely high conductivity, compatibility with both anodes and cathodes, processability, and good mechanical properties.
Clearly, the bottleneck of all-solid-state battery development is no longer maximizing the ionic conductivity of solid electrolytes but has instead shifted toward the integration of the solid electrolyte and electrodes. This challenge of cell integration is largely associated with maintaining chemical and mechanical stability between the electrodes and electrolytes during battery operation, both of which are a major obstacle for solid-state battery development. The compatibility of electrodes and electrolytes is largely determined by the properties of the electrode/electrolyte interface. A good interface between a solid electrolyte and electrode requires fast ion transport, maximum contact area, and chemical stability during cycling. Indeed, in detailed studies, previously claimed stable electrolyte/electrode pairs have often found to degrade through chemical or electrochemical reactions.8,21,26,34,39,46–49
In this work, we focus on the chemical aspect of the cell integration challenge, and present a methodology that combines computational predictions with fast, simple experimental tests that can efficiently screen the compatibility of numerous electrode/electrolyte pairs. We use layered Na transition metal oxide cathodes (NaMO2, M = Cr, Mn, Fe, Co, Ni),50–54 Na metal or Na–Sn alloy anodes,55,56 and two recently reported solid electrolytes with high ionic conductivities (Na3PS430 and Na3PSe415,41) as examples to demonstrate our methodology. The Na ion system was selected for several reasons. First, NIBs have attracted significant attention because of the lower cost and greater abundance of their materials compared with those used in LIBs.57–59 Second, the Na system provides a wider chemical space to explore for cathode materials, enabling synthesis and cycling of many electrode materials for which the Li analogues are electrochemically inactive, such as layered NaFeO2.52,58–60 Finally, compatibility issues have not been systematically studied in the Na solid-state system, which provides us with an opportunity to demonstrate the efficiency of our screening method when applied to unknown systems.
In the following discussion, we will start by introducing the compatibility issues facing solid-state batteries as well as the methodology to examine these issues. Then, the results with respect to the electrochemical stability of the electrolytes and chemical compatibility between the electrodes and electrolytes will be presented. The manuscript concludes with a discussion of the (1) main chemical challenge associated with utilizing an oxide cathode and thiophosphate solid electrolyte, (2) importance of understanding both the chemical and electrochemical decomposition pathways of electrolytes and electrode/electrolyte composites, and (3) role of thermodynamics and kinetics in these reactions. Possible strategies and selection criteria to integrate all-solid-state battery components will also be proposed.
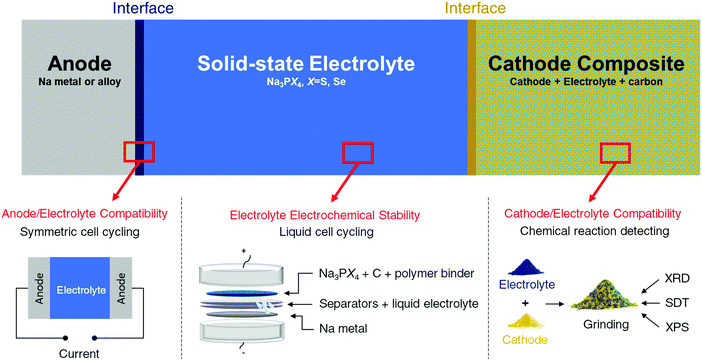
Methodology
Three factors mainly govern the choice of components for all-solid state batteries. Taking Na solid-state systems as an example, the three factors are graphically illustrated in Fig. 1 and are discussed in detail below:(1) Voltage window of the solid electrolyte. The voltage window of the electrolyte determines the cycling range and selection of both electrodes and should thus be considered and determined first.
Prior experimental insights regarding the electrochemical stability of solid-state electrolytes may require reinterpretation. Determination of the stable electrochemical window of a solid electrolyte has been traditionally performed using cyclic voltammetry (CV).18,32,61,62 In this method, the solid electrolyte is pressed into pellets and cycled with Li or Na metal on one side and an inert metal (such as stainless steel, Au, or Pt) on the other side. However, CV often overestimates the electrochemical stability limits of electrolytes. The bulk electrolyte is likely not in equilibrium during a CV scan because of the fast scanning rate and/or imperfect contact with the metal electrodes. Furthermore, because of the poor electronic conductivity of solid electrolytes, the overall decomposition reaction is often slow or limited to a thin region at the interface, thereby limiting the degradation current that can be observed in a CV scan. The situation is very different in a real cell configuration, where the electrolyte is mixed with carbon and the cathode material, providing a facile electron transfer pathway that promotes electrolyte redox reactions. Finally, the relatively small decomposition current detected by the CV method (sometimes less than 1 μA) is difficult to notice compared with the large current created by metal deposition/stripping at low voltage and is often ignored in the CV method. However, this small current could have a catastrophic effect on the long-term cycling of the full cell. Indeed, solid electrolytes previously claimed to be stable based on CV scans62 were later upon more detailed investigation, found to be reactive at typical anode and cathode voltages,63 in agreement with theoretical predictions.6,33,64
Other electrochemical techniques, such as polarization experiments, should be complemented with CV methods to determine the stability window of the solid electrolyte more accurately. In such experiment, the electrolyte is made into electrode and polarized to a given potential or with a constant current. The electrolyte is considered stable at such potential if the capacity delivered below (or above) this potential is close to zero during a galvanostatic or potentiostatic charge (or discharge). In our work, the stability windows of selected electrolytes (Na3PS4 and Na3PSe4) were first computed using density functional theory (DFT) calculations.34 The results were then compared with experimental results obtained from galvanostatic charging/discharging. A similar method was recently employed to evaluate the electrochemical stability windows of Li7La3Zr2O12 garnet and Li10GeP2S12, where the DFT computed and experimentally determined stability windows were in excellent agreement.63 The synthesized solid electrolytes were ground into fine powders and then mixed with carbon and polymer binders to form film-type working electrodes, which were assembled in Swagelok cells with a liquid electrolyte against Na metal. By slowly cycling this cell, the voltage experienced by the bulk electrolyte materials is much better represented by the cell voltage, and a more accurate estimation of the stability window of the materials can be provided. The corresponding charge (or discharge) capacities also indicate whether the electrolyte decomposition is self-limiting. A self-limiting decomposition reaction can be beneficial in widening the electrochemical stability of the electrolyte depending on the physical properties (e.g., ionic and electronic conductivities) of the decomposition products.
(2) Possible reaction between cathode and solid electrolyte. Absolute stability between the cathode and electrolyte is difficult to achieve, and the products of the reaction between the cathode and solid electrolyte can form an interfacial layer between the two. Depending on its properties, this interfacial layer can be detrimental or beneficial to the ionic transport between the two components. A good interface between the electrode and electrolyte must be self-passivating while still being permeable to the working ions.
Based on this information, we tested the compatibility of electrodes and electrolytes by mixing the electrolyte and electrode powders at room temperature. Any bulk change detectable by X-ray diffraction (XRD) indicates that the selected electrolyte and electrode materials are incompatible. The possible reactions between electrodes and electrolytes at elevated temperatures were also evaluated using simultaneous differential scanning calorimetry and thermal gravimetric analysis (SDT) and XRD to determine the onset temperature of reaction and corresponding reaction products. Comparison of these results with the DFT-computed thermodynamic reaction products enabled us to assess the role of kinetics in the electrode/electrolyte reactions, providing additional mechanistic insights.
Besides testing the reaction of the electrolyte with the as-synthesized cathode, studying the compatibility with the charged cathode at high voltages is also important. At higher potential the strong oxidative power of the charged cathode will likely promote the electrolyte decomposition for chalcogenide systems. This chemical compatibility, however, has not yet been systematically investigated.
To investigate the aforementioned issue, partially charged cathodes were prepared through chemical oxidation with highly concentrated iodine in acetonitrile (CH3CN), resulting in cathode powders equivalent to being charged to approximately 3.7 V against Na metal.65,66 The reactions between the charged cathodes and electrolytes were then studied in a similar manner as discussed above.
(3) Possible reaction between anode and solid electrolyte. The compatibility between the anode and electrolyte was examined by cycling anode/electrolyte/anode symmetric cells. If the anode and electrolyte react to form a poorly ionic conductive interfacial layer, the cell potential will increase as the reaction progresses. To prevent possible potential increase due to the mechanical loss of contact, a specially designed pressure cell is used to ensure good contact between electrolyte and electrodes during cycling. Therefore, an increase in the charge and discharge voltages during galvanostatic cycling often signifies an unstable interface between the anode and electrolyte.
Results
I. Electrolyte electrochemical stability
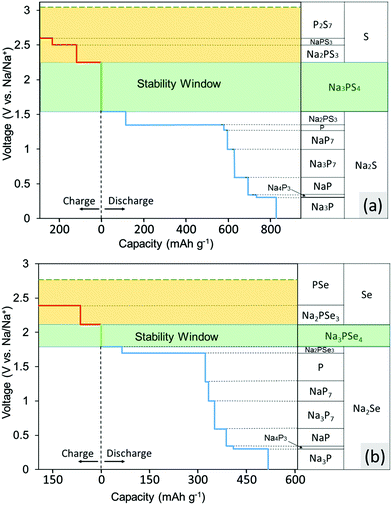
The calculated voltage stability window and decomposition products of Na3PS4 and Na3PSe4 are shown in Fig. 2a and b, respectively. These figures indicate which products the conductor converts into when Na is supplied and extracted at a given potential. The x-axis represents the capacity generated when these decomposition reactions occur per gram of conductor consumed. The results in Fig. 2a indicate that Na3PS4 is electrochemically only stable from 1.55 to 2.25 V against Na metal. Below 1.55 V, Na3PS4 can be reduced and converted into Na2S and other Na–P compounds. Above 2.25 V, in contrast, Na is extracted from Na3PS4, leading to decomposition into Na-deficient phases such as P2S7 and S. Similarly, according to Fig. 2b, Na3PSe4 is stable from 1.80 to 2.15 V against Na metal and decomposes into Na2Se and other Na–P compounds below 1.80 V and Na-deficient phases such as PSe and Se above 2.15 V. Of note is that our calculated stability window is much narrower than experimental values claimed from CV measurements, but in agreement with other theory work.30,41 This discrepancy results either from reaction kinetics, which would delay the onset of decomposition, or intrinsic limitations of the CV measurements. Based on our experimental results, as will be discussed below, the latter is more likely.These calculated voltages assume that diffusion kinetics are not limiting, and thus provide a lower bound of the Na extraction voltage. To investigate the upper limiting case, the voltage for topotactic desodiation of the conductors was calculated. The calculated results indicate that Na3PS4 and Na3PSe4 lose Na at 3.05 V and 2.75 V, respectively. We found furthermore that the voltage for subsequent extraction of Na is lower. Note that these two values indeed provide absolute upper bound for the Na3PX4 (X = S, Se) stability window, as the Na-ion and electron extraction are unlikely to be kinetically limited due to the faster Na-ion mobility in these materials.
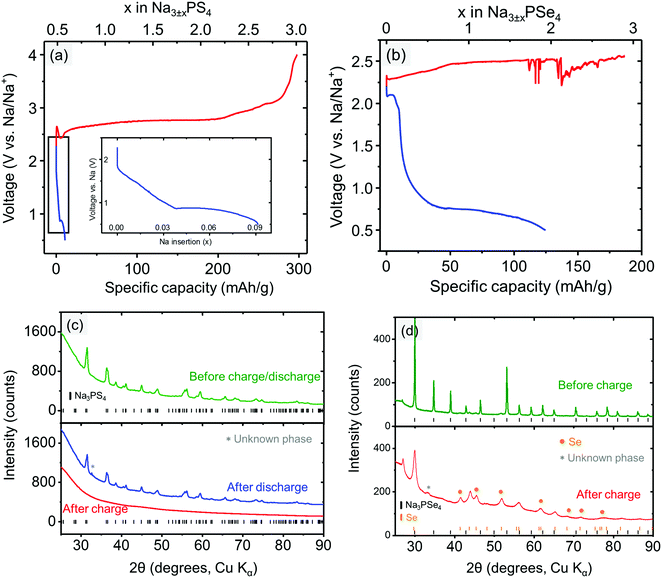
To experimentally determine the electrochemical stability window of the electrolyte materials, Na3PX4 cathodes were “charged” (oxidized) to 4.0 V or “discharged” (reduced) to 0.5 V at a constant current. Upon charging, Na3PS4 exhibited negligible capacity at the beginning of charging (Fig. 3a). However, as the voltage increased above ∼2.65 V, a voltage dip followed by a substantial capacity delivered at approximately 2.7 V was observed. The initial voltage rise is likely due to a nucleation or other activation process, needed to generate the decomposition products of Na3PS4. Therefore, we can assume that the voltage dip at approximately 2.5 V is the onset decomposition voltage of Na3PS4. Approximately 2.5 Na per f.u. can be extracted from Na3PS4 until the cut-off voltage of 4.0 V is reached. The “fully charged” Na3PS4 cathode composite turns completely amorphous as observed in XRD (Fig. 3c).
During the discharging process, a sloping voltage region is first observed at approximately 1.8 V, followed by a redox reaction at approximately 0.9 V, suggesting that Na3PS4 is likely electrochemically unstable below this voltage. The sloping voltage region (1.8–0.9 V) is likely a result of the presence of a small amount of sulfur in the as-prepared Na3PS4 sample. The reduction of sulfur occurs at approximately 2 V.67 Interestingly, fully discharging to the cut-off voltage of 0.5 V only results in a very low capacity (i.e., 0.08 Na intercalation per formula), and the “fully discharged” Na3PS4 shows almost no structural change compared with the pristine cathode composite (Fig. 3c). One possible reason is that Na3PS4 might be passivated by the decomposition products upon discharging. This passivating process may prevent further decomposition of Na3PS4 and widens the apparent reduction limit of Na3PS4. Based on the discussion above, we conclude that the electrochemical stability window of Na3PS4 lies within the range 0.9–2.5 V, which is in much better agreement with the DFT predictions than reported CV measurements, further underscoring the limited reliability of CV techniques to determine the stability limits of solid electrolytes.
Similarly, the stability window of Na3PSe4 was experimentally determined by charging and discharging the Na3PSe4 (mixed with carbon) cathode composite. During the charging process, the decomposition of Na3PSe4 starts at approximately 2.33 V, where a substantial capacity of 110 mA h g−1 or 1.5 Na per formula was delivered in the sloping voltage region of 2.33–2.50 V. Based on DFT calculations, this decomposition process is most likely associated with the production of Se and Na2PSe3. The decomposition products of the “fully charged” Na3PSe4 was experimentally determined by both ex situ and in situ XRD. In the ex situ XRD results presented in Fig. 3d, new Se peaks are observed after the Na3PSe4 cathode composite is “fully charged”, which is in almost perfect agreement with the DFT calculations; in the in situ XRD results (Fig. S1, ESI†), Se was detected to grow in quantity at the expense of Na3PSe4, although the other predicted product (i.e., Na2PSe3) is not observed. We suspect that Na2PSe3 might be present as an amorphous phase. The prolonged voltage plateau at approximately 2.50 V might be a result of the redox shuttle effect caused by dissolved polyselenide molecules,68,69 and the voltage fluctuation could be related to the reaction of the Na metal with the dissolved decomposition products. When the cell was opened after the charging process, the separators and Na metal had both become brown, indirectly supporting the above explanation of the voltage fluctuation. During the discharge process, a noticeable redox reaction occurs at approximately 2.10 V. Similarly, this is likely due to the presence of a small amount of the selenium in the as-prepared Na3PSe4 sample, which is reduced at approximately 2 V.68 Since only a small capacity is delivered in the voltage sloping region (2.10–1.25 V), it is unlikely to arise from the bulk reduction of Na3PSe4. Thus we tentatively assigned 1.25 V as the cathodic stability limit of Na3PSe4. Based on DFT calculations, this process is associated with the production of Na2Se and Na2PSe3. Overall, the stability window of Na3PSe4 was determined to be 1.25–2.35 V, which is again closer to our theoretical predictions than to the CV measurement (Table 4).
II. Compatibility between cathode and electrolyte
| NaCrO2 | NaMnO2 | NaFeO2 | NaCoO2 | NaNiO2 | ||
|---|---|---|---|---|---|---|
| a Denotes compounds which are created through chemical substitution of compounds which are present in the Inorganic Crystal Structure Database (ICSD). | ||||||
| Na3PS4 | Reaction products |
Na3PO4
NaCrS2 |
Na3PO4
NaMnS2a |
Na3PO4
Na3/2(FeS2) FeS2 |
Na3PO4
NaCoS2 |
Na3PO4
Na2S Na2SO4 Na2Ni3S4a |
| Reaction energy (eV per atom) | −0.0970 | −0.2649 | −0.2652 | −0.3516 | −0.4394 | |
| Na3PSe4 | Reaction products |
Na3PO4
NaCrSe2 |
Na3PO4
NaMnSe2a |
Na3PO4
Na2Se FeSe2 FeSe |
Na3PO4
Na2Se Co9Se8 Co5Se8a |
Na3PO4
Na2Se Ni5Se8a Ni3Se4 |
| Reaction energy (eV per atom) | −0.1325 | −0.2138 | −0.2615 | −0.3695 | −0.4541 | |
| Na0.5CrO2 | Na0.5MnO2 | Na0.5FeO2 | Na0.5CoO2 | Na0.5NiO2 | ||
|---|---|---|---|---|---|---|
| Na3PS4 | Reaction products |
Na3PO4
NaCrS2 S Cr2O3 |
Na3PO4
Na2SO4 MnS Na4Mn3S5a |
Na3PO4
Na3/2(FeS2) FeS2 |
Na3PO4
Na2S Na2SO4 Co9S8 |
Na3PO4
Na2SO4 Ni9S8 Ni3S2 |
| Reaction energy (eV per atom) | −0.1429 | −0.3156 | −0.3514 | −0.4376 | −0.5580 | |
| Na3PSe4 | Reaction products |
Na3PO4
Na1/3(CrSe2) Na2/3(CrSe2) |
Na3PO4
Na1/3(MnSe2) Na6MnSe4 MnO |
Na3PO4
Na2Se FeSe2 FeSe |
Na3PO4
Na2Se Co5Se8a CoSe2 |
Na3PO4
Na2Se Ni5Se8a NiSe2 |
| Reaction energy (eV per atom) | −0.1985 | −0.2848 | −0.3730 | −0.4558 | −0.5463 | |
The reactions between the NaxMO2 (x = 1.0 pristine or x = 0.5 desodiated) cathode and Na3PX4 electrolyte can be broadly categorized into two classes (often occurring together):
(1) Anion exchange reactions. For instance, mixing NaCrO2 and Na3PX4 (X = S, Se) can produce NaCrX2 (X = S, Se) and Na3PO4. The exchange of some oxygen from the cathode with the chalcogenide from the electrolyte to form Na3PO4 and metal-chalcogenides is favorable for all the systems we investigated.
(2) Complex redox reactions involving multiple phases with significant structural rearrangements. For example, mixing NaNiO2 and Na3PX4 (X = S, Se) leads to the production of more than three decomposition products and involves transition metal reduction.
According to the onset temperature of each reaction between NaMO2 and Na3PX4 listed in Table 2, two reaction trends are observed:
(1) From NaCrO2 to NaNiO2, the onset temperature decreases, indicating a reduction of the kinetic barrier, which may be related to an increase of the driving force of each reaction (Table 1).
(2) From Na3PS4 to Na3PSe4, the onset temperature also decreases.
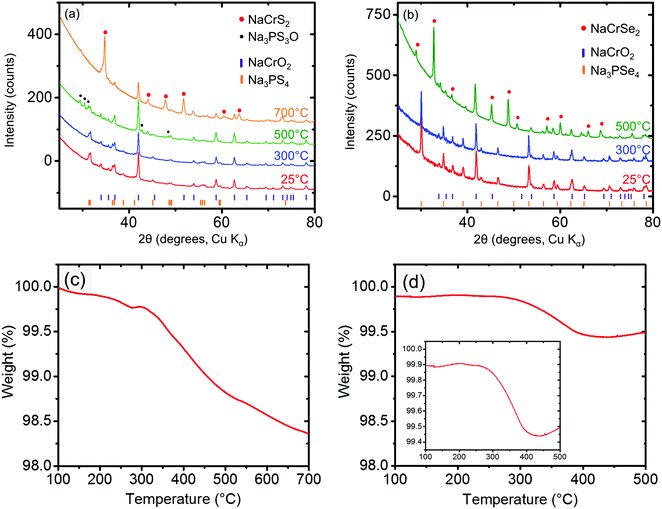
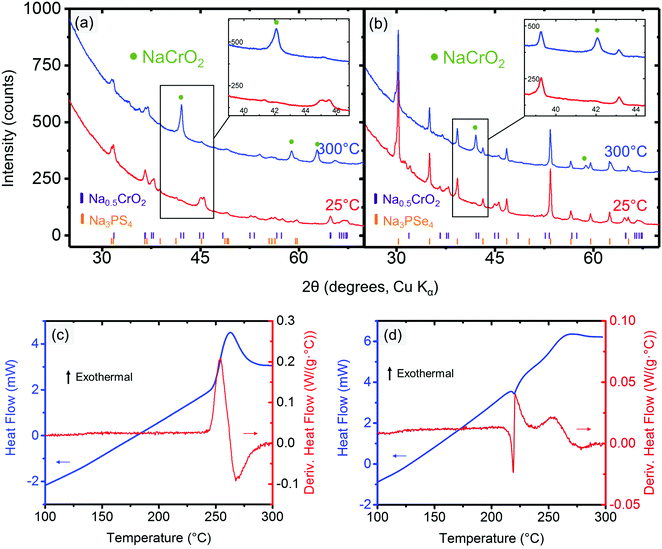
The cathode–electrolyte pairs for which no bulk reactions were observed close to RT (i.e., NaCrO2 and NaMnO2 with Na3PX4) were subjected to combined SDT and XRD characterization. These simple tests were quite informative, as they provided insight into the intriguing interplay between thermodynamics and kinetics in the decomposition reactions. Taking NaCrO2 and Na3PX4 as an example, when these mixtures were heated to below approximately 300 °C, no bulk reaction was observed in the XRD results (Fig. 4a and b). This finding suggests that NaCrO2 and Na3PX4 should be a relatively stable pair that could be used in solid-state batteries at RT. When the reaction temperature was raised to 500 °C, NaCrSe2 (along with excess NaCrO2) was observed in the final products of the reaction between NaCrO2 and Na3PSe4 (green line in Fig. 4b), which partially agrees with the DFT calculation result in Table 1. No other P-containing phases were observed in the XRD result. Because no substantial mass loss (<0.6%) was observed upon heating to 500 °C (Fig. 4d), P-containing phases should still be present in the mixture but in amorphous form. Taken together with the DFT prediction (Table 1), we suspect that amorphous Na3PO4 is present in the heated mixture. However, when the conductor was changed to Na3PS4, the calculated reaction products between NaCrO2 and Na3PS4 with the highest driving force (i.e. NaCrS2 and Na3PO4) were not observed after heating to 500 °C. Instead, Na3PS3O (together with both precursors NaCrO2 and Na3PS4) was observed (green line in Fig. 4a). It is not until 700 °C that the predicted product NaCrS2 (together with excess NaCrO2) starts to appear with the disappearance of Na3PS3O (orange line in Fig. 4a). Although the predicted NaCrS2 might be present in the 500 °C heated mixture in amorphous form, the presence of Na3PS3O in lieu of the predicted product Na3PO4 may indicate a preference for intermediate reaction products over the stable thermodynamic states unless the temperature is very high (e.g. 700 °C). We also note from Table 1 that the reaction energy between NaCrO2 and the selenide conductor is substantially higher than with the sulfide conductor.
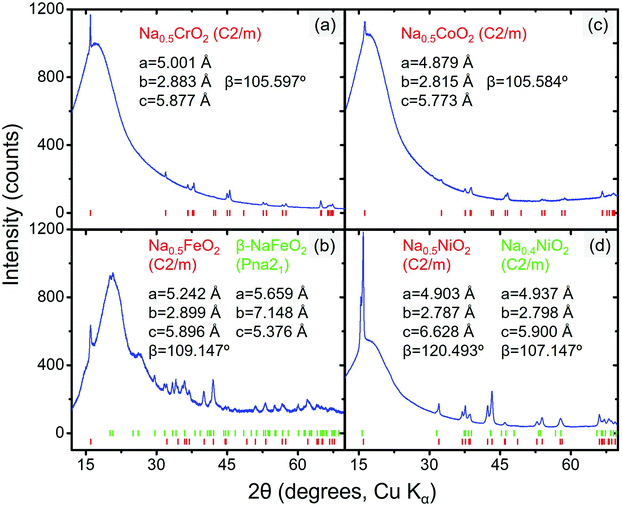 | ||
| Fig. 5 Diffraction patterns of desodiated compound(s) of (a) NaCrO2, (b) NaFeO2, (c) NaCoO2, and (d) NaNiO2. The peak positions and refined structure data are also displayed; the hump at ∼15° in all four figures originates from the Kapton sample holder (the diffraction pattern of the empty sample holder is presented in Fig. S3, ESI†). | ||
When the partially desodiated samples were mixed with Na3PX4, only Na0.5CrO2 was observed to be compatible with Na3PX4 at RT (i.e., no bulk reaction was observed in the XRD results, see Fig. 6a and b). All of the other partially desodiated samples reacted with the electrolyte, and some of the reactions were rather violent. For example, when partially desodiated NaNiO2 was mixed with Na3PX4 in an Ar glove box, sparks were immediately generated and the powder color changed to dark red.
Because Na0.5CrO2 is the only compound compatible with Na3PX4 at RT among our observations, further studies with XRD and SDT at elevated temperatures were performed. In the XRD of mixed Na0.5CrO2 and Na3PX4, we observed that fully sodiated NaCrO2 was regenerated after heating the mixture to 300 °C in reactions with both Na3PSe4 (Fig. 6a) and Na3PS4 (Fig. 6b), suggesting that Na is extracted from the Na3PX4 electrolyte and inserted into Na0.5CrO2, consistent with the thermodynamic anodic potentials predicted for the Na3PX4 electrolytes (2.25 V for Na3PS4 and 2.15 V for Na3PSe4), which are well below the Na0.5CrO2 voltage (∼3.7 V vs. Na/Na+).
This Na insertion to Na0.5CrO2 is similar to a self-discharge reaction, as often observed in rechargeable batteries, leading to decomposition of the electrolyte (i.e. Na3PX4). As shown in Fig. 2, S or Se is likely generated in the decomposition products by oxidizing Na3PX4. In the reaction between Na0.5CrO2 and Na3PSe4, the generation of Se can indeed be observed in our differential scanning calorimetry (DSC) measurements (Fig. 6c), where an endothermal peak is observed at approximately 220 °C, corresponding to the melting point of Se (220.8 °C). The following exothermal peak is attributed to the heat generation of the bulk reaction. In contrast, the generation of S cannot be observed in the reaction between Na0.5CrO2 and Na3PS4. In the DSC result for the reaction between Na0.5CrO2 and Na3PS4 in Fig. 6d, only one exothermal peak is observed at approximately 260 °C reflecting the heat generation of the reaction.
The surface reaction at RT between Na0.5CrO2 and Na3PX4 was investigated by X-ray photoelectron spectroscopy (XPS). After mixing Na0.5CrO2 and Na3PX4 at RT, XPS measurements were performed on the Cr 2p peaks of the mixture. The Cr 2p reference peak positions in Cr3+ and Cr4+ were obtained by fitting the Cr 2p1/2 and 2p3/2 peaks in NaCrO2 (Cr3+ only) and Na0.5CrO2 (Cr3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cr4+ = 1
Cr4+ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), respectively (Fig. 7c and d). The XPS spectrum of the Cr 2p peaks in the mixture of Na0.5CrO2 and Na3PSe4 is presented in Fig. 7b, and the fitting result indicates that the Cr3+/Cr4+ ratio changed from approximately 1.0 in Na0.5CrO2 to 2.423 in the mixed material (Table 3). The reduction of Cr4+ indicates an insertion of Na to Na0.5CrO2. This surface reaction between Na0.5CrO2 and Na3PSe4 at RT cannot be detected in XRD (Fig. 6a), reflecting a slow kinetics and/or a self-passivation reaction mechanism. It is likely that the reaction products form a passivation layer and prevent further reaction, which explains why no bulk reaction is observed at RT in XRD. Based on the above discussion, the surface reaction is likely associated with the production of Se. As the temperature increases to the melting point of Se, the passivation layer becomes unstable and further reaction is activated, which is in good agreement with our observation in DSC (Fig. 6c). When Na0.5CrO2 was mixed with Na3PS4, a lower Cr3+/Cr4+ ratio increase (i.e. less Cr4+ reduction) was observed (Table 3), indicating that less Na was extracted from Na3PS4 in the reaction between Na0.5CrO2 and Na3PS4. This observation is likely due to the slightly lower reactivity of Na3PS4 compared with Na3PSe4, which is in line with the onset temperatures of the reaction between NaMO2 and Na3PX4 (Table 2).
1), respectively (Fig. 7c and d). The XPS spectrum of the Cr 2p peaks in the mixture of Na0.5CrO2 and Na3PSe4 is presented in Fig. 7b, and the fitting result indicates that the Cr3+/Cr4+ ratio changed from approximately 1.0 in Na0.5CrO2 to 2.423 in the mixed material (Table 3). The reduction of Cr4+ indicates an insertion of Na to Na0.5CrO2. This surface reaction between Na0.5CrO2 and Na3PSe4 at RT cannot be detected in XRD (Fig. 6a), reflecting a slow kinetics and/or a self-passivation reaction mechanism. It is likely that the reaction products form a passivation layer and prevent further reaction, which explains why no bulk reaction is observed at RT in XRD. Based on the above discussion, the surface reaction is likely associated with the production of Se. As the temperature increases to the melting point of Se, the passivation layer becomes unstable and further reaction is activated, which is in good agreement with our observation in DSC (Fig. 6c). When Na0.5CrO2 was mixed with Na3PS4, a lower Cr3+/Cr4+ ratio increase (i.e. less Cr4+ reduction) was observed (Table 3), indicating that less Na was extracted from Na3PS4 in the reaction between Na0.5CrO2 and Na3PS4. This observation is likely due to the slightly lower reactivity of Na3PS4 compared with Na3PSe4, which is in line with the onset temperatures of the reaction between NaMO2 and Na3PX4 (Table 2).
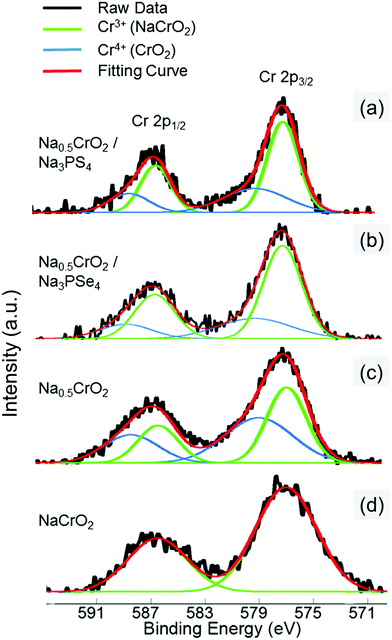 | ||
| Fig. 7 XPS spectra of Cr 2p from the surfaces of (a) mixture of Na0.5CrO2 and Na3PS4 at RT (25 °C), (b) mixture of Na0.5CrO2 and Na3PSe4 at RT (25 °C), (c) Na0.5CrO2, and (d) NaCrO2. | ||
| Sample | Component | Peak position (eV) | Area (a.u.) | Cr3+/Cr4+ ratio | ||
|---|---|---|---|---|---|---|
| 2p3/2 | 2p1/2 | 2p3/2 | 2p1/2 | |||
| Na0.5CrO2/Na3PS4 | Cr3+ | 577.03 | 586.52 | 299 | 149 | 1.869 |
| Cr4+ | 579.09 | 588.52 | 160 | 80 | ||
| Na0.5CrO2/Na3PSe4 | Cr3+ | 577.03 | 586.52 | 344 | 172 | 2.423 |
| Cr4+ | 579.09 | 588.52 | 142 | 71 | ||
| Na0.5CrO2 | Cr3+ | 577.03 | 586.52 | 470 | 234 | 0.997 |
| Cr4+ | 579.09 | 588.52 | 484 | 242 | ||
| NaCrO2 | Cr3+ | 577.03 | 586.52 | 661 | 331 | — |
III. Compatibility between anode and electrolyte
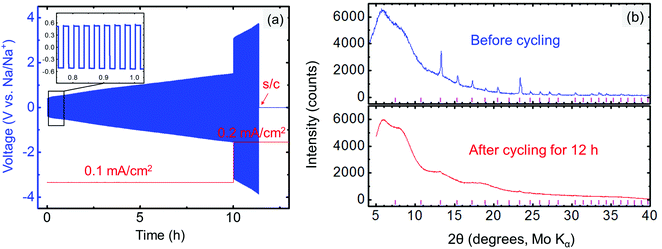
The compatibility between the electrolyte and anode was investigated by cycling the Na/electrolyte/Na symmetric cells under a constant current density (typically 0.1 or 0.2 mA cm−2). The symmetric cell was first galvanostatically cycled at 1 min per cycle. An increasing voltage during cycling is observed in Fig. 8a even at very low current density (0.1 mA cm−2), suggesting an unstable metal/electrolyte interface. The cell failed after approximately 11.4 h of cycling, when Na3PSe4 was fully decomposed into amorphous phases (Fig. 8b), likely Na3P and Na2Se based on our DFT calculations (Fig. 2b). Thus, we conclude that Na3PSe4 is not compatible with a Na metal anode.To improve the compatibility between the anode and electrolyte, a “Na2Sn” alloy with higher potential (∼0.3 V vs. Na/Na+) was synthesized. According to the Na–Sn binary phase diagram,72,73 the two stable phases near this composition are NaSn and Na9Sn4, with the latter being the majority phase. The Na2Sn|Na3PSe4|Na2Sn symmetric cell was galvanostatically cycled at 60 min per cycle. A relatively stable voltage during cycling at low current density (0.1 mA cm−2) is observed in Fig. 9a, indicating enhanced interface stability. However, at a higher current density (0.2 mA cm−2), the interface becomes unstable, and Na2Se was observed after cycling for 40 h (Fig. 9b).
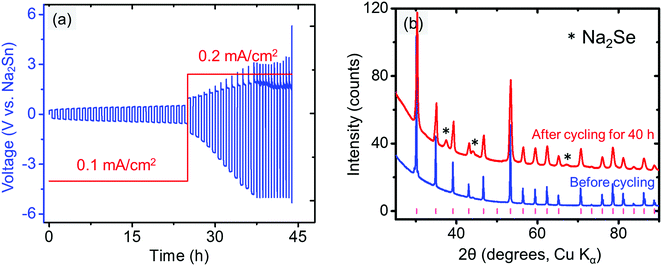 | ||
| Fig. 9 (a) Electrochemical cycling of Na2Sn|Na3PSe4|Na2Sn symmetric cell. (b) XRD patterns of Na3PSe4 before and after cycling for 40 h (60 min per cycle); the tick marks indicate Na3PSe4 peaks. | ||
Because Na metal is reported to be incompatible with Na3PS4 forming Na2S and Na3P decomposition products,74 consistent with our DFT calculation results shown in Fig. 2a, only the compatibility between the Na2Sn anode and Na3PS4 was then investigated by cycling a Na2Sn|Na3PS4|Na2Sn symmetric cell. A stable anode–electrolyte interface was obtained, signified by the approximately constant voltage during cycling at both low and high current densities (Fig. 10). We thus concluded that the “Na2Sn” alloy is a promising anode candidate for use in solid-state batteries employing Na3PS4 solid electrolytes.
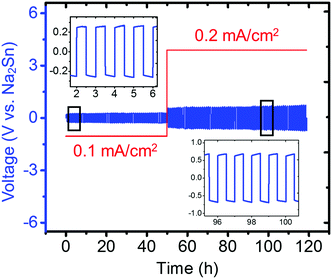 | ||
| Fig. 10 Electrochemical cycling of Na2Sn|Na3PS4|Na2Sn symmetric cell (60 min per charge and discharge). The insets present zoomed-in voltage profiles during cycling from 2–6 h and 96–100 h. | ||
Discussion
We distinguish the pure electrochemical stability of the solid-state electrolyte at various Na chemical potentials (and in contact with Na reservoir) from the chemically-enhanced instability when solid-state electrolyte and cathode chemically interact. The pure electrochemical stability is relevant wherever the solid electrolyte is in contact with the electron reservoir. Hence this occurs at the cathode/electrolyte interface, at a direct contact with the current collector, or through the carbon network present in the electrode. Since Na+ is highly mobile in the solid-state electrolyte, the conductor experiences the full chemical potential of Na applied at these electron contact interfaces. Computationally, we calculate the stability of the conductor in this condition by evaluating the thermodynamic grand potential of the compound under various applied Na chemical potentials, as described in prior work.34 This analysis requires the availability of thermochemical information on a number of competing phases in the phase diagram of the conductor. Such information can for example be found in online resources such as the Materials Project.75 This thermodynamic analysis for the electrochemical stability of the conductor provides a “safe” voltage window, in which there is no driving force at all for decomposition of the conductor. Because the thermodynamic decomposition of the conductor may sometimes require complete bond breaking in the material to form multiple other phases, it may be kinetically inhibited at the operating temperature of the battery. Hence, we also provide a kinetic anodic stability limit by evaluating at which potential, Na+ can simply be extracted topotactically from the conductor together with the oxidation of the anion (S2− or Se2− in our case). Because the material is by definition a fast Na-ion conductor, and anion oxidation is easy, one expects there to be no kinetic barrier for this process. Hence, this topotactic Na extraction voltage can be considered an absolute upper bound for the voltage at which the conductor can operate. To test these computed stability limits we evaluated the conductor as an electrode in an electrochemical cell using liquid electrolyte so that contact problems, often present in full solid state devices, will not mask instabilities. The computational and experimental results summarized in Table 4 clearly indicate that the measured upper voltage limit lies between the thermodynamic upper voltage and the topotactic Na extraction limit, in agreement with our understanding. Table 4 also clearly shows that CV is a poor tool to measure electrochemical stability of solid-state conductors. The poor reliability of CV measurements has led for example to claims that some sulfide conductors have 5 V or even 10 V stability,18,32,76,77 which is counterintuitive, given that a sulfide ion can in general be oxidized between 2–3 V.In contact with the cathode, the conductor (i.e., solid-state electrolyte) can also undergo chemical reactivity. To determine this reactivity, we used a combination of XRD, SDT and XPS to evaluate the reaction products in mixed cathode/electrolyte powders. Through the study of more than 20 cathode/electrolyte reactions between layered Na transition metal oxides (NaMO2, M = Cr, Mn, Fe, Co, Ni) and two solid electrolytes (Na3PX4, X = S, Se), we were able to determine trends and understand the mechanisms behind these reactions. We first determine the thermodynamic driving forces and end-products of the cathode/electrolyte reaction, and then discuss what may happen under more kinetically constrained conditions. There are some common trends that can be understood from Table 1:
(1) On the cathode/conductor interface P strongly prefers bonding to O, resulting in the exchange of O and S/Se between the cathode and conductor, and the formation of PO4 groups. As a result, Na3PO4 is produced for all reactions listed in Table 1.
(2) Some transition metals, even in the discharged redox state can oxidize the chalcogenide anion leading to reaction products that are metallic, have per-sulfide or per-selenide ions, or even sulfate ions. This is the case for the NaFeO2 and NaNiO2 cathodes against both conductors and for the NaCoO2 cathode against the selenide conductor. The fact that the NaCoO2 seems redox stable with the sulfide but not with the selenide is likely due to the fact that the Se2− ion is easier to oxidize than S2−.
Once the cathodes are charged (bottom part of Table 1) oxidation of the anion by reduction of the transition metal is favorable for all cathode/conductor couples, and only local passivation with an electron-insulating layer will protect the conductor. The reaction products that form at the interface are however dependent on chemistry of each cathode. In some cases, elemental S is predicted to occur (e.g. Na0.5CrO2 with Na3PS4) while for other cathode/conductor couples reduced metal sulfides are usually predicted (MnS, FeS2, etc.). The reaction products for the Co and Ni cathode deserve particular attention. Compounds such as Ni9S8 and Co9Se8 are in the pentlandite family and have a structure containing an excess of metal atoms and short metal–metal distance.78,79 Similar metal–metal bonding also exists in other metal-rich chalcogenides such as Ni3S2.80,81 These compounds are metallic and hence will not provide any passivation protection.
Though it is useful to understand the thermodynamic endpoints of the cathode/conductor reaction as shown in Table 1, comparison with the experimentally observed products clearly indicates that these phases do not always form, as would be expected under conditions where kinetics may be limited.
First, when the electrode and electrolyte are in contact, arbitrary amounts of these phases can react, forming an interface layer of decomposition products that can take on, in principle any average composition between the cathode and electrolyte composition depending on the ratio in which they react. This renders many possible reaction pathways plausible. In our previous modeling approach, a mixing parameter x (0 < x < 1) between the electrode and electrolyte was introduced in our calculations.34 By scanning a range of x from 0 to 1, we calculated the reaction enthalpies for all possible reactions and determined the mostly likely reaction as the one with the largest thermodynamic driving force. This approach was largely successful in predicting the decomposition products between electrodes and electrolytes, and indeed, many of the predictions have recently been verified by experiments.48,82–84 However, it is important to keep in mind that in principle all reactions with positive driving force can take place spontaneously, and which ones occur first depends on their kinetics. To make a broader comparison with future experiments possible we have listed in Table S1 (ESI†) possible reaction products that can be formed for each cathode/electrolyte couple. Given these constraints, it is remarkable that many of the experimentally observed products are the ones predicted in the thermodynamic calculations.82,85 This finding may result from the very thin interface layer (nanometer scale) formed, requiring only very short diffusion lengths.
Several of the experimental products we observed can be explained by adding at least a qualitative layer of kinetic constraints on top of the predictions. For example, in the reaction between NaCrO2 and Na3PS4, the theoretically predicted product (Na3PO4) was not observed at temperatures below 700 °C. Instead, the intermediate Na3PS3O was formed at lower temperatures, which may be thought of as an intermediate towards the exchange of S and O in the conductor.
One reaction that however cannot be kinetically limited is the exchange of Na ions between the electrolyte and cathode. As a result, cathodes that are charged above the anodic voltage limit of the conductor will always extract Na from the solid-state electrolyte, at which point the electrolyte will degrade and decompose. This concept rationalizes our experimental observation when Na0.5CrO2 and Na3PSe4 come in contact. The results in Table 1, assuming diffusion is not limited, predicted the formation of Na1/3(CrSe2), Na2/3(CrSe2), and Na3PO4 decomposition products. However, experimentally a more limited reaction is observed whereby Na is extracted from the electrolyte, causing electrolyte decomposition, and producing fully sodiated NaCrO2.
In the two cases discussed above, instead of taking the reaction pathway with the largest thermodynamic driving force, which involves diffusion and rearrangement of elements, a reaction via anion and Na exchange processes is observed. This finding is not surprising as reactions involving well-known mobile species (e.g., Na+) are fast and kinetically favored. Overall, in the analysis of electrode/electrolyte reactions, our results suggest that in addition to the ones with the largest driving forces, other reactions with similar thermodynamic driving forces but faster kinetics (e.g., topotactic Na extraction/insertion) should also be considered in electrode/electrolyte reactions.
With the driving forces that may degrade the cathode/electrolyte interface better understood, one can develop strategies to alleviate these issues. The anion-exchange reaction is mainly driven by the tendency to form the stable phosphate group. Therefore, this type of reaction may be prevented by fully or partially replacing P in the solid electrolytes with other suitable elements that do not exhibit strong bonding preference with O, such as Sb, Ge, Sn, or As. Interestingly, recent studies suggest that a NaCrO2 cathode can be cycled reversibly using a Na3SbS4 solid-state electrolyte, indicating that replacing P with Sb in the sulfide electrolyte resulted in improved compatibility with the oxide cathode.16,19,42 We expect that a similar effect will be observed for Na4SnS4,86 Li4SnS4,87 Li4GeS4,88 Li3AsS4,89 and similar materials. Another possible strategy to prevent the anion exchange is to use polyanion cathodes with stable anion groups such as PO4. Since the O is already in a stable configuration, it is unlikely to participate in the anion exchange reaction. Changing from an oxide-based cathode to a sulfide-based cathode will also mitigate the interface issue, although sulfide-based cathodes will operate at a lower voltage than their oxide counterparts, thus reducing the overall energy density of the batteries. The redox degradation pathway requires transition metal reduction in the cathode. While this seems inevitable in a charged cathode, it may be preventable in the discharged cathode by selecting transition metals that are difficult to reduce (e.g., Cr3+, Mo3+, V3+, Nb3+ and Ti3+). The thermodynamic stability requirement between the conductor and discharged cathode is often more stringent as processing of a solid-state battery may bring this system to elevated temperature. This is not the case for the charged cathode which is usually only exposed to the conductor during room temperature operation.
Although one always has the option to coat the electrode to protect it chemically from the electrolyte,38,39,90 we believe that passivating solid-state electrolytes is equally important and should be explored in future studies. Because the coating is a thin layer, it has less stringent requirements for ionic conductivity than for the bulk electrolyte. This allows many more materials choices than for bulk electrolytes, making the selection of a chemically and electrochemically stable coating material more likely.37 Coating only the cathode still exposes the electrolyte to electronic pathways created by carbon in the cathode. According to our electrolyte stability testing results, it is clear that electronic pathways promote the decomposition of the electrolyte via the extraction of Na+ and oxidation of the anion in the conductor. Therefore, the electrode coating method only solves the cathode/electrolyte interface problem and cannot prevent electrolyte decomposition at voltages beyond its stability window. This issue might not be critical for the cell initially, especially when the cell is cycled at a very high rate, because breakdown of the electrolyte at places other than the cathode interface will initially not degrade cell operation. However, this issue is likely to be detrimental for the long-term cyclability of all-solid-state batteries. We believe that electrolyte coating provides a more effective approach to prevent both electrolyte decomposition and electrolyte/electrode reaction.
Conclusion
We presented a methodology that combines computational and experimental tools to investigate the compatibility between solid electrolytes and electrodes. Relatively simple and rapid XRD and SDT experiments were proven to be very effective in describing the interfacial reactions between electrolytes and electrodes. By applying our method to the Na solid-state system, we were able to determine the voltage windows of the electrolytes (both the thermodynamic-driven lower bound and kinetic-stabilized upper bound), understand the thermodynamics and kinetics behind the reactions between incompatible electrolyte/electrode pairs, and select the most stable components (NaCrO2/Na3PS4/Na–Sn) within our chemical space for an all-solid-state battery. We believe that these data provide crucial information for new solid electrolyte design and electrolyte/electrode interfacial modification and serve as an essential guide for integrating these components. The methodology and insights obtained in this study can also be applied to other electrochemical systems of interest, such as Li-ion solid-state batteries.Experimental
Synthesis of NaMO2
All the NaMO2 cathode materials were prepared by solid-state synthesis. Stoichiometric amounts of the precursors (typically ∼1.0 g) were mixed by ball milling (tungsten carbide ball mill jar, Spex 8000 M mixer per mill) and pressed into 1/2-in pellets. The pellets were then placed in alumina boats and heated at a rate of 10 °C min−1 in appropriate atmospheres until the reaction was completed. The corresponding precursors and heating conditions are listed in Table S2 (ESI†). The samples (except NaMnO2) were cooled to 150 °C at a rate of 30 °C min−1 and immediately transferred to an Ar glovebox. NaMnO2 was quenched to RT after synthesis and then immediately transferred to an Ar glovebox.Synthesis of Na3PX4
Na2X (X = S, Se, Alfa Aesar, 99.8%), red phosphorus (Sigma-Aldrich, ≥99.99% trace metal basis), and S/Se (Sigma-Aldrich, 99.99% trace metal basis) powder were mixed in a stoichiometric ratio in an Ar-filled glovebox. The mixture of the three compounds was then loaded into a BN tube (3 mm inner diameter and 4 mm outer diameter). The tube was wrapped with Al foil and sealed with a stainless steel Swagelok cap (3/8 in) at the open end. The synthesis was performed in a sealed alumina tube furnace, which was purged with Ar gas for 20 min, rapidly ramped to 300 °C within 10 min, and held at the same temperature for 16 h for the reaction. Continuous Ar gas with a flow rate of ∼30 mL min−1 flowed into the sealed furnace during the entire synthesis process. The final products were collected after the furnace was naturally cooled down to RT and were immediately transferred into the glovebox.Synthesis of chemically desodiated Na0.5MO2
Synthesized pristine NaMO2 powder, over-stoichiometric (ten-fold excess) iodine (GSS, 99.8%, beads), and ∼15 mL of acetonitrile (Sigma-Aldrich, 99.8%, anhydrous) were placed in a glass sample vial containing an octagonal magnetic stirring bar. After being wrapped with Al foil to prevent light exposure, the sealed vial was placed on a stirrer and stirred at a speed of 1200 rpm in a Ar glovebox for 4 days. The solution was then centrifuged at 5000 rpm for 7 min. The solid residue was separated from the supernatant and washed with acetonitrile ∼6 times until no iodine was observed in the solvent. After drying in the vacuum chamber of the Ar glovebox for ∼12 h, the final product was transferred into the glovebox and ground into a powder for further characterization.Experimental characterization
XRD analysis was performed using a Rigaku Miniflex diffractometer and Cu Kα radiation. The powder sample was first sealed into a Kapton tube (0.9 mm in diameter, Cole Parmer) in the glovebox and then characterized in the diffractometer, which was equipped with a capillary stage to limit air exposure.SDT measurements were performed using a TA Instruments SDT Q600. Approximately 15 mg of the powder sample was first placed into an alumina sample pan in the glovebox. The filled pan was then placed on the pre-tared cantilever of the analyzer. SDT standard measurements were then performed under continuous Ar flow with a flow rate of 100 mL min−1. The measurement procedure usually involves heating and cooling processes. After equilibrating at 25 °C, the sample was heated to the set temperature at a heating rate of 5 °C min−1. The temperature was held for at least 1 h to complete the reaction before cooling was initiated at a rate of 2 °C min−1. The sample was rapidly transferred to the glovebox after measurement for further characterization.
The working electrode composites were prepared by mixing the synthesized Na3PX4 powder, carbon black, and poly(tetrafluoroethylene) (PTFE) in a weight ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 with a mortar and pestle in an Ar glovebox. This powder mixture was rolled into a thin film using a stainless steel plate and roller. Circular disks of 5/16-in diameter were then punched with a loading of approximately 3–5 mg. These electrodes were assembled into Swagelok cells with Na metal as the counter electrode and 1 M NaPF6 in a 1
5 with a mortar and pestle in an Ar glovebox. This powder mixture was rolled into a thin film using a stainless steel plate and roller. Circular disks of 5/16-in diameter were then punched with a loading of approximately 3–5 mg. These electrodes were assembled into Swagelok cells with Na metal as the counter electrode and 1 M NaPF6 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (volumetric ratio) ethylene carbonate/diethyl carbonate (EC/DEC) solvent mixture as the liquid electrolyte. Two glass fiber separators were used in the cells. The charging and discharging of the Swagelok cells were performed with an Arbin battery cycler.
1 (volumetric ratio) ethylene carbonate/diethyl carbonate (EC/DEC) solvent mixture as the liquid electrolyte. Two glass fiber separators were used in the cells. The charging and discharging of the Swagelok cells were performed with an Arbin battery cycler.
Cyclic voltammetry measurements were conducted to investigate the electrochemical stability window of the solid electrolyte Na3PSe4. A platinum foil as the working electrode and a sodium foil as the counter electrode were attached to each face of the pellet. The potential sweep was performed by using a potentiostat/galvanostat device with a scanning rate of 5 mV s−1 at room temperature.
XPS measurements were performed on a PHI 5400 ESCA/XPS system with a monochromatic Al Kα X-ray source. The powder samples were mixed with PTFE binder (5 wt%) and rolled into thin films in the Ar glovebox. The films were transferred into the XPS system and cleaned using Ar ion milling (3 kV, 25 mA) to remove surface-absorbed C and O. The core-level spectra were fitted using the commonly applied Gaussian peak shapes and Shirley background correction to extract the transition metal valence states based on the ratio of scaled peak areas.
Computational
The calculations for voltage and interfacial stability generally followed the methodology described in greater detail in ref. 34.Phase diagrams and bulk energies
Zero Kelvin phase diagrams were constructed using the pymatgen software package91 and a database of DFT-computed bulk phase energies of materials with crystal structures obtained from the Inorganic Crystal Structure Database (ICSD)92 or generated by applying data-mined chemical substitutions.93 To obtain these bulk energies, we employed DFT within the projector augmented wave (PAW) formalism94 using the generalized gradient approximation (GGA)95 to the exchange–correlation energy as implemented in the Vienna ab initio simulation package (VASP)96 to calculate the formation energy of each electrolyte from the nearest phases present in the NIST-JANAF97 or Kubaschewski98 thermochemical tables or from the elements. To treat the sulfides and selenides equally, we added the formation energy of Na2Se to this dataset.99 We uniquely define the nearest phases as those that define the Gibbs triangle (the low-energy facet) containing the desired composition in the phase diagram. As a result of this methodology, the formation energy input to the phase diagram calculation is exactly the experimentally determined enthalpy for compounds that are present in these thermochemical tables. For other compounds, we use the sum of the experimental formation enthalpies of the nearby phases and the DFT calculated reaction energy from these nearby phases to form the compound of interest. This reduces the formation energy error by minimizing electron transfer in the DFT calculated reactions.For all the VASP calculations, a cutoff energy of 520 eV and a k-point grid of at least 500 per number of atoms were used. We applied the mixing scheme of Jain et al.100 to combine GGA calculations with/without the rotationally invariant Hubbard (+U) correction101,102 to properly treat insulators and metals.
Voltage stability calculations
To calculate the voltage stability of each electrolyte, we calculated the range of Na chemical potential (μNa) over which each electrolyte was observed to be on the convex hull and therefore stable in the relevant 0 K grand potential phase diagram. At the extremes of the stability window, we determined its decomposition products as the compositions defining its associated Gibbs triangle. Topotactic Na extraction voltage (upper kinetic stability limit) is calculated from the energy of removing a single Na atom from a 4-formula unit supercell, constraining the supercell dimensions to that of the stoichiometric bulk material but allowing atomic relaxations.Interfacial stability calculations
To determine the interfacial stability, we determine the reaction between electrode and electrolyte compositions with the highest driving force as first proposed by Richards et al.34 Because arbitrary amounts of either phase can be consumed by this reaction, this process results in a driving force given by the equationwhere ca and cb are the compositions of the electrode and electrolyte, respectively; E[ca] and E[cb] are their bulk energies, respectively; Epd[c] is a function returning the energy of the lowest energy equilibrium of phases at the composition c; and x is a mixing parameter between 0 and 1.
These calculations were not performed at constant Na chemical potential, in slight contrast to the methodologies of ref. 34, to more accurately reflect the experimental conditions used in this work.
Acknowledgements
This work was supported by the Samsung Advanced Institute of Technology. The XPS experiments were performed at the Molecular Foundry, LBNL, supported by the Office of Science, Office of Basic Energy Sciences of the US Department of Energy (Contract No. DE-AC02-05CH11231). This work also used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575.References
- C. Yada, Y. Iriyama, T. Abe, K. Kikuchi and Z. Ogumi, Electrochem. Commun., 2009, 11(2), 413–416 CrossRef CAS.
- A. Hayashi, T. Ohtomo, F. Mizuno, K. Tadanaga and M. Tatsumisago, Electrochem. Commun., 2003, 5(8), 701–705 CrossRef CAS.
- K. Takahashi, K. Hattori, T. Yamazaki, K. Takada, M. Matsuo, S. Orimo, H. Maekawa and H. Takamura, J. Power Sources, 2013, 226, 61–64 CrossRef CAS.
- A. Sakuda, H. Kitaura, A. Hayashi, M. Tatsumisago, Y. Hosoda, T. Nagakane and A. Sakamoto, Chem. Lett., 2012, 41(3), 260–261 CrossRef CAS.
- T. Ohtomo, A. Hayashi, M. Tatsumisago, Y. Tsuchida, S. Hama and K. Kawamoto, J. Power Sources, 2013, 233, 231–235 CrossRef CAS.
- Y. Zhu, X. He and Y. Mo, J. Mater. Chem. A, 2016, 4(9), 3253–3266 CAS.
- J. Xie, N. Imanishi, T. Zhang, A. Hirano, Y. Takeda and O. Yamamoto, J. Power Sources, 2009, 189(1), 365–370 CrossRef CAS.
- M. Tatsumisago, M. Nagao and A. Hayashi, J. Asian Ceram. Soc., 2013, 1(1), 17–25 CrossRef.
- J. G. Kim, B. Son, S. Mukherjee, N. Schuppert, A. Bates, O. Kwon, M. J. Choi, H. Y. Chung and S. Park, J. Power Sources, 2015, 282, 299–322 CrossRef CAS.
- M. Nagao, A. Hayashi and M. Tatsumisago, Electrochim. Acta, 2011, 56(17), 6055–6059 CrossRef CAS.
- M. Nagao, A. Hayashi and M. Tatsumisago, J. Mater. Chem., 2012, 22(19), 10015 RSC.
- J. Burns, A. Kassam, N. Sinha, L. Downie, L. Solnickova, B. Way and J. Dahn, J. Electrochem. Soc., 2013, 160(9), A1451–A1456 CrossRef CAS.
- J. Li, C. Ma, M. Chi, C. Liang and N. J. Dudney, Adv. Energy Mater., 2015, 5(4), 1401408 CrossRef.
- W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim, S. P. Ong, I. Uechi, N. Suzuki and G. Ceder, Nat. Commun., 2016, 7, 11009 CrossRef CAS PubMed.
- S. Bo, Y. Wang and G. Ceder, J. Mater. Chem. A, 2016, 4(23), 9044–9053 CAS.
- H. Wang, Y. Chen, Z. D. Hood, G. Sahu, A. S. Pandian, J. K. Keum, K. An and C. Liang, Angew. Chem., Int. Ed., 2016, 55(30), 8551–8555 CrossRef CAS PubMed.
- P. Knauth, Solid State Ionics, 2009, 180(14–16), 911–916 CrossRef CAS.
- R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148(7), A742–A746 CrossRef CAS.
- L. Zhang, D. Zhang, K. Yang, X. Yan, L. Wang, J. Mi, B. Xu and Y. Li, Adv. Sci., 2016, 3, 1600089 CrossRef PubMed.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14(10), 1026–1031 CrossRef CAS PubMed.
- S. P. Ong, Y. Mo, W. D. Richards, L. Miara, H. S. Lee and G. Ceder, Energy Environ. Sci., 2013, 6(1), 148–156 CAS.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46(41), 7778–7781 CrossRef CAS PubMed.
- J. Wolfenstine, J. Allen, J. Sumner and J. Sakamoto, Solid State Ionics, 2009, 180(14), 961–967 CrossRef CAS.
- V. Thangadurai and W. Weppner, J. Solid State Chem., 2006, 179(4), 974–984 CrossRef CAS.
- J. L. Allen, J. Wolfenstine, E. Rangasamy and J. Sakamoto, J. Power Sources, 2012, 206, 315–319 CrossRef CAS.
- L. J. Miara, W. D. Richards, Y. E. Wang and G. Ceder, Chem. Mater., 2015, 27(11), 4040–4047 CrossRef CAS.
- T. Brousse, P. Fragnaud, R. Marchand, D. Schleich, O. Bohnke and K. West, J. Power Sources, 1997, 68(2), 412–415 CrossRef CAS.
- S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15(21), 3974–3990 CrossRef CAS.
- Y. Inaguma, C. Liquan, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, Solid State Commun., 1993, 86(10), 689–693 CrossRef CAS.
- A. Hayashi, K. Noi, N. Tanibata, M. Nagao and M. Tatsumisago, J. Power Sources, 2014, 258, 420–423 CrossRef CAS.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS.
- A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2012, 3, 856 CrossRef PubMed.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2011, 24(1), 15–17 CrossRef.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2015, 28(1), 266–273 CrossRef.
- T. Minami, A. Hayashi and M. Tatsumisago, Solid State Ionics, 2006, 177(26–32), 2715–2720 CrossRef CAS.
- F. Han, T. Gao, Y. Zhu, K. J. Gaskell and C. Wang, Adv. Mater., 2015, 27(23), 3473–3483 CrossRef CAS PubMed.
- N. Ohta, K. Takada, L. Zhang, R. Ma, M. Osada and T. Sasaki, Adv. Mater., 2006, 18(17), 2226–2229 CrossRef CAS.
- K. Takada, N. Ohta, L. Zhang, K. Fukuda, I. Sakaguchi, R. Ma, M. Osada and T. Sasaki, Solid State Ionics, 2008, 179(27–32), 1333–1337 CrossRef CAS.
- N. Ohta, K. Takada, I. Sakaguchi, L. Zhang, R. Ma, K. Fukuda, M. Osada and T. Sasaki, Electrochem. Commun., 2007, 9(7), 1486–1490 CrossRef CAS.
- I. H. Chu, C. S. Kompella, H. Nguyen, Z. Zhu, S. Hy, Z. Deng, Y. S. Meng and S. P. Ong, Sci. Rep., 2016, 6, 33733 CrossRef CAS PubMed.
- L. Zhang, K. Yang, J. Mi, L. Lu, L. Zhao, L. Wang, Y. Li and H. Zeng, Adv. Energy Mater., 2015, 5(24), 2–6 Search PubMed.
- A. Banerjee, K. H. Park, J. W. Heo, Y. J. Nam, C. K. Moon, S. M. Oh, S. Hong and Y. S. Jung, Angew. Chem., 2016, 128(33), 9786–9790 CrossRef.
- S. Bo, Y. Wang, J. C. Kim, W. D. Richards and G. Ceder, Chem. Mater., 2015, 28(1), 252–258 CrossRef.
- Z. Zhu, I. Chu, Z. Deng and S. P. Ong, Chem. Mater., 2015, 27(24), 8318–8325 CrossRef CAS.
- F. Lalère, J. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, J. Power Sources, 2014, 247, 975–980 CrossRef.
- S. Wenzel, S. Randau, T. Leichtweiß, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, Chem. Mater., 2016, 28(7), 2400–2407 CrossRef CAS.
- K. H. Kim, Y. Iriyama, K. Yamamoto, S. Kumazaki, T. Asaka, K. Tanabe, C. A. J. Fisher, T. Hirayama, R. Murugan and Z. Ogumi, J. Power Sources, 2011, 196(2), 764–767 CrossRef CAS.
- A. Sakuda, A. Hayashi and M. Tatsumisago, Chem. Mater., 2010, 22(3), 949–956 CrossRef CAS.
- S. Wenzel, T. Leichtweiss, D. Krüger, J. Sann and J. Janek, Solid State Ionics, 2015, 278, 98–105 CrossRef CAS.
- S. Komaba, C. Takei, T. Nakayama, A. Ogata and N. Yabuuchi, Electrochem. Commun., 2010, 12(3), 355–358 CrossRef CAS.
- X. Ma, H. Chen and G. Ceder, J. Electrochem. Soc., 2011, 158(12), A1307–A1312 CrossRef CAS.
- N. Yabuuchi, H. Yoshida and S. Komaba, Electrochemistry, 2012, 80(10), 716–719 CrossRef CAS.
- R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10(1), 74–80 CrossRef CAS PubMed.
- P. Vassilaras, X. Ma, X. Li and G. Ceder, J. Electrochem. Soc., 2013, 160(2), A207–A211 CrossRef CAS.
- S. Komaba, Y. Matsuura, T. Ishikawa, N. Yabuuchi, W. Murata and S. Kuze, Electrochem. Commun., 2012, 21, 65–68 CrossRef CAS.
- V. L. Chevrier and G. Ceder, J. Electrochem. Soc., 2011, 158(9), A1011–A1014 CrossRef CAS.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Energy Environ. Sci., 2012, 5(3), 5884–5901 CAS.
- L. P. Wang, L. Yu, X. Wang, M. Srinivasan and Z. J. Xu, J. Mater. Chem. A, 2015, 3(18), 9353–9378 CAS.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4(9), 3680–3688 CAS.
- J. Zhao, L. Zhao, N. Dimov, S. Okada and T. Nishida, J. Electrochem. Soc., 2013, 160(5), A3077–A3081 CrossRef CAS.
- S. Boulineau, M. Courty, J. Tarascon and V. Viallet, Solid State Ionics, 2012, 221, 1–5 CrossRef CAS.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama and K. Kawamoto, Nat. Mater., 2011, 10(9), 682–686 CrossRef CAS PubMed.
- F. Han, Y. Zhu, X. He, Y. Mo and C. Wang, Adv. Energy Mater., 2016, 6, 1501590 CrossRef.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7(42), 23685–23693 CAS.
- R. Moshtev, V. Manev, A. Nassalevska, A. Gushev and G. Pistoia, J. Power Sources, 1989, 26(3–4), 285–292 CrossRef CAS.
- A. I. Popov and D. H. Geske, J. Am. Chem. Soc., 1958, 80(6), 1340–1352 CrossRef CAS.
- Z. Wen, J. Cao, Z. Gu, X. Xu, F. Zhang and Z. Lin, Solid State Ionics, 2008, 179(27), 1697–1701 CrossRef CAS.
- A. Abouimrane, D. Dambournet, K. W. Chapman, P. J. Chupas, W. Weng and K. Amine, J. Am. Chem. Soc., 2012, 134(10), 4505–4508 CrossRef CAS PubMed.
- Z. Chen, Y. Qin and K. Amine, Electrochim. Acta, 2009, 54(24), 5605–5613 CrossRef CAS.
- A. R. Wizansky, P. E. Rauch and F. J. Disalvo, J. Solid State Chem., 1989, 81(2), 203–207 CrossRef CAS.
- J. C. Kim, X. Li, C. J. Moore, S. Bo, P. G. Khalifah, C. P. Grey and G. Ceder, Chem. Mater., 2014, 26(14), 4200–4206 CrossRef CAS.
- V. L. Chevrier and G. Ceder, J. Electrochem. Soc., 2011, 158(9), A1011–A1014 CrossRef CAS.
- Y. Kim, K. Ha, S. M. Oh and K. T. Lee, Chem. – Eur. J., 2014, 20(38), 11980–11992 CrossRef CAS PubMed.
- S. Wenzel, T. Leichtweiss, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2016, 8(41), 28216–28224 CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, APL Mater., 2013, 1(1), 011002 CrossRef.
- M. Murayama, R. Kanno, M. Irie, S. Ito, T. Hata, N. Sonoyama and Y. Kawamoto, J. Solid State Chem., 2002, 168(1), 140–148 CrossRef CAS.
- R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Solid State Ionics, 2000, 130(1), 97–104 CrossRef CAS.
- M. Lindqvist, D. Lundqvist and A. Westgren, Kem. Tidskr., 1936, 48, 156–160 CAS.
- S. Geller, Acta Crystallogr., 1962, 15(12), 1195–1198 CrossRef CAS.
- M. Fleet, Am. Mineral., 1977, 62(3–4), 341–345 CAS.
- J. B. Parise, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36(5), 1179–1180 CrossRef.
- A. Schwöbel, R. Hausbrand and W. Jaegermann, Solid State Ionics, 2015, 273, 51–54 CrossRef.
- P. Hartmann, T. Leichtweiss, M. R. Busche, M. Schneider, M. Reich, J. Sann, P. Adelhelm and J. Janek, J. Phys. Chem. C, 2013, 117(41), 21064–21074 CAS.
- S. Wenzel, T. Leichtweiss, D. Krüger, J. Sann and J. Janek, Solid State Ionics, 2015, 278, 98–105 CrossRef CAS.
- Z. Wang, J. Z. Lee, H. L. Xin, L. Han, N. Grillon, D. Guy-Bouyssou, E. Bouyssou, M. Proust and Y. S. Meng, J. Power Sources, 2016, 324, 342–348 CrossRef CAS.
- H. Chen, Novel Sodium Tin Sulfides As Electrolyte for Solid State Sodium IonBatteries, presented at 18th International Meeting on Lithium Batteries, June 19–24, 2016, 2016.
- G. Sahu, Z. Lin, J. Li, Z. Liu, N. Dudney and C. Liang, Energy Environ. Sci., 2014, 7(3), 1053–1058 Search PubMed.
- I. Seo and S. W. Martin, Preparation and characterization of lithium thio-germanate thin film electrolytes grown by RF sputtering for solid state Li-ion batteries, 2009, p. 153 Search PubMed.
- G. Sahu, E. Rangasamy, J. Li, Y. Chen, K. An, N. Dudney and C. Liang, J. Mater. Chem. A, 2014, 2(27), 10396–10403 CAS.
- H. Kitaura, A. Hayashi, T. Ohtomo, S. Hama and M. Tatsumisago, J. Mater. Chem., 2011, 21(1), 118 RSC.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58(3), 364–369 CrossRef.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Inorg. Chem., 2010, 50(2), 656–663 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169 CrossRef CAS.
- M. Chase, J. Phys. Chem. Ref. Data, 1998, 9, 59 Search PubMed.
- O. Kubaschewski, C. B. Alcock and P. Spencer, Materials Thermochemistry, Pergamon Press, 1993 Search PubMed.
- J. Sangster and A. Pelton, J. Phase Equilib., 1997, 18(2), 185–189 CrossRef CAS.
- A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(4), 045115 CrossRef.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943 CrossRef CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(3), 1505 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ee00534b |
| ‡ Co-authorship. |
| This journal is © The Royal Society of Chemistry 2017 |