Open Access Article
Open Access ArticleCrystal structures and magnetic properties of two series of phenoxo-O bridged dinuclear Ln2 (Ln = Gd, Tb, Dy) complexes†
Marek
Machata
,
Radovan
Herchel
 ,
Ivan
Nemec
,
Ivan
Nemec
 and
Zdeněk
Trávníček
and
Zdeněk
Trávníček
 *
*
Department of Inorganic Chemistry, Regional Centre of Advanced Technologies and Materials, Faculty of Science, Palacký University, 17. listopadu 12, CZ-771 46 Olomouc, Czech Republic. E-mail: zdenek.travnicek@upol.cz
First published on 1st November 2017
Abstract
Six dinuclear lanthanide compounds of the formulae [Ln2(3m-L4)2(L2)2(MeOH)2]·6MeOH (Ln = Gd – 1a, Tb – 1b, and Dy – 1c) and [Ln2(3m-L4)2(L2)2(DMF)2] (Ln = Gd – 2a, Tb – 2b, and Dy – 2c; DMF = N,N-dimethylformamide, H23m-L4 = (2-[(E)-(3-metoxysalicylidene)amino]phenol), and HL2 = 1,3-diphenyl-1,3-diketopropane) were prepared and characterized by elemental analysis, FTIR spectroscopy, thermogravimetric measurements, single-crystal X-ray structural analysis, and magnetometry, and Gd2 and Dy2 compounds by ab initio methods as well. The structural analysis revealed the isostructurallity of the compounds within the series of 1a–c and 2a–c. The analysis of the variable temperature magnetic data showed the presence of a weak antiferromagnetic coupling in the Gd2 compounds (J/cm−1 = –0.13 for 1a and J/cm−1 = –0.17 for 2a). The magnetocaloric effect was studied on compound 2a with the maximum value of −ΔSM = 22.9 J kg−1 K−1 at T = 2.0 K and B = 9 T, which is the highest value among the Gd2 double phenoxo-bridged compounds observed up to now. Both the Dy2 compounds (1c and 2c) exhibit slow-relaxation of magnetization in zero external static magnetic field. Magnetic anisotropy, intradimer magnetic coupling and magnetization blocking barriers were also studied by ab initio methods for 1c and 2c.
Introduction
Lanthanide-based coordination compounds have attracted increasing interest because of their potential applications as luminescent materials,1 catalysts,2 contrast agents in magnetic resonance imaging,3 and molecular magnetic coolers,4 and due to their capability to exhibit slow relaxation of magnetization of molecular origin with potential applications in quantum computing5 and molecular spintronics.6 The last mentioned property refers to a special class of molecular magnetic compounds, so called single molecule magnets (SMMs),7 which exhibit slow relaxation of magnetization due to the presence of an intrinsic barrier of spin reversal (Ueff). This barrier occurs due to the presence of non-negligible magnetic anisotropy on the magnetic centres in the molecules. Lanthanide complexes have become good candidates for SMM preparation, because most of them have a large unquenched orbital momentum causing significant magnetic anisotropy of the metal center.8 Furthermore, when considering polynuclear compounds, it should be noted that in 4f compounds the magnetic coupling between the metal centers is usually very weak. In other words, the magnetic properties of the 4f compounds are dominantly governed by the magnetic anisotropy of the ground term.8 The main negative phenomenon influencing the dynamic magnetic properties of SMMs is fast quantum tunnelling of magnetization (QTM). This may arise from the transverse component of magnetic anisotropy9 and/or magnetic dipolar intermolecular interactions.10 The intermolecular interactions can be suppressed by careful design of the complex molecule and/or magnetic dilution of the sample, as tuning of the magnetic anisotropy is a more complicated task. There are several factors which determine the character of the magnetic anisotropy in lanthanide complexes such as the coordination number,9b the symmetry of the coordination polyhedron11 and its distortion from the ideal symmetry,11a,b and the homogeneity of the electrostatic potential of the ligand field.9a,b,12 Zero-field QTM can also be effectively suppressed by intramolecular exchange coupling in polynuclear compounds13 despite the fact that the coupling between lanthanide atoms is weak.Due to the spin-parity effect, most of the reported 4f based SMMs contain DyIII atoms.7d,14 Depending upon the nuclearity, the ligand field strength and the symmetry of the coordination polyhedron, DyIII SMMs with a large Ueff have been reported15a–c over 800 K.15d–f In order to better understand the magnetism of polynuclear DyIII based SMMs, dinuclear DyIII2 systems have been extensively studied as the simplest example.7d In the design of DyIII2 based SMMs with a large Ueff, the right choice of differently charged ligands forming a heteroleptic coordination sphere turned out to be an even more important factor than the symmetry of the ligand field.9a,b,12,16 One of the successful approaches for the preparation of such compounds is to react the negatively charged N,O-donor phenolate-based ligand Ln− with the dysprosium salt forming thus the {Dy2L2}m+ unit, which might be further ligated by simple inorganic anions and/or solvent molecules.13a,b,17 The utilization of tetradentate Schiff base ligands arising from the condensation of o-vanillin with aromatic amino alcohols has proved to be one of the ways to prepare such compounds.17a,b This type of tetradentate Schiff base ligand provides two distinct coordination pockets ensuring thus the coordination of two metal centres simultaneously, which are often coupled feromagnetically.13a,17a,b Small ligand changes (e.g. different conformations or substitutions of the main and/or auxiliary ligands) result in different coordination environments and thus they can influence the relaxation dynamics.17b It is noteworthy that these compounds often possess an inversion centre and therefore, there is just one symmetry independent magnetic centre in the molecule. This also means that local anisotropic axes are then aligned collinearly.17c,f
Apart from the SMM oriented research of lanthanide compounds, another active area of scientific research is devoted to molecular magnetic coolants. These are materials mostly based on GdIII coordination compounds exhibiting the magnetocaloric effect (MCE).18 The choice of GdIII-based compounds is based on their small magnetic anisotropy and large spin (S = 7/2). Furthermore, a weak superexchange interaction usually present in polynuclear Gd-compounds results in the presence of low-lying excited (almost degenerate) spin states, which are desirable in order to achieve a larger MCE.19
In this work we report on the crystal structures of two new series of LnIII2 complexes with the general formulae [LnIII2(3m-L4)2(L2)2(MeOH)2]·6MeOH (Ln = Gd, Tb, and Dy – 1a–c) and [LnIII2(3m-L4)2(L2)2(DMF)2] (Ln = Gd, Tb, and Dy – 2a–c), where DMF = N,N-dimethylformamide, H23m-L4 = (2-[(E)-(3-metoxysalicylidene)amino]phenol) and HL2 = 1,3-diphenyl-1,3-diketopropane. Their static and dynamic magnetic properties were studied thoroughly by experimental and theoretical methods. Furthermore, MCE was studied for compound 2a. Finally, it must be noted that during the preparation of this report the structure and static and dynamic magnetic properties of 2c were reported.20 Nevertheless, herein we report on the detailed analysis of the relaxation processes in 2c incorporating multiple relaxation pathways.
Results and discussion
Synthesis
Two isostructural LnIII2 series 1a–c and 2a–c were prepared by the reaction of the tetradentate Schiff base ligand H23m-L4 and the bidentate β-diketone ligand HL2 with the corresponding LnIII nitrate (Ln = Gd – 1a, 2a, Tb – 1b, 2b and Dy – 1c, 2c) in the presence of Pr3N (tripropylammine) base in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Fig. 1). The main difference in the preparation of 1a–c and 2a–c series is in the used reaction solvents: compounds 1a–c were prepared by using MeOH only, while 2a–c were synthesized in a MeOH/DMF mixture (20
3 (Fig. 1). The main difference in the preparation of 1a–c and 2a–c series is in the used reaction solvents: compounds 1a–c were prepared by using MeOH only, while 2a–c were synthesized in a MeOH/DMF mixture (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v
1 v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v). In 1a–c, the MeOH molecules are found to be in both the molecular and crystal structures, whereas in 2a–c only the DMF molecules are found to be coordinating directly the metal atoms (vide infra).
v). In 1a–c, the MeOH molecules are found to be in both the molecular and crystal structures, whereas in 2a–c only the DMF molecules are found to be coordinating directly the metal atoms (vide infra).
 | ||
| Fig. 1 Scheme of the synthesis of 1a–c and 2a–c with the depicted solvent molecules incorporated into the molecular structures. | ||
Structure description
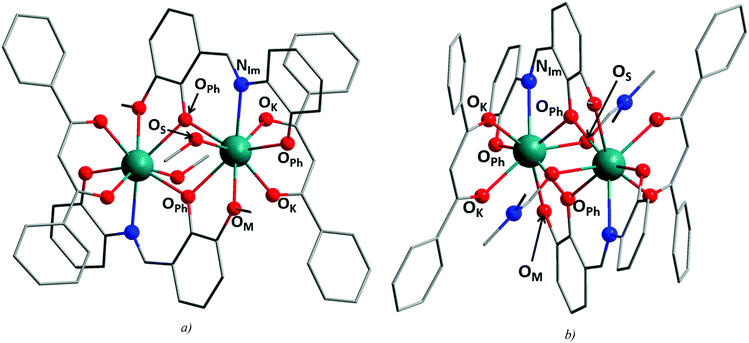
The tetradentate Schiff base ligand H23m-L4 provides four donor atoms for coordination to a central metal atom, i.e. two phenolate oxygen atoms (OPh) after its deprotonation, one methoxy oxygen (OM) and one imino nitrogen atom (NIm). In mononuclear complexes, the dianionic form of the ligand coordinates to the central atom using its NIm and two OPh atoms (a tridentate coordination pocket, {NO2}).21 In polynuclear complexes, all of the donor atoms are involved in coordination in a way that the tridentate {NO2} pocket is formed again and one OM together with one OPh atom (the {O2} donor atom set) forms the second bridging arrangement.21b,22The utilization of the H23m-L4 ligand in the synthesis of metal complexes led to the preparation of polynuclear homometallic transition (NiII4) and inner transition metal (DyIII4, UVI2) coordination compounds.22d,e,23 More often, the preparations of the heterometallic 3d–4f (FeIII2LnIII, MnIII2LnIII2, CoII2LnIII2, NiII2LnIII2, NiII4LnIII2 and NiII8DyIII6) coordination compounds were reported.21b,22a–c,f–i
The basic crystallographic and refinement data for 1a–c and 2a–c are listed in Table S1,† and selected distances and angles for the compounds are summarized in Table 1. The crystal structures of the presented compounds are composed of dinuclear complex molecules with the general formula [Ln2(3m-L4)2(L2)2(solv)2], where solv = MeOH for 1a–c and DMF for 2a–c, and in the case of 1a–c, additional six lattice MeOH molecules are found. In compounds 1a–c and 2a–c, the H23m-L4 ligand binds the Ln atoms in the same way as described above, i.e. one metal centre is coordinated by the {NO2} coordination pocket and simultaneously the same ligand coordinates the second Ln atom by the second {O2} coordination pocket. In this way, a centrosymmetric dimer with the {Ln2O2}4+ core is formed (Fig. 2) and the H23m-L4 ligand occupies five coordination sites on each Ln atom. The additional three coordination sites are occupied by the deprotonated bidentate ketoenol and monodentate solvent ligands making thus the heteroleptic coordination sphere of octacoordinate central atoms.
| 1a | 1b | 1c | 2a | 2b | 2c | |
|---|---|---|---|---|---|---|
| OPh – phenolate oxygen atom, OM – methoxy oxygen atom, NIm – imino nitrogen atom, OK – β-ketoenolate oxygen atom, OS – solvent oxygen atom, OS1, OS2, OS3 – intermolecular solvent oxygen atoms.a Averaged value for three Ln–OPh bond lengths.b Averaged value for two Ln–OK bond lengths.c Intramolecular distances.d Intermolecular distances.e Within the 1D supramolecular chain.f Between the 1D supramolecular chains. | ||||||
| Ln–OPha | 2.339 | 2.325 | 2.313 | 2.338 | 2.329 | 2.312 |
| Ln–OM | 2.5135(15) | 2.5022(13) | 2.4896(13) | 2.503(3) | 2.495(3) | 2.4766(19) |
| Ln–NIm | 2.5055(19) | 2.4893(17) | 2.4791(17) | 2.542(3) | 2.523(3) | 2.508(2) |
| Ln–OKb | 2.313 | 2.301 | 2.287 | 2.337 | 2.324 | 2.308 |
| Ln–OS | 2.4913(15) | 2.4705(13) | 2.4587(14) | 2.433(3) | 2.413(3) | 2.3936(19) |
| Ln–OPh–Ln | 108.06(6) | 108.38(5) | 108.54(5) | 106.28(10) | 106.48(9) | 106.97(7) |
| Ln⋯Lnc | 3.8387(3) | 3.8248(3) | 3.8086(3) | 3.8151(5) | 3.8055(5) | 3.7858(4) |
| Ln⋯Lnd | 10.9275(5)e | 10.8918(4)e | 10.8879(4)e | 8.9439(9) | 8.9239(5) | 8.9039(5) |
| 14.0157(9)f | 14.0147(5)f | 14.0196(5)f | ||||
The bond distances (Table 1) in 1a–c and 2a–c are shorter for the Ln–OPh and Ln–OK (2.29–2.34 Å) than for Ln–OM, Ln–NIm and Ln–OS bonds (2.39–2.54 Å). It should be noted that the Ln–OS bonds are considerably shorter in 2a–c than in 1a–c (2.46–2.49 Å in 1a–c and 2.39–2.43 Å in 2a–c). The shape of the coordination polyhedron in all the compounds was determined by the SHAPE algorithm24 to be a biaugmented trigonal prism (J50) with a significantly smaller distortion from the ideal shape found for 2a–c (4.07–4.16 for 1a–c and 2.13–2.31 for 2a–c).
The phenolate oxygen atoms (OPh) mediate covalent bridging between the metal centres within the {Ln2O2}4+ core with the averaged Ln–OPh distances (in Å) ranging from 2.35 to 2.37 (1a–c) and from 2.36 to 2.39 (2a–c). The corresponding Ln–OPh–Ln bonding angles adopt slightly different values (108.1–108.5° in 1a–c and 106.3–107.0° in 2a–c). The intradimer Ln⋯Ln distances are slightly longer in 1a–c (3.81–3.84 Å) than in 2a–c (3.79–3.82 Å).
The crystal packing in 1a–c significantly differs from that in 2a–c. The adjacent dinuclear complex molecules of 1a–c are connected through two symmetrically related (inversion centre) chains of the hydrogen bonds (Fig. 3, black dashed lines), which assemble the complex molecules into 1D arrays. Each supramolecular chain consists of one coordinated and three lattice MeOH molecules, which are interconnected by the OS–H⋯OS hydrogen bonding. On the end of the chain the MeOH molecule forms hydrogen bonds with the phenolate oxygen atoms of the coordinated Schiff base ligand. All the inchain O–H⋯O hydrogen bonds are rather short with the donor–acceptor distances ranging from 2.66 to 2.73 Å. Next important intermolecular interactions interconnect the neighbouring arrays of the complex molecules by the π–π stacking of the ketoenol aromatic rings with the distances between the centroids in the range of 3.63–3.66 Å for 1a–c. The intermolecular in-chain Ln⋯Ln distances are in the range of 10.89–10.93 Å. The crystal structures of 2a–c contain only weak C–H⋯π, C–H⋯O non-covalent interactions and these will not be described in greater detail. The closest intermolecular Ln⋯Ln distances range from 8.90 to 8.97 Å.
Magnetic properties
Variable temperature DC magnetic measurements for compounds 1a–c and 2a–c are shown in Fig. 4. High temperature data are similar for all the compounds and are constant in the temperature region of 300–100 K with the μeff/μB values of 11.2 (1a), 13.8 (1b), 15.5 (1c), 11.4 (2a), 13.8 (2b), and 15.3 (2c) at 300 K which are close to the spin only values for such systems (Gd2 – 11.2, J = S = 7/2, gJ = 2; Tb2 – 13.8, J = 6, gJ = 3/2 Dy2 – 15.1, J = 15/2, gJ = 4/3). The μeff/μB values for Gd2 compounds remain constant down to approximately 50 K and then decrease to 8.4 and 8.0 at 1.9 K for 1a, and 2a, respectively. Low temperature magnetic data for the Tb2 compounds show a gradual decrease with cooling and below 20 K, the μeff/μB values drop sharply to 11.6 and 11.5 at 1.9 K for 1b, and 2b, respectively. The μeff/μBvs. T data for 1c follow the trend observed for the Tb2 compounds but with a slight increase of μeff/μB below 20 K reaching 14.8 at 1.9 K. Variable temperature magnetic data for 2c display a constant trend down to approximately 25 K followed by a sudden increase to 17.1μB at 1.9 K. The low temperature magnetic behaviour of all the compounds can be attributed to the depopulation of the excited Stark levels as well as magnetic anisotropy and/or antiferromagnetic magnetic interactions for the Gd2 and Tb2 compounds and ferromagnetic interactions in the Dy2 compounds which seems to be stronger for 2c. With regard to the smaller Dy⋯Dy distances for 2c (3.8086(2) Å and 3.7858(4) Å for 1c and 2c, respectively), the observation of the stronger coupling for 2c was expected.Field dependent DC magnetization data measured at 2 and 5 K (Fig. 4) display saturation of the molar magnetization to the expected value of 14 for the Gd2 compounds. The magnetization for the Tb2 and Dy2 compounds does not saturate even at the highest applied fields (10.0, 10.7, 11.0 and 10.7 at 2 K for 1b, 2b, 1c, and 2c, respectively) that can be attributed to the presence of low lying excited states and/or magnetic anisotropy. A rapid increase of magnetization at low magnetic fields for the Dy2 compounds is consistent with ferromagnetic interactions. There have been several reported examples of phenolato bridged Dy2 compounds with ferromagnetic coupling.14b,17a,25
Variable temperature and field DC magnetic data for the Gd2 compounds were fitted using the spin Hamiltonian approach using the formula
 | (1) |
AC susceptibility measurements were performed for the Tb2 (1b and 2b) and Dy2 (1c and 2c) compounds. In the case of Tb2 compounds, no out-of-phase AC susceptibility signal was observed at zero or non-zero static magnetic field. In contrast, both Dy2 compounds exhibited a non-zero out-of-phase AC susceptibility signal already at zero static magnetic field (Fig. 5). The frequency dependence of the χ′′ curves of both 1c and 2c indicates a slow relaxation of magnetization of molecular origin typical of SMMs. However, well-defined maxima on χ′′ susceptibility were observed only for 2c.
 | ||
| Fig. 5 (a–b) Frequency dependent ac susceptibility data recorded in zero DC magnetic field for compound 1c (a) and 2c (b). (c) AC susceptibility data for the DyIII complex 2c at the zero applied external field BDC = 0.0 T. Top: Frequency dependence of χ′ and χ′′ molar susceptibilities. Full points – experimental data, full lines – fitted data using eqn (2). Bottom: Argand (Cole–Cole) plot and fit of the resulting relaxation times to eqn (3) (red line). | ||
Thus, the temperature-dependent experimental data for 2c were possible to analyse with the one-component Debye model (ω = 2πf) as
| χ(ω) = χS + (χT − χS)/[1 + (iωτ)1−α] | (2) |
 | (3) |
| Compound | τ 0 (s) | U (K) | Ref. |
|---|---|---|---|
| a Low temperature behaviour. b High temperature behaviour, H2salaph = 2-{(E)-[(2-hydroxyphenyl)imino]methyl}phenol, H3salhap = 3-{[(E)-(2-hydroxyphenyl)methylidene]amino}propane-1,2-diol, H2ovinh = N-[(E)-(2-hydroxy-3-methoxyphenyl)methylidene]pyridine-4-carbohydrazonic acid, H2ovpch = N-[(E)-(2-hydroxy-3-methoxyphenyl)methylidene]pyridine-2-carbohydrazonic acid, H2napch = N-[(E)-(2-hydroxynaphthalen-1-yl)methylidene]pyridine-2-carbohydrazonic acid. | |||
| 2c | 5.07 × 10−13 | 169 | This work |
| [Dy2(salaph)2(NO3)2(DMF)2] | 4.4 × 10−7(LTB)a | 11 (LTB)a | 17f |
| 3.0 × 10−6 (HTB)b | 12 (HTB)b | ||
| [Dy2(Hsalhap)2(PhCOO)2(MeOH)2] | 2.1 × 10−7 | 45 | 17e |
| [Dy2(ovinh)2(NO3)2(MeOH)2] | 3 × 10−7 | 56 | 17a |
| [Dy2(ovpch)2(NO3)2(H2O)2]·2H2O | 5.3 × 10−7 | 69 | 17b |
| [Dy2(napch)2(NO3)2(MeOH)2]·4MeCN | 1.9 × 10−6 | 41 | 17d |

|
|||
Magnetocaloric properties
With the aim to evaluate the magnetocaloric effect of the herein reported class of GdIII compounds, the magnetization data were measured densely between 1.9 and 10.1 K in various magnetic fields up to 9 T for 2a – Fig. 6. After that, the Maxwell equation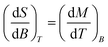 | (4) |
 | (5) |
 | ||
| Fig. 6 Top: The densely-measured magnetization data of 2a. Bottom: The isothermal magnetic entropy change (−ΔSM) of 2a calculated using eqn (5). | ||
The maximal value of −ΔSM = 22.9 J kg−1 K−1 for 2a was found at T = 2.0 K and B = 9 T (Fig. 6). This value is higher than 14.9–20.7 J kg−1 K−1 for other similar double phenoxo-bridged Gd2 compounds.27c,e,29 Recently, we reported on a general relationship for the magnetocaloric effect of GdIII compounds, and two relationships were derived, −ΔSM = 8914 × (Mr/N(Gd))−0.913 and −ΔSM = 39.5cm(Gd)0.364, based on the content of gadolinium expressed either as a relative molecular mass divided by the number of Gd atoms or by a mass concentration (cm = wGd × ρ).30 Then, the estimated magnetocaloric effect for 2a is −ΔSM = 22.7 J kg−1 K−1, and −ΔSM = 27.7 J kg−1 K−1, respectively. These values are close to the experimental one (22.9 J kg−1 K−1), which shows the good prediction capability of these relationships.
Theoretical calculations
Density Functional Theory (DFT) was used to support our findings from fitting the experimental magnetic data for the GdIII compounds. The well-known B3LYP functional was used to calculate high-spin (HS) and broken-symmetry (BS) spin states with ORCA 3.0.3. Then, the energy difference between these states, Δ = εBS − εHS, was utilized in the calculation of the isotropic exchange parameter J following Ruiz's approach as| J = 2Δ/[(S1 + S2)(S1 + S2 + 1)] | (6) |
Furthermore, the post-Hartree–Fock CASSCF calculations were employed in order to better understand the magnetic behaviour of DyIII SMM compounds, namely the ferromagnetic interactions which are evident at low temperatures (Fig. 4) and also different relaxation behaviours (Fig. 5). Thus, the CASSCF calculations were performed with MOLCAS 8.0 for dinuclear molecular fragments [DyLu(3m-L4)2(L2)2(MeOH)2] of 1c and [DyLu(3m-L4)2(L2)2(DMF)2] of 2c, in which one DyIII atom was replaced with a diamagnetic LuIII atom.
Subsequent analysis with the SINGLE_ANISO module of MOLCAS revealed the splitting of the 6H15/2 atomic term into eight Kramers doublets (KD). Each Kramers doublet was then analysed with effective spin Seff = 1/2, which resulted in effective g-tensor values (gx, gy, gz) – Tables 3 and 4.
| E/k (K) | g x | g y | g z | α (°) |
|---|---|---|---|---|
| a α is an angle of gz of the excited state with respect to gz of the ground Kramers doublet. | ||||
| 0 | 0.020 | 0.030 | 19.60 | |
| 225 | 0.899 | 1.836 | 15.52 | 26.0 |
| 296 | 0.370 | 2.474 | 12.23 | 35.4 |
| 376 | 1.411 | 4.777 | 10.17 | 56.2 |
| 438 | 0.062 | 1.907 | 17.07 | 54.5 |
| 461 | 3.045 | 6.307 | 9.61 | 71.8 |
| 553 | 1.131 | 2.056 | 17.43 | 97.3 |
| 768 | 0.044 | 0.094 | 19.71 | 121.0 |
| E/k (K) | g x | g y | g z | α (°) |
|---|---|---|---|---|
| a α is an angle of gz of the excited state with respect to gz of the ground Kramers doublet. | ||||
| 0 | 0.005 | 0.007 | 19.53 | |
| 223 | 0.272 | 0.679 | 15.92 | 11.4 |
| 280 | 1.184 | 2.348 | 16.37 | 64.2 |
| 329 | 9.281 | 6.139 | 2.735 | 132 |
| 411 | 0.609 | 4.166 | 10.96 | 84.2 |
| 489 | 1.022 | 1.557 | 16.36 | 76.6 |
| 514 | 1.277 | 2.171 | 15.86 | 60.4 |
| 639 | 0.161 | 0.363 | 19.40 | 123 |
Evidently, ground states in 1c and 2c possess a very large axial magnetic anisotropy, gx = gy ≈ 0 and gz ≈ 19.5–19.6. The first excited states are separated by 225 and 223 K for 1c, and 2c, respectively, and both have quite large axial magnetic anisotropy (Tables 3 and 4), but gx and gy components are already non-zero. Moreover, the larger deviation of the easy-axis of the g-tensor of the first excited state from the easy-axis of the g-tensor of the ground state is observed for 1c (α = 26.0° for 1c and α = 11.4° for 2c) – (Tables 3 and 4). Next, the plots of the magnetization blocking barrier were constructed for 1c and 2c (Fig. 7), where the values of the transition magnetic moments between Kramers levels are shown and this plot suggests that there is a very low probability of the quantum tunnelling of the ground state and that the relaxation through the first excited states is most probable. To summarize, both compounds should be SMMs in the zero static magnetic field and 2c has predisposition to be a slightly better SMM, because it reveals (i) a better axial type of the magnetic anisotropy of the ground and the first excited states, (ii) a better collinearity of the g-tensors of the first excited and the ground states. In the next step, the POLY_ANISO module was utilized to calculate the DC magnetic properties of 1c and 2c using the data from the SINGLE_ANISO module and the information that Dy atoms are related to each other through inversion symmetry operation. The orientation of the magnetic moments with respect to the Dy⋯Dy connecting line (angle θ) in these centrosymmetric dinuclear compounds is the crucial factor for observing either antiferromagnetic or ferromagnetic dipole–dipole interactions due to the following relationship
 | (7) |
Consequently, for θ < 54.7° the ferromagnetic interaction is expected, whereas for θ > 54.7° the antiferromagnetic interaction is anticipated. Here, we have found that θ = 7.6° for 1c and θ = 9.3° for 2c (Fig. 8), therefore these findings are in agreement with the observed increase of the effective magnetic moment at low temperatures due to the ferromagnetic dipole–dipole interactions (Fig. 9).
This dipolar origin of the ferromagnetic interaction is clearly visible from the comparison of green and blue lines in Fig. 9, where the first green line corresponds to the calculated magnetic properties without dipolar interactions, while the second one comprises the dipolar interactions. In both compounds 1c and 2c, a better agreement with the experimental data was achieved by including additional antiferromagnetic exchange coupling Jex = −0.24 cm−1 for 1c and Jex = −0.16 cm−1 for 2c (red lines in Fig. 9). To summarize, the analysis of magnetic data with the POLYANISO module revealed ferromagnetic dipolar interactions between the DyIII atoms within the dinuclear units accompanied by weak antiferromagnetic superexchange coupling.
Experimental section
Materials
All the purchased chemicals were chemically pure and of analytical reagent grade, and were used without further purification. The preparations of 1a–c and 2a–c are very similar and therefore only the synthesis of 1a will be exemplified in greater detail.[GdIII2(3m-L4)2(L2)2(MeOH)2]·6MeOH (1a)
3-Methoxysalicylaldehyde (0.5 mmol, 0.078 g) and 2-aminophenol (0.5 mmol, 0.055 g) were dissolved in MeOH (15 ml) to obtain an orange solution. A solution of the ligand HL2 (0.5 mmol, 0.112 g) in MeOH (15 ml) and Gd(NO3)3·6H2O (0.5 mmol, 0.226 g) in MeOH (10 ml) were added giving a bright red solution. A solution of Pr3N (tripropylammine, 1.5 mmol, 0.215 g) in 5 cm3 MeOH was dropwise added after 10 min of stirring at room temperature. The resulting yellow solution was filtered and left undisturbed to evaporate the solvent at room temperature. Orange prism shaped crystals were formed after 4 days and collected by filtration. Yield: 36%. Anal. calcd for 1a (C58H44Gd2N2O10·H2O, Mmol = 1261.52 g mol−1): C, 55.2; H, 3.7; N, 2.2, found: C, 55.1; H, 3.5; N, 2.0; IR mid (in cm−1): ν(O–H) = 3594 (w), ν(C–H)aromatic = 3056 (w), ν(C–H)aliphatic = 2938, 2905 (w), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), ν(C
C), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) = 1596, 1549, 1514 (s), ν(C–O) = 1221 (s). TG/DTA data: weight loss of 2.7% found in the 24–136 °C region with the endothermic peak centered at 58 °C (2.8% calcd for 2.5 H2O).
N) = 1596, 1549, 1514 (s), ν(C–O) = 1221 (s). TG/DTA data: weight loss of 2.7% found in the 24–136 °C region with the endothermic peak centered at 58 °C (2.8% calcd for 2.5 H2O).
[TbIII2(3m-L4)2(L2)2(MeOH)2]·6MeOH (1b), [DyIII2(3m-L4)2(L2)2(MeOH)2]·6MeOH (1c)
These compounds were prepared in an identical manner to 1a by replacing Gd(NO3)3·6H2O with the corresponding hydrated nitrate salts (Tb(NO3)3·5H2O, 0.5 mmol, 0.219 g – 1b; Dy(NO3)3·6H2O, 0.5 mmol, 0.230 g – 1c). Compound 1b: Yield 45%. Anal. calcd (C58H44Tb2N2O10·2H2O, Mmol = 1282.88 g mol−1): C, 54.3; H, 3.8; N, 2.2, found: C, 54.3; H, 3.6; N, 2.1; IR mid (in cm−1): ν(O–H) = 3310 (w), ν(C–H)aromatic = 3056 (w), ν(C–H)aliphatic = 2937 (w), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), ν(C
C), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) = 1595, 1550, 1515 (s), ν(C–O) = 1221 (s). TG/DTA data: weight loss of 2.5% found in the 28–142 °C region with the endothermic peak centered at 85 °C (2.8% calcd for 2 H2O). Compound 1c: Yield 42%. Anal. calcd (C58H44Dy2N2O10·2H2O, Mmol = 1292.05 g mol−1): C, 53.9; H, 3.9; N, 2.2, found: C, 53.6; H, 3.6; N, 2.0; IR mid (in cm−1): ν(O–H) = 3315 (w), ν(C–H)aromatic = 3056 (w), ν(C–H)aliphatic = 2937, 2908 (w), ν(C
N) = 1595, 1550, 1515 (s), ν(C–O) = 1221 (s). TG/DTA data: weight loss of 2.5% found in the 28–142 °C region with the endothermic peak centered at 85 °C (2.8% calcd for 2 H2O). Compound 1c: Yield 42%. Anal. calcd (C58H44Dy2N2O10·2H2O, Mmol = 1292.05 g mol−1): C, 53.9; H, 3.9; N, 2.2, found: C, 53.6; H, 3.6; N, 2.0; IR mid (in cm−1): ν(O–H) = 3315 (w), ν(C–H)aromatic = 3056 (w), ν(C–H)aliphatic = 2937, 2908 (w), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), ν(C
C), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) = 1596, 1549, 1515 (s), ν(C–O) = 1221 (s). TG/DTA data: weight loss of 2.6% found in the 28–134 °C region with the endothermic peak centered at 93 °C (2.8% calcd for 2 H2O).
N) = 1596, 1549, 1515 (s), ν(C–O) = 1221 (s). TG/DTA data: weight loss of 2.6% found in the 28–134 °C region with the endothermic peak centered at 93 °C (2.8% calcd for 2 H2O).
[GdIII2(3m-L4)2(L2)2(DMF)2] (2a), [TbIII2(3m-L4)2(L2)2(DMF)2] (2b), [DyIII2(3m-L4)2(L2)2(DMF)2] (2c)
These compounds were prepared following the same procedure in relation to 1a–c, but instead of MeOH (40 cm3) as the reaction solvent, a mixture of MeOH (40 cm3) and DMF (2 cm3) was used. Compound 2a: Yield: 44%. Anal. calcd (C58H44Gd2N2O10·2C3H7NO, Mmol = 1389.70 g mol−1): C, 55.3; H, 4.2; N, 4.0, found: C, 55.6; H, 4.2; N, 3.8; IR mid (in cm−1): ν(C–H)aromatic = 3054 (w), ν(C–H)aliphatic = 2914 (w), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) = 1650 (vs), ν(C
O) = 1650 (vs), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), ν(C
C), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) = 1598, 1551, 1513 (s), ν(C–O) = 1218 (s). Compound 2b: Yield: 52%. Anal. calcd (C58H44Tb2N2O10·2C3H7NO, Mmol = 1393.06 g mol−1): C, 55.1; H, 4.3; N, 4.0, found: C, 54.7; H, 4.2; N, 3.8; IR mid (in cm−1): ν(C–H)aromatic = 3054 (w), ν(C–H)aliphatic = 2916 (w), ν(C
N) = 1598, 1551, 1513 (s), ν(C–O) = 1218 (s). Compound 2b: Yield: 52%. Anal. calcd (C58H44Tb2N2O10·2C3H7NO, Mmol = 1393.06 g mol−1): C, 55.1; H, 4.3; N, 4.0, found: C, 54.7; H, 4.2; N, 3.8; IR mid (in cm−1): ν(C–H)aromatic = 3054 (w), ν(C–H)aliphatic = 2916 (w), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) = 1650 (vs), ν(C
O) = 1650 (vs), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), ν(C
C), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) = 1598, 1551, 1512 (s), ν(C–O) = 1218 (s). Compound 2c: Yield: 50%. Anal. calcd (C58H44Dy2N2O10·2C3H7NO, Mmol = 1402.21 g mol−1): C, 54.8; H, 4.3; N, 4.0, found: C, 54.6; H, 4.3; N, 3.8; IR mid (in cm−1): ν(C–H)aromatic = 3054 (w), ν(C–H)aliphatic = 2914 (w), ν(C
N) = 1598, 1551, 1512 (s), ν(C–O) = 1218 (s). Compound 2c: Yield: 50%. Anal. calcd (C58H44Dy2N2O10·2C3H7NO, Mmol = 1402.21 g mol−1): C, 54.8; H, 4.3; N, 4.0, found: C, 54.6; H, 4.3; N, 3.8; IR mid (in cm−1): ν(C–H)aromatic = 3054 (w), ν(C–H)aliphatic = 2914 (w), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) = 1650 (vs), ν(C
O) = 1650 (vs), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), ν(C
C), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) = 1598, 1551, 1513 (s), ν(C–O) = 1218 (s).
N) = 1598, 1551, 1513 (s), ν(C–O) = 1218 (s).
Methods
Elemental analyses (C, H, N) were performed on a FLASH 2000 CHNS-O Analyzer (ThermoFisher Scientific). The infrared spectra of the complexes were recorded on a ThermoNicolet NEXUS 670 FT-IR spectrometer using the ATR technique in the range of 4000–400 cm−1. The temperature dependent (T = 1.9–300 K, B = 0.1 T) and field dependent (B = 0–7 T, T = 2 and 4.6 or 5 K) magnetization measurements on polycrystalline samples were performed with a MPMS XL-7 Quantum Design SQUID magnetometer. Experimental data were corrected for the diamagnetism of the constituent atoms.X-ray diffraction analysis
X-ray measurements on the selected single crystals of 1a–c and 2b–c were performed on an Oxford Diffraction Xcalibur™2 equipped with a Sapphire 2 CCD detector using the Mo-Kα radiation (λ = 0.71073 Å) and Oxford Cryosystems nitrogen gas-flow apparatus. The CrysAlis program package (version 1.171.33.52, Oxford Diffraction) was used for data collection and reduction.32 X-ray measurement on the single-crystal of 2a was performed on a Bruker D8 Quest diffractometer equipped with a Photon 100 CMOS detector using the Mo-Kα radiation. Data collection, data reduction, and cell parameter refinements were performed using the Bruker Apex III software package.33 The molecular structures were solved by direct methods SHELXS-2014 and all non-hydrogen atoms were refined anisotropically on F2 using the full-matrix least-squares procedure SHELXL-2014.34 All hydrogen atoms were found in differential Fourier maps and their parameters were refined using the riding model with Uiso(H) = 1.2 (CH, CH2, and OH) or 1.5Ueq (CH3).The shape of coordination polyhedra was calculated using the program Shape (version 2.1).24
Theoretical methods
The DFT calculations were performed with the program ORCA 3.0.3.35 The hybrid B3LYP functional36 was used for the calculations of the isotropic exchange constants J for GdIII compounds 1a and 2a following Ruiz's approach37 by comparing the energies of high spin (HS) and broken-symmetry spin (BS) states. The relativistic effects were also included in the calculation with zero order regular approximation (ZORA)38,39 together with the scalar relativistic contracted version of the basis functions def2-TZVP for Gd, N, and O atoms and def2-SVP for C and H atoms.40 We also used the chain-of-spheres approximation to exact exchange (RIJCOSX).41 The molecular geometries were extracted from the experimental X-ray data.The post-Hartree–Fock calculations were performed with the MOLCAS 8.0 program package42 for DyIII compounds 1c and 2c with the geometries experimentally determined by X-ray analysis. The active space of the CASSCF calculations43 comprised nine electrons in seven metal-based f-orbitals, CAS(9,7). The RASSCF method was employed in the CASSCF calculations with the following numbers of multiplets: 21 sextets, 224 quartets and 490 doublets. The spin–orbit coupling based on the atomic mean field approximation (AMFI)44 was taken into account using RASSI-SO with the following numbers of multiplets: 21 sextets, 128 quartets and 130 doublets. The relativistic effects were treated with the Douglas–Kroll Hamiltonian.45 The following basis sets were employed: Dy.ANO-RCC-VQZP, Lu.ANO-RCC-VDZ, O.ANO-RCC-VDZ, N.ANO-RCC-VDZ, C.ANO-RCC-MB and H.ANO-RCC-MB.46 Then, the SINGLE_ANISO module47 and POLY_ANISO module48 were used to calculate all relevant information and magnetic data.
Conclusions
In conclusion, six dinuclear lanthanide complexes [Ln2(3m-L4)2(L2)2(MeOH)2]·6MeOH (Ln = Gd – 1a, Tb – 1b, and Dy – 1c) and [Ln2(3m-L4)2(L2)2(DMF)2] (Ln = Gd – 2a, Tb – 2b, and Dy – 2c) were prepared and thoroughly characterized. It was revealed that the incorporation of different solvent molecules, i.e. MeOH (1a–c) and DMF (2a–c), into the structures of these compounds affected their magnetic properties considerably. The magnetic coupling between the Gd metal centres in 1a and 2a was studied theoretically by the BS-DFT calculations and predicted to be weakly antiferromagnetic in both compounds (in cm−1, J = −0.18 1a, −0.20, 2a), and this is in a very good agreement with the results obtained by the spin Hamiltonian fitting of the experimental magnetic data (in cm−1, J = −0.13 1a, −0.17, 2a). Both Dy2 compounds exhibit ferromagnetic interactions of clearly dipolar character as it was revealed by the theoretical analysis using the Lines model. Different strengths of the magnetic interactions in 1c and 2c were ascribed to different mutual orientations of the magnetic moments within the Dy2 dimers. Single molecule magnet behaviour in zero DC field was found in both Dy2 compounds, but the AC susceptibility measurements revealed the presence of the well-defined maxima only for compound 2c.The magnetocaloric effect was investigated on compound 2a and the experimentally derived value −ΔSM = 22.9 J kg−1 K−1 at T = 2.0 K and B = 9 T is the highest one for the Gd2 double phenoxo-bridged compounds observed up to now.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the National Programme of Sustainability I (LO1305) of the Ministry of Education, Youth and Sports of the Czech Republic.Notes and references
- G. R. Motson, J. S. Fleming and S. Brooker, Adv. Inorg. Chem., 2004, 55, 361–432 CrossRef CAS.
- E. D. Bloch, W. L. Queen and R. Krishna, Science, 2012, 335, 1606 CrossRef CAS PubMed.
- (a) M. Bottrill, L. Kwok and N. J. Long, Chem. Soc. Rev., 2006, 35, 557–571 RSC; (b) E. Debroye and T. N. Parac-Vogt, Chem. Soc. Rev., 2014, 43, 8178–8192 RSC.
- (a) K. A. Gschneidner and V. K. Pecharsky, J. Rare Earths, 2006, 24, 641–647 CrossRef; (b) J. Romero Gómez, R. Ferreiro Garcia, A. de Miguel Catoira and M. Romero Gómez, Renewable Sustainable Energy Rev., 2013, 17, 74–82 CrossRef.
- K. Tordrup and K. Molner, Phys. Rev. A, 2007, 75, 022316 CrossRef.
- J. M. Clemente-Juan, E. Coronado and A. Gaita-Arino, Chem. Soc. Rev., 2012, 41, 7464–7478 RSC.
- (a) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS; (b) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092–3104 RSC; (c) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed; (d) F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278–3288 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- (a) D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770–13778 CrossRef CAS PubMed; (b) S. K. Singh, T. Gupta and G. Rajaraman, Inorg. Chem., 2014, 53, 10835–10845 CrossRef CAS PubMed; (c) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290, 379–392 CrossRef.
- (a) K. R. Meihaus, J. D. Rinehart and J. R. Long, Inorg. Chem., 2011, 50, 8484–8489 CrossRef CAS PubMed; (b) S. N. Konig, N. F. Chilton, C. Maichle-Mossmer, E. M. Pineda, T. Pugh, R. Anwander and R. A. Layfield, Dalton Trans., 2014, 43, 3035–3038 RSC; (c) L. Li, S. Liu, H. Li, W. Shi and P. Cheng, Chem. Commun., 2015, 51, 10933–10936 RSC.
- (a) V. S. Mironov, Y. G. Galyametdinov, A. Ceulemans, C. Gorller-Walrand and K. Binnemans, Chem. Phys. Lett., 2001, 345, 132–140 CrossRef CAS; (b) V. S. Mironov, Y. G. Galyametdinov, A. Ceulemans, C. Gorller-Walrand and K. Binnermans, J. Chem. Phys., 2002, 116, 4673–4685 CrossRef CAS; (c) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 3, 2078–2085 RSC.
- N. F. Chilton, D. Collison, J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551–2557 RSC.
- (a) Y. Guo, G. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H. Zhang, L. F. Chilbotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed; (b) F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830–8833 CrossRef CAS PubMed; (c) T. Fukuda, K. Matsumura and N. Ishikawa, J. Phys. Chem. A, 2013, 117, 10447–10454 CrossRef CAS PubMed; (d) K. Katoh, R. Asano, A. Miura, Y. Horii, T. Morita, B. K. Breedlove and M. Yamashita, Dalton Trans., 2014, 43, 7716–7725 RSC.
- (a) Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953–9963 RSC; (b) P. Zhang, Y.-N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763 CrossRef CAS.
- (a) P.-H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489–9492 CrossRef CAS PubMed; (b) Y. Ma, G. F. Xu, X. Yang, L. C. Li, J. Tang, S. P. Yan, P. Cheng and D. Z. Liao, Chem. Commun., 2010, 46, 8264–8266 RSC; (c) F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976–6780 CrossRef CAS PubMed; (d) R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Commun., 2013, 5, 673–679 CAS; (e) J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 CrossRef CAS PubMed; (f) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- N. F. Chilton, S. K. Langley, B. Moubaraki, A. Soncini, S. R. Batten and K. S. Murray, Chem. Sci., 2013, 4, 1719–1730 RSC.
- (a) P.-H. Lin, T. J. Burchell, R. Clérac and M. Murugesu, Angew. Chem., Int. Ed., 2008, 47, 8848–8851 CrossRef CAS PubMed; (b) Y.-N. Guo, X.-H. Chen, S. Xue and J. Tang, Inorg. Chem., 2011, 50, 9705–9713 CrossRef CAS PubMed; (c) J. Long, F. Habib, P. H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319–5328 CrossRef CAS PubMed; (d) L. Zou, L. Zhao, P. Chen, Y.-N. Guo, Y.-H. Li and J. Tang, Dalton Trans., 2012, 41, 2966–2971 RSC; (e) P. Zhang, L. Zhang, S.-Y. Lin, S. Xue and J. Tang, Inorg. Chem., 2013, 52, 4587–4592 CrossRef CAS PubMed; (f) N. C. Anastasiadis, D. A. Kalofolias, A. Philippidis, S. Tzani, C. P. Raptopoulou, V. Psycharis, C. J. Milios, A. Escuer and S. P. Perlepes, Dalton Trans., 2015, 44, 10200–10209 RSC.
- (a) M. Evangelisti, O. Roubeau, E. Palacious, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606–6609 CrossRef CAS PubMed; (b) F.-S. Guo, J.-D. Leng, J.-L. Liu, Z.-S. Meng and M.-L. Tong, Inorg. Chem., 2012, 51, 405–413 CrossRef CAS PubMed; (c) J.-M. Jia, S.-J. Liu, Y. Cui, S.-D. Han, T.-L. Hu and X.-H. Bu, Cryst. Growth Des., 2013, 13, 4331–4334 Search PubMed; (d) S. Biswas, A. Adhikary, S. Goswami and S. Konar, Dalton Trans., 2013, 42, 13331–13334 RSC; (e) Y.-C. Chen, F.-S. Guo, Y.-Z. Zheng, J.-L. Liu, J.-D. Leng, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, Chem. – Eur. J., 2013, 19, 13504–13510 CrossRef CAS PubMed; (f) Y. Meng, Y.-C. Chen, Z.-M. Zhang, Z.-J. Lin and M.-L. Tong, Inorg. Chem., 2014, 53, 9052–9057 CrossRef CAS PubMed; (g) Y. Yang, Q.-C. Zhang, Y.-Y. Pan, L.-S. Long and L.-S. Zheng, Chem. Commun., 2015, 51, 7317–7320 RSC.
- J. W. Sharples and D. Collison, Polyhedron, 2013, 54, 91–103 CrossRef CAS.
- K. Zhang, D. Liu, V. Vieru, L. Hou, B. Cui, F.-S. Guo, L. F. Chibotaru and Y.-Y. Wang, Dalton Trans., 2017, 46, 638–642 RSC.
- (a) J.-F. Dong, L. Li, Z.-Z. Ji, H. Cui and D.-Q. Wang, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, 1578 Search PubMed; (b) I. Nemec, M. Machata, R. Herchel, R. Boča and Z. Trávníček, Dalton Trans., 2012, 41, 14603–14610 RSC; (c) S. Bag, P. K. Bhaumik, S. Jana, M. Das, P. Bhowmik and S. Chattopadhyay, Polyhedron, 2013, 66, 229–237 CrossRef; (d) M. Hasanzadeh, M. Salehi, M. Kubicki, S. M. Shahcheragh, G. Dutkiewicz, M. Pyziak and A. Khaleghian, Transition Met. Chem., 2014, 39, 623–632 CrossRef CAS.
- (a) K. C. Mondal, G. E. Kostakis, Y. Lan, W. Wernsdorfer, C. E. Anson and A. K. Powell, Inorg. Chem., 2011, 50, 11604–11610 CrossRef CAS PubMed; (b) K. C. Mondal, A. Sundt, Y. Lan, G. E. Kostakis, O. Waldmann, L. Ungur, L. F. Chibotaru, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2012, 51, 7550–7554 CrossRef CAS PubMed; (c) H. Ke, L. Zhao, Y. Guo and J. Tang, Inorg. Chem., 2012, 51, 2699–2705 CrossRef CAS PubMed; (d) K. C. Mondal, G. E. Kostakis, Y. Lan and A. K. Powell, Polyhedron, 2013, 66, 268–273 CrossRef CAS; (e) S. Saha, S. Pal, C. J. Gómez-García, J. M. Clemente-Juan, K. Harms and H. P. Nayek, Polyhedron, 2014, 74, 1–5 CrossRef CAS; (f) K. Griffiths, C. W. D. Gallop, A. Abdul-Sada, A. Vargas, O. Navarro and G. E. Kostakis, Chem. – Eur. J., 2015, 21, 6358–6361 CrossRef CAS PubMed; (g) H. Ke, W. Zhu, S. Zhang, G. Xie and S. Chen, Polyhedron, 2015, 87, 109–116 CrossRef CAS; (h) W.-W. Kuang, C.-Y. Shao and P.-P. Yang, J. Coord. Chem., 2015, 68, 1412–1422 CrossRef CAS; (i) H. Ke, S. Zhang, W. Zhu, G. Xie and S. Chen, J. Coord. Chem., 2015, 68, 808–822 CrossRef CAS.
- R. Kannappan, D. M. Tooke, A. L. Spek and J. Reedijk, Inorg. Chim. Acta, 2006, 359, 334–338 CrossRef CAS.
- (a) M. Llunell, D. Casanova, J. Cicera, P. Alemany and S. Alvarez, SHAPE, Version 2.1, Barcelona, Spain, 2013 Search PubMed; (b) S. Alvarez, Dalton Trans., 2005, 2209–2233 RSC; (c) D. Casanova, P. Alemany, J. M. Bofill and S. Alvarez, Chem. – Eur. J., 2003, 9, 1281–1295 CrossRef CAS PubMed; (d) A. Ruiz-Martínez, D. Casanova and S. Alvarez, Chem. – Eur. J., 2008, 14, 1291–1303 CrossRef PubMed; (e) A. Ruiz-Martínez, D. Casanova and S. Alvarez, Dalton Trans., 2008, 2583–2591 RSC.
- (a) P.-H. Lin, W.-B. Sun, M.-F. Yu, G.-M. Li, P.-F. Yan and M. Murugesu, Chem. Commun., 2011, 47, 10993–10995 RSC; (b) F. Gao, Y.-Y. Li, C.-M. Liu, Y.-Z. Li and J.-L. Zuo, Dalton Trans., 2013, 42, 11043–11046 RSC; (c) J. Zhu, H.-F. Song, P.-F. Yan, G.-F. Hou and G.-M. Li, CrystEngComm, 2013, 15, 1747–1752 RSC; (d) H. Wang, C. Liu, T. Liu, S. Zeng, W. Cao, O. Ma, C. Duan, J. Dou and J. Jiang, Dalton Trans., 2013, 42, 15355–15360 RSC; (e) A.-J. Hutchings, F. Habib, R. J. Holmberg, I. Korobkov and M. Murugesu, Inorg. Chem., 2014, 53, 2102–2112 CrossRef CAS PubMed; (f) E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dorfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Colison, J. van Slageren, E. J. C. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243–5249 CrossRef CAS PubMed; (g) F. Gao, X.-M. Zhang, L. Cui, K. Deng, Q.-D. Zeng and J.-L. Zuo, Sci. Rep., 2014, 4, 5928 CrossRef CAS PubMed.
- The standard deviations were calculated as σi = (Pii−1·S/(N − k))−1/2, where Pij = ∑(δμn/δai·δμn/δaj) and S = ∑(μn − μexpn)2 with n = 1 to N; ai and aj are the fitted parameters, N is the number of the experimental points (sum of temperature and field dependent data), μn and μexpn are the calculated and experimental effective magnetic moments for the given temperature and magnetic field. The σi was then multiplied by Student's t95% to provide confidence limits with 95% probabilities listed in the text.
- (a) X. Mei, X. Wang, J. Wang, Y. Ma, L. Li and D. Liao, New J. Chem., 2013, 37, 3620–3626 RSC; (b) F. Yang, Q. Zhou, G. Zeng, G. Li, L. Gao, Z. Shi and S. Feng, Dalton Trans., 2014, 43, 1238–1245 RSC; (c) W. M. Wang, Y. H. Ren, S. Wang, C. F. Zhang, Z. L. Wu, H. Zhang and M. Fang, Inorg. Chim. Acta, 2016, 453, 452–456 CrossRef CAS; (d) H.-R. Tu, W.-B. Sun, H.-F. Li, P. Chen, Y.-M. Tian, W.-Y. Zhang, Y.-Q. Zhang and P.-F. Yan, Inorg. Chem. Front., 2017, 4, 499–508 RSC; (e) W.-M. Wang, H.-H. Liu, L.-T. He, X.-R. Han, Z.-L. Wu, Y.-G. Ran, J.-Y. Zou and M. Fang, Polyhedron, 2017, 133, 119–124 CrossRef CAS.
- A. M. Tishin and Y. I. Spichkin, The Magnetocaloric Effect and its Applications, IOP Publishing Ltd, 2003 Search PubMed.
- (a) W. M. Wang, H. X. Zhang, S. Y. Wang, H. Y. Shen, H. L. Gao, J. Z. Cui and B. Zhao, Inorg. Chem., 2015, 54, 10610–10622 CrossRef CAS PubMed; (b) H. Y. Shen, W. M. Wang, Y.-X. Bi, H.-L. Gao, S. Liu and J. Z. Cui, Dalton Trans., 2015, 44, 18893–18901 RSC; (c) S.-Y. Wang, W.-M. Wang, H. X. Zhang, S. H.-Y. Shen, L. Jiang, J.-Z. Cui and H.-L. Gao, Dalton Trans., 2016, 42, 3362–3371 RSC.
- R. Herchel, K. Kotrle and Z. Trávníček, RSC Adv., 2017, 7, 30763–30769 RSC.
- J.-D. Leng, J.-L. Liu, W.-Q. Lin, S. Gómez-Coca, D. Aravena, E. Ruiz and M.-L. Tong, Chem. Commun., 2013, 49, 9341–9343 RSC.
- CrysAlis software package, Version 1.171.33.52, Agilent, Technologies, Yarnton, England Search PubMed.
- Bruker. Apex3, Bruker AXS Inc., Madison, Wisconsin, USA, 2015 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (d) P. L. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- (a) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 1999, 20, 1391–1400 CrossRef CAS; (b) E. Ruiz, A. Rodríguez-Fortea, J. Cano, S. Alvarez and P. Alemany, J. Comput. Chem., 2003, 24, 982–989 CrossRef CAS PubMed.
- E. V. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- C. van Wüllen, J. Chem. Phys., 1998, 109, 392–399 CrossRef.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- (a) F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98 CrossRef CAS; (b) R. Izsak and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- (a) F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. Å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed; (b) J. A. Duncan, J. Am. Chem. Soc., 2009, 131, 2416 CrossRef CAS PubMed; (c) G. Karlström, R. Lindh, P. Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrády and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239 CrossRef; (d) V. Veryazov, P.-O. Widmark, L. Serrano-Andres, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635 CrossRef CAS.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- (a) B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef CAS; (b) B. Schimmelpfennig, AMFI, an atomic mean-field spin-orbit integral program, Stockholm University, 1996 Search PubMed.
- (a) N. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CrossRef; (b) B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748 CrossRef CAS.
- (a) B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS PubMed; (b) B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P.-O. Widmark, Chem. Phys. Lett., 2005, 409, 295–299 CrossRef CAS.
- (a) L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed; (b) L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pillet and D. Luneau, J. Am. Chem. Soc., 2008, 130, 12445–12455 CrossRef CAS PubMed; (c) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed; (d) L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, J. Am. Chem. Soc., 2008, 130, 12445–12455 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1574217–1574222. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt03441e |
| This journal is © The Royal Society of Chemistry 2017 |