Solvent-driven azide-induced mononuclear discrete versus one-dimensional polymeric aromatic Möbius cadmium(II) complexes of an N₆ tetradentate helical ligand

Abstract

We report the synthesis and structural characterization of a heteroleptic mononuclear discrete complex [Cd(N₃)₂(L)(MeOH)]·MeOH (1·MeOH) and a one-dimensional coordination polymer of the composition [Cd₃(N₃)₆(L)]_n (2), fabricated from Cd(NO₃)₂·4H₂O and the helical organic ligand benzilbis((pyridin-2-yl)methylidenehydrazone) (L) in the presence of two equivalents of NaN₃. The formation of different structures is driven by the solvent. The former complex is formed in the presence of MeOH, while the latter complex is formed in EtOH. The Cd^II centre in 1·MeOH is trapped by the two pyridyl-imine units of the tetradentate ligand L, two azide ligands and one oxygen atom of one methanol ligand with the CdN₆O coordination polyhedron yielding a square face monocapped trigonal prism. The asymmetric unit of 2 consists of three symmetrically independent atoms of Cd^II, six azide anions and one L. The polymeric structure of 2 is realized through chains of the Cd(N₃)₂ units which are decorated with Cd(N₃)₂L units. The Cd^II atoms from the backbone of the coordination polymer have a distorted octahedral coordination, while the remaining Cd^II atom forms a trigonal prism with two basal planes nearly parallel to each other. In both complexes, the 12π electron chelate ring of the CdL fragment is shown to be aromatic by establishing it as a Möbius object. Hirshfeld surface analysis of 1 in 1·MeOH and L in 2 showed that the structures of both species are highly dominated by H⋯X (X = H, C and N) contacts, of which the latter two are highly favoured, as well as some contribution from highly enriched C⋯C contacts is clearly observed.

---

Introduction

Nature likes helical molecules.¹ Deoxyribonucleic acid, discovered by Watson and Crick in 1953, is the most famous self-organized helicate structure.² The term helicate for a polymetallic helical double-stranded complex was first suggested by Lehn in 1987.³ However, the first known helical double-stranded dinuclear structure was reported in 1976 for the doubly deprotonated octaethyl formylbiliverdine with Zn^II.⁴ Since then, great efforts have been made towards a detailed study of the self-assembly of helicate structures.^5,6 The predesign of coordinating ligands is the most effective strategy to obtain desired helicate metal-containing complexes. However, the use of metal-containing precursors to synthesize helicate systems is much less investigated.^4–6

Non-helical chelating organic ligands, containing suitable donor sites, may give rise to a helical topology upon binding to metal ions^7–10 because in inorganic complexes, the coordination behavior of the metal ions directs the overall topology in a manner that has not been seen in the parent ligand. On the other hand, polydentate Schiff base ligands, comprising two symmetrically related pyridyl coordination sites derived from benzyldihydrazone, in the solid state are monohelical due to the constraint rotation around the C–C bond.^11–13 Upon coordination, the rotating freedom of the two N–N bonds is also restrained, and the ligand can be locked in a twist conformation (Scheme 1).

Scheme 1 Synthesis of complexes 1·MeOH and 2.

Based on Heilbronner's rule, a conjugated system, including 4nπ electrons, can be aromatic if it is Möbius.¹⁴ A Möbius strip can have N number of half-twists designating its order (Fig. 1). Herges and co-workers have reported the first Möbius molecule with the order N of 1.¹⁵ Thereafter, several Möbius molecules of various orders have been reported.^16–22 Datta and co-workers have reported a Cd^II-based mononuclear double helical complex, with fully conjugated ligands, comprising two 13 membered chelate metallocycles with 12π electrons²³ and pointed out that the complex is aromatic and eventually Möbius.²⁴

Fig. 1 (Left) A circular strip, (Middle) a Möbius strip with N = 1 and (Right) a Möbius strip with N = 2. The images adopted from ref. 24.

The nature of a selected metal center is a powerful tool to create the targeted structure. Accordingly, using the Cd^II atom for the formation of hybrid materials is attractive since being a soft metal and exhibiting a variety of coordination numbers it can promote the formation of non-predictable final structures with possible interesting properties. On the other hand, the coordination chemistry of azides had practically not existed prior to the 1960s when the first wide-ranging investigations came out.^25–30 An azide ion is a flexible polydentate ligand that can simultaneously bind several metal ions in different coordination modes. As such, the azide anion is a versatile ligand that can bridge metal centers either end-to-end (μ_1,3) or end-on (μ_1,1) or many other combinations of both possibilities.³¹

When growing crystals from solution, the solvent of crystallization plays a pivotal role in determining the overall structure, crystal system and lattice arrangement. This role can range from influencing the polymorph that is grown to being built into the crystal structure itself to form a solvate. Whereas, in some solvates, the solvent molecules act as space fillers, and in other solvates, the solvent molecules are essential components of the lattice by interacting with the host molecules by specific intermolecular interactions, such as hydrogen bonds. The former type of solvates are classified as inclusion phases, and the latter type of solvates as cocrystals.³² Certain molecular shapes and intermolecular interactions favor the formation of unsolvated crystals.³³ The solvate is stabilized when the incorporated solvent molecule either improves the packing or strengthens the intermolecular interactions in the crystal.³⁴

In this contribution we describe the solvent-driven synthesis and complete structural investigation of mononuclear discrete and one-dimensional polymeric aromatic Möbius Cd(N₃)₂-based complexes constructed from the N₆ tetradentate helical ligand L, derived from benzildihydrazone and 2-acetylpyridine. Notably, it has recently been indicated that an empty s orbital can participate in a Möbius framework of p orbitals.²⁴

Results and discussion

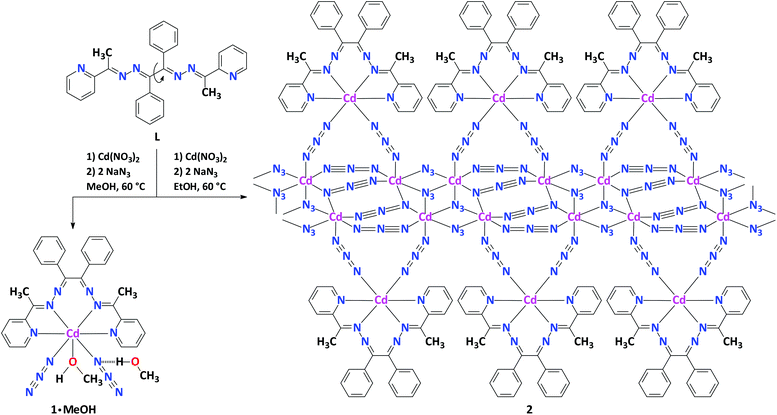
An equimolar one-pot reaction of Cd(NO₃)₂·4H₂O with the organic ligand L in the presence of two equivalents of NaN₃ in MeOH at 60 °C in a branched tube apparatus leads to a heteroleptic mononuclear discrete complex [Cd(N₃)₂(L)(MeOH)]·MeOH (1·MeOH) (Scheme 1). Notably, using the same procedure but in EtOH yielded crystals of the polymeric complex of the composition [Cd₃(N₃)₆(L)]_n (2).

Both compounds 1·MeOH and 2 were obtained in good yields, and were fully characterized by elemental analysis, FTIR spectroscopy, powder and single-crystal X-ray diffraction, and Hirshfeld surface analysis.

According to the single crystal X-ray diffraction data, 1·MeOH and 2 each crystallize in the triclinic space group P1̄. The asymmetric unit of 1·MeOH consists of a single molecule 1 and one lattice methanol (Fig. 2), while the asymmetric unit of 2 consists of three symmetrically independent atoms of Cd^II, six azide anions and one molecule of L (Fig. 3).

Fig. 2 (Left) Crystal structure of 1·MeOH. CH-hydrogen atoms are omitted for clarity. (Right) Coordination polyhedron around the Cd^II atom in the crystal structure of 1·MeOH. Color code: H = black, C = gold, N = blue, O = red, Cd = magenta.

Fig. 3 (Top) Crystal structure of the asymmetric unit of 2. Hydrogen atoms are omitted for clarity. (Bottom) Coordination polyhedra around the Cd^II atoms in the CdL (left) and Cd₂(N₃)₁₀ fragments (right) in the crystal structure of 2. Color code: C = gold, N = blue, Cd = magenta.

In the structure of 1·MeOH the Cd^II centre has a seven coordination geometry bound by the two pyridyl-imine units of the ligand L, two nitrogen atoms of two azide ligands and one oxygen atom of one methanol ligand (Fig. 2). The Cd–N bond distances, corresponding to the four nitrogen atoms of the Schiff-base ligand, range from 2.372(2) Å to 2.533(2) Å, maintaining that Cd–N_Py < Cd–N_imine (Table S1 in the ESI†). Notably, the bond lengths of the azide ligands (2.270(2) and 2.327(2) Å) are significantly shorter than the bonds of the nitrogen donor atoms within the L ligand, indicating a certain amount of π-electron donation.³⁵ Both azide ligands in 1·MeOH are quasi-linear as the average of the N–N–N angle is 178.1°. The coordination polyhedron around the Cd^II center in the structure of 1·MeOH, with a CdN₆O chromophore, can be either a distorted pentagonal bipyramid or a face capped octahedron or a square face monocapped trigonal prism. The latter polyhedron seems to be the best description (Fig. 2), which is further supported by the corresponding face N–N–N bond angles close to 90° (see the file 1-MeOH.cif in the ESI†). The two basal planes of N₂O are nearly parallel to each other and form a 6.8° dihedral angle and the Cd^II ion is displaced by 1.55 and 1.62 Å from the two basal planes. The ligand L in the structure of 1·MeOH adopts a twist helical conformation. This conformation gives rise to a torsion angle of 75.03(6)° for the N–C(Ph)–C(Ph)–N moiety and the coordination leads to significantly different torsion angles of 121.7(2) and 137.72(19)° around the bonds C(Ph)–N–N–C. The torsion angle between two phenyl rings from the twist ligand is of 86.46(10)°.

The crystal packing of 1·MeOH is governed primarily by the methanol ligand and the lattice methanol molecule. The molecules of 1·MeOH are bound together to form dimers (Fig. 4) by means of strong hydrogen bonds between the OH proton of the lattice methanol and the coordinated nitrogen atom of the azide ligand as well as the oxygen atom of the same lattice methanol and the OH proton of the methanol ligand of the second molecule 1 and vice versa (Table S2 in the ESI†). These interactions give a synthon of motif R⁴₄(12) (Fig. 5). The crystal packing of 1·MeOH is further stabilized by face-to-face π⋯π stacking between the pyridyl rings and C–H⋯π interactions formed by both phenyl and one of the pyridyl fragments (Tables S3 and S4 in the ESI†).

Fig. 4 (Top) Hydrogen bonded dimer in the crystal structure of 1·MeOH. (Bottom) 1D polymeric chain in the crystal structure of 2. CH hydrogen atoms are omitted for clarity. Color code: H = black, C = gold, N = blue, O = red, Cd = magenta.

Fig. 5 Top (left) and side (right) views on a homosynthon of motif R⁴₄(12) formed by means of hydrogen bonds between the OH hydrogen atoms of the methanol ligand, lattice methanol and the nitrogen atom of one of the azide ligands and vice versa in the structure of 2. Color code: H = black, C = gold, N = blue, O = red, Cd = magenta.

The polymeric structure of 2 is achieved through the chains of Cd(N₃)₂ units along the crystallographic a axis which are further decorated with Cd(N₃)₂L units (Fig. 4). The two symmetrically independent Cd^II atoms which form the backbone of the coordination polymer each have a distorted octahedral coordination with the Cd–N bond lengths ranging from 2.2702(13) to 2.4428(13) Å (Table S1 in the ESI†). The remaining Cd^II atom, linked to the ligand L, also has a six coordination geometry bound by the two pyridyl-imine units of the ligand L and two nitrogen atoms of two azide ligands (Fig. 3).

The coordination polyhedron around this Cd^II center in the structure of 2, with a CdN₆ chromophore, is best described as a trigonal prism (Fig. 3). The two basal planes of N₃ are nearly parallel to each other and form a 4.6° dihedral angle and the Cd^II ion is displaced by 1.50 and 1.54 Å from the two basal planes. The Cd–N bond distances corresponding to the four nitrogen atoms of the ligand L are almost identical and range from 2.3512(14) to 2.3894(13) Å, maintaining that Cd–N_Py ≈ Cd–N_imine (Table S1 in the ESI†). The bond lengths of the azide ligands within the Cd(N₃)₂L unit are also shorter, however with a lower degree than in the structure of 1·MeOH, than the bonds of the nitrogen donor atoms within the L ligand (Table S1 in the ESI†).

The torsion angle for the N–C(Ph)–C(Ph)–N moiety is of 76.5(2)° while the same angles for the C(Ph)–N–N–C fragment are of 119.18(15) and 125.21(16)°. The torsion angle between two phenyl rings from the twist ligand L is of 88.44(9)°. The shortest and longest Cd⋯Cd separations within the backbone of the coordination polymer are about 3.54 and 5.40 Å, respectively, while the shortest Cd⋯Cd separations between the symmetrically independent metal atoms arising from the backbone of the coordination polymer and the CdL metal center are about 5.62 and 5.89 Å (Table S1 in the ESI†). The azide ligands exhibit a variety of coordination modes, i.e. μ_1,1-N_azide, μ_1,3-N_azide, μ_1,1,1-N_azide and μ_1,1,3-N_azide (Fig. 4).

The crystal packing of 2 is dictated primarily by the face-to-face π⋯π stacking between the pyridyl rings as well as C–H⋯π and N–N⋯π interactions (Table S4 in the ESI†). The latter interactions are formed by the phenyl fragments.

Since the topologies of both complexes, with respect to the organic ligand L, are helical (Fig. 6), enantiomers are expected. Moreover, complexes 1·MeOH and 2 crystallize in the triclinic space group P1̄ and therefore each represents a racemic mixture in the solid state (Fig. 6).

Fig. 6 Space-filling models of the left-handed (left) and right-handed (right) helical nature of the CdL fragment in the crystal structures of 1·MeOH and 2. The phenyl and hydrogen atoms are omitted for clarity. Color code: C = gold, N = blue, Cd = magenta.

Bulk samples of the described complexes were each studied by means of X-ray powder diffraction analysis (Fig. 7). The experimental X-ray powder patterns of the complexes are in full agreement with the calculated powder patterns obtained from single crystal X-ray diffraction, showing that the bulk materials are free from phase impurities.

Fig. 7 Calculated (black) and experimental (red) X-ray powder diffraction patterns of 1·MeOH and 2.

The FTIR spectrum of 1·MeOH contains a wide strong band characteristic for the asymmetric stretching vibration, ν_asym(N₃), of the azide ligands at 2032 cm⁻¹ (Fig. 8). Two intense bands at 2062 and 2108 cm⁻¹ in the FTIR spectrum of 2 were assigned to the same stretching modes of the azide anions but of different coordination modes (Fig. 8).³⁶ The FTIR spectrum of 1·MeOH also displays a broad intense band for the coordinated and lattice methanol ranging from about 3100 to 3700 cm⁻¹ (Fig. 8). The symmetric stretching vibrations, ν_sym(N₃), of the azide ligands are observed in the spectrum of 1·MeOH as a single band at 1438 cm⁻¹, while two bands at 1434 and 1443 cm⁻¹, characteristic for the same symmetric stretching vibrations of azides, are shown in the FTIR spectrum of 2 (Fig. 8). The characteristic bands of the C=C and C=N stretching modes appear in the range of 1560–1600 cm⁻¹ in the spectra of both compounds (Fig. 8).

Fig. 8 FTIR spectra of 1·MeOH (black) and 2 (red).

In order to examine the interactions in the crystal structures of 1 and 2, Hirshfeld surface analysis³⁷ and the corresponding 2D fingerprint plots³⁸ were obtained using CrystalExplorer 3.1.³⁹

Unlike other molecular volumes and surfaces (e.g. van der Waals volumes, solvent-accessible surfaces, solvent-excluded surfaces), Hirshfeld surfaces are not simply a function of the molecular geometry but are only defined within the crystal. Consequently, the Hirshfeld surfaces reflect the interplay between different atomic sizes and intermolecular contacts in the crystal (condensed phase). The Hirshfeld surfaces and volumes are much larger than the conventional ones, generally filling at least 95% of the crystal volume,⁴⁰ compared with more conventional packing coefficients of between 0.65 and 0.80.⁴¹ The Hirshfeld surfaces are obviously packed very tightly in the crystal, at most touching and never overlapping. However, quite unlike any other partitioning or packing scheme, they leave small intermolecular voids, which can be regarded as regions where the crystalline electron density is very low and is not dominated by any single molecule. The use of Hirshfeld surfaces for the analysis of molecular crystal structures encourages the adoption of a whole structure view of intermolecular interactions, rather than concentrating exclusively on assumed interactions. While the discussion of crystal structures in terms of individual interatomic contacts is unavoidable and certainly valuable, a broader picture of intermolecular interactions in the crystal is increasingly desirable; such a picture is available from the Hirshfeld surface. The size and shape of the Hirshfeld surface are intimately related to the chemical environment surrounding the molecule, making it ideal for use when comparing different crystal structures.

According to Hirshfeld surface analysis, for the molecule of 1 in the structure of 1·MeOH the intermolecular H⋯H, H⋯C and H⋯N contacts, comprising 42.3%, 24.1% and 27.4% of the total number of contacts, are the major contributors to the crystal packing (Table 1). The same intermolecular contacts are also the major contributors on the Hirshfeld surface of the ligand L in the structure of 2. However, the intermolecular H⋯H contacts are remarkably less and occupy 29.5%, while a proportion of the H⋯N contacts is more, comprising 35.1% (Table 1). The intermolecular H⋯C contacts on the surface of L in 2 occupy a similar proportion on the surface of 1 and are of 21.3%. The shortest H⋯H contacts are shown in the fingerprint plots of both species as characteristic broad spikes at d_e + d_i ≈ 2.2–2.4 Å (Fig. S1 and S2 in the ESI†). Furthermore, a subtle feature is evident in the fingerprint plot of 1. There is a splitting of the short H⋯H fingerprint. This splitting occurs when the shortest contact is between three atoms, rather than for a direct two-atom contact.³⁷ The H⋯C contacts in the fingerprint plots of both 1 and L in 2 are shown in the form of “wings” (Fig. S1 and S2 in the ESI†) with the shortest d_e + d_i ≈ 2.6 Å. These contacts are recognized as characteristic of C–H⋯π nature.³⁷ It is worth adding that the fingerprint plot of L in 2 exhibits a significant number of points at large d_e and d_i, shown as tails at the top right of the plot (Table 1). These points, similar to those observed in the fingerprint plot of benzene³⁷ and phenyl-containing compounds,^42–47 correspond to the regions on the Hirshfeld surface without any close contacts with nuclei in the adjacent molecules. Notably, the shortest H⋯N contacts in the fingerprint plot of 1 are shown as a sharp spike at d_e + d_i ≈ 1.9 Å (Fig. S1 in the ESI†). These contacts correspond to the O–H⋯N hydrogen bonds (Fig. 2 and 4, Table S2 in the ESI†). The structure of 1 is also characterized by intermolecular H⋯O contacts of 2.1% of which the shortest are shown in the fingerprint plot as a sharp spike at d_e + d_i ≈ 1.9 Å (Fig. S1 in the ESI†). These contacts correspond to the O–H⋯O hydrogen bonds (Fig. 2 and 4, Table S2 in the ESI†). The structures of both species are also described by C⋯C and are of 3.2% and 4.5%, respectively (Table 1), and are shown in the fingerprint plots as the symmetric area on the diagonal at d_e = d_i ≈ 1.7–2.1 Å (Fig. S1 and S2 in the ESI†). These contacts are evidence for π⋯π stacking interactions (Table S3 in the ESI†). Moreover, the Hirshfeld surface of 1 also contains a negligible proportion of the C⋯N contacts of 0.9%, which are shown in the fingerprint plot as the symmetric area on the same diagonal as C⋯C contacts at d_e = d_i ≈ 1.8–2.0 Å (Fig. S1 in the ESI†). Thus, the C⋯N contacts on the molecular surface of 1 are also due to π⋯π stacking between pyridyl rings (Table S3 in the ESI†). Notably, the C⋯N contacts occupy a significantly higher proportion (3.9%) of the Hirshfeld surface area of L in the structure of 2. This is not only due to π⋯π stacking between pyridyl rings (Table S3 in the ESI†) but rather due to N–N⋯π interactions (Table S4 in the ESI†). This is further supported by the shortest C⋯N contacts in the fingerprint plot of L in 2 shown at d_e + d_i ≈ 3.3 Å (Fig. S1 in the ESI†). Close inspection of other intermolecular contacts in the structure of L in 2 also revealed a negligible proportion of the N⋯N contacts (1.6%) and a proportion of the N⋯Cd contacts (3.9%). However, the latter contacts originate from the covalent bonding of L towards the chelated Cd^II center.

Table 1 (Top) Relative contributions of intermolecular contacts to the Hirshfeld surface area and 2D fingerprint plots of observed contacts for 1 in 1·MeOH and L in 2. (Bottom) Hirshfeld contact surfaces and derived “random contacts” and “enrichment ratios” for 1 in 1·MeOH and L in 2^a

	H	C	N	O	H	C	N	Cd
a Values are obtained from CrystalExplorer 3.1.^39 b The enrichment ratios were not computed when the “random contacts” were lower than 0.9%, as they are not meaningful.^48
Contacts (C, %)^a
H	42.3	—	—	—	29.5	—	—	—
C	24.1	3.2	—	—	21.3	4.5	—	—
N	27.4	0.9	0.0	—	35.1	3.9	1.6	—
O/Cd	2.1	0.0	0.0	0.0	0.0	0.0	3.9	0.0
Surface (S, %)
	69.1	15.7	14.2	1.1	57.7	17.1	23.1	2.0
Random contacts (R, %)
H	47.7	—	—	—	33.3	—	—	—
C	21.7	2.5	—	—	19.7	2.9	—	—
N	19.6	0.7	2.0	—	26.7	1.4	5.3	—
O/Cd	1.5	0.3	0.3	0.0	2.3	0.7	0.9	0.0
Enrichment (E)^b
H	0.89	—	—	—	0.89	—	—	—
C	1.11	1.28	—	—	1.08	1.55	—	—
N	1.40	—	0.0	—	1.31	2.79	0.30	—
O/Cd	1.40	—	—	—	0.0	—	4.33	—

---

We have also determined the enrichment ratios (E)⁴⁸ of the intermolecular contacts for both structures to study the propensity of two chemical species to be in contact. The enrichment ratio, derived from Hirshfeld surface analysis, is defined as the ratio between the proportion of actual contacts in the crystal and the theoretical proportion of random contacts. E is larger than unity for a pair of elements with a higher propensity to form contacts, while pairs which tend to avoid contacts yield an E value lower than unity.

The H⋯C, H⋯N and C⋯C contacts as well as H⋯O contacts in 1 are highly favoured in the structure of 1 and L in the structure of 2 since the corresponding enrichment ratios E_HH, E_HN and E_CC are larger than unity (1.08–1.55) (Table 1). This is explained by a relatively higher proportion of these contacts on the total Hirshfeld surface area over a corresponding proportion of random contacts R_HH, R_HN, R_CC and R_HO, respectively (Table 1). Contrarily, the H⋯H contacts on the surface of both species are less favoured (E_HH = 0.89). This is due to a relatively higher amount of random contacts R_HH, despite both molecules being characterised by a high amount of S_H (Table 1). Interestingly, the C⋯N contacts in the structure of L in 2 are remarkably enriched (E_CN = 2.79). This is explained by a significantly higher amount of the C⋯N contacts on the molecular surface together with a lower amount of random contacts R_CN (Table 1). Finally, the structures of L in 2 are characterized by very impoverished N⋯N (E_NN = 0.30) contacts, which are due to a significantly higher proportion of random contacts R_NN compared to a proportion of N⋯N contacts on the molecular surface (Table 1).

Conclusions

In summary, we have obtained and fully structurally characterized a heteroleptic mononuclear discrete complex [Cd(N₃)₂(L)(MeOH)]·MeOH (1·MeOH) and a one-dimensional coordination polymer of the composition [Cd₃(N₃)₆(L)]_n (2), fabricated from Cd(NO₃)₂·4H₂O and the helical organic ligand benzilbis((pyridin-2-yl)methylidenehydrazone) (L) in the presence of two equivalents of NaN₃. The formation of two significantly different structures is exclusively dictated by the solvent nature. Particularly, the former complex is formed in the presence of MeOH as a reaction medium, while the latter complex is formed in EtOH. Thus, different solvent template molecules (MeOH and EtOH) act as structure-directing agents, adjusted by their size and shape, for the Cd(N₃)₂L-system.

According to the single crystal diffraction data the Cd^II centre in 1·MeOH is bound to the tetradentate Schiff-base ligand L, two azide ligands and one methanol ligand with the CdN₆O coordination polyhedron. The asymmetric unit of 2 consists of three symmetrically independent atoms of Cd^II, six azide anions and one molecule of L. The polymeric structure of 2 is achieved through the chains of Cd(N₃)₂ units along the crystallographic a axis which are further decorated with Cd(N₃)₂L units. In both complexes, the 12π electron chelate ring of the CdL fragment is shown to be aromatic by establishing it as a Möbius object.

Experimental

Materials

L was prepared following the reported method as described elsewhere.²² All other reagents and solvents were commercially available and used as received without further purification.

Physical measurements

FTIR spectra were recorded on a Bruker Tensor 27 FTIR spectrometer. Microanalyses were performed using an ElementarVario EL III analyzer.

Hirshfeld surface analysis

The Hirshfeld molecular surfaces³⁷ and their corresponding 2D fingerprint plots³⁸ were generated using the CrystalExplorer 3.1 software³⁹ on the basis of crystal structures. The d_norm (normalized contact distance) surface and the breakdown of the 2D fingerprint plots were used for decoding and quantifying the intermolecular interactions in the crystal lattice. The d_norm is a symmetric function of distances to the surface from the nuclei inside (d_i) and outside (d_e) the Hirshfeld surface, relative to their respective van der Waals radii. 2D fingerprint plots were generated using d_i and d_e in the translated 0.4–3.0 Å range and including reciprocal contacts as a pair of coordinates in 2D histograms. A colour gradient in the fingerprint plots ranging from blue to red is used to visualize the proportional contribution of contact pairs on the global surface.

Enrichment ratio

The enrichment ratio (E)⁴⁸ of a pair of elements (X,Y) is the ratio between the proportion of actual contacts in the crystal and the theoretical proportion of random contacts. E is larger than unity for pairs of elements which have a high propensity to form contacts in crystals, while pairs which tend to avoid contacts with each other yield an E value lower than unity. The E values are calculated from the percentage of contacts, which, in turn, are given by CrystalExplorer 3.1 software,³⁹ between one type or two types of chemical elements in crystal packing.

Synthesis of 1·MeOH and 2

Cd(NO₃)₂·4H₂O (0.154 g, 0.5 mmol), NaN₃ (0.065 g, 1 mmol) and L (0.222 g, 0.5 mmol) were placed in the main arm of a branched tube. MeOH or EtOH (15 mL) was carefully added to fill the arms. The tube was sealed and immersed in an oil bath at 60 °C while the branched arm was kept at ambient temperature. X-ray suitable crystals were formed during the next days in the cooler arm and were filtered off, washed with acetone and diethyl ether, and dried in air.

1·MeOH. Colorless prism-like crystals. Yield: 0.273 g (81%). Anal. calc. for C₃₀H₃₂CdN₁₂O₂ (705.07) (%): C 51.10, H 4.57 and N 23.84; found: C 51.32, H 4.45 and N 23.69.

2 . Colorless prism-like crystals. Yield: 0.148 g (86%). Anal. calc. for C₂₈H₂₄Cd₃N₂₄ (1033.89) (%): C 32.53, H 2.34 and N 32.51; found: C 32.66, H 2.39 and N 32.33.

X-ray powder diffraction

X-ray powder diffraction for bulk samples was carried out using a Rigaku Ultima IV X-ray powder diffractometer. The parallel beam mode was used to collect the data (λ = 1.54184 Å).

Single-crystal X-ray diffraction of 1·MeOH

The X-ray data were collected on an Agilent Technologies SuperNova-Atlas CCD single crystal diffractometer. Data were processed using the CrysAlisPro⁴⁹ program and corrected for absorption using SADABS.⁵⁰ The structure was solved by direct methods,⁵¹ which revealed the positions of all non-hydrogen atoms. These were refined on F² by a full-matrix least-squares procedure using anisotropic displacement parameters.⁵¹ Hydrogen atoms were inserted at calculated positions, except for the hydrogen atoms of the hydroxyl groups, which were located from a difference Fourier map. All hydrogen atoms were included as fixed contributions riding on attached atoms with isotropic thermal displacement parameters 1.2 times those of the respective atom. Certain crystal geometry parameters referred in the discussion were calculated using PLATON.⁵²

Crystal data for 1·MeOH. C₂₉H₂₈CdN₁₂O, CH₄O; M_r = 705.07 g mol⁻¹, T = 100(2) K, triclinic, space group P1̄, a = 9.8020(1), b = 10.3207(1), c = 15.5967(2) Å, α = 94.002(3), β = 94.287(4), γ = 91.342(4)°, V = 1568.92(3) ų, Z = 2, ρ = 1.492 g cm⁻³, μ(Mo-Kα) = 5.979 mm⁻¹, reflections: 29 281 collected, 5582 unique, R_int = 0.032, R₁(all) = 0.0271, wR₂(all) = 0.0654.

Single-crystal X-ray diffraction of 2

The X-ray data were collected on a Bruker Apex2 CCD single crystal diffractometer. Data were processed with the Saint⁵³ program and corrected for absorption using SADABS.⁵⁰ The space group was assigned using XPREP of the Bruker ShelXTL⁵⁴ package, solved with ShelXT⁵⁴ and refined with ShelXL⁵⁴ and graphical interface ShelXle.⁵⁵ All non-hydrogen atoms were refined anisotropically. Hydrogen atoms attached to carbon were positioned geometrically and constrained to ride on their parent atoms.

Crystal data for 2. C₂₈H₂₄Cd₃N₂₄, M_r = 1033.91 g mol⁻¹, T = 223(2) K, triclinic, space group P1̄, a = 8.9122(3), b = 14.7168(5), c = 15.1730(5) Å, α = 111.392(1), β = 92.184(1), γ = 94.028(1)°, V = 1844.04(11) ų, Z = 2, ρ = 1.862 g cm⁻³, μ(Mo-Kα) = 1.773 mm⁻¹, reflections: 70 672 collected, 10 789 unique, R_int = 0.025, R₁(all) = 0.0204, wR₂(all) = 0.0455.

Figures were generated using the program Mercury.⁵⁶

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the University of Maragheh for the financial support of this research. This publication was supported by the “RUDN University Program 5-100”.

References

1. V. G. Machado, P. N. W. Baxter and J.-M. Lehn, J. Braz. Chem. Soc., 2001, 12, 431–462.
2. J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738.
3. J.-M. Lehn, A. Rigault, J. Siegel, J. Harrowfield, B. Chevrier and D. Moras, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 2565–2569.
4. G. Struckmeier, U. Thewalt and J.-H. Fuhrhop, J. Am. Chem. Soc., 1976, 98, 278–279.
5. C. Piguet, G. Bernardinelli and G. Hopfgartner, Chem. Rev., 1997, 97, 2005–2062.
6. M. Albrecht, Chem. Rev., 2001, 101, 3457–3498.
7. M. G. B. Drew, D. Parui, S. De, J. P. Naskar and D. Datta, Eur. J. Inorg. Chem., 2006, 4026–4028.
8. T. Riss-Johannessen, L. P. Harding, J. C. Jeffery, R. Moon and R. C. Rice, Dalton Trans., 2007, 1577–1587.
9. Y. Furusho and E. Yashima, Chem. Rec., 2007, 7, 1–11.
10. A. M. Stadler, N. Kyritsakas, G. Vanghan and J.-M. Lehn, Chem. – Eur. J., 2007, 13, 59–68.
11. Q. Sun, Y. Bai, G. He, C. Duan, Z. Lin and Q. Meng, Chem. Commun., 2006, 2777–2779.
12. M. G. B. Drew, S. De and D. Datta, Inorg. Chim. Acta, 2009, 362, 2487–2291.
13. S. De, M. G. B. Drew and D. Datta, Inorg. Chim. Acta, 2010, 363, 4123–4126.
14. E. Heilbronner, Tetrahedron Lett., 1964, 29, 1923–1928.
15. D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821.
16. R. P. John, M. Park, D. Moon, K. Lee, S. Hong, Y. Zou, C. S. Hong and M. S. Lah, J. Am. Chem. Soc., 2007, 129, 14142–14143.
17. S. De, M. G. B. Drew, H. S. Rzepa and D. Datta, New J. Chem., 2008, 32, 1831–1834.
18. H. S. Rzepa, Inorg. Chem., 2008, 47, 8932–8934.
19. J. Sankar, S. Mori, S. Saito, H. Rath, M. Suzuki, Y. Inokuma, H. Shinokubo, K. S. Kim, Z. S. Yoon, J. Y. Shin, J. M. Lim, Y. Matsuzaki, O. Matsushita, A. Muranaka, N. Kobayashi, D. Kim and A. Osuka, J. Am. Chem. Soc., 2008, 130, 13568–13579.
20. Y. M. Sung, M. C. Yoon, J. M. Lim, H. Rath, K. Naoda, A. Osuka and D. Kim, Nat. Chem., 2015, 7, 418–422.
21. A. Masoumi, M. S. Gargari, G. Mahmoudi, B. Machura, V. Lynch, G. Giester, M. Abedi and P. Hazendonk, Z. Anorg. Allg. Chem., 2015, 641, 1176–1181.
22. G. Mahmoudi, V. Stilinović, M. S. Gargari, A. Bauzá, G. Zaragoza, W. Kaminsky, V. Lynch, D. Choquesillo-Lazarte, K. Sivakumar, A. A. Khandari and A. Frontera, CrystEngComm, 2015, 17, 3493–3502.
23. M. G. B. Drew, S. De and D. Datta, Inorg. Chim. Acta, 2008, 361, 2967–2972.
24. N. K. Shee and D. Datta, Inorg. Chim. Acta, 2016, 453, 339–344.
25. W. Beck, K. Feldl and E. Schuierer, Angew. Chem., Int. Ed. Engl., 1965, 4, 439–440.
26. W. Beck, E. Schuierer and K. Feldl, Angew. Chem., Int. Ed. Engl., 1966, 5, 249.
27. W. Beck, E. Schuierer, P. Pöllmann and W. P. Fehlhammer, Z. Naturforsch., B: Anorg. Chem. Org. Chem. Biochem. Biophys. Biol., 1966, 21, 811–812.
28. W. Beck, W. P. Fehlhammer, P. Pöllmann, E. Schuierer and K. Feldl, Chem. Ber., 1967, 100, 2335–2361.
29. W. Beck, M. Bauder, W. P. Fehlhammer, P. Pöllmann and H. Schächl, Inorg. Nucl. Chem. Lett., 1968, 4, 143–146.
30. W. Beck, W. P. Fehlhammer, P. Pöllmann and H. Schächl, Chem. Ber., 1969, 102, 1976–1987.
31. W. P. Fehlhammer and W. Z. Beck, Anorg. Allg. Chem., 2013, 639, 1053–1082.
32. J. A. R. P. Sarma and G. R. Desiraju, in Crystal Engineering: Design and Application of Functional Solids, ed. K. R. Seddon and M. Zaworotko, Kluwer, Norwell, MA, 1999, pp. 325–356.
33. S. A. Barnett, D. A. Tocher and M. Vickers, CrystEngComm, 2006, 8, 313–319.
34. G. Mahmoudi, A. A. Khandar, J. White, M. P. Mitoraj, H. S. Jena, P. Van Der Voort, N. Qureshi, A. M. Kirillov, K. Robeyns and D. A. Safin, CrystEngComm, 2017, 19, 3075–3025.
35. T. H. Noh, J. H. Kim, Y.-A. Lee, H. Suh and O.-S. Jung, J. Mol. Struct., 2004, 691, 165–169.
36. F. A. Mautner, F. R. Louka, J. Hofer, M. Spell, A. Lefèvre, A. E. Guilbeau and S. S. Massoud, Cryst. Growth Des., 2013, 13, 4518–4525.
37. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
38. M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.
39. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer 3.1, University of Western Australia, 2012.
40. J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Chem. – Eur. J., 1998, 4, 2136.
41. A. I. Kitaigorodsky, Molecular Crystals and Molecules, Academic Press, New York, 1973.
42. D. A. Safin, M. P. Mitoraj, K. Robeyns, Y. Filinchuk and C. M. L. Vande Velde, Dalton Trans., 2015, 44, 16824–16832.
43. M. G. Babashkina, K. Robeyns, Y. Filinchuk and D. A. Safin, New J. Chem., 2016, 40, 1230–1236.
44. D. A. Safin, C. M. L. Vande Velde, M. G. Babashkina, K. Robeyns and Y. Filinchuk, New J. Chem., 2016, 40, 6156–6163.
45. D. A. Safin, K. Robeyns, M. G. Babashkina, Y. Filinchuk, A. Rotaru, C. Jureschi, M. P. Mitoraj, J. Hooper, M. Brela and Y. Garcia, CrystEngComm, 2016, 18, 7249–7259.
46. D. A. Safin, K. Robeyns and Y. Garcia, CrystEngComm, 2016, 18, 7284–7296.
47. D. A. Safin, M. G. Babashkina, M. P. Mitoraj, P. Kubisiak, K. Robeyns, M. Bolte and Y. Garcia, Inorg. Chem. Front., 2016, 3, 1419–1431.
48. C. Jelsch, K. Ejsmont and L. Huder, IUCrJ, 2014, 1, 119–128.
49. Oxford Diffraction, CrysAlis CCD, Oxford Diffraction Ltd, Abingdon, Oxfordshire, England, 2006.
50. G. M. Sheldrick, SADABS. Program for Empirical Absorption Correction of Area Detector Data, University of Göttingen, Germany, 1997.
51. G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8.
52. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
53. Bruker Saint Plus, Saint Plus 8.34A, Bruker AXS Inc., Madison, Wisconsin, USA, 2007.
54. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
55. C. B. Hübschle, G. M. Sheldrick and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 1281–1284.
56. C. F. Macrae, I. J. Bruno, J. A. Chisholm, P. R. Edgington, P. McCabe, E. Pidcock, L. Rodriguez-Monge, R. Taylor, J. van de Streek and P. A. Wood, J. Appl. Crystallogr., 2008, 41, 466–470.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 and S2, Tables S1–S4 and cif files. CCDC 1564162 and 1564163. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt02952g

---