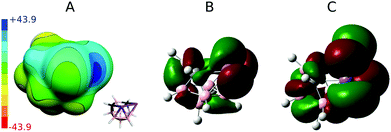A novel stibacarbaborane cluster with adjacent antimony atoms exhibiting unique pnictogen bond formation that dominates its crystal packing

Abstract

We have prepared nido-7,8,9,11-Sb₂C₂B₇H₉, the first cluster with simultaneous Sb–B, Sb–C and Sb–Sb atom pairs with interatomic separations with magnitudes that approach the respective sums of covalent radii. However, the length of the Sb–Sb separation in this cluster is slightly less than the sum of the covalent radii. Quantum chemical analysis has revealed that the crystal packing of nido-7,8,9,11-Sb₂C₂B₇H₉ is predominantly dictated by pnictogen (Pn) bonding, an unconventional σ-hole interaction. Indeed, the interaction energy of a very strong Sb₂⋯H–B Pn-bond in the nido-7,8,9,11-Sb₂C₂B₇H₉ dimer exceeds −6.0 kcal mol⁻¹. This is a very large value and is comparable to the strengths of known Pn-bonds in Cl₃Pn⋯π complexes (Pn = As, Sb).

---

Introduction

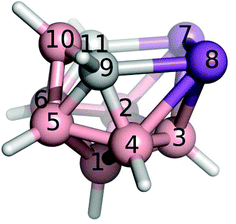
Boron atoms have a remarkable ability to form 3-center-2-electron (3c2e) bonds, which results in an astonishing variety of stable three-dimensional molecular structures composed of triangular B–B–B and B–H–B faces.^1,2 An important class of boranes comprises closo-B_nH_n²⁻ and nido-B_nH_n⁴⁻. BH vertices can be formally replaced by CH⁺, S²⁺, Se²⁺, P⁺, As⁺ and Sb⁺ units which results in a variety of heteroboranes. While carboranes and thiaboranes are common, heteroboranes with heavier main group elements are rare. The first Sb-containing boron clusters to be synthesized were closo-1,2-AsSbB₁₀H₁₀, closo-1,2-Sb₂-B₁₀H₁₀ and nido-7,8-SbCB₉H₁₁⁻ although no crystal structures could be determined.³ The closo-1,2-Sb₂B₁₀H₁₀ compound subsequently allowed a bis(phosphine)metalladistibaborane to be synthesized and crystallized.⁴ However, the Sb₂B₃ pentagonal belt was stabilized by Pd in this cluster. It is often the case that slightly unstable arrangements are capped with a metal atom to help their stabilization.⁵ Inspired by 3-Cl-nido-7,8,9,11-P₂C₂B₇H₉ (1) and 3-I-nido-7,8,9,11-As₂C₂B₇H₉ (2) compounds,^6,7 we have succeeded for the first time in generating a pentagonal belt containing two Sb atoms without having to cap it with a metal atom nido-7,8,9,11-Sb₂C₂B₇H₉ (3, see Fig. 1).

Fig. 1 The molecular structure and atomic numbering of nido-7,8,9,11-Sb₂C₂B₇H₉, 3.

Nowadays, particular attention is paid to σ-hole noncovalent interactions.⁸ The σ-holes are defined as positive electrostatic potential (ESP) areas capable of interacting with electron-rich regions.⁹ They are most often located along the vector of a covalent bond to a halogen (X), chalcogen (Y), or pnictogen (Pn) atom. Consequently, σ-hole interactions are often called X-, Y- or Pn-bonds. These interactions are well known in organic chemistry. A σ-hole is most often characterized by its magnitude (V_s,max); the higher the V_s,max value, the stronger the X-bond. The V_s,max value can be increased by increasing the atomic number of the X atom or by changing the chemical environment. Recently, σ-hole interactions within heteroboranes with positive σ-holes on heteroatoms incorporated have received attention due to the remarkably strong σ-hole interactions.¹⁰ This is counterintuitive when one considers the very low electronegativity of B atoms. It was a phenyl-exo-substituted thiaborane molecule where the σ-hole interactions were first noticed with the resulting formation of an Y-bond that was responsible for the overall packing motif in the crystal structure.^10a A strong X-bond has been observed in the crystal packing of Br-exo-substituted carbaborane.¹¹ Although a series of heteroboranes containing Pn atoms is already known experimentally such as 1 and 2,⁶ no experimental evidence for Pn-bonding in heteroboranes has been reported. Therefore, we used 3 to validate the ability of heteroboranes to form noncovalent Pn-bonds.

Results and discussion

Structural characterization by NMR

The properties of 3 can be inferred from NMR experiments and QM calculations. Table 1 compares experimental and computed ¹¹B NMR chemical shifts, showing excellent agreement between the experimental and computed NMR values with the exception of B(5,6), which are antipodally coupled¹² to the Sb atoms. The discrepancy, which is not unusual for the third row and other heavier elements,¹² indicates that B(5,6) atoms are strongly influenced by Sb(7,8).

Table 1 NMR results for 3^a

	B(1)	B(3)	B(2,4)	B(10)	B(5,6)
a All in ppm with respect to BF3·OEt2. Atomic numbering shown in Fig. 1. b GIAO-MP2/II(def2-TZVP+ECP on Sb)//MP2/cc-pVTZ(def2-TZVP+ECP on Sb).
GIAO^b	−29.3	−15.5	−6.5	−0.4	1.6
Exp.	−30.2	−16.8	−9.2	−1.5	−6.9

---

Aromatic ring currents are observed in 2D and 3D aromatic molecules such as benzene and closo-B₁₂H₁₂²⁻. The nucleus-independent chemical shift (NICS) is a computational method that expresses the absolute magnetic shielding at the center of a 2D or 3D molecule. The NICS values¹³ for various parts of molecule 3 are computed to be −41.7, −44.5, −41.7, −44.9, −22.5 and −17.4 ppm for the Sb–B–B, B–B–B, Sb–Sb–B, and Sb–B–C triangles, center of the molecule, and open pentagonal belt, respectively. These results indicate that the cluster as a whole is of aromatic nature. The fact that the triangles that are closest to antimony are highly aromatic indicates that the Sb atoms donate valence electrons to the corresponding atomic triangles. Even the NICS values that are less negative than −40 ppm are comparable to the aromaticity displayed by the 1,3-dehydro-5,7-adamantanediyl dication and closo-B₁₂H₁₂²⁻ (NICS values of −49.6 and −34.4 ppm, respectively).¹³ The NICS value for the Sb–Sb–C–B–C pentagon of −17.4 ppm is comparable to the values associated with pyrrole and thiophene (NICS values of −17.3 and −14.7 ppm, respectively; more details in ref. 13). The 7,8,9,11-Pn₂C₂B₇H₉ (Pn = P, As) compounds display similar trends of NICS values.

Crystal structure of 3

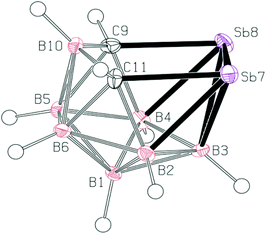
In the crystal structure of 3 (see Fig. 2), four molecules were found in the chiral unit cell. A striking feature of this structure is the well-determined Sb–Sb separation (2.7546(6) Å), which seems to be in line with analogous distances in reduced or over-reduced Sb compounds containing two or more metal atoms. There are several different classes of compounds that could be used for comparison where the Sb–Sb distances are a bit longer than the sum of the covalent radii of 2.8 Å.^14a

Fig. 2 The molecular structure (ORTEP 50% probability level) and atomic numbering of 3. Selected interatomic distances [Å] and angles [°]: Sb7–Sb8 2.7546(6), Sb7–C11 2.225(8), Sb8–C9 2.217(8), C9–B10 1.611(11), B10–C11 1.603(11), B2–Sb7 2.326(9), B3–Sb7 2.458(8), B3–Sb8 2.446(7), Sb8–B4 2.313(8); C9–Sb8–Sb7 89.8(2), C11–Sb7–Sb8 90.61(19), B10–C11–Sb7 115.7(5), B10–C9–Sb8 116.9(5), C11–B10–C9 119.2(6), C9–Sb8–B4 44.5(3), C9–Sb8–B3 77.0(3), B4–Sb8–B3 45.8(3), B4–Sb8–Sb7 92.17(19), B3–Sb8–Sb7 56.03(19), C11–Sb7–B2 44.0(3), C11–Sb7–B3 76.8(3), B2–Sb7–B3 46.1(3), B2–Sb7–Sb8 92.4(2), B3–Sb7–Sb8 55.62(17).

Complexes with Sb–B and Sb–C bonds in a single molecule are very rare.^14b,c The reported Sb–C separation of 3 is elongated by ca. 0.07 Å when compared to the typical C(aromatic)–SbIII distance. Similarly, the Sb–B distances in 3 (range from 2.312 to 2.458 Å) approach the sum of the covalent radii of the constituent atoms, i.e. 2.25 Å.^14a

Electrostatic potential (ESP) analysis

In order to understand Pn-bonding more generally, we analyzed the charge distributions for a series of PnCl₃ and nido-Pn₂C₂B₇H₉ (Pn = P, As, and Sb) molecules. The computed V_s,max and dipole moment (μ) values are summarized in Table 2. Sb has very low electronegativity comparable to that of B but considerably smaller than those values for C and Cl. In accordance with the concept of electronegativity, the Sb atom has highly positive V_s,max values in SbCl₃ of 48.6 kcal mol⁻¹. However, the Sb atoms in 3 also have a very high V_s,max value of 42.7 kcal mol⁻¹ (the σ-hole in between the adjacent Sb atoms; see Fig. 3) despite being bonded to B and C atoms, which are considerably less electronegative than Cl atoms. Interestingly, the Sb vertices have more positive ESP surfaces than the CH vertices (see Fig. 3) and the Sb atoms lie at the center of a partial positive charge within 3. A very large μ of 3 (μ of 4.0 D) also confirms that the center of the Sb–Sb vector is positively charged.

Fig. 3 Computed electrostatic potential (ESP) surface for compound 3 (A). The color range of the ESP in kcal mol⁻¹. The HOMO (B) and LUMO (C) of 3 were derived at the same level of theory as ESP, see computational modeling.

Table 2 Magnitude of σ-holes (V_s,max) on the surfaces of Group V and VII atoms and dipole moments (μ) computed at the HF/cc-pVDZ level in various pnictogen compounds

	V s,max/kcal mol^−1		μ/D
	Group V atoms	Group VII atoms
PCl3	3 × 29.2	3 × 6.7	1.1
AsCl3	3 × 38.6	3 × 2.9	2.1
SbCl3	3 × 48.6	3 × −3.3	3.3
nido-7,8,9,11-P2C2B7H9 (1)	24.8	—	2.0
3-Cl-nido-7,8,9,11-P2C2B7H9	25.4	−3.1	2.8
nido-7,8,9,11-As2C2B7H9	31.1 and 2 × 24.4	—	2.8
3-I-nido-7,8,9,11-As2C2B7H9 (2)	32.2 and 2 × 29.0	8.2	3.5
nido-7,8,9,11-Sb2C2B7H9 (3)	1 × 42.7 and 2 × 25.7	—	4.0

---

Crystal packing and noncovalent interactions

We have studied pairwise interactions in the crystal structure of 3. It was not possible to compare these interactions to the parent nido-7,8,9,11-Pn₂C₂B₇H₉ (Pn = P, As) complexes, as it reveals poor quality crystals, which prevents them from performing reliable X-ray structure determination. Hence, we opted for the halogenated analogues of 1 and 2, for which the crystal structures had already been determined.^6,7 We performed highly accurate MP2.5/CBS calculations for all of the bonding motifs as well as benchmark CCSD(T)/CBS calculations for selected motifs. All the computed interaction energies (ΔE) are summarized in Table 3 (see also Fig. 4). Each molecule of 1 makes two Pn-bonds (P₂⋯H–B and P₂⋯Cl–B). These two Pn-bonds form the A⋯B binding motif which has ΔE of −6.1 kcal mol⁻¹ and was the dominant binding motif for 1. Besides Pn-bonding, molecule 1 also forms a CH⋯Cl–B H-bond and a C–H⋯B–H HH-bond. The H-bonding of 1 is, however, weaker than its Pn-bonding and the ΔE of the A⋯C motif is less negative (−4.4 kcal mol⁻¹).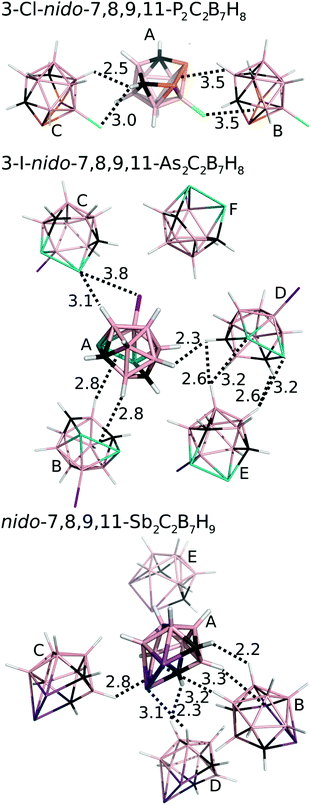

Fig. 4 The most significant/stable interaction motifs from the crystalline structures of 3-Cl-nido-7,8,9,11-P₂C₂B₇H₈ (1), 3-I-nido-7,8,9,11-As₂C₂B₇H₈ (2), and nido-7,8,9,11-Sb₂C₂B₇H₉ (3). Distances are in Å. The color coding as follows: pink – B; black – C; orange – P; green – Cl; white – H; cyan – As; purple – I; magenta – Sb. Positions of H atoms were optimized at the DFT-D3/BLYP/DZVP level.¹¹

Table 3 Interaction energies (ΔE) in kcal mol⁻¹

	Interaction	MP2.5/CCSD(T)
3-Cl-nido-7,8,9,11-P 2 C 2 B 7 H 8
A⋯B	2 × Pn-bonds	−5.93/−6.10
A⋯C	H- and HH-bonds	−4.19/−4.39
3-I-nido-7,8,9,11-As 2 C 2 B 7 H 8
A⋯B	2 × Pn-bonds	−5.98
A⋯C	2 × Pn-bonds	−5.67
D⋯E	Pn- and HH-bonds	−4.52
A⋯D	HH-bond	−3.52
A⋯F	Stacking	−2.66
nido-7,8,9,11-Sb 2 C 2 B 7 H 9
A⋯B	2 × Pn-bond, HH-bond	−6.80/−7.05
A⋯C	Single Pn-bond	−6.22/−6.46
A⋯D	HH-bond, Pn-bond	−4.79
A⋯E	Stacking	−4.10

---

The crystal packing of 2 is also dominated by Pn-bonding, as the binding motifs with most negative ΔE values are stabilized by Pn-bonding. The A⋯B motif of 2 is stabilized by two symmetrical As₂⋯H–B Pn-bonds and has ΔE of −6.0 kcal mol⁻¹. An estimated ΔE of this isolated Pn-bond would thus be about −3 kcal mol⁻¹. The A⋯C motif of 2 has a comparable ΔE of −5.7 kcal mol⁻¹ and is stabilized by As⋯H–B and As⋯I–B Pn-bonds. The other motifs have less negative ΔE values. Among them, the most negative is the D⋯E motif with two As⋯H–B Pn-bonds and ΔE of −4.5 kcal mol⁻¹.

The crystal structure of 3 has two binding motifs with ΔE exceeding −6 kcal mol⁻¹. The A⋯B motif has ΔE of −7.1 kcal mol⁻¹ and is stabilized by multiple interactions, specifically by two Sb⋯H–B Pn-bonds and one C–H⋯H–B HH-bond. On the other side, the A⋯C motif is exclusively formed by a single interaction, namely a Sb₂⋯H–B Pn-bond. ΔE of −6.5 kcal mol⁻¹ computed for this binding motif can thus be considered as ΔE of the isolated Pn-bond. This is a very large value, exceeding ΔE of isolated Pn-bonding of 2 by about 100%. The Pn-bonding of 3 is even slightly more favorable than Pn-bonding in Cl₃Sb⋯N(Me)₃ and Cl₃Sb⋯benzene complexes (ΔE of −5.8 and −6.1 kcal mol⁻¹, respectively).¹⁵

Methods

Synthesis

A solution of arachno-4,6-C₂B₇H₁₃ (0.226 g, 2 mmol, see also Fig. 5) in dichloromethane (20 mL) was treated with proton-sponge (1.5 g, 7 mmol). SbCl₃ (2.0 g, 16 mmol) was added under stirring and cooling to 0 °C. Stirring was continued at room temperature for 4 h and the mixture was then cooled to 0 °C and decomposed by the dropwise addition of water (20 mL). Column chromatography was carried out on a silica gel as the stationary phase (3 g). The solids were mounted onto a silica gel column and the column was eluted with dichloromethane. The chromatography led to the separation of a major yellow fraction of R_f = 0.73 (CH₂Cl₂), which was evaporated to dryness. 0.255 g of yellowish nido-7,8,9,11-Sb₂C₂B₇H₉ was obtained (yield 36%, with respect to the starting material 4,6-C₂B₇H₁₃).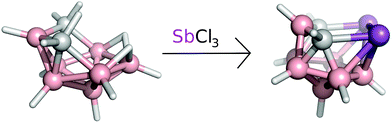

Fig. 5 The reaction scheme of arachno-4,6-C₂B₇H₁₃ with SbCl₃ yielding the nido-7,8,9,11-Sb₂C₂B₇H₉, compound.

Computational modeling

Magnetic shielding was calculated using the GIAO-MP2 method incorporated into Gaussian09¹⁶ utilizing the IGLO-II basis with the MP2/cc-pVTZ geometry (with the TZVP basis set on Sb by Weigend¹⁷ with ECP by Metz¹⁸) and frozen core electrons. Electrostatic potentials were computed at the HF/cc-pVDZ level (for I basis set in ref. 19) using Gaussian09 and Molekel4.3²⁰ programs. It has recently been shown that this basis set size is sufficient for these purposes.²¹

Interaction energy (ΔE) values were calculated for all pairwise interactions of the crystal structures of 1, 2 and 3. All hydrogen atoms were optimized using the DFT-D3/BLYP/DZVP method prior to the energy calculations.¹¹ ΔE for the central molecule with each surrounding molecule was evaluated at MP2.5/CBS using the Turbomole 6.6²² and Cuby4²³ programs. MP2.5/CBS was calculated as the sum of MP2/CBS energy and MP2.5 correction. MP2/CBS was approximated by RI-MP2-F12/cc-pVTZ-F12 for 1.²⁴ In the case of 2 and 3, we used MP2 extrapolation to the CBS from cc-pVTZ to cc-pVQZ (for I and Sb atoms cc-pVTZ-PP and cc-pVQZ-PP pseudopotentials were used).²⁵ The MP2.5 correction term was calculated using the aug-cc-pVDZ basis set. MP2.5/CBS interaction energies were compared to benchmark CCSD(T)/CBS for the interaction motifs of 1 and the most favourable motifs of 3. The CCSD(T) correction term was also determined using the aug-cc-pVDZ basis sets. Counterpoise corrections for basis set superposition error (BSSE) are used for all energy calculations.

Crystallography

Full sets of diffraction data for 3 were collected at 150(2) K using a Bruker D8-Venture diffractometer equipped with a Mo (Mo/K_α radiation; λ = 0.71073 Å) microfocus X-ray (IμS) source, a Photon CMOS detector and an Oxford Cryosystems cooling device.

The frames were integrated using the Bruker SAINT software package using a narrow-frame algorithm. Data were corrected for absorption effects using the Multi-Scan method (SADABS). Data were treated by using XT-version 2014/5 and SHELXL-2014/7 software implemented in an APEX3 v2016.5-0 (Bruker AXS) system.²⁶ Hydrogen atoms were mostly localized on a difference Fourier map; however, to ensure uniformity of treatment of the crystal, all hydrogen atoms were recalculated into idealized positions (riding model) and assigned temperature factors H_iso(H) = 1.2U_eq (pivot atom). H atoms in were placed with C–H distances of 1.1 Å for B–H and C–H bonds in the carborane cage. Hydrogen atoms in the upper rim of the cage were placed according to the appropriate maxima found on the Fourier difference electron density map.

R _int = ∑|F_o² – F_o,mean²|/∑F_o², S = [∑(w(F_o² – F_c²)²)/(N_diffrs – N_params)]^1/2 for all data, R(F) = ∑||F_o| – |F_c||/∑|F_o| for observed data, wR(F²) = [∑(w(F_o² – F_c²)²)/(∑w(F_o²)²)]^1/2 for all data.

Crystallographic data for structural analysis have been deposited with the Cambridge Crystallographic Data Centre, CCDC no. 1553208 for 3.†

Crystallographic data and structural refinement parameters for colorless single crystals of 3: C₂H₉B₇Sb₂, M = 352.26 g mol⁻¹, orthorhombic, Pna2₁, a = 20.4799(12), b = 6.6471(4), c = 6.5803(4) Å, β = 90°, Z = 4, V = 895.79(9) ų, D_c = 2.612 g cm⁻³, μ = 5.946 mm⁻¹, T_min/T_max = 0.583/0.745; −27 ≤ h ≤ 27, −8 ≤ k ≤ 8, −8 ≤ l ≤ 8; 19 233 reflections measured (θ_max = 28.35°), 2223 independent (R_int = 0.1199), 1796 with I > 2σ(I), 106 parameters, S = 1.049, R₁ (obs. data) = 0.0271, wR₂ (all data) = 0.0398; max., min. residual electron density = 1.091, −1.107 e Å⁻³.

Conclusions

To sum up, in compound 3 (nido-7,8,9,11-Sb₂C₂B₇H₉) we have synthesized and crystallized the very first reported cluster containing simultaneously Sb–B, Sb–C and Sb–Sb covalent bonds. In addition to that, the distance between two Sb atoms in the open pentagonal belt of 3 is less than the sum of Sb covalent radii. Further quantum chemical analysis revealed that the most stable crystal motifs in the crystal structure of 3 were directed by Pn-bonding. ΔE of a very strong Sb₂⋯H–B Pn-bond would exceed −6.0 kcal mol⁻¹. For comparison, the Pn-bonding in 3 is more favorable than the reported Pn-bonding in Cl₃Pn⋯N(Me)₃ and is comparable to the Pn-bonding in Cl₃Pn⋯π complexes (Pn = As, Sb). Phosphorus and arsenic can occupy the same positions as Sb in 3. However, in contrast to 3, crystallization of the parent nido-7,8,9,11-Pn₂C₂B₇H₈ (Pn = P, As) has not been possible. Indeed, crystal packing of halogenated 3-X-nido-7,8,9,11-Pn₂C₂B₇H₈ (X = Cl or I; Pn = P, As) derivatives is also dominated by Pn-bonding. We believe that Pn-bonding of nido-7,8,9,11-Pn₂C₂B₇H₉-type compounds offers a tantalizing possibility to further examine the Pn-bonding in a very detailed manner.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the research project RVO 61388963 of the Czech Academy of Sciences. We acknowledge the financial support of the Czech Science Foundation (17-08045S).

References

1. (a) W. N. Lipscomb, Boron Hydrides, Benjamin, New York, 1963; (b) D. Hnyk and D. A. Wann, Challenges and Advances in Computational Chemistry and Physics, in Boron – the Fifth Element, ed. D. Hnyk and M. McKee, Springer, Heidelberg, New York, Dordrecht and London, 2015, ch. 2, vol. 20.
2. K. Wade, Nat. Chem., 2009, 1, 92.
3. (a) J. L. Little, Inorg. Chem., 1979, 18, 1598; (b) L. J. Todd, A. R. Burke, A. R. Garber, H. T. Silverstein and B. N. Storhoff, Inorg. Chem., 1970, 9, 2175 . Note that HOMO of (Me₂PPh)₂Pd⁽²⁺⁾ and SLUMO (the second lowest unoccupied orbital) of the B₉H₉Sb₂⁽²⁻⁾ accounts for the stabilization.
4. S. A. Jasper Jr., S. Roach, J. N. Stipp, J. C. Huffman and L. J. Todd, Inorg. Chem., 1993, 32, 3072.
5. R. N. Grimes, Angew. Chem., Int. Ed., 2003, 42, 1198 . The interaction of the suitable symmetrical d orbitals of a metal with HOMO of the borane-cluster fragment is a driving force for the origination of the metallacarbaboranes.
6. J. Holub, T. Jelínek, D. Hnyk, Z. Plzák, I. Císařová, M. Bakardjiev and B. Štíbr, Chem. – Eur. J., 2001, 7, 1546.
7. L. Mikulášek, B. Grüner, I. Císařová and B. Štíbr, Dalton Trans., 2003, 7, 1332.
8. (a) W. Wang, W. Wang and W. J. Jin, Chem. Rev., 2016, 116, 5072; (b) A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496.
9. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291.
10. (a) J. Fanfrlík, A. Přáda, Z. Padělková, A. Pecina, J. Macháček, M. Lepšík, J. Holub, A. Růžička, D. Hnyk and P. Hobza, Angew. Chem., Int. Ed., 2014, 53, 10139; (b) J. Fanfrlík and D. Hnyk, CrystEngComm, 2016, 18, 8973.
11. J. Fanfrlík, J. Holub, Z. Růžičková, J. Řezáč, P. D. Lane, D. A. Wann, D. Hnyk, A. Růžička and P. Hobza, ChemPhysChem, 2016, 17, 3373.
12. D. Hnyk, E. Vajda, M. Bühl and P. v. R. Schleyer, Inorg. Chem., 1992, 31, 2464 . For the mechanism of the antipodal effect, see. D. Hnyk, D. A. Wann, J. Holub, S. Samdal and D. W. H. Rankin, Dalton Trans., 2011, 40, 5734.
13. P. v. R. Schleyer, Ch. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317.
14. (a) P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186; (b) W. Lu, H. Hu, Y. Li, R. Ganguly and R. Kinjo, J. Am. Chem. Soc., 2016, 138, 6650; (c) C. R. Wade, M. R. Saber and F. P. Gabbai, Heteroat. Chem., 2011, 22, 500.
15. A. Bauza, D. Quinonero, P. M. Deya and A. Frontera, CrystEngComm, 2013, 15, 3137.
16. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
17. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
18. In-Sb(ecp-28): B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563.
19. A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431.
20. (a) P. Flükiger, H. P. Lüthi, S. Portmann and J. Weber, MOLEKEL 4.3, Swiss Center for Scientific Computing, Manno, Switzerland, 2000; (b) S. Portmann and H. P. Lüthi, MOLEKEL: CHIMIA, 2007, vol. 28, p. 555.
21. K. E. Riley, K.-A. Tran, P. Lane, J. S. Murray and P. Politzer, J. Comput. Sci., 2016, 17, 273.
22. R. Ahlrichs, et al., TURBOMOLE V6.2 2010, a development of the University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from http://www.turbomole.com, Turbomole V6, Karlsruhe, Deutschland, 2008.
23. J. Řezáč, J. Comput. Chem., 2016, 37, 1230.
24. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102.
25. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243.
26. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2015, 71, 3.

---

Footnote

† CCDC 1553208. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt02845h

---