Hierarchical and chemical space partitioning in new intermetallic borides MNi₂₁B₂₀ (M = In, Sn)

Abstract

The compounds MNi₂₁B₂₀ (M = In, Sn) have been synthesized and their cubic crystal structure determined (space group Pm3̄m, lattice parameters a = 7.1730(1) Å and a = 7.1834(1) Å, respectively). The structure can be described as a hierarchical partitioning of space based on a reo-e net formed by Ni3 species with large cubical, cuboctahedral and rhombicuboctahedral voids being filled according to [Ni1@Ni3₈], [M@Ni3₁₂], and [Ni2₆@B₂₀@Ni3₂₄], respectively. The [Ni₆@B₂₀] motif inside the rhombicuboctahedral voids features an empty [Ni₆] octahedron surrounded by a [B₂₀] cage recently described in E₂Ni₂₁B₂₀ (E = Zn, Ga). Position-space bonding analysis using ELI-D and QTAIM space partitioning as well as 2- and 3-center delocalization indices gives strong support to an alternative chemical description of space partitioning based on face-condensed [B@Ni₆] trigonal prisms as basic building blocks. The shortest B–B contacts display locally nested 3-center B–B–Ni bonding inside each trigonal prism. This clearly rules out the notion of [Ni₆@B₂₀] clusters and leads to the arrangement of 20 face-condensed [B@Ni2₃Ni3₃] trigonal prisms resulting in a triple-shell like situation Ni2₆@B₂₀@Ni3₂₄(reo-e), where the shells display comparable intra- and inter-shell bonding. Both compounds are Pauli paramagnets displaying metallic conductivity.

---

Introduction

Metal-borides feature a perplexing variety of crystal structures. Numerous and systematic studies suggest that saturation of the valence requirements of the electron-deficient boron constituent is the actual driving force of this complexity.^1–3 In borides, the complexity of boron-based structural units often depends on metal-to-boron ratios, resulting in formation of one-, two-, and three-dimensional arrangements of covalently bonded boron atoms.^1,3–10 Boron-rich materials mostly exhibit a three-dimensional boron partial structure formed by interlinked boron clusters.^3,11,12 Two-dimensional boron networks in turn can be often observed at intermediate metal-to-boron ratios between 3/2 and 2,^3,13,14 whereas, with decreasing boron content, separated chains or rings and, further, isolated boron atoms prevail.^15–19

Therefore, studying the phase diagram at intermediate compositions enables one to follow the structural evolution of and bonding interactions between boron aggregates and metal framework observed in complex intermetallic compounds. The recently discovered compounds MNi₉B₈ (M = Al, Ga)²⁰ represent this structural complexity in an instructive way. There, networks composed of puckered [B₁₆] rings embed arrays of interlinked [M@Ni₁₂] clusters. This extremely unusual crystal structure prompted us to search for isotypic compounds comprising In or Sn as minority elements. However, neither Sn nor In was found to center [Ni₁₂] clusters embedded into 2D boron networks, instead, new compounds MNi₂₁B₂₀ (M = In, Sn) formed. They feature M-filled [Ni₁₂] cuboctahedra and [B₂₀] cages embedded in a Ni atom matrix in such a way that [Ni₆@B₂₀] motifs can be recognized. Arrays formed of [Ni₆@B₂₀] have been recently observed in the crystal structures of Ga₂Ni₂₁B₂₀ ²¹ and Zn₂Ni₂₁B₂₀.²²

In this study, we report on the synthesis, crystal structure, chemical bonding and physical properties of MNi₂₁B₂₀ (M = In, Sn) and place these compounds into context with structurally related metal-rich borides Zn₂Ni₂₁B₂₀ and Cr₂₃C₆ derivatives.

Experimental section

Sample preparation

Powders of tin (Chempur, <100 μm, 99.9 mass%), indium (Alfa Aesar, −325 mesh, 99.99 mass%), nickel (Chempur, −100 mesh, 99.99 mass%) and crystalline boron (Chempur, <100 μm, 99.9 mass%) were used to prepare the SnNi₂₁B₂₀ and InNi₂₁B₂₀ samples via two-step solid state reactions. Mixtures of nickel and boron with a ratio nearly 1 : 1 were pressed into pellets, placed into Al₂O₃ crucibles, sealed in tantalum tubes, and finally enclosed in quartz ampoules. The ampoules were heated to 910 °C, and kept for 7 days. Subsequently, the as-sintered pellets were ground to fine powders (<20 μm), mixed with tin or indium powders with Sn (or In) : Ni ratio 1 : 21. These mixtures were pressed into pellets, heated to 980 °C (for SnNi₂₁B₂₀) or 950 °C (for InNi₂₁B₂₀), and kept for 7 days. Sample handling operations were carried out in argon-filled glove boxes (MBraun, p(O₂/H₂O) ≤ 1 ppm). All resulting samples are stable in air for long time.

X-ray diffraction

Powder X-ray diffraction (XRD) patterns were recorded on a Huber G670 imaging plate Guinier camera using a curved germanium (111) monochromator and Cu K_α1 radiation (λ = 1.540598 Å). Phase analysis and indexing were done using WinXPow program package.²³ Lattice parameters were refined by least-squares fitting with LaB₆ [a = 4.15689(8) Å] as internal standard within the WinCSD program package.²⁴

Single crystal XRD data for SnNi₂₁B₂₀ were collected on a Rigaku AFC 7 diffraction system equipped with a Saturn 724+ CCD using Mo K_α radiation (λ = 0.71073 Å). A multi-scan procedure was used for absorption corrections.

Since for both compounds, SnNi₂₁B₂₀ and InNi₂₁B₂₀, no single crystals of sufficient quality could be obtained, fine powders of both samples with particle size <20 μm were filled and sealed in quartz capillaries (ϕ = 0.5 mm) for high-resolution synchrotron powder XRD experiments. The data were collected at the high-resolution beamline ID22 of the European Synchrotron Radiation Facility (ESRF) in Grenoble, equipped with a multianalyzer stage with nine detectors and Si (111) monochromator (λ = 0.40073 Å, scan step of 0.002°, 1° ≤ 2θ ≤ 40°). Low temperature data were also collected at 100 K and 80 K for SnNi₂₁B₂₀ and InNi₂₁B₂₀, respectively.

For the crystal structure solutions and refinements a direct phase determination method and a full-pattern fitting (powder data) or full-matrix least-square (single-crystal data) procedures were used within WinCSD program package, respectively.²⁴

Metallography

Small pieces were embedded in a conductive resin and then submitted to multistep grinding and polishing processes with final polishing using 0.25 μm diamond powder. The microstructure was investigated on a light-optical microscope (Axioplan2, Zeiss) as well as a field emission scanning electron microscope (JSM-7800F, JEOL). The composition of the observed phase was analyzed by energy dispersive X-ray spectroscopy (EDXS, Quantax 400 EDSX system, Silicon drift detector, Bruker) and wavelength dispersive X-ray spectroscopy (WDXS, SX100, Cameca) using B K_α, Ni K_α, Sn L_α, and In L_α signals and Ni₃B, Sn and InP as standards. The Sn : Ni and In : Ni atomic ratios of the target phases from EDXS were measured to be 1.00(2) : 21.07(2), and 1.00(2) : 21.12(2), respectively. Their compositions from WDXS were measured to be Sn_3.3(1)Ni_51.9(9)B_44.8(9), In_2.6(1)Ni_52.6(9)B_44.8(9), respectively. All values are very close to the ones obtained from crystal structure determination.

Transmission electron microscopy (TEM). Electron diffraction and STEM observations for SnNi₂₁B₂₀ were carried out on a field-emission FEI Tecnai G2 F20 at 200 kV and an aberration-corrected FEI Titan, respectively. Z-Contrast HAADF imaging was performed with a probe convergence angle of 30 mrad and an inner collection angle of 60 mrad. HAADF image simulation was carried out within the QSTEM software package.²⁵

Electronic structure calculations. The electronic structure for SnNi₂₁B₂₀ was investigated on the basis of a full structure optimization carried out with the program FHIaims²⁶ using both the DFT/LDA and the DFT/PBE functional²⁷ and the high-quality basis set (protocol “very tight”), and a 16³k-point mesh. The DFT/PBE method was found to better reproduce the experimental structure. Consequently, the subsequent investigations were performed with this method. For the detailed analysis of chemical bonding the wave-function was calculated with the full-potential APW+lo+LO method implemented in the ELK code.²⁸ On the basis of the wave-function given by ELK, position-space chemical bonding analysis was performed with the program DGrid.²⁹ It invoked topological analysis of the electron density (QTAIM approach³⁰) and the electron localizability indicator (ELI-D).^31–33 For this purpose both scalar fields were calculated for one unit cell on an equidistant grid with about 0.05 bohr mesh size using a 6³k-mesh, rgkmax = 9.0, lmaxapw = 10, and gmaxvr = 18.²⁵ While the QTAIM method yields spatial atomic regions defining the topological atoms,³⁰ topological analysis of ELI-D yields topological definitions of atomic core, bond and lone pair regions. The combination of both exhaustive space partitionings in the ELI-D/QTAIM basin intersection method (similar to ref. 34) yields a topological decomposition of the bond and lone pair regions in terms of the QTAIM atoms. This enables a discussion of bond polarity^34,35 and of multi-center bonding³⁶ on a topological basis.

Furthermore, the 2-center delocalization indices (DIs) between QTAIM atoms, a position-space variant of an effective covalent bond order, were calculated according to ref. 37 and 38. For the computationally demanding calculation of the delocalization indices a reduced k-point mesh of size 2³ had to be used. Extension of this approach to multi-center bonding indices is well known.³⁹ Along this line, 3-center bonding indices were calculated and analyzed with the program DISij⁴⁰ using the previously proposed bond delocalization ratios G⁴¹ as an additional classification tool. Values of G(A,B) for bond A–B are obtained from the ratio between 3-center delocalization and 2-center localization of the bond charge A–B. A value of G(A, B) = 0 indicates a perfect 2-center localization of the bond between atoms A and B, while G(A, B) ≥ 1 indicates the absence of 2-center bonding, where the value of the 2c-DI in the range 0 ≪ δ(A, B) < 1 then only represents a down-sampled value of all the higher-center bond indices. As a rough guide, values 0 ≤ G(A, B) < 0.5 indicate a dominating 2-center bonding scenario, 0.5 < G(A, B) ≤ 1 a dominating three-center bonding scenario. Exemplarily, bond G values of 0.2 and 0.3 are obtained for the diamond structures of C and Ge, respectively, contrasting with G(B, B′) = 1 for the endohedral bonds in closo-B₆H₆²⁻ and CaB₆.³⁸

Physical properties. Temperature-dependent magnetization data of polycrystalline MNi₂₁B₂₀ were measured in a SQUID magnetometer (MPMS XL-7, Quantum Design) in external fields μ₀H from 2 mT to 7 T in the temperature range of 1.8–350 K. The electrical resistivity measurements were performed using a four-point AC method between 1.8 and 320 K on a commercial PPMS system (Quantum Design). Heat capacity was measured by means of a relaxation-type calorimeter on PPMS in the temperature range 1.8–320 K.

Results and discussion

Crystal structure determination

All reflections in the powder synchrotron X-ray diffraction patterns of SnNi₂₁B₂₀ and InNi₂₁B₂₀ samples at 293 K (Fig. 1a and b) were indexed in simple cubic unit cells with lattice parameters a = 7.1834(1) Å and a = 7.1730(1) Å, respectively. Details on crystal data collection are listed in Table 1. Analysis of the extinction conditions indicated possible space groups (SG) P23, Pm3̄, P432, P4̄3m, and Pm3̄m. The SG with highest symmetry Pm3̄m was chosen to determine the crystal structures. The direct phase determination method was used to acquire positions of heavy Sn and Ni or In and Ni atoms, while positions of B were found from difference maps of electron density. Low residuals (R_I = 0.053, R_P = 0.088 and R_I = 0.062, R_P = 0.099 for SnNi₂₁B₂₀ and InNi₂₁B₂₀, respectively) indicate the reliability of the obtained structures.

Fig. 1 Synchrotron powder X-ray diffraction patterns (black dots) of SnNi₂₁B₂₀ (a) and InNi₂₁B₂₀ (b) at 293 K with the calculated profiles (red lines) after full-profile Rietveld refinements.

Table 1 Crystallographic data for SnNi₂₁B₂₀ and InNi₂₁B₂₀ at 293 K from synchrotron diffraction

Composition	SnNi21B20	InNi21B20
Space group	Pm3̄m
a (Å)	7.1834(1)	7.1730(1)
V (Å^3)	370.67(2)	369.06(2)
Calculated density/(g cm^−3)	7.023	7.036
Z	1
λ (Å)	0.40073
2θ range (°)	1 to 40
T/K	293
μ/mm^−1	8.571	8.399
Reflns in measured range	243	240
Refined parameters	15
Refinement method	Full-profile Rietveld
R I; Rp	0.053; 0.088	0.062; 0.099

---

In both crystal structures, [Ni₆] octahedra formed by Ni2 atoms are empty, and distances from their centers to Ni2 are 1.922 Å and 1.931 Å in SnNi₂₁B₂₀ and InNi₂₁B₂₀, respectively. Since B–Ni distances may be similarly short (cf. 1.967 Å in Ni₃B ⁴²) occupation of the octahedra by B is possible. In order to study such a scenario and reduce the thermal vibrations of the B atoms, low temperature synchrotron powder XRD data were collected at 100 K and 80 K, respectively, for SnNi₂₁B₂₀ and InNi₂₁B_20. Details on diffraction data collection are listed in Table S2 in the ESI.‡ However, when additional B atoms were placed at this position, the displacement parameters of B atoms became quite large, indicating that this position should remain unoccupied. This was undoubtedly confirmed by the refinement of the occupation parameter for this position. Final atomic coordinates and anisotropic atomic displacement parameters for the two compounds at 293 K are listed in Table 2, and interatomic distances are listed in Table S1 in the ESI.‡ Corresponding atomic coordinates and anisotropic atomic displacement parameters at 100 K and 80 K are listed in Table S3 in the ESI.‡

Table 2 Atomic coordinates, isotropic and anisotropic displacement parameters (in Ų) for SnNi₂₁B₂₀ and InNi₂₁B₂₀ at 293 K from synchrotron diffraction data

Atom	Site	x	y	z	B iso/Beq	B 11	B 22	B 33	B 12	B 13	B 23
SnNi21B20
Sn	1a	0	0	0	1.67(2)	1.67(4)	B 11	B 11	0	0	0
Ni1	3d	0	0	1/2	1.17(4)	0.93(5)	B 11	1.65(8)	0	0	0
Ni2	6f	1/2	0.2324(2)	1/2	1.10(3)	0.93(3)	1.44(6)	B 11	0	0	0
Ni3	12i	0.28891(7)	x	0	1.23(2)	1.36(2)	B 11	0.98(5)	0.30(3)	0	0
B1	8g	0.2911(6)	x	x	1.0(2)
B2	12j	1/2	0.2007(6)	y	1.00(9)
InNi21B20
In	1a	0	0	0	1.40(2)	1.40(3)	B 11	B 11	0	0	0
Ni1	3d	0	0	1/2	0.97(3)	0.87(4)	B 11	1.16(7)	0	0	0
Ni2	6f	1/2	0.2308(2)	1/2	0.91(2)	0.84(3)	1.05(5)	B 11	0	0	0
Ni3	12i	0.28764(6)	x	0	1.01(2)	1.19(2)	B 11	0.64(4)	0.22(3)	0	0
B1	8g	0.2921(6)	x	x	1.1(2)
B2	12j	1/2	0.1992(5)	y	0.76(7)

---

Despite many efforts, a very small single crystal of moderate quality could be found only for SnNi₂₁B₂₀ for single crystal XRD experiment, while no single crystals could be obtained for InNi₂₁B₂₀. Details on XRD data collection for SnNi₂₁B₂₀ are listed in Table S4 in the ESI.‡ The refined structural model is in good agreement with that obtained from the synchrotron powder XRD data. Final atomic coordinates and anisotropic atomic displacement parameters are listed in Table S5 in the ESI.‡ The single crystal XRD data also unambiguously confirm that the centers of the [Ni₆] octahedra remain empty.

The SnNi₂₁B₂₀ sample was also investigated by (S)TEM. The electron diffraction patterns along relevant zone axes are shown in Fig. 2a. All patterns can be well indexed in a single cubic lattice with the lattice parameters obtained from powder XRD diffraction. In agreement with the results from the powder XRD and single crystal diffraction data, no extinction conditions were observed. The atomic arrangement in the MNi₂₁B₂₀ structure determined from synchrotron diffraction (as shown in Fig. 3–5) is confirmed by HAADF images. HAADF images for SnNi₂₁B₂₀ along [001] and [011] zone axes are shown in the left and right of Fig. 2b, respectively, which is consistent with the simulated images using the structure model solved from synchrotron diffraction data. Moreover, the HAADF images along these two directions also reveal no superstructure formations and defects in SnNi₂₁B₂₀.

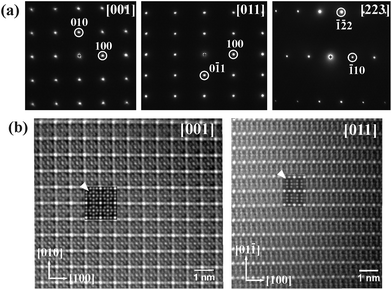Fig. 2 (a) Electron diffraction patterns for SnNi₂₁B₂₀; (b) HAADF images of SnNi₂₁B₂₀ along [001] (left) and [011] (right); the two insets marked with arrows are the simulated images.

Fig. 3 (a) Nickel (small spheres) and tin (large spheres) substructures in high-pressure cubic modification of Ni₃Sn, (b) reo-e framework formed by Ni3 (small white spheres) in MNi₂₁B₂₀ highlighting Sn-centered cuboctahedra (Sn: large white spheres), distorted cubes centered by Ni1 (small turquoise spheres), and the rhombicuboctahedron (outlined by blue lines) with empty octahedron formed by Ni2 (small red spheres) inside.

Fig. 4 Embedding of the [B₂₀] cluster (outlined by bold black lines connecting B atoms visualized as black spheres) in the metal polyhedral framework of (a) MNi₂₁B₂₀ (M = In, Sn) and (b) M₂Ni₂₁B₂₀ (M = Ga, Zn).

Fig. 5 (a) The Ni3₂₄ rhombicuboctadron (blue lines) embedding the [Ni2₆@B₂₀] structural unit: [Ni2₆@B₂₀@Ni3₂₄]; Ni2 – red spheres, Ni3 – grey spheres, B – black spheres. (b) Exhaustion of the rhombicuboctahedron by triangular prims [B2@Ni2₂Ni3₄] which are additionally capped by Ni1 atoms (white spheres). (c) The prisms [B1@Ni2₃Ni3₃] generate the faces of the empty (□@Ni2₆) octahedron at the core of the crystal structure.

Crystal structure discussion. The framework of the structure can be formally described by a hierarchical space partitioning based on the Ni3 atomic species occupying Wyckoff position 12i (x x 0) in SG Pm3̄m. For the ideal case of x = (2 + √2)⁻¹ ≈ 0.2929 the resulting network represents one of 28 possible uniform partitions of 3-dimensional space, which is based on purely mathematical work dating back to Andreini in 1907⁴³ and subsequently completed and extended.^44–46 The network corresponds to number 9 of Grünbaum's original enumeration⁴⁵ and has been named “reo-e” in the Reticular Chemistry Structure Resource database.^47,48

The actual positions of Ni3 atoms with x = 0.28764(6) and 0.28891(7) for M = In, Sn, respectively, slightly deviate from the ideal value, but still lead to a Ni3 network exclusively consisting of interconnected cubes, cuboctahedra and rhombicuboctadra with certain deviations from their ideal Platonic or Archimedean shapes. These polyhedra represent the voids in the Ni3 network, that are found to be filled in a specific way in MNi₂₁B₂₀ (M = In, Sn). The distorted cubic voids are filled by Ni1 atoms according to Ni1@Ni3₈(reo-e). The [Ni1@Ni3₈] polyhedra interconnect filled [M@Ni3₁₂] cuboctahedra. The recently discovered mineral Nisnite⁴⁹ (Ni₃Sn) adopts a Cu₃Au-type of structure, which is constructed from the same [Sn@Ni₁₂] motif (Fig. 3a). This structural arrangement is known as the high pressure modification of Ni₃Sn, which adopts the hexagonal Mg₃Sn structure at ambient pressure,⁵⁰ and [M@Ni₁₂] cuboctahedra are also commonly observed in Cr₂₃C₆-type borides.^51,52 Moreover, in comparison to the In-containing compound, the Ni3–Ni3 distances in the cuboctahedron in the Sn-containing compound are longer, resulting in a spacious Sn-containing cage, consistent with an enlarged B_iso value of Sn (see Tables 2 and 3). The large rhombicuboctahedral voids are found to be filled by a [B₂₀] cage of 8 three-bonded B1 and 12 two-bonded B2 boron atoms surrounding a [Ni2₆] octahedron, which results in a triple-shell-like arrangement Ni1₆@B₂₀@Ni3₂₄(reo-e). The same [Ni₆B₂₀] structural motif has been identified only recently in the isotypic structures of Zn₂Ni₂₁B₂₀ ²² and Ga₂Ni₂₁B₂₀.²¹ Body-centered tetragonal Ga₂Ni₂₁B₂₀ derives from cubic MNi₂₁B₂₀ by a simple shift of the layers formed by the aforementioned rhombicuboctahedra (Fig. 4). However, while [Ni₆@B₂₀@Ni₂₄] rhombicuboctahedra and [Ni@Ni₈] cubes are retained, [M@Ni₁₂] cuboctahedra do not appear in Ga₂Ni₂₁B₂₀. Instead, a bicapped square antiprism [Ga@Ni₁₀] is formed for the coordination of the Ga atoms.

Table 3 Interatomic distances (Å) in polyhedra/or clusters in the structures of SnNi₂₁B₂₀ and InNi₂₁B₂₀

Polyhedra/or clusters		SnNi21B20	InNi21B20
[M@Ni312] cuboctahedron	M–Ni3	2.9350(4)	2.9179(4)
	Ni3–Ni3	2.9350(4)	2.9179(4)
[Ni26@B110B210@Ni324]	B1–B2	1.760(6)	1.764(5)
	Ni2–Ni2	2.719(2)	2.731(2)
	B1–Ni2	2.164(4)	2.154(5)
	B2–Ni2	2.162(5)	2.170(4)
	Ni3–Ni3	2.9350(5)	2.9179(4)
	Ni3–Ni3	3.0327(1)	3.0465(1)
[B1@Ni23Ni33]B23	Ni2–Ni3	2.7176(9)	2.7169(9)
[B2@Ni22Ni34]B12Ni1	B1–Ni3	2.091(4)	2.096(4)
	B2–Ni3	2.186(3)	2.183(3)
[Ni1@Ni38] cube	Ni3–Ni3	2.9350(7)	2.9179(6)
	Ni3–Ni3	3.0327(7)	3.0465(6)
	Ni1–Ni3	2.5703(3)	2.5646(3)
	Ni1–B2	2.039(4)	2.021(4)

---

A complementary view of the [Ni₆B₂₀] motif is obtained focusing on the boron structural chemistry in intermetallic borides with roughly equiatomic boron contents, where capped trigonal prismatic coordination of the boron atoms is frequently observed.^3,5,53 Indeed, the two boron species are found in tricapped trigonal prismatic coordination according to [B1@Ni2₃Ni3₃B2₃] and [B2@Ni2₂Ni3₄B1₂Ni1], where the specific arrangement of the face-condensation at the B1–B2 contacts yields the [Ni1₆@B₂₀@Ni3₂₄] motif described above (Fig. 5). This view automatically implies, that a separate [Ni₆B₂₀] unit does not occur, instead, the [Ni₆B₂₀] motif has to be extended by the outer Ni3 atoms forming the rhombicuboctahedral Ni3₂₄reo-e cage, which is supported by comparison of the relevant interatomic distances (Table 3 and ESI Table S1‡). Comparing B–Ni distances to the inner Ni2₆ octahedron, d(B1–Ni2) = d(B2–Ni2) = 2.16 Å, with those to the outer Ni3₂₄ cage atoms, d(B1–Ni3) = 2.09 Å, d(B2–Ni3) = 2.19 Å, reveals that they are rather similar. This supports the trigonal prismatic coordination assignment. Moreover, distances d(Ni2–Ni2) = 2.72 Å inside the Ni2₆ octahedron are comparable to distances between the inner Ni2 and the outer Ni3 shell, with d(Ni2–Ni3) = 2.72 Å. They are even slightly shorter than the distances d(Ni3–Ni3) = 2.94 Å within the Ni3 framework but longer than the shortest Ni–Ni distances d(Ni1–Ni3) = 2.57 Å. This clearly shows that the interconnecting Ni matrix is not just formed from Ni3 atoms, but includes all Ni atoms of the structure. The most conspicuous feature concerns the distance d(B1–B2) = 1.77 Å, which is rather long for a 2c–2e B–B bond and more comparable to those in deltahedral boron clusters with 3-center bonding although the homoatomic coordination number is only 2 or 3 for B2 and B1, respectively. However, elongated B–B distances are a common feature in intermetallic borides even if they do not display deltahedral boron clusters. This aspect is investigated in detail by analysis of atomic interactions.

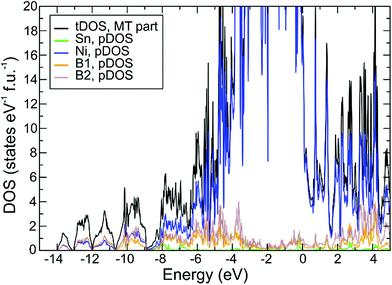
Electronic structure and chemical bonding

The optimized structure displays only small deviations from the experimental one, which points to a faithful representation of the electronic structure by the chosen DFT/PBE method. The calculated density of states DOS (ELK code, Fig. 6) displays a small pseudo gap close to the Fermi energy E_F (set to 0 eV), where DOS(E_F) = 22 states per eV per cell. Decomposition of the total DOS in terms of atomic muffin-tin contributions (pDOS) shows the dominating contributions of Ni 3d states in the region around E_F. Calculation of the center of gravity for each component pDOS yields an energetic sequence value of −6.8 eV and −6.5 eV for B1 and B2, respectively, which correlates with the corresponding number of homoatomic neighbors of each B species, namely 3 and 2. Similar to previous results²⁰ this is considered a hint on the homoatomic interaction being energetically dominating one for the B atoms. Application of this procedure to the Ni atoms’ pDOS yields center of gravity values of −2.3 eV, −2.5 eV, and −2.3 eV for Ni1, Ni2, Ni3, respectively. Given the optimized average distances Ni–B 2.03 Å, 2.16 Å, 2.15 Å (respective experimental values are 2.04 Å, 2.16 Å, and 2.15 Å) for each Ni species, respectively, a correlation of these with the Ni orbitals’ energetic center of gravity cannot be found, most probably because of the different numbers of boron neighbors (4, 8, 6) in each case.

Fig. 6 Electronic density of states (DOS, muffin-tin part) of SnNi₂₁B₂₀.

Position-space chemical bonding analysis yields QTAIM effective charges (Sn^0.51+)(Ni1^0.04−)(Ni2^0.28+)(Ni3^0.23+)(B1^0.31−) (B2^0.19−) which is consistent with the sequence of Allred-Rochow electronegativities 2.0 (B) > 1.8 (Ni) > 1.7 (Sn), although the differences are very small. The boron species display rather small negative effective charges, which look too small to represent a Zintl anion with clear homoatomic 2-center bonds. This issue is clarified in the following analysis employing the electron localizability indicator on the one hand and two- and three-center delocalization indices between QTAIM atoms on the other hand.

The ELI-D distribution (Fig. 7b) yields only three types of local maxima (attractors) in the valence region. For each B1–B2 contact (d(B1–B2)_exp. = 1.77 Å) an attractor lies very close to the internuclear line (light brown localization domains in Fig. 7b). The associated ELI-D basin for the B1–B2 bond attractor displays a population of 3.00 electrons. ELI-D/QTAIM basin intersection reveals that 1.08 and 0.97 e belong to QTAIM atoms B1 and B2, respectively, and the remaining 0.96 e are contributed by 4 neighboring nickel QTAIM atoms 2Ni2 + 2Ni3 (Fig. 7c) spanning the common rectangular face between both [B@Ni₆] trigonal prisms. With this bond basin's effective atomicity of 6 (2B + 4Ni) the situation can be interpreted as a B₂Ni₄ multicenter bonding scenario. Even deeper insight will be gained below from the analysis of 3-center DIs and bond G values. Each Ni2 atom being located in the center of the [B₈] ring takes part in 8 such bonds, each Ni3 atom in 4 such bonds.

Fig. 7 Crystal structure and ELI-D chemical bonding signatures in SnNi₂₁B₂₀: (a) relevant structural features; atomic positions are shown by spheres for Sn (white), Ni1 (dark green), Ni2 (red), Ni3 (green) and B (dark grey); bonds B1–B2 are indicated by yellow lines; trigonal prisms B@Ni₆ by blueish translucent faces; inner Ni2₆ octahedron by red edges, selected trigonal faces of Sn@Ni3₁₂ cuboctahedra related to Sn–Ni3 bonding in translucent grey; (b) ELI-D localization domains for bonds B1–B2 (type 1, light brown, Y_D = 1.30), Ni1–B2 (type 2, magenta, Y_D = 1.23), and Sn–Ni3 (type 3, grey, Y_D = 0.942); (c) ELI-D/QTAIM basin intersection for ELI-D bond basin B1–B2 (type 1), intersected atoms of common prism face 2Ni2 + 2Ni3 are marked by “X”, spatial regions of bond basin belonging to boron, Ni2, Ni3 are colored in grey, light red, and light green, respectively; (d) ELI-D/QTAIM basin intersection of bond basin Ni1–B2 (type 2); intersecting Ni3 + 4Ni1 atoms marked with “X”, spatial regions parts attributed to QTAIM B, Ni1, and Ni3 atoms, are colored in light grey, green and light green, respectively.

The second type of ELI-D attractor is found on the internuclear line B2–Ni1 with d(B2–Ni1)_exp. = 2.16 Å (Fig. 7b, magenta-colored localization domains). The associated ELI-D basin displays a population of 2.50 electrons, which can be decomposed into 1.17 e from B2, 1.32 e from 1 Ni1 (0.59 e) and 4 × 0.18 e from 4 Ni3 atoms. With an effective atomicity of 6 (1 B + 5 Ni) this basin describes a BNi₅ multicenter bonding scenario (Fig. 7d). Each Nil atom takes only part in 4 B2–Ni1 bonds, while each Ni3 atom takes part in 4 B2–Ni1 bonds and 4 B1–B2 bonds.

The third type of ELI-D attractor arises from Sn–Ni3 bonding (d(Sn–Ni3)_exp. = 2.94 Å). The endohedral Sn atoms display a nearly spherical ELI-D distribution with a comparably low value of the structuring index³² of ε ≈ 0.01 for this basin set, which characterizes weak bonding but with a large number of 12 partners. The 24 attractors occur in triangles pointing to the corresponding 3 Ni3 atoms of the 8 trigonal faces of the [Ni3₁₂] cuboctahedron (grey localization domains in Fig. 7b containing 3 attractors). Each of the associated 24 basins is populated by 0.24 electrons. ELI-D/QTAIM intersection reveals them to represent effectively (1 Sn + 1 Ni3)-diatomic polar bonds, with 0.14 e belonging to QTAIM Sn and 0.10 e to Ni3 atom. Each vertex Ni atom is connected to two such basins. All the basins around a Sn atom were merged into a superbasin containing 5.79 electrons, with 3.49 electrons contributed by the QTAIM Sn atom and 2.30 electrons coming from the neighboring 12 Ni3 atoms, i.e. 0.19 e from each.

The bonding situations B–B, B–Ni, and Sn–Ni described above are comparable to the ones discussed recently for GaNi₉B₈ with condensed endohedral clusters [Ga@Ni₁₂] nested with a polyanionic B network to yield multicenter B–B–Ni bonding.²⁰ As an extension to this previous study, the high local symmetry and the smaller unit cell size of SnNi₂₀B₂₁ permits a more detailed investigation of chemical bonding employing a complementary method. Analysis of 2c- and 3-center delocalization indices (DIs) between QTAIM atoms (QTAIM/DI analysis) complemented by bond G values yields direct information of the deviation of the bonding from the classical 2-center case.

The highest 2c-delocalization indices are found between boron atoms, where δ(B1, B2) = 0.53 with bond delocalization ratio G(B1, B2) = 0.84. The high G value indicates a high degree of 3c-bonding character, which is consistent with the clearly fractional effective covalent bond order of the B–B bond and the elongated bond distance d(B–B)_exp. = 1.77 Å (opt. 1.76 Å) observed also for the deltahedral bonds in hexaborides.⁴¹ Decomposition of G(B1, B2) into a sum of all three-center contributions reveals that four similar 3c-DIs of type δ(B1, B2, Ni) play the dominant role. The four Ni atoms involved are just those 2Ni2 and 2Ni3 atoms already identified above with the ELID/QTAIM basin intersection method. They form the surrounding rectangular face of the condensed [B@Ni₆] trigonal prisms (Fig. 5b and c). With their contributions to G(B1, B2) summing up to 71% of the total value they represent the main delocalization channel of the B1–B2 bond. Thus, the B1–B2 contact represents four nested 3-center bonds B–B–Ni. Boron species B1 features three, species B2 two of such contacts.

Ni–B bonding is characterized by nearest-neighbor DIs ranging from δ(Ni1, B) = 0.53 for the shortest (opt. 2.03 Å, exp. 2.04 Å) to δ(Ni2, B) = 0.31 for the longest distance (opt. 2.18 Å, exp. 2.16 Å). The corresponding G(Ni, B) values are found to increase with decreasing 2c-DIs from 0.42 to 0.64 as expected. This marks a gradual transition from a mainly two-center Ni–B bonding regime towards a three-center bonding Ni–B–B one, indicated by the dominating 3-center contributions δ(Ni, B1, B2) to G(Ni, B).

DIs(Ni, Ni) take values between δ(Ni1, Ni3) = 0.25 (opt. 2.58 Å, exp. 2.57 Å) and δ(Ni3, Ni3) = 0.11 (opt. 2.98 Å, exp. 2.94 Å) with remarkably clear 2c-character shown by G(Ni, Ni) ≈ 0.2. These values are roughly similar to the spin-averaged values obtained for fcc-Ni.⁵⁴

The view of a metallic Ni matrix nested with B₂₀ units to form multicenter B–B–Ni bonds is the resulting picture for the MNi₂₀B₂₁ compounds (M = Sn, In). The condensed trigonal prisms [B1@Ni2₃Ni3₃]B2₃ and [B2@Ni2₂Ni3₄]B1₂Ni1 with their three capping atoms are the real building blocks of this motif and a consideration of only [Ni2₆@B₂₀] would be incomplete.

According to the ELI-D/QTAIM intersection method, the endohedral Sn atoms form polar bonds Sn–Ni without evidence for dominating multicenter bonding. This is corroborated by the DI analysis, which yields δ(Sn, Ni) = 0.24 with G(Sn, Ni) = 0.41 being still in the 2-center regime. The sum over all 12 Sn–Ni DIs reveals that 2.9 bonds are effectively formed in total between Sn and the Ni cage atoms.

Physical properties. The molar magnetic susceptibility of SnNi₂₁B₂₀ and InNi₂₁B₂₀ in an external field of μ₀H = 7.0 T is shown in Fig. 8a, and Fig. S1a in the ESI,‡ respectively. Both compounds show Pauli-paramagnetic behavior (with extrapolated values of χ₀ given in Table S6‡) in contrary to the Curie–Weiss like magnetism observed for Zn₂Ni₂₁B₂₀ boride.⁵⁵

Fig. 8 Physical properties of SnNi₂₁B₂₀: (a) temperature-dependent magnetic susceptibility χ(T) in the external magnetic field of μ₀H = 7.0 T; (b) temperature dependence of electrical resistivity ρ(T); (c) temperature dependence of heat capacity c_p(T), the inset shows the fitting by c_p(T) = γT + βT³ + δT⁵ for 3.0 K < T < 10 K.

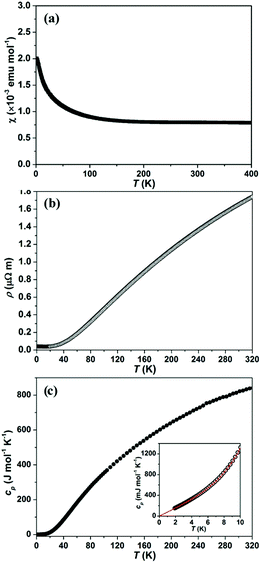
The electrical resistivity as a function of temperatureρ(T) of SnNi₂₁B₂₀ and InNi₂₁B₂₀ (Fig. 8b and Fig. S1b in the ESI‡) shows typical metallic characteristics in accordance with the electronic structure calculations (residual resistivity ρ₀ and the room temperature resistivity ρ(300 K) as well as calculated RRR values are summarized in Table S6‡.

Temperature-dependent heat capacity c_p(T) for SnNi₂₁B₂₀ and InNi₂₁B₂₀ are shown in Fig. 8c and Fig. S1c in the ESI,‡ respectively. Low-T c_p(T) (the insets to Fig. 8c and Fig. S1c in the ESI‡) can be fitted by the model c_p(T) = γT + βT³ + δT⁵, where γ is the Sommerfeld coefficient of the electronic heat capacity, βT³ + δT⁵ are the first terms of the harmonic lattice approximation for the phonon contribution. From the fits (3.0 K < T < 10 K for SnNi₂₁B₂₀ and 2.0 K < T < 10 K for InNi₂₁B₂₀, respectively) the parameters, γ, β and δ as well as the corresponding initial Debye temperatures Θ_D(0) have been evaluated and their values are compiled in Table S6.‡

Conclusions

New borides MNi₂₁B₂₀ (M = In, Sn) were synthesized and their crystal structures were solved from synchrotron powder X-ray diffraction data. The cubic crystal structure can be related to a uniform 3D tiling of space by cuboctahedra, cubes and rhombicuboctahedra, i.e. a filled reo-e net of Ni3 atoms, with unusual [Ni₆@B₂₀] units filling the [Ni₂₄] rhombicuboctahedra leading to [Ni₆@B₂₀@Ni₂₄] triple shell clusters, and M atoms centering the cuboctahedra [M@Ni₁₂]. The triple-shell-like aggregation is the result of the condensation pattern of the two types of boron centered tri-capped trigonal prisms [B@Ni₆X₃], where the capping X₃ features either B₃ or B₂Ni, leading to 3 and 2-bonded B species, respectively. Position-space chemical bonding analysis reveals these prisms to be the chemically relevant building blocks of the structures of MNi₂₁B₂₀ (M = In, Sn), a consideration of only the [Ni₆@B₂₀] part would neglect half of the relevant 3-center B–B–Ni bonds detected by the bonding analysis. Due to their spatial arrangement the [B1@Ni₆B2₃] prisms generate the faces of the empty [Ni₆] octahedron at the core, while the [B2@Ni₆B1₂Ni] prims fill the space in-between them hosting the capping B2 atoms of the [B1@Ni₆B2₃] prisms. This leads to the [B₂₀] units and completes the [Ni₂₄] rhombicuboctahedra on the outside of the clusters. The [M@Ni₁₂] atoms display polar covalent bonds M–Ni, with a small effective bond order leading in sum to a significant number of 2.9 covalent bonds formed between Sn and the Ni cage.

The electronic structure reveals them to be metals, which was corroborated by physical properties measurements indicating metallic conductivity as well as Pauli paramagnetism.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Mr S. Hückmann and Dr H. Borrmann for performing powder X-ray diffraction measurements, Ms P. Scheppan, Ms M. Eckert and Ms. S. Kostmann for the metallographic analysis, Mr R. Koban for assistance with physical property measurements, and Dr W. Schnelle for valuable discussions. We also acknowledge the ORNL's Center for Nanophase Materials Sciences (CNMS), which is sponsored by an Office of Science User Facility, the U.S. Department of Energy (DOE). Qiang Zheng would like to thank Miaofang Chi for her help. The authors thank Dr C. Curfs from ID22 (former beamline ID31) ESRF, Grenoble for assistance with synchrotron data collection. Open Access funding provided by the Max Planck Society.

References

1. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
2. T. Mori, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, J.-C. Bünzli and V. Pecharsky, North-Holland, Amsterdam, 2008, vol. 38, pp. 105–173.
3. P. Rogl, in Inorganic Reactions and Methods, ed. A. P. Hagen, Wiley, 1991,  DOI:10.1002/9780470145289.ch20.
4. T. Mori, in Handbook on the Physics and Chemistry of Rare-Earths, ed. K. A. Gschneidner, J. C. Bunzli and V. K. Pecharsky, Elsevier, Amsterdam, 2007, vol. 38, pp. 105–173.
5. Y. B. Kuz'ma, Crystallochemistry of Borides, Lviv University Publishers, Lviv, 1983.
6. H. Nowotny and P. Rogl, in Boron and Refractory Borides, ed. V. Matkovich, Springer, New York, 1977, ch. 23, pp. 413–438,  DOI:10.1007/978-3-642-66620-9_23.
7. Y. B. Kuz'ma and N. F. Chaban, Binary and Ternary Systems Containing Boron, Metallurgiya, Moscow, 1990.
8. T. Fehlner, J.-F. Halet and J.-Y. Saillard, Molecular clusters: a bridge to solid-state chemistry, Cambridge University Press, 2007.
9. T. Mori, Encyclopedia of Inorganic and Bioinorganic Chemistry, 2012.
10. G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506.
11. L. Pauling and S. Weinbaum, Z. Kristallogr. Kristallgeom. Kristallphys. Kristallchem., 1934, 87, 181–182.
12. P. Blum and F. Bertaut, Acta Crystallogr., 1954, 7, 81–86.
13. Y. B. Kuz'ma, Kristallografiya, 1970, 15, 372–374.
14. P. Rogl and H. Nowotny, Monatsh. Chem., 1974, 105, 1082–1098.
15. A. Westgren, Nature, 1933, 132, 480.
16. Q. Zheng, M. Kohout, R. Gumeniuk, N. Abramchuk, H. Borrmann, Y. Prots, U. Burkhardt, W. Schnelle, L. Akselrud, H. Gu, A. Leithe-Jasper and Y. Grin, Inorg. Chem., 2012, 51, 7472–7483.
17. C. Goerens and B. P. T. Fokwa, J. Solid State Chem., 2012, 192, 113–119.
18. B. P. T. Fokwa, J. von Appen and R. Dronskowski, Chem. Commun., 2006, 4419–4421,  10.1039/b608903h.
19. Q. Zheng, G. Roman, R. Helge, W. Schnelle, Y. Prots, U. Burkhardt, Y. Grin and A. Leithe-Jasper, J. Phys.: Condens. Matter, 2015, 27, 415701.
20. Q. Zheng, F. R. Wagner, A. Ormeci, Y. Prots, U. Burkhardt, M. Schmidt, W. Schnelle, Y. Grin and A. Leithe-Jasper, Chem. – Eur. J., 2015, 21, 16532–16540.
21. Q. Zheng, R. Gumeniuk, W. Schnelle, Y. Prots, U. Burkhardt and A. Leithe-Jasper, Solid State Sci., 2016, 55, 93–97.
22. Z. P. Malik, O. Sologub, A. Grytsiv, G. Giester and P. F. Rogl, Inorg. Chem., 2011, 50, 7669–7675.
23. WinXPow, STOE and Cie GmbH, Darmstadt, 2003.
24. L. Akselrud and Y. Grin, J. Appl. Crystallogr., 2014, 47, 803–805.
25. C. Koch, PhD, Arizona State University, 2002.
26. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. Program ELK, version 2.2.10, http://www.sourceforge.net.
29. M. Kohout, Program DGrid, version 4.7, Radebeul, Germany, 2015.
30. R. F. W. Bader, Atoms in Molecules, Oxford University Press, Oxford, 1990.
31. M. Kohout, Int. J. Quantum Chem., 2004, 97, 651–658.
32. F. R. Wagner, V. Bezugly, M. Kohout and Y. Grin, Chem. – Eur. J., 2007, 13, 5724–5741.
33. A. Martin-Pendas, M. Kohout, M. Blanco and E. Francisco, in Modern Charge-Density Analysis, ed. C. Gatti and P. Macchi, Springer, Heidelberg, 2012, ch. 9, pp. 303–358,  DOI:10.1007/978-90-481-3836-4_9.
34. S. Raub and G. Jansen, Theor. Chem. Acc., 2001, 106, 223–232.
35. D. Bende, F. R. Wagner and Y. Grin, Inorg. Chem., 2015, 54, 3970–3978.
36. D. Bende, Y. Grin and F. R. Wagner, in Heusler Alloys - Properties, Growth, Applications, ed. C. Felser and A. Hirohata, Springer International Publishing, 2016, pp. 133–156.
37. J. G. Angyan, M. Loos and I. Mayer, J. Phys. Chem., 1994, 98, 5244–5248.
38. A. I. Baranov and M. Kohout, J. Comput. Chem., 2011, 32, 2064–2076.
39. R. Bochicchio, R. Ponec, A. Torre and L. Lain, Theor. Chem. Acc., 2001, 105, 292–298.
40. F. R. Wagner, Program DISij, version 7.2.7, Max-Planck-Institut für Chemische Physik fester Stoffe, Dresden, Germany, 2017.
41. C. Börrnert, Y. Grin and F. R. Wagner, Z. Anorg. Allg. Chem., 2013, 639, 2013–2024.
42. G. F. Kayser and F. X. Kayser, J. Alloys Compd., 1996, 233, 74–79.
43. A. Andreini, Mem. Societa Italiana delle Scienze, 1907, 3, 76–129.
44. R. Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, 1st edn, 1979.
45. B. Grünbaum, Geombinatorics, 1994, 4, 49–56.
46. M. Deza and M. Shtogrin, Eur. J. Combinatorics, 2000, 21, 807–814.
47. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.
48. http://rcsr.anu.edu.au .
49. R. Rowe, J. D. Grice, G. Poirier, C. J. Stanley and L. Horváth, Can. Mineral., 2011, 49, 651–656.
50. J. F. Cannon, Effects of high pressure on the structures of AB3 – type layered compounds, Materials Research Society symposium proceedings, 1984, vol. 22, pp. 113–116.
51. D. Kotzott, M. Ade and H. Hillebrecht, J. Solid State Chem., 2009, 182, 538–546.
52. D. Kotzott, M. Ade and H. Hillebrecht, J. Solid State Chem., 2010, 183, 2281–2289.
53. T. Lundström, Pure Appl. Chem., 1985, 57, 1383–1390.
54. F. R. Wagner , unpublished work.
55. Z. Malik, A. Grytsiv, H. Michor, G. Rogl, S. Puchegger, H. Müller, M. Kriegisch, E. Bauer, C. Eisenmenger-Sittner and P. Rogl, J. Alloys Compd., 2013, 550, 302–307.

---

Footnotes

† Dedicated to Professor Dr. Franz Weitzer on the occasion of his 70th birthday.

‡ Electronic supplementary information (ESI) available. CCDC 1560948–1560950, 1561246 and 1561247. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt02501g

§ Present address: Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA.

---