Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A five-coordinate manganese(III) complex of a salen type ligand with a positive axial anisotropy parameter D†
Sergiu
Shova
a,
Angelica
Vlad
a,
Maria
Cazacu
 a,
J.
Krzystek
b,
Lukas
Bucinsky
c,
Martin
Breza
c,
Denisa
Darvasiová
c,
Peter
Rapta
c,
Joan
Cano
a,
J.
Krzystek
b,
Lukas
Bucinsky
c,
Martin
Breza
c,
Denisa
Darvasiová
c,
Peter
Rapta
c,
Joan
Cano
 d,
Joshua
Telser
d,
Joshua
Telser
 *e and
Vladimir B.
Arion
*e and
Vladimir B.
Arion
 *f
*f
aInorganic Polymers Department, “Petru Poni” Institute of Macromolecular Chemistry, Aleea Gr. Ghica Voda 41 A, Iasi 700487, Romania
bNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
cInstitute of Physical Chemistry and Chemical Physics, Slovak University of Technology, Radlinského 9, 81237 Bratislava, Slovak Republic
dInstitut de Ciència Molecular, Universitat de València, Catedrático José Baltrán Martínez 2, 46980 Paterna, Spain
eDepartment of Biological, Chemical and Physical Sciences, Roosevelt University, 430 S. Michigan Avenue, Chicago, Illinois 60605, USA. E-mail: jtelser@roosevelt.edu
fInstitute of Inorganic Chemistry of the University of Vienna, Währinger Strasse 42, A1090 Vienna, Austria. E-mail: vladimir.arion@univie.ac.at
First published on 8th August 2017
Abstract
A new high-spin d4 roughly trigonal–bipyramidal (TBP) manganese(III) complex with a salen type ligand (H2L), namely MnL(NCS)·0.4H2O, has been synthesised and characterised by elemental analysis, ESI mass spectrometry, IR and UV-vis spectroscopy, and spectroelectrochemistry. X-ray diffraction analysis revealed an axial compression of the approximate TBP. Temperature dependent magnetic susceptibility and variable-temperature variable-field (VTVH) magnetisation measurements, as well as high-frequency and -field EPR (HFEPR) spectroscopy, were used to accurately describe the magnetic properties of this complex and, in particular, determine the spin Hamiltonian parameters: g-values and the zero-field splitting (ZFS) parameters D and E. The HFEPR spectra allowed the extraction of fourth order ZFS parameters. Quantum chemical calculations reproduced well the electronic and geometric structures of this unusual complex and, in particular, its electronic absorption spectrum along with the spin Hamiltonian parameters.
Introduction
The manganese(III) ion plays an important role in biological systems, such as photosystem II,1 ribonucleotide reductase,2 and superoxide dismutase.3 It is equally important in molecular magnetism as exemplified by the well-studied family of Mn12 single molecule magnets (SMMs),4 as well as other systems,5 including mononuclear MnIII.6 Among the most appropriate techniques for studying high-spin (HS) manganese(III) complexes is high-frequency and -field EPR spectroscopy (HFEPR), first of all because this spin system usually produces good-quality spectra.7 In addition, although HS manganese(III) systems can also produce X-band EPR spectra,8 extraction of spin Hamiltonian parameters such as the Landé g factor, the magnitude and sign of the axial anisotropy parameter, D, the presence of rhombic anisotropy, E, and fourth order spin Hamiltonian terms is not always possible.9 The magnitude and sign of the anisotropy, however, can provide information on the coordination sphere of manganese(III). Analysis of the literature shows that HFEPR has been applied mainly for the investigation of distorted octahedral and square-pyramidal complexes,6,9–13 although manganese(III) in a rigorously trigonal-bipyramidal (TBP) oxygen donor environment was also quite recently reported,14 providing strong and well-defined EPR signals over the whole frequency region.We recently reported on salen-type Schiff bases derived from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 condensation reactions of 1,3-bis(3-aminopropyl)tetramethyldisiloxane and substituted 2-hydroxybenzaldehydes.15,16 Copper(II) and manganese(III) complexes with these unusual Schiff bases were prepared and investigated by spectroscopic techniques and X-ray crystallography. A feature of note is the formation of a 12-membered central chelate ring, in which the tetramethyldisiloxane unit separates the aliphatic chains, reducing markedly the mechanical strain in the chelate ring via a “shoulder yoke effect”.15 In addition, μ-chlorido-bridged dimanganese(II) complexes17 with macrocyclic Schiff bases were obtained and characterised. These complexes were found to act as catalysts or catalyst precursors for the oxidation of some secondary alcohols to ketones using tert-butyl hydroperoxide as the oxidant in conjunction with low-power microwave irradiation.17 The axially compressed octahedral complex MnL(OAc), where H2L is a Schiff base resulting from 2
2 condensation reactions of 1,3-bis(3-aminopropyl)tetramethyldisiloxane and substituted 2-hydroxybenzaldehydes.15,16 Copper(II) and manganese(III) complexes with these unusual Schiff bases were prepared and investigated by spectroscopic techniques and X-ray crystallography. A feature of note is the formation of a 12-membered central chelate ring, in which the tetramethyldisiloxane unit separates the aliphatic chains, reducing markedly the mechanical strain in the chelate ring via a “shoulder yoke effect”.15 In addition, μ-chlorido-bridged dimanganese(II) complexes17 with macrocyclic Schiff bases were obtained and characterised. These complexes were found to act as catalysts or catalyst precursors for the oxidation of some secondary alcohols to ketones using tert-butyl hydroperoxide as the oxidant in conjunction with low-power microwave irradiation.17 The axially compressed octahedral complex MnL(OAc), where H2L is a Schiff base resulting from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 condensation of 3,5-di-tert-butyl-2-hydroxybenzaldehyde with 1,3-bis(3-aminopropyl)tetramethyldisiloxane,16 appeared to be a suitable candidate for HFEPR investigation. However, we obtained a low quality spectrum of the polycrystalline solid at 10 K that did not permit a spectral analysis. The situation improved slightly when measurements on a low-temperature glass of a dichloromethane (DCM)
1 condensation of 3,5-di-tert-butyl-2-hydroxybenzaldehyde with 1,3-bis(3-aminopropyl)tetramethyldisiloxane,16 appeared to be a suitable candidate for HFEPR investigation. However, we obtained a low quality spectrum of the polycrystalline solid at 10 K that did not permit a spectral analysis. The situation improved slightly when measurements on a low-temperature glass of a dichloromethane (DCM)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene 2
toluene 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
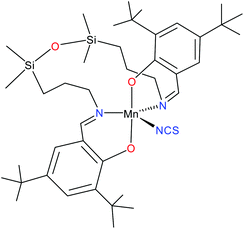
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution of MnL(OAc) were carried out. The lack of resonances in the high-field region of the spectrum indicated a positive axial zero-field-splitting (ZFS) parameter D. By using tunable-frequency EPR,18 the spin Hamiltonian parameters were estimated.16 However, we were unable to explain the low quality of the measured spectra, whether in the solid state or in solution. Being intrigued by these not very favourable results we decided to prepare closely related systems, in which the acetato ligand was replaced by exclusively monodentate ligands, such as NCS− or N3−. Herein we report on the synthesis of a five-coordinate complex, MnL(NCS) (1, see Chart 1), which was characterised by routine spectroscopic techniques (IR and UV-vis), ESI mass spectrometry, and single crystal X-ray diffraction analysis, as well as by spectroelectrochemistry, HFEPR, density functional theory (DFT) and ab initio complete active space self-consistent field (CASSCF) calculations. To our knowledge, HS manganese(III) complexes with an approximate TBP geometry (here, N3eq,O2ax) have not been investigated by HFEPR previously. Although MnIII complexes with a related geometry (TBP: N3eq,Nax,Oax) have been studied by conventional EPR,8 the reliability of the spin Hamiltonian parameters extracted from such single frequency measurements is questionable.9c
1 solution of MnL(OAc) were carried out. The lack of resonances in the high-field region of the spectrum indicated a positive axial zero-field-splitting (ZFS) parameter D. By using tunable-frequency EPR,18 the spin Hamiltonian parameters were estimated.16 However, we were unable to explain the low quality of the measured spectra, whether in the solid state or in solution. Being intrigued by these not very favourable results we decided to prepare closely related systems, in which the acetato ligand was replaced by exclusively monodentate ligands, such as NCS− or N3−. Herein we report on the synthesis of a five-coordinate complex, MnL(NCS) (1, see Chart 1), which was characterised by routine spectroscopic techniques (IR and UV-vis), ESI mass spectrometry, and single crystal X-ray diffraction analysis, as well as by spectroelectrochemistry, HFEPR, density functional theory (DFT) and ab initio complete active space self-consistent field (CASSCF) calculations. To our knowledge, HS manganese(III) complexes with an approximate TBP geometry (here, N3eq,O2ax) have not been investigated by HFEPR previously. Although MnIII complexes with a related geometry (TBP: N3eq,Nax,Oax) have been studied by conventional EPR,8 the reliability of the spin Hamiltonian parameters extracted from such single frequency measurements is questionable.9c
Experimental
Starting materials and physical measurements
The complex [MnL(OAc)]·0.15H2O, where H2L is tetradentate Schiff base with a tetramethyldisiloxane spacer, was prepared according to a procedure described previously16 by a condensation reaction of 3,5-di-tert-butyl-2-hydroxybenzaldehyde with 1,3-bis(3-aminopropyl)tetramethyldisiloxane in the presence of Mn(OAc)2·4H2O in methanol/DCM 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Infrared (IR) spectra of the complex as KBr pellets were recorded on a Bruker Vertex 70 FT-IR spectrometer in transmission mode in the range 400–4000 cm−1 with a resolution of 2 cm−1 and an accumulation of 32 scans at room temperature. Electrospray ionisation mass spectrometry (ESI-MS) was carried out with a Bruker Esquire 3000 instrument and the samples were dissolved in methanol. Elemental analysis was performed at the Microanalytical Laboratory of the University of Vienna with a PerkinElmer 2400 CHN Elemental Analyser (PerkinElmer, Waltham, MA). UV-vis spectra were recorded with a CARY 300 Agilent spectrophotometer in the 200–800 nm range. The path length was 1 cm.
1. Infrared (IR) spectra of the complex as KBr pellets were recorded on a Bruker Vertex 70 FT-IR spectrometer in transmission mode in the range 400–4000 cm−1 with a resolution of 2 cm−1 and an accumulation of 32 scans at room temperature. Electrospray ionisation mass spectrometry (ESI-MS) was carried out with a Bruker Esquire 3000 instrument and the samples were dissolved in methanol. Elemental analysis was performed at the Microanalytical Laboratory of the University of Vienna with a PerkinElmer 2400 CHN Elemental Analyser (PerkinElmer, Waltham, MA). UV-vis spectra were recorded with a CARY 300 Agilent spectrophotometer in the 200–800 nm range. The path length was 1 cm.
Synthesis of MnL(NCS)·0.4H2O (1)
To a solution of MnL(OAc)·0.15H2O (60.0 mg, 0.075 mmol) in DCM (20 ml) was added dropwise under an argon atmosphere a solution of KSCN (11.0 mg, 0.113 mmol) in methanol (15 ml). The mixture was stirred for 2 h at room temperature and then filtered. The filtrate was allowed to stand at room temperature for crystallisation. After three days the product as purple brown sticks was separated by filtration, washed with diethyl ether and dried in air. Yield: 51.6 mg, 86.6%. IR spectrum (KBr pellet), selected bands, νmax: 3469m, 2958w, 2067vs, 1620m, 1554w, 1436w, 1411w, 1251w, 1176vw, 1072w, 746vw, 568vw. ESI mass spectrum (positive) in MeCN/MeOH 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (with 1% H2O): m/z 733.40 [MnIIIL]+, m/z 814.36 [MnIIIL(NCS) + Na]+; negative ion: m/z 791.37 [MnIIL(NCS)]−, m/z 849.35 [MnIIIL(NCS)2]−. UV-vis (MeOH) λ, nm (ε, M−1 cm−1): 231 (36
1 (with 1% H2O): m/z 733.40 [MnIIIL]+, m/z 814.36 [MnIIIL(NCS) + Na]+; negative ion: m/z 791.37 [MnIIL(NCS)]−, m/z 849.35 [MnIIIL(NCS)2]−. UV-vis (MeOH) λ, nm (ε, M−1 cm−1): 231 (36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440), 268sh, 276 (24
440), 268sh, 276 (24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350), 310sh, 355sh, 395 (7290), 480sh, 675 (780).
350), 310sh, 355sh, 395 (7290), 480sh, 675 (780).
X-ray crystallography
Crystallographic measurements for 1 were carried out with an Oxford Diffraction XCALIBUR E CCD diffractometer equipped with graphite-monochromated Mo-Kα radiation. A single crystal was positioned at 40 mm from the detector and 406 frames were measured each for 20 s over 1° scan width. The unit cell determination and data integration were carried out using the ChrysAlis software package from Oxford Diffraction.19 The structure was solved by direct methods using Olex220 software with the SHELXS structure solution program and refined by full-matrix least-squares on F2 with SHELXL-97.21 Atomic displacements for non-hydrogen atoms were refined using an anisotropic model. The hydrogen atoms have been placed at fixed, idealised positions accounting for the hybridisation of the supporting atoms. The molecular plots were obtained using the Olex2 program. Table 1 provides a summary of the crystallographic data together with refinement details, while the bond lengths and angles are summarised in Table S1, ESI, CCDC 1515780.†| a R 1 = ∑||Fo| − |Fc||/∑|Fo|. b wR2 = {∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]}1/2. c GOF = {∑[w(Fo2 − Fc2)2]/(n − p)}1/2, where n is the number of reflections and p is the total number of parameters refined. | |
|---|---|
| Complex | 1 |
| Empirical formula | C41H66.8MnN3O3.4SSi2 |
| Formula weight | 799.35 |
| Temperature/K | 293 |
| Crystal system | Tetragonal |
| Space group |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21c 21c |
| a/Å | 29.3668(8) |
| b/Å | 29.3668(8) |
| c/Å | 11.7840(5) |
| V/Å3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 162.6(7) 162.6(7) |
| Z | 8 |
| D calc/mg mm−3 | 1.045 |
| μ/mm−1 | 0.382 |
| Crystal size/mm3 | 0.05 × 0.15 × 0.30 |
| θ min, θmax (°) | 3.102 to 49.424 |
| Reflections collected | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
| Independent reflections (Rint) | 8548 (0.0903) |
| Data/restraints/parameters | 8548/45/478 |
| R 1 (I > 2σ(I) | 0.0683 |
| wR2b (all data) | 0.1671 |
| GOFc | 1.034 |
| Flack parameter | −0.002(17) |
| Largest diff. peak/hole/e Å−3 | 0.29/−0.23 |
Spectroelectrochemistry
Dichloromethane (puriss; absolute; w(H2O) < 0.001%), analytical grade ferrocene (Fc) purchased from Sigma–Aldrich, and tetrabutylammonium hexafluorophosphate (nBu4NPF6) of puriss. quality from Fluka were all used as received. Cyclic voltammetric experiments were performed under an argon atmosphere using a three-electrode arrangement with a platinum wire as the working electrode, a platinum wire as the counter electrode, and a Ag wire as the pseudo-reference electrode. The cyclic voltammetric studies were performed in a home-made miniature standard electrochemical cell (for 2 mL of solution) using a miniature platinum wire working electrode (platinum wire sealed in a glass capillary). Ferrocene served as the internal redox potential standard and all potentials are referenced to the ferricenium/ferrocene (Fc+/Fc) redox couple. The concentration of 1 in DCM was 0.5 mM both in cyclic voltammetry and spectroelectrochemical experiments. A Heka PG310USB (Lambrecht, Germany) potentiostat with the PotMaster 2.73 software package was used for potential control in voltammetric and spectroelectrochemical studies. In situ ultraviolet–visible–near-infrared (UV-vis-NIR) measurements were performed on Avantes spectrometers, namely Model AvaSpec-2048x14-USB2, equipped with a CCD detector, or Model AvaSpec-NIR256-2.2, equipped with an InGaAs detector. Halogen and deuterium lamps were used as the light sources (Avantes, Model AvaLight-DH-S-BAL). The in situ spectroelectrochemical UV-vis-NIR and cyclic voltammetric experiments were carried out under an argon atmosphere in a special honeycomb spectroelectrochemical cell kit (AKSTCKIT3) with a Pt-microstructured honeycomb working electrode, purchased from Pine Research Instrumentation. The cell was positioned in a CUV-UV cuvette holder (Ocean Optics) connected to a diode-array UV-vis-NIR spectrometer by optical fibers. UV-vis-NIR spectra were processed using the AvaSoft 7.7 software package. Cyclic voltammograms were simulated using DigiElch Professional software from Gamry Instruments (USA, version DigiElch 8.FD).Magnetic measurements
Static direct current (dc) measurements were carried out on 20.6 mg of 1 by powdering and restraining the sample in order to prevent any displacement due to the magnetic anisotropy. Variable-temperature (2.0–300 K) dc magnetic susceptibility under an applied field of 0.25 kG (T < 30 K) and 1.0 kG (T ≥ 20 K), and variable-field (0–5.0 T) magnetisation in the temperature range 2 to 10 K was recorded with a Quantum Design SQUID magnetometer. Variable-temperature (2.0–10 K) alternating current (ac) magnetic susceptibility measurements under ±5.0 G oscillating field at frequencies in the range of 10–1000 Hz were carried out on a crystalline sample under different applied static dc fields in the range 0.0–0.25 kG with a Quantum Design SQUID magnetometer. The magnetic susceptibility data were corrected for the diamagnetism of the constituent atoms and the sample holder. The thermal dependence of the magnetic susceptibility and magnetisation curves was analysed using the XVPMAG program.22HFEPR spectroscopy
HFEPR measurements were made using a spectrometer described elsewhere.23 Complex 1 was investigated both as a loose microcrystalline powder and with the powder immobilised in n-eicosane. HFEPR spectra were simulated using the program SPIN from A. Ozarowski. The following spin Hamiltonian, including fourth order terms, was employed: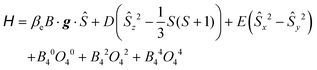 | (1) |
Theoretical calculations
Starting from the experimental X-ray diffraction structure, the geometry of the complex 1 in triplet, quintet and septet ground spin states was optimised at the B3LYP25,26 level of theory without any symmetry restrictions using the Gaussian09 program package.27 Vertical transition energies and oscillator strengths between the initial and final electron states for the electronic absorption spectrum of 1 in a methanolic solution were computed by the TF-DFT method.28 In the next step, the geometry of the most stable system was optimised in a methanolic solution using the standard Integral Equation Formalism Polarisable Continuum Model (IEF-PCM).29 Electronic transitions for the optimised structure of 1 in methanol were evaluated within the TD-B3LYP method30 for the lowest 150 excited states. Standard 6-311G* basis sets31 were used for all atoms. The stability of the obtained structures has been tested by vibrational analysis (no imaginary vibrations). Atomic charges and d electron populations (dx) of relevant atoms were evaluated using natural bond orbital (NBO) analysis.32 The relative free energies of various spin states of the studied complex have been corrected using restricted open-shell single-point calculations (replacing the electron energy in unrestricted energy data) to obtain pure spin states.33 The Molekel software package34 has been used for the visualisation of molecular orbitals and spin densities.ZFS parameters have been evaluated at the BLYP/6-311G* and CASSCF(4,5)/6-311G* levels of theory using the ORCA 3.0.0 software package35,36 (both the experimental and B3LYP/6-311G* optimised geometries have been taken into account). In the case of CASSCF(4,5) the entire quintet and triplet configuration space was employed in the evaluation of the ZFS parameters, i.e. 5 quintets and 35 triplets. The state specific as well as state-averaged quintet CASSCF wave functions have been used for the subsequent evaluation of the ZFS parameters (5 quintets and 35 triplets). The spin–spin interaction has been accounted for via the Multi-Reference Configuration Interaction (MRCI) approach37 for the state-averaged quintet CASSCF(4,5) wave function, denoted sa-MRCI. To estimate also the contribution of dynamic electron correlation effects, the N-Electron Valence State Perturbation Theory to 2nd order (NEVPT2)38 ZFS parameters of a smaller model of 1 (1model) have been provided in Table S2, ESI† (tert-butyl groups have been replaced by hydrogens, see Fig. S1b, ESI†).
Results and discussion
Synthesis
A reaction of MnL(OAc) with KSCN in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 molar ratio in DCM/MeOH 1
1.5 molar ratio in DCM/MeOH 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 afforded the complex MnL(NCS) in 87% yield. The ESI mass spectrum measured in positive ion mode showed peaks with m/z 814.36 and 733.40 attributed to [MnIIIL(NCS) + Na]+ and [MnIIIL]+, respectively. The peaks registered in the negative ion mode at m/z 849.35 and 791.37 could be assigned to [MnIIIL(NCS)2]− and [MnIIL(NCS)]−, respectively. Attempts to precipitate the complex [MnIIIL(NCS)2]− from the reaction mixture by the addition of large countercations, such as NBu4+, failed.
1 afforded the complex MnL(NCS) in 87% yield. The ESI mass spectrum measured in positive ion mode showed peaks with m/z 814.36 and 733.40 attributed to [MnIIIL(NCS) + Na]+ and [MnIIIL]+, respectively. The peaks registered in the negative ion mode at m/z 849.35 and 791.37 could be assigned to [MnIIIL(NCS)2]− and [MnIIL(NCS)]−, respectively. Attempts to precipitate the complex [MnIIIL(NCS)2]− from the reaction mixture by the addition of large countercations, such as NBu4+, failed.
X-ray crystallography
Compound 1 has a molecular structure (Fig. 1) that is constructed from the neutral complexes and traces of co-crystallised water molecules, so that the composition and charge balance are in agreement with the formulation: [MnL(NCS)]·0.4H2O. The N3O2 environment of the manganese(III) ion, which is formed by the deprotonated tetradentate Schiff base ligand L2− and a thiocyanato ligand bonded to the central ion via nitrogen, exhibits an intermediate coordination geometry (τ parameter 0.54) between trigonal-bipyramidal (TBP, τ = 1.00) and square-pyramidal (SPY, τ = 0.00),39 but slightly closer to TBP geometry. In the shape analysis,40 the two ideal geometries can be interconverted following geometrical changes described by a path that connects them. Each value of τ is a measure of the degree of conversion and is bound to the geometry closer to the experimental one, even if it is not on the path. That is why a second parameter, ρ, is defined, which is zero for any geometry on the path and can thus be a measure of additional distortion. For 1, ρ is 13.2%, indicating a high distortion of the metal environment and making more difficult the description of its geometry. However, the high compression along the O1–Mn–O2 axis can be presumed only for the TBP geometry, and that is why it was selected to describe the geometry of 1. A more detailed discussion of this aspect is in the subsection devoted to the electronic structure of 1. The equatorial plane is formed by three nitrogen atoms coordinated to manganese(III) at very close Mn–N distances in the range between 2.032(7) and 2.065(6) Å. The remaining two axial coordination positions are occupied by the phenolato oxygen atoms of the Schiff base ligand at Mn–O1 and Mn–O2 distances of 1.867(4) and 1.859(4) Å, respectively, which are significantly shorter than the Mn–N distances. On the other hand, the N–Mn–N bond angles differ significantly. Two of them: N1–Mn–N3 107.7(3)° and N2–Mn–N3 111.3(3)°, exhibit similar values, while the third one N1–Mn1–N2 141.0(2)° is much larger due to constraints imposed by the tetradentate ligand. It should be noted that TBP coordination for manganese(III) has literature precedence. A family of manganese(III) complexes featuring a TBP N4O donor set with water, hydroxido or oxido groups as terminal ligands with tris(5-cyclohexylimino-pyrrol-2-ylmethyl)amine, tris(5-cyclohexylamino-azafulvene-2-methyl)amine, tris(cyclopentylcarbamoylmethyl)amine or tris[(N′-tert-butylureaylato)-N-ethyl]aminato tripodal ligands is well documented.41–43 A notable example is the heterodimetallic complex [15-crown-5⊃CaII-(μ-OH)-MnIIIMST]+, where [MST]3− = N,N′,N′′-[2,2′,2′′-nitrilotris(ethane-2,1-diyl)]tris(2,4,6-trimethylbenzenesulfonamido), in which a TBP manganese(III) and CaII are bridged via a μ-OH group.44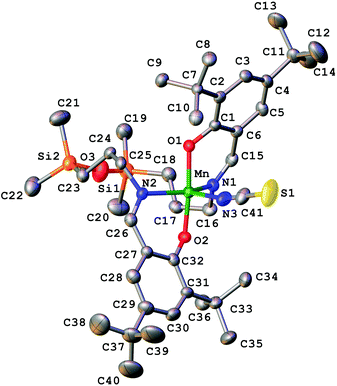 | ||
| Fig. 1 X-ray molecular structure of 1 with the atom labelling scheme and thermal ellipsoids at the 30% probability level. H-atoms are omitted for clarity. | ||
Electronic absorption spectroscopy
The UV-vis spectra of 1 in methanol and DCM are shown in Fig. S2, ESI.† There are very strong (ε > 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1) absorption bands below ca. 300 nm that are due to intraligand π–π* transitions, along with a strong band at 399 nm that may be due to LMCT. Lastly, there is a weaker band (ε = 780 M−1 cm−1) at 675 nm that may be due to a d–d transition hidden by a stronger LMCT band. In the MnIII-doped oxide, at low dopant levels, there is a strong absorption at 620 nm that has been assigned to the transition 5A′1 → 5E′,14 which is allowed with xy polarisation in D3h (ideal TBP) symmetry. The symmetry in 1 is much lower, but we suggest the same assignment as contributing to this visible band. The red shift in 1versus the doped oxide may be due to the weaker axial ligand field of the phenolato ligands as opposed to the oxide donors. The low symmetry of 1 precludes a simple LFT analysis as was done in the doped oxide.
000 M−1 cm−1) absorption bands below ca. 300 nm that are due to intraligand π–π* transitions, along with a strong band at 399 nm that may be due to LMCT. Lastly, there is a weaker band (ε = 780 M−1 cm−1) at 675 nm that may be due to a d–d transition hidden by a stronger LMCT band. In the MnIII-doped oxide, at low dopant levels, there is a strong absorption at 620 nm that has been assigned to the transition 5A′1 → 5E′,14 which is allowed with xy polarisation in D3h (ideal TBP) symmetry. The symmetry in 1 is much lower, but we suggest the same assignment as contributing to this visible band. The red shift in 1versus the doped oxide may be due to the weaker axial ligand field of the phenolato ligands as opposed to the oxide donors. The low symmetry of 1 precludes a simple LFT analysis as was done in the doped oxide.
Cyclic voltammetry and spectroelectrochemistry
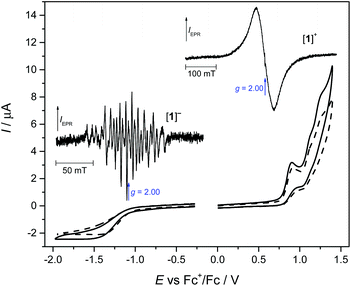
The redox properties of 1 in DCM containing tetrabutylammonium hexafluorophosphate (nBu4NPF6) as the supporting electrolyte were investigated by cyclic voltammetry and in situ spectroelectrochemistry. The resulting electrochemical response at a scan rate of 100 mV s−1 is shown in Fig. 2. Upon oxidation of 1, three oxidation waves are seen: the first being irreversible with a half-peak oxidation potential Ep/2 of +0.84 V and the other two being quasi-reversible at an Ep/2 of +1.08 V and +1.20 V vs. Fc+/Fc. Upon a voltammetric scan in the cathodic region, a broad irreversible reduction wave is observed at Ep/2 = −1.28 V vs. Fc+/Fc at v = 100 mV s−1. This indicates either a slow electron transfer upon oxidation and reduction or (fast) electron transfer followed by an irreversible chemical reaction of [1]− and [1]+.There were no significant changes in the shape of the redox peaks observed upon the second redox cycle (see the dashed line in Fig. 2). To investigate the origin of the reduced and oxidised states of MnL(NCS) after one electron transfer, special ex situ EPR spectroelectrochemical experiments were performed, where the corresponding sample was electrolysed in a home-made electrolytic cell using a large platinum-mesh working electrode at exactly controlled potentials. In particular, coulometric reduction at −1.1 V vs. Fc+/Fc resulted in the passage of an average of 1.1 F (106133 C) of charge per mole of 1. After complete reduction (or oxidation) of [1] in an nBu4NPF6/DCM solution under an argon atmosphere in the region of the first electron transfer, the final solution was inserted under argon into the EPR tube, which was then immediately immersed in liquid nitrogen. The EPR tube was then placed in the pre-cooled EPR cavity and spectra were recorded at 120 K. The corresponding X-band EPR spectra of the one-electron-reduced form [1]− as well as the one-electron-oxidised state [1]+ in a frozen dichloromethane solution measured at 120 K are shown in the insets of Fig. 2. The one-electron reduced state exhibits a rich hyperfine-split EPR spectrum at low temperatures in contrast to the single-line broad isotropic EPR signal (linewidth of about 60 mT) measured for the one-electron oxidised state. Concerning the splitting pattern45 of the observed EPR spectrum, it can be concluded that upon one electron reduction a high-spin MnII species is formed. Specifically, we propose that the spectrum consists of five groups of lines corresponding to the five allowed (ΔMS = ±1) transitions of a 6S state ion of Mn2+ where each group is further split into six lines due to hyperfine interaction with the 55Mn nucleus (100% abundant) with hyperfine splitting of about 7 mT, which is typical of MnII. However, due to the complexity of this spectrum, a quantitative analysis is challenging and is beyond the scope of this paper. Qualitatively, we propose that the ZFS is small compared to the X-band microwave energy and is comparable even to the hyperfine splitting. A B3LYP/6-311G* calculation confirmed the MnII formal oxidation state upon reduction (not shown).
Due to the lack of resolved hyperfine structure, the species generated after one-electron oxidation is less clearly assigned. A B3LYP/6-311G* calculation suggests that the oxidation appears to be ligand centred, forming [MnIIIL˙]+. Alternatively, the broad EPR spectrum of the mono-oxidised [1]+ can be interpreted as the [MnIVL]+ state assuming a very small ZFS and a broad linewidth. Nevertheless, a precise study of the electronic structure of the redox species is beyond the scope of the present paper. We note that the frozen solution of the initial MnIIIL(NCS) in DCM was EPR silent at 120 K at the X-band. This [1]0 state was investigated using HFEPR spectroscopy as discussed in detail below.
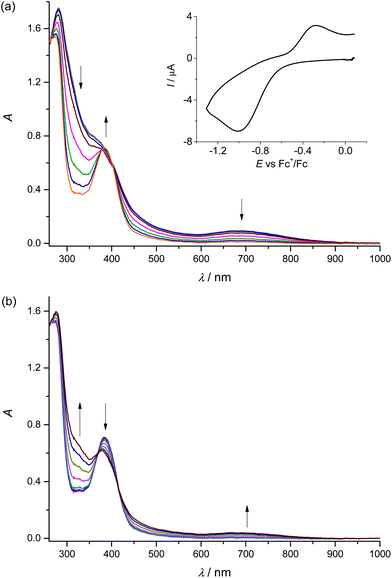
To confirm the chemical reversibility of the first reduction as well as the first oxidation step for complex 1, the in situ spectroelectrochemical UV-vis-NIR and cyclic voltammetric experiments were carried out under an argon atmosphere in a special thin layer honeycomb spectroelectrochemical cell with a microstructured honeycomb working electrode. The in situ UV-vis-NIR spectroelectrochemical experiments revealed that by decreasing the scan rate to 20 mV s−1, the cathodic reduction becomes more electrochemically reversible, confirming the slow electron transfer at this step (see the inset in Fig. 3a).
In the region of the first reduction peak (from −0.4 V to −1.3 V vs. Fc+/Fc), a new optical band at 385 nm emerges. In addition, a decrease of the intensity of the bands of 1 at 280 nm and 690 nm is observed (Fig. 3a). Upon scan reversal the products that are formed upon reduction are partially reoxidised as seen in Fig. 3b. The recovery of the initial optical bands during the voltammetric reverse scan in the region −0.6 V to −0.0 V vs. Fc+/Fc and the lack of any new absorption confirm the chemical reversibility of the redox process at the first reduction peak. Going to even lower scan rates (5 mV s−1) provides almost full recovery of the initial optical bands during the voltammetric reverse scan (see Fig. S3, ESI†).
Upon anodic oxidation of 1 in the region of the first oxidation peak, analogous behaviour was observed with the partial recovery of the initial optical bands during the voltammetric reverse scan (see Fig. S4, ESI†). To understand better the reversibility of each oxidation step, cyclic voltammetry at a low scan rate of 20 mV s−1 was performed using a thin layer cell and a microstructured honeycomb working electrode under an argon atmosphere (Fig. S5, ESI†). No significant changes in the shape of the redox peaks were observed upon multiple redox cycles for the first reduction (Fig. S5a†) and oxidation (Fig. S5b†), confirming the chemically reversible reduction and oxidation of MnIIIL(NCS). Digital simulation of the cyclic voltammograms taken at 20 mV s−1 yielded the formal potential E°′ = −0.66 V vs. Fc+/Fc for the first reduction and E°′ = +0.29 V vs. Fc+/Fc for the first oxidation step, respectively (see dashed lines in Fig. S5a and b). The small rate constant for electron transfer, ks = 1 × 10−5 cm s−1, used in these simulations confirms the slow electron transfer. The chemical reversibility indicates that the coordination number remains constant during the first electron transfer. However, upon scanning onward to the second (Fig. S5c†) and to the third (Fig. S5d†) oxidation peaks, the height of the first reduction peak rapidly decreases after each consecutive scan, indicating irreversible processes which can be tentatively attributed to irreversible ligand-based oxidation, leading to unstable forms of the complex.
Magnetic properties
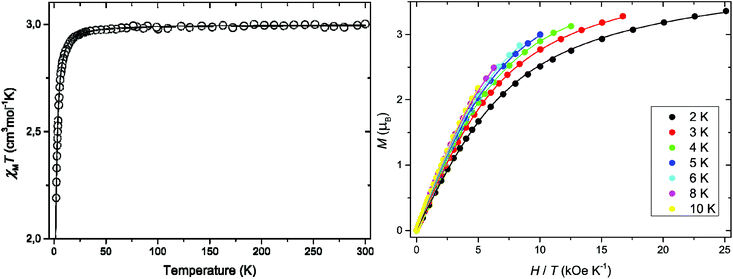
The direct current (dc) magnetic properties of 1 in the form of the χMT versus T (χMT being the dc magnetic susceptibility per MnIII ion) and M versus H/T plots (M being the dc molar magnetisation per mononuclear unit and H the applied magnetic dc field) are shown in Fig. 4. The value of χMT at room temperature (2.98 cm3 mol−1 K) is close to that expected for one magnetically isolated high-spin d4 MnIII ion.46 Upon cooling, χMT remains almost constant until 40 K and then it continuously decreases to attain a value of 2.19 cm3 mol−1 K at 2.0 K (Fig. 4), due to the ZFS of the MnIII ion. The maximum M value for 1 at 2.0 K (3.36 μβ with H = 5.0 kOe) is below that expected for the saturation magnetisation considering a high spin d4 MnIII ion with no ZFS (Ms = gSNβ = 4.0 μβ with S = 2 and g = 2.0). This feature confirms the occurrence of a significant ZFS, the presence of strong magnetic couplings being discarded. Furthermore, variable-field magnetisation data for 1 in the temperature range 2–10 K could not be superimposed at high H/T values, being well below that of the Brillouin function for a quintet spin state (S = 2 with g = 2.0) (Fig. 4). Overall, this supports the presence of appreciable single-ion magnetic anisotropy of the quintet ground state of the high-spin MnIII ion in 1.Both the temperature dependence of the magnetic susceptibility and of the magnetisation curves could be jointly well simulated through the XVPMAG software package,22 the anisotropic spin Hamiltonian being defined as in eqn (1) above (leaving out the fourth order ZFS terms and using only an isotropic g value). The values of the parameters that best described the experimental curves were: g = 1.994, D = +2.74 cm−1, and E = 0.04 cm−1 (E defined with the same sign as D) with F = 1.5 × 10−5. F is the agreement factor defined as F = ∑(φexp − φcalcd)2/∑φexp2, where φ is the observable physical property. The analysis of the variable-temperature–variable-field (VTVH) magnetisation measurements and magnetic susceptibility indicates a positive value of the axial ZFS parameter D and an E/D ratio that is not null, but very small.
The alternating current (ac) magnetic susceptibilities in the form of the χ′M and χ′′Mversus T plots (χ′M and χ′′M being the in-phase and out-of-phase ac magnetic susceptibilities per mononuclear unit, respectively) were measured in different applied static fields (Fig. S6, ESI†). Out-of-phase ac signals are not observed at any magnetic field in agreement with a positive magnetic anisotropy (D) for 1.
To verify the results obtained from magnetic measurements and for a more accurate determination of the spin Hamiltonian parameters we turned to high-frequency and -field EPR (HFEPR) spectroscopy.
HFEPR spectroscopy
Complex 1 when measured as is, i.e., an unconstrained powder, produced strong HFEPR spectra that showed symptoms of field-induced torquing. We did not try to interpret these spectra, and proceeded to experiments on an n-eicosane pellet. The pellet spectra are shown in Fig. 5, accompanied by simulations assuming a perfect powder distribution of the crystallites in space. Additional HFEPR spectra are shown in Fig. S7 and S8, ESI.† The agreement between the simulations and experiments can be described as excellent under the condition D > 0.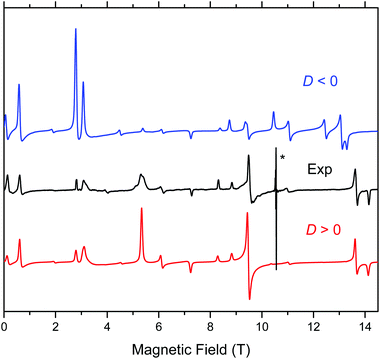 | ||
| Fig. 5 HFEPR spectrum of 1 recorded at 307.2 GHz and 8 K (black trace) accompanied by simulations using spin Hamiltonian parameters as in Table 2. Blue trace: simulations using negative D; red trace: positive D. The asterisk denotes a pair of signals at g values equal to ca. 2.08 and 2.00 originating from an unknown impurity and MnII, respectively. Neither of them is simulated. | ||
Complex 1 produced HFEPR spectra at any temperature between liquid helium and ambient temperature; a room-temperature spectrum, again with a simulation, is shown in Fig. S9, ESI.† The spin Hamiltonian parameters slightly change (decrease) between liquid helium and room temperature (Table 2). The low temperature spin Hamiltonian parameters used in the simulations shown in Fig. 5, S7, and S8, ESI,† were not deduced from the single-frequency spectra shown, but from the 2-D map of turning points as a function of frequency/energy according to the principle of tunable-frequency EPR,18 which is shown in Fig. 6. The parameters are listed in Table 2. The room temperature parameters, in contrast, were estimated from single-frequency spectra alone.
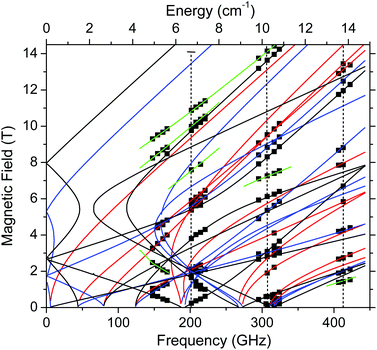 | ||
| Fig. 6 Field vs. frequency/energy map of turning points in complex 1 at 4.5–10 K. Squares are experimental points; curves were simulated using spin Hamiltonian parameters as in Table 2. Red curves: turning points with the magnetic field B0 parallel to the x-axis of the ZFS tensor; blue: B0||y; black: B0||z; green: off-axis turning points. The vertical dashed lines represent the frequencies at which spectra shown, respectively, in Fig. S7,† Fig. 5, and Fig. S8† were recorded. | ||
| T (K) | D (cm−1) | |E| (cm−1) | g x | g y | g z | B 4 0 (10−4 cm−1) | B 4 2 | B 4 4 (10−4 cm−1) |
|---|---|---|---|---|---|---|---|---|
| a Values determined from the fit of full 2D field–frequency dependence of resonances. b Values determined from simulation of selected single frequency spectra. c Values derived from fits of VT dc susceptibility and VTVH magnetisation. d Isotropic g value used for fitting, with no fourth order ZFS terms. | ||||||||
| 4.5–10a | +2.526(4) | 0.443(3) | 2.000(2) | 1.995(3) | 1.998(2) | 4(1) | 0 | −18(6) |
| 293b | 2.48 | 0.374 | 2.000 | 2.000 | 1.995 | — | — | — |
| 2–300c | +2.74 | 0.04 | — | — | 1.994 d | — | — | — |
The positive value of D observed definitively here for 1 is as expected from simple ligand-field theory for a HS d4 system with axial compression,24,47,48 as demonstrated in the molecular structure wherein there are relatively shorter, axial Mn–O bonds and relatively longer Mn–N equatorial bonds. Another reported MnIII complex8 with a distorted TBP geometry likewise gave a positive D value as did a biological 5-coordinate MnIII centre (in manganese superoxide dismutase, MnSOD).49 A six-coordinate complex, [Mn(bpia)(OAc)(OCH3)](PF6) where bpia = bis[(2-pyridyl)-methyl]-[(1-methylimidazol-2-yl)methyl]amine, also exhibited a positive D value, as determined by HFEPR. This complex comprises a cis-N2(eq,am)N2(ax,py)O2(eq) donor set wherein the Mn–O(CH3) bond length is much shorter than those of the other Mn–N,O bonds.11 The magnitude of D found for 1 (+2.5 cm−1) is in the middle of the range spanned by the few known examples. The five-coordinate complex of Gupta et al.8 is on the low end (D = +1.7(5) cm−1), MnSOD has D = +2.10 cm−1, while those seen for MnIII in a TBP oxide lattice and the previously studied compound, MnL(OAc), are at the higher end, respectively (D = +3.0 cm−1(ref. 14 and 50) and +3.35 cm−1),16 with the six-coordinate complex given above having the highest value,11D = +3.526(3) cm−1.51 There are various excited state contributions to the ZFS in such a 5A′1 ground state (using the idealised D3h point group symmetry), so there is no clear structural or electronic basis for a given D value amongst these examples. The rhombicity of 1, as defined by |E/D| = 0.175 (at low T), is quite substantial (the maximum value is 0.333), which qualitatively is a consequence of the very distorted geometry about the MnIII ion (Table 3), in contrast to the axial symmetry of this ion in the oxide lattice.52,53 The ZFS in 1 is quantitatively analysed by computational methods as described in the following section.
| Spin S | 1 | 2 | 3a |
|---|---|---|---|
| a Additional spin density is located at sulfur, oxygens and neighbouring phenyl rings. | |||
| ΔEDFT [kJ mol−1] | 4.469 | 0.000 | 4.202 |
| Δ(EDFT + ZPE) [kJ mol−1] | 4.688 | 0.000 | 3.749 |
| ΔG298 [kJ mol−1] | 5.146 | 0.000 | 3.174 |
| Bond lengths [Å] | |||
| Mn–O1 | 1.881 | 1.881 [1.867(4)] | 2.138 |
| Mn–O2 | 1.883 | 1.881 [1.859(4)] | 2.142 |
| Mn–N1 | 2.026 | 2.105 [2.065(6)] | 2.193 |
| Mn–N2 | 2.026 | 2.104 [2.033(5)] | 2.192 |
| Mn–N3 | 1.875 | 1.976 [2.032(7)] | 2.060 |
| Bond angles [°] | |||
| O1–Mn–N1 | 91.7 | 86.2 [87.7(2)] | 95.3 |
| O1–Mn–N2 | 87.2 | 91.1 [89.9(2)] | 82.3 |
| O1–Mn–N3 | 93.7 | 93.7 [92.9] | 93.0 |
| O1–Mn–O2 | 172.4 | 172.7 [173.1(2)] | 174.3 |
| O2–Mn–N1 | 87.2 | 86.2 [90.0(2)] | 82.2 |
| O2–Mn–N2 | 91.8 | 91.1 [87.8(2)] | 95.2 |
| O2–Mn–N3 | 93.9 | 93.7 [94.1(3)] | 92.7 |
| N1–Mn–N2 | 163.9 | 136.5 [141.0(2)] | 127.9 |
| N1–Mn–N3 | 98.2 | 111.8 [107.7(3)] | 115.9 |
| N2–Mn–N3 | 98.0 | 111.7 [111.3(3)] | 116.2 |
| Mn–N3–C41 | 174.1 | 179.9 [167.0(7)] | 179.7 |
Theoretical calculations
Free energy values at 298 K (G298) indicate the quintet spin state of complex 1 to be most stable (Table 3). Small spin contamination may be concluded in the spin systems under study (compare the spin squares in unrestricted formalism in Table S3 (ESI†) with their theoretical values in Table 3). Unlike its single crystal X-ray diffraction result, the DFT optimised structure indicates complex 1 to adopt the highest possible C2 molecular symmetry (see Table S1, ESI†). Calculated bond distances satisfactorily agree with those from X-ray diffraction within ±0.071 Å (see Table S1, ESI†). Significant differences may be observed only for methyl groups, which can be ascribed to solid state effects, and for the Mn coordination polyhedron, which might be explained by solid state effects or, alternatively, by the pseudo-Jahn–Teller effect in the real structure as well. Nevertheless, the DFT optimised structure of the above polyhedron in all the spin states under study (Table 3) shows practically linear Mn–N3–C41–S units. This along with equal electron density parameters for symmetry equivalent atoms and bonds (Table S4, ESI†) are arguments against the pseudo-Jahn–Teller origin of the above differences. As expected, the d-electron population of the central Mn atom (Table S4, ESI†) is comparable with that for the analogous MnL(OAc) complex reported previously16 (calculated at the B3LYP/6-311G* level of theory as well) indicating the same oxidation state. Analogously, the spin density is concentrated prevailingly at the central Mn atom (see Table S4 and Fig. S10, ESI†).Electronic absorption spectra
TD-DFT calculations of 1 in the quintet spin state in a methanolic solution produced spectral lines in fairly good agreement with experimental data (Table S5, Fig. S2, ESI†). According to our results, the above mentioned weak band at 675 nm corresponds to LMCT from NCS− to manganese(III) (see Fig. 7).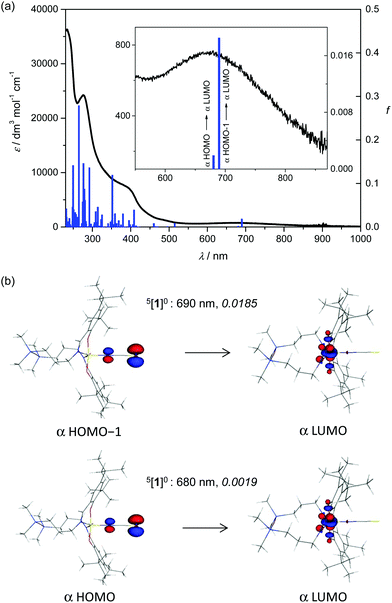 | ||
| Fig. 7 Experimental absorption spectrum of 1 in methanol (black trace) and calculated electronic transitions for the 5[1]0 (blue columns) spin state of the neutral complex. (b) B3LYP orbitals (drawn at ±0.09 au level) contributing dominantly to the calculated (TD-B3LYP, methanol) electronic transitions in the visible region for 5[1]0 (for details see the inset to Fig. 7a); the value in italics is the oscillator strength. | ||
We have found only a few MOs prevailingly located at the Mn atom (e.g., β-LUMO+2 to β-LUMO+5). Thus there are no pure d–d electron transitions that could be identified by theory (see Fig. S11, ESI†). It should be noted that the absorption band with a maximum at 732 nm and an extinction coefficient of 950 M−1 cm−1 for MnL(OAc) in CHCl3 was assigned to LMCT from phenolate moieties to manganese(III).16
Spin Hamiltonian parameters
The agreement between the calculated and experimentally determined ZFS is semi-quantitative (Table 4). Irrespective of the reference geometry (exp/opt) or the theoretical level (BLYP/CASSCF), the calculated D values are positive and close to or above 2 cm−1. The largest D values are found for the sa-CASSCF(4,5) treatments. Although these values are closest to the experimentally determined ones, the missing spin–spin contributions and dynamic correlation effects are expected to increase the final value of D above 3 cm−1. The spin–spin contributions for the sa-CASSCF(4,5) wave function evaluated via the minimal MRCI calculation yielded D values above 3 cm−1 indeed. The BLYP D values are the lowest among the theoretically determined ones; still this approach allows one to estimate the ZFS parameters and spin–spin contributions in cases where CASSCF and MRCI levels are not computationally affordable, respectively. The spin–spin contributions to the D parameter in the BLYP calculations are +0.302 cm−1 and +0.295 cm−1 for the optimised and experimentally obtained geometry, respectively. In the case of sa-CASSCF vs. sa-MRCI comparison, the spin–spin contribution is +0.490 cm−1 and +0.470 cm−1 for the optimised and experimental geometry, respectively. Importantly, the calculated E parameters (BLYP as well as CASSCF) of the experimental geometries are found to be closer to the experimentally determined value. Similarly, the sa-MRCI D value of the experimental geometry is closer to the experimentally determined D value compared to the calculation based on the optimised geometry. The better agreement with the measured values for the calculated ZFS parameters of the experimental geometry has to be assigned to geometrical distortions (bond lengths, angles) of the coordination polyhedron present in the crystal structure. Nevertheless, the orientation of the ZFS eigenvectors remains almost the same (and fully in accordance with the symmetry axes of the coordination polyhedron) irrespective of the geometry used, see Fig. 8. In addition, inclusion of dynamic electron correlation is found to be barely important (0.05 cm−1) for the systems under study, see the comparison of CASSCF and NEVPT2 calculations of the small model compound of 1 (see 1model, Fig. S1b,† magnetic data in Table S2, ESI†). BLYP and CASSCF(4,5) g-values are in excellent agreement with the experimentally determined ones, although their consistent theoretical assessment is often difficult. The sa-CASSCF(4,5) g-values are shifted to lower values for the perpendicular gy and gz components.| Theory | Geometry | D (cm−1) | |E| (cm−1) | g x | g y | g z |
|---|---|---|---|---|---|---|
| CASSCF(4,5) | Opt | +2.284 | 0.131 | 2.000 | 1.991 | 1.992 |
| sa-CASSCF(4,5) | Opt | +2.856 | 0.151 | 2.000 | 1.974 | 1.976 |
| sa-MRCI(4,5) | Opt | +3.347 | 0.190 | — | — | — |
| BLYP | Opt | +2.082 | 0.005 | 2.005 | 1.998 | 1.998 |
| CASSCF(4,5) | Exp | +2.076 | 0.354 | 2.000 | 1.999 | 1.999 |
| sa-CASSCF(4,5) | Exp | +2.662 | 0.522 | 1.999 | 1.973 | 1.982 |
| sa-MRCI(4,5) | Exp | +3.132 | 0.630 | — | — | — |
| BLYP | Exp | +1.965 | 0.331 | 2.005 | 1.998 | 1.999 |
| Experimental (low T) | — | +2.526 | 0.443 | 2.000 | 1.995 | 1.998 |
The orientation of the ZFS tensor should be associated with the symmetry of the ligand field, which in turn is usually connected to the geometry of the coordination sphere. Shape measurements can help establish this connection, and indeed, these measures are useful when massive data sets are analysed, where “odd” cases appear as mild “white noise” that has no significant effect on global behaviour. However, studies on isolated examples can lead to erroneous or misleading conclusions, wherein the symmetry suggested by the shape measurements and the electronic density can disagree. This situation could well arise when a complex has a diverse set of coordinated ligands or donor atoms, such as in 1, where DFT calculations show that the xy orbital is magnetic instead of the z2 orbital, and the axial electronic density of this latter orbital is placed on the O–Mn–O axis. These facts support a TBP rather than an SPY geometry as is shown in Fig. 8 for 1. It is therefore better to use a simple, homoleptic model that also avoids steric effects. The [MnCl5]2− complex satisfies these requirements. Whereas in an ideal SPY geometry, the Jahn–Teller effect becomes apparent leading only to elongated forms in the z-axis, both compressed and elongated forms are possible for the TBP ideal geometry. For the TBP, the compressed form is more stable, but is less so than the elongated SPY. The calculated values of D for the optimised ideal SPY and compressed TBP configurations are negative (−3.56 cm−1) and positive (+3.48 cm−1), in agreement with electronic configurations with empty xy and z2 orbitals, respectively. On the other hand, a less constrained optimisation on the TBP geometry leads to a distorted geometry with a slight bending of the axial axis and two equatorial Cl–Mn–Cl angles larger than 120 degrees, similar to that observed in 1. Thus the optimised TBP geometry should be less idealised than that used for the shape measurements and, therefore, the τ parameter in 1 would be underestimated. A monitoring of the conversion between compressed TBP and elongated SPY conformations in the [MnCl5]2− complex was performed by fixing the shortest equatorial Cl–Mn–Cl bond angle (from 120 to 95 degrees) and relaxing the remaining geometrical parameters. The results are summarised in Fig. S12,† which shows that, as in 1, only the geometries close to the ideal compressed TBP conformation show positive D values. From an electronic, and probably also from a geometrical point of view, this discussion guarantees a description of the geometry of 1 as close to a compressed TBP, which supports a z-axis of the tensor oriented along the O–Mn–O axis (Fig. 8) and D > 0.
Conclusions
The use of 1,3-bis(3-aminopropyl)tetramethyldisiloxane for the preparation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 or 2
2 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 condensation products with substituted 2-hydroxybenzaldehydes and 2,6-diformyl-4-methylphenol, respectively, in the presence of some 3d transition metals allowed the synthesis of metal complexes with open-chain ligands,15,16 μ-chlorido-bridged dimanganese(III) species.17 In the present work a five-coordinate HS (S = 2) MnIII complex, MnL(NCS), 1, with an N3(eq)O2(ax) donor set has been prepared and structurally characterised, providing an unprecedented example of using a salen type ligand for the assembly of a metal complex that has not the square-planar or square-pyramidal geometry. Although the geometry of the MnIII ion is far from ideally TBP, it behaves this way from an electronic point of view, in the observation by HFEPR of a positive axial ZFS (D > 0). This is the consequence of an axial compression and is structurally evidenced in the Mn–O distances being significantly shorter than those for Mn–N. A positive D value has been observed for other MnIII centres with TBP geometry.8,9,14 In contrast to our previous HFEPR study of a related complex,16 and others,36d in this case the spectra are of very high quality, allowing even the extraction of fourth order ZFS parameters. This is only the second such definitive determination for a HS d4 complex with a positive D, the first being in a highly distorted six-coordinate MnIII complex.11 These results are in contrast to the more common, axial elongation case, which yields a negative D value,5,7,9,11–13,54 wherein fourth-order terms have been extracted from doped single crystals, and also from powders.7,55,56 Quantum chemical theory analysis of 1 is remarkably successful, despite the complexity of the molecule, in reproducing the spin Hamiltonian parameters – both the ZFS parameters and the g values, as well as in modelling the experimental geometry. It is now clear that not only the electronic structure of HS MnIII in coordination complexes can be well described theoretically, but also this ion is indeed one of the deliciae of HFEPR,7 regardless of whether its Jahn–Teller active geometry is elongated (D < 0) or compressed (D > 0).
2 condensation products with substituted 2-hydroxybenzaldehydes and 2,6-diformyl-4-methylphenol, respectively, in the presence of some 3d transition metals allowed the synthesis of metal complexes with open-chain ligands,15,16 μ-chlorido-bridged dimanganese(III) species.17 In the present work a five-coordinate HS (S = 2) MnIII complex, MnL(NCS), 1, with an N3(eq)O2(ax) donor set has been prepared and structurally characterised, providing an unprecedented example of using a salen type ligand for the assembly of a metal complex that has not the square-planar or square-pyramidal geometry. Although the geometry of the MnIII ion is far from ideally TBP, it behaves this way from an electronic point of view, in the observation by HFEPR of a positive axial ZFS (D > 0). This is the consequence of an axial compression and is structurally evidenced in the Mn–O distances being significantly shorter than those for Mn–N. A positive D value has been observed for other MnIII centres with TBP geometry.8,9,14 In contrast to our previous HFEPR study of a related complex,16 and others,36d in this case the spectra are of very high quality, allowing even the extraction of fourth order ZFS parameters. This is only the second such definitive determination for a HS d4 complex with a positive D, the first being in a highly distorted six-coordinate MnIII complex.11 These results are in contrast to the more common, axial elongation case, which yields a negative D value,5,7,9,11–13,54 wherein fourth-order terms have been extracted from doped single crystals, and also from powders.7,55,56 Quantum chemical theory analysis of 1 is remarkably successful, despite the complexity of the molecule, in reproducing the spin Hamiltonian parameters – both the ZFS parameters and the g values, as well as in modelling the experimental geometry. It is now clear that not only the electronic structure of HS MnIII in coordination complexes can be well described theoretically, but also this ion is indeed one of the deliciae of HFEPR,7 regardless of whether its Jahn–Teller active geometry is elongated (D < 0) or compressed (D > 0).
Upon one-electron cathodic reduction and anodic oxidation of 1, an analogous behaviour was observed with almost full recovery of the initial optical bands at low scan rates during reverse voltammetric scan, confirming the chemical reversibility of these processes. Digital simulation of the cyclic voltammograms yielded the formal potentials for the first electron transfer and the rate constant for this process, ks = 1 × 10−5 cm s−1. This small value confirms the slow electron transfer. X-band EPR spectra recorded in frozen DCM solutions of [1]− indicated reduction to a MnII species, whilst the one-electron-oxidised state [1]+ may be an MnIV species. Calculations confirmed the reduction of MnIII to MnII, but suggested that the oxidation may be ligand centred. Future work will involve deeper investigation of the redox forms of these salen-type Schiff base complexes with varying metal ions.
Conflicts of interest
The authors declare no competing interest.Acknowledgements
This work was supported by grants from the Romanian Ministry of National Education, CNCS – UEFISCDI under project numbers PN-III-P4-ID-PCE-2016-0642 and PN-II-CT-RO-AT-2013-1 (contract no. 749/2014). We acknowledge financial support from the Austrian Agency for International Cooperation in Education and Research (OEAD) (grant no. SK02/2013 and RO01/2014). This work was supported by the Science and Technology Assistance Agency under contract no. APVV-15-0053 and APVV-15-0079 and by the Slovak Grant Agency VEGA under contract no. 1/0598/16 and 1/0416/17. We thank the HPC Center at the Slovak University of Technology in Bratislava, which is a part of the Slovak Infrastructure of High Performance Computing (SIVVP Project, ITMS code 26230120002, funded by the European Region Development Funds), for computing facilities. Part of this work was done at the NHMFL, Tallahassee, FL, USA, which is funded by the NSF (cooperative agreement no. DMR 1157490), the State of Florida, and the US Department of Energy. We thank Prof. T. David Harris and Jordan A. DeGayner, Northwestern University, for helpful discussions. This work was supported by the MICIIN (Spain) (projects CTQ2016-75671-P and MDM-2015-0538), the Generalitat Valenciana (Spain) (project PROMETEOII/2014/070). Dr Andrew Ozarowski is acknowledged for providing his EPR simulation and fit program SPIN. VBA thanks the COST Action CM1305 (ECOSTBio) for support.References
- V. K. Yachandra, K. Sauer and M. P. Klein, Chem. Rev., 1996, 96, 2927–2950 CrossRef CAS PubMed.
- A. B. Tomter, G. Zoppelaro, N. H. Andersen, H.-P. Hersleth, M. Hammerstad, Å. K. Røhr, G. K. Sandvik, G. E. Nilsson, C. B. Bell, A. L. Barra, E. Blasco, L. Le Pape, E. I. Solomon and K. K. Andersson, Coord. Chem. Rev., 2013, 257, 3–26 CrossRef CAS.
- D. W. Christianson, Prog. Biophys. Mol. Biol., 1997, 67, 217-243–245-252 CrossRef.
- R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011–1026 RSC.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC.
- G. A. Craig, J. J. Marbey, S. Hill, O. Rubeau, S. Parsons and M. Murrie, Inorg. Chem., 2015, 54, 13–15 CrossRef CAS PubMed.
- I. Krivokapic, C. Noble, S. Klitgaard, P. L. W. Tregenna-Piggott, H. Weihe and A.-L. Barra, Angew. Chem., Int. Ed., 2005, 44, 3613–3616 CrossRef CAS PubMed.
- R. Gupta, T. Taguchi, A. S. Borovik and M. P. Hendrich, Inorg. Chem., 2013, 52, 12568–12575 CrossRef CAS PubMed.
- (a) J. Telser, J. Krzystek and A. Ozarowski, J. Biol. Inorg. Chem., 2014, 19, 297–318 CrossRef CAS PubMed; (b) J. Krzystek, A. Ozarowski and J. Telser, Coord. Chem. Rev., 2015, 301–302, 123–133 CrossRef CAS; (c) J. Krzystek and J. Telser, Dalton Trans., 2016, 45, 16751–16763 RSC.
- J. Valejo, A. Pascual-Alvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef PubMed.
- Q. Scheifele, C. Riplinger, F. Neese, H. Weihe, A.-L. Barra, F. Juranyi, A. Podlesnyak and P. L. W. Tregenna-Piggott, Inorg. Chem., 2008, 47, 439–447 CrossRef CAS PubMed.
- C. Mantel, H. Chen, R. H. Crabtree, G. W. Brudwig, J. Pécaut, M.-N. Collomb and C. Duboc, ChemPhysChem, 2005, 6, 541–546 CrossRef CAS PubMed.
- B. Albela, R. Carina, C. Policar, S. Poussereau, J. Cano, J. Guilhem, L. Tchertanov, G. Blondin, M. Delroisse and J.-J. Girerd, Inorg. Chem., 2005, 44, 6959–6966 CrossRef CAS PubMed.
- J. Krzystek, J. Telser, J. Li and M. A. Subramanian, Inorg. Chem., 2015, 54, 9040–9045 CrossRef CAS PubMed.
- A. Soroceanu, M. Cazacu, S. Shova, C. Turta, J. Kožíšek, M. Gall, M. Breza, P. Rapta, T. C. O. Mac Leod, A. J. L. Pombeiro, J. Telser, A. A. Dobrov and V. B. Arion, Eur. J. Inorg. Chem., 2013, 1458–1474 CrossRef CAS.
- M. Cazacu, S. Shova, A. Soroceanu, P. Machata, L. Bucinsky, M. Breza, P. Rapta, J. Telser, J. Krzystek and V. B. Arion, Inorg. Chem., 2015, 54, 5691–5706 CrossRef CAS PubMed.
- M. Alexandru, M. Cazacu, A. Arvinte, S. Shova, C. Turta, B. C. Simionescu, A. Dobrov, E. C. B. A. Alegria, L. M. D. R. S. Martins, A. J. L. Pombeiro and V. B. Arion, Eur. J. Inorg. Chem., 2014, 120–131 CrossRef CAS.
- J. Krzystek, S. A. Zvyagin, A. Ozarowski, S. Trofimenko and J. Telser, J. Magn. Reson., 2006, 178, 174–183 CrossRef CAS PubMed.
- CrysAlis RED, Version 1.171.36.32, Oxford Diffraction Ltd, 2003 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- J. Cano, XVPMAG Package, University of València, Spain, 2013 Search PubMed.
- A. K. Hassan, L. A. Pardi, J. Krzystek, A. Sienkiewicz, P. Goy, M. Rohrer and L.-C. Brunel, J. Magn. Reson., 2000, 142, 300–312 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Paramagnetic Resonance of Transition Ions (Oxford Classic Texts in the Physical Sciences), Oxford University Press, Oxford, UK, 2012 Search PubMed.
- (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5651 CrossRef CAS.
- (a) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS; (b) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- M. J. Frisch et al. , Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013; http://www.gaussian.com Search PubMed.
- (a) R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS; (b) M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS.
- (a) G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed; (b) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS; (b) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS; (c) A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033–1036 CrossRef CAS.
- (a) J. E. Carpenter and F. Weinhold, THEOCHEM, 1988, 169, 41–62 CrossRef; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- V. Bachler, G. Olbrich, F. Neese and K. Wieghardt, Inorg. Chem., 2002, 42, 4179–4193 CrossRef.
- U. Varetto, MOLEKEL 5.4.0.8, Swiss National Supercomputing Centre, Lugano, Switzerland (available via the Internet at: http: //molekel.cscs.ch/wiki/pmwiki.php) Search PubMed.
- ORCA program system: F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- (a) F. Neese, J. Chem. Phys., 2007, 127, 164112 CrossRef PubMed; (b) F. Neese, First principles approach to Spin-Hamiltonian Parameters, in Multifrequency EPR: Theory and Applications, ed. S. K. Misra, Wiley-VCH, 2009, pp. 297–326 Search PubMed; (c) S. Zein and F. Neese, J. Phys. Chem. A, 2008, 112, 7976–7983 CrossRef CAS PubMed; (d) S. Romain, C. Duboc, F. Neese, E. Riviere, L. R. Hanton, A. G. Blackman, C. Philouze, J.-C. Lepretre, A. Deronzier and M.-N. Collomb, Chem. – Eur. J., 2009, 15, 980–988 CrossRef CAS PubMed.
- (a) F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed; (b) C. Duboc, D. Ganyushin, K. Sivalingam, M. N. Collomb and F. Neese, J. Phys. Chem. A, 2010, 114, 10750–10758 CrossRef CAS PubMed.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS; (b) C. Angeli, R. T. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS; (c) C. Angeli, R. T. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and C. G. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356 RSC.
- J. Cirera, P. Alemany and S. Alvarez, Chem. – Eur. J., 2004, 10, 190–207 CrossRef CAS PubMed.
- Y. J. Park, E. M. Matson, M. J. Nilges and A. R. Fout, Chem. Commun., 2015, 51, 5310–5313 RSC.
- Z. Shirin, V. G. Young, Jr. and A. S. Borovik, Chem. Commun., 1997, 1967–1968 RSC.
- C. E. MacBeth, R. Gupta, K. R. Mitchell-Koch, V. G. Young, Jr., G. Lushington, W. H. Thompson, M. P. Hendrich and A. S. Borovik, J. Am. Chem. Soc., 2004, 126, 2556–2567 CrossRef CAS PubMed.
- Y. J. Park, J. W. Ziller and A. S. Borovik, J. Am. Chem. Soc., 2011, 133, 9258–9261 CrossRef CAS PubMed.
- (a) H. N. Ng and C. Calvo, Can. J. Chem., 1972, 50, 3619–3624 CrossRef; (b) A. R. Coffino and J. Peisach, J. Magn. Reson., 1996, 111, 127–134 CrossRef CAS.
- χ M T = (Nβ2g2/3kB) S(S + 1) = 3.0 cm3 mol−1 K with S = 2 and g = 2.0, where N is the Avogadro number, β is the Bohr magneton, and kB is the Boltzmann constant.
- J. S. Griffith, The Theory of Transition Metal Ions, Cambridge University Press, Cambridge, UK, 1964, ch. 4 Search PubMed.
- H. J. Gerritsen and E. S. Sabisky, Paramagnetic resonance of trivalent manganese in rutile (TiO2), Phys. Rev., 1963, 132, 1507–1512 CrossRef CAS.
- K. A. Campbell, E. Yikilmaz, C. V. Grant, W. Gregor, A.-F. Miller and R. D. Britt, J. Am. Chem. Soc., 1999, 121, 4714–4715 CrossRef CAS.
- The ZFS parameters in this system were slightly dependent on the Mn(III) doping level; D = 3.0 cm−1 is of sufficient precision for the present comparison.
- Another six-coordinate complex, [Mn(tolylterpy)2](X)3 (1(X)3; X = BF4, ClO4, PF6; tolyl-terpy = 4′-(4-methylphenyl)-2,2′:6′,2′′-terpyridine) was determined to have a positive D value by magnetometry; HFEPR was unsuccesful.36d.
- The TBP Mn(III) complex studied by Gupta et al.8 is nearly axial: |E/D| = 0.05, while MnSOD exhibited E/D = 0.11; hardly surprising given the low symmetry inherent in a biological centre.
- The six-coordinate [Mn(bpia)(OAc)(OMe)]+ complex also exhibited a large rhombicity: D = +3.526(3) cm−1, E = 0.588(6) cm−1, E/D = 0.167.
- S. Mossin, H. Weihe and A.-L. Barra, J. Am. Chem. Soc., 2002, 124, 8764–8765 CrossRef CAS PubMed.
- G. Aromi, J. Telser, A. Ozarowski, L.-C. Brunel, H.-M. Stoeckli-Evans and J. Krzystek, Inorg. Chem., 2005, 44, 187–196 CrossRef CAS PubMed.
- There is a special case of a MnIII coordination complex with axial elongation for which D > 0.54 This complex, trans-[Mn(cyclam)I2]I, cannot be described by a simple LFT model (i.e., using only the d4 basis set), because of spin delocalisation onto the iodido ligand(s), so that there is contribution from what can be described loosely as [MnIII˙]2+ as well as classically as [MnIIII−]2+. The large SOC from the iodido ligand(s) has a contribution to D that is opposite in sign to that from Mn so that the net ZFS is positive.
Footnote |
| † Electronic supplementary information (ESI) available: Structures of 1 and of the small model compound 1model (Fig. S1), UV-vis spectrum of 1 (Fig. S2), UV-vis-NIR spectra recorded upon oxidation/reduction (Fig. S3 and S4), cyclic voltammograms of 1 and digital simulations (Fig. S5), temperature dependence of the χ′M (right) and χ′′M (left) of 1 in a dc applied static field of 0.0 kG (a), 1.0 kG (b) and 2.5 kG (c) and under ±4.0 G oscillating field at frequencies of 10 (blue), 100 (red) and 1000 Hz (black) (Fig. S6), HFEPR spectra of 1 (Fig. S7–S9), DFT spin density of 1 (Fig. S10), frontier DFT molecular orbitals of 1 (Fig. S11); a plot of D vs. the shortest equatorial ClMnCl angle in [MnCl5]2− (Fig. S12); table of bond lengths and angles for 1 obtained by X-ray experiments and by DFT optimisation (Table S1), calculated ZFS parameters of 1model (Table S2), DFT calculated spin squares (〈S2〉), DFT energies (EDFT), free energies at 298 K (G298) (Table S3), NBO parameters of 1 in various spin states (Table S4), and calculated electron transitions for 1 in methanol (Table S5). CCDC 1515780. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7dt01809f |
| This journal is © The Royal Society of Chemistry 2017 |