Magnetically frustrated synthetic end member Mn₂(PO₄)OH in the triplite–triploidite family

Abstract

The manganese end member of triplite–triploidite series of compounds, Mn₂(PO₄)OH, is synthesized by a hydrothermal method. Its crystal structure is refined in the space group P2₁/c with a = 12.411(1) Å, b = 13.323(1) Å, c = 10.014(1) Å, β = 108.16(1), V = 1573.3 ų, Z = 8, and R = 0.0375. Evidenced in measurements of magnetization M and specific heat C_p, Mn₂(PO₄)OH reaches a long range antiferromagnetic order at T_N = 4.6 K. As opposed to both triplite Mn₂(PO₄)F and triploidite-type Co₂(PO₄)F, the title compound is magnetically frustrated being characterized by the ratio of Curie–Weiss temperature Θ to Néel temperature T_N of about 20. The large value of frustration strength |Θ|/T_N stems from the twisted saw tooth chain geometry of corner sharing triangles of Mn polyhedra, which may be isolated within tubular fragments of a triploidite crystal structure.

---

Introduction

The key factors leading to the suppression of the magnetic ordering temperature as compared to the values of leading exchange interactions in the crystal are reduced dimensionality and frustration. The combination of these factors may result in huge values of the ratio |Θ|/T_N ≥ 50 realized in some triangular or kagomé lattices,^1,2 albeit some recently investigated representatives of this multitude possess a frustration strength |Θ|/T_N ≤ 10.³ Comparable values of the frustration strength are realized in some three-dimensional magnets represented by numerous garnets, pyrochlores or spinels.^4–6 Nevertheless, any object with Curie–Weiss temperature Θ exceeding Néel temperature T_N by an order of magnitude belongs to the field of highly frustrated magnetism. This flourishing field attracts attention as an “excellent playground to discover new states and new properties of matter” including gapped and gapless spin liquids, spin ices, spin nematics, etc.⁷ It should be noted, however, that these ground states should be distinguished from those realized in magnetically ordered, commensurate or incommensurate, magnetic structures due to some degree of frustration.

The geometric frustration in three-dimensional magnets is associated usually with the triangular motif in the arrangement of magnetically active ions. Thus, a three-dimensional network of corner-sharing tetrahedra constitutes the magnetic subsystem in cubic transition metal spinels and in rare-earth pyrochlores. The ferrite structure can be considered as a sequence of frustrated kagomé and triangular layers stacked alternatively to form a three-dimensional arrangement. Significantly more complicated is the magnetic network of frustrating units in garnets represented by interpenetrating rings of corner-sharing triangles. The transition metal based members of the garnet's family exhibit only modest degree of frustration |Θ|/T_N ∼ 3.^8–10 Also, there are three-dimensional heavily frustrated magnets having hyper-kagomé¹¹ or tetragonal pyrogermanate structures,¹² but not many.

In this work, we present a candidate for a frustrated magnet that belongs to a completely different structure type, i.e. triploidite Mn₂(PO₄)OH. The name “triploidite” indicates “near triplite” and specifies a manganese phosphate similar to triplite, Mn₂(PO₄)F, but containing hydroxyl instead of fluorine. A triploidite group of minerals unites isotypic monoclinic phosphates and arsenates with the general formula M₂(TO₄)Z and besides triploidite itself, Mn₂(PO₄)(OH), includes wagnerite, Mg₂(PO₄)F, hydroxylwagnerite, Mg₂(PO₄)(OH), wolfeite, Fe₂(PO₄)(OH) and sarkinite, Mn₂(AsO₄)(OH). All of them crystallize in a space group P2₁/c and have a b cell parameter of about 13 Å. For triplite group of minerals described by the same general formula, the b cell parameter is twice smaller and the monoclinic unit cell is Bravais centered (space group C2/c).¹³ Nevertheless, the crystal structures of minerals of both groups have very similar topologies. Natural mineral phases belonging to the triplite–triploidite supergroup¹⁴ often present solid solutions of Mg/Fe/Mn on one hand and F/OH on the other hand. Recent X-ray diffraction studies of more than 40 mineral samples have shown that their crystal structures may be periodically or aperiodically modulated. It has been suggested that they should be described in the framework of a superspace model with the (3 + 1)-dimensional space group C2/c(0β0)s0 based on the average triplite structure and the modulation vector q = βb*.¹⁵

Besides minerals, the large series of synthetic analogues – mainly phosphates and some arsenates – were obtained and structurally investigated (Table S1†). They are the end members without isomorphic substitutions and thus, no modulations have been noticed in connection with these triplite- or triploidite-like crystal structures. Curiously, synthetic phases with triplite structures present fluoride-phosphate solely, while triploidite-like compounds are possible to grow both as F- or OH-varieties. Despite the fact that many chemical compositions were realized as laboratory prototypes of minerals, the synthetic triploidite Mn₂(PO₄)OH has not been obtained so far. Here, we report the hydrothermal synthesis, crystal structure refinement and thermodynamic properties of Mn₂(PO₄)OH. Unexpectedly, this compound was found to be magnetically frustrated, as opposed to both triplite Mn₂(PO₄)F and triploidite-type Co₂(PO₄)F, but similar to Mn₂(AsO₄)OH.¹⁶ In variance with numerous frustrated antiferromagnets of a pyrochlore or spinel type possessing a three-dimensional triangular magnetic lattice, the Mn₂(PO₄)OH represents a rare case of corner-sharing twisted saw tooth chain magnetic system.

Experimental

Single crystals of Mn₂(PO₄)OH were synthesized under mild hydrothermal conditions. A starting mixture of MnCl₂–H₃PO₄–Na₂B₄O₇ in a 1 : 1 : 1 weight ratio was dissolved in distilled water, sealed in a PTFE-lined stainless-steel pressure vessel (fill factor 80%) and kept at 170° C for 18 days, followed by slow cooling to room temperature. The reaction products were washed with water and dried. The colourless transparent needle-like single crystals of Mn₂(PO₄)(OH) of about 600 μm in length are shown in Fig. 1. These crystals constitute about 70% of the total yield along with fine-crystalline ameghinite, NaB₃O₅(H₂O)₂, as confirmed by X-ray diffraction analysis of a powder sample.

Fig. 1 Photograph of crystals of the title compound.

The composition of the title compound was analyzed with a scanning electron microscope JSM6480LV equipped with an INCA Energy-350 energy dispersive detector and an INCAWave-500 four-crystal wavelength dispersive spectrometer.‡ The measurements were made at 20 kV and 7 nA, and the sample was stable under these conditions. X-ray spectral analysis provided a semi-quantitative result with the Mn : P : O ratios close to 2 : 1 : 5, which is consistent with the results of the X-ray diffraction structural study. No impurity elements were found in the crystals’ composition.

Single crystal X-ray diffraction data were collected at ambient temperature by using MoK_α radiation with an Oxford Diffraction Xcalibur-S area detector diffractometer. Recorded reflection intensities (full sphere of reciprocal space) were corrected for Lorentz and polarization effects, and a numerical absorption correction based on Gaussian integration over a multifaceted crystal model was applied. All calculations were performed in the WinGX32 software package.¹⁷ Atomic scattering factors and anomalous dispersion corrections were taken from the International Tables for Crystallography.¹⁸ The crystal structure was solved via direct methods in the space group P2₁/c with the SHELXT program.¹⁹ Atomic positions were refined against the F² data using SHELXL programs²⁰ with anisotropic displacement parameters for all non-H atoms. Four symmetrically independent H atoms forming hydroxyl groups were obtained by difference-Fourier techniques and refined in an isotropic approximation. The O–H bond lengths were fixed by hard restraints to an empirical value of 0.80 Å in order to obtain comparable H-bond geometry not affected by arbitrary scattering of the refined O–H distances. The main crystallographic characteristics of synthetic triploidite Mn₂(PO₄)OH and experimental parameters for data collection and structure refinement are summarized in Table 1.

Table 1 Crystal information and details of data collection and refinement

Formula	Mn2(PO4)(OH)
Absorption μ [mm^−1]	6.725
Space group	P21/c, Z = 8
a, b, c (Å)	10.0142(8), 13.323(1), 12.411(1)
β (°), V (Å^3)	108.16(1), 1573.3(1)
F(000), density Dcalc [g cm^−3]	1696, 3.747
Crystal size [mm]	0.08 × 0.01 × 0.01
Radiation	MoKα (λ = 0.71073 Å)
Temperature [K]	293(2)
Scanning mode	ω scan
Measuring range	Max θ = 26.50°
h, k, l ranges	−12 ≤ h ≤ 12, −16 ≤ k ≤ 16, −15 ≤ l ≤ 15
Absorption correction	Numerical (Gaussian)
T min, Tmax	0.857, 0.966
R int/Rσ	0.043/0.023
Reflections total/unique/observed [I > 2σ(I)]	23 812/3261/2701
Parameters	306
R (observed refl.)	0.0375
R, wR2 (all refl.)	0.0510, 0.0668
Goodness of fit	1.295
Extinction coefficient	0.00035(5)
δρ (max)/(min) [e Å^−3]	0.491/−0.462

---

The final atom positions are given in Table S2,† while Table 2 reports characteristic distances. The hydrogen bonds’ geometry is presented in Table 3. A bond-valence calculation (Table S3†) has been performed using the algorithm and parameters given in ref. 21. Valence contributions of the H atoms were estimated from O–O distances following the equations from ref. 22; the relationship between the O–O distance and H–O (acceptor) bond valence is calculated from the O–H curve of ref. 23. Data from Table S3† confirm clearly the assignment of O and OH ligands; these data are consistent with the assumed oxidation state of manganese ions, i.e. Mn²⁺.

Table 2 Mn₂(PO₄)OH bond lengths, Å

Mn1-octahedron	Mn2-bipyramid	Mn3-bipyramid
Mn1–O12 2.139(3)	Mn2–O12^#1 2.087(3)	Mn3–O9 2.083(3)
–O4 2.158(3)	–O19 2.099(2)	–O17 2.101(3)
–O6 2.170(3)	–O14 2.116(3)	–O15 2.102(3)
–O16 2.202(2)	–O7 2.134(3)	–O18 2.109(3)
–O5 2.209(3)	–O4 2.189(3)	–O17^#2 2.223(3)
–O7 2.299(3)
<Mn1–O > 2.196	<Mn2–O > 2.125	<Mn3–O > 2.124

---

Mn4-octahedron	Mn5-octahedron	Mn6-bipyramid
Mn4–O9 2.150(3)	Mn5–O12^#4 2.166(3)	Mn6–O5 2.086(3)
–O3 2.185(3)	–O13 2.166(3)	–O10 2.109(3)
–O2 2.194(3)	–O2 2.184(3)	–O18 2.126(3)
–O8 2.196(3)	–O16^#4 2.234(3)	–O19^#5 2.204(3)
–O1^#3 2.237(3)	–O8 2.258(3)	–O20 2.239(3)
–O1 2.239(3)	–O11 2.340(3)
<Mn4–O > 2.200	<Mn5–O > 2.225	<Mn6–O > 2.153

---

Mn7-bipyramid	Mn8-octahedron	P1-tetrahedron
Mn7–O8 2.095(3)	Mn8–O9 2.174(3)	P1–O11^#8 1.534(3)
–O20^#6 2.130(3)	–O6 2.180(3)	–O15^#9 1.540(3)
–O14^#7 2.154(3)	–O11^#6 2.194(3)	–O14^#10 1.547(3)
–O15 2.181(3)	–O5 2.229(3)	–O7 1.548(3)
–O10^#6 2.188(3)	–O13^#6 2.275(3)	<P1–O > 1.542
	–O3 2.320(3)
<Mn7–O > 2.150	<Mn8–O > 2.229

---

P2-tetrahedron	P3-tetrahedron	P4-tetrahedron
Symmetry transformations used to generate equivalent atoms: #1 x, −y + ½, z + ½; #2 −x, −y, −z + 1; #3 −x, −y, −z + 2; #4 x − 1, y, z; #5 x, −y + ½, z − ½; #6 −x, y − ½, −z + 1½; #7 x − 1, −y + ½, z − ½; #8 x + 1, y, z; #9 x + 1, −y + ½, z + ½; #10 −x + 1, −y + 1, −z + 2; #11 −x + 1, −y, −z + 2; #12 −x, y + ½, −z + 1½.
P2–O16^#4 1.535(3)	P3–O17^#1 1.531(3)	P4–O3 1.533(3)
–O13^#1 1.542(3)	–O2 1.536(3)	–O6^#11 1.537(3)
–O18^#1 1.550(3)	–O19 1.542(3)	–O4 1.545(3)
–O1 1.553(3)	–O20 1.546(3)	–O10^#1 1.554(3)
<P2–O > 1.545	<P3–O > 1.539	<P4–O > 1.542

---

Table 3 Geometry of hydrogen bonds

D–H⋯A	d(D–H), Å	d(H⋯A), Å	d(D⋯A), Å	∠(DHA), °
Symmetry transformations used to generate equivalent atoms are as shown in footnotes for Table 2.
O9–H1⋯O13^#6	0.800(1)	2.24(4)	2.784(4)	125(4)
O9–H1⋯O17^#2	0.800(1)	2.33(4)	2.811(4)	120(4)
O5–H2⋯O3	0.800(1)	2.36(3)	2.872(4)	122(4)
O5–H2⋯O4	0.800(1)	2.56(3)	3.003(4)	117(3)
O12–H3⋯O4^#5	0.800(1)	2.36(4)	2.818(4)	117(4)
O12–H3⋯O10	0.800(1)	2.60(3)	3.182(4)	131(4)
O12–H3⋯O11^#8	0.800(1)	2.34(4)	2.885(4)	126(4)
O8–H4⋯O1	0.800(1)	2.65(3)	3.122(4)	120(3)
O8–H4⋯O16^#4	0.800(1)	2.23(4)	2.767(4)	125(4)

---

Results

Crystal structure

The basic structural units of synthetic triploidite, Mn₂(PO₄)OH, are shown in Fig. 2. Eight symmetrically independent Mn²⁺ ions, all in general structural positions are surrounded by six or five oxygen atoms forming octahedra and five-vertex polyhedra. The interatomic Mn–O distances in the Mn-centered octahedra vary from 2.139(3) to 2.340(3) Å. Each of the four MnO₄(OH)₂ octahedra has in its first coordination sphere two OH ligands in the cif-conformation. The morphology of MnO₄(OH) five-vertex polyhedra can be defined as distorted trigonal-bipyramids with Mn–O distances ranging between 2.083(3) and 2.239(3) Å. The shortest bond lengths match Mn–OH contacts in all bipyramids (Table 2). The four non-equivalent P atoms have similarly distorted tetrahedral surroundings with P–O distances that vary from 1.531(3) to 1.554(3) Å, and nearly equal average P–O values of 1.54 Å.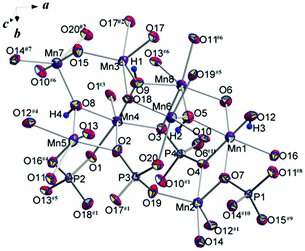

Fig. 2 Basic structural units with atom labeling scheme. Displacement ellipsoids are presented at the 90% probability level. See symmetry codes in footnotes for Table 2.

The positions and refinement of the H atoms has allowed a detailed analysis of the H bonds’ peculiarities (Table 3). The system of O–H–O asymmetrical H bonds between OH groups and O atoms provides additional crosslinking in the structure. With O–O distances between 2.767(4) and 3.182(4) Å, they are classified as weak and very weak bonds. Three of the four hydroxyl groups are involved in bifurcated hydrogen bonding, while the fourth hydrogen atom (H3) forms a trifurcated hydrogen bond. Typically for inorganic compounds, all hydrogen bonds are meaningfully non-linear with O–H⋯O angles ranging between 117(3) and 126(4)°.

Three varieties of topologically distinct strongly corrugated chains built of Mn-centered polyhedra sharing edges and vertices may be distinguished in the crystal structure, as shown in Fig. 3. The chains of the first type are aligned parallel to the b axis of the unit cell and are formed from alternating pairs of sharing edges of MnO₄(OH)₂ octahedra and MnO₄(OH) bipyramids linked through common vertices of neighbouring polyhedra according to the scheme: Mn5O₄(OH)₂ = Mn8O₄(OH)₂–Mn6O₄(OH) = Mn7O₄(OH)–Mn5O₄(OH)₂ = Mn8O₄(OH)₂…, where “=” denotes the shared edges and “–” signifies the shared polyhedron vertices. The same way of alternation (octahedron = octahedron–bipyramid = bipyramid–octahedron = octahedron…) is realized in the chains of the second type ranged along the c axis and built of Mn-centered polyhedra sharing edges and vertices: Mn4O₄(OH)₂ = Mn4O₄(OH)₂–Mn3O₄(OH) = Mn3O₄(OH)–Mn4O₄(OH)₂ = Mn4O₄(OH)₂…. The third sort of chains also parallel to the [001] direction, consists of Mn2- and Mn1-centered polyhedra, which are placed along the chain in the following mode: Mn2O₄(OH) = M14O₄(OH)₂–Mn2O₄(OH) = Mn1O₄(OH)₂–Mn2O₄(OH) = Mn1O₄(OH)₂…, e.g. the octahedra and trigonal bipyramids share edges and vertices, and alternate within this chain in contrast to the case of triplite where an interchange of polyhedra obeys the rule: two octahedra–two bipyramids. Along the a axis the described chains of octahedra and trigonal bipyramids interconnect in a three-dimensional cationic framework through common edges and vertices as shown in Fig. 4. Anionic [PO₄]³⁻ oxo-complexes strengthen the framework by sharing all vertices of tetrahedra with Mn-centered polyhedra (Fig. S1†).

Fig. 3 Three types of chains built by Mn-centered polyhedra that form the cationic framework of the Mn₂(PO₄)OH crystal structure.

Fig. 4 Topological scheme of Mn²⁺ cationic substructure of the synthetic triploidite. Mn²⁺ cations are shown as spheres with numbers. Solid lines indicate edge sharing of MnO₄(OH)₂ octahedra and MnO₄(OH) bipyramids; dotted lines specify vertex sharing of neighbouring polyhedra.

From the magnetic standpoint one can presume that edge-sharing polyhedra are coupled by ferromagnetic exchange interaction, while the vertex-sharing units are coupled by antiferromagnetic exchange interactions.²⁴ The first principles calculation of relative strength of these interactions in Mn₃(PO₄)₂ phases²⁵ in comparison to exchange interactions through [PO₄]³⁻ groups has allowed neglecting the latter.

Physical properties

The properties of Mn₂(PO₄)OH, i.e. magnetization M and specific heat C_p, were investigated using relevant options of “Quantum Design” Physical Properties Measurement System PPMS-9T in the range 2–300 K. The temperature dependence of magnetic susceptibility χ = M/B of Mn₂(PO₄)OH taken at B = 0.1 T is shown in Fig. 5. Below room temperature, the χ(T) dependence follows the Curie−Weiss law χ = χ₀ + C/(T − Θ) modified by the addition of the temperature-independent term χ₀. The fit in the range 200–300 K with χ₀ = 9.6 × 10⁻⁴ emu mol⁻¹ yields Curie constant C = 8.66 emu K mol⁻¹ and Weiss temperature Θ = −88 K. The value of C corresponds to the squared effective magnetic moment μ_eff² = 69.3μ_B² per formula unit, which is in good agreement with the calculated value μ_eff² = ng²S(S + 1)μ_B² = 70μ_B² for two magnetically active Mn²⁺ ions (S = 5/2) per formula unit (n = 2) and g factor g = 2. A large negative value of Θ indicates the predominance of antiferromagnetic exchange interactions at room temperature.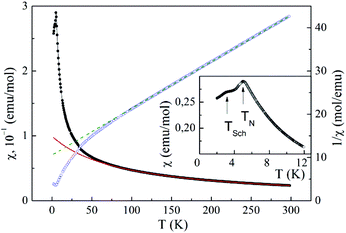

Fig. 5 The temperature dependences of both direct and inverse magnetic susceptibility in Mn₂(PO₄)OH taken at B = 0.1 T. The inset enlarges the low-temperature data.

At about 50 K, the χ(T) dependence deviates upward from the extrapolation of the Curie–Weiss law which evidences the presence of ferromagnetic exchange interactions. The sharp peak at about 5 K marks the transition into a long range antiferromagnetic state. Strictly speaking, the phase transition into a magnetically ordered state is defined by singularity in dχ/dT vs. T dependence, rather than singularity in χ(T) dependence itself, cf. specific heat data. Below this temperature, an additional relatively broad anomaly is seen at T_Sch = 3 K.

The field dependence of magnetization M(B) in Mn₂(PO₄)OH obtained at T = 2 K is shown in Fig. 6. The magnetization increases non-monotonously reflecting tentatively the spin-flop transition marked by a sharp peak in dM/dB vs. B dependence, as shown in the inset to Fig. 6. The low value of spin-flop field B_SF = 0.9 T is consistent with low crystalline anisotropy assumed for Mn²⁺ ions. At B = 9 T, the magnetization reaches only quarter of presumed saturation magnetization of about 10μ_B signaling rather large values of exchange interaction parameters in Mn₂(PO₄)OH.

Fig. 6 The field dependence of magnetization in Mn₂(PO₄)OH at T = 2 K. The arrow at B_SF denotes the spin-flop transition. The inset represents the dM/dB vs. B dependence.

Further evidence of long range magnetic ordering was obtained in measurements of specific heat C_p. Its temperature dependence is shown in Fig. 7. Along with a sharp peak at T_N = 4.6 K two broad Schottky-type anomalies can be seen both below and above the Néel temperature. The low temperature Schottky-type anomaly is more pronounced in C_p/T vs. T presentation of experimental data, as shown in the inset to Fig. 7. The Schottky-type anomalies in both magnetic susceptibility and specific heat could be ascribed to some non-magnetic entity (tentatively hydrogen), since it is virtually insensitive to an external magnetic field.

Fig. 7 The temperature dependence of specific heat in Mn₂(PO₄)OH. The inset visualizes the low temperature Schottky-type anomaly at T_Sch = 3 K.

The magnetic entropy released at T < T_N constitutes about 20% of the total magnetic entropy S_magn = nR ln(2S + 1), where R is the universal gas constant. This fact is in correspondence with a large value of the |Θ|/T_N ratio indicating that magnetic entropy is released mainly at the formation of a short-range correlation regime well above the Néel temperature.

Discussion

Despite the fact that physical properties of both natural and synthetic triplite–triploidite series of compounds are not well documented yet, it is possible to state that the magnetic Mn₂(PO₄)OH phase stands well apart from any other member of this family studied so far. Thus, both triplite Mn₂(PO₄)F and triploidite-type Co₂(PO₄)F compounds²⁶ are characterized by modest frustration strength |Θ|/T_N ∼ 3. The same refers to Fe₂(AsO₄)F with a triplite structure.²⁷

The geometry of strongly corrugated intersecting chains of Mn-centered polyhedra in Mn₂(PO₄)OH (Fig. 3 and 4) does not presume heavy magnetic frustration, at least when the next-nearest-neighbor interactions are not taken into account. These chains are composed of edge- and vertex-sharing units, which presume an alternation of ferromagnetic and antiferromagnetic exchange interactions in accordance with Goodenough–Kanamori–Anderson rules. The competition between antiferromagnetic and ferromagnetic interactions may lead to the suppression of Weiss temperature but does not influence the Néel temperature significantly.

Therefore, the source of heavy frustration is to be seen in the arrangement of Mn-centered polyhedra along the a axis. The vertex-sharing polyhedra in the Mn₂(PO₄)OH crystal structure form the tubular fragment, as shown in Fig. 8a. Within these tubes the twisted saw tooth chain arrangement of vertex-sharing Mn-centered polyhedra can be identified, as shown in Fig. 8b. This arrangement is topologically equivalent to the ribbon cut from the highly frustrated kagomé lattice. The interactions between tubes in the Mn₂(PO₄)OH triploidite structure are provided by edge-sharing polyhedra (see Fig. 4), being tentatively ferromagnetic.

Fig. 8 Tubular structural fragment formed by Mn²⁺ cations shown along the a axis (a). The geometry of corner-sharing twisted saw tooth chain within the tube of Mn atoms (b).

Despite the fact that the Co₂(PO₄)F triploidite-type phase is isostructural to the title compound, it is not heavily frustrated. In the case of Co₂(PO₄)F, the polyhedra within the tubular fragments running along the a axis share both fluorine and oxygen vertices. The presumed difference in bonding through the overlap of d orbitals of Mn²⁺ ions with p orbitals of either F⁻ or O²⁻ ions lifts the frustration. The triplite, Mn₂(PO₄)F, is not frustrated, since no triangular motif can be identified in the crystal structure of this compound organized by edge-sharing octahedra.

Let us note here that phosphate mineral analogues Co₂(PO₄)OH and Cu₂(PO₄)OH can be obtained in completely different structure types, the former showing the spin-glass behavior and the latter showing properties of the spin liquid.²⁸

Conclusions

Summarizing, we have found that synthetic triploidite, Mn₂(PO₄)OH, is characterized by the strength of magnetic frustration comparable to that seen in geometrically frustrated spinels, pyrochlores or garnets. This three-dimensional antiferromagnetic phase possesses the high ratio of magnetic frustration due to the twisted saw tooth chain geometry of antiferromagnetically coupled polyhedra within ferromagnetically coupled tubes. The predominance of antiferromagnetic exchange interactions follows from the large negative value of Weiss temperature. At the same time, the presence of the ferromagnetic exchange interactions in the structure of Mn₂(PO₄)OH is evidenced by a strong deviation of χ(T) from the Curie–Weiss law approaching the Néel temperature. It is definitely of interest to solve eventually the magnetic structure of this compound with quite unusual magnetic topology.

Acknowledgements

We thank E. V. Guseva for the X-ray spectral analysis of the sample and N. V. Zubkova for her help in the X-ray experiment. This work was supported by the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST “MISiS” project K2-2016-066 and by RFBR projects 15-05-06742, 16-02-00021 and 17-02-00211. The work was supported by Act 211 Government of the Russian Federation, contracts 02.A03.21.0004, 02.A03.21.0006 and 02.A03.21.0011.

Notes and references

1. A. P. Ramires, Annu. Rev. Mater. Sci., 1994, 24, 453–480.
2. W. Sun, Y.-X. Huang, S. Nokhrin, Y. Pan and J.-X. Mi, J. Mater. Chem. C, 2016, 4, 8772–8777.
3. D. Boldrin, K. Knight and A. S. Wills, J. Mater. Chem. C, 2016, 4, 10315–10322.
4. T. Yavors'kii, M. Enjalran and M. J. P. Gingras, Phys. Rev. Lett., 2006, 97, 267203.
5. S. T. Bramwell and M. J. P. Gingras, Science, 2001, 294, 1495–1501.
6. E. M. Wheeler, B. Lake, A. T. M. N. Islam, M. Reehuis, P. Steffens, T. Guidi and A. H. Hill, Phys. Rev. B: Condens. Matter, 2010, 82, 140406.
7. C. Lacroix, P. Mendels and F. Mila, ed, Introduction to Frustrated Magnetism, Springer Series in Solid-State Sciences, 2011.
8. G. C. Lau, T. Klimczuk, F. Ronning, T. M. McQueen and R. J. Cava, Phys. Rev. B: Condens. Matter, 2009, 80, 214414.
9. T. Armbruster, C. A. Geiger and G. A. Lager, Am. Mineral., 1992, 77, 512–521.
10. H. Liu, L. Yuan, S. Wang, H. Fang, Y. Zhang, C. Hou and S. Feng, J. Mater. Chem. C, 2016, 4, 10529–10537.
11. Y. Wan and Y. B. Kim, Phys. Rev. B: Condens. Matter, 2016, 94, 224401.
12. A. M. Hallas, J. A. M. Paddison, H. J. Silverstein, A. L. Goodwin, J. R. Stewart, A. R. Wildes, J. G. Cheng, J. S. Zhou, J. B. Goodenough, E. S. Choi, G. Ehlers, J. S. Gardner, C. R. Wiebe and H. D. Zhou, Phys. Rev. B: Condens. Matter, 2012, 86, 134431.
13. H. Strunz and E. H. Nickel, Strunz mineralogical tables. Chemical-structural mineral classification system, 9th edn, Schweizerbart, Stuttgart, 2001.
14. Ch. Chopin, Th. Armbruster, E. Grew, A. Baronnet, C. Leyx and O. Medenbach, Eur. J. Mineral., 2014, 26, 553–565.
15. B. Lazic, Th. Armbruster, Ch. Chopin, E. S. Grew, A. Baronnet and L. Palatinus, Acta Crystallogr., Sect. B: Struct. Sci., 2014, 70, 243–258.
16. I. de Pedro, J. M. Rojo, J. Rius, O. Vallcorba, I. R. de Larramendi, J. Rodríguez Fernandez, L. Lezama and T. Rojo, Inorg. Chem., 2012, 51, 5246–5256.
17. L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854.
18. International Tables for Crystallography, ed. E. Prince, Kluwer, Dordrecht, 3rd edn, Tables 4.2.6.8 and 6.1.14, 2004.
19. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2015, 71, 3–8.
20. G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3–8.
21. I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247.
22. I. D. Brown, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1976, 32, 24–31.
23. I. D. Brown and R. D. Shannon, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1973, 29, 266–282.
24. J. B. Goodenough, Magnetism and the chemical bond, John Wiley and Sons, 1963.
25. O. S. Volkova, L. V. Shvanskaya, E. A. Ovchenkov, E. A. Zvereva, A. S. Volkov, D. A. Chareev, K. Molla, B. Rahaman, T. Saha-Dasgupta and A. N. Vasiliev, Inorg. Chem., 2016, 55, 10692.
26. M. Leblanc, I. Collin-Fèvre and G. Férey, J. Magn. Magn. Mater., 1997, 167, 71–79.
27. T. Berrocal, J. L. Mesa, J. L. Pizarro, M. K. Urtiaga, M. I. Arriortua and T. Rojo, J. Solid State Chem., 2006, 179, 1659–1667.
28. D. Karmakar and J. V. Yakhmi, J. Phys.: Condens. Matter, 2012, 24, 43.

---

Footnotes

† Electronic supplementary information (ESI) available: CIF from single crystal X-ray diffraction study (also deposited in the CSD as entire 43273); tables containing atomic positions and results of BVC, and structural figure. See DOI: 10.1039/c7dt01707c

‡ The analysis was performed at the Laboratory of Local Methods for Matter Investigation of the Department of Petrology at the Faculty of Geology of Moscow State University.

---