Tailoring phase transition temperatures in perovskites via A-site vacancy generation

Abstract

The structures across the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃, 0 ≤ x ≤ 0.6, defect perovskite series were investigated using complementary synchrotron X-ray and neutron powder diffraction data. The locations of second order compositional and temperature dependent phase transitions between the high symmetry cubic Pm3̄m phase and the lower symmetry tetragonal I4/mcm phase were determined. Deviation of the oxygen x coordinate from the high symmetry value and the B–O–B bond angle from 180° as well as the tetragonal strain squared were each found to be suitable order parameters to monitor the transitions. Tolerance factor calculations confirmed that these A-site deficient perovskites retain a higher symmetry to a lower value than their fully occupied counterparts. Therefore, adjusting vacancy concentrations can be employed as a general strategy to design compounds with specifically tailored phase transition temperatures.

---

Introduction

Perovskite type transition metal oxides are a class of materials, which can be represented by the general formula ABO₃. The perovskite type structure is defined by a network of corner linked BO₆ octahedra, with the A-site cations occupying the cavities defined by those octahedra. The ideal perovskite aristotype adopts cubic Pm3̄m symmetry. This is, however, reasonably uncommon, as most perovskite type compounds show some structural distortion.¹ Goldschmidt's tolerance factor can be used to predict whether a perovskite will form with the ideal cubic symmetry based on the relative sizes of the cations present in the structure.² If there is a mismatch between the sizes of the cations then there will be a distortion in that structure. The most common form of distortion observed is octahedral tilting.^3,4ABO₃ perovskites have been shown to exhibit many properties that are useful for, e.g., grain boundary layer capacitors, varistors, electro-optics, ferroelectrics with high dielectric constants, piezoelectrics, high temperature superconductors, ferromagnets, as well as frequency doubling and high memory capacity device applications.^5–8 Complex composition perovskites, with mixed site occupancies, such as PbZr_1−xTi_xO₃ (PZT),^9,10 PbZr_1/3Nb_2/3O₃ (PZN),¹¹ Pb(Mg_1/3Nb_2/3)_1−xTi_xO₃ (PMN-PT)¹² and Ba_1−xSr_xTiO₃ ¹³ are materials which have been shown to display ferroelectric and relaxor ferroelectric behaviour.^14,15 Ferroelectric materials show maximised dielectric constants just below their high temperature phase transitions as well as at morphotropic phase boundaries.^16,17 As a ferroelectric material undergoes structural phase transitions on heating, there are corresponding peaks in the dielectric constant. The peak with the largest dielectric constant tends to be at the high symmetry end, for example BaTiO₃ has its maximum dielectric constant at the transition between cubic and tetragonal symmetries despite two lower temperature phase transitions.^18–20 It has also been shown that for mixed occupancy materials such as PbSc_0.5Ta_0.5O₃ (PST) increasing the level of cation disorder can lead to a corresponding increase in the relaxor behaviour observed.²¹ The most useful and commonly applied ferroelectric and relaxor ferroelectric materials contain lead. Owing to lead's health and environmental impact lead free alternatives to these materials are sought after and compounds with defect perovskite type structures are considered in this context.

An investigation of the Sr_1−xTi_1−2xNb_2xO₃ defect perovskite series showed that a solid solution can be formed with up to 20% vacancies on the A-site, i.e. 0 ≤ x ≤ 0.2. Electron diffraction images taken of Sr_0.8Ti_0.6Nb_0.4O₃ revealed the presence of diffuse intensity streaking, indicating that the compound has the potential to be a relaxor ferroelectric due to short range ordering in the structure.²² The average centrosymmetric cubic Pm3̄m symmetry of the structure is not compatible with ferroelectric, but allows for relaxor ferroelectric behaviour.

Increasing the compositional complexity on the crystallographic B-site enhances the probability of regions of non-homogeneity in the material, and thereby the relaxor ferroelectric properties. Substitution of titanium with zirconium was considered a possible strategy since the analogous zirconium phase, Sr_1−xZr_1-2xNb_2xO₃, 0 ≤ x ≤ 0.25, forms with tetragonal I4/mcm symmetry when x = 0.2.²³ This investigation examined the structural effect of altering the zirconium to titanium ratio across the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃, 0 ≤ x ≤ 0.6, composition range. Additionally, the temperature dependent phase behaviour across the composition range was investigated with the aim of locating phase transitions at which dielectric constants may be optimised.

Experimental

Polycrystalline samples of Sr_0.8Ti_0.6−xZr_xNb_0.4O₃, 0 ≤ x ≤ 0.6, were synthesised via conventional solid state reactions. Compositions x = 0.00, 0.06, 0.12, 0.24, 0.36, 0.48 and 0.60 were prepared for synchrotron X-ray powder diffraction analysis while compositions x = 0.00, 0.06, 0.12, 0.24, 0.36 and 0.60 were prepared for neutron powder diffraction studies. Stoichiometric amounts of the appropriate carbonates and oxides, including SrCO₃ (Sigma Aldrich, 99.9%), BaCO₃ (Aithaca, 99.997%), TiO₂ (Aithaca, 99.999%), ZrO₂ (Aithaca, 99.99%), and Nb₂O₅ (Aithaca, 99.999%), were weighed out and finely ground before calcination and sintering. Sufficient starting materials to prepare 2 g samples for synchrotron X-ray powder diffraction analysis were weighed and ground with acetone using a mortar and pestle. Larger, 10 g, samples were prepared for neutron powder diffraction analysis; these were ball milled for one hour in ethanol to ensure thorough grinding and mixing. The reagents were calcined at 950 °C for 36 h to remove CO₂ and were then sintered at 1400 °C in steps from 24 h to 96 h, until determined pure with the use of a PANalytical X'Pert PRO MPD X-ray diffractometer. The samples were heated at 800 °C in air for a final 24–48 h which restored a white/light grey colour to samples which had become slightly darker grey. Samples were thoroughly reground between heating steps and were pressed into dense pellets (2 g) or rods (10 g) for sintering.

Energy dispersive X-ray spectroscopy was employed utilising a Zeiss Evo 50 scanning electron microscope (SEM) to confirm that the compositions of the synthesised materials matched the nominal compositions. The SEM utilised a LaB₆ filament operating at 15 keV, with a working distance of between 20–30 mm. Samples were dispersed onto carbon tape and carbon coated with a thickness of approximately 25 μm. Compositions were determined using an iXRF Iridium Ultra EDS system and the data were collected and analysed using the AZTEC software at the Australian Microscopy and Microanalysis Research Facility.

High intensity and high resolution synchrotron X-ray powder diffraction (XRD) patterns were collected at room temperature for all compositions. In addition, variable temperature data were collected for members with x ≥ 0.36. X-ray data were collected at the powder diffraction beamline, 10-BM, at the Australian Synchrotron using the MYTHEN microstrip detector and a Si(111) monochromator. The wavelength (λ = 0.826465(1) Å) was accurately determined using LaB₆ (NIST standard 660a). Data were collected for finely ground samples packed into 0.3 mm glass capillaries over the 2θ range 2–82.5° in two 80° frames offset by 0.5° and spliced together. This was necessary to overcome the 0.2° wide gaps between the 16 detector modules. High temperature data were collected using a hot air blower (300 K–1248 K).

Room temperature neutron powder diffraction patterns were collected using the ECHIDNA high resolution powder diffractometer at the OPAL reactor, Australian Nuclear Science and Technology Organisation. Finely ground samples were placed into 9 mm diameter vanadium cans. Diffraction patterns were obtained at room temperature using a wavelength of 1.622 Å from 5–165° (2θ angle) with a step size of 0.05° over a period of 3 h. Structural refinements were performed against both synchrotron X-ray and neutron powder diffraction data using the Rietveld method²⁴ implemented in the refinement program JANA2006.²⁵ The pseudo-Voigt profile shape function was assumed and the backgrounds were modelled using Chebyshev polynomials.

Results and discussion

Room temperature synchrotron X-ray powder diffraction analysis

Structural refinements were performed using the Rietveld method against synchrotron X-ray powder diffraction data. The structures of the Sr_0.8Ti_0.6Nb_0.4O₃ and Sr_0.8Zr_0.6Nb_0.4O₃ end members have been reported with Pm3̄m and I4/mcm symmetry, respectively, where the tetragonal cell has a √2 × √2 × 2 relationship to the cubic unit cell.^22,23 Structural refinements against room temperature synchrotron X-ray powder diffraction data across the composition range are consistent with these reports. The expected phase transition between the lower and higher symmetry structures appears to occur between 0.24 ≤ x ≤ 0.36 (Table 1). The adopted symmetry across the composition range changes from the cubic Pm3̄m symmetry for x = 0.24 to the tetragonal I4/mcm symmetry for x = 0.36. All reflections observed in the synchrotron X-ray diffraction patterns are consistent with the main phase, except in high zirconium content members where a weak reflection is observed compatible with the strongest peak of ZrO₂.²⁶

Table 1 Structural information obtained from Rietveld refinements against synchrotron X-ray powder diffraction data for the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ composition range

	x = 0.00	x = 0.06	x = 0.12	x = 0.24	x = 0.36	x = 0.48	x = 0.60
a (Å)	3.928102(3)	3.942582(3)	3.956674(4)	3.983096(3)	5.664962(9)	5.694282(6)	5.725077(4)
c (Å)					8.01660(2)	8.077236(10)	8.132035(8)
V (Å^3)	60.61057(4)	61.28333(5)	61.94278(6)	63.19203(5)	257.267(6)	261.903(5)	266.540(4)
V (Å^3) (norm)	60.61057	61.28333	61.94278	63.19203	64.31673	65.47579	66.63492
Space group	Pm3̄m	Pm3̄m	Pm3̄m	Pm3̄m	I4/mcm	I4/mcm	I4/mcm
R Bragg [%]	1.45	1.43	1.28	1.50	1.99	2.72	2.44
R p [%]	4.00	4.71	4.53	4.51	3.12	3.16	2.64
GoF	2.76	2.54	2.54	2.44	4.72	4.47	3.94

---

The lower I4/mcm symmetry for compositions close to the zirconium end is evidenced by peak splitting and the presence of superlattice reflections.^3,4,27–29 Peak splitting due to the tetragonal distortion, becomes increasingly difficult to detect as the titanium content is increased. Splitting is observed for x = 0.48 but not for x = 0.36. Superlattice reflections persist further across the series and are present for x = 0.36, but not for x = 0.24. Fig. 1 shows the evolution of the 211 reflection in the tetragonal cell, i.e. 113 in the doubled cubic cell. This is an R-type reflection, which is indicative of out-of-phase tilting.²⁷ Superlattice reflections persisting further across the composition range than detectable peak splitting have also been observed for the related Sr_1−xZr_1−2xNb_2xO₃ system.²³

Fig. 1 Synchrotron X-ray powder diffraction patterns across the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ series revealing the presence of the 211 superlattice reflection (tetragonal setting) present in the patterns for x ≥ 0.36 (see inset).

Refinements of structural models against synchrotron X-ray powder diffraction data reveal a linear relationship between cell volume and zirconium content (Fig. 2), consistent with the larger radius of Zr when compared to Ti.

Fig. 2 Cell volume as determined by refinements against synchrotron X-ray powder diffraction data. Volumes for tetragonal compounds are normalised such that V_norm = a_t/√2 × b_t/√2 × c_t/2.

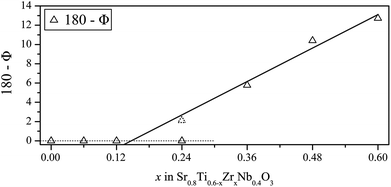
The structural refinements above illustrate the pseudo-symmetry problem in perovskite type compounds. Refinements attempted with tetragonal symmetry for x = 0.12 and x = 0.24 were unstable due to insufficient data to constrain them. However, analysis of bond angles gives some suggestion that at least x = 0.24 forms with tetragonal symmetry. The B–O–B bond angle (Φ) has a value of 180° in the ideal cubic structure, however, octahedral tilting causes deviations from this value. Fig. 3 plots the deviation of the bond angle from 180° (expressed as 180 − Φ) across the composition range. It can be seen that the angles increasingly deviate from 180° as the zirconium content increases. A linear fit was applied to the deviation of the bond angles from 180°, determined by refinement against synchrotron X-ray powder diffraction data. Extrapolation leads to a phase boundary composition of x ≈ 0.15. The value for x = 0.24, when refined with tetragonal symmetry, is indicated in this plot, but was not considered for the line of best fit.

Fig. 3 Deviation of the bond angle Φ from the ideal cubic value of 180° for the B–O–B bond, expressed as 180° − Φ, plotted against composition. The refined value for x = 0.24 from a tetragonal model is shown with a dotted triangle (not used for line of best fit).

As this point falls very close to the line of best fit, it was considered very likely that this composition is tetragonal and thus neutron diffraction experiments were performed for confirmation.

Room temperature neutron powder diffraction analysis

As described earlier, the main differences between the tetragonal and the cubic structures are the cell dimensions and the coordinates of the oxygen atoms. In order to accurately determine the location of the oxygen atoms neutron powder diffraction data were collected at room temperature for both end members of the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ composition range and for members near the phase transition composition, as deduced from refinements against synchrotron X-ray diffraction data. These data allowed the confirmation that the oxygen sites were fully occupied and refinement of anistropic displacement parameters did not lead to any improvement in refinement quality. The x = 0.24 member shows very weak superlattice reflections, which were not observed in the synchrotron X-ray diffraction pattern for that composition. These data were sufficient to successfully refine a structural model with tetragonal symmetry. Consequently the phase transition was determined to occur between x = 0.12–0.24 (Table 2).

Table 2 Structural information obtained from Rietveld refinements against neutron powder diffraction data for the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ series

	x = 0.00	x = 0.06	x = 0.12	x = 0.24	x = 0.36	x = 0.60
a (Å)	3.93076(3)	3.94300(4)	3.9569(4)	5.63400(3)	5.6682(3)	5.72625(6)
c (Å)				7.9659(8)	8.0170(8)	8.13217(13)
V (Å^3)	60.7336(5)	61.3026(6)	61.9508(6)	252.85(13)	257.57(13)	266.65(5)
V (Å^3) (norm)	60.7336	61.3026	61.9508	63.2132	64.3941	66.6634
Space group	Pm3̄m	Pm3̄m	Pm3̄m	I4/mcm	I4/mcm	I4/mcm
R obs [%]	2.68	3.40	4.04	4.81	5.79	3.91
R p [%]	5.09	4.03	4.03	3.12	5.50	4.90
GoF	4.56	5.59	5.35	2.25	3.53	3.38

---

Observing additional superlattice reflections in neutron powder diffraction patterns compared to the X-ray diffraction data is not unusual,^30,31 especially in cases where the deviation from the high-symmetry structure is mainly caused by the movement of oxygen atoms. As oxygen has higher relative scattering power in neutron diffraction,³² it is then understandable that superlattice reflections persist further across the series in the neutron powder diffraction patterns than in the synchrotron X-ray powder diffraction patterns.

In the cubic structure there is one independent oxygen site, (0, 0, 0.5), which splits into two sites in the tetragonal structure, O1 (0, 0, 0.25) and O2 (x, x + 0.5, 0) where x ∼ 0.25. The coordinates of the O1 site are fixed by symmetry while for O2 the x coordinate can be refined. If x = 0.25 for O2 then the structure is equivalent to the cubic structure. The further the coordinate deviates from 0.25 the larger the amount of octahedral tilting in the structure.

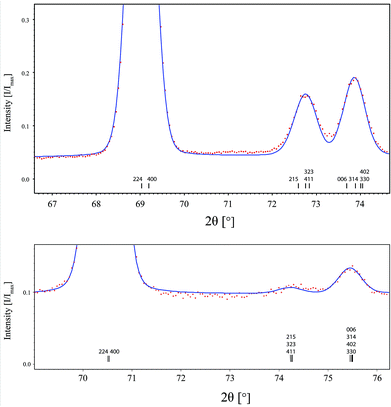
Rietveld refinements were performed for x = 0.12 against neutron powder diffraction data in both the Pm3̄m and I4/mcm settings. The results of these refinements were very similar. The cell parameters for the tetragonal model were within error of being identical, a_norm = 3.9568(2), c_norm = 3.9564(4) and the x coordinate of O2 0.2518(10) is very close to the high symmetry site. For these reasons as well as a slight instability in the tetragonal cell parameters, the cubic model for x = 0.12 was determined to be more appropriate. Fig. 4 shows a zoomed-in portion of the fit for the x = 0.60 (top) and x = 0.24 (bottom) members of the series, highlighting the presence of the strongest superlattice reflection (411) in both. It is just observed for the x = 0.24 composition.

Fig. 4 Plot of neutron powder diffraction data for Sr_0.8Zr_0.60Nb_0.4O₃ (top) and Sr_0.8Ti_0.36Zr_0.24Nb_0.4O₃ (bottom). Observed data are shown in red and the calculated patterns in blue. The strongest superlattice reflection (411) is clearly present for x = 0.60 (end member), but barely observed for x = 0.24.

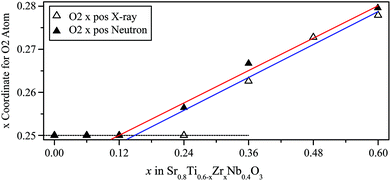
Fig. 5 shows the evolution of the x coordinate of the O2 atom across the composition range as more zirconium is added. Linear fits were applied to the values for the tetragonal members of these plots and extrapolated to x = 0.25. The phase transition composition was determined to be at x ≈ 0.15(3) from X-ray data and x ≈ 0.12(2) from neutron data, i.e. within error of each other.

Fig. 5 Plot of the x coordinate for the O2 atom as determined by Rietveld refinement across Sr_0.8Ti_0.6−xZr_xNb_0.4O₃. x = 0.25 corresponds to the high symmetry site and therefore the cubic structure. The blue line is a linear fit to coordinates calculated from the X-ray data while the red is the linear fit for the neutron data.

Refinements of models against neutron powder diffraction data confirm the linear relationship between cell volume and zirconium content that was observed for X-ray data, while the cell parameters can be seen to increasingly diverge as zirconium content is increased (Fig. 6). The symmetry lowering phase transition in the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ series from cubic Pm3̄m to tetragonal I4/mcm can be explained by the tilting of rigid octahedra. The B-site substitution of the larger zirconium ions for the smaller titanium ions causes an increase in the unit cell dimensions across the composition range (Fig. 6) which results in the octahedral tilts observed.

Fig. 6 Cell parameters a and c across the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ series. Upward pointing triangles represent the cell parameter of the cubic structures. Downward pointing triangles represent the normalised a parameter and circles the normalised c parameter in the tetragonal structures. Tetragonal members are normalised such that a_norm = a_t/√2 and c_norm = c_t/2. Data points determined from refinement against synchrotron data are indicated with empty symbols whilst those from refinement against neutron data have filled symbols.

The octahedral rotations observed in these compounds can be represented by the Glazer notation (a⁰a⁰c⁻),³ corresponding to an out-of-phase tilt along the c-direction, in agreement with the appearance of R-point reflections (e.g. 113, in the doubled cubic cell). The tilts present in this system become more pronounced as the zirconium content is increased, as illustrated in Fig. 7. The observed transition is continuous in nature, as indicated by the change in oxygen coordinates and bond angles, consistent with a second order phase transition. This is not unexpected as it is almost universally so within other perovskites as allowed by the symmetry relationship between these spacegroups.²⁹

Fig. 7 Octahedral tilting in the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ series. Structures displayed are refined against neutron powder diffraction data. From left to right are, cubic x = 0.00 (shown with the same origin and size as the tetragonal unit cell), x = 0.24, x = 0.36 and x = 0.60. Strontium cations are shown in green, with percentage vacancies shown white, titanium/zirconium/niobium cations are grey in the centre of the blue octahedra and oxygen anions are red.

Bond valence sums were calculated for all compositions in the series from the structures resulting from refinement against both X-ray and neutron diffraction data. A full list of bond valence sums is provided as supplementary material in Tables S1 and S2.† Very close agreement was observed between the values obtained from the structures refined against both X-ray and neutron diffraction data, with the maximum deviation for the same compound being ±0.02. The bond valence sum calculations reveal that the Sr²⁺ cation is ideally bonded in the Sr_0.8Ti_0.6Nb_0.4O₃ compound with a bond valence sum of 2.02. As the unit cell expands with increasing zirconium content the Sr²⁺ becomes increasingly under bonded reaching a minimum value of 1.67 for Sr_0.8Zr_0.6Nb_0.4O₃.

Analysing the B-site cations is more complex as this is a shared site. Individual numbers are therefore less reliable as they are calculated for the average B-site when in reality Zr⁴⁺ will have longer bond distances to oxygen than Ti⁴⁺. Despite this, however, trends in the numbers can be indicative. The expectation is that end members should display ideal bonding and as other cations are substituted in, the deviation from ideal should increase. For this system, however, even the end members have two cation types on the B-site. The Nb⁵⁺ and Ti⁴⁺ bond distances to oxygen in an ideal octahedron are very similar and so at the Sr_0.8Ti_0.6Nb_0.4O₃ end we can see that the Ti⁴⁺ cations are ideally bonded at 4.01 and the Nb⁵⁺ at 5.20 are within error of being ideally bonded as well. As Zr⁴⁺ is substituted into the material the average distance from the B cation to the oxygen increases, resulting in a decrease in the bond valence sum. As more Zr⁴⁺ is placed into the structure the average site becomes more ideal for Zr⁴⁺ decreasing from the over bonded 5.34 near the Ti⁴⁺ end towards 4.49 at the Zr⁴⁺ end. Zr⁴⁺ never reaches its ideal bond valence sum due to sharing the site with a significant amount of Nb⁵⁺ even at the Zr⁴⁺ end.

The calculated bond valence sums suggest that the average symmetry for these compounds is complicated by local order. The average polyhedra will locally adjust around highly under-bonded or over-bonded cations leading to strain and consequential compositional ordering. Such local order might be responsible for the diffuse streaking observed in the electron diffraction images of Sr_0.8Ti_0.6Nb_0.4O₃.²² Close to the phase transition there are compositions where all three B-site cations as well as the A-site cation are not ideally bonded, leading to a significant amount of disorder, which could contribute to relaxor ferroelectric behaviour.

Goldschmidt tolerance factors are used to predict and rationalise the compositions at which distortions to lower symmetries might occur in fully occupied perovskites.² To the best of our knowledge, there have been no attempts to calculate tolerance factors for defect perovskites, as there is no radius that can be assigned to a vacancy. Therefore it was necessary to treat the crystallographic A site as if it was fully occupied by Sr²⁺ cations. Tolerance factors were calculated for all members of the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ series using effective ionic radii.³³ As the relative amount of zirconium increases the calculated tolerance factors decrease, suggesting that distortions to lower symmetry are becoming more likely. Rietveld refinements showed that a phase transition from cubic to tetragonal symmetry occurs between the compositions Sr_0.8Ti_0.48Zr_0.12Nb_0.4O₃ and Sr_0.8Ti_0.36Zr_0.24Nb_0.4O₃ (but very close to the former). These correspond to tolerance factors of 0.995 and 0.988, respectively. As more zirconium is added into the structure the tolerance factors decrease further, reaching 0.968 at the end of the composition range, without any further symmetry lowering.

In the closely related defect free series SrTi_1−xZr_xO₃, 0 ≤ x ≤ 1, a very different behaviour is observed. A distortion occurs for a much smaller amount of zirconium present, e.g. SrTi_0.95Zr_0.05O₃ already adopts tetragonal symmetry. As more zirconium is added a second symmetry change is observed, i.e. SrTi_0.4Zr_0.6O₃ forms with orthorhombic symmetry.³⁴ The calculated tolerance factors for these two compositions are 1.006 and 0.975, respectively. Investigations of a related Sr_1−xZr_1−2xNb_2xO₃ series revealed similar behaviour. With an inceasing number of vacancies present higher symmetry phases persisted to lower tolerance factor values.²³ These comparisons show that the presence of A-site vacancies allows the higher symmetry structures to persist further along a similar composition range.

Variable temperature synchrotron X-ray powder diffraction analysis

Variable temperature synchrotron X-ray powder diffraction data were collected for high zirconium content members of the Sr_0.8Ti_0.6−xZr_xNb_0.4O₃ composition range, which display tetragonal symmetry at room temperature. The data for Sr_0.8Zr_0.6Nb_0.4O₃ (Fig. 8) show the coalescence of split reflections and the disappearance of superlattice reflections on heating (see insets). This corresponds to a transition from the low temperature tetragonal (I4/mcm) symmetry to the high temperature cubic (Pm3̄m) symmetry. Rietveld refinements demonstrated that all of the compounds with tetragonal (I4/mcm) symmetry at room temperature adopted cubic (Pm3̄m) symmetry at higher temperature.

Fig. 8 Variable temperature synchrotron X-ray powder diffraction data for Sr_0.8Zr_0.6Nb_0.4O₃. The 211 superlattice reflection (tetragonal setting) is indicated at ∼19.5° 2θ (left inset) and merging superlattice reflections at ∼26.3° 2θ (inset right).

In order to determine the phase transition temperature accurately for each composition the tetragonal strain squared values as a function of temperature were calculated. Tetragonal strain was defined as (c_norm − a_norm)/(c_norm + a_norm). A linear fit was applied and extrapolated to a strain squared of zero, which corresponds to the cubic symmetry being observed.

Fig. 9 shows a representative strain analysis for x = 0.60. The same process was employed for x = 0.48 and x = 0.36. The continuous nature of these changes shows that as with the compositional phase transition, the temperature dependent transition is also second order in nature.

Fig. 9 Tetragonal strain squared for models obtained from structural refinements against synchrotron X-ray powder diffraction data at variable temperatures for Sr_0.8Zr_0.6Nb_0.4O₃. Tetragonal strain is calculated as (c_norm − a_norm)/(c_norm + a_norm) where c_norm and a_norm are normalised cell parameters (c_norm = c_t/2 and a_norm = a_t/√2).

Fig. 10 illustrates the phase transition temperatures from tetragonal to cubic across Sr_0.8Ti_0.6−xZr_xNb_0.4O₃. The x = 0.06, x = 0.12 and x = 0.24 compositions were only investigated at room temperature. A general trend to higher phase transition temperatures can be seen as zirconium content is increased.

Fig. 10 Phase transition temperatures for Sr_0.8Ti_0.6−xZr_xNb_0.4O₃. Triangles represent phase transition temperatures identified by tetragonal strain analysis. The square represents the transition temperature of the Sr_0.8Ti_0.6Nb_0.4O₃ composition as determined by neutron diffraction.²² Circles represent compositions for which data were collected only at ambient temperature. The line of best fit represents the phase transition temperature and was calculated without the circles.

Conclusions

The location of second order compositional and temperature dependent phase transitions between the high symmetry cubic Pm3̄m phase and the lower symmetry tetragonal I4/mcm phase were determined.

It was found that these perovskite type compounds with A-site vacancies, as well as others previously investigated, tended towards higher symmetries than materials of similar composition without vacancies. Through substitution with appropriate heterovalent cations it is therefore possible to introduce vacancies into a perovskite structure in order to achieve higher symmetries. In such vacancy containing structures appropriate tolerance factors for predicting structural distortions are significantly lower than for vacancy free materials. In other words, this can be interpreted as vacancies occupying more space than the fully occupied site. While it might intuitively be expected that surrounding atoms move towards the vacancy to utilise the additional space, consideration of bond valence sums suggests that atoms have to move away from the vacancy to compensate the reduced contribution to their bond valences. As A-site deficient perovskites extend the existence range of higher symmetry phases it is therefore possible to tailor the temperature at which the high symmetry phase transition will occur, and thus the maximum in the dielectric constant.

Analysis of bond valence sums indicates that a high degree of disorder is likely in these materials. When all three metals are present on the B site, particularly near the compositional phase transition, all of the cations are far from being ideally bonded in the average structure. This suggests that there is a likely mix of larger octahedra with Zr⁴⁺ in the centre as well as smaller octahedra with Nb⁵⁺ or Ti⁴⁺ in the centre. As there is no evidence for long range ordering of these octahedra in the diffraction data it is very likely that they are locally ordered throughout the bulk of the material. This local ordering could explain the diffuse intensity observed for Sr_0.8Ti_0.6Nb_0.4O₃ and suggests that these may well be relaxor ferroelectric materials.

Acknowledgements

A part of this work was performed at the powder diffraction beamline of the Australian Synchrotron, Victoria, Australia. Neutron powder diffraction data were collected at the Bragg Institute of the Australian Nuclear Science and Technology Organisation. In addition, the authors acknowledge valuable discussions with Prof. B. J. Kennedy (The University of Sydney).

References

1. R. H. Mitchell, Perovskites: Modern and Ancient, Alamaz Press Inc., Onatrio, Canada, 2002.
2. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
3. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
4. P. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 32–43.
5. V. Ravikumar, R. P. Rodrigues and V. P. Dravid, J. Phys. D: Appl. Phys., 1996, 29, 1799–1806.
6. S. Piskunov, E. Heifets, R. I. Eglitis and G. Borstel, Comput. Mater. Sci., 2004, 29, 165–178.
7. T. Mitsui and W. B. Westphal, Phys. Rev., 1961, 124, 1354–1359.
8. G. A. Smolenskii and V. A. Bokov, J. Appl. Phys., 1964, 35, 915–918.
9. D. Pandey, A. K. Singh and S. Baik, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 192–203.
10. O. Gubanova and D. E. Ellis, Ferroelectrics, 1993, 150, 227–243.
11. G. V. Ramani and D. C. Agrawal, Ferroelectrics, 1993, 150, 291–301.
12. G. C. Cardoso da Costa, L. Wu and A. Navrotsky, J. Mater. Chem., 2011, 21, 1837–1845.
13. M. M. Sutar, A. N. Tarale, S. R. Jigajeni, S. B. Kulkarni, V. R. Reddy and P. B. Joshi, Solid State Sci., 2012, 14, 1064–1070.
14. L. E. Cross, Ferroelectrics, 1987, 76, 241–267.
15. L. E. Cross, Ferroelectrics, 1994, 151, 305–320.
16. J. R. Oliver, R. R. Neurgaonkar and L. E. Cross, J. Am. Ceram. Soc., 1989, 72, 202–211.
17. M. Ahart, M. Somayazulu, R. E. Cohen, P. Ganesh, P. Dera, H.-k. Mao, R. J. Hemley, Y. Ren, P. Liermann and Z. Wu, Nature, 2008, 451, 545–548.
18. J. H. Van Santen and G. H. Jonker, Nature, 1947, 159, 333–334.
19. W. J. Merz, Phys. Rev., 1949, 76, 1221.
20. S. Roberts, Phys. Rev., 1947, 71, 890.
21. N. Setter and L. E. Cross, J. Appl. Phys., 1980, 51, 4356–4360.
22. W. R. Brant, S. Schmid, Q. Gu, R. L. Withers, J. Hester and M. Avdeev, J. Solid State Chem., 2010, 183, 1998–2003.
23. S. Schmid and R. L. Withers, J. Solid State Chem., 2012, 191, 63–70.
24. H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
25. V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352.
26. K. R. Whittle, G. R. Lumpkin and S. E. Ashbrook, J. Solid State Chem., 2006, 179, 512–521.
27. A. M. Glazer, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1975, 31, 756–762.
28. P. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 44–66.
29. C. J. Howard and H. T. Stokes, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 782–789.
30. D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Li and R.-G. Xiong, Science, 2013, 339, 425–428.
31. L. Y. Kraya and R. Kraya, Acta Crystallogr., Sect. B: Struct. Sci., 2013, 69, 105–109.
32. V. F. Sears, Neutron News, 1992, 3, 26–37.
33. R. D. Shannon, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 1976, 32, 751–767.
34. T. K.-Y. Wong, B. J. Kennedy, C. J. Howard, B. A. Hunter and T. Vogt, J. Solid State Chem., 2001, 156, 255–263.

---

Footnotes

† Electronic supplementary information (ESI) available: Tables of bond valence sum calculations, tolerance factor calculations and atomic coordinates. See DOI: 10.1039/c7dt00352h

‡ Current address: Department of Chemistry, Ångström laboratory, Uppsala University, 75121 Uppsala, Sweden.

---