Sequence of phase transitions in (NH₄)₃SiF₇

Abstract

Single crystals of silicon double salt (NH₄)₃SiF₇ = (NH₄)₂SiF₆·NH₄F = (NH₄)₃[SiF₆]F were grown and studied by the methods of polarization optics, X-ray diffraction and calorimetry. A sequence of symmetry transformations with the temperature change was established: P4/mbm (Z = 2) (G₁) ↔ Pbam (Z = 4) (G₂) ↔ P2₁/c (Z = 4) (G₃) ↔ P1̄ (Z = 4) (G₄) ↔ P2₁/c (Z = 8) (G₅). Crystal structures of different phases were determined. The experimental data were also interpreted by a group-theoretical analysis of the complete condensate of order parameters taking into account critical and noncritical atomic displacements. Strengthening of the N–H⋯F hydrogen bonds can be a driving force of the observed phase transitions.

---

1 Introduction

Silicon is the second most abundant element in the Earth's crust. Its double fluoride salt (NH₄)₃SiF₇ = (NH₄)₃SiF₇·NH₄F = (NH₄)₃[SiF₆]F is the main product of fluoride processing of natural silicon-containing raw materials (quartz and silicates of different structure and compositions) with ammonium hydrogen difluoride (NH₄HF₂).^1–5 Fluorination reactions proceed exothermally (even at room temperature) with an entropy reserve. Elemental silicon also interacts with NH₄HF₂ with the formation of (NH₄)₃SiF₇.^6,7 It is accepted in the literature that this salt was first prepared by Marignac in 1859.⁸ He obtained it in the form of square prisms from aqueous fluoride solution. However, similar shape (‘tetrahedral prisms’) crystals were observed by Davy as early as 1812.⁹ The crystal structure of (NH₄)₃SiF₇ was studied in 1942 by Hoard and Williams,¹⁰ and solved using oscillation photographs. In spite of the measurements being performed very carefully and the final model crystal structure being adequate, the authors reported large discrepancies between the calculated and observed reflection amplitudes. They associated these discrepancies with the fluorine anions, for which large temperature corrections should be performed, and pointed out that it would be of interest to obtain diffraction data for (NH₄)₂SiF₆·NH₄F at liquid air temperatures. This task has not been performed until now. Moreover, no data on phase transitions in this compound are available in the literature.

Recently, we found that the isostructural compound (NH₄)₃GeF₇ (space group P4/mbm) underwent several reversible phase transitions below room temperature with an unusual sequence P4/mbm ↔ Pbam ↔ P2₁/c ↔ Pa3̄.¹¹ Moreover, some other fluoride double salts (NH₄)₃M⁴⁺F₇ (M⁴⁺ = Ti⁴⁺, Sn⁴⁺) undergo phase transitions but of different sequences, and a correlation with the M⁴⁺ ionic radius was found.^11–16 Therefore, one might expect the temperature variation would also destabilise the room temperature structure of the silicon double fluoride salt, leading to phase transitions.

In the present paper, a complex study of (NH₄)₃SiF₇ using optical, X-ray, and calorimetric measurements revealed that the succession of structural transformations differs from the sequences observed earlier by us in other related compounds (NH₄)₃M⁴⁺F₇. The crystal structures of all the phases were solved and a reliable model of structural distortions associated with certain order parameters was suggested.

2 Experimental

2.1 Synthesis and crystal growth

Single crystals of a double salt (NH₄)₃SiF₇ were grown from aqueous fluoride solution with an excess of NH₄F or NH₄HF₂. Solid SiO₂, (NH₄)₂SiF₆, NH₄F and NH₄HF₂ of a reagent grade were used. Silicon dioxide (amorphous or quartz) was fluorinated with NH₄HF₂ at 150–200 °C in a Pt or glass-carbon beaker. It should be noted that the reaction began at room temperature itself while grinding together the initial components. A double excess, at least, of NH₄HF₂ was taken relative to the stoichiometric reaction: SiO₂ + 3.5NH₄HF₂ = (NH₄)₃SiF₇ + 0.5NH₃ + 2H₂O. The cake obtained in this way was then water-leached, filtered and colourless prismatic single crystals of (NH₄)₃SiF₇ were formed by slow evaporation of the final solution under ambient conditions. The crystals were recovered by vacuum filtration and air-dried. A large excess of NH₄F was needed to obtain (NH₄)₃SiF₇ in the NH₄F–(NH₄)₂SiF₆–H₂O system.¹⁷ We used a triple excess relative to the stoichiometric reaction: (NH₄)₂SiF₆ + NH₄F = (NH₄)₃SiF₇. For example, 20 g of (NH₄)₂SiF₆ and 12–15 g of NH₄F were mixed and dissolved in 100 ml of deionised water, filtered and slowly evaporated at ambient temperature with the formation of transparent tetragonal prisms. It is not surprising that Davy had observed similar crystals during the addition of excess ammonia to hexafluorosilicic acid (‘the subsilicated fluoric acid’).⁹

2.2 Calorimetric investigations

The temperature stability of the initial tetragonal phase P4/mbm of (NH₄)₃SiF₇ was examined by measurements with a DSM-10M differential scanning microcalorimeter (DSM). Recently it has been shown that among fluorides (NH₄)₃M⁴⁺F₇ there are at least two crystals undergoing a phase transition into the cubic phase Pm3̄m above room temperature at ambient – (NH₄)₃SnF₇ ¹³ – or high – (NH₄)₃TiF₇ ¹⁶ – pressure. Therefore the thermal investigations were performed in a wide temperature range of 100–460 K.

A sample of the powdered compound under study was placed into an aluminium sample holder. Calorimetric measurements were carried out under a helium atmosphere on several samples with a mass of about 0.03–0.06 g. In order to gain information on the hysteretic phenomena associated with the probable structural transformations in (NH₄)₃SiF₇, experiments were carried out using heating and cooling runs with a rate of temperature change dT/dτ of 8 to 32 K min⁻¹. The calibration of the temperature and enthalpy scales was performed using the melting parameters of pure indium as well as tabulated data of enthalpy against temperature for Al₂O₃. The temperature was determined with an accuracy of ±1 K and the uncertainty on the enthalpy and entropy values was estimated to be ±5 J mol⁻¹ and ±0.1 J mol⁻¹ K⁻¹, respectively.

2.3 Optical observations

Optical studies were performed using a polarizing microscope (Axioskop-40) and a Linkam LTS 350 temperature chamber. The investigations were carried out in a quasi-static regime with an accuracy of ±0.1 K in the range of 90–400 K. The birefringence was measured using a Berek compensator (Leica) with an accuracy of ≈0.00001.

2.4 X-ray investigations

Optical experiments proved a complex microtwinning of the crystal under cooling. Currently it seems impossible to solve or refine the crystal structure by single crystal diffraction due to the complex picture of overlapping peaks from different domains. Moreover, a resolution of the single crystal experiment is worse than that of the powder diffraction. Subtle changes of cell parameters can be appropriately investigated by only using a powder diffraction technique, which was chosen in our case.

The powder diffraction data of (NH₄)₃SiF₇ for Rietveld analysis were collected with a Bruker D8 Advance powder diffractometer (Cu-Kα radiation) and a linear VANTEC detector. The beam was controlled by a 0.6 mm fixed divergence slit, 6 mm receiving VANTEC slit and Soller slits. An Anton Paar TTK450 attachment was used for low- and high-temperature measurements.

The diffraction data in the 2θ range 5° to 120° were collected at T = 303 K, T = 213 K, T = 183 K, and T = 133 K (Fig. 1S†). These X-ray patterns were used to solve and refine the crystal structures. Eighteen additional X-ray patterns with smaller exposition time were collected from 133 K to 303 K to identify the space group transformation at phase transition.

The crystal structures of the low-temperature phases were solved by a distortion-mode refinement of X-ray data using the TOPAS 4.2 ¹⁸ program, with a file generated by ISODISPLACE. Amplitudes of critical symmetry-modes were used to find a structural model by the simulated anneal method. Then all atomic coordinates were refined independently by the Rietveld method. Isotropic thermal parameters of Si atoms were refined independently, but all F atoms as well as N atoms had one thermal parameter.

3 Results and discussion

3.1 Calorimetry

No anomalous behaviour of the DSM-signal was observed in experiments above room temperature until the decomposition (∼450 K) of (NH₄)₃SiF₇. Below room temperature, calorimetric studies revealed four anomalies reproducible in the heating and cooling runs, which were suggested to be associated with the successive phase transitions G₁(T₁) ↔ G₂(T₂) ↔ G₃(T₃) ↔ G₄(T₄) ↔ G₅. The background of the DSM-signal(T) dependence, considered to be the lattice contribution into the total DSM-signal, was extracted by polynomial approximation of the experimental data far from the anomalous regions. The quantity determined as the difference between the total DSM-signal and its lattice component is associated with the excess molar heat capacity ΔC_p connected with the order parameters of transformations which will be discussed below.

Fig. 1a depicts the temperature dependence of ΔC_p for one of the samples obtained in experiments with dT/dτ = 8 K min⁻¹. The behavior of ΔC_p at the transformation G₁ ↔ G₂ is typical for the second order: a small asymmetric anomaly characterised by a broad temperature range of the ΔC_p existence below T₁ = 263 ± 1 K, which was detected as the temperature of the ΔC_p maximum. A significant hysteresis in the transition temperatures T₂, T₃, and T₄ as well as its strong dependence on the heating/cooling rate was observed during the thermal cycling. These experimental facts confirm that transformations G₂ ↔ G₃ ↔ G₄ ↔ G₅ are of the first order. Analysis of the T_i dependence on dT/dτ in the heating and cooling modes allowed the determination of the real values of phase transition temperatures and their hysteresis, which were considered as parameters under equilibrium conditions when dT/dτ → 0: T₂ = 198 ± 1 K, δT₂ = 1 K; T₃ = 194 ± 1 K, δT₃ = 2 K; T₄ = 170 ± 1 K, δT₄ = 5 K.

Fig. 1 Temperature dependences of the excess heat capacity (a) and entropy (b) associated with the successive phase transitions G₁ ↔ G₂ ↔ G₃ ↔ G₄ ↔ G₅.

The entropy change associated with the successive phase transitions was determined by integration of the (ΔC_p/T)(T) function. Fig. 1b depicts the temperature behaviour of entropy. Its total value associated with the succession of phase transitions G₁ ↔ G₂ ↔ G₃ ↔ G₄ ↔ G₅ is rather large: ∑ΔS_i = 13.6 ± 3.0 J mol⁻¹ K⁻¹, revealing some order–disorder process in the mechanism of structural distortions. Because a DSM technique is not sensitive to the small excess heat capacity which can exist far below the phase transition point, we did not discuss the value of ΔS_i for individual transformations. For this we plan to perform a more detailed study of heat capacity using an adiabatic calorimeter.

Thus, the calorimetric measurements have shown that the cationic substitution Si → Ge in compounds (NH₄)₃M⁴⁺F₇ is accompanied by a small broadening of the temperature range of the P4/mbm phase stability (T₁ = 280 K in (NH₄)₃GeF₇) and an increase in the number of the phase transformations.¹¹

3.2 Polarization optics

The single crystals of (NH₄)₃SiF₇, like (NH₄)₃GeF₇, have a habitus of elongated rectangular prisms with the developed facets of (110)_t. The four-fold axis is preferably located along the longest edge of the crystal, so the plate-like sample with a (001)_t orientation is very rare. Two of these samples are presented in Fig. 2. The upper crystal consists of two blocks. The left side of this sample has an orientation (110)_t, and extinction along the growth edges. The right-hand block side (Δn_c = 0) is optically isotropic and has an orientation of (001)_t. The uniaxial pressure increase (up to destruction of the sample) did not change the orientation of the fourth-order axis in (NH₄)₃SiF₇, similar to that found earlier for (NH₄)₃GeF₇.¹¹ Thus, silicon and germanium compounds differ from (NH₄)₃TiF₇, where small uniaxial pressure reoriented this axis at 90 degrees.¹⁵

Fig. 2 Observation of crystals (NH₄)₃SiF₇ under polarized light upon cooling: (a) phase G₁, (b) G₂, (c) G₃, (d) G₄, (e and f) G₅. The upper sample consists of two blocks with different orientations of the four-fold axis in the G₁ phase, the lower plate has a (110)_t orientation.

Fig. 2 presents photographs of the (NH₄)₃SiF₇ plates as grown in polarised light. At room temperature the right-hand side of the upper sample is dark; and the left side has a ‘direct extinction’ in accordance with a tetragonal symmetry (G₁-phase) (Fig. 2a). Upon cooling the pattern changes significantly. Below T_1↓ = 263 K the dark area of the sample illuminates (Fig. 2b). The entire crystal illuminates completely or extinguishes along the growth verge (110)_t when the microscope stage is rotated by 90° (G₂-phase).

Further cooling leads to the appearance (disappearance) at T_2↓ = 198 K (T_2↑ = 199 K) of a layered structure with boundaries along [110]_t in the left-hand block (Fig. 2c). Optical indicatrices in the neighbouring twins are disoriented to the direction [110]_t. In the right-hand part of the specimen the direct extinction remains.

Upon cooling below T_3↓ = 191 K (T_3↑ = 192 K), the specimen shows a very complicated twin structure in three orthogonal directions with a ‘floating’ position of extinctions (Fig. 2d). Further cooling reveals an abrupt phase transition at T_4↓ = 162 K (T_4↑ = 167 K) into the tetragonal phase with, at first glance, a dark right side (Fig. 2e). But in contrast to the initial tetragonal phase (Fig. 2a) in the twins with coexistence, ‘direct’ (Fig. 2f), or ‘oblique’ (Fig. 2e) extinctions are observed in the lower (110)_t plate.

The illumination of the dark area of the sample below T_1↓ = 263 K (Fig. 2b) is associated with a reduction of crystal symmetry and the appearance of optical anisotropy along the [001]_t direction. Fig. 3 shows the temperature behaviour of the Δn_c birefringence, which appears at T₁ and smoothly changes near T₂ and T₃, while at T₄ there is a sharp disappearance of Δn_c.

Fig. 3 The appearance of optical anisotropy in the plate (001)_t at T₁, and its change at T₂, T₃, T₄: curve 1 – Δn_c(T). The rotation of the optical indicatrix around [110]_t and [001]_t directions: curve 2 – φ_a(T); curve 3 – φ_c(T); curve 4 – φ_b(T).

The twin structure in very thin plates (∼50 μm) consists of rather large domains in the phase G₅ which allows measurement of the temperature dependence of the birefringence Δn(T) and the angle of rotation of the optical indicatrix φ(T) (Fig. 4).

Fig. 4 Temperature dependence of birefringence Δn(T) of the crystal (NH₄)₃SiF₇ in the plate (110)_t, measured during cooling (curve 1) and heating (curve 2). Curve 3 is Δn(T) in (NH₄)₃GeF₇.¹¹

At room temperature the main birefringence of tetragonal (NH₄)₃SiF₇ (Δn = n_o − n_e = 0.0037) is higher than that in (NH₄)₃GeF₇ (Δn = 0.0034 (ref. 11)) and (NH₄)₃TiF₇ (Δn = 0.0023 (ref. 12)). Fig. 4 shows that the birefringence in the phase G₁ of (NH₄)₃SiF₇ is stable, varying slightly with temperature and gradually decreasing below T₁.

The DSM and polarization-optical studies as well as measuring the birefringence and the rotation angles of the indicatrix in the (NH₄)₃SiF₇ crystal allowed the establishment of the existence of four structural phase transitions between the G₁, G₂, G₃, G₄ and G₅ phases, with different symmetries. According to the temperature dependences of DSM and optical characteristics (Fig. 1, 3 and 4), the character of transitions in (NH₄)₃SiF₇ is the following: the second order for G₁ ↔ G₂, and first order close to the tricritical point for G₂ ↔ G₃ ↔ G₄. Therefore, we assume that a successive lowering of crystal symmetry taking place through three phase transitions at T₁, T₂, and T₃ can be described in the framework of group–subgroup relationships.

The presence of the optical anisotropy Δn_c and the position of extinction along the [110]_t direction reveals the geometry of a new cell in the G₂ phase. The group symmetry of that phase is most likely orthorhombic. Two axes of the unit cell should be perpendicular to the 4-fold axis and directed along the unit cell diagonals of the tetragonal G₁ phase: [110]_t = [010]_or; [110]_t = [100]_or; [001]_t = [001]_or.

The geometry of twinning and rotation of the optical indicatrix only around the [110]_t = [100]_or direction indicates the symmetry of the G₃ phase to be monoclinic P2₁/c11. The screw twofold axis is perpendicular to the former four-fold axis and directed along [100]_or of an orthorhombic unit cell of the G₂ phase. Thus, the successive lowering of symmetry during phase transitions at T₁ and T₂ was established, similar to that observed in (NH₄)₃GeF₇: P4/mbm (G₁) ↔ Pbam (G₂) ↔ P2₁/c (G₃).¹¹

Further temperature lowering leads to an additional cooling decrease in the symmetry of (NH₄)₃SiF₇ at T₃. It can be seen (Fig. 3) that the angle of rotation φ_a is maintained at the lower phase G₄, which is added by the rotation φ_b(T) and φ_c(T) around different axes of the orthorhombic unit cell. Therefore, the crystal symmetry group in this phase can be selected as triclinic P1̄.

The phase transition G₄ ↔ G₅ has a first-order character: there are rapid jumps of extinction angles and birefringence values (Fig. 3). At first glance, the sample in the bottom phase G₅ looks similar to that at room temperature: right-hand dark side (Δn_c = 0) and orange interference colour on the left-hand side (Fig. 2e). All optical data indicate the crystal identification to be tetragonal. However, in the (110)_t plane the observed twins have different positions of extinction. Simultaneous ‘direct’ and ‘oblique’ extinctions are observed (Fig. 2e and f). Thus, the crystal symmetry group in the G₅ phase can be chosen as monoclinic. The above studies show the difference between the monoclinic phases G₃ and G₅, with respect to a two-fold axis. This axis is directed along [110]_t = [100]_or in G₃, but along [110]_t = [010]_or in G₅.

Thus, the polarisation-optical studies suggest the existence of a rather complicated sequence of crystal symmetry changes upon cooling: P4/mbm (G₁) ↔ Pbam (G₂) ↔ P2₁/c11 (G₃) ↔ P1̄ (G₄) ↔ P12₁/c1 (G₅).

A shear deformation with component x₄ (within the orthorhombic cell) appears in phase G₃, causing rotation of the optical indicatrix on the angle φ_a (Fig. 3, curve 2). Additional components of shear deformation x₅ and x₆ appear in the triclinic G₄ phase, causing the indicatrix rotation φ_b and φ_c (Fig. 3, curves 3, 4). A further temperature lowering results in the formation of the monoclinic phase G₅, where the components x₄ and x₆ disappear and x₅ remains, changing its sign (Fig. 3, curve 4). An unusually large angle of indicatrix rotation φ_b ≈ 25° is characteristic of the ‘proper’ ferroelastic transitions when a parameter of transition δ is linearly related to the shear component of the spontaneous deformation δ ≈ x₅.

3.3 X-ray diffraction and group theory analysis

As the crystal structure of (NH₄)₃SiF₇ at room temperature was solved earlier,¹⁰ we used this model (P4/mbm) to make a Rietveld refinement by using TOPAS 4.2.¹⁸ The refinement was stable and gave low R-factors (Table 1 and Fig. 1S(a)†). Atomic coordinates are given in Table 1S,† main bond lengths are given in Table 2, and the crystal structure is presented in Fig. 5a. The compound (NH₄)₃SiF₇ was found to be very pure and all lines were indexed by the P4/mbm phase (Fig. 1S(a)†). Cell parameters after refinement were close to those from ref. 11.

Fig. 5 Crystal structures of (NH₄)₃SiF₇: (a) G₁ phase (P4/mbm) at T = 303 K; (b) G₂ phase (Pbam) at T = 213 K, (c) G₄ phase (P1̄) at T = 183 K; (d) G₅ phase (P2₁/c) at T = 133 K.

Table 1 Main parameters of processing and refinement of the (NH₄)₃SiF₇ sample in four phases

Phase	G1	G2	G4	G5
Temperature, K	303	213	183	133
Sp. Gr.	P4/mbm	Pbam	P1̄	P21/c
a, Å	8.0750(2)	11.3989(5)	5.8256(2)	11.5710(3)
b, Å	8.0750(2)	11.3759(4)	11.3567(4)	11.4073(3)
c, Å	5.8613(2)	5.8343(2)	11.4063(3)	11.4300(3)
α, °	90	90	91.414(3)	90
β, °	90	90	89.808(3)	90.745(2)
γ, °	90	90	90.052(4)	90
V, Å^3	382.19(2)	756.55(5)	754.39(4)	1508.57(6)
Z	2	4	4	8
2θ-interval, °	5–120	5–120	5–120	5–120
Number of refined coordinates and thermal parameters	10	22	66	66
Number of calculated independent reflections	181	642	2286	2263
R wp, %	10.20	10.02	10.26	8.66
R p, %	7.72	7.64	7.38	6.21
R exp, %	3.83	5.94	5.89	3.42
χ ^2	2.66	1.69	1.74	2.54
R B, %	4.74	4.04	3.38	3.95

---

Table 2 Main bond lengths (Å) in the four phases of (NH₄)₃SiF₇

P4/mbm (G1 phase) at T = 303 K
Si1–F2 × 2	1.623(3)	Si1–F3 × 4	1.656(3)
N1–F1 × 2	2.9307(1)	N1–F2 × 4	3.109(3)
N2–F3 × 2	2.848(4)	N2–F1 × 2	2.907(3)
N2–F2 × 2	3.009(1)
Pbam (G2 phase) at T = 213 K
Si1–F3 × 2	1.71(1)	Si1–F4 × 4	1.624(7)
Si2–F2 × 2	1.636(9)	Si2–5 × 4	1.691(7)
N1–F3	2.77(2)	N1–F2	2.84(2)
N1–F1 × 2	2.9207(7)	N1–F5 × 2	3.23(1)
N2–F1	2.88(2)	N2–F4 × 2	2.93(1)
N2–F1	2.94(2)	N2–F2 × 2	2.998(4)
N3–F5 × 2	2.81(1)	N3–F1	2.82(2)
N3–F4 × 2	2.88(1)	N3–F1	2.97(2)
P1̄ (G4 phase) at T = 183 K
Si1–F3 × 2	1.66(1)	Si3–F6 × 2	1.71(2)
Si1–F9 × 2	1.63(2)	Si3–F8 × 2	1.69(2)
Si1–F13 × 2	1.73(2)	Si3–F12 × 2	1.65(2)
Si2–F4 × 2	1.61(2)	Si4–F5 × 2	1.78(2)
Si2–F10 × 2	1.78(2)	Si4–F7 × 2	1.68(2)
Si2–F14 × 2	1.60(2)	Si4–F11 × 2	1.70(2)
N1–F6	2.81(3)	N1–F1	2.91(5)
N1–F1	2.92(5)	N1–F10	2.94(3)
N1–F7	3.02(3)	N1–F3	3.11(3)
N2–F5	2.69(3)	N2–F2	2.88(5)
N2–F4	2.93(3)	N2–F2	2.98(5)
N2–F8	3.01(3)	N2–F3	3.17(3)
N3–F2	2.68(3)	N3–F7	2.76(3)
N3–F13	2.82(3)	N3–F11	2.88(3)
N3–F3	2.92(4)	N3–F1	2.96(3)
N4–F8	2.73(4)	N4–F10	2.75(3)
N4–F1	2.77(3)	N4–F12	2.95(3)
N4–F4	2.98(4)	N4–F14	3.01(3)
N5–F12	2.68(3)	N5–F2	2.77(3)
N5–F6	2.77(4)	N5–F13	2.90(3)
N5–F9^v	2.91(4)	N5–F8	3.02(4)
N6–F2	2.72(3)	N6–F10	2.76(3)
N6–F11	2.80(3)	N6–F14	2.85(3)
N6–F5	2.97(4)	N6–F1	3.01(3)
P21/c (G5 phase) at T = 133 K
Si1–F5 × 2	1.70(1)	Si3–F3 × 2	1.64(2)
Si1–F7 × 2	1.66(1)	Si3–F11 × 2	1.66(1)
Si1–F9 × 2	1.75(1)	Si3–F13 × 2	1.58(1)
Si2–F6 × 2	1.68(1)	Si4–F4 × 2	1.57(2)
Si2–F8 × 2	1.83(1)	Si4–F12 × 2	1.67(1)
Si2–F10 × 2	1.71(1)	Si4–F14 × 2	1.79(1)
N1–F5	2.83(2)	N1–F3	2.84(2)
N1–F11	2.87(2)	N1–F7	2.89(2)
N1–F1	2.90(2)	N1–F2	3.06(2)
N2–F1	2.76(2)	N2–F4	2.85(2)
N2–F2	2.88(2)	N2–F10	3.02(2)
N2–F6	3.02(2)	N2–F6	3.16(2)
N3–F2	2.73(3)	N3–F10	2.78(2)
N3–F12	2.89(2)	N3–F4	2.95(3)
N3–F7	2.96(2)	N3–F3	3.00(3)
N4–F8	2.69(2)	N4–F1	2.72(3)
N4–F14	2.80(2)	N4–F9	2.88(2)
N4–F13	3.01(2)	N4–F4	3.01(3)
N5–F2	2.72(2)	N5–F12	2.79(2)
N5–F9	2.80(2)	N5–F8	2.84(2)
N5–F6	2.87(3)	N5–F13	2.94(2)
N6–F2	2.60(2)	N6–F14	2.73(2)
N6–F7	2.93(2)	N6–F6	2.97(3)
N6–F11	3.01(3)	N6–F10	3.06(2)

---

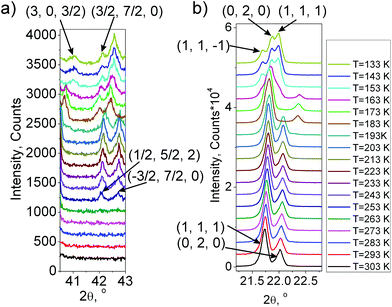
One can see (Fig. 6 and 7a) that the first wave of superstructure peaks appears at T = 253 K. This temperature is 10 K lower than T₁ = 263 K. This is because the powder sample in an X-ray experiment is cooled from the bottom, while diffraction happens only from the top surface, and the result is a temperature gradient in the powder sample. This temperature difference was further taken into account to make measurements in all other experiments. Additional peaks appearing at 253 K can be described by the emergence of instability at (1/2, 1/2, 0) k₁₈-point (M) of the Brillouin zone of the G₁ – P4/mbm unit cell (hereinafter the designation of irreducible representations (irrep) and points of the Brillouin zone are given in accordance with reference books).^19,20 The observation of a similar situation in (NH₄)₃GeF₇ ¹¹ allowed the conclusion that the mechanism of G₁ ↔ G₂ transformation in germanium and silicon compounds should be the same. The M₁⁻⊕M₄⁻ irrep drives this phase transition, and the transformation can be written: , where η₁ and η₂ are components of critical order parameters. The crystal structure for the Rietveld refinement in TOPAS 4.2 was prepared by the ISODISTORT program using the initial G₁ phase (P4/mbm) and M₁⁻⊕M₄⁻ irrep distortion. The refinement was stable and gave low R-factors (Table 1 and Fig. 1S(b)†). Atomic coordinates are given in Table 1S,† main bond lengths are given in Table 2 and the crystal structure is presented in Fig. 5b.

Fig. 6 X-ray powder patterns of (NH₄)₃SiF₇ at different temperatures from 133 K to 303 K.

Fig. 7 Fragment of X-ray powder patterns of (NH₄)₃SiF₇ with: (a) superstructure peaks (3, 0, 3/2) and (1/2, 5/2, 2), which are prohibited in the G₁ tetragonal phase (P4/mbm); (b) structure peaks (1, 1, 1) and (0, 2, 0) of the G₁ tetragonal phase.

Group-theoretical analysis showed that in (NH₄)₃SiF₇, similarly to (NH₄)₃GeF₇, the MF₆ (M = Si, Ge) octahedron was split (MF₆ → M1F₆ + M2F₆) at phase transition P4/mbm ↔ Pbam. The critical irrep M₁⁻⊕M₄⁻ induces the greatest contribution to distortions and leads to the critical shift of fluorine ions along the a and b axes of the orthorhombic phase. These movements can be represented as rotation of the MF₆ octahedron around the 4-fold axis in the tetragonal phase (Fig. 8a and b). The F–N bond lengths vary in the range of 2.907(3)–3.109(3) Å in the tetragonal phase to 2.77(2)–3.23(1) Å (Table 2) in the orthorhombic phase. The decrease of these bond lengths may be due to the formation of N–H⋯F hydrogen bonds. Since SiF₆ octahedra are ordered in the G₁ phase while NH₄ tetrahedra are disordered due to a high local symmetry of one NH₄ site (4/m), the transformation P4/mbm ↔ Pbam can be associated only with the ordering of NH₄ groups. The formation of hydrogen bonds (short N⋯F contacts) after phase transition may serve as an indicator of NH₄ ordering.

Fig. 8 The main distortions of the (NH₄)₃MeF₇ (Me = Si, Ge) crystal structures at phase transitions, leading to rotation of MF₆ octahedra during the transformations in different projections. Dashed red rectangle surrounds the formula unit of different phases. The sequence of G₁ ↔ G₂ ↔ G₃ of the phases is the same for both (NH₄)₃SiF₇ and (NH₄)₃GeF₇, but their G₃ ↔ G₄ phase transitions are different. Further G₄ ↔ G₅ transition exists only in (NH₄)₃SiF₇.

It was impossible to carry out the X-ray measurements in the G₃ phase due to the narrow temperature region of its existence. However, it was found from optical measurements that this phase is monoclinic.

The X-ray experiment in of the G₄ phase (Fig. 1S(c),†Fig. 6 and 7b) reveals that the main peak broadening occurs, but there are no additional superstructure peaks (Fig. 7a); therefore it can be concluded that the G₃ ↔ G₄ phase transition is associated with the emergence of instability at the same (1/2, 1/2, 0) k₁₈-point (M) of the Brillouin zone of P4/mbm. Optical investigations showed a triclinic symmetry of this phase. The space group P1̄ with basis of a tetragonal G₁ phase (0,0,1), (1,1,0), (−1,1,0) fulfills all these conditions. The M₁⁻⊕M₄⁻ and M₅⁻ irreps drive this phase transition and the transformation can be written as:

where (ξ, ε) are other critical order parameters, which are transformed according to M₅⁻ irrep of the sp. gr. P4/mbm. The crystal structure for Rietveld refinement in TOPAS 4.2 was prepared by the ISODISTORT program using M₅⁻ irrep distortion. Refinement was stable and gave low R-factors (Table 1 and Fig. 1S(c)†). Atomic coordinates are presented in Table 1S,† main bond lengths are given in Table 2, and the crystal structure is shown in Fig. 5c. It should be noted that slightly different order parameters of M₅⁻ irrep, namely (ξ, ξ), drive P4/mbm to the P2₁/c phase. Such a phase transition was found in (NH₄)₃GeF₇. Since the phase transition G₁ ↔ G₂ in both compounds (NH₄)₃M⁴⁺F₇ (M⁴⁺ = Si, Ge) is the same, and M₁⁻⊕M₄⁻ with M₅⁻ irreps drive G₂ ↔ G₃ and G₃ ↔ G₄ transitions, the sequence of phase transitions in (NH₄)₃SiF₇ is suggested:
So we can imagine that the main rotations of SiF₆ and GeF₆ octahedra during G₂ ↔ G₃ phase transition are the same (Fig. 8c). After this transformation all similarities between (NH₄)₃SiF₇ and (NH₄)₃GeF₇ vanish. Under G₃ ↔ G₄ transition (NH₄)₃SiF₇ shows transformation P2₁/c ↔ P1̄ (Fig. 8e), but (NH₄)₃GeF₇ showed reconstructive phase transition P2₁/c ↔ Pa3̄ (Fig. 8d). Previously it was found that all NH₄ groups in the Pa3̄ phase of (NH₄)₃GeF₇ are ordered and all hydrogen atoms were localized. The crystal structure of the P1̄ phase of (NH₄)₃SiF₇ shows several rather short F–N bonds: d(N2⋯F5) = 2.69(3) Å, d(N3⋯F2) = 2.68(3) Å, d(N4⋯F8) = 2.73(4) Å, and the range of F–N distances expands to 2.68(3)–3.17(3) Å (Table 2), which indicates the presence of N–H⋯F hydrogen bonds. However, the smallest contact over all N1⋯F contacts, d(N1⋯F6) = 2.81(3) Å, is not very short for a H-bond, therefore some NH₄ disordering could remain in the crystal structure.

Indeed, below T₄, a new phase G₅ in (NH₄)₃SiF₇ was observed, and an additional wave of superstructure peaks appeared (Fig. 6 and 7a). All these new peaks can be described by the emergence of instability at (0, 0, 1/2) k₁₉-point (Z) of the Brillouin zone of the G₁ – P4/mbm unit cell. Indexing shows that a cell in the G₅ phase becomes P2₁/c with twice the cell volume compared to the G₄ phase (P1̄). The M₁⁻⊕M₄⁻, M₅⁻ and Z₁⁺ irreps drive this phase transition, and the transformation can be written as: , where δ is a component of the critical order parameter. Cell parameters and the volume of the G₅ phase (P2₁/c) (NH₄)₃SiF₇ (Table 1 and Fig. 8f) finally became similar to those of the G₄ phase (Pa3̄) in (NH₄)₃GeF₇ (ref. 11, Fig. 8d). The crystal structure G₅ of (NH₄)₃SiF₇ for Rietveld refinement in TOPAS 4.2 was prepared by the ISODISTORT program using the initial G₁ phase (P4/mbm) and M₁⁻⊕M₄⁻, M₅⁻, Z₁⁺ irreps distortion. There are 30 amplitude modes which should be initially varied and their starting values should be found before Rietveld refinement. A simulated annealing procedure in TOPAS 4.2 was used, and a satisfactory model with low R-factors was obtained. The refinement of the obtained model was stable and gave low R-factors (Table 1 and Fig. 1S(d)†). Atomic coordinates are given in Table 1S;† the crystal structure is shown in Fig. 5d. The F–N distances are in the range of 2.60(2)–3.17(2) Å and indicate the formation of N–H⋯F hydrogen bonds. In comparison with the G₄ phase their average values become smaller, and it seems that all NH₄ groups are ordered in the G₅ phase.

It is easy to see that the phase G₁ (P4/mbm) (Fig. 8a), in fact, can be represented as a rotationally distorted antiperovskite ABX₃,²¹ where A = [SiF₆], B = [F] and X = [NH₄], i.e. [SiF₆][F][NH₄]₃. The cubic Pm3̄m phase is a parent phase of antiperovskite²¹ (Fig. 9a), which is not realized in our case. However, taking Pm3̄m as a parent phase, the analysis of sequential orientation changes of F(NH₄)₆ octahedra at phase transitions was performed. It should be noted that SiF₆ were not taken into consideration because they were isolated and didn't form a system of linked octahedra. Therefore, using Glazer's notation²² (Fig. 9b) for the system of linked octahedral F(NH₄)₆, the following scheme was found:

where a⁰ means an absence of any octahedral rotation, c⁺ means in-phase octahedral rotation in all layers along the c-axis, b⁻ means antiphase rotation along the b-axis in the neighboring layers. The value of the F(NH₄)₆ rotation angle, which is associated with c⁺, is approximately equal to ∼10.9°, but rotation angles associated with b⁻ are an order of magnitude lower and equal ∼1.4°. Schemes of the a⁰a⁰c⁺ and a⁰b⁻c⁺ tilt systems are shown in Fig. 9c and d, where rotation values are artificially increased for clarity. Despite the fact that the tilt systems are the same for several phases, the difference between their space groups is associated with changes of SiF₆ positions, which have already been described.

Fig. 9 Relationship between perovskite-type structure and antiperovskite parent Pm3̄m (G₀) phase of [SiF₆][F][NH₄]₃ (a). All possible octahedral tilts in neighboring layers of perovskites and corresponding Glazer's notations (b). Rotation of F(NH₄)₆ octahedra in a⁰a⁰c⁺ (c) and a⁰b⁻c⁺ (d), which are realized under phase transitions.

One can see that the difference between (NH₄)₃SiF₇ and (NH₄)₃GeF₇ is not only in the number and the sequence character (G₃ ↔ G₄ ↔ G₅) of phase transitions. Phase transition P4/mbm ↔ Pa3̄ in (NH₄)₃GeF₇ is reconstructive and cannot be analysed by group-theoretical methods while P4/mbm ↔ P2₁/c transformation in (NH₄)₃SiF₇ can be described in this way. It should be noted that K₃SiF₇,²³ Rb₃SiF₇,²⁴ and Cs₃GeF₇ ²⁵ also have the P4/mbm phase at room temperature, while Tl₃SiF₇ ²⁶ crystallizes in the P3̄1c space group, but nothing is known about their phase transitions.

All patterns from 133 K to 303 K were treated in a similar way and the temperature dependence of cell parameters a, b, c (Fig. 2S(a)†), cell volume V (Fig. 2S(b)†) and angles α, β, γ (Fig. 2S(c)†) were plotted.

Further details of the crystal structures of G₁, G₂, G₃ and G₅ phases may be obtained from Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: (+49)7247-808-666; E-mail: crystdata@fiz-karlsruhe.de; http://www.fiz-karlsruhe.de/request_for_deposited_data.html on quoting the deposition numbers: CSD 432220; 432221; 432222 and 432223, respectively).

4. Conclusions

Single crystals of silicon double salt (NH₄)₃SiF₇ = (NH₄)₂SiF₆·NH₄F = (NH₄)₃[SiF₆]F were grown, and we should recognize that the history of the compound goes back, in fact, more than 200 years. Davy observed tetragonal prisms, which were evidently (NH₄)₃SiF₇, in accordance with the tetragonal structure of this compound. We studied this compound by different methods. Calorimetric measurements revealed the succession of four reversible phase transitions below room temperature: T₁ = 263 ± 1 K; T₂ = 198 ± 1 K; T₃ = 194 ± 1 K; T₄ = 170 ± 1 K, and an absence of transformation into the Pm3̄m phase up to decomposition. It was found that the application of uniaxial pressure does not change the orientation of the four-fold axis of (NH₄)₃SiF₇, similar to (NH₄)₃GeF₇,¹¹ which is in agreement with the fact that they are isostructural at room temperature. Therefore, both (NH₄)₃SiF₇ and (NH₄)₃GeF₇ differ from (NH₄)₃TiF₇ in which the high-pressure parent phase Pm3̄m is attainable.

The polarization-optical studies showed lowering of symmetry during phase transitions at T₁ and T₂, similar to that observed in (NH₄)₃GeF₇. Further cooling (NH₄)₃SiF₇ revealed the existence of a complicated sequence of crystal symmetry changes with the appearance of triclinic P1̄ (G₄) and new monoclinic P12₁/c1 (G₅) phases. The large rotation angles of the indicatrix at G₄ ↔ G₅ phase transition is associated with the ‘proper’ ferroelastic transitions when a parameter of transition δ is linearly related to the shear component of the spontaneous deformation δ ∼ x₅.

Joint XRD and optical analysis allowed us to solve and refine crystal structures of the G₁, G₂, G₃, and G₅ phases, suggest a model of the G₄ phase and define the sequence of symmetry transformations: P4/mbm (Z = 2) (G₁) ↔ Pbam (Z = 4) (G₂) ↔ P2₁/c (Z = 4) (G₃) ↔ P1̄ (Z = 4) (G₄) ↔ P2₁/c (Z = 8) (G₅). Indeed, the sequence of the first three phases of (NH₄)₃SiF₇ coincides with that for (NH₄)₃GeF₇. Then a significant difference arises between them: (NH₄)₃GeF₇ undergoes a reconstructive phase transition to Pa3̄, but (NH₄)₃SiF₇ undergoes two phase transitions, which can be described by group-theoretical methods. The lowest-temperature phases in (NH₄)₃MF₇ (M = Si, Ge) have similar cell parameters, and it seems that all NH₄ groups are fully ordered in them. Therefore, the driving force of all phase transitions in (NH₄)₃MF₇ can be associated with the emergence of N–H⋯F hydrogen bonds, because the value of N⋯F contacts decreases at phase transition under cooling. Suggested order–disorder processes are in accordance with the large values of entropy change.

The final scheme of phase transitions in (NH₄)₃SiF₇, including irreducible representations and corresponding order parameters, can be written as:

In spite of the fact that the Pm3̄m parent phase cannot be obtained under heating/pressure, the final scheme of phase transitions referred to the cubic phase can be expressed as:

Acknowledgements

The reported study was partially supported by RFBR, research project no. 15-02-02009a.

Notes and references

1. N. Laptash and I. Maslennikova, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 112, 012024,  DOI:10.1088/1757-899X/112/1/012024.
2. N. M. Laptash and L. N. Kurilenko, RU Patent, 2306546, 2007.
3. L. N. Kurilenko, N. M. Laptash, E. B. Merkulov and V. Yu. Glushchenko, Electron J. “Investigated in Russia”, 2002, 130/021011, 1465–1471 http://zhurnal.ape.relarn.ru/articles/2002/130.pdf .
4. N. M. Laptash and L. N. Kurilenko, RU Patent, 2157523, 2000.
5. A. M. Abdel-Rehim, J. Therm. Anal., 1997, 48, 177–202.
6. G. Meyer, Z. Anorg. Allg. Chem., 2008, 634, 201–222.
7. C. Plitzko and G. Meyer, Z. Anorg. Allg. Chem., 1996, 622, 1646–1650.
8. M. C. Marignac, Ann. Mines, 1859, 15, 221–290.
9. J. Davy, Philos. Trans. R. Soc. London, 1812, 102, 352–369.
10. J. L. Hoard and M. B. Williams, J. Am. Chem. Soc., 1942, 64, 633–637.
11. S. V. Mel'nikova, M. S. Molokeev, N. M. Laptash and S. V. Misyul, Dalton Trans., 2016, 45, 5321–5327.
12. M. S. Molokeev, S. V. Misyul, I. N. Flerov and N. M. Laptash, Acta Crystallogr., Sect. B: Struct. Sci., 2014, 70, 924–931.
13. I. N. Flerov, M. S. Molokeev, N. M. Laptash, A. A. Udovenko, E. I. Pogoreltsev, S. V. Mel'nikova and S. V. Misyul, J. Fluorine Chem., 2015, 178, 86–92.
14. E. I. Pogoreltsev, E. V. Bogdanov, A. V. Kartashev, M. S. Molokeev, I. N. Flerov and N. M. Laptash, Ferroelectrics, 2016, 501(1), 20–25.
15. S. V. Mel'nikova, E. I. Pogoreltsev, I. N. Flerov and N. M. Laptash, J. Fluorine Chem., 2014, 165, 14–19.
16. E. I. Pogoreltsev, I. N. Flerov, A. V. Kartashev, E. V. Bogdanov and N. M. Laptash, J. Fluorine Chem., 2014, 168, 247–250.
17. J. E. Ricci and J. A. Skarulis, J. Am. Chem. Soc., 1951, 73, 3618–3627.
18. Bruker AXS TOPAS V4, General profile and structure analysis software for powder diffraction data – User's Manual, Bruker AXS, Karlsruhe, Germany, 2008.
19. O. V. Kovalev, Representation of Crystallographic Space Groups, CRC Press, 1993.
20. S. C. Miller and W. F. Love, Tables of Irreducible Representations of the Space Groups and Co-Representations of Magnetic Space Groups, Pruett Press Boulder, Colorado, 1967.
21. B. V. Beznosikov and K. S. Aleksandrov, J. Struct. Chem., 2002, 43, 798–801.
22. A. M. Glazer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 3384–3392.
23. D. L. Deadmore and W. F. Bradley, Acta Crystallogr., 1962, 15, 186–189.
24. B. Hofmann and R. Hoppe, Z. Anorg. Allg. Chem., 1979, 458, 151–162.
25. F. Averdunk and R. Hoppe, J. Less-Common Met., 1989, 146, 137–145.
26. V. A. Shreider, I. M. Vol'pin and Y. E. Gorbunova, Russ. Chem. Bull., 1988, 37, 831–835.

---

Footnotes

† Electronic supplementary information (ESI) available. CSD 432220–432223. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt04874a

‡ S. V. Misyul unfortunately died while this manuscript was in the process of being published.

---