Dielectric relaxation and anhydrous proton conduction in [C₂H₅NH₃][Na_0.5Fe_0.5(HCOO)₃] metal–organic frameworks

Abstract

Metal–organic frameworks (MOFs), in which metal clusters are coupled by organic moieties, exhibit inherent porosity and crystallinity. Although these systems have been examined for vast potential applications, the elementary proton conduction in anhydrous MOFs still remains elusive. One of the approaches to deal with this problem is the utilization of protic organic molecules, to be accommodated in the porous framework. In this work we report the temperature-dependent crystal structure and proton conduction in [C₂H₅NH₃][Na_0.5Fe_0.5(HCOO)₃] metal–organic frameworks using X-ray diffraction and broadband dielectric spectroscopic techniques. The detailed analysis of the crystal structure reveals disorder of the terminal ethylene groups in the polar phase (space group Pn). The structural phase transition from Pn to P2₁/n at T ≈ 363 K involves the distortion of the metal formate framework and ordering of EtA⁺ cations due to the reduction of the cell volume. The dielectric data have been presented in the dynamic window of permittivity formalism to understand the ferroelectric phase transition. The relaxation times have been estimated from the Kramers–Kronig transformation of the dielectric permittivity. A Grotthuss type mechanism of the proton conduction is possible at low temperatures with the activation energy of 0.23 eV. This type of experimental observation is expected to provide new prospective on the fundamental aspect of elementary proton transfer in anhydrous MOFs.

---

Introduction

Metal–organic framework (MOF) compounds composed of anionic metal formate frameworks templated by singly protonated ammonium cations have received enormous scientific attention in recent years due to their attractive ferroelectric,^1–3 ferroelastic,⁴ magnetic,^5,6 multiferroic^7–9 and luminescence^10–12 properties. These remarkable properties are associated with structural changes and thus can be tuned due to a large number of possible combinations between organic cations (mainly alkylammonium cations) and metal ions coordinated by formate linkers. The size and shape of organic cations and hydrogen bonding between these cations and the metal formate framework are essential for making them thermodynamically stable. The most extensive studies on formate MOFs concerned frameworks composed of divalent metal ions with the general formula [cat][M^II(HCOO)₃] that crystallize either in chiral or perovskite-type structures, where cat denotes ammonium,^7,13–16 methylammonium,¹⁷ ethylammonium (EtA⁺),¹⁵ dimethylammonium (DMA⁺),^{4,6,8,10,11,18–21} guanidinium,²² azetidinium,²³ and formamidinium^24,25 ions. According to literature data, [DMA][M^II(HCOO)₃] formates crystallize in the trigonal space group R3̄c with the disordered DMA⁺ cations located in the cages of the network. These compounds show a ferroelectric order close to 160–279 K, which is related to ordering of DMA⁺ cations and order–disorder phase transition.^6,26–29 The replacement of DMA⁺ ions by EtA⁺ ions in Mg(II) and Mn(II) analogues leads to a decrease of room-temperature symmetry to the non-centrosymmetric space group Pna2₁ with ordered EtA⁺ cations.^15,30 It is worth noting that [EtA][Mg(HCOO)₃] undergoes two phase transitions at 374 and 426 K into the trigonal and orthorhombic phase, respectively, with disordered EtA⁺ cations.²⁸

Recent studies also show that divalent metal ions can be substituted by trivalent lanthanide ions¹⁰ or by heterovalent homo-²⁰ or hetero-metallic³ ions. The members of the last group containing Na(I) ions, with the general formula [cat][Na_0.5M^III_0.5(HCOO)₃], where M^III = Fe or Cr, adopt the perovskite-type structure.³ It is reported that [EtA⁺][Na_0.5Fe_0.5(HCOO)₃] (EtANaFe) exhibits a polar structure with the non-centrosymmetric space group Pn at ambient temperature. It undergoes a second-order phase transition close to 360 K and its high-temperature structure becomes monoclinic, space group P2₁/n, with dynamically disordered EtA⁺ cations.³ Based on theoretical calculations, the polarization was estimated as 0.2, 0, and 0.8 μC cm⁻², i.e., lying within the ac plane. The probable driving force of the phase transition is the ordering of EtA⁺ cations accompanied by major distortion of the metal formate framework.³ A proton (H⁺) is coupled to an organic EtA⁺ cation and it forms conventional N–H⋯O hydrogen bonds with the formate oxygen ions.³ The proton is the only ion which has no electron shell of its own.³¹ Thus, it strongly interacts with the electron density of its environment. The donor to acceptor distances, in N–H⋯O hydrogen bonds, range from 2.860(6) to 3.298(7) Å in the polar phase Pn. Proton conduction can be understood through a pathway of sites of equal proton affinity separated by an energy barrier that is as small as possible. Besides, EtA⁺ cations are associated with a more robust H-bond network due to the presence of three H atoms in the NH₃ group compared to DMA⁺. At this juncture, it is essential to note that the efficient proton conduction in the matter depends on (i) the facile movement of H⁺ through the H-bonded network (Grotthuss-type) or motion of the EtA⁺ cation (vehicle-type), (ii) the distance between a proton donor and a proton acceptor (Q) i.e., the static or average Q of most good proton conductors, usually obtained from diffraction experiments, is generally higher than 260 pm which suggests asymmetric, medium, or weak hydrogen bonds and finally (iii) the working experimental window. Several MOF structures have now been reported that conduct at 10⁻³ S cm⁻¹ or higher by incorporating phosphonate groups, or secondary ions such as polycarboxylates or ammonium, as proton transfer sites. For proton conductivity, either organic linkers have been synthesized with sulfonic, phosphonic, carboxylic, or hydroxyl groups that can align themselves in the channels or with proton carriers as guest molecules such as imidazoles, triazoles, ammonium ions, hydroxonium ions, etc.^32–46 We note that the crystalline nature of MOFs provides an excellent platform to examine the possible proton conduction, thus enabling the construction of structure–property relationship due to the long-range order.

In this report, we employ temperature dependent X-ray diffraction (XRD) and broadband dielectric spectroscopy (BDS) techniques to better understand the nature of ferroelectric phase transition and proton conduction in EtANaFe in a wide range of temperature conditions. We select this system because it entails a protic organic cation that facilitates anhydrous proton conduction in a H-bonded network. In addition, we discuss the relationship between structural and electrical properties. A similar approach has also been successfully developed in other MOFs.^47,48

Experimental

Sample synthesis

After description of the synthesis³ EtANaFe crystals were prepared under solvothermal conditions at 140 °C. In a typical experiment, a mixture of FeCl₂ (2 mmol), ethylamine hydrochloride (2 mmol), HCOONa (6 mmol), N-ethylformamide (25 mL), H₂O (20 mL) and HCOOH (0.5 cm³) was heated in a Teflon-lined microwave autoclave for 24 hours. Block light-yellow crystals were obtained by evaporating the solution at room temperature for 1 week. The crystals were filtered from the mother liquid and washed with ethanol.

X-ray diffraction

The X-ray powder diffraction data were collected in reflection mode using a X'Pert PRO X-ray diffraction system equipped with a PIXcel ultra-fast line detector and Soller slits for Cu Kα radiation. For temperature-dependent data, the Anton Paar 1200N High-Temperature Oven Chamber was used. A good match of their powder XRD patterns with the calculated ones based on the single-crystal data (see Fig. S1 and S2 in the ESI†) confirmed the phase purity of the investigated bulk samples. Single-crystal X-ray diffraction data were collected at 297–365 K on the Xcalibur Atlas diffractometer operating in κ geometry, equipped with a two-dimensional CCD detector and Mo Kα radiation (0.71073 Å) source. Data were measured in the ω-scan mode with Δω = 1.0° using the CrysAlis CCD program. CrysAlis PRO software was used for data processing [(Rigaku OD, 2015), CrysAlis PRO, Oxford Diffraction Ltd, Version 1.171.34.44 (release 25-10-2010 CrysAlis171 .NET)]. Empirical absorption correction using spherical harmonics was applied on all data. The structures were solved by direct methods and refined using full-matrix least-squares methods with the SHELXL-97 program package.⁴⁹ Hydrogen atoms were included in geometric positions (C–H ∼ 0.97, N–H ∼ 0.89 Å) and treated as riding atoms with isotropic displacement parameters constrained to 1.2U_eq. of the carrier atom. The details of the crystal, data collection and refinement are presented in Tables 1 and S3.†

Table 1 Experimental details. For all structures: C₁₀H₂₂FeN₂NaO₁₂, M_r = 441.13, Z = 2. Experiments were carried out with Mo Kα radiation. H-atom parameters were constrained. Multi-scan absorption collection using spherical harmonics, implemented in SCALE3 ABSPACK scaling algorithm; CrysAlis PRO 1.171.38.41 (Rigaku Oxford Diffraction, 2015)

	(365 K)	(355 K)	(345 K)	(335 K)
Computer programs: CrysAlis PRO 1.171.38.41 (Rigaku OD, 2015), CrysAlis PRO, Oxford Diffraction Ltd, Version 1.171.34.44 (release 25-10-2010 CrysAlis171 .NET) (compiled Oct 25 2010, 18:11:34), SHELXL2014/7.
Crystal system, space group	Monoclinic, P21/n	Monoclinic, Pn	Monoclinic, Pn	Monoclinic, Pn
Temperature (K)	365	355	345	335
a, b, c (Å)	8.1207 (2), 9.3921 (4), 12.1550 (4)	8.12573 (10), 9.37296 (10), 12.1399 (10)	8.1295 (1), 9.35875 (10), 12.1287 (10)	8.13384 (10), 9.34542 (10), 12.11761 (10)
β (°)	91.124 (3)	91.1731 (10)	91.2117 (10)	91.2564 (10)
V (Å^3)	926.89 (6)	924.41 (2)	922.57 (2)	920.89 (2)
μ (mm^−1)	0.90	0.90	0.90	0.90
Crystal size (mm)	0.22 × 0.17 × 0.16
T min, Tmax	0.951, 1.000	0.954, 1.000	0.954, 1.000	0.959, 1.000
No. of measured, independent and observed [I > 2σ(I)] reflections	10 027, 1754, 1567	10 021, 3372, 3190	10 027, 3371, 3199	9991, 3356, 3222
R int	0.026	0.023	0.022	0.021
(sin θ/λ)max (Å^−1)	0.610	0.609	0.610	0.610
R[F^2 > 2σ(F^2)], wR(F^2), S	0.038, 0.093, 1.24	0.034, 0.089, 1.09	0.029, 0.079, 1.00	0.028, 0.075, 0.97
No. of reflections	1754	3372	3371	3356
No. of parameters	150	238	238	238
No. of restraints	42	7	6	6
Δρmax, Δρmin (e Å^−3)	0.20, −0.29	0.43, −0.30	0.42, −0.25	0.44, −0.25
Absolute structure	—
Absolute structure parameter	—	0.48 (3)	0.47 (2)	0.47 (2)

---

Dielectric spectroscopy

Ambient-pressure dielectric measurements of the examined sample were carried out using a Novocontrol impedance analyzer, having a frequency range from 0.1 Hz up to 1 MHz. Since the obtained single crystals were not big enough to perform single crystal dielectric measurements, pellets made of well-dried samples were measured instead. The pellets were placed between two copper, flat electrodes (diameter 6 mm) of the capacitor with a gap of 0.4 mm. The small signal of amplitude 1 V was applied across the sample. The temperature was controlled by the Novocontrol Quattro Cryosystem, with the use of a nitrogen gas cryostat. The measurements were performed every 1 deg over the temperature range from 280 K up to 400 K. Temperature stability of the samples was better than 0.1 K. It has to be emphasized that measurements were repeated for few pellets and the received results were the same in the range of experimental error.

Results and discussion

Temperature dependent structural study

EtANaFe possesses the perovskite-like metal-formate framework which accommodates EtA⁺ templates in the pseudo-cubic cavities. The room temperature symmetry is polar, Pn, and transforms into the centrosymmetric, P2₁/n, above ∼360 K. In the high-temperature phase the EtA⁺ counterions are disordered over two non-equivalent positions A and B (Fig. 1). At 365 K both positions are occupied in the 0.56/0.44 ratio. The structural phase transition manifests in the distortion of the metal-formate framework and ordering of EtA⁺ cations due to the reduction of the size of the crystal voids and decrease in thermally induced motions. The cavity volume shrinks from 80 ų at 365 K to 75 ų at 355 K, just below the phase transition, and remains unchanged down to room temperature. After the phase transition the rotational motions of the cations are diminished. At room temperature in each cavity only one state from the high-temperature phase is realized. The asymmetric unit contains two non-equivalent cations; both are ordered and interact by N–H⋯O hydrogen bonds with the framework. Fig. S3 (ESI†) illustrates N–H⋯O hydrogen bonds in both structural phases; Table S2† summarizes the hydrogen bonds’ parameters. The amine groups are fixed in the structure though the interactions are of medium and weak strength.⁵⁰ The values of donor–acceptor distances vary from 2.77(2) Å to 3.26(2) Å in phase I and from 2.98(1) Å to 3.23(1) Å in phase II.

Fig. 1 The arrangement of the cations in the EtANaFe crystal; (a) high temperature phase I, T = 365 K, (b) polar phase II, T = 335 K. The A and B orientations are occupied with 0.56/0.44 ratio, respectively. The C cation is disordered over two close positions with ∼0.05/0.95 ratio within 335–355 K range. Both, C and D, are ordered at 297 K.

The EtA⁺ cations are ordered at room temperature. However due to weak anchoring the terminal ethylene groups display thermally inducted vibrations, which manifest in elongated thermal displacement parameters for carbon atoms. The detailed inspection of these motions at higher temperatures, i.e., at 335, 345 and 355 K, reveals notable disorder of the terminal carbon atom in one of the two cations (cation C in Fig. S4†). Due to the negative anisotropic displacement parameters the split-atom model had to be used to properly model the electron density. The occupancy of this additional, split position is almost equal within the error limit in the measured range and vary from 0.05(2) to 0.08(2). Its presence may be a remnant of the process of the cations’ rotations which follow the phase transition and lead to the polar arrangement of the cations, see Fig. 1 and S5.† The distance between the split carbon positions equals 0.77 Å and doesn't change within the 335–355 K range which suggests a static rather than a dynamical character of disorder at these temperatures. Possibly, a small fraction of C cations is trapped during the rotations in the metastable position, which is very close to the final (room temperature) placement. In the Pn phase the spatial arrangement of the EtA⁺ dipole moments gives rise to spontaneous polarization within the (a,c) plane. The symmetry mode analysis reported in ref. 3 also exposes the fact that significant contribution to phase transition and thus to the appearance of spontaneous polarization leads to polar displacements of Na⁺, Fe³⁺cations and formate linkers.

Temperature dependent dielectric study

Fig. 2(a) and (b) depict the frequency-dependent dielectric permittivity, ε′, and loss, ε′′, of EtANaFe for several isotherms between T = 400 K and T = 300 K. A close inspection of the dielectric permittivity spectra presented in Fig. 2a reveals that a dipole relaxation process exists in the material. This relaxation is visible as the gradual step-like change in the frequency dependence of the permittivity and a relaxation peak in the loss spectra (Fig. 2b), respectively. Because both representations provide the same information about the properties of the relaxation process, only one, usually the one associated with the loss spectra, is analyzed. However, as can be seen from the inset, due to a strong overlapping with conductivity, the relaxation process is only slightly visible in the loss spectra. Thus, the direct estimation of the characteristic relaxation times from the loss spectra will lead to large uncertainties of the estimated values. On the other hand, although for the permittivity data the electrode polarization effect is visible with bending up of ε′ at frequency values lower than the dipolar process but this effect only partially masks the relaxation and this process remains much better visible.

Fig. 2 Frequency dependence of (a) the dielectric permittivity (ε′) and (b) loss spectra (ε′′) for selected temperatures. Arrow indicates the direction of shift of the relaxation process on cooling. Inset: representative spectra with depicted relaxation process (orange curve) and conductivity (red line).

As mentioned above, the ε′ and ε′′ are inter-related and provide the same information about the relaxation properties of the material. In the case of highly conducting materials, the loss contribution due to the ohmic conduction of ionic origin should be removed, in order to enable the analysis of the relaxation process hidden below. However, the conductivity subtraction procedure can generate additional inaccuracies in the case of strongly masked dipole relaxation, and consequently the estimated values of the relaxation times can be inaccurate. In this case much more reliable analysis of the relaxation is possible by the use of the logarithmic derivative of the permittivity part, called Kramers–Kronig transformation.^51–53 Therefore, the frequency derivatives were applied to the ε′(f) data measured in the EtANaFe sample and representative spectra are shown in Fig. 3. Unambiguously, the masked dipolar relaxation process becomes clear for all transformed spectra. Comparison of the KK transformed spectra with the dielectric permittivity and loss data measured at 370 K are shown in the inset of Fig. 3. It confirms that the relaxation peak in the derivative data is located at the frequency range for which the relaxation process is observed for the ε′ and ε′′ spectra.

Fig. 3 The Kramers–Kroning transformation from the dielectric permittivity. The arrow indicates the direction of changes of the relaxation process with increasing temperature. Inset: comparison of the frequency dielectric permittivity and loss spectra with the spectra from the Kramers–Kroning transformation (T = 370 K).

For accurate estimation of the characteristic dipolar relaxation times from the Kramers–Kronig transformation, the data were parameterized in the vicinity of the peak maximum with the use of the single Havriliak–Negami function:

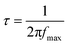whereτ and Δε denote the relaxation time and strength, respectively, ε_∞ is the high-frequency contribution, and parameters α and β describe symmetrical and asymmetrical broadening of the relaxation peak. The relaxation times were calculated from the peak maximum frequency as . Furthermore, the conductivity part of the loss spectra was also parameterized according to the electrodynamics relation , where s is the exponent describing departure from simple ionic temperature behavior with s = −1. In the case of the investigated sample, this departure is small, i.e. about 0.05 down to T_c. For lower temperatures, down to ca. 300 K, the frequency range of the conductivity part in the loss spectra becomes too narrow and too overlapped with the dipole relaxation to perform the reliable estimation of the values of σ (see Fig. S7,† spectrum at T = 330 K). With further cooling, maximum of the dipole process moves out of the experimental window and only a high frequency wing of this process influence the loss spectra. In this temperature range, mainly the part related to the σ remains visible in the loss spectra. Consequently, reliable estimation of the conductivity values becomes again possible (see Fig. S7†).

In order to understand the relaxation dynamics and conductivity, we compare the temperature dependent behavior of the dielectric relaxation times, τ_KK (from the KK transformation), and inverse conductivity, σ_dc⁻¹ as a function of 1000/T (see Fig. 4). In the Arrhenius plot three regions (marked by the vertical arrows), with three different types of thermal activation of the relaxation process, can be recognized, i.e., (a) above T = 363 K (high temperature range), (b) between 330 and 363 K (intermediate temperature range) and (c) below T = 330 K (low temperature range). The structural examination indicates that the dipolar order largely initiates from the reorientational motion or angular jumps of the EtA⁺ cation. Note that T = 360 K (see the inset) corresponds to the ferroelectric phase transition temperature (T_c), where the changes in relaxation dynamics are well visible. At high temperatures, the dipolar reorientations require a high magnitude of the activation energy of the order of 2.27 eV and this result indicates disordered motion of the EtA⁺ cations, in agreement with the structural analysis. Below T_c, the EtA⁺ cations become ordered. This ordering process is observed as a dielectric relaxation with an activation energy of 0.24 eV. It is worth noting that although EtA⁺ cations are ordered below T_c, they still have a significant degree of motions down to about 250 K, as evidenced by the IR data.³ The XRD data also revealed significant thermally induced vibrations of the ethylene groups in the low-temperature phase and some disorder of the terminal carbon atom in one of the two cations in the 335–355 K range which is not observed at room temperature. It is, therefore, likely that the observed increase of the activation energy close to 330 K up to 0.63 eV is related to the change in the dynamics of the ethylene groups. Note that the examined system entails (a) a protic cation controlling the dipolar order and (b) well expanded H-bonded network (see the ESI†); thus it enables efficient proton movement through the material and the conductivity process may couple with the dipolar process. This is evidenced through similar values of the activation energies below and above T_c. At very low temperature, the activation energy of the conductivity process (0.23 eV) is lower compared to the dipolar one (0.63 eV). As the distance (Q) between the proton donor and acceptor increases above T = 360 K, this activation energy of the conductivity process increases up to 1.86 eV. The driving force of this proton transfer can be found in the evolution of O–H distances which is listed in Table S1 (ESI†). It can be seen that the O–H distances decrease with decreasing temperature and are comparable to the values of average Q of most good proton conductors.^29,32 At low temperatures, when proton comes closer to oxygen, the conduction process requires smaller activation energy. Taking into account that hydrogen-bond breaking requires an energy penalty of about 0.11 eV, Grotthuss mechanism conduction processes generally involve activation energies with the magnitude of 0.4 eV. The vehicular mechanism, i.e. transport of larger ionic species with the mass greater than the mass of H⁺, requires significantly larger energy contribution, and as such processes with 0.4 eV generally refers to the latter mechanism.³²

Fig. 4 Relaxation map, i.e. τ_KK, and the inverse conductivity, σ_dc⁻¹ as a function of 1000/T. The inset shows the temperature dependence of ε′ for frequency 1 MHz (black), 0.1 MHz (red) and 10 kHz (blue) displaying the phase transition at T = 363 K.

Conclusions

In summary, we have analyzed the structural and dielectric measurements of the [C₂H₅NH₃][Na_0.5Fe_0.5(HCOO)₃] metal–organic framework. The important results of the study are presented below.

(1) The structural analysis shows the phase transition from Pn to P2₁/n at T ≈ 363 K which is manifested by the distortion of the metal-formate framework and ordering of the EtA⁺ cations.

(2) In the Pn phase the spatial arrangement of the EtA⁺ dipole moments induce spontaneous polarization within the (a,c) plane.

(3) The donor to acceptor distances, in N–H⋯O hydrogen bonds, varies in the range from 2.860(6) to 3.298(7) Å.

(4) We employ the Kramers–Kronig (KK) transformation to reveal the temperature behavior of the dipolar relaxation data, which provide, for the first time, direct evidence of the anhydrous conductivity in the perovskite-like metal-formate framework in its ferroelectric phase.

The broadband dielectric spectroscopy measurements combined with detailed temperature structural investigations clearly indicate the proton conductivity, which can be explained by the Grotthuss mechanism with the activation energy of 0.23 eV. This process is assisted with the structural relaxation caused by the reorientational motion of the protic organic ethylammonium cation.

Acknowledgements

The authors S. N. T. and M. P. are deeply grateful for financial support by the National Science Centre within the framework of the Maestro2 project (Grant No. DEC-2012/04/A/ST3/00337).

Notes and references

1. W. Zhang and R.-G. Xiong, Chem. Rev., 2012, 112, 1163–1195.
2. D. Di Sante, A. Stroppa, P. Jain and S. Picozzi, J. Am. Chem. Soc., 2013, 135, 18126–18130.
3. M. Ptak, M. Mączka, A. Gągor, A. Sieradzki, A. Stroppa, D. Di Sante, J. M. Perez-Mato and L. Macalik, Dalton Trans., 2016, 45, 2574–2583.
4. A. Sieradzki, J. Trzmiel, M. Ptak and M. Mączka, Electron. Mater. Lett., 2015, 11, 1033–1039.
5. G.-C. Xu, X.-M. Ma, L. Zhang, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588–9590.
6. M. Mączka, A. Gągor, B. Macalik, A. Pikul, M. Ptak and J. Hanuza, Inorg. Chem., 2014, 53, 457–467.
7. R. Ramesh, Nature, 2009, 461, 1218–1219.
8. W. Wang, L.-Q. Yan, J.-Z. Cong, Y.-L. Zhao, F. Wang, S.-P. Shen, T. Zou, D. Zhang, S.-G. Wang, X.-F. Han and Y. Sun, Sci. Rep., 2013, 3, 2024.
9. G. C. Xu, W. Yhang, X. M. Ma, Z. H. Chen, L. Yhang, H. L. Cai, Y. M. Wang, R. G. Xiong and S. Gao, J. Am. Chem. Soc., 2011, 133, 14948–14951.
10. Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162.
11. J. Heine and K. Müller-Buschbaum, Chem. Soc. Rev., 2013, 42, 9232–9242.
12. M. Mączka, B. Bondzior, P. Dereń, A. Sieradzki, J. Trzmiel, A. Pietraszko and J. Hanuza, Dalton Trans., 2015, 44, 6871–6879.
13. M. Mączka, A. Pietraszko, B. Macalik and K. Hermanowicz, Inorg. Chem., 2014, 53, 787–794.
14. M. Mączka, M. Ptak and S. Kojima, Appl. Phys. Lett., 2014, 103, 222903.
15. M. Mączka, P. Kadłubański, P. T. C. Freire, B. Macalik, W. Paraguassu, K. Hermanowicz and J. Hanuza, Inorg. Chem., 2014, 53, 9615–9624.
16. M. Mączka, K. Szymborska-Małek, A. Ciupa and J. Hanuza, Vib. Spectrosc., 2015, 77, 17–24.
17. Z. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 15, 2209–2216.
18. M. Mączka, A. Sieradzki, B. Bondzior, P. Dereń, J. Hanuza and K. Hermanowicz, J. Mater. Chem. C, 2015, 3, 9337–9345.
19. A. Ciupa, M. Mączka, A. Gągor, A. Pikul and M. Ptak, Dalton Trans., 2015, 44, 13234–13241.
20. A. Ciupa, M. Mączka, A. Gągor, A. Sieradzki, J. Trzmiel, A. Pikul and M. Ptak, Dalton Trans., 2015, 44, 8846–8854.
21. M. Mączka, A. Pietraszko, L. Macalik, A. Sieradzki, J. Trzmiel and A. Pikul, Dalton Trans., 2014, 43, 17075–17084.
22. A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. Cheetham, H. W. Kroto and S. Picozzi, Angew. Chem., Int. Ed., 2011, 50, 5847–5850.
23. B. Zhou, Y. Imai, A. Kobayashi, Z. M. Wang and H. Kobayashi, Angew. Chem., Int. Ed., 2011, 50, 11441–11445.
24. A. Ciupa, M. Mączka, A. Gągor, A. Pikul, E. Kucharska, J. Hanuza and A. Sieradzki, Polyhedron, 2015, 84, 137–143.
25. M. Mączka, A. Ciupa, A. Gągor, A. Sieradzki, A. Pikul, B. Macalik and M. Drozd, Inorg. Chem., 2014, 53, 5260–5268.
26. P. Jain, N. S. Dalal, B. H. Toby, H. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2008, 130, 10450–11451.
27. P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. J. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625–13627.
28. M. Guo, H. L. Cai and R. G. Xiong, Inorg. Chem. Commun., 2010, 13, 1590–1598.
29. B. PatoDolán, M. Sánchez-Andújar, L. C. Gómez-Aguirre, S. Yáñez-Vilar, J. Lopez-Beceiro, C. Gracia-Fernandez, A. A. Haghighirad, F. Ritter, S. Castro-Garcia and M. A. Señaris-Rodriguez, Phys. Chem. Chem. Phys., 2012, 14, 8498–8501.
30. R. Shang, G. C. Xu, Z. M. Wang and S. Gao, Chem. – Eur. J., 2014, 20, 1146–1158.
31. K. D. Kreuer, Chem. Mater., 1996, 8, 610–641.
32. A. U. Ortiz, A. Boutin, K. J. Gagnon, A. Clearfield and F.-X. Coudert, J. Am. Chem. Soc., 2014, 136, 11540–11545.
33. G. K. H. Shimizu, J. M. Taylor and S. Kim, Science, 2013, 341, 354–355.
34. P. Ramaswamy, N. E. Wong and G. K. H. Shimizu, Chem. Soc. Rev., 2014, 43, 5913–5932.
35. S. Sen, N. N. Nair, T. Yamada, H. Kitagawa and P. K. Bharadwaj, J. Am. Chem. Soc., 2012, 134, 19432–19437.
36. N. C. Jeong, B. Samanta, C. Y. Lee, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 51–54.
37. Y. Ye, L. Zhang, Q. Peng, G.-E. Wang, Y. Shen, Z. Li, L. Wang, X. Ma, Q.-H. Chen, Z. Zhang and S. Xiang, J. Am. Chem. Soc., 2015, 137, 913–918.
38. G. Xu, K. Otsubo, T. Yamada, S. Sakaida and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 7438–7441.
39. V. G. Ponomareva, K. A. Kovalenko, A. P. Chupakhin, D. N. Dybtsev, E. S. Shutova and V. P. Fedin, J. Am. Chem. Soc., 2012, 134, 15640–15643.
40. S. Pili, S. P. Argent, C. G. Morris, P. Rought, V. García-Sakai, I. P. Silverwood, T. L. Easun, M. Li, M. R. Warren, C. A. Murray, C. C. Tang, S. Yang and M. Schröder, J. Am. Chem. Soc., 2016, 138, 6352–6355.
41. J. M. Taylor, S. Dekura, R. Ikeda and H. Kitagawa, Chem. Mater., 2015, 27, 2286–2289.
42. M. Sadakiyo, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2009, 131, 9906–9907.
43. I. Hod, P. Deria, W. Bury, J. E. Mondloch, C.-W. Kung, M. So, M. D. Sampson, A. W. Peters, C. P. Kubiak, O. K. Farha and J. T. Hupp, Nat. Commun., 2015, 6, 8304,  DOI:10.1038/ncomms9304.
44. E. Pardo, C. Train, G. Gontard, K. Boubekeur, O. Fabelo, H. Liu, B. Dkhil, F. Lloret, K. Nakagawa, H. Tokoro, S. Ohkoshi and M. Verdaguer, J. Am. Chem. Soc., 2011, 133, 15328–15331.
45. D. Matoga, M. Oszajca and M. Molenda, Chem. Commun., 2015, 51, 7637–7640.
46. J. A. Hurd, R. Vaidhyanathan, V. Thangadurai, C. I. Ratcliffe, I. L. Moudrakovski and G. K. H. Shimizu, Nat. Chem., 2009, 1, 705–710.
47. Y.-B. Tong, S.-X. Liu, Y. Zou, C. Xue, H.-B. Duan, J.-L. Liu and X.-M. Ren, Inorg. Chem., 2016, 55, 11716–11726.
48. S.-S. Yu, S.-X. Liu and H.-B. Duan, Dalton Trans., 2015, 44, 20822–20825.
49. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
50. T. Steiner, Angew. Chem., 2002, 41, 48–76.
51. A. Molak, M. Paluch, S. Pawlus, J. Klimontko, Z. Ujma and I. Gruszka, J. Phys. D: Appl. Phys., 2005, 38, 1450–1460.
52. M. Wubbenhorst and J. Van Turnhout, J. Non-Cryst. Solids, 2002, 305, 40–49.
53. A. Molak, M. Paluch, S. Pawlus, Z. Ujma, M. Pawełczyk and I. Gruszka, Phase Transitions, 2006, 79, 447–460.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6dt04546d

---