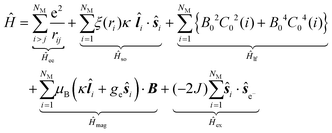Heteroleptic, two-coordinate [M(NHC){N(SiMe₃)₂}] (M = Co, Fe) complexes: synthesis, reactivity and magnetism rationalized by an unexpected metal oxidation state

Abstract

The linear, two-coordinate and isostructural heteroleptic [M(IPr){N(SiMe₃)₂}] (IPr = 1,3-bis(diisopropylphenyl)-imidazol-2-ylidene), formally M^I complexes (M = Co, 3; Fe, 4) were obtained by the reduction of [M(IPr)Cl{N(SiMe₃)₂}] with KC₈, or [Co(IPr){N(SiMe₃)₂}₂] with mes*PH₂, mes* = 2,4,6-tBu₃C₆H₂. The magnetism of 3 and 4 implies Co^II and Fe^II centres coupled to one ligand-delocalized electron, in line with XPS and XANES data; the ac susceptibility of 4 detected a pronounced frequency dependence due to slow magnetization relaxation. Reduction of [Fe(IPr)Cl{N(SiMe₃)₂}] with excess KC₈ in toluene gave the heteronuclear ‘inverse-sandwich’ Fe–K complex 7, featuring η⁶-toluene sandwiched between one Fe⁰ and one K⁺ centre.

---

Introduction

Two-coordinate complexes of 3dⁿ metals (n < 10) remain rare and challenging synthetic targets, calling for fine steric and electronic ligand tuning,¹ although the first example was structurally characterized in 1985.² Their study constitutes a topical area due to their electronic structures (open-shells with diverse spin multiplicities), interesting magnetic properties (e.g. high magnetic moments, ‘single ion magnet’ (SIM) behaviour),³ and stoichiometric and catalytic reactivity.⁴ Insightful modelling of ‘base metal’ catalysts is linked to the mapping of the reactivity of complexes with low coordination numbers.

With the aim to rationally access linear two-coordinate complexes with particularly interesting magnetic properties,⁵ bulky ligands have been used. In general, departure from the exactly linear geometry due to intra- or inter-molecular interactions or other ligand effects has a deleterious effect on the desirably high unquenched orbital magnetism. Thus, alkyl (i.e. C(SiMe₃)₃e.g. in [M{C(SiMe₃)₃}₂]⁻, M = Fe,^6,7 M = Mn⁸) or amido ligands (i.e. –N(SiMe_mPh_(3−m))₂, m = 1, 2; N(SiMe₃)(DiPP), DiPP = 2,6-diisopropylphenyl), have been employed successfully to support linear homoleptic 2-coordinate complexes of Fe,^5a–c,3c,9 Co^5d,9 and Ni^5d,4a and to a lesser extent Cr,^9d,10 Mn^9b,10b and V;¹¹ two-coordinate linear or quasi-linear homoleptic terphenyls, alkoxides and thiolates have also been described.^1,12 Neutral homoleptic complexes with the ubiquitous –N(SiMe₃)₂ form dimers in the solid state or in solution through amido bridging, due to the insufficient steric bulk of the ligand but the anion [Fe{N(SiMe₃)₂}₂]⁻ (ref. 13) is mononuclear and linear. Lately, mononuclear, 2-coordinate homoleptic complexes of Fe,^4g,14 Co,^14b,15 Mn¹⁶ and Cr¹⁷ with the cAAC (cAAC = cyclic AlkylAmino Carbene), and cationic complexes with imidazol-2-ylidene ligands¹⁸ have also been reported.

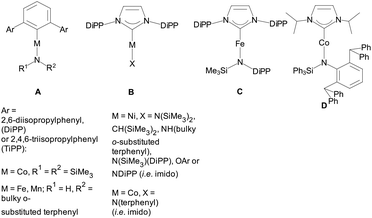
Notwithstanding these synthetic successes, there is only a limited number of linear heteroleptic 2-coordinate complexes A,¹⁹B,^4a,c,e,f,20C ²¹ and D ²² with 3dⁿ (n < 10) metals (Scheme 1). Heteroleptic 3-coordinate NHC amido species have recently been appearing more often.²³

Scheme 1 Heteroleptic two-coordinate complexes of 3d metals.

Herein, we describe the stable, formally 12 and 11 valence electron, virtually linear, 2-coordinate, charge-neutral heteroleptic complexes [M(IPr){N(SiMe₃)₂}] (IPr = N,N′-bis(di-isopropylphenyl)imidazol-2-ylidene, M = Co (3), Fe (4)), respectively, and their remarkable magnetic behaviour; we propose an original, functional model for the interpretation of the latter, supported by probing the oxidation state of the metals with XPS and XANES techniques. We also include some preliminary reactivity studies of 3 and 4.

Results and discussion

Synthesis of 3 and 4

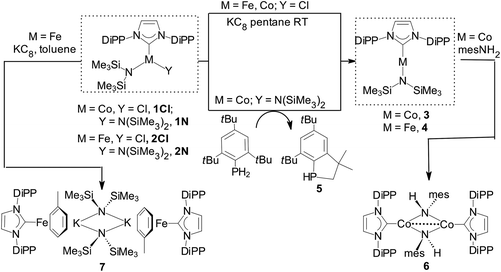
Reduction of [Co(IPr){N(SiMe₃)₂}Cl] (1Cl) with one mol equiv. KC₈ in pentane gave 3 in moderate yields. Preferentially, 3 was obtained from [Co(IPr){N(SiMe₃)₂}₂] (1N) and 1 mol equiv. mes*PH₂, mes* = 2,4,6-tBu₃C₆H₂, in toluene (ca. 70% yield from ca. 1 g of 1N); excess of mes*PH₂ and 3 did not react further under these conditions. The P-containing final product was the phosphaindane 5 (Scheme 2).²⁴ The reduction mechanism with mes*PH₂ (plausible routes are given in the ESI‡) may involve aminyl radicals (˙N(SiMe₃)₂), the involvement of which was also postulated in analogous reactions of [Ni{μ-N(SiMe₃)}(DiPP)]₂ with IPr, which led to a Ni(I) complex.^4a

Scheme 2 Syntheses of the complexes described herein.

Interestingly, reduction of [Co(IMes){N(SiMe₃)₂}Cl] (IMes = 1,3-bis(mesityl)-imidazol-2-ylidene) with KC₈ and of [Co(IMes){N(SiMe₃)₂}₂] with mes*PH₂ led to 3-coordinate [Co(IMes)₂Cl]²⁵ and intractable mixtures, respectively. Reaction of Co–NHC bis(trimethylsilyl)amide complexes with mesPH₂ (mes = 2,4,6-Me₃C₆H₂) yielded Co–NHC phosphinidene species.²⁶

Reduction of [Fe(IPr){N(SiMe₃)₂}Cl] (2Cl) with excess KC₈ in pentane gave 4 in moderate yields (Scheme 2), while reaction of [Fe(IPr){N(SiMe₃)₂}₂] (2N) with mes*PH₂ yielded only [Fe(a-IPr){N(SiMe₃)₂}₂] (a-IPr = abnormally-bound IPr)²⁷ and no 5. Both 3 and 4 are paramagnetic with shifted but relatively sharp lines observable in the ¹H-NMR spectra, which could be assigned by integration.

Determination of the structure of 3 and 4 by X-ray diffraction (Fig. 1)‡ showed that the complexes are isostructural and virtually linear at metal (178.83(7)° and 178.2(2)°, respectively); the M–N(SiMe₃)₂ and the M–C_NHC distances fall into the generally established ranges for these bond types.^13,21,23d Attempts were undertaken to use metrical data in order to support metal oxidation state assignments in 3 and 4, which can formally be described as comprising either M^I centres coordinated to one anionic amido and one neutral IPr ligand, or M^II centres coordinated to one anionic amido and one radical anionic IPr. However, detailed comparison of the M–N(SiMe₃)₂ and M–C_NHC bond distances in 3 and 4 with those in known two-coordinate homoleptic complexes, as well as other two-coordinate analogues (Scheme 1) was inconclusive. Correlation of the metrical data with a metal oxidation state was hampered by the scarcity of relevant identically substituted, two-coordinate complexes in different oxidation states, and the disparate trans-influence of the NHC and amido donor types. In the known homoleptic [Fe{N(SiMe₃)₂}₂]⁻, [Fe(cyIDep)₂]⁺ and [Fe(cAAC)₂]⁺, cyIDep = 1,3-bis(2′,6′-diethylphenyl)-4,5-(CH₂)₄-imidazol-2-ylidene (all assigned as Fe^I complexes), the distances Fe^I–N = 1.9213(6) Å and Fe^I–C_NHC = 1.971(5)–1.996(7) and 1.997(3) Å, respectively, are shorter than the corresponding in 4.^4g,13,18b In addition, the M–N and M–C_NHC distances in 3 and 4 are significantly shorter than those in the three-coordinate [M^II(IPr)(N(SiMe₃)₂)₂] (M = Fe, Co).^23a,d,e However, the Fe–C_NHC distance in 4 is virtually identical to that in the heteroleptic C (Scheme 1), in which Fe^I was implicated. In both 3 and 4 the heterocyclic rings are virtually planar (max. displacement from the mean 5-membered ring plane 0.002 Å); planar is also the environment of the amido N-atoms. In view of the lack of structural or computational data on plausible imidazole-2-ylidene radical anions²⁸ and the previous discussion, it is futile to argue for metrical (ligand) oxidation states²⁹ in 3 and 4. Close in energy, open-shell electronic structures may be attainable under specific conditions (temperature, solvent etc.) by fine ligand tuning, which may also potentially lead to ligand(s) noninnocence. Lastly, in the crystals of 3 and 4 there are no close contacts of the molecules with nearby atoms, implying sufficient electronic stabilization of the two-coordinate structures and the minimal role of sterics and/or dispersion forces serving this purpose. In the crystalline solids the metal centres are at ca. 9.485 and 9.471 Å apart, respectively (self-dilute).

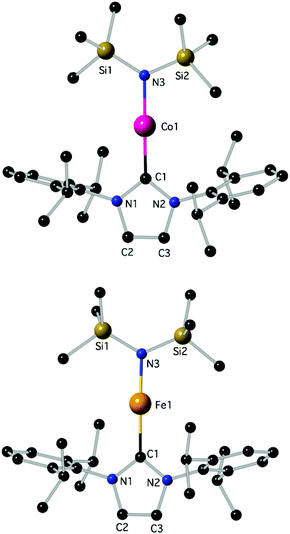Fig. 1 The structures of 3 (top) and 4 (bottom); H-atoms are omitted. Important bond lengths (Å) and angles (°): for 3, C1–Co1: 1.9423(18), C1–N2: 1.368(2), C1–N1: 1.368(2), C2–C3: 1.343(3), C2–N1: 1.381(2), N3–Co1–C1: 178.83(7). For 4, C1–N2: 1.366(7), C1–N1: 1.368(7), C1–Fe1: 2.015(6), C2–C3: 1.336(10), C2–N1: 1.388(8), N3–Fe1: 1.882(5), N3–Fe1: 1.882(5), N3–Fe1–C1: 178.2(2); additional details are given in the ESI.‡

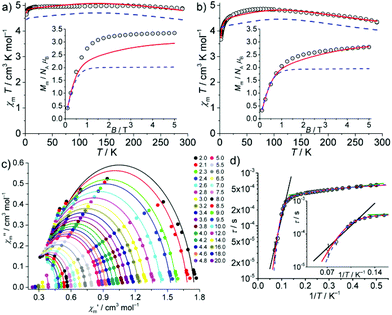
Magnetic studies of 3 and 4

The interpretation of the SQUID magnetometry data of solid samples of 3 and 4 may imply remarkable electronic structures. The static field (dc) susceptibility data (as χ_mT vs. T at 0.1 T and M_mvs. B at 2.0 K) are presented in Fig. 2. For 3, the room-temperature value of χ_mT = 4.88 cm³ K mol⁻¹ (corresponding to μ_eff = 6.25μ_B) is very high. Upon cooling, χ_mT increases to 4.99 cm³ K mol⁻¹ at 170 K, then decreases to 4.92 cm³ K mol⁻¹ at 12 K, and finally drops to 4.65 cm³ K mol⁻¹ at 2.0 K. At this temperature, M_m shows saturation at ca. 3.4N_Aμ_B above B ≈ 2 T. The room temperature value of μ_eff = 6.25μ_B is even higher than the free-ion value (for 3d⁸: L = 3, S = 1, J = 4, g_J = 5/4, μ_eff ≈ g_J[J(J + 1)]^1/2μ_B = 5.59μ_B), which constitutes the upper limit for high spin 3d⁸ mononuclear complexes, thus ruling out the scenario of 3 as a Co^I high-spin complex. Similarly, for 4, χ_mT is 4.37 cm³ K mol⁻¹ at 290 K (corresponding to μ_eff = 5.91μ_B). It increases to 4.85 cm³ K mol⁻¹ at 75 K, and then decreases to 3.67 cm³ K mol⁻¹ at 2.0 K, where M_m is linear in B up to 1 T and reaches 2.8N_Aμ_B at 5 T. The room temperature value of μ_eff = 5.91μ_B is also unusually high for a high spin 3d⁷ Fe^I configuration, but smaller than the free-ion value (L = 3, S = 3/2, J = 9/2, g_J = 4/3, μ_eff ≈ 6.63μ_B). Interestingly, μ_eff values reported in the literature for the majority of linear Co^I and Fe^I complexes^3a,c are significantly smaller, while very few complexes of linear Fe^II centres exhibiting similarly high values have been described. Measurements under various magnetic fields at 290 K did not reveal any ferromagnetic impurities (see Fig. S7‡), corroborating the high intrinsic μ_eff values.

Fig. 2 Temperature dependence of χ_mT of 3 (a) and 4 (b) at 0.1 T; inset: molar magnetization M_mvs. B at 2.0 K. Experimental data: open circles; calculated “M^II + e⁻” model data: solid red lines; related M^II single-ion contribution: dashed blue lines. (c) Cole–Cole plot of the ac susceptibility data of 4 at zero static bias field (T = 2.0–20.0 K); with least-squares fits (solid lines). (d) Relaxation time τ vs. T⁻¹, black (8.5–14 K) and green lines (3.0–5.5 K): fit to Arrhenius expression; blue dashed line: fit considering quantum tunnelling, Raman and Orbach relaxation; red line: fit considering quantum tunneling, Orbach and another Arrhenius-type relaxation.

To account for the observed values, we reasoned that 3 may be characterized by either a 3d⁷4s¹ configuration in a quintet state (S = 2), or by a configuration resulting from the transfer of one electron from the Co^I to the ligand periphery, i.e. localized at one of the ligands or delocalized over the π system of the complex. Analogous considerations for 4 may lead to a 3d⁶4s¹ configuration in a sextet state (S = 5/2), or one electron transferred from Fe^I to one of the ligands, more likely the NHC. Consequently, three different electronic configuration scenarios have been investigated: (i) a single M^I centre (3d^N, M = Co^I: N = 8; M = Fe^I: N = 7); (ii) a single M^II centre (3d^N−1) representing the upper limit for a high spin 3d⁶ electron configuration, with free ion values: L = 2, S = 2, J = 4, g_J = 3/2, μ_eff ≈ 6.71μ_B, to explore the unlikely possibility of decomposition; (iii) a single M^II (3d^N−1) centre interacting with one electron (S = 1/2) via Heisenberg–Dirac–van Vleck exchange coupling that is (de)localized over the ligand/complex (referred hereafter to as the ‘M^II + e⁻’ scenario). In the latter case, maximum μ_eff ≈ 6.86μ_B, and μ_eff ≈ 6.93μ_B corresponding to “3d⁷ + e⁻”and “3d⁶ + e⁻”, respectively, could be envisaged.

Considering the C_∞v ligand field symmetry to be in line with the linear heteroleptic nature of 3 and 4, we employed the ‘full’ model Hamiltonian implemented in CONDON 2.0.³⁰ The corresponding Hamiltonian, neglecting contributions resulting in constant shifts of the total energy, is defined as:

where all operators, but the Heisenberg operator Ĥ_ex, describe the various single-ion contributions (Ĥ_ee: interelectronic repulsion, Ĥ_so: spin–orbit coupling, Ĥ_lf: ligand field effects theory framework, Ĥ_mag: Zeeman effect of an external magnetic field). Ĥ_ee is parameterized by the Racah parameters B and C, Ĥ_so by the one-electron spin–orbit coupling parameter ζ_3d and the orbital reduction factor κ. 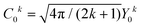The in Ĥ_lf denote the relevant spherical tensors for a given ligand field symmetry and are directly related to the spherical harmonics Y₀^k. B₀^k are the (real) ligand field parameters in the Wybourne notation. The sum index i runs over all N_M valence electrons of the corresponding metal center.

The least-squares fits for the scenarios (i) and (ii) did not yield even remotely acceptable solutions (including considerations of free ions, and physically unlikely parameters, see Fig. S8‡ for a selection of resulting fits). In contrast, the “M^II + e⁻” scenario indeed reproduced the temperature-dependent susceptibility data (SQ = 1.0%; Fig. 2 and Table S6‡). We note that for 3, inclusion of the field-dependent magnetization data at 2.0 K (Fig. 2a, inset) reduces the overall fit quality (SQ = 7.7%). Fitting solely the M_mvs. B data would point (ii) as the preferred scenario, but then the χ_mT vs. T curve would not be reproduced at all (Fig. S8c‡). By employing the “M^II + e⁻” scenario for 4, the least-squares fit yields a reasonable SQ = 2.8% (1.8% when excluding M_mvs. B data). The single ion contribution of the M^II centre is highlighted in Fig. 2 for both complexes.

The scenario “M^II + e⁻” yields small, antiferromagnetic exchange energies J = −0.1 cm⁻¹ (3) and −0.5 cm⁻¹ (4). These results indicate that the additional electron should be assigned to the ligands. Such parameters imply formal triplet (3) or quartet (4) ground states with respect to the whole molecule. We note that DFT calculations of 3 and 4 also support triplet and quartet electronic ground states, respectively; however, at the DFT theory level, only minimal spin delocalization on the ligand is predicted (see the ESI‡ for details).

Since the Heisenberg–Dirac–Van Vleck exchange formalism refers to localized electrons, an unpaired electron localized on a ligand atom is expected to induce a strong exchange interaction. In contrast, within the limitations of the model, the small magnitudes of J hint at (at least partially) delocalized electrons for which various effects, e.g. electron transfer, might compensate each other, yielding a small effective net value. Thus, the fits also reflect the inherent limitations of ligand field theory, where electrons localized at the metal interact with an electrostatic ligand field potential, neglecting further dynamic aspects generated by e.g. the conjugation of the π system.

The in-phase χ′_m and out-of-phase χ′′_m” components of the magnetic ac susceptibility data as a function of temperature (Fig. S9 (3) and S10‡ (4)) show out-of-phase signals for 4, up to ca. 15 K (<1000 Hz) but not for 3. The χ′′_mvs. χ′_m data (Fig. 2c) were analysed in terms of the generalized Debye expression³¹ (solid lines). The dependence of the magnetic relaxation time τ on T⁻¹ is shown in Fig. 2d as the Arrhenius plot. The distribution of relaxation times α (0.04–0.17, mean value 0.12) suggests the existence of multiple relaxation pathways. Notably, the semi-logarithmic Arrhenius plot exhibits two quasi-linear segments between 3.0–5.5 K and 8.5–14 K. Fitting these to the Arrhenius expression τ = τ₀·exp[U_eff/(k_BT)] (attempt time τ₀, effective energy barrier U_eff, Boltzmann constant k_B) yields τ₀ = (3.23 ± 0.03) × 10⁻⁴ s, U_eff = (0.89 ± 0.03) cm⁻¹ for 3.0–5.5 K, and τ₀ = (1.64 ± 0.80) × 10⁻⁶ s, U_eff = (31.0 ± 3.1) cm⁻¹ for 8.5–14 K. Whereas the latter parameters are at the upper limit for typical Orbach relaxation in single ion magnets (SIM), the first is not, thus potentially describing a different process. Note that the effective energy barrier is of the same order as the exchange coupling parameter J. The first process might be thus linked to the potential exchange interaction of the Fe centre and the delocalized electron. We therefore considered two different models for fitting the entire temperature range (2.0–14 K): (a) quantum tunnelling, Orbach and Raman relaxation processes (τ⁻¹ = B + τ₀⁻¹·exp[−U_eff/(k_BT)] + C·Tⁿ), and (b) quantum tunnelling, Orbach relaxation process and another Arrhenius-type relaxation process (τ⁻¹ = B + τ_0,1⁻¹·exp[−U_eff,1/(k_BT)] + τ_0,2⁻¹·exp[−U_eff,2/(k_BT)]). Least-squares fits to (a) (Fig. 2 and S11,‡ blue dashed line) yield B = (1352 ± 152) s⁻¹, τ₀ = (4.56 ± 0.17) × 10⁻⁴ s, U_eff = (2.55 ± 0.52) cm⁻¹, C = (2.88 ± 3.53) × 10⁻⁵ s⁻¹ K^−{n}, and n = 8.02 ± 0.53. Model (b) (Fig. 2 and S11,‡ red line) results in B = (1547 ± 87) s⁻¹, τ_0,1 = (1.01 ± 0.45) × 10⁻⁷ s, U_eff,1 = (56.6 ± 3.1) cm⁻¹, τ_0,2 = (4.03 ± 0.25) × 10⁻⁴ s, and U_eff,2 = (3.59 ± 0.50) cm⁻¹. The fit parameters of (a) describe a system characterized by quantum tunnelling (B) and Raman (C) relaxation processes close to Kramers systems (n = 9), and a process which is not a typical SIM-type Orbach relaxation. Note that there are several other relaxation processes³² compared to the suggested exchange interaction, which are characterized by an Arrhenius law, e.g. the sum process. Model (b) essentially replaces Raman relaxation by Orbach relaxation, while the other fit parameters are almost unchanged. Due to a slightly better goodness-of-fit, the occurrence of an Orbach relaxation process typical of SIMs and fit parameters in the range for similar compounds,^3a–c the SIM characteristics of 4 are better characterized by model (b) than (a), although the nature of the second Arrhenius-type process could not be fully resolved. We note that the magnetization relaxation dynamics of linear Co^I compounds seem to be very sensitive to the ligand field, as was also observed by Meng et al.,^18a which may also be related to the electron delocalization implied in the “M^II + e⁻” scenario.

XPS, EXAFS and XANES studies of 3 and 4

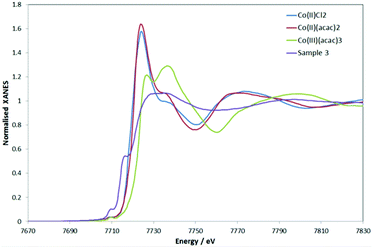
The “M^II + e⁻” scenario was corroborated by the XPS spectra of 3 and 4 (see Fig. S12 and S13 and Table S7‡ for binding energies). The spectrum of 3 showed well-resolved 2p_3/2 and 2p_1/2 peaks (780.7 and 796.4 eV, respectively) in support of Co^II in a soft environment.³³ Strong satellite peaks at 785.7 and 802.1 eV arose from the shake-up transitions of the core photoelectron to metal d and ligand valence levels.^34,35 Their intensity increases with the spin of the metal and the covalency of the metal–ligand bond.^34,35 Overall, the data are consistent with 3 featuring a high-spin Co^II.

The structural analysis of 3 with Co K-edge EXAFS spectroscopy agreed with the crystal structure data (see ESI‡). Remarkably, and in agreement with XPS, the Co K-edge XANES revealed an overall charge of +2 on the Co, with the pre-edge features nicely supporting the linear structure. The Co K-edge XANES of 3, in comparison to some representative Co^II and Co^III compounds, is given in Fig. 3 (the first derivatives of the XANES are given in Fig. S14‡). Although the XANES is known to be dependent on the metal oxidation state (charge) as well as the nature of the ligands and the coordination geometry, Fig. 3 suggests that 3 represents an overall Co²⁺ complex. The first pre-edge feature as seen for 3 can be assigned to pd hybridization, making the dipole forbidden s-to-d transition slightly visible, and the second pre-edge feature originates from hybridization of the Co-p and Co-d (with C-p mostly, and little mixing from N-p, as indicated by simulations (see Fig. S15 in ESI‡)). The high intensity of the second pre-edge is due to the empty character of the orbital, which is indicative of the linear Co. The simulations also suggest the channel of charge redistribution being the aromatic part (i.e. NHC) of the molecule.

Fig. 3 Normalized Co K-edge XANES data on 3 and Co^II and Co^III reference samples.

The XPS spectrum of 4 is less well resolved but globally similar to that of 3. The 2p_3/2 peak is unsymmetrical with a tail on the high-energy side and a broad feature, which is due to the presence of a satellite peak partly overlapping with the 2p_3/2; the 2p_1/2 peak behaves similarly. A deconvolution using a Gaussian/Lorentzian admixture allows distinguishing both components (Table S7‡). The energies of the 2p_3/2 and 2p_1/2 peaks and their satellites are consistent with a Fe^II centre.^29,36 The small intensity of the satellite peaks does not support a high-spin Fe, however, due to the small energy difference between the 2p peaks and their satellites, the intensities of the latter are strongly dependent on the deconvolution mode and base line correction.

Preliminary reactivity studies related to 3 and 4

Reactivity experiments showed that the IPr ligand in 3 and 4 can be displaced by SIPr or IAd, leading to equilibrium mixtures of 3 or 4 and the heteroleptic, 2-coordinate SIPr or IAd analogues, respectively (inferred by ¹H NMR monitoring). Furthermore, the reaction of 4 with Ph–Cl or Me₃SiCH₂–Cl led to mixtures, in which 2Cl is the major paramagnetic component (by comparison of the ¹H NMR spectra with authentic samples). Finally, 3 and 4 react with weak organic protic reagents: for example, the reaction of 3 with mesNH₂, mes = mesityl, 2,4,6-trimethylphenyl, gave after aminolysis of the Co–N(SiMe₃)₂ bond the paramagnetic 6 as red crystals (Scheme 2 and Fig. 4),‡ which was characterized crystallographically. In the centrosymmetric binuclear 6, each Co is coordinated by one IPr and the symmetrically bridging primary mesitylamido ligands (mesNH). The Co₂N₂ core is planar with intermetallic separation of 2.5765(4) Å, supporting the interaction between the Co centres (Σ_{cov. rad} = 2.52 Å), while the bridging mesitylamido ligand adopts a distorted tetrahedral geometry at the N atom, presumably due to steric reasons and the presence of the intermetallic interaction.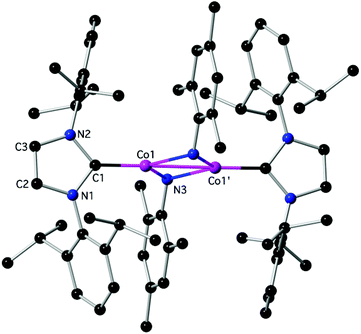

Fig. 4 The structure of 6; H-atoms are omitted. Important bond lengths (Å) and angles (°): C1–N1: 1.3921(17), C1–N2: 1.3965(18), C1–Co1: 1.8897(14), N3–Co1: 2.0387(12), N3–Co1′: 2.0421(12), Co1–Co1: 2.5765(4), N3–Co1–N3′: 101.70(4), C1–Co1–Co1′: 179.03(4), additional details are given in the ESI.‡

Reduction of 2Cl with excess KC₈ in toluene afforded low yields of the yellow-green, paramagnetic 7 which could only be characterized crystallographically (Fig. 5).‡ It is a centrosymmetric, ‘inverse-sandwich’ tetranuclear heterometallic dimer, each monomer containing a η⁶-toluene sandwiched between one Fe⁰ (16e⁻) and one K⁺ centre; the two monomers are connected by two bridging –N(SiMe₃)₂ ligands ligated to the K cations.

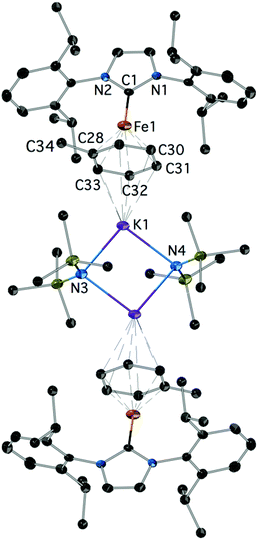Fig. 5 The structure of 7; H-atoms are omitted. Important bond lengths (Å) and angles (°): C1–N1: 1.368(4), C1–N2: 1.370(4), C1–Fe1: 1.988(3), C28–Fe1: 2.061(4), C29–Fe1: 2.070(4), Fe1–K1: 4.520, additional details are given in the ESI.‡

Complex 7 is a rare example of the Fe–NHC η⁶-arene complex;^37,38 [Fe⁰(IPr)(diene)] species were also recently described.³⁹ Interestingly, it could not be obtained by the reduction of 4 in toluene. It is also worth pointing out that mechanistically the formation of 7 is remarkable. The sole source of K is the reducing KC₈ and of –N(SiMe₃)₂ the 2Cl featuring a direct Fe–N(SiMe₃)₂ bond. The formation of 7 may involve a consecutive insertion of the K(toluene) fragment into the Fe–N(SiMe₃)₂ of a transient [IPrFe⁰(N(SiMe₃)₂)]⁻ with or without prior coordination to the metal; [IPrFe⁰(N(SiMe₃)₂)]⁻ is a plausible initial product from the 2e⁻ reduction of 2Cl. Fe–K assemblies have been recently studied with respect to Fe catalysed N₂ activation.⁴⁰

Conclusion

In conclusion, we have developed methods for the synthesis of the heteroleptic two coordinate 3 and 4 using reductive strategies under well defined conditions. 3 and 4 constitute timely additions to the growing family of two-coordinate 3d-organometallics. The unexpected and remarkable finding related to 3 and 4, based on several lines of experimental evidence, is their high magnetic moments, which led to the proposition of an electronic structure model featuring M^II centres and a delocalized electron on the ligand (e.g. IPr) based orbitals. This assignment renders the IPr as a radical anion and therefore electronically non-innocent by definition. Radical anionic NHCs (excluding good π-accepting cAAC) have been rarely established experimentally or invoked in the coordination chemistry of transition metals; for example, radical anions have been detected by ESR after the electrochemical reduction of the ‘Enders carbene’;⁴¹ more recently Apeloig demonstrated the duality of IPr adducts with paramagnetic organometallic species: reaction of IPr with the photochemically generated ‘singlet organometallic radical’ ˙M(CO)₅ (M = Mn, Re) gave adducts, which were formulated as [(IPr˙⁻)(Re⁺(CO)₅)] and [(IPr)(Mn˙(CO)₅)] (i.e. a IPr stabilised organometallic radical) on the basis of EPR spectroscopy and calculations.²⁸ Furthermore, cAAC NHC ligands being excellent π-acceptors have given rise to remarkable, stable 3d complexes in lower oxidation states, in which their electronic non-innocence and open-shell structures have been established.⁴² It is plausible that the higher energy of 3d metal orbitals in combination with the low coordination numbers and the weaker ligand fields may promote non-innocent NHC ligand behaviour in the poor π-accepting IPr and related Arduengo-type NHCs, by closer energy proximity of the metal and ligand orbitals. The coordinated NHC non-innocence under these conditions may also be relevant in catalysis with 3d metal NHC complexes, where ‘underligated’ structures are postulated as common intermediates. The topic of NHC (including Arduengo-type IPr and cAAC) stabilized main group radicals and radical ions has been recently reviewed.⁴³

Although the experimental evidence for the nature of IPr in 3 and 4 is convincing, and DFT calculations support triplet and quartet electronic ground states, respectively, minimal spin delocalization on the ligand is predicted by this methodology (see the ESI‡ for details); this may be a consequence of the well-known limitations of this method with multi-reference structures. Therefore high-level ab initio calculations are desirable to provide a better insight into the electronic structures of 3 and 4.

Experimental

General details on the synthetic methodologies for the new complexes as well as improved synthetic methods for 1Cl and 2Cl can be found in the ESI.‡

[Co(IPr){N(SiMe₃)₂}] (3), method A

A solution of [Co(IPr){N(SiMe₃)₂}₂] (1N) (1.00 g, 1.30 mmol) and mes*PH₂ (0.40 g, 1.43 mmol, 1.1 equiv.) in toluene (20 cm³) was stirred at 45 °C for 3 days, when it changed colour from green to orange-brown. If the starting material was not completely consumed after this period (i.e. <90% conversion by ¹H NMR spectroscopy), more mes*PH₂ (typically 0.10 g, 0.13 mmol, 10%) was added, and the reaction was continued for an additional period of 24 h. After completion, the toluene was removed under reduced pressure and the residue was extracted into ca. 20 cm³ pentane. The pentane solution was concentrated to ca. 6–7 cm³ and cooled to −40 °C for 24 h to yield yellow-orange plates of 3 that were isolated and dried under vacuum. Yield: 0.55 g, 0.90 mmol, ca. 69%. Further concentration of the supernatant and cooling at −40 °C for 2 days gave as a second crop a minor quantity of 3 contaminated with a few green crystals of 1N; this crop was discarded. For C₃₃H₅₅CoN₃Si₂, calculated (%): C 65.09, H 9.10, N 6.90; found (%): C 64.98, H 9.02, N 6.90. ¹H-NMR (C₆D₆): δ, 178.10 (2H, DiPP aromatic), 79.10 (4H, DiPP aromatic), 12.56 (12H, CH(CH₃)₂), 10.21 (18H, N(SiMe₃)₂), −39.18 (2H, CH=CH, imid), −48.8 (4H, CH(CH₃)₂), −152.19 (12H, CH(CH₃)₂) ppm. The ¹H-NMR spectrum in d⁸-THF remains unchanged. NMR spectroscopic analysis of the mother liquor after the second crop revealed the presence of 5 (³¹P δ −75.0 (d)) and a minor unidentified species, δ −60.0 (d of d, J_P–H = 73.0 Hz).

[Co(IPr){N(SiMe₃)₂}] (3), method B

A suspension of [Co(IPr){N(SiMe₃)₂Cl}] (1Cl) (0.25 g, 0.39 mmol) and KC₈ (0.063 g, 0.45 mmol, 1.2 equiv.) in pentane (ca. 30 cm³) was stirred vigorously at room temperature for 24 h giving a yellow-orange reaction mixture and black graphite. The progress of the reaction was monitored by ¹H NMR spectroscopy and, if necessary, more KC₈ was added until conversion was >95%. Finally, the graphite and other solids were filtered off using a syringe filter and glass fibre filter paper. The solids were washed with small amounts of pentane until the washings came out colourless (2 × 5 cm³) and the combined extracts were concentrated to dryness giving a yellow-orange microcrystalline powder, which exhibited an identical ¹H-NMR spectrum to the complex prepared by method A. Yield: 0.10 g, 0.16 mmol, ca. 41%.

[Fe(IPr){N(SiMe₃)₂}] (4)

A suspension of [Fe(IPr){N(SiMe₃)₂}Cl] (2Cl) (0.20 g, 0.31 mmol) and KC₈ (0.065 g, 0.47 mmol, 1.5 equiv.) in pentane (ca. 30 cm³) was stirred vigorously at room temperature for 24 h giving an intense orange-brown reaction mixture and black graphite. If the starting material was not completely consumed after this period (<90% by ¹H NMR) more KC₈ was added (ca. 25 mg) and the reaction was continued for an additional 12 h. Finally, the graphite and other solids were filtered off using a syringe filter and glass fibre filter paper. The solids were washed with small amounts of pentane until washings came out colourless (2 × 5 cm³) and the combined extracts were concentrated and cooled to −40 °C to give the product as intense orange plates. Yield: 0.12 g, 0.19 mmol, ca. 66%. The reaction can be run at 0.50 g scale of 2Cl without any appreciable drop in the yield. X-ray quality crystals were obtained by cooling dilute solutions of 4 in pentane at −40 °C for 24 h. Reproducible elemental analysis data from spectroscopically pure samples could not be obtained, presumably due to the high sensitivity of the complex. ¹H-NMR (C₆D₆): δ, 83.36 (2H, DiPP aromatic), 55.09 (4H, DiPP aromatic), 7.05 (12H, CH(CH₃)₂, in part masked by solvent), −11.59 (18H, N(SiMe₃)₂), −15.24 (2H, CH=CH, imid), −19.22 (4H, CH(CH₃)₂), −78.80 (12H, CH(CH₃)₂) ppm. The ¹H-NMR spectrum in d₈-THF remains unchanged.

Complex 6

To a solution of 3 (0.070 g, 0.12 mmol) in toluene (2 cm³) at room temperature was added 2,4,6-trimethylaniline (mesNH₂, 0.40 cm³ of 0.35 M toluene solution, 0.14 mmol). The reaction mixture was stirred at 80 °C for 8 h and then after cooling to room temperature was evaporated to dryness. The residue was washed with cold pentane and re-dissolved in toluene (1 cm³), the red solution was layered with pentane and allowed to diffuse at −40 °C giving red crystals after one week. Yield: 0.045 g, 0.04 mmol, ca. 64% (based on Co). ¹H-NMR (C₆D₆): δ, 113.4 (6H), 85.1 (br, 12H), 56.7 (4H), 45.7 (2H), 23.0 (4H), −3.9 (6H), −4.1 (three broad overlapping peaks 17H), −34.5 (two single peaks 1H each), −56.7 (1H) ppm; in the diamagnetic region peaks assignable to free IPr (δ, 1.24, 2.90, 6.58 ppm) could also be identified. Magnetic susceptibility, C₆D₆ rt: 3.8μ_B (1.9μ_B per Co).

Complex 7

In a Young's ampoule, a suspension of 2Cl (0.20 g, 0.31 mmol) and KC₈ (0.21 g, 1.55 mmol, 5 equiv.) in toluene (ca. 10 cm³) was heated at 80 °C for 8 h. After cooling, the suspension was evaporated to dryness and the residue was dissolved in pentane (ca. 10 cm³), giving a yellow-green solution, which was concentrated under reduced pressure to ca. 5 cm³ and then evaporated slowly in a stream of nitrogen in a glove box to give yellow green crystals of 7. ¹H-NMR (C₆D₆): the following paramagnetic features of the spectrum are broad: δ, 23.90 (2H), 21.20 (2H), 2.9 (broad, toluene), −1.14 (24H two broad peaks), −4.10 (4H), −7.11 (6H, two broad overlapping peaks), −40.92 (2H) ppm; in addition there are signals in the diamagnetic region that are assignable to IPr (δ, 1.24, 2.90, 6.58) ppm. Satisfactory analytical data could not be obtained for this complex.

Acknowledgements

We thank the USIAS, CNRS, Région Alsace and Eurométropole de Strasbourg for the award of fellowships and a Gutenberg Excellence Chair (to AAD), the CNRS and the MESR (Paris) for funding and Dr L. Karmazin and C. Bailly (Service de Radiocristallographie, Unistra) for the crystal structures, the Diamond Light Source for XAS beam time (BAG project SP8071) and Dr R. J. Thomas and V. Subbiah for performing the XAS experiment. Calculations were performed using HPC resources from GENCI-IDRIS/CINES (Grant 2015-x086894).

Notes and references

1. P. P. Power, Chem. Rev., 2012, 112, 3482–3507.
2. N. H. Buttrus, C. Eaborn, P. B. Hitchcock, J. D. Smith and A. C. Sullivan, J. Chem. Soc., Chem. Commun., 1985, 1380–1381,  10.1039/C39850001380.
3. (a) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147; (b) R. A. Layfield, Organometallics, 2014, 33, 1084–1099; (c) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138; (d) J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491.
4. (a) M. I. Lipschutz, X. Yang, R. Chatterjee and T. D. Tilley, J. Am. Chem. Soc., 2013, 135, 15298–15301; (b) M. I. Lipschutz and T. D. Tilley, Angew. Chem., Int. Ed., 2014, 53, 7290–7294; (c) C. A. Laskowski and G. L. Hillhouse, J. Am. Chem. Soc., 2008, 130, 13846–13847; (d) C. A. Laskowski and G. L. Hillhouse, Chem. Sci., 2011, 2, 321–325; (e) C. A. Laskowski, D. J. Bungum, S. M. Baldwin, S. A. Del Ciello, V. M. Iluc and G. L. Hillhouse, J. Am. Chem. Soc., 2013, 135, 18272–18275; (f) C. A. Laskowski, G. R. Morello, C. T. Saouma, T. R. Cundari and G. L. Hillhouse, Chem. Sci., 2013, 4, 170–174; (g) G. Ung and J. C. Peters, Angew. Chem., Int. Ed., 2015, 54, 532–535; (h) P. L. Holland, Acc. Chem. Res., 2015, 48, 1696–1702.
5. (a) W. M. Reiff, A. M. LaPointe and E. H. Witten, J. Am. Chem. Soc., 2004, 126, 10206–10207; (b) W. M. Reiff, C. E. Schulz, M.-H. Whangbo, J. I. Seo, Y. S. Lee, G. R. Potratz, C. W. Spicer and G. S. Girolami, J. Am. Chem. Soc., 2009, 131, 404–405; (c) W. Alexander Merrill, T. A. Stich, M. Brynda, G. J. Yeagle, J. C. Fettinger, R. D. Hont, W. M. Reiff, C. E. Schulz, R. D. Britt and P. P. Power, J. Am. Chem. Soc., 2009, 131, 12693–12702; (d) A. M. Bryan, W. A. Merrill, W. M. Reiff, J. C. Fettinger and P. P. Power, Inorg. Chem., 2012, 51, 3366–3373.
6. (a) T. Viefhaus, W. Schwarz, K. Hübler, K. Locke and J. Weidlein, Z. Anorg. Allg. Chem., 2001, 627, 715–725; (b) A. M. LaPointe, Inorg. Chim. Acta, 2003, 345, 359–362.
7. J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581.
8. C. Y. Lin, J. C. Fettinger, N. F. Chilton, A. Formanuik, F. Grandjean, G. J. Long and P. P. Power, Chem. Commun., 2015, 51, 13275–13278.
9. (a) R. A. Bartlett and P. P. Power, J. Am. Chem. Soc., 1987, 109, 7563–7564; (b) H. Chen, R. A. Bartlett, H. V. R. Dias, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 1989, 111, 4338–4345; (c) C.-Y. Lin, J.-D. Guo, J. C. Fettinger, S. Nagase, F. Grandjean, G. J. Long, N. F. Chilton and P. P. Power, Inorg. Chem., 2013, 52, 13584–13593; (d) C.-Y. Lin, J. C. Fettinger, F. Grandjean, G. J. Long and P. P. Power, Inorg. Chem., 2014, 53, 9400–9406.
10. (a) I. C. Cai, M. I. Lipschutz and T. D. Tilley, Chem. Commun., 2014, 50, 13062–13065; (b) S. N. König, C. Schädle, C. Maichle-Mössmer and R. Anwander, Inorg. Chem., 2014, 53, 4585–4597.
11. J. N. Boynton, J.-D. Guo, J. C. Fettinger, C. E. Melton, S. Nagase and P. P. Power, J. Am. Chem. Soc., 2013, 135, 10720–10728.
12. (a) D. L. Kays and A. R. Cowley, Chem. Commun., 2007, 1053–1055,  10.1039/B616584B; (b) C. Ni and P. P. Power, Chem. Commun., 2009, 5543–5545,  10.1039/B912312A; (c) T. Hatanaka, R. Miyake, Y. Ishida and H. Kawaguchi, J. Organomet. Chem., 2011, 696, 4046–4050; (d) A. M. Bryan, G. J. Long, F. Grandjean and P. P. Power, Inorg. Chem., 2014, 53, 2692–2698.
13. C. G. Werncke, P. C. Bunting, C. Duhayon, J. R. Long, S. Bontemps and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2015, 54, 245–248.
14. (a) P. P. Samuel, K. C. Mondal, N. Amin Sk, H. W. Roesky, E. Carl, R. Neufeld, D. Stalke, S. Demeshko, F. Meyer, L. Ungur, L. F. Chibotaru, J. Christian, V. Ramachandran, J. van Tol and N. S. Dalal, J. Am. Chem. Soc., 2014, 136, 11964–11971; (b) G. Ung, J. Rittle, M. Soleilhavoup, G. Bertrand and J. C. Peters, Angew. Chem., Int. Ed., 2014, 53, 8427–8431.
15. B. Dittrich, C. M. Wandtke, A. Meents, K. Pröpper, K. C. Mondal, P. P. Samuel, N. Amin Sk, A. P. Singh, H. W. Roesky and N. Sidhu, ChemPhysChem, 2015, 16, 412–419.
16. P. P. Samuel, K. C. Mondal, H. W. Roesky, M. Hermann, G. Frenking, S. Demeshko, F. Meyer, A. C. Stückl, J. H. Christian, N. S. Dalal, L. Ungur, L. F. Chibotaru, K. Pröpper, A. Meents and B. Dittrich, Angew. Chem., Int. Ed., 2013, 52, 11817–11821.
17. P. P. Samuel, R. Neufeld, K. Chandra Mondal, H. W. Roesky, R. Herbst-Irmer, D. Stalke, S. Demeshko, F. Meyer, V. C. Rojisha, S. De, P. Parameswaran, A. C. Stuckl, W. Kaim, J. H. Christian, J. K. Bindra and N. S. Dalal, Chem. Sci., 2015, 6, 3148–3153.
18. (a) Y.-S. Meng, Z. Mo, B.-W. Wang, Y.-Q. Zhang, L. Deng and S. Gao, Chem. Sci., 2015, 6, 7156–7162; (b) Z. Ouyang, J. Du, L. Wang, J. L. Kneebone, M. L. Neidig and L. Deng, Inorg. Chem., 2015, 54, 8808–8816.
19. C. Ni, T. A. Stich, G. J. Long and P. P. Power, Chem. Commun., 2010, 46, 4466–4468.
20. J. Du, L. Wang, M. Xie and L. Deng, Angew. Chem., Int. Ed., 2015, 54, 12640–12644.
21. M. I. Lipschutz, T. Chantarojsiri, Y. Dong and T. D. Tilley, J. Am. Chem. Soc., 2015, 137, 6366–6372.
22. J. Hicks and C. Jones, Organometallics, 2015, 34, 2118–2121.
23. (a) R. A. Layfield, J. J. W. McDouall, M. Scheer, C. Schwarzmaier and F. Tuna, Chem. Commun., 2011, 47, 10623–10625; (b) A. A. Danopoulos, P. Braunstein, N. Stylianides and M. Wesolek, Organometallics, 2011, 30, 6514–6517; (c) B. M. Day, K. Pal, T. Pugh, J. Tuck and R. A. Layfield, Inorg. Chem., 2014, 53, 10578–10584; (d) A. Massard, P. Braunstein, A. A. Danopoulos, S. Choua and P. Rabu, Organometallics, 2015, 34, 2429–2438; (e) A. A. Danopoulos and P. Braunstein, Oil Gas Sci. Technol., 2016, 71, 24.
24. (a) A. H. Cowley, F. Gabbai, R. Schluter and D. Atwood, J. Am. Chem. Soc., 1992, 114, 3142–3144; (b) V. P. W. Böhm and M. Brookhart, Angew. Chem., Int. Ed., 2001, 40, 4694–4696.
25. Z. Mo, D. Chen, X. Leng and L. Deng, Organometallics, 2012, 31, 7040–7043.
26. K. Pal, O. B. Hemming, B. M. Day, T. Pugh, D. J. Evans and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 1690–1693.
27. B. M. Day, T. Pugh, D. Hendriks, C. F. Guerra, D. J. Evans, F. M. Bickelhaupt and R. A. Layfield, J. Am. Chem. Soc., 2013, 135, 13338–13341.
28. B. Tumanskii, D. Sheberla, G. Molev and Y. Apeloig, Angew. Chem., Int. Ed., 2007, 46, 7408–7411.
29. B. Butschke, K. L. Fillman, T. Bendikov, L. J. W. Shimon, Y. Diskin-Posner, G. Leitus, S. I. Gorelsky, M. L. Neidig and D. Milstein, Inorg. Chem., 2015, 54, 4909–4926.
30. (a) M. Speldrich, H. Schilder, H. Lueken and P. Kögerler, Isr. J. Chem., 2011, 51, 215–227; (b) J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Coord. Chem. Rev., 2015, 289–290, 137–148.
31. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
32. K. N. Shrivastava, Phys. Status Solidi B, 1983, 117, 437–458.
33. D. Atzei, D. De Filippo, A. Rossi, R. Caminiti and C. Sadun, Spectrochim. Acta, Part A, 1995, 51, 11–20.
34. P. Brant and R. D. Feltham, J. Electron Spectrosc. Relat. Phenom., 1983, 32, 205–221.
35. A. E. Bocquet, T. Mizokawa, T. Saitoh, H. Namatame and A. Fujimori, Phys. Rev. B: Condens. Matter, 1992, 46, 3771–3784.
36. T. Zell, P. Milko, K. L. Fillman, Y. Diskin-Posner, T. Bendikov, M. A. Iron, G. Leitus, Y. Ben-David, M. L. Neidig and D. Milstein, Chem. – Eur. J., 2014, 20, 4403–4413.
37. B. Blom, G. Tan, S. Enthaler, S. Inoue, J. D. Epping and M. Driess, J. Am. Chem. Soc., 2013, 135, 18108–18120.
38. T. Hashimoto, R. Hoshino, T. Hatanaka, Y. Ohki and K. Tatsumi, Organometallics, 2014, 33, 921–929.
39. H. Zhang, Z. Ouyang, Y. Liu, Q. Zhang, L. Wang and L. Deng, Angew. Chem., Int. Ed., 2014, 53, 8432–8436.
40. K. P. Chiang, S. M. Bellows, W. W. Brennessel and P. L. Holland, Chem. Sci., 2014, 5, 267–274.
41. D. Enders, K. Breuer, G. Raabe, J. Simonet, A. Ghanimi, H. B. Stegmann and J. H. Teles, Tetrahedron Lett., 1997, 38, 2833–2836.
42. S. Roy, K. C. Mondal and H. W. Roesky, Acc. Chem. Res., 2016, 49, 357–369.
43. C. D. Martin, M. Soleilhavoup and G. Bertrand, Chem. Sci., 2013, 4, 3020–3030.

---

Footnotes

† Dedicated to Professor Malcolm L. H. Green on the occasion of his 80th birthday.

‡ Electronic supplementary information (ESI) available: General information on the synthetic methodology, studies of the reactivity, mechanistic considerations, crystal data and detailed list of metrical data and details of the DFT calculations, the magnetochemical measurements and the XPS, EXAFS and XANES studies. CCDC 1469263–1469265 and 1469268. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6dt03565e

---