Open Access Article
Open Access ArticleUnravelling the mechanisms of CO2 hydrogenation to methanol on Cu-based catalysts using first-principles multiscale modelling and experiments†
Matej
Huš
 *,
Drejc
Kopač
*,
Drejc
Kopač
 ,
Neja Strah
Štefančič
,
Damjan Lašič
Jurković
,
Venkata D. B. C.
Dasireddy
,
Neja Strah
Štefančič
,
Damjan Lašič
Jurković
,
Venkata D. B. C.
Dasireddy
 and
Blaž
Likozar
and
Blaž
Likozar
Department of Catalysis and Chemical Reaction Engineering, National Institute of Chemistry, Hajdrihova 19, 1001 Ljubljana, Slovenia. E-mail: matej.hus@ki.si
First published on 24th October 2017
Abstract
A way to address the challenge of carbon dioxide emissions causing global warming and climate change is the heterogeneous catalytic hydrogenation of CO2. When surplus electrical energy is available, hydrogen may be produced and used for conversion of CO2 into fuels and chemicals. Industrially, a multifunctional metallic copper and zinc oxide catalyst on alumina (CZA) is commonly used. Presently, first-principles multiscale modelling was accomplished for a commercial-like catalyst (Zn3O3/Cu) and three other Cu/metal oxide combinations (Cr3O3/Cu, Fe3O3/Cu, and Mg3O3/Cu), synthesised via co-precipitation, characterised and experimentally tested. Ab initio plane wave density functional theory calculations were performed using different structural models to elucidate the adsorption of intermediates and elementary reaction steps, considering thermodynamics and kinetics. The results were fed into mean-field micro-kinetic expressions to calculate the conversion and selectivity in a continuous flow stirred-tank reactor vessel for various temperatures and pressures. Kinetic Monte Carlo simulations were used to obtain the detailed surface coverage, turnover frequency and catalytic performance. Although no experimental input besides the structure was applied for physico-chemical mechanism description, measurements were in agreement with theoretical predictions. It was shown that the formate species pathway (HCOO → H2COO → H2COOH → H2CO → H3CO) predominates on the examined Cu-based catalysts, although there are variations in the rate determining steps and the most abundant surface intermediate fractions. Whereas Zn3O3/Cu exhibited the highest conversion and a moderate CH3OH product selectivity, the former was lower for Mg3O3/Cu. Interestingly, Cr3O3/Cu was optimal in terms of yield, but with extremely low CH3OH productivity, while Fe3O3/Cu performed poorly overall. Our results highlight the superiority of Zn3O3/Cu, combining the estimations on micro-, meso- and reactor operation scales. Insights beyond traditional activity experiments may be attained and employed in full-scale reactor engineering and optimisation.
1. Introduction
Technological breakthroughs that have revolutionized our world have been made possible by abundant energy. Historically, humanity has used accumulated solar energy, which has been stored in various forms. Coal and oil have been the cheapest and most plentiful energy sources and thus heavily relied upon. This, however, represents a great environmental burden, necessitating scientific approaches to tackle it.Burning oil and coal is not a carbon neutral process because the carbon that is released as carbon dioxide has not been in the atmosphere for millions of years. Thus it irreversibly increases the concentration of atmospheric CO2, which has been linked to global warming and ocean acidification. This problem can be avoided if carbon neutral energy sources are used, such as biomass, hydro, wind or nuclear energy. In the near future, the full transition towards carbon neutral economy is unfortunately not foreseeable. Thus, the problem of increasing carbon dioxide concentrations must be addressed proactively.1
One of the most promising methods for fixation of captured carbon dioxide is its catalytic hydrogenation to methanol at concentrated sources, such as in thermal power plants. In doing so, methanol is obtained, which is often a more convenient way of storing energy than H2 itself. Methanol is both a clean energy source with a neutral carbon footprint and a versatile chemical for a number of chemical processes.
Several industrial methods for methanol production with hydrogenation of CO and CO2 already exist. Mostly, syngas mixtures at high pressures up to 100 bar and temperatures of 200–300 °C are used. Although several non-copper catalysts have been proposed in the literature,2–5 industrial processes use mainly copper/zinc/alumina (CZA) catalysts due to their low price and durability. They are prepared by a co-precipitation method to yield active Cu clusters and ZnO nanoparticles.6 Effective catalysts have a high Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio and large exposed Cu surfaces. Catalyst activity scales linearly with the accessible Cu surface area.7,8 However, pure Cu is only weakly effective, proving that there is strong synergy between Cu and ZnO.9–11 In the quest for the most effective and inexpensive catalyst, the secondary metal (Zn), support and method of synthesis are varied.
Zn ratio and large exposed Cu surfaces. Catalyst activity scales linearly with the accessible Cu surface area.7,8 However, pure Cu is only weakly effective, proving that there is strong synergy between Cu and ZnO.9–11 In the quest for the most effective and inexpensive catalyst, the secondary metal (Zn), support and method of synthesis are varied.
Considerable research efforts have been devoted to establishing the exact mechanism of this reaction. Most of the intermediates involved cannot be followed experimentally, therefore one must speculate about their existence based on other available experimental data and ab initio studies. Historically, two mechanisms have been proposed. Carbon dioxide is either hydrogenated on the carbon atom, yielding HCOO and following the formate route (H2COO, H2COOH, CH2O, CH3O), or hydrogenated on the oxygen atom, yielding COOH and following the reverse water–gas shift route. Most theoretical work on copper-based catalysts gives credence to the former method. In our previous work on spinel-type CuZnAl2O4, density functional theory (DFT) screening of all conceivable intermediates and elementary steps showed the formate pathway to predominate.12 Other authors have reached similar conclusions on related catalysts. Grabow and Mavrikakis performed DFT simulations and microkinetic modelling on Cu(111) and confirmed the formate pathway.13 Studt et al. studied the reaction on stepped copper surfaces with HCOO, HCOOH and H2COO intermediates.14 DFT calculations and kinetic Monte Carlo from Yang et al.'s study on metal-doped Cu corroborated the formate pathway on pure Cu(111) and Au/Cu(111), while other noble metal dopants favoured the RWGS pathway.15 Behrens et al. studied the reaction on Cu(111), Cu(211) and Zn-doped Cu(211) and confirmed the formate pathway mechanism.10 The combined experimental and theoretical study by Kattel et al. confirmed this,16 although there is some discussion whether Zn becomes oxidised or attaches to formate.17 Nakatsuji and Hu studied this reaction on Cu(100) and Zn/Cu(100) and also established the formate pathway as the main source of methanol.18 Zhao et al., however, argued that on Cu(111), direct hydrogenation of CO2 to HCOO is a mechanistic dead-end due to the high activation energies for further conversion of HCOO, and instead proposed an alternative pathway catalysed by co-adsorbed water.19 Several studies also focused on more subtle effects, such as interface effects of Cu/ZnO by Tang et al.20
This work is a significant extension of our previous endeavour, which focused on DFT calculations,12 albeit using a different atomistic model. Four copper-based catalysts were synthesised, characterised and computationally studied. The secondary metals were Zn, Mg, Cr and Fe, present in their oxide form. An atomistic model simple enough to be computationally tractable and complex enough to account for the synergy of the Cu and metal oxide was formulated. Using DFT, adsorption energies and the complete energetics (barriers, energy changes, and vibrational analysis) were calculated. These data were fed into a complex microkinetic (MK) model with two types of reaction sites to study selectivity, conversion and equilibrium coverages in a continuous stirred-tank reactor (CSTR). Results were then contrasted with kinetic Monte Carlo (kMC).
The paper is structured as follows. After the Introduction in section 1, the experimental, theoretical, and computational methods are outlined in section 2. Experimental work is sketched in section 2.1. The DFT (section 2.2), MK (section 2.3), and kMC (section 2.4) methodologies are thoroughly explained. Results are reported in section 3, separately for DFT-calculated adsorption modes (section 3.1), reaction pathways and rates (section 3.2), MK modelling (section 3.3) and kMC results (section 3.4). Then, the results from different methods are compared among themselves and contrasted with the experimental data. The reasons for agreement and discrepancies are discussed (section 4), followed by a short conclusion (section 5).
2. Methodology
2.1. Catalyst synthesis and characterisation
Cu/M/Al catalysts (Cu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al = 50
Al = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20, M = Zn, Mg, Cr, and Fe) were prepared by a co-precipitation method.21 Details can be found in ref. 12. The catalysts were then dried for 12 h at 90 °C and further calcined in a positive flow of air at 300 °C for 4 h.
20, M = Zn, Mg, Cr, and Fe) were prepared by a co-precipitation method.21 Details can be found in ref. 12. The catalysts were then dried for 12 h at 90 °C and further calcined in a positive flow of air at 300 °C for 4 h.
To obtain the necessary parameters for microkinetic modelling, characterisation was performed with temperature programmed desorption (H2-TPD) and a Brunauer–Emmett–Teller (BET) surface area measurement, as described in ref. 12. The dispersion of copper was measured using dissociative N2O-chemisorption, as described in ref. 22.
For catalytic testing, a GHSV of 6000 h−1 for a mixture of CO2 and H2 (CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2 = 1
H2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) was used. The reactor pressure (20, 30, 40, 50 bar for different runs) and temperature (200, 220, 240, 260, 280, 300 °C for different runs) were kept constant for each run.
3) was used. The reactor pressure (20, 30, 40, 50 bar for different runs) and temperature (200, 220, 240, 260, 280, 300 °C for different runs) were kept constant for each run.
2.2. DFT calculations
As the best compromise between accuracy and computational cost, the Perdew–Burke–Ernzerhof (PBE) functional was selected.25,26 Ultrasoft pseudopotentials from scalar-relativistic calculations were used. To account for the insufficient description of van der Waals interactions by DFT methods, a modified semi-empirical Grimme dispersion correction was included.27 Convergence testing showed that a kinetic energy cut-off of 300 eV and a wavefunction cutoff of 2400 eV sufficed to obtain well converged results. The metallic nature of the catalyst was taken into account by using Gaussian spreading of width 0.1 Ry for Brillouin zone integration. It was sampled on a Monkhorst-Pack mesh with 8 × 8 × 1 points.28 A convergence threshold of 10−8 Ry for self-consisted cycles was selected. For geometric optimisation of adsorbates, residual forces were required to drop below 10−3 Ry per au and energy change per step below 10−4 Ry.
For gaseous species calculations, a large (25 × 25 × 25 Å) cubic cell was used. As there is no periodicity to account for, the Brillouin zone was sampled at a single point (Γ) and no dipole correction was used.
To seek transition states, the nudge elastic band (NEB) method was used.29 After preliminary identification of the transition state structure, it was determined with the climbing image approach until forces orthogonal to the reaction pathway dropped below 0.05 eV Å−1.30 Vibrational analysis was carried out to ensure that each transition state structure had exactly one imaginary frequency, corresponding to the movement along the reaction coordinate. For adsorbed species, zero-point energy (ZPE) correction was calculated from the vibrational component only, perturbing only adsorbate atoms
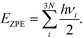 | (1) |
Adsorption energies of reactants, intermediates and products were calculated as
| ΔEads = Eadsorbed − Ecatalyst − Especies + ΔEZPE. | (2) |
The reaction barrier (EA, activation energy) and reaction energy (ΔE) for each elementary step were calculated in a standard fashion as
| EA = ETS − Ereactant | (3) |
| ΔE = Eproduct − Ereactant. | (4) |
This allowed us to obtain the reaction rates as
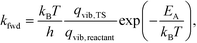 | (5) |
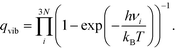 | (6) |
The equilibrium constants are obtained from
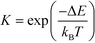 | (7) |
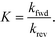 | (8) |
For adsorbed hydrogen atoms, surface diffusion was explicitly taken into account as an elementary reaction, when hydrogen migrates from one fcc site on Cu to the adjacent one.
The kinetic constants for adsorption and desorption are obtained from collision theory. The rate of adsorption can be evaluated if we assume that the sticking probability equals unity as
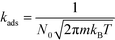 | (9) |
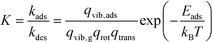 | (10) |
To account for the bifunctional nature of the catalyst and the synergistic effects of Cu and the metal oxide, a small cluster of M3O3 (M = Zn, Mg, Fe, Cr) was deposited on top of the catalyst in a 5 × 5 supercell (see Fig. 1). Several positions were tested to identify the one with the lowest energy. In this manner, we reproduce both the synergistic effect of metal/metal–oxide contact and the effect of a defect (step or terrace).
 | ||
Fig. 1 Modelled active site of the M3O3/Cu catalyst (from top left, clockwise M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn, Mg, Cr, Fe) consists of M3O3 deposited atop of the Cu(111) plane. Reactions proceed at the interphase boundary. Zn, Mg, Cr, Fe) consists of M3O3 deposited atop of the Cu(111) plane. Reactions proceed at the interphase boundary. | ||
Admittedly, such an “inverse” model is particularly useful to describe the SMSI (strong metal–support interaction) state,31 which is for instance well established in Cu/ZnO. The same model was chosen for other metals, despite them being somewhat harder (Cu/MgO) or more easily reducible (FeOx), to allow for easier comparison. Structurally different models would probably quantitatively better describe each particular set of measurements, but would obscure fundamental properties we wish to explore across different metals. One should also keep in mind that this is one possible type of active site, as oxides can also be partially or totally reduced at high temperatures and hydrogen pressures.32
Work on pure Cu and Zn-doped Cu also showed that the active site might be located at a twin boundary, i.e. at a step size and not a terrace site. Our models, however, include oxides.10
The active site of the catalyst is the interface of Cu and M3O3. Throughout the calculations, the top two Cu layers, M3O3 and adsorbed species were allowed to relax fully, while the bottom Cu layers were frozen in their bulk positions.
2.3. Microkinetic modelling
In order to investigate the effects of different catalyst compositions on CO2 hydrogenation, a micro-kinetic model, which is based on 33 reversible elementary steps (vide infraTable 2 for stable adsorbates and Table 3 for surface reactions), was developed. A thorough methanol synthesis reaction network with 26 distinct species and seven of them also in the bulk (gaseous phase) was considered, also taking into account possible formation of by-products such as formaldehyde and formic acid. The model includes all pathways as calculated using DFT without any assumptions regarding the rate determining step. The mean-field micro-kinetic model was used to predict the reaction kinetics. All surface reaction (kfwd, krev) and adsorption rates (kads, kdes) were taken directly from DFT calculations and transition state theory or collision theory, respectively. To improve model stability and decrease computation times, all reaction rates were scaled. When scaled by a factor of 10−3, the results were the most in-line with the general observations reported in the methanol synthesis field and our experimental results.Methanol synthesis is performed under dynamic conditions where reactant gases continuously flow through the reactor. To simulate this and to have similar conditions as those in kMC simulations, our model is based on the continuous stirred-tank reactor (CSTR). Simulation conditions were chosen based on typical experimental set-ups. First, temperature dependence (480–680 K with increments of 20 K) was tested at 40 bar. Subsequently, pressure dependence (20–60 bar with increments of 10 bar) was checked at 540 K. During all simulations, the initial molar ratio between CO2 and H2 was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and the gas hourly space velocity (GHSV) was set to 6000 h−1 with no other gases present in the influent. The reactor volume was 1 ml. The number of active sites was inferred from the H2-TPD results. As shown later in Fig. 4 and Table 2, all intermediates except H* and CO* bind to the copper–metal interface active site, while the latter bind to copper. For this reason we de-convoluted the H2-TPD profiles to three different peaks, with the α peak attributed to copper sites (*) and the β and γ peaks to interface sites (#).
3 and the gas hourly space velocity (GHSV) was set to 6000 h−1 with no other gases present in the influent. The reactor volume was 1 ml. The number of active sites was inferred from the H2-TPD results. As shown later in Fig. 4 and Table 2, all intermediates except H* and CO* bind to the copper–metal interface active site, while the latter bind to copper. For this reason we de-convoluted the H2-TPD profiles to three different peaks, with the α peak attributed to copper sites (*) and the β and γ peaks to interface sites (#).
The initial values of the gas composition are specified as written below and initially no species are bound to the catalyst's surface
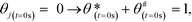 | (11) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), respectively.
1), respectively.
Active sites must be either free or covered by an intermediate:
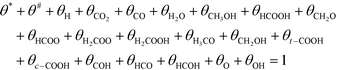 | (12) |
The corresponding rate equations for surface reactions (cf.Table 3 for numbering) can be written either as
| ri = ki·θj·θ* or # − k−i·θj·θj | (13) |
| ri = ki·θj·θj − k−i·θj·θ* or # | (14) |
In elementary reaction i = 7, where only the cis–trans configuration is changed, the rate equation is written as:
| ri = ki·θj − k−i·θj | (15) |
For the adsorption and desorption reactions, the rates are defined as:
| ri = ki·pj·θjn − k−i·θjn, | (16) |
Reactions are indexed to i, while adsorbate species and intermediates are indexed to j. The forward reaction constants ki are calculated from the DFT results from eqn (5) and the reverse constants k−i from eqn (7) and (8).
Mass balances of surface-bound species are defined as
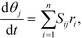 | (17) |
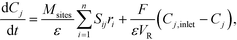 | (18) |
Micro-kinetic simulations were carried out with MATLAB®, a script-based numerical computing environment by MathWorks Inc. Using the systematic approach described above, a system of 26 non-linear ordinary differential equations was obtained. The system is not solvable analytically; therefore numerical methods were used to obtain a solution. Although only steady state reactor operation was required, a transient solution was calculated as the stability of the system would prevent any noticeable computational savings with steady-state solvers. Because the system is numerically very stiff, the usual Runge–Kutta methods proved to be too unstable. Instead, we had to resort to more stiff-orientated solvers. MATLAB's built-in solver ode23s was used. This solver is based on backwards differential formulas, an implicit method widely used for solving stiff systems. Such solvers use variable orders of the said formulas. The system was solved successfully for a sufficient time to achieve a steady state.
After simulation CO2 conversion was calculated as:
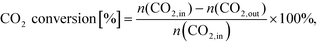 | (19) |
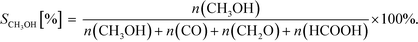 | (20) |
2.4. kMC simulations
Kinetic Monte Carlo (kMC) simulations are nowadays widely used in theoretical chemistry applications, and are gaining particular importance in the field of heterogeneous catalysis.33,34 In combination with the atom-scale DFT computations, kMC provides a mesoscopic description of reactor performance, enabling the studies of catalyst kinetics in a stochastic manner.35 Using kMC, we can statistically evaluate the surface chemistry kinetics, and ultimately estimate the activity, selectivity, conversion, etc. of a catalyst under operating conditions.In this paper, we used the kMC software package Zacros.34 Zacros employs the graph-theoretical kMC framework, which apart from simulating adsorption, desorption, diffusion, and reactions on lattices, allows for treatment of complex chemistries such as multidentate species or complex neighbouring lattice site coverage. The catalysts that we study in this paper are alloys of Cu and metal (Zn, Mg, Fe, Cr) oxides, which due to complex geometries require accurate handling of adsorbate lateral interactions and active site occupancies.
Following the methanol synthesis pathway presented in Fig. 5 and using the DFT obtained results, we set up our kMC simulations. Species formation energies were mapped with Zacros using DFT obtained absolute energies using the standard procedure.36,37 We defined a custom periodic cell lattice (size of 48 × 48 cells) with unit cell vectors α = (4.78, 0.0) Å and β = (2.39, 4.14) Å, representing the geometry of our Cu alloys. These values correspond to the position of Cu atoms in pure Cu(111). We used two distinct active site types (their ratio being 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), because DFT simulations showed that hydrogen atoms and CO tend to adsorb on Cu, while other intermediates favour the interface between Cu and the dopant metal (M3O3 cluster). In total, the lattice consists of 4608 active sites. In this model, this cluster acts as a surface defect where the reaction takes place. Intermediates with two oxygen atoms were considered bidentate, adsorbing on two neighbouring distinct-type sites. The pre-exponential factors for each reaction were obtained as in ref. 36 and 38, where the temperature and pressure dependence was taken into account through rotational, translational, and vibrational partition functions.
1), because DFT simulations showed that hydrogen atoms and CO tend to adsorb on Cu, while other intermediates favour the interface between Cu and the dopant metal (M3O3 cluster). In total, the lattice consists of 4608 active sites. In this model, this cluster acts as a surface defect where the reaction takes place. Intermediates with two oxygen atoms were considered bidentate, adsorbing on two neighbouring distinct-type sites. The pre-exponential factors for each reaction were obtained as in ref. 36 and 38, where the temperature and pressure dependence was taken into account through rotational, translational, and vibrational partition functions.
Overall, the methanol synthesis model consists of 19 lattice and 7 gaseous species and 32 reversible reaction steps (see Tables 2 and 3 and Fig. 5). To avoid unnecessary and physically unimportant repetition of some steps, which would render simulations intractably time-consuming, hydrogen surface diffusion and CO2 adsorption had to be slowed down by a factor of 104. According to Prats et al., such modifications speed up the simulations considerably without significantly affecting the results.39
Also, in Zacros the gas molar fraction is treated as constant throughout the reaction and we used a H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 = 3
CO2 = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio throughout our simulations. Therefore desorption of HCOOH and CH2O had to be turned off, since both are prone to desorption but due to the constant gaseous phase composition could never re-adsorb. Our experimental results show negligible amounts of formed HCOOH and CH2O, warranting this approximation in the model.
1 molar ratio throughout our simulations. Therefore desorption of HCOOH and CH2O had to be turned off, since both are prone to desorption but due to the constant gaseous phase composition could never re-adsorb. Our experimental results show negligible amounts of formed HCOOH and CH2O, warranting this approximation in the model.
3. Results
3.1. Experimental
| Cu/Zn | Cu/Mg | Cu/Cr | Cu/Fe | |
|---|---|---|---|---|
| Cu metallic surface area (m2 g−1) | 48 | 35 | 21 | 29 |
| Cu metal dispersion (%) | 28 | 27 | 17 | 23 |
| Surface area (m2 g−1) | 96 | 85 | 29 | 24 |
| H2-TPD (μmol g−1) | 9.5 | 7.3 | 5.8 | 6.1 |
It is believed that the reducible nature of copper species and the copper surface area are important parameters for the catalytic performance of copper-based catalysts.40–42 A linear relationship between CO2 conversion on Cu-based catalysts and their exposed Cu surface area is often reported.43,44 In the present study, trends of the catalytic activity are consistent with the exposed Cu surface area and Cu+/Cu0 ratio.
The amount of chemisorbed hydrogen on the catalyst surface is influenced by the second metal (M), being the highest for Cu/Zn, followed by Cu/Mg, Cu/Fe, and Cu/Cr. It has been reported in the literature that higher amounts of chemisorbed hydrogen are also due to the formation of subsurface hydrogen.45
Surface area is the largest for Cu/Mg, followed by Zn, Cr, and Fe. The relatively low surface area of Cu/Cr and Cu/Fe catalysts (in comparison to Cu/Zn and Cu/Mg) could be caused by blocking of the alumina pores with the crystallites of chromium and iron oxides.46,47
The metal dispersion of all tested catalysts ranges from 17 to 37%, while the Cu metallic surface area remains in the range 21–35 m2 g−1. In particular, the Cu/Cr catalyst showed lower dispersion and surface area than other catalysts. In general, for catalysts prepared with co-precipitation, small catalyst crystallites are correlated with higher dispersion and BET surface area.48 Our results confirm this. The Cu metallic surface area follows the order: Cu/Mg > Cu/Zn = Cu/Fe > Cu/Cr.
 | ||
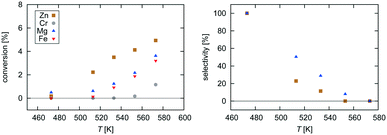
| Fig. 2 Experimental data for pressure dependence of selectivity towards CH3OH and conversion of CO2 for the investigated Zn3O3/Cu and Mg3O3/Cu catalysts at T = 533 K and GHSV = 6000 h−1. | ||
Selectivity is shown only for Zn3O3/Cu and Mg3O3/Cu catalysts as they have the best conversion. As expected, the selectivity sharply drops with increasing temperature as RWGS becomes more favourable and more CO is formed. The slightly higher selectivity of Mg3O3/Cu is in agreement with micro-kinetic modelling (see Fig. 7 later on), but the overall lower conversion makes this catalyst less suitable anyway. Note that this trend reverses under high pressure.
Pressure dependence was investigated only for Zn3O3/Cu and Mg3O3/Cu catalysts at 533 K and GHSV = 6000 h−1. Upon increasing the pressure, the chemical potential of CO2 and H2 is higher, resulting in higher catalyst surface coverage. As expected, conversion increases as pressure is increased. From simple thermodynamic analysis it follows that selectivity must increase with pressure, also shown by our data. A slight decrease in selectivity over Mg3O3/Cu when going from 20 to 30 bar is attributed to experimental uncertainty. It is experimentally known that at low pressures, methanol is formed via the formate route, but at higher pressure the RWGS route also becomes accessible.45 We see that except at 20 bar, the selectivity of the Zn3O3/Cu catalyst is better than that of Mg3O3/Cu.
3.2. Adsorption modes
In Table 2, we show the calculated ZPE-corrected adsorption energies for all the species considered. We list the adsorption energies for each catalyst and the adsorption site. Hydrogen and carbon monoxide bond exclusively to the pure copper surface, while other species can bond to both the M3O3/Cu interface and pure Cu. To keep the model reasonably manageable, we consider only adsorption modes to the interface for these species. Preliminary computations showed that this interaction is in all cases more favourable than binding to pure Cu, which is both an understandable and desirable property of the model.| Adsorbate | Site | E ads ZPE (eV) | |||
|---|---|---|---|---|---|
| Zn3O3/Cu | Mg3O3/Cu | Cr3O3/Cu | Fe3O3/Cu | ||
| Stable molecules | |||||
| H | Cu | −2.18 | −2.21 | −2.28 | −2.18 |
| CO2 | Interface | −0.23 | −0.80 | −0.69 | 0.00 |
| H2O | Interface | −0.79 | −1.25 | −0.72 | −0.67 |
| CO | Cu | −0.65 | −1.37 | −1.42 | −0.81 |
| HCOOH | Interface | −0.59 | −1.28 | −0.83 | −0.70 |
| CH2O | Interface | −0.90 | −1.46 | −1.60 | −0.85 |
| CH3OH | Interface | −1.09 | −1.51 | −0.91 | −0.94 |
| Intermediates | |||||
| HCOO | Interface | −3.13 | −3.75 | −3.44 | −2.99 |
| H2COO | Interface | −4.83 | −5.22 | −5.56 | −4.76 |
| H2COOH | Interface | −2.92 | −3.10 | −2.78 | −2.84 |
| t-COOH | Interface | −2.16 | −2.96 | −2.60 | −2.22 |
| c-COOH | Interface | −2.30 | −2.93 | −2.63 | −2.26 |
| HCO | Interface | −1.92 | −2.38 | −2.59 | −1.79 |
| COH | Interface | −3.08 | −3.65 | −3.80 | −2.96 |
| HCOH | Interface | −2.64 | −2.90 | −2.92 | −2.25 |
| CH2OH | Interface | −1.77 | −2.24 | −1.81 | −1.68 |
| CH3O | Interface | −2.84 | −3.16 | −3.48 | −2.60 |
| OH | Interface | −3.49 | −3.99 | −4.04 | −3.24 |
| O | Interface | −5.59 | −6.08 | −6.36 | −5.28 |
As follows from basic thermodynamics, adsorption energies are negative. For adsorption to be spontaneous, it has to be exothermic. Molecules lose degrees of freedom upon adsorption, thus decreasing the entropy of the system, which must be offset by a greater release of energy for the Gibbs free energy to be negative.
Hydrogen binds dissociatively to the pure copper surface with very similar adsorption energies (around −2.20 eV). This is the only activated adsorption (cf.Table 3), as its activation energies range from 0.39 eV on Cr3O3/Cu to 0.55 eV on the Mg3O3/Cu catalyst. Carbon dioxide shows great variations in its affinity to bind to the catalyst. CO2 does not bind to Cu/Fe and only weakly physisorbs to Zn3O3/Cu (−0.23 eV), indicative of an Eley–Rideal mechanism. Mg3O3/Cu and Cr3O3/Cu, however, bind CO2 quite strongly (−0.80 and −0.69 eV, respectively), following the Langmuir–Hinshelwood mechanism. In all three instances, CO2 binds in a bent configuration, with one oxygen atom interacting with the secondary metal and the carbon atom binding to copper. Mg3O3/Cu and Cr3O3/Cu strongly bind CO, as well (−1.37 and −1.42 eV, respectively), as opposed to the moderate interaction of CO with Zn3O3/Cu and Fe3O3/Cu (−0.65 and −0.81 eV, respectively). CO binds in the vicinity of the interface but not at the interface, perpendicularly to the copper surface with the carbon atom interacting with copper. Water binds with its oxygen atom to the secondary metal, while its hydrogen atoms point towards the copper surface. In a similar fashion, HCOOH, CH2O and CH3OH also bind to the secondary metal through their oxygen atoms. CH2O adopts a planar orientation, while HCOOH and CH3OH orient their hydroxyl hydrogen atoms towards the Cu surface.
| i | Elementary reaction | In eV | Zn3O3/Cu | Mg3O3/Cu | Cr3O3/Cu | Fe3O3/Cu |
|---|---|---|---|---|---|---|
| 1 | H2 + 2* → 2 H* (dis. ads.) | E A | 0.47 | 0.55 | 0.39 | 0.53 |
| ΔE | −0.13 | −0.20 | −0.33 | −0.13 | ||
| 2 | H* → H* (diffusion) | E A | 0.16 | 0.20 | 0.24 | 0.16 |
| 3 | CO2** → CO* + O* | E A | 0.60 | 0.57 | 0.78 | 1.03 |
| ΔE | +0.06 | −0.57 | −1.02 | −0.06 | ||
| 4 | H* + CO2** → HCOO** + * | E A | 0.59 | 0.47 | 0.71 | 0.12 |
| ΔE | −0.65 | −0.68 | −0.41 | −0.80 | ||
| 5 | HCOO** → HCO* + O* | E A | 1.70 | 1.93 | 1.78 | 1.89 |
| ΔE | +0.74 | +0.41 | −0.40 | +1.05 | ||
| 6 | H* + CO2** → t−COOH** | E A | 0.71 | 0.76 | 0.88 | 0.64 |
| ΔE | +0.10 | −0.10 | +0.21 | −0.24 | ||
| 7 | t-COOH** → c-COOH** | E A | 0.44 | 0.55 | 0.54 | 0.56 |
| ΔE | −0.07 | +0.10 | +0.06 | +0.03 | ||
| 8 | H* + t-COOH** → HCOOH** + * | E A | 0.60 | 0.60 | 0.56 | 0.49 |
| ΔE | −0.15 | −0.01 | +0.15 | −0.20 | ||
| 9 | c-COOH** → OH* + CO* | E A | 0.69 | 1.03 | 0.84 | 0.96 |
| ΔE | −0.18 | −0.77 | −1.18 | −0.13 | ||
| 10 | H* + HCOO** → H2COO** + * | E A | 0.90 | 1.23 | 0.74 | 1.10 |
| ΔE | +0.32 | +0.58 | −0.01 | +0.24 | ||
| 11 | H2COO** → CH2O* + O* | E A | 0.55 | 0.81 | 0.49 | 1.09 |
| ΔE | +0.14 | −0.52 | −0.60 | +0.44 | ||
| 12 | H* + HCOO** → HCOOH** + * | E A | 0.92 | 0.81 | 1.14 | 0.77 |
| ΔE | +0.60 | +0.57 | +0.77 | +0.36 | ||
| 13 | HCOOH** → HCO* + OH* | E A | 0.80 | 0.95 | 0.82 | 1.21 |
| ΔE | −0.06 | −0.35 | −1.05 | +0.41 | ||
| 14 | H* + HCOOH* → H2COOH** + * | E A | 0.46 | 0.78 | 0.74 | 0.74 |
| ΔE | −0.51 | +0.03 | −0.04 | −0.32 | ||
| 15 | H* + H2COO** → H2COOH** + * | E A | 0.32 | 0.89 | 0.93 | 0.42 |
| ΔE | −0.23 | +0.02 | +0.74 | −0.21 | ||
| 16 | H2COOH** → CH2O* + OH* | E A | 0.81 | 0.68 | 0.03 | 0.68 |
| ΔE | +0.16 | −0.73 | −1.23 | +0.37 | ||
| 17 | H* + CO* → HCO* + * | E A | 0.60 | 0.59 | 0.64 | 0.70 |
| ΔE | +0.03 | +0.31 | +0.22 | +0.31 | ||
| 18 | H* + CO* → COH* + * | E A | 1.24 | 1.92 | 1.80 | 1.48 |
| ΔE | +0.63 | +0.81 | +0.78 | +0.91 | ||
| 19 | H* + COH* → HCOH* + * | E A | 0.65 | 0.57 | 0.50 | 0.51 |
| ΔE | −0.45 | −0.11 | +0.09 | −0.18 | ||
| 20 | H* + HCO* → CH2O* + * | E A | 0.41 | 0.29 | 0.55 | 0.33 |
| ΔE | −0.29 | −0.35 | −0.22 | −0.37 | ||
| 21 | H* + HCO* → HCOH* + * | E A | 0.93 | 0.91 | 1.06 | 0.98 |
| ΔE | +0.15 | +0.39 | +0.65 | +0.41 | ||
| 22 | H* + HCOH* → CH2OH* + * | E A | 0.55 | 0.39 | 0.83 | 0.22 |
| ΔE | −0.52 | −0.69 | −0.18 | −0.83 | ||
| 23 | H* + CH2O* → CH2OH* + * | E A | 0.46 | 0.36 | 1.07 | 0.67 |
| ΔE | −0.08 | +0.05 | +0.68 | −0.04 | ||
| 24 | H* + CH2O* → CH3O* + * | E A | 0.38 | 0.37 | 0.62 | 0.20 |
| ΔE | −0.79 | −0.52 | −0.64 | −0.61 | ||
| 25 | H* + CH2OH* → CH3OH | E A | 0.72 | 0.63 | 0.79 | 0.57 |
| ΔE | −0.92 | −0.84 | −0.61 | −0.86 | ||
| 26 | H* + CH3O* → CH3OH* + * | E A | 0.46 | 0.42 | 0.80 | 0.31 |
| ΔE | −0.20 | −0.27 | +0.71 | −0.29 | ||
| 27 | H* + O* → OH* + * | E A | 0.74 | 0.88 | 0.57 | 0.85 |
| ΔE | −0.20 | −0.19 | +0.12 | −0.28 | ||
| 28 | H* + OH* → H2O + * | E A | 0.50 | 0.47 | 0.82 | 0.38 |
| ΔE | −0.18 | −0.10 | +0.53 | −0.31 |
While the formate species (HCOO) binds in a monodentate and bidentate configuration on the pure copper surface,19 it binds solely as bidentate on stepped surfaces.12 This is also the case in our model, with HCOO binding in a tilted orientation with one oxygen to the metal atom and the other oxygen to copper. Hydroxycarbonyl (COOH) exists in two orientations, either cis or trans with respect to the C–O bond. Their adsorption energies are similar, although c-COOH binds marginally more strongly (except for Cu/Mg).
Another crucial intermediate is H2COO,49 which plays a vital role in methanol synthesis. It binds to the metal atom with one oxygen and to copper with another oxygen atom. H2COOH is another important intermediate. It binds to the metal atom with the oxygen atom and to copper through its hydroxyl group, similarly to HCOOH. The methoxy fragment (CH3O) assumes a similar configuration to methanol, i.e. it binds to the interface through its oxygen atom.
HCO and COH behave noticeably differently. Although both bind to the interface through the oxygen atom and to copper with carbon, HCO assumes a planar orientation, while COH sits upright, similar to CO. HCOH is the only species that binds to the metal atom through carbon and not oxygen. CH2OH is oriented similarly to HCO.
Hydroxyl (OH) binds to the interface in a planar orientation through the oxygen atom. Atomic oxygen preferentially binds to the copper plane.
It should be noted that oxygen-containing species bind more strongly to the Mg3O3/Cu and Cr3O3/Cu catalysts than to Zn3O3/Cu and Fe3O3/Cu. This can be easily explained; Mg is considerably more electropositive than Zn and Fe. Cr on the other hand normally preferentially assumes the oxidation state +3, meaning that it is coordinatively unsaturated with oxygen atoms in the model Cr3O3 moiety. Nevertheless, stronger adsorption to Mg3O3/Cu and Cr3O3/Cu reflects better catalytic performance, as shown by microkinetic modelling.
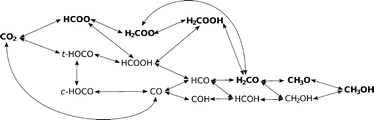
3.3. Reaction pathways
A complex network of possible elementary reactions yielding methanol from CO2 can be constructed. In addition to formate and reverse water–gas shift (RWGS) pathways, various side pathways with somewhat exotic intermediates (such as HOCOH, HOCHOH or COH) can be proposed. Since our previous work12 and literature review showed the formate and RWGS pathways to predominate,13,15 we limit our investigations to these two pathways, resulting in the scheme shown in Fig. 5.In Table 3, we list all the elementary reaction steps considered with their respective activation barriers and reaction energies on the four investigated catalysts. We also include the dissociative hydrogen adsorption and hydrogen surface diffusion since both processes are activated. From the activation barriers and activation energies, the reaction rates (not shown) in the transition state theory (TST) approximation were calculated as explained in the Methodology section and used in the microkinetic modelling.
It is already well established that the hydrogen spill-over is an important bottleneck in the CO2 hydrogenation reaction. This fact is nicely reflected in the model used, as hydrogen binds to Cu(111) but the reaction then proceeds at the interface. Therefore, hydrogen surface diffusion on Cu(111) is also important. This is a fast reaction with activation energies ranging from 0.16 eV on Zn3O3/Cu to 0.24 eV on Cr3O3/Cu (cf. kMC methodology for necessary artificial downscaling of this reaction rate). The spill-over effect is cumulatively accounted for as hydrogen surface diffusion over Cu(111) and its transfer from Cu(111) to the interface during the elementary reaction steps.
First, adsorbed or gaseous CO2 is hydrogenated to HCOO. On pure Cu(111), this reaction has a moderate activation energy of 0.62 eV,19 which is slightly lowered on Zn3O3/Cu and Mg3O3/Cu catalysts (0.59 and 0.47 eV, respectively) and higher on Cr3O3/Cu (0.71 eV). It is less straight-forward to compare this value with the activation energy on Fe3O3/Cu (0.12 eV) because of a different reaction mechanism.
HCOO could in principle dissociate to HCO and O, but on account of the extremely large activation energies (1.7 eV or larger), it does not. Instead, it forms either H2COO on Zn3O3/Cu (0.90 eV) and Cr3O3/Cu (0.74 eV) or HCOOH on Mg3O3/Cu (0.81 eV) and Fe3O3/Cu (0.77 eV). On pure Cu(111), the activation barrier for the formation of H2COO is 1.20 eV and for HCOOH it is 0.70 eV.19 This demonstrates the effect of Zn in particular in lowering the overall activation energy and guiding the reaction towards the desirable route. On Zn3O3/Cu, H2COO is hydrogenated to H2COOH, while on Cr3O3/Cu it directly dissociates to H2CO and O. On Mg3O3/Cu and Fe3O3/Cu, HCOOH is hydrogenated to H2COOH. When H2COOH is formed, it is then cleaved into CH2O and OH.
On all catalysts, CH2O is preferentially hydrogenated to CH3O, although on Cr3O3/Cu non-negligible amounts of CH2OH can also form. Either intermediate is then hydrogenated to the final product methanol. All these activation energies are lower than on Cu(111).
On Zn3O3/Cu and Fe3O3/Cu, CO can either desorb or react further to HCO. On Mg3O3/Cu and Cr3O3/Cu, CO is bound more strongly and will preferentially react to HCO. In neither case is COH formed upon hydrogenation of CO. HCO is then further hydrogenated in the consecutive steps to H2CO, CH3O and CH3OH, the last two steps being the same as in the formate pathway.
In any case, CO cannot form through the formate pathway but via RWGS.
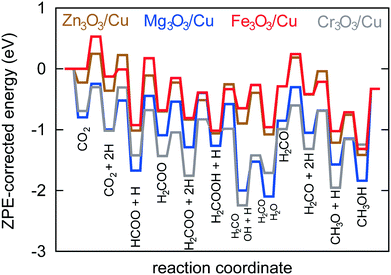
In Fig. 6, a potential energy surface for the most probable route on all catalysts is shown.
3.4. Microkinetic modelling
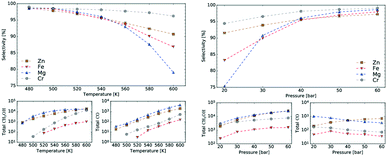
Mean-field microkinetics modelling was used to predict the reaction kinetics from first principles, i.e. reaction rates obtained taken directly from DFT calculations. The calculated selectivities towards methanol and total CO2 conversion for all four catalysts are shown as a function of temperature and pressure in Fig. 7 and 8, respectively.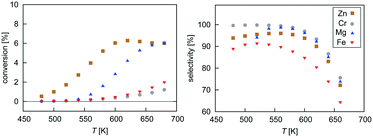 | ||
| Fig. 7 Temperature dependence of selectivity towards CH3OH and conversion of CO2 for all four investigated catalysts from microkinetic modelling at p = 40 bar and GHSV = 6000 h−1. | ||
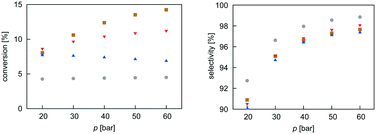 | ||
| Fig. 8 Pressure dependence of selectivity towards CH3OH and conversion of CO2 for all four investigated catalysts from microkinetic modelling at T = 540 K and GHSV = 6000 h−1. Colour code as in Fig. 7. | ||
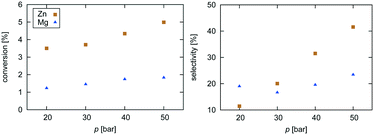
At low temperatures, high selectivities towards methanol are obtained for all catalysts. For the Mg3O3/Cu catalyst, conversion below 520 K was too low for a meaningful determination of the selectivity. Methanol synthesis from carbon dioxide is an exothermic process, favoured at low temperatures and high pressures. However, high temperatures are needed for a reasonable conversion. Accordingly, selectivities decreased with increasing temperature for all catalysts while conversions increased. Among the catalysts, the highest selectivity was exhibited by Cr3O3/Cu, but its conversion was the lowest. On the other hand, the Zn3O3/Cu catalyst had the highest conversion and a reasonable selectivity, making it the most suitable for methanol production. This is in agreement with the fact that Zn3O3/Cu is predominantly used in industry.
As expected from thermodynamic considerations, an increase in selectivity and conversion with increasing pressure was observed, as shown in Fig. 8. The effect is most pronounced on Zn3O3/Cu. The only exception was observed for the Mg3O3/Cu catalyst, where conversion showed a peculiar decrease with increasing pressure. This is due to catalyst surface saturation.
To sum it up, Zn3O3/Cu showed the best activity among all catalysts considered, especially at lower temperatures, which are more suitable for industrial processes. This is both expected and understandable, since industrially Zn3O3/Cu is used almost exclusively.
3.5. Insights from kinetic Monte Carlo
kMC simulations for each of the four catalysts were performed at various temperatures (ranging from 480 K to 600 K) and pressures (ranging from 20 bar to 60 bar). For each simulation, we randomly chose an initial random seed. We studied how the overall selectivity towards methanol, relative frequencies of the reaction steps, and lattice coverage change over time as a function of temperature and pressure.The simulations ran for five days (elapsed wall time 432![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s), each on a single core, reaching the typical simulation times between 10−4 s and 10−2 s, depending on the pressure, temperature, and catalyst. On average, 3 × 107 kMC steps (events) occurred during a simulation.
000 s), each on a single core, reaching the typical simulation times between 10−4 s and 10−2 s, depending on the pressure, temperature, and catalyst. On average, 3 × 107 kMC steps (events) occurred during a simulation.
Fig. 9 shows selectivity towards methanol at various temperatures and pressures for each catalyst. The selectivity peaks at 97% for high pressure and low temperature for each catalyst type but drops with decreasing pressure and increasing temperature (i.e. at 600 K selectivity for Mg3O3/Cu catalyst drops below 80%). The best catalysts in terms of selectivity are Cr3O3/Cu and Zn3O3/Cu, which also show the most stable behaviour across the whole temperature and pressure range. Fig. 9 also shows the production of CH3OH and CO in terms of the total number of molecules produced in the simulations, again as a function of temperature or pressure. We see that the temperature dependence is much stronger than the pressure dependence. This is expected as higher temperatures accelerate the rate of all reactions. Trends in selectivity and CH3OH and CO production are in good agreement with experimental data (cf. sections 3.1 and 4).
As seen in Fig. 7, HCOO is the most abundant species on the surface until very late. This is in line with recent studies which show that formation of methanol is mainly controlled by the surface coverage of formate and hydrogen at the steady state.50
To show the behaviour of the active catalyst in more detail, we plot in Fig. 10 (see also the ESI† for the animated video) a snapshot of the lattice coverage for the Cr3O3/Cu catalyst at T = 500 K and P = 40 bar upon reaching a steady state and temporal evolution of lattice coverage and gaseous fraction composition. In the top plot, the most abundant intermediates on the lattice are CH3O and H, which recombine into CH3OH. This particular reaction is among the most frequent reactions for the Cr3O3/Cu catalyst, as depicted in Fig. 11.
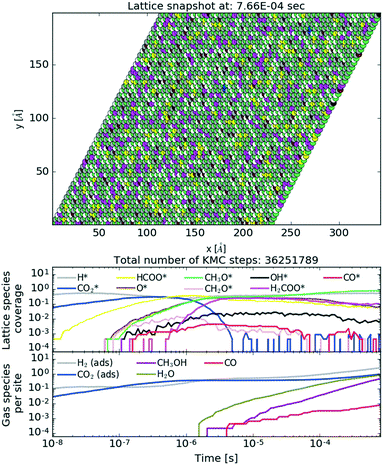 | ||
| Fig. 10 Lattice snapshot plot at 8 × 10−4 s (top) with temporal evolution of lattice coverage (middle) and gas fraction composition (bottom) for the Cr3O3/Cu catalyst. See the ESI† for the animated video. | ||
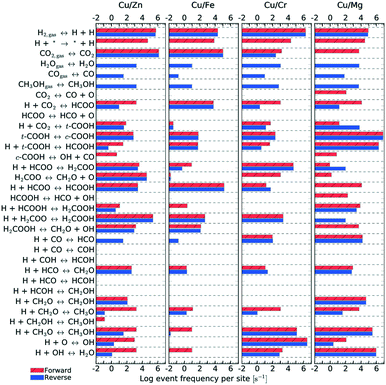 | ||
| Fig. 11 Elementary step frequency for the case of T = 500 K and P = 40 bar, for all four types of catalysts. Red steps indicate forward reactions, while blue ones indicate reverse reactions. | ||
From the lattice coverage evolution in Fig. 10, we see that the stationary conditions on the lattice are reached after ∼5 × 10−6 s; thereafter production of gaseous species follows at a constant rate. Similar timescales are also apparent for other studied catalysts. Our simulations reached typical times of 10−3 s, which is sufficient to reach steady state conditions. To make sure of that, one simulation for the Zn3O3/Cu catalyst at T = 500 K and P = 40 bar was run for twice as long (wall time of 10 days). The obtained results were consistent.
Fig. 11 shows the frequency of the reaction steps for all four catalysts for T = 500 K and P = 40 bar. The frequency is defined as the number of instances a particular reaction step occurred per active site divided by the total simulation time. The event frequency distribution shows that the reaction pathway towards methanol production differs among the catalysts (cf. section 4). There are greater differences observed between Mg3O3/Cu and Fe3O3/Cu catalysts, which have much poorer selectivities. In contrast, Zn3O3/Cu and Cr3O3/Cu have better selectivity and are also more comparable.
4. Discussion
We have synthesised a commercial-like ZnxOy/Cu catalyst for carbon dioxide hydrogenation to methanol and three variants where Zn has been substituted with Mg, Fe and Cr. These three metals have been chosen as the most active ones among a larger battery of synthesised catalysts (including Ca, Sr, Ba, Ni, Mn, Co). Although a commercial catalyst could have been purchased, we opted for in-house synthesis. This allowed us to avoid potential effects of unwanted components (binders, stabilisers etc.) and impurities that might be present in the commercial catalyst.The activity of all four synthesised catalysts has been tested experimentally. Extensive multiscale modelling has been performed to account for the observed trends in catalytic activity, conversion and selectivity. Our aim was to describe their performance solely from catalyst characterisation (Table 1) and first-principles calculations without any input of catalytic performance and then compare these results with experimental data.
In catalyst modelling, a compromise had to be struck between the veracity of the catalyst description, computational tractability and comparability of the four tested catalysts. In reality, every catalyst has many different active sites. In addition to different surface planes, kinks, steps, defects and lattice strain also play important roles.51,52 Experimentally observed catalytic activity is thus an amalgam of activities of all present active sites, while in DFT calculations we can only manageably follow the reaction on one active surface. Thus, a M3O3 active cluster deposited on Cu(111) has been selected as the most suitable depiction of the active site.
It should be noted that M3O3 is a model cluster and by no means the only or even predominant structure in the real catalyst. To thoroughly analyse the exact oxide stoichiometry on the catalyst, a comprehensive thermodynamic analysis would have to be performed. This would further complicate an already complex model, which focuses on the kinetic considerations and not phase stability.
A comprehensive reaction pathway with all possible interconversions has been proposed (Fig. 5) and calculated (Tables 2 and 3). Although often used to predict the most probable reaction route and rate-determining steps, solely DFT results cannot provide this information in the case of a complex and intertwined reaction scheme. In our case, we see that the hydrogenation of CO2 first leads to HCOO and not t-COOH. In further reactions, however, their reversibility means that the actual pathway will be more complex than a simple potential energy surface (Fig. 4) would lead us to assume. Thus, a micro-kinetic analysis is essential.
In our micro-kinetic model, no assumptions about the reaction pathway have been made. Instead, all possible reactions have been included. This means that the included reactions spanned a large range of rates, making the model numerically challenging. Due to the stiffness of the system, the ode23s solver was used with very tight convergence criteria and short time steps. All reaction steps were scaled down but our preliminary testing showed that this did not impact the results noticeably. The calculation times (wall time) also varied from a few seconds to a few hours, depending on the conditions imposed (temperature, pressure, GHSV, influx composition). To test the reliability of the results, we made sure that the output did not vary upon changing the convergence criteria and that trends across temperatures and pressures did not show any outliers.
From micro-kinetic modelling, selectivity towards methanol and conversion were obtained for each catalyst under various operating conditions. Selectivities show expected trends. In general, they decrease with temperature and are above 90% in the operating range. This is consistent with our choosing the four most active catalysts among many synthesised. It might seem odd that the Cr3O3/Cu catalyst exhibits the highest selectivity but it is only marginally higher than those of Mg3O3/Cu and Zn3O3/Cu. However, the conversion of Cr3O3/Cu and Fe3O3/Cu catalysts is very poor, making their overall activity low. We see that conversion on Zn3O3/Cu and Mg3O3/Cu catalysts plateaus above 650 K, reaching thermodynamic equilibrium. For pressure dependence, the anticipated and experimentally measured effects are smaller, again evidenced by micro-kinetic modelling. In general, selectivity and conversion should increase with pressure, which is also the case except for conversion on Mg, where a slight decrease with pressure is observed.
Micro-kinetics employs a mean-field approximation. Thus, it only deals with average values for surface coverage with each species. In reality, surface diffusion plays an important role and two reactants can only react if they are adsorbed on adjacent sites. In our case, this limitation is not particularly severe because catalysts can be considered covered with atomic hydrogen (evidenced also by kinetic Monte Carlo simulations), which is one reactant in all elementary reactions with two reactants. For decomposition reactions (e.g. H2COOH* → H2CO* + OH*), an empty site is needed in the vicinity of the adsorbed species. This is implicitly accounted for with treating all species with two oxygen atoms as bidentate. Such an assumption is well founded on DFT-obtained geometries (Fig. 4).
From kMC simulations, we see that selectivity towards methanol is favoured at low temperatures and high pressures, as expected from thermodynamics and experiments. kMC results compare favourably with those of micro-kinetic modelling, although they differ in some details. This is expected and cannot be avoided since the methods use different assumptions. kMC is not a mean-field approach but instead explicitly treats every active site on the catalytic surface. It is thus crucial to accurately describe adsorption and surface diffusion. Although we performed micro-kinetic modelling for a CSTR, which is the closest to the conditions in kMC, they are not the same. In current kMC implementation in Zacros, the gas composition above the catalyst is considered constant. Any side products that would possibly desorb (such as HCOOH or CH2O) can never re-adsorb due to their gaseous phase concentration being zero. To avoid this, desorption of stable side products (except for CO) has been switched off. Micro-kinetic modelling and experiments showed that this is a reasonable assumption.
kMC can also provide information on the relative frequency of particular elementary steps, which helps determine the dominant reaction pathway, which cannot be surmised from micro-kinetic modelling. As shown in Fig. 11, the relative frequencies span many orders of magnitude. Adsorption of CO2 and hydrogen surface diffusion were artificially slowed down as described in section 2.4. Therefore, only the selectivities are meaningful and we do not report the conversions. A productivity measure is the total number of CH3OH and CO molecules produced during the runtime of the simulation, which is reported for the same time for all catalysts.
From the relative frequencies, we see that the reaction pathway is slightly different on different catalysts. On Zn3O3/Cu, the following intermediates are formed: HCOO, H2COO, H2COOH, CH2O, CH2OH and CH3O. On Fe3O3/Cu and Cr3O3/Cu, CH2OH does not form. On Mg3O3/Cu, HCOOH is an important intermediate, as well. This is also the only catalyst where direct CO2 dissociation into CO and O occurs. In line with the generally low activity and selectivity of Fe3O3/Cu, we see that all reactions are less frequent on this catalyst. When comparing the catalysts with the best selectivity (Zn3O3/Cu and Cr3O3/Cu), we notice additional differences, such as CH2O (which is then further hydrogenated to methanol) being produced mainly from H2COOH on Zn3O3/Cu and from H2COO on Cr3O3/Cu.
The overall agreement between experimental results, micro-kinetic modelling and kinetic Monte Carlo simulations is remarkable. Exact reproduction of experimental data is currently out of scope even for state-of-the-art theoretical methods, but very good approximations can be achieved. It should be noted that this model is an approximation of the real conditions and cannot be expected to quantitatively recapture every experimental nuance. There is admittedly room for improvement. For instance, for CO and several other species multiple adsorption modes could be considered. As CO binds less strongly on Cu(111) far from the interface, this would increase its production and bring theoretical predictions even more in line with experimental measurements. However, such extensions are beyond the scope of this work.
Experimentally, conversion is the highest for Zn3O3/Cu, followed by Mg3O3/Cu, Fe3O3/Cu and Cr3O3/Cu (Fig. 2). This is exactly the same order as that obtained from microkinetics (Fig. 7). Selectivity is better for Mg3O3/Cu than for Zn3O3/Cu at moderate pressures. Again, microkinetics provides the same information. The same trend is also discovered by kMC simulations at moderate temperatures (up to 540 K). At higher temperatures, however, the trend is different as the selectivity on Mg3O3/Cu plummets. Similarly, pressure dependence trends show very good agreement.
5. Conclusions
Among several synthesised copper-based catalysts for CO2 hydrogenation to methanol, the four best performing ones were selected. Experimental testing across a wide range of temperatures and pressures was performed to determine and quantify their activity. A comprehensive reaction framework of all possible elementary steps was established. An atomistic model for each catalyst was constructed based on the characterisation data. All reactions were calculated from first-principles using each model. Results were used for micro-kinetic modelling and kinetic Monte Carlo simulations.Very good agreement between experimental measurements of catalytic activity and modelling data is a strong indication that the proposed model is correct. Remarkably, although absolutely no input from experimental data on catalytic activity was used for modelling, first-principles modelling very well described the temperature and pressure trends in selectivity and conversion. This agreement allows us to trust additional data that only theoretical methods could provide, such as coverage and relative reaction step frequency.
Several conclusions can be drawn from the presented data. First and foremost, the formate pathway has been irrefutably proved to account for the bulk of methanol production, both by DFT analysis alone and statistics from kMC simulations. It predominates on all copper-based catalysts regardless of the second metal. Secondly, the superiority of the Zn3O3/Cu catalyst has been proved experimentally and computationally. No other copper-based catalyst has been found to have better of similar performance. Thirdly, we have shown that micro-kinetic modelling and kMC simulations present an important complement to DFT results, as naïve interpretation and back-of-the-envelope estimations of the latter do not offer adequate insight into the reaction mechanism.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was made possible by funding from the EU Framework Programme for Research and Innovation Horizon 2020 under grant agreement No. 637016 (Project MefCO2) and the Slovenian Research Agency (ARRS) through Core Grant P2-0152.References
- C. Song, Catal. Today, 2006, 115, 2–32 CrossRef CAS.
- O. Martin and J. Pérez-Ramírez, Catal. Sci. Technol., 2013, 3, 3343 CAS.
- J. Toyir, P. Ramírez de la Piscina, J. L. G. Fierro and N. Homs, Appl. Catal., B, 2001, 34, 255–266 CrossRef CAS.
- C. A. Huff and M. S. Sanford, J. Am. Chem. Soc., 2011, 133, 18122–18125 CrossRef CAS PubMed.
- J. Graciani, K. Mudiyanselage, F. Xu, A. E. Baber, J. Evans, S. D. Senanayake, D. J. Stacchiola, P. Liu, J. Hrbek, J. F. Sanz and J. A. Rodriguez, Science, 2014, 345, 546–550 CrossRef CAS PubMed.
- I. Kasatkin, P. Kurr, B. Kniep, A. Trunschke and R. Schlögl, Angew. Chem., 2007, 119, 7465–7468 CrossRef.
- M. Kurtz, N. Bauer, C. Büscher, H. Wilmer, O. Hinrichsen, R. Becker, S. Rabe, K. Merz, M. Driess, R. A. Fischer and M. Muhler, Catal. Lett., 2004, 92, 49–52 CrossRef CAS.
- G. C. Chinchen, K. C. Waugh and D. A. Whan, Appl. Catal., 1986, 25, 101–107 CrossRef CAS.
- R. Burch, S. E. Golunski, M. S. Spencer, M. Bettahar, K. C. Waugh, K. C. Waugh and D. A. Whan, J. Chem. Soc., Faraday Trans., 1990, 86, 2683 RSC.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897 CrossRef CAS PubMed.
- M. Behrens, S. Zander, P. Kurr, N. Jacobsen, J. Senker, G. Koch, T. Ressler, R. W. Fischer and R. Schlögl, J. Am. Chem. Soc., 2013, 135, 6061–6068 CrossRef CAS PubMed.
- M. Huš, V. D. B. C. Dasireddy, N. Strah Štefančič and B. Likozar, Appl. Catal. B Environ., 2017, 207, 267–278 CrossRef.
- L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384 CrossRef CAS.
- F. Studt, F. Abild-Pedersen, J. B. Varley and J. K. Nørskov, Catal. Lett., 2013, 143, 71–73 CrossRef CAS.
- Y. Yang, J. Evans, J. A. Rodriguez, M. G. White, P. Liu, L. C. Grabow, J. A. Dumesic, M. Mavrikakis, I. Chorkendorff, P. Liu, J. F. Sanz and J. Hrbek, Phys. Chem. Chem. Phys., 2010, 12, 9909 RSC.
- S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299 CrossRef CAS PubMed.
- J. Nakamura, T. Fujitani, S. Kuld, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2017, 357 DOI:10.1126/science.aan8074.
- H. Nakatsuji and Z.-M. Hu, Int. J. Quantum Chem., 2000, 77, 341–349 CrossRef CAS.
- Y.-F. Zhao, Y. Yang, C. Mims, C. H. F. Peden, J. Li and D. Mei, J. Catal., 2011, 281, 199–211 CrossRef CAS.
- Q.-L. Tang, W.-T. Zou, R.-K. Huang, Q. Wang and X.-X. Duan, Phys. Chem. Chem. Phys., 2015, 17, 7317–7333 RSC.
- N. Ahmed, Y. Shibata, T. Taniguchi and Y. Izumi, J. Catal., 2011, 279, 123–135 CrossRef CAS.
- V. D. B. C. Dasireddy and B. Likozar, Fuel, 2017, 196, 325–335 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- A. Kokalj, J. Mol. Graphics Modell., 1998, 17, 176–179 CrossRef , 215–6.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- M. Vandichel, A. Moscu and H. Grönbeck, ACS Catal., 2017, 7431–7441 CrossRef CAS.
- S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974 CrossRef CAS PubMed.
- K. Reuter, in Modeling and Simulation of Heterogeneous Catalytic Reactions, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011, pp. 71–111 Search PubMed.
- M. Stamatakis and D. G. Vlachos, ACS Catal., 2012, 2, 2648–2663 CrossRef CAS.
- M. Stamatakis, J. Phys.: Condens. Matter, 2015, 27, 13001 CrossRef PubMed.
- M. Stamatakis and D. G. Vlachos, J. Chem. Phys., 2011, 134, 214115 CrossRef PubMed.
- J. Nielsen, M. d'Avezac, J. Hetherington and M. Stamatakis, J. Chem. Phys., 2013, 139, 224706 CrossRef PubMed.
- D. Kopač, M. Ogrizek, M. Huš and B. Likozar, Catal. Sci. Technol. DOI:10.1021/acs.jpcc.7b04985.
- H. Prats, L. Álvarez, F. Illas and R. Sayós, J. Catal., 2016, 333, 217–226 CrossRef CAS.
- G. C. Chinchen, K. C. Waugh and D. A. Whan, Appl. Catal., 1986, 25, 101–107 CrossRef CAS.
- M. Kurtz, N. Bauer, C. Büscher, H. Wilmer, O. Hinrichsen, R. Becker, S. Rabe, K. Merz, M. Driess, R. A. Fischer and M. Muhler, Catal. Lett., 2004, 92, 49–52 CrossRef CAS.
- J. Díez-Ramírez, F. Dorado, A. R. de la Osa, J. L. Valverde and P. Sánchez, Ind. Eng. Chem. Res., 2017, 56, 1979–1987 CrossRef.
- T. Phongamwong, U. Chantaprasertporn, T. Witoon, T. Numpilai, Y. Poo-arporn, W. Limphirat, W. Donphai, P. Dittanet, M. Chareonpanich and J. Limtrakul, Chem. Eng. J., 2017, 316, 692–703 CrossRef CAS.
- S. Xiao, Y. Zhang, P. Gao, L. Zhong, X. Li, Z. Zhang, H. Wang, W. Wei and Y. Sun, Catal. Today, 2017, 281, 327–336 CrossRef CAS.
- R. Sahki, O. Benlounes, O. Chérifi, R. Thouvenot, M. M. Bettahar and S. Hocine, React. Kinet., Mech. Catal., 2011, 103, 391–403 CrossRef CAS.
- S. Lowell, J. E. Shields, M. A. Thomas and M. Thommes, Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density, Springer Netherlands, 2004 Search PubMed.
- G. Leofanti, M. Padovan, G. Tozzola and B. Venturelli, Catal. Today, 1998, 41, 207–219 CrossRef CAS.
- A. M. Venezia, V. La Parola and L. F. Liotta, Catal. Today, 2017, 285, 114–124 CrossRef CAS.
- X.-K. Gu and W.-X. Li, J. Phys. Chem. C, 2010, 114, 21539–21547 CAS.
- P. Wu and B. Yang, ACS Catal., 2017, 7, 7187–7195 CrossRef CAS.
- I. Kasatkin, P. Kurr, B. Kniep, A. Trunschke and R. Schlögl, Angew. Chem., 2007, 119, 7465–7468 CrossRef.
- M. M. Günter, T. Ressler, B. Bems, C. Büscher, T. Genger, O. Hinrichsen, M. Muhler and R. Schlögl, Catal. Lett., 2001, 71, 37–44 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Animation with kMC results. See DOI: 10.1039/c7cy01659j |
| This journal is © The Royal Society of Chemistry 2017 |