Active colloids with collective mobility status and research opportunities
Jie
Zhang
a,
Erik
Luijten
 b,
Bartosz A.
Grzybowski
b,
Bartosz A.
Grzybowski
 c and
Steve
Granick
c and
Steve
Granick
 *c
*c
aDepartment of Materials Science and Engineering, University of Illinois, Urbana, IL 61801, USA
bDepartments of Materials Science and Engineering, Engineering Sciences and Applied Mathematics, and Physics and Astronomy, Northwestern University, Evanston, IL 60208, USA
cIBS Center for Soft and Living Matter and UNIST, Ulsan 689-798, South Korea. E-mail: sgranick@ibs.re.kr
First published on 1st August 2017
Abstract
The collective mobility of active matter (self-propelled objects that transduce energy into mechanical work to drive their motion, most commonly through fluids) constitutes a new frontier in science and achievable technology. This review surveys the current status of the research field, what kinds of new scientific problems can be tackled in the short term, and what long-term directions are envisioned. We focus on: (1) attempts to formulate design principles to tailor active particles; (2) attempts to design principles according to which active particles interact under circumstances where particle–particle interactions of traditional colloid science are augmented by a family of nonequilibrium effects discussed here; (3) attempts to design intended patterns of collective behavior and dynamic assembly; (4) speculative links to equilibrium thermodynamics. In each aspect, we assess achievements, limitations, and research opportunities.
Introduction
There is mounting interest in the emergence of collective mobility in systems of self-propelled objects that transduce energy into mechanical work to drive their motion, most commonly through fluids. Examples include motor proteins1 in biology, whose motion is driven by the consumption of ATP; synthetic particles including nanoparticles and colloids, whose motion is driven by chemical reactions at their interface;2 synthetic micro-robots whose rules of interaction with their neighbors are programmed;3 and collective structures in the living world of organisms, from the microscopic and macroscopic living world with examples from bacteria colonies4 to bird flocks5 and schools of fish,6 respectively. Without wishing to minimize the important differences between these examples, we express the hope that the collective behavior of all these systems, each of which presents nontrivial intellectual challenges, can be understood from simple physical principles with predictive generality. There is also hope for potential benefits to society when these new materials are applied cleverly in technological applications. Beyond fundamental questions of physics, chemistry and biology, active matter also presents numerous engineering opportunities, from the efficient delivery of drugs to the design of “living” materials with structures and functionalities that would be impossible to achieve in passive materials.7,8The rules of interaction can be relatively simple for colloids, which facilitates computer simulation (whereas the rules of law and order that govern the emergence of bacterial colonies, important as they are, would be enormously more difficult to affirm precisely). It has been argued, noting that the minimum size of living systems is micrometer-sized just as for colloidal particles, that similar physical rules may be fundamental to both of them.9 The rules of interaction possible in colloidal systems can also be extended to include some of the attributes of living systems. For example, considering that self-replication is an essential attribute of living systems, efforts are underway to “fertilize” the replication of colloids.10–12 Indeed, study of active colloidal matter is sometimes justified by the hope to understand some essential aspects of living matter in a testbed of components whose relevant variables can be controllably modulated, allowing their consequences to be explored systematically.
We focus on needs and opportunities in the following emerging areas:
• Designing active particles. We seek to articulate general design principles that may help to cross-fertilize a literature that is scattered among different research communities.
• Designing particle–particle interactions. We will refer to this as “communication”. The interactions of traditional colloid science (DLVO and hydrophobic interactions, for example)13 are augmented by a family of time-dependent nonequilibrium interactions.
• Towards designing collective structures. Colloid-sized particles, even when active, are small enough to display Brownian motion also. Accordingly, systems of such particles can explore more of phase space than when driven merely deterministically. How, in designing new structures, can one balance control and randomness to encourage “evolution” in desired directions? In the colloid world, structures and features can sometimes be selected, according to the dynamic rules of interaction, to produce states that are relatively stable, in the sense that their lifetime is long. What determines the lifetime of specific structures and dynamical patterns? What is the role of initial conditions? Is it useful to intervene in the spirit of a Maxwell's Demon14 to promote desired structures during the evolution process?
1. Designing active particles
This review is not concerned with planes and trains or other macroscopic vehicles as active particles because, though self-propelled, their motion is deterministic. More interesting and inevitable at the microscopic scale is to have active motion with stochasticity also present for each of the moving particles. Thus, the motion of active particles generally becomes random over long times and distances: this is so with most of the natural and artificial swimmers such as Janus colloids and bacteria, and even many animals in the wild,15 so active motion is relevant only over restricted times and distances, which for colloids/bacteria and animals would be drastically different.A burgeoning literature shows many ways to achieve self-propulsion. Examples include motion produced by the local gradient field of certain molecular species (e.g., hydrogen peroxide),2 the response to external magnetic,16 electric,17,18 light,19–22 thermal fields,23 and even ultrasound.24 Beyond the important differences between how to implement these different approaches, these mechanisms indeed share the feature that motion of colloidal-sized objects will retain elements of stochasticity. We choose to categorize particles according to three dimensions: shape/geometry, constituent material, and nature of the liquid medium in which they are suspended. The interplay of these dimensions produces many possibilities, some of them illustrated in Fig. 1. Later we will also discuss coupling with other particles.
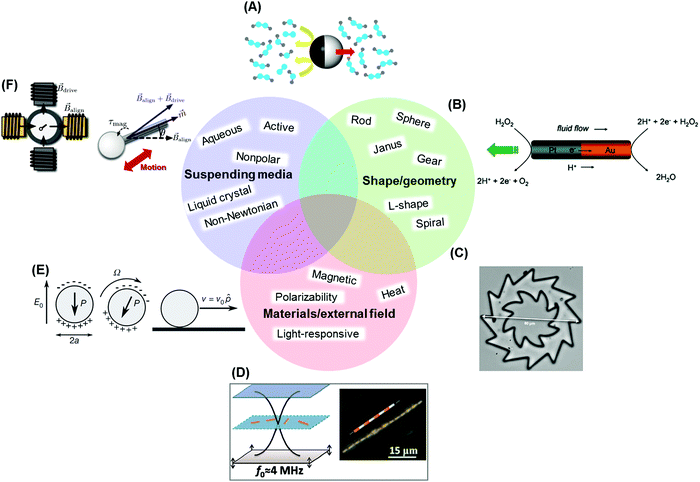 | ||
| Fig. 1 Illustrative designs of active particles. (A) Schematic illustration of a Janus swimmer fueled by partial catalysis of hydrogen peroxide. The black region denotes the catalytically active hemisphere. Hydrogen peroxide, water, and oxygen molecules are represented explicitly. The red arrow shows the direction of motion. Reproduced from ref. 33 with permission from Elsevier, copyright 2016. (B) Self-electrophoresis propulsion mechanism of a bimetallic nanorod. Reproduced from ref. 34, with permission from the American Chemical Society, copyright 2006. (C) Optical microscopy images of microfabricated gears suspended in water. The gear can be driven to rotate anti-clockwise rotation by an active bath of E. coli cells. Reproduced from ref. 35, with permission from the United States National Academy of Sciences, copyright 2010. (D) Metallic microrods are levitated to the nodal plane in an acoustic cell by ultrasonic standing waves (left), and assemble into spinning chains (right). Reproduced from ref. 24, with permission from the American Chemical Society, copyright 2012. (E) Schematic of the Quincke rotation mechanism for a colloidal roller with electric polarization P. Reproduced from ref. 29 with permission from Nature Publishing Group, copyright 2013. (F) Geometrically polar particle, a rod with a bead on one end (right panel), reciprocally rotated using magnetic fields. The configuration of the magnetic field is shown on the left. The particle is immersed in a wormlike micellar (WLM) solution susceptible to the formation of shear bands and other localized structures due to shear-induced reorganization of its microstructure. The nonlinearities present in this WLM solution break time-reversal symmetry under certain conditions, and enable propulsion provided the Deborah number is selected appropriately. Reproduced from ref. 36 with permission from AIP Publishing, copyright 2014. | ||
Present research status
Rod-shaped active particles are also studied frequently (Fig. 1B, D and F). Their shape encourages them to align, either without a preferred direction (known as nematic order), or with a distinct head and tail (known as polar order and analogous to ferromagnetic order of magnets).26 Polar order is observed in some bacteria, fish, and birds.27 To model this, the celebrated model of Vicsek, proposed in 1995, is based on the spin models commonly used to model phase transitions.28 Later, alignment interactions were also implemented experimentally even for spherical particles whose symmetry was broken in other ways, for example by the Quincke instability29 (Fig. 1E) or by electrostatic imbalance.18
Directed motion can also result from the interplay between particle shape and random mechanical agitation of the entire system. Examples include the action of ultrasound waves on elongated rod particles,24 surface waves on droplets,30 and specially designed granular walkers on a periodically agitated plate.31 Introducing chiral shapes to single particles can produce chiral or circular motion. For example, L-shaped swimmers, powered by catalytic action on one arm, swim in circles32 and gear-shaped objects, suspended in a uniform solution of bacteria, are induced to rotate in a preferred direction (Fig. 1C).
Without the need for catalytic chemical reactions, self-propulsion of Janus particles driven by an alternating current (AC) electric field relies on the differential polarizability of these particles, so that propulsion results from asymmetric flow of nearby aqueous ions.17 In principle, any particles with asymmetric response to an electric field can be propelled similarly: not only metal–dielectric Janus particles, but also dimers, provided that the two dielectric sides differ in composition, geometry, or surface charges.47 Metal–dielectric Janus particles also permit propulsion induced by a temperature gradient between the two hemispheres of the particles, a process known as self-thermophoresis.23 The absorption of defocused laser energy by the metal hemisphere generates a local temperature gradient that drives the particle motion towards either the colder or the warmer direction, depending on the solvent and the particles, with the mechanistic details under debate.48–50
Lastly, response to time-dependent magnetic fields can allow anisotropic particles to perform complex motions that would not be easily achieved in other ways. Examples include semi-flexible rods that respond like flagella,51 chiral rigid spirals that move forward while rotating,52 and Janus spheres in a precessing magnetic field that synchronize their motion.16 The last example proves that synchronization of low Reynolds number motion can result not only from the usual hydrodynamic coupling53,54 but also from magnetic response.
When particles diffuse in nematic and cholesteric liquid crystals, the anisotropic structure of these oriented fluids guides Brownian motion in preferred directions.56 Isotropic spheres can move in a specific direction when suspended in nematic liquid crystals and a direct current (DC) or even an AC electric field is applied. This is because the electric field, distorting the liquid crystal structure surrounding the particles, opens a path of least resistance for particle motion. When motile organisms such as bacteria are suspended within liquid crystals, their trajectories and collective behavior can also be significantly modified; they likewise move preferentially in paths of least resistance.57 Embedded in liquid crystals, molecular motors that perturb the local order in one spot can produce a cascade of reorientation far away. For example, a chiral molecular motor has been shown to drive the reorganization of macroscopic-sized liquid crystalline films, producing reversible color change.58
In allowing one to direct particle motility in a desired direction, viscoelastic media can be useful as well, as the frictional resistance depends on the shear rate. This holds not just for polymer solutions but also for biological media such as cell plasma and the extracellular matrix.59 In such media, propulsion can be achieved if the particle changes shape, even when these shape changes are reciprocal. For example, propulsion of a micro-scallop operated by a reciprocal but asymmetric actuation sequence has been realized in hyaluronic acid, a shear-thinning solution found in several biological systems, as well as in a suspension of fumed silica particles, a shear-thickening fluid with high viscosity.60 Another type of microswimmer, whose self-propulsion is achieved by a local concentration gradient of a critical polymer mixture under laser illumination, has been reported to have orientation-dependent anisotropic response to external forces in viscoelastic media.61
Future prospects
There is insufficient integration between the community of physical scientists who focus on active matter, and those chemical scientists whose expertise is to prepare colloids and nanoparticles with sophisticated shapes. The latter community is expert in producing, for example, designed aspect ratio,62 flat facets,63 interacting patches, and printed particles,32,64 so there is clear potential for synergy. Physical scientists tend to work with known materials, and this can even create a tendency for many of them to work with essentially the same type of particle (Janus particles, for example). Upon surveying the current literature, we note that there is a trend to use complex-shaped objects65 for the purpose of equilibrium self-assembly, but complex shapes also hold promise as a mechanism to produce particle motility by breaking geometric and chemical symmetry. Indeed, most of what is known so far about collective behavior in active matter concerns spheres and rod shapes26 only. To achieve better control of particle transport behavior, different types of propulsion mechanism may be designed orthogonally (to be independent of each other) though they act on the same batch of particles.66Too little is known about how particle behavior alters in response to changes in the surrounding environment. The simple Janus particle motif shows a rich variety of response depending on whether thin paramagnetic metallic coatings on one hemisphere are placed in magnetic, electric, or laser heating fields, because such fields are so effective in exploiting the differential magnetic susceptibility,16 polarizability,18,67,68 and heat absorbance23 of the two sides. When this principle is extended to more complex geometrical and chemical shapes, one can anticipate opportunities for multi-level control and coupling to achieve useful complex behavior. Particle behavior could also be optimized by programming experimental parameters, based on real-time information of the experimental system, toward specific goals.69,70
We suggest that another area of opportunity can involve more use of chemical design. It is reasonable to anticipate new research opportunities from field-induced chemical reactions and chemical feedback loops (reaction–diffusion systems). For example, there is potential for advances that make more use of electrochemistry: carbon particles can be polarized under an electric field to produce electrochemical reactions that deposit metal on one side.71 This approach can probably be generalized such that electrochemical reactions on other types of particle may be used to initiate propulsion if these reactions cause asymmetric chemical and fluid flows around the particle.
2. Designing particle–particle interactions (“Communication”)
When particles self-assemble at equilibrium, structures depend on energies of interaction that are well understood—electrostatic, van der Waals, hydrophobic, and so on.13,72 But active systems are governed by more complex particle interactions that also depend on time and history.13,67 End results are sensitive to the path taken, which offers new possibilities for design, especially involving feedback control of the system over spatial-temporal scales.72Present research status
For catalytic swimmers powered by self-electrophoresis, a chemical gradient surrounds each particle. When neighboring particles are sufficiently close to sense this gradient, the result is so-called “phoretic” attraction.21 It has been modeled analytically with predictions concerning the inverse-square dependence of radial velocity on separation confirmed by experiments (Fig. 2A).21
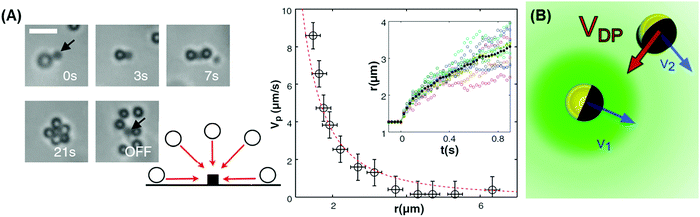 | ||
| Fig. 2 Examples of chemical communication between active colloids. (A) To characterize the chemical field, a hematite cube was immobilized on a surface and surrounded by colloidal tracers. Blue light was turned on at t = 0 s, triggering the decomposition of hydrogen peroxide on the hematite surface. Tracers were attracted to the hematite until physical contact. This attraction is isotropic with particles coming from all directions, excluding advective flow that must be divergence-free as an explanation. When the light is turned off, the attraction ceases and the tracers diffuse away. Radial velocity Vp extracted from the ensemble average of the tracer drift in the inset scales as r−2 (r is the separation), as expected for phoretic attraction to a reaction source. Reproduced from ref. 21 with permission from the American Association for the Advancement of Science, copyright 2013. (B) Schematic showing two self-propelled Janus particles moving with phoretic velocities v1 and v2, creating a surrounding density gradient that induces a diffusiophoretic motion of the particles toward each other with a drift velocity VDP ∝ ∇c, where c is the concentration of the solute. For simplicity, only the chemical gradient for the bottom particle is indicated. Reproduced from ref. 2 with permission from the American Physical Society, copyright 2012. | ||
Overlapping chemical fields around neighboring self-propelled particles cause coupling of the resulting influences on other particles that are poorly understood as, in general, chemical fields vary both spatially and temporally. Pioneering work by Keller and Segel rationalized the role of chemical sensing in pattern and cluster formation of bacteria based on a mean-field description that takes into consideration the diffusion of bacteria, chemicals, and the drift induced by chemical sensing.76 Bocquet and coworkers worked out a similar model to describe the clustering of active chemotactic colloids in which the solute concentration gradient around Janus particles induces a corresponding diffusiophoretic drift of other particles.2,77 More specifically, a Keller–Segel description can be used to describe the dynamics of a collection of 2D active particles in a global chemoattractant field with effective diffusion coefficients for the self-propelled particles and chemoattractant and a reaction rate that gives rise to self-propelled motion at the surface of each particle. This model predicts a critical number of particles above which aggregates would form, and the prediction was compared favorably with experiment.2 Recently, Brady and coworkers worked out a many-particle solute concentration field that allows dynamic simulation of the motion of many reactive Janus particles, and demonstrated exponentially screened long-ranged interactions.78 The self-propulsion of such chemically communicating particles contributes to collective behavior by allowing coexistence of dilute and dense regions, whereas uniformly reactive particles would only form loosely packed clusters without the coexistence of differential density regions.78
We emphasize now a spectacular example of experimental work on collective behavior of active colloids, in which hydrodynamic communications between particles are not only essential but can be expressed in a simple pairwise additive form. This is based on a notable phenomenon, discovered long ago by the German physicist Georg Quincke,86 that an insulating sphere suspended in an electrically conducting fluid rotates in response to sufficiently strong electric field. More than a century later, Bartolo and coworkers reported that so-called “Quincke rollers” align with each other as a result of competing electrostatic and hydrodynamic interactions29 and this could be described in detail mathematically. The hydrodynamic term in the effective interaction induces polar ordering while competing with rotational diffusion, leading to a transition from an isotropic state to a macroscopically ordered state that can be described even by a mean-field approach.29 It has been argued that the form of the effective interactions between these rollers is not specific and can be deduced from general considerations of global rotational invariance.29
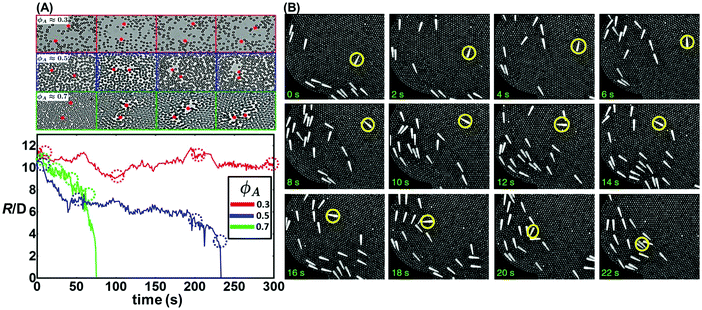 | ||
| Fig. 3 Long-range interactions mediated by intervening passive particles whose size is similar to the active particles. (A) Experimental snapshots of active magnetic spinners in passive media with area fractions ϕA = 0.3 (red), 0.5 (blue), and 0.7 (green), and corresponding particle trajectories. The bottom panel shows the particle distance with time at different packing fractions. Reproduced from ref. 88 with permission from the United States National Academy of Sciences, copyright 2016. (B) A monolayer of millimetre-sized tapered brass rods is suspended in a background of aluminium beads on a vibrating surface. Series of experimental images showing a polar rod brought into alignment with the rest of the flock as a consequence of bead flow. Reproduced from ref. 90 with permission from Nature Publishing Group, copyright 2014. | ||
Over even larger distances on the scale of millimetres, Ramaswamy and coworkers reported the transition from random arrangement to flocking of motile tapered rods in a medium of spherical beads, provided that the bead area fraction was sufficiently high (Fig. 3B).90 Note that this system is a dry granular system: the rods were rendered motile by vibrating the supporting surface, and they interacted through the medium of intervening spherical beads, which transmitted orientational information about the rods. In contrast to momentum transfer in the vertical direction governed by friction with the sample chamber, lateral transmission of momentum in the particle plane was dominated by an effective viscosity arising from tangential forces between the beads and rods, both with each other and with their own species. A simplified continuum theory treating the system as fluid could rationalize the flocking behavior, but did not explain why flocking occurred even at such high bead concentrations that the medium crystallized.90
Dynamic systems of Janus colloids in aqueous suspension that respond to magnetic and electric fields offer the opportunity to combine concepts of dynamic self-assembly and synchronization.16 Similar to the up-and-down bobbing (“nutation”) of a revolving gyroscope, micron-sized Janus particles thinly coated on one hemisphere with nickel can be made to rotate with a DC bias in a precessing magnetic field (Fig. 4A). With each particle retaining phase freedom, magnetic interactions with neighboring particles produce dynamical coupling and the possibility to synchronize. Sufficiently strong coupling between two such oscillators can lock them into synchronized motion with a well-defined phase difference (Fig. 4B). At this point their geometric centers rotate around a common central axis while each particle's rotation has slowed slightly. The physical origin of this synchronization is the spatially and time-dependent anisotropic magnetic dipolar interaction, with interesting consequences when even more such oscillators synchronize, described in a later section.
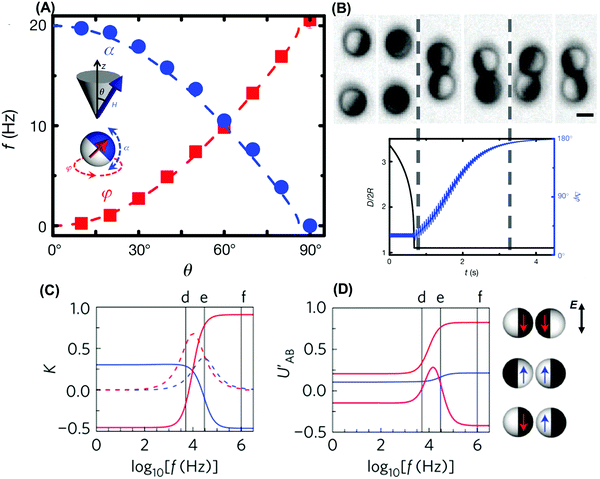 | ||
| Fig. 4 Electromagnetic dipolar interactions between Janus colloids. (A) The Janus director (red arrow) rotates around the precession axis z (angle φ) while oscillating perpendicularly (α), in a precessing field H with precession angle θ. The measured frequency is consistent with prediction (dashed line). Reproduced from ref. 16, with permission from Nature Publishing Group, copyright 2012. (B) Image sequence of two approaching particles at precession angle θ = 25°, corresponding to the distance D and phase difference Δφ also plotted versus time. Reproduced from ref. 16, with permission from Nature Publishing Group, copyright 2012. (C) Calculated real (solid) and imaginary (dashed) dipole coefficients K plotted against frequency f for dielectric (blue) and metallic (red) hemispheres. Reproduced from ref. 18, with permission from Nature Publishing Group, copyright 2016. (D) Calculated dipolar interaction UAB′ for different interacting pairs at contact as shown schematically on the right, normalized by the interaction between two metallic hemispheres at infinite frequency. Reproduced from ref. 18 with permission from Nature Publishing Group, copyright 2016. | ||
In systems where it is convenient to use electric fields, their use allows one to induce anisotropic interactions and propulsion when Janus particles are suspended in aqueous media. As AC fields induce differential charges on the two Janus sides, motility perpendicular to the applied field results with so-called induced-charge electrophoresis17 as the propulsion mechanism. The differential charges arising in this process on each side can be described with effective dipole moments displaced in position from the geometrical center of the sphere.18 These off-center interaction sites provide a rich design space for interactions between the particles as they are propelled by the electric field, producing torques that can change the orientations and trajectories of neighboring particles. As the dipoles on each hemisphere are, to first approximation, independent, various possibilities are offered by the permutations of repulsion between parallel dipoles and attraction between antiparallel dipoles, depending on whether the dominant interactions act on the forward moving or the trailing side of the particles. The magnitude of the dipoles, and thus the interactions between identical particles, then can be tuned by a single parameter, the frequency of the AC electric field. Fig. 4C and D illustrate a theoretical analysis that approximates the electrokinetic effects in the physical system via effective dipoles, each of them with real and imaginary dielectric response. The collective behavior resulting from such communication combined with dynamic effects will be discussed in a later section. Under certain circumstances, the situation may demand considering more complexity. For example, when particles are close enough, the dipole approximation may fail and interactions cease to be additive due to changes in particle charge.91
Future prospects
Not enough attention has been given yet to switching the rules of particle communication with time as collective structures develop. Potentially, this approach could be implemented using sequences of electric, magnetic, light, and even chemical fields (such as the Belousov–Zhabotinsky oscillating reaction),92 and reaction–diffusion processes,72 to program the elementary interactions. It is interesting that in the limit of rapid oscillations between the carefully chosen states, the resulting structures from dynamical interactions may be described by an effective averaged potential that may not be easily accessible by means of static interactions.93,94As one step towards implementing this concept, Sherman and Swan proposed the notion of “toggled interactions” to achieve temporal control of interactions between self-assembling components.95 Their simulations and theory show that time-dependent, periodically toggled attractions can avoid kinetic barriers, generating well-ordered crystalline domains in a dispersion of nanoparticles that interact via a short-ranged isotropic potential. The resulting state diagram differs from its equilibrium counterpart and includes the temporal pattern of the interactions applied (“toggling protocol”) as an important control parameter. This approach allows one to design rapidly assembling crystals with low defect density and even crystals that in equilibrium would be metastable.95 In the future, we expect more novel structures to be designed in this spirit. A natural extension will be to apply toggled communication sequences to active particles and their dynamic interactions. These predictions from theory and simulation remain to be tested experimentally.
Beyond binary toggled interactions, one can also oscillate properties that vary continuously. Simulations by Szleifer and coworkers analyzed what happens when colloid charge is regulated by oscillating pH in the aqueous medium.94 Modeling a binary mixture of particles coated with weak acids and weak bases (Fig. 5A and B), they compared the period of pH oscillation to the relevant diffusion time scale. When the pH oscillated more rapidly than the time over which particles diffuse over their own diameter, structures arose spontaneously from the effective time-averaged potential. Provocatively, oscillations at lower frequencies generated structures that at fixed pH would not form: dimers, fibers, and honeycombs (Fig. 5C).
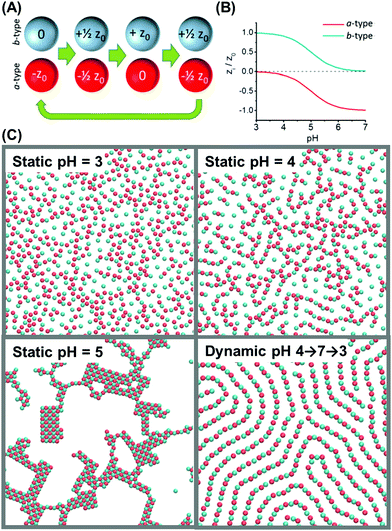 | ||
| Fig. 5 Dynamic self-assembly of particles in a pH-oscillating medium. (A) The model system is composed of equal numbers of a-type and b-type particles: a-type particles model pH-responsive negatively charged colloids with pKa = 5, with charge −z0 at pH = 7 and no charge at pH = 3; b-type particles model pH-responsive positively charged colloids with pKa = 5, with charge +z0 at pH = 3 and no charge at pH = 7. (B) Colloidal charge as a function of pH. (C) Snapshots of simulation results at different static and dynamic pH. Panels A–C are reproduced from ref. 94, with permission from the United States National Academy of Sciences, copyright 2014. | ||
In these simulations, the energy dissipation per oscillation cycle, which depended on the rate of the pH oscillation, was highest at the transition between order and disorder. This prediction from simulation is interesting, as the rate of energy dissipation has been proposed to be relevant to “nonequilibrium thermodynamics”,96 and it would be highly significant if the probability of nonequilibrium steady states generally correlates with their respective rates of energy dissipation. Looking to the future, to test this concept experimentally will be problematical, as it will not be easy to evaluate friction, ion flow, and excited-state chemical reactions, all of which enter the accounting of energy dissipation.
On the experimental side, optical control of colloids is in the midst of rapid development. Beyond providing a means to manipulate the local temperature gradient and colloid–solvent interactions to drive particle motion,97 optical techniques offer additional powerful control. In the past this method has been widely used to trap colloidal particles and study microscopic processes in biological systems, such as the unzipping of DNA and proteins.98 The potential has been demonstrated of multiple optical traps in the same suspension by using spatial light modulation technology.99,100 With this approach, one can produce optical forces that fluctuate both spatially and temporally, and we note the study by Di Leonardo and coworkers in which a dynamic speckle pattern was used to switch colloid transport from subdiffusive to superdiffusive.101 Dynamical optical traps have also been used to test fundamental issues of nonequilibrium thermodynamics.102 The practical ease of this technology, and the multiple uses to which it can be put, make it likely that research exploiting optical control of colloid–colloid interactions will advance in prominence.
Beyond these approaches based on using elementary physical interactions to produce collective behavior, there exists the contrasting approach in which communication rules are programmed deterministically. A pioneering study has created swarms of millimetre-sized robots just by programming the nearest-neighbor interactions into computer chips.3 It is intriguing as well as challenging to extend this concept to objects in fluid environments. It is not yet known how small the interacting agents can be.
3. Towards designing collective structures
From complete knowledge of how two individual particles interact, emergent behavior and collective properties may result when dealing with many particles: “More is different”, as P. W. Anderson wrote long ago,103 and the dangers of reductionism are worth keeping in mind. The discussion below considers first the matter of collective states, then dynamic self-assembly of active particles.Present research status (collective dynamic states)
A take-home message from a large body of work is that flocking structures first recognized in living systems do not necessarily require the intelligence or the instinctive decision-making of living organisms. Beyond examples of flocks and herds of organisms, patterns of collective behavior are likewise achieved when filaments of microtubules104 and actin organize under the action of molecular motors,105–107 when self-propelled colloids interact with appropriate rules of engagement,2,97 when granular matter is agitated suitably,90 and when rolling particles interact in fluids.29 The phenomenon of motility-induced phase separation is another spectacular phenomenon, first studied in bacterial collective motion and subsequently generalized to non-living active systems.108–111 In these systems of self-propelled hard (inert) spheres, activity induces coexistence between a high-density solid and a low-density fluid. The theoretical foundation for this is discussed below in a section about effective free energy.Active colloids show how to implement such ideas with model experiments outside the biological world. Quincke rotors (introduced above) are the first colloid system in which directional motion of a population was observed experimentally (Fig. 6A–D).29 The mechanism to adopt polar alignment was surmised to be dominated by short-range hydrodynamic interactions. Theoretical analysis confirmed that this sufficed, and a conventional Boltzmann-like kinetic–theory framework was used to derive the equations of motion that describe the macroscopic density and polarization fields. A mean-field phase transition from isotropic rest state to a macroscopically ordered swimming state resulted from competition between polar ordering and rotational diffusion, and this occurred when the particle concentration exceeded a critical volume fraction independent of the particle velocity, in good agreement with the experiment (Fig. 6E). The giant density fluctuation observed in other active systems was suppressed here,116 as a result of subtle experimental reasons (long-range hydrodynamic interaction). As a reductionist viewpoint based solely on considering alignment interactions would have missed this point, this sensitivity to system-specific parameters illustrates the potential pitfalls of over-generalizing based on assuming one has full knowledge of the relevant microscopic interactions. In a second colloid system, Janus particles powered by induced-charge electrophoresis, the motile particles repelled each other electrostatically at the forward-facing hemisphere18 and the resulting torque temporarily aligned neighboring pairs of particles, producing coherent swarms of particles when the particle concentration was sufficiently high. There is an interesting materials science twist to this problem. Because swarms nucleate randomly in different spatial locations, the swarms swim in random directions and can collide. Experiments show that vortices result.18
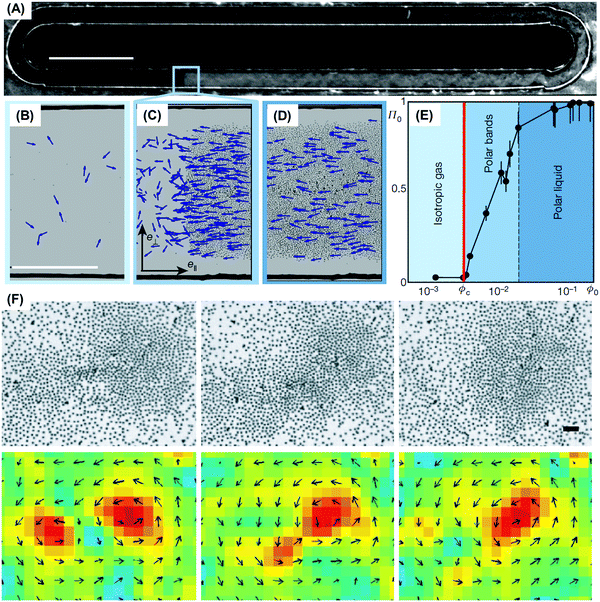 | ||
| Fig. 6 Flocking of active colloids. (A) Dark-field images of roller particles that spontaneously form a microscopic band propagating along the channel. Scale bar: 5 mm. (B–D) Enlarged view of (B) isotropic gas, (C) propagating band, and (D) homogeneous polar liquid. (E) Modulus of the average polarization plotted versus the area fraction. Panels A–E are reproduced from ref. 29, with permission from Nature Publishing Group, copyright 2013. (F) In an independent system, active Janus particles, each with a strong repulsive head, align to develop local polar order. Scale bar: 40 μm. Vortices with the same polarity merge. Reproduced from ref. 18, with permission from Nature Publishing Group, copyright 2016. | ||
Extending the concept to chain macromolecules, actin filaments with motion powered by myosin molecular motors, Bausch and coworkers found that alignment induced by binary collisions was too weak to account for the ordering transition from random order to polar nematic patterns.117 They studied how this depended on the concentration of actin and found that the density needed to form polar order decreased quadratically with filament length, indicating that multi-filament collisions drove the observed ordering phenomenon. This was interpreted to signify a significant contribution from non-additivity and to call into question the conditions of validity when using the Boltzmann equation to link the macroscopic behavior of self-propelled particles to the microscopic dynamics of its constituents. The intuitive assumption of simplified binary collisions is attractive in its theoretical simplicity, but probably should be investigated skeptically according to the system of interest, especially for systems involving active molecules that are polydisperse and flexible as was the case here.54,106 To explore these matters in additional experimental systems would be desirable.
It is noteworthy that all these experiments were performed in 2D or quasi-2D systems. Preliminary computational investigation of 3D behavior was included in the study just discussed,18 and a very recent experimental study showed that the third dimension is necessary for the transition of active microtubule gels from turbulent to coherent motion.118 More investigation of collective behavior in 3D systems by experiment and simulation would be desirable.
Possible scenarios become even richer, and even more dynamic states are predicted, when particle–particle interactions are anisotropic. A state diagram of self-organized dynamic states was computed, for active Janus particles interacting by electrostatic imbalance between the two hemispheres, using molecular dynamics simulations of particles in 2D.18 Regimes of gas, swarming, clustering, and chain formation were observed, as summarized in Fig. 7. Torques arising from electrostatic imbalance modulated the orientations of particles in proximity with consequences depending strongly on whether the particles were head-repulsive or tail-repulsive. Head-repulsive particles adopted the swarming state discussed in the previous section but tail-repulsive particles experienced torques tending to maximize distance between the tails of particles in proximity. This encouraged jammed clusters in which the resulting high local density in turn promoted further cluster growth.108,111 However, chains resulted from head-to-tail attraction of neighboring spheres when the two hemispheres possessed opposite dipoles or charges of similar magnitude, with the possibility to close into rings.18 The computed state diagrams were consistent with experiments in which most of states could be realized by controlling a single parameter, frequency of the applied AC electric field (Fig. 4C and D).
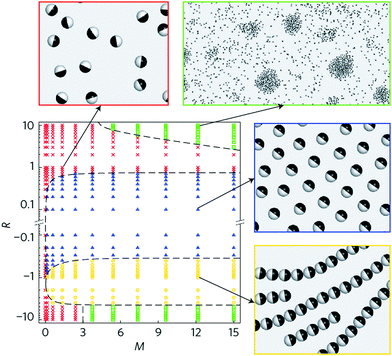 | ||
| Fig. 7 Dynamic state diagram from 2D simulations. R is the ratio of the dipole moment on the tail and head of the Janus particles. M is the dipolar repulsive force between two spheres at contact, normalized by the swimming force. In this 2D system, the dipoles are perpendicular to the sample plane, hence either parallel or antiparallel, and particles (head-to-head) with dipoles in parallel orientation repel. Red, green, blue, and yellow regions represent isotropic, clustering, swarming, and chain-forming states, respectively. Simulation snapshots for the four different phases are shown, with corresponding parameter choices (R, M) indicated by the arrows. Only the cluster state is sensitive to M, because the nucleation of small clusters requires local reorientation of multiple particles, a process possible only if particles are given enough time to reorient before they separate again. The timescale of reorientation is determined by the competition between interaction strength and particle motility, precisely what is quantified by M. Reproduced from ref. 18, with permission from Nature Publishing Group, copyright 2016. | ||
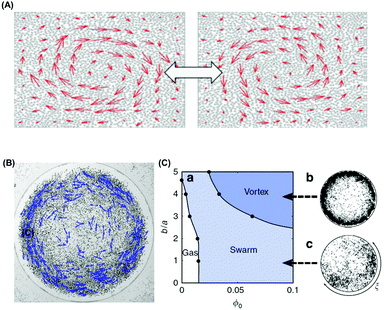 | ||
| Fig. 8 Active colloids that spontaneously form vortices. (A) Collective dynamic oscillation between clockwise and anti-clockwise vortices. Reproduced from ref. 124, with permission from the Royal Society of Chemistry, copyright 2017. (B) Snapshot of a vortex of Quincke rollers. The dark dots show the position of one half of the ensemble of rollers. The blue vectors represent their instantaneous speed. (C) The numerical phase diagram of the confined population is composed of three regions: isotropic gas, swarm coexisting with a gaseous phase, and the vortex state. The parameter b is the range of the repulsive forces normalized by particle radius a. Panels B–C are reproduced from ref. 82, with permission from Nature Publishing Group, copyright 2015. | ||
Present research status (dynamic self-assembly)
Whereas the examples in the previous section concerned collective motion, we now consider structure formation when moving objects self-assemble. Combining synchronization with dynamic self-assembly, colloidal Janus spheres were suspended in aqueous suspension under the influence of precessing magnetic fields.16 Individual particles in such a field revolve circularly with an extra velocity component normal to the circular motion, like a gyroscope. Collectively, they assembled into structures consisting of filamentous tubes in which synchronization of the constituent particles was key to understanding their stability (Fig. 9A and B). Simple dynamic criteria analogous to the tidal locking of the moon and earth were found to describe how their stability depended on the precession angle (Fig. 9C and D), as the rotation rate of the self-assembled tubes must be consistent with the allowed rotation rates of individual spheres within it.16 The filaments were normally achiral, but the use of a different type of Janus particles, with same nickel coating on paramagnetic spheres instead of non-magnetic silica spheres allowed one to form chiral filaments.16 This synchronization thus could be exploited to control collective behavior. For this scheme of self-assembly to work, each constituent particle must possess phase freedom to adapt to the presence of other particles when “communicating” with them.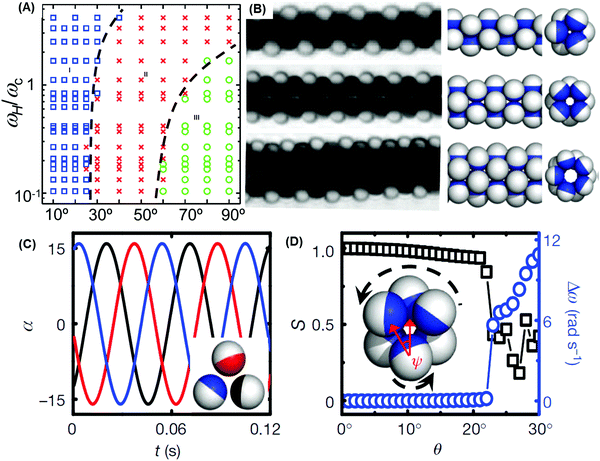 | ||
| Fig. 9 Synchronized assembly of filamentous microtubes of paramagnetic Janus particles. (A) Dynamic state diagram in the ωH−θ plane where ωH is the precession frequency and θ the precession angle. Blue, red, and green regions represent microtubes, zig-zag chains, and planar sheets, respectively. (B) Observed images (left) and corresponding models of microtubes parallel to the precession axis. (C) Illustration of phase locking of the oscillation angle for cross-sections of particles in a (330) microtube, simulated at θ = 18°. (D) Order parameter and difference in rotation frequency between constituent particle and microtube. (A–D) Are reproduced from ref. 16, with permission from Nature Publishing Group, copyright 2012. | ||
Cluster formation was the subject of a different study in which active and passive particles were mixed. In this aqueous suspension of Janus spheres mixed with a minority of silica beads, subjected to AC electric fields, clusters formed in one example because the Janus spheres were mutually repulsive but attracted to the passive silica spheres. The final structure depended on the sequence of steps in which the clusters formed (Fig. 10A) and could be selected to differ from what would have been the most favorable electrostatic configuration at equilibrium. Bifurcation between two possible rotating structures via simple tuning of experimental parameters was achieved, thus demonstrating a useful dependence on “processing” history.67 Process engineering comprises a huge aspect of materials technology but receives limited attention in the active matter community.
In a second example of finite cluster formation, interactions between Janus particles were tuned from repulsive to attractive; the result was that because the active particles tended to form chains, spirals with longer arms formed when the system's stoichiometry involved an excess of active particles.68 This produced filaments of active particles attached to passive particles and the resulting spiral clusters rotated like pinwheels. Asymmetric arm lengths were tolerated as all particle elements along each arm were self-propelled. The concept of VIP, “very important particles”, was introduced to express that chirality and stability of the active structures were most sensitive to the presence of only a few of the constituent particles. Small perturbations to the relative particle orientation within a given cluster, whether from random internal fluctuations or from interactions with nearby clusters, resulted in cascading conformational changes. It is noteworthy that the associations of each particle in a cluster were reversible. This allowed the system to achieve a steady state through an evolutionary process in which alternative structures were explored stochastically before finding the most stable structure consistent with the constraint of pinwheel rotation (Fig. 10B–D). Configurations for which the collective motion was most compatible with the motion of its constituent individual particles were “selected” by this biased “evolution”.68
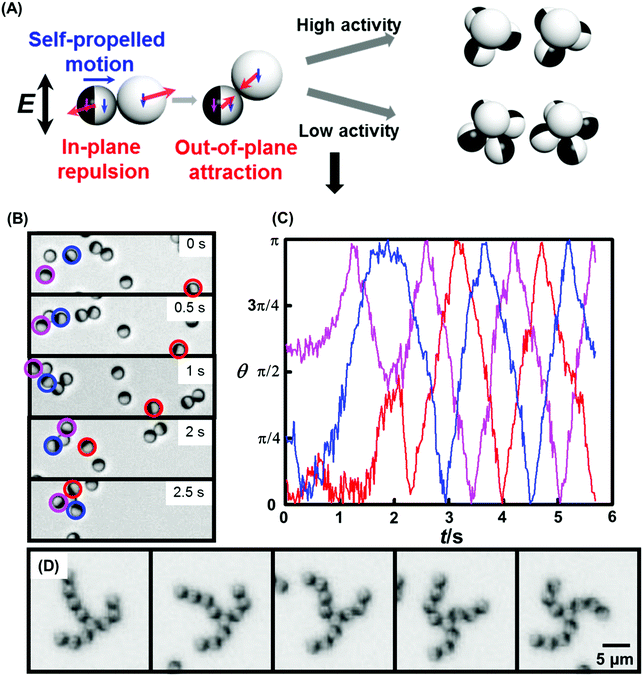 | ||
| Fig. 10 Dynamic assembly of chiral colloidal rotors. (A) One inert silica particle is lifted slightly from the bottom of the sample cell to allow attraction to either three or four active Janus particles, producing tetrahedral rotors (“low activity”) or square pyramidal rotors (“high activity”). Reproduced from ref. 67, with permission from Wiley-VCH, copyright 2016. (B) Time sequence of microscope images shows the simultaneous assembly and coordination of a three-armed pinwheel. Blue, red, and magenta circles indicate the identity of participating particles. (C) History of orientation for the three labeled particles in (B). Starting after about 2 s elapsed time, the three active particles coordinate their motion and have fixed orientation differences. Noise in these curves reflects jiggling of particle orientation. (D) Coordination process of a pinwheel with longer arms over two seconds. Panels B–D are reproduced from ref. 68, with permission from the Royal Society of Chemistry, copyright 2016. | ||
Future prospects
The active matter community began by trying to understand the physical origins of active structures in the living world (herds of animals,5 flocks of birds,125 schools of fish,27 swarms of insects,126 and even colonies of bacteria127), and extend them to create analogous structures using synthetic active matter.18,29,81,82 In times to come, increasing interest is likely to focus on understanding leadership,128 dissidence129 and the effect of obstacles.81 The notion of planning has been introduced: classical alignment interactions can give single particles the ability to anticipate the future orientation of their neighboring particles.130 As these trends continue, the interests of active matter scientists may come to overlap increasingly with those of social scientists. Fascinating spatial-temporal patterns, such as Turing patterns, form as a result of the coupling of reaction and diffusion of different chemical species in a system,131 and also provide inspiration for general non-equilibrium systems, including collective dynamics of active colloids.Regarding self-assembly in conjunction with active matter, selection criteria are not simply the outcome of static free energy minimization familiar from equilibrated systems, as they may compete with dynamic criteria. Too little is understood about this, as it is unclear conceptually what is minimized when ultimate structures are selected. To build a database of possibilities, experiments and simulations of additional systems are desirable, and one can hope to formulate the lifetime distribution of alternative configurational structures. In seeking predictive capabilities, it is likely that machine learning will prove to be useful, just as it is already useful in other areas of knowledge that in the present state of understanding must be guided by empirical approaches.132–136
4. Speculative links to equilibrium thermodynamics
It is especially pleasing when known ideas can be extended to describe non-equilibrium situations, as the paucity of general concepts capable of predicting new possibilities limits the development of any research field. The work by Vicsek28 inaugurated efforts that sought to understand far-from-equilibrium physical phenomena by what amounts to a perturbation analysis, making analogies to what is known regarding equilibrium systems. Moreover, experiments show that systems whose underlying motion stems from active mobility often can be modelled as random walks; there are numerous examples of this, from run-and-tumble bacteria to synthetic active particles, and even animals or human beings and their stock markets.137 While these systems display persistent motion over limited times and distances, stochasticity causes them to average over long times into diffusive states with the important exception of systems that can be glassy.138 From this point of view, one can motivate on physical grounds various attempts to link the transport behavior of active particles to that of passive Brownian particles, and hence to notions of statistical thermodynamics that are predicated on the existence of thermal energy. Here we introduce additional examples.Present research status
Cates and Tailleur showed that by coarse-graining microscopic dynamics, and with certain assumptions and integrability conditions, one may view an active particle as an isothermal passive Brownian particle with an effective potential emerging purely from activity, with no actual force field acting on the particle. From this point of view, a system of active particles is equivalent to a fluid of passive Brownian particles described by an effective free-energy functional.108 However, in active matter, violations of detailed balance are necessarily present microscopically. Mapping onto an equivalent equilibrium system is possible only when the violations of detailed balance disappear upon coarse-graining.
Even when this condition of integrability is not satisfied, a local functional dependence of the motility on particle density may hold and so may the notion of an effective potential as well as a mapping onto equilibrium conditions.140 This argument predicts a phase separation of the active system, in the case of no specific interactions between particles, into dense and dilute fluid phases. An alternative argument for this surprising conclusion is that by breaking the usual detailed balance of equilibrium thermodynamics, self-propelled particles tend to accumulate in spatial positions where they move most slowly.108 Physical reasons for slowdown at high density can be many, from steric97 to biochemical,141 so the conclusion does not appear to depend on details of the mechanism.
The notion of effective temperature can also be motivated from distinctively different arguments. Another perspective comes from Poon and coworkers, who considered how “depletion forces” promote phase separation of active bacteria by adding non-absorbing polymers to the suspension.145 In the “depletion interaction” of equilibrium colloid science, attraction between colloidal particles is induced by adding to the suspension non-adsorbing polymer or additional smaller colloids; the entropic attraction resulting from minimization of excluded volume can lead to phase separation of the larger colloids.146 This physical picture changed drastically when motile bacteria were used instead of colloids. To reach the point of phase separation, stronger interparticle attraction was required than at equilibrium; the active system suppressed phase separation even though the actual interparticle potential was believed to be nearly the same. One approach to interpret these experiments was the postulation of an “active” force that partly balances the attractive force, which would imply an effective potential that is shallower and has slightly shorter range than the actual equilibrium potential. In an alternative interpretation, there is an elevated effective temperature, in this case Teff ≈ 3T, and the interparticle potential is unchanged. This is much below the estimate of 104 K implied by the argument of the previous paragraph in which enhanced diffusivity is attributed to effective temperature through the Einstein relation. Considering the entropic origin of the equilibrium depletion effect,146 these interpretations of effective temperature appear to take into account the influence of activity on system entropy.
A third approach is not to seek to replace the thermal temperature with a different “temperature” but instead look for an equivalent quantity, not necessarily with the same physical units. This approach was taken in a study that used a combination of experiment and simulation to examine a quasi-2D system of Janus colloids whose mobility was driven by AC induced-charge electrophoresis under conditions where the swimmers were restricted to orbit in circles, clockwise or anticlockwise, driven by a superposed 2D rotating magnetic field.66 In-phase particles never collided, whereas those orbiting out of phase had the opportunity to collide with one another. In this system, collisions resulting from the external energy sources play the role of temperature. Statistical analysis of the computer and laboratory experiments showed quantitative agreement with hallmarks of statistical thermodynamics for binary phase behavior, including the archetypal phase diagram with equilibrium critical exponents, Gaussian displacement distributions, and capillarity.66 This quantitative agreement with equilibrium expectations from statistical thermodynamics, observed in this decidedly non-equilibrium system, appear to constitute the only such example at the time that this review was written. The observed agreement with equilibrium anticipations is believed to originate in the fact that external energy input was applied to all particles equally. But despite the pleasing predictive capabilities of this effective temperature concept and its speculative potential to describe other systems that would likewise perform 3D periodic motion where collisions are statistically significant, the concept of a single effective temperature is useful in describing only one-phase situations and the approach to phase separation.66
In a loosely confined, vertically vibrated, dry granular gas, quasi-2D gas–liquid spinodal decomposition reminiscent of a regular liquid was observed.147 This was explained as reflecting negative compressibility in the homogeneous system, resulting from excess kinetic energy of the dilute phase due to resonant motion of the particles. The explanation may seem exotic, but the dynamics of this phase separation indicated that the characteristic length scale grew with time to the power 1/3, compatible with a standard scenario described by the Cahn–Hillard theory. Behavior consistent with Laplace's equation was also found, likewise suggesting existence of a surface tension. The surface tension calculated from Laplace's equation and the pressure tensor showed good agreement, both giving a value around 10−3 N m−1, and the phenomenon was further confirmed to arise mainly from anisotropy in the kinetic part of the pressure tensor.147
Possibly counterintuitively, negative interfacial tension has been inferred in simulations of active matter.148 The negative sign was inferred from the excess mechanical stress, whereas the stiffness governing interfacial fluctuations was positive. Pressure was found to have two contributions: a tensor from physical interactions, and a scalar from active motion.149 Active pressure was highest in the dilute region but dropped considerably in the dense region, for intuitive physical reasons, as the particle motion was most hindered in the dense phase so that orientation and actual displacement were least correlated. The finding of negative mechanical interfacial tension for phase-separated active Brownian particles implies that energy is released when the interfacial length increases. However, this should not be taken literally, as this “negative work” is not available to the system, but is part of the work that is done by the particles to drive the surrounding fluid.148 If one accepts the validity of this interpretation of the simulations, it appears problematic to imagine combining a negative surface tension and proper interfacial fluctuations into descriptions based on an effective free energy. In thermal equilibrium, the same free-energy functional determines the probability of all fluctuations, but this seems less likely to hold for systems away from thermal equilibrium.
Future prospects
As one of the principal parameters of equilibrium thermodynamics, temperature measures randomly fluctuating degrees of freedom of all constituent particles that give rise to the thermal energy which agitates and tends to organize equilibrium matter. To date, several definitions of effective temperature out-of-equilibrium have been advanced, but speculatively. This provides motivation to do better. Among the examples presented above, the third example notably looks for an equivalent quantity to temperature, not necessarily with the same units as thermal temperature, which nonetheless plays a comparable role. This we consider to be a promising path to follow in seeking to evaluate the usefulness of the effective temperature concept in other out-of-equilibrium systems. Lastly, we note that the possibilities of inhomogeneous “effective temperature”, especially gradients, have been explored to only a limited extent. High- and low-temperature regions eventually equilibrate toward the same in equilibrium systems but not necessarily in nonequilibrium systems.665. Perspective and outlook
It is the objective of this review to present a snapshot in time of this field. “Active matter”, sometimes interpreted as “living materials”, constitutes a rapidly growing field of fundamental study that it is reasonable to hope may find applications of practical use.7,8 In the foregoing, we have outlined:• Why we believe that microscopic understanding of collective mobility of active matter constitutes a new frontier in science and achievable technology.
• Beyond the current status of the field, what kinds of new scientific problems can be tackled in the short term, and what long-term directions are envisioned.
• Why this field's scientific potential cannot be fully met by working within just a single discipline but requires the interdisciplinary collaboration of physicists, chemists, biologists, and engineers.
This review emphasizes experiment, but we note that the vivid contrast of these out-of-equilibrium systems with better-understood thermal systems likewise excites the imagination of theorists. The conceptual toolbox to describe it is in a period of rapid development based on theory and simulation,26,108 the difficulty being that these systems do not evolve from state to state governed by minimization of their free energy, as in the case of equilibrium statistical mechanics. Regarding experiment, this review emphasizes colloidal-sized particles suspended in liquid, while mentioning dry granular systems with relevant problems.
This type of system, potentially useful for engineering,7,8 also offers the immense simplification that it can be studied with relative ease in the laboratory. Active colloidal particles meet key criteria that matter to experimentalists. First, they can be sufficiently large (a few hundreds of nm to a few μm) to be observed using light microscopy in situ with high spatial and temporal resolution for long times. Second, they can be sufficiently small to be biased by random thermal energy, while concurrently active motility also operates. Third, they can be designed and produced in large numbers, monodisperse in size, shape, and chemical functionality, allowing direct observation of how individual particle motility scales up to bulk behavior while also permitting control of the particle–particle interactions through variation of the functionality. Opportunities involving active nanoparticles present another obvious exciting candidate for analysis, but binary additive interactions are less likely in those systems as the typical range of particle–particle interactions is comparable to the particle size. This review therefore does not discuss active nanoparticles.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank taxpayers who supported this work through the Korean IBS (Institute for Basic Science), project code IBS-R020-D1, and through the US National Science Foundation, award no. DMR-1610796.References
- M. Schliwa and G. Woehlke, Nature, 2003, 422, 759–765 CrossRef CAS PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- M. Rubenstein, A. Cornejo and R. Nagpal, Science, 2014, 345, 795–799 CrossRef CAS PubMed.
- A. Sokolov and I. S. Aranson, Phys. Rev. Lett., 2012, 109, 248109 CrossRef PubMed.
- M. Ballerini, N. Calbibbo, R. Candeleir, A. Cavagna, E. Cisbani, I. Giardina, V. Lecomte, A. Orlandi, G. Parisi, A. Procaccini, M. Viale and V. Zdravkovic, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1232–1237 CrossRef CAS PubMed.
- U. Lopez, J. Gautrais, I. D. Couzin and G. Theraulaz, Interface Focus, 2012, 2, 693–707 CrossRef PubMed.
- J. Li, P. Angsantikul, W. Liu, B. E. de Ávila, S. Thamphiwatana, M. Xu, E. Sandraz, X. Wang, J. Delezuk, W. Gao, L. Zhang and J. Wang, Angew. Chem., Int. Ed., 2017, 56, 2156–2161 CrossRef CAS PubMed.
- J. Orozco, D. Vilela, G. Valdes-Ramirez, Y. Fedorak, A. Escarpa, R. Vazquez-Duhalt and J. Wang, Chem. – Eur. J., 2014, 20, 2866–2871 CrossRef CAS PubMed.
- W. C. K. Poon, Proc. Int. Sch. Phys. “Enrico Fermi”, 2013, 184, 317–386 CAS.
- H. Tanaka, Z. Zeravcic and M. P. Brenner, Phys. Rev. Lett., 2016, 117, 238004 CrossRef PubMed.
- Z. Zeravcic and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1748–1753 CrossRef CAS PubMed.
- M. E. Leunissen, R. Dreyfus, R. J. Sha, T. Wang, N. C. Seeman, D. J. Pine and P. M. Chaikin, Soft Matter, 2009, 5, 2422–2430 RSC.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 3rd edn, 2011 Search PubMed.
- C. G. Knott, Quote from undated letter from Maxwell to Tait, Cambridge University Press, 1911 Search PubMed.
- F. Bartumeus, M. G. E. Da Luz, G. M. Viswanathan and J. Catalan, Ecology, 2005, 86, 3078–3087 CrossRef.
- J. Yan, M. Bloom, S. C. Bae, E. Luijten and S. Granick, Nature, 2012, 491, 578–582 CrossRef CAS PubMed.
- S. Gangwal, O. J. Cayre, M. Z. Bazant and O. D. Velev, Phys. Rev. Lett., 2008, 100, 058302 CrossRef PubMed.
- J. Yan, M. Han, J. Zhang, C. Xu, E. Luijten and S. Granick, Nat. Mater., 2016, 15, 1095–1100 CrossRef CAS PubMed.
- J. Stenhammar, R. Wittkowski, D. Marenduzzo and M. E. Cates, Sci. Adv., 2016, 2, e1501850 Search PubMed.
- J. Palacci, S. Sacanna, S. H. Kim, G. R. Yi, D. J. Pine and P. M. Chaikin, Philos. Trans. R. Soc., A, 2014, 372, 20130372 CrossRef PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS PubMed.
- I. Buttinoni, G. Volpe, F. Kummel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- H. R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed.
- W. Wang, L. A. Castro, M. Hoyos and T. E. Mallouk, ACS Nano, 2012, 6, 6122–6132 CrossRef CAS PubMed.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143 CrossRef CAS.
- S. V. Viscido, J. K. Parrish and D. Grunbaum, Mar. Ecol.: Prog. Ser., 2004, 273, 239–249 CrossRef.
- T. Vicsek, A. Czirok, E. Benjacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226–1229 CrossRef CAS PubMed.
- A. Bricard, J. B. Caussin, N. Desreumaux, O. Dauchot and D. Bartolo, Nature, 2013, 503, 95–98 CrossRef CAS PubMed.
- H. Ebata and M. Sano, Sci. Rep., 2015, 5, 8546 CrossRef CAS PubMed.
- N. Koumakis, A. Gnoli, C. Maggi, A. Puglisi and R. Di Leonardo, New J. Phys., 2016, 18, 113046 CrossRef.
- F. Kummel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
- S. J. Ebbens, Curr. Opin. Colloid Interface Sci., 2016, 21, 14–23 CrossRef CAS.
- W. F. Paxton, P. T. Baker, T. R. Kline, Y. Wang, T. E. Mallouk and A. Sen, J. Am. Chem. Soc., 2006, 128, 14881–14888 CrossRef CAS PubMed.
- R. Di Leonardo, L. Angelani, D. Dell'Arciprete, G. Ruocco, V. Iebba, S. Schippa, M. P. Conte, F. Mecarini, F. De Angelis and E. Di Fabrizio, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9541–9545 CrossRef CAS PubMed.
- D. A. Gagnon, N. C. Keim, X. N. Shen and P. E. Arratia, Phys. Fluids, 2014, 26, 103101 CrossRef.
- M. J. Xuan, J. X. Shao, X. K. Lin, L. R. Dai and Q. He, ChemPhysChem, 2014, 15, 2255–2260 CrossRef CAS PubMed.
- W. Gao, M. D'Agostino, V. Garcia-Gradilla, J. Orozco and J. Wang, Small, 2013, 9, 467–471 CrossRef CAS PubMed.
- R. F. Dong, Q. L. Zhang, W. Gao, A. Pei and B. Y. Ren, ACS Nano, 2016, 10, 839–844 CrossRef CAS PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- H. Ke, S. R. Ye, R. L. Carroll and K. Showalter, J. Phys. Chem. A, 2010, 114, 5462–5467 CrossRef CAS PubMed.
- L. F. Valadares, Y. G. Tao, N. S. Zacharia, V. Kitaev, F. Galembeck, R. Kapral and G. A. Ozin, Small, 2010, 6, 565–572 CrossRef CAS PubMed.
- Y. J. Wu, Z. G. Wu, X. K. Lin, Q. He and J. B. Li, ACS Nano, 2012, 6, 10910–10916 CrossRef CAS PubMed.
- W. Gao, S. Sattayasamitsathit, J. Orozco and J. Wang, J. Am. Chem. Soc., 2011, 133, 11862–11864 CrossRef CAS PubMed.
- M. Manjare, B. Yang and Y. P. Zhao, Phys. Rev. Lett., 2012, 109, 128305 CrossRef PubMed.
- S. J. Wang and N. Wu, Langmuir, 2014, 30, 3477–3486 CrossRef CAS PubMed.
- F. D. Ma, X. F. Yang, H. Zhao and N. Wu, Phys. Rev. Lett., 2015, 115, 208302 CrossRef PubMed.
- S. Duhr and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19678–19682 CrossRef CAS PubMed.
- P. Naumann, N. Becker, S. Datta, T. Sottmann and S. Wiegand, J. Phys. Chem. B, 2013, 117, 5614–5622 CrossRef CAS PubMed.
- A. L. Sehnem, A. M. F. Neto, R. Aquino, A. F. C. Campos, F. A. Tourinho and J. Depeyrot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042311 CrossRef CAS PubMed.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS PubMed.
- W. Gao, X. M. Peng, A. Pei, C. R. Kane, R. Tam, C. Hennessy and J. Wang, Nano Lett., 2014, 14, 305–310 CrossRef CAS PubMed.
- J. Kotar, L. Debono, N. Bruot, S. Box, D. Phillips, S. Simpson, S. Hanna and P. Cicuta, Phys. Rev. Lett., 2013, 111, 228103 CrossRef PubMed.
- V. Schaller, C. Weber, E. Frey and A. R. Bausch, Soft Matter, 2011, 7, 3213–3218 RSC.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- O. D. Lavrentovich, Curr. Opin. Colloid Interface Sci., 2016, 21, 97–109 CrossRef CAS.
- S. Zhou, A. Sokolov, O. D. Lavrentovich and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1265–1270 CrossRef CAS PubMed.
- R. Eelkema, M. M. Pollard, J. Vicario, N. Katsonis, B. S. Ramon, C. W. M. Bastiaansen, D. J. Broer and B. L. Feringa, Nature, 2006, 440, 163 CrossRef CAS PubMed.
- A. E. Patteson, A. Gopinath and P. E. Arratia, Curr. Opin. Colloid Interface Sci., 2016, 21, 86–96 CrossRef CAS.
- T. Qiu, T. C. Lee, A. G. Mark, K. I. Morozov, R. Munster, O. Mierka, S. Turek, A. M. Leshansky and P. Fischer, Nat. Commun., 2014, 5, 5119 CrossRef CAS PubMed.
- J. R. Gomez-Solano, A. Blokhuis and C. Bechinger, Phys. Rev. Lett., 2016, 116, 138301 CrossRef PubMed.
- V. R. Dugyala, S. V. Daware and M. G. Basavaraj, Soft Matter, 2013, 9, 6711–6725 RSC.
- M. Sindoro, N. Yanai, A. Y. Jee and S. Granick, Acc. Chem. Res., 2014, 47, 459–469 CrossRef CAS PubMed.
- A. Sokolov, M. M. Apodaca, B. A. Grzybowski and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 969–974 CrossRef CAS PubMed.
- D. W. Sinkovits and E. Luijten, Nano Lett., 2012, 12, 1743–1748 CrossRef CAS PubMed.
- M. Han, J. Yan, S. Granick and E. Luijten, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7513–7518 CrossRef CAS PubMed.
- J. Zhang, J. Yan and S. Granick, Angew. Chem., Int. Ed., 2016, 55, 5166–5169 CrossRef CAS PubMed.
- J. Zhang and S. Granick, Faraday Discuss., 2016, 191, 35–46 RSC.
- T. Mano, J. B. Delfau, J. Iwasawa and M. Sano, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E2580–E2589 CrossRef CAS PubMed.
- F. D. Ma, S. J. Wang, D. T. Wu and N. Wu, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6307–6312 CrossRef CAS PubMed.
- G. Loget, J. Roche and A. Kuhn, Adv. Mater., 2012, 24, 5111–5116 CrossRef CAS PubMed.
- I. R. Epstein and B. Xu, Nat. Nanotechnol., 2016, 11, 312–319 CrossRef CAS PubMed.
- A. Baskaran and M. C. Marchetti, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15567–15572 CrossRef CAS PubMed.
- M. E. Taga and B. L. Bassler, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 14549–14554 CrossRef CAS PubMed.
- D. Kagan, P. Calvo-Marzal, S. Balasubramanian, S. Sattayasamitsathit, K. M. Manesh, G. U. Flechsig and J. Wang, J. Am. Chem. Soc., 2009, 131, 12082–12083 CrossRef CAS PubMed.
- E. F. Keller and L. A. Segel, J. Theor. Biol., 1970, 26, 399–415 CrossRef CAS PubMed.
- R. Golestanian, Phys. Rev. Lett., 2012, 108, 038303 CrossRef PubMed.
- W. Yan and J. F. Brady, J. Chem. Phys., 2016, 145, 134902 Search PubMed.
- E. Bertin, M. Droz and G. Gregoire, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 022101 CrossRef PubMed.
- I. Shani, T. Beatus, R. H. Bar-Ziv and T. Tlusty, Nat. Phys., 2014, 10, 140–144 CrossRef CAS.
- A. Morin, N. Desreumaux, J.-B. Caussin and D. Bartolo, Nat. Phys., 2017, 13, 63–68 CrossRef CAS.
- A. Bricard, J. B. Caussin, D. Das, C. Savoie, V. Chikkadi, K. Shitara, O. Chepizhko, F. Peruani, D. Saintillan and D. Bartolo, Nat. Commun., 2015, 6, 7470 CrossRef CAS PubMed.
- L. L. Zhu, E. Lauga and L. Brandt, Phys. Fluids, 2012, 24, 051902 CrossRef.
- O. S. Pak, L. L. Zhu, L. Brandt and E. Lauga, Phys. Fluids, 2012, 24, 103102 CrossRef.
- A. Boymelgreen, G. Yossifon and T. Miloh, Langmuir, 2016, 32, 9540–9547 CrossRef CAS PubMed.
- G. Quincke, Ann. Phys., 1896, 295, 417–486 CrossRef.
- M. Tasinkevych and D. Andrienko, Condens. Matter Phys., 2010, 13, 33603 CrossRef.
- J. P. Steimel, J. L. Aragones, H. L. Hu, N. Qureshi and A. Alexander-Katz, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4652–4657 CrossRef CAS PubMed.
- J. Dzubiella, H. Löwen and C. N. Likos, Phys. Rev. Lett., 2003, 91, 248301 CrossRef CAS PubMed.
- N. Kumar, H. Soni, S. Ramaswamy and A. K. Sood, Nat. Commun., 2014, 5, 4688 CrossRef CAS PubMed.
- C. A. S. Batista, R. G. Larson and N. A. Kotov, Science, 2015, 350, 1242477 CrossRef PubMed.
- H. Kitahata, N. Yoshinaga, K. H. Nagai and Y. Sumino, Chem. Lett., 2012, 41, 1052–1054 CrossRef CAS.
- M. Tagliazucchi and I. Szleifer, Faraday Discuss., 2016, 186, 399–418 RSC.
- M. Tagliazucchi, E. A. Weiss and I. Szleifer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9751–9756 CrossRef CAS PubMed.
- Z. M. Sherman and J. W. Swan, ACS Nano, 2016, 10, 5260–5271 CrossRef CAS PubMed.
- I. Prigogine, Phys.-Usp., 1980, 131, 185–207 CAS.
- I. Buttinoni, J. Bialke, F. Kummel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- U. Bockelmann, P. Thomen, B. Essevaz-Roulet, V. Viasnoff and F. Heslot, Biophys. J., 2002, 82, 1537–1553 CrossRef CAS PubMed.
- D. Kumar, S. Ghosh and S. Bhattacharya, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 013202 CrossRef PubMed.
- D. G. Grier, Nature, 2003, 424, 810–816 CrossRef CAS PubMed.
- S. Bianchi, R. Pruner, G. Vizsnyiczai, C. Maggi and R. Di Leonardo, Sci. Rep., 2016, 6, 27681 CrossRef CAS PubMed.
- D. Y. Lee, C. Kwon and H. K. Pak, Phys. Rev. Lett., 2015, 114, 060603 CrossRef PubMed.
- P. W. Anderson, Science, 1972, 177, 393–396 CAS.
- T. Sanchez, D. T. N. Chen, S. J. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- V. Schaller, C. A. Weber, B. Hammerich, E. Frey and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 19183–19188 CrossRef CAS PubMed.
- S. Kohler, V. Schaller and A. R. Bausch, Nat. Mater., 2011, 10, 462–468 CrossRef PubMed.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- R. Wittkowski, A. Tiribocchi, J. Stenhammar, R. J. Allen, D. Marenduzzo and M. E. Cates, Nat. Commun., 2014, 5, 4351 CAS.
- J. Stenhammar, D. Marenduzzo, R. J. Allen and M. E. Cates, Soft Matter, 2014, 10, 1489–1499 RSC.
- J. Stenhammar, A. Tiribocchi, R. J. Allen, D. Marenduzzo and M. E. Cates, Phys. Rev. Lett., 2013, 111, 145702 CrossRef PubMed.
- G. Gregoire and H. Chate, Phys. Rev. Lett., 2004, 92, 025702 CrossRef PubMed.
- A. P. Solon, H. Chate and J. Tailleur, Phys. Rev. Lett., 2015, 114, 068101 CrossRef PubMed.
- H. Chate, F. Ginelli, G. Gregoire, F. Peruani and F. Raynaud, Eur. Phys. J. B, 2008, 64, 451–456 CrossRef CAS.
- A. P. Solon and J. Tailleur, Phys. Rev. Lett., 2013, 111, 078101 CrossRef CAS PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS PubMed.
- R. Suzuki, C. A. Weber, E. Frey and A. R. Bausch, Nat. Phys., 2015, 11, 839–844 CrossRef CAS PubMed.
- K. T. Wu, J. B. Hishamunda, D. T. N. Chen, S. J. DeCamp, Y. W. Chang, A. Fernandez-Nieves, S. Fraden and Z. Dogic, Science, 2017, 355, eaal1979 CrossRef PubMed.
- Y. Fily, S. Henkes and M. C. Marchetti, Soft Matter, 2014, 10, 2132–2140 RSC.
- G. S. Redner, A. Baskaran and M. F. Hagan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012305 CrossRef PubMed.
- R. Grossmann, P. Romanczuk, M. Bar and L. Schimansky-Geier, Phys. Rev. Lett., 2014, 113, 258104 CrossRef CAS PubMed.
- D. Grossman, I. S. Aranson and E. Ben Jacob, New J. Phys., 2008, 10, 023036 CrossRef.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chate and K. Oiwa, Nature, 2012, 483, 448–452 CrossRef CAS PubMed.
- H. Jiang, H. Ding, M. Pu and Z. Hou, Soft Matter, 2017, 13, 836–841 RSC.
- G. Roberts, Anim. Behav., 1996, 51, 1077–1086 CrossRef.
- J. D. Villa, Ann. Entomol. Soc. Am., 2004, 97, 111–116 CrossRef.
- D. B. Kearns, Nat. Rev. Microbiol., 2010, 8, 634–644 CrossRef CAS PubMed.
- J. Herbert-Read, Curr. Biol., 2015, 25, R1127–R1129 CrossRef CAS PubMed.
- I. Watts, M. Nagy, T. B. de Perera and D. Biro, Biol. Lett., 2016, 12, 20160544 CrossRef PubMed.
- A. Morin, J. B. Caussin, C. Eloy and D. Bartolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 012134 CrossRef PubMed.
- S. Kondo and T. Miura, Science, 2010, 329, 1616–1620 CrossRef CAS PubMed.
- J. Carrasquilla and R. G. Melko, Nat. Phys., 2017, 13, 431–434 CrossRef CAS.
- S. S. Schoenholz, E. D. Cubuk, D. M. Sussman, E. Kaxiras and A. J. Liu, Nat. Phys., 2016, 12, 469–472 CrossRef CAS.
- E. Y. Lee, B. M. Fulan, G. C. L. Wong and A. L. Ferguson, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13588–13593 CrossRef CAS PubMed.
- A. W. Long, J. Zhang, S. Granick and A. L. Ferguson, Soft Matter, 2015, 11, 8141–8153 RSC.
- E. D. Cubuk, S. S. Schoenholz, J. M. Rieser, B. D. Malone, J. Rottler, D. J. Durian, E. Kaxiras and A. J. Liu, Phys. Rev. Lett., 2015, 114, 108001 CrossRef CAS PubMed.
- Y. H. Liu, P. Cizeau, M. Meyer, C. K. Peng and H. E. Stanley, Physica A, 1997, 245, 437–440 CrossRef.
- M. Sanopoulou and J. H. Petropoulos, J. Non-Cryst. Solids, 1991, 131, 827–830 CrossRef.
- M. E. Cates and J. Tailleur, Eur. Phys. J., 2013, 101, 20010 CAS.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS PubMed.
- P. Ghosh, J. Mondal, E. Ben-Jacob and H. Levine, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E2166–E2173 CrossRef CAS PubMed.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304 CrossRef PubMed.
- T. C. Lee, M. Alarcon-Correa, C. Miksch, K. Hahn, J. G. Gibbs and P. Fischer, Nano Lett., 2014, 14, 2407–2412 CrossRef CAS PubMed.
- S. Ebbens, R. A. L. Jones, A. J. Ryan, R. Golestanian and J. R. Howse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 015304 CrossRef PubMed.
- J. Schwarz-Linek, C. Valeriani, A. Cacciuto, M. E. Cates, D. Marenduzzo, A. N. Morozov and W. C. K. Poon, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4052–4057 CrossRef CAS PubMed.
- Y. Mao, M. E. Cates and H. N. W. Lekkerkerker, Physica A, 1995, 222, 10–24 CrossRef CAS.
- J. P. D. Clewett, K. Roeller, R. M. Bowley, S. Herminghaus and M. R. Swift, Phys. Rev. Lett., 2012, 109, 228002 CrossRef PubMed.
- J. Bialke, J. T. Siebert, H. Löwen and T. Speck, Phys. Rev. Lett., 2015, 115, 098301 CrossRef PubMed.
- S. C. Takatori and J. F. Brady, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032117 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |




