Mastering the non-equilibrium assembly and operation of molecular machines
Cristian
Pezzato
a,
Chuyang
Cheng
a,
J. Fraser
Stoddart
 *a and
R. Dean
Astumian
*a and
R. Dean
Astumian
 *b
*b
aDepartment of Chemistry, Northwestern University, 2145 Sheridan Road, Evanston, Illinois 60208-3113, USA. E-mail: stoddart@northwestern.edu; Fax: +1-847-491-1009; Tel: +1-847-491-3793
bDepartment of Physics, University of Maine, 5709 Bennet Hall, Orono, ME 04469-5709, USA. E-mail: astumian@maine.edu; Fax: +1-207-581-3441; Tel: +1-207-581-1024
First published on 24th March 2017
Abstract
In mechanically interlocked compounds, such as rotaxanes and catenanes, the molecules are held together by mechanical rather than chemical bonds. These compounds can be engineered to have several well-defined mechanical states by incorporating recognition sites between the different components. The rates of the transitions between the recognition sites can be controlled by introducing steric “speed bumps” or electrostatically switchable gates. A mechanism for the absorption of energy can also be included by adding photoactive, catalytically active, or redox-active recognition sites, or even charges and dipoles. At equilibrium, these Mechanically Interlocked Molecules (MIMs) undergo thermally activated transitions continuously between their different mechanical states where every transition is as likely as its microscopic reverse. External energy, for example, light, external modulation of the chemical and/or physical environment or catalysis of an exergonic reaction, drives the system away from equilibrium. The absorption of energy from these processes can be used to favour some, and suppress other, transitions so that completion of a mechanical cycle in a direction in which work is done on the environment – the requisite of a molecular machine – is more likely than completion in a direction in which work is absorbed from the environment. In this Tutorial Review, we discuss the different design principles by which molecular machines can be engineered to use different sources of energy to carry out self-organization and the performance of work in their environments.
Key learning points(1) Generalization of equilibrium relations to non-equilibrium steady states.(2) Microscopic reversibility can be used to calculate the work absorbed from or done on the environment by a molecular machine. (3) The power stroke model is conceptually incorrect for catalysis-driven motors, including all biomolecular motors. (4) Mechanically interlocked molecules provide a platform for developing new technologies as well as a set of tools for studying self-organisation. |
Introduction
All living things are dissipative structures, that is, their form and function results from the continual absorption, transduction, and dissipation of external energy.1 By contrast, the function of most molecular materials used in present technologies derives from their equilibrium properties. Although some recent examples, such as liquid crystal displays, use externally driven switching between equilibrium states, none function by using the continuous input of external energy to maintain the material in a non-equilibrium steady state.Recent research on Mechanically Interlocked Molecules2 (MIMs), such as catenanes3 and rotaxanes,4 offers glimpses of opportunities to create an entirely new type of technology based on using input energy to maintain a designed material in a non-equilibrium steady state.5–7 Further, the ability to design molecules that absorb energy to create dissipative structures will provide a better understanding of the thermodynamic and kinetic constraints under which living systems operate. In order to exploit the capabilities of MIMs fully, it is necessary to have a firm grasp of the fundamental theory required to use different types of input energy – light, external modulation of the chemical or physical environment, or catalysis of a non-equilibrium chemical reaction – to drive a molecular system away from thermodynamic equilibrium. Applying ideas from the theory of stochastic conformational pumping8,9 developed10 in the mid-1980s, we discuss here how MIMs can be made to undergo directed motion and to function as motors and pumps – i.e., as artificial molecular machines (AMMs) – and how external energy can be used for the self-assembly of complex structures. In this Tutorial Review, we make no pretense at completeness, referencing instead several reviews11–14 for details on the synthesis and applications of MIMs. Here, we focus on the thermodynamics and kinetics of AMMs, and on how theory guides the design principles for constructing the molecular machines of the future.
Interlocked molecules as switches
Early efforts to harness the potential of MIMs focused on the relative ease with which catenanes and rotaxanes can operate as on/off switches, triggered by external stimuli such as light, modulation of pH, redox potential, or other aspects of their chemical or physical environment. Two examples are shown in Fig. 1a and b. Rotaxanes provide a platform to create diverse molecular architectures, such as daisy chains (Fig. 1c) or molecules with palindromic structures (Fig. 1d), in which an external stimulus causes two components to move relative to one another. In order to exploit such motion in the context of AMMs, an additional ingredient must be added, namely, the ability to attach to and detach from an external load,13 be it mechanical, electrical, or chemical.Using rotaxanes to drive a chemical reaction away from equilibrium
One approach to this problem of attachment and detachment, where we focus on assigning the AMM a molecular task, is shown in Fig. 2. The motion of two small cyclobis(paraquat-p-phenylene) (CBPQT4+) rings, shown in dark blue, in a palindromic rotaxane is linked to a very slow chemical reaction A–B ⇌ A + B, where A–B is an adduct of some sort with an equilibrium constant Keq. The rotaxane, by binding to the components A and B and to the adduct A–B provides a pathway that allows equilibration of the reaction more rapidly than would be the case in free solution, i.e., the rotaxane acts as a catalyst. In addition to the two rings, the rotaxane comprises two 1,5-dioxynaphthalene units (DNP) shown in scarlet, and two redox-switchable viologen units, shown in dark blue (V2+) or violet (V˙+) depending on their redox condition. In the oxidised state, the two CBPQT4+ rings reside on the two DNP sites by virtue of favourable donor–acceptor interactions, while, in the reduced state, the rings (i.e., CBPQT2(˙+)) move onto V˙+ to form a stabilised trisradical species. The kinetic cycle shown in Fig. 2 illustrates the coupling between redox potential , the relative ring positions, and the chemical reaction between A and B. Here and elsewhere in this Tutorial Review, energies (including redox potentials) are given in terms of the thermal energy per molecule kBT, where kB is Boltzmann's constant and T is the temperature in Kelvin.
, the relative ring positions, and the chemical reaction between A and B. Here and elsewhere in this Tutorial Review, energies (including redox potentials) are given in terms of the thermal energy per molecule kBT, where kB is Boltzmann's constant and T is the temperature in Kelvin.
We have illustrated in Fig. 2 a situation in which the rotaxane is designed to have a large affinity constant K for the adduct A–B when the rings are close together, and a small affinity constant K′ for the components A and B when the rings are far apart. In most cases in the literature, the operations of AMMs are represented with single arrows for the sake of clarity. Here, we stress the importance of having a dynamic view of systems where every process has its corresponding microscopic reverse. Non-equilibrium behaviour results from favouring or preventing some trajectories over others, all of which are possible at equilibrium. External energy is a tool for selecting specific pathways, not for creating new pathways. In order to stress the dynamic nature of the transitions, we have opted here to use double arrows for representing all chemical processes.
Each clockwise cycle through the oxidised and reduced states shown in Fig. 2 results in breaking the adduct A–B into its component parts, A and B, and conversely, each counterclockwise redox cycle results in linking A and B to form the adduct A–B. The equilibrium constants can be written in terms of the equilibrium concentrations of A, B, and A–B, of the redox potential, and of the basic free energies of the four states, K* = [A–B]|eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eGF*−GB*,
eGF*−GB*, 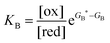 , K = [A]|eq[B]|eq
, K = [A]|eq[B]|eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eGF−GB and
eGF−GB and  . The product of the equilibrium constants is, by microscopic reversibility, the overall equilibrium constant (Keq) for the catalyzed chemical process
. The product of the equilibrium constants is, by microscopic reversibility, the overall equilibrium constant (Keq) for the catalyzed chemical process
 | (1) |
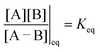 | (2) |
The ratio 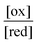 will also attain equilibrium in the bulk, as determined by the redox potential of the components. On account of thermal noise, the components of an individual AMM will undergo fluctuations between being reduced and oxidised, and between being bound and free. These fluctuations, however, are reversible and there is no dissipation and no net conversion, A–B ⇌ A + B or red ⇌ ox. In the thermodynamic limit, the bulk concentrations of [A–B], [A], [B], [red], and [ox] are constant. An individual rotaxane-based machine undergoes dynamic fluctuations characteristic of chemical equilibria in which each transition is just as likely as the reverse of that transition.
will also attain equilibrium in the bulk, as determined by the redox potential of the components. On account of thermal noise, the components of an individual AMM will undergo fluctuations between being reduced and oxidised, and between being bound and free. These fluctuations, however, are reversible and there is no dissipation and no net conversion, A–B ⇌ A + B or red ⇌ ox. In the thermodynamic limit, the bulk concentrations of [A–B], [A], [B], [red], and [ox] are constant. An individual rotaxane-based machine undergoes dynamic fluctuations characteristic of chemical equilibria in which each transition is just as likely as the reverse of that transition.
The situation is very different if we modulate the chemical environment back and forth externally between being highly oxidising, 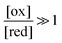 , and highly reducing,
, and highly reducing, 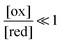 . Because of the different affinities associated with the adduct and the individual components, the external modulation induces clockwise cycling through the states, leading to the breaking of the adduct into its component parts. Under oxidising conditions, the system exists entirely in the states with the rings far apart and equilibrates according to K. Under reducing conditions, the system exists entirely in the states with the rings close together and equilibrates according to K*. After many redox cycles, the concentrations of [A], [B], and [A–B] adjust to attain the ratio
. Because of the different affinities associated with the adduct and the individual components, the external modulation induces clockwise cycling through the states, leading to the breaking of the adduct into its component parts. Under oxidising conditions, the system exists entirely in the states with the rings far apart and equilibrates according to K. Under reducing conditions, the system exists entirely in the states with the rings close together and equilibrates according to K*. After many redox cycles, the concentrations of [A], [B], and [A–B] adjust to attain the ratio 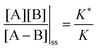 which can be rewritten using eqn (1) as
which can be rewritten using eqn (1) as
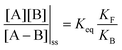 | (3) |
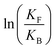 is the net work done in a clockwise cycle passing through the four states on oxidation of the machine at high redox potential and reduction at low redox potential. The association constants, K and K*, which are linked to KF and KB by microscopic reversibility, are designable properties of the interaction between A–B, A and B, and the rings. By appropriate design, the degrees of freedom of the molecular machine can be coupled with those of a chemical reaction such that externally driven fluctuations and the concomitant dissipation of energy can be used to drive the reaction away from equilibrium in a desired direction.
is the net work done in a clockwise cycle passing through the four states on oxidation of the machine at high redox potential and reduction at low redox potential. The association constants, K and K*, which are linked to KF and KB by microscopic reversibility, are designable properties of the interaction between A–B, A and B, and the rings. By appropriate design, the degrees of freedom of the molecular machine can be coupled with those of a chemical reaction such that externally driven fluctuations and the concomitant dissipation of energy can be used to drive the reaction away from equilibrium in a desired direction.
Rethinking macromolecular catalysis – stochastic conformational pumping
The mechanism by which a time-dependent modulation causes directional cycling is known10 as electro-conformational coupling. It has been discussed15–19 in the context of the effect of oscillating electric fields on trans-membrane biomolecular pumps. More recently the mechanism has been termed stochastic conformational pumping8 since, in principle, any time-dependent thermodynamic or chemical parameter can be used to drive the system away from equilibrium.20–22 Molecules with many degrees of freedom are effective at absorbing energy from non-equilibrium fluctuations in the environment, from cycling near a thermal vent, or from diurnal cycles of light and dark, etc. If these molecules also act as catalysts, some of the absorbed energy, instead of being dissipated into the environment, can be transduced to drive a chemical reaction to a non-equilibrium steady state, thereby storing chemical energy. A simple example based on the Michaelis–Menten mechanism for enzyme catalysis23 is described in Fig. 3. In the absence of an external driving force, the enzyme will catalyze the reaction toward the final equilibrium , where the superscript 0 indicates the value of the rate constant in the absence of non-equilibrium driving. In the presence of an oscillating or fluctuating external driving force, f(t), the rate constants are time-dependent and are given by the Arrhenius form ki(t) = k0i
, where the superscript 0 indicates the value of the rate constant in the absence of non-equilibrium driving. In the presence of an oscillating or fluctuating external driving force, f(t), the rate constants are time-dependent and are given by the Arrhenius form ki(t) = k0i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ezif(t), i = ±1, ±2, reflecting that both the energies of the states and the energies of the barriers between them depend on time. The exponent zif(t) is a conjugate pair of intensive [f(t)] and extensive (zi) thermodynamic parameters.24 Possible zi includes molecular volume, molecular dipole moment, molecular entropy, or number of molecules, with f(t) being pressure, electric field, temperature, or chemical potential, respectively. The steady state ratio in the presence of a high frequency oscillation f(t) can be written23 as the product of the equilibrium constant and an exponential time average over the energy absorbed from the field
ezif(t), i = ±1, ±2, reflecting that both the energies of the states and the energies of the barriers between them depend on time. The exponent zif(t) is a conjugate pair of intensive [f(t)] and extensive (zi) thermodynamic parameters.24 Possible zi includes molecular volume, molecular dipole moment, molecular entropy, or number of molecules, with f(t) being pressure, electric field, temperature, or chemical potential, respectively. The steady state ratio in the presence of a high frequency oscillation f(t) can be written23 as the product of the equilibrium constant and an exponential time average over the energy absorbed from the field  . The rate is
. The rate is 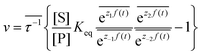 where
where  .
.
 | ||
Fig. 3 (a) Illustration of the effect of time-dependent modulation on a Michaelis–Menten enzyme. In general, the conformation of the bound state of the enzyme (EL) is different than that of the unbound state (E). Transitions between these two states provide a mechanism by which the enzyme can absorb energy from external fluctuations, and some of this energy can be transduced to drive the catalyzed reaction SP away from equilibrium. (b) Plots of the concentrations [P] and [S] as a function of time in the presence of external oscillations as shown in (a). The reaction starts at equilibrium  and is driven by a high-frequency oscillation toward a non-equilibrium steady state ratio and is driven by a high-frequency oscillation toward a non-equilibrium steady state ratio  . (c) A fit of the theoretical frequency response plotted with data taken from the work of Liu et al.15 on the experimentally observed ATP-independent Na+ (squares) and K+ (triangles) currents driven through the Na, K-ATPase by an applied ac electric field, where r(t) and ε(t) vary in an out-of-phase manner with one another. . (c) A fit of the theoretical frequency response plotted with data taken from the work of Liu et al.15 on the experimentally observed ATP-independent Na+ (squares) and K+ (triangles) currents driven through the Na, K-ATPase by an applied ac electric field, where r(t) and ε(t) vary in an out-of-phase manner with one another. | ||
If the overall equilibrium between S and P is not influenced by the driving force, the coefficients in the exponent obey the relation z+1 + z−1+ z+2 + z−2 = 0. Then, the condition 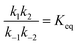 holds at every instant, despite the driving. Such a situation, with z+1= 1, z+2 = −1, and z−1, z−2 = 0, is shown in Fig. 3a. The effect of the oscillation on the energy levels of the enzyme, depicted in Fig. 3a, can be described in terms of two ratios, (i) the time-dependent affinity for the substrate,
holds at every instant, despite the driving. Such a situation, with z+1= 1, z+2 = −1, and z−1, z−2 = 0, is shown in Fig. 3a. The effect of the oscillation on the energy levels of the enzyme, depicted in Fig. 3a, can be described in terms of two ratios, (i) the time-dependent affinity for the substrate, 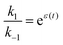 , where ε(t) = (z+1 − z−1)f(t) is a thermodynamic quantity related to the well depth in Fig. 3a, and (ii) the ratio of the dissociation rates,
, where ε(t) = (z+1 − z−1)f(t) is a thermodynamic quantity related to the well depth in Fig. 3a, and (ii) the ratio of the dissociation rates, 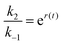 , where r(t) = (z+2 − z−1)f(t) is a kinetic quantity that depends only on the difference in the barrier heights, and r0 is the difference between the two barrier heights in the absence of a driving force. The dissipation depends only on ε(t) – i.e., each time a substrate or product binds when the energy of the Michaelis complex is a minimum and a product or substrate is released when the energy of the Michaelis complex is a maximum (the most likely possibility), an amount of energy, Δε, is dissipated in the environment. Note that the effectiveness of energy transduction, however, depends on both ε(t), and r(t): if either ε or r are time independent, there is no pumping.
, where r(t) = (z+2 − z−1)f(t) is a kinetic quantity that depends only on the difference in the barrier heights, and r0 is the difference between the two barrier heights in the absence of a driving force. The dissipation depends only on ε(t) – i.e., each time a substrate or product binds when the energy of the Michaelis complex is a minimum and a product or substrate is released when the energy of the Michaelis complex is a maximum (the most likely possibility), an amount of energy, Δε, is dissipated in the environment. Note that the effectiveness of energy transduction, however, depends on both ε(t), and r(t): if either ε or r are time independent, there is no pumping.
When ε(t) and r(t) oscillate 90° out of phase with one another, the oscillation can cause adiabatic pumping, where the energy absorbed by the enzyme is converted almost entirely into mechanical, electrical or chemical work done on the environment.16,20 The phase lag can occur because of the conformational relaxation of the enzyme, a dissipative process. The energy waste can be very small in comparison to the work done. The frequency response is shown in Fig. 3c, where the data points are from experiments on ac field-driven Na+ and K+ pumping reported by one15 of us. At first glance, based on the non-monotonic dependence of current versus frequency, it is tempting to conclude that the pumping arises because of “resonance” between the enzyme and the applied field. Succumbing to this temptation would be both mistaken and misleading. In fact, the physics behind the response shown in Fig. 3c is that of dispersion, the mechanism by which energy is dissipated in the environment, and not resonance, a mechanism by which potential and kinetic energy are almost perfectly interconverted as when a singer's voice shatters a wine glass.
Now consider a model24 in which the bound-state energy and the energy barrier for binding the substrate fluctuate together dichotomically between their highest level (dashed orange lines) and their lowest level (solid orange line), and where Δr = Δε, i.e., with z+1 = 1, z+2 = −1, and z−1, z−2 = 0 as shown in Fig. 3a. The forward rate constants are then k1 = k01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e±Δε/2 and k2 = k02
e±Δε/2 and k2 = k02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e∓Δε/2 while the backward rate constants do not depend on Δε. There are four energetically distinct paths,
e∓Δε/2 while the backward rate constants do not depend on Δε. There are four energetically distinct paths,  , by which the substrate S can be converted to product P – (1) binding the substrate when ε is small and releasing the product when ε is large,
, by which the substrate S can be converted to product P – (1) binding the substrate when ε is small and releasing the product when ε is large,  ; (2) binding the substrate when ε is large and releasing the product when ε is small,
; (2) binding the substrate when ε is large and releasing the product when ε is small,  ; (3) binding the substrate when ε is small and releasing the product when ε is small,
; (3) binding the substrate when ε is small and releasing the product when ε is small, 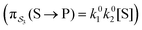 ; (4) or binding the substrate when ε is large and releasing the product when ε is large
; (4) or binding the substrate when ε is large and releasing the product when ε is large 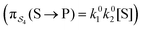 . The products of rate constants for each path,
. The products of rate constants for each path,  , are the un-normalized path probabilities. Each of the four paths has a microscopic reverse in which P is transformed to S. The reverse path probabilities
, are the un-normalized path probabilities. Each of the four paths has a microscopic reverse in which P is transformed to S. The reverse path probabilities  are all k0−1k0−2[P] since the backward rate constants do not depend on Δε. The ratio of the probability for the conversion S → P to the probability for the conversion P → S is
are all k0−1k0−2[P] since the backward rate constants do not depend on Δε. The ratio of the probability for the conversion S → P to the probability for the conversion P → S is
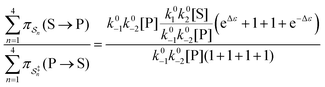 | (4) |
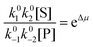 with Δμ being the chemical potential difference between S and P. This calculation can also be expressed24 in terms of cycle kinetic diagrams. The steady state concentration ratio [P]/[S] can be easily calculated by setting the net probabilities equal,
with Δμ being the chemical potential difference between S and P. This calculation can also be expressed24 in terms of cycle kinetic diagrams. The steady state concentration ratio [P]/[S] can be easily calculated by setting the net probabilities equal,  to get
to get  .
.
The significance of stochastic conformational pumping for enzyme catalysis, and for molecular machines in general, can be understood23 as follows. Consider a simple chemical reaction, 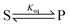 , at equilibrium,
, at equilibrium, 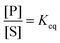 . Next, some high-frequency external oscillation or fluctuation is applied to the system. The chemical reaction itself does not absorb energy from the fluctuation and hence remains in equilibrium. If a small amount of an enzyme that catalyzes the reaction, while absorbing and dissipating energy from the applied fluctuation, is added to the system, the chemical reaction, without further interference, moves away from equilibrium to reach a new steady state using some of the energy absorbed by the enzyme, the rest of which is dissipated. The efficiency of this energy transduction can be, in practice, quite high, and is fundamentally bounded only by unity. The take-away message is that every enzyme, and indeed every catalytic macromolecule, because of its many degrees of freedom into which external energy can be absorbed, has the possibility to serve as a molecular machine. We can generalize this result for understanding synthetic molecular machines using the principle of microscopic reversibility.
. Next, some high-frequency external oscillation or fluctuation is applied to the system. The chemical reaction itself does not absorb energy from the fluctuation and hence remains in equilibrium. If a small amount of an enzyme that catalyzes the reaction, while absorbing and dissipating energy from the applied fluctuation, is added to the system, the chemical reaction, without further interference, moves away from equilibrium to reach a new steady state using some of the energy absorbed by the enzyme, the rest of which is dissipated. The efficiency of this energy transduction can be, in practice, quite high, and is fundamentally bounded only by unity. The take-away message is that every enzyme, and indeed every catalytic macromolecule, because of its many degrees of freedom into which external energy can be absorbed, has the possibility to serve as a molecular machine. We can generalize this result for understanding synthetic molecular machines using the principle of microscopic reversibility.
Unreasonable effectiveness of equilibrium-like theory
There has been much recent progress in the theory of non-equilibrium thermodynamics, especially as applied to individual molecular machines. Perhaps the most significant development is the use of, and deeper appreciation of, the principle of microscopic reversibility25 for single trajectories by which,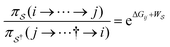 | (5) |
 denotes some trajectory leading from state i to state j,
denotes some trajectory leading from state i to state j, 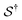 denotes the microscopic reverse of that trajectory,
denotes the microscopic reverse of that trajectory,  is the product of the rate constants for the transitions in the trajectory, ΔGij is the free energy change of the molecule associated with a transition from state i to state j, and
is the product of the rate constants for the transitions in the trajectory, ΔGij is the free energy change of the molecule associated with a transition from state i to state j, and 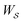 is the excess work, i.e., the energy transferred between the molecule and the environment, in the trajectory
is the excess work, i.e., the energy transferred between the molecule and the environment, in the trajectory 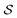 by any external driving force, including binding and release of the ligand (e.g., substrate and product in the case of an enzyme) that acts on the system in the transition. The free energy change is, of course, path-independent. At equilibrium
by any external driving force, including binding and release of the ligand (e.g., substrate and product in the case of an enzyme) that acts on the system in the transition. The free energy change is, of course, path-independent. At equilibrium  is also path-independent (e.g., for an enzyme in the absence of a time-dependent external driving force,
is also path-independent (e.g., for an enzyme in the absence of a time-dependent external driving force,  , in going from the “free” to “bound” state, is either the chemical potential of S or of P, which at equilibrium are equal) but away from equilibrium
, in going from the “free” to “bound” state, is either the chemical potential of S or of P, which at equilibrium are equal) but away from equilibrium  depends on the details of the specific path
depends on the details of the specific path  , and may be positive or negative. For single transitions the form given in eqn (5) is familiar from effects of voltage on opening/closing transitions for ion channels,26 or the effects of external force on stretching/contraction of polymers.27 For continuous dynamical processes, this equation is most easily derived25,28 in the context of the Onsager–Machlup thermodynamic “action” theory,29 a variational principle that allows calculation of the most probable trajectory given an ensemble of possible trajectories.
, and may be positive or negative. For single transitions the form given in eqn (5) is familiar from effects of voltage on opening/closing transitions for ion channels,26 or the effects of external force on stretching/contraction of polymers.27 For continuous dynamical processes, this equation is most easily derived25,28 in the context of the Onsager–Machlup thermodynamic “action” theory,29 a variational principle that allows calculation of the most probable trajectory given an ensemble of possible trajectories.
Many scientists are quick to point out that Onsager's theory is valid only near equilibrium in the linear regime. While this interpretation is correct, the phrasing is quite misleading. Onsager and Machlup29 explicitly clarify the regime of validity of their theory, explaining that “The essential physical assumption about the irreversible processes is that they are linear, i.e., that the fluxes are proportional to the forces that cause them.” This requirement holds microscopically for any process where the ratio between the inertial force and the viscous drag force is very small, i.e., the requirement holds30 at low Reynolds number. Hence, all motions of synthetic and bio-molecular machines in solution,31 where the inertial force (mass times acceleration) is negligible in comparison to the viscous force (velocity times coefficient of viscous drag), are appropriately described in terms of the Onsager–Machlup theory. These two scientists' work,29 aside from providing a seminal proposal of a variational principle for calculating the most probable trajectory of a stochastic system, is notable for its emphasis on the importance of paths (trajectories) between states rather than on the states themselves. This situation is manifest in the present treatment by recognising that the excess work terms are associated not with the states i and j, but with the paths 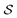 and
and  .
.
As in equilibrium theory, the ratio of the concentrations in states i and j at a non-equilibrium steady state can be calculated as the sum of the probabilities of all paths leading from j to i divided by the sum of the probabilities of paths leading from i to j,
 | (6) |
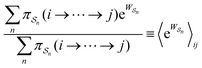 is the exponential of the excess work, i.e., the energy transferred between the molecule and the environment, averaged over the ensemble of trajectories leading between state j and i. In the absence of an external driving force
is the exponential of the excess work, i.e., the energy transferred between the molecule and the environment, averaged over the ensemble of trajectories leading between state j and i. In the absence of an external driving force  is the same for all n, and hence the ratio of the concentrations is given by the familiar Boltzmann factor. In the presence of an external driving force
is the same for all n, and hence the ratio of the concentrations is given by the familiar Boltzmann factor. In the presence of an external driving force 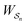 does depend on the path. The ratio is shifted toward state i if, on average, work is done on the molecule by the driving force in going from state j to i, and in favor of state j if, on average, work is done on the molecule by the driving force in going from state i to j. The effect of a non-equilibrium driving force on molecular machines arises because input work favours those trajectories with positive
does depend on the path. The ratio is shifted toward state i if, on average, work is done on the molecule by the driving force in going from state j to i, and in favor of state j if, on average, work is done on the molecule by the driving force in going from state i to j. The effect of a non-equilibrium driving force on molecular machines arises because input work favours those trajectories with positive  and disfavours those with negative
and disfavours those with negative  .
.
Eqn (6) must be carefully interpreted. If, for example, we identify state i as an assembled or organized state and state j as a disassembled or unorganized state comprised of elementary components, and make the natural but mistaken interpretation of  as the average of the exponential of the “dissipation”, it would be easy to conclude that self-assembly in the presence of dissipation is as natural as a ball rolling downhill since the dissipation can never be negative. The factor
as the average of the exponential of the “dissipation”, it would be easy to conclude that self-assembly in the presence of dissipation is as natural as a ball rolling downhill since the dissipation can never be negative. The factor 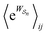 is actually the average of the exponential of the work exchanged with the environment when the system undergoes transition from state j to i. Since the excess work can be negative, then
is actually the average of the exponential of the work exchanged with the environment when the system undergoes transition from state j to i. Since the excess work can be negative, then 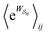 can be less than one, in which case the external driving force favours transition from i to j. When we examine closely the requirements for self-assembly, we find that, in fact, highly intelligent design on the part of the synthetic chemist is necessary to allow a system to use external energy to self-assemble. It is simply not the case that shining light on a random clump of atoms is enough to lead to self-assembly of complex structures. Input energy is certainly necessary, but is not sufficient for non-equilibrium self-assembly. The goal of the synthetic chemist in designing a molecular machine for self-assembly, or to accomplish mechanical, electrical or chemical work, is to engineer a situation in which the kinetic pre-factors
can be less than one, in which case the external driving force favours transition from i to j. When we examine closely the requirements for self-assembly, we find that, in fact, highly intelligent design on the part of the synthetic chemist is necessary to allow a system to use external energy to self-assemble. It is simply not the case that shining light on a random clump of atoms is enough to lead to self-assembly of complex structures. Input energy is certainly necessary, but is not sufficient for non-equilibrium self-assembly. The goal of the synthetic chemist in designing a molecular machine for self-assembly, or to accomplish mechanical, electrical or chemical work, is to engineer a situation in which the kinetic pre-factors  of each thermodynamic term in the sum in eqn (6) are very small except for those multiplying paths in which the external driving force is coupled to the desired output. For more details concerning stochastic thermodynamics and molecular motors the interested reader should consult one of the recent reviews32–34 on this topic. We can best understand the implications of eqn (6) for the design of molecular machines in the context of a specific example – an artificial molecular pump that uses externally driven oscillation of the redox potential to cause self-assembly of small rings onto a dumbbell component.
of each thermodynamic term in the sum in eqn (6) are very small except for those multiplying paths in which the external driving force is coupled to the desired output. For more details concerning stochastic thermodynamics and molecular motors the interested reader should consult one of the recent reviews32–34 on this topic. We can best understand the implications of eqn (6) for the design of molecular machines in the context of a specific example – an artificial molecular pump that uses externally driven oscillation of the redox potential to cause self-assembly of small rings onto a dumbbell component.
Energy-driven self-assembly by an artificial molecular pump
Two of us presented5 an artificial molecular pump (Fig. 4) recently that uses energy from externally driven oscillations of the redox potential to concentrate several rings on a dumbbell component. The process represents true non-equilibrium self-assembly of a dissipative structure – if the redox oscillations are stopped the system falls apart. The machine is made of a CBPQT4+ ring that threads onto a dumbbell (DB3+) comprising a viologen (V2+) recognition site, a 3,5-dimethylpyridinium (PY+) group on one end to serve as an electrostatically switchable barrier for threading the ring onto the dumbbell, an isopropylphenylene (IPP) group that serves as a steric “speed bump”, separating the recognition site from a long oligomethylene-collecting chain, and a bulky 2,6-diisopropylphenyl stopper. The energy landscape for threading the ring onto the dumbbell depends on whether the ring and the dumbbell are oxidised (lower profile in Fig. 4) or reduced (upper profile in Fig. 4).At equilibrium, the ratio between the probability of finding the system assembled with a ring on the collecting chain ([Aox] + [Ared]) to the probability of finding the system disassembled with no ring on the chain ([Dox] + [Dred]), is
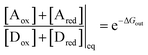 | (7) |
By externally changing the redox potential back and forth between reducing and oxidising conditions, the energy profile is made to switch back and forth between the upper state and the lower state, giving rise to stochastic pumping8 by an energy ratchet31 mechanism as described in Fig. 5, where, for simplicity's sake, we focus on the kinetic of threading just one ring.
 | ||
| Fig. 5 Kinetic diagram describing how external oscillation of the redox potential drives dissipative assembly of CBPQT4+ rings onto a collecting chain. Under reducing conditions the system equilibrates between states Dred and Ired, and under oxidizing conditions between Iox and Aox. Over many cycles reducing and oxidizing conditions the system eventually reaches a steady state in which the net equilibrium between assembled and disassembled molecules is governed by the product KDI,redKIA,ox. Refer to Fig. 4 for the structural formulas. | ||
There are several thermodynamic identities that connect the K's,
 | (8) |
| KDI,redKIA,red = KDI,oxKIA,ox= e−ΔGout. | (9) |
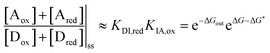 | (10) |
 is the work absorbed when the components are oxidised while in state I. The second equality in eqn (10) is obtained by using the thermodynamic identities eqn (8) and (9).
is the work absorbed when the components are oxidised while in state I. The second equality in eqn (10) is obtained by using the thermodynamic identities eqn (8) and (9).
We can develop intuition about the mechanism of pumping by considering modifications to the design of the pump. For example, if we exchange the PY+ group with the IPP steric “speed bump”, the transitions Dred ⇌ Ired and Iox ⇌ Aox would become blocked kinetically. This alteration would have the effect of changing the sign of ΔΔG*‡ − ΔΔG‡. The single remaining pathway would then be Dred ↔ Dox ⇌ Iox ↔ Ired ⇌ Ared ↔ Aox and we would find that large-amplitude oscillations of the redox potential would lead to the steady state ratio between assembled and disassembled molecules  . The external driving force in this case would favour disassembly, not assembly, relative to the equilibrium case. Non-equilibrium self-assembly requires, in addition to dissipation, intelligent design on the part of the synthetic chemist. We also observe that, in contrast to equilibrium thermodynamics, the free energies of the intermediate states and of the transition states play an important role in determining the steady state ratio maintained by the external driving force. If ΔG − ΔG* = 0, the steady state in the presence of redox potential oscillations is the same as the equilibrium ratio, irrespective of the barriers heights. Further, if the difference of the barrier heights between the bulk and the recognition site and between the recognition site and the collecting chain are the same under both oxidising and reducing conditions, there is no energy-driven assembly (or disassembly) irrespective of the value of ΔG − ΔG*. The possibilities are summarised in Table 1.
. The external driving force in this case would favour disassembly, not assembly, relative to the equilibrium case. Non-equilibrium self-assembly requires, in addition to dissipation, intelligent design on the part of the synthetic chemist. We also observe that, in contrast to equilibrium thermodynamics, the free energies of the intermediate states and of the transition states play an important role in determining the steady state ratio maintained by the external driving force. If ΔG − ΔG* = 0, the steady state in the presence of redox potential oscillations is the same as the equilibrium ratio, irrespective of the barriers heights. Further, if the difference of the barrier heights between the bulk and the recognition site and between the recognition site and the collecting chain are the same under both oxidising and reducing conditions, there is no energy-driven assembly (or disassembly) irrespective of the value of ΔG − ΔG*. The possibilities are summarised in Table 1.
| ΔG − ΔG* | ΔΔG*‡ − ΔΔG‡ | ||
|---|---|---|---|
| <0 | 0 | >0 | |
| <0 | Disassembly | No change | Assembly |
| 0 | No change | No change | No change |
| >0 | Assembly | No change | Disassembly |
Are these results universal? Do both kinetic (barrier heights) and thermodynamic (free energies of the states of the molecule) parameters control self-assembly irrespective of the mechanism by which dissipation is introduced into the system? The answer is no. If dissipation arises from catalysis of a non-equilibrium chemical reaction, we find, perhaps surprisingly, that the free energies of the intermediate states (i.e., ΔG and ΔG*) are irrelevant, and that the directionality – assembly or disassembly – is determined solely by kinetic parameters, including the state-dependent gating of the catalysed reaction according to the mechanical state of the pump.
Autonomously driven molecular pumps
Biological molecular machines are driven, not by external fluctuation or oscillation of some chemical property (e.g., redox potential, pH) but by catalysis of a chemical reaction, often ATP hydrolysis or ion transport across a membrane. Consequently, attempts to design autonomously driven molecular machines have been at the forefront of recent research. We can contemplate this possibility in the context of the rotaxane pump illustrated in Fig. 6 but where there are two molecular species that can oxidise/reduce the rotaxane.14 | ||
| Fig. 6 Kinetic diagram illustrating how, in principle, a catalyzed process ox1 + red2 ⇌ ox2 + red1 can drive assembly. By microscopic reversibility we see that the overall steady state ratio between assembled and disassembled molecules is independent of the free energies of the intermediate states Ired and Iox, (i.e., independent of KDI,red, and KIA,ox) and depends instead on the specificity of the mechanical states for the two redox reactions, and on the overall free energy released in the redox reaction Δμ. Refer to Fig. 4 for the structural formulas. | ||
Each mechanical state facilitates the overall process ox1 + red2 ⇌ ox2 + red1, which releases an amount of energy  for each completion in the forward direction, and absorbs energy Δμ for each completion in the reverse direction. The principle of microscopic reversibility36,37 constrains the rate constants for oxidation/reduction. The most obvious constraint is
for each completion in the forward direction, and absorbs energy Δμ for each completion in the reverse direction. The principle of microscopic reversibility36,37 constrains the rate constants for oxidation/reduction. The most obvious constraint is
 | (11) |
 | (12) |
 | (13) |
 | (14) |
 ,
,  ,
, 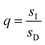 , and L = s−1D + sIeΔμ. The most salient feature of this relationship is that the steady state ratio between assembled and disassembled structures does not depend on the free energy of either intermediate state Iox (ΔG), or of Ired (ΔG*). Instead, for Δμ > 0, the term in brackets is greater than unity if q < 1, is less than unity if q > 1, and is unity if q = 1. While the difference in energies of the intermediate states, ΔG − ΔG*, is irrelevant for determining whether input energy from a catalysed reaction facilitates non-equilibrium self-assembly, or disassembly, the parameter ΔΔG*‡ − ΔΔG‡ remains important – changing the sign changes the dissipation-driven tendency to assemble or disassemble. The possibilities are summarised in Table 2.
, and L = s−1D + sIeΔμ. The most salient feature of this relationship is that the steady state ratio between assembled and disassembled structures does not depend on the free energy of either intermediate state Iox (ΔG), or of Ired (ΔG*). Instead, for Δμ > 0, the term in brackets is greater than unity if q < 1, is less than unity if q > 1, and is unity if q = 1. While the difference in energies of the intermediate states, ΔG − ΔG*, is irrelevant for determining whether input energy from a catalysed reaction facilitates non-equilibrium self-assembly, or disassembly, the parameter ΔΔG*‡ − ΔΔG‡ remains important – changing the sign changes the dissipation-driven tendency to assemble or disassemble. The possibilities are summarised in Table 2.
| ln(q) | ΔΔG*‡ − ΔΔG‡ | ||
|---|---|---|---|
| <0 | 0 | >0 | |
| <0 | Disassembly | No change | Assembly |
| 0 | No change | No change | No change |
| >0 | Assembly | No change | Disassembly |
In a recent review,38 two of the authors of this Tutorial Review discussed directionally controlled threading of a ring and an axle39–42 in which switching between two states causes transport of a ring along an axle, threading from one side and de-threading from the other. They noted that “the attractive interactions associated with the recognition sites in both the hydrogen bonding and donor–acceptor cases are only weakened – that is, they do not become repulsive when switched off. The consequence is that the potential to perform useful work is severely limited and leads to low energy conversion efficiencies. The pumping efficiencies can only be improved if large enthalpic changes can be realised when the recognition sites are switched off – that is, when the sites become repulsive. By employing radical-pairing interactions as the source of the recognition between CBPQT2(˙+) rings and viologen radical cations under reducing conditions, when the highly stable trisradical complex is oxidized, the reinstatement of six positive charges gives rise to strong Coulombic repulsions with a lot more potential for real work to be done.” This observation is indeed seen to be the case with the radical pair-based recognition used in the pump driven by external oscillations (Fig. 4 and 5). The interaction between the ring and recognition site in the reduced form is strongly attractive, but the interaction in the oxidised form is strongly repulsive. The theoretical analysis of the catalysis-driven pump presents a very different picture in which the repulsion/attraction between the ring and the recognition site is inconsequential and the steady state occupancy of the collecting chain depends solely on the gating of the driving reaction by an information ratchet mechanism.31,42
We can gain insight into the fundamental difference between energy and information ratchets by stepping back and recognizing that there are three types of pathways leading from the disassembled to the assembled states: (1) forward ( ) paths in which the environment does excess work, W, on the molecule; (2) backward reverse (
) paths in which the environment does excess work, W, on the molecule; (2) backward reverse ( ) paths in which the molecule does excess work, W, on the environment; (3) neutral (
) paths in which the molecule does excess work, W, on the environment; (3) neutral ( ) processes in which no excess work is done. Each type of process has a microscopic reverse
) processes in which no excess work is done. Each type of process has a microscopic reverse  ,
, 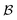 ,
, 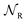 , respectively, leading from the assembled to the disassembled states. According to eqn (6) we can then write
, respectively, leading from the assembled to the disassembled states. According to eqn (6) we can then write
 | (15) |
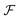 and
and 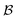 paths and hence of
paths and hence of  and
and  paths but, in general, there will be a greater number of
paths but, in general, there will be a greater number of  paths, which is accounted for by assigning a multiplicity, m. The approach described by eqn (15) is inspired by a general theory for biomolecular motors.34
paths, which is accounted for by assigning a multiplicity, m. The approach described by eqn (15) is inspired by a general theory for biomolecular motors.34
For external modulation, where reduction and oxidation occur at either low or high redox potential, the work absorbed when the molecule is oxidised in the intermediate state is W = ΔG − ΔG*. If, by design, W ≫ 1, we recover eqn (10) as a very good approximation.
For processes driven by catalysis, reduction and oxidation occur at a fixed redox potential, but by several different paths so that W = Δμ. We also have an explicit relation34 for the ratio 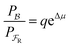 , leading immediately to eqn (14).
, leading immediately to eqn (14).
The irrelevance of the intermediate state free-energies derived for the hypothetical chemically driven pump shown in Fig. 6 is quite general, and is based firmly on the principle of microscopic reversibility.36,37 This result implies something quite important regarding the mechanism of ATP and ion-transport-driven molecular machines, such as muscle (action-myosin), kinesin, FoF1-ATPase, the flagellar motor, and many other biological molecular machines. The power-stroke mechanism, presented in almost every textbook of biochemistry, biophysics, and cell biology, is simply conceptually incorrect.
In order to appreciate this widespread conceptual error, let us consider two AMMs, one a light-driven machine40 where the constraints of microscopic reversibility are inapplicable to the photochemical processes,8 and for which a power-stroke is clearly important,43 and the other a catenane-based chemically driven motor6 that is superficially very similar in terms of the kinetic mechanism, but where the conclusions for optimal design are very different when the constraints of microscopic reversibility36,37 are used in the analysis.
Light-driven directional translation
Recently Ragazzon et al.40 described a very simple mechanism for using light energy to drive directional transit of an axle through a ring as shown in Fig. 7. These authors used a molecular axle with end groups that impede, but do not prevent, the threading of a macrocyclic ring – a 2,3-dinaphtho[24]crown-8 ether – to assemble a pseudorotaxane. One end group is a photo-switchable azobenzene unit (lime or orange color), and the other end group is a passive methylcyclopentyl group, represented as a gray sphere. Between the two end groups lies an ammonium recognition site for the crown ether represented as a blue cylinder. In the ground state, the azobenzene is in the less bulky (E)-isomeric form and so a crown ether, with strong affinity for the ammonium recognition site, threads onto the molecular axle predominately (in fact almost completely) over the (E)-azobenzene terminus. Upon absorption of a photon, the azobenzene in its excited state undergoes isomerisation to the (Z)-azobenzene form, which is more bulky than the (E)-azobenzene form, and which also destabilizes the interaction between the macrocycle and the ammonium recognition site. The resulting dethreading of the ring occurs almost entirely over the passive methylcyclopentyl group. In a cycle of threading, excitation, dethreading, de-excitation, threading, the ring undergoes directional motion along the molecular axle. Similar results were obtained for a different system,41 where explicit density functional theory calculations were described as verifying the general features of the energy landscapes. In neither of these cases40,41 was the transport energetically demanding44 since the ring starts and ends in the same bulk reservoir. The mechanism for the directional transport is shown in Fig. 7a. In bright, broad-spectrum, light, the excitation rates are the same irrespective of whether the molecular axle is threaded or not, ψ1,hν = ψ2,hν, and similarly the de-excitation rates do not depend on whether the axle is or is not threaded, ϕ1,hν = ϕ2,hν. Thus, the ratio of the probability to complete a clockwise cycle in preference to a counterclockwise cycle (i.e., the ratio of the probability for a ring to pass over the axle in the order azobenzene, recognition site, passive stopper to the probability to pass over the axle in the order passive stopper, recognition site, azobenzene) is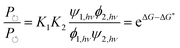 | (16) |
 | ||
| Fig. 7 (a) Graphical representation with structural formulas and (b) energy profiles for the operation of the light-driven directional translation of a small ring over a molecular axle reported by Ragazzon et al.40 We have drawn the illustration with a repulsive interaction between the macrocycle and the ammonium recognition site, when in the actual molecule this interaction is simply less attractive than in the ground state. Eqn (16) quantifies the effect of the energies independent of the drawings. | ||
The result, summarised in eqn (16), is schematically explained in Fig. 7b in terms of an energy ratchet. In the ground state, the barrier over the azobenzene is lower than that over the passive barrier, and the recognition site is attractive, resulting in the crown ether threading over the azobenzene group. In the excited state, the barrier over the passive methylcyclopentyl group is lower than that over the active azobenzene group. The recognition site is drawn as being repulsive in the excited state for clarity, although in the molecule, the recognition site is simply less attractive than in the ground state. The process of de-threading can, with a repulsive interaction, be very reasonably described as a power stroke in which azobenzene, in undergoing transition from the (E)- to the (Z)-form, pushes the crown ether over the methylcyclopentyl group. Now, let us consider a formally similar catenane rotor that is driven by catalysis of an energy-releasing chemical reaction.
Chemical catalysis-driven directional rotation
In a landmark paper, Wilson et al.6 reported recently on the design of a catenane-based rotor driven by catalytic conversion of fluoroenylmethoxycarbonyl chloride (Fmoc-Cl) to dibenzofulvene as shown in Fig. 8. Their achievement, which represents the first experimental demonstration of an AMM fueled by a catalytic reaction, is similar in concept to the ATP hydrolysis and ion transport-driven molecular machines of biology.45 Here, although we focus on a slightly simplified mechanism, it is one that incorporates all the essential features of the autonomously driven rotor described by Wilson.6 | ||
| Fig. 8 A chemically-driven catenane motor based on that of Wilson et al.6 (a) A strongly exergonic reaction – the conversion of Fmoc-Cl (red sphere) into dibenzofulvene – is harnessed with an hydroxyl site (red polygon) in the [2]catenane. (b) Graphical representation for the operation of the catenane motor. The larger, black, ring has two different recognition sites (orange and aqua regions) between which the smaller pink ring shuttles. There is a molecular speed bump indicated by the yellow sphere, and a hydroxyl site indicated by the red polygon. Contrary to what one might think based on the equilibrium constants K1 and K2, the probability of realising a counterclockwise motion (illustrated with a light gray semi-circle) is greater than for a clockwise cycle and is independent of K1 and K2. (c) The binding of Fmoc and the release of dibenzofulvene causes switching of the energy barrier and recognition site interaction energy. At first glance the diagram appears identical to the energy ratchet shown in Fig. 7b, but when we incorporate microscopic reversibility into the ψi and ϕi we see that the setup functions as an information ratchet, and with the experimental conditions Δμ > 0, and kon1F > kon2F, the most probable direction is from right to left, opposite to the direction predicted for an energy ratchet mechanism. | ||
The system comprises a small ring – shown in pink – moving on a cyclic track with two recognition sites illustrated by the orange and aqua regions. A catalytic site near the orange region can bind a “protecting group”, Fmoc, and catalyse its conversion to dibenzofulvene, followed by dissociation of dibenzofulvene to the bulk. In this process (Fig. 8a), the difference in free energy of Fmoc-Cl and dibenzofulvene is dissipated.
How can the energy released by conversion of Fmoc-Cl to dibenzofulvene be used to drive unidirectional rotation of the pink ring around the track? A very natural approach, by analogy with the radical pair-based recognition mechanism introduced by two of us16 into our synthetic molecular pump, is to incorporate a strongly repulsive interaction between the protecting group (red sphere) and the pink ring, thus engineering a power stroke for the mechanical transition in which the pink ring circumrotates from the orange to the aqua recognition site, following attachment of the Fmoc protecting group. This thought experiment would seem to lead to clockwise cycling in which the pink ring sees the components in the order orange recognition site, yellow speed bump, aqua recognition site, red catalytic site, orange recognition site, etc. This simple idea, however, does not work when the fuel is provided by the energy released during catalysis of a chemical reaction. A repulsive interaction that facilitates the mechanical transition of the pink ring to the aqua recognition site inevitably hinders the chemical reaction leading to the attachment of the protecting group. Instead, the motor, as described by Wilson et al.,6 undergoes counterclockwise cycling, where the directionality is determined by the fact that, on account of steric effects, binding Fmoc to the active site is faster when the ring is in the distal position at the aqua recognition site than when it is in the proximal position at the orange recognition site. The experimental condition actually leads to counterclockwise cycling in which the pink ring sees the components in the order orange recognition site, red catalytic site, aqua recognition site, yellow speed bump, orange recognition site, etc., as seen experimentally.6
The best way to recognise the futility of incorporating a power stroke is by writing down the immutable constraints of microscopic reversibility36,37 and work out the consequences. Firstly, we note that ψi,Δ and ϕi,Δ are not elementary rate constants, but rather the sum of “off” and “on” rates for Fmoc-Cl and dibenzofulvene, respectively, ψi,Δ = (koffiF + koffiD) and ϕi,Δ = (koniF + koniD). The constraints of microscopic reversibility36,37 are 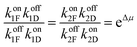 and
and  . When inserted into the expression for the ratio of clockwise and counterclockwise probabilities, we find
. When inserted into the expression for the ratio of clockwise and counterclockwise probabilities, we find
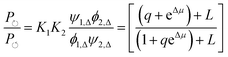 | (17) |
 can, by use of microscopic reversibility, be expressed in terms of only the off rates. Using microscopic reversibility, we find that because kon1F > kon2F by steric hindrance, then q > 1, the ratio in eqn (17) is less than unity, and hence the system undergoes counterclockwise rotation through its states. Neither Δμ nor q depend on the free-energies of any of the four states in the kinetic diagram in Fig. 8b.
can, by use of microscopic reversibility, be expressed in terms of only the off rates. Using microscopic reversibility, we find that because kon1F > kon2F by steric hindrance, then q > 1, the ratio in eqn (17) is less than unity, and hence the system undergoes counterclockwise rotation through its states. Neither Δμ nor q depend on the free-energies of any of the four states in the kinetic diagram in Fig. 8b.
It is important to recognize that in, e.g., a “stopped-flow” kinetic experiment designed to test for a “power stroke” where Fmoc is rapidly added to a solution of the catenane motor, the resulting transient rearrangement of the small pink ring would, in fact, be predominately clockwise, with net transition of the pink ring from the orange site to the aqua one over the yellow speed bump following attachment of the protecting group. A further “stopped-flow” experiment removing the protecting group would also be followed by transient clockwise transitions in which there would be net transfer of the pink ring from the aqua site to the orange one over the unoccupied catalyst. Both of these results would, from a naïve perspective, seem to be consistent with the predictions of a power-stroke mechanism. It is only in conjunction with the principle of microscopic reversibility that the kinetic data could be used to construct a correct theory of the steady state catalysis-driven motion. Stopped-flow experiments are often used in attempts to decipher the mechanisms of biomolecular motors. The discussion here illustrates the caution that must be exercized in interpreting experimental results.
The power-stroke model is wrong for motors driven by chemical catalysis
The cycle illustrated in Fig. 8b, and the energy diagram in Fig. 8c, are each drawn intentionally as a trompe l'oeil. It is not wrong in any particular detail but does lead the eye to draw the incorrect conclusion that the motion is most probably clockwise in Fig. 8b and left to right in Fig. 8c, due to a power stroke. In other words, (i) the pink ring undergoes transition from the aqua site to the orange one over the unoccupied catalyst, (ii) the protecting group becomes attached to the catalyst, followed (iii) by the transition of the pink ring from the orange site to the aqua one over the yellow speed bump – the power stroke – after which (iv) the protecting group dissociates and the cycle repeats. Instead, the backward trajectory, in which (i′) the protecting group is attached when the pink ring is on the aqua recognition site, (ii′) the ring undergoes transition from aqua site to the orange site over the yellow speed bump (yes, energetically uphill), (iii′) the protecting group dissociates from the catalytic site, and (iv′) the ring moves from the orange site to the aqua site over the unoccupied catalyst, is the more probable. The directionality is enforced by having the binding of Fmoc and dissociation of dibenzofulvene more likely than the binding of dibenzofulvene and the dissociation of Fmoc (i.e., Δμ > 0) and by having the rate of binding of Fmoc slower when the ring is nearby than when the ring is far away.The literature is rife with misleading models involving two asymmetric energy surfaces with transitions between them. Following observation that the systems are “far-from-equilibrium” many authors assign rate constants for the transitions between the surfaces ad libitum for mathematical convenience rather than for thermodynamic consistency with the principle of microscopic reversibility. They then go on to draw incorrect conclusions, augmented with Kiplingesque “just so stories” to accompany a diagram like the one in Fig. 8c. Blackmond,36 in the context of the origins of chirality in molecular systems, describes, in a wonderfully evocative and appropriately disparaging way, models that are not consistent with microscopic reversibility as “when pigs fly” chemistry. Regrettably, flying pig models of molecular machines often reinforce preconceived, but incorrect notions of how molecular machines work. By assigning the rate constants in Fig. 8 such that ψ1,Δ = ψ2,Δ and ϕ1,Δ = ϕ2,Δ, we immediately arrive at the false conclusion that the power stroke is important for determining directionality. In contrast, assignments that are consistent with microscopic reversibility show that in fact the “power stroke” is not important at all for determining directionality.
True progress towards a thermodynamic theory of molecular machines34 requires an intellectually disciplined approach in which fundamental constraints, be they the Bose–Einstein relations for light-driven machines or the relations of microscopic reversibility for thermally activated processes, are rigorously applied without regard for preconceived, macroscopically based notions about how molecular machines ought to work.
Equilibrium or not equilibrium, that is the question
If we were to watch by some yet undeveloped high resolution microscopic method a sequence of 8 to 10 transitions of an individual molecular machine, there would be no way of determining whether the system was or was not in thermodynamic equilibrium while carrying out these transitions. The character of the physical motion by which a single AMM (or bio-MM) carries out its function is the same at and away-from thermodynamic equilibrium. The individual trajectories away-from-equilibrium are just equilibrium trajectories with a statistical weighting that is different than that at equilibrium, depending on the presence and type of fuel supplied to drive the system.46 The trajectories comprise waiting times in which a ring moves diffusively near a single recognition site, and transit times in which the ring undergoes a transition from one recognition site to another. The waiting times which are, in general, much longer than the transit time, are inverse of what chemists know to be the rate constant. The transit times in contrast are very short. Any realistic movie of a molecular machine would be incredibly boring, with 99.99 percent of the movie devoted to diffusion near a recognition site, and only 0.01 percent (or less) of the movie devoted to the actual motion.47 That part involving net motion from one station to another is the same at and away-from-equilibrium.25 At or very-near thermodynamic equilibrium, there will be both forward and backward transitions, but away-from-equilibrium, there will be predominately forward transitions. The waiting times depend on the concentration of the substrate. A “faster” motor moves faster not because of a greater velocity but rather because of a shorter waiting time. This realization registers an important distinction because it makes clear why frictional dissipation is not all that relevant in the case of molecular machines. When these machines are attached to microscale spheres, or other objects that must move through a viscous medium, frictional dissipation is important, but not at the scale of individual molecules.Eqn (6), derived from the Onsager and Machlup approach29 and based on Onsager's theory of microscopic reversibility, provides a powerful way to understand the effect of external driving on steady populations among states of a molecule, as well as on how the driving influences the relative frequencies of specific pathways linking the different states. When the driving is in the form of light, or of external modulation of the chemical or thermodynamic environment, specific pathways can be favoured by engineering repulsive interactions between components of a machine that drives a power stroke. In contrast, when the driving is provided by a non-equilibrium catalysed reaction, repulsive (or attractive) interactions can play no role whatsoever. The required sculpting of the energy landscape34 must be accomplished by tailoring the energy barriers to shepherd the reaction along the desired pathway, where the motion itself is driven by thermal noise.
Over-emphasis on the fact that, by some measures, AMMs operate far-from-equilibrium also leads to misunderstanding regarding the physics of their motion. Some authors write of violent kicks delivered to molecular machines by the reactions they catalyze, of molecular motors executing judo throws, of enzymes stepping on landmines, of macromolecules being struck by hammers to give rise to resonant phenomena, and of enzymes ringing like bells while playing the symphony of life. These depictions have nothing whatsoever to do with the way that molecular machines work. While the probability distribution for a molecular machine amongst its possible states is doubtless very different than the Boltzmann distribution expected at equilibrium, the physical motions of molecular machines are very close to equilibrium. The role of input work is to select preferentially, from amongst the ensemble of equilibrium trajectories, those that accomplish the desired function, and suppress those that impede the accomplishment of that function. For more information on the relationship between synthetic motors and biomolecular motors see, in addition to ref. 45, see the review ref. 34 in which recent work on computational studies of the FoF1 ATP synthase and on myosin is discussed and shows that in these systems, too, the principle of microscopic reversibility precludes operation by a power-stroke mechanism. The work focusses on elucidating the energy landscape that governs the function of these molecules.
Why microscopic reversibility is so important
We can appreciate the importance of understanding microscopic reversibility36,37 in the context of recently published work of Collins et al.7 who describe a chemically powered unidirectional rotor based on a palladium redox cycle illustrated schematically in Fig. 9. A mono-substituted benzene plays the role of the rotor, shown in dark blue, while a more complex biaryl sulfoxide plays the role of the stator, shown in scarlet. By sequentially changing the chemical environment of the molecule, the rotor is caused to undergo 360° directional cycling about the stator as detected by NMR spectroscopy following each cycle of the external changes in the environment. The strain developed when palladium binds to the molecule, and again, when it dissociates, is essential for operation of the motor by external manipulation of the chemical environment. The authors go on to suggest that the design provides a blueprint for an autonomous rotor, and that under the right conditions this molecule could operate autonomously by binding Pd(II) catalyzing its reduction to Pd(0), releasing Pd(0), and continuing to cycle using the difference in the chemical potential between Pd(II) and Pd(0) to fuel continual rotation.7 Let us examine this question in the context of the four-state model shown in Fig. 10 which captures the essential ingredients – two mechanical states, proximal (1) and distal (2) (relative to the tip of the triangle) and two chemical states, bound or not bound to Pd.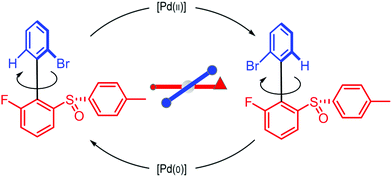 | ||
| Fig. 9 Schematic illustration of a rotary motor driven by a palladium redox cycle proposed by Collins et al.7 Based on the observation that externally manipulating the reaction conditions to interconvert between Pd(0) and Pd(II) leads to directional rotation, the authors suggested that the rotor could be driven autonomously by maintaining a constant chemical potential difference between Pd(0) and Pd(II). | ||
The authors argue that the energy difference of the configurations by which K1, K2 > 1 is essential for directional rotation. Indeed, in their experiments where the reaction conditions are externally changed this is true. However, from microscopic reversibility, for an autonomous rotor driven by a catalytic conversion, Pd(II) → Pd(0), it is not necessary to have shifted equilibria to obtain net rotation, and in fact K1= K2 = 1 will optimise the velocity of the motor. What is necessary is to find some way of designing an allosteric interaction such that the rotor in the proximal position is highly specific for Pd(II) and the rotor in the distal position is highly specific for Pd(0). As a result, Pd(II) – at high chemical potential – would most probably bind when the motor is in the proximal state, and that Pd(0) – at low chemical potential – would most probably dissociate when the motor is in the distal state, a condition concomitant with 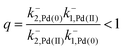 . This is a clear example where theory can guide experimental design of a molecular machine.
. This is a clear example where theory can guide experimental design of a molecular machine.
Prospective
Having clarified the thermodynamic and kinetic aspects by which AMMs operate, we should point out where, in our opinion, the next steps in the field might take us. We envision two potential developments for AMMs in the near future. The first one, despite being obvious, yet not straightforward to achieve in practical terms, is the integration of AMMs into complex chemical networks, where molecular tasks (e.g., see Fig. 2) are precisely organized in space and synchronized in time. For example, considering the recent progress of functional molecular switches into MOF,48 one may envision a MOF-based system where multiple AMMs are able to work in concert, varying the outcome of a cascade of reactions depending on the type of energy supplied, or inducing and amplifying the directional motion of multiple components in a controlled manner.Another way, perhaps less intuitive, regards the implementation of the above described pump operation into polymeric materials (i.e., polyrotaxanes49), where multiple rings are confined onto chains that display no binding affinity towards them. The resulting enthalpically and entropically demanding structures represent a goal that is impossible to achieve using the available repertoire of chemical reactions or supramolecular approaches, and, being away-from-equilibrium, are expected to display unprecedented mechanical and physico-chemical properties.
Conclusions and outlook
As noted recently by Jean-Marie Lehn,50 perhaps the biggest question in science is how did complex matter arise and self-organize to form life. He goes on to reflect that “It is the task of chemistry to decipher what lies behind this word, to fill in the steps that progressively led to matter of increasing complexity”.The fundamental physical principle of microscopic reversibility provides a tantalizing glimpse towards a theory of self-organization based on a simple extension of the familiar relation of equilibrium thermodynamics to one for a not necessarily equilibrium steady state
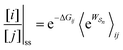 | (18) |
 is the exponential of the work absorbed from/done on the environment in going from state j to state i averaged over all paths leading between j and i. At equilibrium, this general equation leads back to the familiar Boltzmann expression since the excess energy,
is the exponential of the work absorbed from/done on the environment in going from state j to state i averaged over all paths leading between j and i. At equilibrium, this general equation leads back to the familiar Boltzmann expression since the excess energy,  , is the same for each path.
, is the same for each path.
The simplicity of eqn (18) obscures the fact that  is, in general, quite difficult to calculate. Unlike ΔGij, which depends only on the free-energies of the molecular states i and j, away from equilibrium
is, in general, quite difficult to calculate. Unlike ΔGij, which depends only on the free-energies of the molecular states i and j, away from equilibrium  depends on each entire path
depends on each entire path 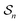 connecting the states, and the average must be taken over all the many paths
connecting the states, and the average must be taken over all the many paths  . Those trajectories that absorb energy from the non-equilibrium source are favored by a large value
. Those trajectories that absorb energy from the non-equilibrium source are favored by a large value 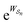 , but the relative probabilities can also be kinetically controlled by the factors
, but the relative probabilities can also be kinetically controlled by the factors  in eqn (6). The former, thermodynamic terms, dominates the mechanism for energy ratchets (including light driven processes, and processes driven by external modulation of chemical or physical parameters), but only the latter, kinetic factors (kinetic gating) play a role in determining the direction of a catalysis-driven molecular machine. The reason for this is that, for a catalysis-driven machine, the relationships between the thermodynamic factors are constrained by the principle of microscopic reversibility.
in eqn (6). The former, thermodynamic terms, dominates the mechanism for energy ratchets (including light driven processes, and processes driven by external modulation of chemical or physical parameters), but only the latter, kinetic factors (kinetic gating) play a role in determining the direction of a catalysis-driven molecular machine. The reason for this is that, for a catalysis-driven machine, the relationships between the thermodynamic factors are constrained by the principle of microscopic reversibility.
Progress in developing a theory of non-equilibrium steady states is fueled by consideration of specific molecules, with MIMs as prime examples. Chemistry, unlike either biology or physics, is able to make the object of its study, and then use that object as a concrete reference point for detailed experimental and theoretical analysis.
The artificial pump reported by two of us5 (Fig. 4–6) is complex enough to accomplish a challenging function – the use of external energy to maintain a non-equilibrium steady state between assembled and disassembled forms – but simple enough to allow for analysis using standard kinetic and thermodynamic models of chemistry.14 Similarly, recent molecules that facilitate directional transport of chemical rings along molecular rods, driven by light or external pumping, provide a specific foil against which directional rotation of two rings relative to one another, driven by chemical catalysis, can be compared. Despite formal similarity of the kinetic mechanisms describing the two systems driven by different fuels, we recognize, by applying the principle of microscopic reversibility to the catalysis-driven machine, that the design principles are entirely different. This realisation leads to a very tangible and important result – the power stroke model that has served as the preeminent description of ATP and ion-transport driven biomolecular machines, is simply conceptually wrong for these systems. All chemically driven molecular motors function as information ratchets31 in which kinetic gating, and not repulsive or attractive interactions, determines the directionality. Pushing and pulling is not only not necessary, it is not even useful.
The detailed kinetic analysis of molecular systems can, at times, seem tedious in comparison to sweeping statements about new and novel thermodynamic relations that provide a pathway toward a physical theory of the origin of life. However, it is only through the rigorous application of fundamental physical principles such as microscopic reversibility or the Bose–Einstein relations, that the essential back and forth between theory and experimental investigation of synthetically manipulable chemical systems can be carried out to provide insight into the basic mechanisms of self-organization. MIMs not only provide opportunities for the development of new materials that can take advantage of the possibilities for harnessing a variety of external energy in technology, but also serve as a remarkable laboratory for developing a more complete understanding of how molecules can undergo self-organization to form complex entities to perform the essential functions of life.
Acknowledgements
This work was supported by the Non-equilibrium Energy Research Center which is an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0000989.Notes and references
- P. Glandsdorff and I. Prigogine, Thermodynamics of Structure, Stability and Fluctuations, Wiley-Interscience, New York, 1971 Search PubMed.
- C. J. Bruns and J. F. Stoddart, The Nature of the Mechanical Bond: From Molecules to Machines, Wiley, New Jersey, 2016 Search PubMed.
- C. O. Dietrich-Buchecker, J.-P. Sauvage and J.-P. Kintzinger, Tetrahedron Lett., 1983, 24, 5095–5098 CrossRef CAS.
- P. L. Anelli, N. Spencer and J. F. Stoddart, J. Am. Chem. Soc., 1991, 113, 5131–5133 CrossRef CAS PubMed.
- C. Cheng, P. R. McGonigal, S. T. Schneebeli, H. Li, N. A. Vermeulen, C. Ke and J. F. Stoddart, Nat. Nanotechnol., 2015, 10, 547–553 CrossRef CAS PubMed.
- M. R. Wilson, J. Solà, A. Carlone, S. M. Goldup, N. Lebrasseur and D. A. Leigh, Nature, 2016, 534, 235–240 CrossRef CAS PubMed.
- B. Collins, J. C. M. Kistemaker, E. Otten and B. L. Feringa, Nat. Chem., 2016, 8, 860–866 CrossRef CAS.
- R. D. Astumian, Annu. Rev. Biophys., 2011, 40, 289–313 CrossRef CAS PubMed.
- N. A. Sinitsyn, J. Phys. A: Math. Theor., 2009, 42, 193001 CrossRef.
- T. Y. Tsong and R. D. Astumian, Prog. Biophys. Mol. Biol., 1987, 50, 1–45 CrossRef CAS PubMed.
- J. M. Abendroth, O. S. Bushuyev, P. S. Weiss and C. J. Barrett, ACS Nano, 2015, 9, 7746–7768 CrossRef CAS PubMed.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- A. Coskun, M. Banaszak, R. D. Astumian, J. F. Stoddart and B. A. Grzybowski, Chem. Soc. Rev., 2012, 41, 19–30 RSC.
- C. Cheng, P. R. McGonigal, J. F. Stoddart and R. D. Astumian, ACS Nano, 2015, 9, 8672–8688 CrossRef CAS PubMed.
- D. S. Liu, R. D. Astumian and T. Y. Tsong, J. Biol. Chem., 1990, 265, 7260–7267 CAS.
- R. D. Astumian, Phys. Rev. Lett., 2003, 91, 118102 CrossRef PubMed.
- Y. C. Kim, L. A. Furchtgott and G. Hummer, Phys. Rev. Lett., 2009, 103, 268102 CrossRef PubMed.
- M. L. López, M. Queralt-Martín and A. Alcaraz, Nanoscale, 2016, 8, 13422–13428 RSC.
- Y. Zhang, C.-T. Lai, B. J. Hinds and G. C. Schatz, J. Phys. Chem. C, 2016, 120, 14495–14501 CAS.
- R. D. Astumian, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19715–19718 CrossRef CAS.
- S. Rahav, J. Horowitz and C. Jarzynski, Phys. Rev. Lett., 2008, 101, 140602 CrossRef PubMed.
- N. A. Sinitsyn and I. Nemenman, Phys. Rev. Lett., 2007, 99, 220408 CrossRef CAS PubMed.
- R. D. Astumian and B. Robertson, J. Am. Chem. Soc., 1993, 115, 11063–11068 CrossRef CAS.
- R. D. Astumian, P. B. Chock, T. Y. Tsong and H. V. Westerhoff, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 6416–6435 CrossRef CAS.
- M. Bier, I. Derényi, M. Kostur and R. D. Astumian, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 6422–6432 CrossRef CAS.
- D. Sigg, J. Gen. Physiol., 2014, 144, 7–26 CrossRef CAS PubMed.
- S. Walcott, J. Chem. Phys., 2008, 128, 215101 CrossRef PubMed.
- P. Muzikar, J. Phys. Chem. B, 2016, 120, 5720–5723 CrossRef CAS PubMed.
- L. Onsager and S. Machlup, Phys. Rev., 1953, 91, 1505–1512 CrossRef CAS.
- E. M. Purcell, Am. J. Phys., 1977, 45, 3–11 CrossRef.
- R. D. Astumian and I. Derényi, Eur. Biophys. J., 1998, 27, 474–489 CrossRef CAS PubMed.
- D. Chowdhury, Phys. Rep., 2013, 529, 1–197 CrossRef CAS.
- U. Seifert, Rep. Prog. Phys., 2012, 75, 126001 CrossRef PubMed.
- R. D. Astumian, S. Mukherjee and A. Warshel, ChemPhysChem, 2016, 17, 1719–1741 CrossRef CAS PubMed.
- W. P. Jencks, Annu. Rev. Biochem., 1997, 66, 1–18 CrossRef CAS PubMed.
- D. G. Blackmond, Angew. Chem., Int. Ed., 2009, 48, 2648–2654 CrossRef CAS PubMed.
- R. D. Astumian, Nat. Nanotechnol., 2012, 7, 684–688 CrossRef CAS PubMed.
- C. Cheng and J. F. Stoddart, ChemPhysChem, 2016, 17, 1780–1793 CrossRef CAS PubMed.
- M. Baroncini, S. Silvi, M. Venturi and A. Credi, Angew. Chem., Int. Ed., 2012, 51, 4223–4226 CrossRef CAS PubMed.
- G. Ragazzon, M. Baroncini, S. Silvi, M. Venturi and A. Credi, Nat. Nanotechnol., 2015, 10, 70–75 CrossRef CAS PubMed.
- H. Li, C. Cheng, P. R. McGonigal, A. C. Fahrenbach, M. Frasconi, W.-G. Liu, Z. Zhu, Y. Zhao, C. Ke, J. Lei, R. M. Young, S. M. Dyar, D. T. Co, Y.-W. Yang, Y. Y. Botros, W. A. Goddard III, M. R. Wasielewski, R. D. Astumian and J. F. Stoddart, J. Am. Chem. Soc., 2013, 135, 18609–18620 CrossRef CAS PubMed.
- A. Carlone, S. M. Goldup, N. Lebrasseur, D. A. Leigh and A. Wilson, J. Am. Chem. Soc., 2012, 134, 8321–8323 CrossRef CAS PubMed.
- J. Conyard, K. Addison, I. A. Heisler, A. Cnossen, W. R. Browne, B. L. Feringa and S. R. Meech, Nat. Chem., 2012, 4, 547–551 CrossRef CAS PubMed.
- C. Cheng, P. R. McGonigal, W.-G. Liu, H. Li, N. A. Vermeulen, C. Ke, M. Frasconi, C. L. Stern, W. A. Goddard III and J. F. Stoddart, J. Am. Chem. Soc., 2014, 136, 14702–14705 CrossRef CAS PubMed.
- M. Schliwa and G. Woehlke, Nature, 2003, 422, 759–765 CrossRef CAS PubMed.
- R. Ballardini, V. Balzani, A. Credi, M. T. Gandolfi and M. Venturi, Acc. Chem. Res., 2001, 34, 445–455 CrossRef CAS PubMed.
- P. B. Moore, Annu. Rev. Biophys., 2012, 41, 1–19 CrossRef CAS PubMed.
- Q. Chen, J. Sun, P. Li, I. Hod, P. Z. Moghadam, Z. S. Kean, R. Q. Snurr, J. T. Hupp, O. K. Farha and J. F. Stoddart, J. Am. Chem. Soc., 2016, 138, 14242–14245 CrossRef CAS PubMed.
- K. Kato, T. Yasuda and K. Ito, Polyrotaxane and Slide-Ring Materials, Monographs in Supramolecular Chemistry, Royal Society of Chemistry, Cambridge, 2016 Search PubMed.
- J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 2013, 52, 2836–2850 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |








