Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dispersity effects in polymer self-assemblies: a matter of hierarchical control†
Kay E. B.
Doncom
a,
Lewis D.
Blackman
a,
Daniel B.
Wright‡
a,
Matthew I.
Gibson
 ab and
Rachel K.
O’Reilly
ab and
Rachel K.
O’Reilly
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry, CV47AL, UK. E-mail: rachel.oreilly@warwick.ac.uk
bWarwick Medical School, University of Warwick, Coventry, CV47AL, UK
First published on 9th June 2017
Abstract
Advanced applications of polymeric self-assembled structures require a stringent degree of control over such aspects as functionality location, morphology and size of the resulting assemblies. A loss of control in the polymeric building blocks of these assemblies can have drastic effects upon the final morphology or function of these structures. Gaining precise control over various aspects of the polymers, such as chain lengths and architecture, blocking efficiency and compositional distribution is a challenge and, hence, measuring the intrinsic mass and size dispersity within these areas is an important aspect of such control. It is of great importance that a good handle on how to improve control and accurately measure it is achieved. Additionally dispersity of the final structure can also play a large part in the suitability for a desired application. In this Tutorial Review, we aim to highlight the different aspects of dispersity that are often overlooked and the effect that a lack of control can have on both the polymer and the final assembled structure.
Key learning points1. What do we mean by dispersity within polymers?2. What methods do we have to reliably measure the dispersity within polymers and their self-assembled structures? 3. How do polymer properties relate to assembly structure and function? 4. Do we always need control on lower hierarchical levels in order to obtain well-defined higher order structures? 5. In what instances are controlled polymers and assemblies required? |
Introduction
Amphiphilic block copolymers, like small molecule surfactants, can form a range of nanostructures in a selective solvent. These polymeric self-assembled nanostructures are finding more potential applications and uses as a result of the higher stability and robustness that the polymers infer on the particles, due to their low critical aggregation concentrations and the ability to contain discrete functionalized domains within the assembly. There are many factors that can impact the properties of the self-assembled structure, some are a result of the self-assembly process, such as preparation pathway, and some are factors that are inherent to the polymers of which these nanoparticles comprise, such as molar mass variation, block ratio variation and compositional variation. Hence, it is important to consider these aspects individually and the impact that they can have on the desired properties of the assembled structure. The size distribution of self-assembled structures is often reported in scientific articles, but there are fewer reports of how dispersity in polymer composition and functionality can affect the overall properties of the nanoparticle. In this Tutorial Review, we aim to highlight the different areas, both in the polymer building blocks and the assembly route, which can impact the properties of the final structures. We also discuss whether control on the polymer scale is always needed to impart control over the nanoparticles formed and highlight areas where absolute control over the self-assembled structure, in terms of dispersity and functionality, are indeed required.Controlling and determining polymer dispersity in polymers
Polymer length dispersity
Before considering the effect of dispersity on a self-assembled system, one must consider the effect of variation within the building blocks of the nanoparticle, i.e. the polymer chains. Advances in living polymerization techniques such as ionic polymerization, and more recently reversible deactivation radical polymerization (RDRP) techniques, which will be the main focus of this Tutorial Review, have paved the way for the synthesis of well-defined block copolymers. Although the molar mass distributions of polymers prepared by these techniques are narrow when compared to free-radical processes for instance, some level of dispersity remains. The most commonly studied form of dispersity amongst polymer chains is that of their molar mass; this is assessed by studying both the breadth and shape of the molar mass distribution. Commonly, size exclusion chromatography (SEC) is used to reveal this information, however care should be taken when considering the absolute values obtained by this analysis technique. The obtained retention time for a polymer chain moving along the SEC column is related to the hydrodynamic volume of the chain in solution, assuming no chemical interaction with the SEC column, as opposed to its molar mass. Typically, the distribution of retention times is transformed mathematically into a distribution of molar masses by use of a series of calibrants of known narrow molar mass distributions, however one must consider the similarity of the solution behavior between the sample polymer and the calibrant standard. More accurate results can be obtained by use of a multi-detector SEC setup that employs the use of a multi-angle light scattering (MALS) and/or an intrinsic viscosity detector in conjunction with a refractive index (RI) or ultraviolet (UV) detector. For additional information regarding SEC, the reader is referred to the following text.1 Additionally, more advanced techniques employing 2D chromatography, such as SEC coupled to an affinity column, or liquid chromatography under critical conditions of absorption, coupled to information rich detectors such as those discussed above, as well as FT-IR or NMR spectroscopy, or ESI-ToF and MALDI-ToF MS exist.2 These advanced techniques can give information on not only length but also compositional dispersity, and can even decipher polymer chains of identical length that vary only in their end group.The calculated molar mass distribution obtained can be described in terms of different molar mass averages, of which we shall consider the number average molar mass (Mn) and the weight average molar mass (Mw). These are defined in eqn (1) and (2), respectively, where Ni is the number of chains with mass Mi. The dispersity (ĐM) of the polymer is the ratio of these two molar mass averages as shown in eqn (3) and is generally considered a measure of the broadness of a polymer's molar mass distribution. However, the standard deviation (Sn) associated with a polymer's Mn is given in eqn (4).3
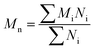 | (1) |
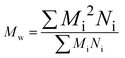 | (2) |
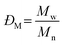 | (3) |
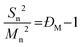 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1. This means that for the 20 kg mol−1 polymer, 95% of its chains fall between 8.6–31.4 kg mol−1 (±2Sn), whereas for the 200 kg mol−1 polymer with an identical ĐM, 95% of the molar mass distribution falls between 86–314 kg mol−1. This is something that should be considered when comparing the dispersity of polymer samples with significantly different molar masses. Additionally, this shows that although the latter polymer is relatively well-defined, with a ĐM value that is reasonable from an RDRP process, 95% of its molar mass distribution occupies a molar mass range of 228 kg mol−1. As such, even polymers with ĐM values as low as 1.01 cannot be considered well defined in terms of its molar mass, when compared to an entity with a single molar mass. In this case, an Mn = 100 kg mol−1 polymer of ĐM = 1.01 occupies a molar mass range between 80–120 kg mol−1 in 95% of its chains. Polymer molar mass, and the dispersity thereof, is a factor that affects numerous polymer properties including the glass transition temperature (Tg), processability, viscosity and strength, resistance and wear.5 As will be discussed later in this review, polymer dispersity can also have an effect on the properties of the self-assembled structures, such as morphology and size. As such, there have been a few reports in recent years that have focused on tuning the ĐM and shape of a polymer's molar mass distribution, whilst keeping other properties, such as Mn, constant. Recently, Fors and coworkers were able to tune both the breadth and shape of the molar mass distribution of a series of polymers synthesized by nitroxide-mediated polymerization (NMP).4 Here, the authors used different total addition times of the nitroxide initiator to the polymerization, at a constant addition rate, which led to the preparation of polymers with a controlled ĐM. Additionally, by using different addition rate profiles, the shape of the molar mass distribution could also be controlled. The authors used an asymmetry factor (As) to describe the symmetry of the shape of the distribution, the calculation of which is defined in eqn (5).4 The values for B and A are the deviations of the molar mass of the upper and lower 10% of the distribution, respectively, from the molar mass of the peak of the distribution (Mp) (Fig. 1).
000 g mol−1. This means that for the 20 kg mol−1 polymer, 95% of its chains fall between 8.6–31.4 kg mol−1 (±2Sn), whereas for the 200 kg mol−1 polymer with an identical ĐM, 95% of the molar mass distribution falls between 86–314 kg mol−1. This is something that should be considered when comparing the dispersity of polymer samples with significantly different molar masses. Additionally, this shows that although the latter polymer is relatively well-defined, with a ĐM value that is reasonable from an RDRP process, 95% of its molar mass distribution occupies a molar mass range of 228 kg mol−1. As such, even polymers with ĐM values as low as 1.01 cannot be considered well defined in terms of its molar mass, when compared to an entity with a single molar mass. In this case, an Mn = 100 kg mol−1 polymer of ĐM = 1.01 occupies a molar mass range between 80–120 kg mol−1 in 95% of its chains. Polymer molar mass, and the dispersity thereof, is a factor that affects numerous polymer properties including the glass transition temperature (Tg), processability, viscosity and strength, resistance and wear.5 As will be discussed later in this review, polymer dispersity can also have an effect on the properties of the self-assembled structures, such as morphology and size. As such, there have been a few reports in recent years that have focused on tuning the ĐM and shape of a polymer's molar mass distribution, whilst keeping other properties, such as Mn, constant. Recently, Fors and coworkers were able to tune both the breadth and shape of the molar mass distribution of a series of polymers synthesized by nitroxide-mediated polymerization (NMP).4 Here, the authors used different total addition times of the nitroxide initiator to the polymerization, at a constant addition rate, which led to the preparation of polymers with a controlled ĐM. Additionally, by using different addition rate profiles, the shape of the molar mass distribution could also be controlled. The authors used an asymmetry factor (As) to describe the symmetry of the shape of the distribution, the calculation of which is defined in eqn (5).4 The values for B and A are the deviations of the molar mass of the upper and lower 10% of the distribution, respectively, from the molar mass of the peak of the distribution (Mp) (Fig. 1).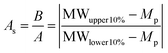 | (5) |
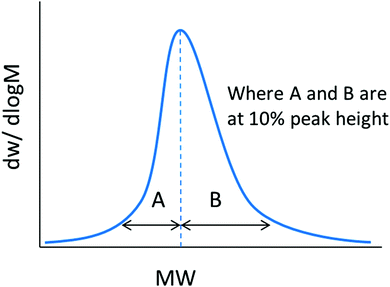 | ||
| Fig. 1 Depiction of the calculation of the asymmetry factor (As) for a molar mass distribution. Adapted from ref. 4 with permission from the American Chemical Society, copyright 2016. | ||
Polymer block dispersity
By their very nature, block copolymers will show discrepancies in both the length of each block and their respective end-group fidelity. This will typically depend on the type of polymerization(s) employed. For instance, ring opening metathesis polymerization (ROMP) and ionic polymerizations that are truly “living” in character generally show better end-group fidelity of the growing chain between each chain extension than RDRP processes by virtue of the fact that chain termination does not occur. However, one must also consider the inherent limitations of these techniques such as backbiting in ROMP, which can lead to branching and therefore dispersity in the polymer chain's architecture and hydrodynamic volume, or the lack of functional group compatibility in ionic polymerizations. Additionally, the block sequence control in living ring opening polymerizations (ROP) is limited by transesterification reactions and unwanted initiation from contaminants such as water. Furthermore, intermolecular chain transfer to polymer in ROP results in shuffling of the polymer segments, and therefore leads to dispersity in the monomer or block sequence. This behavior is subtle as it results in a broadening of the molar mass distribution but no change in Mn as the total number of chains remains constant. RDRP techniques have gained popularity owing to their tolerance to a wide variety of different chemistries in the monomer and being less synthetically taxing than ionic polymerizations. In the case of RDRP, techniques that make use of the persistent radical effect, such as ATRP and NMP, often show the most promising efficiency in the subsequent chain extension of macroinitiators (also referred to as the blocking efficiency) because of the lack of a requirement for a second small molecule initiator. However, since termination is still a contributing factor in these techniques, “dead” chains that will not chain extend in subsequent polymerizations can still arise. Keddie has discussed a further complication in synthesizing block copolymers by reversible addition fragmentation chain transfer (RAFT) polymerization.6 Although typically very low concentrations are employed, the need for an initiator means that some chains from the polymerization of the first block will be initiator derived and will bear this functionality at the α-end group. Therefore, if a specific functional moiety (e.g. targeting ligand, fluorescent dye, etc.) of the chain transfer agent was expected to be present on the α-end group, 100% functionalization of the chains will not be achieved in the case of RAFT polymerization. Additionally, some chains undergo termination so functionality at the ω-end group will also be lost in these cases. Whilst important for homopolymers, both these factors become even more so when considering the synthesis of block copolymers. After just a single chain extension of a homopolymer (A) to synthesize a diblock copolymer (AB), the polymer sample will contain a mixture of both dead and living RAFT CTA-derived AB diblock copolymer chains, both dead and living initiator-derived AB diblock copolymer chains, both dead and living initiator-derived B homopolymer chains, and dead initiator- and RAFT CTA-derived A homopolymer chains (see Fig. 2).6 The contribution of initiator-derived chains can be minimized by methods developed by Perrier and coworkers.7 Here, monomers that show high propagation rates, and therefore high kp/(kt)1/2, such as acrylamides, were employed at high concentrations, in aqueous media, in order to increase the overall reaction rate. Crucially, this allowed for very small initiator equivalents to be used in order to reduce the amount of initiator-derived chain ends but still allow for reasonable reaction times. The low degree of termination coupled with the excellent end-group retention resulting from the low initiator concentration allowed for the synthesis of multiblock copolymers with low dispersities by RAFT polymerization in a one-pot process.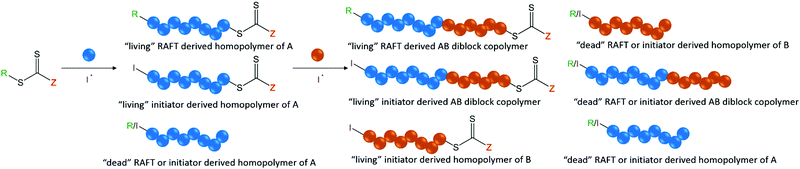 | ||
| Fig. 2 The various polymer species formed during a chain extension by RAFT polymerization. Figure adapted from ref. 6 with permission from the Royal Society of Chemistry, copyright 2014. | ||
Even though block copolymers may have poor blocking efficiency, they may not necessarily have a poor length dispersity and vice versa. For example, Matyjaszewski and coworkers investigated the use of activators regenerated by electron transfer atom transfer radical polymerization (ARGET ATRP) to achieve polymer distributions with controllable ĐM. By varying the catalyst loadings in the polymerization, the ĐM values of a series of poly(methyl acrylate) and poly(styrene) homopolymers could be controlled. At very low catalyst amounts (<5 ppm), the polymers showed relatively high ĐM values up to 2.0, however they still retained their end group functionality and were able to undergo successful chain extensions to form diblock copolymers with narrow molar mass distributions.8
Harrisson and coworkers carried out statistical analyses on both real and theoretical precision polymers prepared by different synthetic techniques.9 Using a monomer (B) that could not homopolymerize into a growing polymer chain and targeting a polymer of composition A10–B1–C10, single monomer addition resulted in only 12.5% of chains actually displaying this exact composition. Similarly, the addition of a rapidly polymerizing monomer into a slowly polymerizing mixture resulted in only 4.6% of chains containing just one unit of monomer B, at position 11, in the polymer chain. The probability of finding monomer B in the target position was also found to increase with increasing DP of B; there is a 95% chance of finding monomer B at the midpoint (in this case position 16) if the target composition is A10B11C10 compared with just a 17.5% chance for A10B1C10 (position 11).
For (multi)block copolymers synthesized by coupling chemistries employed using the end group, such as click chemistries, the assessment of the success of the coupling reaction becomes increasingly complicated as the dispersity of the two constituent blocks increases. By investigating the quantitative click conjugation of theoretical molar mass distributions, Barner-Kowollik found that the conjugation of polymers led to conjugates with a lower ĐM than their constituent blocks, and Mn values equal to the sum of the Mn values of their constituent blocks, regardless of constituent block dispersity.10 The author showed that when conjugating polymers with narrow molar mass distributions (ĐM < 1.10), a clear shift in the entire distribution could be observed with no significant change in the overall shape of the distribution. However, when conjugating polymers with ĐM > 2.0, although the Mn of the conjugate equaled the Mn of the constituent blocks, the peak molar mass (Mp) decreased relative to the higher molar mass block. Although the conjugate appeared to have a lower molar mass than one of its constituent blocks, on closer inspection of the overall distribution, fewer lower molar mass species existed in the conjugate, which allowed Mn to increase despite the decrease in Mp. For constituent blocks with vastly different Mn and ĐM values, the ideal shape of the molar mass distribution for a quantitatively conjugated block copolymer was found to be bimodal, when analyzed by SEC (Fig. 3). This was rationalized by considering that a distribution obtained by using a refractive index detector of an SEC calculated the number of repeat units at a certain molar mass, not the number of chains at a certain molar mass. By calculating the concentration (i.e. number distribution) and plotting against molar mass in a linear plot, the distributions of the conjugates were found to be unimodal and of higher molar mass than their constituent block copolymers.10
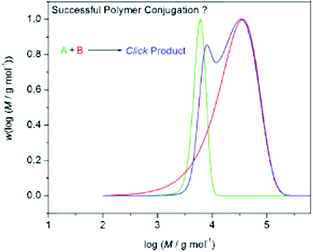 | ||
| Fig. 3 Expected theoretical distributions obtained from conjugation of two polymer distributions in a quantitative process. Two constituent blocks, one with a narrow molar mass distribution (green) and one with a broad molar mass distribution (red) form a conjugate block with a bimodal molar mass distribution (blue) when quantitatively conjugated together. Reproduced from ref. 10 with permission from John Wiley & Sons Ltd, copyright 2009. | ||
It is important to stress from considering the above examples, that molar mass values, and molar mass distributions obtained from SEC, are not always particularly informative for block copolymers, although commonly employed. Two polymer chains within a distribution can have an identical molar mass but can ultimately be very different in terms of their hydrophilic to hydrophobic ratio, block volume ratio in solution, degree of functionality and overall block sequence. These challenges can lead to a loss of control or understanding when considering block copolymer self-assembly, particularly when close to a phase boundary, which can lead to ill-defined morphologies in certain cases.
End group fidelity
Because of the inherent challenges in controlling and understanding the dispersity in block copolymers, it is possible to achieve a pseudo block copolymer by utilizing an end group on a homopolymer, where the end group resembles a second block of differing solvophilicity to the homopolymer chain. This can obviously reduce the dispersity, particularly in the length, of a system to that contained within the single polymerized block. Du et al. designed a series of RAFT chain transfer agents, based on a common, commercially available RAFT CTA, with differing hydrophobic functionalities on the α- and ω-ends.11 These RAFT agents were then used to homopolymerize hydrophilic monomers to form hydrophilic homopolymers with hydrophobic end groups. It was found that these homopolymers underwent self-assembly in aqueous solution, driven by the hydrophobicity of the end groups. However, it is important to consider that when functionalizing a polymer, either by a post-polymerization method or by introducing the functionality into the end groups before polymerization, the amount of functionalization can introduce another level of dispersity between polymer chains. As mentioned in the previous section, RAFT chain transfer agents can contain two different functionalities, but one or both of these can be lost on some chains during the polymerization. Post-polymerization methods do not always yield 100% functionalization either, however by employing highly efficient chemistries, the dispersity in end group functionality between chains can be reduced.12 Analysis techniques, such as NMR spectroscopy, that are often used to calculate the degree of functionalization always carry a level of error, as well as showing an average of all the components of the sample, so it is often difficult to accurately state that every single chain within the sample contains the desired end block. Instead, one should use a variety of complementary techniques dependent upon the end group in question, such as MALDI-ToF-MS, UV-Vis spectroscopy, including the UV trace obtained from SEC analysis, elemental analysis, FT-IR spectroscopy and fluorescence spectroscopy. However, one must also consider that these techniques often consider averages across the sample and carry their own associated errors. It is worth considering such effects when using chain transfer agents or similar that end up attached to the polymer chain and whether hydrophobic functionality introduced by this method can act as a pseudo block.Polymer compositional dispersity
Copolymerization is typically employed to tune the properties of a polymer chain, or of a block within a block copolymer. For instance, copolymerization of monomers with very different hydrophilicities can lead to the tuning of the copolymer's overall hydrophilicity, or even introduce thermoresponsive properties in certain solvents. Copolymerization can also be used to introduce functionality (e.g. for targeting, sensing, responsiveness or catalysis) along a section of a block copolymer. Although copolymerization is a robust method for achieving such properties, copolymerization itself introduces another dimension of dispersity in the location of functionality along the polymer chain. Compositional dispersity, for instance differences in the degree of functionality along the length of each polymer chain (also known as compositional drift) or variation in the degree of functionality between chains, is a factor that can play a major role in polymer performance and function. The average composition of a polymer chain can be obtained relatively easily using NMR spectroscopy or in some cases elemental analysis, however determining the dispersity in a polymer's composition is challenging since two polymer chains with similar molar masses within a single sample can possess different functionality loadings. Considering that polymer chains with different compositions may not behave similarly in solution, compositional dispersity may lead to a broadening of the dispersity of a polymer's higher order self-assembled structures, be it in terms of size, volume, shape etc. Additionally, variation in the distribution and loading of a functional group may then affect other properties of the self-assembled structure. For example in a nanoreactor, poorly defined functionality location may impact the nanoreactors’ catalytic capabilities.Commonly, reactivity ratios are employed to ascertain the compositional distribution along a copolymer chain. Note that this method only applies to RDRP, or other “controlled” polymerization techniques and not to free radical polymerizations. A plot of fAvs. FA is often fit to a non-linear least squares (NLLS) method to obtain values for rA and rB.13,14 These reactivity ratio values yield theoretical information on the compositional distribution throughout the copolymer. For instance, if both rA and rB are close to zero, neither monomer preferentially reacts with itself and so an alternating copolymer structure is predicted. If rA and rB are close to one, the monomers show no preference for either monomer and so a random distribution of the monomers throughout the chains is obtained. As the values increase to greater than one, the monomers preferentially react with themselves so homopolymerization dominates, although if single incidents of cross-propagation occur, a block-like structure is obtained. In the extreme case where both rA and rB ≫ 1, copolymerization does not occur, leading exclusively to homopolymerization. In the case where the reactivity ratios are very different from one another (e.g. if rA ≫ 1 ≫ rB), compositional drift is likely to occur. This is where, for an RDRP process, in the initial stages of the reaction, both A- and B-terminal growing chains preferentially react with monomer A. As the reaction proceeds, the concentration of monomer A rapidly decreases, where the concentration of monomer B remains roughly constant, making the chances of monomer B addition higher, which outweighs the preference for monomer A addition. This change in monomer preference leads to asymmetrically functionalized gradient copolymers. Note that such methods yield point estimates for rA and rB but a 95% joint confidence interval should also be obtained in order to determine the uncertainty associated with these values, and therefore the uncertainty in the monomer distribution along the chain.15
Copolymerization in ring opening polymerizations that proceed via an “activated monomer” mechanism is further complicated by virtue of the fact that the actual reactive monomer species are the activated versions of the cyclic monomers and not the cyclic monomers themselves. Therefore, measurement of the reactivity ratios is challenging as the relative concentrations of the active monomers does not always match the feed ratios and as such careful consideration of the relative equilibria must be employed.
The use of reactivity ratios to predict the overall composition along a chain can be very powerful because the various polymer compositions produced cannot be distinguished by standard techniques such as SEC or NMR spectroscopy of the prepared polymers. As such, understanding the architecture of the polymer distribution, which is necessary for understanding the polymer's solution behavior, can only be achieved using specialized techniques such as reactivity ratio determination15 and those discussed further below.
13C NMR spectroscopy was a technique employed by Kaur and Brar to observe this compositional distribution throughout a polymer chain synthesized by ATRP.16 Firstly, they calculated the reactivity ratios between methyl methacrylate (M) and n-butyl acrylate (B), which showed different reactivity ratios (rM = 2.17, rB = 0.42) implying a moderate gradient copolymer would form. In order to experimentally measure this phenomenon, the authors compared the 13C NMR spectra across a range of monomer feeds at different conversions during the copolymerizations and compared the relative integrals of the dyads consisting of MB, MM and BB compositions, and both M-centered (MMM, BMM, and BMB) and B-centered (BBB, MBB, and MBM) triads. The results showed that BB dyads increased as a function of conversion, whereas MM dyads decreased in relative intensity. The same corresponding trends were also observed for BBB and MMM triads. The results were in good agreement with the compositional drift predicted from the reactivity ratios.
Both compositional and molar mass dispersity can have drastic implications on the solvent interaction parameter and the packing parameter, respectively, and therefore the self-assembly behavior of block copolymers. As such, when considering dispersity in block copolymers, not only the molar mass dispersity but also dispersity in the composition, end groups, block order and blocking efficiency must be considered when designing these polymers for use in self-assembly.
Self-assembly
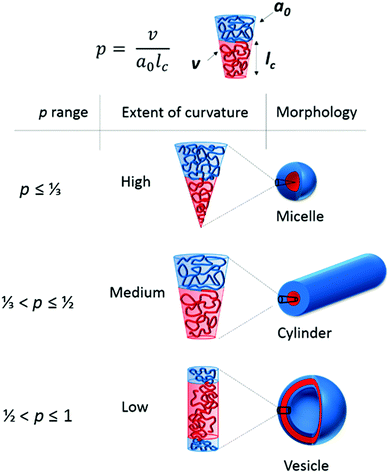
It is necessary at this point to give a brief overview of the aspects that affect the self-assembly of polymers in aqueous solution. For more detailed literature please refer to the relevant section in the ESI.† When amphiphilic block copolymers are dispersed into a selective solvent (or solvent mixture) the polymers spontaneously self-assemble in dilute solution into a range of structures on the nanoscale, similar to those adopted by surfactant molecules in solution, with the most commonly formed structures being spherical micelles.17 The vast range of nanostructure morphologies formed at equilibrium is governed by the minimization of free energy between the two blocks in solution (polymer–polymer interaction parameter, χAB) and between each block and the surrounding solvent (polymer–solvent interaction parameters, χAS and χBS).18 This is typically dictated by the relative volume fractions (f), the solvophobicity, and the degree of polymerization of each block, and is strongly related to the packing parameter by which surfactant micelles abide.The packing parameter of surfactant molecules as investigated by Israelachvili, Mitchell and Ninham19 is a simple concept that allows the relationship between surfactant molecular structure (such as head group area, a0, hydrophobic tail length, lc and volume of the hydrophobic segment, v) and the resulting particle morphology to be understood using a critical packing parameter, p, where p = v/a0lc (Fig. 4). Altering these parameters leads to the molecule adopting a different interfacial curvature and therefore a different morphology. Amphiphilic block copolymers can be considered mimics of these small molecule surfactants where the hydrophobic block is a mimic of the surfactant tail and the hydrophilic block is a mimic of the polar head group.20 Spherical micelles, with high curvature, are formed when p ≤ ⅓, cylinders between ⅓ < p ≤ ½ and when ½ < p ≤ 1, vesicles are formed (Fig. 4). It should be noted that this situation applies to structures at equilibrium, which is true in the majority of cases for surfactants. However, block copolymers can also adopt structures that are kinetically trapped, out-of-equilibrium structures that cannot be predicted in this way and relate instead to the self-assembly process. For instance, the use of a cosolvent that is a common solvent for both blocks to aid the transition into the selective solvent is more likely to result in morphologies closer to their equilibrium structures than direct dissolution in the selective solvent. In practice, p is extremely difficult to calculate and therefore only occasionally used. Instead the hydrophilic and hydrophobic mass fractions, which relate to the volume fractions, are more commonly considered parameters.21 One must also consider the relative volume changes that occur when considering different monomers, e.g. monomers containing branched side chains, such as 2-ethylhexyl methacrylate, occupy more volume than their linear counterparts of the same mass.
By controlling the volume fraction of each block through polymerization methods, specific morphologies can be targeted. Altering the hydrophilicity of one block will also cause a shift in both the volume fraction of the block and in the polymer–solvent interaction parameter. This control over both hydrophilic and hydrophobic domains and overall polymer architecture allows access to a rich range of nanostructure phases in solution. However, dispersity within the block copolymers close to a phase boundary could result in a hydrophobic/hydrophilic distribution that exists on either side of the phase boundary, which in turn will result in a mixture of morphologies at equilibrium. Possible implications of this include obtaining a mixed morphology phase, as will be exemplified later in the review. It is important to stress that the morphology predicted by the packing parameter is the morphology adopted at thermodynamic equilibrium. If the polymers cannot reach thermodynamic equilibrium then intermediate morphologies may be formed, with the ultimate morphology predicted by p never being reached. However, a discussion of such cases is beyond the scope of this review.
Size distribution within self-assembled structures
After self-assembly to form polymeric nanostructures several analysis techniques can be utilized in order to study their properties. These include both scattering and microscopic analyses, of which some will be discussed herein. For further information regarding more advanced techniques such as small angle X-ray and neutron scattering (SAXS and SANS) and a broader overview of microscopy techniques, the reader is referred to the following text.22 One such property is the size and the size distribution of the particles in solution. A common method to analyze this is to use dynamic light scattering (DLS). Light scattering techniques analyze a large number of particles and therefore give excellent statistics. For a more in depth discussion on light scattering techniques the reader is referred to the following texts.22,23 In order to obtain the diffusion coefficient and therefore information on the size of the particles in solution one must first obtain the electric field and intensity autocorrelation functions, g1(q, t) and g2(q, t). The intensity autocorrelation function, g2(q, t), can be expressed in terms of the decay in scattered intensity as in eqn (6).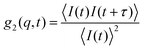 | (6) |
| g2(q, t) = 1 + f[g1(q, t)]2 | (7) |
Assuming a Gaussian distribution of particle sizes, this dispersity can be expressed, as a dispersity (Đ), in terms of the standard deviation of the distribution and the mean size of the sample, see eqn (8).
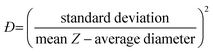 | (8) |
It should be noted that one drawback to DLS analysis is that the hydrodynamic diameter obtained for the particle is that of a hard sphere that moves at the same speed in solution as the particle in question. For this reason, sizes obtained by DLS may not be representative for non-spherical morphologies. Quite often benchtop DLS instruments only measure at one or two angles. This can lead to large errors in the particle size obtained, particularly when multiple populations are present in the sample.25 There are more sophisticated instruments that are able to measure at a range of angles and these give advanced information, such as better analysis of multi-modal particle size distributions and can also give information on the interaction between the particles. However, even sophisticated instruments cannot distinguish between particles with little difference in size, instead giving an average particle size or sizes. Practically, a difference of 3 times the diameter is needed to be able to distinguish two different populations. For example, in one study three monomodal samples of polystyrene beads of 220 nm, 330 nm and 410 nm were mixed and it was observed that DLS analysis gave a broad intensity distribution, weighted towards the larger particles, rather than separating the different populations.26 This demonstrates how dispersity observed in DLS is not always a result of a continuum of sizes, but can also be caused by discrete populations of a similar size. Therefore it is important to use a range of complementary techniques to fully characterize any sample.
Static light scattering (SLS) uses the same principles as DLS but uses the mean value of the scattered light rather than the fluctuations over a given time period.22,23 Experiments are often performed over a range of angles (θ) and at multiple concentrations (c). The Zimm equation (eqn (9)) can then be used to obtain information about the molar mass (Mw) and the radius of gyration (Rg) of the scatterers. Here, A2 is the second virial coefficient, c is the sample concentration and K and Rθ are defined in the ESI.†
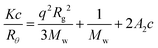 | (9) |
Combining DLS and SLS allows for information about size and molar mass to be obtained simultaneously. If the molar mass of the polymer is known then the molar mass of the self-assembled particle can be used to give an aggregation number, Nagg, defined as the number of polymer chains per particle. This is important in determining differences between similar particles, for example, two particles may have a similar size when measured in solution but widely different aggregation numbers. This dispersity could result in differences in functional behavior, as the aggregation number relates to the density of chains and therefore the two particles will have different core densities, and a different number of chains making up the corona, which if used for a functional application such as targeting in nanomedicine, could be crucial parameters.
Combining the hydrodynamic size information, RH, from DLS and the Rg from SLS can give information on the morphology of the particles. Rg/RH values are representative of different density of morphologies. Rg/RH value of 0.775 suggests a homogeneous sphere, i.e. a spherical micelle whereas a Rg/RH value of 1 is indicative of a hollow sphere and therefore suggests a vesicular morphology. Values of Rg/RH > 1 account for extended structures in solution, for example a flexible polymer chain has an Rg/RH of between 1.5–1.7 whereas a rigid rod has Rg/RH > 2.27 This parameter can also allow for comparison between two similarly sized particles and can give information on the internal structure of each particle.
Complementary techniques to such solution based scattering methods are in the form of microscopy. One of the most widespread methods used to visualize particles is transmission electron microscopy (TEM). Most commonly this is done in the dry state; although cryogenic TEM (cryo-TEM) is becoming more widely used it is still prohibitive for many research groups due to lack of access to the specialized equipment, the high expense and a lack of technical expertise. In dry state TEM particles are dried to a substrate, commonly on a grid containing a carbon based film support or, more recently, atomically thin graphene oxide,28 and depending on the phase contrast between the sample and the support, a high atomic number stain (e.g. uranyl acetate, phosphotungstic acid etc.) that selectively binds to either the sample or to the grid may be applied. Very recently, Lieberwirth and coworkers have also described the use of low vapor pressure trehalose solutions, which are typically used for the analysis of biological samples, as well as ionic liquids as embedding free-standing solvents for ambient temperature TEM analysis of polymer nanoparticles in solution.29
Microscopy techniques, such as TEM, are useful in visualizing the morphology of the particles and by performing tomography can give information about the 3D shape of the particle and some information on internal structure. It is worth keeping in mind that the particles observed in dry state TEM are no longer hydrated and this could affect the morphology and size observed. Additionally, using high trehalose concentrations necessary for ambient temperature liquid phase TEM analysis also alters the solution environment of the polymer nanoparticles, which may affect its solution behavior. There has been progress in the use of liquid cell TEM to analyze particles directly in solution without the need for cryogenic temperatures, however this relatively new field has yet to be used widely by the scientific community.30
To obtain the average particle size after TEM analysis it is common to utilize some imaging software, the most commonly used being ImageJ, and to measure individual particles. Some software packages allow for automatic particle size measuring but one should be aware of some of the limitations of this technique. In order for automatic particle sizing to be employed, the particles must satisfy several criteria. They must be spherical, isolated and have a high contrast compared to the background. If these criteria apply then automatic software can be a useful tool for measuring the size of a large number of particles. A threshold value must be set to allow the software to distinguish what “brightness” equates to a particle and what “brightness” equates to background. Setting the threshold too low or too high can result in the loss of small or large particles, giving an inaccurate representation of the sizes of the particles in the solution. There are also semi-automatic methods whereby one can select a large number of particles and then manually remove any aggregates or other objects not of interest from the measurements. These automatic methods are useful in generating size measurements from a large number of particles, important when comparing to light scattering methods that look at >109 particles in a given measurement. However, the particles must still have a good contrast with the background grid and even automated particle counting analyses do not produce anywhere near the statistical relevance of averaging techniques such as light scattering. This highlights a key difference as light scattering techniques give intensity-weighted distributions and microscopy yields a number-weighted distribution. The majority of publications report the average size obtained by TEM ± Sn. As stated previously, this range of ±Sn only accounts for 68% of the size distribution, hence this should be kept in mind when analyzing particle sizes.
Often it is difficult to utilize this software when imaging polymer self-assemblies. Polymeric nanoparticles are often low contrast due to their hydrocarbon nature and drying effects often bring them into contact on the TEM grid. The use of a stain to increase the contrast can cause problems within the automatic software if the background staining is not even across the grid or if there are artefacts caused by the stain. Other potential problems for using the automatic software is the presence of multiple morphologies, or non-spherical morphologies. In most automatic image analysis software, the size of the particle is calculated either by taking the area of the particle, or by taking the average of the maximum and minimum particle dimensions. For spherical particles, either of these methods will be suitable, but for non-spherical particles, this may not lead to accurate results. Worms for example are often highly anisotropic in length. In these instances manual particle counting must be performed. This is more time consuming and has the potential to be more subjective. The researcher must be disciplined to ensure that they measure all particles within a given area and not be tempted to “cherry-pick” the particles that most suit their hypothesis. It is also important that a significant number of particles are counted, and the number required to obtain good statistics will vary according to the distribution of sizes observed. Ideally, enough particles will be counted that a Gaussian distribution can be fitted to the histogram of sizes, with the outermost populations reaching full width at a quarter maximum peak height. Therefore using microscopy methods in conjunction with light scattering methods gives the best possible analysis.
Does polymer mass dispersity affect morphology?
As has been described in a previous section, whilst great care is often taken to gain control over the polymerization conditions and therefore produce a well-defined polymer in the hope that this will give a well-defined self-assembled structure, some dispersity in the system will remain. It can be thought of that dispersity within a block copolymer affects not only the length distribution but also the relative volume fractions of the different blocks within the copolymer. For example, a diblock copolymer where one block has a greater length dispersity than the other will mean that the length of the block with the broader molar mass distribution varies more throughout the sample than the block with the narrower molar mass distribution and so chains with an overall higher molar mass effectively have a lower volume fraction of the latter block. In an amphiphilic block copolymer this will result in the solvophilic/solvophobic volume fractions varying throughout the sample. Since the volume fraction is related to the packing parameter, different polymers within the same sample will prefer to adopt different interfacial curvatures and hence the final morphology adopted may not be that predicted by the average solvophilic volume fraction (Fig. S1A, ESI†). This is particularly true if the block ratio of the copolymer sits close to a phase boundary. Additionally, a longer solvophobic block will result in an increase in the interaction parameter between the core block and the surrounding solvent, providing another driving force for potential morphological variety.This inhomogeneity resulting from polymer block dispersity has been demonstrated to occur in bulk self-assembly. For instance, Hillmyer and Lynd found that for a high interaction parameter polymer, poly(ethylene-co-propylene)-block-poly(lactide), increasing the dispersity of the block copolymer from 1.16 to 1.34 whilst keeping the Mn constant at ca. 15 kg mol−1, resulted in an increase in the domain spacing of the lamellar phase of the bulk self-assembly.31 For lower molar mass (weakly segregating, low interaction parameter) block copolymers, they found that entirely different morphologies, namely lamellar, cylinder and gyroid phases, could be obtained using block copolymers that only varied in their molar mass dispersity.31
This same phenomenon also occurs in solution self-assembly. Eisenberg and coworkers looked at the effect of the dispersity of the corona block in a poly(styrene-b-acrylic acid) (PS-b-PAA) diblock copolymer upon the final morphology achieved when assembled in water.32,33 Dispersity was artificially broadened by mixing polymers with very low dispersity (ĐM < 1.05) and identical PS block lengths but different PAA chain lengths in order to create a range of polymers with the same overall average chain length but ĐM ranging from 1.1 to 2.2.32 At low ĐM, large ill-defined vesicles with a broad size range were formed. Increasing the dispersity of the system resulted in smaller vesicles with a narrower size range, and the appearance of spheres. This decrease in vesicle size with increasing dispersity was a result of segregation between chains of different lengths (Fig. S1B, ESI†). In a highly disperse sample the inherent variation in polymer length led to there being fewer chains with the average length and instead a greater number of longer and shorter chains, near the extremes of the size distribution. The short chains preferentially segregated on the inside wall of the vesicles, whilst the longer chains tended to favor the outside wall, where they are less confined. Hence, this led to more repulsion on the outer surface of the vesicles and therefore a higher curvature and smaller vesicles. Equally, shorter chains in the center of the vesicle allowed for a higher curvature to be adopted. Excessive repulsion between longer chains eventually lead to spheres forming (Fig. S1B, ESI†). The phenomenon of asymmetry in polymer vesicles has been used by Meier and coworkers to afford directionality to the assembly of a transmembrane protein into a polymersome membrane formed from an ABC triblock copolymer with intentionally different chain lengths of the corona-forming A and C blocks.34
The effect of dispersity within the hydrophobic block has also been demonstrated.35 Mahanthappa and coworkers synthesized a triblock copolymer of poly(ethylene oxide-b-1,4-butadiene-b-ethylene oxide), PEO–PB–PEO. The PEO blocks had ĐM ≤ 1.25 whereas the 1,4-butadiene block had a higher ĐM of 1.75. The average chemical composition was expected to give vesicles as the predominant morphology. Since the dispersity of the 1,4-butadiene block was greater, polymers that had an overall longer block length would have therefore had a higher weight fraction of PB, wB, a lower weight fraction of PEO, wO, and hence preferred to adopt a different interfacial curvature compared to shorter chains that had a higher wO. This was demonstrated in a sample with an average wO of 24%, a weight fraction of PEO where vesicles would be expected to form. Instead cryo-TEM images revealed the presence of spheres, worms and vesicles. The authors converted the wO value into a volume degree of polymerization (Nv,tot) and, by comparing this to a known morphology diagram for PEO–PB copolymers with a low dispersity, were able to mark the composition cut off that corresponds to each morphology regime. This demonstrated that although the sample had a large portion of chains that preferred to adopt a vesicular morphology, there were also significant fractions that preferred to form worms and spheres. Samples that contained higher wO resulted in quite different behavior. At wO of 42 and 58% the expected morphology was spherical micelles, and whilst all chemical compositions of the polymers within the distribution fall within the spherical micelle phase, the differing chain lengths caused by the dispersity favor different sized spherical micelles. Rather than a range of micelle sizes, elongated micelles with tapered ends, similar to an American football shape, were observed by cryo-TEM. This was rationalized by different length hydrophobic chains relocating within the micelle to satisfy their preferred curvature, similar to the chain segregation in vesicles described earlier (see Fig. 6).
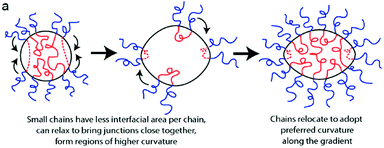 | ||
| Fig. 6 Schematic demonstrating how the polymers with different lengths of hydrophobic block migrate within the nanostructure to satisfy their preferred interfacial curvature, hence forming elongated micelles. Reprinted with permission from ref. 35. Copyright 2012 American Chemical Society. | ||
These experimental findings are also backed up by theoretical simulations. Yang and coworkers investigated the effect of dispersity in the polymer chain on the morphology adopted in solution.36 Self-consistent field theory (SCFT) was used to artificially induce dispersity within a polymer by mixing two AB diblock copolymers of differing chain lengths. When investigating the effect of dispersity within the hydrophilic block the overall average block length was kept constant at 27 but the hydrophilic block length varied, creating samples with ĐM ranging from 1.00 to 2.56. For simplicity's sake, the hydrophobic block had no length dispersity (ĐM = 1.00) in the simulations. For the sample with both blocks of ĐM = 1.00, the polymers adopted a vesicular morphology in solution. But as the dispersity increased, and the hydrophilic block length increased, the assemblies transitioned from vesicles to a mixture of vesicles, worms and spheres and finally to spheres and large compound micelles (LCM). The segregation of the different hydrophilic block lengths was further investigated and, as in Eisenberg's work, it was found that the segregation of the longer blocks on the outside of the vesicles and the shorter hydrophilic chains on the inside of the vesicles caused an increase in curvature and therefore induced the morphology change. A similar morphological trend was observed when the dispersity in the hydrophobic block was varied from 1.0 to 1.97, keeping the hydrophilic block with no length dispersity. However, at very short hydrophobic block lengths (DPB < 6) the diblock copolymer acted as a hydrophilic copolymer, being found equally distributed throughout solution.
These simulations used two distinct polymer chain lengths to artificially create the dispersity, which is not particularly representative of a disperse polymer sample. However Jiang et al. also used SCFT in a similar manner but where dispersity was characterized by a continuous molar mass distribution.37 Increasing the dispersity, from 1.0 to 2.0, caused a decrease in the vesicles sizes owing to the segregation of the short and longer polymer chains into the inner and outer walls of the vesicles, respectively, eventually leading to spherical micelles at high dispersity of 3.4. Similar observations were made whether the hydrophilic or hydrophobic block was the more disperse.
Whilst these previous examples suggest that dispersity within the polymer can affect the morphology that the self-assembled structure adopts in solution, there are also many reports that find that well-defined self-assembled structures can be produced from ill-defined block copolymers. Recently Sawamoto and coworkers synthesized statistical copolymers of poly(ethylene glycol methyl ether methacrylate) (PEGMA) and dodecyl methacrylate (DMA) with hydrophobic content between 20 mol% and 50 mol%, varying block lengths and low ĐM between 1.2–1.4.38 These copolymers self-assembled in water and the overall size of the particles were determined by the hydrophobic content of the polymer. The size and molar mass of the particles was independent of polymer molar mass at a given DMA mol%, as assessed by SEC in the selective aqueous solvent. This allowed easy tuning of the aggregation number of these polymers in water, as the Nagg was inversely proportional to the DP. The control over aggregation number could be especially useful when considering functionalization of specific domains within polymeric nanoparticles. Polymers with much broader ĐM (2.3–2.4) when analyzed as unimers in DMF were also found to display such self-assembly behavior. These ill-defined polymers self-assembled into particles with low ĐM (1.2–1.3) when analyzed by aqueous SEC. The smaller chains within the distribution assembled into multi-chain aggregates, whilst the longer chains intramolecularly assembled into single chain nanoparticles of similar sizes to the corresponding chains with narrow molar mass distributions (see Fig. 7).
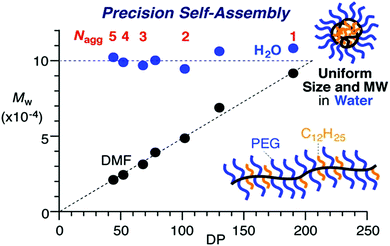 | ||
| Fig. 7 Graph depicting the constant Mw of the assembled particles in water, formed from statistical copolymers of poly(ethyleneglycol methyl ether methacrylate) (PEGMA) and dodecyl methacrylate (DMA) as the DP of the overall polymer increases. In DMF the polymers do not assemble, therefore Mw increased with DP. Adapted with permission from ref. 38. Copyright 2016 American Chemical Society. | ||
Therefore, whether dispersity within a polymer necessarily results in dispersity within the self-assembled structure is not as clear. Also a narrow size distribution, Đ, does not indicate that all particles are the same. Indeed, as shown in the example above, particles of similar sizes assembled from the same polymer can have different properties, such as aggregation number, leading to differences in such factors as core density or repulsion between corona chains. It is also worth noting that dispersity within a structure is not solely confined to size distributions. Distribution within a polymer in terms of functionality location will therefore translate into the structure and may affect such properties of compartmentalization. When targeting specific applications, such as nanoreactors with functionalized cores, such differences can affect the efficiency of the particle.
Why does distribution within self-assembled particles matter?
One way of targeting, by encouraging accumulation of drugs in tumor vasculature, is by use of the enhanced permeability and retention (EPR) effect. The theory behind the EPR effect lies in tumor architecture. Blood vessels in tumors are dilated and more permeable than in normal tissue and the endothelial cells in tumors are poorly aligned and have larger gaps between them. In addition, tumor cells often have poor lymphatic drainage systems. These defects allow for macromolecules and nanoparticles in the blood plasma to pass into tumors, with the poor lymphatic drainage causing the macromolecules to accumulate in tumor tissues, an effect known as passive targetting.39 On this basis, it is possible to accumulate polymer prodrugs, or drug loaded nanoparticles, at the tumor site. Conversely, low molar mass drugs do not show the same accumulation effect because they rapidly diffuse back into the circulating blood and are cleared by the kidneys (see Fig. 8). However, solely utilizing the EPR effect to target tumor tissues has been shown to be inefficient. Chan and coworkers recently conducted a review of literature on nanoparticle-based targeting from the last 10 years and found that, on average, less than 1% of the nanoparticle dose was actually delivered to a solid tumor.40 Polymeric-based drugs also offer other advantages, such as immune system avoidance, prolonged half-life of drugs in blood plasma and suppressed antigenicity.
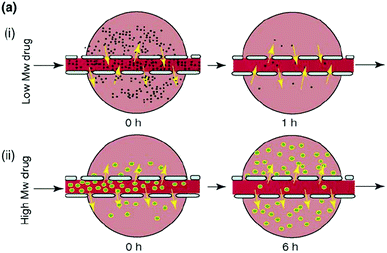 | ||
| Fig. 8 Depiction of a low molecular weight drug entering the tumor tissues but rapidly diffusing out again once the concentration of drug in the blood plasma decreases and the diffusion of a larger Mw drug into the tumor tissue and its accumulation there as a result of its size limiting diffusion back into the bloodstream. Reproduced from ref. 39 with permission from Elsevier, copyright 2006. | ||
Polymeric nanoparticles take these advantages one step further. They can encapsulate hydrophilic and hydrophobic drugs and, by incorporation of stimuli-responsive blocks, can release their payloads in a controlled fashion. They have extended blood circulation times as a result of their size, being too large for rapid renal clearance (glomerular filtration).41
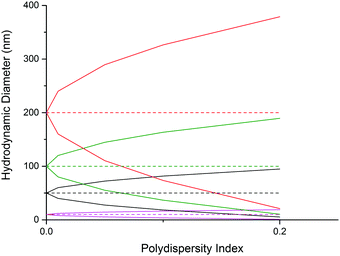
For use in such applications, it is important to consider the factors that dispersity within the nanoparticle may have. We have previously discussed how a low Đ by light scattering methods can still equate to a quite considerable range of sizes in the sample. This size range may be problematic as it leads to different circulation times and clearance pathways for differently sized nanoparticles.42 Different tumor types have different sized cut offs for nanoparticle accumulation, as a result of their different blood vessels nanoparticles that are larger than 200 nm generally do not accumulate in tumor tissues.43 Therefore when considering this type of passive targeting it is important that the entire size range of the morphologies in the system are able to be accumulated within the tumor tissue, otherwise the system will have low efficiency as the larger particles cannot diffuse into the tissues. The clearance pathways of the particle should also be considered. For example, particles smaller than 5 nm (<40 kDa) are rapidly filtered by the kidneys whereas particles larger than 8 nm are not.44 A broad distribution of sizes could cause a significant amount of the delivery sample to fall either side of these cut-offs, with great implications related to the targeted dose of drug.
Additionally, when considering the size difference one should also think about the variation in volume within the range of nanoparticles. A particle with a Dh = 100 nm with a Đ of 0.1 will range from 36–164 nm. This equates to a volume range of 2.44 × 104 nm3 to 2.31 × 106 nm3, with the particles at the larger end of the spectrum having a volume over 94 times greater than that of the smallest particles in solution. This could affect the efficiency of drug encapsulation and causes difficulties in deducing the exact concentration of drug being delivered to the target site, which could have potential safety implications. It will also drastically alter the nanoparticle's diffusion behavior and may result in increased or decreased circulation times or alternative cell uptake mechanisms becoming dominant, which could affect the targeting selectivity or specificity of the nanoparticle.
However, once again it is important to recognize how these factors can be affected by dispersity within the nanoparticle, in a previous example, Sawamoto and coworkers demonstrated that amphiphilic copolymers formed aggregates of the same size but differing aggregation number based on the size of the polymer.38 Considering the case where the corona-forming blocks or end groups of the assembling polymer contain the targeting moiety or surface charge, such a variation in Nagg can lead to a difference in surface functionalization of the nanoparticle. A particle comprising of fewer chains will have a lower density of targeting groups than a more densely packed particle of similar size. For example, consider the hypothetical situation where the end group of a corona-forming block is utilized as a means of introducing a targeting ligand on the surface of a particle, assuming 100% end group functionality and that the corona chains are well hydrated such that the end groups are presented on the particle's outer-most surface at the corona–solvent interface. In this situation, a core–shell spherical micelle with RH = 100 nm and Nagg = 50 has approximately 4 × 10−4 ligands per nm2. It follows that a spherical micelle with an identical size but twice the molar mass contains twice the ligand density on its surface. In contrast, dispersity in the radii of the particles follows a squared relationship in affecting the ligand density. For instance, a micelle with an identical Nagg of 50 only has to decrease its radius by a factor of √2, to an RH of 71 nm, in order to double its ligand density on its surface. If considering mixed morphologies present in the block copolymer self-assembly, the situation gets more complicated; for instance vesicles typically show Nagg values in the thousands so a vesicle of the same size as the aforementioned core–shell micelle will display a ligand density orders of magnitude higher. Therefore in these hypothetical examples it is clear that the surface ligand density is an interplay between the particles’ morphology, size and molar mass and so dispersity in any of these factors can lead to drastic deviations from the mean ligand density. Practically, this could have implications in multivalent binding interactions and diffusion/uptake pathways of the particle mixture.
Additionally, the same variation in surface density in particles with well-controlled Nagg could also be a result of poor end group modification, whereby the nanoparticle will then be comprised of a mixture of polymeric chains, those that bear the desired tag and those that do not. This may have implications in binding strength and efficiency and therefore affect the delivery of the therapeutic. Fakhari et al. investigated the optimum ligand density for binding to carcinomic human basal epithelial cells and for uptake.47 A cyclic peptide, cLABL, was used as the targeting ligand and poly(DL-lactic-co-glycolic acid) used as the polymeric core of the nanoparticles, stabilized by Pluronic® block copolymers. By using a mixture of differently functionalized Pluronic® stabilizers (either modified with the ligand or non-modified), nanoparticles with varying surface densities of the peptide could be synthesized. It was found that an intermediate ligand surface density (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 or 25
50 or 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 ratio of modified to non-modified Pluronic®) maximized cellular uptake, with lower uptake values being seen for low or very high levels of surface functionalization. This demonstrates that for each system there will be an optimum level of nanoparticle functionalization for cellular binding and therefore changes in surface functionalization, either through differences in aggregation number between particles or through inefficient end group modification, can affect the desired properties of the nanoparticle.
75 ratio of modified to non-modified Pluronic®) maximized cellular uptake, with lower uptake values being seen for low or very high levels of surface functionalization. This demonstrates that for each system there will be an optimum level of nanoparticle functionalization for cellular binding and therefore changes in surface functionalization, either through differences in aggregation number between particles or through inefficient end group modification, can affect the desired properties of the nanoparticle.
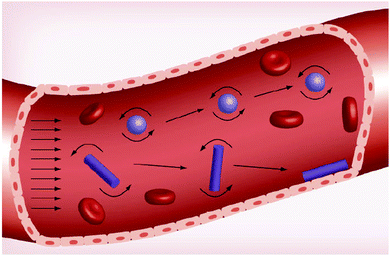 | ||
| Fig. 9 Effect of nanoparticle morphology on the margination towards the outside walls of the blood vessel. Reproduced from ref. 46 with permission from Future Medicine Ltd, copyright 2013. | ||
Where chemical functionality is located within the particle can also have an effect upon the function of the particle. The location of functionality will be mainly determined by the polymerization technique, reactivity of the monomers and chain architecture. Compositional control within the polymer structure will play a large part in determining location control in the self-assembled nanoparticle. Block copolymerization techniques allow for a clear divide between hydrophilic/hydrophobic segments of the polymer and can also clearly divide between functional/non-functional or different functionalities. Often the functional chemical group is introduced to the hydrophobic fraction of an amphiphilic block copolymer by copolymerization with a non-functional hydrophobic monomer. Variations within the copolymerization will mean that there is a compositional drift across the polymer chain, as discussed previously. This will therefore translate into a drift in the composition of the cores of the self-assembled structures. Note that this will be weighted towards the monomer feed ratios employed. It is also only possible to predict statistically where the functionality will reside (e.g. having an increased chance of being located at a chain end).
Compositional drift within the core block could lead to enough of a copolymer gradient that effectively the majority of the functional monomer is located towards one end of the block, resulting in a functional density either nearer the core–corona interface or the center of the hydrophobic core. This could result in phase segregation within the core, or even lead to unpredicted morphologies. Conversely, discrepancies in the amount of functionality within the hydrophobic block between chains may not affect the average micelle core functionality as each particle will consist of a randomized population of polymer chains. This demonstrates an example whereby a lack of control at one hierarchical level does not necessarily contribute to a loss of control at a higher level.
Conclusions
It is crucial to consider the different factors that can affect dispersity within a self-assembled system. By controlling various aspects in the polymer chains, e.g. functionality, block ratio, interaction parameter, molar mass and chain architecture, it is possible to predict and control the properties of the self-assembly and therefore the solution behavior. Consideration of dispersity in other aspects of the polymeric building blocks, such as length, blocking efficiency and compositional distribution has also been discussed as well as the dispersity within the self-assembled systems, such as morphology ranges, final sizes and density of surface functionalization. Such considerations are important when considering such polymeric assemblies for advanced applications, such as in drug delivery or as nanoreactors. Examples have been given where a lack of control at the polymer level leads to poorly-defined self-assemblies and solution behaviors, as well as times where block copolymer dispersity does not correlate to dispersity in polymer self-assemblies. We hope this tutorial review sheds light on the factors that influence block copolymer solution self-assembly and behavior and enables readers to consider how polymer design can be used to fine-tune particle properties for specific applications.References
- S. Mori and H. G. Barth, Size Exclusion Chromatography, Springer, 1999 Search PubMed.
- H. Pasch, Polym. Chem., 2013, 4, 2628–2650 RSC.
- A. Rudin and P. Choi, The Elements of Polymer Science & Engineering, Academic Press, Boston, 3rd edn, 2013, pp. 63–87 Search PubMed.
- D. T. Gentekos, L. N. Dupuis and B. P. Fors, J. Am. Chem. Soc., 2016, 138, 1848–1851 CrossRef CAS PubMed.
- P. C. Hiemenz and T. P. Lodge, Polymer Chemistry, CRC Press, New York, 2nd edn, 2007 Search PubMed.
- D. J. Keddie, Chem. Soc. Rev., 2014, 43, 496–505 RSC.
- G. Gody, T. Maschmeyer, P. B. Zetterlund and S. Perrier, Nat. Commun., 2013, 4, 2505 Search PubMed.
- A. Plichta, M. Zhong, W. Li, A. M. Elsen and K. Matyjaszewski, Macromol. Chem. Phys., 2012, 213, 2659–2668 CrossRef CAS.
- G. Gody, P. B. Zetterlund, S. Perrier and S. Harrisson, Nat. Commun., 2016, 7, 10514 CrossRef PubMed.
- C. Barner-Kowollik, Macromol. Rapid Commun., 2009, 30, 1625–1631 CrossRef CAS PubMed.
- J. Du, H. Willcock, J. P. Patterson, I. Portman and R. K. O'Reilly, Small, 2011, 7, 2070–2080 CrossRef CAS PubMed.
- H. Willcock and R. K. O'Reilly, Polym. Chem., 2010, 1, 149–157 RSC.
- A. M. Van Herk and T. Dröge, Macromol. Theory Simul., 1997, 6, 1263–1276 CrossRef CAS.
- B. G. Manders, W. Smulders, A. M. Aerdts and A. M. van Herk, Macromolecules, 1997, 30, 322–323 CrossRef CAS.
- K. J. Sykes, S. Harrisson and D. J. Keddie, Macromol. Chem. Phys., 2016, 217, 2310–2320 CrossRef CAS.
- A. S. Brar and S. Kaur, Polym. J., 2005, 37, 316–323 CrossRef CAS.
- G. Riess, Prog. Polym. Sci., 2003, 28, 1107–1170 CrossRef CAS.
- I. A. Nyrkova and A. N. Semenov, Faraday Discuss., 2005, 128, 113–127 RSC.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, Biochim. Biophys. Acta, 1977, 470, 185–201 CrossRef CAS.
- S. Jain and F. S. Bates, Science, 2003, 300, 460–464 CrossRef CAS PubMed.
- M. Dionzou, A. Morere, C. Roux, B. Lonetti, J. D. Marty, C. Mingotaud, P. Joseph, D. Goudouneche, B. Payre, M. Leonetti and A. F. Mingotaud, Soft Matter, 2016, 12, 2166–2176 RSC.
- J. P. Patterson, M. P. Robin, C. Chassenieux, O. Colombani and R. K. O'Reilly, Chem. Soc. Rev., 2014, 43, 2412–2425 RSC.
- W. Schärtl, Light Scattering from Polymer Solutions and Nanoparticle Dispersions, Springer-Verlag Berlin Heidelberg, Berlin, 2007 Search PubMed.
- D. E. Koppel, J. Chem. Phys., 1972, 57, 4814–4820 CrossRef CAS.
- K. Fischer and M. Schmidt, Biomaterials, 2016, 98, 79–91 CrossRef CAS PubMed.
- W. Anderson, D. Kozak, V. A. Coleman, Å. K. Jämting and M. Trau, J. Colloid Interface Sci., 2013, 405, 322–330 CrossRef CAS PubMed.
- S. Yusa, S. Ohno, T. Honda, H. Imoto, Y. Nakao, K. Naka, Y. Nakamura and S. Fujii, RSC Adv., 2016, 6, 73006–73012 RSC.
- J. P. Patterson, A. M. Sanchez, N. Petzetakis, T. P. Smart, T. H. Epps III, I. Portman, N. R. Wilson and R. K. O'Reilly, Soft Matter, 2012, 8, 3322–3328 RSC.
- P. Renz, M. Kokkinopoulou, K. Landfester and I. Lieberwirth, Macromol. Chem. Phys., 2016, 217, 1879–1885 CrossRef CAS.
- J. P. Patterson, P. Abellan, M. S. Denny, C. Park, N. D. Browning, S. M. Cohen, J. E. Evans and N. C. Gianneschi, J. Am. Chem. Soc., 2015, 137, 7322–7328 CrossRef CAS PubMed.
- N. A. Lynd and M. A. Hillmyer, Macromolecules, 2005, 38, 8803–8810 CrossRef CAS.
- O. Terreau, L. Luo and A. Eisenberg, Langmuir, 2003, 19, 5601–5607 CrossRef CAS.
- O. Terreau, C. Bartels and A. Eisenberg, Langmuir, 2004, 20, 637–645 CrossRef CAS PubMed.
- R. Stoenescu, A. Graff and W. Meier, Macromol. Biosci., 2004, 4, 930–935 CrossRef CAS PubMed.
- A. L. Schmitt, M. H. Repollet-Pedrosa and M. K. Mahanthappa, ACS Macro Lett., 2012, 1, 300–304 CrossRef CAS.
- X. Li, P. Tang, F. Qiu, H. Zhang and Y. Yang, J. Phys. Chem. B, 2006, 110, 2024–2030 CrossRef CAS PubMed.
- Y. Jiang, T. Chen, F. Ye, H. Liang and A.-C. Shi, Macromolecules, 2005, 38, 6710–6717 CrossRef CAS.
- Y. Hirai, T. Terashima, M. Takenaka and M. Sawamoto, Macromolecules, 2016, 49, 5084–5091 CrossRef CAS.
- A. K. Iyer, G. Khaled, J. Fang and H. Maeda, Drug Discovery Today, 2006, 11, 812–818 CrossRef CAS PubMed.
- S. Wilhelm, A. J. Tavares, Q. Dai, S. Ohta, J. Audet, H. F. Dvorak and W. C. W. Chan, Nat. Rev. Mater., 2016, 1, 16014 CrossRef CAS.
- A. M. Jhaveri and V. P. Torchilin, Front. Pharmacol., 2014, 5, 77 Search PubMed.
- C. Allen, D. Maysinger and A. Eisenberg, Colloids Surf., B, 1999, 16, 3–27 CrossRef CAS.
- A. Nagayasu, K. Uchiyama and H. Kiwada, Adv. Drug Delivery Rev., 1999, 40, 75–87 CrossRef CAS PubMed.
- J. Liu, M. Yu, C. Zhou and J. Zheng, Mater. Today, 2013, 16, 477–486 CrossRef CAS.
- V. P. Torchilin, Pharm. Res., 2006, 24, 1–16 CrossRef PubMed.
- R. Toy, P. M. Peiris, K. B. Ghaghada and E. Karathanasis, Nanomedicine, 2013, 9, 121–134 CrossRef PubMed.
- A. Fakhari, A. Baoum, T. J. Siahaan, K. B. Le and C. Berkland, J. Pharm. Sci., 2011, 100, 1045–1056 CrossRef CAS PubMed.
- P. Decuzzi and M. Ferrari, Biomaterials, 2006, 27, 5307–5314 CrossRef CAS PubMed.
- G. Sharma, D. T. Valenta, Y. Altman, S. Harvey, H. Xie, S. Mitragotri and J. W. Smith, J. Controlled Release, 2010, 147, 408–412 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional references, figures regarding how dispersity relates to morphology and table of size dependence on dispersity range. See DOI: 10.1039/c6cs00818f |
| ‡ Current Address: Department of Chemistry & Biochemistry, University of California, La Jolla, San Diego, CA, USA. |
| This journal is © The Royal Society of Chemistry 2017 |