The effect of hydronium ions on the structure of phospholipid membranes

Abstract

This work seeks to identify the mechanisms by which hydronium ions (H₃O⁺) modulate the structure of phospholipid bilayers by studying the interactions of H₃O⁺ with phospholipids at the molecular level. For this, we carried out multiple microsecond-long unrestrained molecular dynamics (MD) simulations of a POPC bilayer at different H₃O⁺ concentrations. The results show that H₃O⁺ accumulates at the membrane surface where it displaces water and forms strong and long-lived hydrogen bonds with the phosphate and carbonyl oxygens in phospholipids. This results in a concentration-dependent reduction of the area per lipid and an increase in bilayer thickness. This study provides an important molecular-level insight into the mechanism of how H₃O⁺ modulates the structure of biological membranes and is a critical step towards a better understanding of the effect of low pH on mammalian and bacterial membranes.

---

1 Introduction

Phospholipids are the major components of cell membranes in all living organisms.¹ Phospholipid bilayers are thus routinely used as model systems for mammalian and bacterial membranes to investigate their structural, chemical and physical properties.² Besides lipid composition, environmental factors such as temperature, salt concentration, ionic strength and pH affect the properties of membranes and lipid bilayers, including their structure, level of fluidity, interfacial tension, conduction and ion permeability. The effect of temperature,^3–5 pressure^6,7 and salt^8–11 on lipid bilayers has been studied extensively over the past decades. In contrast, less is known on the effect of pH on the structure of membranes despite its important role in a range of biological processes, including the stability and integrity of the lysosomal membrane,¹² the formation of cholesterol-enriched domains¹³ and drug partitioning.^14,15 Furthermore, extracellular acidosis has been associated with inflammation¹⁶ and various pathological states (for example tumour growth,^17,18 ischaemic stroke¹⁹ and epileptic seizures²⁰). The effect of pH on biological membranes is also relevant to understanding how some organisms have adapted to living in extreme pH environments²¹ and the design of acidophilic bacteria for bio-mining and other biotechnology applications.²²

Most studies on the effect of pH on membranes have focused on the physical, electrical and mechanical properties of phospholipid bilayers rather than the molecular interactions of the hydronium ions with the phospholipids. As summarised by Koynova and Caffrey,²³ at a pH < 3 in the bulk aqueous solution, a range of fully hydrated, saturated diacyl and dialkyl glycerophospholipids bilayers, including phosphatidylcholines and phosphatidylcholine analogues show an increased lamellar gel-to-liquid crystalline phase-transition temperature.^24–29 Furthermore, using a range of experimental techniques such as micropipette aspiration, fluorescence spectroscopy and electrophoresis, Zhou and Raphael characterised the mechanical and electrical properties of a 2-oleoyl-1-stearoyl-sn-glycero-3-phosphocholine (SOPC) bilayer at pH 2–9.³⁰ Based on measurements of ζ-potential and dipole moments, the authors concluded that pH-induced changes in membrane bending stiffness stemmed from alterations in interfacial rather than intra-membrane electrostatics. In another study, Petelska and Figaszewski proposed a theoretical model to describe the effect of pH on interfacial tension in the vicinity of the isoelectric point of a phosphatidylcholine lipid bilayer based on interfacial tension measurements of a solvent-formed egg phosphatidylcholine bilayer.³¹ The authors then extended their model to describe the adsorption of the H⁺ and OH⁻ ions to the surface of phosphatidylcholine and phosphatidylserine bilayers for pH ranges within and outside the isoelectric point.³² Whilst these studies provided some insight into the effect of pH on macroscopic properties of phospholipid bilayers, they did not provide structural information at the molecular level of solvent-free bilayers. That is, none of the methods used can report on the molecular interactions between lipids and H₃O⁺ or OH⁻ ions, and how these interactions might differ from and compete with hydrogen bonding of lipids with H₂O. Indeed, rather than studying the effect of protons and hydronium ions on the phospholipid bilayer, most experimental and theoretical studies have focused on the transfer of protons or hydronium ions across the surface of biological membranes, a process critical to energy metabolism.^33–38 In addition, the intricate interactions of water with phospholipids, in particular how interfacial water can cross-link phospholipid head groups via hydrogen bonds, has been investigated experimentally and in simulations.^9,39–44

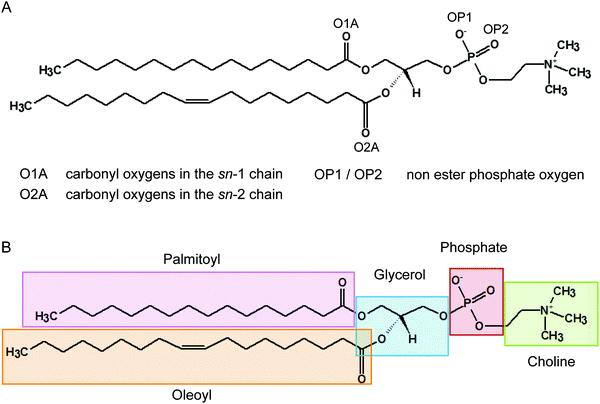
It has been recognised for some time that water can cross-link phospholipid head groups via hydrogen bonding to the oxygens present at the interface.^41–43 Glycerophospholipids provide a number of hydrogen-bonding sites. In phosphatidylcholines such as POPC (2-oleoyl-1-palmitoyl-sn-glycero-3-phosphocholine) these include the carbonyl oxygens in the sn-1 (referred to as O1A) and sn-2 chains (O2A) and the two non-ester phosphate oxygens (OP1 and OP2), as illustrated in Fig. 1. Note, the oxygens OP1 and OP2 are chemically equivalent through resonance and both P–O bonds have a 1.5-bond character owing to sharing of the negative charge. Recently, Cranfield et al. proposed a model to account for the pH-induced structural changes in model membranes through the modification of water–lipid hydrogen bonds.⁴⁵ Specifically, the conductance and capacitance of tethered phospholipid bilayers in bathing solutions at acidic and alkaline pH were determined using AC impedance spectroscopy and DC-ramped amperometry. In addition, the thickness and water content of the bilayers were examined using neutron reflectometry. It was suggested that the variations in membrane conductivity and water penetration into the bilayer observed at low pH was caused by H₃O⁺ ions competing with and disrupting water-bridged intermolecular hydrogen bonds between lipid molecules. Furthermore, it was hypothesised that the observed decrease in area per lipid was due to an enhanced stability of hydrogen bonds of H₃O⁺ with the phosphate and carbonyl oxygens in lipids.

Fig. 1 Structure of a POPC lipid molecule showing the hydrogen bonding sites on the carbonyl and phosphate oxygens (A) and chemical moieties (B). The oxygens OP1 and OP2 are chemically equivalent through resonance.

In this study, we examine the interactions of H₃O⁺ ions with a POPC bilayer at a molecular level using multiple microsecond-long unrestrained molecular dynamics (MD) simulations at H₃O⁺ concentrations of 0.4 and 0.04 M. While bulk-phase concentrations of 0.4 M and 0.04 M for the hydronium ion may seem high (equivalent to bulk-phase pH values of about 0.5 and 1.5, respectively), a range of experimental^33,35,46,47 and computational^48–51 studies have suggested that the H₃O⁺ concentration is significantly higher on the membrane surface than in the bulk water phase, and that the interfacial water layer may act as a barrier for ions which would contribute to retarding surface-to-bulk H₃O⁺ equilibration and separating the surface of a membrane from the bulk. Indeed, calculations of the potential of mean force of the hydrated excess proton near phospholipid bilayers in atomistic simulations have indicated that the interfacial pH could be as low as 3 when the pH of the bulk water region was taken as 7.⁵¹ This would imply that in the experiments performed by Cranfield et al.⁴⁵ at a bulk-phase pH of 5, the local concentration in hydronium ions at the surface of the model membranes could be within a range comparable to that used in the simulations.

In summary, the results presented here show that H₃O⁺ ions accumulate at the water–lipid interface where they displace water. The H₃O⁺ ions form short and long-lived hydrogen bonds with the phosphate and carbonyl oxygens with a particular preference for the sn-2 carbonyl oxygen. The strong hydrogen bond network results in a decrease of the area per lipid and an increase in the bilayer thickness in agreement with previous experimental studies⁴⁵ and consistent with the increase in the lamellar gel-to-liquid crystalline phase-transition temperature in phosphatidylcholines and phosphatidylcholine analogues.^24–29 The combined results from these simulations are supportive of the hypothesis by Cranfield et al. that the strong hydrogen bonding capacity of H₃O⁺ is the origin of the pH-induced changes in the structure of phospholipid membranes.⁴⁵

2 Experimental

Model systems

Three simulation systems were examined with H₃O⁺ concentrations, denoted [H₃O⁺], of 0, 0.04 M and 0.4 M (Table 1). Each system consisted of a preassembled bilayer of 512 POPC molecules and at least 13 000 water molecules; that is, at least 45 water molecules per lipid to ensure a fully hydrated state. The POPC bilayer in the absence of H₃O⁺ ions was taken from previous studies.^52,53 The system consisting of a POPC bilayer with 0.04 M and 0.4 M [H₃O⁺] were prepared by randomly adding 16 and 164 H₃O⁺ ions, respectively.

Table 1 Overview of simulation systems listing the number of H₃O⁺ ions added and the resulting H₃O⁺ concentrations. Each simulation system contains a preassembled bilayer of 512 POPC molecules. The simulations for the neutral system were taken from previous studies^52,53

System name	H3O^+ ions	[H3O^+]	Simulations (μs)
Neutral	—	—	2 × 1
0.04 M	16	0.04 M	3 × 1
0.4 M	164	0.4 M	3 × 1

---

Simulation parameters

All simulations were performed using GROMACS version 4.6.7,⁵⁴ in conjunction with the GROMOS 54A7 force field⁵⁵ and parameters for POPC developed by Poger et al.⁵³ This force field has been shown to reproduce a range of lipid-packing, chain-ordering and hydration properties of phosphatidylcholine bilayers.^52,53,56,57 Parameters for the H₃O⁺ ion compatible with the GROMOS 54A7 force field were obtained from the Automated Topology Builder (ATB; http://https://atb.uq.edu.au).^58,59 Briefly, the partial charges of the oxygen and hydrogen atoms were −0.587e and 0.529e, respectively, giving an overall charge of +1 to the ion. The O–H bond length and the H–O–H angle were set to 0.0983 nm and 109.50°, respectively (see also Fig. S1 in the ESI†). The structure and parameter files can be downloaded from the ATB (molid 3859). The ATB has been thoroughly tested and validated using a large set of small molecules to reproduce hydration free enthalpies. Parameters are produced based on QM calculations and charge group partitioning⁶⁰ optimised for small molecules used in biomolecular simulations. The model used for the hydronium ion in this study, in particular the atomic partial charges and the ion geometry, was similar to other models employed successfully in previous simulation studies.^61–67 Such a model does not allow for bond-breaking or creation and therefore ignores any proton hopping as proposed in the Grotthuss mechanism.^68,69 Likewise, it is assumed that the excess proton is localised on a single water molecule forming a hydronium cation, rather than being delocalised over multiple water molecules and changing between different species, such as the Eigen (H₉O₄⁺) and Zundel cations (H₅O₂⁺).^68,70 Solvent water was described using the simple point charge (SPC) water model.⁷¹ All systems were subject to rectangular periodic boundary conditions. The systems were simulated using a 2 fs time step. Both temperature and pressure were maintained close to their reference values of 303 K and 1 bar, respectively, using the Berendsen weak-coupling method.⁷² For temperature coupling, a time constant of 0.1 ps was used. For semi-isotropic pressure coupling a time constant of 1 ps alongside an isothermal compressibility of 4.65 × 10⁻⁵ bar⁻¹ were used. The LINCS algorithm⁷³ was used to constrain the lengths of all bonds in lipids. Nonbonded interactions were evaluated using a single-range cutoff scheme whereby interactions within a 1.4 nm cutoff were calculated at every step and the pair list was updated every 5 steps. Previous work with the GROMOS force field used a twin-range cutoff scheme but its association with the current implementation of the integrator in GROMACS leads to artefacts in the collective properties of a lipid bilayer.⁷⁴ Despite some loss in computational efficiency, using a single-range cutoff scheme was found to counterbalance those artefacts.⁷⁴ To correct for the truncation of electrostatic interactions beyond 1.4 nm a reaction-field correction⁷⁵ with a relative dielectric constant (ε_r) of 62 was applied. The systems with 0.04 and 0.4 M [H₃O⁺] were simulated in triplicate and the reference system without H₃O⁺ ions was simulated in duplicate, each time using randomly assigned starting velocities. All simulations were 1 μs long.

Changing the protonation state of the phosphate group in POPC as a result of the high concentration in hydronium ions used in the simulations was not considered insofar as the value of the pK_a of the phosphate group in phosphatidylcholines has remained unclear given the various estimates reported including 0.8,⁴² <1,⁷⁶ 1.0,⁴¹ 1.3,⁷⁷ <1.5²⁸ and 2.25.⁷⁸ Even for the isolated phosphate group alone, a pK_a value as low as −1.54 has been proposed for dimethyl phosphate.⁵¹ In addition, those estimates relied on critical assumptions that intrinsically limited their accuracy. For example, Monceli et al.⁷⁹ determined a value of pK_a of 0.8 assuming that the area per lipid was constant and corresponded to that of a fluid-phase phosphatidylcholine bilayer (0.65 nm²), and that the properties of interfacial water, that is the water layer residing near the membrane surface, was the same as those of bulk water, in particular the dielectric permittivity. However, both of those assumptions have proven arguable since it was shown that variations in pH induced phase transition in lipid bilayers.^23,29,30,80

Setup of membrane simulation systems

The systems containing 0.04 M and 0.4 M [H₃O⁺] were generated by adding 16 and 164 H₃O⁺ ions in the water slab, respectively, to the 521 POPC lipid bilayer at neutral pH (Table 1). The positive net charge of the systems containing H₃O⁺ ions was neutralised by adding Cl⁻ anions. Additional Na⁺ and Cl⁻ ions were used to obtain a final concentration of 0.15 M NaCl. All the ions (H₃O⁺, Na⁺ and Cl⁻) were added to the hydrated systems by replacing water molecules selected randomly. Each system was energy-minimised using a steepest-descent algorithm and then simulated for 5 ns with all lipid atoms position-restrained to allow the water and ions to relax, followed by the production simulations.

Setup of ‘bulk’ water simulation systems

To validate the parameters of H₃O⁺ a 40 ns simulation of ‘bulk’ water with 0.04 M [H₃O⁺] and 0.15 M NaCl was carried out. For this, a cubic box of side lengths 6.5 nm containing 9081 water molecules and 6 randomly positioned H₃O⁺ ions was created. The positive charge of the system was neutralised with 6 Cl⁻ anions and additional Na⁺ and Cl⁻ ions were used to obtain a final concentration of 0.15 M NaCl. The system was energy-minimised using a steepest-descent algorithm and then simulated for 40 ns saving frames every 2 ps.

Data analysis

Unless stated otherwise trajectories from independent simulations were analysed separately. Analysis was carried out using GROMACS tools⁵⁴ and the MDAnalysis package.⁸¹ The area per lipid was calculated using the lateral dimensions of the box (in the xy plane) divided by the number of lipids per leaflet. The bilayer thickness was derived from the electron density profile of the phosphorus atoms of the system along the bilayer normal (taken as the z axis) and corresponded to the distance between the two maxima of the electron density. Distribution of distances between H₃O⁺ ions were calculated using oxygen–oxygen distances from the last 500 ns of the trajectory. For hydrogen bonding analysis, a 0.35 nm cut-off for the radius and a 30° for the angle were used. Contacts between phosphorus atoms in the POPC molecules and H₃O⁺ ions and water, respectively, were calculated using the centre of mass of the P atom, the H₃O⁺ ions and water, respectively, and a 0.4 nm cut-off. Unless otherwise stated, uncertainties are given as ±1 standard deviation.

3 Results

The results section is divided into four parts: (i) validation of the H₃O⁺ model, (ii) the effect of H₃O⁺ ions on the structure of the lipid bilayer; (iii) the accumulation and location of the H₃O⁺ ions in the lipid bilayer; and (iv) the hydrogen bonding network in the phosphate, glycerol and carbonyl of the lipid bilayer.

Validation of the H₃O⁺ model

Over the past three decades a wide range of force-field parameters for the hydronium ion have been proposed. The geometric parameters (bond lengths and angles) used as well as the partial charges, van der Waals parameters, the presence or absence of polarisability, and the inclusion of virtual sites in these models vary considerably (see ref. 61–67, 82 and 83 and references therein). In the classical model presented here, the partial charges are 0.529e and −0.587e on the hydrogen and oxygen, respectively, and the Lennard-Jones parameters for the oxygen atom are ε = 0.84 kJ mol⁻¹ and σ = 0.29 nm (see also Fig. S1, ESI†). These parameters are based on DFT calculations (B3LYP/6-31G*) and charge group assignments that have been optimised for small molecules in biomolecular simulations,⁶⁰ and implemented on the ATB.^58,59 Also, our model of H₃O⁺ is consistent with the force field and SPC water model used in our simulations of the hydrated bilayers.

As a validation of our model of H₃O⁺, a 40 ns simulation of 0.04 M H₃O⁺ in water with 0.15 M NaCl was carried out. The radial distribution function (RDF; Fig. S2, ESI†) between the oxygen in H₃O⁺ and the oxygen in water shows a first peak at 0.25 nm. This is in excellent agreement with earlier simulation studies of H₃O⁺ in solution using classical non-polarisable force fields for H₃O⁺.^61,62 The RDF also agrees well with simulations using a more complex model of H₃O⁺ that takes into account the interaction of an exchange charge distribution of the charge-transfer complex.⁸³

Effect of H₃O⁺ ions on membrane structure

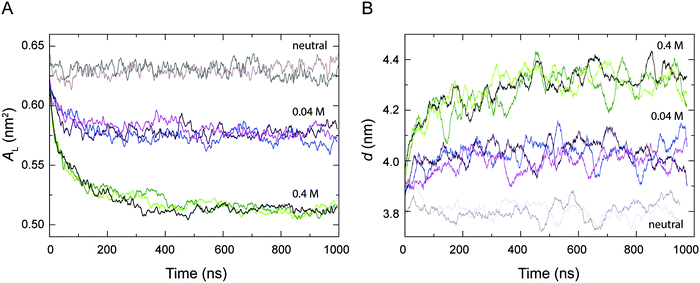
The area per lipid A_L and the bilayer thickness d are important properties to describe the structure and the degree of packing within a bilayer, which are thus indicative of the level of fluidity of a lipid bilayer.⁵⁶Fig. 2 shows the time-dependent variation of A_L and d calculated from the simulations of a POPC lipid bilayer with 0.04 M and 0.4 M H₃O⁺ in comparison to the A_L and d from the simulations of a POPC bilayer in the absence of H₃O⁺ (referred to as neutral). As can be seen, all the systems reached equilibrium within about 0.5 μs and A_L and d fluctuated around their average values over the last 0.5 μs. In the absence of H₃O⁺ ions, the average values for A_L and d over the last 0.5 μs of the two simulations were 0.628 ± 0.007 nm² and 3.80 ± 0.16 nm, respectively. This is in good agreement with simulation and experimental values previously reported for a fluid-phase POPC bilayer.^53,56,84,85 In contrast, A_L decreased and d increased at higher H₃O⁺ concentrations, that is A_L = 0.572 ± 0.006 nm² and d = 4.02 ± 0.14 nm at 0.04 M [H₃O⁺], and A_L = 0.514 ± 0.003 nm² and d = 4.32 ± 0.13 nm, at 0.4 M [H₃O⁺] over the last 0.5 μs of the three simulations.

Fig. 2 Effect of H₃O⁺ ions on the structure of a POPC lipid bilayer from 1 μs of unrestrained MD simulation. Area per lipid (A_L) (A) and membrane thickness (d) (B) as a function of time from simulations of neutral POPC (grey, brown) and in the presence of 0.04 M [H₃O⁺] (blue, magenta, indigo) and 0.4 M [H₃O⁺] (black, light green, dark green). A_L and d are shown as moving averages over 100 and 50 data points, respectively.

Accumulation of H₃O⁺ ions at the water–lipid interface

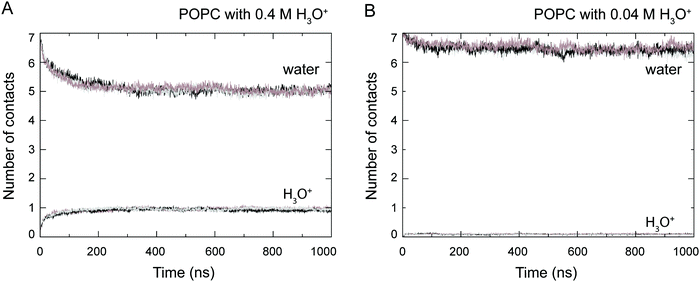
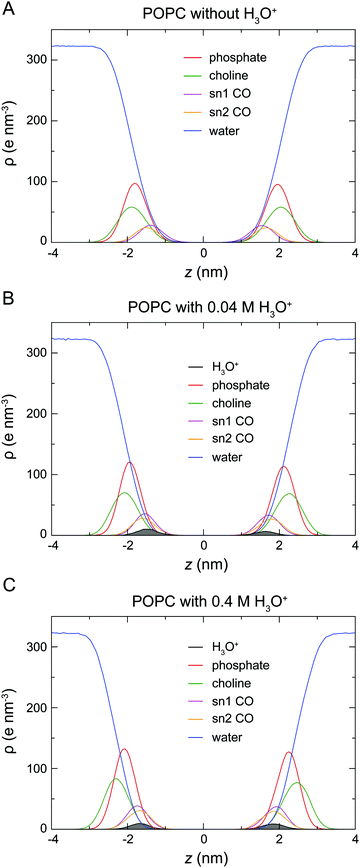
At the start of the simulation, the H₃O⁺ ions were randomly distributed in the bulk solvent. Shortly after the start of the simulation the H₃O⁺ ions migrated to the water–lipid interface as reflected in the sharp increase in the average number of contacts formed between the phosphorus atom (P) and H₃O⁺ ions at the cost of contacts between P and water molecules (Fig. 3). The time-dependent variation of these contacts suggests that the number of H₃O⁺ ions at the water–lipid interface reached a steady state after about 300–400 ns. This is consistent with the convergence of the area per lipid and the bilayer thickness (Fig. 2), which further highlights that the simulations were at equilibrium over the last 0.5 μs of simulation. For the rest of the simulations the H₃O⁺ ions remained at the water–lipid interface.

Fig. 3 Number of contacts between phosphorus atoms in the POPC molecules and H₃O⁺ ions and water, respectively, calculated from simulations of a POPC lipid bilayer in the presence of 0.4 M [H₃O⁺] (A) and 0.04 M [H₃O⁺] (B). Data from the three independent simulations is shown (grey, black and brown). The number of contacts are normalised by the number of lipids in the system.

To determine the location of the hydronium ions at the water–lipid interface, the electron density profiles of the phosphate, choline, sn-1 carbonyl and sn-2 carbonyl groups as well as water and H₃O⁺ ions along the bilayer normal were calculated using data from the last 0.5 μs of the simulations. Fig. 4 displays the electron density profiles from simulations of POPC in the absence of H₃O⁺ (A) and in the presence of 0.04 M [H₃O⁺] (B) and 0.4 M [H₃O⁺] (C). For clarity, the density of H₃O⁺ from simulations with 0.04 M [H₃O⁺] has been multiplied by 10. Comparing the density profiles of water in the three graphs shows a receding of the water density from the centre of the bilayer with increasing H₃O⁺ concentration. This effect is absent in the simulations of POPC without H₃O⁺ ions and thus further confirms that water at the membrane surface is being displaced by H₃O⁺ ions. Furthermore, the position of the electron density for H₃O⁺ reveals that H₃O⁺ ions are located below the phosphate group close to the carbonyl groups.

Fig. 4 Electron density profiles of a POPC lipid bilayer in the absence of H₃O⁺ (A) and in the presence of 0.04 M [H₃O⁺] (B) and of 0.4 M [H₃O⁺] (C). Each density profile shows the electron density ρ as a function of the distance from the centre of the bilayer z for the phosphate (red), choline (green), sn-1 (magenta) and sn-2 (orange) carbonyl groups as well as water (blue) and H₃O⁺ ions (black) calculated from the last 0.5 μs of the simulations. For clarity, the density of H₃O⁺ from simulations with 0.04 M H₃O⁺ (B) has been multiplied by 10.

Hydrogen bonding of H₃O⁺

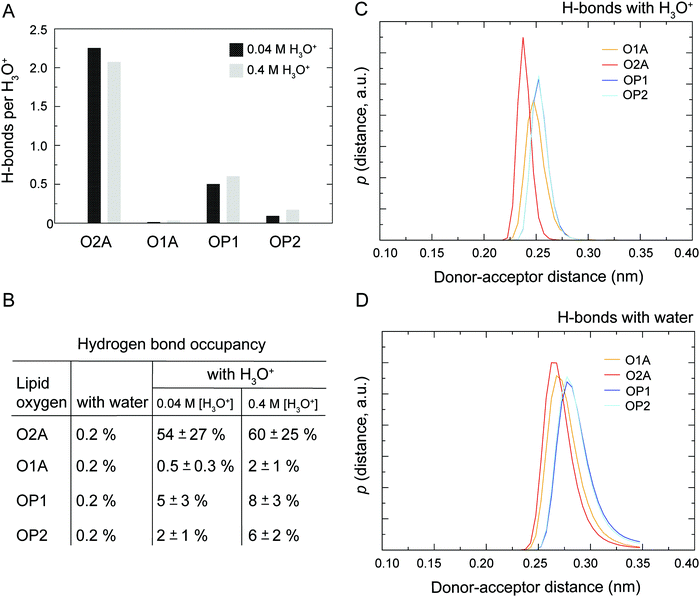
As illustrated in Fig. 1 the POPC molecule has several hydrogen-bonding sites through which it can interact with H₃O⁺ and H₂O. Fig. 5A shows histograms of hydrogen bonds per H₃O⁺ ions for the different lipid oxygens calculated from the last 200 ns of the 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺] simulations. The carbonyl oxygen in the sn-2 chain O2A formed between 2.0 to 2.5 hydrogen bonds per H₃O⁺ while the non-ester phosphate oxygens OP2 and OP1 formed about 1.0 and 0.5 hydrogen bonds per H₃O⁺, respectively. In contrast, the carbonyl oxygen in the sn-1 chain O1A formed almost no hydrogen bond with the H₃O⁺ ion. These results suggest that H₃O⁺ has a strong preference for the carbonyl oxygen in the sn-2 chain. The lifetime of the hydrogen bonds was estimated by calculating the occupancy, that is, the fraction of time during which the hydrogen bond is present. Fig. 5B lists the occupancy of hydrogen bonds formed by the different lipid oxygens with water and H₃O⁺ ions. For a given oxygen, the occupancy was averaged over the three independent simulations of a POPC lipid bilayer in the presence of 0.04 [H₃O⁺] and 0.4 [H₃O⁺], respectively. As can be seen, the hydrogen bonds for all lipid oxygens exhibited greater occupancies for H₃O⁺ than for water, in particular for O2A. For all oxygen, there is no significant difference between the 0.4 [H₃O⁺] and 0.04 [H₃O⁺] simulations suggesting that the effect is not dependent on the specific H₃O⁺ concentration.

Fig. 5 Hydrogen bonds (H-bonds) between lipid oxygens. (A) Histograms of H-bonds per H₃O⁺ ions for the different lipid oxygens calculated from simulations of a POPC lipid bilayer in the presence of 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺]. For each oxygen, the number of H-bonds were averaged over the last 200 ns of the simulation from the three independent trajectories. (B) Occupancy of H-bond formed by the different lipid oxygens with water and H₃O⁺ ions, respectively. For each oxygen, the occupancy was calculated over the full lengths of the trajectory and then averaged over the three independent simulations a POPC lipid bilayer in the presence of 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺], respectively. (C and D) Probability distribution of donor–acceptor distances distance for the hydrogen bonds formed by the lipid oxygens with the H₃O⁺ ion (C) and water (D) calculated from the last 500 ns of simulations of POPC in the presence of 0.4 M [H₃O⁺]. In summary, the analysis indicates that H₃O⁺ forms stronger and longer-lived hydrogen bonds with the lipid oxygen compared to H₂O.

Fig. 5C and D show the probability distribution of the donor–acceptor distance for the hydrogen bonds formed by the lipid oxygens with H₃O⁺ (5C) and water (5D). Comparison of the two plots shows that for both H₃O⁺ and water the average hydrogen bond distance is the shortest for O2A, followed by O1A. The bonds with OP1 and OP2 are the longest. However, for all four lipid oxygens the average hydrogen bond distances are slightly shorter for H₃O⁺ compared to water. In addition, the distribution for the hydrogen bonds with H₃O⁺ are narrower.

Bonding arrangement of lipids around the H₃O⁺ ion

Next, we investigated the packing of lipids around H₃O⁺ ions. To determine the most likely arrangement of lipids around H₃O⁺ a list of all possible hydrogen-bonding arrangements for the H₃O⁺ was prepared. For example, a H₃O⁺ ion can be interacting with two O2A oxygens and one OP1 oxygen or one O2A oxygen and two OP1 oxygens or one O2A, one OP1 and one OP2 etc. The occurrence of each possible arrangements over the full-length of the 1 μs simulation was calculated as the frequency of finding all lipid oxygen within 0.2 nm of a given H₃O⁺. The data was averaged over the three independent simulations with 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺], respectively. The occurrence for the four most populated arrangements is shown in Table 2. Comparing the data from simulations with 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺] shows that the standard deviations are much larger for simulations with 0.04 M [H₃O⁺] due to the much lower number of the H₃O⁺ ions (16 vs. 164). Nevertheless, the order of the four most populated arrangements is the same in two simulation systems.

Table 2 Occurrence for the different arrangements of lipid oxygen observed in simulation of POPC in the presence of 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺]. Occurrences were calculated using the full-length of the 1 μs simulation and a 0.2 nm cut-off, and averaged over the three independent simulations of 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺], respectively. In each arrangement, the H₃O⁺ ion interacts with three oxygen from three lipid molecules. Errors are standard deviations

Arrangement	Occupancy
	0.04 M [H3O^+] (%)	0.4 M [H3O^+] (%)
2 O2A, 1 OP1	45 ± 11	36 ± 1
3 O2A	24 ± 11	19 ± 2
2 O2A, 1 OP2	7 ± 1	11 ± 1
1 O2A, 2 OP1	4 ± 3	6 ± 0

---

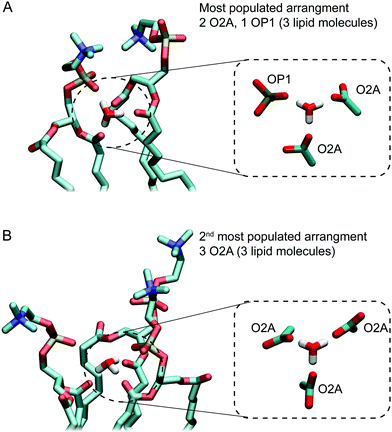
Fig. 5A and B show examples of the two arrangements with the highest occurrences. Together, these account for almost two thirds of hydrogen bonding arrangements across the 3 μs of the 0.04 M [H₃O⁺] and 0.4 M [H₃O⁺] simulations. In the most populated arrangement (42%), H₃O⁺ interacts with two O2A oxygen and one OP1 oxygen (Fig. 5A). In the second most common arrangement (22%), H₃O⁺ hydrogen bonds with three O2A oxygen (Fig. 5A). In both cases, the ion is surrounded by three lipids.

4 Discussion

Despite the important role of pH in biological processes and the association of acidosis with various pathophysiological states little is known about the effect of the H₃O⁺ ion on the structure of phospholipid membranes. In this study, we aimed to characterise the molecular interactions with the H₃O⁺ ion and phospholipids and its effect of the structure of a phospholipid bilayer. For this we carried out unrestrained MD simulations of POPC lipid bilayers in the presence 0.04 M and 0.4 M [H₃O⁺] and combined this with data from simulations of POPC in the absence of H₃O⁺.⁶

Analysis of the structure of the bilayers showed that in simulations with 0.04 M and 0.4 M H₃O⁺ the area per lipid A_L dropped by about 8% and 18% compared to a fluid-phase POPC bilayer without H₃O⁺ ions (Fig. 2A). At the same time the bilayer thickness d increased by about 6% at 0.04 M H₃O⁺ and 14% at 0.4 M H₃O⁺ (Fig. 2B). This would indicate that the presence of H₃O⁺ ions induced a reduction in the level of the fluidity of the bilayer. These observations are consistent with recent neutron reflectometry experiments on phospholipids that showed an increase in the outer leaflet tail thickness of about 4% as the pH was decreased from 9 to 5,⁴⁵ as well as the gel-like characteristics and the reduced elasticity observed in SOPC bilayers at pH 2.³⁰ In addition, a number of studies have shown that for bulk pH < 3, the lamellar gel-to-liquid crystalline phase-transition temperature for a range of phosphatidylcholines and phosphatidylcholine analogues is increased by about 10 °C.^{23,25,26,28,29,63} The concomitant change in A_L and d can be interpreted in terms of the critical packing parameter (CPP). For a system of constant molecular volume, the molecular shape can be determined by the CPP defined as the ratio v/(a₀l), where v is the hydrated molecular volume, a₀ is the interfacial molecular area and l is the length of the lipid chains. The CPP can reflect a property of a heterogeneous molecular assembly where the individual components which may include lipids, sterols and peptides can combine to provide an averaged CPP. The membrane geometry influenced by the averaged CPP will modulate the physical properties of the membrane such as membrane thickness and conduction.^86,87 That the POPC bilayer remained planar (CPP∼1) in all simulations at 0.04 M and 0.4 M [H₃O⁺] suggests that the term a₀l approximated as A_Ld was constant at both [H₃O⁺] concentrations and that the increase in d closely matched the decrease in A_L.

The analysis of the location and hydrogen bonding of H₃O⁺ enabled us to identify the molecular interactions that underlie these changes. Results from the electron density profiles indicate that H₃O⁺ sequesters into the water–lipid interface where it displaces water. The H₃O⁺ ion accumulates slightly below the phosphate group close to the carbonyl oxygens (Fig. 4). This agrees with previous simulations studies of a proton excess or hydrated protons at the surface of DMPC,⁵⁰ DOPC or DOPE bilayers.^49,51 In these studies, the free energy profiles showed a strong membrane surface affinity for the protons and the H₃O⁺ was shown to interact with both the phosphate and carbonyl oxygen. These observations from simulations are in line with the results from measurements of the ζ-potential by Zhou and Raphael³⁰ which indicated that H₃O⁺ ions alter the interfacial electrostatics by acting as counterions at the water–lipid interface. The same study also reported that there are no changes in the intra-membrane electric properties, as measured by the dipole moment. This suggest that H₃O⁺ ions do not enter the hydrophobic core of the membrane, which is also in agreement with the data from our simulations.

The hydrogen bond analysis suggests that the H₃O⁺ ions show a preference for the carbonyl oxygen in the sn-2 chain (O2A) followed by the non-ester phosphate oxygen (OP1). There are little to no hydrogen bonds formed by H₃O⁺ and the other non-ester phosphate oxygen (OP2) and the sn-1 carbonyl oxygen (O1A). The three hydrogen bonding sites on H₃O⁺ combined with this preference means that the majority of the time H₃O⁺ is surrounded by three lipid molecules forming hydrogen bonds with either three O2A or two O2A and one OP1 oxygens, as depicted in Fig. 6. This is consistent with the observations reported previously in which the pH dependence of POPC which contains ester carbonyl groups resulted in a 245-fold change in conduction between pH 5 and pH 9 of the bulk solution compared to an 8-fold change in conduction for an ether-lipid containing no carbonyls.⁴⁵ Previous simulations of hydrated protons with DOPC bilayers suggested that in the deep interface region, closer to the hydrophobic core, a distorted Zundel cation (H₅O₂⁺) can bridge between the phosphate and carbonyl oxygen.⁵¹ Note that the results from this study cannot be directly compared to data from this study as in our simulations a hydronium cation was used where the excess proton is localised on a single water molecule rather than a Zundel cation.

Fig. 6 The two most common hydrogen bonding networks formed by H₃O⁺ ions and POPC lipids observed in simulations of a POPC lipid bilayer in the presence of 0.4 M [H₃O⁺] and 0.04 M [H₃O⁺]. (A) In the most populated arrangement a H₃O⁺ ion forms hydrogen bonds with the sn-2 carbonyl oxygens (O2A) from two lipids and the non-ester oxygen (OP1) from a third lipid. (B) The second most common arrangement in which H₃O⁺ ion forms hydrogen bonds with the sn-2 carbonyl oxygens (O2A) from three lipids.

Combined, these results clearly indicate that H₃O⁺ ions form a distinct hydrogen bonding network with the polar lipid oxygen that is different from the one formed by water molecules. Even at low pH the concentration of water (55 M) and Na⁺ ions (0.15 M) exceeds the concentration of H₃O⁺ by at least 3 orders of magnitude, yet it is the interactions of H₃O⁺ with the lipid head groups that alter the structure of the membrane. The small size and positive charge of H₃O⁺ results in a high-field strength providing it with the ability to form strong non-covalent interactions with the polar oxygen in the lipid molecules. In our simulations, this is evident in the shorter and longer-lived hydrogen bonds of H₃O⁺ when compared to the ones by H₂O. The lifetimes of the hydrogen bonds and the relative occupancies for the different lipid arrangements is likely distorted by the absence of ability for proton transfer. To obtain accurate lifetimes for hydrogen bonds and relative stabilities of the different bonding arrangement would require the use of a model that allows for proton hopping and charge transfer delocalization, which is beyond the scope of this study. Nevertheless, on a qualitative level the longer-lived H-bonds observed in our simulations are in agreement with significantly reduced proton transfer rates at membrane surface reported in previous simulations.⁵⁰ The increased stability of hydrogen bonds formed by the H₃O⁺ ion can also be related to the diffusion of protons and hydronium ions across membrane surfaces. For example, based on the energetics and mobility of protons near a solvated DMPC bilayer Wolf et al.⁵⁰ observed anomalous diffusion “characterized by a short subdiffusive regime (1 ns) and a subsequent superdiffusive regime” where the subdiffusive regime results from the H₃O⁺ ion being tightly bound to lipids. Similarly, Yamashita and Voth⁵¹ reported that the “lateral diffusion coefficients are 1 order of magnitude smaller in the interface region than in bulk water for all the lipids.”

Overall, the simulations are consistent with the model of lipid bilayers and biological membranes in a low-pH environment that has emerged from a range of experimental studies. Specifically, lipid bilayers and membrane undergo a reduction in the decrease in area per lipid that stems from an increase in the stability of the hydrogen bonds between lipids and hydronium ions H₃O⁺. At high H₃O⁺ concentration (that is acidic pH), H₃O⁺ ions accumulate at the membrane interface where they form strong hydrogen bond networks with the carbonyl and phosphate oxygen. This results in a condensation of the lipids onto the H₃O⁺ ion resulting in a reduced area per lipid A_L.

5 Conclusions

To the best of our knowledge this is the first study that reports, at the molecular level, the interactions between H₃O⁺ and phospholipids and its effect on the structure of phospholipid bilayers. Our results indicate that the H₃O⁺ ions partition into the water–lipid interface where they displace water and form strong and long-lived hydrogen bonds with the phospholipid phosphate and carbonyl oxygens. These strong interactions result in a reduced area per lipid and an increased bilayer thickness. In order to quantitatively predict this effect, more concentrations would need to be examined but this was beyond the scope of the present study. Additional studies will also be required to investigate this effect in more complex membranes.

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

This work was supported by resources provided of the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia, as well as with the assistance of resources provided at the NCI National Facility systems at the Australian National University through the National Computational Merit Allocation Scheme supported by the Australian Government. This work was supported in part by Australian National Health and Medical Research Council Early Career Fellowship to ED.

References

1. G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124.
2. G. Pabst, N. Kučerka, N. Mu-Ping and J. Katsaras, Liposomes, Lipid Bilayers and Model Membranes: From Basic Research to Application, CRC Press, 2016.
3. R. Basu, S. De, D. Ghosh and P. Nandy, Physica A, 2001, 292, 146–152.
4. A. Blicher, K. Wodzinska, M. Fidorra, M. Winterhalter and T. Heimburg, Biophys. J., 2009, 96, 4581–4591.
5. S. L. Veatch and S. L. Keller, Biochim. Biophys. Acta, Mol. Cell Res., 2005, 1746, 172–185.
6. R. Chen, D. Poger and A. E. Mark, J. Phys. Chem. B, 2011, 115, 1038–1044.
7. R. Winter, Curr. Opin. Colloid Interface Sci., 2001, 6, 303–312.
8. A. Aroti, E. Leontidis, M. Dubois and T. Zemb, Biophys. J., 2007, 93, 1580–1590.
9. M. L. Berkowitz and R. Vácha, Acc. Chem. Res., 2012, 45, 74–82.
10. H. I. Petrache, T. Zemb, L. Belloni and V. A. Parsegian, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7982–7987.
11. J. Song, J. Franck, P. Pincus, M. W. Kim and S. Han, J. Am. Chem. Soc., 2014, 136, 2642–2649.
12. A. C. Carreira, R. F. M. de Almeida and L. C. Silva, Sci. Rep., 2017, 7, 3949.
13. D. A. Redfern and A. Gericke, J. Lipid Res., 2005, 46, 504–515.
14. S. D. Krämer, A. Braun, C. Jakits-Deiser and H. Wunderli-Allenspach, Pharm. Res., 1998, 15, 739–744.
15. K.-J. Schaper, H. Zhang and O. A. Raevsky, Quant. Struct.-Act. Relat., 2001, 20, 46–54.
16. J. A. Kellum, M. Song and J. Li, Crit. Care, 2004, 8, 331.
17. L. E. Gerweck and K. Seetharaman, Cancer Res., 1996, 56, 1194–1198.
18. Y. Kato, S. Ozawa, C. Miyamoto, Y. Maehata, A. Suzuki, T. Maeda and Y. Baba, Cancer Cell Int., 2013, 13, 89.
19. Y. Huang and J. O. McNamara, Cell, 2004, 118, 665–666.
20. A. E. Ziemann, M. K. Schnizler, G. W. Albert, M. A. Severson, M. A. Howard Iii, M. J. Welsh and J. A. Wemmie, Nat. Neurosci., 2008, 11, 816–822.
21. M. de Rosa, A. Gambacorta, B. Nicolaus and W. D. Grant, J. Microbiol., 1983, 129, 2333–2337.
22. H. N. Khaleque, J. P. Ramsay, R. J. Murphy, A. H. Kaksonen, N. J. Boxall and E. L. Watkin, Genome Announc., 2017, 5, e01469–e01416.
23. R. Koynova and M. Caffrey, Biochim. Biophys. Acta, Biomembr., 1998, 1376, 91–145.
24. J. M. Boggs, G. Rangaraj and K. M. Koshy, Chem. Phys. Lipids, 1986, 40, 23–34.
25. G. Cevc, J. Biochem., 1987, 26, 6305–6310.
26. G. Cevc, J. Phys., 1989, 50, 1117–1134.
27. G. Cevc, A. Watts and D. Marsh, J. Biochem., 1981, 20, 4955–4965.
28. H. Eibl and P. Woolley, Biophys. Chem., 1979, 10, 261–271.
29. H. Träuble and H. Eibl, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 214–219.
30. Y. Zhou and R. M. Raphael, Biophys. J., 2007, 92, 2451–2462.
31. A. D. Petelska and Z. A. Figaszewski, Biophys. J., 2000, 78, 812–817.
32. A. D. Petelska and Z. A. Figaszewski, Biochim. Biophys. Acta, Biomembr., 2002, 1561, 135–146.
33. M. Brändén, T. Sandén, P. Brzezinski and J. Widengren, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19766–19770.
34. B. Gupta, O. Haas and G. G. Scherer, J. Appl. Polym. Sci., 1994, 54, 469–476.
35. J. Heberle, J. Riesle, G. Thiedemann, D. Oesterhelt and N. A. Dencher, Nature, 1994, 370, 379–382.
36. S. J. Marrink, F. Jähnig and H. J. Berendsen, Biophys. J., 1996, 71, 632–647.
37. J. F. Nagle and R. A. Dilley, J. Bioenerg. Biomembr., 1986, 18, 55–64.
38. H. L. Tepper and G. A. Voth, Biophys. J., 2005, 88, 3095–3108.
39. J. Fitter, R. E. Lechner and N. A. Dencher, J. Phys. Chem. B, 1999, 103, 8036–8050.
40. F. Foglia, M. J. Lawrence, C. D. Lorenz and S. E. McLain, J. Chem. Phys., 2010, 133, 145103.
41. M. Pasenkiewicz-Gierula, Y. Takaoka, H. Miyagawa, K. Kitamura and A. Kusumi, J. Phys. Chem. A, 1997, 101, 3677–3691.
42. M. Pasenkiewicz-Gierula, Y. Takaoka, H. Miyagawa, K. Kitamura and A. Kusumi, Biophys. J., 1999, 76, 1228–1240.
43. R. H. Pearson and I. Pascher, Nature, 1979, 281, 499–501.
44. W. Zhao, D. E. Moilanen, E. E. Fenn and M. D. Fayer, J. Am. Chem. Soc., 2008, 130, 13927–13937.
45. C. G. Cranfield, T. Berry, S. A. Holt, K. R. Hossain, A. P. Le Brun, S. Carne, H. Al Khamici, H. Coster, S. M. Valenzuela and B. Cornell, Langmuir, 2016, 32, 10725–10734.
46. O. A. Gopta, D. A. Cherepanov, W. Junge and A. Y. Mulkidjanian, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13159–13164.
47. C. J. Slevin and P. R. Unwin, J. Am. Chem. Soc., 2000, 122, 2597–2602.
48. A. Mashaghi, P. Partovi-Azar, T. Jadidi, M. Anvari, S. P. Jand, N. Nafari, M. R. R. Tabar, P. Maass, H. J. Bakker and M. Bonn, J. Phys. Chem. B, 2013, 117, 510–514.
49. A. M. Smondyrev and G. A. Voth, Biophys. J., 2003, 85, 864–875.
50. Maarten G. Wolf, H. Grubmüller and G. Groenhof, Biophys. J., 2014, 107, 76–87.
51. T. Yamashita and G. A. Voth, J. Phys. Chem. B, 2010, 114, 592–603.
52. D. Poger and A. E. Mark, J. Chem. Theory Comput., 2012, 8, 4807–4817.
53. D. Poger, W. F. van Gunsteren and A. E. Mark, J. Comput. Chem., 2010, 31, 1117–1125.
54. B. Hess, C. Kutzner, D. van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
55. N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843–856.
56. D. Poger, B. Caron and A. E. Mark, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1556–1565.
57. D. Poger and A. E. Mark, J. Chem. Theory Comput., 2010, 6, 325–336.
58. K. B. Koziara, M. Stroet, A. K. Malde and A. E. Mark, J. Comput.-Aided Mol. Des., 2014, 28, 221–233.
59. A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037.
60. S. Canzar, M. El-Kebir, R. Pool, K. Elbassioni, A. K. Malde, A. E. Mark, D. P. Geerke, L. Stougie and G. W. Klau, J. Comput. Biol., 2013, 20, 188–198.
61. D. J. Bonthuis, S. I. Mamatkulov and R. R. Netz, J. Chem. Phys., 2016, 144, 104503.
62. A. A. Chialvo, P. T. Cummings and J. M. Simonson, J. Chem. Phys., 2000, 113, 8093–8100.
63. L. X. Dang, J. Chem. Phys., 2003, 119, 6351–6353.
64. B. J. Gertner and J. T. Hynes, Faraday Discuss., 1998, 110, 301–322.
65. I. Kusaka, Z. G. Wang and J. H. Seinfeld, J. Chem. Phys., 1998, 108, 6829–6848.
66. S. Urata, J. Irisawa, A. Takada, W. Shinoda, S. Tsuzuki and M. Mikami, J. Phys. Chem. B, 2005, 109, 4269–4278.
67. R. Vácha, V. Buch, A. Milet, J. P. Devlin and P. Jungwirth, Phys. Chem. Chem. Phys., 2007, 9, 4736–4747.
68. N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462.
69. C. J. T. Grotthuss, Ann. Chim. Phys., 1806, 58, 54–74.
70. J. M. J. Swanson, C. M. Maupin, H. Chen, M. K. Petersen, J. Xu, Y. Wu and G. A. Voth, J. Phys. Chem. B, 2007, 111, 4300–4314.
71. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Inter molecular Forces, ed. B. Pullman, Springer, Netherlands, 1981, ch. 21, vol. 14, pp. 331–342.
72. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
73. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
74. S. Reißer, D. Poger, M. Stroet and A. E. Mark, J. Chem. Theory Comput., 2017, 13, 2367–2372.
75. I. G. Tironi, R. Sperb, P. E. Smith and W. F. van Gunsteren, J. Chem. Phys., 1995, 102, 5451–5459.
76. E. London and G. W. Feigenson, J. Lipid Res., 1979, 20, 408–412.
77. M. S. Fernández and E. Calderón, Berichte der Bunsengesellschaft für physikalische Chemie, 1991, 95, 1669–1674.
78. M. Gutman and E. Nachliel, Biochim. Biophys. Acta, Bioenerg., 1990, 1015, 391–414.
79. M. R. Moncelli, L. Becucci and R. Guidelli, Biophys. J., 1994, 66, 1969–1980.
80. D. P. Siegel, J. L. Burns, M. H. Chestnut and Y. Talmon, Biophys. J., 1989, 56, 161–169.
81. N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327.
82. D. E. Sagnella and G. A. Voth, Biophys. J., 1996, 70, 2043–2051.
83. U. W. Schmitt and G. A. Voth, J. Chem. Phys., 1999, 111, 9361–9381.
84. N. Kučerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771.
85. N. Kučerka, S. Tristram-Nagle and J. F. Nagle, J. Membr. Biol., 2006, 208, 193–202.
86. C. G. Cranfield, S. T. Henriques, B. Martinac, P. Duckworth, D. J. Craik and B. Cornell, Langmuir, 2017, 33, 6630–6637.
87. S. Nizalapur, K. K. K. Ho, O. Kimyon, E. Yee, T. Berry, M. Manefield, C. G. Cranfield, M. Willcox, D. S. Black and N. Kumar, Org. Biomol. Chem., 2016, 14, 3623–3637.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06776c

---