Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploration of H2 binding to the [NiFe]-hydrogenase active site with multiconfigurational density functional theory†
Geng
Dong
a,
Ulf
Ryde
 a,
Hans Jørgen
Aa. Jensen
a,
Hans Jørgen
Aa. Jensen
 b and
Erik D.
Hedegård
b and
Erik D.
Hedegård
 *a
*a
aDepartment of Theoretical Chemistry, Lund University, Chemical Centre, P. O. Box 124, SE-221 00 Lund, Sweden. E-mail: ulf.ryde@teokem.lu.se; erik.hedegard@teokem.lu.se
bDepartment of Physics, Chemistry and Pharmacy, University of Southern Denmark, DK-5230 Odense M, Denmark
First published on 24th November 2017
Abstract
The combination of density functional theory (DFT) with a multiconfigurational wave function is an efficient way to include dynamical correlation in calculations with multiconfiguration self-consistent field wave functions. These methods can potentially be employed to elucidate reaction mechanisms in bio-inorganic chemistry, where many other methods become either too computationally expensive or too inaccurate. In this paper, a complete active space (CAS) short-range DFT (CAS–srDFT) hybrid was employed to investigate a bio-inorganic system, namely H2 binding to the active site of [NiFe] hydrogenase. This system was previously investigated with coupled-cluster (CC) and multiconfigurational methods in the form of cumulant-approximated second-order perturbation theory, based on the density matrix renormalization group (DMRG). We find that it is more favorable for H2 to bind to Ni than to Fe, in agreement with previous CC and DMRG calculations. The accuracy of CAS–srDFT is comparable to both CC and DMRG, despite much smaller active spaces were employed than in the corresponding DMRG calculations. This enhanced efficiency at the smaller active spaces shows that CAS–srDFT can become a useful method for bio-inorganic chemistry.
1 Introduction
Quantum mechanical (QM) methods today play a prominent role in many branches of chemical science. In particular, Kohn–Sham density functional theory (DFT) has made a large impact owing to its computational efficiency and often accurate results.1–5 However, for systems with dense frontier orbital manifolds and with degenerate or near-degenerate electronic states, DFT can be inaccurate, which is often seen for transition-metal complexes in biological systems.6 Thus, methods that can handle such cases are needed. The coupled cluster (CC) methods can be highly accurate, but they may also deteriorate for multiconfigurational systems and are considerably more expensive, if at all feasible. The alternative is to employ a multiconfigurational wave function. One of the most common multiconfigurational methods is the complete active space (CAS) approach, in which the orbitals are divided into active and inactive spaces. Within the active space, all configurations are included in a full configuration interaction (full-CI) calculation, thus incorporating any multiconfigurational character. Combining the CAS with a self-consistent field (SCF) procedure leads to the complete active space self-consistent field (CASSCF) method.7–12 On the one hand, the accuracy of CAS-based methods depends on the size of the active space, in which all important orbitals should be included. On the other hand, the computational effort also rises steeply with the size of the active space so that traditional CAS implementations are restricted to about 16–18 orbitals. This puts limitations on the type of systems that can be studied; for instance, systems with two transition metals are normally already too large. Methods that allow more orbitals in the active space have been introduced in recent years, for example the density matrix renormalization group (DMRG) method.13–20Another serious problem is that all CAS methods, even with very large active spaces, neglect a major part of the dynamical correlation. To recover the missing dynamical correlation, perturbation theory is normally employed after a CASSCF or DMRG–SCF calculation, as done in CASPT216,21–24 or NEVPT2.20,25,26 However, the perturbation correction comes with additional computational cost.
An efficient method to recover the dynamical correlation in multiconfigurational methods is to merge DFT with a multiconfigurational wave function, thereby capitalizing on the efficient treatment of semi-local dynamical electron correlation within DFT methods. Simultaneously, such a hybrid method has the advantage that the multiconfigurational wave function can include static correlation.27–31 In this paper, we explore the multiconfigurational short-range DFT (MC–srDFT) method. It exploits the concept of range separation of the two-electron repulsion operator to merge DFT with a multiconfigurational wave function. With a recent extension of the MC–srDFT method to a polarizable embedding framework,32–34 the method can also be employed on biological systems, and the method may be a promising approach to use for metalloenzymes. However, the MC–srDFT method has mostly been benchmarked for s- and p-block atoms, diatomic molecules,30,35–40 and organic systems.41–44 Studies of transition metals are more rare.40,45 Before addressing full enzymes, we first need to ensure that the results of the MC–srDFT are in agreement with previous accurate calculations for biologically relevant cases and this is the purpose of the present paper.
We investigate the binding of H2 to the active site of [NiFe] hydrogenase, for which previous studies have given ambiguous results. On the one hand, experimental studies with CO or Xe gas-diffusion have predicted that H2 binds to Ni.46–48 On the other hand, Fe is the expected binding site from the organometallic perspective.49,50 Various DFT studies have predicted that H2 binds to Ni or to Fe with the active site in the Ni(II) singlet, or even to Fe in the triplet state51–57 (see Table 1 of ref. 58 for an overview). We have recently investigated the H2 binding site by using CCSD(T), cumulant approximated DMRG–CASPT2,58 and DFT-based calculations with the big-QM approach,59 the latter with 819 atoms in the QM region. In this study, we compare results obtained with the MC–srDFT method with the previous CCSD(T) and DMRG–CASPT2 results, and show that MC–srDFT comes to the same conclusions. We furthermore study the method's dependence on the size of the active space and the employed basis set.
| Method | Basis | ΔEH2 |
|---|---|---|
| a With 3s,3p correlation obtained from CCSD(T). | ||
| CAS(10,10)–srPBE | B1 | 15.1 |
| CAS(14,14)–srPBE | B1 | 17.0 |
| CAS(16,16)–srPBE | B1 | 16.8 |
| CAS(14,14)–srPBE | B2 | 15.2 |
| CAS(14,14)–srPBE | B3 | 13.9 |
| DMRG(22,22)–CASPT258 | ANO-RCC | 17.7 |
DMRG(22,22)–CASPT2a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
ANO-RCC | 11.9 |
| CCSD(T)58 | ANO-RCC | 18.1 |
| TPSS58 | def2-QZVPD | 25.6 |
2 Computational method
2.1 The MC–srDFT method
The MC–srDFT method is a hybrid between wave function theory (WFT) and density functional theory (DFT). The method relies on the range-separation of the two-electron repulsion operator into long-range and short-range parts30,60| ĝee(1,2) = ĝlree(1,2) + ĝsree(1,2). | (1) |
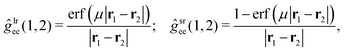 | (2) |
Ĥ[ρ] = ĥ + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) srHxc[ρ] + ĝlree, srHxc[ρ] + ĝlree, | (3) |
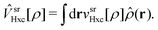 | (4) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r) is the density operator and vsr,μHxc is the short-range adapted, μ-dependent Hartree exchange–correlation potential
(r) is the density operator and vsr,μHxc is the short-range adapted, μ-dependent Hartree exchange–correlation potential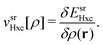 | (5) |
For the range-separation parameter, most studies on range-separated DFT hybrids66,67 employ values between 0.33–0.5 Bohr−1. For MC–srDFT, a value of μ = 0.4 Bohr−1 has been suggested based on natural occupation numbers and differences between the HF–srDFT and CAS–srDFT ground-state energies of small organic systems.31 Benchmark studies on excitation energies41,42,44 for organic systems have confirmed that this value provides accurate results. Using both MP2–srPBE and CAS–srPBE models, we have tested a range of μ values (see the ESI,† Table S1). These results show that μ values between 0.5 and 0.3 gives relative energies of H2–Fe and H2–Ni close to the energies obtained with DMRG and CCSD(T). Since μ = 0.4 is both accurate and consistent with previous suggestions, we here employ μ = 0.4 Bohr−1.
All calculations were carried out with a development version of the DALTON program.68,69 Further details about the MC–srDFT method, as well as the implementation, can be found elsewhere.70
2.2 Model systems and basis sets
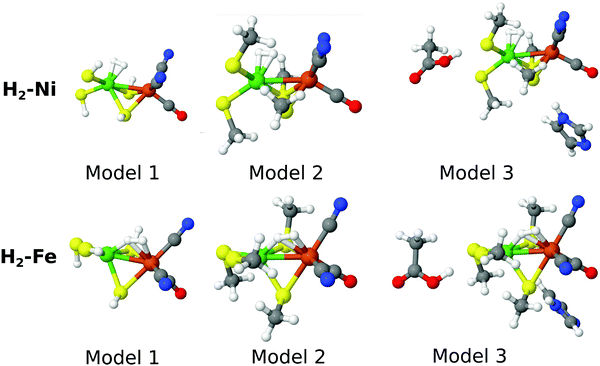
As the name indicates, the active site of [NiFe] hydrogenase consists of a Ni ion and a Fe ion. The former is coordinated to four Cys residues, two of which are also bridging to the Fe ion. The latter also coordinates one CO and two CN− ligands. In this paper, we compare the stability of two binding modes of H2 to this site, viz. binding side-on to Ni or to Fe. The two binding modes will be called H2–Ni and H2–Fe, and they are shown in Fig. 1 (note that H2 actually bridges the two metal ions in the H2–Fe binding mode). In analogy with our previous study,58 we used for each state three models of increasing size, also shown in Fig. 1. In the smallest model 1, the four cysteine ligands were modeled by HS− groups, whereas in the other two models they were modeled by CH3S−. In the largest model 3, two second-sphere residues were included, Glu34 and His88 (residue numbering according to the crystal structure with PDB entry 1H2R71), modeled by acetic acid and imidazole, respectively. The structures were taken from our previous study58 and were optimized with the combined quantum mechanics and molecular mechanics (QM/MM) approach at the TPSS/def2-SV(P) level of theory72–75 in the singlet state. Thus, both the Ni and Fe ions are in the low-spin +II oxidation state, corresponding to the spectroscopic Ni–SIa state of [NiFe] hydrogenase.76 The calculations presented here were carried out with three basis sets of increasing size, denoted as B1–B3. For the smallest one (named B1), the cc-pVTZ77,78 basis set was employed for the Ni and Fe ions, and the cc-pVDZ77 basis set was used for the other atoms. The effect of increasing the basis set was investigated by using the cc-pVTZ basis set on all atoms except H, for which the cc-pVDZ basis set was used. This basis set resembles the ANO-type basis set employed in ref. 58 and is denoted B2. In addition, we have added a calculation with a basis set similar to B2, but in which the H2 molecule bound to Ni or Fe is also described with the cc-pVTZ basis set. Thus, the important H2-molecule is (in contrast to ref. 58) also described with a triple-zeta basis set. We denoted this last basis set as B3. The MC–srDFT method has during this study undergone development to become more efficient and this effort is ongoing. Still, a large number of inactive electrons does pose a challenge for the current implementation of MC–srDFT. Therefore the basis sets B2 and B3 were used only for model 1. It should be emphasized that this is not a challenge of the method itself and standard techniques (e.g. Cholesky decomposition) can straightforwardly be applied to MC–srDFT. Relativistic effects were considered by using a standard second-order Douglas–Kroll–Hess (DKH2) Hamiltonian.79–812.3 Selection of active spaces
The selection of the active space is of highest importance for an MCSCF calculation and different strategies have been proposed for this selection. One strategy has been to rely on identifying orbitals from the chemical context.82 For transition metal complexes, this has typically led to the suggestion that all 3d orbitals and a few ligand orbitals should be included, and preferably also an additional (double-shell) of 3d′ orbitals. A different strategy relies on selecting orbitals based on natural occupation numbers from methods where the predicted occupation numbers are qualitatively correct. This could be either MP283 or a computationally cheap CI method. Typically, one would select orbitals with occupation numbers significantly different from 2 or 0. Rules for the selection of active spaces are not as well established for short-range DFT methods. Occupation numbers based on MP2–srDFT have previously been discussed84 and it was noted these natural occupation numbers are much closer to 2.0 and 0.0 than their MP2 counterparts. This is expected because the short-range density functional effectively includes the dynamical Coulomb-hole correlation. Hence, orbitals with occupation numbers below 1.98 or above 0.02 in MP2–srDFT or MC-srDFT can be expected to show strong correlation and should preferably be included in the active spaces. Importantly, since we here investigate the relative energy of two species, the chosen active spaces of the two species must be comparable.The MP2–srPBE occupation numbers for the two complexes (model 1) are compiled in Tables S2 and S3 (ESI†), and our initial selection of orbitals for the CAS–srDFT calculations was based on these. Tables S2 and S3 (ESI†) also contain occupation numbers for a number of different μ values, but we focus here on μ = 0.4 Bohr−1. Occupation numbers with a similar magnitude should preferably be included as a group and we have initially selected a CAS(10,10) space, for which there is a clear change in occupation numbers between the selected 10 orbitals and the orbitals not included (for both H2–Ni and H2–Fe). A larger active space is more challenging to define: for H2–Ni, selecting CAS(12,12) or CAS(14,14) will mean including and excluding orbitals with rather similar MP2–srPBE occupation numbers. The CAS(16,16) choice seems better, but this is rather large. On the other hand, for H2–Fe, CAS(10,10) or CAS(16,15) seems appropriate based on the MP2–srDFT occupation numbers.
Considering that the MP2–srPBE occupation numbers might not reflect the “true” occupation number (i.e. occupation numbers obtained with a full-CI-srPBE approach), we initially investigated CAS(10,10), CAS(14,14) and CAS(16,16) for both species. The corresponding CAS–srPBE occupation numbers are also shown in Tables S2 and S3 (ESI†). For CAS(16,16), we started to include orbitals with either very high or very low occupation numbers (above 1.99 or below 0.01), which affects the convergence. The CAS(16,16)–srPBE calculation for H2–Fe also shows that the occupation numbers for the last two orbitals in what would correspond to a CAS(12,12) become even closer than for the MP2–srPBE calculation. Hence, CAS(12,12) will become unstable and is prone to get stuck in the local minima, which was confirmed by a trial calculation with this active space. The orbitals causing these difficulties are involved in the Fe–CN and Fe–CO bonds, and care must be taken to include these orbitals uniformly in the two states. This is done in CAS(14,14), which is the largest active space that can be considered balanced (and it is also feasible for the larger models 2 and 3).
Visual inspection of the CAS(14,14) orbitals in Fig. 2 shows that this active space includes the Ni 3d-orbitals, the H2 and metal–ligand (CO π-type) orbitals, although the orbitals are more delocalized than the pure DMRG-SCF (or CASSCF) orbitals in ref. 58 and 85. Further reduction of the active space to CAS(10,10), leads to exclusion of orbitals that are partly on hydrogen and the Ni ion, and we therefore prefer to include these two orbitals (i.e. orbitals 4, 5, 13 and 14 are included for H2–Ni in Fig. 2, compared to Fig. S2, ESI†). Furthermore, the occupation number of the Ni orbital in H2–Ni (orbital 4 in Fig. 2) is around 1.98 in the CAS(14,14) calculations and thus rather close to two of the other orbitals in the active space. This indicates that this orbital should be included.
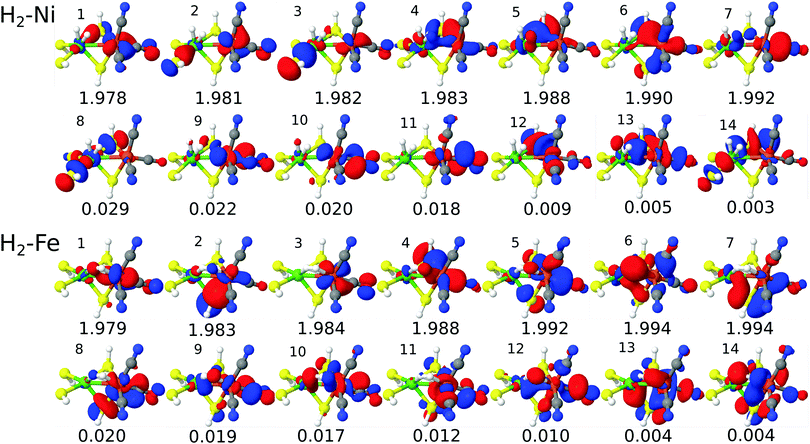 | ||
| Fig. 2 Active natural orbitals and their occupation numbers from the CAS(14,14)–srPBE calculation on model 1. | ||
Expanding the calculations to CAS(16,16), introduces orbitals that are mainly on bridging sulfur atoms and can be considered less important. For instance, for H2–Ni, the additional orbitals compared to CAS(14,14) are orbitals 8 and 14 in Fig. S5 (ESI†). Although we here focus on CAS(14,14), it should be noted that the effect on the calculated (relative) energies is in fact small (2 kJ mol−1 and below), as will be discussed in the next section. For models 2 and 3, we also focus on CAS(14,14), but we have employed both CAS(10,10) and CAS(14,14) active spaces to probe the effect of the active spaces for these larger models as well. The corresponding active space orbitals are shown in the ESI.† Finally, we note that we also attempted to select orbitals based on calculations with larger μ values, but this procedure was less satisfactory (shortly discussed in the ESI†).
3 Results and discussion
In this study, we have compared the results of CAS–srPBE with previously published CCSD(T) and cumulant approximated DMRG–CASPT2 calculations for the two binding modes of H2 to the active site of [NiFe] hydrogenase.58 We discuss first the smallest model (model 1) and then the two larger models (models 2 and 3) in separate sections.3.1 Calculations with model 1
The energy difference between the H2–Ni and H2–Fe states (ΔEH2) calculated with the CAS–srPBE method is compared to previous CCSD(T) and DMRG–CASPT2 results in Table 1. We report CAS–srPBE results with the CAS(10,10), CAS(14,14) and CAS(16,16) active spaces. In all cases, CAS–srPBE predicts that the H2–Ni state is most stable, in agreement with the CCSD(T) and DMRG–CASPT2 results. The effect of expanding the active space from CAS(10,10)–srPBE to CAS(14,14)–srPBE is only 2 kJ mol−1 (see the Methods section for a description of the orbitals within the two active spaces). The CAS(10,10)–srPBE model predicts that H2–Ni is 15 kJ mol−1 more stable, whereas the difference with CAS(14,14)–srPBE is 17 kJ mol−1. For the largest active space, CAS(16,16), the obtained energy difference changes by only 0.2 kJ mol−1. Hence, there is little effect on the relative energies when expanding the active space and the CAS(14,14) active space seems to be sufficiently large for the systems studied here.The CAS(14,14)–srPBE results with both the B1 and B2 basis sets (17 and 15 kJ mol−1) are in good agreement with the result obtained with DMRG(22,22)–CASPT2 (18 kJ mol−1), although those calculations employed a significantly larger active space. Hence, the treatment of semi-local, dynamical correlation by the srDFT part allows for the use of significantly smaller active spaces compared to traditional MR methods. It should be noted that the CAS–srPBE calculations also show a rather modest basis set dependence. The basis sets increase from B1 to B2 only lowers the obtained energy-difference by 2 kJ mol−1. Further increasing it to B3 lowers the energy-difference by another 1 kJ mol−1, yielding a final result of 14 kJ mol−1.
At this point we emphasize that recent studies have noted that multireference perturbation theory to the second order does not always recover the 3s,3p correlation well.86Table 1 also reports a DMRG(22,22)–CASPT2 result obtained without the 3s,3p correlation, but including an estimate of this semi-core correlation from CCSD(T). The resulting energy difference was then 12 kJ mol−1.58 Thus, our best CAS(14,14)-srPBE result (14 kJ mol−1) is within 2 kJ mol−1 of this corrected DMRG–CASPT2 value, and within 4 kJ mol−1 of the CCSD(T) result. From the above discussion, we can thus conclude that both CAS(14,14)–srPBE and DMRG(22,22)–CASPT2 reproduce the CCSD(T) data well.
3.2 Calculations with models 2 and 3
Next, we carried out CAS–srPBE calculations also for the two larger models 2 and 3 as shown in Fig. 1. The results are shown in Table 2 and are compared to the corresponding results obtained with DMRG–CASPT2. It can be seen that the two approaches give similar trends: the energy differences increase in model 2 (24–39 kJ mol−1), whereas inclusion of the models of two nearby amino-acids counteracts this increase, so that in model 3, the energy difference decreases again to 8–19 kJ mol−1. For all three models, H2–Ni is thus consistently predicted to be the most stable state and the CAS(14,14)–srPBE results are quite close to that of DMRG(22,22)–CASPT2. From Table 2, it can be seen that the differences from CAS(14,14)–srPBE are 5 and 10 kJ mol−1 for model 2, depending on whether the DMRG–CASPT2 included the 3s,3p correlation from CCSD(T) or not. The corresponding differences for model 3 are even smaller, 1 and 5 kJ mol−1.| Method | Basis | ΔEH2 | |
|---|---|---|---|
| Model 2 | Model 3 | ||
| a With 3s,3p correlation obtained from CCSD(T). b Extrapolated with the energy difference between CCSD(T) and DMRG(22,22)–CASPT2 for model 1, the latter with the 3s,3p correlation obtained from CCSD(T). | |||
| CAS(10,10)–srPBE | B1 | 24.3 | 7.9 |
| CAS(14,14)–srPBE | B1 | 27.7 | 10.5 |
| DMRG(22,22)–CASPT258 | ANO-RCC | 37.7 | 15.2 |
DMRG(22,22)–CASPT2a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
ANO-RCC | 33.0 | 11.1 |
DMRG(22,22)–CASPT2b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
ANO-RCC | 39.2 | 17.3 |
| TPSS58 | def2-QZVPD | 34.0 | 18.5 |
In ref. 58, it was noted that CCSD(T) was beyond the computational resources for models 2 and 3, but an estimate of a CCSD(T) result could be obtained by correcting the DMRG–CASPT2 results for models 2 and 3 with the energy difference between CCSD(T) and DMRG–CASPT2 from model 1. With this correction, the results were 39 and 17 kJ mol−1 for models 2 and 3, respectively. Compared to these values, CAS(14,14)–srPBE underestimates the energy difference by 11 and 6 kJ mol−1 for models 2 and 3. Judging from the results with the smallest model, the difference is expected to decrease by 2 kJ mol−1 with the larger B2 basis set. These differences are certainly acceptable and below the other error sources. For instance, going from cluster model 3 to a much larger model for the protein was found to increase the energy difference by approximately 25 kJ mol−1 in favor of the H2–Ni state. This estimate comes from the difference 42.2 − 18.5 = 23.7 kJ mol−1, where the first number is ΔEH2 from big-QM calculations with a 819 atom QM model,58 whereas the second number is ΔEH2 for model 3 (both calculated with TPSS). Indeed, effects of this magnitude (and above) in relation to QM-cluster size is not unusual in proteins, as has been documented many times in the literature (see e.g.ref. 87 and 88 and references therein). In later studies, we aim at including protein effects using e.g. a polarizable embedding model.32 With the big-QM environment correction, our CAS(14,14)–srPBE energy difference would change from 10.5 kJ mol−1 to 10.5 + 23.7 = 32.2 kJ mol−1. Adding also the dispersion and thermal corrections,58 the final predicted CAS(14,14)–srPBE/big-QM-corrected value becomes 42.1 kJ mol−1, giving unambiguously the same general conclusion as with CCSD(T) and DMRG-CASPT2.
4 Conclusions
In this paper, CAS–srPBE calculations were performed on three models of H2 bound to [NiFe]-hydrogenase. Our results indicate that H2 binding to Ni is more stable than the binding to Fe, which is consistent with previous calculations with the CCSD(T) and DMRG–CASPT2 methods.58 Our CAS–srPBE calculations with reduced active spaces (CAS(10,10), CAS(14,14) and CAS(16,16)) gave results close to the CAS(22,22) active space used in the previous DMRG–CASPT2 calculations.For all the employed model systems, the effect of extending the active space from CAS(10,10) to CAS(14,14) was found to be small (around 2 kJ mol−1). For model 1, we further employed CAS(16,16), which only gave rise to a change of 0.2 kJ mol−1. This is a good indication that the calculations converge with respect to the choice of active space. The effect of increasing the basis set was also quite modest: for model 1, an increase in the basis set from cc-pVDZ to cc-pVTZ for all C, N, O and S atoms changed the CAS(14,14)–srPBE energy difference by only 3 kJ mol−1. Thus, both the effect of increasing the active space and the effect of the basis set is much lower than that of other sources of error. For instance, a change of 7 kJ mol−1 was obtained by employing the 3s,3p correlation obtained from either CCSD(T) or DMRG–CASPT2 and the effect of the surrounding protein was 25 kJ mol−1.
For the larger models 2 and 3, the CAS(10,10)–srPBE and CAS(14,14)–srPBE results agree with the CCSD(T) extrapolated DMRG–CASPT2 results to within 4–9 kJ mol−1. This is similar to the difference between the best DMRG(22,22)–CASPT2 and CCSD(T) results for model 1, 6 kJ mol−1.
Hence, our results support MC–srDFT as a new valuable tool for bio-inorganic chemistry, with an accuracy similar to that of DMRG–CASPT2 but at a much lower computational cost (in a fully optimized implementation). The lower computational cost is achieved by means of the much smaller active spaces needed and by the replacement of the perturbation correction of CASPT2 with DFT integration.
Although the performance of CAS–srPBE is encouraging for applications in metalloenzymes, further improvements are possible: for instance, the accuracy of the srDFT functional can be improved. This could be achieved by either including the exact (short-range) DFT exchange or by including the kinetic energy dependence in the same way as in meta-GGA functionals.89
Finally, it would also be interesting to address the triplet spin-states of the two H2–Ni and H2–Fe intermediates. This will require extension of our current MC–srDFT implementation to functionals that depend on spin-densities, and this development is currently ongoing.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This investigation has been supported by grants from the Swedish Research Council (project 2014-5540), the Carlsberg Foundation (project CF15-0208), the European Commission, the China Scholarship Council, and COST Action CM1305 (ECOSTBio). The computations were performed on computer resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc at Lund University and HPC2N at Umeå University, and on computer resources on Abacus 2.0 provided by the Danish e-infrastructure Cooperation.References
- K. Burke, J. Chem. Phys., 2012, 136, 150901 CrossRef PubMed.
- J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226 RSC.
- M. A. L. Marques and E. K. U. Gross, Annu. Rev. Phys. Chem., 2004, 55, 427–455 CrossRef CAS PubMed.
- M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- B. Kirchner, F. Wennmohs, S. Ye and F. Neese, Curr. Opin. Chem. Biol., 2007, 11, 134–141 CrossRef CAS PubMed.
- K. Pierloot, Int. J. Quantum Chem., 2011, 111, 3291–3301 CrossRef CAS.
- K. Ruedenberg, L. M. Cheung and S. T. Elbert, Int. J. Quantum Chem., 1979, 16, 1069–1101 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, J. Chem. Phys., 1981, 74, 2384–2396 CrossRef.
- H. J. Aa. Jensen and P. Jørgensen, J. Chem. Phys., 1984, 80, 1204–1214 CrossRef.
- J. Olsen, D. L. Yeager and P. Jørgensen, Adv. Chem. Phys., 1983, 54, 1–176 CrossRef CAS.
- H. J. Aa. Jensen and H. Ågren, Chem. Phys., 1986, 104, 229–250 CrossRef.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef PubMed.
- G. K. L. Chan, J. Chem. Phys., 2004, 120, 3172–3178 CrossRef CAS PubMed.
- K. H. Marti and M. Reiher, Phys. Chem. Chem. Phys., 2011, 13, 6750–6759 RSC.
- S. Wouters and D. Van Neck, Eur. Phys. J. D, 2014, 68, 1–20 CrossRef CAS.
- Ö. Legeza, J. Röder and B. Hess, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125114 CrossRef.
- S. Keller, M. Dolfi, M. Troyer and M. Reiher, J. Chem. Phys., 2015, 143, 244118 CrossRef PubMed.
- T. Yanai, Y. Kurashige, W. Mizukami, J. Chalupský, T. Nguyen Lan and M. Saitow, Int. J. Quantum Chem., 2014, 115, 283–299 CrossRef.
- L. Freitag, S. Knecht, A. Celestino and M. Reiher, J. Chem. Theory Comput., 2017, 13, 451–459 CrossRef CAS PubMed.
- K. Andersson, P.-Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- Y. Kurashige and T. Yanai, J. Chem. Phys., 2011, 135, 094104 CrossRef PubMed.
- Y. Kurashige, J. Chalupsky, T. N. Lan and T. Yanai, J. Chem. Phys., 2014, 141, 174111 CrossRef PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- S. Guo, M. A. Watson, W. Hu, Q. Sun and G. K.-L. Chan, J. Chem. Theory Comput., 2016, 12, 1583–1591 CrossRef CAS PubMed.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- C. M. Marian and N. Gilka, J. Chem. Theory Comput., 2008, 4, 1501–1515 CrossRef CAS PubMed.
- G. L. Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef PubMed.
- A. Savin and H.-J. Flad, Int. J. Quantum Chem., 1995, 56, 327–332 CrossRef CAS.
- E. Fromager, J. Toulouse and H. J. Aa. Jensen, J. Chem. Phys., 2007, 126, 074111 CrossRef PubMed.
- J. M. Olsen, K. Aidas and J. Kongsted, J. Chem. Theory Comput., 2010, 6, 3721–3734 CrossRef CAS.
- E. D. Hedegård, J. M. H. Olsen, S. Knecht, J. Kongsted and H. J. Aa. Jensen, J. Chem. Phys., 2015, 114, 1102–1107 Search PubMed.
- E. D. Hedegård and M. Reiher, J. Chem. Theory Comput., 2016, 12, 4242–4253 CrossRef PubMed.
- A. Savin, in Recent Developments and Applications of Modern Density Functional Theory, Elsevier, Amsterdam, 1996, p. 327 Search PubMed.
- J. G. Ángyán, I. C. Gerber, A. Savin and J. Toulouse, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 012510 CrossRef.
- E. Fromager and H. J. Aa. Jensen, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 022504 CrossRef.
- E. Fromager, R. Cimiraglia and H. J. Aa. Jensen, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 024502 CrossRef.
- E. Goll, H.-J. Werner and H. Stoll, Phys. Chem. Chem. Phys., 2005, 7, 3917–3923 RSC.
- E. Fromager, S. Knecht and H. J. Aa. Jensen, J. Chem. Phys., 2013, 138, 084101 CrossRef PubMed.
- M. Hubert, E. D. Hedegård and H. J. Aa. Jensen, J. Chem. Theory Comput., 2016, 12, 2203–2213 CrossRef CAS PubMed.
- M. Hubert, H. J. Aa Jensen and E. D. Hedegård, J. Phys. Chem. A, 2016, 120, 36–43 CrossRef CAS PubMed.
- E. D. Hedegård, N. H. List, H. J. Aa. Jensen and J. Kongsted, J. Chem. Phys., 2013, 139, 044101 CrossRef PubMed.
- E. D. Hedegård, Mol. Phys., 2016, 115, 26–38 CrossRef.
- J. M. H. Olsen and E. D. Hedegård, Phys. Chem. Chem. Phys., 2017, 19, 15870–15875 RSC.
- H. Ogata, Y. Mizoguchi, N. Mizuno, K. Miki, S. Adachi, N. Yasuoka, T. Yagi, O. Yamauchi, S. Hirota and Y. Higuchi, J. Am. Chem. Soc., 2002, 124, 11628–11635 CrossRef CAS PubMed.
- Y. Montet, P. Amara, A. Volbeda, X. Vernede, E. C. Hatchikian, M. J. Field, M. Frey and J. C. Fontecilla-Camps, Nat. Struct. Biol., 1997, 4, 523–526 CrossRef CAS PubMed.
- A. Volbeda and J. C. Fontecilla-Camps, Dalton Trans., 2003, 4030–4038 RSC.
- G. J. Kubas, in Metal Dihydrogen and σ-Bond Complexes: Structure, Theory and Reactivity (Modern Inorganic Chemistry), ed. J. P. Fackler Jr., Springer, 2006 Search PubMed.
- P. E. M. Siegbahn and M. R. A. Blomberg, in Oxidative Addition Reactions (Theoretical Aspects of Homogeneous Catalysis, Applications of Ab Initio Molecular Orbital Theory), ed. P. W. van Leeuwen, K. Morokuma and J. H. van Lenthe, Springer, 1995 Search PubMed.
- P. E. M. Siegbahn, J. W. Tye and M. B. Hall, Chem. Rev., 2007, 107, 4414–4435 CrossRef CAS PubMed.
- M. Bruschi, M. Tiberti, A. Guerra and L. De Gioia, J. Am. Chem. Soc., 2014, 136, 1803–1814 CrossRef CAS PubMed.
- S. Q. Niu, L. M. Thomson and M. B. Hall, J. Am. Chem. Soc., 1999, 121, 4000–4007 CrossRef CAS.
- M. Pavlov, M. R. A. Blomberg and P. E. M. Siegbahn, Int. J. Quantum Chem., 1999, 73, 197–207 CrossRef CAS.
- H. Wu and M. B. Hall, C. R. Chim, 2008, 11, 790–804 CrossRef CAS.
- P. Jayapal, M. Sundararajan, I. H. Hillier and N. A. Burton, Phys. Chem. Chem. Phys., 2008, 10, 4249–4257 RSC.
- D. S. Kaliakin, R. R. Zaari and S. A. Varganov, J. Phys. Chem. A, 2015, 119, 1066–1073 CrossRef CAS PubMed.
- G. Dong, Q. M. Phung, S. Hallaert, K. Pierloot and U. Ryde, Phys. Chem. Chem. Phys., 2017, 19, 10590–10601 RSC.
- L. Hu, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 640–649 CrossRef CAS PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- J. Toulouse, F. Colonna and A. Savin, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 062505 CrossRef.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151 CrossRef CAS.
- R. Pollet, A. Savin, T. Leininger and H. Stoll, J. Chem. Phys., 2002, 116, 1250–1258 CrossRef CAS.
- E. Fromager, Mol. Phys., 2015, 113, 419–434 CrossRef CAS.
- E. Goll, H.-J. Werner, H. Stoll, T. Leininger, P. Gori-Giorgi and A. Savin, Chem. Phys., 2006, 329, 276–282 CrossRef CAS.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS PubMed.
- Dalton, a molecular electronic structure program, development version, see http://daltonprogram.org/, 2017.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansk, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- J. K. Pedersen, PhD thesis, University of Southern Denmark, 2004.
- Y. Higuchi, H. Ogata, K. Miki, N. Yasuoka and T. Yagi, Structure, 1999, 7, 549–556 CrossRef CAS PubMed.
- U. Ryde and M. H. M. Olsen, Int. J. Quantum Chem., 2001, 81, 335–347 CrossRef CAS.
- U. Ryde, J. Comput.-Aided Mol. Des., 1996, 10, 153–164 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- W. Lubitz, H. Ogata, O. Rüdiger and E. Reijerse, Chem. Rev., 2014, 114, 4081–4148 CrossRef CAS PubMed.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- B. A. Hess, Phys. Rev. A, 1985, 32, 756–763 CrossRef CAS.
- B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748 CrossRef CAS.
- V. Veryazov, P.-Å. Malmqvist and B. O. Roos, Int. J. Quantum Chem., 2011, 111, 3329–3338 CrossRef CAS.
- H. J. Aa. Jensen, P. Jørgensen, H. Ågren and J. Olsen, J. Chem. Phys., 1988, 88, 3834 CrossRef.
- E. D. Hedegård, F. Heiden, S. Knecht, E. Fromager and H. J. Aa. Jensen, J. Chem. Phys., 2013, 139, 184308 CrossRef PubMed.
- M. G. Delcey, K. Pierloot, Q. M. Phung, S. Vancoillie, R. Lindh and U. Ryde, Phys. Chem. Chem. Phys., 2014, 16, 7927–7938 RSC.
- K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537–553 CrossRef CAS PubMed.
- U. Ryde, Methods Enzymol., 2016, 577, 119–158 CAS.
- S. Sumner, P. Söderhjelm and U. Ryde, J. Chem. Theory Comput., 2013, 9, 4205–4214 CrossRef CAS PubMed.
- E. Goll, M. Ernst, F. Moegle-Hofacker and H. Stoll, J. Chem. Phys., 2009, 130, 234112 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional active space orbital plots as well as MP2–srPBE and CAS–srPBE orbital occupation numbers. See DOI: 10.1039/c7cp06767d |
| This journal is © the Owner Societies 2018 |