XANES study of vanadium and nitrogen dopants in photocatalytic TiO2 thin films†
Zakaria
El Koura
a,
Giacomo
Rossi
b,
Marco
Calizzi
b,
Lucia
Amidani
c,
Luca
Pasquini
 *b,
Antonio
Miotello
a and
Federico
Boscherini
b
*b,
Antonio
Miotello
a and
Federico
Boscherini
b
aDepartment of Physics, Università degli Studi di Trento, Via Sommarive 14, 38123 Povo (Trento), Italy
bDepartment of Physics and Astronomy and CNISM, Alma Mater Studiorum Università di Bologna, Viale C. Berti Pichat 6/2, 40127 Bologna, Italy. E-mail: luca.pasquini@unibo.it
cESRF – The European Synchrotron, Grenoble, France
First published on 22nd November 2017
Abstract
We report an X-ray absorption near edge structure (XANES) study of vanadium (V) and nitrogen (N) dopants in anatase TiO2 thin films deposited by radio-frequency magnetron sputtering. Measurements at the Ti K and V K edges were combined with soft X-ray experiments at the Ti L2,3, O K and N K edges. Full potential ab initio spectral simulations of the V, O and N K-edges were carried out for different possible configurations of substitutional and interstitial dopant-related point defects in the anatase structure. The comparison between experiments and simulations demonstrates that V occupies substitutional cationic sites (replacing Ti) irrespective of the film structure and dopant concentration (up to 4.5 at%). On the other hand, N is found both in substitutional anionic sites (replacing O) and as N2 dimers within TiO2 interstices. The dopants’ local structures are discussed with reference to the enhanced optical absorption and photocatalytic activity achieved by (co)doping.
Introduction
Titanium dioxide (TiO2) is a prominent photocatalyst, because it is chemically stable, abundant, nontoxic and economically viable.1–4 Photogenerated holes and electrons in TiO2 have a suitable potential to promote redox reactions, which can be employed for environmental cleaning (air, water, and soil) as well as in photoelectrochemical water splitting.2,5,6 However, because of its wide band gap (≈3.2 and 3.0 eV in the anatase and rutile polymorphs, respectively), only the UV fraction of the solar spectrum (3–5% of total) can be exploited for photocatalytic processes. Therefore, the sensitization of TiO2 to visible light by band gap modification has been a subject of intense research in the last few decades.1,7,8 One can envisage three different schemes to achieve this goal via doping in TiO2: (1) downward shift of the conduction band minimum (CBM); (2) upward shift of the valence band maximum (VBM), and (3) introduction of impurity states in the band gap.Since the conduction band consists mostly of Ti 3d states, numerous studies have focused on the incorporation of metallic ions, particularly 3d transition metals (TMs), as dopants capable of lowering the CBM and/or introducing intra-gap impurity levels below the CBM.9–12 Metal-doped TiO2 materials indeed show a red-shift of the optical absorption edge or a color center. Systematic theoretical investigations show that this effect originates from intra-gap states. For instance, the 3d elements: V, Cr, Mn, Fe and Co create donor states, the positions of which shift to lower energies with increasing atomic number.13 V-doping of TiO2 has proved effective in increasing the photocatalytic activity of TiO2 and has been the subject of several investigations.9,14–18
Even if TM-doping of TiO2 enhances sunlight absorption, its influence on the overall photocatalytic activity, and more specifically on the visible-light-activity, is a rather complex subject and conflicting results are reported in the literature.14 In fact, a stronger absorption of visible photons is a necessary but not sufficient requisite to realize a good photocatalyst. Two further requirements are: (i) the photoexcited electron energy should be above the reduction level and the photogenerated hole energy below the oxidation level, and (ii) the dopant-induced states should be mixed with the band states of TiO2 in order to efficiently transfer the photoexcited carriers to reactive sites at the catalyst surface. Dopants acting as recombination centers of photogenerated charge carriers are detrimental to photocatalysis,19 whereas surface traps associated with dopants may increase the carriers’ lifetime and availability for redox processes.20 The contrasting results reported in the literature about the effect of specific TM dopants on photocatalysis may therefore be due to the use of different preparation methods, which result in dissimilar microstructure and dopant dispersion in the matrix. For example, Yamashita et al.21 studied Fe-doped bulk TiO2 as obtained by ion-implantation or the sol–gel method. In the case of Fe doping by sol–gel, a small shift of the absorption band to the visible light regions is observed as opposed to the larger shift observed in the case of ion-implanted TiO2 where the defects induced by implantation play a relevant role.
In 2001, Asahi et al. demonstrated that N-doped TiO2 has significant photocatalytic activity under visible light and explained the observed effect on the basis of band structure calculations.22 N-Doping induces acceptor states above the VBM, effectively lowering the band gap.23 The visible light photocatalytic activity of N-doped TiO2 has been confirmed by many researchers and other nonmetal anionic dopants such as S, C and I have been widely studied (see ref. 1 and references therein).
The two schemes of cation and anion doping can be combined to prepare codoped TiO2.24 In recent papers, we have shown that V–N-codoped TiO2 thin films prepared by radio-frequency magnetron sputtering are efficient photocatalysts under visible-light irradiation, with better performance than singly-doped V-TiO2 and N-TiO2 both in photoelectrochemical water splitting18,25 and photocatalytic degradation of organic water pollutants.26
A detailed analysis of the dopant's local structure and chemistry is essential to improve the physico-chemical understanding of material's properties and to optimize the functionality of (co-)doped TiO2. In this paper, we pursue this goal using X-ray Absorption Spectroscopy (XAS) coupled with ab initio full potential simulations of the X-ray Absorption Near Edge Structure (XANES).
The XANES region conveys details on the oxidation state, local geometry and density of unoccupied electronic states, and is particularly powerful for the investigation of dopants.27,28 The interpretation of the XANES at a dopant's absorption edge can be supported by density functional theory (DFT) electronic structure calculations and finite difference numerical methods,29–34 which permit the spectral features for different dopant sites to be simulated, as will be shown in the present investigation.
Several XAS studies of dopants in TiO2-based nanostructured materials have appeared in the literature. Li et al.35 and Rodríguez-Torres et al.36 have investigated Nd- and Fe-doped anatase nanoparticles (NPs), respectively. They observed that Nd3+ and Fe3+ cations substitutionally replace Ti4+ ones in anatase NPs, with increased cation-oxygen first shell bond lengths. A recent study37 of Nb dopants also supports a substitutional site. Stewart et al. have examined the influence of N-doping on the structure and electronic properties of anatase NPs.38 Qualitative XAS measurements aimed at the characterization of the V local structure and oxidation state in V-doped TiO2 have been reported by Yamashita et al.,8 Wu and Chen,9 and Avansi et al.39 An early attempt to compare experimental spectra with simulations of the V K-edge XANES in V-TiO2 was reported by Izumi et al.,40 but the simulations failed to reproduce the essential features of the data. Recently, we have reported a good agreement between the simulated XANES for a substitutional V cation and the experimental data obtained on V-TiO2 NPs prepared by gas phase condensation.41
In this work, we report XANES measurements carried out both with hard X-rays at the Ti and V K-edges and with soft X-rays at the Ti L2,3, O K, and N K edges. High energy resolution fluorescence detected (HERFD)-XANES were also collected at the V K edge using scattered beam crystal analyzers. XANES data are interpreted with the support of state-of-the-art ab initio calculations based on a structural picture determined by DFT. We have investigated both singly-doped V-TiO2 and codoped V–N-TiO2.
Our results show that the local environment of the V dopant and host Ti are very similar, irrespective of the V content (up to about 4.5 at%), degree of crystallinity and phase purity, supporting the picture of substitutional V cations in the TiO2 lattice. On the other hand, N is found both as a substitutional anion and as N–N dimers located in interstices within the TiO2 lattice.
Experimental and theoretical methods
Sample preparation and characterization
Pure, V-doped (V-TiO2), and V–N-codoped (V–N-TiO2) TiO2 thin films were deposited on glass substrates by radio frequency (RF) magnetron sputtering using a ceramic TiO2 target (purity 99.99%) and Ar (99.9% purity) as a working gas. The RF power used was 150 W and the Ar pressure was kept constant at 8 × 10−3 mbar in all the depositions. V-TiO2 films were obtained by placing V pieces (purity 99.9%) over the TiO2 target. The V content can be tuned by varying the mass of V attached to the target. V–N-TiO2 codoped films were deposited by introducing a controlled N2 flux, which increased the chamber pressure to 1.1 × 10−2 mbar. Crystalline films were obtained using a constant substrate temperature of 350 ± 2 °C throughout the deposition process, as reported in our previous work.42 Amorphous films, identified by the suffix “-am” hereafter, were obtained keeping the substrate temperature below 70 °C.Raman spectroscopy was carried out using a LabRam Aramis Jobin-Yvon Horiba microRaman system equipped with a 100× objective and He–Ne laser source (632.8 nm).
Scanning Electron Microscopy (SEM) was carried out with a JEOL JSM-7001F field emission SEM (FE-SEM) operated at 20 kV and equipped with an Energy Dispersive X-ray Spectroscopy detector (EDS, Oxford INCA PentaFETx3). The thickness of the films, as measured from SEM cross-sectional images, was 240 ± 20 nm (Fig. S1, ESI†). We deposited films with V/(V + Ti) atomic fractions of 2.4 ± 0.5 at% and 4.5 ± 0.5 at%, as determined by EDS. The N content was estimated from X-ray Photoelectron Spectroscopy (XPS) in a previous study,25 yielding an atomic ratio N/(N + O) of 4.0 ± 0.7 at%.
XAS measurements and data analysis
XAS measurements at the Ti and V K-edges were performed at the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. Most experiments were carried out at the BM23 beamline,43 where thin film samples were measured in Total Fluorescence Yield (TFY) using a Vortex Si drift diode detector. The energy resolution of the Si drift diode could not discriminate between the quite close Ti Kβ (4931.8 eV) and V Kα (4945–4952 eV) fluorescence lines, and their partial overlap leads to a lower signal to noise ratio in the V K-edge spectra. As a result, it was difficult to identify clearly the fine details of the V K post-edge XANES region with this setup. In addition, the signal-to-noise ratio in the V K-edge EXAFS region was not sufficient to allow a quantitative analysis. Reference compounds of several Ti and V oxides were also measured in transmission mode at BM23 (see the ESI† for further details).V K-edge XANES using the High Energy Resolution Fluorescence Detection (HERFD) XANES setup at the ID26 beamline were subsequently measured on the crystalline film samples (V-TiO2 and V–N-TiO2). The gain in energy resolution in the post-edge region allows for a direct comparison to reference anatase XANES, as it will be discussed later on.
Soft XAS measurements were performed at the BEAR beamline44 of the Elettra synchrotron, in Trieste, Italy. XANES at the Ti and V L2,3-edges and at the O K-edge were collected in total electron yield (TEY) mode, by measuring the drain current from the sample to ground. The N K-edge XANES was measured in total fluorescence yield (TFY) using a Si drift diode equipped with a soft X-ray transparent window.
The XAS measurements did not detect any meaningful difference among films with different V content. Therefore, we will only report XAS data of V-TiO2 and V–N-TiO2 films with the V content V/(V + Ti) = 4.5 ± 0.5 at%, which display slightly better statistics compared to those with 2.4 ± 0.5 at% V.
Ab initio XANES simulations
Simulations of the theoretical XANES spectra were performed using doped TiO2 structural models, calculated with Quantum ESPRESSO,45 as input for FDMNES.29,46 Quantum ESPRESSO is a software based on the plane wave algorithm45,47 that performs DFT calculations, iterating a super-cell (obtained joining one or more crystals unit cells), to simulate the physics of an infinite crystal structure. In our case, we used clusters of 2 × 2 × 2 anatase unit cells containing from 96 to 98 atoms. Fig. 1 displays the local structure around the dopants for all stable configurations obtained relaxing the doped systems, while the full cluster structures are reported in Fig. S2 (ESI†). The simulated doping percentages are realistic and similar to the experimental ones. We analyzed two models for V-doped anatase, labelled as VTi (substitutional V in a Ti site) and Vi (V interstitial). For V–N-codoped anatase we considered 6 different models, labelled M#, where # indicates the model number. In these 6 models, N occupies substitutional or interstitial sites, which are either close or far from a substitutional V. We also considered N dimers having the initial N–N distance of the N2 molecule. Finally, since the V–N-TiO2 film contained a minority fraction of rutile, we also examined a model (M7) with substitutional N and V in a rutile cluster of 72 atoms. The crystallographic parameters of the relaxed doped super-cells are listed in Table S1 (ESI†). The full atomic coordinate sets in Cartesian units are provided in a separate archive. The starting dopant configuration and the relaxed local structures of all models are detailed in Table S2 (ESI†).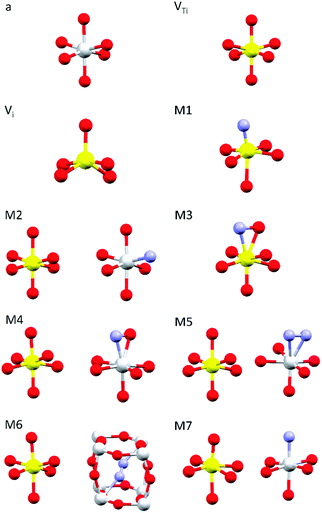 | ||
| Fig. 1 Dopant-related relaxed local structures for V-doped and V–N-codoped TiO2. Ti in grey, V in yellow, O in red and N in blue. a: anatase TiO2; VTi: substitutional V in anatase; Vi: interstitial V in anatase; M1–M6: V–N-codoped anatase; M7: V–N-codoped rutile. When two clusters are displayed, the dopants are located in non nearest neighbour sites. Detailed information is given in Tables S1–S2 (ESI†); the structures of the simulated full clusters are displayed in Fig. S2 (ESI†). | ||
For the calculation of theoretical XANES spectra we used FDMNES,29,46 an ab initio software based on a full potential approach that overcomes the muffin-tin approximation.48 The first step is a self-consistent field calculation, performed with time independent DFT methods, necessary to determine the charge density of the unperturbed system starting from a charge density obtained from the superposition of the atomic ones. The cluster Coulomb potential necessary to evaluate the transition matrix elements is evaluated starting from the charge density solving the Poisson equation. The energy dependence of exchange correlation potentials is evaluated using the local density approximation (LDA). Considering dipole and quadrupole contributions the absorption cross section is evaluated according to Fermi's golden rule shown in eqn (1) were ℏω is the incoming photon energy and α the fine structure constant:
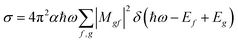 | (1) |
The transition matrix elements |Mgf| from the ground state |ψg〉 to the final state |ψf〉 are calculated using eqn (2), where ε is the incoming photon polarization and k its wavevector:
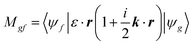 | (2) |
The excited states |ψf〉 generating XANES oscillations are then evaluated solving the Schrödinger equation using the finite difference method,49 which consists in constructing a space grid and discretizing the Schrödinger equation on its points. These states are represented in terms of spherical harmonics. If the potential is non-spherical but can be written as in eqn (3), then the final states can be expressed as in eqn (4), where aflm are coefficients determined by continuity conditions and blml′m′(r) are the radial solutions of the Schrödinger's equation.
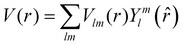 | (3) |
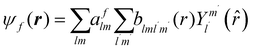 | (4) |
In order to account for the presence of the core–hole excitation, an excited configuration for the absorber is considered in the calculation of the final states.
The coordinate sets used as input (provided as supplementary electronic archive) were calculated as replicas of the Quantum Espresso super-cells. This procedure is fully justified, because of the plane wave algorithm used for the structural optimization. For each simulation, we considered a cluster containing all the atoms comprised within a sphere of radius 6.5 Å centered on the absorber. The self-consistent field (SCF) calculation, instead, was performed on a sphere of radius 4.00 Å surrounding the absorber. To be consistent with the Quantum ESPRESSO calculations we used the Perdew exchange correlation functional. Further details about FDMNES exchange correlation potentials and DFT calculations can be found in the literature.29,50 All spectra were convoluted using the standard FDMNES Γ function, to take into account the core–hole lifetime broadenings. This function is also designed to suppress all the filled levels lying below the Fermi level that are automatically computed during the SCF calculation. However, the Γ function is not meant to simulate exactly the broadening induced by the finite experimental resolution. Since we are mainly interested in the energy position of the spectral features, no further convolution was applied to the calculated spectra. As a consequence, the simulated spectra may exhibit sharper line-shapes compared to the experimental ones.
Results
Raman spectroscopy
Raman spectra of V-TiO2 and V–N-TiO2 films deposited at a substrate temperature of 350 °C are presented in Fig. 2(a). The Raman spectrum of V-TiO2 matches very well the one reported in the literature for anatase TiO2.51,52 It exhibits the characteristic five peaks of the anatase phase (marked “a” in Fig. 2(a)) at 141 cm−1, 197 cm−1, 399 cm−1, 515 cm−1 and 639 cm−1, which are attributed to the Eg, Eg, B1g, A1g–B1g, and Eg modes, respectively.53 Other peaks attributable to Raman modes of rutile TiO2 or vanadium oxides are not detected, confirming that the V-TiO2 sample is constituted solely by anatase. Moreover, the peak widths indicate a good crystalline quality.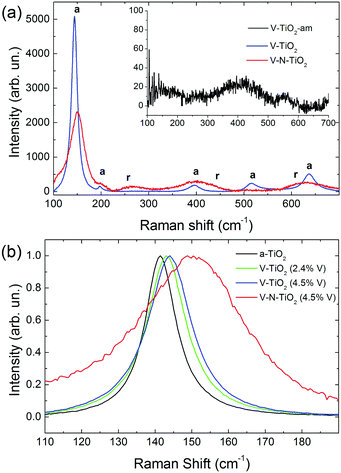 | ||
| Fig. 2 (a) Raman spectra of V-TiO2 and V–N-TiO2; the inset in (a) shows the Raman spectrum of amorphous film V-TiO2-am; a and r represent the position of Raman peaks due to anatase and rutile respectively, according to the literature.51 (b) Detail of the main Raman peak, normalized to the same maximum intensity, for pure anatase (a-TiO2), V-TiO2 films with different V contents (2.4 and 4.5 at%), and V–N-TiO2. | ||
Differently, the Raman spectrum of V–N-TiO2 indicates that anatase coexists with rutile and suggests a lower crystallinity compared to V-TiO2. The presence of rutile is revealed by the broad feature at about 260 cm−1, which is generally attributed to a multi-photon process.51 In addition, the two main peaks of rutile at 447 (Eg) and 610 (A1g) cm−1 overlap with the aforementioned B1g and Eg features of anatase at 399 and 639 cm−1. The weak B1g mode of rutile at about 143 cm−1 is not resolved at all due to its superposition to the intense anatase peak at 141 cm−1 (named hereafter Eg(1)). All spectral features of both anatase and rutile in V–N-TiO2 exhibit significant increase of the Full Width at Half Maximum (FWHM). This broadening is particularly strong for the Raman feature at 515 cm−1, which is still present although hardly visible in Fig. 2(a). In addition, Fig. 2(b) shows that the main anatase peak in V–N-TiO2 is blue-shifted compared to reference TiO2. The singly-doped V-TiO2 samples also present a blue-shift and a broadening, which increase slightly with the doping level but are much smaller than that for codoped V–N-TiO2 (Fig. 2(b)).
X-ray diffraction (XRD) data previously published on similar samples26 provide a picture consistent with Raman analysis, showing that: (i) the anatase crystallite size in V–N-TiO2 is ∼9 nm compared to ∼55 nm of V-TiO2, and (ii) codoping induces the formation of about 30 wt% of the rutile phase with a crystallite size of ∼8 nm.
The smaller crystallite size in codoped films contributes to the broadening and blue-shifting of the Raman spectral features, a well-known effect that arises from phonon confinement,54,55 while in an “infinite” crystal only optical phonons near the Brillouin zone center (wavevector q ≈ 0) are involved in first-order Raman scattering, and in a nanocrystal of size D a range of q vectors (as large as Δq ≈ 1/D) is accessible due to the uncertainty principle. As a consequence, Raman peaks are both asymmetrically broadened and either blue- or red-shifted, depending on the slope of the optical phonon dispersion relation near q = 0. The anatase Eg(1) peak turns out to be blue-shifted, in agreement with our results.54,55 According to calculations and experimental data available for the Eg(1) peak,54,55 and assuming a crystallite size D of 9 nm as in V–N-TiO2, a blue-shift between 2 and 4 cm−1 and a FWHM of 15 cm−1 are expected. These values are significantly smaller than the blue-shift of 9 cm−1 and the FWHM of 35 cm−1 observed in V–N-TiO2 (Fig. 2(b)).
Assuming D ∼ 55 nm as in V-TiO2 samples, no blue-shifting and broadening are expected compared to bulk reference anatase. However, the V-TiO2 samples do exhibit a distinct blue-shifting and broadening: the FWHMs are ∼13 cm−1 (2.4 at% V) and ∼15 cm−1 (4.5 at% V), both larger than pure anatase where FWHM ∼ 10 cm−1 (Fig. 2(b)). These comparisons suggest that, in addition to phonon confinement, other factors affect Raman spectral features, particularly for the codoped material. These factors may be searched in the incorporation of dopants within the TiO2 matrix, causing a local lattice distortion and introducing bonds with different force constants compared to pure TiO2. This interpretation is qualitatively consistent with the doping level dependence in V-TiO2 and with the more pronounced effect observed in the codoped material where the fraction of foreign atoms is higher. In the codoped material, the elevated density of grain boundaries due to the small crystallite size, may also induce elastic strains at the interfaces and increase the fraction of interfacial atoms with modified force constants. These microstructural features are likely to affect the Raman spectral characteristics, bringing about shifting and broadening effects in addition to those related to phonon confinement.
No Raman peaks are detected in the thin films deposited at low temperature (inset of Fig. 1(a)), indicating that these films are amorphous.
Local environment of host atoms
 | ||
| Fig. 3 Pre-edge (left) and full XANES (right) of the Ti K-edge measured on the thin film samples and on anatase and rutile TiO2 reference compounds. | ||
The quantitative EXAFS analysis of the local structure around Ti in V-TiO2 films and reference anatase is summarized in Table S3 (ESI†). The magnitude of the Fourier transform and the relative fits, of good quality, are displayed in Fig. S3 (ESI†). The most prominent features in the spectra are due to, in order of increasing distance, the six O nearest neighbors and the Ti atoms in higher coordination shells. As anticipated, Table S3 (ESI†) shows that the corresponding interatomic distances and Debye Waller factors do not depend on the V content. Moreover, they are consistent with those of reference anatase within the experimental uncertainties.
The V-TiO2-am film, deposited below 70 °C, displays a very broad lineshape in both pre- and main edge XANES regions. Moreover, the onset of the main edge is significantly shifted towards low energy. These observations, besides confirming the amorphous character of the film suggested by Raman spectroscopy, point to a possible oxygen deficiency, which may be responsible for the red-shift of the X-ray absorption edge.
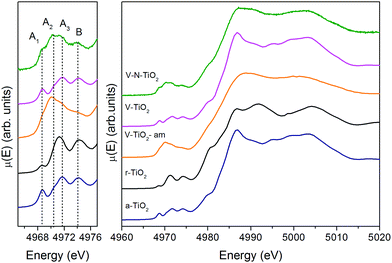
The spectrum of the V–N-TiO2 film exhibits both anatase-like features and signatures of disorder. In particular, the A2 pre-edge peak is higher than in V-TiO2 and reference anatase. This is reminiscent of the higher intensity observed at the energy position of the A2 peak in the amorphous samples. Moreover, in the case of anatase nanoparticles with a size in the 2–60 nm range, it was shown that with decreasing particle size and increasing surface-to-volume ratio, the intensity of the A2 peak increases relative to the A3 peak.59 Therefore, the A2 peak is generally associated with lower coordination Ti sites such as those present at surfaces or grain boundaries. The V–N-TiO2 film thus appears to contain a relevant fraction of such unsaturated Ti sites, which are likely located at interfaces between nanocrystallites (grain boundaries) due to the lower film crystallinity. In addition, the shoulder at 4980 eV on the increasing part of the main edge is higher than in anatase. An inspection at the same feature in the spectrum of rutile suggests that this difference may originate from the presence of rutile in the V–N codoped film, in agreement with Raman spectroscopy. The post-edge features of the V–N-codoped sample are broadened in comparison with anatase, again because of the lower film crystallinity and of the coexistence of the two polymorphs.
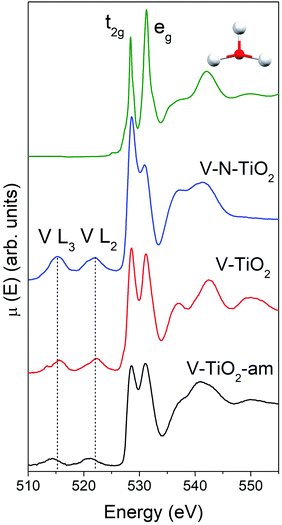
The Ti L2,3-edge XANES, reported in Fig. S4 (ESI†), are consistent with the picture derived from Raman spectroscopy and K-edge XAS. The spectrum of the V-TiO2 film matches very well with the anatase reported in the literature.60 The L2,3 absorption edges reflect transitions from Ti 2p core levels, split by the spin–orbit coupling, into Ti 3d antibonding states in the conduction band. For both L2 and L3 edges, the crystal field of the surrounding O atoms splits the 3d band into t2g and eg subbands. Codoping with N results in less sharp spectral features. More severe broadening is observed in the amorphous film deposited below 70 °C.
The main peaks centered at about 528.5 eV and 531.2 eV correspond to excitations from the O 1s core level into the Ti 3d-related conduction band, which is split into t2g and eg subbands described above. The subsequent maxima at about 537 and 543 eV are due to transitions into antibonding O 2p and Ti 4sp-related bands. All these typical anatase features are reproduced remarkably well by the calculated XANES displayed in Fig. 4, testifying the reliability of the scheme adopted for the simulations. Again, the amorphous nature of V-TiO2-am is witnessed by the broadening of its spectral feature. The 535–545 eV region of V–N-TiO2 appears less structured probably because the features of anatase and rutile overlap. In fact, in this energy region rutile has three broad features slightly shifted compared to the two anatase features. Fig. 4 also shows the V L2,3 lines, which are located at lower energy than the O K-edge. These lines are weak and featureless, therefore little information can be gained from their analysis.
Local environment of V dopants: V K-edge
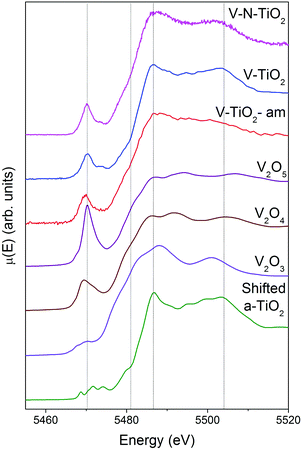
XAS spectra at the V K-edge were measured with the aim of determining the V incorporation site in the TiO2 thin films. V K-edge spectra of the thin film samples are reported in Fig. 5 along with those of V2O3, VO2 and V2O5 reference oxides, plotted in order of increasing V oxidation state from bottom to top (3+, 4+ and 5+), recalling the linear relation between the energy of the spectral features and the oxidation state.61,62 We also report for comparison the anatase spectra shifted by +500 eV (i.e., the energy difference between V and Ti K-edges).Firstly, we note that the amorphous film V-TiO2-am exhibits broad spectral features, indicating a rather disordered V environment, in analogy to the previously described Ti environment in the same film. In comparison, the V-TiO2 and V–N-TiO2 samples display sharpened spectra along with a blue-shift of the main edge. This blue-shift can be observed also at the V L2,3 lines (Fig. 4) and may indicate an oxygen deficiency in the amorphous state, as already suggested for Ti.
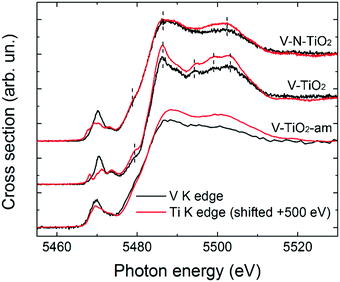
The pre-edge of the films is characterized by a sharp peak at 5470 eV followed by a weak shoulder at higher photon energy. These pre-edge features display similarities to those found in reference oxides VO2 and V2O5: they are due to dipole and quadrupole transitions to bound hybridized orbitals originating from O p and V d atomic orbitals.61 In particular, the peak height is very close to VO2, while its energy position is intermediate between VO2 and V2O5. On the other hand, the main edge parts of the spectra do not bear a good correspondence to those of reference oxides; especially noticeable is the energy onset of the main edge, which is significantly shifted to higher energies in the thin films with respect to the reference oxides. Interestingly, the V K-edge spectra of the thin films are very similar to the corresponding Ti K-edge spectra shifted by +500 eV, as far as the main edge region is concerned. This comparison is displayed in Fig. 6 making use of the V K-edge HERFD-XANES, which reveal a particularly striking similarity.
Local environment of N dopants: N K-edge
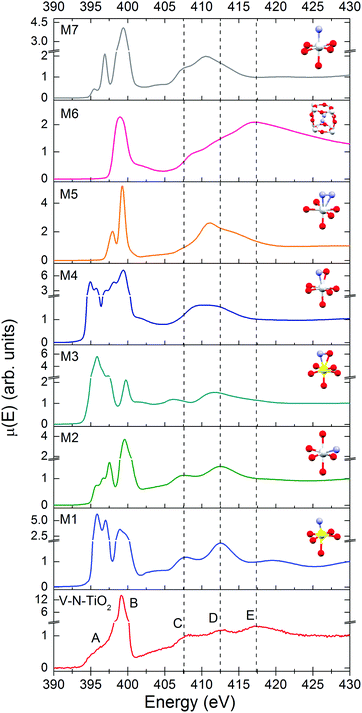
The N K-edge measured for the N–V-TiO2 film, shown in the bottom panel of Fig. 7 and in Fig. S5 (ESI†), is characterized by a very intense white line at about 399 eV (labeled B) with a weak shoulder at lower energy (labeled A). This contrasts with the O K-edge, where two lines of similar intensities are observed for the same sample and were also reported in the literature for both anatase and rutile.60 At higher energy, the spectrum displays three broad bands indicated by the vertical dashed lines, centered at 407.5, 412.5, and 417.5 eV and labeled C, D, and E. Fig. 7 also displays the simulated XANES for the models M1–M7 related to various N dopant configurations. The identification of N species from the comparison between experiment and simulations will be dealt with in the Discussion section.Discussion
V local structure
The comparison of the V K edge with the shifted Ti K edge strongly suggests that V substitutionally occupies Ti cationic sites in the anatase lattice. The simulations of V K-edge XANES for substitutional and interstitial V in anatase, shown in Fig. 8, support this hypothesis. In fact, the simulation model VTi represents very well the main edge part of the experimental spectrum, which does not resemble any of the reference vanadium oxides. The model also catches reasonably well the intensity of the pre-edge features and their energy position with respect to the main edge. Differently, the simulation model Vi fails to describe the essential pre-edge and main edge XANES features.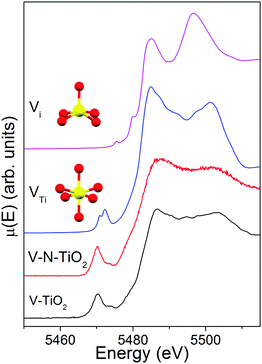 | ||
| Fig. 8 V K-edge XANES spectra of V-TiO2 and V–N-TiO2 films compared to simulations for a substitutional and interstitial V4+ cation in the anatase lattice. | ||
The simulation was carried out for a neutral cluster, resulting in a 4+ oxidation state and a higher local electron density compared to Ti for the V ion, the extra-electron of which remains localized. This situation is physically plausible because it is known that the donor transition level of substitutional V4+ lies deep in the anatase gap, from 0.7 eV13,26 to 1.36 eV63 below the CBM. Such energy difference is too high to permit that a macroscopic fraction of V ions attains a 5+ oxidation state by donating the excess electron to the anatase conduction band at room temperature. According to our DFT results, the V–O distances (1st and 2nd neighbors) for substitutional V in a cationic site are very similar to those for a Ti4+ cation in anatase. In particular, for a substitutional V4+ the four O nearest neighbors in the basal plane contract inwards by ∼0.027 Å and the two apical O atoms move inwards by ∼0.030 Å. This is consistent with the similar radius of V4+ and Ti4+ ions.17 In summary, the simulations of the V K-edge XANES confirm that the major contribution to the experimental spectrum of V-dopants arises from substitutional V4+ cations in the anatase lattice.
N local structure
In order to assess the N species in the V–N-TiO2 sample, we compare in Fig. 7 the experimental XANES with the simulations for models M1–M7. In model M2, N is in a NO configuration, replacing O in an anionic site with no V among its nearest neighbors. The XANES calculated for this model matches qualitatively the main experimental characteristics, in particular the significantly higher intensity of the B peak compared to the A feature and the energy positions of all features from A to D. Model M1 and M3 represent respectively a NO and a (NO)O configuration with one V as nearest neighbor; both models are not satisfactory in that they yield an A line more intense than the B line. Models M4 and M5 depict a (NO)O and a (N2)O configuration, respectively, without V neighbors: these models clearly fail in describing almost all features. Moreover, for model M4, it was not possible to reach a full relaxation of the cluster by DFT calculations, suggesting that this configuration is not stable. Model M7, i.e. a NO configuration in rutile, shows a different structure at high energy, which is characteristic of rutile64 and does not account for the C–E features. Interestingly, model M6, which represents a N2 dimer in an interstitial site (N2)i, is the only one that accounts for feature E, and additionally predicts a single white line exactly at the energy position of B. The calculated N–N distance for this model is 1.11 Å, quite close to the interatomic distance in the free N2 molecule (1.10 Å).It appears therefore that a single N configuration is not able to describe, even qualitatively, the experimental N K XANES. The comparison with the simulations suggests that N is mainly present in two species: (i) substitutional NO anions without V neighbors (model M2), and (ii) N2 dimers in interstitial sites (N2)i (model M6). The presence of two different N species is consistent with N 1s XPS measurements on similar samples,25 which show two main broad peaks at different binding energies (BE). The lower BE (394–396 eV) can be associated with NO, which is the most reduced species,65 while the higher BE (398–402 eV) is compatible with different defects: (NO)i65, (N2)i66, and N2 adsorbed at surface defects.67 The cross-check with our bulk-sensitive XANES in TFY mode therefore permits the (N2)i defect in the N–V-TiO2 film to be singled out, in addition to substitutional NO. This conclusion is further strengthened by previous reports of a strong N K-edge white line in TiO2 containing the (N2)i defect, namely oxidized TiN66 and TiO2 annealed under NH3.68 On this basis, we interpret the intense white line as a distinct signature of the (N2)i defect. Our experimental finding also agrees with DFT calculations,68 which indicate that N atoms incorporated in the bulk of TiO2 tend to recombine forming interstitial N2 dimers. In addition, it is possible that N2 molecules adsorbed on the surface of the growing film remain trapped during the sputtering process. It is important to stress at this point that we are not in the presence of gaseous N2 bubbles within the film: if it were so, a vibrational structure would be clearly visible in the white line, as shown for instance in N-doped ZnO.69 This is not our case, as demonstrated by the zoomed-in view of the white line in Fig. S5 (ESI†).
Useful as they are for the interpretation of experimental data and identification of dopant configurations, the XANES simulations do not provide quantitative information about their relative abundance. There are two principal reasons for this. First, a true fit should be carried out varying the atomic coordinates, but this is hardly doable without using high performance computing, because full potential calculations are very time consuming; the second is more fundamental: DFT, used for the evaluation of the Coulomb potentials, is a ground state theory that must be approximated to obtain XANES spectra related to core–hole excited states.
Connection with deposition method and photocatalytic properties
The obtained structural and electronic picture of V and N dopants may be connected with the film deposition method, resulting in good photocatalytic properties for the V-TiO2 and V–N-TiO2 films, as reported in our previous publications.25,26First of all, the efficient incorporation of V as a substitutional cation is not trivial and may be traced to the atom-by-atom film growth. The substrate temperature, sufficiently high to promote crystallization during growth, is too low to allow for long-range cationic diffusion.70 Therefore, despite the positive enthalpy of formation of about 1 eV41,63 for the V substitutional defect, the segregation of V and the formation of vanadium oxide is limited by the slow kinetics. Other preparation recipes may yield only a partial insertion of V in substitutional sites. For instance, by using a microemulsion method, Kubacka et al.17 obtained enhanced photo-activity of V-doped anatase up to 2.5 at% V. The subsequent decrease of photo-activity for doping levels of about 5 at% and above was attributed to a significant fraction of segregated vanadate-type (V5+) clusters. Moreover, even at low V-doping levels, only about 10–20% of the overall V atoms were estimated to occupy substitutional cationic sites.
Second, also the observed N-related defects are peculiar of the adopted preparation procedure, and other synthesis recipes for N-TiO2 may lead to quite different N-containing species. For instance, in N-TiO2 prepared by using a sol–gel method, only the XPS peak at higher BE around 400 eV was observed and attributed to interstitial N-containing species, while the XPS peak at lower energy, associated with NO, was not detected.71 Drera et al. studied by XANES and XPS rutile N-TiO2 films prepared by reactive RF sputtering under conditions similar to ours, apart from a much higher substrate temperature of 750 °C, needed for the growth of rutile.64 They found only a weak XPS signature in favor of molecular N2 adsorbed at surface defects, while substitutional NO dominated the XANES spectrum. The comparison with our results suggests that RF reactive sputtering yields NO substitutional anions, while there is no evidence in favor of the Ni interstitial. The absence of (N2)i in rutile films of Drera et al. may be due to the higher substrate temperature, by which N2 species trapped near the surface can surmount a surface energy barrier and be released in the gas phase, as suggested by DFT calculations.67 According to a recent review,1 NO is effective in photocatalysis under visible light because it introduces levels slightly above the VBM. These levels enhance light absorption in the visible range leaving a photogenerated hole deep enough to promote several oxidation reactions. Whether interstitial complexes like (N2)i observed in our films are photocatalytically active or not is still under debate.1
Regarding the V oxidation state, a distinction must be made between bulk-like and near-surface sites, the latter being particularly relevant to photocatalysis. Specific chemical information on the near-surface layers can be obtained by X-ray photoelectron spectroscopy (XPS), which indeed detected both V4+ and V5+ oxidation states, as reported in our previous publication.25 Fig. S6 (ESI†) displays a zoomed-in view of the pre-edge features of the V-TiO2 film compared to reference V oxides and to V-doped TiO2 NPs (3.5 at% V, mainly anatase) prepared by gas-phase condensation.41 In general, the pre-edge lineshape depends on the oxidation state of the absorber, its local point symmetry, and the elemental composition of its first coordination shell. Therefore, a comparison between V dopants in TiO2 and V oxides is not straightforward. Nevertheless, we can clearly notice that the pre-edge peak height in the NPs is intermediate between VO2 and V2O5, while in the V-TiO2 film it is similar to VO2. On account of the positive correlation between the pre-edge peak height and the V oxidation state demonstrated on a series of V-containing glasses,72 it appears that both V4+ and V5+ cations contribute to the pre-edge peak of the V-doped TiO2 NPs, whereas the contribution of V5+ cations is hardly discernible in the films’ case. This may be connected with the different surface-to-volume ratio of the two systems. In fact, in the films with a thickness of 240 nm, the surface-to-volume ratio is 1 to 2 orders of magnitude lower than in NPs with a diameter of about 10 nm. The contribution of near-surface sites to the XANES spectra will be downscaled accordingly and XAS essentially probes the bulk of the films. In summary, the film vs. NPs and the XAS vs. XPS comparisons are consistent with the idea that V5+ is associated with near-surface sites, while V4+ represents the dominant oxidation state in bulk-like sites. This conclusion agrees with a theoretical study suggesting that V4+ may be the dominant state within the TiO2 structure while V5+ is likely the major chemical state at the surface of the material.73 V5+ is likely in the form of ultra-small V2O5 clusters at the surface. These were suggested to act as electron scavengers favoring the reduction of adsorbed species, with a positive influence on photo-activity.26
Conclusions
We have been able to elucidate the nature of V- and N-related defects in TiO2 thin films grown by RF sputtering with enhanced visible light photocatalytic activity. We showed that V occurs as a VTi substitutional anion, with oxidation states 4+ in the bulk and 5+ in the near surface region. On the other hand, N is found in two species, i.e. as a substitutional NO anion – not neighboring VTi – and as (N2)i interstitial dimers.Ab initio simulations of XANES spectra, carried out for different dopant configurations, were extremely useful for the identification of the defects. The same experimental/theoretical combined approach may be applied to determine the local environment of other dopants used to enhance sunlight absorption and visible light photo-activity of semiconductor photocatalysts.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to N. Bazzanella for SEM observations and EDX analyses and to C. Degli Esposti Boschi for help and stimulating discussions on DFT simulations.References
- R. Asahi, T. Morikawa, H. Irie and T. Ohwaki, Chem. Rev., 2014, 114, 9824 CrossRef CAS PubMed.
- A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515 CrossRef CAS.
- J. Nowotny, T. Bak, M. K. Nowotny and L. R. Sheppard, Int. J. Hydrogen Energy, 2007, 32, 2609 CrossRef CAS.
- F. Fresno, R. Portela, S. Suárez and J. M. Coronado, J. Mater. Chem. A, 2014, 2, 2863 CAS.
- J. Tang, J. R. Durrant and D. R. Klug, J. Am. Chem. Soc., 2008, 130, 13885 CrossRef CAS PubMed.
- H. Zhang, G. Chen and D. W. Bahnemann, J. Mater. Chem., 2009, 19, 5089 RSC.
- L. Amidani, A. Naldoni, M. Malvestuto, M. Marelli, P. Glatzel, V. Del Santo and F. Boscherini, Angew. Chem., Int. Ed., 2015, 54, 5413 CrossRef CAS PubMed.
- N. Serpone and A. V. Emeline, J. Phys. Chem. Lett., 2012, 3, 673 CrossRef CAS PubMed.
- W. Choi, A. Termin and M. R. Hoffmann, J. Phys. Chem., 1994, 98, 13669 CrossRef.
- W. Li, Y. Wang, H. Lin, S. Ismat Shah, C. P. Huang, D. J. Doren, S. A. Rykov, J. G. Chen and M. A. Barteau, Appl. Phys. Lett., 2003, 83, 4143 CrossRef CAS.
- M. Takeuchi, H. Yamashita, M. Matsuoka, M. Anpo, T. Hirao, N. Itoh and N. Iwamoto, Catal. Lett., 2000, 67, 135 CrossRef CAS.
- R. Dholam, N. Patel, M. Adami and A. Miotello, Int. J. Hydrogen Energy, 2009, 34, 5337 CrossRef CAS.
- T. Umebayashi, T. Yamaki, H. Itoh and K. Asai, J. Phys. Chem. Solids, 2002, 63, 1909 CrossRef CAS.
- J. Choi, H. Park and M. R. Hoffmann, J. Phys. Chem. C, 2010, 114, 783 CAS.
- H. Yamashita, M. Harada, J. Misaka, M. Takeuchi, K. Ikeue and M. Anpo, J. Photochem. Photobiol., A, 2002, 148, 257 CrossRef CAS.
- J. C.-S. Wu and C.-H. Chen, J. Photochem. Photobiol., C, 2004, 163, 509 CrossRef CAS.
- A. Kubacka, A. Fuerte, A. Martínez-Arias and M. Fernández-García, Appl. Catal., B, 2007, 74, 26 CrossRef CAS.
- R. Dholam, N. Patel and A. Miotello, Int. J. Hydrogen Energy, 2011, 36, 6519 CrossRef CAS.
- S. Ikeda, N. Sugiyama, B. Pal, G. Marcí, L. Palmisano, H. Noguchi, K. Uosaki and B. Ohtani, Phys. Chem. Chem. Phys., 2001, 3, 267 RSC.
- Y. Tamaki, A. Furube, M. Murai, K. Hara, R. Katoh and M. Tachiya, Phys. Chem. Chem. Phys., 2007, 9, 1453 RSC.
- H. Yamashita, M. Harada, J. Misaka, M. Takeuchi, B. Neppolian and M. Anpo, Catal. Today, 2003, 84, 191 CrossRef CAS.
- R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269 CrossRef CAS PubMed.
- M. V. Dozzi and E. Selli, J. Photochem. Photobiol., C, 2013, 14, 13 CrossRef CAS.
- D. Gu, Y. Lu, B. Yang and Y. Hu, Chem. Commun., 2008, 2453 RSC.
- Z. El Koura, N. Patel, R. Edla and A. Miotello, Int. J. Nanotechnol., 2014, 11, 1017 CrossRef CAS.
- N. Patel, R. Jaiswal, T. Warang, G. Scarduelli, A. Dashora, B. L. Ahuja, D. C. Kothari and A. Miotello, Appl. Catal., B, 2014, 150–151, 74 CrossRef CAS.
- M. Katsikini, F. Boscherini and E. C. Paloura, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 241 CrossRef CAS.
- A. Stavrinadis, J. S. Pelli Cresi, F. d’Acapito, C. Magén, F. Boscherini and G. Konstantatos, Chem. Mater., 2016, 28, 5384 CrossRef CAS.
- O. Bunău and Y. Joly, J. Phys.: Condens. Matter, 2009, 21, 345501 CrossRef PubMed.
- Y. Joly, D. Cabaret, H. Renevier and C. R. Natoli, Phys. Rev. Lett., 1999, 82, 2398 CrossRef CAS.
- L. Signorini, L. Pasquini, L. Savini, R. Carboni, F. Boscherini, E. Bonetti, A. Giglia, M. Pedio, N. Mahne and S. Nannarone, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195423 CrossRef.
- F. Boscherini, in X-Ray Absorption Spectroscopy of Semiconductors, ed. C. S. Schnor and M. Ridgway, Springer-Verlag, Berlin-Heidelberg, 1st edn, 2015, pp. 77–97 Search PubMed.
- F. Boscherini, in Characterization of Semiconductor Heterostructures and Nanostructures, ed. C. Lamberti and G. Agostini, Elsevier B.V., 2nd edn, 2013, pp. 259–310 Search PubMed.
- F. Boscherini, in Synchrotron Radiation: Basics, Methods and Applications, ed. F. Boscherini, C. Meneghini and S. Mobilio, Springer-Verlag, Berlin-Heidelberg, 1st edn, 2015, pp. 485–498 Search PubMed.
- W. Li, A. I. Frenkel, J. C. Woicik, C. Ni and S. I. Shah, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155315 CrossRef.
- C. E. Rodríguez-Torres, A. F. Cabrera, L. A. Errico, C. Adán, F. G. Requejo, M. Weissmann and S. J. Stewart, J. Phys.: Condens. Matter, 2008, 20, 135210 CrossRef.
- C. Marchiori, G. Di Liberto, G. Soliveri, L. Loconte, L. Lo Presti, D. Meroni, M. Ceotto, C. Oliva, S. Cappelli, G. Cappelletti, C. Aieta and S. Ardizzone, J. Phys. Chem. C, 2014, 118, 24152 CAS.
- S. J. Stewart, M. Fernández-García, C. Belver, B. S. Mun and F. G. Requejo, J. Phys. Chem. B, 2006, 110, 16482 CrossRef CAS PubMed.
- W. Avansi, R. Arenal, V. R. de Mendonça, C. Ribeiro and E. Longo, CrystEngComm, 2014, 16, 5021 RSC.
- Y. Izumi, F. Kiyotaki, H. Yoshitake, K. Aika, T. Sugihara, T. Tatsumi, Y. Tanizawa, T. Shido and Y. Iwasawa, Chem. Commun., 2002, 2402 RSC.
- G. Rossi, M. Calizzi, V. Di Cintio, S. Magkos, L. Amidani, L. Pasquini and F. Boscherini, J. Phys. Chem. C, 2016, 120, 7457 CAS.
- E. Binetti, Z. El Koura, N. Patel, A. Dashora and A. Miotello, Appl. Catal., A, 2015, 500, 69 CrossRef CAS.
- BM23-XAS beamline, http://www.esrf.eu/home/UsersAndScience/Experiments/MEx/BM23.html, June 2017.
- Elettra Sincrotrone BEAR beamline, http://www.elettra.trieste.it/it/lightsources/elettra/elettra-beamlines/bear/bear.html, June 2017.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- S. A. Guda, A. A. Guda, M. A. Soldatov, K. A. Lomachenko, A. L. Bugaev, C. Lamberti, W. Gawelda, C. Bressler, G. Smolentsev, A. V. Soldatov and Y. Joly, J. Chem. Theory Comput., 2015, 11, 4512 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1953, 92, 603 CrossRef CAS.
- J. Strikwerda, Finite Difference Schemes and Partial Differential Equations, Society for Industrial and Applied Mathematics, 2nd edn, 2004 Search PubMed.
- Y. Joly, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125120 CrossRef.
- H. L. Ma, J. Y. Yang, Y. Dai, Y. B. Zhang, B. Lu and G. H. Ma, Appl. Surf. Sci., 2007, 253, 7497–7500 CrossRef CAS.
- H. C. Choi, Y. M. Jung and S. B. Kim, Vib. Spectrosc., 2005, 37, 33–38 CrossRef CAS.
- T. Ohsaka, J. Phys. Soc. Jpn., 1980, 48, 1661–1668 CrossRef CAS.
- V. Swamy, A. Kuznetsov, L. S. Dubrovinsky, R. A. Caruso, D. G. Shchukin and B. C. Muddle, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184302 CrossRef.
- S. Balaji, Y. Djaoued and J. Robichaud, J. Raman Spectrosc., 2006, 37, 1416–1422 CrossRef CAS.
- P. Glatzel, M. Sikora and M. Fernández-García, Eur. Phys. J. – Spec. Top., 2009, 169, 207–214 CrossRef.
- F. Farges, G. Brown and J. Rehr, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1809–1819 CrossRef CAS.
- F. Bohr, M. F. Ruiz-López and A. Muñoz-Páez, Catal. Lett., 1993, 20, 59–71 CrossRef CAS.
- V. Luca, J. Phys. Chem. C, 2009, 113, 6367–6380 CAS.
- S. O. Kucheyev, T. van Buuren, T. F. Baumann, J. H. Satcher, T. M. Willey, R. W. Meulenberg, T. E. Felter, J. F. Poco, S. A. Gammon and L. J. Terminello, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 245102 CrossRef.
- J. Wong, F. W. Lytle, R. P. Messmer and D. H. Maylotte, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 5596–5610 CrossRef CAS.
- L. Whittaker, T.-L. Wu, C. J. Patridge, G. Sambandamurthy and S. Banerjee, J. Mater. Chem., 2011, 21, 5580–5592 RSC.
- J. Osorio-Guillén, S. Lany and A. Zunger, Phys. Rev. Lett., 2008, 100, 036601 CrossRef PubMed.
- G. Drera, M. C. Mozzati, P. Galinetto, Y. Diaz-Fernandez, L. Malavasi, F. Bondino, M. Malvestuto and L. Sangaletti, Appl. Phys. Lett., 2010, 97, 012506 CrossRef.
- R. Asahi and T. Morikawa, Chem. Phys., 2007, 339, 57–63 CrossRef CAS.
- F. Esaka, K. Furuya, H. Shimada, I. Imamura, N. Matsubayashi, H. Sato, A. Nishijima, A. Kawana, H. Ichimura and T. Kikuchi, J. Vac. Sci. Technol., A, 1997, 15, 2521–2528 CAS.
- A. Nambu, J. Graciani, J. A. Rodriguez, Q. Wu, E. Fujita and F. J. Sanz, J. Chem. Phys., 2006, 125, 94706 CrossRef CAS PubMed.
- H. Chen, A. Nambu, W. Wen, J. Graciani, Z. Zhong, J. C. Hanson, E. Fujita and J. A. Rodriguez, J. Phys. Chem. C, 2007, 111, 1366–1372 CAS.
- P. Fons, H. Tampo, A. V. Kolobov, M. Ohkubo, S. Niki, J. Tominaga, R. Carboni, F. Boscherini and S. Friedrich, Phys. Rev. Lett., 2006, 96, 45504 CrossRef PubMed.
- K. Hoshino, N. L. Peterson and C. L. Wiley, J. Phys. Chem. Solids, 1985, 46, 1397–1411 CrossRef CAS.
- C. Di Valentin, E. Finazzi, G. Pacchioni, A. Selloni, S. Livraghi, M. C. Paganini and E. Giamello, Chem. Phys., 2007, 339, 44–56 CrossRef CAS.
- S. R. Sutton, J. Karner, J. Papike, J. S. Delaney, C. Shearer, M. Newville, P. Eng, M. Rivers and M. D. Dyar, Geochim. Cosmochim. Acta, 2005, 69, 2333–2348 CrossRef CAS.
- A. Vittadini, M. Casarin, M. Sambi and A. Selloni, J. Phys. Chem. B, 2005, 109, 21766–21771 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06742a |
| This journal is © the Owner Societies 2018 |