The significance of the amorphous potential energy landscape for dictating glassy dynamics and driving solid-state crystallisation

Abstract

The fundamental origins surrounding the dynamics of disordered solids near their characteristic glass transitions continue to be fiercely debated, even though a vast number of materials can form amorphous solids, including small-molecule organic, inorganic, covalent, metallic, and even large biological systems. The glass-transition temperature, T_g, can be readily detected by a diverse set of techniques, but given that these measurement modalities probe vastly different processes, there has been significant debate regarding the question of why T_g can be detected across all of them. Here we show clear experimental and computational evidence in support of a theory that proposes that the shape and structure of the potential-energy surface (PES) is the fundamental factor underlying the glass-transition processes, regardless of the frequency that experimental methods probe. Whilst this has been proposed previously, we demonstrate, using ab initio molecular-dynamics (AIMD) simulations, that it is of critical importance to carefully consider the complete PES – both the intra-molecular and inter-molecular features – in order to fully understand the entire range of atomic-dynamical processes in disordered solids. Finally, we show that it is possible to utilise this dependence to directly manipulate and harness amorphous dynamics in order to control the behaviour of such solids by using high-powered terahertz pulses to induce crystallisation and preferential crystal-polymorph growth in glasses. Combined, these findings provide compelling evidence that the PES landscape, and the corresponding energy barriers, are the ultimate controlling feature behind the atomic and molecular dynamics of disordered solids, regardless of the frequency at which they occur.

---

Introduction

Over the past several decades, a number of theories have been proposed that attempt to predict the temperature-dependent behaviour of disordered solids; however a clear consensus regarding the fundamental mechanism at or near the glass-transition temperature (T_g) has not yet been achieved.¹ However, as originally proposed by Goldstein² and expanded on by others,^3,4 it has been suggested that the underlying shape and structure of the potential energy surface (PES) is responsible for dictating properties, including the dynamics, of glassy materials. Dielectric spectroscopy has become the standard technique for experimentally investigating the relaxational dynamics associated with the glass-transition,^5,6 and such measurements have uncovered a number of characteristic relaxation fingerprints that occur within particular frequency windows, with the two most common being the primary α-relaxation (≈10⁻⁶–10³ Hz), corresponding to entire-molecule rearrangement, and the secondary Johari–Goldstein (JG) β (≈10⁻⁶–10⁹ Hz) relaxation, which has been suggested as a representing a special class of secondary relaxations strongly linked to the a number of physical properties.^7–9 But while dielectric spectroscopy probes the (relatively low) frequency relaxation of electric-dipole vectors, numerous other techniques have been used to characterise the properties and glass-transition temperatures of glasses, including neutron scattering,¹⁰ Brillouin light scattering (BLS),¹¹ dynamical mechanical analysis (DMA),¹² Raman scattering¹³ and, more recently, terahertz time-domain spectroscopy (THz-TDS),¹⁴ amongst many others.^15,16 In general, each of these methods were found to be sufficiently sensitive for detecting the α- and β-relaxation fingerprints, as well as the corresponding glass transitions (e.g. T_gα and T_gβ), which are loosely defined as the slowing of the corresponding dielectric relaxation processes beyond time scales that are readily detected by experiment (≈100 s).¹⁷ It is important to clarify that T_gβ has only recently been explored in-depth,^14,18,19 and it represents the vitrification of the β-relaxation process as originally described by Johari and Goldstein.²⁰

There have been attempts to link the experimental observations at frequencies exceeding the dielectric relaxations (such as mid-infrared, Raman or terahertz spectroscopies) to the fundamental process of collective translational and (hindered) rotational motions by means of a coupling process.²¹ However, given that most of these measurements probe processes that occur on drastically shorter timescales (femtoseconds to picoseconds probed in the infrared/terahertz vs. milliseconds to seconds for the relaxation processes associated with α- and β-relaxation) a more fundamental origin must exist that links the slow relaxation process with all the other experimental data. Given the importance of the PES on the properties of glasses, it is possible to explain the frequency-independence of the relaxation processes as a manifestation of the PES structure. Importantly, we believe that it is critical to explicitly consider the molecular nature of the solids, their complete intra- and inter-molecular interactions, and the corresponding anharmonicity in their PES, particularly the inter-molecular anharmonicity (responsible for thermal expansion). While there exists a large body of work related to this topic, with a wide variety of theories having been proposed over the years,^22–25 it is not surprising that this level of detail has not yet been achieved since such considerations are far from trivial to implement into theoretical models.^26–29 However, this work will demonstrate how important both of these factors are for understanding the origins of glassy dynamics, and that previous oversimplifications might be the cause of certain discrepancies in the quantitative agreement between theory and experiment. This interpretation is aligned with the coupling model, which is based on the corresponding anharmonicity in inter-molecular interactions, and helps to explain the origins of the inter-molecular dynamics (inclusive of any cage-rattling motions) within the context of a PES picture.

Such a dependence implies that the manipulation of the condensed phase molecular dynamics according to the PES structure should have a clear effect on the physical properties of disordered solids, which has effectively been shown on previous studies involving vapour deposition of molecular glass-formers.^30,31 Terahertz radiation is an ideal tool to investigate this, since the low-frequencies excite large-amplitude motions of entire molecules, and has indeed been shown to guide disordered processes, such as governing protein–ligand binding and driving biomolecular DNA mechanisms.^32,33 This work extends this by using high-powered terahertz pulses to drive solid-state crystallisation in amorphous pharmaceutical solids. Such experiments add to the strong evidence in support of the PES picture of disordered dynamics, and that related phenomena can be directed through this fundamental understanding.

Results and discussion

Given that such a wide range of methods, spanning large frequency regimes, produce comparable results when studying amorphous dynamics, an in-depth experimental and theoretical examination of a well-studied molecular glass-former, sorbitol, was performed to investigate any possible relationship between the various techniques. Fig. 1 shows experimental results from THz-TDS, mid-infrared Fourier-transform infrared spectroscopy (FTIR) and DMA measurements, complemented by BLS measurements by Ruta et al.,³⁴ as well as theoretical ab initio molecular-dynamics (AIMD) simulations results, all plotted as a function of temperature. The results clearly show that each of these experimental methods are capable of sensing both of the glass transition temperatures, T_gα and T_gβ, as well as the change in the temperature dependence in the regions above and below both of these (traditionally linked to the α-relaxation above T_gα, the β-relaxation below T_gα and above T_gβ, and a third region below T_gβ). While each of the techniques are capable of sensing the glass transitions (see ESI† for individual plots) there are slight discrepancies between the actual value of the temperatures between the techniques (≈±5 K), which is still subject to interpretation. Additionally, the absolute values of T_g are known to be slightly dependent on the heating/cooling rate as well as the thermal history of the sample,³⁵ however in the case of this study these relatively minor temperature shifts were minimised by using very slow cooling rates as well as the lack of significance on the overall aim of this work, which is related to the universality of the observed phenomena. Furthermore, to highlight that the results presented in this work are not simply confined to small-molecule or hydrogen bonded systems like sorbitol, and as originally suggested based on previous reports,^18,19Fig. 1 also contains results from BLS,³⁶ neutron-scattering mean-squared-displacement (MSD),³⁷ and deuteron nuclear magnetic resonance (²H-NMR) spin–lattice relaxation³⁸ measurements on ortho-terphenyl (OTP), and neutron-scattering MSD,³⁹ positron spectroscopy (PS),^40,41 quasi-elastic light scattering (QELS),³⁹ and dielectric spectroscopy⁴² for polymethyl methacrylate (PMMA), which exhibit the same temperature-dependent behaviour as described for sorbitol, although with different values for T_gα and T_gβ. It is important to comment that as noted previously,^18,19 these data represent the detection of T_gα and T_gβ across time-scales spanning over 15 orders of magnitude, indicating that a fundamental link between the processes must exist.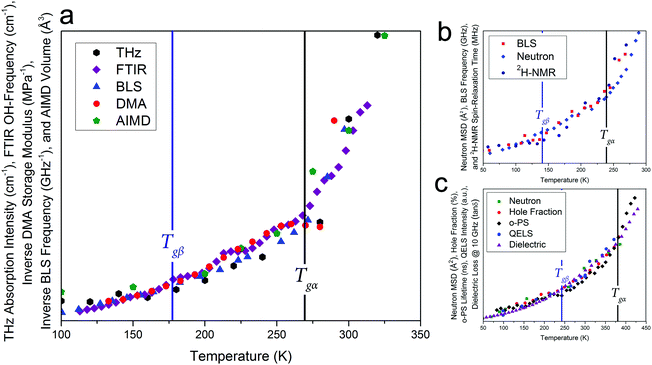

Fig. 1 (a) Experimental variable-temperature data from THz-TDS, FTIR, BLS,³⁴ DMA, and theoretical AIMD-simulated volume for amorphous sorbitol, showing changes in the temperature dependence at the α and β glass-transitions, (b) BLS linewidths,³⁶ neutron MSD,³⁷ and ²H-NMR spin–lattice relaxation³⁸ data for ortho-terphenyl, and (c) neutron MSD,³⁹ PS hole-fraction,⁴⁰o-PS lifetime,⁴¹ QELS,³⁹ and 10 GHz dielectric loss⁴² data for PMMA, all showing similar behaviour. The DSC-determined values for T_gα (black vertical lines) and the THz-TDS determined T_gβ for sorbitol,⁴³ DSC-determined T_gβ for OTP,⁴⁴ and the dielectric determined T_gβ for PMMA⁴² (blue vertical lines), are shown. It should be noted that the identification of T_gβ has been previously reported.^18,19 The data are plotted with different vertical axes (not shown, see ESI† for individual plots).

There is a clear agreement between the data obtained from all techniques in both the temperatures of the glass transitions and the relative change in the three regions that are typically attributed to the α- and β-relaxations. However, it is somewhat surprising that, while the fundamental α- and β-relaxations occur at relatively low frequencies (kHz to MHz) in dielectric spectroscopy, their associated dynamics can also be observed at much higher frequencies. For example, THz-TDS covers the spectral region of 0.1–3 THz i.e. frequencies some nine orders of magnitude greater than the fundamental α-relaxation process. There have been attempts to reconcile these observations within the context of the coupling model,⁴⁵ which argues that spectral changes observed at terahertz frequencies are coupled to their fundamental relaxations via a so-called ‘fast process’, typically referred to as ‘cage-rattling’ motion.^17–19,21 However, given that a wide range of methods all yield similar results, even though they are based on very different measurement principles and probe molecular properties over a wide range of energies, it is possible, and indeed likely, that a more fundamental feature, that is, the PES, that relates the experimental observations and atomic-level interactions. This is what is suggested in the coupling model, but rather than limit the application to ‘cage-rattling’ dynamics, we propose that the PES, both intramolecular and inter-molecular, is responsible for dictating the complete inter-molecular dynamics, inclusive of any cage-rattling motions.⁴⁶ This is particularly important in the case of organic molecular-solids, as the low-frequency mode-types are often a mixture of intra- and inter-molecular motions that cannot be easily separated from one another.⁴⁷

FTIR analysis

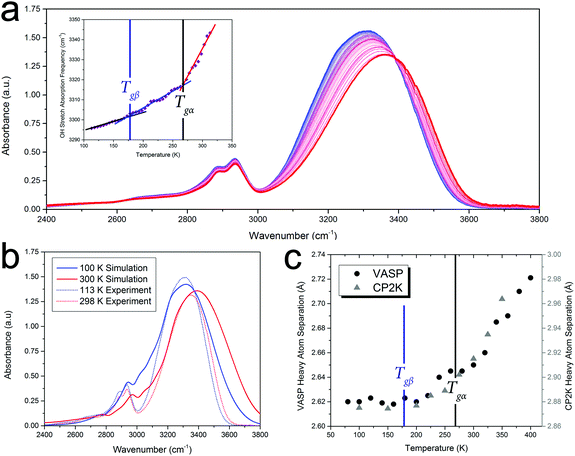
In order to highlight the importance of the PES structure (including inter-molecular anharmonicity) on glassy dynamics, the FTIR absorption data, specifically the OH vibrational stretch absorption for sorbitol, will be used as an illustrative example of the proposed hypothesis. Analysis of the FTIR data also reveals that the glass-transition temperatures are fundamental characteristics of the PES (rather than an exclusive low-frequency relaxation that couples to higher-frequency phenomena) since the OH stretching vibration has a cycle time of ≈60 fs, which is 11–20 orders of magnitude higher than the characteristic time of the α-relaxation motion. Since the strengths of covalent OH-bonds are highly influenced by their inter-molecular interactions (i.e. hydrogen bonds), the OH-stretch absorption characteristics can provide a measure of the inter-molecular interactions in the solid, an important component since traditional structural analyses (e.g. X-ray diffraction) are not easily applied to disordered media and precise inter-molecular information is difficult to extract.

Fig. 2 shows the FTIR spectra of amorphous sorbitol from 113–313 K acquired in 5 K increments. The frequency of the OH-stretch peak in the IR-absorption spectra exhibits the same temperature-dependent variation as measured using the other techniques, as shown in Fig. 1, with clear changes in the slope being observed at both T_gα and T_gβ (Fig. 2 inset). The origins of the temperature-induced frequency shift must arise from a change in the OH-bond strength. Since the OH-bond potential energy surface is relatively hard (with the first excited vibrational level occurring at ≈5100 cm⁻¹, equivalent to ≈7300 K), only the vibrational ground state is populated under ambient conditions, indicating that the change in the OH-bond strength must arise from temperature-altered inter-molecular interaction strengths rather than higher order vibrational transitions (which would be expected to exhibit an anharmonically-caused red-shift in frequency with increasing temperature, rather than the observed blue-shift). Further evidence for this is the lack of any significant changes with temperature in the CH-bond stretch that occurs at ≈2900 cm⁻¹, since the CH-bond is not significantly influenced by inter-molecular interactions and there is little change in the CH-bond strength itself as a function of temperature.

Fig. 2 (a) Mid-IR spectra of amorphous sorbitol from 113 K (blue) to 313 K (red), with the OH bond-stretching frequency plotted as a function of temperature in the inset (with linear trends in the three regions shown); (b) simulated IR absorption spectra from the CP2K AIMD simulations at 100 and 300 K; (c) and the average heavy-atom (hydrogen bonded oxygens) bond distance throughout the MD trajectory as a function of temperature, using two different AIMD software packages.

Ab initio molecular dynamics (AIMD)

To help interpret the atomic-level details associated with the dynamics of glasses, ab initio molecular dynamics (AIMD) simulations of sorbitol were performed. These simulations differ from the classical MD method, which uses empirical interatomic potentials, in that the PES (and associated atomic forces) are recalculated at every time step of the MD simulation, and hence take into account the delicate and dynamic nature of the inter-molecular interactions. The AIMD simulations of amorphous sorbitol were performed using both CP2K⁴⁸ and VASP.⁴⁹ Amorphous models were generated by progressively reducing the density of a 10-molecule gas-phase system and allowing for equilibration (of energy and temperature) via NVT simulations until the density of the solid was reached, followed by a series of NPT simulations to determine the density as a function of temperature. Finally, NVT simulations were performed on the various NPT-generated structures to determine the atomic dynamics of the system at constant temperature and volume.

The AIMD simulations enable the atomic-level mechanisms that occur in amorphous sorbitol to be uncovered. For example, the vibrational dynamics of the system can be determined via the Fourier transform of the dipole-moment autocorrelation function,^50,51 and the results are in good agreement with the experimental data (Fig. 2(b)), providing validation in the utilised theoretical model. Furthermore, the calculations can provide information that is difficult to obtain experimentally, for example the average hydrogen bond distance as a function of temperature (Fig. 2), which also follows the trend described in Fig. 1(c).

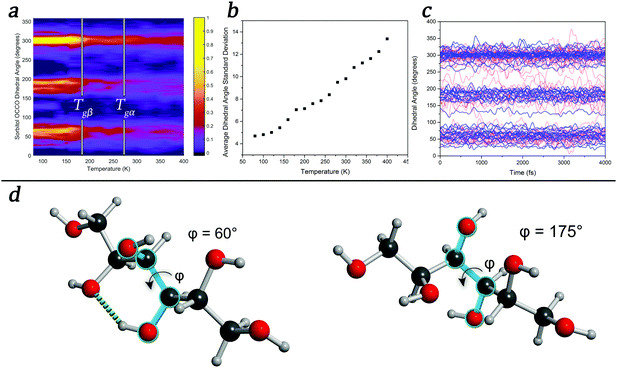
To further explore the temperature-induced changes in the dynamics of the system, an analysis of the OCCO dihedral angles of sorbitol in the glassy state was performed at a number of temperatures. The results, shown in Fig. 3, show that there exist three distinct structural features corresponding to dihedral angles of approximately 60°, 180°, and 300°, with sub-maxima within the regions emerging as the temperature is decreased (Fig. 3(a)), in agreement with a previous report.⁵² It is significant that the onset of the localised sub-regions occurs near 260 K, corresponding to the T_gα of sorbitol, while significant localisation occurs near 180 K, corresponding to the T_gβ of sorbitol. An analysis of the time-evolution of dihedral angles in glassy sorbitol helps to uncover the changes in atomic dynamics that occur as a function of temperature in such disordered molecular solids. For instance, low-temperature simulations (T < T_gβ) show only small-magnitude oscillations of each dihedral angle about its respective average value, with little to no structural rearrangement occurring, implying that the molecules are confined to the sub-minima in the PES. However, as the temperature is increased above T_gβ and through T_gα, the magnitude of the oscillations increases and fluctuations in the sub-minima populations become increasingly prevalent, as shown in the average dihedral angle standard deviation shown in Fig. 3(b). Additionally, above T_gα, there are an increasing number of large-scale conformational changes, evidenced by jumps between the principal dihedral angle basins over the course of the simulation (Fig. 3(c)). This is direct evidence confirming previous theories related to dihedral-angle changes determined by FTIR and NMR studies, where large changes in absorption corresponding to dihedral angle vibrational motions were observed as a function of temperature.^53,54

Fig. 3 (a) Population of amorphous- and liquid-sorbitol OCCO dihedral angles as a function of temperatures; (b) average dihedral-angle standard deviation over a 4 ps range of time as a function of temperature; (c) comparison of the 100 K (blue) and 400 K (red) time-evolving dihedral angle; (d) models of a sorbitol molecule with two possible dihedral angle configurations defined in terms of blue bonds, in which an intra-molecular hydrogen bond (dotted green) is broken.

These effects can also shed light on the ‘intramolecular’ versus ‘intermolecular’ hypotheses regarding the origins of the JG-β relaxation.^8,17,55 For example, the well-studied glass former, ortho-terphenyl (OTP), is regularly referred to as being ‘rigid’ in the literature, and has been used as a benchmark in the debate surrounding the origins of the JG-β relaxation. A simple simulation of the gas-phase vibrational properties (using DFT in CP2K) of a single-molecule of OTP puts this description in dispute, however, since there exist a number of lower-frequency features in the vibrational spectrum (<400 cm⁻¹) that are torsional type motions of the OTP ring moieties. These motions will be thermally excited at ambient conditions (using the Boltzmann relation for a 400 cm⁻¹ transition yields an excited state population of ≈13% at 298 K), and will contribute to the overall spectral response of OTP. We propose that, rather than restrict a description of the type of motions involved in the various relaxation processes to being either internal or external, it is better to simply refer to the nature of the PES and the energies of the various dynamical variables.

As Goldstein originally hypothesised,² the AIMD results for sorbitol show that below T_gα structural changes are localised, while temperatures above T_gα lead to large-scale conformational rearrangements of the molecules. While this phenomenon is clearly associated with overcoming potential-energy barriers, the origins are slightly more complex, as the barrier heights (and indeed the entire PES) are as dynamic as are the processes themselves. This arises because the PES, which dictates the atomic dynamics and structures, evolves in time as the interactions themselves change, with various factors influencing its structure at any time. For example, inter-molecular anharmonicity, which is responsible for thermal expansion, can lead to a larger accessible free volume of the particles with increasing temperature, which in turn can weaken the inter-molecular interaction strength and thereby lower potential energy barriers for conformational rearrangements.

These conclusions highlight the importance of accounting for a varying PES as a function of time in MD simulations, a factor that classical MD simulations are not capable of reproducing. This also has implications for the coupling model,⁴⁵ where the changing of the PES as a function of time (and temperature) means that the relative coupling between molecules is dynamic and must be accounted for. However as previously mentioned, the PES is not only dependent on static atomic positions, as any change in these values will cause a corresponding change in the PES. For example, changing a single dihedral angle (as shown in Fig. 3(d)) results in the breaking of an intra-molecular hydrogen bond. A new hydrogen bond can easily form along this direction, provided that the OH group can readily rotate so as to take advantage of this, which can occur throughout the time-evolution of the system. Thus, forming a model of amorphous dynamics would require every combination of structures and interactions to be known. Given these conclusions, the glass transitions and temperature-dependent dynamics can be related to the number of accessible states that the system has, implying that a thermodynamic partition function might be an appropriate means of predicting such phenomena. However, because the PES is both temperature- and time-dependent (since the various conformations that the molecules can achieve will change the PES accordingly), the expression would become much more complex, depending on both the temperature and time-dependent barriers. Thus, while the problem might appear intuitively simplistic, it becomes highly complex to solve analytically. However, approaches to its solution are currently under investigation.

Inducing crystallisation with high-power terahertz pulses

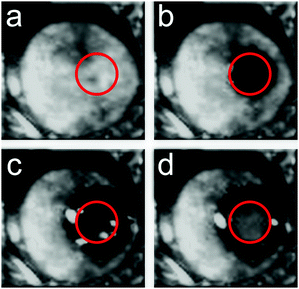
Given that the PES and the corresponding inter-molecular anharmonicity have been indicated to be behind the dynamics of glasses, harnessing these effects could lead to control over the physical properties of amorphous materials. To test this hypothesis, experiments were carried out on the FLARE instrument at the FELIX free-electron laser facility which allowed an investigation of how (molecular) amorphous solids respond to high-power pulses of low-frequency radiation. Given that such low-frequency pulses are not able to significantly heat the sample,⁵⁶ changes in the material upon irradiation by high-power pulses can be induced by excitation to higher-order vibrational states due to the significant anharmonicity in the inter-molecular PES, since pure harmonic systems are forbidden from undergoing such transitions. Due to significant anharmonicity in the inter- and intra-molecular interactions, such excitations can lead to increased displacements from the molecular pseudo-equilibrium positions (i.e. the potential energy minima), thereby allowing the molecules to move into new conformations. Furthermore, since the secondary glass transition temperature corresponds to energies in the terahertz range (200 K corresponds to a thermal wavelength of ≈4.2 THz), such experiments can serve to push the molecules over their potential barriers.

Samples of amorphous indomethacin (C₁₉H₁₆ClNO₄), a popular active pharmaceutical ingredient (API), were prepared by melt quenching from a molten liquid and were exposed to the focused terahertz beam (1.5 mm diameter) with an average power of 200 mW (power density of 3 MW cm⁻²) operating at a frequency of 1.56 THz, chosen due to the presence of an absorption feature in the crystalline form near this frequency. After 1 minute of exposure to the terahertz beam, visual inspection showed that a clear transparent region had formed at the focal point of the beam, which did not extend beyond this region (Fig. 4b). Subsequently, after an additional 4 minutes of exposure (5 minutes total), a crystalline region had formed within the beam spot (Fig. 4c), with the transparent region extending slightly beyond the focal point of the beam. Continued exposure (10 minutes total) resulted in the entire focus region of the beam converting to a crystalline phase (Fig. 4d). It is important to note that other than the focal point of the beam and the extension region (which is in direct contact with the beam focus spot), there was no discernible change in the rest of the sample. Further characterisation with THz-TDS showed that the crystalline areas, both within the focus of the beam and the area that extended outwards, contained a mixture of α and γ polymorphs of indomethacin. However, the region within the focal point of the beam contained a larger proportion of the γ form, indicating that the intense terahertz pulses were preferentially promoting one form over the other. It is important to note that while temperature is known to have an effect on the polymorphic outcome of indomethacin,⁵⁷ it is not believed to be the origin of the observed phenomena, as these effects were also observed when the sample was placed under active cooling, helping to highlight that the terahertz radiation, rather than thermal effects, was responsible.

Fig. 4 Images of indomethacin while under exposure to FLARE. (a) Freshly prepared sample at room temperature, (b) 1 minutes after exposure, showing formation of transparent region (c) 5 minutes after exposure, showing the initial formation of crystalline region within the beam spot, (d) 10 minutes after exposure, showing a clear formation of crystalline region within the spot of the beam. The beam spot of FLARE is highlighted in red circles.

A similar behaviour was observed in samples of amorphous API carbamazepine (C₁₅H₁₂N₂O), which were exposed to a 1.0 THz beam, again chosen due to the resonance found in the crystalline spectrum. In the absence of any external perturbation, carbamazepine regularly crystallises on heating in the Form III polymorph.⁵⁸ However, upon exposure to the FLARE terahertz beam, the crystallised region within the focus only contained Form I, while the edges of the sample, which were in contact with the copper sample holder that was subsequently heated while exposed to FLARE to in an attempt to speed crystallisation, contained the expected Form III. These results strongly indicate that the intense terahertz radiation produced by FLARE is capable of inducing crystallisation, as well as preferentially promoting particular polymorphic forms. Detailed information can be found in the ESI.†

The results from the FLARE experiments, together with the interpretation of the large-scale conformational rearrangement of molecules associated with overcoming potential-energy barriers at T_gβ, fully explains our previous observation regarding the critical role of T_gβ for the crystallisation process from a disordered solid.⁵⁹ Additionally, these results are in agreement with previous studies using gamma-rays, where in that particular work the authors observed that upon irradiation their sample underwent significant ageing thought to be caused by structural rearrangement due to pushing molecules over their energy barriers.⁶⁰ In samples of a quench-cooled melt of naproxen (C₁₄H₁₄O₃), which contained crystalline nucleation seeds due to an insufficient cooling rate, we found that upon heating the crystallisation rate increased dramatically at temperatures above T_gβ and full crystallisation was observed at temperatures well below T_gα. Whilst our simple method of quench-cooling molten APIs can reliably produce stable glasses in most cases, this is not the scenario for naproxen – even when quenching the melt to liquid nitrogen temperatures – given its extremely high propensity to crystallise and limited heat transfer in our experimental apparatus. The resulting solid is hence mostly disordered, but there exists significant near-range order between a large number of molecules. For a system like this, further nucleation and crystal growth requires only the subtle movement of neighbouring molecules and no significant translational or (hindered) rotational motions, and as the potential-energy barriers that govern the conformational rearrangement are exceeded (at T_gβ), the crystallisation process can commence much more readily. This idea also explains why we observe the formation of different polymorphs during the stimulated crystallisation process by FLARE compared to the crystallisation at high temperatures. The near-range order in the disordered solid will determine the crystal structure that can form during FLARE excitation, as only the weak potential-energy barriers that are linked to the large-scale conformational rearrangement of molecules are pumped by the terahertz beam, implying there is no significant enhancement of the translational or (hindered) rotational motions associated with the terahertz stimulation. It is therefore not surprising that the polymorph formed during such crystallisation is not necessarily that with the lowest energy crystal structure, but the only that which is structurally closest to the near-range structure in the disordered solid. There is empirical evidence that different polymorphs may result from crystallising from melt-quenced, spray-dried, lyophilised or cryo-milled amorphous solids.⁶¹ It is important to note that while the net-outcome of these experiments produces crystalline phases, there is no evidence for or against other possible outcomes due to the terahertz radiation, for example accelerated aging or rejuvenation of the amorphous solid itself. Future experiments will have to confirm whether this is predetermined by the existing near-range order, as suggested in the literature, and whether it is hence possible to selectively crystallise different polymorphic forms from such disordered solids, e.g. by terahertz stimulation.

For a fully disordered solid (i.e. no crystal nuclei present) we hypothesise that no crystallisation is possible at temperatures below T_gβ as the molecular interactions are confined by localised energy minima. It is only at temperatures above T_gβ that large-scale conformational changes can take place that provide sufficient molecular mobility for crystal nuclei to form. However, whilst crystallisation will be possible at such temperatures it will be a very slow process for most materials as there is not sufficient free volume available in the solid for translational or rotational motions to take place. As the temperature increases further the density of the solid decreases as the amount of free volume increases until at T_gα there is sufficient mobility and free volume available for the glass transition to take place. Whether or not a material will fully crystallise at temperatures T_gβ < T < T_gα, or indeed at all, will depend on the molecular size, flexibility and inter-molecular bond strength of the molecule.

Conclusions

Understanding the temperature-dependent atomic dynamics of amorphous solids can be understood within the context of the structure of the potential-energy surface (PES). By comparing the experimental temperature-dependent results from a multitude of measurement techniques, it is clear that the observations must originate from a shared fundamental origin, in this case the PES, a concept originally proposed by Goldstein. The atomic dynamics can be fully described by interpretation of the consequence of the shape of the PES, and this picture provides a comprehensive connection to the previously suggested coupling model in order to explain the link between the fundamental dielectric relaxation processes and higher-frequency observations. By using ab initio molecular-dynamics simulations we are able to highlight the critical role that ‘soft’ interactions, such as intra-molecular torsional potentials, have on the glass-transition processes. Finally, we show that these principles can be used in applications by exciting amorphous molecular solids with high-power terahertz radiation, where it is possible to actively induce processes, such as crystallisation and atypical crystal-polymorph formation, by selectively perturbing the dynamics allowed by the shape of the PES. This study shows the important link to the PES for the understanding of amorphous solids. It further highlights the crucial role of weak forces for the material behaviour in applications as diverse as amorphous drug stability, durability of polymers, and the solid electrolyte interphase of batteries, amongst others.

Author contributions

M. T. R., S. R. E, and J. A. Z. designed the project, interpreted the data, and wrote the paper. M. T. R. performed the THz-TDS experiments. E. O. K., H. G., K. L, and T. R. designed and performed the DMA experiments. J. S. performed the FTIR experiments and J. S. and T. M. K. analysed the data. M. T. R. and M. K. performed the AIMD simulations. J. S., N. Y. T., D. D. A., W. v. d. Z., B. R., and J. A. Z. performed the FLARE experiments, and D. M. and M. T. R. processed and analysed the data. All authors contributed to the discussion of the results.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

M. T. R., M. K., S. R. E., and J. A. Z. thank the UK Engineering and Physical Sciences Research Council for funding (EP/N022769/1). The research leading to these results has received funding from the European Community's Seventh Framework Programme (FP7/2007–2013) under grant agreement 312284. T. M. K. would like to acknowledge the Royal Society International Exchanges Scheme as well as the Royal Society of Chemistry JWT Jones Travelling Fellowship for support. M. T. R and J. A. Z thank Ian Bethune for his valuable computational support. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). The authors would like to thank David Williams, Bio-Organic Chemistry at Nijmegen, for help acquiring the DSC measurements of indomethacin. Further data to support this manuscript can be found with the electronic preprint at DOI: 10.26434/chemrxiv.5328235.v1.

References

1. K. L. Ngai, J. Non-Cryst. Solids, 2007, 353, 709–718.
2. M. Goldstein, J. Chem. Phys., 2003, 51, 3728–3739.
3. S. Sastry, P. G. Debenedetti and F. H. Stillinger, Nature, 1998, 393, 554.
4. P. G. Debenedetti, F. H. Stillinger, T. M. Truskett and C. J. Roberts, J. Phys. Chem. B, 1999, 103, 7390.
5. A. Cavagna, Phys. Rep., 2009, 476, 51–124.
6. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267.
7. K. L. Ngai, J. Chem. Phys., 1998, 109, 6982–6994.
8. K. L. Ngai and M. Paluch, J. Chem. Phys., 2004, 120, 857–873.
9. Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer Berlin Heidelberg, 2003.
10. J. M. Carpenter and D. L. Price, Phys. Rev. Lett., 1985, 54, 441–443.
11. D. Heiman, D. S. Hamilton and R. W. Hellwarth, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19, 6583–6592.
12. P. G. Royall, C.-y. Huang, S.-w. J. Tang, J. Duncan, G. Van-de Velde and M. B. Brown, Int. J. Pharm., 2005, 301, 181–191.
13. H. Liem, J. Cabanillas-Gonzalez, P. Etchegoin and D. D. C. Bradley, J. Phys.: Condens. Matter, 2004, 16, 721–728.
14. J. Sibik, S. R. Elliott and J. A. Zeitler, J. Phys. Chem. Lett., 2014, 5, 1968–1972.
15. D. H. Gracias, D. Zhang, L. Lianos, W. Ibach and Y. R. Shen, Chem. Phys., 1999, 245, 277–284.
16. D. Fragiadakis and P. Pissis, J. Non-Cryst. Solids, 2007, 353, 4344–4352.
17. K. L. Ngai, S. Capaccioli, M. Thayyil and D. Prevosto, J. Phys. Chem. B, 2015, 119, 8800–8808.
18. K. L. Ngai, S. Capaccioli, D. Prevosto and L. M. Wang, J. Phys. Chem. B, 2015, 119, 12502–12518.
19. K. L. Ngai, S. Capaccioli, D. Prevosto and L. M. Wang, J. Phys. Chem. B, 2015, 119, 12519–12525.
20. G. P. Johari and M. Goldstein, J. Chem. Phys., 2003, 53, 2372–2388.
21. K. L. Ngai, Philos. Mag., 2004, 84, 1341–1353.
22. G. Biroli and J. P. Bouchaud, The Random First-Order Transition Theory of Glasses: A Critical Assessment, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2012, vol. 267.
23. J. D. Bryngelson and P. G. Wolynes, J. Phys. Chem., 1989, 93, 6902–6915.
24. A. Cavagna, I. Giardina and G. Parisi, J. Phys. A: Math. Gen., 1997, 30, 7021–7038.
25. J. C. Phillips and M. F. Thorpe, Solid State Commun., 1985, 53, 699–702.
26. A. Glensk, B. Grabowski, T. Hickel and J. Neugebauer, Phys. Rev. Lett., 2015, 114, 195901.
27. A. Saksaengwijit and A. Heuer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061503.
28. D. J. Wales, M. A. Miller and T. R. Walsh, Nature, 1998, 394, 758–760.
29. M. Micoulaut, Europhys. Lett., 2002, 58, 830–836.
30. S. Singh, M. D. Ediger and J. J. de Pablo, Nat. Mater., 2013, 12, 139–144.
31. S. F. Swallen, K. L. Kearns, M. K. Mapes, Y. S. Kim, R. McMahon, M. D. Ediger, T. Wu, L. Yu and S. Satija, Science, 2007, 315, 353.
32. D. A. Turton, H. M. Senn, T. Harwood and A. J. Lapthorn, Nature, 2014, 5, 028103.
33. M. González-Jiménez, G. Ramakrishnan, T. Harwood, A. J. Lapthorn, S. M. Kelly, E. M. Ellis and K. Wynne, Nat. Commun., 2016, 7, 11799.
34. B. Ruta, G. Monaco, F. Scarponi and D. Fioretto, Philos. Mag., 2008, 88, 3939–3946.
35. N. T. Correia, C. Alvarez, J. Ramos and M. Descamps, Chem. Phys., 2000, 252, 151–163.
36. G. Monaco, S. Caponi, R. Di Leonardo, D. Fioretto and G. Ruocco, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, R7595–R7598.
37. E. Bartsch, F. Fujara, M. Kiebel, H. Sillescu and W. Petry, Ber. Bunsenges. Phys. Chem., 1989, 93, 1252–1259.
38. W. Schnauss, F. Fujara and H. Sillescu, J. Chem. Phys., 1992, 97, 1378.
39. E. Duval, A. Mermet, N. Surovtsev, J. F. Jal and A. J. Dianoux, Philos. Mag. B, 2009, 77, 457–461.
40. H. A. Hristov, B. Bolan, A. F. Yee, L. Xie and D. W. Gidley, Macromolecules, 1996, 29, 8507–8516.
41. N. Qi, Z. Q. Chen and A. Uedono, Radiat. Phys. Chem., 2015, 108, 81–86.
42. E. M. Amrhein and F. H. Mueller, Trans. Faraday Soc., 1968, 64, 666–676.
43. J. Sibik, E. Y. Shalaev and J. A. Zeitler, Phys. Chem. Chem. Phys., 2013, 15, 11931–11942.
44. H. Fujimori and M. Oguni, Solid State Commun., 1995, 94, 157–162.
45. K. L. Ngai, J. Phys.: Condens. Matter, 2003, 15, S1107–S1125.
46. K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, 2011.
47. S. P. Delaney, D. Pan, S. X. Yin and T. M. Smith, Cryst. Growth Des., 2013, 13, 2943–2952.
48. J. Hutter, J. VandeVondele, M. Iannuzzi, M. Iannuzzi, J. Vandevondele, F. Schiffmann, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
50. M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622.
51. M. T. Ruggiero and J. A. Zeitler, J. Phys. Chem. B, 2016, 120, 11733–11739.
52. A. Lerbret, P. E. Mason, R. M. Venable, A. Cesàro, M. L. Saboungi, R. W. Pastor and J. W. Brady, Carbohydr. Res., 2009, 344, 2229–2235.
53. W. Kossack, K. Adrjanowicz, M. Tarnacka, W. K. Kipnusu, M. Dulski, E. U. Mapesa, K. Kaminski, S. Pawlus, M. Paluch and F. Kremer, Phys. Chem. Chem. Phys., 2013, 15, 20641–20650.
54. R. Lefort, P. Bordat, A. Cesaro and M. Descamps, J. Chem. Phys., 2007, 126, 014511.
55. K. L. Ngai, S. Pawlus, K. Grzybowska, K. Kaminski, S. Capaccioli and M. Paluch, Macromolecules, 2015, 48, 4151–4157.
56. H. Hoshina, H. Suzuki, C. Otani, M. Nagai, K. Kawase, A. Irizawa and G. Isoyama, Sci. Rep., 2016, 6, 27180.
57. M. Yoshioka, B. C. Hancock and G. Zografi, J. Pharm. Sci., 1994, 83, 1700–1705.
58. W. Liu, L. Dang, S. Black and H. Wei, J. Chem. Eng. Data, 2008, 53, 2204–2206.
59. J. Sibik, K. Löbmann, T. Rades and J. A. Zeitler, Mol. Pharmaceutics, 2015, 12, 3062–3068.
60. R. Calemczuk and E. Bonjour, J. Non-Cryst. Solids, 1981, 43, 427–432.
61. P. Karmwar, K. Graeser, K. C. Gordon, C. J. Strachan and T. Rades, Int. J. Pharm., 2011, 417, 94–100.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06664c

‡ Present address: F. Hoffmann-La Roche AG, Konzern-Hauptsitz, Basel, Switzerland.

§ Present address: ASM Laser Separation International, Beuningen, The Netherlands.

¶ Present address: ASML, Veldhoven, The Netherlands.

---