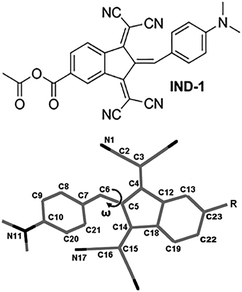
Unusual response to environmental polarity in a nonlinear-optical benzylidene-type chromophore containing a 1,3-bis(dicyanomethylidene)indane acceptor fragment†
Kaspars
Traskovskis
 *a,
Arturs
Bundulis
b and
Igors
Mihailovs
ab
*a,
Arturs
Bundulis
b and
Igors
Mihailovs
ab
aRiga Technical University, Faculty of Materials Science and Applied Chemistry, 3/7 Paula Valdena Street, Riga LV-1048, Latvia. E-mail: kaspars.traskovskis@rtu.lv; Tel: +371 29148070
bInstitute of Solid State Physics, University of Latvia, 8 Kengaraga Street, Riga LV-1063, Latvia
First published on 29th November 2017
Abstract
One of the strongest known electron-accepting fragments used in the synthesis of organic dyes for applications in nonlinear optics (NLO) is 1,3-bis(dicyanomethylidene)indane (BDMI). By studying a benzylidene-type push–pull chromophore bearing a 5-carboxy-BDMI electron-acceptor and 4-(dimethylamino)aniline donor fragment, we demonstrate that this class of compounds can show unusual response to the polarity of the surrounding medium. The combined results of UV-Vis absorption spectrometry, NMR experiments and computational modeling indicate that the studied compound undergoes a geometrical transformation that involves an increase in the torsion angle ω between the aniline and indane ring systems with the rise of the polarity of the surrounding medium. This process is partly facilitated by an increased rotational freedom around ω in more polar solvents, as detected experimentally by NMR and predicted by calculations. Regarding the practical application aspects, computations predict that the solvent-polarity-induced increase of torsion ω would lead to a notable decrease in the first hyperpolarizability (β) value. This was detected experimentally, as hyper-Rayleigh scattering (HRS) data showed a drop in the compound's NLO activity from βHRS(532)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = 513 × 10−30 esu in toluene to βHRS(532)
= 513 × 10−30 esu in toluene to βHRS(532)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 249 × 10−30 esu in acetonitrile. This places limitations on the NLO applications of the studied compound and its structural analogues, as the surrounding medium (solvent of polymer matrix) with the lowest possible polarity needs to be used to maximize their NLO efficiency.
249 × 10−30 esu in acetonitrile. This places limitations on the NLO applications of the studied compound and its structural analogues, as the surrounding medium (solvent of polymer matrix) with the lowest possible polarity needs to be used to maximize their NLO efficiency.
Introduction
Nonlinear optics is one of the most extensively researched fields of photonics that involves practical use of organic materials.1–4 Due to the unique physical properties of their delocalized π-electron systems, organic substances can reach nonlinear optical (NLO) response levels that surpass those of the currently used inorganic materials by more than one order of magnitude. Generally, NLO activity of a molecule is characterized by its first hyperpolarizability (β). The vast majority of the large-β-value compounds are highly dipolar chromophores of type “electron donor–π-electron bridge–electron acceptor.” Numerous theoretical and practical studies have provided a fairly good understanding of the structural requirements for highly efficient NLO materials. The increase in β can be correlated with the strength of the electron-donating and -accepting fragments of the chromophore5,6 as well as with the length and electron-transferring ability of the π-electron bridge systems.7,8According to the two-state model,9,10 the electronic ground state of a conjugated π-electron system can be expressed as a combination of two limiting classical (Lewis) structures (or basis states): the neutral (push–pull) one and the charge-separated (zwitterionic) one, thus describing an actual partially ionic electronic structure (an intermediate of both). Depending on the prevalence of one or the other state, the nonlinear optical characteristics of the dipolar π-electron systems can change drastically, and maximal β is usually attained when the molecule assumes a configuration that lies between push–pull and cyanine-like (i.e., centrosymmetrical) structure.11 The charge distribution, bond configuration and consequentially NLO characteristics of chromophores can be significantly altered by the polarity of the surrounding medium (e.g. solvent, polymer matrix).12–14 For example, two-fold increase in β for some push–pull chromophores has been reported by increasing the solvent polarity.15 This means that a complete understanding of the molecule's interaction with the medium is needed to evaluate the results of experimental NLO measurements reliably and to maximize the performance of the developed materials.
One of the strongest known electron-accepting fragments used in high-performance NLO-active chromophores is 1,3-bis(dicyanomethylidene)indane (BDMI).16–21 The low cost and high chemical and thermal stability of the corresponding compounds makes BDMI a promising structural building block. In our previous study we presented an improved chemical design of BDMI by attaching a carboxyl group to its 5 position (5A-BDMI) with the intention to introduce a chemically linkable fragment for subsequent attachment of solubility-enhancing or site-isolating functional fragments.22 As it was found, reactions of 5A-BDMI with different 4-aminobenzaldehydes yielded only E-configuration benzylidenes, providing an additional tool of structural control over the geometry of the NLO active molecules. In this study we take a closer look at the solvent-polarity dependence of the molecular geometry, and linear and nonlinear optical properties in 5A-BDMI-based benzylidene IND-1 (Fig. 1). By analyzing UV-Vis, NMR, and hyper-Rayleigh scattering (HRS) data as well as carrying out quantum chemical modeling to explain the experimental observations, we demonstrate that BDMI-based chromophores can show unusual responses to the surrounding medium that need to be taken into account to maximize their molecular and macroscopic NLO efficiency.
Results and discussion
Absorption spectra
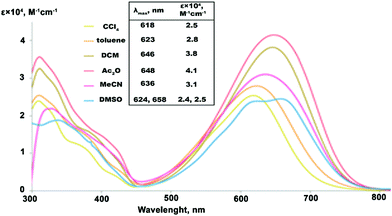
The solvatochromic response of the studied compounds was measured in 6 solvents of varied polarity (Fig. 2). In the series of low to medium polarity solvents, CCl4 (dielectric constant εr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.2), toluene (εr
2.2), toluene (εr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.4), DCM (εr
2.4), DCM (εr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.9) and Ac2O (εr
8.9) and Ac2O (εr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.0), the lowest-energy absorption band of IND-1 shows a steady batochromic shift of 30 nm. Such behavior is common for neutral ground state push–pull type compounds, where electronic excitation can be associated with an increase in molecular dipole moment. At the same time the molar absorption coefficient (ε) of the bands substantially grows in response to medium polarity, reaching its maximum in Ac2O with a 60% increase in comparison with the value measured in CCl4. In strongly polar solvents starting with MeCN (εr
20.0), the lowest-energy absorption band of IND-1 shows a steady batochromic shift of 30 nm. Such behavior is common for neutral ground state push–pull type compounds, where electronic excitation can be associated with an increase in molecular dipole moment. At the same time the molar absorption coefficient (ε) of the bands substantially grows in response to medium polarity, reaching its maximum in Ac2O with a 60% increase in comparison with the value measured in CCl4. In strongly polar solvents starting with MeCN (εr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5), however, the solvatochromic response changes drastically. The absorption intensity starts to fall, with ε values in DMSO (εr
37.5), however, the solvatochromic response changes drastically. The absorption intensity starts to fall, with ε values in DMSO (εr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46.7) dropping to the level initially observed in CCl4. At the same time a reversed hypsochromic behavior of the bands can be detected, as an absorption maxima exhibits a blue shift by 12 nm in MeCN if compared to the spectra measured in less polar Ac2O – a behavior that can be attributed to a zwitterionic structure. Additionally, the spectrum of IND-1 in DMSO starts to exhibit a multi-peak vibrational fine structure. Similarly shaped fine structures can be found in the spectra of 5A-BDMI anions,22 thus indicating a large contribution of the charge-separated (zwitterionic) resonance form. The observed highly non-linear solvatochromic response indicates that notable structural transformations take place in IND-1 depending on the polarity of the surrounding medium.
46.7) dropping to the level initially observed in CCl4. At the same time a reversed hypsochromic behavior of the bands can be detected, as an absorption maxima exhibits a blue shift by 12 nm in MeCN if compared to the spectra measured in less polar Ac2O – a behavior that can be attributed to a zwitterionic structure. Additionally, the spectrum of IND-1 in DMSO starts to exhibit a multi-peak vibrational fine structure. Similarly shaped fine structures can be found in the spectra of 5A-BDMI anions,22 thus indicating a large contribution of the charge-separated (zwitterionic) resonance form. The observed highly non-linear solvatochromic response indicates that notable structural transformations take place in IND-1 depending on the polarity of the surrounding medium.
NMR spectra
In order to evaluate the influence of solvent polarity on the structure of IND-1, a series of NMR experiments were performed (Fig. 3). 1H-NMR spectra in different polarity solvents were initially obtained. In C6D6 an additional set of signals can be observed that cannot be found in the spectra taken in other solvents. Based on 1H-NMR data of structurally comparable benzylidene-1,3-indanediones, the newly found signals can be attributed to the Z-isomer of IND-1.22 The X-ray analysis of the crystalline material used in these experiments unambiguously shows the presence of only the E-isomer,22 and thus it is evident that isomerization of IND-1 with rotation around the C5–C6 bond takes place in C6D6 solution. The detected ratio of E/Z isomers is 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In comparison, no observation of similar signal splitting pattern was made in other, more polar solvents. Slight peak splitting was detected in CD3CN, but in this case it is caused by the partial hydrolysis of the reactive anhydride group in the presence of trace water. The lack of observable isomerization in more polar solvents does not rule out the fact that the process is happening. If the energy barrier of the rotation around C5–C6 bond is low enough, such structural transformation would fall outside of the NMR time scale, and the spectrum would represent the average conformation of E/Z isomers. Such indications of the increased conformational freedom of IND-1 can indeed be found with the increase in solvent polarity. Specifically, a substantial broadening of the isolated proton signal H8/H21 can be observed in the 1H-NMR spectra in the solvent sequence CDCl3 → (CD3)2SO. Due to the sterical overcrowding caused by a bulky BDMI structural fragment, IND-1 assumes a non-planar, asymmetrically out-of-plane deformed geometry.22 Protons H8/H21 reside in the most sterically hindered region of the molecule and are highly susceptible to shielding effects of the BDMI fragment. In the case of increased conformational freedom it is expected that this proton signal would broaden due to the increased amount of viable conformations. The broadening of the corresponding C8/C21 signal is even more pronounced in the 13C-NMR spectra (Fig. 3b).
1. In comparison, no observation of similar signal splitting pattern was made in other, more polar solvents. Slight peak splitting was detected in CD3CN, but in this case it is caused by the partial hydrolysis of the reactive anhydride group in the presence of trace water. The lack of observable isomerization in more polar solvents does not rule out the fact that the process is happening. If the energy barrier of the rotation around C5–C6 bond is low enough, such structural transformation would fall outside of the NMR time scale, and the spectrum would represent the average conformation of E/Z isomers. Such indications of the increased conformational freedom of IND-1 can indeed be found with the increase in solvent polarity. Specifically, a substantial broadening of the isolated proton signal H8/H21 can be observed in the 1H-NMR spectra in the solvent sequence CDCl3 → (CD3)2SO. Due to the sterical overcrowding caused by a bulky BDMI structural fragment, IND-1 assumes a non-planar, asymmetrically out-of-plane deformed geometry.22 Protons H8/H21 reside in the most sterically hindered region of the molecule and are highly susceptible to shielding effects of the BDMI fragment. In the case of increased conformational freedom it is expected that this proton signal would broaden due to the increased amount of viable conformations. The broadening of the corresponding C8/C21 signal is even more pronounced in the 13C-NMR spectra (Fig. 3b).
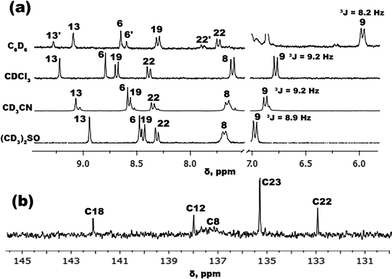 | ||
| Fig. 3 (a) IND-11H-NMR spectra of representative aromatic signals in solvents of different polarity; (b) IND-113C-NMR spectral region showing broadening of the C8 signal in CDCl3. | ||
Solvent-dependent variations in composition of the electronic ground state in IND-1 can be examined by measuring the vicinal coupling constant 3JH9–H8 at the proton signal H9. During the push–pull-type charge transfer, the electron-donating aniline fragment of a chromophore molecule undergoes a transformation of its double bond configuration from mostly aromatic to mostly quinoidal. It is expected that with more pronounced quinoidal nature the constant 3JH9–H8 would increase, as the C–C bond between the corresponding carbon atoms shortens in this process.23 Looking at the obtained 3JH9–H8 values (Fig. 3a), the push–pull charge transfer level of IND-1 is not linearly dependent on solvent polarity. A predictable increase of aniline ring quinoidality is observed in the solvent sequence C6D6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CDCl3, indicated by a coupling constant change from 8.2 to 9.2 Hz. However, with the further medium polarity increase in CD3CN and (CD3)2SO, the 3JH9–H8 value does not increase and even starts to drop, from 9.2 to 8.9 Hz. This indicates that push–pull electron transfer in strongly polar solvents becomes obstructed, most likely by an increased torsion angle ω (C14–C5–C6–C7).
CDCl3, indicated by a coupling constant change from 8.2 to 9.2 Hz. However, with the further medium polarity increase in CD3CN and (CD3)2SO, the 3JH9–H8 value does not increase and even starts to drop, from 9.2 to 8.9 Hz. This indicates that push–pull electron transfer in strongly polar solvents becomes obstructed, most likely by an increased torsion angle ω (C14–C5–C6–C7).
Quantum chemical calculations
In order to explain the previously discussed experimental data, a series of quantum chemical simulations were performed. The geometry, charge separation level and electronic transitions of IND-1 in different polarity media were initially calculated (Table 1). The experimental data suggest that with a rising solvent polarity the conformational freedom of IND-1 increases, and the electronic configuration of the compound assumes a state with a more pronounced zwitterionic nature. In terms of molecular geometry these transformations would result in a structure where the torsion angle ω between the planes of the indane system and aniline ring would be approaching the 90° mark, away from the initial partly-planar state. On the other hand, based on the structures of the known zwitterionic-ground-state BDMI-based chromophores,24 such a process would lead to the planarization of the indane ring system due to the release of sterical strain between the electron-donor and -acceptor fragments of the molecule. Thus, to fully characterize the degree of geometrical deformations of IND-1, in calculations we used two parameters: torsion ω(C14–C5–C6–C7) and a complex parameter ISDI that accounts for the degree of geometrical deformations in the indane ring system by summing up four possible geometrical deviations from a fully planar structure (see Table 1). The obtained results of the calculations reveal a very weak solvatochromic behavior of IND-1, e.g., the change in dihedral ω is less than 1.5°, which amounts to just 12% of its average value, generally slowly rising from vacuum to DMSO, with an outlier of chloroform. In order to screen the possibilities of application of other methodological approaches we checked the solvatochromic behavior by running calculations with eight other density functionals (described in the Experimental section), but did not notice any major differences (see Fig. S3 in the ESI†), including for meta functionals such as M06-2X. The corresponding vibrational mode energy (though strongly coupled to the anhydride group) showed a similar (lack of) trend. This seems to indicate that none of the tested functionals considered the dihedral in question relevant for adaptation to a medium of particular polarity (both for van der Waals and SAS cavities). It was therefore decided to use CAM-B3LYP for most of the subsequent calculations, because this functional has arguably one of the best asymptotic behaviors in geometry parameters and is assessed as the best at the description of spectral transitions of IND-1 (see the Experimental section).| Medium | ω [°] | ISDIb [°] | BLA(1)c | MK charge on indaned | APT charge on indaned | λ S1 [nm] | f S1 | λ S2 [nm] | f S2 | β HRS(0),g 10−30 esu | β HRS(532),h 10−30 esu |
|---|---|---|---|---|---|---|---|---|---|---|---|
a Torsion angle C14–C5–C6–C7.
b ISDI (indane-system deformation index) parameter is calculated as the sum of indane ring deformations (higher value corresponds to a more deformed structure). ISDI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (360 – bond-to-bond angle sum at atom C5) + |torsion angle C13–C12–C4–C3| + |torsion angle C19–C18–C14–C15| + |torsion angle C18–C14–C5–C4|.
c BLA parameter calculated following path C3–C4–C5–C6–C7–C8–C9–C10. It perfectly correlates with BLA of C5–C6–C7.
d Including the anhydride part; the rest of the molecule was considered the aniline region (with complimentary positive total charge).
e Wavelength of the corresponding transition.
f Oscillator strength of the corresponding transition.
g Calculated molecular static first hyperpolarizability, averaged over components as to be comparable with HRS experimental data.31
h Experimentally determined values; these are resonance-enhanced due to proximity of the second-harmonic scattering wavelength to those of optical transitions. Zero frequency extrapolation was avoided to prevent an underestimation of the parameter. (360 – bond-to-bond angle sum at atom C5) + |torsion angle C13–C12–C4–C3| + |torsion angle C19–C18–C14–C15| + |torsion angle C18–C14–C5–C4|.
c BLA parameter calculated following path C3–C4–C5–C6–C7–C8–C9–C10. It perfectly correlates with BLA of C5–C6–C7.
d Including the anhydride part; the rest of the molecule was considered the aniline region (with complimentary positive total charge).
e Wavelength of the corresponding transition.
f Oscillator strength of the corresponding transition.
g Calculated molecular static first hyperpolarizability, averaged over components as to be comparable with HRS experimental data.31
h Experimentally determined values; these are resonance-enhanced due to proximity of the second-harmonic scattering wavelength to those of optical transitions. Zero frequency extrapolation was avoided to prevent an underestimation of the parameter.
|
|||||||||||
| Vacuum | 10.69 | 55.41 | 0.041 | −0.598 | −0.873 | 465 | 0.40 | 416 | 0.37 | 48 | — |
| Toluene | 10.66 | 50.08 | 0.038 | −0.680 | −0.945 | 487 | 0.32 | 435 | 0.39 | 59 | 513 ± 52 |
| CHCl3 | 11.75 | 50.39 | 0.037 | −0.676 | −0.982 | 489 | 0.32 | 438 | 0.40 | 66 | 497 ± 40 |
| DCM | 11.11 | 52.84 | 0.036 | −0.675 | −1.025 | 488 | 0.33 | 439 | 0.42 | 72 | — |
| MeCN | 11.35 | 52.70 | 0.035 | −0.668 | −1.053 | 491 | 0.32 | 441 | 0.43 | 76 | 249 ± 23 |
| DMSO | 12.03 | 49.48 | 0.035 | −0.707 | −1.025 | 493 | 0.33 | 442 | 0.46 | 73 | — |
In agreement with the predictions based on analogous structures, the indane ring system generally becomes less deformed during the change of ω, as is shown by ISDI (most planar in DMSO, least planar in vacuum; toluene point is an outlier). The calculated bond-length alternation (BLA) parameter values show a steady exponential drop with increasing solvent polarity (dependent not on either ω or ISDI but rather on some intricate combination of them). However, in DMSO the value of BLA is still relatively large and positive, indicating a strong neutral ground-state character.25 The charge separation level in IND-1 increases with solvent polarity (except for DMSO, where it drops; probably the reason is that the increase in indane planarity outweighs the increase in the value of ω). Note that the reverse but very weak behavior is observed in the case of Merz–Singh–Kollman26,27 (electrostatic-potential-derived) charges, even if using a 64× denser grid than the Gaussian 09 default to ensure trend consistency.
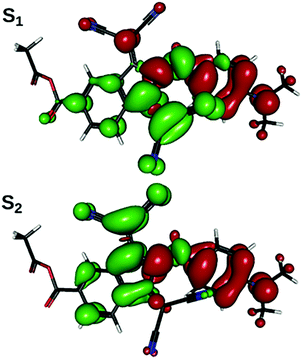
The computational analysis of the electronic transitions reveals that the lowest-energy absorption band of the studied chromophores consists of two transitions, S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 and S2
S0 and S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0, in which electron density shifts from the aniline ring to the region of indane, centered around one or the other of the two dicyanomethylene groups (Fig. 4). As is expected from the results of structural optimizations, the slow change in molecular geometry with the increase in solvent polarity determines a slow change in spectral properties (Table 1). Correlation can be drawn between the transition energy and some combination of ω and BLA: in general, weakly bathochromic solvatochromism is predicted for IND-1. No notable band shape and intensity transformations are present, as indicated by oscillator strength values; the intra-band weight, however, shifts gradually from S1
S0, in which electron density shifts from the aniline ring to the region of indane, centered around one or the other of the two dicyanomethylene groups (Fig. 4). As is expected from the results of structural optimizations, the slow change in molecular geometry with the increase in solvent polarity determines a slow change in spectral properties (Table 1). Correlation can be drawn between the transition energy and some combination of ω and BLA: in general, weakly bathochromic solvatochromism is predicted for IND-1. No notable band shape and intensity transformations are present, as indicated by oscillator strength values; the intra-band weight, however, shifts gradually from S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 to S2
S0 to S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 transition, producing some faint negative solvatochromism, as is also observed in experiments. It is interesting to note that the transition energies computed are off from the experimental band maximum even by as much as 0.6 eV. This is rather unusual, as range-separated DFT usually yields better transition wavelengths than the global hybrids (which provide better results in the absolute values in our case) specifically by making these wavelengths shorter.28,29 On the other hand, in particular cases like cyanines29 and condensed heteroaromatics29,30 modern TD-DFT implementations still happen to produce errors of the scale mentioned.
S0 transition, producing some faint negative solvatochromism, as is also observed in experiments. It is interesting to note that the transition energies computed are off from the experimental band maximum even by as much as 0.6 eV. This is rather unusual, as range-separated DFT usually yields better transition wavelengths than the global hybrids (which provide better results in the absolute values in our case) specifically by making these wavelengths shorter.28,29 On the other hand, in particular cases like cyanines29 and condensed heteroaromatics29,30 modern TD-DFT implementations still happen to produce errors of the scale mentioned.
It is obvious therefore that the previously discussed results of quantum chemical modeling do not give a consistent explanation to the observed NMR data, and linear and especially (as discussed latter) nonlinear optical properties. It must be taken into consideration that those calculated values represent a static structure in its optimized, lowest-energy state, so any possible effects of structural dynamics are being ignored; as are specific solvent effects due to the use of PCM. Hence, in an actual medium the molecule can have rather different value of average ω, being in addition surrounded by available internal-rotational (vibrational) states. As this torsion is probably the most significant coordinate of thermal motion, we a performed potential energy surface (PES) scan for IND-1 by setting the torsion ω to various values and optimizing the rest of the molecule in the corresponding medium (Table 2; see Table S1 in ESI† for additional ω values). Although it is usually advised to use meta functionals for barrier studies,32–34 and we also found that M06-2X Gibbs energy barriers are more consistent than those computed with CAM-B3LYP, we have faced considerable convergence problems with the meta functionals (see the Experimental section), and decided to use CAM-B3LYP for scan-relevant computations, as range-separated hybrid functionals also do perform fairly well for barriers.32,33,35 Conformations explored range from the almost planar E-isomer to the fully twisted (ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90°) structure to the Z-isomer. As is predicted, with increased torsion ω the value of the ISDI parameter steeply falls, and at 90° the indane ring assumes the most planar configuration. The calculated BLA parameter values in the ω
90°) structure to the Z-isomer. As is predicted, with increased torsion ω the value of the ISDI parameter steeply falls, and at 90° the indane ring assumes the most planar configuration. The calculated BLA parameter values in the ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11–40° range are typical for those of the neutral ground state structures.25 Starting from ca. 55°, these become negative, indicating the dominance of the zwitterionic resonance form. The increased charge separation is also reflected by both charge types, which increase in absolute value in the range of negative BLA. Before that, MK charges are just oscillating, whereas the APT ones are decreasing (probably attributable to different vibration modes of classical and zwitterionic forms).
11–40° range are typical for those of the neutral ground state structures.25 Starting from ca. 55°, these become negative, indicating the dominance of the zwitterionic resonance form. The increased charge separation is also reflected by both charge types, which increase in absolute value in the range of negative BLA. Before that, MK charges are just oscillating, whereas the APT ones are decreasing (probably attributable to different vibration modes of classical and zwitterionic forms).
| ω [°] | ISDI [°] | BLA(1) | APT charge on indane | MK charge on indane | ΔEa [kcal mol−1] | ΔEb [kcal mol−1] | λ S1 [nm] | f S1 | λ S2 [nm] | f S2 | β HRS(0), 10−30 esu |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a Relative energy of conformation from the bottom of the E isomer well. b The same parameter but calculated for the corresponding conformations in benzene. c E isomer. d Z isomer. | |||||||||||
| 11.3c | 52.70 | 0.035 | –1.05 | –0.67 | 0.00 | 0.00 | 507 | 0.32 | 458 | 0.43 | 76.2 |
| 30.1 | 41.35 | 0.023 | −1.15 | −0.76 | 0.98 | 1.08 | 508 | 0.46 | 466 | 0.33 | 69.6 |
| 50.1 | 26.75 | 0.005 | −1.22 | −0.80 | 3.84 | 4.16 | 526 | 0.53 | 474 | 0.20 | 51.6 |
| 70.0 | 23.41 | −0.014 | −1.25 | −1.05 | 8.24 | 8.94 | 573 | 0.42 | 478 | 0.20 | 29.9 |
| 90.1 | 7.27 | −0.056 | −1.04 | −1.34 | 14.44 | 16.03 | 848 | 0.02 | 493 | 0.26 | 25.8 |
| 110.4 | 9.00 | −0.014 | −1.29 | −0.85 | 8.84 | 9.60 | 588 | 0.35 | 486 | 0.20 | 25.1 |
| 130.1 | 23.07 | 0.011 | −1.22 | −0.64 | 3.77 | 3.97 | 517 | 0.51 | 484 | 0.19 | 51.6 |
| 150.2 | 47.65 | 0.030 | −1.09 | −0.71 | 0.65 | 0.66 | 479 | 0.29 | 494 | 0.43 | 69.3 |
| 157.7d | 53.69 | 0.034 | −1.05 | −0.66 | 0.41 | 0.32 | 478 | 0.29 | 492 | 0.42 | 73.2 |
Regarding the calculated electronic transitions S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 and S2
S0 and S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
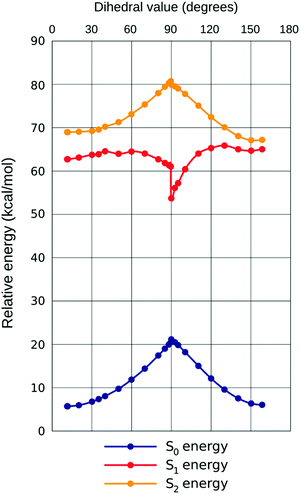
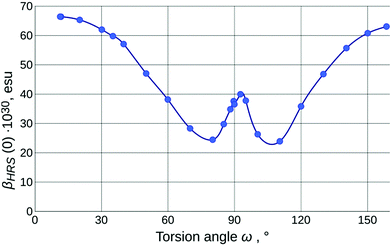
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0, a notable nonlinearity can be observed in the response to increasing ω. This is best rationalized by plotting all three PES together (example for chloroform given in Fig. 5, demonstrating the close qualitative resemblance of situations in all three solvents). Initially (until approximately ω
S0, a notable nonlinearity can be observed in the response to increasing ω. This is best rationalized by plotting all three PES together (example for chloroform given in Fig. 5, demonstrating the close qualitative resemblance of situations in all three solvents). Initially (until approximately ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40° in all solvents considered) all three states are developing in the same direction, with most quickly rising for S0 (hence the small bathochromic shift for both transitions, somewhat larger for S2
40° in all solvents considered) all three states are developing in the same direction, with most quickly rising for S0 (hence the small bathochromic shift for both transitions, somewhat larger for S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0). Then, however, states S1
S0). Then, however, states S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and
and![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 start approaching one another, resulting in plummeting energy of the first transition (shift ca. 5× that for S2
S0 start approaching one another, resulting in plummeting energy of the first transition (shift ca. 5× that for S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0, in energy dimension). The oscillator strength (f) of the first transition is climbing, but that of the second one is descending until ω
S0, in energy dimension). The oscillator strength (f) of the first transition is climbing, but that of the second one is descending until ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40°, with the sum of both remaining nearly constant; this can be rationalized through planarization of the indane 5-membered ring, increasing quantum interference effects on the efficiency of both transitions. Both transitions are inherently asymmetric due to non-equality of both dicyanomethylene groups (one is in-plane with the rest of the molecule, another one is not), but this cannot explain the increase in asymmetry when this sterically induced bias is removed by increasing ω. The difference in quantum interference patterns, the true cause of the increasing asymmetry, is caused by an electron-accepting carboxylic group in 5A-BDMI, which by cross-conjugation stabilizes the charge transfer involving the C4-centered dicyanomethylene group. Beginning with ω = 40°, fS2 stabilizes while fS1 drops down to almost zero at ω = 90°. In this region, as revealed by NTO plots, S2
40°, with the sum of both remaining nearly constant; this can be rationalized through planarization of the indane 5-membered ring, increasing quantum interference effects on the efficiency of both transitions. Both transitions are inherently asymmetric due to non-equality of both dicyanomethylene groups (one is in-plane with the rest of the molecule, another one is not), but this cannot explain the increase in asymmetry when this sterically induced bias is removed by increasing ω. The difference in quantum interference patterns, the true cause of the increasing asymmetry, is caused by an electron-accepting carboxylic group in 5A-BDMI, which by cross-conjugation stabilizes the charge transfer involving the C4-centered dicyanomethylene group. Beginning with ω = 40°, fS2 stabilizes while fS1 drops down to almost zero at ω = 90°. In this region, as revealed by NTO plots, S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 starts to localize on the indane part of the molecule, while its counterpart withdraws to aniline; yet both transitions spread over both structural regions until the very adjacency of the turning point at ω = 90°. This is caused by the loss of the conjugation between the aniline and indane π-electronic subsystems. In this region, transition S1
S0 starts to localize on the indane part of the molecule, while its counterpart withdraws to aniline; yet both transitions spread over both structural regions until the very adjacency of the turning point at ω = 90°. This is caused by the loss of the conjugation between the aniline and indane π-electronic subsystems. In this region, transition S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 displays a characteristic saw-tooth, which means that the real rotation path in the first excited state is more complicated than just the change of a single dihedral;36 this is obviously linked to the considerable non-planarity of the 5-membered ring of indane. As the second transition is much less affected by the change of the dihedral, it also shows almost no sign of such ‘saw-tooth’, following the pattern in the ground state. Seeing no ‘saw-tooth’ for the ground state, we reckon that the change in ω represents the real internal rotation path sufficiently well. In the region of the Z-isomer, it is observed that λ and f oscillate for both transitions, as the S1 and S2 states approach each other and mix together. We have also performed a less detailed scan with the same CAM-B3LYP on TPSSh-optimized geometries, because this functional provided the largest range of dihedral values during the full optimization study in various solvents. However, no notable differences in trends of electronic states were observed (see Fig. S5 in the ESI†).
S0 displays a characteristic saw-tooth, which means that the real rotation path in the first excited state is more complicated than just the change of a single dihedral;36 this is obviously linked to the considerable non-planarity of the 5-membered ring of indane. As the second transition is much less affected by the change of the dihedral, it also shows almost no sign of such ‘saw-tooth’, following the pattern in the ground state. Seeing no ‘saw-tooth’ for the ground state, we reckon that the change in ω represents the real internal rotation path sufficiently well. In the region of the Z-isomer, it is observed that λ and f oscillate for both transitions, as the S1 and S2 states approach each other and mix together. We have also performed a less detailed scan with the same CAM-B3LYP on TPSSh-optimized geometries, because this functional provided the largest range of dihedral values during the full optimization study in various solvents. However, no notable differences in trends of electronic states were observed (see Fig. S5 in the ESI†).
The resulting behavior of the composite band is an initially small bathochromic shift with hyperchromism, as the energetic gap between both bands narrows until ω = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40° while the combined f value also slightly increases (from 0.75 to 0.81). After the 40° mark, the bands begin to separate, with the total intensity dropping noticeably. The same parabolic behavior of the absorption intensity can be observed in the solvatochromism experimental data, where similar changes in ε values of IND-1 were detected depending on solvent polarity. In fact, the evolution of bands can also explain the perceived negative solvatochromism in the most polar solvents: as the medium polarity grows, the higher-energy transition gains a little in intensity, while the lower-energy one loses it considerably. In addition, both transitions show only a marginal red shift in this range of polarity. As a result, the maximum of the band formed by both transitions should shift to higher energies – which is actually observed experimentally. This suggests that in the response to growing polarity of the surrounding medium the dominating conformational population of the molecules assumes gradually larger values of torsion angle ω.
40° while the combined f value also slightly increases (from 0.75 to 0.81). After the 40° mark, the bands begin to separate, with the total intensity dropping noticeably. The same parabolic behavior of the absorption intensity can be observed in the solvatochromism experimental data, where similar changes in ε values of IND-1 were detected depending on solvent polarity. In fact, the evolution of bands can also explain the perceived negative solvatochromism in the most polar solvents: as the medium polarity grows, the higher-energy transition gains a little in intensity, while the lower-energy one loses it considerably. In addition, both transitions show only a marginal red shift in this range of polarity. As a result, the maximum of the band formed by both transitions should shift to higher energies – which is actually observed experimentally. This suggests that in the response to growing polarity of the surrounding medium the dominating conformational population of the molecules assumes gradually larger values of torsion angle ω.
It should be mentioned that absolute transition energy values that are similar to those observed in the experiments appear only at the very proximity to the saddle point. In the absence of some multi-molecular processes unaccounted for it seems highly improbable for IND-1 to remain steadily in such a geometry; possibly part of this discrepancy is explained by the aforementioned inaptitude of range-separated density functionals.
Another argument that speaks in favor of this hypothesis is provided by comparison of E/Z-isomerization barriers in solvents of different polarity. Table 2 presents electronic energies of different conformations, while in Table 3 the barriers calculated from the more reliable Gibbs free energies are given. A notable deviation in ΔE between the two solvents can be observed starting from ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30°, where the computed structure in benzene is of slightly higher relative energetic cost; this comes to a significant difference at ω = 90°. According to the Eyring–Polanyi transition state theory, under room temperature conditions this would lead to an E/Z-isomerization rate constant difference of several orders (103 s−1 in MeCN vs. 10−1 s−1 in benzene). Such a difference in the time scale of the process is in accordance with NMR data, where both isomers were detected in C6D6, in contrast to more polar solvents. As a consequence, it can be assumed that it is less likely for IND-1 to assume conformations with higher ω in low-polarity solvents.
30°, where the computed structure in benzene is of slightly higher relative energetic cost; this comes to a significant difference at ω = 90°. According to the Eyring–Polanyi transition state theory, under room temperature conditions this would lead to an E/Z-isomerization rate constant difference of several orders (103 s−1 in MeCN vs. 10−1 s−1 in benzene). Such a difference in the time scale of the process is in accordance with NMR data, where both isomers were detected in C6D6, in contrast to more polar solvents. As a consequence, it can be assumed that it is less likely for IND-1 to assume conformations with higher ω in low-polarity solvents.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (SAS, nelst)) for the rotation of IND-1 around the C5–C6 double bond, corresponding to the torsion angle ω
(SAS, nelst)) for the rotation of IND-1 around the C5–C6 double bond, corresponding to the torsion angle ω
| Medium | CAM-B3LYP/6-311G(d,p) | M06-2X/6-311G(d,p) | ||||||
|---|---|---|---|---|---|---|---|---|
ΔG‡anti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a [kcal mol−1] a [kcal mol−1] |
ΔG‡syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b [kcal mol−1] b [kcal mol−1] |
k anti [s−1] | k syn [s−1] | ΔG‡anti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a [kcal mol−1] a [kcal mol−1] |
ΔG‡syn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b [kcal mol−1] b [kcal mol−1] |
k anti [s−1] | k syn [s−1] | |
| a Gibbs activation free energy and the corresponding force constant from the side of the E isomer. b Same from the side of the Z isomer. c Unfortunately, we could not converge the minimum geometry of the syn isomer. | ||||||||
| Benzene | 18.00 | 15.86 | 0.2 | 7 | 16.85 | —c | 1 | —c |
| Toluene | 15.70 | 12.64 | 9 | 1669 | 16.39 | 13.79 | 3 | 240 |
| CHCl3 | 15.09 | 16.24 | 26 | 4 | 15.47 | 14.02 | 14 | 163 |
| MeCN | 13.02 | 13.71 | 874 | 273 | 14.09 | 12.18 | 143 | 3627 |
The Gibbs energy (hence the population) of the Z-isomer in benzene (toluene) has significantly higher values (ΔG) in comparison with their E-counterparts, and at the lowest energy configuration the difference is slightly above 2 (3) kcal mol−1. This is in an agreement with the X-ray structural analysis of IND-1 that shows the presence of only the E-isomer. While a slight population of Z-isomer is expected to be present in solutions of the compound, the slow process of crystallization apparently causes a selective precipitation of the compound in its more stable form. Again, the difference between both isomers is rationalized by the quantum interference, for in the case of the E-isomer the carboxylic-group-promoted conjugation path runs along the more coplanar of the two regions around the dicyanomethylene groups, the one centered around C4.
Nonlinear optical properties
The values of the calculated static first-order hyperpolarizability (βHRS(0); further just βHRS) of IND-1 in solvents of different polarity are given in Table 1. The maximal NLO efficiency is predicted in ACN, with a 4% drop in DCM and 16% drop in toluene. Such behavior is typical for neutral ground-state push–pull systems and can be explained by the stabilization of the charge separated resonance form in more polar solvents.15 Interestingly, a 6% drop is also predicted in DMSO, probably due to some intricate interplay between geometry changes (reflected also in APT charges and fS1).As is clear from the previous discussion, the results of the calculations for energetically optimized structures are not consistent with experimental observations; the twist around torsion ω needs to be taken into account to model the solvatochromic response of IND-1 accurately. The results of this modeling (Table 2 and Fig. 6) indicate a steady drop of βHRS with increasing ω, as it is expected, due to the loss of conjugation between the aniline and indane fragments. At the 80° mark the orientationally averaged βHRS(0) value is expected to drop by 62% (β0 even more so). The predicted temporary increase in hyperpolarizability in the 80°–90° range is in accordance with the three-level model proposed by Kuzyk et al.37 This model suggests that the first hyperpolarizability becomes larger when the target energy level of the first electronic transition lowers and at the same time increasingly departs from the rest of the excited states. This requirement is met by the behavior of steeply falling S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 and relatively steady S2
S0 and relatively steady S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
← ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 transition.
S0 transition.
The experimental hyperpolarizability values were determined by the HRS technique in toluene (εr = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.4), CHCl3 (εr =
2.4), CHCl3 (εr = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.8) and ACN (εr =
4.8) and ACN (εr = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5) (Table 1). The acquired βHRS(532) values demonstrate a medium-polarity response that is in full agreement with the assumption that in more polar solvents IND-1 populates states with larger value of torsion ω (either by wider conformational freedom or by more pronounced influence of solvent-specific effects). The highest βHRS was measured in toluene, while in CHCl3 it dropped by 4% and in ACN by 52%. Assuming that in toluene the structure is maximally planar, a rough estimate of the actual ω value in the other two solvents can be made using the model outlined in Fig. 6. Multiplying the experimental value of toluene by the coefficient of the computed βHRS ratio for E-isomers in both solvents, then normalizing the βHRS torsion-angle dependence to this value, we can conjecture that the dominating conformational population of IND-1 resides at around the 37° mark in CHCl3 and around the 80° mark in ACN. The last figure seems quite improbable, in particular because there is no associated major change in electronic transitions observed experimentally; we can at least rule out the influence of the Z-isomer, as the ω-dependence of βHRS(0) is rather symmetric around the ω =
37.5) (Table 1). The acquired βHRS(532) values demonstrate a medium-polarity response that is in full agreement with the assumption that in more polar solvents IND-1 populates states with larger value of torsion ω (either by wider conformational freedom or by more pronounced influence of solvent-specific effects). The highest βHRS was measured in toluene, while in CHCl3 it dropped by 4% and in ACN by 52%. Assuming that in toluene the structure is maximally planar, a rough estimate of the actual ω value in the other two solvents can be made using the model outlined in Fig. 6. Multiplying the experimental value of toluene by the coefficient of the computed βHRS ratio for E-isomers in both solvents, then normalizing the βHRS torsion-angle dependence to this value, we can conjecture that the dominating conformational population of IND-1 resides at around the 37° mark in CHCl3 and around the 80° mark in ACN. The last figure seems quite improbable, in particular because there is no associated major change in electronic transitions observed experimentally; we can at least rule out the influence of the Z-isomer, as the ω-dependence of βHRS(0) is rather symmetric around the ω = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90° point. It is probably also not the effect of decomposition due to laser radiation, as absorption spectra taken after measurements did not show any remarkable change. On the other hand, it is known that in “wet” ACN (and in other hydrogen-bond-donating media, as alcohol solutions) the IND-1 absorption peak features major hypochromism with the addition of band splitting, resembling the spectrum of the 5A-BDMI anion (i.e., indicating totally split conjugation, as around the ω = 90° point). Although no such changes were found in absorption spectra of ACN solutions used for HRS, they may occur locally at the focal point of the laser beam. This is one probable reason for the unexpectedly small values of βHRS observed in acetonitrile. Another one is connected with the inability of CAM-B3LYP to predict absolute values of electronic transition energies for IND-1 (vide supra). As hyperpolarizability is intrinsically a property of the same nature, we can expect the lesser performance of this functional also for β values. It would be expected, however, that it underestimates β, as the electronic transition energies are overestimated (see ref. 37). This confirms that some unexplored molecular-level processes take place at the focal point of the laser beam.
90° point. It is probably also not the effect of decomposition due to laser radiation, as absorption spectra taken after measurements did not show any remarkable change. On the other hand, it is known that in “wet” ACN (and in other hydrogen-bond-donating media, as alcohol solutions) the IND-1 absorption peak features major hypochromism with the addition of band splitting, resembling the spectrum of the 5A-BDMI anion (i.e., indicating totally split conjugation, as around the ω = 90° point). Although no such changes were found in absorption spectra of ACN solutions used for HRS, they may occur locally at the focal point of the laser beam. This is one probable reason for the unexpectedly small values of βHRS observed in acetonitrile. Another one is connected with the inability of CAM-B3LYP to predict absolute values of electronic transition energies for IND-1 (vide supra). As hyperpolarizability is intrinsically a property of the same nature, we can expect the lesser performance of this functional also for β values. It would be expected, however, that it underestimates β, as the electronic transition energies are overestimated (see ref. 37). This confirms that some unexplored molecular-level processes take place at the focal point of the laser beam.
Summary and conclusions
The experimental data of UV-Vis absorption, NMR, HRS and computational modeling show that the studied benzylidene chromophore IND-1 undergoes a solvent-polarity-dependent geometrical transformation that involves an increase in the torsion angle between the aniline and indane ring systems with the rise of medium polarity and probably with the occurrence of solvent-specific interactions. As a result, in some strongly polar solvents the NLO properties of the compound are shown to be affected heavily, leading to a decrease in molecular hyperpolarizability (by 52% in ACN in comparison with toluene, but also by 4% in CHCl3 where one could expect an increase due to increase in polarity). This finding puts notable restrictions on experimental procedures and practical application aspects involving IND-1 and its structural analogues. Specifically, it is not advised to use a surrounding medium (solvent or polymer matrix) with high polarity if maximal NLO performance of compounds is desired. It is worth noting that such behavior is opposite to some of the previously investigated coplanar push–pull chromophores that favor more polar surrounding conditions. These findings can also be of relevance for other applications exploiting the HRS effect (such as analytical, biophysical and supramolecular chemistry).38The following assumptions can be made about the conformational changes and solvatochromism of IND-1:
(1) A greater twist of torsion ω between the planes of indane and aniline corresponds to greater contribution of the zwitterionic structure to the ground state. Thus, in polar solvents, which favor a charge-separated state over the mostly-neutral one, the twist must become more pronounced. To some extent the increase in ω can be facilitated by specific solvent interactions and photochemistry in high-intensity optical fields.
(2) The experimentally observed nonlinear behavior of the UV-Vis absorption band of IND-1 is in agreement with computational modeling predictions, which are as follows. Initially, in response to increasing ω different evolution of the two lowest-energy transitions leads to an initial intensification and moderate bathochromic shift of the combined band. In the ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
> ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40° range, with the intensity difference now in favor of the higher-energy transition, this leads to the perceived reversal of solvatochromism and drop of intensity.
40° range, with the intensity difference now in favor of the higher-energy transition, this leads to the perceived reversal of solvatochromism and drop of intensity.
(3) The calculations and NMR data show that the energy of the rotational barrier between the planes of indane and aniline in IND-1 notably decreases with increased polarity of the surrounding medium, thus favoring the probability of the twisted conformations. This provides evidence for the theoretical reasoning outlined in the first point.
Experimental section
Materials and instruments
Synthesis of acetic (E)-1,3-bis(dicyanomethylene)-2-[4-(dimethylamino)benzylidene]-2,3-dihydro-1H-indene-5-carboxylic anhydride (IND-1) is outlined elsewhere.22 The material used in the study was the compound's benzene solvate crystals acquired from an acetic anhydride solution using the vapor diffusion method (using benzene as the volatile fraction). Analytical grade solvents used in the spectral measurements were purchased from Alfa Aesar. DMSO and MeCN were additionally dried over CaH2 before use. The NMR spectra were obtained on a Bruker Avance 300 MHz spectrometer, using solvent residue as an internal reference. The UV-Vis spectra in solutions (typical concentrations – 1 × 10−5–4 × 10−5 mol L−1) were recorded with a Perkin Elmer Lambda 35 spectrometer using 0.5 cm quartz cuvettes.HRS measurements
The studied solutions (C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–5 × 10−5 mol L−1) were contained in 10 × 2 mm photometric quartz cells. The hyper-Rayleigh scattering (HRS) experiments were carried out using a 1064 nm Nd:YAG laser that generated 10 ns laser pulses at 1 kHz repetition frequency. To adjust the laser power, we used a half-wave plate and Glan–Taylor polarizer. The beam was focused upon the sample solution using a lens with focal length f
1–5 × 10−5 mol L−1) were contained in 10 × 2 mm photometric quartz cells. The hyper-Rayleigh scattering (HRS) experiments were carried out using a 1064 nm Nd:YAG laser that generated 10 ns laser pulses at 1 kHz repetition frequency. To adjust the laser power, we used a half-wave plate and Glan–Taylor polarizer. The beam was focused upon the sample solution using a lens with focal length f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mm. Scattered light was collected by two plano-convex lenses in 90° and 270° angle geometry with respect to the incident beam and detected by two photon-counting channels. To reduce external influence on the detected signal, the intensity of HRS-generated double-frequency light was measured in a time window synchronized with the laser pulse. A detected second harmonic (SH) signal can be generated not only by the HRS process, but also by two-photon luminescence (TPL). To separate the influences of both effects on the HRS signal, we place SH 532 nm filters with different full widths at half maximum (FWHM) before the photon counting channels (3 and 10 nm). The FWHM of the TPL signal is usually considerably wider than that of HRS. Therefore, the TPL and HRS contributions in the measured SH intensity depend on the spectral bandwidth of the detection system. In this case we assume that the HRS contribution is the same for both channels while TPL depends on the SH 532 nm filter bandwidth. To calculate βHRS values for the studied samples, we used chloroform as an internal reference (βHRS = 0.49 × 10−30 esu).
3 mm. Scattered light was collected by two plano-convex lenses in 90° and 270° angle geometry with respect to the incident beam and detected by two photon-counting channels. To reduce external influence on the detected signal, the intensity of HRS-generated double-frequency light was measured in a time window synchronized with the laser pulse. A detected second harmonic (SH) signal can be generated not only by the HRS process, but also by two-photon luminescence (TPL). To separate the influences of both effects on the HRS signal, we place SH 532 nm filters with different full widths at half maximum (FWHM) before the photon counting channels (3 and 10 nm). The FWHM of the TPL signal is usually considerably wider than that of HRS. Therefore, the TPL and HRS contributions in the measured SH intensity depend on the spectral bandwidth of the detection system. In this case we assume that the HRS contribution is the same for both channels while TPL depends on the SH 532 nm filter bandwidth. To calculate βHRS values for the studied samples, we used chloroform as an internal reference (βHRS = 0.49 × 10−30 esu).
Quantum chemical calculations
All the quantum chemical calculations were performed using Gaussian 09, rev. D.01.39 All the optimizations/thermochemistry calculations used force constants obtained with the current method, and in the end no imaginary frequencies were found in the output, confirming that the structure is a true minimum. Convergence criteria were left at the default levels, though sometimes the two-electron integral accuracy had to be increased to 10−11. The effect of the integral grid was checked by comparing the results for M11 with the standard FineGrid and with UltraFine ones, and no significant differences were discovered (even better convergence was not guaranteed by using UltraFine).In order to select an appropriate method, we compared various calculated geometry parameters of IND-1 with the X-ray analysis data. The final choice of the functional was made by considering asymptotic behavior of them in various real media (vacuum, tetrachloromethane, toluene, tetrahydrofuran (THF), dichloromethane (DCM), acetic anhydride, nitromethane, acetonitrile (ACN), dimethylsulfoxide (DMSO)), as well as (for van der Waals cavity tests, which showed very similar results) in three fictitious ones (with dielectric constants εr = 65; 81; 100 and εr∞ = 3), modeled with a simple, resource-effective conductor-like polarizable continuum model (CPCM).40,41 These dependencies were checked for up to 10 density functionals (APFD,42 B3LYP,43 TPSSh,44 M06-2X,45 LC-BLYP,46 LC-ωPBE,47 ωB97X,48 ωB97XD,49 CAM-B3LYP50 and M11;51 not all calculations converged for every solvent, especially with meta functionals) with the 6-311G(d,p)52 basis set. For the main parameter of this study, the C14–C5–C6–C7 dihedral, among the best were CAM-B3LYP and M06-2X; the largest absolute range was obtained with TPSSh and is 5.9°, 34% of the average value for this functional; the largest relative range was obtained with M11 (3.4° and 37%). Despite local functionals (incl. TPSSh) showing the broadest window of ω values, they also predict its maximum in DCM, without rise in DMSO, which triggered us to continue using CAM-B3LYP, as we also needed to obtain excited-state energies at every point, for which this functional was found to be optimal (see below). Although it is usually advised to use meta functionals for barrier studies,32–34 we faced considerable problems with converging geometry optimizations (both full and partial) for this class of functionals when they have large percentage of HF-like exchange admixed (this is the reason why we have almost no data with M06-HF but is also manifested with M06-2X, M11 and BMK, the ones we have checked for the barrier calculations). The values of barriers computed from purely electronic energies are similar between CAM-B3LYP and M06-2X, and more consistent with M06-2X when Gibbs energies are used. Hence, we have chosen M06-2X values for barriers, while the potential energy scan around the dihedral mentioned was still performed with CAM-B3LYP due to its better computational stability and because the examples in the literature show that range-separated hybrid functionals also do perform fairly for barriers.32,33,35
In addition to geometry parameters, the quality of electronic transition solvatochromism was checked for the same functionals (in the state-specific (relaxed-density) time-dependent DFT approximation), and CAM-B3LYP showed overall the best results for the combined task when compared to the experiment and some reference calculations with SAC-CI/6-31G(d′)//CAM-B3LYP/6-311G(d,p). This is illustrated in Fig. S1 and S2 in the ESI† (see also the captions of these two figures). Literature analysis also has shown that this functional is one of the best for optical transitions.29,53 Therefore, we chose to perform further calculations (LR-TD-DFT electronic spectrum and CPKS polarizabilities) at the CAM-B3LYP/6-311G(d,p)//CAM-B3LYP/6-311G(d,p) level. SAS cavity was also chosen for full and partial optimization studies, and non-electrostatic terms of dispersion, Pauli repulsion and cavity formation (nelst) were included into the model. The SAC-CI54 (see ESI† for the extended reference list) calculations were performed with full orbital window and with LevelTwo accuracy level. A relatively small basis set 6-31G(d′)55,56 from Petersson et al. was used. CBS methods for these were dictated by limited computational resources available. The CAM-B3LYP/6-311G(d,p) geometry was utilized for SAC-CI calculations to avoid high computational burden and because the effect of geometry on the shape of the predicted spectra was confirmed to be much less important than that of the functional chosen for the TD-DFT procedure.
A study considering the effect of changing dihedral C14–C5–C6–C7 was carried out as a set of partial optimizations with the dihedral mentioned frozen. For these partially optimized structures, spectra and polarizabilities were calculated. Polarizabilities calculated with 6-311G(d,p) and with 6-311+G(d,p) are almost perfectly correlated (slope 0.95, R2 = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.999 for ACN) save the region of 89°–100°, so we chose to use the same basis for all the DFT calculations. The functional used for hyperpolarizability computations is also CAM-B3LYP, as is frequently suggested in the literature.57,58
0.999 for ACN) save the region of 89°–100°, so we chose to use the same basis for all the DFT calculations. The functional used for hyperpolarizability computations is also CAM-B3LYP, as is frequently suggested in the literature.57,58
Atomic charges were computed using the atomic polar tensor (APT) model,59 as well as the Merz–Singh–Kollman scheme.26,27 Natural transition orbital (NTO)60 difference plots were obtained using the cubegen utility of Gaussian 09 and Gabedit.61 Avogadro62 was also used for visualization.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support for this work was provided by the Riga Technical University through the Scientific Research Project Competition for Young Researchers No. ZP-2016/8.References
- M. J. Cho, D. H. Choi, P. A. Sullivan, A. J. P. Akelaitis and L. R. Dalton, Prog. Polym. Sci., 2008, 33, 1013–1058 CrossRef CAS.
- L. R. Dalton, P. A. Sullivan and D. H. Bale, Chem. Rev., 2010, 110, 25–55 CrossRef CAS PubMed.
- W. Wu, J. Qin and Z. Li, Polymer, 2013, 54, 4351–4382 CrossRef CAS.
- W. Wu, R. Tang, Q. Li and Z. Li, Chem. Soc. Rev., 2015, 44, 3997–4022 RSC.
- L. T. Cheng, W. Tam, S. H. Stevenson, G. R. Meredith, G. Rikken and S. R. Marder, J. Phys. Chem., 1991, 95, 10631–10643 CrossRef CAS.
- F. Liu, Y. Yang, H. Wang, J. Liu, C. Hu, F. Huo, S. Bo, Z. Zhen, X. Liu and L. Qiu, Dyes Pigm., 2015, 120, 347–356 CrossRef CAS.
- D. R. Kanis, M. A. Ratner and T. J. Marks, Chem. Rev., 1994, 94, 195–242 CrossRef CAS.
- M. Blanchard-Desce, V. Alain, P. V. Bedworth, S. R. Marder, A. Fort, C. Runser, M. Barzoukas, S. Lebus and R. Wortmann, Chem. – Eur. J., 1997, 3, 1091–1104 CrossRef CAS.
- J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 CrossRef CAS.
- S. R. Marder, D. N. Beratan and L. T. Cheng, Science, 1991, 252, 103–106 CAS.
- I. D. Albert, T. J. Marks and M. A. Ratner, J. Phys. Chem., 1996, 100, 9714–9725 CrossRef CAS.
- A. Abbotto, L. Beverina, S. Bradamante, A. Facchetti, C. Klein, G. A. Pagani, M. Redi-Abshiro and R. A. Wortmann, Chem. – Eur. J., 2003, 9, 1991–2007 CrossRef CAS PubMed.
- F. Terenziani, S. Ghosh, A. C. Robin, P. K. Das and M. Blanchard-Desce, J. Phys. Chem. B, 2008, 112, 11498–11505 CrossRef CAS PubMed.
- C. K. Wang, Y. H. Wang, Y. Su and Y. Luo, J. Chem. Phys., 2003, 119, 4409–4412 CrossRef CAS.
- D. H. Bale, B. E. Eichinger, W. Liang, X. Li, L. R. Dalton, B. H. Robinson and P. J. Reid, J. Phys. Chem. B, 2011, 115, 3505–3513 CrossRef CAS PubMed.
- S. S. Sun, C. Zhang, L. R. Dalton, S. M. Garner, A. Chen and W. H. Steier, Chem. Mater., 1996, 8, 2539–2541 CrossRef CAS.
- S. S. Sun, C. Zhang, L. R. Dalton, S. M. Garner, A. Chen and W. H. Steier, Polymer, 1998, 39, 4977–4981 CrossRef CAS.
- J. M. Raimundo, P. Blanchard, L. Michaux, J. Roncali, I. Ledoux-Rak and R. Hierle, Chem. Commun., 2000, 1597–1598 RSC.
- M. Rutkis, A. Jurgis, V. Kampars, A. Vembris, A. Tokmakovs and V. Kokars, Mol. Cryst. Liq. Cryst., 2008, 485, 903–914 CrossRef CAS.
- F. Borbone, A. Carella, L. Ricciotti, A. Tuzi, A. Roviello and A. Barsella, Dyes Pigm., 2011, 88, 290–295 CrossRef CAS.
- A. R. Morales, A. Frazer, A. W. Woodward, H. Y. Ahn-White, A. Fonari, P. Tongwa, T. Timofeeva and K. D. Belfield, J. Org. Chem., 2013, 78, 1014–1025 CrossRef CAS PubMed.
- K. Traskovskis, V. Kokars, A. Tokmakovs, I. Mihailovs, E. Nitiss, M. Petrova, S. Belyakov and M. Rutkis, J. Mater. Chem. C, 2016, 4, 5019–5030 RSC.
- J. B. Pawliczek and H. Günther, Tetrahedron, 1970, 26, 1755–1769 CrossRef CAS.
- A. Capobianco, A. Esposito, T. Caruso, F. Borbone, A. Carella, R. Centore and A. Peluso, Eur. J. Org. Chem., 2012, 2980–2989 CrossRef CAS.
- G. Bourhill, L. T. Cheng, C. B. Gorman, G. Lee, S. R. Marder, J. W. Perry, M. J. Perry and B. G. Tiemann, Proc. SPIE, 1994, 2143, 153 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- B. H. Besler, K. M. Merz Jr. and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439 CrossRef CAS.
- M. E. Casida, THEOCHEM, 2009, 914, 3–18 CrossRef CAS.
- D. Jacquemin and C. Adamo, Top. Curr. Chem., 2016, 368, 347–376 CrossRef CAS PubMed.
- A. Prlj, B. F. E. Curchod, A. Fabrizio, L. Floryan and C. Corminboeuf, J. Phys. Chem. Lett., 2015, 6, 13–21 CrossRef CAS PubMed.
- T. Verbiest, K. Clays and V. Rodriguez, Second-Order Nonlinear Optical Characterization Techniques: An Introduction, CRC Press, Boca Raton, 2009 Search PubMed.
- R. Peveratti and D. G. Truhlar, Philos. Trans. R. Soc., A, 2014, 372, 20120476 CrossRef PubMed.
- P. O. Hubin, D. Jacquemin, L. Leherte, J.-M. André, A. C. T. van Duin and D. P. Vercauteren, Theor. Chem. Acc., 2012, 131, 1261 CrossRef.
- A. Haloui and E. Haloui, J. Phys. Org. Chem., 2014, 27, 430–439 CrossRef CAS.
- H. Choi, Y. C. Park, Y. S. Lee, H. An and K. K. Baeck, Chem. Phys. Lett., 2013, 580, 32–36 CrossRef CAS.
- J. Gálvez, J. I. López Sánchez and A. Guirado, Comput. Theor. Chem., 2015, 1069, 40–47 CrossRef.
- M. G. Kuzyk, J. Pérez-Moreno and S. Shafei, Phys. Rep., 2013, 529, 297–398 CrossRef.
- P. K. Das, J. Phys. Chem. B, 2006, 110, 7621–7630 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- A. Austin., G. A. Petersson, M. J. Frisch, F. J. Dobek, G. Scalmani and K. Throssel, J. Chem. Theory Comput., 2012, 8, 4989–5007 CrossRef CAS PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS; (b) P. Stephens, F. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119(23), 12129 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem., 2006, 110, 5121–5129 CrossRef CAS PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- (a) Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 210, 8425 CrossRef PubMed; (b) O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed; (c) O. A. Vydrov, J. Heyd, A. Krakau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106 CrossRef PubMed; (d) O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817 CrossRef CAS.
- K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef CAS.
- H. Nakatsuji and K. Hirao, J. Chem. Phys., 1978, 68, 2053–2065 CrossRef CAS.
- G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193 CrossRef CAS.
- G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090 CrossRef CAS.
- S.-I. Lu, Theor. Chem. Acc., 2015, 134, 1589 CrossRef.
- I. W. Bulik, R. Zaleśny, W. Bartkowiak, J. M. Luis, B. Kirtman, G. E. Scuseria, A. Avramopoulos, H. Reis and M. G. Papadopoulos, J. Comput. Chem., 2013, 34, 1775–1784 CrossRef CAS PubMed.
- J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333–8336 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- A. Allouche, J. Comput. Chem., 2012, 32, 174–182 CrossRef PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06333d |
| This journal is © the Owner Societies 2018 |