Polyaniline and CN-functionalized polyaniline as organic cathodes for lithium and sodium ion batteries: a combined molecular dynamics and density functional tight binding study in solid state†
Yingqian
Chen
 a,
Johann
Lüder
a,
Johann
Lüder
 a,
Man-Fai
Ng
a,
Man-Fai
Ng
 b,
Michael
Sullivan
b and
Sergei
Manzhos
b,
Michael
Sullivan
b and
Sergei
Manzhos
 *a
*a
aDepartment of Mechanical Engineering, Faculty of Engineering, National University of Singapore, Block EA #07-08, 9 Engineering Drive 1, Singapore 117575, Singapore. E-mail: mpemanzh@nus.edu.sg; Fax: +65 6779 1459; Tel: +65 6516 4605
bInstitute of High Performance Computing, Agency for Science, Technology and Research, 1 Fusionopolis Way, #16-16 Connexis, Singapore 138632, Singapore
First published on 27th November 2017
Abstract
We present the first atomistic-scale simulation of the discharge process of polymeric cathode materials for electrochemical batteries in solid state. The oxidation of polyaniline (PANI) and of cyano groups (CN) functionalized PANI induced by coordination to the electrolyte anions is computed and voltage curves are estimated. To deal with the large required numbers of atoms and structures, a combination of molecular dynamics and density functional tight binding (DFTB) is used. The DFTB is benchmarked to density functional theory (DFT) calculations using different functionals to confirm its accuracy. The voltages computed with the solid state model are in good agreement with available experimental data and ab initio models based on oligomers. The solid state model also predicts substantially increased voltage with PANI functionalized with cyano groups.
Introduction
Organic active electrode materials for lithium and sodium ion batteries possess a range of significant advantages including abundant and cheap feedstock, potentially low-cost synthesis, and ease of disposal.1,2 Specifically, they do not necessarily require toxic or poisonous components like some transition or rare earth metals. Importantly, organic electrode materials have shown high performance in Li as well as in Na ion batteries, with key parameters such as specific capacities, voltages, energy densities, cycle rates covering or exceeding values achieved with inorganic materials.1–8 The performance of many organic materials with Na is comparable to that with Li, which is not the case for most inorganic electrode materials.9–14 This bodes well for sustainability and scalability required especially for large-scale stationary applications.Organic electrode materials can operate by oxidation or reduction.2,15,16 Specifically, materials operating by oxidation have shown high voltages suitable for cathodic operation, while those operating by reduction are often more suitable as anodes.2,17 In the oxidation mechanism (often called 'dual ion'), the active organic material does not coordinate to Li and Na. It is oxidized and coordinates to the anion of the Li/Na salt, in the battery charged state. During discharge, the active material is reduced back to neutral state as the anions coordinate to Li/Na atoms released by the anode. For this type of organic battery, there is in principle no difference in the performance of the redox mechanism for lithium and sodium ions when the same solvent and anion (e.g. Li/Na–ClO4 in carbonate based solvents) are used.16
One promising organic cathode material operating by oxidation is polyaniline (PANI).16,18–20 It possesses a reasonably high oxidation potential (voltage) of about 4 V vs. Li+/Li21 and a high theoretical specific capacity of about 300 mA h g−1. It suffers from irreversible conversion to pernigraniline base at high degrees of oxidation, which limits usable capacity to about 150 mA h g−1.21,22 It would also be desirable to increase the voltage and thereby energy density, for operation with actively developed high-voltage electrolytes. In ref. 16, we reported a computational density functional theory (DFT) study of PANI oligomers functionalized with several different functional groups and proposed that functionalization with cyano groups on the nitrogen should simultaneously increase the voltage by about 1.3 V and increase stability, as dissociation of H from the –NH– would be prevented in principle.
The oligomeric model in ref. 16 was used due to limitations of DFT, specifically, due to the CPU cost which makes calculations in aggregate (i.e. solid) state impractical for polymeric systems. For many inorganic solids, lithiation/sodiation can be computed with DFT due to small sizes of the unit cells and the periodicity of the crystal, which make relatively reliable predictions of voltage–capacity curves possible based on models containing dozens, and rarely more than a hundred atoms.23 In the case of polymeric materials like PANI, the degree of disorder is substantial with multiple local minima and coordination environments, requiring large and multiple simulation cells containing many hundreds or thousands of atoms. Systems of such size would be costly to compute with DFT; further, not only system size but also the number of optimization steps could be very large (thousands in this work) and impractical with DFT. We previously showed that, for materials operating by reduction, aggregate state can have a significant effect on the voltage.24,25 Also, the oxidation mechanism requires calculation of the oxidation potential, which is numerically difficult for models using large amount of pristine (i.e. without counter-anions) material, or calculations with counterions which require large and non-unique simulation cells with different amounts of counterions.
Here, we model the voltage curve of PANI in aggregate state, to compare the results with the oligomeric model, and to confirm in the aggregate state the effects of functionalization with cyano groups (CN) on the voltage predicted by the oligomeric model in ref. 16. To deal with the large size of the simulation cell and multiple structures, we use forcefield based molecular dynamics to generate and pre-optimize structures and self-consistent charge density functional tight binding (SCC-DFTB)26 to re-optimize them and to compute oxidation potentials. DFTB is an approximation to DFT which is about three orders of magnitude faster. It has been well parameterized for purely organic systems. It could be a powerful method specifically for modeling of organic electrode materials operating by oxidation, as Li and Na need not be included in the model. To the best of our knowledge, DFTB has not been used for this purpose and its accuracy in this application has not been documented. We therefore also compare DFTB to DFT calculations using different functionals to estimate its expected accuracy.
Methods
Amorphous solid PANI was simulated in cubic simulation cells. Most calculations were done on cells comprised of five PANI chains (each with ten monomers, containing a total of 610 atoms for pristine and 660 atoms for functionalized PANI) constructed using the Amorphous Cell module implemented in Materials Studio 8.0.27 Cells containing ten PANI chains (of ten monomers each) were also produced to test the model as described below. All calculations were carried out using COMPASSII forcefield.28,29 Atomic charges were forcefield assigned while the electrostatic and van der Waals forces were controlled by the Ewald method (threshold = 0.0001 kcal mol−1) and the atom based method (cutoff = 15.5 Å), respectively. Four initial amorphous structures were constructed and refined for each cell. Density and temperature were set at 1.36 g cm−3 and 298 K, respectively. Ring spearing was checked for all cells. Optimizations were carried out on the resulting cells using the Forcite module. Energy and force thresholds were set at 0.0001 kcal mol−1 and 0.005 kcal mol−1 Å−1, respectively. No lattice relaxation was included in the construction and optimization stages in order to avoid large structural changes due to the large initial forces. The optimized cell with the lowest energy was chosen for molecular dynamics (MD) simulations. MD simulations were carried out using the Forcite module. Temperature and pressure were controlled by the Nose method (Q ratio = 0.01) and the Berendsen method (decay constant = 0.1 ps), respectively. The program's default values are adopted. With these values set for our systems, the target temperature at each MD stage can be reached within the simulation time. The equilibration process was carried out for 17 stages (a total of 1890 ps) with NVT canonical ensemble used for annealing and NPT isothermal–isobaric ensemble used for equilibration.30 The details of the MD calculations are summarized in Table S1 in ESI.† The averaged density after equilibration process is about 1.2 g cm−3 for both pristine and functionalized PANI. For studies of the oxidation of the amorphous PANI solid, ClO4 anions were incorporated into the amorphous structure. 18 different configurations (i.e. different numbers of ClO4 anions within the PANI solid) representing different degrees of oxidation were considered. For each configuration, ten random structures were generated using the Amorphous Cell module and optimized (both atoms and lattices) using the Forcite module. The lowest energy structure of each configuration was selected for further analysis with DFTB.SCC-DFTB26 calculations were performed in DFTB+31 for both PANI oligomers (4 and 8 monomers) and solid state. The 3ob-3-1 parameter set was used, together with DFTB3 (third order density functional tight binding),32 which improves the accuracy of estimation for non-covalent interactions. Dispersion corrections were also considered by using UFF parameters.33 Geometries were optimized until forces on all atoms were below 0.02 eV Å−1 and voltages were converged. For PANI in solid state, periodic simulation cells (about 18 × 18 × 18 Å3) were used with the Brillouin zone sampled at the Γ point.
DFT calculations were performed in Gaussian 0934 only for oligomers (tetramers). B3LYP,35–38 PBE39 and ωB97XD40,41 functionals were used, together with 6-31+g(d,p) basis set. Specifically, ωB97XD was found to reproduce CCSD(T)42 values most accurately. In our previous study, we have found this basis set is sufficient for describing oxidation of PANI oligomers.16 To compare with oligomers computed with DFTB+, no solvent effects were considered. Spin polarization was considered for open-shell systems.
Considering the reactions at electrodes during the discharge (assuming that LiClO4/NaClO4 is used as the salt in the electrolyte), the absolute oxidation potential Eabs is calculated as:
| Eabs(PANIn+/PANI) ≅ −[E(PANI) + nE(ClO4−) − E(PANIn+·n(ClO4−))]/ne |
| E(ClO4−) = [E(PC·mNaClO4) − E(PC·mNa+)]/m |
Results and discussion
Comparison of DFT and DFTB
We first compared the oxidation potential computed with DFTB/3ob-3-1 and with DFT using different functionals. To this end, an oligomer model with four PANI monomers is used in DFT calculations. We previously showed that a tetramer provides oxidation potentials/voltages within 0.1 eV compared to larger oligomers.16 To this oligomer, one, two, three and four ClO4 anions were attached corresponding to degrees of oxidation 25%, 50%, 75% and 100%, respectively. The degree of oxidation here means the fraction of PANI monomers which coordinate to the anion; it is also equal to the ratio of the number of positive charges on PANI to the number of monomers. Due to DFTB calculations being done only in spin-restricted formalism, in DFTB, an octamer was used with two and six ClO4 anions attached, to maintain an even number of electrons on PANI (see ESI† for the structures). Also, we observed in some DFTB calculations (including oligomers and solid state at high degree of oxidation), that some H atoms in the –NH– groups undergo dissociation; for this reason, the coordination of ClO4 anions to PANI oligomer was optimized with fixed PANI coordinates which were then optimized with respective methods. We also observed that at full oxidization of functionalized PANI in solid state computed in DFTB oxygen dissociation from the anion occurred. For those cases, we repeated the DFTB computation with a different starting configuration of similar total energy from MD simulations where no unphysical reaction occurred. Fig. 1 shows four structures of ClO4-coordinated PANI oligomers computed in DFT with the ωB97XD functional. The structures computed with other methods are shown in ESI.† These calculations are done in vacuum and with explicit anions (contrary to the calculations of ref. 16 and 47 which used implicit solvation of organic cations) to account for the fact that implicit solvation is not implemented in DFTB+ and to relate to solid state calculations which necessarily use explicit anions. Fig. 2 compares the absolute oxidation potentials of PANI oligomers at different degrees of oxidation computed with different methods. It is found that DFTB calculations agree very well with ωB97XD results. In ref. 16, we compared several DFT functionals for the calculation of the oxidation potential of PANI oligomers and identified ωB97XD as the most suitable, specifically, the oxidation potentials computed with ωB97XD were within 0.05 V of those computed with CCSD(T).42 Given the approximations on which DFTB relies,48,49 the agreement between DFTB results and ωB97XD results is likely helped by error cancellation. Nevertheless, our results indicate that reasonable accuracy can be obtained with DFTB for the PANI–ClO4 system.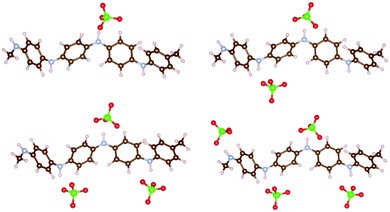 | ||
| Fig. 1 PANI oligomer coordinated to one, two, three and four ClO4 anions representing degrees of oxidation of 25%, 50%, 75% and 100%, respectively. The structures are computed with DFT/ωB97XD. Atom color code here and elsewhere: C – brown, N – blue, H – pink, Cl – green, O – red. Visualization here and elsewhere by VESTA.46 | ||
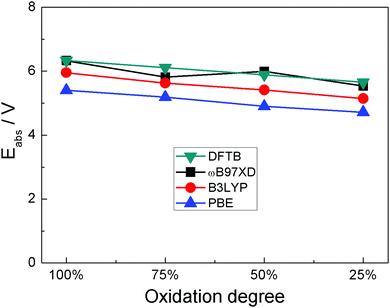 | ||
| Fig. 2 Absolute oxidation potentials at different degrees of oxidation of polyaniline computed with PBE, B3LYP and ωB97XD DFT functionals and with DFTB. | ||
DFTB modeling of oxidation and voltage curve in solid state
Simulation cells with different amounts of ClO4 were used to model different degrees of oxidation. As an example, a simulation cell containing 24 ClO4 units (corresponding to 48% oxidation) is shown in Fig. 3. Structures with different numbers of anions are shown in ESI.† The resulting computed absolute oxidation potentials are plotted in Fig. 4. The generated structures are not unique; therefore, one must ensure that the computed values are for structures reasonably close to the global minimum. We use two indicators of how close our structures are to the global minimum: (i) the shape of the curve (filled circles or filled rhombuses) in Fig. 4. If there is a significant chance that the obtained structures are far from the global minimum, the curve would be very jagged, as it is computed for a nearly continuous increase in the number of counterions. The curve with filled circles in Fig. 4 is somewhat jagged but with oscillations on the order of 0.1 V which we deem acceptable. (ii) For one degree of oxidation (specifically, 24%), we computed oxidation potentials of pristine PANI with different spatial positions of ClO4 anions, which have higher total energy, as well as using a larger simulation cell containing twice as many PANI strands and their computed oxidation potentials are given as open circles and green triangles, respectively, in Fig. 4. All these structures are shown in ESI.† The spread of these values represents a sort of “worst case scenario” for error in oxidation potential due to the use of structures far from the global minimum and of insufficient size. The spread is about 0.2 V and would still represent an acceptable level of error in many cases, specifically, in comparative studies.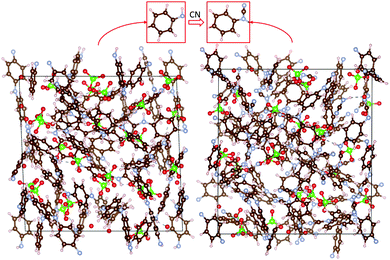 | ||
| Fig. 3 Simulation cells at 48% oxidation. On the left (the right), the cell contains five PANI chains with ten monomers (five functionalized PANI chains with ten monomers). Each cell contains 24 ClO4 anions. The monomer units of PANI and CN-functionalized PANI are highlighted above the simulation cells. Atom color scheme as in Fig. 1. | ||
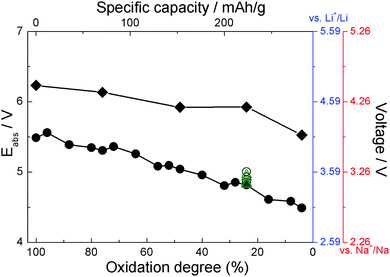 | ||
| Fig. 4 The absolute oxidation potentials (left axis) and estimated voltages (right axes, blue for Li and red for Na) for PANI (filled circles) and functionalized PANI (filled rhombuses) at different degrees of oxidation. Open circles indicate the potentials obtained from pristine PANI at 24% oxidation with different spatial positions of ClO4 anions. Open green triangles indicate the potential obtained from PANI at 24% oxidation using a larger unit cell. The structures are shown in ESI.† | ||
The right ordinate axes in Fig. 4 are estimated voltages in a Li-ion battery vs. Li+/Li (using 1.41 V for Li+/Li potential16) and in a Na-ion battery vs. Na+/Na (using 1.74 V for Na+/Na potential, see ESI†). The degree of oxidation is related to specific capacity which is also indicated in the figure. The voltage curve is in good agreement with experimental data and with the oligomer model for pristine PANI.16,21,50,51 Experimental voltage curves are in the range of ∼3–4 V vs. Li+/Li.21,50,51 We note that in experiment it is difficult to disambiguate between the degree of oxidation of PANI strands and the degree to which oxidation affects different regions/domains of PANI.
Fig. 4 also shows the oxidation potentials and expected voltages for solid state PANI functionalized with cyano groups. These structures are shown in Fig. 3 and ESI.† The solid state calculations with DFTB confirm an increase in the voltage by functionalization with cyano groups, by about 0.7–1.1 V depending on the degree of oxidation. Mainly electronic effects cause the increased voltage. The HOMO (highest occupied molecular orbital) of CN-functionalized solid state PANI (−5.01 eV) is about 0.6 eV more stable than in solid state PANI (HOMO at −4.43 eV) which is caused by the stabilizing effect of the electron withdrawing CN-groups.16 This is in good agreement with that predicted by DFT in an oligomer model using implicit solvation, namely a voltage increase of 1.3 V.16 This is significant because (i) it establishes the expected accuracy of the DFTB method with existing parameterizations for modeling of organic electrode materials operating by oxidation, (ii) it gives higher confidence to the proposition that functionalization with cyano groups will lead to significantly higher voltages; we hope this will guide experimental design.
Conclusions
We have performed simulations of voltage–capacity curves of organic cathode materials operating by oxidation, polyaniline (PANI) and functionalized polyaniline. The simulations were performed in solid state with the help of DFTB, which was benchmarked to DFT on small model systems. We have therefore established applicability of DFTB for modeling of organic electrode materials operating by oxidation. DFTB possesses a significant cost advantage over DFT and makes calculations of simulation cells with hundreds to several thousand atoms routine,52–54 which allows building more realistic models compared to DFT. We therefore hope that this work opens way to further use of DFTB for modeling of organic batteries. We note that this approach is especially attractive when the mechanism is oxidation, as Li or Na need not be included in the model, which avoids the need for an accurate parameterization for these elements. For materials operating by reduction (coordinating to Li/Na) DFTB has still not been shown to provide good accuracy.The computed voltage–capacity curve for PANI in solid state is in good agreement with experimental data and with the previously reported oligomer model. More importantly, we have confirmed in the more realistic solid state model that functionalization of PANI with cyano groups on the nitrogen would lead to a significant increase of the voltage, by about 1.1 V. It was already suggested that such functionalization would also inhibit the conversion to pernigraniline base which leads to irreversible capacity loss and thereby increase reversible capacity.16 We therefore hope that our result will incite experimental investigations of functionalized PANI.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Ministry of Education of Singapore AcRF Tier 2 grant MOE2014-T2-2-006.Notes and references
- Y. L. Liang, Z. L. Tao and J. Chen, Adv. Energy Mater., 2012, 2, 742–769 CrossRef CAS.
- Z. Song and H. Zhou, Energy Environ. Sci., 2013, 6, 2280–2301 CAS.
- Y. NuLi, Z. Guo, H. Liu and J. Yang, Electrochem. Commun., 2007, 9, 1913–1917 CrossRef CAS.
- K. Koshika, N. Sano, K. Oyaizu and H. Nishide, Chem. Commun., 2009, 836–838, 10.1039/B818087C.
- T. Suga, H. Ohshiro, S. Sugita, K. Oyaizu and H. Nishide, Adv. Mater., 2009, 21, 1627–1630 CrossRef CAS.
- A. Abouimrane, W. Weng, H. Eltayeb, Y. Cui, J. Niklas, O. Poluektov and K. Amine, Energy Environ. Sci., 2012, 5, 9632–9638 CAS.
- Y. Park, D. S. Shin, S. H. Woo, N. S. Choi, K. H. Shin, S. M. Oh, K. T. Lee and S. Y. Hong, Adv. Mater., 2012, 24, 3562–3567 CrossRef CAS PubMed.
- L. Zhao, J. M. Zhao, Y. S. Hu, H. Li, Z. B. Zhou, M. Armand and L. Q. Chen, Adv. Energy Mater., 2012, 2, 962–965 CrossRef CAS.
- D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A803–A811 CrossRef CAS.
- F. Legrain, O. I. Malyi and S. Manzhos, Solid State Ionics, 2013, 253, 157–163 CrossRef CAS.
- O. Malyi, V. V. Kulish, T. L. Tan and S. Manzhos, Nano Energy, 2013, 2, 1149–1157 CrossRef CAS.
- O. I. Malyi, T. L. Tan and S. Manzhos, Appl. Phys. Express, 2013, 6, 027301 CrossRef.
- M. Ge, J. Rong, X. Fang and C. Zhou, Nano Lett., 2012, 12, 2318–2323 CrossRef CAS PubMed.
- S. Komaba, Y. Matsuura, T. Ishikawa, N. Yabuuchi, W. Murata and S. Kuze, Electrochem. Commun., 2012, 21, 65–68 CrossRef CAS.
- P. Novák, K. Müller, K. S. V. Santhanam and O. Haas, Chem. Rev., 1997, 97, 207–282 CrossRef.
- Y. Chen and S. Manzhos, J. Power Sources, 2016, 336, 126–131 CrossRef CAS.
- J. Lüder, F. Legrain, Y. Chen and S. Manzhos, MRS Commun., 2017, 7, 523–540 CrossRef.
- E. T. Kang, K. G. Neoh and K. L. Tan, Prog. Polym. Sci., 1998, 23, 277–324 CrossRef CAS.
- J. Y. Shimano and A. G. MacDiarmid, Synth. Met., 2001, 123, 251–262 CrossRef CAS.
- J.-W. Jeon, Y. Ma, J. F. Mike, L. Shao, P. B. Balbuena and J. L. Lutkenhaus, Phys. Chem. Chem. Phys., 2013, 15, 9654–9662 RSC.
- Y. Lan-sheng, S. Zhong-qiang and L. Ye-dong, J. Power Sources, 1991, 34, 141–145 CrossRef.
- G. D'Aprano, M. Leclerc and G. Zotti, Macromolecules, 1992, 25, 2145–2150 CrossRef.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS.
- Y. Chen and S. Manzhos, Phys. Chem. Chem. Phys., 2016, 18, 1470–1477 RSC.
- Y. Chen and S. Manzhos, Phys. Chem. Chem. Phys., 2016, 18, 8874–8880 RSC.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268 CrossRef CAS.
- BIOVIA Materials Studio 8.0, Dassault Systemes Biovia, Cambridge, UK, 2015.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- BIOVIA (2015) COMPASS, COMPASS-II, Forcite, Discover and Materials Studio Software, BIOVIA, San Diego, CA, http://accelrys.com/products/collaborative-science/biovia-materials-studio/.
- X. Chen, C. Yuan, C. K. Y. Wong and G. Zhang, J. Mol. Model., 2012, 18, 2333–2341 CrossRef CAS PubMed.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS PubMed.
- Y. Yang, H. Yu, D. York, Q. Cui and M. Elstner, J. Phys. Chem. A, 2007, 111, 10861–10873 CrossRef CAS PubMed.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- É. Brémond, M. Savarese, N. Q. Su, Á. J. Pérez-Jiménez, X. Xu, J. C. Sancho-García and C. Adamo, J. Chem. Theory Comput., 2016, 12, 459–465 CrossRef PubMed.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- K. Hernandez-Burgos, S. E. Burkhardt, G. G. Rodriguez-Calero, R. G. Hennig and H. D. Abruna, J. Phys. Chem. C, 2014, 118, 6046–6051 CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- N. Dardenne, X. Blase, G. Hautier, J.-C. Charlier and G.-M. Rignanese, J. Phys. Chem. C, 2015, 119, 23373–23378 CAS.
- P. Koskinen and V. Mäkinen, Comput. Mater. Sci., 2009, 47, 237–253 CrossRef CAS.
- M. Elstner and G. Seifert, Philos. Trans. R. Soc., A, 2014, 372, 20120483 CrossRef PubMed.
- A. G. MacDiarmid, L. S. Yang, W. S. Huang and B. D. Humphrey, Synth. Met., 1987, 18, 393–398 CrossRef CAS.
- E. Song and J. W. Choi, Nanomaterials, 2013, 3, 498–523 CrossRef CAS PubMed.
- S. Manzhos, G. Giorgi and K. Yamashita, Molecules, 2015, 20, 3371 CrossRef CAS PubMed.
- W. Li, K. Kotsis and S. Manzhos, Phys. Chem. Chem. Phys., 2016, 18, 19902–19917 RSC.
- S. Arabnejad, K. Yamashita and S. Manzhos, Phys. Chem. Chem. Phys., 2017, 19, 7560–7567 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details of MD calculations and Na/Na+ potential, periodic simulation cell of NaClO4 in explicit solvent, lowest-energy structures of PANI oligomers coordinated to different numbers of ClO4 anions, computed with different functionals, optimized structures of PANI and functionalized PANI at different degrees of oxidation. See DOI: 10.1039/c7cp06279f |
| This journal is © the Owner Societies 2018 |
