The electron density of delocalized bonds (EDDB) applied for quantifying aromaticity

Abstract

In this study the recently developed electron density of delocalized bonds (EDDB) is used to define a new measure of aromaticity in molecular rings. The relationships between bond-length alternation, electron delocalization and diatropicity of the induced ring current are investigated for a test set of representative molecular rings by means of correlation and principal component analyses involving the most popular aromaticity descriptors based on structural, electronic, and magnetic criteria. Additionally, a qualitative comparison is made between EDDB and the magnetically induced ring-current density maps from the ipsocentric approach for a series of linear acenes. Special emphasis is given to the comparative study of the description of cyclic delocalization of electrons in a wide range of organic aromatics in terms of the kekulean multicenter index KMCI and the newly proposed EDDB^k index.

---

Introduction

Aromaticity is an important and extensively used concept in chemistry. It plays a fundamental role in predicting and rationalizing the structure, spectroscopy, reactivity, and magnetic properties of countless number of chemical species that have closed 2D or 3D circuits. Like many other concepts in chemistry, aromaticity has not been precisely defined.¹ In practice, however, it is determined enumeratively on the basis of distinctive properties of aromatic species. These properties regard inter alia increased stability with respect to the (linear) unsaturated counterparts without cyclic delocalization of π-electrons (energetic criterion),² vanishing or significantly reduced alternation of bond lengths (structural criterion),³ and large magnetic anisotropies accompanied by abnormal chemical shifts (magnetic criterion).⁴ From the electronic-structure point of view, aromatic stabilization is usually caused by cyclic delocalization of electrons and as such it can be quantified by different delocalization indices (DI).^5,6 Indeed, the precise relation between energy and delocalization indices, originally proposed by Rafat and Popelier,⁷ has been shown to be very useful for measuring the aromatic stabilization energy of aromatic molecules;^8,9 very recently the exact algebraic relationship between DI and the interatomic exchange–correlation energies has also been established.¹⁰

Among all the ways to quantify aromaticity through the “ground-state” criteria (energetic, structural, and electronic), there are descriptors that have gained enormous recognition and wide acceptance: the aromatic stabilization energy (ASE),² harmonic oscillator model of aromaticity (HOMA),^11–13 and different types of the multicenter delocalization indices (MCDI).^14–18 In turn, one of the most popular aromaticity descriptors based on the response properties is the nucleus-independent chemical shift (NICS) and its various derivatives.^4,19,20 Despite the unquestionable success and popularity of these aromaticity indices, some of their imperfections still cuts back their applicability to relatively small and simple systems. In particular, design of isodesmic and homodesmotic reaction scenarios to determine ASE is very difficult in practice and it leaves room to a lot of arbitrariness.² The principal problem with HOMA, in turn, is the necessity of parametrization of bond lengths for an idealized reference molecule, which obviously cannot be chosen unambiguously. Consequently, the practical use of HOMA is limited to aromatic and heteroaromatic systems since the parameters for chemical bonds with metal atoms are not available.³ Furthermore, the parametrization of HOMA should be performed using the same quantum-chemical method as used in calculations of equilibrium geometries of the molecule under study, since routinely computed HOMA with the experimentally determined parameters is bound to suffer from large and unsystematic errors.¹³ The magnetic-based measures of aromaticity, like NICS, have also been criticised for their complexity (NICS relies on the condensation of potentially complicated patterns of induced currents to a single number, especially in the case of fused aromatic rings),^21–26 methodological shortcomings (aromaticity evaluation using NICS is limited mainly to planar units of similar size),^6,20,27 and interpretative mistiness (quoting Prof. P. Bultinck, “…a multicenter delocalization is a necessary condition for a diatropic ring current to exist, provided that there are proper virtual molecular orbitals to excite to.”).^28–32 Finally, the DI-based indices (especially MCDI), unlike the aromaticity measures described above, enable one to study most of the types of aromaticity that can be found in literature.⁶ Also, the MCDIs are the only descriptors that passed a set of rigorous tests for aromaticity quantifiers.^33–35 Unfortunately, the main disadvantage connected with calculation of MCDI is their computational cost – at the level of one-determinant wavefunction with moderate basis set one cannot use multicenter delocalization indices to evaluate aromaticity of the molecular fragments containing more than a dozen of atoms.⁶ Thus, for large molecular rings, the analysis of aromatic stabilization using MCDI is applicable only within the framework of simple approximations like Hückel's or pseudo-π methods and for limited range of cases.³⁶

Recently the original method of the electron density of delocalized bonds (EDDB) has been proposed to facilitate quick qualitative analysis of different bond-conjugation patterns and to provide a bird's-eye view on the global aromaticity and resonance effects in molecular systems that due to their size and complex structure are the major challenge for the currently used tools.^37,38 However, in a number of preliminary tests EDDB turned out to be highly capable of providing also a quantitative evaluation of electron delocalization in many diversified aromatic rings and simultaneously free from the aforementioned shortcomings of the commonly used aromaticity indices.³⁹ This work provides a comprehensive view on the performance of the electron density of delocalized bonds in quantification of local aromaticity by comparative study with other well-known descriptors based on structural, magnetic and electronic criteria. Special emphasis is given to the analysis of cyclic delocalization of π-electrons in terms of the newly proposed EDDB-based index and the kekulean multicenter index. Since the former does not strictly take into account the cooperativity of all atomic centers in cyclic delocalization of electrons, as the latter does, the results will show if and to what extent the multicenter sharing effects are important for reliable description of organic aromatics.

Electron density of delocalized bonds

Electron density of delocalized bonds derives from the original method of the electron density (ED) partitioning that has been introduced to provide a uniform approach to quantify electron delocalization in molecular systems.⁴⁰ It makes use of the age-old concept of bond-order orbitals as well as the recently developed bond-orbital projection formalism^41–45 to probe different levels of electron delocalization by decomposition of ED into density layers representing electrons localized on atoms (inner shells, lone pairs), EDLA(r), electrons localized between atomic pairs (typical two-center bonds), EDLB(r), and electrons delocalized between conjugated bonds (multicenter electron sharing), EDDB(r):

ED(r) = EDLA(r) + EDLB(r) + EDDB(r). (1)

Fig. 1a presents the results of such electron density partitioning in the case of the pyridine molecule (only valence electrons included). The last component called electron density of delocalized bonds is of our special interest in the context of aromatic stabilization effect, especially if we consider aromaticity as a property of the ground-state electron density in the spirit of the first Hohenberg–Kohn theorem of the conceptual density functional theory (DFT).⁴⁶ Formally, the electron density of delocalized bonds is defined in the basis of natural atomic orbitals (NAO),⁴⁷ {χ_μ(r)}, but any other representation of the well-localized orthonormalized atomic orbitals can be used as well:^48–50where the corresponding EDDB matrix readsIn the above equation P represents the standard charge and bond-order matrix,⁵¹C_αβ is a matrix of linear-combination coefficients of the appropriately orthogonalized^52,53 two-center bond-order orbitals (2cBO),⁴²λ_αβ stands for a diagonal matrix collecting the corresponding 2cBO occupation numbers, ε_αβ represents a diagonal matrix of the bond-conjugation factors,³⁷ and Ω denotes the system of conjugated bonds. For a typical Lewis-like (localized) bond A_α–B_β all the elements of ε_αβ are close to zero, while in the case of delocalized (conjugated) bonds there is at least one diagonal element in ε_αβ close to 1. The definition of ε_αβ involves a series of projections of localized 2cBO onto their three-center counterparts, followed by the projection onto the delocalized (in nature) occupied molecular orbitals (MO).⁴⁰ Formal definition of this projection cascade is deeply rooted in the formalism of the orbital communication theory by Nalewajski^54–58 and as such it falls outside the framework of this work. But it should be mentioned that the trace of the resulting DB-density matrix, D^DB, can be straightforwardly interpreted as the population of electrons delocalized through the system of conjugated bonds, Ω. For the purpose of this work, Ω is restricted to represent only the cyclic delocalization of electrons due to the resonance of the kekulean forms. For instance, in the case of the 5-membered rings (5-MR) Ω contains five chemical bonds as follows:

Ω = {(A₁ − A₂),(A₂ − A₃),(A₃ − A₄),(A₄ − A₅),(A₅ − A₁)}. (4)

The resulting electron population, in this paper denoted simply by EDDB^k, does not account for the cross-ring electron delocalization, which for most of the organic aromatics in this study do not play an important role (or at least does not change the qualitative picture of the electron delocalization pattern) and can be simply ignored (see Table S1 in ESI†). Although the EDDB^k index is used here as a local aromaticity descriptor, one should realize that, by default (i.e. without specified Ω), the EDDB(r) function considers conjugations between all the chemical bonds in a molecule, and, as such, it can be used to evaluate global aromatic stabilization³⁸ or to study the non-local resonance effects in conjugated aromatic rings (in both ground- and excited states).⁵⁹

Fig. 1 (a) Different levels of electron delocalization from the one-electron density decomposition scheme by eqn (1) for pyridine (only valence electrons); (b) global EDDB(r) function for the LEU-LYS-GLU-GLN-PRO-ARG-HIS-PHE-TYR-TRP decapeptide (colored fragments indicate aromatic rings). Method: HF/6-311G**//PM6.

It has to be emphasized that EDDB is far more efficient than MCDI, especially in the case of highly accurate wavefunctions of large molecular systems. For instance, the calculation of MCDI takes from a dozen of seconds to several hours depending on the size of the ring and the computational method used, while the EDDB calculation takes less than 1 s for all the aromatic rings considered in this study regardless of their size.³⁹ Even the determination of global aromaticity/resonance effects in molecules containing hundreds of atoms, like the decapeptide depicted in Fig. 1b, is very fast and takes less than 40 s if the appropriate threshold for the 2cBO occupations is used and much less than 10 minutes otherwise.³⁹ Such speed-up is possible because within the EDDB formalism the multicenter electron sharing is approximated by means of decoupled three-atomic local resonances representing conjugations between the adjacent bonds only (cf. the Bridgeman–Empson method).⁶⁰ Further reduction of computational time can be achieved by using the natural minimal basis (NMB) instead of the default (full) NAO-representation.

Computational details

Two test sets of molecules have been used in our study. Test set T1, partially based on the set proposed by Andrzejak et al.¹³ and presented in Fig. 2, contains both Hückel's aromatic and antiaromatic systems (including the polycyclic aromatic hydrocarbons of different topology) that rely on cyclic conjugation of 2p orbitals and involve only carbon atoms. For such homogeneous group of molecular rings with only C–C and C=C bonds it is reasonable to expect the differences between aromaticities reflected by different criteria to be more or less related.

Fig. 2 The T1 test set of molecular rings used to benchmark the performance of different aromaticity descriptors.

We have chosen the following descriptors as the most representative and commonly used aromaticity measures that can be found in literature:

• Harmonic oscillator model of aromaticity (HOMA),^11–13 which is a normalized measure of the energetic consequences of deviations of bond lengths in the molecular ring from the corresponding optimum values for an idealized aromatic system.

• The axial component of the nucleus-independent chemical shift calculated at 1 Å above the ring centroid, NICS(1)_zz,^4,19,20 which quantifies diatropicity/paratropicity of the induced ring current by means of the effective magnetic shielding.

• The kekulean multicenter index (KMCI),^14–18 which directly quantifies cyclic delocalization of electrons in aromatic rings. Our preliminary studies indicate that the KMCI values for all aromatic species from both test sets tightly correlate (R² = 1.00) with those of MCI – the multicenter index originally proposed by Bultinck et al.¹⁵ that implicitly takes into account the cross-ring delocalization of electrons. However, since MCI is far more computationally expensive and offers virtually no advantage over KMCI (at least for the studied systems) its use in this benchmark is not necessary; the MCI values are included in Table S1 in ESI.† In view of the well-known problems of the multicenter indices with the ring-size extensivity, in order to perform the correlation and principal component analysis (PCA) involving the entire T1 set of 5-, 6-, and 7-MR molecules we used the nth root of the original index, denoted by KMCI^1/n (see Fig. 3a and 4a), as suggested in the literature.^6,16

Fig. 3 The arrays of the R²-values multiplied by 100 for linear (below the diagonal) and exponential, if available (above the diagonal) correlations between EDDB^k and different aromaticity indices calculated using (a) the entire set of molecules from T1 as well as (b, c, and d) within the corresponding subsets of aromatic rings of the same size, i.e. 5-, 6-, and 7-MRs, respectively; for polycyclic hydrocarbons ATI is used instead of NICS(1)_zz. The numbers in the column on the right side of each array stand for the percentage of explained variance by first component in PCA (more details in the text). Method: CAM-B3LYP/def2-TZVPP, equilibrium geometries.

Fig. 4 Correlation between EDDB^k and different aromaticity indices (a–h) for the entire test set T1 (black) as well as the subsets of 5- (blue), 6- (green), and 7-membered rings (red). The r-squared coefficients in brackets refer to the unnormalized KMCI. Method: CAM-B3LYP/def2-TZVPP, equilibrium geometries.

• Average two-center index (ATI),¹⁵ which measures the average effect of the electron delocalization between three para-related atoms in a benzenoid unit. Its use is thus limited to 6-membered rings only. ATI has the same theoretical foundations as the well-known para-delocalization index (PDI) by Poater et al.^5,62 but it involves a Hilbert-space partitioning within the basis of atomic orbitals instead of Bader's atoms-in-molecule (AIM)⁶⁵ or the fuzzy-atomic space (FAS).⁶¹

• Shannon aromaticity (SA),⁶³ which measures the Kullback–Leibler distance of the bonding electron density distribution in aromatic ring from uniformity; SA is a non-referential index.

• Fluctuation index of aromaticity (FLU),^5,64 which has a similar interpretation as the SA index but depends upon parameters determined for an idealized aromatic system.⁶⁴

• Ellipticity index of aromaticity (EL),⁶⁶ which measures bonding electron density deformations reflected in negative eigenvalues of the Hessian matrix of the electronic density in the bond critical point (BCP).

• Density of the total electron energy at the ring critical point (H_RCP),⁶⁷ which is one of the AIM parameters that has been proven to serve as a quantitative measure of aromaticity in a number of molecular rings.⁶⁸

Formal definitions of all the above listed indices can be found in the source papers as well as in the manual of the MultiWFN program,⁶⁹ which has been used to calculate HOMA (with parameters for the C–C bond calculated consistently according to ref. 9) as well as ATI and KMCI (both in the NAO basis). To calculate H_RCP, FLU, SA, and EL the analysis of electron density distribution within the framework of quantum theory of atoms in molecules has been performed using AIMAll program.⁷⁰ Although the electronic indices calculated using different partitioning schemes may sometimes give rise to different aromaticity predictions,⁷¹ our preliminary studies show that the NAO-based indices like KMCI and ATI are fully equivalent to their AIM- and FAS-based counterparts, i.e. I_Ring and PDI, respectively (the r-squared coefficients are very close to 1.00 in all cases); the I_Ring and PDI values are included in Table S1 in ESI.† The NICS(1)_zz values have been determined for all systems (using the Gaussian 09 package⁷²) except for polycyclic aromatic hydrocarbons, for which NICS is ill-defined, owing to its proven non-local character caused by mixing of different ring currents.^21–25 The EDDB^k indices have been obtained using the NBO6 software⁷³ and the script program written by one of the authors (DS).⁷⁴ The corresponding EDDB(r) maps have been generated by means of the standard tools from the Gaussian 09 package (formchk and cubegen programs). The CAM-B3LYP⁷⁵/def2-TZVPP⁷⁶ calculations with full geometry optimizations have been performed using Gaussian 09. The correlation and principal component analyses based on appropriately scaled aromaticity indices (scaling factors can be found in Table S1 in ESI†) have been carried out using the R-package⁷⁷ and their results are summarized in Fig. 3 and 4, while the complete results of the benchmark calculations are collected in Tables S1 and S2 in ESI.†

Test set T2 contains more diverse types of aromatic systems and has been used to assess if and to what extent the cyclic delocalization patterns in aromatic rings predicted by KMCI can be reproduced by the newly proposed index EDDB^k; a more comprehensive study involving the AIM-based counterpart of KMCI and other indices based on different criteria of aromaticity can be found elsewhere.^33–35 The T2 set is based on the collection of tests originally designed by Solà et al.³³ to evaluate new aromaticity indicators proposed in the literature and it accumulates chemical experience about the expected trends in aromaticity changes in the following systems: distorted benzene, substituted benzene, metal complexes, penta- and heptafulvenes, claromatic systems, heteroaromatic systems, as well as the aromatic transition states in selected chemical reactions. All the test molecules are depicted in Fig. 6–8. KMCI and EDDB^k indices were calculated at the B3LYP/6-311++G** theory level (equilibrium geometries) using Gaussian 09 and are listed in Fig. 6 and 7 (results for distorted benzene and two chemical reactions); Fig. 8 presents a summary of the results for other species from the test set, which are displayed and briefly described in Fig. S1–S5 in ESI.†

Results and discussion

Correlation and principal component analysis

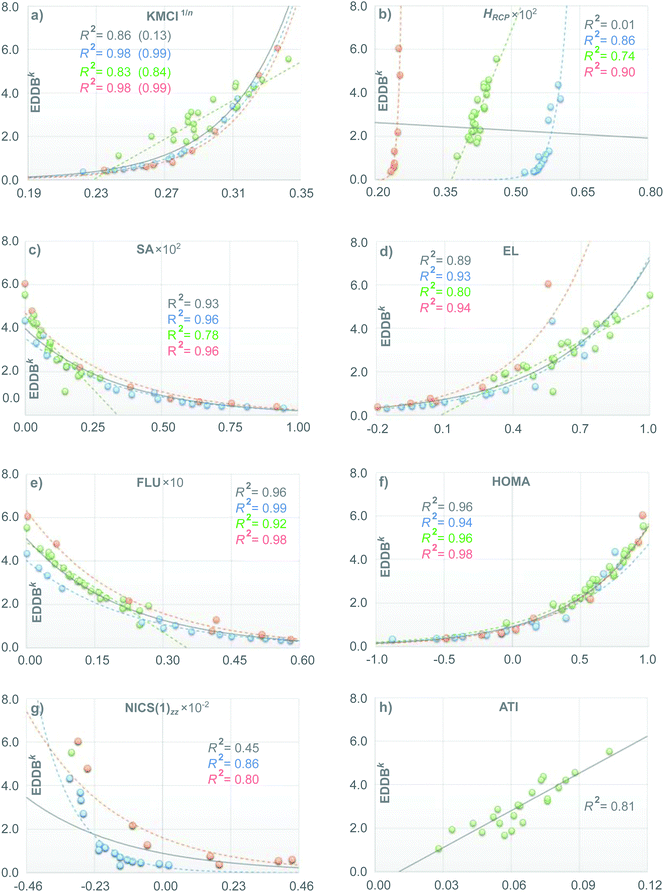
Let us first consider the results of the correlation and principal component analyses performed using the T1 set of molecules. Fig. 3 collects arrays of the R² coefficients multiplied by 100 for linear (below the diagonal) and exponential, if available (above the diagonal) correlations between different aromaticity indices calculated using the entire set of molecules from T1 (Fig. 3a) as well as within the corresponding subsets of aromatic rings of the same size (Fig. 3b–d for 5-, 6-, and 7-MR, respectively). The numbers in the column on the right side of each array represent the percentage of variance explained by the first principal component (PVE1C); the second and higher components are much smaller and, therefore, neglected in further analysis. Boxed numbers refer to the entire set of indices while the numbers below represent the effect of the cummulative exclusions (in the order given by Roman numerals in brackets) of the corresponding indices from the analysis; for detailed explanation see below. Fig. 4 illustrates in detail the results of the correlation analyses between EDDB^k and other aromaticity indices considered in this study.

Even a cursory glance at Fig. 3a (as well as Fig. 4b and g) indicates that the ring-size extensivity issue⁶ makes H_RCP and NICS(1)_zz incomparable with the rest of aromaticity descriptors when molecular rings of different size are considered.⁷⁸ On the other hand, reasonable linear correlation (with R² coefficients close to or greater than 0.90) can be observed within the set of SA, EL, FLU and HOMA indices, while their correlation with EDDB^k is mainly non-linear in character, but still relatively tight (up to R² = 0.96 for HOMA). This is clearly shown in Fig. 4c–f. The fact that aromaticity changes predicted by different aromaticity measures may not necessarily be linearly proportional to each other is quite obvious. It should be noticed, however, that here the exponential relation between EDDB^k (a quantity based on bond-order orbitals) and HOMA (an index involving bond lengths) explicitly refers to the bond-distance/bond-order correlation originally established by Pauling.⁷⁹ As follows from Fig. 3a, in turn, the renormalized multicenter index, KMCI^1/n, seems to fall slightly behind EDDB^k, SA, EL, FLU, and HOMA with r-squared coefficients in the range of 0.70 to 0.90 (excluding H_RCP and NICS(1)_zz), but it still performs dramatically better than the original KMCI for size-differentiated aromatic rings (see Fig. 4a and Table S2a in ESI†).

The results of PCA indicate that PVE1C for the entire set of aromaticity indices calculated for all aromatic rings from T1 equals 78% (see Fig. 3a). However, consecutive eliminations of indices with the smallest contributions to the first component (and significant contributions to the second one) from the set systematically improve PVE1C. In particular, by eliminating the H_RCP measure from the set PVE1C grows to a value of 87%, then by exclusion of NICS(1)_zz it reaches 91%, next, elimination of EL increases PVE1C up to 93%, and so on; red numbers indicate PVE1Cs for the last two indices remaining after exclusion of all other aromaticity measures (here FLU and SA). In fact, it should not be surprising that two mutually linked indices (in a sense both quantify uniformity of the electron distribution in aromatic ring) remain at the end of the procedure. But for our purposes the final effect is not as important as the partial result of elimination of a specific descriptor: the smaller the PVE1C growth, the better. In this context, EDDB^k (eliminated as the fourth in order) gives rise to relatively small increase of PVE1C by 2 percent points (pp), i.e. from 93% to 95%; basically the same is true for the T1 subsets of 5- (+2pp), 6- (+2pp) and 7-membered rings (0pp). Generally, if one regards size-differentiated rings separately (Fig. 3b–d) PVE1Cs for the entire set of aromaticity indices are close to 90%, which means that all the criteria of aromaticity used in this study give a more or less consistent picture of aromatic stabilization for the set T1. Moreover, a closer inspection of the antecedent PVE1C values reveals that in each case EDDB^k is in the subset of only a few descriptors with the rate of at least 96% of variance explained in the case of monocyclic aromatics (Fig. 3b and d) and at least 95% in the polycyclic aromatic hydrocarbons (Fig. 3c).

The effect of the ring-size extensivity issue of the original (unnormalized) kekulean multicenter index is clearly shown in Fig. 4a, in which the correlation with the EDDB^k index is analyzed. Apparently, KMCI^1/n is superior to KMCI (R²-values in brackets) if one wants to compare aromaticity of rings of different size; at the same time renormalization of KMCI seems to give only a slight adjustment to the r-squared coefficients when we consider rings of different size separately. One should realize, however, that the situation dramatically changes e.g. in the case of NICS(1)_zz, where the correlation coefficients for the entire test set T1 speaks in favor of the original KMCI. Indeed, accordingly to Table S2a in ESI,† renormalization of KMCI decreases R² from 0.67 (exponential correlation) to 0.36 (linear correlation). This particular should not be surprising, since the nucleus-independent chemical shift is known to share the lack of ring-size extensivity with the unnormalized multicenter index.^6,20 In contrast, when regarding 5- and 7-MRs separately renormalization of KMCI has negligible impact on the correlation with NICS(1)_zz (see Tables S2b and d in ESI†). It should also be mentioned that excluding 1,3-cyclopentadiene from the subset of 5-MRs significantly improves the correlation with NICS(1)_zz of both cyclic delocalization measures, KMCI and EDDB^k, i.e. the corresponding correlation coefficients rise from 0.79 to 0.97 (KMCI) and from 0.86 to 0.94 (EDDB^k), i.e. by 23% and 9%, respectively. When the AIM-based counterpart of KMCI (i.e. the I_Ring index) is considered, the R² value increases by nearly 60% (unpublished results). Thus, it seems that EDDB^k performs slightly better than KMCI regarding the correspondence between magnetic and electronic criteria of aromaticity, especially when both Hückel's aromatic and antiaromatic systems are taken into account.

A closer look at Fig. 4e and f reveals that the correlation of EDDB^k with FLU and HOMA is relatively tight regardless of whether we consider rings of different size separately or collectively. Additionally, in the case of SA (Fig. 4c), excluding the central ring (27) in triphenylene from the 6-MR subset of T1 significantly improves the correlation with EDDB^k (as well as with other indices like HOMA and FLU) giving rise to R² = 0.95. On the other hand, it follows from Fig. 4a, b, d and h that in the case of polycyclic aromatic hydrocarbons the correlation with KMCI^1/n, H_RCP, EL and ATI is significantly weaker. This effect is associated with a more general problem of the definition of local aromaticity in polycyclic systems.^21,22 A good example here are linear acenes as they have been a subject of heated debate in literature, owing to dramatic discrepancies between local aromaticity descriptions provided by different aromaticity criteria (“the anthracene problem”).^{21,22,80–83}

The aromaticity indices based on magnetic and structural criteria predict increasing aromaticity going from terminal to the central ring, while the electronic aromaticity indices like I_Ring, PDI, or H_RCP predict the opposite trend.^33,34,84 It has recently been demonstrated, however, that in the latter group of indices the results dramatically depend on the choice of the exchange–correlation functional at the DFT theory level and as such they are somewhat less reliable at least in the case of polyacenes.⁸⁴ In this context, the EDDB^k index gives virtually the same predictions as HOMA and FLU (regardless of the level of the theory). Furthermore, even the qualitative comparison of the global EDDB(r) maps with the magnetically induced ring-current density maps from the ipsocentric approach^4,23,85 presented in Fig. 5 clearly show that, despite fundamental methodological differences (induced ring-current density is a response property that occurs only in the presence of an external magnetic field while the cyclic delocalization of electrons is a ground-state property that is present irrespective of the presence or absence of an external magnetic field), both approaches lead to the same conclusions about local aromaticity of acenes as those from HOMA and FLU calculations.

Fig. 5 Contours of the (global) electron density of delocalized bonds and the corresponding maps of the ring-current density from the ipsocentric approach for the first four acenes (only the π-type molecular orbitals were taken into account). Method: B3LYP/6-311G**, equilibrium geometries. CRD(r) maps reproduced from ref. 85 with permission from Elsevier.

Aromaticity of distorted benzene rings

As an archetypical aromatic molecule, benzene can be used to assess the performance of aromaticity descriptors in a series of in-plane deformation modes such as bond length alternation (BLA) and clamping (CLA), as well as the out-of-plane distortions such as pyramidalization (PYR), boat-like (BOA) and chair-like (CHA) deformations (see Fig. 6). These types of distortions are very often observed in large and strained benzene-based molecular systems like graphene, nanotubes, and fullerenes, and they generally alter the cyclic delocalization of electrons leading to reduction of the aromatic character of benzenoid units.⁸⁶ In principle, the reference-based electronic aromaticity descriptors (e.g. FLU) perform reasonably well, since, by definition, they measure the deviation of particular electronic-structure properties from benzene. Some of the electronic criteria of aromaticity, however, are quite insensitive to most of the distortion modes (e.g. PDI).^33,34 As Fig. 6 clearly shows, both KMCI and the recently proposed EDDB^k index perfectly and in full compliance reproduce the expected decrease of cyclic delocalization when a distortion is applied. Both indices consistently identify the bond length alternation as the most “resonance killing” deformation in a benzenoid unit while pyramidalization and the boat-like deformation are found to affect π-bond delocalization to a very limited extent (less than 5%). Interestingly, in the case of BLA the EDDB^k index is clearly more sensitive than KMCI as it predicts reduction of aromaticity for about 85% in comparison to the about 45% reduction predicted by KMCI. Since for the bond-alternation parameter ΔR = 0.25 Å we actually get the hypothetical structure of 1,3,5-cyclohexatriene with highly localized double bonds, the result by EDDB seem to be even more reliable than those predicted by KMCI. To rationalize the difference between sensitiveness of EDDB and KMCI in this particular case one has to realize that in the former we approximate the effect of bond resonance from the perspective of each C–C bond in a ring (decoupled local resonances), while in the latter we actually do not measure the chemical resonance at all but rather the effect of cooperativity of all atomic centers in electron delocalization. Indeed, from the multicenter electron sharing perspective the reduction of cyclic delocalization of π-electrons is somewhat balanced by the enhanced electron delocalization within the Lewis-like (two-center) π-bonds. Thus, in this particular case EDDB^k seems to account strictly for the bond-resonance stabilization rather than cyclic delocalization of electrons. It should be mentioned, however, that according to our unpublished results, for the archetypical Hückel's antiaromatic molecule, 1,3-cyclobutadiene, no discrepancy is observed between EDDB^k and KMCI, and both indices predict no resonance/cyclic delocalization of electrons.

Fig. 6 Different benzene distortions together with the corresponding KMCI and EDDB^k values as well as the EDDB(r) contour maps. KMCI values have been multiplied by 10³. Method: B3LYP/6-311++G**.

Aromaticity changes along the reaction path

The interplay between aromaticity and reactivity is of vital importance in organic chemistry since a considerable number of chemical reactions involve species with a clear aromatic or antiaromatic character. The concept of transition state-aromaticity plays a key role in pericyclic, pseudopericyclic, and non-pericyclic reactions, properly determining and allowing one to understand the reaction mechanism.⁸⁷ For the purpose of this comparative study, let us consider two simple reactions involving aromatically stabilized transition states: the standard Diels–Alder (DA) cycloaddition and the acetylene trimerization. In the case of the former, it is well-known that the reaction takes place through a boat-like aromatic transition state thus giving rise to a peak of cyclic electron delocalization in the ring at the vicinity of the TS along the reaction path. For the latter, an increase of aromaticity is expected when going from reactants to transition state. After this point significant reduction of the aromatic character is observed until a final increase due to formation of benzene as a product. The trends of aromaticity changes in both reactions are known to be perfectly reproduced by all electronic indices except for FLU, which depends critically on the model aromatic molecules chosen as a reference. Therefore, it cannot be used to study reactivity.^33,34 Admittedly, aromaticity indices based on magnetic criteria properly reproduce the shape of the curve in the trimerization reaction, but they incorrectly identify the transition state with σ-delocalized bonds to be even more aromatic than benzene itself.^33,34

Fig. 7 presents plots of KMCI and EDDB^kvs. the reaction coordinate for both reactions. Analysis of these plots leads to the conclusion that despite some minor differences in the shape of curves, both aromaticity indices precisely identify the σ-aromatic transition state and the π-aromatic product of the acetylene trimerization (here the product is correctly identify as more aromatically stabilized than the corresponding TS) as well as the aromatic TS in the Diels–Alder cycloaddition. The EDDB(r) contour maps show very clearly that TS in the DA reaction has a boat-like structure with characteristic cyclic delocalization pattern in the plane between butadiene and ethylene fragments.⁸⁸ Moreover, although both TS and the product of the trimerization reaction are to a similar extent stabilized by resonance (according to the EDDB^k values, the difference is less than 10%) it is quite obvious even from the first look at the EDDB(r) contours that TS is stabilized by cyclic delocalization of σ-electrons while the final product represents a typical for organic aromatics π-delocalization pattern.

Fig. 7 Plot of KMCI and EDDB^kvs. the reaction coordinate for (a) the Diels–Alder cycloaddition and (b) the acetylene trimerization. For TS and products the EDDB(r) contour maps are displayed with the corresponding values of both indices. KMCI values have been multiplied by 10³. Method: B3LYP/6-311++G**.

Heteroaromatics, claromatics, fulvenes, and others

It has been pointed out by Krygowski et al. that substitution to an aromatic ring, either electron-donating or electron-accepting groups, decreases aromaticity of the ring as it leads to partial localization of π-electrons.^89,90 A similar behavior is observed when a metal atom is complexed to benzene, as in the case of (η⁶-C₆H₆)Cr(CO)₃.^33,34,91 All the electronic indicators of aromaticity like PDI, FLU, KMCI/MCI, etc. were shown to perfectly reproduce these trends, in contrast to the indices based on structural and magnetic criteria, which for some substituted benzenes predict higher aromatic stabilization than for benzene itself.^33,34 For the effects of atom- and ring-size dependence, it was also shown that electronic indices of aromaticity, especially the appropriately normalized multicenter index, are superior to the rest of aromaticity descriptors.^16,33,34

Three additional groups of aromatic systems complete the T2 set of molecules: heteroaromatics, claroaromatics and fulvenes. The first one was originally proposed to predict the proper trend of aromaticity changes along a well-established heteroaromatic series including five aza-derivatives of benzene and five heterocyclic compounds of type C₄H₄X (where X = CH⁻, NH, O, CH₂, BH, CH⁺); the second group was designed to test the effect of fusing aromatic rings represented by five Clar systems, while the third subset was used to assess the expected trend of aromaticity in 5-MR and 7-MR fulvenes with different substituents.³³ In general, all the electronic aromaticity indices were reported to pass the three tests.^33,34 The only exceptions concern the series of pentafulvenes, which are particularly difficult to assess by aromaticity quantifiers as they display a tunable aromatic character (sometimes being termed “aromatic chameleons”⁹²). Magnetic and structural indices are in most cases also in line with the expected trends for all three tests, except a single incorrect prediction that C₄H₄NH is more aromatic than C₅H₅⁻.^33,34

How does the EDDB^k index deal with the above mentioned tests? The answer to this question is provided by Fig. 8, which displays a summary of calculations for all 47 test systems used to compare the performance of EDDB^k and KMCI; detailed results with comments are collected in Fig. S1–S5 in ESI.† The presented results leave no doubt: the index based on the electron density of delocalized bonds predicts exactly the same trends of aromaticity changes as the kekulean multicenter index. Furthermore, in the overwhelming majority of cases these predictions are in full agreement with general expectations.^16,33,34 There are only three systems for which significant discrepancies between the expectations and the predictions based on both indices are observed: 23, 32, and 42. In fact, discrepancies between different aromaticity criteria are very common for heteroaromatic species, because in such systems proportionality of the energetic effects of aromatic stabilization and the electron delocalization may depend on the heteroatoms present in the system.^12,93–97 Nevertheless, EDDB^k index perfectly reproduce the predictions by KMCI, which clearly shows that the bond-orbital projection formalism behind the EDDB approach provides a widely applicable and reliable tool for quantitative evaluation of the multicenter electron sharing and aromatic stabilization effects (at least in the case of organic species). It should be pointed out, however, that the situation might be different in the cases, for which cyclic delocalization of electrons cannot be represented with the resonant covalent forms (e.g. in small charged aromatic rings, metal clusters, etc.) or when the strong cross-ring interactions appear. Then, according to our preliminary (unpublished) studies, EDDB^k and KMCI can predict slightly different trends of aromaticity changes; a detailed analysis of this issue will be published elsewhere.

Fig. 8 Summary of the five tests used to compare the performance of EDDB^k and KMCI as an aromaticity quantifiers. The complete results with brief comments are collected in Fig. S1–S5 in ESI.†

Conclusions

Throughout recent decades, several dozen types of chemical aromaticity have been reported in the literature.⁹⁸ As far as the physicochemical and electronic-structure properties are concerned, many of those concepts differ much from the archetypical π-aromaticity of the benzene molecule. It stimulated research towards quantification of the aromatic stabilization effect. Every now and then new quantitative criteria of chemical aromaticity are introduced in the literature. Different criteria, on which the quantifiers are based and their sometimes inconsistent predictions has led to aromaticity concept reputation being somewhat tarnished and often criticised, both in its conceptual and methodological layer.^99,100 One may add – the criticism often being undeserved since, even on the level of a qualitative theory, the usefulness of the aromaticity concept, in the context of structure and reactivity prediction of a whole bunch of organic molecules, cannot be overestimated.¹⁰⁰ One must admit, however, that among others introducing new aromaticity measures makes sense nowadays if their performance has the advantage over the already existing descriptors or they enable one to study molecular systems that due to their size and structure are the major challenge for currently used tools.^6,100

The results presented in this work clearly show that the EDDB method safely fulfils the above conditions. For a wide spectrum of organic compounds, the EDDB^k index predicts the same trends of aromaticity changes as most of the aromaticity indices from different criteria. What is more, EDDB(r) maps allow for easy identification of resonance-stabilised regions and for tracing of aromaticity changes due to chemical reactions. The comparison of electronic populations from EDDB to other aromaticity measures in the first test proves that the proposed ground-state electron density partitioning in eqn (1) can be considered reliable, and the extracted density layer corresponding to the delocalized bonds (EDDB) in fact seems to be closely related to the properties being characteristic for aromatic rings. In turn, a detailed comparison of EDDB to KMCI shows that for a majority of studied aromatic rings the cyclic delocalization of electrons can be reliably approximated within the framework of the decoupled local resonances at incomparably lower computational cost.

The current implementation of the EDDB method, called RunEDDB, works with both RHF and UHF one-determinant wavefunctions and involves the Hilbert-space partitioning within representation of natural atomic orbitals, which is widely available for most of the popular quantum-chemistry packages through NBO⁷³ and JaNPA¹⁰¹ interfaces. RunEDDB is still under active development and is freely available on the author's website.⁷⁴

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research was supported in part by the Faculty of Chemistry at Jagiellonian University (grant K/DSC/001469, DS), Foundation for Polish Science (FNP START 2015, stipend 103.2015, DS), National Science Centre, Poland (NCN SONATA, grant 2015/17/D/ST4/00558, DS) as well as the PL-Grid Infrastructure of the Academic Computer Centre CYFRONET with the calculations performed on the cluster platform “Prometheus”. MS thanks for the support of the Ministerio de Economa y Competitividad of Spain (Project CTQ2014-54306-P), Generalitat de Catalunya (project number 2014SGR931, Xarxa de Referència en Qumica Teòrica i Computacional, and ICREA Academia prize), and European Fund for Regional Development (FEDER grant UNGI10-4E-801). Calculations using the Gaussian09 set of codes were partially carried out in Wroclaw Center for Networking and Supercomputing (http://www.wcss.wroc.pl). Access to HPC machines and licensed software is gratefully acknowledged by JD. HS thanks the Warsaw University of Technology for supporting this work. DS extends his special thanks to all the co-authors for their constant support and encouragement without which this work would have never been accomplished.

References

1. J. Grunenberg, Int. J. Quantum Chem., 2017, 117, e25359.
2. M. K. Cyrański, Chem. Rev., 2005, 105, 3773.
3. T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Chem. Rev., 2014, 114, 6383.
4. R. Gershoni-Porannea and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597.
5. J. Poater, M. Duran, M. Solà and B. Silvi, Chem. Rev., 2005, 105, 3911.
6. F. Feixas, E. Matito, J. Poater and M. Solà, Chem. Soc. Rev., 2015, 44, 6434.
7. M. Rafat and P. L. A. Popelier, Topological Atom-Atom Partitioning of Molecular Exchange Energy and its Multipolar Convergence, in The quantum theory of atoms in molecules: from solid state to DNA and drug design, ed. C. F. Matta and R. J. Boyed, Wiley, Weinheim, 2007, p. 121.
8. C. Foroutan-Nejad, Z. Badri and R. Marek, Phys. Chem. Chem. Phys., 2015, 17, 30670.
9. C. Foroutan-Nejad and Z. Badri, Phys. Chem. Chem. Phys., 2016, 18, 11693.
10. E. Francisco, D. M. Crespo, A. Costales and A. Martin-Pendas, J. Comput. Chem., 2017, 38, 816.
11. J. Kruszewski and T. M. Krygowski, Tetrahedron Lett., 1972, 13, 3839.
12. T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385.
13. M. Andrzejak, P. Kubisiak and K. Zborowski, Struct. Chem., 2013, 24, 1171.
14. M. Giambiagi, M. S. de Giambiagi, C. D. dos Santos and A. P. de Figueiredo, Phys. Chem. Chem. Phys., 2000, 2, 3381.
15. P. Bultinck, R. Ponec and S. V. Damme, J. Phys. Org. Chem., 2005, 18, 706.
16. J. Cioslowski, E. Matito and M. Solà, J. Phys. Chem. A, 2007, 111, 6521.
17. W. Heyndrickx, P. Salvador, P. Bultinck, M. Solà and E. Matito, J. Comput. Chem., 2011, 32, 386.
18. J. M. Mercero, E. Matito, F. Ruipérez, I. Infante, X. Lopez and J. M. Ugalde, Chem. – Eur. J., 2015, 21, 9610.
19. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. Eikema-Hommes, J. Am. Chem. Soc., 1996, 118, 6317.
20. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842.
21. P. Bultinck, Faraday Discuss., 2007, 135, 347.
22. E. Steiner, P. W. Fowler, A. Soncini and L. W. Jenneskens, Faraday Discuss., 2007, 135, 309.
23. S. Fias, P. Fowler, J. L. Delgado, U. Hahn and P. Bultinck, Chem. – Eur. J., 2008, 14, 3093.
24. S. Fias, S. V. Damme and P. Bultinck, J. Comput. Chem., 2008, 29, 358.
25. S. Fias, S. V. Damme and P. Bultinck, J. Comput. Chem., 2010, 31, 2286.
26. J. Poater, M. Solà, R. G. Viglione and R. Zanasi, J. Org. Chem., 2004, 69, 7537.
27. C. Foroutan-Nejad, S. Shahbazian and P. Rashidi-Ranjbar, Phys. Chem. Chem. Phys., 2010, 12, 12630.
28. P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217.
29. P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1.
30. J. N. A. F. Gomez and R. B. Mallion, Chem. Rev., 2001, 101, 1349.
31. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, J. Chem. Theory Comput., 2013, 9, 4789.
32. L. Zhao, R. Grande-Aztatzi, C. Foroutan-Nejad, J. M. Ugalde and G. Frenking, ChemistrySelect, 2017, 2, 863.
33. F. Feixas, E. Matito, J. Poater and M. Solà, J. Comput. Chem., 2008, 29, 1543.
34. M. Solà, F. Feixas, J. O. C. Jiménez-Halla, E. Matito and J. Poater, Symmetry, 2010, 2, 1156.
35. F. Feixas, J. O. C. Jiménez-Halla, E. Matito, J. Poater and M. Solà, J. Chem. Theory Comput., 2010, 6, 1118.
36. P. Bultinck, M. Mandado and R. Mosquera, J. Math. Chem., 2008, 43, 111.
37. D. W. Szczepanik, E. Zak, K. Dyduch and J. Mrozek, Chem. Phys. Lett., 2014, 593, 154.
38. D. W. Szczepanik, M. Andrzejak, K. Dyduch, E. Zak, M. Makowski, G. Mazur and J. Mrozek, Phys. Chem. Chem. Phys., 2014, 16, 20514.
39. The effectiveness of bond conjugation – a new criterion of aromaticity, http://eddb.nazwa.pl/attendances/2016-06-07.pdf#page=11, (accessed July 2017).
40. D. W. Szczepanik, Comput. Theor. Chem., 2016, 1080, 33.
41. D. W. Szczepanik and J. Mrozek, J. Math. Chem., 2013, 51, 1388.
42. D. W. Szczepanik and J. Mrozek, J. Math. Chem., 2013, 51, 1619.
43. D. W. Szczepanik and J. Mrozek, Comput. Theor. Chem., 2013, 1023, 83.
44. D. W. Szczepanik and J. Mrozek, Comput. Theor. Chem., 2013, 1026, 72.
45. D. W. Szczepanik, Comput. Theor. Chem., 2017, 1100, 13.
46. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
47. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
48. D. W. Szczepanik and J. Mrozek, Comput. Theor. Chem., 2012, 996, 103.
49. D. W. Szczepanik and J. Mrozek, J. Chem., 2013, 2013, 684134.
50. D. W. Szczepanik and J. Mrozek, J. Math. Chem., 2013, 51, 2687.
51. M. S. Giambiagi, M. Giambiagi and F. E. Jorge, J. Phys. Sci., 2014, 39, 1259.
52. D. W. Szczepanik and J. Mrozek, Chem. Phys. Lett., 2012, 521, 157.
53. D. W. Szczepanik and J. Mrozek, Comput. Theor. Chem., 2013, 1008, 15.
54. R. F. Nalewajski, D. W. Szczepanik and J. Mrozek, Adv. Quantum Chem., 2011, 61, 1.
55. D. W. Szczepanik and J. Mrozek, J. Math. Chem., 2011, 49, 562.
56. D. W. Szczepanik and J. Mrozek, J. Theor. Comput. Chem., 2011, 10, 471.
57. R. F. Nalewajski, D. W. Szczepanik and J. Mrozek, J. Math. Chem., 2012, 50, 1437.
58. D. W. Szczepanik, E. Zak and J. Mrozek, Comput. Theor. Chem., 2017, 1115, 80.
59. M. Andrzejak, D. W. Szczepanik and Ł. Orzeł, Phys. Chem. Chem. Phys., 2015, 17, 5328.
60. A. J. Bridgeman and C. J. Empson, New J. Chem., 2008, 32, 1359.
61. I. Mayer and P. Salvador, Chem. Phys. Lett., 2004, 383, 368.
62. J. Poater, X. Fradera, M. Duran and M. Solà, Chem. – Eur. J., 2003, 9, 400.
63. S. Noorizadeh and E. Shakerzadeh, Phys. Chem. Chem. Phys., 2010, 12, 4742.
64. E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2005, 122, 014109.
65. R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford University Press, New York, 1990.
66. J. Dominikowska and M. Palusiak, Struct. Chem., 2012, 23, 1173.
67. M. Palusiak and T. M. Krygowski, Chem. – Eur. J., 2007, 13, 7996.
68. A. Mohajeri and A. Ashrafi, Chem. Phys. Lett., 2008, 458, 378.
69. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
70. T. A. Keith, AIMAll Professional program, http://aim.tkgristmill.com (accessed: October 2014).
71. E. Matito, P. Salvador, M. Duran and M. Solà, J. Phys. Chem. A, 2006, 110, 5108.
72. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
73. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013.
74. D. W. Szczepanik, RunEDDB, available at: http://www.eddb.info (accessed on March 2017).
75. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51.
76. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
77. The R Project for Statistical Computing, http://www.r-project.org (accessed July 2017).
78. A. A. Ebrahimi, R. Ghiasi and C. Foroutan-Nejad, THEOCHEM, 2010, 941, 47.
79. L. Pauling, J. Am. Chem. Soc., 1947, 69, 542.
80. P. v. R. Schleyer, M. Manoharan, H. Jiao and F. Stahl, Org. Lett., 2001, 3, 3643.
81. G. Portella, J. Poater, J. M. Bofill, P. Alemany and M. Solà, J. Org. Chem., 2005, 70, 2509.
82. P. Bultinck, R. Ponec and R. Carbó-Dorca, J. Comput. Chem., 2007, 28, 152.
83. P. W. Fowler and W. Myrvold, J. Phys. Chem. A, 2011, 115, 13191.
84. D. W. Szczepanik, M. Solà, M. Andrzejak, B. Pawełek, J. Dominikowska, M. Kukułka, K. Dyduch, T. M. Krygowski and H. Szatylowicz, J. Comput. Chem., 2017, 38, 1640.
85. E. Steiner and P. W. Fowler, Chem. Phys. Lett., 2002, 364, 259.
86. F. Feixas, E. Matito, J. Poater and M. Solà, J. Phys. Chem. A, 2007, 111, 4513.
87. P. v. R. Schleyer, J. I. Wu, F. P. Cosso and I. Fernández, Chem. Soc. Rev., 2014, 43, 4909.
88. F. P. Cosso, I. Morao, H. Jiao and P. v. R. Schleyer, J. Am. Chem. Soc., 1999, 121, 6737.
89. T. M. Krygowski, K. Ejsmont, B. T. Stepień, M. K. Cyrański, J. Poater and M. Solà, J. Org. Chem., 2004, 69, 6634.
90. T. M. Krygowski and B. T. Stepień, Chem. Rev., 2005, 105, 3482.
91. F. Feixas, J. O. C. Jiménez-Halla, E. Matito, J. Poater and M. Solà, Pol. J. Chem., 2007, 81, 783.
92. M. Rosenberg, C. Dahlstrand, K. Kilsa and H. Ottosson, Chem. Rev., 2014, 114, 5379.
93. A. R. Katritzky, P. Barczynski, G. Musumarra, D. Pisano and M. Szafran, J. Am. Chem. Soc., 1989, 111, 7.
94. K. Jug and A. M. Köster, J. Phys. Org. Chem., 1991, 4, 163.
95. A. R. Katritzky, M. Karelson, S. Sild, T. M. Krygowski and K. Jug, J. Org. Chem., 1998, 63, 5228.
96. A. R. Katritzky, K. Jug and D. C. Oniciu, Chem. Rev., 2001, 101, 1421.
97. M. K. Cyrański, T. M. Krygowski, A. R. Katritzky and P. v. R. Schleyer, J. Org. Chem., 2002, 67, 1333.
98. M. Solà, Aromaticity, in Encyclopedia of Physical Organic Chemistry, ed. Z. Wang, Wiley, Weinheim, 2017, vol. 1, p. 511.
99. R. Hoffmann, Am. Sci., 2015, 103, 18.
100. M. Solà, Front. Chem., 2017, 5, 22.
101. T. Y. Nikolaienko, L. A. Bulavin and D. M. Hovorun, Comput. Theor. Chem., 2014, 1050, 15.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06114e

---