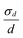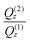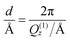Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effect of benzocaine and propranolol on phospholipid-based bilayers
G.
Mangiapia
 *a,
M.
Gvaramia
ab,
L.
Kuhrts
*a,
M.
Gvaramia
ab,
L.
Kuhrts
 a,
J.
Teixeira
c,
A.
Koutsioubas
a,
J.
Teixeira
c,
A.
Koutsioubas
 a,
O.
Soltwedel
d and
H.
Frielinghaus
a,
O.
Soltwedel
d and
H.
Frielinghaus
 a
a
aForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science Außenstelle am Heinz Maier-Leibnitz Zentrum, Lichtenbergstraße 1, D-85747 Garching, Germany. E-mail: mangiapia.gaetano@alice.it
bIvane Javakhishvili Tbilisi State University, 1 Chavchavadze Avenue, GE-0179 Tbilisi, Georgia
cLaboratoire Léon Brillouin (CEA-CNRS), CEA-Saclay, F-91191 Gif-sur-Yvette CEDEX, France
dHeinz Maier-Leibnitz Zentrum, Technische Universität München, Lichtenbergstraße 1, D-85747 Garching, Germany
First published on 31st October 2017
Abstract
Cell membranes play a fundamental role in protecting the cell from its surroundings, in addition to hosting many proteins with fundamental biological tasks. A study of drug/lipid interactions is a necessary and important step in fully clarifying the role and action mechanism of active ingredients, and shedding light on possible complications caused by drug overdosage. In this paper, the influence of benzocaine and propranolol drugs on the structure of L-α-phosphatidylcholine-based membranes has been investigated by means of neutron reflectivity, grazing incidence small angle neutron scattering, and small/ultra-small angle neutron scattering. Investigations allowed discovering a stiffening of the membranes and the formation of stalks, caused by the presence of benzocaine. On the other hand, disordered bilayers (lamellar powders) and highly curved structures were found in the presence of propranolol. The results obtained may be rationalized in terms of the molecular structures of drugs and may serve as a starting point for explaining the toxic behavior in long-term and overdosage scenarios.
Introduction
Cell membranes consist mainly of lipid bilayers as their structural unit.1 In turn, these bilayers are composed of phospholipids, amphiphilic molecules formed by a functionalized hydrophilic phosphate head esterified with two fatty acid chains.The main task of a cell membrane is essentially to protect the cell from its surroundings, acting as a selective barrier between the internal cytoplasm and the extracellular environment.2 Part of its selectivity is due to the presence of different proteins (known as membrane proteins) that are embedded in the lipid bilayer. The biological functions of these proteins also include the possibilities of activating cell signaling, triggering intracellular signaling pathways, and interacting with external substances, including active ingredients.3 To this aim, most of the drugs designed or used in pharmacological therapies target membrane proteins,4 like channel blockers or protein binding inhibitors.5
For the above mentioned reasons, most of the action mechanism studies, or pharmacokinetic investigations, are exclusively focused on drug/protein interactions, while a possible drug/phospholipid interaction is usually neglected. This approach, aside from being not fully justified, neglects some key aspects of the interaction between active ingredients and cellular systems. Concerning this, even in the presence of a specific drug interaction with a particular receptor, a partial drug uptake by the cell membrane may significantly influence the pharmacokinetic properties of the drug, such as its delivery, distribution, and elimination, modulating the overall efficacy of the administration. The second key aspect to consider for a proper and meaningful investigation concerns the structure of the target protein. In fact, action mechanism and pharmacological studies require, for a correct understanding, that the protein has the same conformation assumed inside the cell membrane, which is possible only when the protein is embedded in a lipid bilayer membrane. A scenario in which the protein is extracted from the bilayer, purified, and studied is hardly possible, because of its sensitive nature that often results in a denaturation process once extracted.
For what has been said, a study of drug/lipid interactions appears to be a necessary and important step in fully understanding and properly evaluating the role played by the two different interactions – drug/protein and drug/phospholipid. Such a study is also important, when combined with complementary investigations, for developing and finding new active ingredients with improved pharmacokinetic characteristics. Indeed, in a limited number of cases, different families of drugs such as antibiotics,6–9 antimycotics, and10,11 antipsychotics,12,13 as well as anticancer agents,14,15 have been studied from the point of view of their possible interaction with lipids,16 even through simulation studies.17 It has often been found that, even in the absence of a specific drug/membrane interaction, the binding of the drug to the membrane reduces the availability of the free drug, making the pharmacological effects blander.18–20
The high complexity shown by cell membranes makes their physico-chemical and biophysical interactions with drugs very challenging to investigate. To this aim, simplified membrane systems, like liposomes,21 giant unilamellar vesicles,22 Langmuir monolayers,23 or solid supported membranes,24 have been developed for their capability to mimic closely the natural lipid bilayer.
In this paper we report an investigation of the interaction of benzocaine and propranolol active ingredients with SoyPC phospholipid-based bilayers. Biomimetic model membranes, such as liposomes and lamellar phases, represent very good alternatives to natural membranes, since they allow investigating drug/membrane interactions under very precise and reproducible conditions, without departing from those that are the main features of a cell bilayer.
Benzocaine, chemically the ethyl ester of the 4-aminobenzoic acid, is a local anesthetic normally used as a pain reliever or for treatment of oral ulcers. It is the active ingredient of many non-prescription drugs, including those used for numb teething treatments; it is very commonly administered and it is estimated that around 30 billion doses are annually taken in the U.S.A.
Propranolol is a beta blocker medication. It is used for the treatment of high blood pressure and hyperthyroidism and in some cardiac arrhythmia scenarios.
Investigations at the nanoscale level have been carried out by means of Neutron Reflectivity (NR), Grazing Incidence Small Angle Neutron Scattering (GISANS), and Small/Ultra-Small Angle Neutron Scattering (SANS/USANS). Combination of these techniques is able to provide detailed information both on the supramolecular structures formed25 and on bilayer characteristics,26,27 highlighting eventual variations caused by drug addition. In particular, NR is able to probe the nanoscopic characteristics of the bilayers in a very accurate way, providing information about the extensions of hydrophobic and hydrophilic domains inside the bilayers: part of this accuracy is due to the capability of neutrons to depend on the nuclear composition of the sample, rather than on its electron density, like in the X-ray analogue technique. On the other hand, SANS measures the average structures in the volume probed and is ideal for examining the shape and size of supramolecular aggregates formed.
The results obtained from our investigations will show how the addition of very simple molecules (like those studied here) may modify very strongly the properties of the double layer. These findings strengthen the idea that a simple drug/protein study carried out by neglecting a (possible) interaction with the double layer may lead to a misleading or an incomplete picture of the system. Moreover, it will be noted how the present approach, involving complementary neutron-based techniques, is able to give valuable information about the systems investigated.
Going into detail, it will be seen that the two drugs exhibit different behaviors: benzocaine tends to stiffen the phospholipid-based double layer and to bend it locally with the formation of stalks, whereas propranolol causes a strong degree of disorder in the double layer, promoting the formation of distorted lamellae and structures with high curvature.
Experimental
Materials
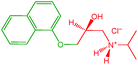
SoyPC (mainly composed of 1,2-dilinoleoyl-sn-glycero-3-phosphocholine, purity 95%, averaged molecular weight 775.037 a.m.u.) was obtained from Avanti Polar Lipids Inc. (Alabaster, AL, USA). Benzocaine (purity 98%, molecular weight 165.19 a.m.u.) and propranolol (in the hydrochloride form, purity ≥99%, molecular weight 295.80 a.m.u.) were purchased from Sigma Aldrich (Taufkirchen, Germany). All the molecular structures, as well as the molecular volumes and the scattering length densities (SLD) of hydrophobic and hydrophilic portions, highlighted in green and red colors, respectively, are reported in Table 1.Heavy water (minimum isotopic enrichment >99.8%, molecular weight 20.0276 a.m.u.) was obtained from ARMAR Chemicals (Leipzig, Germany) and used for the preparation of all the samples.
2-Propanol (molecular weight 60.10 a.m.u.) and trichloromethane (molecular weight 119.38 a.m.u.) pure for HPLC analysis were both purchased from Bachem (Bubendorf, Switzerland).
All chemicals were used as received, without further purification.
Preparation of samples for NR/GISANS experiments
Each sample used for NR and GISANS investigations was prepared starting from a standard solution of SoyPC in 2-propanol: to this aim, a selected amount of SoyPC was dissolved in the secondary alcohol, so as to achieve a molar ratio of ≅2 mol% between the phospholipid and the solvent, and a total volume of ≅15 ml. The mixed components were stirred to ensure complete dissolution of the phospholipid in the solvent. Afterwards, always under stirring, an appropriate amount of a 2-propanol-based stock solution of the drug (benzocaine or propranolol) was slowly added until a clear one-phase system was obtained.Each of the prepared solutions was deposited on an ultrapolished Si block (r.m.s. roughness <2 Å, dimensions: 15.0–5.0–2.0 cm3) obtained from Andrea Holm GmbH (Tann, Germany): an O-ring in a custom-made scaffold allowed the solution to stay on top of the silicon block. The block was levelled out by means of a spirit level. Subsequently, the solution was allowed to evaporate at room temperature and at a reduced pressure (∼250 mbar) for 8 h, in order to avoid the formation of bubbles inside the liquid phase due to a drastic decrease of the pressure. After that, the system was kept under a pressure of few millibars (<10−3 mbar) for 16 h for removing all the residual isopropanol, leading to a SoyPC/drug layer of macroscopic size (1–2 mm thick). Just after this step, the silicon block was mounted into a custom made sample cell (sketched in Fig. 1), filled with heavy water and studied through NR and GISANS experiments. The cell was equipped with a cover glass, allowing visually inspecting the SoyPC/drug layer and checking for eventual air bubbles formed after injection of D2O. Ocular inspection of the layer after the NR/GISANS investigations allowed excluding, in all prepared samples, a deterioration of the film coverage during the measurements.
All the silicon block active surfaces used for the experiments were carefully cleaned before their use through the RCA treatment.30
Preparation of samples for SANS/USANS experiments
Samples used for small angle scattering experiments were prepared starting from a stock solution, obtained by dissolving a suitable amount of SoyPC in pure chloroform, in order to achieve a concentration of ≅1 mg ml−1. Appropriate amounts of this mother solution were transferred into different round-bottom glass vials. Subsequently, suitable quantities of chloroform-based stock solutions containing the drug to be investigated were added, in order to have a pre-fixed molar ratio between the drug and phospholipid. The dissolution of the components was promoted by a slight warming (≅40 °C) and a very short sonication treatment (≅5 min). Afterwards, a thin film was obtained for every sample, through slow evaporation of the chloroform in a stream of argon, to prevent lipid oxidation. The lipid films were hydrated, and all the resulting suspensions were vortexed and then gently sonicated (≅30 min). Subsequently, an aliquot of each suspension was repeatedly extruded through a polycarbonate membrane of 100 nm pore size, 11 times. The final (molal) concentration of SoyPC was in all cases 5.0 mmol kg−1; drug concentrations were chosen accordingly to the pre-fixed molar ratio.NR and GISANS experiments
NR and GISANS measurements were performed at MARIA, N-REX, and TREFF instruments, installed at MLZ (Maier-Leibnitz Zentrum), Garching, Germany. In an NR experiment, the specular reflectivity R is measured as a function of the scattering vector component Qz along the direction z perpendicular to the interface: under the Born approximation, and in the limit of large Qz values (i.e. low R values), the reflectivity is dependent on the Fourier transform of the scattering length density profile ρ(z) along this direction:31The function ρ(z), the scattering length density at the various z values, is dependent on the local composition and allows obtaining information on the lipid bilayer at the nanoscale.
Even if in NR experiments the scattering plane is perpendicular to the sample plane, measurements always provide data containing both the specular contribution and the diffuse scattering coming from Qx = 0, where x represents the direction perpendicular both to z and to the detector plane. Anyway, the diffuse contribution is usually orders of magnitude smaller than the specularly reflected signal.32
On the other hand, in a GISANS investigation, where a non-null component of the scattering vector along a direction perpendicular to z is present, information about eventual lateral correlations inside the sample is easily accessible.33
At MARIA,34 the wavelength of the neutrons was set at λ = 10 Å for NR and at λ = 5.0 Å for GISANS investigations, with a wavelength spread of Δλ/λ ≤ 0.10 by means of a velocity selector. In the NR configuration, an elliptically curved focusing guide along the vertical direction allowed obtaining a beam size of 10 × 0.1 mm2; in the GISANS setup, a pinhole collimation setting was used, with a beam aperture of 16 × 2 mm2. The sample-to-detector distance was fixed at 1.91 m, whereas a rotating table allowed modulating the incident angle. This configuration allowed collecting data in the 3.3 × 10−3 < Qz/Å−1 < 0.31 range for NR and 0 < Qz/Å−1 < 0.25; −0.15 < Qy/Å−1 < 0.15 for GISANS, with y being the direction perpendicular to z and parallel to the detector plane. Because of its high-flux and low-background characteristics, MARIA is able to detect reflectivity values down to 10−6 with relatively short time measurements (≅1.5–2 h per sample). In GISANS mode, the measurements were mostly performed below the critical angle θ(cr) of total internal reflection: in this case an evanescent wave propagating into the sample occurred, allowing collecting information over the complete surface region down to the depth of this wave.
At NREX,35 a wavelength of λ = 4.28 Å with a wavelength spread of Δλ/λ ≤ 0.03 was used, by means of a HOPG crystal. A slit size of 50 × 1.0 mm2 was used for defining the incident beam, whereas scattered neutrons were detected by means of a 3He detector set at 2.46 m from the sample position. With this configuration, data in the 5.6 × 10−3 < Qz/Å−1 < 0.26 range were collected in NR mode and 0 < Qz/Å−1 < 0.12; 0 < Qy/Å−1 < 0.10 in the GISANS setup.
At the neutron reflectometer TREFF,36 a wavelength of 4.7 Å was used, by means of a graphite monochromator able to provide a wavelength resolution of Δλ/λ ≤ 0.03. Specular intensities were recorded in θ/2θ scan mode, with an incident beam of 0.4 × 60 mm2, covering the 9.1 × 10−4 < Qz/Å−1 < 0.25 range.
All the measurements were carried out at room temperature, using the custom made cell, as described in Fig. 1.
SANS/USANS experiments
SANS/USANS measurements were carried out by means of KWS-1 and KWS-3 diffractometers, at MLZ (Maier-Leibnitz Zentrum), Garching, Germany. Additional experiments were also performed with the TPA diffractometer, at LLB (Laboratoire Léon Brillouin), Saclay, France.At KWS-1,37 neutrons with an average wavelength of λ = 5.0 Å and a wavelength spread Δλ/λ ≤ 0.10 were used. A two-dimensional 128 × 128 pixel-based array scintillation detector set at three different collimation (C)/sample-to-detector (D) distances (namely C8/D2, C8/D8, and C20/D20, with all distances in meters) measured neutrons scattered from the samples. These configurations allowed collection of data in the scattering vector modulus (Q = 4π/λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2)) range between 0.0028 and 0.40 Å−1, with θ being the scattering angle. The investigated samples were contained in a closed quartz cell, in order to prevent the solvent evaporation, and were kept under measurement for a period so as to have at least 2 million counts of neutrons. The obtained raw data were corrected for background and empty cell scattering, and then radially averaged. Detector efficiency corrections and transformation to absolute scattering cross sections were executed with a secondary plexiglass standard.38
sin(θ/2)) range between 0.0028 and 0.40 Å−1, with θ being the scattering angle. The investigated samples were contained in a closed quartz cell, in order to prevent the solvent evaporation, and were kept under measurement for a period so as to have at least 2 million counts of neutrons. The obtained raw data were corrected for background and empty cell scattering, and then radially averaged. Detector efficiency corrections and transformation to absolute scattering cross sections were executed with a secondary plexiglass standard.38
At KWS-3,39 an incident neutron wavelength λ = 12.8 Å (wavelength spread Δλ/λ ≤ 0.2) was used, while the sample-to-detector distance was fixed at 9.6 m. KWS-3 uses a double focusing mirror principle to access to a very small angle region; a bidimensional detector with square pixels of 0.35 mm in size allowed collecting data ranging between 6 × 10−4 and 2 × 10−3 Å−1.
At TPA,40 neutrons with a wavelength of 12 Å were used, with a wavelength spread Δλ/λ ≤ 0.11. A multibeam design of the collimation system and a high resolution two dimensional image plate detector located at 6.27 m from the sample position allowed collecting data in the 4 × 10−4 < Q/Å−1 < 4.7 × 10−3 range: data corrected for background and empty cell scattering were radially averaged and rescaled to the small-angle data collected at KWS-1. To this aim, a scale factor was evaluated in order to have the smallest sum of the squares of the differences of the two datasets in the range in which the overlap between the two instruments occurred.
All the measurements were carried out at room temperature.
Results
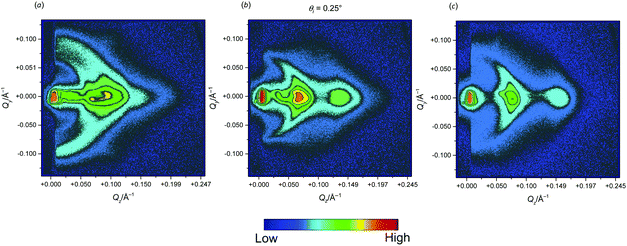
In Fig. 2(a) and (b), NR data are reported for SoyPC/benzocaine and SoyPC/propranolol systems, respectively. Inspection of data allows recognizing different behaviors shown by the two different drugs. | ||
| Fig. 2 NR data collected for (a) SoyPC/benzocaine and (b) SoyPC/propranolol systems in D2O, according to the reported legends. To allow for a better visualization, data have been multiplied by a scale factor, as indicated. In plot (a) solid curves have been obtained by fitting of the Parratt algorithm to the experimental data, as described in the text. In plot (b) Bragg reflections have been highlighted with arrows of different colors, according to their Qz positions and connections (see the Discussion section). For an accurate determination of peak positions, a Gaussian function, or a sum of two Gaussian functions for partially overlapped peaks, has been fitted to the experimental data in proximity to the maxima, and reported as solid curves. Non-detected peaks or weak peaks whose positions deviate from that of a lamellar arrangement are indicated with dashed arrows (see also Table 4). | ||
For systems containing benzocaine, the presence of two Bragg peaks at Q(1)z ≅ 0.1 Å−1 and Q(2)z = 2·Q(1)z is clearly visible. This characteristic is also observed for the system without the drug, although the position of the peaks is shifted to lower Qz values: according to the method used for lodging the SoyPC/drug mixtures on to the Si-based blocks, all these features may be explained by assuming the formation of a lamellar phase composed of the repetition of several bilayers on the support, separated by water layers. Two additional features are clearly visible by careful perusal of Fig. 2(a): (i) the presence of a weakly pronounced reflection at Q(1/2)z ≅ 0.05 Å−1 and (ii) the presence of two different critical angles highlighted by two different slopes shown by data. The first critical angle appears to be very small, i.e. smaller than or comparable to the minimum angle attained during reflectivity scans (Q(cr,1)z ≅ 0.002 Å−1), whereas the second is located around Q(cr,2)z ≅ 0.012 Å−1. Both these characteristics occur only in the presence of benzocaine, while they are absent for the pure SoyPC system.
Data for the above described systems were analyzed by means of the Parratt formalism,41 describing the scattering length density distribution, along the z direction, in terms of a stack of distinct layers. In this analysis, the Si substrate was modeled as an infinite-thick planar surface covered with a thin layer of oxide (SiO2).42 The Parratt approach uses a transition matrix for each layer, able to correlate the amplitude of the neutron wave propagating in a certain layer with the behavior in the previous adjacent layer.43 A set of matrices minimizing the sum of the squares of the differences between the experimental and the calculated reflectivities were found, characterizing the thickness, scattering length density, solvation (solvent volume fraction), and interfacial roughness of the different layers. These calculations were implemented in the MOTOFIT application:44 all the parameters were varied until the optimum fit to the data was found. Although more than one set of parameters can very often be found for a given experimental dataset, the number of these possible sets was significantly reduced by a prior knowledge of the system, which allows imposing a range of values for each parameter to be optimized, as well as a certain number of constraints, avoiding the occurrence of meaningless values. For example, the two thicknesses belonging to the opposite hydrophilic portions of the bilayers were constrained to be equal to each other. Data obtained from the analysis of the systems are reported in Fig. 3.
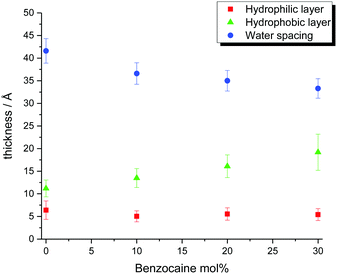 | ||
| Fig. 3 Thicknesses of SoyPC-based bilayers in the presence of benzocaine, obtained through the Parratt algorithm, according to the reported legend. | ||
Reflectivity data collected for SoyPC bilayers in the presence of propranolol show, on the other hand, a more complex behavior: multiple peaks with high broadness are visible. The positions of some reflections are, again, typical of a lamellar arrangement, but, differently from what has been seen for SoyPC/benzocaine systems, here the peaks appear broad and some of them overlap. This behavior is particularly apparent for the system with 10 mol% of propranolol: the most intense reflection is observed at Q(1a)z ≅ 0.0790 Å−1, along with two correlated peaks at Q(2a)z ≅ 0.158 Å−1 and Q(3a)z ≅ 0.235 Å−1. Besides these peaks, additional maxima are clearly present in the spectrum; in particular, a peak is visible at Q(1b)z ≅ 0.0618 Å−1, with its shoulder-like shape due to the high signal connected to the Bragg reflection at Q(1a)z that partially masks its position. Other peaks most likely correlated with Q(1b)z appear at Q(2b)z ≅ 0.124 Å−1 and at Q(3b)z ≅ 0.186 Å−1 (the latter being rather weak). These reflectivity data appear as the result of the presence of different structures, and are not susceptible of a simple quantitative analysis.
As mentioned, the study of the interaction of the active ingredients with the bilayers was also carried out in the bulk, by means of SANS/USANS. To this aim, Fig. 4 and 5 show the scattering cross sections obtained for SoyPC/benzocaine and SoyPC/propranolol systems, including both suspensions subjected to simple sonication and suspensions extruded afterwards. Analogously to what has been seen for reflectivity data, a different trend of cross sections is observed for the two systems. Some differences also occur when extruded and simply sonicated systems are compared.
Sonicated suspensions in the presence of benzocaine, as well as the drug-free SoyPC suspension, show a narrow peak located at Q ≅ 0.1 Å−1, as also observed for NR data. In the low Q region, cross sections scale with a power law, i.e. (dΣ/dΩ) ∝ Q−α, where the slope α ranges between 2 and 4. On the other hand, for sonicated suspensions in the presence of propranolol, the Bragg peak observed for samples containing benzocaine is absent, and data at low Q scale with a power law (dΣ/dΩ) ∝ Q−2. In all cases no Guinier regime is observed in the Q range covered by SANS/USANS investigations: this behavior is consistent with the opalescent appearance of the simple sonicated suspensions, indicating aggregates whose linear dimensions are larger than the typical wavelength of visible light (≅ 500 nm), although samples containing propranolol appeared less opalescent than benzocaine-based suspensions. All these features are typical of the presence of liposomes in all the suspensions: the presence of Bragg peaks and that of a power law with 2 < α < 4 are typical features of the existence of multilamellar liposomes, whereas for SoyPC/propranolol systems unilamellar liposomes are responsible for the scattering pattern detected. In all cases, the slope α of the power law observed at low Q values is connected to the lamellarity of the aggregates.45
Scattering arising from multilamellar liposomes may be described assuming the liposomes as a collection of randomly oriented assemblies of lamellar stacks, neglecting their curvature, since the Guinier region is completely missing. For such structures, the theoretical cross section of a sample containing ns randomly oriented stacks per unit volume has been obtained by Kotlarchyk and Ritzau:46
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉 in eqn (1) refer to averages both over the distribution of layer thicknesses and over that of interlamellar distances.46
〉 in eqn (1) refer to averages both over the distribution of layer thicknesses and over that of interlamellar distances.46
Scattering coming from unilamellar liposomes may be described by a single bilayer form factor:
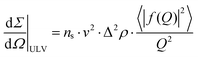 | (2) |
Analysis of experimental cross sections collected for SoyPC/benzocaine has shown that the best description has been obtained by modeling the system as a mixture of multilamellar and a small amount of unilamellar vesicles, summing up eqn (1) and (2); on the other hand, for SoyPC/propranolol a description in terms of unilamellar vesicles has been proved to be suitable for the analysis. In all the fitting procedures, a constant term, (dΣ/dΩ)incoh, has been added, which represents the incoherent contribution to the cross section measured, mainly due to the presence of hydrogen atoms. Data obtained from the analysis of the systems are reported in Table 2.
| System | α | N | τ/Å | i τ | d/Å | |
|---|---|---|---|---|---|---|
| SoyPC | 2.76 ± 0.04 | 7.3 ± 0.4 | 31.5 ± 2.5 | 1.16 ± 0.08 | 60.9 ± 1.4 | 0.11 ± 0.04 |
| SoyPC/benzocaine (10 mol%) | 2.64 ± 0.03 | 8.1 ± 0.3 | 31.8 ± 2.9 | 1.12 ± 0.07 | 61.5 ± 1.2 | 0.10 ± 0.03 |
| SoyPC/benzocaine (20 mol%) | 2.76 ± 0.04 | 7.5 ± 0.3 | 32.0 ± 2.7 | 1.22 ± 0.12 | 63.1 ± 1.5 | 0.10 ± 0.03 |
| SoyPC/benzocaine (30 mol%) | 2.72 ± 0.04 | 8.4 ± 0.3 | 32.2 ± 2.8 | 1.15 ± 0.09 | 62.9 ± 1.7 | 0.11 ± 0.03 |
| SoyPC/propranolol (10 mol%) | 2.04 ± 0.04 | — | 41.3 ± 1.2 | 1.06 ± 0.05 | — | — |
| SoyPC/propranolol (20 mol%) | 2.08 ± 0.05 | — | 40.8 ± 0.6 | 1.09 ± 0.07 | — | — |
| SoyPC/propranolol (30 mol%) | 1.97 ± 0.04 | — | 40.8 ± 0.4 | 1.11 ± 0.07 | — | — |
When data for simply sonicated suspensions are compared with the corresponding data obtained for suspensions subjected to extrusion, substantial differences can be detected. For SoyPC/benzocaine, a typical trend ascribable to unilamellar liposomes is observed in the medium and high Q regions, i.e. (dΣ/dΩ) ∝ Q−2 when 5 × 10−3 < Q/Å−1 < 7 × 10−2, similar to what has been observed for sonicated SoyPC/propranolol systems. Anyway, differently from the latter case, data at low Q for SoyPC/benzocaine suspensions reveal an excess of scattering that quantitative analysis shows to be attributable to a residual presence of multilamellar liposomes, although in this case their fraction is low.
Finally, SoyPC/propranolol extruded suspensions show the unique presence of unilamellar liposomes that, differently from what has been seen for the corresponding simply sonicated systems, are unquestionably smaller, with the Guinier regime being clearly visible when Q < 2 × 10−3 Å−1. All data for the extruded systems are reported in Table 3: quantitative analysis for such systems is similar in many respects to the corresponding description adopted for sonicated suspensions, with the main difference being the model for describing the scattering coming from unilamellar liposomes. In this case a form factor of a hollow sphere with a polydisperse aqueous core has been adopted. This model is justified by the presence of the Guinier regime for unilamellar vesicles at very low Q values, weakly detectable for SoyPC/benzocaine suspensions (because of the scattering coming from multilamellar vesicles) and clearly shown for SoyPC/propranolol systems.
| System | R core/Å | i R core | τ/Å | N | d/Å | |
|---|---|---|---|---|---|---|
| SoyPC | 407 ± 6 | 1.09 ± 0.05 | 33.0 ± 1.2 | 6 ± 2 | 62.1 | 0.10 |
| SoyPC/benzocaine (10 mol%) | 398 ± 6 | 1.09 ± 0.06 | 35.9 ± 1.5 | 4.4 ± 1.5 | 62.1 | 0.10 |
| SoyPC/benzocaine (20 mol%) | 395 ± 7 | 1.09 ± 0.05 | 36.3 ± 1.4 | 3.5 ± 1.5 | 62.1 | 0.10 |
| SoyPC/benzocaine (30 mol%) | 408 ± 6 | 1.09 ± 0.04 | 36.3 ± 1.5 | 3.5 ± 1.7 | 62.1 | 0.10 |
| SoyPC/propranolol (10 mol%) | 471 ± 7 | 1.12 ± 0.05 | 36.0 ± 1.8 | — | — | — |
| SoyPC/propranolol (20 mol%) | 521 ± 7 | 1.10 ± 0.05 | 37.0 ± 1.9 | — | — | — |
| SoyPC/propranolol (30 mol%) | 529 ± 7 | 1.09 ± 0.04 | 35 ± 2 | — | — | — |
Discussion
In the present work we focused on the study of the perturbation effects produced on the lipid bilayer by molecules used as active ingredients for some treatment, trying to correlate such effects with the drug molecular structure. Generally speaking, the perturbation effects may depend on the hydrophobicity/hydrophilicity degree of the active ingredient, on its molecular shape and on possible attractive or repulsive interactions (e.g. electrostatic) that can be established: all these factors contribute in a complex way to (eventually) perturb the phospholipid packing. To this aim, the concept of the packing factor, introduced by Israelachvili, Mitchell, and Ninham,47 has been proved to be useful, because of its capability to explain, justify and very often predict the molecular self-assembly behavior in surfactant solutions. The packing factor Ns is defined as | (3) |
Quantitative analysis of membrane characteristics was performed for SoyPC/benzocaine systems. It showed that SoyPC is organized on the Si substrate as a stack of bilayers, formed by their repetition on the support, separated by layers of water. Besides these repeating layers, a thin (≅15 Å) water layer was found to be directly stratified on the SiO2 layer (≅2 nm), covering, in turn, the Si block. In all cases, the roughness values of the interfaces ranged between 2 Å and 7 Å. Extensions of the hydrophobic and hydrophilic portions of the bilayers, as well as the dimensions of the water spacing, are plotted in Fig. 3 for the drug concentrations investigated. Inspection of data reveals a certain effect on the bilayer caused by the presence of the drug: inclusion of benzocaine reduces the repetition distance among the bilayers, but not in a monotonic fashion. For the pure SoyPC system, this distance is found to be ≅2π/Q(1)z = 65.2 Å, which reaches its minimum value for 10 mol% of the drug (59.8 Å) and slightly increases again for 20 mol% and 30 mol% (61.9 Å and 62.7 Å, respectively). Although these values are independent of any theoretical model, analysis of Fig. 3, based on the Parratt algorithm, shows that this trend is the outcome of two different tendencies: (i) the water spacing that slightly decreases with increase of the drug content (even taking into account the uncertainty affecting the data) and (ii) the thickness of the hydrophobic portion of the bilayer, which is progressively enlarged as soon as the drug amount is increased. Concerning the latter parameter, it is interesting to note that the C1–C18 distance measured in the linoleic acid (the precursor of the main species in SoyPC) is 19.2 Å.49 Although this value refers to the crystallographic distance, and although the average thickness of the hydrophobic portion of the bilayers seldom exceeds 1.8 times the fully extended length of the hydrocarbon chains,50 it is nevertheless still higher than the experimental thicknesses found, ranging from 11.2 to 19.2 Å – a symptom of an interdigitation or tilting of the hydrophobic chains. Generally speaking, there are manifold circumstances where interdigitation phenomena are observed. The most important are the asymmetry of the chains forming the phospholipid tail (i.e. one chain has more than 5–6 methylene groups with respect to the other one),51 the application of high pressures,52,53 and the solubilization of molecules able to promote or increase intermolecular lateral repulsions.54,55 In particular, the last point is what we are concerned about, since solubilized species inside the bilayer may increase (or mitigate) lateral repulsions, enhancing (or reducing) the interdigitation/tilting phenomena. It has been argued56 that the repulsions occurring in the interfacial region of the bilayer initially promote a progressive tilting of the lipid chains, for adapting the chains to the large interfacial molecular area. Increasing the tilting angle increases, in turn, the torsional and angular tensions in the lipid chain: beyond a certain threshold, the tilt cannot be further increased, and hydrocarbon interdigitation occurs.
Analysis of the hydrophobic layer thickness shows, indeed, that the insertion of benzocaine reduces the above described phenomena, as an increase of the thickness is observed with increasing content of the drug. The presence of two cis double bonds in the hydrocarbon backbone introduces kinks, preventing efficient packing of the hydrophobic chains in the bilayer, as can be seen in Fig. 6.57 It can be argued that the insertion of benzocaine is able to promote a better packing of the chains, being capable of “filling” the space that is created in consequence of the reduction of chain tilting/interdigitation. In any case, it has to be taken into account that the final packing is a compromise between the reduction (or increase) of repulsive interactions between the hydrophobic chains and a possible reduction (or increase) of repulsive interactions between the polar heads, as will be glimpsed in the following. The thickness of the hydrophilic portion is roughly constant in the concentration range studied: benzocaine has a small hydrophilic portion represented by the amine functional group and its insertion does not dramatically modify this part of the bilayer.
 | ||
| Fig. 6 “Ball and stick” representation of the 1,2-dilinoleoyl-sn-glycero-3-phosphocholine molecule (main component of SoyPC) in the staggered conformation. | ||
Finally, it is interesting to discuss and rationalize the presence of two other features appearing in SoyPC/benzocaine reflectivity data, shortly mentioned in the Results section: namely the presence of two possible critical angles and the appearance of weak reflections at Q(1/2)z ≅ 0.05 Å−1, both of these features occurring only in the presence of the drug.
There are two distinct sudden changes in slope in data trends, for systems containing benzocaine: the first is close to the minimum angle reached during investigations, namely Q(cr,1)z ≅ 0.002 Å−1, whereas the second is located around Q(cr,2)z ≅ 0.012 Å−1. Their presence might be ascribed to the different contrast Δρ = ρinf − ρSi existing between the “final” (infinite) layer and the “initial” Si layer: the contrast value determines the critical scattering vector modulus Q(cr)z at which total reflection occurs:
 | (4) |
The presence of macroscopically thick patches of bilayer material with a scarce penetration of D2O among the bilayers may rationalize the results observed: these patches, for which D2O is not “seen” as the final layer (for the purposes of the critical angle determination), coexist with normally hydrated portions of the bilayers. It has to be assumed that the sizes of these “islands” of scarcely hydrated material are bigger than the coherence volume of the incident beam, as the two angles would not be visible otherwise. Application of eqn (4) for ρinf = ρD2O gives a value (0.0146 Å−1) very close to the observed Q(cr,2)z. On the other hand, a reliable estimation of Δρ for the poorly hydrated phospholipid stacks is hardly possible because of the unknown penetration degree of water; it can only be argued that it must be smaller than the corresponding difference found for water, which is in qualitative agreement with the experimental observation that Q(cr)1 < Q(cr)2 (as can also be seen from Table 1). A similar phenomenon has been described for sodium poly-(styrenesulfonate) based films on silicon, where two critical angles arising from the silicon/film and silicon/air interfaces were observed in X-ray reflectivity investigations.58
A possible nanoscopic interpretation for the presence of patches in SoyPC/benzocaine systems might be the partial suppression of bilayer fluctuations. Fluctuations promote the detachment of the bilayers and the subsequent penetration of the solvent among the layers. The presence of benzocaine reduces the strength of these fluctuations, from which we may infer a higher rigidity of the bilayer. On the other hand, in the SoyPC and SoyPC/propranolol systems, bilayers fluctuate much more, showing the typical critical angle of the Si/D2O interface. This hypothesis may be proven through Grazing Incidence Neutron Spin-Echo Spectroscopy (GINSES) investigations. At present, the low counting rate is the main limitation for such a technique, because of the limited scattering volume that comprises only the volume covered by the evanescent wave. However, improvements for dealing with this drawback are currently under development.59
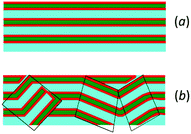
Most interesting is the appearance, for all the systems in the presence of benzocaine, of a small maximum at Q(1/2)z ≅ 0.05 Å−1, besides the first and second order Bragg peaks arising from the multilayer structure. The main point is represented by the position of this reflection that is, for all the concentrations investigated and within the experimental uncertainty, half the value of the first Bragg peak, i.e. Q(1/2)z = Q(1)z/2. A rational justification of such behavior is a local formation, in the bilayers, of stalks in the lamellar arrangement, which will then result in twice the typical repetition distance, resulting in turn in the appearance of a peak at half the value of the first Bragg peak (as sketched in Fig. 7). The formation of stalks, which are real crystal-like defects in the lipid arrangement, has to be ascribed to the capability of benzocaine to induce localized structures with a negative curvature of the bilayer membrane: such bending can only be the result of a global increase of the packing factor Ns with respect to the value assumed in pure SoyPC bilayers. Actually, it has already been seen that addition of benzocaine promotes a packing of hydrophobic chains that progressively resembles that existing in the crystal. The existence of stalks suggests that, at the same time, less repulsive interactions among the phospholipid heads occur. In turn, these interactions affect the global value of a0, i.e. the molecular area at the aggregate surface. A simple analysis carried out by Tanford48,60 shows that a0 is dependent on a headgroup repulsion parameter (β) and on the interfacial free energy (σ):  . A decrease of β results in an increase of the packing factor Ns, favoring, after all, the formation of morphologies with negative curvatures: the better packing of the hydrophobic chains, which tends to decrease Ns, is overcompensated by the improved interactions among the polar heads, leading to a global increase of Ns. In any case, it has to be highlighted that these structures are formed in a low content, due to the lower intensities of the associated Bragg peaks.
. A decrease of β results in an increase of the packing factor Ns, favoring, after all, the formation of morphologies with negative curvatures: the better packing of the hydrophobic chains, which tends to decrease Ns, is overcompensated by the improved interactions among the polar heads, leading to a global increase of Ns. In any case, it has to be highlighted that these structures are formed in a low content, due to the lower intensities of the associated Bragg peaks.
It has often been supposed that the formation of such defects is the prelude to a transition to non-lamellar phases.61 Indeed, the formation of hexagonal and tetragonal lattices has been found62 for the investigation of phospholipid-based membranes in the presence of the ibuprofen active ingredient, which is connected to the presence of similar stalks in the double layer arrangement. With the aim of investigating a possible similar situation in our system, selected GISANS scans have been performed – most of them below the critical angle of total internal reflection of the Si/D2O interface. In this case, eventual lateral correlations are probed inside the bilayers, up to the depth Λevw of the evanescent wave given by
Analysis of images reveals that starting from low angles a spot located at Qz ≅ 0.1 Å−1 and corresponding to the Bragg peak arising from the lamellar arrangement of bilayers appears. Its intensity increases as θi increases, since the penetration depth of the evanescent wave is progressively enlarged, so that a higher scattering of the lamellar bilayer structure is observed. Although not appreciable when θi < 0.1°, a Debye–Scherrer ring starts to appear at θi = 0.14°, which is indicative of an increasing amount of disordered lamellae, i.e. bilayers having an increased curviness with respect to the ideal situation corresponding to a parallel alignment of the phospholipid membranes. However, it has to be noted that the Debye–Scherrer ring does not stretch over the whole detector, suggesting that the disordering of the lamellar areas is far from being complete but rather deviates by only a few degrees from a perfect parallel ordering. Interestingly, no reflections arising from crystalline structures inside the double layer are detected, suggesting that the formed stalks are isolated, i.e. are not distributed according to the existence of a lattice. Based on the NR/GISANS results, we may point out that the presence of stalks inside the bilayer arrangement, the incomplete Si surface coverage with fully hydrated bilayers, and the imperfect parallel alignment of the bilayer with respect to the Si surface are the main sources for the non-perfect description of data by the Parratt model, i.e. the non-exact fitting of the curves in Fig. 2(a).
Much more complicated appear to be the NR data obtained for the SoyPC/propranolol system. As mentioned in the Results section, the inclusion of propranolol drastically changes reflectivity trends: analysis of data reported in Fig. 2(b) reveals, differently from what has been seen for the systems in the presence of benzocaine, the existence of multiple peaks. These peaks are broad and some of them overlap partially, compelling to describe the system in a qualitative fashion. It could be reasonable to analyze the positions of the peaks in terms of the possible existence of lamellae, as already seen for SoyPC/benzocaine systems and as normally observed for systems prepared as described in the Experimental section.62 To this aim, peaks appearing in NR data are highlighted in Fig. 2(b) by regrouping their Qz values with arrows having the same color; positions found are reported in Table 4, according to the grouping operated. In all cases no more than two sets have been found. Analysis of the positions found for the reflections shows, indeed, quite a complex trend. For the SoyPC system, as already described above, the positions of the Bragg peaks are easily described, both qualitatively and quantitatively, in terms of a (fairly ordered) lamellar phase composed of the repetition of several bilayers on the support. On the other hand, for SoyPC/propranolol systems, even at 10% mol of the drug, the data show a richer behavior. For this lowest amount, five maxima are clearly visible: analysis of their positions shows that they are correlated in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Q-ratio (or 1
2 Q-ratio (or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3), with the second set (the one located at higher Q and highlighted with grey arrows) being clearly visible, whereas the primary reflection of the first set (indicated with a black arrow) appears as a shoulder because of the high signal connected to the primary peak of the second pair. Trends become complicated for higher amounts of propranolol. At 20% mol, one peak series is clearly visible (up to the third reflection) having the primary maximum so high and broad to make the detection of the primary Bragg peak at smaller Q hardly detectable. At 30% mol, the latter peak is even not visible (with its expected position being indicated with the black dashed arrow). Analysis of the positions of the maxima indicates two repetition distances for 10% and 20% mol propranolol of 80 Å and 102 Å, and 101 Å and 125 Å, respectively. Furthermore, inspection of GISANS 2-D detector images (Fig. 9) reveals the appearance of diffuse Debye–Scherrer rings around the reflections, stronger than the corresponding rings observed for systems in the presence of benzocaine.
3), with the second set (the one located at higher Q and highlighted with grey arrows) being clearly visible, whereas the primary reflection of the first set (indicated with a black arrow) appears as a shoulder because of the high signal connected to the primary peak of the second pair. Trends become complicated for higher amounts of propranolol. At 20% mol, one peak series is clearly visible (up to the third reflection) having the primary maximum so high and broad to make the detection of the primary Bragg peak at smaller Q hardly detectable. At 30% mol, the latter peak is even not visible (with its expected position being indicated with the black dashed arrow). Analysis of the positions of the maxima indicates two repetition distances for 10% and 20% mol propranolol of 80 Å and 102 Å, and 101 Å and 125 Å, respectively. Furthermore, inspection of GISANS 2-D detector images (Fig. 9) reveals the appearance of diffuse Debye–Scherrer rings around the reflections, stronger than the corresponding rings observed for systems in the presence of benzocaine.
| System | Q (1) z /Å−1 | Q (2) z /Å−1 | Q (3) z /Å−1 | |||
|---|---|---|---|---|---|---|
| SoyPC | 0.0964 | 0.191 | 1.98 | 65.2 | ||
| SoyPC/propranolol (10 mol%) | 0.0790 | 0.158 | 2.00 | 79.5 | ||
| 0.0618 | 0.124 | 0.187 | 2.01 | 2.99 | 102 | |
| SoyPC/propranolol (20 mol%) | 0.0625 | 0.125 | 0.187 | 2.00 | 2.99 | 101 |
| 0.0466 (?) | 0.101 | 2.17 | 135 | |||
| SoyPC/propranolol (30 mol%) | 0.0752 | 0.143 (?) | 1.90 | 83.6 | ||
| ? | 0.127 |
The indications found can be ascribed to the presence, even at the lowest amount of propranolol investigated, of a powder of lamellar regions in the scattering volume. Likely, the presence of a condensed ring in the molecular structure of propranolol and the contemporaneous charge existing at physiological pH induce strong disorder in the lipid bilayer arrangement: the polycyclic moiety has less conformational freedom than the single aromatic group present in the benzocaine structure. Consequently, propranolol has a smaller or nearly null capability to act as “filler” and is unable to efficiently occupy the space created in consequence of the reduction of tilting/interdigitation of SoyPC hydrophobic chains. Furthermore, differently from what has been seen for SoyPC/benzocaine systems, the charge existing in the hydrophilic region increases the repulsive interactions in the hydrophilic region, promoting the formation of highly curved structures. These two factors may result in the formation of lamellar powders, as schematically displayed in Fig. 10.
In sum, in the presence of benzocaine only a very limited local disorder of lamellar arrangement (along with the formation of negatively curved structures inside the lamellar phase) occurred, so that the NR data were still describable in terms of the Parratt model. On the other hand, the presence of propranolol has a much stronger effect that may not be interpreted as a simple deviation from the perfect parallel ordering, as also highly evidenced by NR data.
It is interesting to compare the strong perturbative effects on the bilayer arrangement due to propranolol addition, with the results found by Pereira-Leite and collaborators.63 The authors investigated the interaction of propranolol with bilayers composed of egg phosphatidylcholine (EPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC). In particular, they observed a decrease of the gel–sol transition temperature due to the presence of the drug, as well as a reduction of the order parameter associated with the transition. These pieces of evidence are consistent with the results found in the presence of SoyPC: a stronger disorder caused by the presence of propranolol is connected to a less efficient packing of the double layer that results in a gel–sol transition temperature smaller than the one corresponding to the pure phospholipid. The behavior observed for propranolol is also found for other drugs, although with different characteristics.64
The results obtained from the NR/GISANS analysis of SoyPC bilayers in the presence of benzocaine and propranolol drugs allow foreseeing what should be the characteristics of such bilayers under bulk conditions, i.e. in water dispersions: under these conditions liposomes are formed. Unless a certain amount of mechanical energy is transferred to liposomes during their preparation (e.g. in the case of extrusion of aqueous suspensions), the size and characteristics of a population of liposomes are the result of a complex balance between the entropy of mixing65 and bilayer curvature elasticity.66–68 In the limit of large liposomes, with dimensions much larger than the surfactant size, the curvature energy per unit area of bilayer fc is given by65
 | (5) |
![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) being the bending moduli, depending, in turn, on the elastic constants determined by the head–head and tail–tail interactions. Finally, c1 and c2 indicate the two local curvatures, whereas cs represents the spontaneous (i.e. minimum-energy) radius of curvature. In the case of a bilayer with relatively high curvature, as appears to be the case for SoyPC/propranolol systems, the energy required for hypothetically adding a further bilayer to the liposome (i.e. for increasing the lamellarity) can overcome the attractive interaction between bilayers: in this case, a limited number of lamellae associated with a single liposome may be observed. In the most extreme cases, unilamellar liposomes are exhibited. Observations from NR and GISANS data could suggest the formation of oligolamellar or even unilamellar liposomes for aqueous suspensions prepared in the presence of propranolol, whereas a higher number of lamellae is expected when benzocaine is used.
being the bending moduli, depending, in turn, on the elastic constants determined by the head–head and tail–tail interactions. Finally, c1 and c2 indicate the two local curvatures, whereas cs represents the spontaneous (i.e. minimum-energy) radius of curvature. In the case of a bilayer with relatively high curvature, as appears to be the case for SoyPC/propranolol systems, the energy required for hypothetically adding a further bilayer to the liposome (i.e. for increasing the lamellarity) can overcome the attractive interaction between bilayers: in this case, a limited number of lamellae associated with a single liposome may be observed. In the most extreme cases, unilamellar liposomes are exhibited. Observations from NR and GISANS data could suggest the formation of oligolamellar or even unilamellar liposomes for aqueous suspensions prepared in the presence of propranolol, whereas a higher number of lamellae is expected when benzocaine is used.
Analysis of SANS trends shows, indeed, that this is the case: unilamellar liposomes are exclusively observed in the SoyPC/propranolol system, independently of the preparation method adopted (simple sonication or extrusion), whereas multilamellar liposomes are observed for SoyPC/benzocaine sonicated suspensions. The results obtained through the fitting of theoretical models described in the Results section are reported in Tables 2 and 3. For SoyPC/benzocaine systems, multilamellar liposomes with an average lamellarity of N ≅ 7 are observed: these liposomes coexist with a small fraction of unilamellar structures. Although unilamellar liposomes would be expected to coexist with liposomes having a smaller lamellarity (2 ≤ N ≤ 5), it is important to note that in the adopted model, where no polydispersity for N is considered, the number of layers is generally only approximately estimated; it determines the upturn in scattering at low Q values where the total thickness of the stack is seen.69,70 The essential bilayer characteristics obtained from the analysis of NR data are retained for liposomes studied in an aqueous environment by means of SANS investigations. The values of bilayer thickness τ agree, as a rule, to the corresponding data obtained from NR data, although they are slightly overestimated: small discrepancies are normally present depending on the approximation degree of the model adopted for the fitting analysis. In the present case, for example, a homogeneous SLD profile has been assumed for the bilayer. Moreover, the strong Bragg peaks observed give a repetition distance of the bilayer arrangement very close to the values extracted through NR analysis.
The high curvature of bilayers produces, in SoyPC/propranolol systems, only unilamellar liposomes, even without any extrusion process, see Fig. 4(b). Ocular inspections of suspensions have shown a lower turbidity when compared to the corresponding SoyPC/benzocaine samples, suggesting the presence of smaller liposomes. Anyway, their linear size is still too large to make the Guinier region fall in the Q range covered by SANS/USANS measurements. Bilayer thicknesses appear to be comparable to the corresponding values obtained for benzocaine-based dispersions.
Analysis of the systems subjected to the extrusion of the prepared suspensions shows the presence of bilayers having lateral dimensions similar to those observed for simply sonicated systems. On the other hand, the characteristics of SoyPC-based liposomes are, at large scales, mainly influenced by the preparation method adopted: large liposomes (having radius R ≫ 500 nm) occur when the phospholipid suspensions are only sonicated, whereas relatively small liposomes (R ≅ 400 nm) are produced if the aqueous suspensions are also subjected to extrusion. Generally speaking, in the presence of extrusion processes, vesicle dimensions are often (but not always) grossly determined by the pore size of the membrane used (100 nm in the present preparation). Exceptions to this typical rule are observed when elastic deformations of the liposomes occur during their crossing of the pores of the membrane used in the extrusion process.71
Also the liposome lamellarity and the size polydispersity are influenced by the extrusion process: for the extruded SoyPC/benzocaine systems, the partial tendency of the liposomes to form unilamellar structures has been observed, as proved by SANS data, even if a small residue of the scattering still arises from multilamellar structures. The extrusion process is considered to be a reliable methodology to produce unilamellar vesicles,72 even if in some cases, because of rearrangement phenomena, it has also been found to produce multilamellar aggregates,73 or even more complex morphologies.74 The general trend is here fulfilled, even if the small fraction of multilamellar aggregates suggests that a higher amount of energy, i.e. a higher number of extrusion steps, has to be provided for a further or total reduction of the multilamellar aggregates.
Finally, it is worthy of note that although the prepared liposomes, analogously to most of the natural phospholipids, are found to be metastable, their lifetime (which is of the order of months, at least) does not have any appreciable effect on the timescale covered by the investigations carried out.
Conclusions
In this paper, the influence of benzocaine and propranolol active ingredients on SoyPC-based bilayers has been investigated. Despite their small and simple chemical structures, marked and different effects of these two drugs have been found: on one hand, benzocaine induces a locally highly negative bending of the bilayer membrane, a result of a better packing of phospholipid hydrophobic chains and a closer distance between polar adjacent heads. Over large length scales, only a slight disorder from a perfect parallel ordering is observed.On the other hand, propranolol, because of its structure and of the presence of charged heads (occurring under physiological conditions), promotes the formation of highly curved bilayers. This has been observed both in NR/GISANS investigations, where a high disorder typical of the formation of lamellar powders exists, and in SANS experiments, where only unilamellar liposomes have been observed.
It is important to recognize that the drug concentrations investigated in the present study are beyond the dosage in any medical posology. Nonetheless, it may be argued that a correlation exists between the effects observed at the expense of the bilayers and the complications due to high drug dosages, where a local excess of active ingredient is in all cases present. A possible structural modification of the bilayer may nevertheless cause a change in the mobility of membrane proteins, reducing or even inhibiting their biological function, giving rise to possible serious cell damages.75
A further point to be reaffirmed concerns the necessity, shown by results obtained, to check for eventual interactions between the active ingredients and the phospholipid-based bilayer. The methodology adopted here combining NR, GISANS, and SANS/USANS has been proven to be helpful for characterizing, at the nanoscale, the main features of the bilayer. Integration with GINSES is desirable to integrate the structural information with the bilayer dynamics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Jülich Centre for Neutron Science, Maier-Leibnitz Center, Max Planck Institute for Solid State Research and Laboratoire Léon Brillouin are fully acknowledged for their excellent support and for provision of beam time. One of us (MG) thanks the Georgian Shota Rustaveli National Science Foundation for financial support (contract number 04/02).Notes and references
- G. M. Cooper and R. E. Hausman, The Cell: A Molecular Approach, Sinauer Associates, 2016 Search PubMed.
- B. Alberts, A. Johnson, J. Lewis, D. Morgan, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Sixth Edition, Taylor & Francis Group, 2014 Search PubMed.
- W. Lim, B. Mayer and T. Pawson, Cell Signaling: principles and mechanisms, Taylor & Francis Group, 2014 Search PubMed.
- M. A. Yildirim, K. I. Goh, M. E. Cusick, A. L. Barabasi and M. Vidal, Nat. Biotechnol., 2007, 25, 1119–1126 CrossRef CAS PubMed.
- P. Cohen, Nat. Rev. Drug Discovery, 2002, 1, 309–315 CrossRef CAS PubMed.
- A. Grancelli, A. Morros, M. E. Cabanas, O. Domenech, S. Merino, J. L. Vazquez, M. T. Montero, M. Vinas and J. Hernandez-Borrell, Langmuir, 2002, 18, 9177–9182 CrossRef CAS.
- T. Guinan, C. Godefroy, N. Lautredou, S. Pace, P. E. Milhiet, N. Voelcker and F. Cunin, Langmuir, 2013, 29, 10279–10286 CrossRef CAS PubMed.
- K. Hoc-Wydro, J. Kapusta, A. Jagoda, P. Wydro and P. Dynarowicz-Latka, Chem. Phys. Lipids, 2007, 150, 125–135 CrossRef PubMed.
- Z. Sajjadiyan, N. Cheraghi, S. Mohammadinejad and L. Hassani, J. Biol. Phys., 2017, 43, 127–137 CrossRef CAS PubMed.
- A. Ambrosini, G. Bossi, S. Dante, B. Dubini, L. Gobbi, L. Leone, M. G. P. Bossi and G. Zolese, Chem. Phys. Lipids, 1998, 95, 37–47 CrossRef CAS.
- S. Goncalves, A. Teixeira, J. Abade, L. N. de Medeiros, E. Kurtenbach and N. C. Santos, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 1420–1426 CrossRef CAS PubMed.
- Y.-W. Jiang, G. Gao, Z. Chen and F.-G. Wu, New J. Chem., 2017, 41, 4048–4057 RSC.
- A. V. Agasosler, L. M. Tungodden, D. Cejka, E. Bakstad, L. K. Sydnes and H. Holmsen, Biochem. Pharmacol., 2001, 61, 817–825 CrossRef CAS PubMed.
- S. S. Feng, K. Gong and J. Chew, Langmuir, 2002, 18, 4061–4070 CrossRef CAS.
- A. Preetha, N. Huilgol and R. Banerjee, Colloids Surf., B, 2006, 53, 179–186 CrossRef CAS PubMed.
- C. Peetla, A. Stine and V. Labhasetwar, Mol. Pharmaceutics, 2009, 6, 1264–1276 CrossRef CAS PubMed.
- A. Yousefpour, H. Modarress, F. Goharpey and S. Amjad-Iranagh, J. Mol. Model., 2017, 23, 1–18 CrossRef CAS PubMed.
- J. A. McLure, J. O. Miners and D. J. Birkett, Br. J. Clin. Pharmacol., 2000, 49, 453–461 CrossRef CAS PubMed.
- S. Nagar and K. Korzekwa, Drug Metab. Dispos., 2012, 40, 1649–1652 CrossRef CAS PubMed.
- D. A. Smith, L. Di and E. H. Kerns, Nat. Rev. Drug Discovery, 2010, 9, 929–939 CrossRef CAS PubMed.
- A. Doisy, J. E. Proust, T. Ivanova, I. Panaiotov and J. L. Dubois, Langmuir, 1996, 12, 6098–6103 CrossRef CAS.
- S. Smeazzetto, F. Tadini-Buoninsegni, G. Thiel, D. Berti and C. Montis, Phys. Chem. Chem. Phys., 2016, 18, 1629–1636 RSC.
- G. Brezesinski and H. Mohwald, Adv. Colloid Interface Sci., 2003, 100, 563–584 CrossRef PubMed.
- E. T. Castellana and P. S. Cremer, Surf. Sci. Rep., 2006, 61, 429–444 CrossRef CAS.
- W. T. Heller and K. C. Littrell, Methods Mol. Biol., 2009, 544, 293–305 CAS.
- C. F. Majkrazk, N. F. Berk, S. Krueger and U. A. Perez-Salas, Neutron Scattering Biol., 2006, 225–263 CAS.
- M. Loesche, Synth. Microstruct. Biol. Res., [Proc. Int. Conf.], 3rd, 1992, 91–108 CAS.
- R. S. Armen, O. D. Uitto and S. E. Feller, Biophys. J., 1998, 75, 734–744 CrossRef CAS PubMed.
- P. Gianni and L. Lepori, J. Solution Chem., 1996, 25, 1–42 CrossRef CAS.
- W. Kern and D. A. Puotinen, RCA Rev., 1970, 31, 187–206 CAS.
- J. Daillant and A. Gibaud, X-ray and neutron reflectivity: principles and applications, Springer, Berlin, 2009 Search PubMed.
- O. H. Seeck and E. Kentzinger, in Neutron Scattering. Lectures of the JCNS Laboratory Course held at Forschungszentrum Jülich and the research reactor FRM II of TU Munich., ed. T. Brückel, G. Heger, D. Richter and R. Zorn, Forschungszentrum Jülich GmbH, Jülich, 2007, ch. 5, vol. 38 Search PubMed.
- S. K. Sinha, E. B. Sirota, S. Garoff and H. B. Stanley, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 2297–2311 CrossRef.
- S. Mattauch, A. Koutsioubas and S. Pütter, J. Large-Scale Res. Facil., 2015, 1, A8 CrossRef.
- Y. Khaydukov, O. Soltwedel and T. Keller, J. Large-Scale Res. Facil., 2015, 1, A38 CrossRef.
- Neutron Optics – Instrument Service – Science & Projects – MLZ – Heinz Maier-Leibnitz Zentrum, http://www.mlz-garching.de/neutron-optics.
- H. Frielinghaus, A. Feoktystov, I. Berts and G. Mangiapia, J. Large-Scale Res. Facil., 2015, 1, A28 CrossRef.
- G. D. Wignall and F. S. Bates, J. Appl. Crystallogr., 1987, 20, 28–40 CrossRef CAS.
- V. Pipich and Z. Fu, J. Large-Scale Res. Facil., 2015, 1, A31 CrossRef.
- S. Desert, V. Thevenot, J. Oberdisse and A. Brulet, J. Appl. Crystallogr., 2007, 40, S471–S473 CrossRef CAS.
- L. G. Parratt, Phys. Rev., 1954, 95, 359–369 CrossRef.
- G. Fragneto-Cusani, J. Phys.: Condens. Matter, 2001, 13, 4973–4989 CrossRef CAS.
- R. J. Roe, Methods of X-ray and neutron scattering in polymer science, Oxford University Press, New York, 2000 Search PubMed.
- A. Nelson, J. Appl. Crystallogr., 2006, 39, 273–276 CrossRef CAS.
- H. Frielinghaus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051603 CrossRef PubMed.
- M. Kotlarchyk and S. M. Ritzau, J. Appl. Crystallogr., 1991, 24, 753–758 CrossRef CAS.
- J. N. Israelachvili, D. J. Mitchell and B. W. Ninham, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1525–1568 RSC.
- R. Nagarajan, Langmuir, 2002, 18, 31–38 CrossRef CAS.
- F. D. Gunstone, J. L. Harwood and A. J. Dijkstra, The lipid handbook with CD-ROM, CRC Press, Boca Raton, 2007 Search PubMed.
- D. F. Evans and H. K. Wennerström, The colloidal domain: where physics, chemistry, biology, and technology meet, Wiley-VCH, New York, 1999 Search PubMed.
- S. W. Hui, J. T. Mason and C. Huang, Biochemistry, 1984, 23, 5570–5577 CrossRef CAS PubMed.
- L. F. Braganza and D. L. Worcester, Biochemistry, 1986, 25, 2591–2596 CrossRef CAS PubMed.
- R. Chen, D. Poger and A. E. Mark, J. Phys. Chem. B, 2011, 115, 1038–1044 CrossRef CAS PubMed.
- R. V. McDaniel, T. J. McIntosh and S. A. Simon, Biochim. Biophys. Acta, Biomembr., 1983, 731, 97–108 CrossRef CAS.
- M. L. Manca, I. Castangia, P. Matricardi, S. Lampis, X. Fernandez-Busquets, A. M. Fadda and M. Manconi, Colloids Surf., B, 2014, 117, 360–367 CrossRef CAS PubMed.
- N. E. Nagel, G. Cevc and S. Kirchner, Biochim. Biophys. Acta, Biomembr., 1992, 1111, 263–269 CrossRef CAS.
- H. Martinez-Seara, T. Rog, M. Pasenkiewicz-Gierula, I. Vattulainen, M. Karttunen and R. Reigada, J. Phys. Chem. B, 2007, 111, 11162–11168 CrossRef CAS PubMed.
- R. Steitz, W. Jaeger and R. von Klitzing, Langmuir, 2001, 17, 4471–4474 CrossRef CAS.
- H. Frielinghaus, M. Gvaramia, G. Mangiapia, S. Jaksch, M. Ganeva, A. Koutsioubas, S. Mattauch, M. Ohl, M. Monkenbusch and O. Holderer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2017, 871, 72–76 CrossRef CAS.
- C. Tanford, The hydrophobic effect: formation of micelles and biological membranes, Wiley, New York, 1973 Search PubMed.
- J. M. Seddon and R. H. Templer, in Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, North-Holland, 1995, ch. 3, vol. 1, pp. 97–160 Search PubMed.
- S. Jaksch, F. Lipfert, A. Koutsioubas, S. Mattauch, O. Holderer, O. Ivanova, H. Frielinghaus, S. Hertrich, S. F. Fischer and B. Nickel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022716 CrossRef PubMed.
- C. Pereira-Leite, C. Carneiro, J. X. Soares, C. Afonso, C. Nunes, M. Lúcio and S. Reis, Eur. J. Pharm. Biopharm., 2013, 84, 183–191 CrossRef CAS PubMed.
- C. Nunes, G. Brezesinski, J. L. F. C. Lima, S. Reis and M. Lucio, Soft Matter, 2011, 7, 3002–3010 RSC.
- S. A. Safran, P. A. Pincus, D. Andelman and F. C. Mackintosh, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 1071–1078 CrossRef CAS.
- P. Herve, D. Roux, A. M. Bellocq, F. Nallet and T. Gulikkrzywicki, J. Phys. II, 1993, 3, 1255–1270 CrossRef CAS.
- D. C. Morse and S. T. Milner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 5918–5945 CrossRef CAS.
- B. D. Simons and M. E. Cates, J. Phys. II, 1992, 2, 1439–1451 CrossRef CAS.
- M. Vaccaro, R. Del Litto, G. Mangiapia, A. M. Carnerup, G. D'Errico, F. Ruffo and L. Paduano, Chem. Commun., 2009, 1404–1406 RSC.
- R. D. Harvey, N. Ara, R. K. Heenan, D. J. Barlow, P. J. Quinn and M. J. Lawrence, Mol. Pharmaceutics, 2013, 10, 4408–4417 CrossRef CAS PubMed.
- S. Lesieur, C. Grabielle-Madelmont, M.-T. Paternostre and M. Ollivon, Anal. Biochem., 1991, 192, 334–343 CrossRef CAS PubMed.
- B. Mui, L. Chow and M. J. Hope, Methods Enzymol., 2003, 367, 3–14 CAS.
- G. D'Errico, A. Silipo, G. Mangiapia, G. Vitiello, A. Radulescu, A. Molinaro, R. Lanzetta and L. Paduano, Phys. Chem. Chem. Phys., 2010, 12, 13574–13585 RSC.
- G. Mangiapia, M. Vaccaro, G. D'Errico, H. Frielinghaus, A. Radulescu, V. Pipich, A. M. Carnerup and L. Paduano, Soft Matter, 2011, 7, 10577–10580 RSC.
- M. J. Saxton, Biophys. J., 1987, 52, 989–997 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2017 |