Quantum stochastic trajectories: the Smoluchowski–Bohm equation
Received
6th September 2017
, Accepted 20th November 2017
First published on 20th November 2017
Abstract
Molecular systems are quantum systems, but the complete characterization of molecular motions within a fully quantum framework might appear to be an unfeasible task because it would require that the actual nuclear positions are established at any time. One would like to use a quantum molecular trajectory that defines the instantaneous nuclear positions and satisfies the predictions of quantum mechanics in terms of its statistical properties. Even though it can be proven that the single Bohm trajectory provides a representation of the quantum molecular trajectory, this solves the issue only on a theoretical ground: exact solutions of the Schrödinger–Bohm dynamical system are extremely computationally demanding. Therefore, we derive a stochastic equation of Smoluchowski type from the Schrödinger–Bohm dynamics, through projection operator techniques, in order to characterize the molecular motions of open quantum systems. The main quantum features of the motions emerge from the equilibrium distribution, i.e., the wave function's squared modulus integrated on the environment degrees of freedom. Furthermore, we verify the accuracy of the stochastic equation by comparing its predictions with those of the deterministic dynamics for a model system of six interacting harmonic oscillators. The indisputable advantage of this full quantum mechanical approach is that of representing the molecular dynamics, which controls important phenomena like vibrational relaxation, conformational transitions and activated processes, in a self consistent way and at the low computational cost of solving simple stochastic equations.
1 Introduction
Many phenomena, such as chemical reactions, conformational changes and protein folding, are closely related to the time evolution of the spatial position of the nuclei in the molecules. Due to this reason, the accurate characterization of molecular geometry and of molecular motions is fundamental in chemistry. On the one hand, common methodologies rely on classical molecular dynamics (or its quantum correction as ab initio molecular dynamics)1–3 in order to establish rigorously the nuclear positions at any time. Several applications of these kinds of approaches are available in the literature with the purpose of examining both the dynamics of the molecular scaffold (as the photoisomerization of azobenzene) and the intermolecular geometry (as the hydrogen bond network in a cluster of water molecules).4–7 On the other hand, one would like to use quantum methods because of the quantum nature of molecular systems.8 However, the probabilistic character of the wave function prevents a univocal identification of the instantaneous positions of the nuclei. This issue cannot be avoided even if one might select the most probable configuration of the system at a given time when dealing with a localized wave function as the wave packets employed in the scattering analysis.9–12
A proposal for the quantum molecular trajectory on the basis of the Bohm coordinates has been presented by us in a recent publication.13 This trajectory defines rigorously the particle positions at any time, as in classical mechanics, but without contradicting the predictions of quantum mechanics which are recovered from the sampling of the time dependent trajectory. The Bohm theory is a formulation of quantum mechanics that characterizes a quantum system according to both the time dependent configuration, i.e., the positions of all the quantum particles, and the wave function.14–16 The configuration evolves in time by drawing a continuous trajectory that solves the Bohm equation. In the original formulation, the agreement between Bohm theory and the standard formulation of quantum mechanics is established by introducing the suitable ensemble of trajectories emerging from all the possible initial configurations. This representation is also known in the literature as hydrodynamic interpretation.17 In contrast, in our approach a single Bohm trajectory is considered with the purpose of identifying rigorously the time-dependent positions of the system components. Such a trajectory can be used to represent the molecular geometry and the molecular motions within a full quantum framework. Indeed this representation is fully congruent with quantum mechanics: the probabilistic predictions derived from the wave function are recovered in terms of the configuration distribution generated by the single Bohm trajectory. Evidence to this regard have been found with the calculated Bohm trajectory of a model system.18 Afterwards, such an equivalence was proven in ref. 13 where we have introduced the phase space representation for the independent dynamical variables together with the Liouville operator for the corresponding distribution.
On the other hand, the hydrodynamic interpretation17 provides an alternative, but equivalent picture in terms of an ensemble of quantum trajectories that collectively reproduce the evolution of the wave function. Such a point of view has been exploited by Wyatt and coworkers by designing algorithms for the self-consistent evolution of the trajectories in order to calculate the wave function dynamics.19,20 It has been applied to a variety of molecular phenomena, from the reactive scattering to the tunneling processes,21–23 and it shares with our approach the same identification of the quantum trajectories according to the Bohm equation. The essential difference is the use of a single Bohm trajectory by us, instead of their ensemble reproducing the wave function, in order to evaluate the molecular motions as well as the quantum observables. In ref. 13 and 18 we have presented the statistical tools required to characterize the single Bohm trajectory.
Albeit our method is completely general, it has strong limitations from the computational point of view. First of all, it requires the full knowledge of the time dependent wave function for the closed (isolated) quantum system through the solution of the Schrödinger equation. Secondly, given the wave function that determines the velocity field for the Bohm coordinates, one has to integrate numerically the Bohm equation that has a rather stiff behaviour in order to obtain the time dependent positions. Therefore, it appears that the full calculation of the Bohm trajectory is confined to model systems with few degrees of freedom.
In this work we intend to overcome the high computational cost of determining exactly the quantum molecular trajectory, by introducing its stochastic representation. As a matter of fact, stochastic methods are shared by several fields of Physical Chemistry,24 for example in the description of the kinetics of chemical reactions by considering explicitly the fluctuations on the number of molecules of the components.25–28 We recall a recent analysis of the two-state kinetics that takes into account the noise effects on the measured concentrations.29 Furthermore, stochastic methodologies are extremely powerful for the study of the dynamics of macromolecules of biological interest.30,31 Recent applications concern the correlation between the internal dynamics and the overall motion of proteins.32–34 On the other hand, we stress that our stochastic representation is applied to the Bohm coordinates only and, therefore, from the methodological point of view it is completely different from the dissipative or stochastic extension of the Schrödinger equation.35–39
We aim to represent the molecular motions of open quantum systems that are defined by the degrees of freedom to be used for characterizing the geometry of the molecule of interest. For instance, when a conformational change is occurring, the motion of the solvent molecules is less significant than the dynamics of the degrees of freedom that define the molecular conformation. The appropriate tool for this objective is supplied by the projection operator techniques, like Mori–Zwanzig procedures in classical mechanics,40–43 to be applied to the Liouville representation for the Schrödinger–Bohm dynamics.13 By examining the case of a generic open quantum system in equilibrium with the environment, we derive a Fokker–Planck equation of Smoluchowski type (the Smoluchowski–Bohm equation), for the probability density on the corresponding Bohm coordinates. Then, the main quantum features of the dynamics are taken into account through the equilibrium density distribution that corresponds to the square modulus of the wave function of the isolated system to be integrated on the degrees of freedom of the environment. As long as projection techniques necessarily supply approximated representation to the underlying deterministic dynamics, it is important to make a comparison between the two descriptions at least in model systems. To this purpose, we shall employ a system of six interacting harmonic oscillators, with one oscillator playing the role of the open system.
The benefits of using the Smoluchowski–Bohm equation are twofold. First of all, it is derived within a full quantum framework where the molecular motions are well defined according to the quantum molecular trajectory. Secondly, it preserves the low computational cost that characterizes the stochastic methodologies. These two features suggest that our approach could find useful applications in reproducing molecular dynamics in the quantum regime like tunnelling or activated processes at low temperature.
The paper is organized as follows. In Section 2 the description of the molecular systems according to a single Bohm trajectory is summarized, by recalling its statistical characterization presented in ref. 13 because of its relevance to the use of Mori–Zwanzig projection operators. The projection operator technique is introduced in Section 3 in all generality, while in Section 4 we derive the Smoluchowski–Bohm equation and its corresponding Langevin equation. In Section 5 we introduce the model system of six interacting harmonic oscillators, which is employed in Section 6 to compare the predictions of the stochastic equations with those of the exact dynamics.
2 The quantum trajectory and the Liouville equation
In the framework of Bohm theory, the state of isolated quantum systems is described by the configuration Q(t) and the quantum pure state |Ψ(t)〉 together.14–16 For a system composed of n degrees of freedom, the configuration includes the corresponding n coordinates, Q(t) = (Q1(t),Q2(t),…,Qn(t)). The evolution of the quantum state is described by the Schrödinger–Bohm dynamics that is determined by the Bohm equation, for the coordinates, and the Schrödinger equation, for the quantum pure state,| | 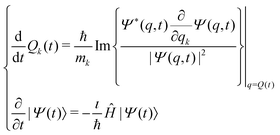 | (1) |
for k = 1, 2,…,n, where Ĥ is the Hamiltonian operator, Qk(t) is the coordinate of the k-th degree of freedom with an associated mass mk and the wave function Ψ(q,t) is the coordinate representation of the quantum pure state, Ψ(q,t) = 〈q|Ψ(t)〉. According to eqn (1), the time evolution of (Q(t),|Ψ(t)〉) follows a deterministic dynamics: given the initial condition (Q(0),|Ψ(0)〉), a uniquely defined state at arbitrary time t is determined by solving eqn (1):| |  | (2) |
In this way the time evolution of the configuration Q(t) draws a quantum continuous trajectory, i.e., the Bohm trajectory. As argued in previous work,13 the Bohm trajectory Q(t) can be used to define the actual positions of all the particles composing molecular systems including nuclei and, therefore, to characterize the molecular motions. In this way the molecular motions are described within a full quantum framework, since the predictions of standard quantum mechanics (e.g., expectation values) correspond to the statistical properties of the trajectory itself.13
Furthermore, the Schrödinger–Bohm dynamics can be represented according to the mathematical theory of the dynamical system44 where the state X(t) of a generic system belonging to an appropriate manifold Ω evolves in time according to a system of ordinary differential equations like
| | 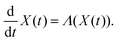 | (3) |
This is particularly useful, since it allows the straightforward use of projection operator techniques,
40–43 commonly employed in the analysis of classical dynamics, for inferring stochastic equations also in the framework of Bohm theory. In the following, we summarize the fundamental steps for representing the Schrödinger–Bohm dynamics of
eqn (1) according to a differential equation like that of
eqn (3), whereas the details are reported in
ref. 13.
First of all it is assumed that time-dependent pure state |Ψ(t)〉 belongs to an N dimensional Hilbert space, called active space,
| | 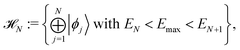 | (4) |
that is the Hilbert subspace due to eigenstates |
ϕj〉 of the Hamiltonian operator
Ĥ with eigenvalues
Ej smaller than the energy cutoff
Emax. For a given initial pure state, the cutoff parameter
Emax must be chosen according to the largest energy of its eigenstate components. The pure state |
Ψ(
t)〉 is expressed as superposition of the eigenstates |
ϕj〉
| | 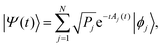 | (5) |
where the coefficients 〈
ϕj|
Ψ(
t)〉 are specified in polar form according to the constant populations {
Pj} and the time dependent phases {
Aj(
t)} with
Aj(
t) =
Aj(0) + (
Ej/
ħ)
t. By dealing with a normalized representation |
Ψ(
t) of the pure state, the ensemble of populations results to be normalized too,
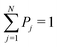
. Since the pure state of
eqn (5) is fully identified by the set of phases
A(
t) = (
A1(
t),
A2(
t),…,
AN(
t)) once the populations are established, a complete description of the Schrödinger–Bohm dynamics is recovered by considering also the Bohm coordinates according to the time dependent variable
X(
t),
| | | X(t) := (Q(t), A(t)) ∈ ΩP, | (6) |
belonging to the manifold
ΩP =
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
× [0,2π)
N = {(
q,
α)} = {
x}, where
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif)
represents the configuration space while [0,2π) is the domain of each phase variable. The subscript
P of
ΩP highlights the parametric dependence on the population set
P of the map supplied by
eqn (5) between each element of the manifold
ΩP and a specific pure state |
Ψ(
t)〉. In our notation the capital letters,
i.e.,
X(
t) = (
Q(
t),
A(
t)), tag the actual system state whereas the corresponding lowercase symbols,
i.e.,
x = (
q,
α), are used for the generic element of the manifold
ΩP. For instance, a distribution (probability density)
ρΩP on the manifold
ΩP will be described by the function
ρΩP(
x,
t) depending on the point
x ∈
ΩP and in general on the time.
In order to translate the Schrödinger–Bohm dynamics into an evolution equation for the X(t) parametrization of the state, the wave function Ψ(q,t) = 〈q|Ψ(t)〉 is derived from eqn (5)
| | 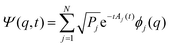 | (7) |
where
ϕj(
q) = 〈
q|
ϕj〉 are the
q-representation of the eigenstates |
ϕj〉. Then, by substitution of this wave function into the Schrödinger–Bohm
eqn (1), one obtains the first order differential equations for
X(
t) = (
Q(
t),
A(
t)), which can be specified like in
eqn (3),
| | 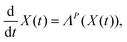 | (8) |
where the velocity field
ΛP(
x) is denoted with the superscript
P to highlight its parametric dependence on the populations
P. As found in
ref. 13, the
n +
N components of the velocity field
ΛP(
x) are given as
| | 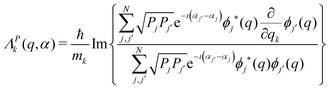 | (9) |
with
k = 1, 2,…,
n and
j = 1, 2,…,
N.
Eqn (9) is equivalent to the Bohm equation in
eqn (1) for the coordinates, while
eqn (10) specifies the phase's rates of change d
Aj(
t)/d
t =
Ej/
ħ according to the Schrödinger equation.
The Liouville equation for a generic probability density ρΩP(x,t) on the manifold ΩP in correspondence of the dynamics specified by eqn (8) is given as
| | 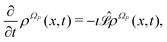 | (11) |
with the following Liouville operator
13| | 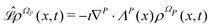 | (12) |
where ∇
P = (∂/∂
q1,…,∂/∂
qn,∂/∂
α1,…,∂/∂
αN) is the gradient operator in the space
ΩP. The stationary solution of the Liovuille equation,
i.e., the equilibrium density distribution,
| | 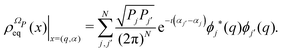 | (13) |
has a fundamental role in the projection procedure leading to stochastic equations. The factor 1/(2π)
N has been included in
eqn (13) in order to ensure the normalization of the equilibrium distribution
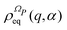
by integration on the coordinates
q and the phases
α. We stress that
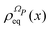
is proportional to the square modulus of the wave function if the phase dependence is replaced by the time dependence,
i.e.,
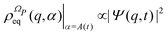
.
3 Stochastic modelling of Bohm dynamics
In this section we employ the projection operator procedure40–43 in order to recover a stochastic representation of Bohm dynamics for an open quantum system. Let us assume that the variables X(t) of eqn (6), representing the actual quantum state, can be separated into two sets,| | | X(t) = (XR(t),XI(t)) ∈ ΩP = ΩR × ΩI, | (14) |
where XR(XI) is the set of the relevant (irrelevant) variables belonging to the submanifold ΩR(ΩI). The label R tags the subset of X variables that are classified as relevant so XR(t) = {Xi(t)}i∈R. The projection procedure allows the definition of time-dependent marginal distributions on the relevant variables ρR(xR,t) that can be employed to represent (approximately) the XR(t) dynamics as an independent stochastic process. At this stage the precise identification of the set XR (and XI) is not essential and it will be specified later on.
From the projection of the Liouville equation, namely eqn (11) for Bohm theory, according to the procedure in ref. 41 (summarized in the Appendix) by assuming a memoryless kernel, one obtains the Fokker–Planck equation for probability density ρR(xR,t) on the submanifold ΩR. We employ the following projection operator 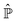 onto the submanifold ΩR
onto the submanifold ΩR
| | 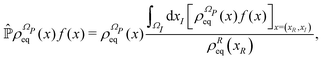 | (15) |
where
f(
x) is a generic function of
x and
ρReq(
xR) is the equilibrium density distribution as recovered from the integration of
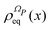
on the irrelevant variables,
| | 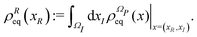 | (16) |
The resulting Fokker–Planck equation is
| | 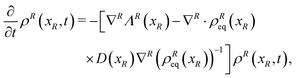 | (17) |
where the term between square brackets identifies the Fokker–Planck operator, ∇
R = {∂/∂
xi} with
i ∈
R and
ΛR(
xR) are the gradient operator and the averaged velocity field, respectively, for the relevant variables. The
i-th element of the averaged velocity field
ΛRi(
xR) describes the deterministic drift of the
i-th relevant variable and it is specified as
| | 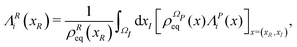 | (18) |
for
i ∈
R. The matrix
D(
xR) (see its definition in the Appendix) can be interpreted as the diffusion matrix like for the diffusion of a classical Brownian particle. It should be stressed that the projection procedure defines in all generality a diffusion matrix
D which is dependent on the relevant variables
xR,
D =
D(
xR), even if such a dependence is often neglected in the practical applications of stochastic models.
Furthermore, there is a formal correspondence between the Fokker–Planck equation and the Langevin equation where the fluctuations induced by the irrelevant variables are modelled according to a multidimensional white noise ζ(t).24 The Langevin equation corresponding to eqn (17) is specified as
| | 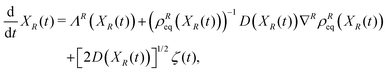 | (19) |
where the first two terms on the r.h.s represent the deterministic contributions, while the third term accounts for the fluctuating dynamics.
This projection procedure allows one to recover different stochastic models from the Liouville equation according to the specific choices for the relevant variables xR amongst the full set x = (q,α) of variables. In the following we shall examine a particular realization leading to a Fokker–Planck equation of Smoluchowski type for Bohm coordinates.
4 The Smoluchowski–Bohm equation
As already mentioned in the introduction, we aim to use stochastic modelling in order to characterize the dynamics of an open quantum system according to the quantum molecular trajectory, but without solving exactly eqn (1). For example, one can be interested in the conformational dynamics of a molecule interacting with the solvent. In this regard, the conformational degrees of freedom represent the open quantum system of interest S, while the enviroment E is composed of the remaining degrees of freedom. Then the coordinates q can be separated in two subsets, q = (qS,qE). The set qS = {qk}k∈S includes the coordinates corresponding to the interesting degrees of freedom, e.g., the conformational ones, while the set qE = {qk}k∈E includes the other coordinates.
Like with classical stochastic methods, only the coordinates qS are selected as elements of the set of relevant variables: they characterize the molecular motions we are interested in, e.g., the conformational dynamics. Unlike classical mechanics, we also have to establish if the phase variables α have to be classified as the relevant or the irrelevant variables. Since the phases represent the wave function, they are global variables: the wave function, and so the phases, cannot be associated with a limited portion of the whole system, such as the open system S. Thus, we consider the phases as irrelevant variables and, therefore, the sets of relevant and irrelevant variables are given as
| | | xR = (qS), xI = (qE,α). | (20) |
In the following we will further comment on the implication of classifying the phases as irrelevant variables. The general Fokker–Planck
eqn (17) can be specified for such a choice of variables with explicit relations for the equilibrium density distribution
ρReq(
xR) and the averaged velocity field
ΛR(
xR) defined in
eqn (16) and (18), respectively.
First of all, one should notice that the α dependence of the integrands in eqn (16) and (18), see the definition of 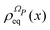 and ΛP(x) in eqn (13) and (9), is controlled by imaginary exponentials like exp(−ıαl′ + ıαl). Thus, the integration on the phases in eqn (16) and (18) can be performed explicitly by exploiting the orthogonality of the Fourier components. Secondly, the whole Hilbert space
and ΛP(x) in eqn (13) and (9), is controlled by imaginary exponentials like exp(−ıαl′ + ıαl). Thus, the integration on the phases in eqn (16) and (18) can be performed explicitly by exploiting the orthogonality of the Fourier components. Secondly, the whole Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) can be identified with the tensor product between the Hilbert space
can be identified with the tensor product between the Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S for the open system S and the Hilbert space
S for the open system S and the Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) E for the environment E,
E for the environment E, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S ⊗
S ⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) E. By employing the generic basis sets {|ηlS〉} and {|χlE〉} for
E. By employing the generic basis sets {|ηlS〉} and {|χlE〉} for ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S and
S and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) E, respectively, the eigenfunctions {ϕj(q)} of the Hamiltonian operator Ĥ can be represented in the form
E, respectively, the eigenfunctions {ϕj(q)} of the Hamiltonian operator Ĥ can be represented in the form
| | 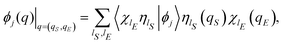 | (21) |
with
ηlS(
qS) = 〈
qS|
ηlS〉 and
χlE(
qE) = 〈
qE|
χlE〉.
Eqn (21) allows one to specify the
qS and
qE dependence of
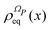
and of
ΛP(
x) through
eqn (13) and (9). The integration on
qE coordinates in
eqn (16) and (18) is performed by exploiting the orthogonality of the basis functions
χlE(
qE). In this way, the equilibrium density distribution
ρReq(
xR) can be identified with
| | 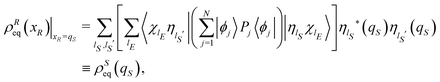 | (22) |
where we introduce the symbol
ρSeq(
qS) in order to emphasize that the coordinates of the open system
S are the only relevant variables,
xR =
qS. Note that, in the absence of degeneracy in the Hamiltonian spectrum,
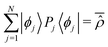
is the time average of the density matrix operator
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif)
= |
Ψ(
t)〉〈
Ψ(
t)|.
45,46 Therefore, the terms between square brackets in
eqn (22) correspond to the time average of the elements of the reduced density matrix
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif)
(
t) := Tr
E{|
Ψ(
t)〉〈
Ψ(
t)|} on the basis {|
ηlS〉}, and the equilibrium density distribution
ρSeq(
qS) can be rewritten as
| | 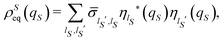 | (23) |
where
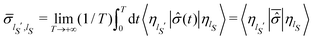
. The same equilibrium density distribution is obtained from the time average of the squared modulus of the wave function of
eqn (7) by integration on the environmental degrees of freedom
| | 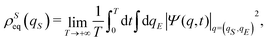 | (24) |
so establishing a correspondence between the equilibrium distribution
ρSeq(
qS) and the wave function
Ψ(
q,
t) itself.
By operating, as done for the equilibrium density distribution, one recovers the explicit dependence of the averaged velocity field ΛR(xR) on the open system coordinates qS,
| | 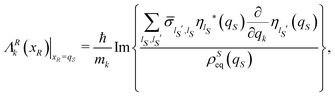 | (25) |
with
k ∈
S.
The simple structure of Smoluchowski type for diffusion processes24 emerges when the average velocity field vanishes everywhere: ΛRk(xR)|xR=qS = 0 for any possible coordinate qS of the open system and for any component k ∈ S. As a matter of fact, this condition is realized when the isolated system is described by a real Hamiltonian operator, which is the ordinary mechanical Hamiltonian including the kinetic energy and the potential energy. We recall that an operator ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is real if for any element |ψ〉 of its domain represented by a real function of the coordinates, also its transform
is real if for any element |ψ〉 of its domain represented by a real function of the coordinates, also its transform ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) |ψ〉 corresponds to a real function in the coordinate representation. An obvious implication is that the eigenfunctions ϕj(q) of the Hamiltonian Ĥ can be specified by real functions and, therefore, the time average density matrix
|ψ〉 corresponds to a real function in the coordinate representation. An obvious implication is that the eigenfunctions ϕj(q) of the Hamiltonian Ĥ can be specified by real functions and, therefore, the time average density matrix 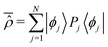 is a real operator too. Furthermore, also the time average reduced density matrix
is a real operator too. Furthermore, also the time average reduced density matrix 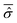 is a real operator in consideration of its definition as the partial trace of
is a real operator in consideration of its definition as the partial trace of 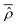 , i.e.,
, i.e., 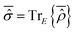 . One can then choose a basis set {|ηlS〉} with elements represented by real functions of the coordinates so deriving real values for the elements
. One can then choose a basis set {|ηlS〉} with elements represented by real functions of the coordinates so deriving real values for the elements 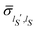 of the reduced density matrix. Correspondingly, the term between curly brackets in eqn (25) results to be real with vanishing values for the average velocity field. We stress the generality of this conclusion due to the independence on the basis set {|ηlS〉} of the velocity field of eqn (25).
of the reduced density matrix. Correspondingly, the term between curly brackets in eqn (25) results to be real with vanishing values for the average velocity field. We stress the generality of this conclusion due to the independence on the basis set {|ηlS〉} of the velocity field of eqn (25).
By taking into account these previous considerations, hereafter we shall assume that the velocity field is missing with the following Fokker–Planck operator ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) S for the evolution of the distribution ρS(qS,t) on the open system coordinates qS
S for the evolution of the distribution ρS(qS,t) on the open system coordinates qS
| | 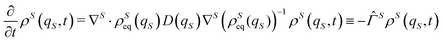 | (26) |
where ∇
S = {∂/∂
qk} with
k ∈
S. The associated Langevin equation,
| | 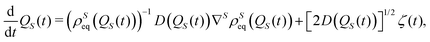 | (27) |
describes a diffusion process sampling the
qS domain,
i.e., the configuration space corresponding to the open system, according to the equilibrium distribution
ρSeq(
qS). These two equations are formally equivalent to the classical Smoluchowski equation and the corresponding Langevin equation,
24 respectively. For this reason, we refer to
eqn (26) as the Smoluchowski–Bohm equation. The main features of the quantum dynamics are taken into account by the equilibrium density distribution
ρSeq(
qS), which is generated by the wave function of the whole isolated system through
eqn (24).
The Smoluchowski–Bohm equation governing the quantum molecular trajectory of the open system is the key result of our analysis. In our opinion it represents a rather interesting outcome because of its simple formal structure and because it establishes a direct connection with the well-known diffusion processes. However, one should not forget that the Smoluchowski–Bohm equation, as a result of a projection procedure according to the choice of the relevant variables made in eqn (20), necessarily represents an approximation of the full deterministic description provided by eqn (1). Like for similar treatments of classical dynamics, one wonders how accurate is such an approximation and what are the conditions assuring its validity.
In particular, a major issue arises: is it legitimate to neglect the effects of the phases by classifying them amongst the irrelevant variables? According to eqn (7), the phases A(t) determine the time evolution of the wave function for the isolated system and so of the reduced density matrix ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) for the open system. On the other hand, with the Smoluchowski–Bohm equation the dynamics of
(t) for the open system. On the other hand, with the Smoluchowski–Bohm equation the dynamics of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) is completely neglected and it is replaced by its time average
(t) is completely neglected and it is replaced by its time average 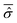 in the calculation of the equilibrium distribution by means of eqn (23). Therefore, the Smoluchowski–Bohm equation appears to be justified whenever the time dependence of
in the calculation of the equilibrium distribution by means of eqn (23). Therefore, the Smoluchowski–Bohm equation appears to be justified whenever the time dependence of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) does not have significant deviations from its time average. However, when the evolution of the reduced density matrix of an open system is exactly evaluated according to the Schrödinger equation, an explicit time dependence is necessarily recovered. Of particular interest is the case of an open quantum system in equilibrium with the environment when the time dependence of
(t) does not have significant deviations from its time average. However, when the evolution of the reduced density matrix of an open system is exactly evaluated according to the Schrödinger equation, an explicit time dependence is necessarily recovered. Of particular interest is the case of an open quantum system in equilibrium with the environment when the time dependence of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) is characterized by random type fluctuations of small amplitude about the average, see Fig. 1 of ref. 47 for the results of a simple model system. In our opinion this is the situation where the use of the Smoluchowski–Bohm equation is appropriate by neglecting the effects of weak and incoherent fluctuations of
(t) is characterized by random type fluctuations of small amplitude about the average, see Fig. 1 of ref. 47 for the results of a simple model system. In our opinion this is the situation where the use of the Smoluchowski–Bohm equation is appropriate by neglecting the effects of weak and incoherent fluctuations of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t). However, whether such a situation is realized or not depends on the pure state Ψ(q,t) of the isolated quantum system, in particular on the initial wave function Ψ(q,0). One can always select a particular form of Ψ(q,0) for the isolated system in a non-equilibrium state leading to an initial relaxation of the reduced density matrix before reaching the equilibrium controlled by the above mentioned small fluctuations of random type. As long as the initial relaxation is not taken into account by the averaged reduced density matrix
(t). However, whether such a situation is realized or not depends on the pure state Ψ(q,t) of the isolated quantum system, in particular on the initial wave function Ψ(q,0). One can always select a particular form of Ψ(q,0) for the isolated system in a non-equilibrium state leading to an initial relaxation of the reduced density matrix before reaching the equilibrium controlled by the above mentioned small fluctuations of random type. As long as the initial relaxation is not taken into account by the averaged reduced density matrix 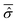 , the Smoluchowski–Bohm equation is unable to reproduce the behaviour of the open quantum system under this condition. These considerations point out that the use of the Smoluchowski–Bohm equation is legitimate only when the open quantum system is in equilibrium with the environment.
, the Smoluchowski–Bohm equation is unable to reproduce the behaviour of the open quantum system under this condition. These considerations point out that the use of the Smoluchowski–Bohm equation is legitimate only when the open quantum system is in equilibrium with the environment.
In this framework one can also examine the effects of the environment size. It has been demonstrated, see ref. 45 and 48 for detail, that the fluctuation intensity of the reduced density matrix of a subsystem, i.e., the open quantum system, decreases with the size of the environment, up to vanish in the macroscopic limit. These fluctuations becomes totally irrelevant and the instantaneous reduced density matrix can be identified with its average, 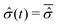 , provided that the equilibrium condition applies to the isolated system composed of the open quantum system and the macroscopic environment. Correspondingly, the time average is not required in eqn (24) in order to establish a relation between the equilibrium distribution ρSeq(qS) of the open system and the instantaneous wave function Ψ(q,t) of the isolated system. In such a situation the environment acts like a thermal bath with a well-defined temperature T and, if the interactions with the open system are weak enough, one can evaluate the reduced density matrix according to the canonical statistics49
, provided that the equilibrium condition applies to the isolated system composed of the open quantum system and the macroscopic environment. Correspondingly, the time average is not required in eqn (24) in order to establish a relation between the equilibrium distribution ρSeq(qS) of the open system and the instantaneous wave function Ψ(q,t) of the isolated system. In such a situation the environment acts like a thermal bath with a well-defined temperature T and, if the interactions with the open system are weak enough, one can evaluate the reduced density matrix according to the canonical statistics49
| | ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) C = exp(−ĤS/kBT)/Z, C = exp(−ĤS/kBT)/Z, | (28) |
where
ĤS is the Hamiltonian of the open quantum system,
kB is the Boltzmann constant and
Z is the corresponding partition function. In this way, an explicit form for the equilibrium distribution of
eqn (23) can be obtained from the quantum description of the open system according to its Hamiltonian
ĤS. This is certainly the most common and interesting situation when examining the specific degrees of freedom of a molecule in equilibrium with a macroscopic environment.
It should be stressed that the Fokker–Planck equations, or higher order partial differential equations, have often been employed for the analysis of quantum dynamics and ref. 50 presents their useful summary. A prominent role is usually attributed to the Wigner–Moyal equation51,52 deriving from the expansion of the time evolution equation for the Wigner distribution, and to the Caldeira–Leggett equation53 obtained according to the influence-functional method of Feynman and Vernon. The latter describes, as our Smoluchowski–Bohm equation, an open system and it includes dissipation coefficients like the diffusion coefficients in our case. Besides the common mathematical framework of the Fokker–Planck-like equations, there is a deep methodological difference between our procedure and these theories as long as they are aimed to derive a probabilistic description from the quantum pure state, i.e., the wave function, of the isolated system. In our method, in contrast, the building blocks include both the quantum pure state and the Bohm trajectory with the reduction to the Smoluchowski–Bohm equation for the relevant Bohm coordinates by projecting out the pure state degrees of freedom, which is by integrating on the phases. Such a methodological difference determines a different functional form for the probability density: a distribution on the (Bohm) coordinates in our case in opposition to the distribution on both coordinates and momenta in the case of the Wigner–Moyal or Caldeira–Leggett equation. To the best of our knowledge, in the literature there are no proposal analogous to our method. It represents a new line of research to be explored in order to fully assess its capabilities and its benefits with respect to more traditional approaches.
In conclusion, we have derived the Smoluchowski–Bohm equation for describing approximately the dynamics of the degrees of freedom composed of an open system and inferred that the stochastic description should be appropriate when the open system is in equilibrium. On the other hand, the direct comparison between the predictions of the stochastic equations resulting from the projection procedure and the results of the full deterministic dynamics represents the main tool for assessing the validity of the Fokker–Planck description. Thus, like for classical dynamics problems, we have adopted the strategy for a direct comparison between the predictions of the Smoluchowski–Bohm equation and the results of the deterministic dynamics. Correspondingly, a suitable quantum system whose full deterministic evolution is accessible through the numerical solution of eqn (1) has to be selected. The model system which has been employed for this purpose is described in the next section, while in the following one we present the result of the comparison with the stochastic representation.
5 Model system
We consider a system composed of n interacting harmonic oscillators that could represent n interacting vibrational degrees of freedom. The set q = (q1,q2,…,qn) includes the coordinates for each oscillator. By hypothesis, the first oscillator is taken as the open quantum system of interest S; the other oscillators play the role of the environment. Since this model system is rather similar to the system of n planar rotors examined in ref. 18 we characterize it by briefly summarising its main features, whereas the details for the calculations are reported in that reference.
The Hilbert space for the whole system is the tensor product of the Hilbert space for each oscillator, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 1 ⊗
1 ⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 2 ⊗⋯⊗
2 ⊗⋯⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n. Each element of the space
n. Each element of the space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) k can be fully specified by means of the orthonormal basis set {|ζlk〉}, whose coordinate representation is specified in the following
k can be fully specified by means of the orthonormal basis set {|ζlk〉}, whose coordinate representation is specified in the following
| | 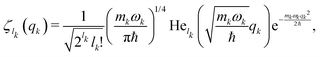 | (29) |
with
lk = 0, 1, 2,…, and He
lk (•) the
lk-th Hermite polynomial. Each function
ζlk(
qk) is the
lk-th eigenfunction of the harmonic Hamiltonian operator
Ĥ(0)k describing the
k-th oscillator
| | 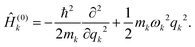 | (30) |
with eigenvalues
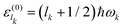
, and where
mk (
ωk) is the corresponding mass (resonance angular frequency). The Hamiltonian of the whole system is specified as
| | 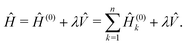 | (31) |
In the above equation
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif)
represents the interactions between the oscillators and the parameter
λ sets the magnitude of the interactions. The operator
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif)
aims to produce a generic coupling amongst the oscillators and it is modelled according to a random matrix (see below).
Because of the identification of the first oscillator as the open system S of interest with the other oscillators playing the role of the environment, the operator Ĥ(0)1 becomes the open system Hamiltonian, ĤS = Ĥ(0)1, with its eigenvalues and eigenfunctions specified as 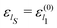 and ηlS(qS) = ζl1(q1), respectively; the corresponding Bohm coordinates is tagged with QS(t). Thus, the open system is described by only one degree of freedom whose stochastic dynamics is determined by a one-dimensional Fokker–Planck equation including a scalar diffusion coefficient D(qS).
and ηlS(qS) = ζl1(q1), respectively; the corresponding Bohm coordinates is tagged with QS(t). Thus, the open system is described by only one degree of freedom whose stochastic dynamics is determined by a one-dimensional Fokker–Planck equation including a scalar diffusion coefficient D(qS).
We employ numerical methods in order (i) to determine the eigenstates of the full system Hamiltonian Ĥ, (ii) to select the initial wave function, (iii) to compute the Bohm trajectory, and (iv) to solve the stochastic equations. First of all, we identify the Hamiltonian eigenstates |ϕj〉 through the numerical diagonalization of the matrix representation of the Hamiltonian Ĥ. For this purpose, we consider the basis set {|l〉} whose elements |l〉 are provided by the system eigenstates in the absence of interaction ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) :
:
where
l = (
l1,
l2,…,
ln) and
| | 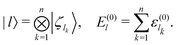 | (33) |
Hereafter, it is assumed that the examined pure state belongs to a finite dimensional subspace
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
′ (the “computational” Hilbert space) of the whole infinite Hilbert space
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
=
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 1
1 ⊗
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 2
2 ⊗ ⋯ ⊗
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n
n of the model system. We define
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
′ as the Hilbert space generated by the basis set {|
l〉} that includes only the eigenstates of
Ĥ(0) with eigenenergies
E(0)l smaller than the truncation energy cutoff
Etr:
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif)
′ := {⊕
l|
l〉 with
E(0)l <
Etr}. A diagonal matrix with elements
E(0)l is recovered for the representation of
Ĥ(0) Hamiltonian on the basis set |
l〉, whereas the operator
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif)
has been modelled with a random matrix whose elements are Gaussian distributed according to the following statistical constraints:
54,55| | 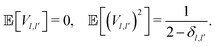 | (34) |
The eigenstates of
Ĥ are identified by linear combinations of the basis set elements |
l〉 according to the numerical diagonalization that, from a technical view point, has been performed by employing the software routine
Armadillo, a C++ linear algebra library.
56 Of course the use of a finite number of elements for the basis set {|
l〉} is strictly necessary in order to perform the numerical diagonalization. As long as the interaction potential
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif)
is a perturbation compared to
Ĥ(0), the diagonalization of the full Hamiltonian is influenced mainly by the coupling amongst basis elements |
l〉 with similar energies
E(0)l. Consequently, the effects of the basis set truncation are more pronounced for the Hamiltonian
Ĥ eigenstates |
ϕj〉 whose eigenenergies are closed to the truncation energy cutoff
Etr. In order to deal with an efficient truncation scheme with negligible effects on the pure state dynamics, the truncation energy cutoff
Etr must be significantly larger than the energy cutoff
Emax defining the active space
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) N
N of
eqn (4), which includes the examined pure state of the system. In such a case, the calculation of the eigenstates belonging to
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) N
N are weakly effected by the truncation. A more detailed discussion about this issue can be found in
ref. 18.
Let us now examine the procedure of the selection of the initial pure state |Ψ(0)〉. As emphasized in the previous section, the Smoluchowski–Bohm equation is suitable to describe an open quantum system in equilibrium with the environment. Then, in order to compare its predictions with those of the deterministic dynamics of the isolated system, we have to choose a quantum pure state for the equilibrium condition. The issue of the relation between the pure state of the isolated system and the thermodynamic equilibrium has been examined in the past on a general ground.49,57 It has been shown that if the pure state is randomly chosen from the uniform distribution on the Bloch sphere for the active Hilbert space, the quantum properties are typical of the equilibrium condition. The same strategy has been adopted in our calculations by employing the RPSE (Random Pure State Ensemble) procedure.47,58 One has to establish the N populations P and the N initial phases A(0) that specify the components of |Ψ(0)〉 along the basis set elements |ϕj〉 according to eqn (5). The populations are selected by sampling an auxiliary set of N − 1 independent random variables (one population is determined by the normalization condition) uniformly distributed in the unitary domain [0,1).58 Note that the choice of the populations P corresponds to select the dynamical space ΩP where the dynamics of (Q(t),A(t)) occurs (see Section 2). On the other hand, since the phases are independently and uniformly distributed, each phase is randomly chosen in its principal domain [0,2π). Once the initial pure state has been established, the solution of the Schrödinger equation is specified at an arbitrary time according to eqn (5) by inserting the time dependence of the phases Aj(t) = Aj(0) + (Ej/ħ)t.
For solving numerically the Bohm equation, that is the first of eqn (1), and computing the deterministic Bohm trajectory of the oscillators, we adopted the Runge–Kutta method at the 4-th order.59 The Langevin equation has been solved by employing the Euler method,59 which is computationally less expensive than the Runge–Kutta method. As a matter of fact, the Euler method, which is unstable in the case of deterministic equations, results in an efficient algorithm for stochastic equations because of the white noise term.
6 Deterministic dynamics vs. stochastic dynamics
In this section, we first of all characterize the quantum features of the oscillator representing the open quantum system, such as the time average reduced density matrix and the probability distribution ρSeq(qS). Secondly, we focus on the behaviour and the statistical properties of the Bohm trajectory QS(t) of its coordinate, which is established by solving numerically the deterministic eqn (1). Thirdly, we compare these results with the stochastic representation of the oscillator as provided by the Smoluchowski–Bohm equation. The operating conditions of the model system correspond to an open quantum system which is weakly coupled to the environment. In order to provide a simple analytical interpretation of the stochastic dynamics, we introduce also its Gaussian approximation described by the classical Ornstein–Uhlenbeck process.24
For the sake of simplicity, we examine six (n = 6) identical oscillators, mk = m and ωk = ω∀k, with the intensity parameter λ = 0.001ħω for the random matrix coupling ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) in order to mimic the condition of weak interaction between the open quantum system and the environment. The energy cutoffs for the truncation and the active space are set to Etr = 10.5ħω and to Emax = 9.5ħω, respectively. Correspondingly, the dimension of the computational Hilbert space is 1716, while the dimension of the active space is N = 924. We anticipate that in the analysis of the results of the calculations, we shall employ 2π/ω as the time unit and
in order to mimic the condition of weak interaction between the open quantum system and the environment. The energy cutoffs for the truncation and the active space are set to Etr = 10.5ħω and to Emax = 9.5ħω, respectively. Correspondingly, the dimension of the computational Hilbert space is 1716, while the dimension of the active space is N = 924. We anticipate that in the analysis of the results of the calculations, we shall employ 2π/ω as the time unit and 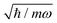 as the coordinate unit for the oscillator.
as the coordinate unit for the oscillator.
The initial wave function has been generated according to the RPSE procedure. Then, from the diagonalization of the full Hamiltonian, we obtain its eigenstates |ϕj〉 which allow the calculation of the averaged reduced density matrix 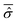 , see eqn (22) and (23). On the basis of the oscillator eigenfunctions, ηlS(qS) = ζlS(qS) of eqn (29), the matrix representation of
, see eqn (22) and (23). On the basis of the oscillator eigenfunctions, ηlS(qS) = ζlS(qS) of eqn (29), the matrix representation of 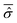 results to be almost diagonal:
results to be almost diagonal: 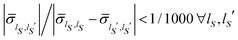 . The resulting values for the diagonal elements
. The resulting values for the diagonal elements ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) lS,lS of the averaged reduced density matrix are reported in Table 1. They steeply decrease in magnitude with the oscillator eigenenergies
lS,lS of the averaged reduced density matrix are reported in Table 1. They steeply decrease in magnitude with the oscillator eigenenergies 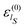 , and this behaviour might suggest the equivalence with the canonical density matrix of eqn (28). However, in order to verify it, the temperature must be identified. For this purpose, we have interpreted the calculated value of the ratio between the first two diagonal elements according to the canonical statistics, i.e.,
, and this behaviour might suggest the equivalence with the canonical density matrix of eqn (28). However, in order to verify it, the temperature must be identified. For this purpose, we have interpreted the calculated value of the ratio between the first two diagonal elements according to the canonical statistics, i.e., ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0,0/
0,0/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 1,1 = exp((ε(0)1 − ε(0)0)/kBT), so obtaining a thermal energy factor of kBT = 1.661ħω. Then, the elements of the canonical density matrix can be evaluated and they are reported in Table 1 between parenthesis. Clearly, significant deviations emerge from the comparison with the result of the full calculation for the model system. We can conclude that even if the RPSE procedure has been employed to select typical pure states, which is representative of the equilibrium condition, thermal equilibrium states described according to the canonical states are not generated by the model system. This is due to the fact that the environment is too small to reproduce the thermodynamical behaviour of a truly thermal bath at a given temperature, which can be recovered only with a sufficiently larger number of oscillators.
1,1 = exp((ε(0)1 − ε(0)0)/kBT), so obtaining a thermal energy factor of kBT = 1.661ħω. Then, the elements of the canonical density matrix can be evaluated and they are reported in Table 1 between parenthesis. Clearly, significant deviations emerge from the comparison with the result of the full calculation for the model system. We can conclude that even if the RPSE procedure has been employed to select typical pure states, which is representative of the equilibrium condition, thermal equilibrium states described according to the canonical states are not generated by the model system. This is due to the fact that the environment is too small to reproduce the thermodynamical behaviour of a truly thermal bath at a given temperature, which can be recovered only with a sufficiently larger number of oscillators.
Table 1 Diagonal elements of the equilibrium reduced density matrix ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) lS,lS, with, between parentheses, their canonical values for comparison
lS,lS, with, between parentheses, their canonical values for comparison
|
l
S
|
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) l
S
,lS
l
S
,lS
|
| 0 |
0.496 (0.456) |
| 1 |
0.272 (0.250) |
| 2 |
0.139 (0.137) |
| 3 |
0.0618 (0.0749) |
| 4 |
0.0234 (0.0410) |
| 5 |
6.71 × 10−3 (0.0224) |
| 6 |
1.14 × 10−3 (0.0123) |
| 7 |
6.50 × 10−7 (6.73 × 10−3) |
The equilibrium density distribution ρSeq(qS) represents according to eqn (23) and (24) the time average of the wave function distribution for the open system coordinate. Because of the harmonic potential, a confined distribution is recovered as displayed in Fig. 1. As a matter of fact, its shape is reproduced by the normal (Gaussian) distribution
| | 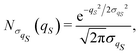 | (35) |
with a null average for the variable and the optimized value
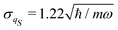
for the variance. However, significant deviations are evident in comparison with the exact one as in
Fig. 1, particularly, for the too slowly decaying tails at large values of the coordinate
qS.
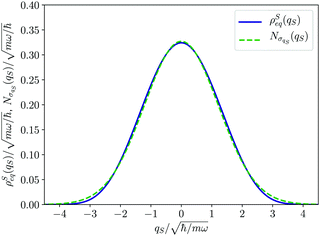 |
| | Fig. 1 Equilibrium density distribution ρSeq(qS) of the qS coordinate (solid blue line) and its Gaussian approximation  with the variance with the variance 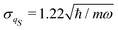 (dashed green line). (dashed green line). | |
Different deterministic trajectories, for the given quantum pure state |Ψ(t)〉, are obtained depending on the choice of the initial condition Q(0) for the coordinates, but they supply an equivalent statistical description of the dynamical process. In the following we present and examine the results for the particular trajectory arising when all the oscillators have an initial position at the bottom of the potential, Qi = 0 ∀i = 1, 2,…,n. We adopted a time step Δt = 1.6 × 10−3 2π/ω for the numerical integration of the Bohm equation and verified that the trajectory does not change significantly within the correlation time if one decreases the time step of integration. The computed trajectory QS(t) is displayed in Fig. 2 and one can observe a fluctuating dynamics in the presence of a confinement like for similar classical problems. Furthermore, by sampling the values of the coordinate along the trajectory QS(t), one can determine the corresponding distribution wSeq(qS) which allows the calculation of the time average 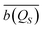 of any observable specified as a function b(QS) of the Bohm coordinate,
of any observable specified as a function b(QS) of the Bohm coordinate,
| | 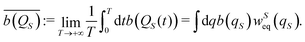 | (36) |
The distribution
wSeq(
qS) is displayed in
Fig. 3. Its rough profile is due to the finite time window
T of the calculated trajectory
QS(
t) (in the calculation
T = 6 × 10
3 2π/
ω). As a matter of fact, the resulting distribution becomes smoother as the window
T increases without changing the underlying profile.
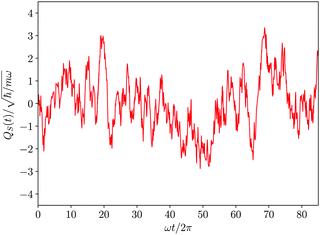 |
| | Fig. 2 Deterministic time evolution of the Bohm coordinate of the first oscillator composing the model system. | |
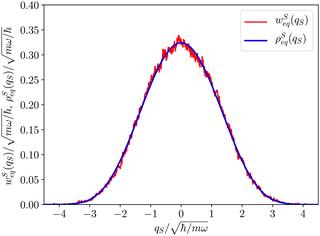 |
| | Fig. 3 Distribution wSeq(qS) (red line) of the Bohm coordinate corresponding to the first oscillator calculated from the sampling of its deterministic trajectory QS(t). For comparison the equilibrium distribution ρSeq(qS) (blue line) derived from the reduced density matrix is also reported. | |
For the sake of comparison in Fig. 3 we have also reported the equilibrium distribution ρSeq(qS) derived from the reduced density matrix. The equivalence of wSeq(qS), in spite of the roughness of its calculated profile, with ρSeq(qS) is clearly evident and this, in our opinion, represents an important result. The two distributions ρSeq(qS) and wSeq(qS), even if both are referred to the same variable qS for the coordinate of the first oscillator, derive from different kinds of information: the former from the reduced density matrix generated by the wave function, the latter from the sampling of the deterministic Bohm trajectory. Then, this equivalence cannot be taken for granted at all and it could be considered a peculiar result of the quantum dynamics of the Bohm coordinate. Such an issue has been examined in detail by us in a previous comunication13 where we have shown that the equivalence derives for the ergodicity of the Bohm dynamics. An analogy exists with the ergodicity of classical statistical mechanics,60 since in both cases one examines the equivalence between statistical distribution along a system's trajectory, in the one hand, and the stationary distribution in the phase space as supplied by the Liouville equation, on the other hand. On a general ground ergodicity is normally observed in complex systems characterized by a chaotic dynamics. On the other hand, Bohm trajectories are characterized by a strong chaotic behaviour also for simple systems composed of few degrees of freedom.61–64 This is mainly due to the instabilities of the velocity field of the Bohm coordinates because of the singularities of 1/|Ψ(q,t)|q=Q(t)2 (see the first of eqn (1)). If |Ψ(q,t)|q=Q(t) ≃ 0 the Schrödinger–Bohm dynamics produces abrupt changes of coordinates Q(t) that erase the memory of the previous configuration. In ref. 13, we have formally proven that the trajectory QS(t) samples the corresponding configuration space according to ρSeq(qS), because of the loss of correlation due to the chaotic dynamics. In conclusion, the equivalence between the two distributions displayed in Fig. 3 represents the numerical evidence of the ergodicity of the Bohm coordinate in the particular case of our model system for the oscillator coupled to the environment composed of the other oscillators.
In order to identify the time scales of the fluctuations of the Bohm coordinate QS(t) during its deterministic evolution, we employ the auto-correlation functions for functions b(QS) of the oscillator coordinate
| | 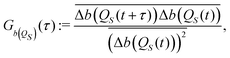 | (37) |
where the overline denotes the time average like in
eqn (36) and
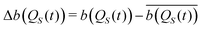
. Note that these correlation functions have been defined in a normalized form such that they start from a unitary value:
Gb(QS)(
τ)|
τ=0 = 1. They are computed by averaging directly Δ
b(
QS(
t +
τ))Δ
b(
QS(
t)) for 0 ≤
t ≤
T −
τ along the calculated trajectory within the given time window
T. The most interesting correlation function is certainly
GQS(
τ) for the coordinate
QS itself,
i.e.,
b(
QS) =
QS, which is drawn in red in
Fig. 4. Its monotonic and exponential-like decrease up to vanish is clear evidence of the loss of correlation during the evolution of the Bohm coordinate
QS(
t), which originates from the chaotic nature of the Bohm coordinate motion. This ensures that the choice of their initial values
Qk(0) is irrelevant, since they start to loose the memory of the initial conditions after times of the order of the correlation time
τC which can be estimated as
τC = 1.86 2π/
ω. According to the analysis of
ref. 13, the loss of correlation is at the origin of the ergodicity of the Bohm coordinate leading to the equivalence of the distributions displayed in
Fig. 3. It should be noted that some kind of wobbling in the profile of the correlation function
GQS(
τ) displayed in
Fig. 4 appears particularly at times longer than the correlation time. This is an effect of the finite time window
T of the calculated trajectory, which tends to disappear by enlarging
T significantly.
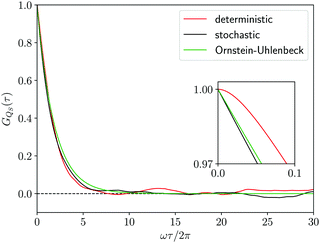 |
| | Fig. 4 Correlation function GQS(τ) of the coordinate QS(t) of the first oscillator from the deterministic trajectory (red line), from the stochastic trajectory corresponding to the Smoluchowski–Bohm equation (black line) and from the Ornstein–Uhlenbeck process (green line). In the inset an enlargement of the initial decay of the correlation function is reported. | |
Let us now analyze the Bohm coordinate dynamics according to the stochastic representation deriving from the projection procedure, which is the Smoluchowski–Bohm eqn (26) or equivalently the Langevin type eqn (27). As mentioned in the previous section, we have preferred to solve numerically the Langevin type equation in order to deal explicitly with the stochastic representation for the evolution of QS(t), from which both the time average and the correlation functions can be directly computed like for the deterministic dynamics. In order to implement such a procedure, however, the two fundamental ingredient of the Smoluchowski–Bohm eqn (26), i.e., the equilibrium density distribution ρSeq(qS) and the coordinate dependent diffusion coefficient D(qS), has to be recognized.
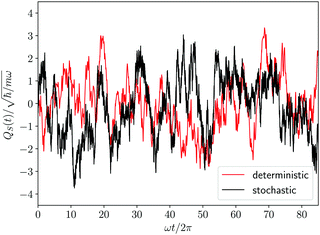
As already discussed, for our model system the equilibrium distribution ρSeq(qS) can be exactly computed through eqn (23) and the resulting profile is displayed in Fig. 1. The projection procedure provides a formal definition of the diffusion coefficient according to eqn (52) of the Appendix. However, such a definition does not have an operational value, since it requires the calculation of a correlation function with a projected Liouville operator 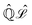 whose effects on the time evolution are hardly estimated. The same problem arises in classical stochastic treatments65 so that the diffusion coefficient (or the friction coefficient) is considered as a parameter to be evaluated independently of the projection procedure. For instance, in the case of the Brownian motion the diffusion coefficient is identified according to the proportionality between the mean squared displacement and the time. The same point of view will be assumed for the Smoluchowski–Bohm equation. In particular we assume that the qS dependence of the diffusion coefficient is negligible, i.e., D(qS) = D, similarly to what is often done in the applications of classical stochastic methods. Its value is selected by optimizing the agreement with the autocorrelation function GQS(τ) calculated with the deterministic dynamics. According to the Smoluchowski–Bohm eqn (26), the diffusion coefficient sets the time scale of the diffusion motion. Then, the trajectory QS(t) obtained as a solution of the Langevin type eqn (27) can be used to represent the stochastic motion with a different diffusion coefficient by simply scaling the time axis. Since the same rule holds for the correlation functions, we have calculated GQS(τ) from the stochastic trajectory for a given value of D, and then we have optimized the time scale in order to obtain the best fit with the deterministic correlation function reported in Fig. 4. Using this procedure, we have obtained for the stochastic motion of the oscillator coordinate an effective diffusion coefficient D = 0.1273ħ/m and the resulting correlation function is also reported in Fig. 4. The initial part of a stochastic trajectory QS(t) is reported in Fig. 5 together with the same deterministic trajectory of Fig. 2 for the sake of comparison. Clearly, they share the same features of the fluctuating dynamics. By visual inspection, the deterministic trajectory could be apparently interpreted as another stochastic trajectory deriving from a different realization of the noise term.
whose effects on the time evolution are hardly estimated. The same problem arises in classical stochastic treatments65 so that the diffusion coefficient (or the friction coefficient) is considered as a parameter to be evaluated independently of the projection procedure. For instance, in the case of the Brownian motion the diffusion coefficient is identified according to the proportionality between the mean squared displacement and the time. The same point of view will be assumed for the Smoluchowski–Bohm equation. In particular we assume that the qS dependence of the diffusion coefficient is negligible, i.e., D(qS) = D, similarly to what is often done in the applications of classical stochastic methods. Its value is selected by optimizing the agreement with the autocorrelation function GQS(τ) calculated with the deterministic dynamics. According to the Smoluchowski–Bohm eqn (26), the diffusion coefficient sets the time scale of the diffusion motion. Then, the trajectory QS(t) obtained as a solution of the Langevin type eqn (27) can be used to represent the stochastic motion with a different diffusion coefficient by simply scaling the time axis. Since the same rule holds for the correlation functions, we have calculated GQS(τ) from the stochastic trajectory for a given value of D, and then we have optimized the time scale in order to obtain the best fit with the deterministic correlation function reported in Fig. 4. Using this procedure, we have obtained for the stochastic motion of the oscillator coordinate an effective diffusion coefficient D = 0.1273ħ/m and the resulting correlation function is also reported in Fig. 4. The initial part of a stochastic trajectory QS(t) is reported in Fig. 5 together with the same deterministic trajectory of Fig. 2 for the sake of comparison. Clearly, they share the same features of the fluctuating dynamics. By visual inspection, the deterministic trajectory could be apparently interpreted as another stochastic trajectory deriving from a different realization of the noise term.
 |
| | Fig. 5 Stochastic evolution (black line) of the coordinate of the first oscillator as obtained from the Langevin-like equation. For comparison, the deterministic counterpart of Fig. 2 is also reported (red line). | |
The comparison in Fig. 4, between the correlation functions resulting from the deterministic motion and the stochastic motion, allows one to ascertain the effectiveness of the projection procedure leading to the Smoluchowski–Bohm equation for the open quantum system. One should take into account that, like in classical mechanics, projection procedures can generate only approximations to the true (deterministic) dynamics. Therefore, deviations should be expected in advance and one would like to reproduce with a simple stochastic model the main features of the deterministic motion, without truly quantitative agreement. According to these guidelines, we can conclude that unexpected good agreement is found, much better than in relevant classical problems like, for instance, in the comparison between the velocity correlation function obtained from Molecular Dynamics simulations and from the Brownian motion model.66 In our case the deterministic and the stochastic correlation functions share an exponential-like profile with rather small deviations.
Essential differences emerge only at short times. The deterministic dynamics is time reversible and, therefore, the corresponding correlation function is an even function of time so that dGQS(τ)/dτ|τ=0 = 0. This reversibility is absent in the Fokker–Planck equations, as well as in other stochastic models having a semi-group evolution describing dissipation phenomena, so that the corresponding correlation functions are no more even functions of time, i.e., dGQS(τ)/dτ|τ=0 ≠ 0. Such a difference is evident by examining the inset in Fig. 4 which magnifies the correlation function in a time domain much shorter than the correlation time. We can conclude that this fundamental difference in the time parity does not have a significant effect on the comparison between the two correlation functions, since it cannot be visually detected if the overall profile is examined without considering the inset in Fig. 4.
The correlation functions, besides the direct averaging along a stochastic trajectory, can be calculated also by solving the Fokker–Planck eqn (26) obtaining the following relation24
| | 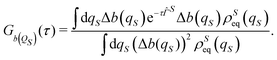 | (38) |
By expanding the function
b(
qS)
ρSeq(
qS) on the basis of the eigenfunctions of the Fokker–Planck operator,
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) Sξj
Sξj(
qS)
ρSeq(
qS) =
λjξj(
qS)
ρSeq(
qS), the correlation function is decomposed according to a multi-exponential decay due to the ensemble of independent diffusion modes
ξj(
qS) each of them characterized by the relaxation time
τj = 1/
λj. In particular, analytical approximations can be derived by replacing the exact equilibrium distribution
ρSeq(
qS) with its Gaussian approximation
of
eqn (35), since in this case the Smoluchowski–Bohm equation becomes equivalent to the classical Ornstein–Uhlenbeck process.
24 Then the independent diffusion modes are specified according to the Hermite polynomials,
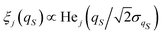
for
j = 0, 1, 2,…, with the following relaxation time for
j ≠ 0:
| | 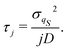 | (39) |
In this way, the following Ornstein–Uhlenbeck approximations are obtained for the correlation functions of the first powers of the coordinate,
| | 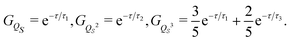 | (40) |
In particular one recovers for the correlation function
GQS(
τ) of the oscillator coordinate the interpretation as a monoexponential decay of the slowest diffusion mode with relaxation time
τ1. The comparison in
Fig. 4 shows that the Ornstein–Uhlenbeck process provides a rather good approximation to the results of the averaging along the stochastic trajectory: only small deviations emerge because of the contributions of faster relaxation modes in the stochastic trajectory. Indeed, as long as the equilibrium distribution
ρSeq(
qS) is not exactly reproduced by the Gaussian distribution
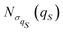
, the expansion of the function
b(
qS) =
qS on the basis of the true diffusion modes
ξj(
qS) of the Smoluchowski–Bohm equation includes also small contributions from those with
j > 1.
To complete the comparison between the deterministic and the stochastic trajectory, in Fig. 6 we have reported also the correlation functions GQS2(τ) and GQS3(τ) for the second and the third power of the oscillator coordinate, together with the corresponding Ornstein–Uhlenbeck approximations of eqn (40). The same level of agreement of Fig. 4 in the comparison between the deterministic and stochastic results it is found also for these further correlation functions. In our opinion, this supports even more strongly the Smoluchowski–Bohm description. Indeed, one might justify the agreement found in Fig. 4 as a mere consequence of the fitting of the diffusion coefficient D. However, such agreement is recovered also for other correlation functions whose relaxation, according to the Ornstein–Uhlenbeck approximation of eqn (40), is driven by different independent diffusion modes. Let us suppose that the true dynamics of the oscillator coordinate is driven by a stochastic equation different from the Smoluchowski–Bohm eqn (26), for instance a strong collision process.67 The corresponding correlation functions would be controlled by the independent strong collision modes, i.e., the eigenfunctions of the strong collision operator, which have the same relaxation time. In this case the Smoluchowski–Bohm equation, because of the different relaxation times, would be unable to reproduce the set of different correlation functions, even if the diffusion coefficient has been adjusted to reproduce the time dependence of GQS(t). In conclusion, the agreement in the comparison of different correlation functions demonstrates the capability of the Smoluchowski–Bohm equation to reproduce correctly the dynamical process characterizing the coordinate evolution of the open quantum system represented by the selected oscillator.
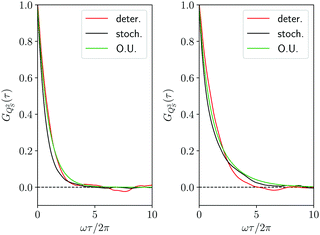 |
| | Fig. 6 Correlation functions of the observables QS2(t) and QS3(t) with the same representation of Fig. 4. | |
7 Conclusions
In this work we introduced the methods that should allow the practical use of the quantum molecular trajectory to represent the molecular motions. Indeed, in its original formulation of ref. 13 requiring the full deterministic solution for the wave function and all the Bohm coordinates, it can hardly be employed for the systems of Chemical interest with a large number of degrees of freedom because of the high computational cost of exactly solving the dynamical problem. Therefore, by means of projection operator techniques, we have derived the stochastic equations representing approximately the dynamics of a set of relevant coordinates of interest. In particular, by focusing on an open quantum system in equilibrium with the environment, we have obtained the Smoluchowski–Bohm equation describing the dynamics as a diffusion process. The accuracy of the stochastic predictions has been verified through the comparison with the deterministic quantum molecular trajectory for a model system of six interacting harmonic oscillators with one oscillator playing the role of the open system.
The benefit of this approach is that of representing quantum dynamics using a Fokker–Planck equation of Smoluchowski type. It should allow a full quantum analysis of several problems which usually are treated as classical stochastic processes. For instance, one might examine activated processes and characterize their dynamics by adapting Kramers theory to our formalism.68–70 The identification of the reaction paths according to a quantum stochastic trajectory could be a major future outcome of the Smoluchowski–Bohm approach.
In order to model specific systems according to the Smoluchowski–Bohm equation, two fundamental ingredients have to be defined: the equilibrium probability density ρSeq(qS) and the diffusion coefficient D. We recall that the main quantum features of the open system are taken into account by the equilibrium density distribution ρSeq(qS) that corresponds to the square modulus of the wave function integrated on the environmental degrees of freedom. It can be calculated according to eqn (23) from the time averaged reduced density matrix 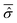 of the open quantum system. Let us consider the common situation of an open quantum systems weakly interacting with a large enough environment acting as a thermal bath at a given temperature T. Then the time averaged reduced density matrix
of the open quantum system. Let us consider the common situation of an open quantum systems weakly interacting with a large enough environment acting as a thermal bath at a given temperature T. Then the time averaged reduced density matrix 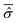 of the open quantum system49,57 can be replaced by its canonical form of eqn (28). This corresponds to the case of an open system in thermal equilibrium with the environment, which has a paramount importance in chemical studies in relation to the observation of a small system, such as a particular molecule or a set of its degrees of freedom, weakly interacting with the surroundings. In this case, through the canonical reduced density matrix one can obtain the equilibrium distribution by means of a suitable model of the open system Hamiltonian ĤS.
of the open quantum system49,57 can be replaced by its canonical form of eqn (28). This corresponds to the case of an open system in thermal equilibrium with the environment, which has a paramount importance in chemical studies in relation to the observation of a small system, such as a particular molecule or a set of its degrees of freedom, weakly interacting with the surroundings. In this case, through the canonical reduced density matrix one can obtain the equilibrium distribution by means of a suitable model of the open system Hamiltonian ĤS.
Let us consider the issue of choice of the diffusion coefficient D which determines the time scale of the fluctuating dynamics of the open system coordinates. For classical stochastic models the brownian motion theory provides estimates of D on the basis of the Stokes–Einstein relation, at least for a simple type of dynamical process. Unfortunately, analogous procedures are not available for correlating the diffusion coefficient of the Smoluchowski–Bohm equation with the quantum properties of the open system and of the environment. A clear understanding of the phenomena determining the values of the diffusion coefficient is still an open problem which is worthwhile to be examined in future investigations. Some information might be recovered from the behaviour of the simple model system. For instance, with the model system of six interacting harmonic oscillators, we have found that by decreasing the strength parameter of the interaction in eqn (31) with respect to the case illustrated in Section 6, the value of the diffusion coefficient is not modified. This points out that, at least in the particular motional regime explored in these calculations, the diffusion coefficient of the open quantum system is independent of the interactions with the environment, and therefore, it is controlled by the entanglement between the two partners. At the actual stage, however, given the lack of general information about the diffusion coefficient, it has to be considered as a free parameter of the stochastic description, which could be optimized by comparison with experimental data.
The new procedure introduced in this work opens a new line of research on the analysis of quantum molecular motions, which has to be fully exploited in order to assess its capabilities. At this stage one can recognize its major benefit in the simple and self-consistent representation of few selected degrees of freedom without the need for considering the evolution of the full quantum pure state. On the other hand, the identification of the diffusion coefficient for the Smoluchowski–Bohm equation is still an open issue which calls for further deeper studies.
Conflicts of interest
There are no conflicts to declare.
Appendix
According to ref. 41, a Fokker–Planck equation for time dependent probability distributions on the relevant variables only ρR(xR,t) can be derived from the Liouville equation| | 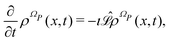 | (41) |
by employing the projection operator| | 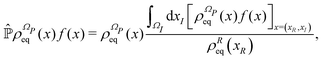 | (42) |
where f(x) is a generic function of x and ρReq(xR) is the equilibrium density distribution as recovered from the integration of 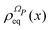 on the irrelevant variables. Since the projection operator is linear and time independent, the Liouville equation can be written as a pair of equations
on the irrelevant variables. Since the projection operator is linear and time independent, the Liouville equation can be written as a pair of equations| | 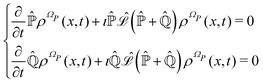 | (43) |
where 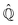 is defined in such a way that
is defined in such a way that 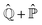 is the identity operator. The second equation in (43) can be formally solved for
is the identity operator. The second equation in (43) can be formally solved for 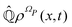 and the solution can be substituted in the first equation in (43) (see ref. 42). In this way a closed equation for the projected probability density
and the solution can be substituted in the first equation in (43) (see ref. 42). In this way a closed equation for the projected probability density 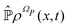 is obtained,
is obtained,| | 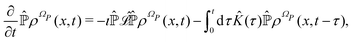 | (44) |
where the kernel operator ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ),
(τ),| | 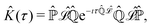 | (45) |
represents the memory effects due to the whole process. Eqn (44) it is still an exact equation for the evolution of 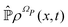 . The only assumption concerns the initial density distribution ρΩP(x,0): since it is arbitrary and we are interested in the probability density of the relevant variables, it has been selected in such a way that
. The only assumption concerns the initial density distribution ρΩP(x,0): since it is arbitrary and we are interested in the probability density of the relevant variables, it has been selected in such a way that 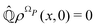 . According to eqn (42),
. According to eqn (42), 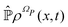 can be specified as
can be specified as| | 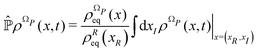 | (46) |
and the result of the integration is the marginal density distribution ρR(xR,t) with respect to the irrelevant variables:| | 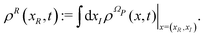 | (47) |
In order to derive the Fokker–Planck equation for the probability density ρR(xR,t), eqn (44) has to be simplified by assuming that the dynamical process involving the relevant variables is memoryless. This means formally that the kernel operator ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ) does not vanish only for small values of τ:
(τ) does not vanish only for small values of τ: ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ) ≃ 0 for τ > ε with ε as a small number. Then, the following approximation results to be justified
(τ) ≃ 0 for τ > ε with ε as a small number. Then, the following approximation results to be justified| | 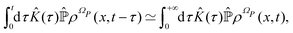 | (48) |
as long as the difference between ρΩP(x,t−τ) and ρΩP(x,t) is negligible for time differences τ corresponds to a non-vanishing kernel ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ). Furthermore, the upper integration boundary can be brought to infinity when a generic time t is considered. If eqn (48) holds, eqn (44) corresponds to a partial differential equation of Fokker–Planck type.
(τ). Furthermore, the upper integration boundary can be brought to infinity when a generic time t is considered. If eqn (48) holds, eqn (44) corresponds to a partial differential equation of Fokker–Planck type.
In order to verify this equivalence, the operators on the r.h.s. of eqn (44) have to be made explicit. This is only a matter of mathematical handling of the operators and we report the final results. As regards to the first set of operators acting on ρΩP(x,t) on the r.h.s. of eqn (44), they can be specified according to the following equation:
| | 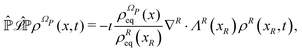 | (49) |
where ∇
R = {∂/∂
xi}, the
i-th element of the averaged velocity field
ΛR(
xR) is specified by
eqn (25) and the index
i runs on the relevant variables
R only,
i ∈
R.
As regards to the kernel operator, the term 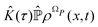 can be specified as
can be specified as
| | 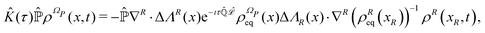 | (50) |
where Δ
ΛRi(
x) =
ΛPi(
x) −
ΛRi(
xR) with
i ∈
R. By integration on the
τ variable according to
eqn (48) and by performing the projection
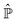
, one obtains
| | 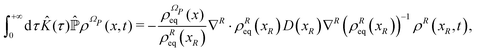 | (51) |
where the matrix of the diffusion coefficients is defined according to the following equation:
| | 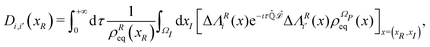 | (52) |
with
i,
i′ ∈
R. By inserting the result of
eqn (49) and (51) into
eqn (44), one obtains the final Fokker–Planck operator,
| | ![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) R = ∇RΛR(xR) − ∇R·ρReq(xR)D(xR)∇R(ρReq(xR))−1, R = ∇RΛR(xR) − ∇R·ρReq(xR)D(xR)∇R(ρReq(xR))−1, | (53) |
in agreement with the Fokker–Planck equation of
eqn (17).
Acknowledgements
The authors acknowledge the support by Univesità degli Studi di Padova through 60% grants and the project P-DiSC#08BIRD2016-UNIPD.
References
-
Modern Methods and Algorithms of Quantum Chemistry, ed. J. Grotendorst, John-von-Neumann-Inst. for Computing, 2000 Search PubMed.
- J. M. Millam, V. Bakken, W. Chen, W. L. Hase and H. B. Schlegel, J. Chem. Phys., 1999, 111, 3800–3805 CrossRef CAS.
- T. Helgaker, E. Uggerud and H. J. A. Jensen, Chem. Phys. Lett., 1990, 173, 145–150 CrossRef CAS.
- A. Petrone, G. Donati, P. Caruso and N. Rega, J. Am. Chem. Soc., 2014, 136, 14866–14874 CrossRef CAS PubMed.
- M. Wohlgemuth, V. Bonačić-Koutecký and R. Mitrić, J. Chem. Phys., 2011, 135, 054105 CrossRef PubMed.
- E. Titov, G. Granucci, J. P. Götze, M. Persico and P. Saalfrank, J. Phys. Chem. Lett., 2016, 7, 3591–3596 CrossRef CAS PubMed.
- D. C. Clary, Science, 2016, 351, 1267–1268 CrossRef CAS PubMed.
- A. G. Császár, C. Fábri, T. Szidarovszky, E. Mátyus, T. Furtenbacher and G. Czakó, Phys. Chem. Chem. Phys., 2012, 14, 1085–1106 RSC.
- S. C. Althorpe and D. C. Clary, Annu. Rev. Phys. Chem., 2003, 54, 493–529 CrossRef CAS PubMed.
- N. Balakrishnan, C. Kalyanaraman and N. Sathyamurthy, Phys. Rep., 1997, 280, 79–144 CrossRef CAS.
- W. Xie, L. Liu, Z. Sun, H. Guo and R. Dawes, J. Chem. Phys., 2015, 142, 064308 CrossRef PubMed.
- H. Tamura, S. Nanbu, T. Ishida and H. Nakamura, J. Chem. Phys., 2006, 124, 084313 CrossRef PubMed.
- F. Avanzini and G. J. Moro, J. Phys. Chem. A, 2017, 121, 5352–5360 CrossRef PubMed.
- D. Bohm, Phys. Rev., 1952, 85, 166–179 CrossRef CAS.
- D. Bohm, Phys. Rev., 1952, 85, 180–193 CrossRef CAS.
-
P. R. Holland, The Quantum Theory of Motion, Cambridge University Press, 1995 Search PubMed.
- E. Madelung, Z. Phys., 1927, 40, 322–326 CrossRef.
- F. Avanzini, B. Fresch and G. J. Moro, Found. Phys., 2016, 46, 575–605 CrossRef.
- C. L. Lopreore and R. E. Wyatt, Phys. Rev. Lett., 1999, 82, 5190–5193 CrossRef CAS.
-
R. E. Wyatt, Quantum Dynamics with Trajectories – Introduction to Quantum Hydrodynamics, Springer, 2005 Search PubMed.
- R. E. Wyatt, J. Chem. Phys., 1999, 111, 4406–4413 CrossRef CAS.
- D. Babyuk, R. E. Wyatt and J. H. Frederick, J. Chem. Phys., 2003, 119, 6482–6488 CrossRef CAS.
- K. H. Hughes and R. E. Wyatt, Phys. Chem. Chem. Phys., 2003, 5, 3905–3910 RSC.
-
C. W. Gardiner, Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences, Springer-Verlag, New York, 1986 Search PubMed.
- D. T. Gillespie, Physica A, 1992, 188, 404–425 CrossRef CAS.
- D. T. Gillespie, Annu. Rev. Phys. Chem., 2007, 58, 35–55 CrossRef CAS PubMed.
- D. T. Gillespie, A. Hellander and L. R. Petzold, J. Chem. Phys., 2013, 138, 170901 CrossRef PubMed.
- F. Wu, T. Tian, J. B. Rawlings and G. Yin, J. Chem. Phys., 2016, 144, 174112 CrossRef PubMed.
- J.-H. Prinz, J. D. Chodera and F. Noé, Phys. Rev. X, 2014, 4, 011020 Search PubMed.
- F. Hirata and K. Akasaka, J. Chem.
Phys., 2015, 142, 044110 CrossRef PubMed.
- H. C. R. Klein and U. S. Schwarz, J. Chem. Phys., 2014, 140, 184112 CrossRef PubMed.
- Y. E. Ryabov and D. Fushman, J. Am. Chem. Soc., 2007, 129, 3315–3327 CrossRef CAS PubMed.
- V. Wong, D. A. Case and A. Szabo, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 11016–11021 CrossRef CAS PubMed.
- Y. Ryabov, G. M. Clore and C. D. Schwieters, J. Chem. Phys., 2012, 136, 034108 CrossRef PubMed.
- A. Sanz, R. Martnez-Casado, H. Peñate-Rodrguez, G. Rojas-Lorenzo and S. Miret-Artés, Ann. Phys., 2014, 347, 1–20 CAS.
- S. Garashchuk, V. Dixit, B. Gu and J. Mazzuca, J. Chem. Phys., 2013, 138, 054107 CrossRef PubMed.
- A. P. Polychronakos and R. Tzani, Phys. Lett. B, 1993, 302, 255–260 CrossRef.
- M. D. Kostin, J. Chem. Phys., 1972, 57, 3589–3591 CrossRef CAS.
-
H. Breuer and F. Petruccione, The Theory of Open Quantum Systems, OUP, Oxford, 2007 Search PubMed.
- S. Nakajima, Prog. Theor. Phys., 1958, 20, 948–959 CrossRef.
- R. Zwanzig, J. Chem. Phys., 1960, 33, 1338–1341 CrossRef CAS.
- R. Zwanzig, Physica, 1964, 30, 1109–1123 CrossRef.
-
D. Henderson, Physical Chemistry: An Advanced Treatise – Mathematical Methods, Elsevier Science, 2012, vol. XIB Search PubMed.
-
D. V. Anosov and V. I. Arnold, Dynamical Systems I: ordinary differential equations and smooth dynamical systems, Springer Berlin Heidelberg, 1989 Search PubMed.
- B. Fresch and G. J. Moro, J. Chem. Phys., 2010, 133, 034509 CrossRef PubMed.
- B. Fresch and G. J. Moro, J. Chem. Phys., 2010, 133, 034510 CrossRef PubMed.
- B. Fresch and G. J. Moro, J. Chem. Phys., 2011, 134, 054510 CrossRef PubMed.
- B. Fresch and J. G. Moro, Eur. Phys. J. B, 2013, 86, 1–13 CrossRef.
- S. Goldstein, J. L. Lebowitz, R. Tumulka and N. Zanghì, Phys. Rev. Lett., 2006, 96, 050403 CrossRef PubMed.
- C. J. Trahan and R. E. Wyatt, J. Chem. Phys., 2003, 119, 7017–7029 CrossRef CAS.
- E. Wigner, Phys. Rev., 1932, 40, 749–759 CrossRef CAS.
- J. E. Moyal, Proc. Cambridge Philos. Soc., 1949, 45, 99–124 CrossRef.
- A. Caldeira and A. Leggett, Physica A, 1983, 121, 587–616 CrossRef.
- E. P. Wigner, SIAM Rev., 1967, 9, 1–23 CrossRef.
- T. A. Brody, J. Flores, J. B. French, P. A. Mello, A. Pandey and S. S. M. Wong, Rev. Mod. Phys., 1981, 53, 385–479 CrossRef CAS.
-
C. Sanderson, Technical Report, NICTA, 2010.
- S. Popescu, A. J. Short and A. Winter, Nat. Phys., 2006, 2, 754–758 CrossRef CAS.
- B. Fresch and G. J. Moro, J. Phys. Chem. A, 2009, 113, 14502–14513 CrossRef CAS PubMed.
-
W. H. Press, S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, Numerical Recipes, Cambridge University Press, 2007 Search PubMed.
-
A. Khinchin, Mathematical Foundations of Statistical Mechanics, Dover Publications, 1949 Search PubMed.
- C. Efthymiopoulos, C. Kalapotharakos and G. Contopoulos, J. Phys. A: Math. Theor., 2007, 40, 12945 CrossRef.
- H. Wu and D. Sprung, Phys. Lett. A, 1999, 261, 150–157 CrossRef CAS.
- O. F. de Alcantara Bonfim, J. Florencio and F. C. Sá Barreto, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6851–6854 CrossRef.
- H. Frisk, Phys. Lett. A, 1997, 227, 139–142 CrossRef CAS.
-
R. Zwanzig, Nonequilibrium Statistical Mechanics, Oxford University Press, 2001 Search PubMed.
- A. Rahman, Phys. Rev., 1964, 136, A405–A411 CrossRef.
-
H. Risken, The Fokker–Planck Equation, Springer-Verlag Berlin Heidelberg, 1989 Search PubMed.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- G. A. Voth and R. M. Hochstrasser, J. Phys. Chem., 1996, 100, 13034–13049 CrossRef CAS.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  * and
Giorgio J.
Moro
* and
Giorgio J.
Moro
 *
*
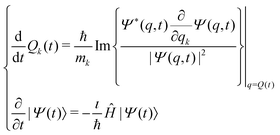

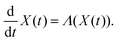
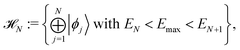
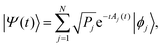
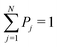 . Since the pure state of eqn (5) is fully identified by the set of phases A(t) = (A1(t), A2(t),…,AN(t)) once the populations are established, a complete description of the Schrödinger–Bohm dynamics is recovered by considering also the Bohm coordinates according to the time dependent variable X(t),
. Since the pure state of eqn (5) is fully identified by the set of phases A(t) = (A1(t), A2(t),…,AN(t)) once the populations are established, a complete description of the Schrödinger–Bohm dynamics is recovered by considering also the Bohm coordinates according to the time dependent variable X(t),![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) × [0,2π)N = {(q,α)} = {x}, where
× [0,2π)N = {(q,α)} = {x}, where ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) represents the configuration space while [0,2π) is the domain of each phase variable. The subscript P of ΩP highlights the parametric dependence on the population set P of the map supplied by eqn (5) between each element of the manifold ΩP and a specific pure state |Ψ(t)〉. In our notation the capital letters, i.e., X(t) = (Q(t),A(t)), tag the actual system state whereas the corresponding lowercase symbols, i.e., x = (q,α), are used for the generic element of the manifold ΩP. For instance, a distribution (probability density) ρΩP on the manifold ΩP will be described by the function ρΩP(x,t) depending on the point x ∈ ΩP and in general on the time.
represents the configuration space while [0,2π) is the domain of each phase variable. The subscript P of ΩP highlights the parametric dependence on the population set P of the map supplied by eqn (5) between each element of the manifold ΩP and a specific pure state |Ψ(t)〉. In our notation the capital letters, i.e., X(t) = (Q(t),A(t)), tag the actual system state whereas the corresponding lowercase symbols, i.e., x = (q,α), are used for the generic element of the manifold ΩP. For instance, a distribution (probability density) ρΩP on the manifold ΩP will be described by the function ρΩP(x,t) depending on the point x ∈ ΩP and in general on the time.
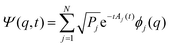
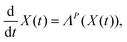
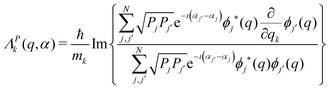
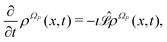
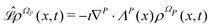
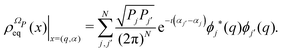
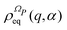 by integration on the coordinates q and the phases α. We stress that
by integration on the coordinates q and the phases α. We stress that 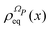 is proportional to the square modulus of the wave function if the phase dependence is replaced by the time dependence, i.e.,
is proportional to the square modulus of the wave function if the phase dependence is replaced by the time dependence, i.e., 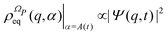 .
.
 onto the submanifold ΩR
onto the submanifold ΩR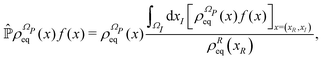
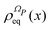 on the irrelevant variables,
on the irrelevant variables,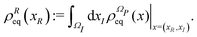
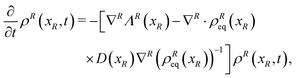
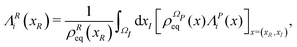
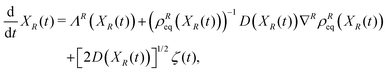
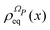 and ΛP(x) in eqn (13) and (9), is controlled by imaginary exponentials like exp(−ıαl′ + ıαl). Thus, the integration on the phases in eqn (16) and (18) can be performed explicitly by exploiting the orthogonality of the Fourier components. Secondly, the whole Hilbert space
and ΛP(x) in eqn (13) and (9), is controlled by imaginary exponentials like exp(−ıαl′ + ıαl). Thus, the integration on the phases in eqn (16) and (18) can be performed explicitly by exploiting the orthogonality of the Fourier components. Secondly, the whole Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) can be identified with the tensor product between the Hilbert space
can be identified with the tensor product between the Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S for the open system S and the Hilbert space
S for the open system S and the Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) E for the environment E,
E for the environment E, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S ⊗
S ⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) E. By employing the generic basis sets {|ηlS〉} and {|χlE〉} for
E. By employing the generic basis sets {|ηlS〉} and {|χlE〉} for ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) S and
S and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) E, respectively, the eigenfunctions {ϕj(q)} of the Hamiltonian operator Ĥ can be represented in the form
E, respectively, the eigenfunctions {ϕj(q)} of the Hamiltonian operator Ĥ can be represented in the form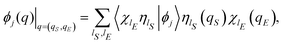
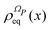 and of ΛP(x) through eqn (13) and (9). The integration on qE coordinates in eqn (16) and (18) is performed by exploiting the orthogonality of the basis functions χlE(qE). In this way, the equilibrium density distribution ρReq(xR) can be identified with
and of ΛP(x) through eqn (13) and (9). The integration on qE coordinates in eqn (16) and (18) is performed by exploiting the orthogonality of the basis functions χlE(qE). In this way, the equilibrium density distribution ρReq(xR) can be identified with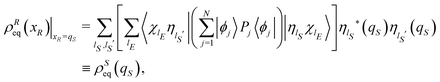
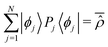 is the time average of the density matrix operator
is the time average of the density matrix operator ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) = |Ψ(t)〉〈Ψ(t)|.45,46 Therefore, the terms between square brackets in eqn (22) correspond to the time average of the elements of the reduced density matrix
= |Ψ(t)〉〈Ψ(t)|.45,46 Therefore, the terms between square brackets in eqn (22) correspond to the time average of the elements of the reduced density matrix ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) := TrE{|Ψ(t)〉〈Ψ(t)|} on the basis {|ηlS〉}, and the equilibrium density distribution ρSeq(qS) can be rewritten as
(t) := TrE{|Ψ(t)〉〈Ψ(t)|} on the basis {|ηlS〉}, and the equilibrium density distribution ρSeq(qS) can be rewritten as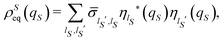
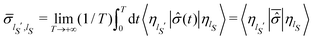 . The same equilibrium density distribution is obtained from the time average of the squared modulus of the wave function of eqn (7) by integration on the environmental degrees of freedom
. The same equilibrium density distribution is obtained from the time average of the squared modulus of the wave function of eqn (7) by integration on the environmental degrees of freedom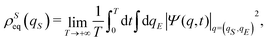
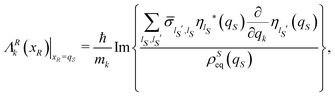
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is real if for any element |ψ〉 of its domain represented by a real function of the coordinates, also its transform
is real if for any element |ψ〉 of its domain represented by a real function of the coordinates, also its transform ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) |ψ〉 corresponds to a real function in the coordinate representation. An obvious implication is that the eigenfunctions ϕj(q) of the Hamiltonian Ĥ can be specified by real functions and, therefore, the time average density matrix
|ψ〉 corresponds to a real function in the coordinate representation. An obvious implication is that the eigenfunctions ϕj(q) of the Hamiltonian Ĥ can be specified by real functions and, therefore, the time average density matrix 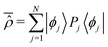 is a real operator too. Furthermore, also the time average reduced density matrix
is a real operator too. Furthermore, also the time average reduced density matrix 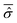 is a real operator in consideration of its definition as the partial trace of
is a real operator in consideration of its definition as the partial trace of 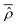 , i.e.,
, i.e., 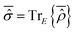 . One can then choose a basis set {|ηlS〉} with elements represented by real functions of the coordinates so deriving real values for the elements
. One can then choose a basis set {|ηlS〉} with elements represented by real functions of the coordinates so deriving real values for the elements 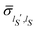 of the reduced density matrix. Correspondingly, the term between curly brackets in eqn (25) results to be real with vanishing values for the average velocity field. We stress the generality of this conclusion due to the independence on the basis set {|ηlS〉} of the velocity field of eqn (25).
of the reduced density matrix. Correspondingly, the term between curly brackets in eqn (25) results to be real with vanishing values for the average velocity field. We stress the generality of this conclusion due to the independence on the basis set {|ηlS〉} of the velocity field of eqn (25).![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) S for the evolution of the distribution ρS(qS,t) on the open system coordinates qS
S for the evolution of the distribution ρS(qS,t) on the open system coordinates qS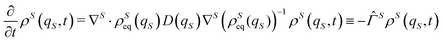
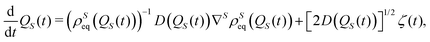
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) for the open system. On the other hand, with the Smoluchowski–Bohm equation the dynamics of
(t) for the open system. On the other hand, with the Smoluchowski–Bohm equation the dynamics of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) is completely neglected and it is replaced by its time average
(t) is completely neglected and it is replaced by its time average  in the calculation of the equilibrium distribution by means of eqn (23). Therefore, the Smoluchowski–Bohm equation appears to be justified whenever the time dependence of
in the calculation of the equilibrium distribution by means of eqn (23). Therefore, the Smoluchowski–Bohm equation appears to be justified whenever the time dependence of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) does not have significant deviations from its time average. However, when the evolution of the reduced density matrix of an open system is exactly evaluated according to the Schrödinger equation, an explicit time dependence is necessarily recovered. Of particular interest is the case of an open quantum system in equilibrium with the environment when the time dependence of
(t) does not have significant deviations from its time average. However, when the evolution of the reduced density matrix of an open system is exactly evaluated according to the Schrödinger equation, an explicit time dependence is necessarily recovered. Of particular interest is the case of an open quantum system in equilibrium with the environment when the time dependence of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) is characterized by random type fluctuations of small amplitude about the average, see Fig. 1 of ref. 47 for the results of a simple model system. In our opinion this is the situation where the use of the Smoluchowski–Bohm equation is appropriate by neglecting the effects of weak and incoherent fluctuations of
(t) is characterized by random type fluctuations of small amplitude about the average, see Fig. 1 of ref. 47 for the results of a simple model system. In our opinion this is the situation where the use of the Smoluchowski–Bohm equation is appropriate by neglecting the effects of weak and incoherent fluctuations of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t). However, whether such a situation is realized or not depends on the pure state Ψ(q,t) of the isolated quantum system, in particular on the initial wave function Ψ(q,0). One can always select a particular form of Ψ(q,0) for the isolated system in a non-equilibrium state leading to an initial relaxation of the reduced density matrix before reaching the equilibrium controlled by the above mentioned small fluctuations of random type. As long as the initial relaxation is not taken into account by the averaged reduced density matrix
(t). However, whether such a situation is realized or not depends on the pure state Ψ(q,t) of the isolated quantum system, in particular on the initial wave function Ψ(q,0). One can always select a particular form of Ψ(q,0) for the isolated system in a non-equilibrium state leading to an initial relaxation of the reduced density matrix before reaching the equilibrium controlled by the above mentioned small fluctuations of random type. As long as the initial relaxation is not taken into account by the averaged reduced density matrix  , the Smoluchowski–Bohm equation is unable to reproduce the behaviour of the open quantum system under this condition. These considerations point out that the use of the Smoluchowski–Bohm equation is legitimate only when the open quantum system is in equilibrium with the environment.
, the Smoluchowski–Bohm equation is unable to reproduce the behaviour of the open quantum system under this condition. These considerations point out that the use of the Smoluchowski–Bohm equation is legitimate only when the open quantum system is in equilibrium with the environment.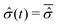 , provided that the equilibrium condition applies to the isolated system composed of the open quantum system and the macroscopic environment. Correspondingly, the time average is not required in eqn (24) in order to establish a relation between the equilibrium distribution ρSeq(qS) of the open system and the instantaneous wave function Ψ(q,t) of the isolated system. In such a situation the environment acts like a thermal bath with a well-defined temperature T and, if the interactions with the open system are weak enough, one can evaluate the reduced density matrix according to the canonical statistics49
, provided that the equilibrium condition applies to the isolated system composed of the open quantum system and the macroscopic environment. Correspondingly, the time average is not required in eqn (24) in order to establish a relation between the equilibrium distribution ρSeq(qS) of the open system and the instantaneous wave function Ψ(q,t) of the isolated system. In such a situation the environment acts like a thermal bath with a well-defined temperature T and, if the interactions with the open system are weak enough, one can evaluate the reduced density matrix according to the canonical statistics49![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) C = exp(−ĤS/kBT)/Z,
C = exp(−ĤS/kBT)/Z,![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 1 ⊗
1 ⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 2 ⊗⋯⊗
2 ⊗⋯⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n. Each element of the space
n. Each element of the space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) k can be fully specified by means of the orthonormal basis set {|ζlk〉}, whose coordinate representation is specified in the following
k can be fully specified by means of the orthonormal basis set {|ζlk〉}, whose coordinate representation is specified in the following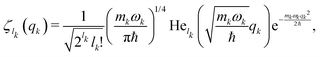
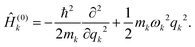
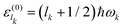 , and where mk (ωk) is the corresponding mass (resonance angular frequency). The Hamiltonian of the whole system is specified as
, and where mk (ωk) is the corresponding mass (resonance angular frequency). The Hamiltonian of the whole system is specified as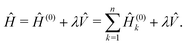
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) represents the interactions between the oscillators and the parameter λ sets the magnitude of the interactions. The operator
represents the interactions between the oscillators and the parameter λ sets the magnitude of the interactions. The operator ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) aims to produce a generic coupling amongst the oscillators and it is modelled according to a random matrix (see below).
aims to produce a generic coupling amongst the oscillators and it is modelled according to a random matrix (see below).
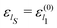 and ηlS(qS) = ζl1(q1), respectively; the corresponding Bohm coordinates is tagged with QS(t). Thus, the open system is described by only one degree of freedom whose stochastic dynamics is determined by a one-dimensional Fokker–Planck equation including a scalar diffusion coefficient D(qS).
and ηlS(qS) = ζl1(q1), respectively; the corresponding Bohm coordinates is tagged with QS(t). Thus, the open system is described by only one degree of freedom whose stochastic dynamics is determined by a one-dimensional Fokker–Planck equation including a scalar diffusion coefficient D(qS).![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) :
: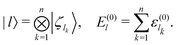
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ′ (the “computational” Hilbert space) of the whole infinite Hilbert space
′ (the “computational” Hilbert space) of the whole infinite Hilbert space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) =
= ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 1 ⊗
1 ⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) 2 ⊗ ⋯ ⊗
2 ⊗ ⋯ ⊗ ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n of the model system. We define
n of the model system. We define ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ′ as the Hilbert space generated by the basis set {|l〉} that includes only the eigenstates of Ĥ(0) with eigenenergies E(0)l smaller than the truncation energy cutoff Etr:
′ as the Hilbert space generated by the basis set {|l〉} that includes only the eigenstates of Ĥ(0) with eigenenergies E(0)l smaller than the truncation energy cutoff Etr: ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ′ := {⊕l|l〉 with E(0)l < Etr}. A diagonal matrix with elements E(0)l is recovered for the representation of Ĥ(0) Hamiltonian on the basis set |l〉, whereas the operator
′ := {⊕l|l〉 with E(0)l < Etr}. A diagonal matrix with elements E(0)l is recovered for the representation of Ĥ(0) Hamiltonian on the basis set |l〉, whereas the operator ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) has been modelled with a random matrix whose elements are Gaussian distributed according to the following statistical constraints:54,55
has been modelled with a random matrix whose elements are Gaussian distributed according to the following statistical constraints:54,55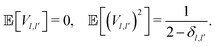
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is a perturbation compared to Ĥ(0), the diagonalization of the full Hamiltonian is influenced mainly by the coupling amongst basis elements |l〉 with similar energies E(0)l. Consequently, the effects of the basis set truncation are more pronounced for the Hamiltonian Ĥ eigenstates |ϕj〉 whose eigenenergies are closed to the truncation energy cutoff Etr. In order to deal with an efficient truncation scheme with negligible effects on the pure state dynamics, the truncation energy cutoff Etr must be significantly larger than the energy cutoff Emax defining the active space
is a perturbation compared to Ĥ(0), the diagonalization of the full Hamiltonian is influenced mainly by the coupling amongst basis elements |l〉 with similar energies E(0)l. Consequently, the effects of the basis set truncation are more pronounced for the Hamiltonian Ĥ eigenstates |ϕj〉 whose eigenenergies are closed to the truncation energy cutoff Etr. In order to deal with an efficient truncation scheme with negligible effects on the pure state dynamics, the truncation energy cutoff Etr must be significantly larger than the energy cutoff Emax defining the active space ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) N of eqn (4), which includes the examined pure state of the system. In such a case, the calculation of the eigenstates belonging to
N of eqn (4), which includes the examined pure state of the system. In such a case, the calculation of the eigenstates belonging to ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) N are weakly effected by the truncation. A more detailed discussion about this issue can be found in ref. 18.
N are weakly effected by the truncation. A more detailed discussion about this issue can be found in ref. 18.
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) in order to mimic the condition of weak interaction between the open quantum system and the environment. The energy cutoffs for the truncation and the active space are set to Etr = 10.5ħω and to Emax = 9.5ħω, respectively. Correspondingly, the dimension of the computational Hilbert space is 1716, while the dimension of the active space is N = 924. We anticipate that in the analysis of the results of the calculations, we shall employ 2π/ω as the time unit and
in order to mimic the condition of weak interaction between the open quantum system and the environment. The energy cutoffs for the truncation and the active space are set to Etr = 10.5ħω and to Emax = 9.5ħω, respectively. Correspondingly, the dimension of the computational Hilbert space is 1716, while the dimension of the active space is N = 924. We anticipate that in the analysis of the results of the calculations, we shall employ 2π/ω as the time unit and 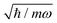 as the coordinate unit for the oscillator.
as the coordinate unit for the oscillator.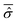 , see eqn (22) and (23). On the basis of the oscillator eigenfunctions, ηlS(qS) = ζlS(qS) of eqn (29), the matrix representation of
, see eqn (22) and (23). On the basis of the oscillator eigenfunctions, ηlS(qS) = ζlS(qS) of eqn (29), the matrix representation of 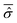 results to be almost diagonal:
results to be almost diagonal: 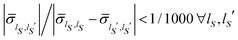 . The resulting values for the diagonal elements
. The resulting values for the diagonal elements ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) lS,lS of the averaged reduced density matrix are reported in Table 1. They steeply decrease in magnitude with the oscillator eigenenergies
lS,lS of the averaged reduced density matrix are reported in Table 1. They steeply decrease in magnitude with the oscillator eigenenergies 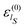 , and this behaviour might suggest the equivalence with the canonical density matrix of eqn (28). However, in order to verify it, the temperature must be identified. For this purpose, we have interpreted the calculated value of the ratio between the first two diagonal elements according to the canonical statistics, i.e.,
, and this behaviour might suggest the equivalence with the canonical density matrix of eqn (28). However, in order to verify it, the temperature must be identified. For this purpose, we have interpreted the calculated value of the ratio between the first two diagonal elements according to the canonical statistics, i.e., ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 0,0/
0,0/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) 1,1 = exp((ε(0)1 − ε(0)0)/kBT), so obtaining a thermal energy factor of kBT = 1.661ħω. Then, the elements of the canonical density matrix can be evaluated and they are reported in Table 1 between parenthesis. Clearly, significant deviations emerge from the comparison with the result of the full calculation for the model system. We can conclude that even if the RPSE procedure has been employed to select typical pure states, which is representative of the equilibrium condition, thermal equilibrium states described according to the canonical states are not generated by the model system. This is due to the fact that the environment is too small to reproduce the thermodynamical behaviour of a truly thermal bath at a given temperature, which can be recovered only with a sufficiently larger number of oscillators.
1,1 = exp((ε(0)1 − ε(0)0)/kBT), so obtaining a thermal energy factor of kBT = 1.661ħω. Then, the elements of the canonical density matrix can be evaluated and they are reported in Table 1 between parenthesis. Clearly, significant deviations emerge from the comparison with the result of the full calculation for the model system. We can conclude that even if the RPSE procedure has been employed to select typical pure states, which is representative of the equilibrium condition, thermal equilibrium states described according to the canonical states are not generated by the model system. This is due to the fact that the environment is too small to reproduce the thermodynamical behaviour of a truly thermal bath at a given temperature, which can be recovered only with a sufficiently larger number of oscillators.![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) lS,lS, with, between parentheses, their canonical values for comparison
lS,lS, with, between parentheses, their canonical values for comparison
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) l
S
,lS
l
S
,lS
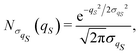
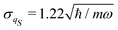 for the variance. However, significant deviations are evident in comparison with the exact one as in Fig. 1, particularly, for the too slowly decaying tails at large values of the coordinate qS.
for the variance. However, significant deviations are evident in comparison with the exact one as in Fig. 1, particularly, for the too slowly decaying tails at large values of the coordinate qS.

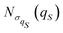 with the variance
with the variance 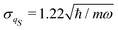 (dashed green line).
(dashed green line).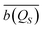 of any observable specified as a function b(QS) of the Bohm coordinate,
of any observable specified as a function b(QS) of the Bohm coordinate,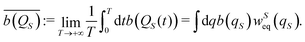

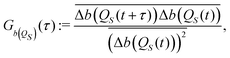
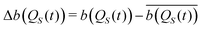 . Note that these correlation functions have been defined in a normalized form such that they start from a unitary value: Gb(QS)(τ)|τ=0 = 1. They are computed by averaging directly Δb(QS(t + τ))Δb(QS(t)) for 0 ≤ t ≤ T − τ along the calculated trajectory within the given time window T. The most interesting correlation function is certainly GQS(τ) for the coordinate QS itself, i.e., b(QS) = QS, which is drawn in red in Fig. 4. Its monotonic and exponential-like decrease up to vanish is clear evidence of the loss of correlation during the evolution of the Bohm coordinate QS(t), which originates from the chaotic nature of the Bohm coordinate motion. This ensures that the choice of their initial values Qk(0) is irrelevant, since they start to loose the memory of the initial conditions after times of the order of the correlation time τC which can be estimated as τC = 1.86 2π/ω. According to the analysis of ref. 13, the loss of correlation is at the origin of the ergodicity of the Bohm coordinate leading to the equivalence of the distributions displayed in Fig. 3. It should be noted that some kind of wobbling in the profile of the correlation function GQS(τ) displayed in Fig. 4 appears particularly at times longer than the correlation time. This is an effect of the finite time window T of the calculated trajectory, which tends to disappear by enlarging T significantly.
. Note that these correlation functions have been defined in a normalized form such that they start from a unitary value: Gb(QS)(τ)|τ=0 = 1. They are computed by averaging directly Δb(QS(t + τ))Δb(QS(t)) for 0 ≤ t ≤ T − τ along the calculated trajectory within the given time window T. The most interesting correlation function is certainly GQS(τ) for the coordinate QS itself, i.e., b(QS) = QS, which is drawn in red in Fig. 4. Its monotonic and exponential-like decrease up to vanish is clear evidence of the loss of correlation during the evolution of the Bohm coordinate QS(t), which originates from the chaotic nature of the Bohm coordinate motion. This ensures that the choice of their initial values Qk(0) is irrelevant, since they start to loose the memory of the initial conditions after times of the order of the correlation time τC which can be estimated as τC = 1.86 2π/ω. According to the analysis of ref. 13, the loss of correlation is at the origin of the ergodicity of the Bohm coordinate leading to the equivalence of the distributions displayed in Fig. 3. It should be noted that some kind of wobbling in the profile of the correlation function GQS(τ) displayed in Fig. 4 appears particularly at times longer than the correlation time. This is an effect of the finite time window T of the calculated trajectory, which tends to disappear by enlarging T significantly.
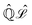 whose effects on the time evolution are hardly estimated. The same problem arises in classical stochastic treatments65 so that the diffusion coefficient (or the friction coefficient) is considered as a parameter to be evaluated independently of the projection procedure. For instance, in the case of the Brownian motion the diffusion coefficient is identified according to the proportionality between the mean squared displacement and the time. The same point of view will be assumed for the Smoluchowski–Bohm equation. In particular we assume that the qS dependence of the diffusion coefficient is negligible, i.e., D(qS) = D, similarly to what is often done in the applications of classical stochastic methods. Its value is selected by optimizing the agreement with the autocorrelation function GQS(τ) calculated with the deterministic dynamics. According to the Smoluchowski–Bohm eqn (26), the diffusion coefficient sets the time scale of the diffusion motion. Then, the trajectory QS(t) obtained as a solution of the Langevin type eqn (27) can be used to represent the stochastic motion with a different diffusion coefficient by simply scaling the time axis. Since the same rule holds for the correlation functions, we have calculated GQS(τ) from the stochastic trajectory for a given value of D, and then we have optimized the time scale in order to obtain the best fit with the deterministic correlation function reported in Fig. 4. Using this procedure, we have obtained for the stochastic motion of the oscillator coordinate an effective diffusion coefficient D = 0.1273ħ/m and the resulting correlation function is also reported in Fig. 4. The initial part of a stochastic trajectory QS(t) is reported in Fig. 5 together with the same deterministic trajectory of Fig. 2 for the sake of comparison. Clearly, they share the same features of the fluctuating dynamics. By visual inspection, the deterministic trajectory could be apparently interpreted as another stochastic trajectory deriving from a different realization of the noise term.
whose effects on the time evolution are hardly estimated. The same problem arises in classical stochastic treatments65 so that the diffusion coefficient (or the friction coefficient) is considered as a parameter to be evaluated independently of the projection procedure. For instance, in the case of the Brownian motion the diffusion coefficient is identified according to the proportionality between the mean squared displacement and the time. The same point of view will be assumed for the Smoluchowski–Bohm equation. In particular we assume that the qS dependence of the diffusion coefficient is negligible, i.e., D(qS) = D, similarly to what is often done in the applications of classical stochastic methods. Its value is selected by optimizing the agreement with the autocorrelation function GQS(τ) calculated with the deterministic dynamics. According to the Smoluchowski–Bohm eqn (26), the diffusion coefficient sets the time scale of the diffusion motion. Then, the trajectory QS(t) obtained as a solution of the Langevin type eqn (27) can be used to represent the stochastic motion with a different diffusion coefficient by simply scaling the time axis. Since the same rule holds for the correlation functions, we have calculated GQS(τ) from the stochastic trajectory for a given value of D, and then we have optimized the time scale in order to obtain the best fit with the deterministic correlation function reported in Fig. 4. Using this procedure, we have obtained for the stochastic motion of the oscillator coordinate an effective diffusion coefficient D = 0.1273ħ/m and the resulting correlation function is also reported in Fig. 4. The initial part of a stochastic trajectory QS(t) is reported in Fig. 5 together with the same deterministic trajectory of Fig. 2 for the sake of comparison. Clearly, they share the same features of the fluctuating dynamics. By visual inspection, the deterministic trajectory could be apparently interpreted as another stochastic trajectory deriving from a different realization of the noise term.
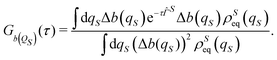
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) Sξj(qS)ρSeq(qS) = λjξj(qS)ρSeq(qS), the correlation function is decomposed according to a multi-exponential decay due to the ensemble of independent diffusion modes ξj(qS) each of them characterized by the relaxation time τj = 1/λj. In particular, analytical approximations can be derived by replacing the exact equilibrium distribution ρSeq(qS) with its Gaussian approximation
Sξj(qS)ρSeq(qS) = λjξj(qS)ρSeq(qS), the correlation function is decomposed according to a multi-exponential decay due to the ensemble of independent diffusion modes ξj(qS) each of them characterized by the relaxation time τj = 1/λj. In particular, analytical approximations can be derived by replacing the exact equilibrium distribution ρSeq(qS) with its Gaussian approximation 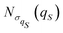 of eqn (35), since in this case the Smoluchowski–Bohm equation becomes equivalent to the classical Ornstein–Uhlenbeck process.24 Then the independent diffusion modes are specified according to the Hermite polynomials,
of eqn (35), since in this case the Smoluchowski–Bohm equation becomes equivalent to the classical Ornstein–Uhlenbeck process.24 Then the independent diffusion modes are specified according to the Hermite polynomials, 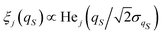 for j = 0, 1, 2,…, with the following relaxation time for j ≠ 0:
for j = 0, 1, 2,…, with the following relaxation time for j ≠ 0: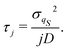
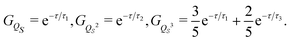
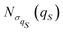 , the expansion of the function b(qS) = qS on the basis of the true diffusion modes ξj(qS) of the Smoluchowski–Bohm equation includes also small contributions from those with j > 1.
, the expansion of the function b(qS) = qS on the basis of the true diffusion modes ξj(qS) of the Smoluchowski–Bohm equation includes also small contributions from those with j > 1.

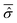 of the open quantum system. Let us consider the common situation of an open quantum systems weakly interacting with a large enough environment acting as a thermal bath at a given temperature T. Then the time averaged reduced density matrix
of the open quantum system. Let us consider the common situation of an open quantum systems weakly interacting with a large enough environment acting as a thermal bath at a given temperature T. Then the time averaged reduced density matrix 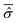 of the open quantum system49,57 can be replaced by its canonical form of eqn (28). This corresponds to the case of an open system in thermal equilibrium with the environment, which has a paramount importance in chemical studies in relation to the observation of a small system, such as a particular molecule or a set of its degrees of freedom, weakly interacting with the surroundings. In this case, through the canonical reduced density matrix one can obtain the equilibrium distribution by means of a suitable model of the open system Hamiltonian ĤS.
of the open quantum system49,57 can be replaced by its canonical form of eqn (28). This corresponds to the case of an open system in thermal equilibrium with the environment, which has a paramount importance in chemical studies in relation to the observation of a small system, such as a particular molecule or a set of its degrees of freedom, weakly interacting with the surroundings. In this case, through the canonical reduced density matrix one can obtain the equilibrium distribution by means of a suitable model of the open system Hamiltonian ĤS.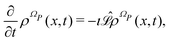
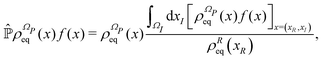
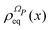 on the irrelevant variables. Since the projection operator is linear and time independent, the Liouville equation can be written as a pair of equations
on the irrelevant variables. Since the projection operator is linear and time independent, the Liouville equation can be written as a pair of equations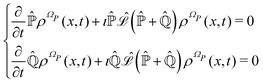
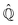 is defined in such a way that
is defined in such a way that 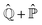 is the identity operator. The second equation in (43) can be formally solved for
is the identity operator. The second equation in (43) can be formally solved for 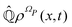 and the solution can be substituted in the first equation in (43) (see ref. 42). In this way a closed equation for the projected probability density
and the solution can be substituted in the first equation in (43) (see ref. 42). In this way a closed equation for the projected probability density 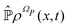 is obtained,
is obtained,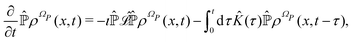
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ),
(τ),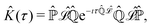
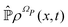 . The only assumption concerns the initial density distribution ρΩP(x,0): since it is arbitrary and we are interested in the probability density of the relevant variables, it has been selected in such a way that
. The only assumption concerns the initial density distribution ρΩP(x,0): since it is arbitrary and we are interested in the probability density of the relevant variables, it has been selected in such a way that 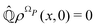 . According to eqn (42),
. According to eqn (42), 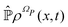 can be specified as
can be specified as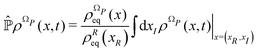
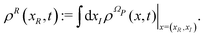
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ) does not vanish only for small values of τ:
(τ) does not vanish only for small values of τ: ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ) ≃ 0 for τ > ε with ε as a small number. Then, the following approximation results to be justified
(τ) ≃ 0 for τ > ε with ε as a small number. Then, the following approximation results to be justified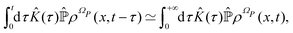
![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (τ). Furthermore, the upper integration boundary can be brought to infinity when a generic time t is considered. If eqn (48) holds, eqn (44) corresponds to a partial differential equation of Fokker–Planck type.
(τ). Furthermore, the upper integration boundary can be brought to infinity when a generic time t is considered. If eqn (48) holds, eqn (44) corresponds to a partial differential equation of Fokker–Planck type.
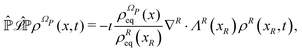
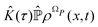 can be specified as
can be specified as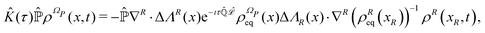
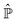 , one obtains
, one obtains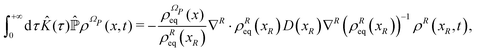
![[capital Gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e132.gif) R = ∇RΛR(xR) − ∇R·ρReq(xR)D(xR)∇R(ρReq(xR))−1,
R = ∇RΛR(xR) − ∇R·ρReq(xR)D(xR)∇R(ρReq(xR))−1,

