Structures and infrared spectra of calcium phosphate clusters by ab initio methods with implicit solvation models
Tzu-Jen
Lin
 *a and
Cheng-Chau
Chiu
*a and
Cheng-Chau
Chiu
 b
b
aDepartment of Chemical Engineering, Chung Yuan Christian University, 200 Chung Pei Road, Chung Li District, Taoyuan City, 32023, Taiwan. E-mail: tzujenlin999@gmail.com
bInstitute of Atomic and Molecular Sciences, Academia Sinica, No. 1, Roosevelt Rd., Sec. 4, Taipei, 10617, Taiwan
First published on 27th November 2017
Abstract
Since the first detection of pre-nucleation clusters during the formation of calcium phosphate minerals, determining such clusters’ compositions and structures has become crucial for understanding the early-stage nucleation of these minerals in solutions. In previous experimental studies, the composition and sizes of pre-nucleation clusters have been calculated, but their structural information has been difficult to determine because they are very small (<1 nm). In this study, we examined the structures and infrared spectra of small- and medium-sized calcium phosphate clusters using ab initio calculations combined with implicit solvation models. Adding solvent effects increased the possibility of the existence of alternative configurations of calcium phosphate clusters other than their compact configurations. The calcium atoms had a tendency to be located outside of the clusters to coordinate with water molecules in the aqueous environment. The computed infrared spectra of extended small calcium phosphate clusters captured some of the features measured in the in situ infrared spectra, which supports the network structures proposed by large-scale molecular dynamics studies and X-ray adsorption near-edge spectra. The relative stabilities of medium-sized Ca9(PO4)6 clusters with respect to the stability of Posner's cluster in water were also reviewed. We found that in water, alternative structures with low symmetry or large dipole moments had lower energies than Posner's cluster.
Introduction
In 2008, Gebauer1 and Sommerdijk2 studied long-lived pre-nucleation calcium carbonate clusters by using equilibrium thermodynamics and observed them through cryotransmission electron microscopy (cryo-TEM). They found the structure of the cluster to be different from that of bulk counterparts. On the basis of their findings, Gebauer and coworkers1,3,4 proposed an alternative theory of nucleation – the so-called non-classical nucleation theory. Classical nucleation theory assumes that ions or atoms pack in the same fashion as they do in a small part of the bulk crystal, and that the interface energy of the packed ions or atoms is equal to that of the completely formed surfaces. By contrast, the nonclassical theory states that stable pre-nucleation clusters form and they subsequently collide and coalesce, resulting in the growth of amorphous nanoparticles and eventually leading to the formation of an ordered crystal phase. Since this theory's proposal, determining the details and behaviors of pre-nucleation clusters has become important to the understanding of the nucleation of minerals.5–9In recent experiments, the appearance of stable pre-nucleation clusters in calcium phosphate systems has been observed. Wang10 observed stable nanosized clusters in solution without any organic template through atomic force microscopy (AFM), and Sommerdijk11 observed clusters with an average diameter of 0.87 ± 0.2 nm through high-resolution cryo-TEM. The cluster sizes in both experimental observations suggested that the observed clusters were Posner's clusters12 (Ca9(PO4)6), even though the structure details of these clusters could not be determined. In recent experimental studies, pre-nucleation calcium phosphate clusters in solution have been investigated. Using in situ cryo-TEM, DeYoreo and Sommerdijk13 detected calcium triphosphate clusters, [Ca2(HPO4)3]2−, and suggested that they were the building blocks for the formation of amorphous calcium phosphate. Qun Zhang14 used synchrotron X-ray adsorption near-edge spectroscopy (XANES) at the calcium K-edge spectrum to probe calcium phosphate clusters in the early stages of crystallization, and suggested that the most abundant component of the clusters in solution was Ca(η2-PO4)2L2 (L = H2O or η1-PO4). Qun Zhang proposed that these clusters would subsequently form network structures. Tian-Lan Zhang15 used in situ XANES, ex situ X-ray diffraction, continuous pH measurements, and coordination chemistry to propose an improved Posner's cluster, Ca9(PO4)6(H2O)30, in which the eight calcium atoms are coordinated with water molecules except that at the center of the cluster.
Determining the structure of pre-nucleation clusters in solution is highly challenging because their sizes are nearly or less than 1 nm. Theoretical calculations provide alternative methods to overcome this challenge. Treboux16–18 conducted pioneer studies on calcium phosphate clusters through theoretical calculations. He systematically examined calcium phosphate clusters such as Ca3(PO4)2 and Ca9(PO4)6 through ab initio calculations, and showed that the clusters preferred compact arrangements with D3h and S6 symmetry, respectively. The structure of the Ca9(PO4)6 cluster with S6 symmetry was close to that of Posner's cluster. However, Treboux's studies were performed in vacuo and did not consider solvent effects. Recent theoretical studies have begun to include solvent effects. de Leeuw19 used ab initio molecular dynamics (AIMD) combined with umbrella sampling to determine the stability of calcium phosphate clusters in an aqueous environment. The AIMD study demonstrated that the structure of the pre-nucleation calcium phosphate cluster was Ca(η2-HPO42−)2(η1-HPO42−)(H2O)2, in which the calcium ion was sevenfold-coordinated. Furthermore, de Leeuw20 employed classical molecular dynamics to study the aggregation of calcium and phosphate ions in water, and the results showed that these ions preferred to aggregate into a structure similar to Posner's cluster.
With such diverse information available in the literature, it would not be trivial to investigate the stable structures of calcium phosphate clusters in an aqueous environment by using affordable simulation methods. In this study, we selected ab initio methods rather than classical molecular dynamics to evaluate the structure of calcium phosphate clusters because the performance and accuracy of the force field parameters of mineral ions is still uncertain.5,21,22 In addition, force field parameters usually have to be tuned for specific chemical and physical conditions, which could lead to case-dependent parameters. AIMD can include solvent effects, but is computationally demanding, thus leading to limited system sizes and sampling times. Therefore, we employed compromise methods, ab initio calculations combined with implicit solvation models, for our study. We compared optimized structures of small calcium phosphate clusters in vacuo and in water, and then re-examined the relative stability of medium-sized Ca9(PO4)6 clusters with respect to the stability of Posner's cluster in vacuo and in water. Furthermore, we computed the infrared spectra of calcium phosphate clusters. Previous theoretical studies have focused on the infrared spectra of hydroxyapatite or carbonate-substituted hydroxyapatite crystals.23,24 Boldeskul obtained the infrared spectra of calcium phosphate clusters, but the structure information of the calcium phosphate clusters in that study was elusive.25 In this study, we attempted to correlate the computed infrared spectra of calcium phosphate clusters with their in situ Fourier transform infrared (FTIR) spectra.13
Theoretical calculations
We began our investigation by studying small calcium phosphate clusters such as [Ca(PO4)]1− [Ca(PO4)2]4−, [Ca2(PO4)]1+, [Ca2(PO4)2]2−, [Ca2(PO4)3]5−, and Ca3(PO4)2 both in vacuo and in water. This helped us to identify the structural features of calcium phosphate clusters in an aqueous environment. Then, we studied Ca9(PO4)6 clusters in vacuo and in water. We examined the 39 Ca9(PO4)6 clusters mentioned in Treboux's18 study. These Ca9(PO4)6 clusters were created from compact structures with a high point group symmetry such as S6, Td, Th, and D3d. The orientation of the phosphate ions was then changed to form low-symmetry structures from the high symmetry structures, leading to the final 39 stable Ca9(PO4)6 clusters. These clusters were arranged in a body-centered fashion. The calcium atoms were located at the center and corners of the cubic structure, and the phosphate ions were located at the six facets of the cubic structure. We employed the notation used in Treboux's work. For example, CS-7, where the letter before the dashed line denotes the point group symmetry of the initial structure, which is CS. The number after the dashed line denotes the energy rank of Ca9(PO4)6 clusters with CS symmetry in Treboux's study.18 Latter in our investigation, we found that the ranks in Treboux's work were different from those given by our calculations. In addition, the optimized structures in our calculations mostly lost their starting symmetry. Nevertheless, we retained Treboux's notation in this study.The optimized structures and relative energies of calcium phosphate clusters were evaluated by density functional theory (DFT).26,27 Calcium phosphate clusters are highly polar and contain big phosphate anions. The meta GGA hybrid M06-2X functional shows good performance not only for main group thermochemistry, but also for anionic systems.28,29 6-31+G(d) basis sets were implemented for geometry optimizations, and this was followed by single-point calculations conducted using the same functional with 6-311+G(d) basis sets. Solvent effects were included by employing an SMD solvation model.30 The SMD solvation model is an extension of the SM8 (The 8 generation of universal Solvation Model) solvation model which was parameterized by a large training set and developed by Cramer and Truhlar.31 The “D” in SMD stands for “density”, which means the solvation model is based on the polarized continuous quantum mechanical charge density of the solute. The performance of the SMD solvation model has been tested for a broad range of systems.32,33 The infrared spectra of calcium phosphate clusters in water were on the basis of harmonic approximation, and were computed by using M062X/6-31+G(d) with the SMD solvation model. All DFT calculations were conducted by using Gaussian 09, Revision E.01.34 In this study, no explicit water molecules were considered because the number and placements of water molecules would have made the simulations unmanageable and beyond the capability of the computational resources in our lab.
Results and discussion
Structures of small calcium phosphate clusters
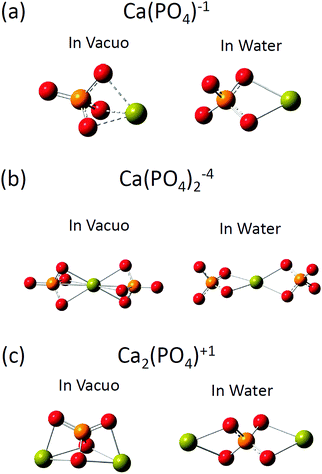
The optimized structures of [Ca(PO4)]1−, [Ca(PO4)2]4−, and [Ca2(PO4)]1+ clusters in vacuo and in water are shown in Fig. 1, and selected structural parameters of the clusters are presented in Table 1. Three initial configurations were considered for the geometry optimizations of [Ca(PO4)]1−: the calcium atom was put on the top, side, and face site of the phosphate ion. In vacuo, these three initial configurations converged to a structure in which the calcium atom located at the face site of the phosphate ion (see Fig. 1(a)). The shorter Ca–O bond lengths and the longer P–O bond lengths of [Ca(PO4)]1−in vacuo, than those in water, indicated that the Ca–O interactions were much stronger in vacuo than in water. In vacuo, the calcium atom in [Ca(PO4)]1− maximized Ca–O bond interactions by coordinating three oxygen atoms of the phosphate ion. The O–P–O angles of the phosphate ion were 100° and 117.8°, which indicated that the strong Ca–O interactions distorted the tetrahedral structure of the phosphate ion. By contrast, the optimized structure of [Ca(PO4)]1− in water was a different atomic arrangement. Rather than coordinating with three oxygen atoms of the phosphate ion, the calcium atom preferred coordinating with only two oxygen atoms of the phosphate ion, and the O–P–O angles were 109.5°, indicating that the phosphate ion maintained a tetrahedral structure. The optimized structure of [Ca(PO4)]1− in water indicated that maximization of the Ca–O bond interactions between calcium and phosphate ions was not the only criterion to form a stable structure in an aqueous environment. However, another factor that must be considered is the coordination between the calcium atom and water molecules. The two-oxygen-coordinated calcium atom in [Ca(PO4)]1− in water had more space to coordinate with water molecules than the three-oxygen-coordinated calcium atom in [Ca(PO4)]1−in vacuo. The optimized structures of [Ca(PO4)2]4−, and [Ca2(PO4)]1+ clusters in vacuo and in water demonstrated a similar trend to that of [Ca(PO4)]1−. In vacuo, the calcium and phosphate ions in [Ca(PO4)2]4− and [Ca2(PO4)]1+ formed a close packed configuration, and the Ca–O coordination numbers were 6 and 3, respectively. The calcium atoms of these two clusters located at the face site of the phosphate ions (see Fig. 1(b) and (c)). The strong Ca–O interactions were also observed based on the large variation of O–P–O angles in the distorted phosphate ions of [Ca(PO4)2]4− and [Ca2(PO4)]1+in vacuo. In water, the calcium atom in these two structures preferred to reside not at the face sites of the phosphate ions but at the edge sites, and the phosphate ions maintained their tetrahedral structures. In addition, the Ca–O coordination numbers of [Ca(PO4)2]4− and [Ca2(PO4)]1+ reduced to 4 and 2, respectively. The optimized structures of [Ca(PO4)]1−, [Ca(PO4)2]4−, and [Ca2(PO4)]1+ clusters in water support the experiment results of K-edge XANES spectra obtained by Zhang.14 Zhang proposed that the stable pre-nucleation clusters were Ca(η2-PO4)2L2 (L = H2O or η1-PO4) in which the calcium atom coordinated with two phosphate ions through the two oxygen atoms in each ion.| Environment | [Ca(PO4)]1− | [Ca(PO4)2]4− | [Ca2(PO4)]1+ | |||
|---|---|---|---|---|---|---|
| Vacuo | Water | Vacuo | Water | Vacuo | Water | |
| Ca–O distance (Å) | 2.251 | 2.418 | 2.509 | 2.443 |
2.400
2.307 |
2.446 |
|
Calcium coordinated
P–O bond lengths (Å) |
1.621 | 1.580 | 1.588 | 1.578 |
1.523
1.634 |
1.565 |
|
Calcium uncoordinated
P–O bond lengths (Å) |
1.499 | 1.555 | 1.533 | 1.558 | N.A. | N.A. |
| O–P–O angles (°) |
100.0
117.8 |
109.5 |
102.9
115.5 |
109.5 | 93–128 | 109.5 |
| Ca–O coordination number | 3 | 2 | 6 | 4 | 3, 3 | 2, 2 |
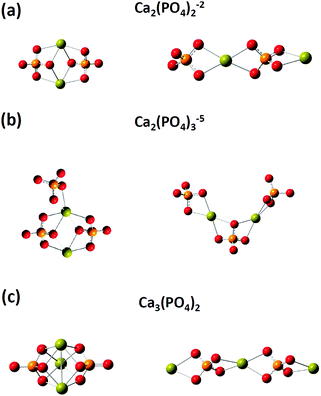
We then investigated the optimized structures of [Ca2(PO4)2]2− [Ca2(PO4)3]5− and Ca3(PO4)2 clusters in water. We constructed two configurations for each cluster. One was a compact configuration, and the other was an extended configuration (see Fig. 2). The compact configuration was constructed by maximizing Ca–O coordination, thus the calcium atoms were placed between phosphate ions. The extended configuration was constructed to verify the experimental conjecture that pre-nucleation clusters would aggregate into network structures or liquid-like ionic polymers.5,14Table 2 shows that the Ca–O coordination numbers in the compact configurations of [Ca2(PO4)2]2− [Ca2(PO4)3]5− and Ca3(PO4)2 clusters are higher than those of the extended configurations. In the compact configuration of [Ca2(PO4)2]2− and Ca3(PO4)2 clusters, the Ca–O distances were converged to 2.466 Å and 2.493 Å, respectively. This indicated that the strengths of Ca–O interactions in these two clusters were consistent. By contrast, the variation of Ca–O distances in the extended configurations of [Ca2(PO4)2]2− and Ca3(PO4)2 clusters indicated the different strengths of Ca–O interactions in these two clusters. In the [Ca2(PO4)3]5− cluster, different strengths of Ca–O interactions were in both compact and extended configuration based on the Ca–O distances ranging from 2.439 Å to 2.497 Å. The calcium-uncoordinated P–O bond lengths of [Ca2(PO4)2]2−, [Ca2(PO4)3]5−, and Ca3(PO4)2 clusters in water, no matter whether in the compact or extended configuration, were 1.53–1.55 Å, which were much shorter than the P–O bond lengths of a free phosphate ion in water. Based on DFT calculations combined with the implicit solvation model, we discovered that the compact configurations of [Ca2(PO4)2]2−, [Ca2(PO4)3]5−, and Ca3(PO4)2 clusters in water all had lower energies than their extended counterparts. The close-packed configurations of [Ca2(PO4)2]2− and [Ca2(PO4)3]5− clusters had 15 kcal mol−1 lower energies than their extended configurations, and the close-packed configuration of the Ca3(PO4)2 cluster had 25 kcal mol−1 lower energies than its extended configurations. This was mainly because of the higher Ca–O coordination number of the compact configurations than those of the extended configurations. The extended configurations gave much more space for coordination with water molecules in an aqueous environment than the close-packed configurations, but they also had less Ca–O bond interactions inside the clusters at the same time. As the calcium phosphate clusters grew, the Ca–O coordination number in the cluster seemed to be a dominant factor for creating stable structures. Although, the extended configurations had higher energies than the compact configurations, it was still difficult to deny their existence in water. We later found that the extended configurations captured some features of the measured in situ FTIR spectra of the clusters. The relative energies of the extended and compact configurations of [Ca2(PO4)2]2− [Ca2(PO4)3]5− and Ca3(PO4)2 clusters may need to be determined by AIMD where the clusters are solvating with numbers of explicit water molecules.
| Configuration | [Ca2(PO4)2]2− | [Ca2(PO4)3]5− | Ca3(PO4)2 | |||
|---|---|---|---|---|---|---|
| Compact | Extended | Compact | Extended | Compact | Extended | |
| Ca–O distance | 2.466 |
2.439
2.444 2.467 |
2.445–2.497 | 2.439–2.474 | 2.493 |
2.441
2.462 |
|
Ca-coordinated
Ca–O bond |
1.567
1.586 |
1.565
1.579 |
1.565–1.585 | 1.565–1.587 | 1.575 | 1.565 |
| Ca-uncoordinated Ca–O bond | 1.546 | 1.558 |
1.547
1.559 |
1.546
1.557 |
1.535 | N.A. |
| Ca–O coordination number | 4, 4 | 2, 4 | 4, 6 | 4, 4 | 4, 4, 4 | 2, 4, 2 |
| Relative energy | 0 | 16.1 | 0 | 13.5 | 0 | 24.6 |
Infrared spectra of small calcium phosphate clusters
The computed infrared spectra of the [Ca(PO4)]1− cluster are shown in Fig. 3, and the P–O stretching modes of the cluster were compared with those of a free phosphate ion in water. For a free phosphate ion, the P–O stretching frequency was between 965 and 970 cm−1, and the P–O bond lengths were 1.57 Å. For the [Ca(PO4)]1− cluster, the P–O stretching mode was split into two regions. One located at 928 cm−1, and the other having two peaks at 1000 cm−1 and 1015 cm−1. This was because the calcium atom increased the P–O bond length to 1.58 Å via Ca–O interactions on one side of the phosphate ion, leading to weaker P–O bonds and a lower stretching frequency than the free phosphate ion. On the other side of the phosphate ion, the calcium-uncoordinated P–O bond length decreased to 1.555 Å, resulting in stronger P–O covalent bonds and higher stretching frequency than the free phosphate ion. The two peaks at 1000 cm−1 and 1015 cm−1 were attributed to in-phase and out-of-phase P–O stretching respectively. From the computed infrared spectra of the [Ca(PO4)]1− cluster, we found that the P–O stretching in phosphate ions was sensitive to Ca–O interactions. The computed infrared spectra of the [Ca(PO4)2]4− cluster had a similar trend as that of the [Ca(PO4)]1− cluster, but the spectra of the [Ca2(PO4)]1+ cluster exhibited a slight difference to that of the [Ca(PO4)]1− cluster. The P–O stretching modes of the [Ca2(PO4)]1+ cluster shifted to 980 cm−1 and 1020 cm−1, which were higher than the stretching mode of a free phosphate ion in water. These two peaks corresponded to in phase and out of phase P–O stretching modes, and the shift was attributed to the decreased P–O bond lengths, 1.565 Å, in the [Ca2(PO4)]1+ cluster.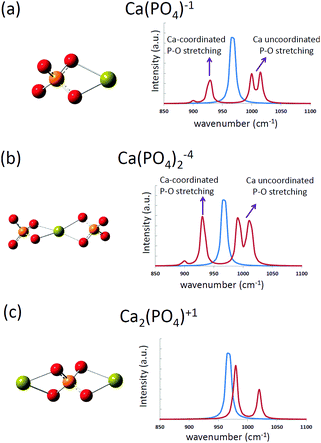 | ||
| Fig. 3 The computed infrared spectra of (a) [Ca(PO4)]1−, (b) [Ca(PO4)2]4−, and (c) [Ca2(PO4)]1+ clusters in water. The blue curves represent the computed spectrum of a free phosphate ion in water. | ||
The computed infrared spectra of the extended and compact configurations of [Ca2(PO4)2]2−, [Ca2(PO4)3]5−, and [Ca3(PO4)2] clusters are presented in Fig. 4. The profile of infrared spectra of the compact configurations exhibited sharp peaks, and the profile of the extended configurations showed a distribution character especially in the extended [Ca2(PO4)2]2− cluster. The calcium-coordinated P–O stretching frequencies were mostly located between 900 cm−1 and 1025 cm−1. The calcium uncoordinated P–O stretching frequencies were located at 1050 cm−1, and the stretching frequency shifts higher at 1085 cm−1 in the case of the compact Ca3(PO4)2 cluster. As mentioned in the previous section, the Ca–O interactions in the compact configurations are more consistent than those of the extended configurations based on their Ca–O distances. This lead to the sharp P–O stretching peaks in the infrared spectra of the compact configurations. By contrast, the P–O bonds experienced different strengths of Ca–O interactions in the extended configurations, leading to the distributed P–O stretching peaks in the infrared spectra. The in situ FTIR spectrum at an early stage of calcium phosphate nucleation is given in Fig. 4(d).13 The P–O stretching mode corresponds to a broad distribution between 950 cm−1 and 1150 cm−1. Based on the computed infrared spectra, P–O bonds of the phosphate ions in the calcium phosphate clusters may feel different strengths of Ca–O interactions at the early stage of nucleation, and the configuration of calcium phosphate clusters was extended rather than compact. We already knew that from an energy perspective, the extended configurations of [Ca2(PO4)2]2−, [Ca2(PO4)3]5− and Ca3(PO4)2 clusters are not as stable as their compact counterparts. Nevertheless, by comparing the computed and in situ infrared spectra, we cannot rule out the possibility of their existence in water. As mentioned in the previous section, the relative stability of these compact and extended configurations should be further examined by using AIMD simulations.
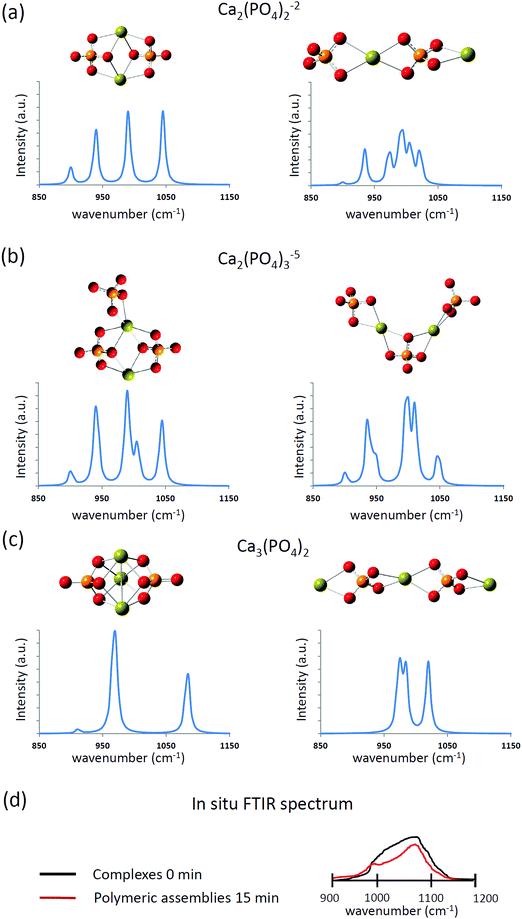 | ||
| Fig. 4 The computed infrared spectra of (a) [Ca2(PO4)2]2−, (b) [Ca2(PO4)3]5−, and (c) Ca3(PO4)2 clusters in water. (d) The sketched in situ FTIR spectrum based on ref. 13. | ||
Structures and infrared spectra of Ca9(PO4)6 clusters
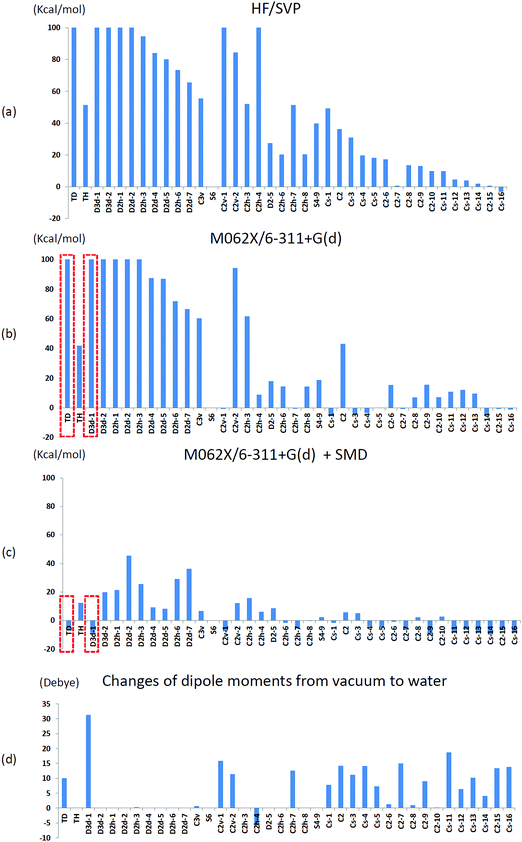
We initially used the same theoretical method as that used by Treboux, the Hartree–Fock method with Ahlrichs SVP basis sets,35 to determine the relative energies of the 39 optimized Ca9(PO4)6 clusters mentioned in his work. We set the energy of an S6 isomer as a reference because the structure of the S6 isomer was almost identical to that of Posner's cluster. Fig. 5(a) shows the relative energies of the 39 optimized Ca9(PO4)6 clusters. The relative energies showed the same trend as that described in Treboux's work. Thirteen structures had relative energies less than 20 kcal mol−1 with respect to the S6 isomer, and most of them were low-symmetry structures such as C2 and CS symmetry. The structures with high-symmetry such as Td, Th, D3d, D2d, D2h, and C3v symmetry, had higher relative energies. Because of the limited computational power 15 years ago, Treboux obtained these 39 optimized structures through geometry optimization with symmetry constraints. We then optimized these structures without any symmetry constraint in addition to using modern density functional M06-2X and the larger basis sets 6-31+g(d). Fig. 5(b) shows the relative energies of the fully relaxed structures. After lifting the symmetry constraints during geometry optimizations, 22 structures had relative energies less than 20 kcal mol−1 with respect to the S6 isomer. We discovered that C2v-1, C2h-4, and CS-1 clusters exhibited drastic changes of 40–200 kcal mol−1 in their relative energies, and the final relative energies of these three structures were within 10 kcal mol−1 with respect to the S6 isomer after the symmetry constraints were lifted. By contrast, the lifting of constraints during geometry optimizations did not influence the structures that began with high-symmetry such as Td, Th, D3d, D2h, D2d, and C3v symmetry. This may be because leaving their local minimum was difficult for these highly symmetric structures, but easy for structures possessing lower symmetry. In order to find possible low-lying states of calcium phosphate clusters in water, we did not impose symmetry constraints in further investigations.We then conducted geometry optimizations for the 39 Ca9(PO4)6 clusters in combination with the SMD solvation model, and the relative energies and the change of dipole moments in vacuo and in water are presented in Fig. 5(c) and (d), respectively. Surprisingly, only five structures had relative energies higher than 20 kcal mol−1 with respect to the S6 isomer. Solvent effects lowered the relative energies of the low symmetry structures, and these structures generally exhibited a considerable dipole moment change in water compared with in vacuo. Moreover, solvent effects greatly reduced the relative energies of Ca9(PO4)6 clusters starting in high-symmetry configurations. Most of these optimized structures did not maintain their starting symmetry after geometry optimizations in water. Td, D3d-1, and CS-14 clusters were the most stable clusters with respect to the S6 cluster in water, and the relative energies were −6.7, −8.7, and −9.8 kcal mol−1, respectively. Stott relaxed calcium phosphate clusters which were extracted from hydroxyapatite crystals without symmetry restrictions, and discovered that the structure has lower energy than Posner's cluster by about 1.3 eV using HF and B3LYP in vacuo.36 We examined the structure by the theoretical method used in this study, and the relative energy with respect to the S6 isomer was only −2.6 kcal mol−1 in water.
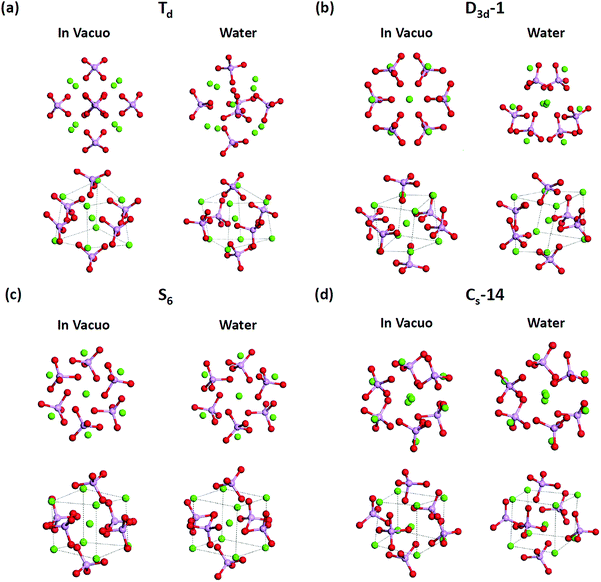
T d and D3d-1 structures were notable, and their structures and structural information in vacuo and in water are presented in Fig. 6 and Table 3. The relative energies of the Td and D3d-1 clusters were 387 and 162 kcal mol−1 with respect to the S6 isomer, respectively, without considering solvent effects, but −6.7 and −8.7 kcal mol−1, respectively, when solvent effects were included. The optimized structures of Td and D3d-1 had zero dipole moments in vacuo, but had dipole moments of 10 and 31 D, respectively, in water. The considerable dipole moment of the D3d-1 cluster in water could be attributed to its optimized structure in water. Fig. 6 displays fully relaxed Td, D3d-1, S6, and CS-14 clusters in vacuo and in water, and the optimized structure of Td and D3d-1 clusters in water were very different from their optimized structures in vacuo. In vacuo, the optimized structure of Td and D3d-1 clusters maintained their highly symmetric structures, but their structures became relaxed in water shown in Fig. 6. The histogram of Ca–O distance in Td and D3d-1 clusters in vacuo and in water also showed an obvious demonstration of the structural character of these two clusters (see Fig. 7). The histograms of Ca–O distance in Td and D3d-1 clusters showed a sharp distribution in vacuo rather than a broad distribution in water. This indicated that considerable structural changes lead to large changes in dipole moment of these two structures in vacuo and in water. By contrast, the changes of the Ca–O distance histogram in S6 and CS-14 clusters between in vacuo and in water were not as obvious as the change in Td and D3d-1 clusters. The small changes in the structures of S6 and CS-14 clusters lead to the small differences of dipole moments in vacuo and in water. In the case of D3d-1, the relaxed structure in water resembles a pyramid. Two of the six phosphate ions are displaced to the lower part of the cluster. Therefore, the distribution of phosphate ions in the upper and lower parts of the D3d-1 cluster was 2-to-4. The displaced phosphate ions create an imbalanced charge distribution in the cluster, leading to an enormous dipole moment. This polar molecule was, however, stable in an aqueous environment, which is consistent with the like-dissolves-like principle.
| Cluster | Relative energy (kcal mol−1) | Dipole moment (Debye) | Ca–Ca distances of hexahedron (Å) | |||
|---|---|---|---|---|---|---|
| In vacuo | Water | In vacuo | Water | In vacuo | Water | |
| T d | 387 | −6.7 | 0 | 10 | 4.28 | 4.42 ± 0.45 |
| D 3d-1 | 162 | −8.7 | 0 | 31.3 | 3.58, 4.13 | 4.43 ± 0.45 |
| S 6 | 0 | 0 | 0 | 0 | 3.84, 4.40 | 4.33 ± 0.02 |
| C S-14 | −4.7 | −9.8 | 1.9 | 6 | 4.05 ± 0.35 | 4.30 ± 0.32 |
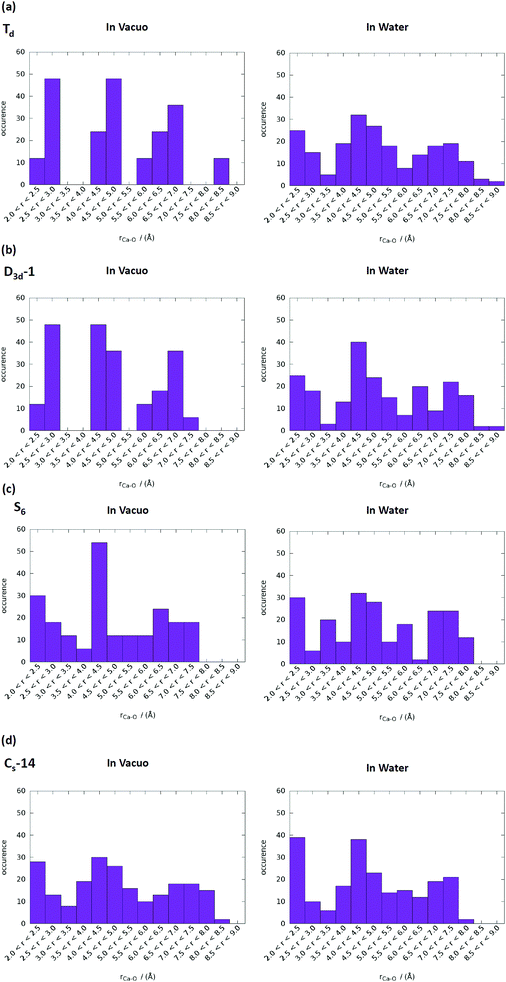 | ||
| Fig. 7 Ca–O distance distributions in vacuo and in water of (a) Td, (b) D3d-1, (c) S6, and (d) CS-14 clusters. The range of P–O bond lengths was from 2 to 9 Å with an increment of 0.5 Å. | ||
T d and D3d-1 clusters exhibited large Ca–Ca side length variations of the calcium hexahedron being in vacuo and in water. The Ca–Ca side lengths of the calcium hexahedron in the D3d-1 cluster in vacuo were only 4.13 Å and 3.58 Å listed in Table 3. In water, these lengths were increased to 4.43 ± 0.45 Å, with the largest increase being to 5.2 Å. For the Td cluster, the Ca–Ca side lengths were 4.28 Å in vacuo and 3.87–5.32 Å in water. The increase in the Ca–Ca side lengths from vacuum to water was also observed in S6 and CS-14 clusters, with increases of approximately 0.3–0.7 Å, which were not as apparent as those in the D3d-1 and Td clusters. The increase in the Ca–Ca side lengths of the calcium hexahedron in Ca9(PO4)6 clusters in water indicated that the calcium atoms had a tendency to be located at the surface of the clusters. This deduction is consistent with the simulation results for the small calcium phosphate clusters described in previous sections.
The computed infrared spectra of D3d-1, S6, and CS-14 clusters are shown in Fig. 8. The computed infrared spectra of D3d-1 and CS-14 clusters have different features than the spectrum of the S6 cluster. The S6 cluster exhibited three sharp peaks at 965 cm−1, 995 cm−1, and 1055 cm−1 in the infrared spectrum, and the D3d-1 and CS-14 clusters exhibited broad distributions between 960 cm−1 and 1085 cm−1 in the spectra. The sharp distribution of P–O bond lengths (see Fig. 9) of the S6 cluster in water indicated that the P–O bonds experienced consistent Ca–O interactions in the ordered cluster. Therefore, the computed infrared spectrum of the S6 cluster in water exhibited sharp peaks. By contrast, the P–O bond length had broad distributions in the less ordered D3d-1 and CS-14 clusters in water, which indicated that the P–O bonds experienced different strengths of Ca–O interactions. This lead to broad distributions of infrared spectra in these two clusters. The broad distribution in the in situ FTIR spectrum at an early stage of nucleation gradually transformed into a sharp peak at 1030 cm−1 as nucleation continued (Fig. 8(d)). This indicated that the some calcium phosphate clusters transformed from disordered to ordered structures during the nucleation process. Nevertheless, the measured spectrum also exhibited broad distributions at frequencies higher than 1030 cm−1 as nucleation continued, and not all calcium phosphate clusters aggregate into an ordered structure such as the S6 cluster. The broad distribution at frequencies higher than 1030 cm−1 indicated that the calcium phosphate clusters may aggregate into a less ordered structure such as D3d-1 and CS-14 clusters. The incoherence between the computed and measured IR spectra was the frequencies over 1050 cm−1 in D3d-1, S6, and CS-14 clusters. This was because the outermost P–O bonds of phosphate ions are always coordinated with ions in solutions and protonated in experiments, which was not considered in our simulation models. The coordination of ions or protonation of P–O bonds lowers the P–O stretching frequencies as mentioned in previous sections.
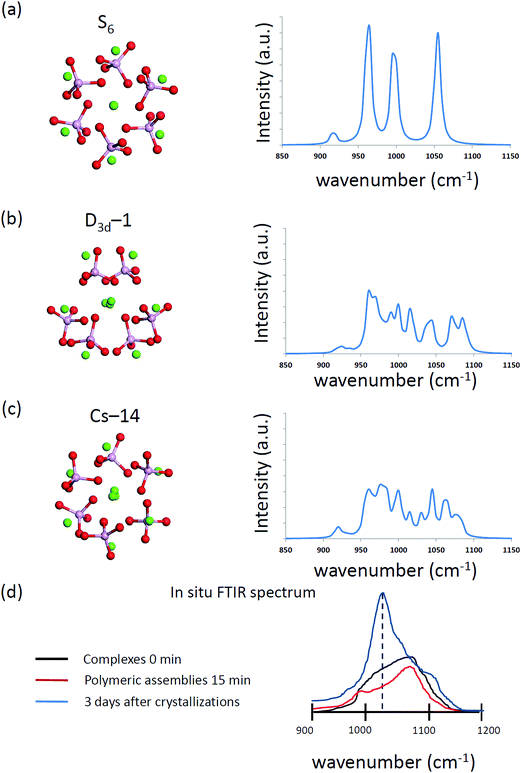 | ||
| Fig. 8 The simulated vibration spectrum of (a) S6, (b) D3d-1, and (c) CS-14 Ca9(PO4)6 clusters in water. (d) The sketched in situ FTIR spectrum based on ref. 13. | ||
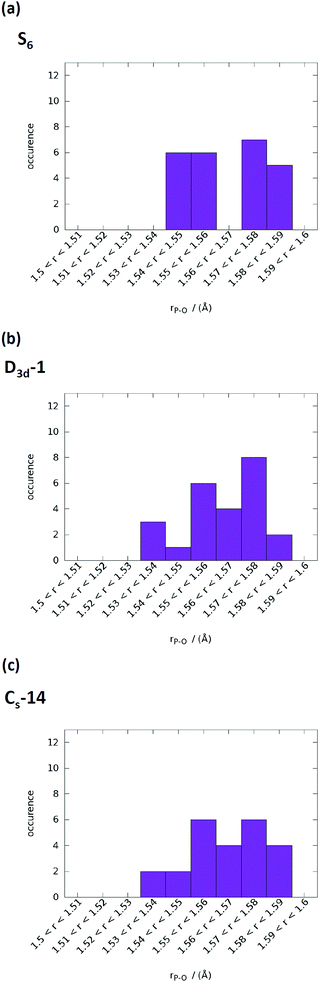 | ||
| Fig. 9 P–O bond length distributions in water of (a) S6, (b) D3d-1, and (c) CS-14 clusters. The range of P–O bond lengths was from 1.5 to 1.6 Å with an increment of 0.01 Å. | ||
Conclusions
In this study, we used ab initio methods combined with implicit solvation models to examine small and medium-sized calcium phosphate clusters. The optimized structures of [Ca(PO4)]1−, [Ca(PO4)2]4−, and [Ca2(PO4)]1+ clusters in water showed that stable structures can be achieved by balancing the Ca–O interactions inside and outside of the clusters. The calcium atoms formed Ca–O bonds with the phosphate ions inside the clusters and also had a tendency to coordinate with oxygen atoms of water molecules in an aqueous environment. On the basis of computed infrared spectra of small-sized calcium phosphate clusters, it was deduced that the P–O stretching modes in calcium phosphate clusters were sensitive to calcium coordination. Although [Ca2(PO4)2]2−, [Ca2(PO4)3]5−, and Ca3(PO4)2 clusters with extended configurations in water had higher energies than their compact counterparts, their computed infrared spectra were correlated with in situ FTIR spectra. The relative stabilities of the extended configurations with respect to their compact configurations should be further validated by including explicit water molecules. The relative stabilities of 39Ca9(PO4)6 clusters studied by Treboux were also examined. Solvent effects increased the number of possible configurations of Ca9(PO4)6 clusters to that allowed by the packings of these clusters in vacuo. In water, the calcium atoms in these clusters had a tendency to migrate to the surface of the clusters. Surprisingly, we identified two alternative Ca9(PO4)6 clusters that had different atomic arrangements and lower energies than a compact Posner's cluster. One structure was the Ca9(PO4)6 cluster with low-symmetry, and the other was similar to a pyramid with an asymmetric distribution of phosphate ions, leading to enormous dipole moments that contributed to its stability in an aqueous environment. In addition, the computed infrared spectra of these two Ca9(PO4)6 clusters were correlated with measured in situ FTIR spectra.This study indicated that there could be many candidate structures with similar or even lower energies than Posner's cluster in an aqueous environment. This study was the initial search for calcium phosphate clusters in an aqueous environment. Ab initio methods combined with implicit solvation models appeared to provide an efficient approach to determining the structural features of mineral clusters in an aqueous environment, although the calculations of accurate relative energies may require the solvation of mineral clusters by explicit water molecules in theoretical calculations. Combining implicit solvation models and advanced algorithms such as ab initio random structure searching (AIRSS)37 would be worthwhile for conducting a detailed search for pre-nucleation calcium phosphate clusters in an aqueous environment in the future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Ministry of Science and Technology, Taiwan (105-2218-E-033-010-MY2). The author is grateful for the generous allocation of computational resources provided by the National Center for High-Performance Computing, Taiwan.References
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
- E. M. Pouget, P. H. H. Bomans, J. A. C. M. Goos, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Science, 2009, 323, 1455–1458 CrossRef CAS PubMed.
- D. Gebauer and H. Cölfen, Nano Today, 2011, 6, 564–584 CrossRef CAS.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergstrom and H. Colfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- J. Baumgartner, A. Dey, P. H. H. Bomans, C. Le Coadou, P. Fratzl, N. A. J. M. Sommerdijk and D. Faivre, Nat. Mater., 2013, 12, 310–314 CrossRef CAS PubMed.
- H.-J. Li, D. Yan, H.-Q. Cai, H.-B. Yi, X.-B. Min and F.-F. Xia, Phys. Chem. Chem. Phys., 2017, 19, 11390–11403 RSC.
- J. Scheck, B. Wu, M. Drechsler, R. Rosenberg, A. E. S. Van Driessche, T. M. Stawski and D. Gebauer, J. Phys. Chem. Lett., 2016, 7, 3123–3130 CrossRef CAS PubMed.
- G. C. Wang, Q. Wang, S. L. Li, X. G. Ai and C. G. Fan, Sci. Rep., 2014, 4, 5082 CrossRef CAS PubMed.
- L. Wang, S. Li, E. Ruiz-Agudo, C. V. Putnis and A. Putnis, CrystEngComm, 2012, 14, 6252–6256 RSC.
- A. Dey, P. H. H. Bomans, F. A. Müller, J. Will, P. M. Frederik, G. de With and N. A. J. M. Sommerdijk, Nat. Mater., 2010, 9, 1010–1014 CrossRef CAS PubMed.
- A. S. Posner and F. Betts, Acc. Chem. Res., 1975, 8, 273–281 CrossRef CAS.
- W. J. E. M. Habraken, J. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. H. Bomans, P. M. Frederik, J. Laven, P. van der Schoot, B. Aichmayer, G. de With, J. J. DeYoreo and N. A. J. M. Sommerdijk, Nat. Commun., 2013, 4, 1507 CrossRef PubMed.
- Q. Zhang, Y. Jiang, B.-D. Gou, J. Huang, Y.-X. Gao, J.-T. Zhao, L. Zheng, Y.-D. Zhao, T.-L. Zhang and K. Wang, Cryst. Growth Des., 2015, 15, 2204–2210 CAS.
- L.-W. Du, S. Bian, B.-D. Gou, Y. Jiang, J. Huang, Y.-X. Gao, Y.-D. Zhao, W. Wen, T.-L. Zhang and K. Wang, Cryst. Growth Des., 2013, 13, 3103–3109 CAS.
- N. Kanzaki, G. Treboux, K. Onuma, S. Tsutsumi and A. Ito, Biomaterials, 2001, 22, 2921–2929 CrossRef CAS PubMed.
- G. Treboux, N. Kanzaki, K. Onuma and A. Ito, J. Phys. Chem. A, 1999, 103, 8118–8120 CrossRef CAS.
- G. Treboux, P. Layrolle, N. Kanzaki, K. Onuma and A. Ito, J. Phys. Chem. A, 2000, 104, 5111–5114 CrossRef CAS.
- G. Mancardi, U. Terranova and N. H. de Leeuw, Cryst. Growth Des., 2016, 16, 3353–3358 CAS.
- G. Mancardi, C. E. Hernandez Tamargo, D. Di Tommaso and N. H. de Leeuw, J. Mater. Chem. B, 2017, 5, 7274–7284 RSC.
- P. Raiteri, R. Demichelis and J. D. Gale, Methods Enzymol., 2013, 532, 3–23 CAS.
- P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634 CrossRef CAS PubMed.
- M. Corno, C. Busco, B. Civalleri and P. Ugliengo, Phys. Chem. Chem. Phys., 2006, 8, 2464–2472 RSC.
- G. Ulian, G. Valdrè, M. Corno and P. Ugliengo, Am. Mineral., 2013, 98, 752–759 CrossRef CAS.
- L. F. Sukhodub, I. E. Boldeskul, A. N. Kalinkevich and V. D. Khavryutchenko, Condens. Matter Phys., 2006, 9, 669–680 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- C. J. Cramer and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 760–768 CrossRef CAS PubMed.
- J. Ho, Phys. Chem. Chem. Phys., 2015, 17, 2859–2868 RSC.
- J. Ho and M. Z. Ertem, J. Phys. Chem. B, 2016, 120, 1319–1329 CrossRef CAS PubMed.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- X. Yin and M. J. Stott, J. Chem. Phys., 2003, 118, 3717–3723 CrossRef CAS.
- J. P. Chris and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
| This journal is © the Owner Societies 2018 |