On the selectivity of the NaChBac channel: an integrated computational and experimental analysis of sodium and calcium permeation

Abstract

Ion channel selectivity is essential for their function, yet the molecular basis of a channel's ability to select between ions is still rather controversial. In this work, using a combination of molecular dynamics simulations and electrophysiological current measurements we analyze the ability of the NaChBac channel to discriminate between calcium and sodium. Our simulations show that a single calcium ion can access the Selectivity Filter (SF) interacting so strongly with the glutamate ring so as to remain blocked inside. This is consistent with the tiny calcium currents recorded in our patch-clamp experiments. Two reasons explain this scenario. The first is the higher free energy of ion/SF binding of Ca²⁺ with respect to Na⁺. The second is the strong electrostatic repulsion exerted by the resident ion that turns back a second potentially incoming Ca²⁺, preventing the knock-on permeation mechanism. Finally, we analyzed the possibility of the Anomalous Mole Fraction Effect (AMFE), i.e. the ability of micromolar Ca²⁺ concentrations to block Na⁺ currents. Current measurements in Na⁺/Ca²⁺ mixed solutions excluded the AMFE, in agreement with metadynamics simulations showing the ability of a sodium ion to by-pass and partially displace the resident calcium. Our work supports a new scenario for Na⁺/Ca²⁺ selectivity in the bacterial sodium channel, challenging the traditional notion of an exclusion mechanism strictly confining Ca²⁺ ions outside the channel.

---

1 Introduction

Voltage gated sodium channels (Navs) play a key role in the onset and propagation of electric signals in excitable cells due to their involvement in the rising branch of the action potential.¹ Their physiological importance makes them potential targets for a wide range of drugs including anticonvulsants, antiarrhythmics and local anaesthetics.^2,3

The eukaryotic members of this family of channels are composed by a single polypeptide chain folded in four homologous domains each comprising a voltage sensor subdomain (helices S1–S4) and a pore domain (helices S5–S6 and the intervening P-loop).⁴ Due to the large size and structural complexity, so far it has not been possible to attain high resolution crystal structures of eukaryotic Navs. This is why the smaller prokaryotic Navs (Fig. 1) represent amenable model systems for simulation and experimental studies. Prokaryotic Navs are homotetrameric proteins whereby each subunit exhibits the same organization of the four domains of eukaryotic Navs.⁵ The Selectivity Filter (SF) of bacterial Navs, located in the P-loop of the pore domain, is characterized by a conserved ring of four glutamates (EEEE-ring).⁶ It is noteworthy that the EEEE-ring can also be found in voltage gated calcium channels while mammalian sodium channels exhibit an asymmetric, conserved DEKA locus.⁷ In NaChBac, the first discovered bacterial sodium channel identified in Bacillus halodurans,⁸ as well as in other prokaryotic Navs, a further link with calcium channels is at the level of the SF sequence that conforms to the pattern FxxxTxExW typical of eukaryotic calcium channels. Moreover, mutagenesis experiments on NaChBac showed that serine to aspartate mutations switch the channel from sodium selective to calcium selective.⁹

Fig. 1 Structure of the NaChBac channel. Side (a) and top (b) view of the superposition of the NaChBac homology model (blue) with the NavMs template (red). Each of the four identical subunits comprises transmembrane helices S5 and S6 as well as a linking region including the turret loop, P1-helix, the selectivity filter (SF) and P2-helix. The glutamates of the NaChBac SF are portrayed in cyan as van der Waals spheres. Side (c) and top (d) view of the NaChBac SF at the end of 100 ns simulation at equilibrium. For the sake of clarity in the side view only the first and third chains are portrayed. The Thr189, Leu190 and Glu191 residues respectively involved in sites IN, CEN and HFS are shown in a ball-and-stick representation. Only backbone atoms are shown for Thr189 and Leu190. At the end of the simulation the SF is occupied by a calcium ion (orange bead) solvated by 7 water molecules and directly interacting with a glutamate side-chain.

Ion channel selectivity is a topic of intensive investigation not only for its biochemical relevance but also in view of the potential use of artificial nanopores as a tool for the separation of molecular mixtures.^10,11 Ion channel selectivity has traditionally been associated with high-affinity binding. However, the observation of flux rates of up to 10⁷ ions per second through individual channel proteins would appear to be incompatible with high-affinity binding and consequent slow release of the transported ion.¹² This problem is often referred to as ion selectivity paradox.

Much is known about the K⁺/Na⁺ selectivity of potassium channels like KcsA.¹³ The Na⁺/K⁺ selectivity of prokaryotic Navs has been recently investigated on the NavAb channel from Arcobacter butzleri. A study⁵ based on the crystal structure of the channel suggests the glutamates of the SF to form a high field strength binding site. According to Eisenman's theory,¹⁴ due to its smaller radius, the Na⁺ ion could establish a closer contact, and thus a stronger Coulombic interaction with the glutamates, at variance with the bulkier K⁺ ion. In this view, sodium selectivity would be driven by a better compensation of the desolvation cost. This situation is somewhat related to what happens in medium-sized carbon or graphene nanopores whose selectivity to small ions is related to the ability of the latter to retain their full hydration shell without incurring in desolvation costs.¹⁵ This scenario is different from the one emerging from Molecular Dynamics (MD) studies of the NavAb channel.¹⁶ According to these studies despite the ability of the K⁺ ion to maintain a complete hydration shell as it advances along the SF, the ion would be incapable of fitting inside the EEEE-ring keeping the coordinating waters in the optimal geometric arrangement.

The ability of prokaryotic Navs to discriminate between sodium and calcium ions is even more elusive. Due to the similarity with eukaryotic calcium channels, a possible conceptual framework could be represented by the charge/space competition model.¹⁷ According to this model, the negatively charged EEEE-ring tends to attract into the SF as many cations as are necessary to balance its charge. In this Coulombic interaction divalent cations like calcium are favoured with respect to monovalent ones like sodium. The high density of cations drawn into the SF, however, determines electrostatic repulsion that favours smaller ions that can be accommodated at a larger interatomic distance inside the SF. Unfortunately, since sodium and calcium have almost equal radii the model would predict calcium selectivity while it is experimentally known⁸ that the NaChBac channel is sodium selective.

Details on the Na⁺/Ca²⁺ discrimination mechanism can only be attained by simulation studies at atomistic resolution. In a simulation study on NavAb,¹⁸ Corry showed that the single-ion Potential of Mean Force (PMF) of both Na⁺ and Ca²⁺ features a main minimum in correspondence of the HFS site and two secondary minima near the CEN site. Calcium advancement between the latter two minima is opposed by a barrier of 8.0 kcal mol⁻¹ possibly resulting from the desolvation cost. It was noted¹⁸ that even if this barrier can be lowered to 4.5 kcal mol⁻¹ in case of a knock-on mechanism, it is still high enough to enforce a selectivity ratio P_Na/P_Ca ∼ 10 observed experimentally. A similar result was attained in a work by Ke et al.,¹⁹ but in this case the barrier preventing Ca²⁺ advancement was ascribed to a sub-optimal coordination geometry of this ion with respect to Na⁺.

In this work we address the problem of Na⁺/Ca²⁺ selectivity in the NaChBac channel via joint experimental and computational study. Even though NaChBac was the first discovered bacterial voltage dependent sodium channel, computational studies on this system were very limited²⁰ because no crystal structure was available. Since the NaChBac channel is the first Nav channel studied experimentally,^8,9 the majority of computational studies on prokaryotic Navs, including those mentioned above,^18,19 used experimental measurements of the NaChBac channel as a benchmark comparison despite differences in the electrophysiological measurements of different Nav channels. In turn, published experimental investigations^8,9 of NaChBac reported different selectivity ratios that makes the value P_Na/P_Ca vaguely defined. Therefore the experimental part of this study is designed to determine the sodium/calcium selectivity ratio in simplified conditions which could be more readily related to those used in the MD simulations. Additionally, we experimentally consider the mole fraction effect on the conductance of the NaChBac channel. The latter effect is often studied for clarifying preferential selectivity.²¹ For the computational part we use the recently built²² homology model of NaChBac (Fig. 1). By means of equilibrium and metadynamics simulations of this model it was shown²² that Na⁺ permeation occurs through a knock-on mechanism involving two but possibly even three ions. Further it was demonstrated²² that single-channel patch-clamp recordings of sodium current are in an excellent correspondence with the currents predicted from the unbiased simulation using linear response theory. In the present study the analysis of the homology NaChBac model is extended to the Ca²⁺–protein interaction.

By means of MD equilibrium simulations, supported by whole-cell patch-clamp recordings, we show that a single Ca²⁺ ion can access the SF and it strongly binds inside. We explain this behaviour in terms of the higher free energy of binding of Ca²⁺ to the SF and in terms of the strong electrostatic repulsion that the resident ion exerts on a second, potentially incoming ion. Differences between sodium and calcium ion interaction with NaChBac were analyzed in terms of ion's hydration and coordination, binding sites and binding energy of ions. Since the isomerization of glutamate side-chains in the EEEE-ring of the SF received a considerable attention,^19,23 this phenomenon is also discussed in the corresponding section of the ESI.‡ Finally, we addressed the issue of the Anomalous Mole Fraction Effect, i.e. the influence of relative ion concentrations in two-species mixtures on the channel conductance. Our whole-cell current recordings in the presence of mixtures of Na⁺ and Ca²⁺ show two distinct conductance patterns depending on the ion species used in the initial pure bath. 2D-metadynamics simulations show that the existence of the two patterns is related to a by-pass mechanism for Na⁺ permeation in the presence of a resident Ca²⁺.

2 Methods

2.1 Unbiased simulations

A homology model of the pore domain of the NaChBac channel was built using as a template the NavMs channel that features about 46% sequence identity. The details of the model building as well as of the simulations in 0.5 M NaCl are provided elsewhere.²² The protocol for the simulations in 0.5 M CaCl₂ was as follows. The NaChBac homology model was embedded in a bilayer comprising 248 molecules of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and solvated by 15 712 water molecules. We added 162 calcium ions and 316 chloride ions so as to neutralize the charge of the channel and reach a final concentration of 0.5 M CaCl₂. Overall the system comprised 87 226 atoms. All simulations were performed with the NAMD 2.11b2²⁴ suite of programs using the ff14SB²⁵ force field for the protein, the Lipid14 force-field²⁶ for the phospholipids and the calcium parameters from Bradbrook et al.²⁷ The system first underwent 10 000 steps of conjugate gradient minimization. The equilibration was organized in six stages whereby harmonic constraints applied to the backbone, side-chains, phospholipid heads and dihedral angles were gradually released. Further details on the equilibration protocol are provided in ref. 22 and the values of the force constants used in the six stages can be found in Table S1 of the ESI.‡ The production run was carried out in the isothermal isobaric (NPT) ensemble for 105 ns. Pressure was kept at 1 atm by the Nose–Hoover Langevin piston method while temperature was kept at 300 K by coupling to a Langevin thermostat with a damping coefficient of 1 ps⁻¹. Long-range electrostatic interactions were evaluated with the smooth particle mesh Ewald algorithm. For the short-range non-bonded interactions, we used a cutoff of 12 Å with a switching function at 10.0 Å. The integration time step was 2 fs, and the bonds between hydrogen and heavy atoms were fixed to eliminate the most rapid oscillatory motions.

2.2 Metadynamics simulations

In order to simplify the terminology, metadynamics simulations biasing one or two ions to explore the SF while all other ions are excluded from this region will be referred to as 1D- and 2D-metadynamics respectively. The 1D-metadynamics simulation was started from the final frame of the 105 ns unbiased NPT simulation where a single ion was trapped in the neighborhood of the EEEE-ring. The biased collective variable was defined as the z-component of the distance vector between the ion in the SF and the center of mass (COM) of the C_αs of the four glutamates of the EEEE-ring. The space explored by the z reaction coordinate was restricted to lie within the range [−10 : 10] Å by 100 kcal mol⁻¹ Å⁻² walls. The transversal mobility of the ion was also restricted by the same means within a circle of radius 4.0 Å centered on an axis parallel to the z-axis passing through the center of mass of the C_αs of the glutamates of the EEEE-ring. Energy Gaussians with an initial height of 0.005 kcal mol⁻¹ and a width of 0.25 Å were deposited every 0.4 ps. In order to avoid over-filling artifacts, we used well-tempered metadynamics²⁸ with a virtual temperature parameter ΔT = 2697 K. The choice of the ΔT parameter was based on a preliminary standard metadynamics run (data not shown) which allowed estimation of the height of the energy barriers at about E* ≈ 6.0 kcal mol⁻¹. The virtual temperature parameter was then chosen to satisfy the relation R(T + ΔT) ≈ E*. The sampling was improved by applying a spherical harmonic restraint from the COM of the EEEE-ring to prevent the remaining Ca²⁺ ions from the outer bulk from entering the SF during the long sampling. The total length of the sampling slightly exceeded 140 ns (144 ns).

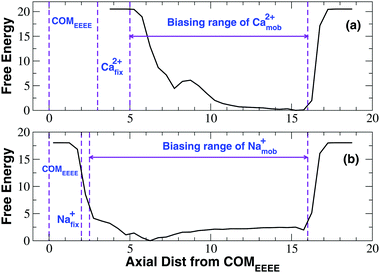
The 1D-metadynamics simulation with a fixed calcium ion and a mobile calcium ion was started from the final frame of the unbiased NPT run. In this conformation a single calcium ion is accommodated in the SF at the level of the EEEE-ring. This ion was harmonically restrained to its initial position with a force constant of 50 kcal mol⁻¹ Å⁻². The center of mass of the alpha-carbons of the EEEE-ring was also constrained to its initial position with a force constant of 100 kcal mol⁻¹ Å⁻². The ion chosen to be biased was moved from the bulk solvent to a position along the channel axis 10 Å above the COM of the EEEE-ring. The ion was biased to move along the z-axis in an 11 Å interval. If the origin of the reference system is set to coincide with the COM of the EEEE-ring, the mobility range of the ion is [5 : 16] Å and it was limited by semi-harmonic walls with a force constant of 100 kcal mol⁻¹ Å⁻². The distance of closest approach between the mobile ion and the fixed ion is thus set to 2 Å to avoid instabilities in the electrostatic forces. The calcium ions other than the fixed and biased ion are harmonically excluded from a spherical region with a radius of 15 Å centered on the COM of the EEEE-ring. The simulation length slightly exceeded 100 ns (117 ns). All other settings were identical to those of the 1D-metadynamics simulation for a single ion inside the SF.

An analogous 1D-metadynamics simulation was also performed with a fixed and a mobile sodium ion. This simulation was started from a typical configuration of the unbiased simulation in NaCl where two ions occupy the SF. In order to make this initial arrangement more comparable to that of the simulation with the fixed and mobile calcium ions, the conformation of the sodium system was aligned to that of the calcium system using all protein atoms. The innermost sodium ion in the SF was then moved to make its position coincide with that of the fixed calcium ion. Conversely, the outermost sodium ion was moved along the channel axis up to a level corresponding to that of the mobile calcium ion. Considering that the repulsion between sodium ions is weaker than that between calcium ions, the mobile Na⁺ was biased to move along an axial interval of 13.5 Å so that its distance of closest approach with the fixed sodium is 0.5 Å. Setting the origin of the reference system in the COM of the EEEE-ring the mobility range of the mobile Na⁺ ion was thus [2.5 : 16] Å. All other settings were identical to those of the simulation with a fixed and a mobile calcium.

In the 2D-metadynamics simulation, a sodium and a calcium ion initially in sites HFS and CEN were biased to explore the selectivity filter using as collective variables the z-components of the distance vectors between the two ions and the center of mass of the EEEE-ring. The simulation protocol was the same as in the 1D-metadynamics except that the virtual temperature parameter ΔT was set to 5700 K to assure the overcoming of all energy barriers while the initial height of the energy gaussians was increased to 0.6 kcal mol⁻¹ and the deposition interval was reduced to 0.1 ps to reduce the convergence time. The simulation was run for 310 ns.

2.3 Electrophysiology

The NaChBac (GenBank accession number BAB05220) cDNA construct encoding 274 amino acid residues was synthesised by EPOCH Life Science (http://www.epochlifescience.com), subcloned into the mammalian cell expression vector pTracer-CMV2 (Invitrogen) and transiently transfected into CHO cells with TransIT-2020 (Mirus Bio). Transfected cells were identified by GFP fluorescence using an inverted fluorescence microscope (Nikon TE2000-s) and used for electrophysiological investigation 24–48 hours after transfection.

Whole-cell voltage clamp recordings were performed at room temperature (20 °C) using an Axopatch 200A (Molecular Devices, Inc.) amplifier. Patch-clamp pipettes were pulled from borosilicate glass (Kimax, Kimble Company, USA) and had resistances of 2.2 to 2.6 MOhm when filled with pipette solution 1 (PS1), which contained (in mM) 120 Cs-methanesulfonate, 20 Na-gluconate, 5 CsCl, 10 EGTA, and 20 HEPES, pH 7.4 (adjusted with 1.8 mM CsOH) or of 6.8 to 7.2 MOhm when filled with pipette solution 2 (PS2), which contained (in mM) 90 NMDG, 5 Choline-Cl, 10 EGTA, 20 HEPES, pH 7.4 (adjusted with 3 mM HCl). Bath solution was either SBS-Na (in mM: 132 Na-methanesulfonate, 5 NaCl, 10 HEPES and 10 glucose, pH 7.4) (adjusted with 3.6 mM NaOH; total [Na⁺] ∼ 140 mM), SBS-Ca (in mM: 93 Ca-methanesulfonate, 5 CaCl₂, 10 HEPES and 10 glucose, pH 7.4) (adjusted with 2.2 mM Ca(OH)₂; total [Ca²⁺] ∼ 100 mM) or SBS-Cs (in mM: 95 Cs-methanesulfonate, 5 CsCl, 10 HEPES and 10 glucose, pH 7.4) (adjusted with 0.4 mM CsOH; total [Cs⁺] ∼ 100 mM). Table S2 (ESI‡) details modifications of these bath solutions.

Note that although there was no evidence in the present study of endogenous Ca²⁺ activated Cl⁻ channels which have been previously reported in CHO cells,²⁹ as a precaution against possible interference from endogenously expressed Cl⁻ channel activity, experiments were conducted using methanesulfonate salts as a replacement for Cl⁻. Furthermore, Cs⁺ has been found to be impermeant for NaChBac (ref. 30 but also see Fig. S4B and S5C, ESI‡). Consequently currents recorded in the present study represent Na⁺ or/and Ca²⁺ flow.

Whole cell currents were recorded at least 3 minutes after obtaining whole cell configuration to ensure complete equilibration of the pipette solution and cytosol. The bath solution was grounded using a 3 M KCl agar bridge; the liquid junction potential determined experimentally (as described by Neher³¹) agreed with that calculated (using the JPCalc program, Clampex, Axon Instruments, Inc.) and was accounted for in the analysis. The recording chamber volume was approximately 200 μl and was continuously exchanged by a gravity-driven flow/suction arrangement at a rate of ∼2 ml min⁻¹; to ensure complete exchange of the bath solution, electrophysiological recordings were initiated at least 3 minutes after the onset of solution change. Osmolarities of all solutions were measured using a Wescor vapor pressure osmometer (model 5520) and adjusted with sorbitol to maintain a constant osmolarity during solution changes.

The results were analysed using Clampfit 10.1 software (Molecular Devices) and OriginPro 8 (OriginLab Corporation). Pooled data are presented as means ± SEM(n), where n is the number of independent experiments.

3 Results

3.1 Characterization of the Na⁺/Ca²⁺ selectivity via the patch-clamp recordings

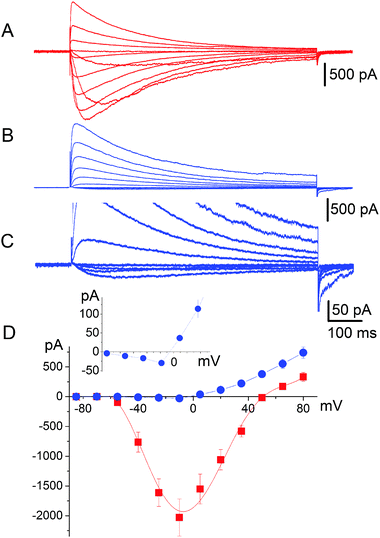
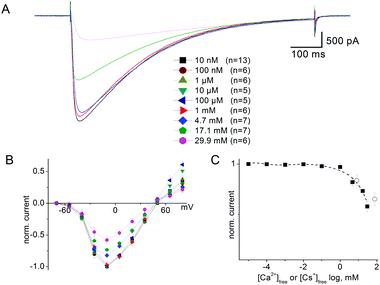
It has long been known³³ that in general voltage-gated sodium channels are impermeable to calcium. This piece of evidence, however, does not provide an unambiguous description of the selectivity mechanism. Traditionally, it was believed that calcium was simply not capable of interacting with the SF of sodium channels.³² On the contrary our electrophysiological analysis revealed that tiny inward calcium currents can indeed be recorded, which would obviously not be possible if the calcium ions were completely excluded from the channel.

Current–voltage data were collected by recording responses to a consecutive series of step pulses from a holding potential of −100 mV at intervals of −15 mV beginning at +95 mV in SBS-Na followed by perfusion with a bath solution in which Na⁺ was completely replaced with 100 mM Ca²⁺ (SBS-Ca) or Cs⁺ (SBS-Cs). Consistent with the previously reported results,^8,9 cells expressing NaChBac channels exhibited time-dependent depolarisation-activated currents in SBS-Na, which completely inactivated within one second following activation (Fig. 2A). Plotting whole cell peak current (I_peak) against voltage revealed that E_rev (50.3 ± 0.68 mV; n = 17) was close to the equilibrium voltage for Na⁺ (E_Na = 49.97 mV using PS1) consistent with these currents representing Na⁺ flux (Fig. 2D). Complete replacement of extracellular Na⁺ with Ca²⁺ abolished most of the inward current consistent with Na⁺ permeation through NaChBac. However (and as previously reported⁸), in those cells exhibiting large (≥1500 pA) NaChBac-mediated Na⁺ currents, small inward currents (representing about 3–5% of the Na⁺ current) were apparent following complete replacement of Na⁺ with Ca²⁺ (Fig. 2B and C) and this was consistent with a small but finite Ca²⁺ permeability (Fig. 2D). The permeability ratio (P_Ca/P_Na) was determined from whole cell Ca²⁺ current reversal potentials (E_rev) according to standard procedure.^33,34 The presented results provide E_rev = −4.7 ± 1.0 mV (n = 12) and the selectivity ratio P_Ca/P_Na = 0.19, which is close to the value reported by Yue et al.⁹ It should be noted that these currents were not the result of incomplete Na⁺ removal as they were stable for 15 min after perfusion with SBS-Ca and were not apparent in SBS-Cs (in which Na⁺ is completely replaced with Cs⁺; see Fig. S4A and B, ESI‡). Furthermore, these currents were not the result of endogenous channel activity as they were not present in control non-transfected cells or cells transfected with the empty vector.

Fig. 2 Permeability of NaChBac to Ca²⁺. Representative whole cell current recordings obtained from CHO cells expressing NaChBac using SP1 and (A) 140 mM extracellular Na⁺ (SBS-Na) or (B) 100 mM extracellular Ca²⁺ (SBS-Ca). (C) Same as panel (B) but using an amplified scale to illustrate the small inward Ca²⁺ currents. (D) Current–voltage relationship of mean peak whole cell currents and illustration of E_rev values of 50.3 ± 0.68 mV (n = 17) and E_rev = −4.7 ± 1.0 mV (n = 12) for currents recorded in 140 mM Na⁺ (red squares) and 100 mM Ca²⁺ (blue circles) respectively.

We further confirmed that the small inward Ca²⁺ currents resulted from NaChBac activity using the L226P NaChBac mutant. The L226P mutation changes the gating of the channel so that it activates at hyperpolarised voltages and removes inactivation.³⁵ Fig. S5A (ESI‡) shows that cells expressing L226P NaChBac mutant channels exhibited hyperpolarisation-activated inward currents (characteristic for the L226P NaChBac mutant) in bath solution following complete replacement of Na⁺ by Ca²⁺ consistent with NaChBac-mediated small Ca²⁺ currents (Fig. S5B and D, ESI‡); note that the inward current was absent in SBS-Cs (Fig. S5C, ESI‡).

3.2 Unbiased MD simulations of Na⁺ and Ca²⁺ ions

The observation of tiny (pA) inward calcium currents as opposed to large (nA) sodium currents suggests that both ions are capable of interacting with the SF but the mechanism of interaction is expected to be radically different. In order to gain a molecular level insight into these differences, we performed long timescale MD equilibrium simulations of the NaChBac system bathed in a CaCl₂ solution following the same protocol employed to study the channel in the presence of NaCl.²² Similar to that reported for the simulation in the NaCl solution, water molecules permeate spontaneously in the channel accessing from both the lower and the upper bath. The number of water molecules in the cavity of the channel in the axial range −20 < z < 10 Å increases during the first 20 ns of the simulation and thereafter oscillates around a plateau level of about 80 water molecules. However, as illustrated in Fig. 3, the time course of the number of calcium ions occupying the SF (axial range −10 < z < 24 Å) is dramatically different from that observed in the simulation in the NaCl solution (see Fig. 3). When NaChBac was simulated in the NaCl bath, a sodium ion accessed the EEEE-ring at the end of the equilibration after 1 ns of simulation. A second ion entered the SF after 5 ns determining a stable arrangement with an ion in the CEN site (at the level of the backbone carbonyls of the leucines of the SF) and a second ion in the HFS site (interacting with the side-chains of the glutamates of the EEEE-ring). The number of sodium ions in the SF thereafter hardly ever decreased below two and frequent transient events of access of a third ion could be observed. Conversely, when the channel is simulated in the presence of CaCl₂ a single calcium ion can be steadily accommodated into the SF but only at a rather late stage of the simulation (after 35 ns). This ion mainly resides at the level of site HFS where it interacts with the glutamates of the EEEE-ring. The number of ions in the SF will thereafter remain constant. It is also interesting to compare the time evolution of the number of water molecules and protein-supplied oxygen atoms coordinating the ions inside the SF. This analysis is discussed in detail in the ESI‡ (section Time evolution of hydration and coordination of ions and Fig. S3).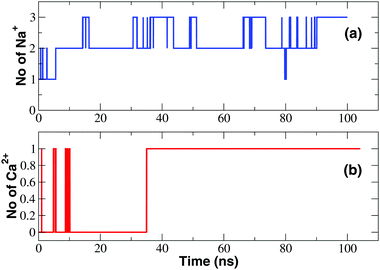

Fig. 3 Occupancy of the SF. (a) Time course of the number of Na⁺ ions in the SF; (b) time evolution of the number of Ca²⁺ ions in the SF.

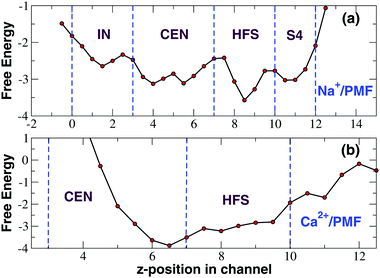
The time-course of calcium occupancy of the SF depicted in Fig. 3 shows that a single Ca²⁺ ion is stably accommodated in the SF. The time-course however does not show whether this calcium ion resides in a single location or can occupy alternative binding sites. To investigate this further we computed a PMF as a function of the position of the ions along the channel axis. As shown in Fig. 4, the PMF derived from the NPT simulation in a NaCl bath reveals the existence of four binding sites IN, CEN, HFS and S4, the first three of which correspond to the ones identified in the homologous NavAb channel. In sites IN and CEN sodium interacts with the backbone carbonyls of the threonine- and leucine-ring of the SF respectively. In site HFS the ion interacts with the side-chains of the glutamates of the EEEE-ring. In site S4 sodium mostly interacts with the side-chains of the serines of the SF. The PMF derived from an unbiased NPT simulation in the presence of a CaCl₂ bath is dramatically different (Fig. 4) with a single very deep minimum corresponding to the upper part of site CEN and the full HFS site. Calcium thus appears to be sandwiched between the LLLL-ring and the EEEE-ring but it mostly interacts with the negatively charged side-chains of the glutamates of the SF. This electrostatic interaction is so strong that calcium is bound to remain in the 5 < z < 10 Å range of the SF while sodium ion can freely span the whole filter region corresponding to the 0 < z < 12 Å axial range.

Fig. 4 Potential of mean force (kcal mol⁻¹) of sodium (a) and calcium ion (b) as a function of the axial position (Å) in the SF. The PMFs have been computed from two 100 ns unbiased simulations in the NPT ensemble.

3.3 Analysis of Ca²⁺ hydration and coordination

In order to characterize the state of hydration and coordination of sodium and calcium ions at different levels along the channel axis, in Fig. 5 we plot the average number of oxygen atoms interacting with sodium or calcium in transversal bins with a height of 2.0 Å. For both Na⁺ and Ca²⁺ there is a central region of the channel that during the finite timescale of our simulation the ions could not reach. In this region the number of coordinating oxygens per internal ion was thus arbitrarily set to zero. Due to its higher permeability, this excluded region for sodium only ranges from −16.0 to −8.0 Å while in the case of calcium it is much larger extending from −18.0 to 4.0 Å. The coordination patterns of sodium and calcium are radically different. In the bulk solvent Na⁺ ions are coordinated on average by 5.5 water molecules. At the level of both the inner (−34.0 to 20.0 Å) and the outer (6.0 to 16.0 Å) mouth, the channel narrows causing a drop to 3.5 in the number of coordinating water oxygens. The total number of coordinating oxygens however remains unchanged since the displaced water oxygens are replaced by an approximately equal number of oxygens provided by the protein. In particular, at the intracellular mouth of the channel, sodium interacts with an oxygen provided by the side chain of E236 and the carboxy-terminal group COO– of K237. Conversely, in the SF region it is possible to discriminate the coordination pattern of bin 8.0–10.0 Å corresponding to site HFS, where Na⁺ interacts with a glutamate and the adjacent serine of the TLESWAS sequence, and a distinct coordination pattern of the 10.0–14.0 Å region corresponding to site S4 where sodium interacts with one or two serines of the SF.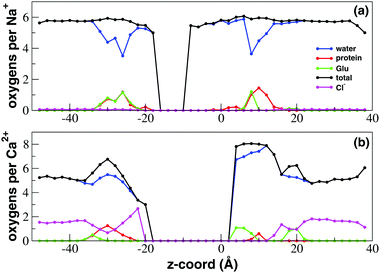

Fig. 5 Ion coordination and hydration inside the NaChBac channel. Number of coordinating oxygens and chlorides in axial bins with a height of 2.0 Å computed using a cutoff distance of 3.5 Å for Ca²⁺–oxygen and Ca²⁺–Cl⁻, of 3.2 Å for Na⁺–oxygen and 3.5 Å for Na⁺–Cl⁻ (see calculations of the radial distribution function (RDF) in the ESI,‡ Fig. S1 and S2). (a) Sodium coordination; (b) calcium coordination. Blue line: number of coordinating oxygens provided by water; green line: coordinating oxygens contributed by the glutamates of the EEEE-ring; red line: oxygens contributed by other protein residues; black line: total number of coordinating oxygens; magenta line: number of coordinating chlorides.

In the bulk solvent calcium ions are coordinated on average by 5 water molecules. When calcium accesses the SF (4.0 < z < 10.0 Å) however, it does not undergo any desolvation but the number of coordinating water molecules instead increases on average to 7 while the ion also interacts electrostatically with the side-chain of a glutamate of the EEEE-ring. When the Ca²⁺ ion enters the SF thus there appears to be no replacement of water-provided with protein-provided oxygens, but an exchange of anionic ligands occurs. In fact, as illustrated in the radial distribution function (RDF) in ESI,‡ Fig. S2, when calcium is in the bulk solution, the first coordination shell contains one or two chloride ions that are lost when Ca²⁺ enters the SF. The chloride ion appears to be replaced by one or two oxygens of a negatively charged glutamate side-chain. This replacement mechanism is clear from Fig. 5 where the average number of coordinating chlorides as a function of the axial position in the channel is shown. Outside the channel the average number of chlorides is about 1.5 in agreement with the Ca²⁺–Cl⁻ RDF in ESI,‡ Fig. S2. As soon as calcium enters into the SF the number of coordinating chlorides drops to zero while calcium establishes interactions with the glutamates of the SF. A similar behaviour can be observed at the cytoplasmic mouth of the channel where the decrease in the number of coordinating chlorides is paired to the increase in the number of interactions with the terminal COO⁻ groups of the four chains. A peak in chloride coordination can be observed in the −28.0 < z < −22.0 Å range. In this region, already corresponding to the central cavity of the channel, clusters of calcium and chloride ions occupy a near-axial position where they do not interact with any protein residue.

The ability of calcium not to lose any water of its hydration shell could possibly be due to the higher solvation free energy of calcium with respect to sodium. As detailed in the ESI‡ (section Details on calculation of free energies of binding), using a free energy perturbation (FEP) approach, we estimated free energies of solvation of −93.49 and −355.47 kcal mol⁻¹ for Na⁺ and Ca²⁺ respectively. The fact that the free energy of solvation of calcium is about three times and a half higher than that of sodium might explain why calcium keeps its whole solvation shell upon entering into the SF. This behaviour is also consistent with the dynamics of exchange of water molecules between different coordination shells around metal ions studied by Di Tommaso et al.⁴¹ In particular, these authors reported that the frequency of water exchange in the first shell of calcium decreases as the halide concentration increases. Therefore, electrolytes in solution strongly stabilize the first hydration shell of Ca²⁺. In the same paper the authors studied the influence of different concentrations of alkali halides on calcium hydration. They discovered that a single calcium ion in a water environment features about 7 water molecules in its first hydration shell, but this number drops to a value between 4 and 6 in the presence of different concentrations of another salt not containing calcium. In the ESI‡ we show that a similar decrease in the hydration number results from the increase of the concentration of CaCl₂. The change in hydration of calcium as it accesses the SF of NaChBac can now be interpreted in the light of this pattern. When the calcium ion is in the bulk, it finds itself in a medium with high CaCl₂ concentration (0.5 M) and it thus adopts a low hydration number around 5. When the ion enters into the SF it is exposed to an environment where there are no other CaCl₂ molecules. It is thus in the same conditions as a single calcium ion in a waterbox and it subsequently adopts a high hydration number (around 7).

The calcium behaviour can thus be summarized in these terms. When calcium is in the bulk it is surrounded by 5 water molecules and one or two chlorides. The tight binding of chloride (ion pairs) limits the hydration number to 5 because chloride displaces at least a couple of potentially interacting water molecules. When calcium enters into the SF, the coordinating chlorides are displaced and replaced by the oxygens of a negatively charged glutamate residue. The interaction with glutamate apparently does not prevent the interaction with other water molecules and calcium attains its full hydration shell of 7 waters.

The additional water molecules that surround calcium in the SF with respect to bulk solvation probably act as bridges between the calcium ion and the glutamate side-chains that are too far to directly interact with the ion. It is interesting to note that the increase in the number of coordinating waters only occurs at the level of the SF. At the level of the intracellular mouth of the channel the number of coordinating waters, despite exhibiting a local maximum, reaches a level comparable to the bulk coordination number. Calcium also interacts with one or two oxygen atoms provided by the carboxy-terminal group COO⁻ of Lys237. It is noteworthy that in this region the C-terminal COO⁻ groups of the four chains and the side-chains of Glu236 are too far from one another for water molecules to act as bridges between them and the calcium ion. This coordination pattern highlights another difference with respect to the mode of coordination of sodium. While Na⁺ ions especially at the level of the SF interact with both negatively charged and polar (but neutral) groups, calcium shows a marked preference for anionic binding partners selectively interacting with carboxylate groups belonging to either glutamate side-chains or the C-terminus. This pattern can also be recognized in the [18.0–22.0] Å axial region where calcium interacts with the side chains of Glu172 or Glu204 that form a ring of eight negatively charged residues lined along the extracellular rim of the channel. While calcium interacts on average with one oxygen from Glu172 or Glu204, Na⁺ interacts on average with 0.1 oxygens from these residues so that the interaction can be considered negligible.

3.4 Binding sites of Ca²⁺ in the SF via 1D metadynamics simulations

The unbiased equilibrium simulations of NaChBac in a NaCl and CaCl₂ solution show that sodium ions move more freely than calcium in the SF. In particular, the PMF shown in Fig. 4 suggests that calcium remains stuck in a deep minimum in the upper region of the CEN site from which it cannot further proceed toward the central cavity of the channel. In principle this scenario could represent a transient behaviour and it cannot be a priori excluded that on longer timescales a single Ca²⁺ ion could cross the SF. In order to attain a more reliable reconstruction of the free energy profile we performed 1D-metadynamics simulations biasing a single ion to explore the SF. The simulation was started from the final frame of our 105 ns unbiased NPT simulation where a single ion was trapped at the boundary between the CEN and HFS sites. The metadynamics simulation was run for 144 ns and the z-component of the distance vector between the ion in the SF and the center of mass (COM) of the alpha–carbons of the glutamates of the EEEE-ring was selected as the collective variable. Since the axial position of the COM of the EEEE-ring is at about 5.5 Å, the resulting PMF in Fig. 6 has been translated accordingly to simplify the comparison with the PMF from the unbiased simulation illustrated in Fig. 4.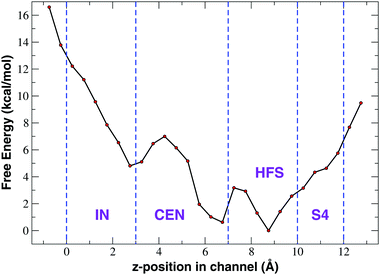

Fig. 6 Potential of mean force of Ca²⁺ as a function of the axial position derived from 1D-metadynamics.

As can be noted from Fig. 6, the 1D-metadynamics PMF is much richer than the one derived from the unbiased simulation (Fig. 4(b)). While the PMF from the unbiased simulation features a single minimum at the border between sites CEN and HFS, the free energy profile reconstructed through metadynamics shows three distinct minima. The deepest minima are located in sites HFS and CEN and they are separated by a barrier of about 3.0 kcal mol⁻¹. This barrier can be easily overcome at room temperature which means that an incoming calcium ion can reach as far as the CEN site. The third minimum is located at the boundary between site IN and site CEN and could be reached by an ion coming from the minimum in site CEN only after overcoming a barrier of 6.0 kcal mol⁻¹. This barrier thus represents the bottleneck that prevents the further advancement of the calcium ion into the Central Cavity. From a molecular point of view, on analyzing conformations sampled in the three minima, it can be noted that while calcium resides in the minimum corresponding to site HFS, it interacts with the side-chains of E191 of the EEEE-ring and of the adjacent S192. The barrier between the minima in sites HFS and CEN corresponds to a situation when the weakening of the interaction with the glutamates of the EEEE-ring is not yet compensated by the interaction with the carbonyls of L190 on the four chains. When calcium dwells in the minimum in site CEN it interacts with the leucines of the LLLL-ring while still feeling the electrostatic interaction of the glutamates of the EEEE-ring (ion–ion interactions are longer-ranged than ion-dipole interactions). At the level of the barrier between the minima in sites IN and CEN the attraction from the glutamates of the EEEE-ring is definitely lost while the weakening of the interactions with the leucines of the LLLL-ring is not yet compensated by the interaction with the backbone carbonyls of the threonines of the TTTT-ring. When Ca²⁺ moves from this barrier to the minimum in site IN, finally the energy decreases again due to the simultaneous interaction with the C=O dipoles of the TTTT-ring and LLLL-ring.

3.5 Analysis of Ca²⁺ binding in the SF

The unbiased and 1D-metadynamics simulations of NaChBac in a CaCl₂ solution show that at variance with sodium, the calcium ion is trapped in the SF and cannot further proceed to the central cavity of the channel. In evaluating the observed failure of calcium to cross the SF and access the central cavity of the channel, it is important to consider the finite duration of our simulations. The small inward calcium currents highlighted by our patch-clamp measurements suggest that full permeation events could possibly occur on a longer time-scale. However, the small amplitude of the Ca²⁺ current, amounting to a few percent of the Na⁺ current, supports the existence of a high energy barrier so that calcium permeation can be regarded as a rare event. Two reasons, both related to calcium charge, can be put forward to explain this scenario:

(1) Due to its double charge with respect to sodium, the calcium ion interacts more strongly with the negatively charged glutamates of the EEEE-ring.

(2) A knock-on mechanism is precluded due to the strong electrostatic repulsion that a calcium ion bound in the SF exerts on a second, potentially incoming Ca²⁺ ion.

3.5.1 Free energies of binding. In order to test the first hypothesis we computed the free energy of binding of sodium and calcium to the NaChBac SF. The calculations were performed employing an Alchemical Free Energy Perturbation (FEP) double annihilation protocol.³⁶ More specifically, as illustrated in Fig. 7, the ion binding process was decomposed into the three steps of a thermodynamic cycle:

Fig. 7 Thermodynamic cycle delineating the reversible association of an ion to the selectivity filter (SF) of the NaChBac channel. The notation “0” refers to an ion decoupled from its environment setting to zero both electrostatic and van der Waals interactions. The left vertical leg represents the annihilation of an ion in the bulk solvent. The right vertical leg depicts the vanishing of an ion in complex with the SF. The lower horizontal branch describes the transfer of a ghost ion from the solvent to the SF. The upper horizontal branch represents the real binding reaction whose free energy must be determined.

(1) The ion in the bulk solution is first decoupled from its environment by gradually switching off the electrostatic and van der Waals interaction. The free energy change in this step is ΔG^bulk_annihil.

(2) The ghost ion no longer interacting with its environment is bound to the SF of the NaChBac channel. Since the ion interacts with neither the solvent nor the protein, this step has a zero free energy change.

(3) The ghost ion in the SF of the channel is recoupled with its environment by gradually restoring the electrostatic and van der Waals interactions. The variation of free energy in this stage is ΔG^SF_create = −ΔG^SF_annihil.

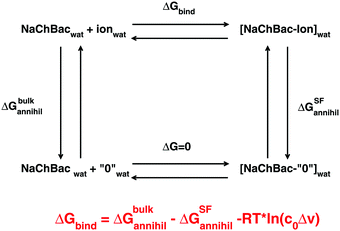
From a practical point of view this cycle can be implemented through a double annihilation protocol based on two distinct simulations: annihilation of a sodium or calcium ion in the bulk and annihilation of an ion complexed to the SF of the channel. In the latter simulation in order to avoid the so-called wandering ligand problem, the ion must be harmonically constrained to its initial position. In fact, on uncoupling a substrate from its environment, this ligand becomes free to drift away from its binding sites finding itself in unnatural positions. The geometric restraint limits the entropy of the ligand thus affecting its free energy. Roux and coworkers showed³⁷ that the effect of the restraint on the free energy can be quantified as −RT ln(c₀Δv), where Δv is the effective volume the ligand is constrained in while c₀ is the standard state concentration of 1 mol per liter (1/1661 Å⁻³). Conversely, no constraint is required during the annihilation of the ion in the bulk since the solvent is considered isotropic so that the drift of the ion away from the initial position leaves the free energy unchanged. The free energy of ion binding can thus be computed as

ΔG_bind = ΔG^bulk_annihil − ΔG^SF_annihil − RT ln(c₀Δv) (1)

Further details on the protocol for computing the free energy of binding are provided in the ESI‡ (section Details on calculation of free energies of binding and Fig. S6–S8). Using eqn (1), the free energy of binding of the sodium ion can be evaluated as 93.49 − 95.20 + 0.69 = −1.02 kcal mol⁻¹. In a similar way, the free energy of binding of Ca²⁺ was 355.47 − 360.60 + 1.61 = −3.52 kcal mol⁻¹. The fact that for both ions ΔG^SF_annihil > ΔG^bulk_annihil suggests that the interactions between the sodium or calcium ions and the glutamates of the EEEE-ring are stronger than the interactions of these ions with the water molecules in the bulk solvent. More importantly, our calculations thus show that the free energy of binding of calcium to the SF of NaChBac (−3.52 kcal mol⁻¹) is more than three times as large as the corresponding ΔG_bind of the sodium ion (−1.02 kcal mol⁻¹). On computing the ΔG_bind we note that calcium binding to the SF is favoured by −2.5 kcal mol⁻¹ with respect to sodium binding. Considering that at room temperature RT = 0.6 kcal mol⁻¹, the thermodynamic advantage of Ca²⁺ over Na⁺ is estimated to be −4.16 RT. These results suggest that calcium interacts in a very stable way with the glutamates of the SF and is thus very unlikely to leave spontaneously its binding site.

3.5.2 Barriers to the knock-on mechanism. The free energies of binding computed through the alchemical FEP approach showed that calcium interacts in a very stable way with the glutamates of the EEEE-ring so that it is unlikely to spontaneously leave its binding site. However, a calcium ion in the SF could be electrostatically pushed by another incoming calcium ion, enacting a knock-on mechanism similar to the one observed for the sodium ion.²² In order to evaluate this possibility we performed a 1D-metadynamics simulation with a calcium ion constrained into the SF and a second calcium ion biased to explore the region above the fixed ion. In order to compare the possibility of the knock-on mechanism in the calcium and sodium system, we also performed an analogous 1D-metadynamics simulation with a fixed and a mobile sodium ion.

The free energy profile shown in Fig. 8 reveals that the mobile calcium ion experiences a barrier of about 6.0 kcal mol⁻¹ when it is at a distance of about 5.5 Å from the fixed ion. As the mobile ion is moved further closer to the fixed ion, the energy decreases by 1.5 kcal mol⁻¹ in correspondence of a minimum at a distance of 4.5 Å from the fixed ion. Basically, as the mobile ion comes closer and closer to the fixed ion, the electrostatic repulsion exerted by the latter becomes stronger and stronger determining a high energy barrier. At a closer distance this repulsion is partially mitigated by the attraction exerted by the negatively charged glutamates of the EEEE-ring, but this effect is still overwhelmed by the Ca²⁺–Ca²⁺ repulsion so that the minimum at 4.5 Å separation corresponds to a high free energy level and it is scarcely populated. This scenario suggests that the second incoming ion could not come close enough to the ion already inside the SF to push it in a deeper position inside the channel. A knock-on mechanism involving two ions is thus unlikely to occur.

Fig. 8 Potential of mean force (kcal mol⁻¹) of calcium (a) and sodium (b) when one ion is kept fixed and the other is biased to explore the SF in a 1D-metadynamics simulation. The collective variable is the z-component of the distance vector with respect to the center of mass of the EEEE-ring (Å).

Fig. 8 also reveals the PMF computed from the simulation with a fixed and a mobile sodium ion. The curve shows a profile very different with respect to that of the calcium simulation. In fact, in the calcium simulation, as the mobile ion comes closer and closer to the fixed ion the free energy increases monotonically peaking at the barrier at 5.5 Å separation. Conversely, as the mobile sodium ion moves closer and closer to its fixed counterpart, the free energy decreases monotonically producing a minimum at 4.0 Å separation. This scenario suggests that in the case of sodium the electrostatic attraction exerted by the negative glutamates of the EEEE-ring is dominant with respect to the repulsion exerted by the fixed ion. The main minimum of the free energy is separated by a barrier at 3.0 Å separation from a secondary minimum at about 2.7 Å separation. Consistent with the less intense repulsion between sodium ions, the barrier corresponds to a closer approach between the two ions and its height is only 1.5 kcal mol⁻¹. The secondary minimum possibly stems from the specific setting of the simulation where the innermost ion was constrained to its initial position. Indeed when we reconstructed the permeation mechanism by means of the Nudged Elastic Band approach²² we recognized a typical knock-on mechanism. In particular we noted that the incoming ion never comes closer than 3.0–3.5 Å from the ion inside the SF. When this separation is reached the electrostatic repulsion is sufficiently strong such that the innermost ion is pushed further inside the SF enacting the knock-on mechanism. It can thus be suggested that the knock-on mechanism occurs when the mobile ion reaches the main minimum at 4.0 Å separation shown in Fig. 8(b). The secondary minimum would never appear because the two ions would never reach the corresponding level of separation.

3.6 Anomalous mole fraction effect

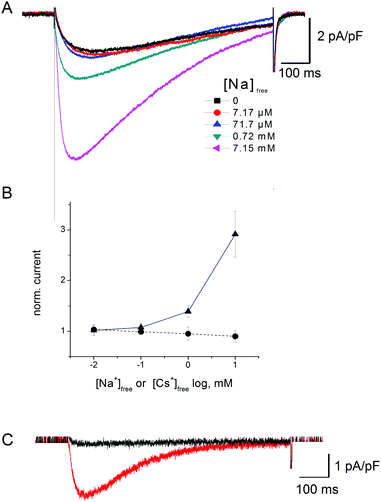
The expression “Anomalous Mole Fraction Effect” (AMFE) refers in the present study to the ability of micromolar calcium concentrations to significantly affect sodium currents in ion channels. This issue is extremely important for NaChBac because both our unbiased and metadynamics simulations support a scenario whereby a single calcium ion accesses the SF and remains stuck therein. The high free energy of binding makes Ca²⁺ difficult to displace from its binding site in the SF, so that in principle it may block sodium permeation and display AMFE phenomenology. We addressed this issue by means of an integrated strategy based on both electrophysiological measurements and MD simulations.

3.6.1 Experimental analysis of AMFE. To explore the interaction of Na⁺ and Ca²⁺ in the pore of NaChBac we recorded NaChBac-mediated currents in bath solutions containing mixtures of varying Na⁺ and Ca²⁺ concentrations. Specifically we conducted two sets of experiments using (1) bath solution SBS-Na to which Ca²⁺ was added to activities ranging from 10 nM to 29.9 mM (Fig. 9) and (2) bath solution SBS-Ca to which Na⁺ was added to activities ranging from 7.17 μM to 7.15 mM (Fig. 10). For each combination of concentration the current in response to a depolarising step to −10 mV was measured. The details of bath solution modifications are listed in Table S2 (ESI‡).

Fig. 9 Effect of extracellular Ca²⁺ on NaChBac-mediated Na⁺ currents. (A) Representative whole cell current recordings obtained from CHO cells expressing NaChBac using SP1 in response to a depolarising voltage step from −100 mV to −10 mV in SBS-Na containing Ca²⁺ activities ranging from 10 nM to 29.9 mM. (B) Current voltage relationship of mean peak current obtained in SBS-Na containing Ca²⁺ activities ranging from 10 nM to 29.9 mM. Currents were normalized to the peak current recorded from the same cell in SBS-Na containing 10 nM Ca²⁺; error bars represent SEM of mean values determined from at least 5 independent experiments. (C) Plot of mean peak inward currents from (B) against increasing Ca²⁺ activities ([Ca²⁺]_free; closed squares) normalized to peak inward currents recorded in SBS-Na containing 10 nM Ca. Open circles are as closed squares but in SBS-Na supplemented with 7.67 and 72.72 mM [Cs⁺]_free.

Fig. 10 Effect of extracellular Na⁺ on NaChBac-mediated Ca²⁺ currents. (A) Representative whole cell current recordings obtained from CHO cells expressing NaChBac using SP2 and SBS-Ca supplemented with Na⁺ in response to a depolarising step from −100 mV to −10 mV. (B) Plot of mean peak inward current in SBS-Ca supplemented with Na⁺ (closed triangles) or Cs⁺ (closed circles); current values are normalised to peak inward currents recorded in SBS-Ca. Values are means ± SEM from at least 5 independent experiments. (C) Representative whole cell current recordings obtained from CHO cells expressing NaChBac using SP2 and SBS-Cs (in black) supplemented with 10 mM Na⁺ (in red) in response to a depolarising step from −100 mV to −10 mV.

NaChBac-mediated Na⁺ currents in SBS-Na supplemented with Ca²⁺ (Fig. 9A) exhibited a partial reduction of inward current but this was only apparent in the presence of mM Ca²⁺ (approximately 40% reduction in inward current in the presence of 29.9 mM [Ca²⁺]_free) (Fig. 9C). Similar experiments were performed in which Cs⁺ was added to SBS-Na to understand the nature of this blockade. As shown in Fig. S4B (ESI‡), addition of Cs⁺ to SBS-Na also resulted in reduction of the inward current similar to that observed following the addition of Ca²⁺ (Fig. 9C) suggesting that this reduction resulted mainly from a general cation effect which was not specific to Ca²⁺ entry into the pore.

Fig. 10 shows the results of the addition of low concentrations of extracellular Na⁺ on the tiny (∼50 pA) NaChBac-mediated Ca²⁺ currents (i.e. recorded in SBS-Ca supplemented with Na⁺). To remove interference from Na⁺ efflux currents, these experiments were performed in Na⁺-free pipette media (PS2; see Methods). As shown in Fig. 10B, addition of low concentrations of Na⁺ to SBS-Ca (i.e. low Na⁺ in saturating concentrations of Ca) resulted in increasing inward current. This increase in current most likely reflects, at least in part, Na⁺ influx in addition to Ca²⁺ influx. This is based on the observations that (1) addition of Cs⁺ to SBS-Ca did not result in an increase in inward current (Fig. 10B) indicating that the effect was specific for Na⁺ and (2) that equivalent addition of Na⁺ to SBS-Cs (Cs⁺ being impermeant) resulted in an increase in peak current which was equivalent to that observed following the addition of Na⁺ to SBS-Ca (Fig. 10C). Specifically, addition of 10 mM Na⁺ (7.15 mM activity) to SBS-Ca resulted in 3.6 ± 1.75 pA pF⁻¹ (n = 5) increase in peak inward current and addition of 10 mM Na⁺ (8.1 mM activity) to SBS-Cs resulted in 2.17 ± 1.23 pA pF⁻¹ (n = 5) increase in peak inward current: p = 0.27.

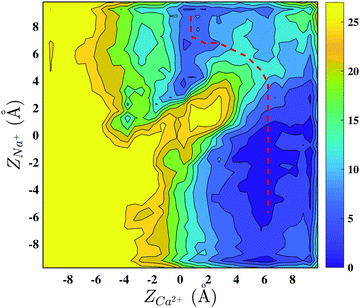
The first set of experiments excludes the AMFE in agreement with previous studies.³⁸ However, the second set of measurements of currents in mixed Na⁺/Ca²⁺ solutions reveals that despite the occupancy of Ca²⁺ in the SF, Na⁺ is still able to cross the NaChBac channel, with the possible explanation being that Na⁺ is able to bypass the resident Ca²⁺. In order to clarify the mechanism, we performed a metadynamics simulation biasing a calcium and a sodium ion to explore the NaChBac SF.

3.6.2 Computational analysis of AMFE. In order to clarify the sodium permeation mechanism when the channel is occupied by a single calcium ion, we ran a 2D-metadynamics simulation using as collective variables the z-components of the distance vectors of a sodium and a calcium ion with respect to the center of mass of the alpha-carbons of the glutamates of the EEEE-ring. The simulation was started from an initial conformation where the Na⁺ and Ca²⁺ ions were located in sites HFS and CEN respectively, mimicking the access of a sodium ion in a SF already occupied by a calcium ion in the most stable binding site identified by our equilibrium and metadynamics simulations (Fig. 4 and 6). The bidimensional PMF reported in Fig. 11 was computed after 300 ns of simulation. The PMF shows that the calcium ion spends most of its time close to or above the EEEE-ring at z ≥ 0.0 Å where it was initially located. Conversely, the sodium ion mainly dwells in two main basins in the upper and lower part of the SF. These two basins, however, are not disconnected but the sodium ion can move from one another through a bridge region in the upper-right corner of the contour plot. Following a minimum free energy path the following permeation route could be envisaged. The path starts from a situation with a calcium ion bound at the level of the EEEE-ring and a sodium ion outside the SF at z = 8 Å. Then the sodium ion moves down, reducing its distance from calcium. When the two ions are sufficiently close, calcium moves up, while sodium moves further down. In other words the sodium ion overcomes or by-passes the calcium ion and then proceeds all the way down to the end of the SF, while calcium remains close to the upper margin of the SF. This mechanism seems to show that, in agreement with experimental data, a calcium ion in the channel is not able to stop sodium ion permeation, but the permeation barrier increases. This mechanism appears to be similar to the one identified by Corry¹⁸ in the homologous NavAb channel. The barriers that the sodium ion must overcome along the lowest energy pathway are also similar amounting to ∼6.0 kcal mol⁻¹ in NaChBac and ∼5.0 kcal mol⁻¹ in NavAb.

Fig. 11 Potential of mean force for one calcium and one sodium ion in the channel. The two collective variables represent the axial distance of the two ions with respect to the center of mass of the EEEE-ring. The free energy is expressed in kcal mol⁻¹ and contour lines correspond to 3 kcal mol⁻¹ intervals. The red dashed line represents the approximate lowest energy pathway that a Na⁺ ion must follow to permeate through the pore overcoming a resident Ca²⁺ ion.

4 Conclusions

Ion channel selectivity is an area of intensive research due to the biochemical importance of the issue and the potential applications for the design of artificial nanopores for the separation of mixtures of chemicals.^10,11 In this paper the Na⁺/Ca²⁺ selectivity of the NaChBac channel has been investigated employing an integrated approach based on MD simulations and electrophysiological measurements.

As a preliminary step of our work, as detailed in ref. 22, we built a new homology model of NaChBac. Several prokaryotic sodium channel orthologues have recently been determined in Magnetococcus marinus (NavMs),⁴²Arcobacter butzleri (NavAb),⁵Rickettsiales sp. (NavRh)³⁸ and Alkalilimnicola ehrlichei (NavAe).⁴³ These structures capture sodium channels in different states of their functional cycle and a careful comparison⁴⁴ provides insights into the functioning of the channel. In particular the NavAb channel (PDB ID: 3RVY) was captured in the closed state characterized by an open SF but an occluded activation gate. Conversely the NavMs channel was crystallized in the open conformation where both the SF and the activation gate are open (PDB ID: 4F4L and 3ZJZ). Finally, NavRh (PDB ID: 4DXW) can be considered to be in the inactivated form where both pore and SF are collapsed. An accurate comparison of NavAb and NavMs showed a similar arrangement of the SF suggesting that this region should be uncoupled from the activation gate that appears to be the only region involved in the open–close transition. This process is now believed to involve a twist in the middle of the S6 helix at the level of a critical glycine or threonine residue. The twist that starts as a relatively small change in the middle of the helix is translated to a motion of more than 5.0 Å at the end of S6 that forms the activation gate. We took advantage of this rich library of structures of prokaryotic sodium channels to make a new homology model of NaChBac. In 2008 Shafrir et al.⁴⁵ had already proposed a homology model based on two different templates: the Kv1.2/2.1 chimera (PDB ID: 2R9R) and the Kv1.2 channel (PDB ID: 3LUT). The reliability of this model, however, was limited by the poor sequence similarity of sodium and potassium channels (the sequence identities of Kv1.2 and Kv1.2/2.1 chimera for NaChBac were 22.5% and 23.5% respectively). We therefore chose to model the open structure of the NaChBac channel using as a template the fully open structure of the NavMs channel (3ZJZ) that features 45.6% sequence identity with NaChBac. Thanks to a steady increase in its reliability, homology modeling is becoming a standard tool in molecular biology.⁴⁶ The accuracy of a comparative model is related to the percentage sequence identity between template and target.⁴⁷ High-accuracy comparative models are based on more than 50% sequence identity to their templates which leads to a root mean square (RMS) error for the main-chain atoms of approximately 1.0 Å. Medium-accuracy comparative models are based on 30 to 50% sequence identity. They tend to have about 90% of the main-chain modeled with 1.5 Å RMS error. Finally, low-accuracy comparative models are based on less than 30% sequence identity leading to fairly inaccurate structural predictions. The 45% sequence identity between NavMs and NaChBac thus places our model at the boundary between medium- and high-accuracy models which means that our model has accuracy comparable to that of a low-resolution X-ray structure. The subsequent equilibration using a state-of-the-art force field is then expected to further reduce the gap between the computed structure and the real one.

The first key finding of our work is that a single calcium ion can indeed access the selectivity filter, but the ion interacts so strongly with the glutamates of the EEEE-ring that it is stuck inside. This finding is far from trivial. In fact, it has been long known³³ that sodium channels are generally impermeable to calcium, but the mechanism of this differential permeability was not clear. In their seminal work Ganesh et al.³² analyzed the mechanism of sodium and calcium permeation through simulations of simplified models of selectivity filters. They discovered that the model SF of calcium channels operates through a preferential binding mechanism interacting with both Na⁺ and Ca²⁺ but with a preference for the latter. By contrast, the model SF of sodium channels was observed to work through an exclusion mode confining the calcium ion outside the channel, in the extracellular bath. This interpretation scheme is challenged by our patch-clamp recordings showing small, but non-negligible inward calcium currents that would be impossible if Ca²⁺ was confined in the extracellular space. Our electrophysiological results confirm the high selectivity and permeability of Na⁺ as previously reported.^8,9,30 On the other hand, the observed finite NaChBac-mediated Ca²⁺ influx, which was only detectable in cells which were highly expressing NaChBac and exhibiting large NaChBac-mediated Na⁺ whole cell currents, is consistent with early reports of Ca²⁺ permeation through NaChBac.⁸ However, this phenomenon has been ignored in subsequent reports. In the present study we have used the different activation kinetics of the L226P mutant to confirm that the small Ca²⁺ current is indeed mediated by NaChBac (and therefore confirming Ca²⁺ occupancy in the pore). This permitted the use of carefully designed solutions to investigate Na⁺ permeation in the presence of Ca²⁺ and thus gain novel insights into the cation permeation process in the channel pore. Our computational and experimental results are consistent with the findings of Ke et al.¹⁹ on the NavAb channel, where a single calcium ion was observed to access the SF without transiting to the central cavity in the timespan of a 100 ns equilibrium simulation.

The access of a calcium ion into the SF of NaChBac, after all, should not be surprising. In fact, as already discussed, the SF of NaChBac conforms to the consensus sequence FxxxTxExW of eukaryotic calcium channels and shares the EEEE-locus. Since experimental studies of eukaryotic calcium channels³⁹ have shown that they are continually occupied by at least one Ca²⁺, the presence of a calcium ion in the NaChBac SF is not unexpected. What is really surprising then is that this calcium ion is rarely released into the central cavity to complete the permeation process. We identified two reasons for this behaviour. First of all, by performing alchemical transformations with the FEP approach, we estimated that the free energy of binding of calcium to the SF is 3.5 times higher than that of sodium. This implies that calcium is unlikely to spontaneously leave the thermodynamically stable binding site at the level of the EEEE-ring. Even if the Ca²⁺/SF interaction is strong, calcium could still be displaced from its binding site as a result of an electrostatic kick exerted by a second incoming Ca²⁺ ion. In this way calcium permeation would be based on a knock-on mechanism just like sodium permeation in the same channel.²² Our metadynamics simulation with a calcium ion fixed near the EEEE-ring and a mobile calcium ion biased to explore the region above the first one, however, reveals a high free energy barrier, and thus strong electrostatic repulsion that turns the incoming ion back into the bulk, likely preventing the knock-on mechanism resulting from two-ion interactions.

This explanation is different from the one proposed by Corry¹⁸ and Ke et al.¹⁹ According to Corry, the limited calcium permeability in NavAb is due to the narrowing of the channel in the region between the four glutamates of the EEEE-ring and the backbone carbonyls of the neighbouring leucine-ring. The channel narrowing would induce a massive desolvation of both sodium and calcium, but the latter would pay a higher, uncompensated dehydration cost leading to a free energy barrier preventing its further advancement. This scenario is not supported by our simulations. In fact, while for Na⁺ we observed a hydration and coordination pattern comparable to the one reported by Corry, Ca²⁺ behaved in a completely different way. In a 0.5 M solution of CaCl₂, calcium appeared to be coordinated by 5 water molecules and one or two chloride ions. Upon accessing the SF, the chlorides are replaced by negatively charged glutamate side-chains while the number of coordinating waters is further increased to 7, possibly because the channel is locally narrow enough to allow water molecules to act as bridges between calcium and glutamate side chains. Both Corry's interpretation and ours are within the framework of the Eisenman model¹⁴ stating that ion permeability depends on the balance between the desolvation penalty and the enthalpic gain of ion/SF electrostatic interaction. The two interpretations, however, differ in the relative weights assigned to the desolvation and electrostatic terms, which may result from the different parameterization of the force field. Even if neither our simulations nor Corry's have been performed using a polarizable force field, as it is often recommended⁴⁰ for the simulation of divalent cations, our results on calcium hydration and coordination are consistent with calculations by Di Tommaso et al.,⁴¹ who used a sophisticated classical force field specifically designed to reproduce calcium behaviour in ab initio simulations (see discussion in the ESI‡).

The presence of a calcium ion stably bound to the EEEE-ring potentially opens the way to the AMFE, since the resident Ca²⁺ ion could prevent the permeation of Na⁺. Our current measurements in the presence of Na⁺/Ca²⁺ mixtures show that calcium can significantly decrease sodium current only at millimolar concentrations so that no AMFE actually occurs. A possible mechanism of sodium permeation in the presence of a resident calcium was unveiled by a 2D-metadynamics simulation biasing a Na⁺ and a Ca²⁺ ion to explore the SF. The axial–axial PMF shows a by-pass mechanism equivalent to the one identified by Corry in NavAb.¹⁸ The minimum energy permeation pathway, however, implies the overcoming of a free energy barrier of ∼6.0 kcal mol⁻¹ which suggests sodium current attenuation larger than the experimental one. A possible explanation of this behaviour lies in the protonation state of the EEEE-ring. While in our simulation the EEEE-ring was assumed to be in the fully charged −4 state, protonation of individual glutamates may loosen the Ca²⁺/SF attraction favouring the displacement of Ca²⁺ towards the extracellular margin of the SF that occurs during the by-pass mechanism. Another possible explanation is based on the observation that a single Na⁺ ion finds it difficult to cross the NaChBac SF even when it is empty, so that permeation occurs through a knock-on mechanism involving 2 or 3 ions.²² It can therefore be speculated that a knock-on mechanism could be required to cross the SF also when this is occupied by a resident calcium ion. A rigorous test of this hypothesis would require Umbrella Sampling or metadynamics simulations biasing two sodium ions and one calcium ion to explore the SF. Due to the long expected convergence time this simulation was not attempted in the current work.

A final issue addressed by our work is the isomerization of glutamate side-chains in the EEEE-ring that we discuss in detail in the ESI.‡ In their work on NavAb Chakrabarti et al.²³ reported a dunking of E177 side-chains bringing their carboxylate groups from out-facing to protruding into the lumen. This finding was only partially confirmed by Ke et al.,¹⁹ who observed a shift from −70° to 45° of the χ₂ angle of E177 only in the presence of calcium while the SF remained rigid in the presence of sodium. In our simulations on NaChBac the side-chains of E191 are initially oriented towards the extracellular bath and subsequently bend toward the interior of the channel. We observed this behavior in the presence of both sodium and calcium, but in the latter case the shift between χ₂ = −75° and χ₂ = 50° is more evident and can be clearly correlated to the entrance of the Ca²⁺ ion. When NaChBac is simulated at equilibrium in a NaCl solution the SF is always occupied by at least two Na⁺ ions and the glutamate side-chains spend more time in the χ₂ = 50° orientation to coordinate the resident sodium ions. Overall, this conformational rearrangement might represent a shift between a conformation favouring the capture of cations in the bulk and another conformation stabilizing the ions in the SF. Indeed, by this movement the side chains of the EEEE-ring might actually chaperon the incoming cation to its most stable binding sites.

Notes

Data related to this research are openly available from the University of Warwick archive at http://wrap.warwick.ac.uk/92905.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors gratefully acknowledge financial support from EPSRC (grant EP/M016889/1 and EP/M015831/1). Project: Ionic Coulomb blockade oscillations and the physical origins of permeation, selectivity, and their mutation transformations in biological ion channels. Computational facilities were provided by the MidPlus Regional Centre of Excellence for Computational Science, Engineering and Mathematics, under EPSRC grant EP/K000128/1, and by the University of Warwick Scientific Computing Research Technology Platform.

References

1. B. Hille, Ionic Channels of Excitable Membranes, Sinauer, Sunderland, MA, 3rd edn, 2001.
2. S. England and M. J. de Groot, Br. J. Pharmacol., 2009, 158(6), 1413–1425.
3. A. Mike and P. Lukacs, Curr. Mol. Pharmacol., 2010, 3(3), 129–144.
4. R. Koishi, H. Xu, D. Ren, B. Navarro, B. W. Spiller, Q. Shi and D. E. Clapham, J. Biol. Chem., 2004, 279(10), 9532–9538.
5. J. Payandeh, T. Scheuer, N. Zheng and W. A. Catterall, Nature, 2011, 475, 353–358.
6. H. Terlau, S. H. Heinemann, W. Stühmer, M. Pusch, F. Conti, K. Imoto and S. Numa, FEBS Lett., 1991, 293(1–2), 93–96.
7. S. H. Heinemann, H. Terlau, W. Stühmer, K. Imoto and S. Numa, Nature, 1992, 356(6368), 441–443.
8. D. Ren, B. Navarro, H. Xu, L. Yue, Q. Shi and D. E. Clapham, Science, 2001, 294, 2372–2375.
9. L. Yue, B. Navarro, D. Ren, A. Ramos and D. E. Clapham, J. Gen. Physiol., 2002, 120, 845–853.
10. J. Cichelli and I. Zharov, J. Am. Chem. Soc., 2006, 128(25), 8130–8131.
11. Y. Caspi, D. Zbalda, H. Cohen and M. Elbaum, Nano Lett., 2008, 8(11), 3728–3734.
12. F. Bezanilla and C. F. Armstrong, J. Gen. Physiol., 1972, 60, 588–608.
13. B. Roux, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 153–171.
14. G. Eisenman and R. Horn, J. Membr. Biol., 1983, 76, 197–225.
15. B. Corry, MRS Bull., 2017, 42, 306–310.
16. B. Corry and M. Thomas, J. Am. Chem. Soc., 2012, 134, 1840–1846.
17. D. Boda, M. Valisko, D. Henderson, B. Eisenberg, D. Gillespie and W. Nonner, J. Gen. Physiol., 2009, 133(5), 497–509.
18. B. Corry, PeerJ, 2003, 1, e16.
19. S. Ke, E.-M. Zangerl and A. Stary-Weinzinger, Biochem. Biophys. Res. Commun., 2013, 430, 1272–1276.
20. A. F. Barber, V. Carnevale, S. G. Raju, C. Amaral, W. Treptow and M. L. Klein, Biochim. Biophys. Acta, 2012, 1818, 2120–2125.
21. R. K. Finol-Urdaneta, Y. Wang, A. Al-Sabi, C. Zhao, S. Y. Noskov and R. J. French, J. Gen. Physiol., 2014, 143(2), 157–171.
22. C. Guardiani, P. M. Rodger, O. A. Fedorenko, S. K. Roberts and I. A. Khovanov, J. Chem. Theory Comput., 2017, 13, 1389–1400.
23. M. Chakrabarti, C. Ing, J. Payandeh, N. Zheng, W. A. Catterall and R. Pomes, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(28), 11331–11336.
24. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
25. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
26. C. J. Dickson, B. D. Madej, A. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879.
27. G. M. Bradbrook, T. Gleichmann, S. J. Harrop, J. Habash, J. Raftery, J. Kalb, J. Yariv, I. H. Hillier and J. R. Helliwell, J. Chem. Soc., Faraday Trans., 1998, 94(11), 1603–1611.
28. A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603.
29. N. Gamper, J. D. Stockand and M. S. Shapiro, J. Pharmacol. Toxicol. Methods, 2005, 51, 177–185.
30. P. G. DeCaen, Y. Takahashi, T. A. Krulwich, M. Ito and D. E. Clapham, eLife, 2014, 3, e04387.
31. E. Neher, Methods Enzymol., 1992, 207, 123–131.
32. P. S. R. Ganesh, B. Chanda, S. K. Gupta, M. K. Mathew and J. Chandrasekhar, Proteins: Struct., Funct., Genet., 2000, 38, 384–392.
33. B. Hille, J. Gen. Physiol., 1972, 59(6), 637–658.
34. Y. M. Sun, I. Favr, L. Schild and E. Moczydlowski, J. Gen. Physiol., 1997, 110(6), 693–715.
35. Y. Zhao, T. Scheuer and W. A. Catterall, Proc. Natl. Acad. Sci. U. S. A., 2004, 101(51), 17873–17878.
36. C. Chipot and A. Pohorille, Free Energy Calculations, ed. C. Chipot and A. Pohorille, Springer-Verlag Berlin, Heidelberg, 2007, ch. 2.
37. J. Wang, Y. Deng and B. Roux, Biophys. J., 2006, 91, 2798–2814.
38. X. Zhang, W. Ren, P. DeCaen, C. Yan, X. Tao, L. Tang, J. Wang, K. Hasegawa, T. Kumasaka, J. He, J. Wang, D. E. Clapham and E. Yan, Nature, 2012, 486(7401), 130–134.
39. P. Hess and R. W. Tsien, Nature, 1984, 309, 453–456.
40. A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045.
41. D. Di Tommaso, E. Ruiz-Agudo, N. H. de Leeuw, A. Putnis and C. V. Putnis, Phys. Chem. Chem. Phys., 2014, 16, 7772–7785.
42. E. C. McCusker, C. Bagneris, C. E. Naylor, A. R. Cole, N. D'Avanzo, C. G. Nichols and B. A. Wallace, Nat. Commun., 2012, 3, 1102.
43. D. Shaya, F. Findeisen, F. Abderemane-Ali, C. Arrigoni, S. Wong, S. R. Nurva, G. Loussouarn and D. L. Minor Jr., J. Mol. Biol., 2014, 426, 467–483.
44. C. Bagneris, C. E. Naylor, E. C. McCusker and B. A. Wallace, J. Gen. Physiol., 2015, 145(1), 5–16.
45. Y. Shafrir, S. R. Durell and H. R. Guy, Biophys. J., 2008, 95, 3650–3662.
46. Z. Xiang, Curr. Protein Pept. Sci., 2006, 7(3), 217–227.
47. D. Baker and A. Sali, Science, 2001, 294, 93–96.

---

Footnotes

† We dedicate the paper to the memory of Mark P Rodger who passed away in March 2017. We are greatly indebted to him for contributions to our research.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05928k

§ These authors contributed equally to this work.

---