Quantitative DFT modeling of product concentration in organometallic reactions: Cu-mediated pentafluoroethylation of benzoic acid chlorides as a case study

Abstract

DFT calculations are widely used for computing properties, reaction mechanisms and energy profiles in organometallic reactions. A qualitative agreement between the experimental and the calculated results seems to usually be enough to validate a computational methodology but recent advances in computation indicate that a nearly quantitative agreement should be possible if an appropriate DFT study is carried out. Final percent product concentrations, often reported as yields, are by far the most commonly reported properties in experimental metal-mediated synthesis studies but reported DFT studies have not focused on predicting absolute product amounts. The recently reported stoichiometric pentafluoroethylation of benzoic acid chlorides (R-C₆H₄COCl) with [(phen)Cu(PPh₃)C₂F₅] (phen = 1,10-phenanthroline, PPh₃ = triphenylphosphine) has been used as a case study to check whether the experimental product concentrations can be reproduced by any of the most popular DFT approaches with high enough accuracy. To this end, the Gibbs energy profile for the pentafluoroethylation of benzoic acid chloride has been computed using 14 different DFT methods. These computed Gibbs energy profiles have been employed to build kinetic models predicting the final product concentration in solution. The best results are obtained with the D3-dispersion corrected B3LYP functional, which has been successfully used afterwards to model the reaction outcomes of other simple (R = o-Me, p-Me, p-Cl, p-F, etc.) benzoic acid chlorides. The product concentrations of more complex reaction networks in which more than one position of the substrate may be activated by the copper catalyst (R = o-Br and p-I) are also predicted appropriately.

---

Introduction

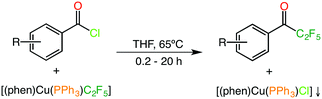
DFT calculations have become a powerful tool and are nowadays widely used in many fields including organometallic, catalysis and coordination chemistry studies.¹ The synergistic application of experiment and calculations has also evolved with time, allowing the development of both fields and producing results that would be hardly achievable by any of the isolated techniques alone. In this sense, DFT calculations have started corroborating experimental results in a post-experimental manner, e.g. in determining reaction mechanisms and selectivities when rational chemical intuition and mechanistic experimental techniques have been exhausted. More recently, computations have started to be used in concert with experiments or even prior to them, taking the lead in the discovery of new reactions and chemical systems.² In most cases a qualitative agreement between experiments and calculations seems to be enough to validate the results, probably because a quantitative agreement is much more difficult – or even impossible – to achieve. Nevertheless, thorough computational DFT explorations, usually including benchmarking processes,³ have been reported to reach a nearly quantitative agreement in predicting properties as complex as the spin crossover transition temperatures of metal complexes,⁴ the enantiomeric excess of organic reactions,⁵ and the Gibbs energy profiles,⁶ reaction barriers⁷ and energy spans⁸ for organometallic catalytic reactions, thus establishing the foundations for the computational quantitative prediction of other relevant chemical properties. One of the most important quantities in chemistry is the reaction yield of a process, which is by far the most usually reported result in organometallic and homogeneous catalysis studies. In these reports, the yield often adopts the form of percent concentration of the final product instead of the real isolated amount of product. To date, no method has been published to computationally allow the reproduction of the final product concentrations, and thus a direct way of comparing the experimental data with a computed Gibbs energy profile does not seem evident, although both magnitudes are closely related through kinetics. Simple kinetics is all that is needed to obtain the transient concentration of any species (or the final yield of a product) involved in a reaction from the corresponding Gibbs energy profile. In practice, converting the Gibbs energy profiles into rate constants, and then employing those to build a kinetic model that simulates an experimental reaction run can do this. Having a computational method that reproduces the experimental outcome of a reaction could also allow making predictions for other substrates and similar catalytic systems, and could be a useful tool for validating a reaction mechanism. Of course, this is a complex procedure given that the relationship between the computed Gibbs energy profiles and the rate constants, those determining the concentration of the species over time, is exponential, which means that the calculations have to be extremely accurate. This study explores whether the experimental reaction concentrations in solution can be reproduced by the most typical DFT approaches with enough accuracy. The copper-mediated pentafluoroethylation of benzoic acid chlorides reported by Grushin et al.⁹ has been chosen as a suitable test case (Scheme 1). In this reaction, the mixed [(phen)Cu(PPh₃)C₂F₅] (phen = 1,10-phenanthroline, PPh₃ = triphenylphosphine) reagent is employed to efficiently fluoroalkylate a broad variety of benzoic acid chlorides. This copper complex has been experimentally obtained by reacting “ligandless” CuC₂F₅ in the presence of PPh₃ and 1,10-phenanthroline, and has been structurally characterized by X-Ray diffraction. THF is a convenient solvent for this reaction because the [(phen)Cu(PPh₃)Cl] by-product is poorly soluble and precipitates out as the pentafluoroethylation occurs.

Scheme 1 Cu-Mediated pentafluoroethylation of benzoic acid chlorides.

This reaction seems to be an ideal candidate for checking the performance of computational chemistry by modeling the final product concentrations because (i) it is a stoichiometric reaction and thus no catalyst recycling has to be taken into account, although technically this should not be a problem, (ii) no by-products other than [(phen)Cu(PPh₃)Cl] are obtained, which implies that competing pathways leading to stable alternative intermediates can be ruled out, (iii) the reaction mechanism leading to the final product has been proposed to simply consist of an oxidative addition/reductive elimination sequence, while a radical mechanism has been discarded by experimental evidence, and (iv) the final product concentration of product is not the usual isolated yield but that measured by in situ¹⁹F-NMR, ensuring the accuracy of the collected data (usually below 5% error). In all cases, the experimentally reported yield corresponds to the percentage concentration of the corresponding pentafluoroethylated product in solution.

The adopted computational approach mimics the methodology usually employed in experimental metal-mediated studies. First, a functional screening is carried out aiming to find the best computational settings for reproducing the results obtained in the pentafluoroethylation of benzoic acid chloride. To this end, several density functionals have been tested following the standard techniques employed in computational homogeneous catalysis studies. After that, the methodology providing the best results is applied to other substrates, i.e. mono- and polysubstituted benzoic acid chlorides in order to check its performance in reactions with increasing complexity. Of course, carrying out a more complete screening of methods (with other density functionals, different basis sets, etc.) is possible but lies beyond the aim of this work. In contrast, this report focuses on demonstrating that good results can be obtained with a computationally affordable methodology.

Computational details

All the structures have been fully optimized in tetrahydrofuran (PCM, see below) using the Gaussian09¹⁰ suite of programs with 14 different functionals: BP86,¹¹ B3LYP,¹² CAM-B3LYP,¹³ B3PW91,^12c,14 PBE,¹⁵ LC-wPBE,¹⁶ PBE0,^15,17 TPSS,¹⁸ B97D,¹⁹ wB97xD,²⁰ M06-L,²¹ MN12SX,²² M06²³ and M06-2X.²³ In the optimization process, the standard 6-31G*²⁴ basis set is used for all H, C, N, O, F, P and Cl atoms while the Stuttgart triple zeta basis set (SDD),²⁵ along with the associated ECP to describe the core electrons, has been employed for Cu, Br and I. Tight convergence criteria as well as ultrafine integration grids have been used in order to ensure satisfactory convergence. This is necessary because some of the species under study present a number of low frequency vibrational modes (<100 cm⁻¹) that contribute significantly to the entropy and have to be properly computed. In all cases, the solvation energies are computed with the (IEF-PCM)²⁶ continuum dielectric solvation model using the SMD²⁷ radii and non-electrostatic terms. The dispersion correction terms have been included in the optimization process, except for B97D, wB97xD and MN12SX, by using the D3 method of Grimme.²⁸ These computational settings are named BS1. In all cases, frequency calculations are carried out to ensure the nature of stationary points and transition states. During the reviewing process of this work, one of the referees suggested computing at least one example without including the dispersion correction. Thus, the pentafluoroethylation of benzoic acid chloride has been computed using the B3LYP functional without dispersion. As should be expected, the computed reaction profile is seriously affected whenever two molecules come together or one molecule splits into two fragments. The Gibbs energies obtained with these calculations produce a very large energy barrier that indicates the reaction should not work under the experimental conditions, demonstrating the importance of including the dispersion correction. Details about these calculations can be found in the ESI† (Table S1). Additional single point calculations, including solvation and dispersion corrections, on the optimized geometries for each functional are employed to obtain improved Gibbs energy values with larger basis sets (BS2). The aug-cc-pVTZ-PP²⁹ basis set including polarization and the associated electron core potential has been employed for Cu, Br and I while the 6-311+G**^24c,30 all-electron basis set is used for all the other atoms. Single point calculations with the DLNPO-CCSD(T)³¹ method have been carried out in selected cases for validating the accuracy of the DFT functionals. The ORCA³² package has been employed to run these calculations with two different basis sets: def2-TZVPP³³ and aug-cc-pVTZ,³⁴ and their corresponding auxiliary Coulombic counterparts.³⁵ The computed Gibbs energies have been corrected to use a standard state corresponding to species in solution with a standard concentration of 1 M. Unless otherwise stated, all the Gibbs energy values in the text correspond to those computed with the larger basis sets BS2 including PCM-SMD solvation and the D3 dispersion terms at 65 °C. The detailed procedure to obtain these Gibbs energy values is described in the ESI.†

The construction of the kinetics simulations has been done with the COPASI³⁶ software. The rate constants of all the forward and backward steps in the catalytic cycle have been extracted from the computed DFT energy differences using the methodology described in the ESI.† These rate constants have been fed into the kinetic models, which use the simple mass action law to describe the reaction and allow the calculation of the transient concentrations at different times. The detailed procedure to obtain the rate constants is described in the ESI.†

Results and discussion

As mentioned above, the experimental observations suggest that the pentafluoroethylation of benzoic acid chloride follows a catalytic oxidative addition/reductive elimination sequence like the one shown in Scheme 2. In order to check the validity of this proposal, the chemical species along this catalytic cycle and other alternative options have been computed with the B3LYP functional.

Scheme 2 Detailed mechanism for the Cu-mediated pentafluoroethylation of benzoic acid chloride (relative Gibbs energy values (in kcal mol⁻¹) has been obtained with the B3LYP functional, NN ligand = phen).

In the proposed catalytic cycle, the reaction starts with the dissociation of the phosphine ligand from the coordinatively saturated copper(I) complex [(phen)Cu(PPh₃)C₂F₅] (I) to form the tricoordinated complex II. This step is slightly endergonic by +4.8 kcal mol⁻¹. A plausible transition state for this process has been sought and not found; however, a linear transit exploration of the associated reaction coordinate, i.e. the elongation of the Cu–P bond, reveals that the energy goes up steadily in the transformation of I into II, ruling out the possibility of having a transition state governing this step (Fig. S1, ESI†). The benzoic acid chloride then comes in to form intermediate III. The interplay between the substrate and the metal is quite subtle and a direct strong interaction of the carbonyl group with the copper was not found in any case (nor with other functionals). In fact, this complex seems to be stabilized by two factors. The first one corresponds to a π-stacking interaction between the phenanthroline ligand and the aromatic ring of the benzoic acid chloride. The second interaction is a short contact (around 2.4 Å) between one of the fluorine atoms of the pentafluoroethyl group and one of the hydrogen atoms of the benzoic acid chloride. This process is also endergonic but the overall energy required to get to this intermediate (+6.0 kcal mol⁻¹) is still acceptable. The approach of the substrate to the copper complex is not subject to an energy barrier and is more likely to be controlled by diffusion processes. Other activation pathways could also be plausible at these initial stages; these should involve a single electron transfer (SET) between the substrate and the copper(I) complexes I or II. Nevertheless, these processes have been discarded by experiments and should not play a crucial role in the reaction mechanism. Indeed, the computed Gibbs energies for these SET steps between benzoic acid chloride plus I and II are +44.0 and +46.8 kcal mol⁻¹, respectively; completely blocking these radical pathways. Once III is formed, the oxidative addition of the C–Cl bond onto the copper center, controlled by the corresponding transition state (OATS), takes place. This process, which leads to the formation of the copper(III) complex IV, has an affordable barrier of 22.3 kcal mol⁻¹. In complex IV, the copper center adopts a square pyramidal structure with one of the nitrogen atoms of the phenanthroline ligand occupying the axial position while the incoming chloride and carbonyl substituent are placed cis to each other in the equatorial plane. Other oxidative addition transition states have been computed in order to explore the possibility of reaching other copper(III) isomers related to IV. Unfortunately, those complexes have been found to be much higher in energy or to evolve during optimization to complexes where the chloride and the carbonyl groups are placed trans to each other, which should not be possible. The dissociation of chloride during the oxidative addition process, which should generate the positively charged intermediate [(phen)Cu(C₂F₅)(COC₆H₅)]⁺, also seems unlikely since this complex lies at +25.8 kcal mol⁻¹, even higher than OATS. The Gibbs energy of the triplet-state copper(III) structure analogous to IV is more than 20 kcal mol⁻¹ higher in energy (overall +32.0 kcal mol⁻¹) than the singlet species and thus this pathway can be safely discarded. All in all, it seems that the only plausible copper(III) intermediate for the reaction to proceed happens to be complex IV. From there, the C–C₂F₅ reductive elimination, governed by the corresponding transition state RETS, produces the pentafluoroethylated ketone. This stage requires an overall Gibbs energy investment of 25.8 kcal mol⁻¹ and is the highest point along the catalytic cycle. After the reductive elimination, the product remains, as in complex III, weakly bound to the metal fragment [(phen)CuCl] (V). At this point, the relative Gibbs energy value has already become negative (−10.8 kcal mol⁻¹) probably because of the new C–C bond formation. The final product PhCOC₂F₅ then dissociates to form complex VI and is replaced by PPh₃, which produces the insoluble [(phen)Cu(PPh₃)Cl] (VII) compound. These two steps are exergonic by 7.3 and 6.5 kcal mol⁻¹, respectively, and very likely to be controlled by diffusion. The computed Gibbs energies indicate that the reaction barrier for the whole pentafluoroethylation process is 25.8 kcal mol⁻¹, calculated as the energy difference between the starting materials and the reductive elimination transition state (RETS). This barrier seems quite right for a relatively slow reaction that provides a 95% conversion in 18 hours at 65 °C (see below). The proposed mechanism shown in Scheme 2 complies with the experimental observations: (1) it consists of an oxidative addition/reductive elimination sequence, (2) radical processes, such as a single electron transfer between the initial catalyst (or complex II) and benzoic acid chloride, or the formation of triplet-state copper(III) species, are not possible and (3) the only products obtained are [(phen)Cu(PPh₃)Cl] and the pentafluoroethylated ketone. These results indicate that the proposed mechanism should be the one governing the pentafluoroethylation of benzoic acid chloride with [(phen)Cu(PPh₃)C₂F₅]. Therefore, the reaction sequence shown in Scheme 2 was fully computed with 13 additional density functionals, and their corresponding Gibbs energies at 65 °C are shown in Table 1.

Table 1 Computed Gibbs energy profiles (in kcal mol⁻¹) for the Cu-mediated pentafluoroethylation of benzoic acid chloride with different functionals

Functional	I	II	III	OATS	IV	RETS	V	VI	VII
BP86	0.0	13.0	10.6	22.2	9.3	25.2	3.2	−6.7	−20.3
B3LYP	0.0	4.8	6.0	22.4	11.0	25.8	−10.8	−18.1	−24.6
CAM-B3LYP	0.0	3.8	6.5	22.5	13.1	27.2	−13.6	−21.6	−27.3
B3PW91	0.0	9.4	8.9	24.0	12.6	26.5	−5.7	−14.2	−26.1
PBE	0.0	9.2	10.3	19.3	9.1	24.6	−3.9	−10.8	−19.5
LC-wPBE	0.0	9.5	9.5	27.5	16.8	30.1	−9.9	−16.6	−26.7
PBE0	0.0	6.9	7.8	21.8	12.7	25.7	−12.6	−18.7	−27.0
TPSS	0.0	8.7	9.9	21.0	5.8	22.8	−2.6	−10.0	−19.7
B97D	0.0	4.3	4.3	19.7	10.6	24.0	−5.3	−13.8	−21.1
wB97xD	0.0	5.8	7.0	24.3	16.9	29.0	−12.2	−20.1	−26.2
M06-L	0.0	9.9	9.7	19.2	3.8	19.7	−7.6	−15.4	−23.1
MN12SX	0.0	0.3	2.7	18.8	1.7	21.6	−13.8	−22.0	−23.7
M06	0.0	8.8	7.4	22.7	13.7	26.3	−7.7	−15.0	−23.7
M06-2X	0.0	2.1	2.8	23.6	20.9	22.3	−19.7	−28.0	−28.7

---

The shape of the Gibbs energy profiles is similar for all the functionals tested. The relative Gibbs energies go up from I to III; the tricoordinated copper complex II normally lies in between those two values although in some cases, e.g. BP86 and B3PW91, this order is reversed. The Gibbs energy then rises to overcome the oxidative addition transition state (OATS), goes down when intermediate IV is formed and rises again to jump over the reductive elimination transition state (RETS). In the last steps, i.e.V, VI and VII, the Gibbs energy goes successively down. In most cases, the overall reaction barrier corresponds to the Gibbs energy difference between the starting materials (I) and the reductive elimination transition state (RETS); the only exception is the M06-2X functional, with which the oxidative addition transition state (OATS) is 1.3 kcal mol⁻¹ higher in energy than RETS. The values of the energy barriers span across more than 10 kcal mol⁻¹, with M06-L and LC-wPBE showing the lowest (19.7) and highest (30.1) values, respectively. In general, the lowest barriers are obtained with the pure functionals (M06-L, TPSS), while the hybrid functionals (B3PW91, M06) tend to produce higher values. It has to be noted that the three long-range corrected functionals tested: CAM-B3LYP, LC-wPBE and wB97xD, provide the highest reaction barriers (27.2, 30.1 and 29.0 kcal mol⁻¹, respectively). With the computed Gibbs energy profiles in hand, a comparison with the experimental results should be possible. Unfortunately, the Gibbs energy of activation for the pentafluoroethylation of benzoic acid chloride was not measured in the original report. The only available data are the concentration in solution of the final product, which was measured by in situ¹⁹F-NMR. Thus, in order to establish a comparison between the experimental and computed data, the theoretical Gibbs energy profiles have been converted into rate constants that are, in turn, transformed into a product concentration by a kinetic model. The reaction mechanism shown in Scheme 2 is composed of two different kinds of processes, and their corresponding rate constant types have to be computed differently (see ESI† for details). Reaction stages proceeding without a barrier – the associative and dissociative steps – are assumed to proceed under diffusion control and their rate constants are estimated as in previous reports.⁶ Under these conditions, the rate constant for the associative process is computed as k = 8k_BT/3η, where k_B is Boltzmann's constant, T is the temperature, N_A is Avogadro's number and η is the solvent viscosity at that temperature.³⁷ For tetrahydrofuran at 65 °C and 1 atm, η has been estimated to be 0.308 mPa s, yielding a diffusion-controlled rate constant of 2.433 × 10¹⁰ M⁻¹ s⁻¹. The corresponding dissociative rate constants are easily obtained through the formulation of the thermodynamic equilibrium constant K and the computed Gibbs energy difference between the intermediates involved. In contrast, the rate constants of all the steps governed by a transition state are computed with the Eyring–Polanyi equation: k = (k_BT/h)exp(−ΔG^‡/RT), where k_B is Boltzmann's constant, T is the temperature, h is Planck's constant, ΔG^‡ is the activation Gibbs energy and R is the gas constant. The forward (k_f) and backward (k_b) rate constants are computed independently using their corresponding activation energies. The computed rate constants extracted from the Gibbs energy profile are fed to the COPASI program along with the reaction conditions, e.g. starting concentrations of the species, reaction time, etc., and the kinetic models are built. 14 kinetic models, one for each density functional method present in Table 1, were then simulated to run for 18 hours. The transient concentration of the PhCOC₂F₅ product obtained with each functional is shown in Fig. 1. As expected, the density functional methods having lower barriers produce a faster generation of the pentafluoroalkylated ketone product. It may be observed that none of the employed functionals provides a perfectly accurate result; this is not completely surprising given that the relationship between some of the rate constants and the activation energies is exponential. Therefore, a small deviation in the Gibbs energy calculation implies a large error in the computed product concentration. In addition, the Eyring–Polanyi equation derives from the transition state theory (TST), which is an approximate theory and is obtained making a series of assumptions that are far from being fulfilled in many cases. This implies that applying TST for computing product concentrations may also introduce some errors in the final outcome. In order to avoid these problems, molecular dynamic simulations could be used; however, these types of calculations are more computationally expensive than DFT.

Fig. 1 Computed concentration (%) of PhCOC₂F₅ over time obtained with different DFT methods. The dashed line indicates the experimental final concentration (90%) obtained in an 18 hour run.

Even so, some of the hybrid functionals (PBE0, B3LYP and M06) produce remarkably close results (93, 92 and 87%, respectively) to those obtained in the experiments (90% in 18 hours). The computed barriers for these three functionals are quite close and the difference between the B3LYP and M06 values is only 0.5 kcal mol⁻¹. The barrier for the experimental system seems to correspond to an average value between those two, e.g. raising the B3LYP RETS to 26.0 kcal mol⁻¹ produces a product concentration of exactly 90%. In contrast, the pure functionals produce very fast reactions that yield more than 90% of the pentafluoroethylated product in less than 3 hours, e.g. M06-L, MN12SX, TPSS, B97D and PBE. Although M06-2X accounts for the highest amount of Hartree–Fock exchange (54%), and should be expected to be slower than the rest of the hybrid functionals, it produces quite a low barrier and, in consequence, a very fast reaction. In the end, it seems that this functional is not describing the system properly, as could be deduced from the relative Gibbs energies obtained for OATS, IV and RETS: 23.6, 20.9 and 22.3 kcal mol⁻¹, respectively. The BP86 and B3PW91 functionals are too fast (96%) and too slow (84%), respectively, although their barriers differ by just 1.3 kcal mol⁻¹. On the other hand, the long-range corrected functionals, CAM-B3LYP, LC-wPBE and wB97xD, display very high barriers of 27.2, 31.0 and 29.0 kcal mol⁻¹, respectively, which imply very slow reactions and a much lower final concentration (73, 16 and 32%) than the one reported experimentally. In order to check the overall accuracy of the functionals tested, the Gibbs energies of the whole catalytic cycle were recomputed using higher level DLNPO–CCSD(T) calculations with two different basis sets: def2-TZVPP and aug-cc-PVTZ. The accuracy of DLPNO-CCSD(T) has been assessed on either full CCSD(T) or experimental sets of data, including transition metal-mediated reactions.³⁸ The geometries cannot be reoptimized when using this methodology because a large amount of time would be needed; therefore, the structures obtained with the B3LYP functional, the ones giving closer results to the experiments, have been used as input for these calculations. The computed Gibbs energy profiles obtained with this methodology can be found in Table S2 (ESI†). As before, the highest barrier for the DLNPO-CCSD(T) computed profiles corresponds to the Gibbs energy difference between the starting materials (I) and the reductive elimination transition state (RETS): 25.2 and 25.4 kcal mol⁻¹ for the calculations employing the def2-TZVPP and aug-cc-PVTZ basis sets, respectively. The final product concentrations derived from these Gibbs energy profiles are 96% and 93%, slightly higher than those found with the lower level DFT approach. These results, which are very similar to the ones found above, validate the usage of the DFT methodologies for studying the pentafluoroethylation reaction of benzoic acid chloride and indicate that the reactivity for other related substrates could be predicted by using the same approach. B3LYP is the functional of choice for all the subsequent studies since it gives the most accurate prediction for the reaction of benzoic acid chloride and, in addition, is faster and shows a better convergence than PBE0 and M06.

Thus, the B3LYP functional has been used to compute the Gibbs energy profile and the product concentration in solution for the pentafluoroethylation reaction of different monosubstituted benzoic acid chlorides (Table 2 and Table S3 in the ESI†). These substrates include a variety of substituents in different ring positions. The computed Gibbs energy profiles for all the explored substrates display the same pattern found for the benzoic acid chloride; the Gibbs energy rises from I to OATS, drops when IV is formed and then rises again to surpass the reductive elimination barrier (RETS), which is again the highest point along the reaction pathway. After that, the energy goes subsequently down with the formation of V, VI plus the pentafluoroethylated ketone and VII. The experimental and computed product concentrations obtained in the pentafluoroethylation of monosubstituted benzoic acid chlorides are shown in Table 2.

Table 2 Experimental and computed product concentrations obtained in the pentafluoroethylation of monosubstituted benzoic acid chlorides

Substrate	Time (h)	Exp. (%)	Calc. (%)
a Reaction carried out at room temperature.
C6H5COCl	18	90	92
C6F5COCl^a	10 minutes	85	68
o-F-C6H4COCl	1.5	95	90
p-F-C6H4COCl	3	93	90
o-Cl-C6H4COCl	6	95	88
p-Cl-C6H4COCl	3	92	85
o-Me-C6H4COCl	6	90	95
p-Me-C6H4COCl	18	93	85
m-CF3-C6H4COCl	2	94	92
p-MeO-C6H4COCl	20	81	87

---

It may be noted that, although the results are not perfect, quite a good agreement is found for practically all the studied systems. The highest deviation is found for pentafluorobenzoic acid chloride (C₆F₅COCl), the difference between the computed and experimental product concentrations is 17%, in favor of the latter. This substrate has a computed Gibbs energy barrier as low as 21.1 kcal mol⁻¹ that seems to be, however, insufficiently low to correctly predict the final outcome of the reaction. It has to be noted, though, that the time lapse for this reaction is very short (600 s) and thus a small deviation in the Gibbs energies may have a higher impact on the computed concentrations. The errors found for the rest of the substrates are lower and range between 2–8%. In most cases, the final computed concentrations in solution are slightly lower than those found experimentally, indicating that the calculated Gibbs energy profiles produce higher barriers than the ones associated with the experiments. On the other hand, the computed concentrations for the electron-rich o-methyl and p-methoxy substrates are found to be higher than the experimental ones, which means that the computed barriers are lower than they should be. This is not a general result for this kind of substrate since p-methylbenzoic acid chloride shows the reverse behavior. The best agreement is found for m-trifluoromethylbenzoic acid, which displays just a 2% error. The errors associated with these calculations of the Gibbs energy barriers are quite low and well within the intrinsic uncertainty related to the DFT method employed. The “real” activation barriers, those needed to exactly match the experimental results, were estimated as above by adjusting the height of the relative Gibbs energy of RETS for each substrate. The mean error between all the computed and estimated “real” barriers is just 0.6 kcal mol⁻¹, with a maximum value of 1.1 kcal mol⁻¹ for C₆F₅COCl. These results clearly confirm that the methodology employed is on the right track and demonstrate that concentrations in solution for a given reaction can be accurately computed with DFT methods.

The same methodology can be successfully applied to reactions involving substrates with more than one reactive position, i.e. o-BrC₆H₄COCl and p-IC₆H₄COCl (Scheme 3). For those substrates, there are two pathways leading to three different pentafluoroethylated products, where C₂F₅ replaces the acid chloride (P1), the halide on the ring (P2) or both (P3). Each of these processes involves a similar reaction sequence as the one described above, a complete schematic description of these reactions and the associated Gibbs energy profiles can be found in Schemes S1, S2 and Table S4 in the ESI.†

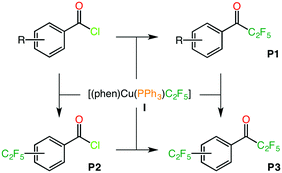Scheme 3 Possible products generated in the pentafluoroethylation of o-BrC₆H₄COCl and p-IC₆H₄COCl with complex I.

The Gibbs energy profile network obtained for these substrates is more complex than those obtained with the simple benzoic acid chlorides but the general shape for each individual pentafluoroethylation process remains, i.e. the Gibbs energy goes up from the starting complex to the corresponding oxidative addition transition state, then goes down when the copper(III) intermediate is formed, and rises again to jump over the reductive elimination transition state, which is in all cases the highest point along the reaction coordinate. The comparison between the experimental and computed final product concentrations for the pentafluoroethylation of o-BrC₆H₄COCl and p-IC₆H₄COCl with complex I can be found in Table 3. The computed substrate and product transient concentrations are shown in Fig. 2. In the case of p-IC₆H₄COCl, two different experiments were reported and both have been studied. In the first one, the reaction conditions were kept the same as above. In contrast, the second experiment was carried out with 0.5 equivalents of para-iodobenzoic acid chloride.

Table 3 Experimental and computed product concentrations for the pentafluoroethylation of o-BrC₆H₄COCl and p-IC₆H₄COCl

Substrate	Time (h)	Product	Exp. (%)	Calc. (%)
a With 0.5 equivalents of p-I-C6H4COCl.
o-BrC6H4COCl	3	o-BrC6H4COC2F5	50	59
		o-C2F5C6H4COCl	10	11
		o-C2F5C6H4COC2F5	15	9
p-IC6H4COCl	1	p-IC6H4COC2F5	21	26
		p-C2F5C6H4COCl	14	5
		p-C2F5C6H4COC2F5	30	27
p-IC6H4COCl^a	4	p-IC6H4COC2F5	n/a	16
		p-C2F5C6H4COCl	n/a	1
		p-C2F5C6H4COC2F5	72	74

---

Fig. 2 Computed concentrations of complex I (orange), substrate (blue, X = o-Br, p-I) and products (P1 = red, P2 = green and P3 = purple) for the pentafluoroethylations of o-BrC₆H₄COCl and p-IC₆H₄COCl. (*0.5 equivalents of p-IC₆H₄COCl.)

The agreement between the experimental and calculated product concentrations is quite good for both substrates. In the case of o-BrC₆H₄COCl, the major product of the reaction is o-BrC₆H₄COC₂F₅ (P1) while the concentration of the other pentafluoroethylated products remain around 10% (Fig. 2, left). The Gibbs energy barrier computed for each pentafluoroethylation process provides a qualitative interpretation of these results (Scheme 4, left). As may be observed, the barrier leading to o-BrC₆H₄COC₂F₅ (P1) is relatively low (25.5 kcal mol⁻¹) and thus this product is the fastest one to appear; however, getting to P3 from P1 is much more complicated since the energy barrier governing this transformation is higher (26.9 kcal mol⁻¹). This implies that P1, once formed, remains stable in the reaction medium and only a minor amount of it would be transformed into P3 over time. On the other hand, the barrier leading to o-C₂F₅C₆H₄COCl (P2) is slightly higher than the one leading to P1, and thus P2 is obtained as the minor product in the competition for the first pentafluoroethylation process.

Scheme 4 Computed Gibbs energy barriers (in kcal mol⁻¹) for the pentafluoroethylation processes of o-BrC₆H₄COCl (left) and p-IC₆H₄COCl (right).

The barrier connecting P2 and P3 has practically the same height and indicates that this transformation should be also slow. The difference in height between the P1 → P3 and P2 → P3 barriers seems to indicate that most of the o-C₂F₅C₆H₄COC₂F₅ (P3) should be obtained from P2. However, the kinetic model states that 72% (6.5% overall) of P3 comes from P1; this is probably because the amount of this latter product is always in a higher concentration than that of P2 and thus the transformation of P1 into P3 has a higher probability of occurring. In the case of p-IC₆H₄COCl, the barriers for the first pentafluoroethylation processes, i.e. those leading to p-IC₆H₄COC₂F₅ (P1) and p-C₂F₅C₆H₄COCl (P2), are practically the same, indicating that both products should be formed equally fast. However, the barriers leading to p-C₂F₅C₆H₄COC₂F₅ (P3): P1 → P3 and P2 → P3, differ by more than 1 kcal mol⁻¹ in favor of the latter, which is also lower than the barriers for the first pentafluoroethylation stages. This explains why the amount of P1 remains always higher than that of P2; the low P2 → P3 barrier states that P2 is readily transformed into P3. Under stoichiometric conditions (Fig. 2, middle), the pentafluoroethylating agent (I) disappears faster than the substrate p-IC₆H₄COCl (38% left at the end), indicating that the copper catalyst I reacts preferentially with other species, most probably with P2. Indeed, the amount of P3 obtained in the stoichiometric 1 hour run (27%) has been confirmed to come preferentially from P2; 67% of the total P3 is obtained by the reaction of P2 with I, while only 33% of P3 comes from P1. These effects are even more noticeable in the reaction where half the amount of p-IC₆H₄COCl is employed as substrate (Fig. 2, right). As may be observed, the amount of P2 rises slightly at the start of the reaction but rapidly decreases as the yield of P3 increases. On the other hand, P1 appears and reaches a maximum yield of around 25% in the first moments of the reaction, and then it starts to go progressively down as it becomes transformed into P3. The computed concentration of the doubly pentafluoroethylated product (P3) is very similar to the one observed experimentally (74 vs. 72%). On the other hand, the experimental results for P1 and P2 in this reaction were not reported and thus they cannot be compared with the ones computed here. The results obtained for these substrates confirm that the calculation of concentrations in solution is also possible for more complex reaction networks, including those where more than one reactive position is available.

Conclusions

The modeling of reaction yields in solution for the copper-mediated pentafluoroethylation of benzoic acid chlorides has been successfully explored with relatively simple DFT methods. Out of the 14 employed methods, the B3LYP-D3 dispersion corrected density functional has produced the best results, comparable to those obtained with more modern and sophisticated approaches such as DLNPO-CCSD(T). The selected methodology allows also reproducing the concentration in solution of the products for differently substituted benzoic acid chlorides and for other systems with increasing complexity, where the substrate has more than one reacting position.

As a whole, this work should be understood as a demonstration of what can be achieved with an accurate usage of DFT calculations. A proper screening of the methodology allows the prediction of a property as complex as that of a transient concentration in solution. This procedure could allow the prediction of the reaction outcome for other untested substrates or similar mediated (or even catalytic) systems and could be even used to validate a possible reaction mechanism. Of course, the methodology employed in this report is not general and an individual screening should be carried out for each reaction studied including a diverse range of density functionals and, if needed, different basis sets and solvation methods. A fundamental aspect of these kinds of studies, which unfortunately could not be applied in this work, consists of checking the predictive power of the selected methodology for reactions that have not been explored experimentally. For this reason, the parallel development of experiments and calculations is a must and should be strongly encouraged in the near future.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been supported by the Spanish Ministerio de Economía y Competitividad (MINECO, grants TQ2015-64579-C3-1-P and CTQ2015-68770-R).

References

1. (a) J. Jover and N. Fey, Chem. – Asian J., 2014, 9, 1714–1723; (b) T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586; (c) S. Santoro, M. Kalek, G. Huang and F. Himo, Acc. Chem. Res., 2016, 49, 1006–1018; (d) T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319; (e) X. Zhang, L. W. Chung and Y.-D. Wu, Acc. Chem. Res., 2016, 49, 1302–1310.
2. (a) J. Jover, F. M. Miloserdov, J. Benet-Buchholz, V. V. Grushin and F. Maseras, Organometallics, 2014, 33, 6531–6543; (b) A. B. Durr, G. Yin, I. Kalvet, F. Napoly and F. Schoenebeck, Chem. Sci., 2016, 7, 1076–1081; (c) T. Sperger, H. C. Fisher and F. Schoenebeck, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 226–242.
3. (a) H. Jacobsen and L. Cavallo, ChemPhysChem, 2012, 13, 562–569; (b) T. Weymuth, E. P. A. Couzijn, P. Chen and M. Reiher, J. Chem. Theory Comput., 2014, 10, 3092–3103; (c) Y. Minenkov, E. Chermak and L. Cavallo, J. Chem. Theory Comput., 2016, 12, 1542–1560; (d) T. Bligaard, R. M. Bullock, C. T. Campbell, J. G. Chen, B. C. Gates, R. J. Gorte, C. W. Jones, W. D. Jones, J. R. Kitchin and S. L. Scott, ACS Catal., 2016, 6, 2590–2602.
4. (a) K. P. Jensen and J. Cirera, J. Phys. Chem. A, 2009, 113, 10033–10039; (b) J. Cirera and E. Ruiz, J. Mater. Chem. C, 2015, 3, 7954–7961; (c) J. Cirera and E. Ruiz, Inorg. Chem., 2016, 55, 1657–1663.
5. Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093–6107.
6. (a) C. L. McMullin, J. Jover, J. N. Harvey and N. Fey, Dalton Trans., 2010, 39, 10833–10836; (b) L. E. Rush, P. G. Pringle and J. N. Harvey, Angew. Chem., Int. Ed., 2014, 53, 8672–8676.
7. (a) K.-B. Cho, E. J. Kim, M. S. Seo, S. Shaik and W. Nam, Chem. – Eur. J., 2012, 18, 10444–10453; (b) I. Kalvet, K. J. Bonney and F. Schoenebeck, J. Org. Chem., 2014, 79, 12041–12046; (c) E. Lyngvi, I. A. Sanhueza and F. Schoenebeck, Organometallics, 2015, 34, 805–812.
8. (a) S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110; (b) T. R. Ramadhar and R. A. Batey, Comput. Theor. Chem., 2011, 976, 167–182; (c) K. Rohmann, M. Hölscher and W. Leitner, J. Am. Chem. Soc., 2016, 138, 433–443.
9. L. I. Panferova, F. M. Miloserdov, A. Lishchynskyi, M. Martínez Belmonte, J. Benet-Buchholz and V. V. Grushin, Angew. Chem., Int. Ed., 2015, 54, 5218–5222.
10. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
11. (a) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824; (b) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
12. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (b) B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
13. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
14. (a) J. P. Perdew, in Electronic Structure of Solids ‘91, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, 1991, vol. 11; (b) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687; (c) J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978; (d) J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539; (e) K. Burke, J. P. Perdew and Y. Wang, in Electronic Density Functional Theory: Recent Progress and New Directions, ed. J. F. Dobson, G. Vignale and M. P. Das, Plenum, 1998.
15. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
16. (a) O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 234109; (b) O. A. Vydrov, J. Heyd, A. Krukau and G. E. Scuseria, J. Chem. Phys., 2006, 125, 074106; (c) O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109.
17. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6169.
18. J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
19. (a) A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560; (b) S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
20. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
21. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
22. R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191.
23. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
24. (a) R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728; (b) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261; (c) P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222.
25. (a) T. H. Dunning and P. J. Hay, in Modern Theoretical Chemistry, ed. H. F. Schaefer III, Plenum, New York, 1976, vol. 3, pp. 1–28; (b) A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431–1441.
26. (a) D. J. Tannor, B. Marten, R. Murphy, R. A. Friesner, D. Sitkoff, A. Nicholls, B. Honig, M. Ringnalda and W. A. Goddard, J. Am. Chem. Soc., 1994, 116, 11875–11882; (b) B. Marten, K. Kim, C. Cortis, R. A. Friesner, R. B. Murphy, M. N. Ringnalda, D. Sitkoff and B. Honig, J. Phys. Chem., 1996, 100, 11775–11788.
27. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
28. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
29. (a) K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123; (b) K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296.
30. (a) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301; (b) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
31. (a) C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106; (b) C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
32. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. (a) T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023; (b) D. E. Woon and T. H. Dunning Jr., J. Chem. Phys., 1993, 98, 1358–1371; (c) N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
35. (a) K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290; (b) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124.
36. S. Hoops, S. Sahle, R. Gauges, C. Lee, J. Pahle, N. Simus, M. Singhal, L. Xu, P. Mendes and U. Kummer, Bioinformatics, 2006, 22, 3067–3074.
37. K. J. Laidler, Chemical Kinetics, Harper & Row, New York, 3rd edn, 1987.
38. Y. Minenkov, E. Chermak and L. Cavallo, J. Chem. Theory Comput., 2015, 11, 4664–4676 and references therein.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05709a

---