Order–disorder phase transition in an anhydrous pyrazole-based proton conductor: the enhancement of electrical transport properties

Abstract

The crystal structure of 1H-pyrazol-2-ium hydrogen oxalate has been studied at 100 K. It consists of two-dimensional layers built with one-dimensional chains that contain pyrazolium and oxalate acids bonded by N–H⋯O and O–H⋯O hydrogen bonds. According to the X-ray data and the Quantum Theory of Atoms in Molecules, it was shown that weak and moderate hydrogen bonds are present in the crystal at room temperature. The thermal stability was studied with the DSC, TGA, and DTG methods: three endothermic peaks are observed at 384, 420, and 469 K. Conductivity measurements have been performed in the temperature range from 300 to 433 K. At 383 K the pyrazole–oxalic acid framework loses its rigidity and the crystal undergoes an ordered–disordered phase transition. At this temperature, the value of the activation energy of proton conductivity changes from 1.14 to 2.31 eV. The proton conduction pathways and the transport mechanism have been studied with theoretical methods.

---

Introduction

During the last decade, there has been continued considerable interest in the study of proton conducting materials for applications in solid-state hydrogen fuel cells, electrochemical devices, and hydrogen storage.^1–6 Materials with amphoteric nitrogen-containing heterocyclic molecules were proposed by Kreuer et al.⁷ as interesting alternatives to polymer membrane electrolyte fuel cells (PEMFCs) based on water solvated protons as their conducting media. Nitrogen-containing heterocyclic molecules such as imidazole, pyrazole, and benzimidazole^7–12 are attractive for proton conducting media because the energy barriers for proton transfer in the hydrogen bonds between the nitrogen atoms are lower in comparison with those of the hydrogen bonds between less polarizable oxygen atoms.¹³ Moreover, the proton conducting materials under anhydrous conditions have advantage over those based on water solvated protons because their conductivity does not depend on the relative humidity and their operating temperature range can be extended to temperatures higher than 100 °C.

Recently, a new proton conducting material 1H-pyrazol-2-ium hydrogen oxalate was synthesized based on a nitrogen-containing heterocycle and dicarboxylic acid.¹⁴ The pyrazole molecule, like other nitrogen-containing heterocycles (triazole, imidazole, benzimidazole), crystallizes in layer crystal structures held together by a hydrogen bond network, where protons can easily migrate through the crystal within the layers.^15–22 In the case of proton conductors, several proton diffusion mechanisms such as the Grotthuss process, the translocation mechanism, the vehicle mechanism, proton tunneling, and the solitonic mechanism have been proposed to explain the conducting properties.^23,24

The present study was carried out to provide detailed structural, electrical, and optical properties of this new proton conducting material. To yield more information on the nature of an anomaly observed at 383 K in the conductivity measurements, we performed detailed studies in the temperature range from 300 to 433 K. At 383 K the value of the activation energy of proton conductivity changes from 1.14 to 2.31 eV. What is interesting is the fact that despite the increase in the value of the activation energy, the electrical conductivity increases. With an increase in temperature from 300 up to 433 K, a dramatic increase in conductivity of seven orders of magnitude is observed. One of the main objectives of our study is to confirm by other experimental methods the occurrence of this anomaly and to clarify its nature. In order to understand its conductive properties, we have performed optical and thermal investigations and structural analysis. Moreover, Density Functional Theory (DFT) and Quantum Theory of Atoms in Molecules (QTAIM) calculations have been performed as well. In our opinion, libration and rotations of molecules in the crystal arise and increase with heating of the sample so that the pyrazole–oxalic acid framework loses its rigidity and the crystals undergo an ordered–disordered phase transition.

Materials and methods

Synthesis procedure

The 1H-Pyrazol-2-ium hydrogen oxalate crystals were obtained from a saturated aqueous solution containing pyrazole (Sigma-Aldrich, purity 98%) and oxalic acid dihydrate (Sigma-Aldrich ≥99%) in the mole ratio 1 : 1. The dissolved solutions were mixed using a magnetic stirrer at 40 °C. The crystallization was carried out by slow evaporation of the solvent at room temperature (about 25 °C), according to the procedure described in ref. 22. Single crystal plates of 10 mm length, 4 mm width, and 2 mm thick were obtained.

Experimental methods

The thermal properties of 1H-pyrazol-2-ium hydrogen oxalate crystals were investigated by means of differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA). The DSC measurements were performed with a Netzsch DSC 200 calorimeter in a helium atmosphere. The samples were about 7 mg; scan rate 5, 10, 15, and 20 K min⁻¹. The measurements were performed from 300 to 550 K. The TGA measurements were carried out with a Perkin-Elmer TGA 4000 instrument in a nitrogen atmosphere from 300 to 550 K with a heating rate of 10 K min⁻¹. The results of the DSC measurements show that there are no characteristic bands associated with the presence of water molecules in the studied system.

The single-crystal data sets of the sample were collected at 100 K on a 4-circle X’Calibur diffractometer (Oxford Diffraction) using graphite monochromated Mo radiation (λ = 0.71073 Å). CrysAlis software version 170.33.42 was used for data processing. An empirical absorption correction was applied using spherical harmonics implemented in the SCALE3 ABSPACK scaling algorithm. The structure was solved by direct methods and refined by the full-matrix least-squares method by means of the SHELXL-13 program package. All the non-hydrogen atoms were treated anisotropically and the N-bound H atoms and CH₂ were located in a difference Fourier map and refined isotropically.

The real and imaginary parts of the electric impedance of the investigated compound were investigated in the frequency range from 0.1 Hz to 10 MHz by means of a computer-controlled Alpha A High-Frequency Analyzer (Novocontrol GmbH). The temperature of the sample was stabilized with an accuracy of 0.1 K using a Quatro Cryosystem. For conductivity measurements cylindrical pellets 2.13 mm thick and 5.3 mm in diameter were prepared from a powder obtained by milling of the crystals in an agate mortar. The powder was pressed under 30 MPa for 1 min at room temperature to form a pellet. Next, its surfaces were electroded with Hans Wolbring GmbH silver paste.²⁵

The optical properties were investigated with a Bruker Equinox 55 spectrometer combined with an FT-IR Hyperion 2000 microscope in the spectral range from 650 to 17 000 cm⁻¹ with the spectral resolution of 2 cm⁻¹. The spectra were measured perpendicular to the (01̄1) crystallographic (natural) plane. The sample was stuck onto the KBr window and polished with diamond powder until transmittance spectra measurements were possible. The vibrational and electronic transitions were investigated versus temperature using a cryostat made by Linkam corporation from 300 to 410 K. The Raman spectrum was recorded with the excitation line in the NIR range (laser, λ_ext = 785 nm) on a Jobin-Yvon HORIBA LabRAM HR 800 spectrometer connected to a CCD detector within the range from 250 to 2000 cm⁻¹ with a spectral resolution better than 2 cm⁻¹. The laser power at the sample was kept below 1 mW to avoid thermal and photochemical degradation.

Computational methods

The intermolecular interactions were analyzed using the Bader theory performed with the AIMAll program.²⁶ The 6-311++G(d,p) Pople style basis set and the B3LYP hybrid density functional which combines Becke's three-parameter nonlocal exchange potential with the nonlocal correlation functional of Lee, Yang, and Parr^27,28 were used. We investigate the topological properties of the critical points of a system containing six molecules bound by O–H⋯O and N–H⋯O hydrogen bonds.

To study the molecular structure, the quantum chemical calculations were performed with the Gaussian 03 set of codes.²⁹ For all the calculations, the initial geometry obtained from the X-ray studies was applied. The flipping energy barrier of a molecule and hydrogen bonding interactions were determined by employing a Potential Energy Scan (PES). The scanning of energy was performed by changing the dihedral angle in the investigated system or the position of the proton within the hydrogen bond. The quantum chemical calculations were performed at the MP2/6-31G(d) theory level.

Results and discussion

The crystal structure of 1H-pyrazol-2-ium hydrogen oxalate

The structure of the 1H-pyrazol-2-ium hydrogen oxalate crystal belongs to a triclinic system with P1̄ space group and with a = 3.6202(1) Å, b = 9.8258(3) Å, c = 10.4146(3) Å, α = 117.336(3)°, β = 95.831(2)°, γ = 94.177(2)°, V = 324.39(2) ų, and Z = 2 at room temperature. The unit cell has an inversion. It was found to consist of two-dimensional layers lying parallel to the (1̄1̄2) plane, shifted relative to each other by an amount of 3.5 Å. The distance between the atoms in different layers is never less than twice the van der Waals radius of the atoms. The layers are built with one-dimensional chains extending in the [111] direction. The single chain contains pyrazole cations attached to the carboxyl groups of acids by N–H⋯O bonds and anions formed centrosymmetric dimers through cyclic O–H⋯O hydrogen-bonding associations (see Fig. 1). Detailed studies of the structure of the investigated material are presented in Tables S1–S7 (see ESI†) and they show good compatibility with the results obtained by other authors^14,30 (see ESI,† Table S8).

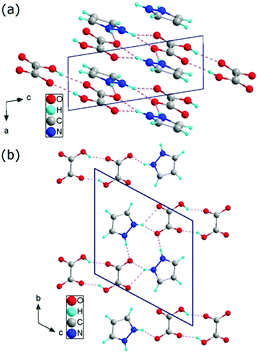Fig. 1 Crystallographic structure of 1H-pyrazol-2-ium hydrogen oxalate in the ac plane (a) and in the bc plane (b).

Hydrogen-bond interaction analysis

In the 1H-pyrazol-2-ium hydrogen oxalate, there are numerous N–H⋯O and O–H⋯O hydrogen bonds (see Fig. 2). The layer-type structure of the investigated proton-conducting material can be represented as consisting of chains formed along the [111] direction with a system of hydrogen bonds between the pyrazole ions and the carboxyl groups of the oxalic acids.

Fig. 2 Crystallographic structure of 1H-pyrazol-2-iumhydrogen oxalate crystal (a); the dotted line between the atoms symbolizes the hydrogen bond. Representation of bonding interactions analyzed using the Quantum Theory of Atoms in Molecules (QTAiM) (b); the green circle corresponds to the bond critical point (BCP) of the H⋯O bond path.

There are three distinct hydrogen bonds: N(X)–H(X)⋯O(X) (d_N⋯O = 2.70 Å and d_N⋯O = 2.92 Å) between a hydrogen oxalic ion acting as the proton donor and a pyrazole molecule acting as a proton acceptor and O(X)–H(X)⋯O(X) (d_O⋯O = 2.66 Å) between oxalic acid molecules (see Table 1); the projections of the hydrogen bonds are shown in Fig. 2. In the crystal at room temperature, taking into account the geometrical parameters of the D–H⋯A bonds, all of the above-mentioned hydrogen bonds can be considered as moderate hydrogen bonds.³¹

Table 1 Geometrical parameters of D–H⋯A hydrogen bonds (in Ångstrom and in degree) and QTAIM parameters (in atomic unit) corresponding to the H⋯O bond critical points (BCPs). Note: the values at BCP: the electron density, ρ_BCP; Laplacian of electron density, ∇²ρ_BCP; the kinetic electron energy density, G_BCP; the potential electron energy density, V_BCP; the total electron energy density; H_BCP

D–H⋯A	d D–H [Å]	d H⋯A [Å]	d D⋯A [Å]	∠D–H⋯A [°]	ρ BCP [a.u.]	∇^2ρBCP [a.u.]	G BCP [a.u.]	V BCP [a.u.]	H BCP [a.u.]
N10–H11⋯O2	0.88	1.83	2.70	168.31	0.034314	0.128697	0.03113	−0.03010	0.001039
N8–H9⋯O2	0.88	1.89	2.70	152.75	0.029678	0.120722	0.02764	−0.02511	0.002538
N8–H9⋯O5	0.88	2.31	2.92	126.17	0.012542	0.051023	0.01057	−0.00840	0.002179
O1–H4⋯O3	0.86	1.87	2.66	152.69	0.025078	0.123777	0.02680	−0.02267	0.004139

---

Based on Bader theory,³² we analyzed critical points³³ and their topological properties at the bond critical point BCP, such as: the electron densities (ρ_BCP), their Laplacians (∇²ρ_BCP), the potential electron energy density (V_BCP), the kinetic electron energy density (G_BCP), and the total electron energy density (H_BCP). At the critical point, there are the following relationships between topological parameters:

0.25∇²ρ_BCP = 2G_BCP + V_BCP, (1)

H_BCP = G_BCP + V_BCP. (2)

Kinetic electron energy density G_BCP has a positive value, whereas the potential electron energy density V_BCP has a negative value. If the absolute value of V_BCP is two times as high as the G_BCP value, the Laplacian ∇²ρ_BCP is negative. The Rozas group³⁴ proposed a classification of hydrogen bonds using topological parameters: for weak and moderate hydrogen bond interactions ∇²ρ_BCP and H_BCP values are positive, for strong hydrogen bond interactions ∇²ρ_BCP is positive and H_BCP is negative, and for a very strong hydrogen bond interaction the ∇²ρ_BCP and H_BCP values are negative. For the 1H-pyrazol-2-ium hydrogen oxalate crystal, the values of ∇²ρ_BCP and H_BCP are positive which indicates them as closed-shell interactions.

Thermal stability analysis

Knowledge of the thermal stability of 1H-pyrazol-2-ium hydrogen oxalate is important for the interpretation of temperature investigations of conducting and spectral properties. It was studied with the DSC, TGA, and DTG methods and the results are presented in Fig. 3, which shows the scans on heating at 5, 10, 15, and 20 K min⁻¹ scan rates in the temperature range of 300–550 K.

Fig. 3 Differential scanning calorimetry scans (DSC) recorded for 5, 10, 15, and 20 K min⁻¹ scan rates (upper panel), thermogravimetric analysis (TGA) (lower panel; red line), and derivative thermogram (DTG) (lower panel; blue line) of 1H-pyrazol-2-ium hydrogen oxalate crystals.

In the investigated compound, we observe at T₃ an intense endothermic peak that is due to melting and decomposition processes. Its onset temperature is observed at about 463 K and it attains the maximum degradation rate at about 469 K. The second endothermic peak is present at T₂ = 420 K. The position of this feature depends on the heating scan rates and it is observed at 435, 440, 441, and 448 K for 5, 10, 15, and 20 K min⁻¹, respectively. This peak is related to the sublimation process. It was confirmed by us using Raman scattering measurements (see ESI,† Fig. S1). The spectra of the investigated compound were compared to the material which was deposited on a quartz plate placed directly above the crystal. From the TGA measurements, it is known that there are three major weight losses: the first one in the temperature range from 377 to 388 K with a value of 1.2%, the second from 413 to 428 K with a weight loss of 3.7%.

The third weight loss starts at 463 K and ends at 488 K with a value 97.1%. The derivative thermogram (DTG) shows the anomaly at about T₁ = 384 K.

We examined these phenomena by measuring infrared spectra. For single crystals of 1H-pyrazol-2-ium hydrogen oxalate, absorbance spectra in the temperature range from room temperature up to 395 K were investigated. At the same time measurements of infrared spectra were performed and the optical surface of the crystal was observed by means of an optical microscope. Above 395 K, a significant degradation of the crystal surface associated with the mass loss was observed; this was confirmed by TGA measurements. This fact demonstrates that the structure rigidity and intermolecular interactions decrease as temperature increases.

For several normal modes, spectral parameters of infrared bands have been thoroughly investigated as a function of temperature. Fig. 4 and 5 show the temperature evolution of peak position and half-width for the selected bands observed at 1172, 1415, and 1589 cm⁻¹, for which one can observe a distinct anomaly at about 380 K. The first band is related to the ring breathing mode of pyrazolium and the other two are associated with the presence of the deprotonated carboxyl group, symmetric and asymmetric COO^– stretching vibration.^30,35,36 The increase in the width of the infrared bands associated with the dynamics of carboxyl groups indicates that above the temperature of 380 K in the system we are dealing with a structural disorder associated with oxalate. Band broadening suggests the presence of reorientation of oxalic acid ions at specific locations in the crystal. This means that the anomaly at 380 K can be related to the transition between the ordered and disordered phases. Such temperature dependence of the bandwidth indicates also that a plastic phase above 380 K can be present in our investigated system.

Fig. 4 Absorption spectra of 1H-pyrazol-2-ium hydrogen oxalate crystals presented for two spectral regions where the bands related to ring breathing mode (a) and symmetric and asymmetric COO⁻ stretching vibration (b) can be observed.

Fig. 5 Temperature evolution of the peak center (a) and bandwidth (b) of infrared bands observed at 1172 (ν_ring; upper panel), 1415 (ν_sym(COO⁻); middle panel), and 1589 cm⁻¹ (ν_asym(COO⁻); lower panel).

The nature of this transition will be discussed in detail in the ‘Proton conduction pathway analysis’ section.

Electrical property investigations

For 1H-pyrazol-2-ium hydrogen oxalate, the temperature dependence of the electrical conductivity has been investigated from 300 to 433 K. The sample was a cylindrical pellet made of powdered salt. For that reason, two contributions to the electrical conductivity have to be taken into account in the interpretation of experimental data. The first one is related to the grain interior while the second one to the grain boundaries. For fitting the experimental data the Cole–Cole formula for double RC parallel equivalent circuits connected in series was used:where R₁ denotes the resistance of the first contribution, R₂ is the resistance of the sum of two contributions (the crystalline and grain boundaries), C₁ and C₂ mean electrical capacities of circuits 1 and 2, α₁ and α₂ are Cole–Cole parameters, and ω = 2πν is the angular frequency of the measuring field. Such an approach is commonly used in the analysis of the complex impedance response in polycrystalline samples and in ceramics.^25,37

The measurement of the complex impedance Z*(ω) = Z′ − iZ′′ for the 1H-pyrazol-2-ium hydrogen oxalate was obtained at a constant temperature in the frequency range from 0.1 Hz up to 10 MHz. Fig. 6 shows the dependence of the imaginary part Z′′ of the impedance of the real part Z′ (Nyquist plot) for selected temperatures. In order to determine the dc conductivity of the investigated sample, we have performed fits separately for both dependencies Z′(ν) and Z′′(ν) at given temperatures (see the insets of Fig. 6).

Fig. 6 Examples of complex impedance plots for 1H-pyrazol-2-ium hydrogen oxalate. Note: insets present fits of the experimental data at 373 K (a) and 433 K (b).

Fig. 7 shows the dc conductivity of the investigated proton conductor versus the inverse temperature; the maximum conductivity amounts to 2 × 10⁻⁵ S m⁻¹ at 433 K. It has been described by the Arrhenius law:

where σ₀ means the pre-exponential factor, E_a is the activation energy, and k is the Boltzmann constant. The activation energy is equal to 1.14 and 2.31 eV, below and above 383 K, respectively. It can be seen that the temperature at which the change of the slope of the Arrhenius law is observed is in good agreement with the endset temperature (388 K) of the T₁ transition.

Fig. 7 Arrhenius plots of dc conductivity of 1H-pyrazol-2-ium hydrogen oxalate. Note: the anomaly can be found at 383 K.

The above-mentioned contributions for conductivity, taken into account for powdered samples, are not a well-defined semicircular response in the experimental data. Unfortunately, we were not able to grow sufficiently large crystals to measure the conductivity of a single crystal sample. We can give only information on the average conductivity and the activation energy. To overcome this limitation, we carried out temperature-dependent spectroscopic studies of single crystals.

We examined the anomaly observed at 383 K by measuring the visible-near IR spectrum. Initially, the electron spectra were recorded at room temperature; then the crystal was heated at a heating rate of 2 K min⁻¹ and kept at 410 K for 1 h, before being cooled down to room temperature. Finally, the spectrum for the heat-treated crystal was measured at room temperature (see Fig. 8; curve (b)). During this experiment, the surface of the crystal was monitored under an optical microscope as well.

Fig. 8 Absorbance spectra of 1H-pyrazol-2-ium hydrogen oxalate single crystals recorded at room temperature before (green line) (a) and after heat treatment (purple line) (b).

In Fig. 8 the two spectra differ from one another. This shows that the anomaly observed at 383 K is not a reversible transition and is most likely related to an order–disorder transition. For each of the spectra, two bands A and B consisting of multiple components can be observed. For the A band one can find transitions at 11 350 cm⁻¹ (1.41 eV), 12 150 cm⁻¹ (1.51 eV), and 13 050 cm⁻¹ (1.61 eV).

The intensity of this feature is more or less unchanged as opposed to the B band, where a significant increase for the heat-treated crystal is observed. In the broad B band, the following transitions can be distinguished: 14 200 cm⁻¹ (1.76 eV), 14 800 cm⁻¹ (1.83 eV), 15 450 cm⁻¹ (1.92 eV), and 16 250 cm⁻¹ (2.01 eV). In addition to these bands in the spectrum, one can observe a group of bands at around 6100 cm⁻¹ (0.76 eV) and 4200 cm⁻¹ (0.52 eV). P. Karthiga Devi and co-worker³⁰ for 1H-pyrazol-2-ium hydrogen oxalate observe a strong band at 5 eV, which they interpret as a manifestation of the energy gap. In addition, weak bands at about 925 nm (1.34 eV) and 600 nm (2.06 eV) can also be found in Fig. 3 in ref. 30; the position of these features agrees with the A and B band's position. Unfortunately, the authors do not discuss the origin of these bands.

We believe that in the disordered phase, in one-dimensional conductive chains, defects can be observed. The appearance of such phenomena affects the increase in activation energy. In the section below, we will try to propose the types of defects that can be realized in the crystal and the possible pathways of the proton below and above the order–disorder phase transition.

Proton conduction pathway analysis

For 1H-pyrazol-2-ium hydrogen oxalate, we studied the proton transport mechanism with theoretical methods. At the beginning of our considerations, we assumed that the conductivity of protons in the crystal is along the [111] direction parallel to the one-dimensional chains within the individual layers in the (1̄1̄2) plane (see Fig. 9). This assumption results directly from the analysis of the crystallographic structure obtained for room temperature. The distance between atoms in different layers shows that the transport of protons may take place in layers along the chains.

Fig. 9 A view of the one-dimensional chain in 1H-pyrazol-2-ium hydrogen oxalate crystals (projection on the (1̄1̄2) plane).

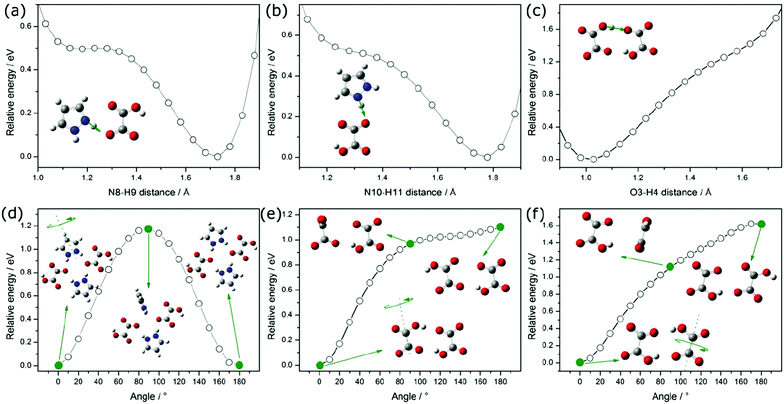
We took into account the two main components that can be distinguished in the mechanism of proton transport: (1) intrabond motion: proton motion within double-well N–H⋯O and O–H⋯O hydrogen bonds from one potential minimum to the other, (2) interbond motion: proton motion between hydrogen bonds, during which rotations of pyrazole and carboxyl groups cause the link of a double-minimum H-bond to be broken and the proton is transferred to the nearest vacant position with the formation of a new hydrogen bond. The proton motion related to the reorientations, according to the NMR,²⁰ is a much faster process than the double-well jump motion within the hydrogen bonds. For our proton conducting material, we have determined the energetic barrier³⁸ within the double-well hydrogen bonds. For all types of hydrogen bonds in the system, it is similar and equals about 0.15 eV. The transfer of a proton from one site to another with the destruction of the old H-bond and the formation of a new one has been presented in Fig. 10(a–c). The DFT studies of molecular motions revealed that the pyrazole cations undergo an 180° flip around the pseudo 2-fold axis with an activation energy of 1.17 eV (see Fig. 10(d)) and carboxyl groups in oxalic acids flip around the C–C bond axis with an activation energy of 1.10 eV (see Fig. 10(e)). The determined activation energy is in agreement with that obtained from the Arrhenius plot for electric conductivity measurements in the range from 300 to 383 K (E_a = 1.14 eV). In our opinion, the probability and frequency of appearance of molecule rotation in the crystal increase with heating. Thus, the pyrazole–oxalic acid framework loses its rigidity and 1H-pyrazol-2-ium hydrogen oxalate can undergo an ordered–disordered phase transition at 383 K. At this temperature, the value of the activation energy of proton conductivity is changed from 1.14 to 2.31 eV. What is interesting is the fact that despite the increase in the value of the activation energy the electrical conductivity increases by seven orders of magnitude from 300 up to 433 K. Similar behavior was observed for the Li₆Y(BO₃)₃ ionic conductors by the Lopez-Bermudez group,³⁹ which considers that the observation of two different linear regions in the Arrhenius graph indicates the competition between two or more diffusion mechanisms.⁴⁰

Fig. 10 Potential Energy Scan (PES) performed for the translational movement of a proton between pyrazole and oxalic acid (a–c); structures show two local minima, resulting from hydrogen bonding interactions. Potential energy scan obtained for the rotation of the pyrazolium around its pseudo 2-fold axis (d) and the rotation of carboxyl groups in oxalic acids around the C–C bond axis (e and f).

In order to explain the nature of proton transport in 1H-pyrazol-2-ium hydrogen oxalate above the phase transition, we propose an additional mechanism that can be found in the high-temperature range: (I) the elementary proton transfer process consists of two steps: pyrazolium cations hindered rotation by 45° inducing cross-linking between previously isolated H-bonded chains in neighboring layers and the translation of the proton between two equilibrium sites in the newly created N–H⋯O (see Fig. 11), resulting in an pyrazole–oxalic acid defect and (II) the proton transfer process where the carboxyl group in oxalic acids hindered rotation by 70° inducing cross-linking between isolated H-bonded chains and the translation of the proton between two equilibrium sites in the created O–H⋯O hydrogen bond (see Fig. 11), resulting in a carboxyl group of oxalic acid–carboxyl group of oxalic acid defect.

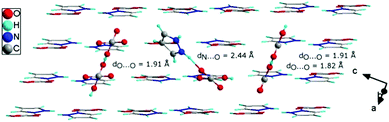Fig. 11 The crystallographic structure of 1H-pyrazol-2-ium hydrogen oxalate with different types of defects (see the text) that may occur above the phase transition.

At sufficiently high temperatures, it can be assumed that it will be possible to rotate the whole oxalic acid molecule around the C–C bond axis; (III) the proton transfer process is performed between oxalic acids (see Fig. 11). Such a rotation requires a greater activation energy in comparison with the processes discussed above. For the case where we have an isolated dimer made up of two oxalic acid ions, we have shown that the activation energy of such a molecular rotation is about 1.62 eV (see Fig. 10(f)). In general, the activation energy is determined by many effects: the interaction between hopping ions, the interaction between hopping ions and phonons, and the configuration of surrounding ions, etc. If we take into account the impact of phonon vibrations in the high-temperature region and the impact of the dimer's closest environment, then the activation energy of such a process would be even greater than 1.62 eV. On the basis of theoretical considerations and experimental results, the activation energy can be estimated at about 2 eV; in an optical measurement, the band B is observed from 1.7 to 2.1 eV, whereas in conductivity measurements, above 383 K E_a equals 2.31 eV. A similar mechanism of proton transport to what we proposed above consisting of two basic steps, proton motion within a double-well hydrogen bond and HSO₄ rotation, is observed also in superprotonic phases of hydro- and deuterosulfate and selenate proton conductors.⁴¹

For the investigated material, defects can propagate rather fast by phonon-assisted tunneling, or classical hopping of protons, between the two minima in the N–H⋯O and O–H⋯O bonds along the H-bonded chains. The flip of rotating components in the crystal can be activated thermally and through phonons. The formation of defects provides protonic conductivity in the direction perpendicular to the layers. In our opinion, with the increase in the number of conduction paths, the dimensionality of the investigated system increases, which has implications for the value of conductivity in a high-temperature region. On the other hand, the formation of defects affects the size of the activation energy as well. In addition, allowing the existence of interactions between the layers at high temperatures explains in someway their reversibility of the phase transformation at 383 K. If we heat the system above the transition temperature and then cool it down to room temperature, defects will be frozen in the system. This was experimentally confirmed by the presence of the B band in the spectrum (see Fig. 8). Keolopile et al.⁴² showed that the oxalic acid dimer is a very stable structure due to the fact that the inter- and intramolecular hydrogen bonds are present inside the dimer.⁴³

Conclusions

The crystal structure of 1H-pyrazol-2-ium hydrogen oxalate consists of two-dimensional layers built with one-dimensional conducting chains. According to the X-ray data performed at room temperature, the system of weak or moderate hydrogen bonds and strong anisotropy of electrical conductivity can be expected. The conductivity measurement reveals that at 383 K the value of the activation energy of proton conductivity changes from 1.14 to 2.31 eV. The observation of two different linear regions in the Arrhenius graph indicates the competition between different diffusion mechanisms. The results of QTAIM calculations show that in the investigated system weak interactions such as van der Waals or hydrogen bond interactions should be observed. Three endothermic peaks are observed at 384, 420, and 469 K. The peak at 469 K is due to melting and decomposition processes, whereas the peak at 420 K is related to the sublimation process. At 384 K the ordered–disordered phase transition is present and it is due to the fact that libration and rotations of molecules in the crystal arise and increase with heating of the sample so that the pyrazole–oxalic acid framework loses its rigidity. In the disordered phase, in one-dimensional conductive chains, there are defects, the appearance of which affects the increase in activation energy. The formation of defects provides protonic conductivity between the layers.

Conflicts of interest

There are no conflicts to declare.

References

1. T. Norby, Nature, 2001, 410, 877–878.
2. S. M. Haile, D. A. Boysen, C. R. I. Chisholm and R. B. Merle, Nature, 2001, 410, 910–913.
3. J. Tollefson, Nature, 2010, 464, 1262–1264.
4. M. Sadakiyo, T. Yamada and H. Kitagawa, J. Am. Chem. Soc., 2009, 131, 9906–9907.
5. J. A. Hurd, R. Vaidhyanathan, V. Thangadurai, Ch. I. Ratcliffe, I. L. Moudrakovski and G. K. H. Shimizu, Nat. Chem., 2009, 1, 705–710.
6. G. K. H. Shimizu, J. M. Taylor and S. Kim, Science, 2013, 341, 354–355.
7. K. D. Kreuer, A. Fuchs, M. Ise, M. Spaeth and J. Maier, Electrochim. Acta, 1998, 43, 1281.
8. K. G. Herz, K. D. Kreuer, J. Maier, G. Scharfenberger, M. F. H. Schuster and W. H. Meyer, Electrochim. Acta, 2003, 48, 2165.
9. K. D. Kreuer, J. Membr. Sci., 2001, 185, 29–39.
10. M. Schuster, W. H. Meyer, G. Wegner, H. G. Herz, M. Ise, M. Schuster, K. D. Kreuer and J. Maier, Solid State Ionics, 2001, 145, 85–92.
11. M. F. H. Schuster, W. H. Meyer, M. Schuster and K. D. Kreuer, Chem. Mater., 2004, 16, 329–337.
12. J. Weber, ChemSusChem, 2010, 3, 181–187.
13. S. Scheiner, Acc. Chem. Res., 1994, 27, 402–408.
14. C.-H. Yu and R.-Q. Zhu, Acta Crystallogr., 2012, E68, o1911.
15. K. Pogorzelec-Glaser, J. Garbarczyk, Cz. Pawlaczyk and E. Markiewicz, Mater. Sci., 2006, 24, 245–252.
16. K. Pogorzelec-Glaser, Cz. Pawlaczyk, A. Pietraszko and E. Markiewicz, J. Power Sources, 2007, 173, 800–805.
17. A. Rachocki, K. Pogorzelec-Glaser, A. Pietraszko and J. Tritt-Goc, J. Phys.: Condens. Matter, 2008, 20, 505101.
18. P. Ławniczak, K. Pogorzelec-Glaser, Cz. Pawlaczyk, A. Pietraszko and L. Szcześniak, J. Phys.: Condens. Matter, 2009, 21, 345403.
19. P. Ławniczak, M. Zdanowska-Frączek, Z. J. Frączek, K. Pogorzelec-Glaser and Cz. Pawlaczyk, Solid State Ionics, 2012, 225, 268–271.
20. A. Rachocki, K. Pogorzelec-Glaser, P. Ławniczak, M. Pugaczowa-Michalska, A. Łapiński, B. Hilczer, M. Matczak and A. Pietraszko, Cryst. Growth Des., 2014, 14, 1211–1220.
21. S. Zięba, A. Mizera, K. Pogorzelec-Glaser and A. Łapiński, Spectrochim. Acta, Part A, 2017, 180, 224–233.
22. K. Pogorzelec-Glaser, A. Rachocki, P. Ławniczak, A. Pietraszko, Cz. Pawlaczyk, B. Hilczer and M. Pugaczowa-Michalska, CrystEngComm, 2013, 15, 1950–1959.
23. Ph. Colomban, Proton Conductors, Cambridge University Press, Cambridge, 1992.
24. W. Münch, K. D. Kreuer, W. Silvestri, J. Maier and G. Seifert, Solid State Ionics, 2001, 145, 437–443.
25. Impedance Spectroscopy Theory, Experiment and Applications, ed. E. Barsoukov and J. R. Macdonald, J. Wiley & Sons, New Jersey, 2005.
26. A. Todd and T. K. Keith, AIMAll (Version 10.05.04), Gristmill Software, Overland Park KS, USA, 2017, http://aim.tkgristmill.com.
27. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
28. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Hona, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03 (Revision B.03), Gaussian, Inc., Pittsburgh PA, 2003.
30. P. Karthiga Devi and K. Venkatachalam, Mater. Chem. Phys., 2016, 186, 210–219.
31. G. A. Jeffrey, An introduction to hydrogen bonding, Oxford University Press, New York, 1997, pp. 11–14.
32. C. Matta and R. J. Boyd, Quantum Theory of Atoms in Molecules: Recent Progress in Theory and Application, Wiley-VCH, New York, 2007.
33. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
34. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11164.
35. R. Y. M. Huang, R. Pal and G. Y. Moon, J. Membr. Sci., 1999, 160, 101–113.
36. F. Leroux, J. Gachon and J.-P. Besse, J. Solid State Chem., 2004, 177, 245–250.
37. T. van Dijk and A. J. Burggraaf, Phys. Status Solidi A, 1981, 63, 229–240.
38. X. Lu, H. Jain and O. Kanert, J. Non-Cryst. Solids, 1994, 172-174, 1436–1440.
39. B. Lopez-Bermudez, W. G. Zeier, S. Zhou, A. J. Lehner, J. Hu, D. O. Scanlon, B. J. Morgan and B. C. Melot, J. Mater. Chem. A, 2016, 4, 6972.
40. R. J. Cava and E. A. Rietman, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 6896–6902.
41. R. Blinc, J. Dolinšek, G. Lahajnar and I. Zupančič, Phys. Status Solidi B, 1984, 123, K83–K87.
42. Z. G. Keolopile, M. R. Ryder and M. Gutowski, J. Phys. Chem. A, 2014, 118, 7385–7391.
43. S. A. Blair and A. J. Thakkar, Chem. Phys. Lett., 2010, 495, 198–202.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05708c

---