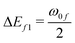Interplay of twist angle and solvents with two-photon optical channel interference in aryl-substituted BODIPY dyes†
Received
19th August 2017
, Accepted 9th October 2017
First published on 11th October 2017
Abstract
Channel interference plays a crucial role in understanding the physics behind multiphoton absorption processes. In this work, we study the role of channel interference and solvent effects on the two-photon absorption in aryl-substituted boron dipyrromethene (BODIPY) dyes, a class of intramolecular charge-transfer (ICT) molecules. For this purpose, we consider fourteen dyes of this class with various donor/acceptor substitutions at the para position of the phenyl ring and with or without methyl (–CH3) substitution on the BODIPY moiety. The presence of a methyl group on the BODIPY moiety affects the dihedral angle significantly, which in turn affects the one- (OPA) and two-photon absorption (TPA) properties of the molecules. Among the molecules studied, the one having the strong electron-donating dimethylamino group and no methyl substitution at the BODIPY moiety is found to have the highest TPA cross section. Our few-state model analysis shows that the large TPA activity of this molecule is due to the all positive contributions from different channel interference terms. Change in dielectric constant of the medium is found to have a profound impact on both the magnitude and sign of the channel interference terms. The magnitude of destructive channel interference gradually decreases with decreasing solvent polarity and becomes constructive in a low-polarity solvent. We also study the effect of rotating the phenyl ring with respect to the BODIPY moiety on the TPA activity. In the gas phase and in different solvents, we found that channel interference is changed from destructive to constructive on twisting the molecule. These results are explained by considering different dipole-, energy- and angle-terms appearing in the expression of a two-state model.
1 Introduction
Of late, studies of two-photon absorption (TPA) properties of intramolecular charge-transfer (ICT) based molecules have increased because of their numerous technological applications, such as in optical switching, optical data storage and as probes for two-photon microscopy, to name a few.1–6 Several strategies have been adopted to optimize the TPA in charge-transfer based molecules, such as altering the strength of donor and/or acceptor groups and introducing additional donor/acceptor groups to perturb the charge separation and extend the conjugation network.7–11 One of the important aspects of studying TPA is to find molecules with large TPA cross sections, whereas another is the study of structure–property relationships to rationalize the physics behind the TPA activity, enabling one to design novel molecules with desired TPA cross sections. Boron dipyrromethene (BODIPY) dyes are well known for their strong absorption and relatively sharp fluorescence emission with high quantum yields.12,13 It has also been reported that the absorption and emission properties of BODIPY dyes can be conveniently tuned by altering the substitution pattern in the BODIPY framework, which in turn can push their fluorescence into the near-infrared region. Excellent thermal and photochemical stability and negligible triplet-state formation are other advantages of these dyes when designing materials for technological applications. The molecules investigated here (Fig. 1) belong to the class of aryl-substituted BODIPY dyes. Tang and coworkers14 have reported experimental studies of the ICT processes in this class of dyes. They have also reported that substitution of the phenyl ring attached to the BODIPY ring decreases the quantum yield of fluorescence compared to BODIPY alone. On the other hand, substitution of methyl groups in the BODIPY moiety of phenyl-substituted BODIPY restricts the rotation of the phenyl group, leading to an enhancement of the quantum yield of fluorescence of these molecules. Although several studies have been devoted to the study of charge-transfer properties of BODIPY dyes,14,15 studies of their TPA activity are scarce. Some experimental and theoretical studies of TPA in BODIPY and related molecules were recently reported by Belfield et al.16 and Feng et al.17 The nonlinear optical (NLO) response properties of aryl-substituted BODIPY dyes were recently reported18 and it was shown that the charge-transfer processes in these molecules are mostly unidirectional. From the molecular orbital pictures of these molecules, it was inferred that the charge transfer occurs from the donor-substituted aryl ring to the BODIPY moiety. Substitution of acceptor group either alone or in conjunction with methyl group substitution in the BODIPY moiety could alter the charge-transfer pathway. It was also found that the strength of the donor/acceptor substitution as well as rotation of the phenyl ring relative to the BODIPY moiety affect the NLO response properties of these molecules. Apart from altering the substitution pattern and the solvent, an important principle when designing molecules with large TPA cross section lies in a phenomenon called ‘channel interference’. This refers to the constructive or destructive interference between two optical pathways for the two-photon transition in a given molecule. The energies of the involved electronic states and the angle between two transition dipole moment vectors involved in the process determine the constructive or destructive nature of the alternative pathways. This analysis was first proposed by Ågren and co-workers19 for two-dimensional systems wherein only two components of the transition moment vectors are involved. Alam et al.20–22 proposed a general model that can be used for any molecule, irrespectively of its dimensionality.
 |
| | Fig. 1 All fourteen molecules considered in this work. The dihedral angle used for studying the effect of rotation is shown by the red colored bonds. | |
In this contribution, we use the aforesaid analysis tools to study the one- and two-photon absorption properties of charge-transfer based dyes (shown in Fig. 1) belonging to the aryl-substituted BODIPY family. The results are analyzed in terms of a two-state model. The effect of changing the dielectric constant of the medium on the one-photon absorption (OPA) and TPA properties of the most two-photon active aryl-substituted BODIPY molecule (molecule 3 in Fig. 1) is studied. We have also examined how changes in the dihedral angle between the aryl and BODIPY moieties affect the TPA cross section of this molecule.
2 Computational details
The Cartesian coordinates for the gas-phase, ground-state optimized geometry of all the fourteen molecules are taken from a recent work by one of the authors18 and correspond to geometry optimizations at the CAM-B3LYP/6-31+G(d,p) level of theory. The corresponding solvent phase (CH3CN, CH2Cl2 and C6H12) ground-state geometries of the most TPA active molecule (molecule 3 in Fig. 1) have been optimized at the same level of theory using the Gaussian program package.23 The static (and optical) dielectric constants of the three solvents CH3CN, CH2Cl2 and C6H12 are, respectively, 36.640 (1.806), 8.93 (2.020) and 2.02 (2.028). We have also performed a harmonic vibrational frequency analysis of the optimized structures to verify that all are minima on their respective potential energy surfaces. The optimized Cartesian coordinates in the solvents are reported in Tables S1–S3 in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The solvent effects are taken into account using the polarizable continuum model (PCM) of Tomasi and co-workers.25,26 After geometry optimizations and frequency analyses, the OPA and TPA properties of all the molecules are calculated using time-dependent density functional linear and quadratic response theories using the CAM-B3LYP functional27 and the aug-cc-pVDZ basis set, as implemented in the DALTON program package.28,29 Recently, Leonardo et al.30 reported the TPA cross section of some disubstituted BODIPY dyes using their theoretical–experimental studies that revealed that the time-dependent density functional theory (TD-DFT) results are consistent with the experimental values. For both the OPA and TPA calculations in the gas phase, the five lowest singlet-excited states have been considered. However, for the specific study of molecule 3, the excited state having the largest TPA cross section is considered. For studying the effects of rotation of the two parts of molecule 3 on its TPA cross section, we changed the dihedral angle (θ, as shown in Fig. 1) between the phenyl and BODIPY moieties from 0° to 90° at an interval of 10° and calculated the OPA and TPA properties for each dihedral angle at the same level of theory. The geometries of the rotated systems have not been re-optimized. For the solvent calculations, the non-equilibrium formulation of the PCM quadratic response theory is used.31,32 In all solvent calculations, we used atom-centered cavities with the same radius as that used in the Gaussian program package. The radii of the cavities on each of the H, B, C, N and F atoms are 1.4430 Å, 2.0415 Å, 1.9255 Å, 1.8300 Å, and 1.6820 Å respectively. Note that at 40° dihedral angle in the CH2Cl2 solvent, we faced a numerical problem with the convergence of the quadratic response function. We circumvented this situation by using a 41° dihedral angle in place of 40°. To study the contributions of different optical channels to the TPA of molecule 3, we performed two- and three-state model calculations using the generalized few-state model expression of Alam et al.20,22 The transition dipole moment between two excited states, required for few-state model calculations, is calculated using the double residue of the quadratic response function,33,34 at the same level of theory using the DALTON program package.28,29
24 The solvent effects are taken into account using the polarizable continuum model (PCM) of Tomasi and co-workers.25,26 After geometry optimizations and frequency analyses, the OPA and TPA properties of all the molecules are calculated using time-dependent density functional linear and quadratic response theories using the CAM-B3LYP functional27 and the aug-cc-pVDZ basis set, as implemented in the DALTON program package.28,29 Recently, Leonardo et al.30 reported the TPA cross section of some disubstituted BODIPY dyes using their theoretical–experimental studies that revealed that the time-dependent density functional theory (TD-DFT) results are consistent with the experimental values. For both the OPA and TPA calculations in the gas phase, the five lowest singlet-excited states have been considered. However, for the specific study of molecule 3, the excited state having the largest TPA cross section is considered. For studying the effects of rotation of the two parts of molecule 3 on its TPA cross section, we changed the dihedral angle (θ, as shown in Fig. 1) between the phenyl and BODIPY moieties from 0° to 90° at an interval of 10° and calculated the OPA and TPA properties for each dihedral angle at the same level of theory. The geometries of the rotated systems have not been re-optimized. For the solvent calculations, the non-equilibrium formulation of the PCM quadratic response theory is used.31,32 In all solvent calculations, we used atom-centered cavities with the same radius as that used in the Gaussian program package. The radii of the cavities on each of the H, B, C, N and F atoms are 1.4430 Å, 2.0415 Å, 1.9255 Å, 1.8300 Å, and 1.6820 Å respectively. Note that at 40° dihedral angle in the CH2Cl2 solvent, we faced a numerical problem with the convergence of the quadratic response function. We circumvented this situation by using a 41° dihedral angle in place of 40°. To study the contributions of different optical channels to the TPA of molecule 3, we performed two- and three-state model calculations using the generalized few-state model expression of Alam et al.20,22 The transition dipole moment between two excited states, required for few-state model calculations, is calculated using the double residue of the quadratic response function,33,34 at the same level of theory using the DALTON program package.28,29
3 Results and discussion
All the fourteen molecules considered in this work are shown in Fig. 1. H and –CH3 are used as R-groups, whereas for the X-group, H, –NH2, –N(CH3)2, –NO2, –CN, –CH3 and –CHO are used. The presence of a methyl group in the BODIPY moiety increases the dihedral angle (θ) in all these molecules, as is evident from the data given in Table 1. The value of θ is between 50°–60° for molecules with R = –H, whereas for those having R = –CH3, θ is around 90°. We notice that for the molecules having R = –CH3, θ does not vary on changing the X-group. However, for those having R = –H, the dihedral angle gradually decreases with increasing electron-donating power of the X-group and increases with increasing electron-withdrawing power of the X-group, as given in Table 1.
Table 1 Dihedral angle (θ) in the gas-phase optimized geometries of all fourteen molecules studied
| R |
X |
θ (°) |
R |
X |
θ (°) |
| –H |
–N(CH3)2 |
−50.50 |
–CH3 |
–N(CH3)2 |
−89.88 |
| –H |
–NH2 |
−51.69 |
–CH3 |
–NH2 |
−89.68 |
| –H |
–CH3 |
−55.52 |
–CH3 |
–CH3 |
−89.92 |
| –H |
–H |
−56.94 |
–CH3 |
–H |
−89.81 |
| –H |
–CHO |
−58.33 |
–CH3 |
–CHO |
−90.01 |
| –H |
–CN |
−58.47 |
–CH3 |
–CN |
−90.00 |
| –H |
–NO2 |
−59.02 |
–CH3 |
–NO2 |
−90.11 |
3.1 One-photon absorption
The one-photon absorption (OPA) strength of a molecular system is measured by the dimensionless oscillator strength (δ1P), which is proportional to the square of the transition dipole moment between the two states involved and proportional to the corresponding excitation energy. Here, we studied the OPA cross section for a transition from the ground state |S0〉 to the lowest five singlet-excited states (|Si〉, i = 1, 2, …, 5). For a S0 → Si transition, δ1P is given as| |  | (1) |
where ω0i and μ0i are the excitation energy and magnitude of the corresponding transition dipole moment vector, respectively.
A comparison of the OPA strength of all the fourteen molecules in gas phase is shown in Fig. 2, while the absorption energies, the corresponding oscillator strengths and the orbitals involved in the OPA process along with their contributions are shown in Tables S4 and S5 in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The first excited state of all these molecules has the largest oscillator strength and in most of the cases is the only one-photon active state among the five excited states considered. However, in some of the molecules, there exists a second large one-photon active state; for instance, the fourth excited state in molecules 2 and 9, the second excited state in molecules 3 and 7, the third excited state in molecule 11 and the fifth excited state in molecule 13. We note that the value of θ has a significant impact on the OPA of these molecules, which in turn is controlled by the size of the R-group on the BODIPY moiety. For instance, for molecules having R = –CH3, θ is close to 90° and such molecules have a single dominating one-photon active state. On the other hand, for molecules with R = –H, the dihedral angle is around 50°–60° and for these molecules, there exists a second large one-photon active state. Furthermore, the molecules with R = –CH3 have larger δ1P values than the molecules with R = –H. An examination of the S0 → Si excitation energies and the corresponding transition dipole moments (Fig. 2) indicate that the variation of the oscillator strength follows the corresponding variation in transition dipole moments rather than the excitation energies. There are no significant variations in the excitation energies of a particular excited state among the molecules considered here. The orbitals involved in the dominant transitions in all these molecules are given in the ESI† (Tables S4 and S5).24 We note that the dominant transitions (i.e., S0 → S1) in all the molecules with R = –H are short-range local transitions, mainly a rearrangement of electron density in the BODIPY moiety. In contrast, for molecules having R = –CH3, the dominant transitions are a mixture of both long- and short-range orbital transitions. This is also consistent with the orbital pictures in ref. 18 and the Λ parameter35 provided in the ESI.†
24 The first excited state of all these molecules has the largest oscillator strength and in most of the cases is the only one-photon active state among the five excited states considered. However, in some of the molecules, there exists a second large one-photon active state; for instance, the fourth excited state in molecules 2 and 9, the second excited state in molecules 3 and 7, the third excited state in molecule 11 and the fifth excited state in molecule 13. We note that the value of θ has a significant impact on the OPA of these molecules, which in turn is controlled by the size of the R-group on the BODIPY moiety. For instance, for molecules having R = –CH3, θ is close to 90° and such molecules have a single dominating one-photon active state. On the other hand, for molecules with R = –H, the dihedral angle is around 50°–60° and for these molecules, there exists a second large one-photon active state. Furthermore, the molecules with R = –CH3 have larger δ1P values than the molecules with R = –H. An examination of the S0 → Si excitation energies and the corresponding transition dipole moments (Fig. 2) indicate that the variation of the oscillator strength follows the corresponding variation in transition dipole moments rather than the excitation energies. There are no significant variations in the excitation energies of a particular excited state among the molecules considered here. The orbitals involved in the dominant transitions in all these molecules are given in the ESI† (Tables S4 and S5).24 We note that the dominant transitions (i.e., S0 → S1) in all the molecules with R = –H are short-range local transitions, mainly a rearrangement of electron density in the BODIPY moiety. In contrast, for molecules having R = –CH3, the dominant transitions are a mixture of both long- and short-range orbital transitions. This is also consistent with the orbital pictures in ref. 18 and the Λ parameter35 provided in the ESI.†
 |
| | Fig. 2 Oscillator strengths, transition dipole moments and excitation energies for S0 → Si, (i = 1, 2,…,5) transitions in all the fourteen molecules in gas phase. | |
3.2 Two-photon absorption
The TPA activity is measured in terms of the TP transition probability (δ2P), which depends on not only the molecular system, but also the polarization of the incident light. Here, we studied TPA caused by linearly polarized light. The expression for δ2P in a molecular system when a single beam of linearly polarized monochromatic light is used is given as36| |  | (2) |
where the indices α, β represent the Cartesian coordinates {x,y,z} and Sαβ is the αβ'th component of the two-photon transition moment S. For S0 → Sf transitions, Sαβ can be written as a sum-over-states expression| | 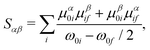 | (3) |
where μαij represents the α'th component of the μij transition dipole moment vector. Other terms have their usual meanings. In this work, we will use three different methods to calculate the value of δ2P, viz. quadratic response theory, a two-state and a three-state model, and we will use δ2PResp, δ2P2SM and δ2P3SM to denote which model has been used to calculate δ2P.
A comparison of the TPA activity of the first five singlet-excited states of all the fourteen molecules in the gas phase is shown in Fig. 3. The vacuum phase TPA data of molecules (1–14) obtained from the quadratic response theory as well as through two- and three-state model calculations are reported in Tables S6 and S7 in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 To the best of our knowledge, except for molecule 2, none of the other molecules considered for the present study has been studied experimentally for two-photon absorption. The reported experimental37 TPA cross section of molecule 2 is 4 GM, which is very small and is consistent with our theoretically calculated value. It is interesting to note that unlike the OPA plot (Fig. 2), the TPA plot is much less crowded as only a few molecules are found to have significant TPA cross sections. The TPA cross section of molecule 3 dominates over all the other 13 molecules. Molecule 7 has the second largest TPA cross section and molecules 11 and 9 are the third and fourth most TPA-active molecules. The ratios of δ2PResp of these four molecules are 1
24 To the best of our knowledge, except for molecule 2, none of the other molecules considered for the present study has been studied experimentally for two-photon absorption. The reported experimental37 TPA cross section of molecule 2 is 4 GM, which is very small and is consistent with our theoretically calculated value. It is interesting to note that unlike the OPA plot (Fig. 2), the TPA plot is much less crowded as only a few molecules are found to have significant TPA cross sections. The TPA cross section of molecule 3 dominates over all the other 13 molecules. Molecule 7 has the second largest TPA cross section and molecules 11 and 9 are the third and fourth most TPA-active molecules. The ratios of δ2PResp of these four molecules are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50
0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.19
0.19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.13. Molecules 3 and 7 are structurally similar – molecule 3 has –N(CH3)2 as the X-group, whereas molecule 7 has –NH2 (Fig. 1). It is interesting to note that unlike the trend observed for the OPA cross section, the molecules with R = –H have significantly larger TPA cross sections than those with R = –CH3. This can be correlated with the synergistic effect of θ and the nature of the X- and R-groups.
0.13. Molecules 3 and 7 are structurally similar – molecule 3 has –N(CH3)2 as the X-group, whereas molecule 7 has –NH2 (Fig. 1). It is interesting to note that unlike the trend observed for the OPA cross section, the molecules with R = –H have significantly larger TPA cross sections than those with R = –CH3. This can be correlated with the synergistic effect of θ and the nature of the X- and R-groups.
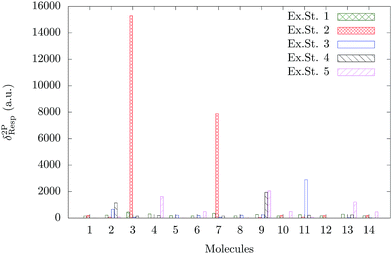 |
| | Fig. 3 TPA strength of the first five excited states of all the fourteen molecules in gas phase. | |
3.2.1 Few-state models.
To rationalize the large TPA cross section of molecule 3, we used few-state models,20,22 more specifically, the two- and three-state models. The few-state model calculations are based on the generalized few-state model expression initially developed for TPA by Alam, Chattopadhyaya and Chakrabarti,20 and then further generalized by Alam, Beerepoot and Ruud.22 The main feature of the latter22 is that the transition probabilities can be calculated for any multiphoton absorption process including any number of intermediate states. One of the main advantages of the generalized few-state model is that it can identify which excited states contribute most significantly to the overall TPA activity of a given system. Furthermore, it describes the TPA process as a sum of contributions from the interference of different optical channels. Depending on the transition dipole moment vectors involved and their relative orientations, these interferences can contribute constructively or destructively to the overall TPA activity and hence the model provides a deeper understanding of the physical process. Nevertheless, one must keep in mind that few-state models may give misleading results if the most-contributing states are not included in the calculation. For this reason it is instructive always to use few-state model results with reference to some standard methods, such as quadratic response theory. The few-state model expression for the two-photon transition probability, δ2PFSM, is given as22| | 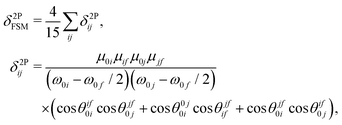 | (4) |
where δ2Pij represents the value of δ2P due to the interference between the optical channels S0 → Si → Sf and S0 → Sj → Sf, and θcdab represents the angle between the transition dipole moment vectors μab and μcd. Note that μaa represents the dipole moment of the ath state. Other terms have their usual meaning. The channel interference terms involved in the 2SM expressions are given as| | 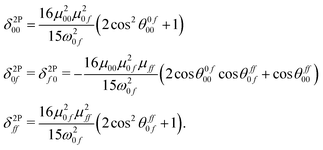 | (5) |
These four terms also appear in the expression for the 3SM. There are three additional terms of the same form as δ2P0i, δ2Pii and δ2Pif, with the first and the last ones appearing twice in the 3SM. ‘i’ is here an intermediate state. The quadratic response and the 2SM results for the first five excited states in all the fourteen molecules in the gas phase are presented in Table 2. Note that unlike the 2SM, the 3SM is not unique in the sense that the latter involves an intermediate state. For example, if we construct a 3SM for the third excited state and if we have data for five excited states, a total of four 3SM will be possible with the first, second, fourth and fifth excited states as intermediates. Furthermore, each 3SM contains a total of six unique channel interference terms (i.e., δ terms). All these considerations complicate the analysis and are part of the reason why we do not present the 3SM results in Table 2. In addition, the 3SM provides only very minor improvements in the δ2PFSM values when going from the 2SM to the 3SM. In all these molecules, the magnitudes of the additional 3SM terms (i.e., δ2P0i, δ2Pii and δ2Pif) are very small compared to those of the 2SM terms (i.e., δ2P00, δ2Pff and δ2P0f). The full few-state model output data can be found in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The results in Table 2 show that the δ2P00 and δ2Pff terms in many cases have large positive values that are almost completely compensated by the destructive contribution from δ2P0f. Let us, for instance, consider the 2SM result for the first excited state in molecule 5. This molecule contains the strongest electron-donating group (–N(CH3)2), as is also the case for the molecule with the largest TPA, molecule 3, but it shows a very low TPA cross section. For molecule 5, the contributions from the δ2P00 and δ2Pff terms are 5.440 × 103 a.u. and 6.600 × 103 a.u., respectively. The total contribution from these two terms is therefore 12.040 × 103 a.u., which is very close to the highest TPA cross section (δ2P2SM = 15.300 × 103 a.u.) among the fourteen molecules. However, this is largely compensated by the negative contribution from δ2P0f (−11.984 × 103 a.u.), reducing the overall TPA cross section of the first excited state in molecule 5 to only 0.056 × 103 a.u. A close inspection of the transition moments involved and their relative orientations reveals that for this molecule, all the transition dipole moment terms involved have relatively large values, μ00 = 2.923 a.u., μ01 = 2.674 a.u., and μ11 = 3.221 a.u., respectively, due to the strong electron-donating group, and these vectors orient themselves in such a way that all the cosine terms are positive (cos
24 The results in Table 2 show that the δ2P00 and δ2Pff terms in many cases have large positive values that are almost completely compensated by the destructive contribution from δ2P0f. Let us, for instance, consider the 2SM result for the first excited state in molecule 5. This molecule contains the strongest electron-donating group (–N(CH3)2), as is also the case for the molecule with the largest TPA, molecule 3, but it shows a very low TPA cross section. For molecule 5, the contributions from the δ2P00 and δ2Pff terms are 5.440 × 103 a.u. and 6.600 × 103 a.u., respectively. The total contribution from these two terms is therefore 12.040 × 103 a.u., which is very close to the highest TPA cross section (δ2P2SM = 15.300 × 103 a.u.) among the fourteen molecules. However, this is largely compensated by the negative contribution from δ2P0f (−11.984 × 103 a.u.), reducing the overall TPA cross section of the first excited state in molecule 5 to only 0.056 × 103 a.u. A close inspection of the transition moments involved and their relative orientations reveals that for this molecule, all the transition dipole moment terms involved have relatively large values, μ00 = 2.923 a.u., μ01 = 2.674 a.u., and μ11 = 3.221 a.u., respectively, due to the strong electron-donating group, and these vectors orient themselves in such a way that all the cosine terms are positive (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1100 = 1.00, cos
θ1100 = 1.00, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0100 = 0.03 and cos
θ0100 = 0.03 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1101 = 0.03). From eqn (5), it then follows that δ2P0f becomes negative. This is the case for most of the molecules considered in this work. Exceptions do exist, such as the first four excited states in molecule 6, second excited state in molecule 5, all five excited states in molecules 9 and 10 etc., where the low TPA cross section is mainly due to very low values of the dipole moment vectors. This illustrates that a small TPA cross section does not necessarily result from the small magnitude of the transition dipole moment vectors involved, but also the relative orientations of these vectors. Optimization of TPA cross sections thus cannot only focus on maximizing the contributing transition dipole vectors. For the second excited states in molecules 3 and 7 (the two largest TPA-active systems), all the δ2P terms have positive values and are larger than in any of the other molecules in the gas phase. The angle terms (the terms in parenthesis in eqn (5)) are also positive and close to the maximum value of +3. Furthermore, in molecule 3, the presence of a strong electron-donating group (–N(CH3)2) makes the dipole moments involved very large, making the second excited state in molecule 3 the state with the largest TPA. A pictorial representation of the different transition moment and dipole moment vectors in molecule 3 is provided in Fig. S4 of the ESI.†
θ1101 = 0.03). From eqn (5), it then follows that δ2P0f becomes negative. This is the case for most of the molecules considered in this work. Exceptions do exist, such as the first four excited states in molecule 6, second excited state in molecule 5, all five excited states in molecules 9 and 10 etc., where the low TPA cross section is mainly due to very low values of the dipole moment vectors. This illustrates that a small TPA cross section does not necessarily result from the small magnitude of the transition dipole moment vectors involved, but also the relative orientations of these vectors. Optimization of TPA cross sections thus cannot only focus on maximizing the contributing transition dipole vectors. For the second excited states in molecules 3 and 7 (the two largest TPA-active systems), all the δ2P terms have positive values and are larger than in any of the other molecules in the gas phase. The angle terms (the terms in parenthesis in eqn (5)) are also positive and close to the maximum value of +3. Furthermore, in molecule 3, the presence of a strong electron-donating group (–N(CH3)2) makes the dipole moments involved very large, making the second excited state in molecule 3 the state with the largest TPA. A pictorial representation of the different transition moment and dipole moment vectors in molecule 3 is provided in Fig. S4 of the ESI.†
Table 2 Quadratic response theory and 2SM results for TPA of the first five excited states in all the fourteen molecules in gas phase. All the δ2P values are reported in orders of 103 a.u.
| # |
δ
2PResp
|
2SM |
# |
δ
2PResp
|
2SM |
|
δ
2P00
|
2δ2P0f |
δ
2P
ff
|
δ
2P2SM
|
δ
2P00
|
2δ2P0f |
δ
2P
ff
|
δ
2P2SM
|
| # represents the molecule's numbering. |
| 1 |
0.155 |
2.339 |
−5.347 |
3.056 |
0.048 |
8 |
0.168 |
4.444 |
−9.819 |
5.427 |
0.052 |
| 0.198 |
0.090 |
−0.190 |
0.100 |
0.000 |
0.002 |
0.000 |
0.001 |
0.001 |
0.002 |
| 0.000 |
0.201 |
−0.452 |
0.254 |
0.003 |
0.207 |
0.167 |
−0.353 |
0.186 |
0.001 |
| 0.003 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.357 |
−0.783 |
0.431 |
0.004 |
| 0.001 |
0.000 |
−0.001 |
0.002 |
0.001 |
0.009 |
0.049 |
−0.078 |
0.031 |
0.002 |
|
|
| 2 |
0.217 |
2.553 |
−6.013 |
3.540 |
0.080 |
9 |
0.271 |
0.015 |
−0.123 |
0.244 |
0.137 |
| 0.068 |
0.195 |
−0.473 |
0.287 |
0.009 |
0.041 |
0.001 |
−0.011 |
0.027 |
0.017 |
| 0.659 |
0.049 |
−0.078 |
0.031 |
0.002 |
0.248 |
0.001 |
−0.006 |
0.016 |
0.010 |
| 1.140 |
1.642 |
0.003 |
0.000 |
1.645 |
1.940 |
0.013 |
0.499 |
4.886 |
5.398 |
| 0.089 |
0.009 |
0.014 |
0.006 |
0.029 |
2.060 |
0.000 |
−0.011 |
0.162 |
0.151 |
|
|
| 3 |
0.452 |
6.408 |
−14.684 |
8.412 |
0.136 |
10 |
0.163 |
0.029 |
−0.059 |
0.081 |
0.052 |
| 15.300 |
14.093 |
6.551 |
0.762 |
21.406 |
0.192 |
0.001 |
−0.002 |
0.002 |
0.001 |
| 0.058 |
0.434 |
−1.034 |
0.615 |
0.016 |
0.002 |
0.000 |
−0.000 |
0.001 |
0.001 |
| 0.143 |
0.846 |
−2.073 |
1.271 |
0.043 |
0.001 |
0.001 |
−0.002 |
0.005 |
0.004 |
| 0.006 |
0.103 |
−0.100 |
0.024 |
0.027 |
0.499 |
0.000 |
−0.001 |
0.901 |
0.901 |
|
|
| 4 |
0.307 |
0.008 |
−0.098 |
0.305 |
0.215 |
11 |
0.254 |
3.185 |
−7.456 |
4.364 |
0.093 |
| 0.004 |
0.001 |
−0.009 |
0.038 |
0.029 |
0.068 |
0.239 |
−0.577 |
0.348 |
0.010 |
| 0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
2.900 |
2.081 |
1.754 |
0.369 |
4.204 |
| 0.198 |
0.000 |
−0.007 |
0.025 |
0.018 |
0.207 |
0.676 |
−1.636 |
0.991 |
0.030 |
| 1.630 |
0.000 |
−0.028 |
0.763 |
0.735 |
0.071 |
0.010 |
0.012 |
0.004 |
0.026 |
|
|
| 5 |
0.179 |
5.440 |
−11.984 |
6.600 |
0.056 |
12 |
0.164 |
2.915 |
−6.600 |
3.736 |
0.051 |
| 0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.202 |
0.111 |
−0.235 |
0.124 |
0.000 |
| 0.215 |
0.200 |
−0.420 |
0.221 |
0.001 |
0.000 |
0.252 |
−0.564 |
0.315 |
0.003 |
| 0.001 |
0.446 |
−0.979 |
0.537 |
0.004 |
0.002 |
0.000 |
0.000 |
0.000 |
0.000 |
| 0.007 |
0.095 |
−0.116 |
0.035 |
0.015 |
0.001 |
0.000 |
−0.001 |
0.002 |
0.001 |
|
|
| 6 |
0.160 |
0.042 |
0.008 |
0.000 |
0.050 |
13 |
0.293 |
0.839 |
−2.225 |
1.550 |
0.164 |
| 0.004 |
0.000 |
0.000 |
0.003 |
0.003 |
0.000 |
0.000 |
−0.000 |
0.000 |
0.000 |
| 0.190 |
0.002 |
−0.001 |
0.000 |
0.001 |
0.033 |
0.062 |
−0.176 |
0.132 |
0.018 |
| 0.001 |
0.003 |
0.000 |
0.000 |
0.004 |
0.242 |
0.016 |
−0.052 |
0.043 |
0.007 |
| 0.484 |
0.002 |
0.078 |
0.792 |
0.873 |
1.210 |
0.508 |
1.718 |
2.108 |
4.335 |
|
|
| 7 |
0.351 |
4.998 |
−11.480 |
6.595 |
0.113 |
14 |
0.164 |
0.552 |
−1.318 |
0.818 |
0.051 |
| 7.890 |
7.016 |
3.803 |
0.545 |
11.365 |
0.195 |
0.022 |
−0.047 |
0.026 |
0.001 |
| 0.058 |
0.355 |
−0.848 |
0.506 |
0.013 |
0.013 |
0.000 |
−0.002 |
0.017 |
0.016 |
| 0.155 |
0.651 |
−1.604 |
0.987 |
0.035 |
0.000 |
0.028 |
−0.072 |
0.048 |
0.004 |
| 0.006 |
0.028 |
−0.016 |
0.002 |
0.015 |
0.475 |
0.014 |
−0.196 |
0.952 |
0.769 |
3.2.2 Solvent effect on TPA process.
In the gas phase, the second excited state in molecule 3 has the strongest TPA cross section among the five singlet-excited states of the fourteen molecules studied. The aforesaid result probably arises from a combination of a strong electron-donating group –N(CH3)2 and the relative orientations of the involved transition dipole moment vectors. Therefore, it would be interesting to study the TPA process in molecule 3 in more detail. In particular, we will focus on the solvent effect on the TPA process of this particular state. To do this, we performed quadratic response as well as few-state model analysis of the TPA process in molecule 3 in three different solvents, viz., C6H12, CH2Cl2 and CH3CN. The results are presented in Table 3. The highest TPA-active state of molecule 3 in the gas phase and in C6H12 is the second excited state, whereas it is the first excited state in the other two solvents. However, in all the cases, we deal with the same excited state, confirmed by the nature of the orbitals involved (Fig. S3 in ESI†).
Table 3 TPA data for molecule 3 in gas phase and in three solvents, viz. C6H12,CH2Cl2 and CH3CN. All the δ2P values are given in the order of 103 a.u. The μ-terms are in atomic units
| Solvent |
δ
2PResp
|
2SM |
δ
2P3SM
|
μ
00
|
μ
0f
|
μ
ff
|
|
δ
2P00
|
2δ2P0f |
δ
2P
ff
|
δ
2P2SM
|
| Gas phase |
15.300 |
14.093 |
6.551 |
0.762 |
21.406 |
20.400 |
3.716 |
2.090 |
0.864 |
| C6H12 |
31.100 |
30.238 |
11.399 |
1.074 |
42.711 |
40.282 |
4.288 |
2.473 |
0.808 |
| CH2Cl2 |
37.000 |
52.728 |
−4.367 |
0.090 |
48.452 |
51.900 |
4.993 |
2.648 |
0.207 |
| CH3CN |
35.500 |
60.036 |
−15.115 |
0.951 |
45.872 |
43.505 |
5.218 |
2.670 |
0.657 |
From the results, it is apparent that there is a significant increase in the TPA activity of molecule 3 when going from gas phase to a solvent. However, a small decrease in the TPA cross section is observed when the solvent is changed from the moderately polar CH2Cl2 to the highly polar CH3CN solvent or to the less polar C6H12. This is consistent with the general observations that the donor–π–acceptor systems show larger TPA activity in moderately polar solvents as compared with that in very high or very low-polarity solvents.38–40 The trend of δ2P obtained from the 2SM and 3SM calculations is consistent with the response theory results. However, the former overestimates the latter. We notice that the ratio δ2P2SM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ2PResp gradually decreases with increasing solvent polarity. The corresponding ratios in gas phase, C6H12, CH2Cl2 and CH3CN solvents are 1.399
δ2PResp gradually decreases with increasing solvent polarity. The corresponding ratios in gas phase, C6H12, CH2Cl2 and CH3CN solvents are 1.399![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.373
1.373![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.309
1.309![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.292. When going from 2SM to 3SM, the agreement with the response theory results improves slightly in gas phase and in C6H12 and CH3CN. However, the difference between the 2SM and 3SM results is small, indicating that the terms δ2P0i, δ2Pii and δ2Pif (i.e., those appearing only in the 3SM) contribute little to the overall TPA activity. For brevity, only the contributions of the terms involved in the 2SM are shown in Table 3. The full 2SM and 3SM results are provided in the ESI.†
1.292. When going from 2SM to 3SM, the agreement with the response theory results improves slightly in gas phase and in C6H12 and CH3CN. However, the difference between the 2SM and 3SM results is small, indicating that the terms δ2P0i, δ2Pii and δ2Pif (i.e., those appearing only in the 3SM) contribute little to the overall TPA activity. For brevity, only the contributions of the terms involved in the 2SM are shown in Table 3. The full 2SM and 3SM results are provided in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The larger TPA cross section of molecule 3 in CH2Cl2 than in either gas phase or the other two solvents can be explained by considering the terms contributing to the 2SM. It is interesting to note that in both gas phase and in the three solvents, δ2P00 is the largest contributing term, whereas δ2Pff has the smallest contribution (Table 3). In all cases, the angle terms, i.e., the term in parenthesis in eqn (5) are close to the maximum value of +3. Furthermore, as is evident from Table 3, μ00 in the gas phase is much smaller than in the three solvents and hence δ2P00 in the gas phase is much smaller than in solvent. The most interesting result is δ2P0f: in gas phase and in C6H12, δ2P0f contributes constructively, but in the other two solvents it has destructive contributions. Interestingly, with the decrease in polarity of the solvent, the magnitude of destructive contribution of δ2P0f gradually decreases and becomes constructive in a solvent with very low polarity. Similar results were reported by Alam et al.41 for two through-space charge-transfer systems. Molecule 3 is the first through-bond charge-transfer system where a change in the nature of channel interference is observed with a change in solvent polarity. As is evident from eqn (5), the expression for δ2P0f already has a negative sign, and all the terms except the cosine of the angles are inherently positive quantities. This clearly reflects that the orientations of the three dipole moment vectors (μ00, μ0f and μff) are such that the corresponding angle term (the term in parenthesis) is negative in the gas phase and in C6H12, but is positive in the other two solvents. This is supported by the calculated values of the cosine of the angle between dipoles involved. The values of cos
24 The larger TPA cross section of molecule 3 in CH2Cl2 than in either gas phase or the other two solvents can be explained by considering the terms contributing to the 2SM. It is interesting to note that in both gas phase and in the three solvents, δ2P00 is the largest contributing term, whereas δ2Pff has the smallest contribution (Table 3). In all cases, the angle terms, i.e., the term in parenthesis in eqn (5) are close to the maximum value of +3. Furthermore, as is evident from Table 3, μ00 in the gas phase is much smaller than in the three solvents and hence δ2P00 in the gas phase is much smaller than in solvent. The most interesting result is δ2P0f: in gas phase and in C6H12, δ2P0f contributes constructively, but in the other two solvents it has destructive contributions. Interestingly, with the decrease in polarity of the solvent, the magnitude of destructive contribution of δ2P0f gradually decreases and becomes constructive in a solvent with very low polarity. Similar results were reported by Alam et al.41 for two through-space charge-transfer systems. Molecule 3 is the first through-bond charge-transfer system where a change in the nature of channel interference is observed with a change in solvent polarity. As is evident from eqn (5), the expression for δ2P0f already has a negative sign, and all the terms except the cosine of the angles are inherently positive quantities. This clearly reflects that the orientations of the three dipole moment vectors (μ00, μ0f and μff) are such that the corresponding angle term (the term in parenthesis) is negative in the gas phase and in C6H12, but is positive in the other two solvents. This is supported by the calculated values of the cosine of the angle between dipoles involved. The values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θff00 and cos
θff00 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0f00 are −1.0 in the gas phase and in C6H12 but +1.0 in the other two solvents. The largest TPA cross section in CH2Cl2 is a result of the large magnitude of δ2P00 and the small value of the destructive δ2P0f. Interestingly, the reasons for the decrease in δ2P2SM when moving from CH2Cl2 to CH3CN and to C6H12 are different. When moving from CH2Cl2 to the polar CH3CN solvent, the compensation of δ2P00 by the destructive δ2P0f increases and hence δ2P2SM decreases. On the other hand, when moving from CH2Cl2 to the low-polar C6H12 solvent, the magnitudes of the corresponding dipole moment vectors decrease and hence the corresponding δ2P2SM is also decreased.
θ0f00 are −1.0 in the gas phase and in C6H12 but +1.0 in the other two solvents. The largest TPA cross section in CH2Cl2 is a result of the large magnitude of δ2P00 and the small value of the destructive δ2P0f. Interestingly, the reasons for the decrease in δ2P2SM when moving from CH2Cl2 to CH3CN and to C6H12 are different. When moving from CH2Cl2 to the polar CH3CN solvent, the compensation of δ2P00 by the destructive δ2P0f increases and hence δ2P2SM decreases. On the other hand, when moving from CH2Cl2 to the low-polar C6H12 solvent, the magnitudes of the corresponding dipole moment vectors decrease and hence the corresponding δ2P2SM is also decreased.
3.2.3 Variation of TPA activity with dihedral angle.
Alam, Chattopadhyaya and Chakrabarti42 studied the effect of rotating two rings in o-betaine on the relative orientations of the transition dipole moments, channel interference and hence the TPA process in the molecule. They42 reported that for a particular dihedral angle, the TPA activity is maximized. The present system also has such a dihedral angle, viz. C1–C2–C3–C4 between the phenyl ring and the BODIPY moiety (shown in Fig. 1 as θ). In Table 3, we have already seen that there is a change in the nature of the channel interference when going from gas phase to a solvent or on decreasing polarity of solvents. These results make it interesting to study the effect of rotation about θ on the nature and magnitude of channel interference in molecule 3. Fig. 4 shows the variation of δ2PResp and δ2P2SM with θ in gas phase and in the three solvents. The variation of OPA and TPA properties of molecule 3 with varying C1–C2–C3–C4 dihedral angle in the gas phase and in the three solvents is shown in Tables S8–S11, in the ESI,†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 respectively. It is interesting to note that in gas phase and in C6H12, the variations of δ2P are very slow at the beginning, in particular from θ = 0° to θ = 50°. Thereafter, there is a rapid decrease in δ2P until it reaches a minimum at θ = 90°. On the other hand, in the other two solvents, the variation of δ2P is faster at the beginning, increasing significantly when going from a θ of 0° to 50°. A further increase in θ causes a rapid decrease similar to that observed in the gas phase and in C6H12. δ2P attains a maximum value for θ around 40°–50°.
24 respectively. It is interesting to note that in gas phase and in C6H12, the variations of δ2P are very slow at the beginning, in particular from θ = 0° to θ = 50°. Thereafter, there is a rapid decrease in δ2P until it reaches a minimum at θ = 90°. On the other hand, in the other two solvents, the variation of δ2P is faster at the beginning, increasing significantly when going from a θ of 0° to 50°. A further increase in θ causes a rapid decrease similar to that observed in the gas phase and in C6H12. δ2P attains a maximum value for θ around 40°–50°.
 |
| | Fig. 4 Variation of TPA strength of highest TP active excited state in molecule-3 against the dihedral angle. Solid lines represent “quadratic response theory results,” whereas dashed lines represent the 2SM results. The ‘‘+” point type represents the gas phase results, whereas *, □ and ● point types represent the results in C6H12, CH2Cl2 and CH3CN solvents, respectively. | |
To investigate these results in more detail, we considered the changes in different channel interference contributions and also that of all the different terms in each of the δ2Pij appearing in the 2SM expression. We divided the expression of δ2Pij, eqn (5), into four parts22
| |  | (6) |
where
Pij is the prefactor, which is the same

for each
δ2Pij, and
Dij is the contribution from the magnitude of the (transition) dipole moments and hence is named the
D-term.
Eij and
Aij in
eqn (6) are the contributions from the excitation energies and angle between the transition dipole moments, respectively.
The variations of each of the δ2Pij and that of the total δ2P2SM with θ are shown in Fig. 5. Similarly, the variations of all the D-, A- and E-terms are shown in Fig. 6–8 respectively. The variations of different transition dipole moments (μ00, μ0f and μff) and the cosine of the angle between them are presented in the ESI† (Fig. S1 and S2).24 The contributions from different optical channels involved in 2SM calculations on the two-photon activity of molecule 3 with varying θ are shown in Tables S12 and S13 in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24Fig. 8 shows that the variations of the E-terms are the same in gas phase and in the three solvents. Thus, the variation of δ2Pij is mainly controlled by the D and A terms. Furthermore, Fig. 7 shows that all the angle terms are either +3 or −3. Only some of the A0f terms have negative values. The other two A terms are always positive, as expected from eqn (5). For 0° ≤ θ ≤ 30°, in the gas phase and in C6H12, A0f is positive and for the rest, it is negative. In the other two solvents CH2Cl2 and CH3CN, A0f is positive only for the ranges 0°–40° and 0°–50°, respectively. The variations of A0f (which is the only term controlling the sign of channel interference) indicate a change in nature of the corresponding δ2P0f term when the molecule is twisted. This is visible in Fig. 5.
24Fig. 8 shows that the variations of the E-terms are the same in gas phase and in the three solvents. Thus, the variation of δ2Pij is mainly controlled by the D and A terms. Furthermore, Fig. 7 shows that all the angle terms are either +3 or −3. Only some of the A0f terms have negative values. The other two A terms are always positive, as expected from eqn (5). For 0° ≤ θ ≤ 30°, in the gas phase and in C6H12, A0f is positive and for the rest, it is negative. In the other two solvents CH2Cl2 and CH3CN, A0f is positive only for the ranges 0°–40° and 0°–50°, respectively. The variations of A0f (which is the only term controlling the sign of channel interference) indicate a change in nature of the corresponding δ2P0f term when the molecule is twisted. This is visible in Fig. 5.
 |
| | Fig. 5 Contribution of different optical channels on TP activity of molecule 3 in gas phase (top left), in C6H12 (top right), CH2Cl2 (bottom left) and in CH3CN (bottom right). | |
 |
| | Fig. 6 Variation of different D-terms involved in 2SM in gas phase (top left), in C6H12 (top right), CH2Cl2 (bottom left) and in CH3CN (bottom right) in molecule 3. D00 = μ200μ20f, D0f = μ00μ20fμff and Dff = μ20fμ2ff. | |
 |
| | Fig. 7 Variation of different A terms involved in 2SM in gas phase (top left), in C6H12 (top right), CH2Cl2 (bottom left) and in CH3CN (bottom right) in molecule 3. A00 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0f00 + 1, A0f = 2 θ0f00 + 1, A0f = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0f00 θ0f00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θff0f + cos θff0f + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θff00 and Aff = 2 θff00 and Aff = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θff0f + 1. θff0f + 1. | |
 |
| | Fig. 8 Variation of different E-terms involved in 2SM in gas phase (top left), in C6H12 (top right), CH2Cl2 (bottom left) and in CH3CN (bottom right) in molecule 3. E00 = ΔE201, E0f = ΔE01ΔEf1 and Eff = ΔE2f1, where  and and 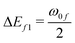 . . | |
After discussing the constructive/destructive nature of different δ terms, let us now discuss their magnitudes. The variations of different δ terms in Fig. 5 show that in both the gas phase and the three solvents, δ2P00 and δ2Pff are respectively the largest and the smallest contributing terms. The former gradually decreases when twisting the molecule, whereas δ2Pff oscillates. These variations can be explained by considering the variation of the corresponding transition moments (see Fig. S1 and S2 in ESI†).24 We note that with increase in θ, μ00 does not vary much, as compared to μ0f. Thus, the large values of δ2P00 are due to the larger values of both μ00 and μ0f, but its decrease with increasing θ is really due to the drastic decrease in μ0f. The second-most contributing channel interference term is δ2P0f, which also decreases when the molecule is twisted until it reaches a very small value at θ = 40°–50°. When increasing θ further, first it slightly increases and then again falls to a very small value. This is true in both the gas phase and the three solvents. As shown in the ESI,†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24μff also shows a similar variation, which indicates that the oscillation of δ2P0f is due to this dipole moment. For θ = 40°–50°, all the δ terms have moderate, but positive values (or a small negative value) and hence in this range for the dihedral angle, the overall δ2P2SM acquires the maximum value.
24μff also shows a similar variation, which indicates that the oscillation of δ2P0f is due to this dipole moment. For θ = 40°–50°, all the δ terms have moderate, but positive values (or a small negative value) and hence in this range for the dihedral angle, the overall δ2P2SM acquires the maximum value.
4 Conclusions
We have studied the channel interference in the two-photon absorption (TPA) processes in fourteen aryl-substituted BODIPY dyes using quadratic response theory and generalized few-state model analysis. We have also studied the effect of twisting of the aryl ring with respect to the BODIPY moiety, and the polarity of the medium on the TPA process and channel interference in the BODIPY dye with the largest TPA activity. The twist angle has been found to depend on the substituent on the BODIPY moiety as well as on the nature of the substituent on the phenyl ring. The TPA activity is found to be strongly affected by the change in the twist angle. All molecules having a methyl substituent on the BODIPY moiety have twist angles close to 90° and show very low TPA cross sections. Only molecule 3 in Fig. 1, having no substituent on the BODIPY moiety and a strong electron-donating group in the para position on the phenyl group, shows a large TPA activity, with the largest TPA cross section obtained for the moderately polar solvent CH2Cl2. With decreasing solvent polarity, the magnitude of the only destructive channel interference term (δ2P0f) gradually decreases, even changing to a constructive term in solvents of very low polarity. This is due only to the relative orientations of the involved transition moment vectors. The channel interference also changes when the molecule is twisted. Irrespective of the nature of the solvent, δ2P0f is destructive for small twist angles (θ = 0°–50°) and constructive for θ = 60°–90°. For small twist angles, the large and constructive contribution of δ2P00 is largely compensated by the destructive contribution from δ2P0f. On the other hand, for large dihedral angles, all terms become very small. However, for θ = 40°–50°, all the constructive channel interference terms have moderate values, whereas the destructive one (if any) has a very small value. The TPA cross section thus achieves its maximum value in this range of the twist angle.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has received support from the Research Council of Norway through a FRIPRO grant (Grant No. 250743, 262695).
References
- F. Ricci, B. Carlotti, B. Keller, C. Bonaccorso, C. G. Fortuna, T. Goodson, F. Elisei and A. Spalletti, J. Phys. Chem. C, 2017, 121, 3987–4001 CAS.
- K. P. Divya, S. Sreejith, P. Ashokkumar, K. Yuzhan, Q. Peng, S. K. Maji, Y. Tong, H. Yu, Y. Zhao, P. Ramamurthy and A. Ajayaghosh, Chem. Sci., 2014, 5, 3469–3474 RSC.
- M. Pawlicki, H. Collins, R. Denning and H. Anderson, Angew. Chem., Int. Ed., 2009, 48, 3244–3266 CrossRef CAS PubMed.
-
F. Kajar and J. M. Nunzi, Functional organic and polymeric materials, John Wiley & Sons Ltd., New York, 3rd edn, 2000 Search PubMed.
- W. R. Zipfel, R. M. Williams and W. W. Webb, Nat. Biotechnol., 2003, 21, 1369–1377 CrossRef CAS PubMed.
- B. H. Cumpston, S. P. Anathavel, S. Barlow, D. L. Dyer, J. E. Ehrlich, L. L. Erskine, A. A. Heikal, S. Kueble, I.-Y. S. Lee, D. McCord-Maughon, J. Qin, H. Rockel, M. Rumi, X.-L. Wu, S. R. Marder and J. Perry, Nature, 1999, 398, 51–54 CrossRef CAS.
- M. Rumi, J. E. Ehrlich, A. A. Heikal, J. W. Perry, S. Barlow, Z. Hu, D. McCord-Maughon, T. C. Parker, H. Röckel, S. Thayumanavan, S. R. Marder, D. Beljonne and J.-L. Brédas, J. Am. Chem. Soc., 2000, 122, 9500–9510 CrossRef CAS.
- P. N. Day, K. A. Nguyen and R. Pachter, J. Chem. Phys., 2006, 125, 094103 CrossRef PubMed.
- K. S. Kim, S. B. Noh, T. Katsuda, S. Ito, A. Osuka and D. Kim, Chem. Commun., 2007, 2479–2481 RSC.
- L. Cristian, I. Sasaki, P. G. Lacroix, B. Donnadieu, I. Asselberghs, K. Clays and A. C. Razus, Chem. Mater., 2004, 16, 3543–3551 CrossRef CAS.
- C. Katan, S. Tretiak, M. H. V. Werts, A. J. Bain, R. J. Marsh, N. Leonczek, N. Nicolaou, E. Badaeva, O. Mongin and M. Blanchard-Desce, J. Phys. Chem. B, 2007, 111, 9468–9483 CrossRef CAS PubMed.
- A. Loudet and K. Burgess, Chem. Rev., 2007, 107, 4891–4932 CrossRef CAS PubMed.
- K. Umezawa, A. Matsui, Y. Nakamura, D. Citterio and K. Suzuki, Chem. – Eur. J., 2009, 15, 1096–1106 CrossRef CAS PubMed.
- R. Hu, E. Lager, A. Aguilar-Aguilar, J. Liu, J. W. Y. Lam, H. H. Y. Sung, I. D. Williams, Y. Zhong, K. S. Wong, E. Peña-Cabrera and B. Z. Tang, J. Phys. Chem. C, 2009, 113, 15845–15853 CAS.
- M. T. Whited, N. M. Patel, S. T. Roberts, K. Allen, P. I. Djurovich, S. E. Bradforth and M. E. Thompson, Chem. Commun., 2012, 48, 284–286 RSC.
- B. Sui, M. V. Bondar, D. Anderson, H. J. Rivera-Jacquez, A. E. Masunov and K. D. Belfield, J. Phys. Chem. C, 2016, 120, 14317–14329 CAS.
- X. Liu, J. Zhang, K. Li, X. Sun, Z. Wu, A. Ren and J. Feng, Phys. Chem. Chem. Phys., 2013, 15, 4666–4676 RSC.
- R. Misra, J. Phys. Chem. C, 2017, 121, 5731–5739 CAS.
- P. Cronstrand, Y. Luo and H. Ågren, Chem. Phys. Lett., 2002, 352, 262–269 CrossRef CAS.
- M. M. Alam, M. Chattopadhyaya and S. Chakrabarti, Phys. Chem. Chem. Phys., 2012, 14, 1156–1165 RSC.
- M. M. Alam, M. Chattopadhyaya, S. Chakrabarti and K. Ruud, Acc. Chem. Res., 2014, 47, 1604–1612 CrossRef CAS PubMed.
- M. M. Alam, M. T. P. Beerepoot and K. Ruud, J. Chem. Phys., 2017, 146, 244116 CrossRef PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford, CT, 2013 Search PubMed.
- M. M. Alam, R. Misra and K. Ruud, ESI† and raw output files of channel interference study is available at http://dx.doi.org/10.18710/LHCGYQ.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- Dalton, a molecular electronic structure program, Release Dalton2013.4, see http://daltonprogram.org., 2014.
- L. W. T. Barros, T. A. S. Cardoso, A. Bihlmeier, D. Wagner, D. K. Kolmel, A. Horner, S. Brase, C. H. Brito Cruz and L. A. Padilha, Phys. Chem. Chem. Phys., 2017, 19, 21683–21690 RSC.
- L. Frediani, Z. Rinkevicius and H. Ågren, J. Chem. Phys., 2005, 122, 244104 CrossRef PubMed.
- L. Frediani, H. Ågren, L. Ferrighi and K. Ruud, J. Chem. Phys., 2005, 123, 144117 CrossRef PubMed.
- P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, J. Chem. Phys., 2002, 117, 9630–9645 CrossRef.
- H. Hettema, H. J. A. Jensen, P. Jørgensen and J. Olsen, J. Chem. Phys., 1992, 97, 1174–1190 CrossRef CAS.
- M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, J. Chem. Phys., 2008, 128, 044118 CrossRef PubMed.
- M. T. P. Beerepoot, D. H. Friese, N. H. List, J. Kongsted and K. Ruud, Phys. Chem. Chem. Phys., 2015, 17, 19306 RSC.
- D. Zhang, Y. Wang, Y. Xiao, S. Qian and X. Qian, Tetrahedron, 2009, 65, 8099–8103 CrossRef CAS.
- D. Cvejn, E. Michail, K. Seintis, M. Klikar, O. Pytela, T. Mikysek, N. Almonasy, M. Ludwig, V. Giannetas, M. Fakis and F. Bures, RSC Adv., 2016, 6, 12819–12828 RSC.
- M. Wielgus, R. Zaleśny, N. A. Murugan, J. Kongsted, H. Ågren, M. Samoc and W. Bartkowiak, ChemPhysChem, 2013, 14, 3731–3739 CrossRef CAS PubMed.
- K. Zhao, L. Ferrighi, L. Frediani, C.-K. Wang and Y. Luo, J. Chem. Phys., 2007, 126, 204509 CrossRef PubMed.
- M. M. Alam, M. Chattopadhyaya, S. Chakrabarti and K. Ruud, J. Phys. Chem. Lett., 2012, 3, 961–966 CrossRef CAS PubMed.
- M. M. Alam, M. Chattopadhyaya and S. Chakrabarti, J. Phys. Chem. A, 2012, 116, 8067–8073 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05679f |
| ‡ Present address: Department of Organic Chemistry, Weizmann Institute of Science, Rehovot 76100, Israel. |
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Ramprasad
Misra‡
*a,
Ramprasad
Misra‡
 b and
Kenneth
Ruud
b and
Kenneth
Ruud
 a
a

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The solvent effects are taken into account using the polarizable continuum model (PCM) of Tomasi and co-workers.25,26 After geometry optimizations and frequency analyses, the OPA and TPA properties of all the molecules are calculated using time-dependent density functional linear and quadratic response theories using the CAM-B3LYP functional27 and the aug-cc-pVDZ basis set, as implemented in the DALTON program package.28,29 Recently, Leonardo et al.30 reported the TPA cross section of some disubstituted BODIPY dyes using their theoretical–experimental studies that revealed that the time-dependent density functional theory (TD-DFT) results are consistent with the experimental values. For both the OPA and TPA calculations in the gas phase, the five lowest singlet-excited states have been considered. However, for the specific study of molecule 3, the excited state having the largest TPA cross section is considered. For studying the effects of rotation of the two parts of molecule 3 on its TPA cross section, we changed the dihedral angle (θ, as shown in Fig. 1) between the phenyl and BODIPY moieties from 0° to 90° at an interval of 10° and calculated the OPA and TPA properties for each dihedral angle at the same level of theory. The geometries of the rotated systems have not been re-optimized. For the solvent calculations, the non-equilibrium formulation of the PCM quadratic response theory is used.31,32 In all solvent calculations, we used atom-centered cavities with the same radius as that used in the Gaussian program package. The radii of the cavities on each of the H, B, C, N and F atoms are 1.4430 Å, 2.0415 Å, 1.9255 Å, 1.8300 Å, and 1.6820 Å respectively. Note that at 40° dihedral angle in the CH2Cl2 solvent, we faced a numerical problem with the convergence of the quadratic response function. We circumvented this situation by using a 41° dihedral angle in place of 40°. To study the contributions of different optical channels to the TPA of molecule 3, we performed two- and three-state model calculations using the generalized few-state model expression of Alam et al.20,22 The transition dipole moment between two excited states, required for few-state model calculations, is calculated using the double residue of the quadratic response function,33,34 at the same level of theory using the DALTON program package.28,29
24 The solvent effects are taken into account using the polarizable continuum model (PCM) of Tomasi and co-workers.25,26 After geometry optimizations and frequency analyses, the OPA and TPA properties of all the molecules are calculated using time-dependent density functional linear and quadratic response theories using the CAM-B3LYP functional27 and the aug-cc-pVDZ basis set, as implemented in the DALTON program package.28,29 Recently, Leonardo et al.30 reported the TPA cross section of some disubstituted BODIPY dyes using their theoretical–experimental studies that revealed that the time-dependent density functional theory (TD-DFT) results are consistent with the experimental values. For both the OPA and TPA calculations in the gas phase, the five lowest singlet-excited states have been considered. However, for the specific study of molecule 3, the excited state having the largest TPA cross section is considered. For studying the effects of rotation of the two parts of molecule 3 on its TPA cross section, we changed the dihedral angle (θ, as shown in Fig. 1) between the phenyl and BODIPY moieties from 0° to 90° at an interval of 10° and calculated the OPA and TPA properties for each dihedral angle at the same level of theory. The geometries of the rotated systems have not been re-optimized. For the solvent calculations, the non-equilibrium formulation of the PCM quadratic response theory is used.31,32 In all solvent calculations, we used atom-centered cavities with the same radius as that used in the Gaussian program package. The radii of the cavities on each of the H, B, C, N and F atoms are 1.4430 Å, 2.0415 Å, 1.9255 Å, 1.8300 Å, and 1.6820 Å respectively. Note that at 40° dihedral angle in the CH2Cl2 solvent, we faced a numerical problem with the convergence of the quadratic response function. We circumvented this situation by using a 41° dihedral angle in place of 40°. To study the contributions of different optical channels to the TPA of molecule 3, we performed two- and three-state model calculations using the generalized few-state model expression of Alam et al.20,22 The transition dipole moment between two excited states, required for few-state model calculations, is calculated using the double residue of the quadratic response function,33,34 at the same level of theory using the DALTON program package.28,29

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The first excited state of all these molecules has the largest oscillator strength and in most of the cases is the only one-photon active state among the five excited states considered. However, in some of the molecules, there exists a second large one-photon active state; for instance, the fourth excited state in molecules 2 and 9, the second excited state in molecules 3 and 7, the third excited state in molecule 11 and the fifth excited state in molecule 13. We note that the value of θ has a significant impact on the OPA of these molecules, which in turn is controlled by the size of the R-group on the BODIPY moiety. For instance, for molecules having R = –CH3, θ is close to 90° and such molecules have a single dominating one-photon active state. On the other hand, for molecules with R = –H, the dihedral angle is around 50°–60° and for these molecules, there exists a second large one-photon active state. Furthermore, the molecules with R = –CH3 have larger δ1P values than the molecules with R = –H. An examination of the S0 → Si excitation energies and the corresponding transition dipole moments (Fig. 2) indicate that the variation of the oscillator strength follows the corresponding variation in transition dipole moments rather than the excitation energies. There are no significant variations in the excitation energies of a particular excited state among the molecules considered here. The orbitals involved in the dominant transitions in all these molecules are given in the ESI† (Tables S4 and S5).24 We note that the dominant transitions (i.e., S0 → S1) in all the molecules with R = –H are short-range local transitions, mainly a rearrangement of electron density in the BODIPY moiety. In contrast, for molecules having R = –CH3, the dominant transitions are a mixture of both long- and short-range orbital transitions. This is also consistent with the orbital pictures in ref. 18 and the Λ parameter35 provided in the ESI.†
24 The first excited state of all these molecules has the largest oscillator strength and in most of the cases is the only one-photon active state among the five excited states considered. However, in some of the molecules, there exists a second large one-photon active state; for instance, the fourth excited state in molecules 2 and 9, the second excited state in molecules 3 and 7, the third excited state in molecule 11 and the fifth excited state in molecule 13. We note that the value of θ has a significant impact on the OPA of these molecules, which in turn is controlled by the size of the R-group on the BODIPY moiety. For instance, for molecules having R = –CH3, θ is close to 90° and such molecules have a single dominating one-photon active state. On the other hand, for molecules with R = –H, the dihedral angle is around 50°–60° and for these molecules, there exists a second large one-photon active state. Furthermore, the molecules with R = –CH3 have larger δ1P values than the molecules with R = –H. An examination of the S0 → Si excitation energies and the corresponding transition dipole moments (Fig. 2) indicate that the variation of the oscillator strength follows the corresponding variation in transition dipole moments rather than the excitation energies. There are no significant variations in the excitation energies of a particular excited state among the molecules considered here. The orbitals involved in the dominant transitions in all these molecules are given in the ESI† (Tables S4 and S5).24 We note that the dominant transitions (i.e., S0 → S1) in all the molecules with R = –H are short-range local transitions, mainly a rearrangement of electron density in the BODIPY moiety. In contrast, for molecules having R = –CH3, the dominant transitions are a mixture of both long- and short-range orbital transitions. This is also consistent with the orbital pictures in ref. 18 and the Λ parameter35 provided in the ESI.†

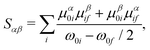
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 To the best of our knowledge, except for molecule 2, none of the other molecules considered for the present study has been studied experimentally for two-photon absorption. The reported experimental37 TPA cross section of molecule 2 is 4 GM, which is very small and is consistent with our theoretically calculated value. It is interesting to note that unlike the OPA plot (Fig. 2), the TPA plot is much less crowded as only a few molecules are found to have significant TPA cross sections. The TPA cross section of molecule 3 dominates over all the other 13 molecules. Molecule 7 has the second largest TPA cross section and molecules 11 and 9 are the third and fourth most TPA-active molecules. The ratios of δ2PResp of these four molecules are 1
24 To the best of our knowledge, except for molecule 2, none of the other molecules considered for the present study has been studied experimentally for two-photon absorption. The reported experimental37 TPA cross section of molecule 2 is 4 GM, which is very small and is consistent with our theoretically calculated value. It is interesting to note that unlike the OPA plot (Fig. 2), the TPA plot is much less crowded as only a few molecules are found to have significant TPA cross sections. The TPA cross section of molecule 3 dominates over all the other 13 molecules. Molecule 7 has the second largest TPA cross section and molecules 11 and 9 are the third and fourth most TPA-active molecules. The ratios of δ2PResp of these four molecules are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50
0.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.19
0.19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.13. Molecules 3 and 7 are structurally similar – molecule 3 has –N(CH3)2 as the X-group, whereas molecule 7 has –NH2 (Fig. 1). It is interesting to note that unlike the trend observed for the OPA cross section, the molecules with R = –H have significantly larger TPA cross sections than those with R = –CH3. This can be correlated with the synergistic effect of θ and the nature of the X- and R-groups.
0.13. Molecules 3 and 7 are structurally similar – molecule 3 has –N(CH3)2 as the X-group, whereas molecule 7 has –NH2 (Fig. 1). It is interesting to note that unlike the trend observed for the OPA cross section, the molecules with R = –H have significantly larger TPA cross sections than those with R = –CH3. This can be correlated with the synergistic effect of θ and the nature of the X- and R-groups.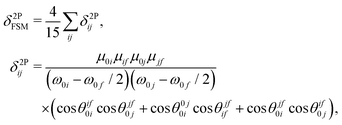
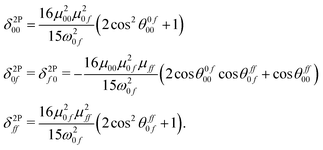
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The results in Table 2 show that the δ2P00 and δ2Pff terms in many cases have large positive values that are almost completely compensated by the destructive contribution from δ2P0f. Let us, for instance, consider the 2SM result for the first excited state in molecule 5. This molecule contains the strongest electron-donating group (–N(CH3)2), as is also the case for the molecule with the largest TPA, molecule 3, but it shows a very low TPA cross section. For molecule 5, the contributions from the δ2P00 and δ2Pff terms are 5.440 × 103 a.u. and 6.600 × 103 a.u., respectively. The total contribution from these two terms is therefore 12.040 × 103 a.u., which is very close to the highest TPA cross section (δ2P2SM = 15.300 × 103 a.u.) among the fourteen molecules. However, this is largely compensated by the negative contribution from δ2P0f (−11.984 × 103 a.u.), reducing the overall TPA cross section of the first excited state in molecule 5 to only 0.056 × 103 a.u. A close inspection of the transition moments involved and their relative orientations reveals that for this molecule, all the transition dipole moment terms involved have relatively large values, μ00 = 2.923 a.u., μ01 = 2.674 a.u., and μ11 = 3.221 a.u., respectively, due to the strong electron-donating group, and these vectors orient themselves in such a way that all the cosine terms are positive (cos
24 The results in Table 2 show that the δ2P00 and δ2Pff terms in many cases have large positive values that are almost completely compensated by the destructive contribution from δ2P0f. Let us, for instance, consider the 2SM result for the first excited state in molecule 5. This molecule contains the strongest electron-donating group (–N(CH3)2), as is also the case for the molecule with the largest TPA, molecule 3, but it shows a very low TPA cross section. For molecule 5, the contributions from the δ2P00 and δ2Pff terms are 5.440 × 103 a.u. and 6.600 × 103 a.u., respectively. The total contribution from these two terms is therefore 12.040 × 103 a.u., which is very close to the highest TPA cross section (δ2P2SM = 15.300 × 103 a.u.) among the fourteen molecules. However, this is largely compensated by the negative contribution from δ2P0f (−11.984 × 103 a.u.), reducing the overall TPA cross section of the first excited state in molecule 5 to only 0.056 × 103 a.u. A close inspection of the transition moments involved and their relative orientations reveals that for this molecule, all the transition dipole moment terms involved have relatively large values, μ00 = 2.923 a.u., μ01 = 2.674 a.u., and μ11 = 3.221 a.u., respectively, due to the strong electron-donating group, and these vectors orient themselves in such a way that all the cosine terms are positive (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1100 = 1.00, cos
θ1100 = 1.00, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0100 = 0.03 and cos
θ0100 = 0.03 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1101 = 0.03). From eqn (5), it then follows that δ2P0f becomes negative. This is the case for most of the molecules considered in this work. Exceptions do exist, such as the first four excited states in molecule 6, second excited state in molecule 5, all five excited states in molecules 9 and 10 etc., where the low TPA cross section is mainly due to very low values of the dipole moment vectors. This illustrates that a small TPA cross section does not necessarily result from the small magnitude of the transition dipole moment vectors involved, but also the relative orientations of these vectors. Optimization of TPA cross sections thus cannot only focus on maximizing the contributing transition dipole vectors. For the second excited states in molecules 3 and 7 (the two largest TPA-active systems), all the δ2P terms have positive values and are larger than in any of the other molecules in the gas phase. The angle terms (the terms in parenthesis in eqn (5)) are also positive and close to the maximum value of +3. Furthermore, in molecule 3, the presence of a strong electron-donating group (–N(CH3)2) makes the dipole moments involved very large, making the second excited state in molecule 3 the state with the largest TPA. A pictorial representation of the different transition moment and dipole moment vectors in molecule 3 is provided in Fig. S4 of the ESI.†
θ1101 = 0.03). From eqn (5), it then follows that δ2P0f becomes negative. This is the case for most of the molecules considered in this work. Exceptions do exist, such as the first four excited states in molecule 6, second excited state in molecule 5, all five excited states in molecules 9 and 10 etc., where the low TPA cross section is mainly due to very low values of the dipole moment vectors. This illustrates that a small TPA cross section does not necessarily result from the small magnitude of the transition dipole moment vectors involved, but also the relative orientations of these vectors. Optimization of TPA cross sections thus cannot only focus on maximizing the contributing transition dipole vectors. For the second excited states in molecules 3 and 7 (the two largest TPA-active systems), all the δ2P terms have positive values and are larger than in any of the other molecules in the gas phase. The angle terms (the terms in parenthesis in eqn (5)) are also positive and close to the maximum value of +3. Furthermore, in molecule 3, the presence of a strong electron-donating group (–N(CH3)2) makes the dipole moments involved very large, making the second excited state in molecule 3 the state with the largest TPA. A pictorial representation of the different transition moment and dipole moment vectors in molecule 3 is provided in Fig. S4 of the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ2PResp gradually decreases with increasing solvent polarity. The corresponding ratios in gas phase, C6H12, CH2Cl2 and CH3CN solvents are 1.399
δ2PResp gradually decreases with increasing solvent polarity. The corresponding ratios in gas phase, C6H12, CH2Cl2 and CH3CN solvents are 1.399![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.373
1.373![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.309
1.309![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.292. When going from 2SM to 3SM, the agreement with the response theory results improves slightly in gas phase and in C6H12 and CH3CN. However, the difference between the 2SM and 3SM results is small, indicating that the terms δ2P0i, δ2Pii and δ2Pif (i.e., those appearing only in the 3SM) contribute little to the overall TPA activity. For brevity, only the contributions of the terms involved in the 2SM are shown in Table 3. The full 2SM and 3SM results are provided in the ESI.†
1.292. When going from 2SM to 3SM, the agreement with the response theory results improves slightly in gas phase and in C6H12 and CH3CN. However, the difference between the 2SM and 3SM results is small, indicating that the terms δ2P0i, δ2Pii and δ2Pif (i.e., those appearing only in the 3SM) contribute little to the overall TPA activity. For brevity, only the contributions of the terms involved in the 2SM are shown in Table 3. The full 2SM and 3SM results are provided in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 The larger TPA cross section of molecule 3 in CH2Cl2 than in either gas phase or the other two solvents can be explained by considering the terms contributing to the 2SM. It is interesting to note that in both gas phase and in the three solvents, δ2P00 is the largest contributing term, whereas δ2Pff has the smallest contribution (Table 3). In all cases, the angle terms, i.e., the term in parenthesis in eqn (5) are close to the maximum value of +3. Furthermore, as is evident from Table 3, μ00 in the gas phase is much smaller than in the three solvents and hence δ2P00 in the gas phase is much smaller than in solvent. The most interesting result is δ2P0f: in gas phase and in C6H12, δ2P0f contributes constructively, but in the other two solvents it has destructive contributions. Interestingly, with the decrease in polarity of the solvent, the magnitude of destructive contribution of δ2P0f gradually decreases and becomes constructive in a solvent with very low polarity. Similar results were reported by Alam et al.41 for two through-space charge-transfer systems. Molecule 3 is the first through-bond charge-transfer system where a change in the nature of channel interference is observed with a change in solvent polarity. As is evident from eqn (5), the expression for δ2P0f already has a negative sign, and all the terms except the cosine of the angles are inherently positive quantities. This clearly reflects that the orientations of the three dipole moment vectors (μ00, μ0f and μff) are such that the corresponding angle term (the term in parenthesis) is negative in the gas phase and in C6H12, but is positive in the other two solvents. This is supported by the calculated values of the cosine of the angle between dipoles involved. The values of cos
24 The larger TPA cross section of molecule 3 in CH2Cl2 than in either gas phase or the other two solvents can be explained by considering the terms contributing to the 2SM. It is interesting to note that in both gas phase and in the three solvents, δ2P00 is the largest contributing term, whereas δ2Pff has the smallest contribution (Table 3). In all cases, the angle terms, i.e., the term in parenthesis in eqn (5) are close to the maximum value of +3. Furthermore, as is evident from Table 3, μ00 in the gas phase is much smaller than in the three solvents and hence δ2P00 in the gas phase is much smaller than in solvent. The most interesting result is δ2P0f: in gas phase and in C6H12, δ2P0f contributes constructively, but in the other two solvents it has destructive contributions. Interestingly, with the decrease in polarity of the solvent, the magnitude of destructive contribution of δ2P0f gradually decreases and becomes constructive in a solvent with very low polarity. Similar results were reported by Alam et al.41 for two through-space charge-transfer systems. Molecule 3 is the first through-bond charge-transfer system where a change in the nature of channel interference is observed with a change in solvent polarity. As is evident from eqn (5), the expression for δ2P0f already has a negative sign, and all the terms except the cosine of the angles are inherently positive quantities. This clearly reflects that the orientations of the three dipole moment vectors (μ00, μ0f and μff) are such that the corresponding angle term (the term in parenthesis) is negative in the gas phase and in C6H12, but is positive in the other two solvents. This is supported by the calculated values of the cosine of the angle between dipoles involved. The values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θff00 and cos
θff00 and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0f00 are −1.0 in the gas phase and in C6H12 but +1.0 in the other two solvents. The largest TPA cross section in CH2Cl2 is a result of the large magnitude of δ2P00 and the small value of the destructive δ2P0f. Interestingly, the reasons for the decrease in δ2P2SM when moving from CH2Cl2 to CH3CN and to C6H12 are different. When moving from CH2Cl2 to the polar CH3CN solvent, the compensation of δ2P00 by the destructive δ2P0f increases and hence δ2P2SM decreases. On the other hand, when moving from CH2Cl2 to the low-polar C6H12 solvent, the magnitudes of the corresponding dipole moment vectors decrease and hence the corresponding δ2P2SM is also decreased.
θ0f00 are −1.0 in the gas phase and in C6H12 but +1.0 in the other two solvents. The largest TPA cross section in CH2Cl2 is a result of the large magnitude of δ2P00 and the small value of the destructive δ2P0f. Interestingly, the reasons for the decrease in δ2P2SM when moving from CH2Cl2 to CH3CN and to C6H12 are different. When moving from CH2Cl2 to the polar CH3CN solvent, the compensation of δ2P00 by the destructive δ2P0f increases and hence δ2P2SM decreases. On the other hand, when moving from CH2Cl2 to the low-polar C6H12 solvent, the magnitudes of the corresponding dipole moment vectors decrease and hence the corresponding δ2P2SM is also decreased.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 respectively. It is interesting to note that in gas phase and in C6H12, the variations of δ2P are very slow at the beginning, in particular from θ = 0° to θ = 50°. Thereafter, there is a rapid decrease in δ2P until it reaches a minimum at θ = 90°. On the other hand, in the other two solvents, the variation of δ2P is faster at the beginning, increasing significantly when going from a θ of 0° to 50°. A further increase in θ causes a rapid decrease similar to that observed in the gas phase and in C6H12. δ2P attains a maximum value for θ around 40°–50°.
24 respectively. It is interesting to note that in gas phase and in C6H12, the variations of δ2P are very slow at the beginning, in particular from θ = 0° to θ = 50°. Thereafter, there is a rapid decrease in δ2P until it reaches a minimum at θ = 90°. On the other hand, in the other two solvents, the variation of δ2P is faster at the beginning, increasing significantly when going from a θ of 0° to 50°. A further increase in θ causes a rapid decrease similar to that observed in the gas phase and in C6H12. δ2P attains a maximum value for θ around 40°–50°.

 for each δ2Pij, and Dij is the contribution from the magnitude of the (transition) dipole moments and hence is named the D-term. Eij and Aij in eqn (6) are the contributions from the excitation energies and angle between the transition dipole moments, respectively.
for each δ2Pij, and Dij is the contribution from the magnitude of the (transition) dipole moments and hence is named the D-term. Eij and Aij in eqn (6) are the contributions from the excitation energies and angle between the transition dipole moments, respectively.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24Fig. 8 shows that the variations of the E-terms are the same in gas phase and in the three solvents. Thus, the variation of δ2Pij is mainly controlled by the D and A terms. Furthermore, Fig. 7 shows that all the angle terms are either +3 or −3. Only some of the A0f terms have negative values. The other two A terms are always positive, as expected from eqn (5). For 0° ≤ θ ≤ 30°, in the gas phase and in C6H12, A0f is positive and for the rest, it is negative. In the other two solvents CH2Cl2 and CH3CN, A0f is positive only for the ranges 0°–40° and 0°–50°, respectively. The variations of A0f (which is the only term controlling the sign of channel interference) indicate a change in nature of the corresponding δ2P0f term when the molecule is twisted. This is visible in Fig. 5.
24Fig. 8 shows that the variations of the E-terms are the same in gas phase and in the three solvents. Thus, the variation of δ2Pij is mainly controlled by the D and A terms. Furthermore, Fig. 7 shows that all the angle terms are either +3 or −3. Only some of the A0f terms have negative values. The other two A terms are always positive, as expected from eqn (5). For 0° ≤ θ ≤ 30°, in the gas phase and in C6H12, A0f is positive and for the rest, it is negative. In the other two solvents CH2Cl2 and CH3CN, A0f is positive only for the ranges 0°–40° and 0°–50°, respectively. The variations of A0f (which is the only term controlling the sign of channel interference) indicate a change in nature of the corresponding δ2P0f term when the molecule is twisted. This is visible in Fig. 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24μff also shows a similar variation, which indicates that the oscillation of δ2P0f is due to this dipole moment. For θ = 40°–50°, all the δ terms have moderate, but positive values (or a small negative value) and hence in this range for the dihedral angle, the overall δ2P2SM acquires the maximum value.
24μff also shows a similar variation, which indicates that the oscillation of δ2P0f is due to this dipole moment. For θ = 40°–50°, all the δ terms have moderate, but positive values (or a small negative value) and hence in this range for the dihedral angle, the overall δ2P2SM acquires the maximum value.