Open Access Article
Open Access ArticleA combined NMR and DFT study of conformational dynamics in lanthanide complexes of macrocyclic DOTA-like ligands†
Jan
Blahut
 a,
Petr
Hermann
a,
Petr
Hermann
 *a,
Zdeněk
Tošner
*a,
Zdeněk
Tošner
 b and
Carlos
Platas-Iglesias
b and
Carlos
Platas-Iglesias
 c
c
aDepartment of Inorganic Chemistry, Faculty of Science, Charles University, Hlavova 2030/8, Prague 2, 128 43, Czech Republic. E-mail: petrh@natur.cuni.cz
bFaculty of Science, Charles University, Hlavova 2030/8, Prague 2, 128 43, Czech Republic
cCentro de Investigaciones Científicas Avanzadas (CICA) and Departamento de Química, Facultade de Ciencias, Universidade da Coruña, 15071 A Coruña, Galicia, Spain
First published on 6th September 2017
Abstract
The solution dynamics of the Eu(III) complexes of H4dota (1,4,7,10-tetraazacyclododecane-1,4,7,10-tetracarboxylic acid) and H5do3ap (1,4,7,10-tetraazacyclododecane-4,7,10-tris(carboxymethyl)-1-methylphosphonic acid, bound in both monoprotonated and fully deprotonated forms) were investigated by using a combination of NMR measurements and DFT calculations. In solution, an equilibrium between the square antiprismatic (SAP) and twisted-square antiprismatic isomers (TSAP) of these complexes is present. These two isomers interconvert by rotation of the pendant arms or inversion of the cyclen chelate rings. 1D EXSY NMR spectra were used to determine these exchange rates with unprecedented accuracy. It was found that the two processes occur at different rates. Additional variable-temperature measurements allowed determination of the corresponding activation parameters for the two processes. DFT calculations were then used to obtain mechanistic information at the molecular level. The results show that the cyclen inversion pathway involves stepwise inversion of the four chelate rings formed upon metal ion coordination. However, the arm rotation process may operate through a synchronous rotation of the pendant arms or a stepwise mechanism depending on the system. A mixed cluster-continuum approach was required to improve the agreement between experimental and calculated activation parameters for the arm rotation process. The obtained results will aid the design of MRI contrast agents. Furthermore, the methodology developed in this work can be further applied for the investigation of other dynamic paramagnetic systems, e.g. peptides with Ln(III) probes or natively paramagnetic metalloproteins.
1 Introduction
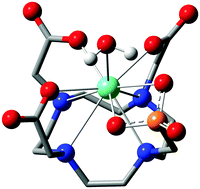
Since the early 1980s, when the first lanthanide(III) complexes of H4dota were prepared (H4dota = 1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic acid),1 great efforts have been made to understand and describe the conformational properties and dynamics of these and structurally related compounds in solution. The efforts have been mainly driven by the wide range of applications of the complexes in different fields, especially in biology and medicine in various techniques of molecular imaging. In the [Ln(dota)]− complexes and related systems, the metal ion is coordinated to the four nitrogen atoms of the macrocycle, which define the N4 plane, and four oxygen atoms of the pendant arms (referred to as the O4 plane). Usually, an additional coordination position is occupied by a water molecule which caps the O4 plane (Fig. 1).2 The relative torsion of the N4 and O4 planes results in two possible orientations of the pendant arms (Δ or Λ) while the chelate rings of the macrocyclic cyclen unit may adopt two different conformations (δδδδ or λλλλ). As a result, four conformational isomers are possible which are observed as two enantiomeric pairs. One enantiomeric pair [Δ(λλλλ)/Λ(δδδδ)] presents a square antiprismatic (SAP) coordination geometry, whereas the Λ(λλλλ)/Δ(δδδδ) enantiomeric pair adopts a twisted-square antiprismatic (TSAP) coordination geometry. The exchange between the SAP and TSAP forms can occur via pendant arm rotation or macrocycle chelate ring inversion, while the combination of these two processes results in interconversion between the enantiomers.3 While direct enantiomerization has also been postulated,4 there is no experimental evidence supporting such a concerted arm-rotation and ring-inversion pathway and, likely, a high activation energy barrier disables it.5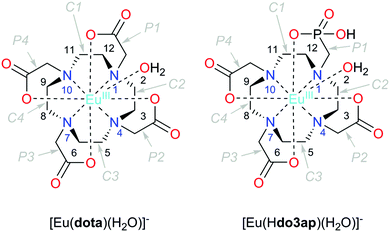 | ||
| Fig. 1 Structure of the complexes discussed in this work with an atom and cyclen chelate/pendant arm numbering scheme. The TSAP isomers are depicted in both cases. | ||
The relative abundance of the SAP and TSAP isomers is affected by both the lanthanide(III) ion and the nature of the ligand. Generally, abundance of the SAP isomers increases on going to the right across the lanthanide series while an increase in the steric demand of the pendant arms increases the abundance of the TSAP form.6,7 A rational control of the TSAP/SAP ratio in solution favoring one isomer or another is of key importance for many applications of these types of complexes. For instance, TSAP isomers present much faster exchange rates of the coordinated water molecule which, in the case of the [Gd(dotam)(H2O)]3+ complex (dotam = tetraamide of H4dota), was shown to be ∼50 times faster than that for the SAP form.8–10 The water exchange rate of the coordinated water molecule is an important parameter that affects the efficiency of gadolinium-based contrast agents (CAs) for magnetic resonance imaging (MRI).11 A slow water exchange is also critical for the design of MRI contrast agents based on the chemical exchange saturation transfer (CEST) approach.12 Because two isomeric forms are present in solution, it is also problematic to use lanthanide complexes with dota-like ligands as paramagnetic probes in protein structure studies,13 for the determination of drug binding sites,14 and in the design of CEST12,15 and PARASHIFT16,17 MRI CAs. Other properties are expected to be influenced by this isomerism as well, such as the magnetic anisotropy and symmetry axis orientation in Dy3+ complexes,18 or the nuclear relaxation rate of 89Y complexes for application in dynamic nuclear polarization.19 Last but not least, isomeric composition affects luminescence properties9 and the enantioselectivity of organic reactions using dota-like complexes as catalysts.20
NMR spectroscopy is a powerful method that allows determination of isomer composition as well as their interconversion dynamics even in the steady-state. The application of NMR to Ln3+ complexes was reviewed by Babilov,21 and the most important methods and their limitations are briefly discussed below. First, the dynamics of the system can be followed by analyzing changes in the line-shape with temperature. Activation energies can be determined either by simple estimation of exchange rates from the coalescence temperature or by more rigorous line-shape fitting. While this method is straightforward and relatively sensitive, it requires a reasonable estimate of the temperature dependence of chemical shifts and transverse relaxation rates. This can be relatively simple for diamagnetic systems but, for paramagnetic complexes, the paramagnetically induced shift and relaxation rates complicate the analysis. Other problems arise from signal overlap and complicated signal behaviour when the exchange process involves more than two sites, which is often the case in dota-like systems. Nevertheless, this technique has been relatively successfully applied for diamagnetic La3+ and Lu3+ complexes and/or employing 13C and 31P NMR spectra which are less affected by paramagnetic effects and are less crowded.7,21–26
A second group of NMR techniques is based on selective inversion4,5,24 or selective saturation27 of a selected NMR resonance and following signal intensities after a delay during which the exchange takes place. These approaches also suffer from signal overlap, especially in complexes of dota derivatives with low symmetry. This problem can be alleviated by using 2D pulse sequences such as 2D-EXSY.28,29 While being very useful for a qualitative description of the dynamics of the system, it is difficult to obtain quantitative results due to the problematic integration of 2D cross-peaks suffering from phase and baseline distortions.
Theoretical calculations can provide detailed information about the mechanism of dynamic processes at the molecular level experienced by lanthanide(III) complexes in solution. Both classical30 and ab initio31–33 molecular dynamics (AIMD) have been used to investigate lanthanide(III) complexes. However, the parametrization of force fields to be used for f-block elements is not a trivial task. In contrast, AIMD offer a robust tool to investigate lanthanide(III) complexes in solution, but their high computational cost rarely allows simulations exceeding a hundred picoseconds. Pollet et al.34 used metadynamics to gain information on the water exchange rates of a gadolinium(III) complex, a process that occurs at the time scale of hundreds of nanoseconds. However, conformational dynamics of dota-like complexes take place at the time scale of tens of milliseconds at room temperature, which cannot be reached with the currently available computational resources. Thus, information on the conformational dynamics of lanthanide(III) complexes has been generally obtained by exploring the potential energy surface of the system of interest, which provides the relevant energy minima and transition states and the associated energy profile.35 While this approach suffers from some limitations, in particular related to the treatment of solvent effects, it has been shown to provide useful information at the molecular level complementary to experimental studies.36
Herein we report thorough NMR analysis of the conformational dynamics of the Eu3+ complexes with the (dota)4− anion and with protonated and deprotonated forms of the (do3ap)5− anion (Fig. 1), which provides exchange rates and activation parameters with unprecedented accuracy. DFT calculations will subsequently be presented to reveal details of the mechanisms responsible for the isomer interconversion.
2 Results and discussion
2.1 1H MNR spectra
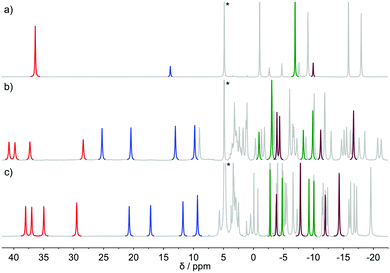
The 1H NMR spectrum of [Eu(dota)(D2O)]− recorded at 5 °C (Fig. 2) is in agreement with that reported previously.28 The spectrum consists of two sets of six signals with different intensities, which correspond to the SAP and TSAP isomers, each showing an effective C4 symmetry. The equilibrium constant characterizing the isomer equilibrium reaction SAP ⇆ TSAP was determined by integration of signals at δ(1H) = 36.32 and 13.76 ppm yielding Kintegral = 0.21. This value is in good agreement with the values reported previously.3 The synthesis and NMR spectra of [Eu(do3ap)(D2O)]2− were also published previously;6 however no spectral assignments were provided. The phosphonate group of the SAP and TSAP isomers were found to experience protonation processes characterized by pKa values of 6.0 (TSAP) and 5.5 (SAP).6 Thus, 1H NMR spectra at two pD values were recorded to investigate the conformational dynamics of both the protonated and non-protonated forms of the complex. The C1 symmetry of the two isomers present in solution results in two sets of 24 1H NMR signals and two 31P NMR resonances.The conformational dynamics of [Eu(dota)(D2O)]− was investigated by focusing on two signals in its 1H NMR spectrum, namely on the macrocyclic chelate ring axial protons that are directed opposite to the pendant arms, and the corresponding geminal equatorial protons (SAP: 36.3 ppm (axial) and −7.0 ppm (equatorial); TSAP: 13.8 ppm (axial) and −10.1 ppm (equatorial)).28,37 For the [Eu(Hdo3ap)(D2O)]− and [Eu(do3ap)(D2O)]2− complexes, the analogous proton signals were identified using a combination of 2D 1H EXSY and 1H–1H COSY experiments (Table S1 and Fig. S2, ESI†). The four signals of axial protons of the cyclen unit that point opposite to the pendant arms are observed in the range ∼28–40 ppm for the SAP isomers, and between 10 and 25 ppm for the TSAP isomers. These spectral ranges are typical for Eu3+ complexes of H4dota and dota-tetraamide derivatives.38 The equilibrium constants Kintegral obtained from the integration of the 1H NMR axial proton resonances (red and blue in Fig. 2) are 0.88 and 1.42 for the [Eu(Hdo3ap)(D2O)]− and [Eu(do3ap)(D2O)]2− complexes, respectively. The increase in the population of the TSAP isomer upon replacing carboxylate group(s) by bulkier phosphonate arm(s) is well documented, and has been attributed to steric effects.6,7
2.2 1D-EXSY experiments
The conformational dynamics of [Eu(dota)(D2O)]−, [Eu(Hdo3ap)(D2O)]− and [Eu(do3ap)(D2O)]2− were investigated using an optimized variant of the 1D EXSY experiment. The pulse sequence starts with a selective excitation block realized using a selective refocusing pulse during a spin echo. It is followed by an exchange period τM during which the magnetization is stored along the z-axis and a spectrum is recorded after the final 90° pulse (eqn (1)).| 90° − δ − 180°(sel) − δ − 90° − τM − 90° − FID | (1) |
Relatively fast relaxation and exchange rates, especially at high temperature, impose a strong requirement to minimize both the duration of an echo, 2δ, and the mixing period τM. For slowly relaxing diamagnetic systems, z gradients are used to improve the performance of the selective 180° pulse, and an inversion pulse (accompanied with gradients) is used during the mixing in order to suppress unwanted magnetization pathways.39 For the title paramagnetic samples, the gradients were replaced by a phase cycle that combines EXORCYCLE on the 180°(sel) pulse, EXORCYCLE on the last 90° pulse, and a two-step cycle of the first pulse in order to reduce T1 relaxation effects by ±z alternation of the selected magnetization before mixing. In total, the phase cycle has 32 steps that presents no complication for systems with short T1 relaxation, allowing fast repetition. Note that the measured magnetization effectively evolves to zero for long mixing times.39
Additional considerations should be taken into account when designing the selective refocusing pulse, as both the chemical exchange and relaxation processes take place during the pulse. While the exact description is beyond the scope of this paper, one can qualitatively state that in order to avoid significant loss of signal intensity, the pulse length should be shorter than the characteristic exchange and/or relaxation times. In the present case, the characteristic exchange and relaxation times are approximately 2 × 10−2 s, and thus pulses longer than ≈5 ms should be avoided. On the other hand, short pulses are less selective. Using a Gauss pulse length of 5 ms results in re-focusing of all resonances within the range of ≈200 Hz. This problem is particularly relevant in EXSY experiments when proximate signals are involved in chemical exchange (e.g. undesired partial refocusation of the signal of TSAP axial protons when applying the 180°(sel) pulse to the resonance of SAP axial protons). Due to this restriction in signal separation, the 1D-EXSY experiments in [Eu(do3ap)(D2O)]2− and [Eu(Hdo3ap)(D2O)]− at all temperatures and in [Eu(dota)(D2O)]− at temperatures above 5 °C were performed selecting axial proton signals (6–40 ppm), which are well isolated (Fig. 2). In the case of [Eu(dota)(D2O)]− at 5 °C, equatorial signals were also used. The same set of experiments was performed for 31P TSAP and SAP signals of [Eu(do3ap)(D2O)]2−, and [Eu(Hdo3ap)(D2O)]− at 5 °C as well.
2.3 Data analysis
The exchange rates characterizing the conformational dynamics of the complexes investigated in this work were determined by analyzing the evolution of the signal integral as a function of τM through numerical solution of Bloch-McConnell eqn (2),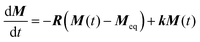 | (2) |
 | (3) |
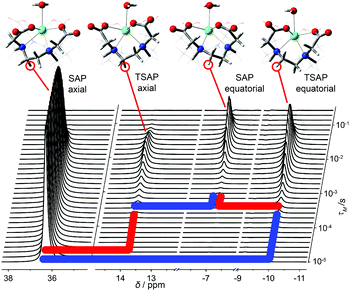
The exchange rates and relaxation times of [Eu(dota)(D2O)]− were obtained at 5 °C from a simultaneous fitting of four datasets measured starting from selected magnetization at the frequencies of the SAPax (36.3 ppm), TSAPax (13.8 ppm), SAPeq (−7.1 ppm) and TSAPeq (−10.1 ppm) protons. The four rate constants and the four relaxation rates were used as global variables during the fitting procedure, while Meq and M(0) were used as local variables for each dataset. Fig. 3 shows the 1H NMR spectra used to obtain one of these datasets by applying the 180°(sel) pulse at the frequency of the SAPax resonance (36.3 ppm). At short τM values only the signal of the SAP axial protons is observed while the signals of the remaining three protons gradually emerge upon increasing τM as the chemical exchange progresses. The signal evolution of the three resonances encodes kinetic information of a different exchange pathway, as illustrated in Fig. 3. The interconversion between SAPax and TSAPax protons occurs by rotation of the pendant arms. Interconversion between SAPax ⇆ TSAPeq requires the inversion of the cyclen unit, while the SAPax ⇆ SAPeq exchange requires both arm rotation and ring inversion. The intensity of the three signals observed due to chemical exchange fades away at long τM values due to T1 relaxation and the applied phase cycle.
Fig. 4 shows four datasets used to determine the exchange rates and relaxation times in [Eu(dota)(D2O)]−. A nice fit of the experimental data was obtained by analyzing these four data sets simultaneously. The same procedure was applied to the [Eu(do3ap)(D2O)]2− and [Eu(Hdo3ap)(D2O)]− systems at 5 °C by using eight datasets. In these cases, the four axial protons of the SAP isomer and the four axial protons of the TSAP isomer were selectively excited (these resonances are well isolated from the remaining 1H NMR signals, see blue and red signals in Fig. 2). The resulting fits are presented in the ESI† (Fig. S4a and S5a). All the exchange and relaxation rates determined from the analysis of the 1D EXSY data are compiled in Table 1.
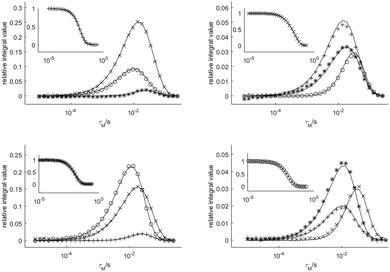 | ||
| Fig. 4 Relative areas of the four signals of [Eu(dota)(D2O)]− as a function of the mixing time obtained from 1D-EXSY experiments at 5 °C. The insets show the evolution of the magnetization of the signal to which the refocusing selective 180° pulse was applied. Symbols: TSAPax (+), SAPeq (×), TSAPeq (*), SAPax (○). The solid lines represent the simultaneous fit of all four data sets using eqn (2). | ||
| Parameter | Anion | ||
|---|---|---|---|
| dota 4− | Hdo3ap4− | do3ap 5− | |
| a k/s−1 are exchange rates, R1/s−1 are longitudinal relaxation rates, and K denotes equilibrium constants calculated as KEXSY = (kPendSAP + kCycleSAP)/(kPendTSAP + kCycleTSAP) or determined from integration of the 1H proton signals of TSAP/SAP axial protons (Kintegral). | |||
| k PendSAP | 5.58(6) | 23.2(5) | 99.7(3) |
| k CycleSAP | 10.60(7) | 19.6(6) | 21.0(3) |
| k PendTSAP | 25.80(7) | 25.0(5) | 71.7(3) |
| k CycleTSAP | 52.30(8) | 23.0(6) | 15.5(2) |
| K EXSY | 0.207(5) | 0.89(9) | 1.39(4) |
| K integral | 0.21 | 0.88 | 1.42 |
| R 1Ax. SAP | 69.1(1) | 69.4(9) | 73.2(4) |
| R 1Eq. SAP | 22.53(7) | 20(3) | 16(2) |
| R 1Ax. TSAP | 47.6(2) | 54.1(9) | 58.9(3) |
| R 1Eq. TSAP | 18.3(1) | 22(3) | 23(2) |
In agreement with the literature,6 the dominant isomer of [Eu(dota)(D2O)]− is the SAP isomer while the TSAP isomer is the dominant species for [Eu(do3ap)(D2O)]2− and the population of SAP and TSAP isomers is very similar for [Eu(Hdo3ap)(D2O)]−. Therefore, the TSAP → SAP interconversion is faster than the SAP → TSAP interconversion in [Eu(dota)(D2O)]−, while the situation is reversed for [Eu(do3ap)(D2O)]2− and the two processes are characterized by similar rates for [Eu(Hdo3ap)(D2O)]−. The equilibrium constants for the SAP ⇆ TSAP equilibrium reaction obtained from the exchange rates (KEXSY = (kPendSAP + kCycleSAP)/(kPendTSAP + kCycleTSAP)) are in excellent agreement with those obtained from 1H spectral integration (Table 1) and confirms the accuracy of our analysis.
In the case of [Eu(dota)(D2O)]−, the TSAP ⇆ SAP interconversion processes are dominated by the ring inversion mechanism which is approximately twice as fast as the arm rotation (Table 1). The arm rotation and ring inversion processes proceed with comparable rates for [Eu(Hdo3ap)(D2O)]−. Deprotonation of the phosphonate pendant arm does not have an important effect on the rates characterizing the ring inversion pathway; however, it dramatically accelerates the arm rotation pathway for the TSAP → SAP interconversion (from 25.0 s−1 to 71.7 s−1), and even more for the reverse process (from 23.2 s−1 to 99.7 s−1, Table 1). These results are in a good agreement with the results of 31P 1D-EXSY experiments where only the sum of arm rotation and ring inversion can be principally detected (see Fig. S6, S7 and Table S5, ESI†).
The SAPax ⇆ SAPeq exchange process represents the mutual interconversion of the SAP enantiomers and requires both arm rotation and inversion of the cyclen chelate rings. Fig. 3 shows that magnetization transfer to SAPeq protons occurs with some delay with respect to the TSAPax and TSAPeq protons. The same effect can be observed in Fig. 4 for all protons exchanging by racemization with those chosen for the 180°(sel) pulse. These results indicate that enantiomerization follows concatenated arm rotation and ring inversion mechanisms.
As the EXSY experiments were not designed to measure relaxation rates (their effect is partially suppressed by phase cycling), they were determined with lower accuracy than exchange rates. Nevertheless, in all cases the axial protons present faster relaxation rates than the equatorial ones, which is caused by their shorter distance from the Eu3+ central ion compared to the equatorial protons.40 The relaxation rates determined for axial protons of SAP geometries are faster than those observed for TSAP isomers while equatorial protons show comparable relaxation rates in both isomers. This can be attributed, at least in part, to shorter Eu···Hax distances in the SAP isomers (3.849 and 3.931 Å for the SAP and TSAP isomers of [Eu(dota)(D2O)]− respectively, according to the DFT calculations presented below), and quite similar distances for the equatorial protons (4.550 and 4.579 Å for the same SAP and TSAP isomers, respectively).
2.4 Activation parameters
Variable-temperature 1H 1D-EXSY experiments were also conducted at 15, 25 and 35 °C by applying the same procedures described in the previous section for 5 °C. Measurements at lower temperature were not possible due to hardware and solvent limitations while, at higher temperatures, extensive signal broadening occurs due to chemical exchange. The exchange rates determined at four temperatures (5, 15, 25 and 35 °C) were used to determine the activation enthalpy ΔH‡ and activation entropy ΔS‡ of each exchange process using the Eyring equation (4), where all symbols have their usual meaning.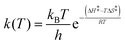 | (4) |
The activation parameters obtained for the TSAP/SAP exchange processes indicate that arm rotation is driven mainly by enthalpy factors, since entropic contribution is close to zero.
The ΔS‡ values characterizing the arm rotation path of the SAP isomers take values lower than 10 J K−1 mol−1. The reverse process in [Eu(do3ap)(D2O)]2− is characterized by a negative activation entropy (ΔS‡PendTSAP = −17(2) J K−1 mol−1) that deviates from this trend. Although this difference could be associated with a different mechanism, it can also be associated with an enthalpy–entropy compensation effect due to the simplified model applied, and/or an insufficient temperature range accessible in our experiments.41
The activation entropies obtained for the ring inversion process are consistently negative. However, a comparison with data reported for related systems is not straightforward. This is either because of the high uncertainty of the data,29 or the different hydration numbers of the SAP and TSAP isomers in the case of the Lu3+-dota complex, which determines the entropy of the transition state.23 Despite this, the activation entropy reported for the La3+-dota complex (ΔS‡CycleTSAP −21.4 J K−1 mol−1) is consistent with our results.7 The strong negative values obtained herein in some cases (ΔS‡CycleSAP = −54(11) J K−1 mol−1 for [Eu(do3ap)(D2O)]2− and ΔS‡CycleTSAP = −43(4) J K−1 mol−1 for [Eu (Hdo3ap)(D2O)]−) are associated with rather low activation enthalpies (ΔH‡CycleSAP = 45(3) kJ mol−1 for [Eu(do3ap)(D2O)]2− and ΔH‡CycleTSAP = 49(1) kJ mol−1 for [Eu(Hdo3ap)(D2O)]−), which again suggests an enthalpy–entropy compensation effect.
2.5 DFT calculations
DFT calculations were used to gain an insight into the mechanisms responsible for the conformational dynamics of [Eu(dota)(H2O)]−, [Eu(do3ap)(H2O)]2− and [Eu(Hdo3ap)(H2O)]− at the molecular level. Following previous studies, we employed the large core relativistic effective pseudopotential of Dolg,42,43 which includes 46 + 4f6 electrons of Eu3+ in the core, in combination with Pople's 6-31+G(d,p) basis set to describe the ligand atoms. The hybrid meta-GGA functional M06 was used throughout.44 Bulk solvent effects were considered by using a polarized continuum model (see computational details below). The two pathways responsible for TSAP/SAP exchange (arm rotation and cyclen inversion) were studied separately as there is no experimental evidence of the composite mechanism.Geometry optimizations of the [Eu(dota)(H2O)]−, [Eu(do3ap)(H2O)]2− and [Eu(Hdo3ap)(H2O)]− complexes provided the expected SAP and TSAP isomers as local energy minima. The structure calculated for the SAP isomer of [Eu(dota)(H2O)]− presents average Eu–Ocarboxylate and Eu–N distances of 2.390 and 2.725 Å, respectively, which compare well with the average experimental values obtained from X-ray diffraction measurements (Eu–O = 2.394 and Eu–N = 2.680 Å).45 The ring-inversion process responsible for the SAP → TSAP interconversion pathway calculated for the three systems is a four-step process; it involves the stepwise inversion of each of the five-membered chelate rings, resulting from the coordination of the macrocyclic unit. This stepwise mechanism is in line with previous studies performed on cyclen-based complexes using HF and DFT methods.5,35,46
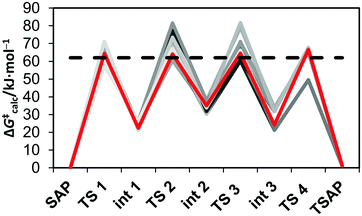
Several pathways are possible for the inversion of the cyclen unit of [Eu(dota)(H2O)]− depending on the sequence of ethylenediamine units that change conformation from δ to λ. The lowest energy path corresponds to the inversion of cyclen chelate rings following the sequence C2 → C3 → C4 → C1 (see Fig. 1 for labeling). The calculated activation free energy, as estimated for the transition state (TS) with the highest energy along the minimum energy pathway (ΔG‡calc = 61.9 kJ mol−1, Table 3), is in excellent agreement with the experimental value (ΔG‡CycleSAP = 62.7 ± 0.9 kJ mol−1). For [Eu(do3ap)(H2O)]2− and [Eu(Hdo3ap)(H2O)]−, the paths with the lowest energy correspond to the sequences C3 → C1 → C4 → C2 and C2→ C3 → C4 → C1, respectively, with the inversion of C2 (ΔG‡calc = 66.6 kJ mol−1) and C3 (ΔG‡calc = 60.6 kJ mol−1) being the steps with the highest activation energies (Fig. 5). The agreement between the experimental and calculated activation free energies is very good in both cases. However, one should bear in mind that our calculations provide several pathways with very similar activation energies, with 3, 12 and 7 paths having activation free energies within 5 kJ mol−1 for [Eu(dota)(H2O)]−, [Eu(do3ap)(H2O)]2− and [Eu(Hdo3ap)(H2O)]−, respectively. Thus, it is likely that several of them can play a role in the SAP → TSAP interconversion process (Fig. 5 and ESI†).
Our calculations provide negative ΔS‡ values, in agreement with the experimental data (Table 3). An analysis of the different contributions to the total ΔS‡ (ESI†) indicates that the vibrational contribution is the main factor leading to negative values due to the reduction of intramolecular vibrational frequencies. Inspection of the geometries of the SAP isomers and the transition states responsible for the SAP → TSAP interconversion shows that the inversion of the cyclen chelate rings provokes an important lengthening of the Eu–N distances. Thus, the largest contribution to the negative ΔS‡ values can be attributed to a reduction of the vibrational frequencies of low-frequency modes involving the relative displacement of the lanthanide(III) ion and the nitrogen atoms of the cyclen chelate rings.47
| Parameter | Anion | ||
|---|---|---|---|
| dota 4− | Hdo3ap4− | do3ap 5− | |
| a ΔH‡/kJ mol−1, ΔS‡/J K−1 mol−1 and ΔG‡ (25 °C)/kJ mol−1 are activation enthalpy, activation entropy and Gibbs energy (calculated from ΔH‡ and ΔS‡ at 25 °C), respectively. | |||
| ΔH‡PendSAP | 66.0(6) | 61.8(7) | 58.3(5) |
| ΔH‡CycleSAP | 58.8(4) | 54(1) | 45(3) |
| ΔH‡PendTSAP | 57(1) | 61.1(6) | 53.4(7) |
| ΔH‡CycleTSAP | 55(1) | 49(1) | 59(2) |
| ΔS‡PendSAP | 7(2) | 4(2) | 4(2) |
| ΔS‡CycleSAP | −13(1) | −26(4) | −54(11) |
| ΔS‡PendTSAP | −9(5) | 2(2) | −17(2) |
| ΔS‡CycleTSAP | −14(4) | −43(4) | −10(7) |
| ΔG‡PendSAP | 64(1) | 61(1) | 57(1) |
| ΔG‡CycleSAP | 62.7(9) | 62(2) | 62(7) |
| ΔG‡PendTSAP | 61(3) | 60(1) | 58(1) |
| ΔG‡CycleTSAP | 59(2) | 62(2) | 62(4) |
| Anion | ΔG‡CycleSAP | ΔS‡CycleSAP | ΔH‡CycleSAP |
|---|---|---|---|
| a ΔH‡/kJ mol−1, ΔS‡/J K−1 mol−1 and ΔG‡ (25 °C)/kJ mol−1. The experimental values are provided in parentheses. | |||
| dota 4− | 61.9 (62.7) | −3.3 (−13) | 63.8 (58.8) |
| Hdo3ap4− | 60.6 (62.0) | −8.8 (−26) | 57.9 (54) |
| do3ap 5− | 66.6 (62.0) | −15 (−54) | 62.2 (45) |
According to the calculations, the arm rotation process is synchronous (i.e. the process involves only one transition state) in both [Eu(dota)(H2O)]− and [Eu(Hdo3ap)(H2O)]− but follows a stepwise pathway for [Eu(do3ap)(H2O)]2−. The synchronous mechanisms of [Eu(dota)(H2O)]− and [Eu(Hdo3ap)(H2O)]− involve the simultaneous rotation of all four pendant arms. The activation free energies obtained from these calculations are 71.4 ([Eu(dota)(H2O)]−) and 85.5 ([Eu(Hdo3ap)(H2O)]−) kJ mol−1. These values considerably exceed the experimental values of 64 and 61 kJ mol−1 (Table 3), respectively. Nevertheless, the value calculated for [Eu(dota)(H2O)]− represents a significant improvement with respect to that obtained for [Lu(dota)]− in the gas phase (82.0 kJ mol−1).7 Thus, the introduction of bulk solvent effects with a polarized continuum appears to bring the calculated activation energies closer to the experimental values. This suggests that solvent effects play an important role in the arm rotation process of negatively charged pendant arms.
The polarized continuum model used in this work represents an improvement with respect to previous studies, but it still shows some limitations to account for specific solute–solvent interactions (i.e. hydrogen bonds involving second-sphere water molecules and the negatively charged pendant arms). For instance, it has been shown previously that the explicit inclusion of a few second-sphere water molecules was critical to compute accurate Ln–Owater bond distances and 17O hyperfine coupling constants in lanthanide(III) complexes.48,49 To test the effect of an explicit second hydration shell, the arm-rotation process on the [Eu(dota)(H2O)]−·2H2O system was investigated. It includes two explicit second-sphere water molecules involved in hydrogen bonds with the coordinated water molecule and oxygen atoms of the carboxylate groups (Fig. S12, ESI†). The inclusion of two second-sphere water molecules results in a significant shortening of the calculated Eu–Owater bond distance from 2.583 to 2.491 Å for the SAP isomer, the latter value being in good agreement with the value observed in the solid state (2.480 Å).45 The synchronous transition state obtained for this system provides a calculated ΔG‡ value of 60.0 kJ mol−1, which is in close agreement with the experimental value of 64(1) kJ mol−1 (Table 3). For [Eu(Hdo3ap)(H2O)]−, the inclusion of the explicit water molecules also results in the decrease in the arm rotation activation energy (81.9 kJ mol−1), but the effect is not as large as for [Eu(dota)(H2O)]−. However, a similar trend in the Eu–Owater bond distance of the SAP isomer was followed; the distances are 2.584 and 2.492 Å for the [Eu(Hdo3ap)(H2O)]− complex and the [Eu(Hdo3ap)(H2O)]−·2H2O system, respectively.
The energy profile calculated for the stepwise rotation of the pendant arms in [Eu(do3ap)(H2O)]2− is shown in Fig. 6 and Table 4. The first step of the pathway corresponds to the rotation of the phosphonate pendant arm, which changes its coordination mode from mono – to bidentate (Fig. 7). Subsequent rotation of the three acetate pendant arms results in SAP → TSAP interconversion. The activation free energy estimated from the energy of the transition state with the highest energy is 42.6 kJ mol−1 (Table 5). This value is somewhat lower than the experimental one (57(1) kJ mol−1, Table 2). We attribute this discrepancy to an overestimation of the stability of the intermediates with the bidentate phosphonate group; this is related to the limitations of continuum solvation models to provide an adequate description of the hydration of the negatively double-charged phosphonate groups. In order to understand this effect, the rate determining step was re-optimized with two second-sphere water molecules. The corresponding activation energy (51.2 kJ mol−1) is in reasonable agreement with the experiment. The Eu–Owater bond distance of the SAP isomer is 2.633 and 2.593 Å for [Eu(do3ap)(H2O)]2− and [Eu(do3ap)(H2O)]2−·2H2O respectively, which is consistent with the trends discussed above.
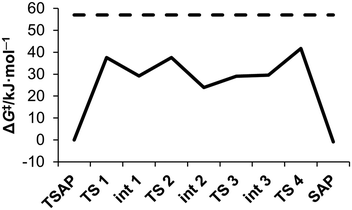 | ||
| Fig. 6 Calculated energy profile of successive arm rotation of [Eu(do3ap)(H2O)]2− at 25 °C (full line); compared to experimental activation energy ΔG‡PendTSAP (dashed line). For geometry of each intermediate (Int #) and transition state (TS #), see the ESI.† | ||
The results obtained for the arm rotation mechanism show that adding second-sphere water molecules results in a more accurate description of the system. In principle, the model could be further improved by increasing the number of explicit second-sphere water molecules. However, our attempts in this direction failed because the increasing number of soft degrees of freedom disables transition state geometry optimization. However, alternative molecular dynamics or metadynamics simulations34,50 are not effective enough to reach the long (ms) trajectories required to describe the TSAP ↔ SAP interconversion.
2.6 Conclusions
The dynamics of lanthanide(III) complexes with ligands structurally related to H4dota in solution is critical for the behaviour of these systems if they are applied as MRI CAs. One of the most important dynamic processes occurring in complexes of the dota-like ligands is the exchange between the SAP and TSAP geometries of the coordination polyhedron. This exchange can occur via pendant arm rotation or cyclen inversion. Though many publications have focused on the description of this complicated motion, the rates of these processes were not measured accurately.In this work, we determined arm rotation and cyclen inversion rates separately by utilization of a modified EXSY NMR pulse sequence in combination with full Bloch-McConnell-based data analysis. In addition, we also reported the corresponding activation barriers. A detailed insight into the mechanisms of these motions at the molecular level was obtained using DFT calculations.
The calculated activation parameters for the cyclen-inversion process are in excellent agreement with the experimental ones, including the activation entropies. The activation barriers computed with DFT for the arm rotation pathway present larger deviations from the experimental values. However, we showed that this is mainly due to deficient modelling of solvent effects by PCM as the arm rotation process involves flipping of the negatively charged pendant arms. Propitiously, using a mixed cluster-continuum model that includes two explicit second-sphere water molecules results in activation parameters which are in better agreement with the experiment for the arm rotation process. We believe that the results reported here represent an important contribution to a better understanding the dynamics of these important complexes.
Furthermore, the NMR methodology described here could be, in principle, applied to investigations of the dynamics of complex paramagnetic systems (i.e. proteins with open-shell ions) thanks to the paramagnetically-induced shifts which avoid extensive signal overlap and increase the range of observable exchange rates.
3 Experimental and computational section
3.1 Reagents and materials
The ligands, H4dota and H5do3ap, were prepared according the literature procedures.1,6 Samples of the Eu3+ complexes for NMR studies were obtained by dissolving the corresponding ligand (100 mg) in water (4 mL) and adding 0.95 equiv. of EuCl3·6H2O. Then, 5% aq. LiOH was slowly added to reach pH 11 and the mixture was stirred overnight at 60 °C. The absence of free Eu3+ ions was tested by reaction with xylenol orange in acetate buffer at pH 6.7.51 The solution was then evaporated to dryness and the residue was re-dissolved in D2O (Euriso-top, 99.96% D) for the NMR measurements. The pD of the samples was adjusted by addition of dilute solutions of DCl or LiOD in D2O.3.2 NMR spectroscopy
NMR experiments were performed on a Bruker AVANCE III 600 and 400 MHz spectrometers, the former equipped with a cryoprobe. The temperature of the sample was calibrated using pure MeOH (below 15 °C) and ethylene glycol (above 15 °C) by measuring the chemical shift differences between the two 1H NMR signals.52,53 Particular care was taken to ensure that the sample reached thermal equilibrium before the data acquisition started. The acquired FID data were then analyzed using MestReNova software.54 A 50 Hz exponential apodization was applied prior to the Fourier transform, followed by phase and baseline corrections. The signals of axial and equatorial protons of both isomers were integrated for the data analysis. In the case of signal overlap, the signal pattern was deconvoluted into Lorenzian–Gaussian curves using MestReNova tools. The dependence of signal integral values with mixing time was fitted using self-written procedures in the MATLAB R2015b®55 environment. The activation enthalpies and entropies (ΔH‡ and ΔS‡) were determined using MATLAB by fitting the temperature dependence of exchange rates using the Eyring equation (4).3.3 Computational details
All calculations presented in this work were performed using Gaussian 09 (Revision D.01).56 Full geometry optimizations of transition states and energetic minima were performed employing DFT within the meta-GGA approximation using M0657 exchange–correlation functional. For all atoms except Eu3+, the 6-31+G(d,p) basis set was employed. The large core effective core potential of the Stuttgart family (including 46 + 4f6 electrons in core, ECP52MWB)43 and the associated (7s6p5d)/[5s4p3d] basis set were used for Eu3+. An UltraFine integration grid and the default SCF energy convergence threshold (10−8) were used in all calculations. All the calculations were performed employing a polarization continuum model to account for bulk solvent effects (water) and the solvent accessible surface to define the solute cavity. The identities of all stationary points (0 imaginary frequencies) and transition states (1 imaginary frequency) were confirmed by frequency analysis.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The investigations were supported by the Czech Science Foundation (16-03156S; to J. B.), by the Grant Agency of Charles University (1076016, to J. B.) and the Ministry of Education of the Czech Republic (LTC 170607, to J. B. and P. H.; project is connected to the EU COST CA15209 Action). Computational resources were provided by the CESNET LM2015042 and the CERIT Scientific Cloud LM2015085, provided under the program “Projects of Large Research, Development, and Innovations Infrastructures”. C. P.-I. thanks Ministerio de Economía y Competitividad (CTQ2013-43243-P) for generous financial support.Notes and references
- J. F. Desreux, Inorg. Chem., 1980, 19, 1319–1324 CrossRef CAS.
- D. Parker, R. S. Dickins, H. Puschmann, C. Crossland and J. A. K. Howard, Chem. Rev., 2002, 102, 1977–2010 CrossRef CAS PubMed.
- S. Aime, M. Botta, M. Fasano, M. P. M. Marques, C. F. G. C. Geraldes, D. Pubanz and A. E. Merbach, Inorg. Chem., 1997, 36, 2059–2068 CrossRef CAS PubMed.
- F. A. Dunand, S. Aime and A. E. Merbach, J. Am. Chem. Soc., 2000, 122, 1506–1512 CrossRef CAS.
- L. S. Natrajan, N. M. Khoabane, B. L. Dadds, C. A. Muryn, R. G. Pritchard, S. L. Heath, A. M. Kenwright, I. Kuprov and S. Faulkner, Inorg. Chem., 2010, 49, 7700–7709 CrossRef CAS PubMed.
- J. Rudovský, P. Cígler, J. Kotek, P. Hermann, P. Vojtíšek, I. Lukes, J. A. Peters, L. Vander Elst and R. N. Muller, Chem. – Eur. J., 2005, 11, 2373–2384 CrossRef PubMed.
- M. Purgel, Z. Baranyai, A. de Blas, T. Rodríguez-Blas, I. Bányai, C. Platas-Iglesias and I. Tóth, Inorg. Chem., 2010, 49, 4370–4382 CrossRef CAS PubMed.
- S. Aime, A. Barge, M. Botta, A. S. De Sousa and D. Parker, Angew. Chem., Int. Ed., 1998, 37, 2673–2675 CrossRef CAS.
- B. C. Webber and M. Woods, Inorg. Chem., 2012, 51, 8576–8582 CrossRef CAS PubMed.
- M. Woods, S. Aime, M. Botta, J. A. K. Howard, J. M. Moloney, M. Navet, D. Parker, M. Port and O. Rousseaux, J. Am. Chem. Soc., 2000, 122, 9781–9792 CrossRef CAS.
- The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, ed. A. Merbach, L. Helm and É. Tóth, John Wiley & Sons, Ltd, Chichester, UK, 2013 Search PubMed.
- S. Viswanathan, Z. Kovacs, K. N. Green, S. J. Ratnakar and A. D. Sherry, Chem. Rev., 2010, 110, 2960–3018 CrossRef CAS PubMed.
- W. M. Liu, M. Overhand and M. Ubbink, Coord. Chem. Rev., 2014, 273–274, 2–12 CrossRef CAS.
- U. Brath, S. I. Swamy, A. X. Veiga, C.-C. Tung, F. Van Petegem and M. Erdélyi, J. Am. Chem. Soc., 2015, 137, 11391–11398 CrossRef CAS PubMed.
- T. Krchová, A. Gálisová, D. Jirák, P. Hermann and J. Kotek, Dalton Trans., 2016, 3486–3496 RSC.
- T. Krchová, V. Herynek, A. Gálisová, J. Blahut, P. Hermann and J. Kotek, Inorg. Chem., 2017, 56, 2078–2091 CrossRef PubMed.
- P. Harvey, A. M. Blamire, J. I. Wilson, K.-L. N. A. Finney, A. M. Funk, P. Kanthi Senanayake and D. Parker, Chem. Sci., 2013, 4, 4251–4258 RSC.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- L. Lumata, A. K. Jindal, M. E. Merritt, C. R. Malloy, A. D. Sherry and Z. Kovacs, J. Am. Chem. Soc., 2011, 133, 8673–8680 CrossRef CAS PubMed.
- R. S. Dickins, S. Gaillard, S. P. Hughes and A. Badari, Chirality, 2005, 17, 357–363 CrossRef CAS PubMed.
- S. P. Babailov, Prog. Nucl. Magn. Reson. Spectrosc., 2008, 52, 1–21 CrossRef CAS.
- F. K. Kálmán, Z. Baranyai, I. Tóth, I. Bányai, R. Király, E. Brücher, S. Aime, X. Sun, A. D. Sherry and Z. Kovács, Inorg. Chem., 2008, 47, 3851–3862 CrossRef PubMed.
- S. Aime, A. Barge, M. Botta, M. Fasano, J. Danilo Ayala and G. Bombieri, Inorg. Chim. Acta, 1996, 246, 423–429 CrossRef CAS.
- F. A. Dunand, R. S. Dickins, D. Parker and A. E. Merbach, Chem. – Eur. J., 2001, 7, 5160–5167 CrossRef CAS.
- M. Elhabiri, S. Abada, M. Sy, A. Nonat, P. Choquet, D. Esteban-Gómez, C. Cassino, C. Platas-Iglesias, M. Botta and L. J. Charbonnière, Chem. – Eur. J., 2015, 21, 6535–6546 CrossRef CAS PubMed.
- M. Mato-Iglesias, T. Rodríguez-Blas, C. Platas-Iglesias, M. Starck, P. Kadjane, R. Ziessel and L. Charbonniére, Inorg. Chem., 2009, 48, 1507–1518 CrossRef CAS PubMed.
- S. P. Babailov, A. G. Coutsolelos, A. Dikiy and G. A. Spyroulias, Eur. J. Inorg. Chem., 2001, 303–306 CrossRef CAS.
- S. Hoeft and K. Roth, Chem. Ber., 1993, 126, 869–873 CrossRef CAS.
- V. Jacques and J. F. Desreux, Inorg. Chem., 1994, 33, 4048–4053 CrossRef CAS.
- O. V. Yazyev, L. Helm, V. G. Malkin and O. L. Malkina, J. Phys. Chem., 2005, 109, 10997–11005 CrossRef CAS PubMed.
- A. Lasoroski, R. Vuilleumier and R. Pollet, J. Chem. Phys., 2014, 141, 14201 CrossRef PubMed.
- A. Lasoroski, R. Vuilleumier and R. Pollet, J. Chem. Phys., 2013, 139, 104115 CrossRef PubMed.
- A. Ramírez-Solís, J. I. Amaro-Estrada, J. Hernández-Cobos and L. Maron, J. Phys. Chem. A, 2017, 121, 2293–2297 CrossRef PubMed.
- R. Pollet, N. N. Nair and D. Marx, Inorg. Chem., 2011, 50, 4791–4797 CrossRef CAS PubMed.
- U. Cosentino, A. Villa, D. Pitea, G. Moro, V. Barone and A. Maiocchi, J. Am. Chem. Soc., 2002, 124, 4901–4909 CrossRef CAS PubMed.
- C. Platas-Iglesias, Eur. J. Inorg. Chem., 2012, 2023–2033 CrossRef CAS.
- M. P. M. Marques, C. F. G. C. Geraldes, A. D. Sherry, A. E. Merbach, H. Powell, D. Pubanz, S. Aime and M. Botta, J. Alloys Compd., 1995, 225, 303–307 CrossRef CAS.
- C. Kumas, W. S. Fernando, P. Zhao, M. Regueiro-Figueroa, G. E. Kiefer, A. F. Martins, C. Platas-Iglesias and A. D. Sherry, Inorg. Chem., 2016, 55, 9297–9305 CrossRef CAS PubMed.
- K. Stott, J. Stonehouse, J. Keeler, T.-L. Hwang and A. J. Shaka, J. Am. Chem. Soc., 1995, 117, 4199–4200 CrossRef CAS.
- S. Aime, L. Barbero, M. Botta and G. Ermondi, J. Chem. Soc., Dalton Trans., 1992, 225–228 RSC.
- L. Liu and Q. X. Guo, Chem. Rev., 2001, 101, 673–695 CrossRef CAS PubMed.
- M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1993, 85, 441–450 CrossRef CAS.
- M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194 CrossRef CAS.
- A. Roca-Sabio, M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Comput. Theor. Chem., 2012, 999, 93–104 CrossRef CAS.
- M. R. Spirlet, J. Rebizant, J. F. Desreux and M. F. Loncin, Inorg. Chem., 1984, 23, 359–363 CrossRef CAS.
- M. Regueiro-Figueroa, B. Bensenane, E. Ruscsák, D. Esteban-Gómez, L. J. Charbonnière, G. Tircsó, I. Tóth, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Inorg. Chem., 2011, 50, 4125–4141 CrossRef CAS PubMed.
- G. Brehm, M. Reiher and S. Schneider, J. Phys. Chem. A, 2002, 106, 12024–12034 CrossRef CAS.
- D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas, L. Helm and C. Platas-Iglesias, ChemPhysChem, 2012, 13, 3640–3650 CrossRef PubMed.
- M. Regueiro-Figueroa and C. Platas-Iglesias, J. Phys. Chem. A, 2015, 119, 6436–6445 CrossRef CAS PubMed.
- R. Pollet, C. S. Bonnet, P. Retailleau, P. Durand and É. Tóth, Inorg. Chem., 2017, 56, 4317–4323 CrossRef CAS PubMed.
- A. Barge, G. Cravotto, E. Gianolio and F. Fedeli, Contrast Media Mol. Imaging, 2006, 1, 184–188 CrossRef PubMed.
- C. Ammann, P. Meier and A. Merbach, J. Magn. Reson., 1982, 46, 319–321 CAS.
- M. L. Kaplan, F. A. Bovey and H. N. Cheng, Anal. Chem., 1975, 47, 1703–1705 CrossRef CAS.
- MestReNova, Version 11.0.1-17801, Mestrelab Research S.L., Santiago de Compostela, 2016.
- MATLAB and Optimisation Toolbox 7.3 Release R2015b, The MathWorks, Inc., Natick, Massachusetts, United States, DERIVESTsuite, available viahttp://www.mathworks.com.
- Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05296k |
| This journal is © the Owner Societies 2017 |