Symmetry and dynamics of FHF⁻ anion in vacuum, in CD₂Cl₂ and in CCl₄. Ab initio MD study of fluctuating solvent–solute hydrogen and halogen bonds

Abstract

FHF⁻ anion is a classic example of a central-symmetric strongly hydrogen bonded system that has been intensively investigated both experimentally and theoretically. In this paper we focus on solvent effects on symmetry, structure and dynamics of the anion. The FHF⁻ anion is studied in vacuum, dissolved in CH₂Cl₂ and dissolved in CCl₄ by ab initio molecular dynamics simulations. We show that CH₂Cl₂ molecules form CH⋯F hydrogen bonds with lone pairs of fluorine atoms, while CCl₄ molecules form halogen bonds. These specific non-covalent solvent–solute interactions are cooperatively coupled to the FHF⁻ hydrogen bonds. The fluctuation of solvent molecules’ positions is the driving force changing the FHF⁻ hydrogen bond geometry. Most of the time, the anion is solvated asymmetrically, which leads to the asymmetric bridging particle position, though the time-averaged D_∞h symmetry is retained. Interestingly, this transient asymmetrization of FHF⁻ is more pronounced in CCl₄, than in CH₂Cl₂. We show that the ¹H and ¹⁹F NMR chemicals shifts react sensitively to the changes of anion's geometry and the limiting chemical shifts of free solvated FH and F⁻ are strongly solvent-dependent.

---

Introduction

The geometric, energetic and spectroscopic properties of hydrogen bonded complexes are susceptible to the structure and dynamics of the surrounding medium. For example, in molecular crystals and in hydrophobic pockets of biomolecules steric factors and local polarity often determine the bridging proton position.^1,2 In solutions, the thermal fluctuations of solvent dipoles in the solvation shell and specific solvent–solute interactions may significantly influence the structure of a hydrogen bonded complex.^3–6 In particular, in the case of formally symmetric hydrogen bonds transient asymmetric solvation shell structures (which may include counterions for charged systems) may break the overall symmetry of the complex.⁴ For example, Perrin et al. have studied the solvent effects on the symmetry of an intramolecular (OHO)⁻ hydrogen bond in case of symmetric counter cation placement⁷ and have coined the term “solvatomers”⁸ to describe conformations (sometimes true isomers) that differ in solvation. In ref. 9 authors argue that the observation of an equilibrium between two strongly hydrogen-bonded tautomers of a formally symmetric NHN system could be due to the reorganization of the solvent, switching between two asymmetric solvation patterns. It has been proposed to detect experimentally the presence of an equilibrium by performing its isotopic perturbation (H/D or ¹⁶O/¹⁸O replacement).^7,10,11

Recently we have studied by a combination of ab initio molecular dynamics simulations (ab initio MD) and experimental low-temperature combined NMR/UV-Vis spectroscopy¹² strongly OHO-bonded anionic complex of 4-nitrophenolate and acetic acid dissolved in CD₂Cl₂.¹³ In this system an effective double-well proton potential is realized and the fast reversible proton transfer in the OHO bond is driven by the solvent–solute interactions. While the overall effect of solvation by a polar medium is clearly present,¹⁴ the primary driving force of proton transfer was shown to be the formation and breakage of weak CH⋯O=C hydrogen bonds between solvent molecules and the “free” carbonyl group of the acetic acid. Expanding the line of research to neutral OHN-bonded complexes, a series of complexes formed by chloroacetic acid and substituted pyridines has been studied by low-temperature combined NMR/IR spectroscopy.¹⁵Ab initio MD simulations carried out for the complex of acetic acid with 2-methylpyridine dissolved in dichloromethane have revealed that the proton transfer from the molecular OH⋯N to the zwitterionic O⁻⋯HN⁺ form occurs in the picosecond time range and it is driven by the cooperative interaction of the OHN hydrogen bond and CH⋯O=C bonds with solvent molecules. In contrast to liquid solutions, in molecular crystals with OHN hydrogen bonds, where the surrounding medium is essentially static (and stabilization of zwitterionic structures is less likely¹⁶), the proton tautomerism is often suppressed.¹⁷ For charged systems with intramolecular (NHN)⁺ hydrogen bonds the solvent and counter-anion effects have been previously studied experimentally^18,19 and computationally.²⁰ In ref. 19 it was argued that the increase of the solvent polarity leads to the separation of the (NHN)⁺-bonded complex and its counteranion and in average results in the symmetrisation of the (NHN)⁺ bridge. The nuclear quantum effects on distribution of bridging proton position could be accounted for by using path integral molecular dynamics simulations (PIMD). Recently, this approach has been applied to short OHO,²¹ OHN²² and other hydrogen bonds, including intramolecular ones²³ and the ones found inside the active sites of enzymes.²⁴

One of the most famous examples of an extremely strong and short symmetric hydrogen bond is FHF⁻ anion. The recent estimates give the gas phase complexation energy around 44 kcal mol⁻¹.²⁵ In the gas phase the bridging proton is located at the geometric centre between two fluorines (D_∞h point group of symmetry for the anion), as confirmed by IR spectroscopy^26–28 The experimental value of FHF⁻ vibrational frequencies are ν₁ = 583 cm⁻¹ (symmetric stretch) ν₂ = 1286 cm⁻¹ (bending) and ν₃ = 1331 cm⁻¹ (asymmetric stretch).²⁷ Deuteration of the complex results in so-called anomalous Ubbelohde effect:^29,30 the F⋯F distance slightly shortens in FDF⁻, as compared to FHF⁻.²⁶ This could be rationalized in terms of a smaller special spread of the deuteron's vibrational wave function, which allows two fluorines to come closer to each other.³¹ Apart of the Ubbelohde effect, the equilibrium structure of FDF⁻ anion is similar to that of FHF⁻. The symmetry of the FHF⁻ (FDF⁻) anion remains unbroken in noble gas matrices³² and in KHF₂ (KDF₂) crystals.³³ In a recent paper Grabowski² has analyzed the available crystal structures including FHF⁻ fragment and found out that while in some cases the gas-phase symmetry D_∞h is preserved, in many other cases it is deformed due to interactions with the surrounding medium, mainly by the formation of external hydrogen bonds. In a polar aprotic medium, such as a mixture of liquefied gases CDF₂/CDF₂Cl the FHF hydrogen bond in the FHF⁻NBu₄⁺ complex retains its average symmetry, as evidenced by the positive value of the primary H/D isotope effect³⁴ (δD − δH > 0.32 ppm; δH = 16.6 ppm³⁵). However, the situation depends on the strength of the intermolecular interactions: in the presence of a strongly interacting counter-cation, such as 2,4,6-trimethylpyridinium,³⁶ the transient symmetry of FHF⁻ is broken, though in the NMR time scale two fluorine atoms stay chemically equivalent due to the rapid rotation of the anion.

The FHF⁻ anion is a popular system for theoretical investigations. The small number of atoms allows for high-precision calculations of the multidimensional potential energy surface (PES).^37,38 It has been demonstrated that in the gas phase the potential for the proton stretching motion is highly anharmonic and has a “flat-bed” single-well shape, which leads to the delocalization of the bridging particle near the H-bond center. Depending on the level of theory used, the calculations of the vibrational frequencies using the multidimensional PES show some spread around the experimental values. In some cases computed frequencies match rather well – difference less than 10 cm⁻¹ – with the experiment.^39–42 Upon increase of the F⋯F distance a barrier for the proton motion appears and grows, eventually rising above the zero-point energy level and creating a dual maximum shape of the proton wave function.⁴³ It could be argued that in a condensed medium such double well potential is realized along the proton transfer coordinate that includes the solvent molecule motions.⁴⁴

The NMR parameters of FHF⁻ anion have been computed by several authors.^35,41,45 The results show the low-field bridging proton chemical shift and high values of the ¹J_HF and ^2hJ_FF coupling constants for the isolated anion, which reproduce rather well the available experimental data. Additionally, in ref. 46 various vibrational contributions to the resulting value of the positive primary H/D isotope have been discussed and in ref. 47 the solvent-induced temperature dependencies of NMR parameters of FHF⁻ anion were analyzed. Recently published results of the gas phase path integral molecular dynamics study (MP2/6-31++G**)⁴⁸ of FHF⁻ and FDF⁻ have reproduced the main features of the anion: D_∞h symmetry, anomalous Ubbelohde effect on the F⋯F distance upon deuteration and the narrower distribution of D positions, as compared to H. It has also been reported that despite the linear configuration of three atoms in the optimized geometry of the anion the most probably structure in the gas phase is bent (more on that in Discussion).

In this work we present the results of ab initio MD investigation of FHF⁻ anion in three environments: in vacuum and in two explicit solvents, CH₂Cl₂ and CCl₄. Our main interest is to gain an atomistic understanding of how specific solvent–solute interactions (symmetric or not) break the transient symmetry of the anion. Here by symmetry we mean the position of the bridging proton between two fluorine atoms (D_∞h for the central position, C_∞v for the asymmetric linear position and C_s for asymmetric non-linear one). We aim to analyse the ensemble of solvatomers and corresponding distribution of spectroscopic parameters (NMR and IR) in condensed medium.⁴⁹ The main source of the solvent–solute interactions is expected to be the interaction of the fluorine lone pairs with the CH protons (for CH₂Cl₂) and with the sigma-holes on the halogen atoms (for CH₂Cl₂ and CCl₄). The counterion effects are not considered in this paper. Small cations such as K⁺ or Na⁺ would strongly interact with the anion, perturb the solvation shell and mask the specific solvent–solute non-covalent interactions. Large bulky counterions used in experiments (pyridinium,³⁶ tetrabutylammonium,³⁵ and even larger systems⁵⁰) are less active, but the perturbation of the solvation shell would also break the potential symmetry of the solvation shell.

Computational details

Ab initio MD simulations of the complexes were performed using the CP2K⁵¹ simulation package. We chose GPW⁵² method, the BLYP-D2^53–55 DFT functional, together with a DZVP-MOLOPT-GTH^56,57 basis sets for all atoms. The simulations were performed in an NVT ensemble at 300 K using a global CSVR thermostat⁵⁸ with 500 fs time constant. All hydrogen atoms were simulated as deuterium atoms, which allowed us to increase the time step to 1 fs, but throughout the paper we will refer to them as to protons. The selected time step is at least 10 times shorter than the period of the expected highest-frequency nuclear vibrational motion in the system (CD stretching), which satisfies the usual criterion proposed for the Born–Oppenheimer MD.⁵⁹ The employed SCF convergence was 10⁻⁶ a.u. and plane wave cutoff was set to 450 Ry. The molecular dynamics was done in a cubic periodic box with a side length of 15 Å. We have run three trajectories: for a FHF⁻ in vacuum, in dichloromethane (CH₂Cl₂) and in tetrachloromethane (CCl₄). For the trajectories in condensed phase the solvent cells were previously equilibrated (energy minimization followed by 6 ps AIMD run). Then the complexes were inserted into the solvent box by calculating the molecular volume of the overlapping van der Waals radii of its atoms and removing the equivalent volume of solvent molecules calculated in the same way. This resulted in a box containing 33 CH₂Cl₂ molecules and FHF⁻ at a density 1.4 g cm⁻³ and 22 CCl₄ molecules at a density 1.68 g cm⁻³. The systems were equilibrated for 5 ps, and then the simulation continued for another 11 ps (vacuum) or 25 ps (CH₂Cl₂ and CCl₄) which were used for data sampling. We used VMD⁶⁰ and TRAVIS^61,62 for trajectory analysis.

Chemical shifts were calculated in CP2K with the all-electron GAPW^63,64 method and PBE0⁶⁵ functional, employing locally dense basis sets: pcSseg-2^66–68 basis set on hydrogen and fluorine atoms and 6-31G* basis set for carbon and chlorine atoms. A number of random snapshots were extracted from every trajectory (30 for FHF⁻ in vacuum, 100 for FHF⁻ in CH₂Cl₂ and CCl₄). For the solvated systems all solvent molecules were included in calculations. Isotropic magnetic shielding constants for ¹H and ¹⁹F were referenced to tetramethylsilane and CFCl₃ in vacuum, respectively.

Results

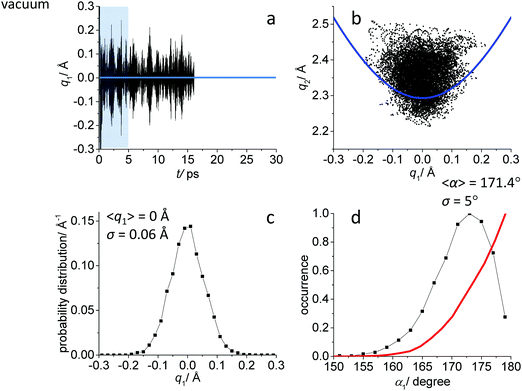
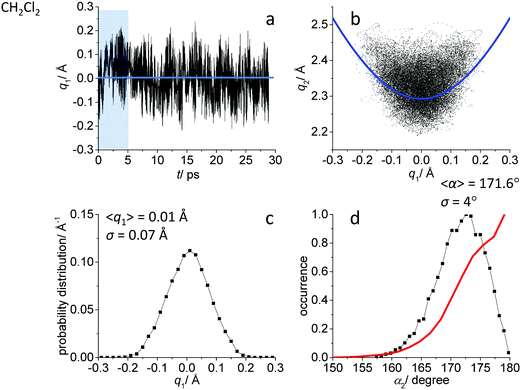
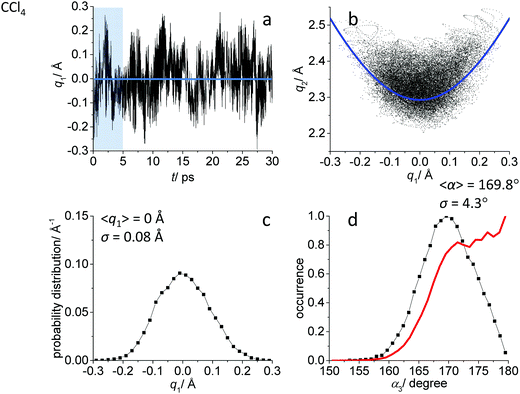
While the detailed description of the results of ab initio MD simulations concerning the solvation shell structure will be given in Discussion, here we present general information about the structure of the FHF⁻ anion itself, according to the calculated trajectories. In all cases – in vacuum or dissolved in an aprotic solvent – FHF⁻ anion exhibits strong and short hydrogen bond, that does not break during the simulation. Geometric parameters of the FHF⁻ anion fluctuate around equilibrium values and the characteristics of these fluctuations depend on the medium. For convenience, we introduce here linear combinations of interatomic distances for the description of FHF⁻ hydrogen bond as q₁ = 1/2(r_FH − r_HF) and q₂ = r_FH + r_HF. For a linear hydrogen bond these parameters have a clear physical meaning: q₁ represents the shift of the proton from the centre of the hydrogen bond and q₂ represents its overall length. The change of the q₁ sign corresponds to proton crossing the centre of the H-bond (the center of the F⋯F distance). Note that the sign of q₁ value is defined by the numbering of fluorine atoms, which in our case was chosen arbitrary and kept consistently during the analysis.

In Fig. 1–3 the data for FHF⁻ in vacuum, dissolved in CH₂Cl₂ and dissolved in CCl₄ are given, respectively. The following characteristic are plotted: (a) the time dependence of the hydrogen bond asymmetry parameter q₁; (b) the interdependence of q₁ and the overall hydrogen bond length parameter q₂; (c) the probability distribution of q₁ values and (d) the occurrence of different FHF angles with cone correction (red curve) and without it (black curve).

Fig. 1 Ab initio MD trajectory analysis: geometry of FHF⁻ anion in vacuum. (a) The time dependence of q₁ = 1/2(r_FH − r_HF). (b) The interdependence of q₁ and q₂ = r_FH + r_HF. (c) The probability distribution of q₁ values. (d) The occurrence of different FHF angles α with cone correction (red curve) and without it (black curve). For more details see text.

Fig. 2 Ab initio MD trajectory analysis: geometry of FHF⁻ anion dissolved in CH₂Cl₂. (a) The time dependence of q₁ = 1/2(r_FH − r_HF). (b) The interdependence of q₁ and q₂ = r_FH + r_HF. (c) The probability distribution of q₁ values. (d) The occurrence of different FHF angles α with cone correction (red curve) and without it (black curve). For more details see text.

Fig. 3 Ab initio MD trajectory analysis: geometry of FHF⁻ anion dissolved in CCl₄. (a) The time dependence of q₁ = 1/2(r_FH − r_HF). (b) The interdependence of q₁ and q₂ = r_FH + r_HF. (c) The probability distribution of q₁ values. (d) The occurrence of different FHF angles α with cone correction (red curve) and without it (black curve). For more details see text.

Fig. 1a, 2a and 3a show that in all cases the bridging particle crosses the midpoint of the hydrogen bridge (q₁ = 0 Å) many times during the simulation. In Fig. 1b, 2b and 3b we show the interdependence of q₁ and q₂ parameters, which is barely noticeable in Fig. 1b and becomes progressively more apparent in Fig. 2b and 3b. For future reference, we have added to the Fig. 1b, 2b and 3b a curve, corresponding to the previously established q₁–q₂ correlation. This correlation represents FHF⁻ geometry changes along the proton transfer reaction pathway in vacuum. The curve was constructed according to ref. 69 and stems from the so-called valence bond order model of hydrogen bonded complexes:^70–72

p₁ + p₂ = 1, p₁ = exp(−(r_FH − r⁰)/b); p₂ = exp(−(r_HF − r⁰)/b), (1)

where p₁ and p₂ are called bond orders, r⁰ = 0.897 Å and b = 0.36 Å. The parameter r⁰ has the meaning of the F⋯H distance in a hypothetical free FH molecule, while b describes how rapidly the FH bond order falls with the F⋯H distance (in other words, the parameter b is chosen in such a way that the equation p₁ + p₂ = 1 is better fulfilled). From eqn (1) one can derive that

q₂ = 2r⁰ + 2q₁ + 2b ln(1 + exp(–2q₁/b)). (2)

The probability distributions of q₁ values are shown in Fig. 1c, 2c and 3c (see also the distribution of F⋯H distances in Fig. S1 in ESI†). Quite expectedly, considering the symmetry of the system, these distributions are centred at q₁ = 0 Å, which corresponds to the central-symmetric anion. The reasons why there are changes in the widths and general shapes of distributions will be given in Discussion. The probability distributions of q₂ and F⋯F distance r_FF for all three studied systems are shown in Fig. S1 in ESI.† For three systems (FHF⁻ in vacuum, in CH₂Cl₂ and in CCl₄ medium) these distributions for each parameter are qualitatively similar. However, there are some changes in the shapes, which will be discussed below.

Finally, in Fig. 1d, 2d and 3d we demonstrate that the average structure of FHF⁻ anion is linear in vacuum and in solution. This topic deserves some comments. The bent structures are progressively less and less energetically favoured when FHF angle α deviates from linearity. Nevertheless, the statistical weight of the bent structures increases proportionally to the sin(α). As a result, the distributions of angles start to show maxima at α < 180°. In other words, the most probable structure of the FHF⁻ anion is bent, even in vacuum. For example, the most probable angle α equals to 171.4° for FHF⁻ in vacuum, 171.6° in CH₂Cl₂ and 169.8° in CCl₄ (these values are close to each other, suggesting that there is not really a difference in the stability of the bent geometries). However, if one performs so called cone correction, which takes into account the statistical weight of each value of the angle α, one obtains the distribution functions as shown in Fig. 1d, 2d and 3d as red curves. In all cases the cone-corrected most probable (most energetically favoured) FHF angle α is 180°.

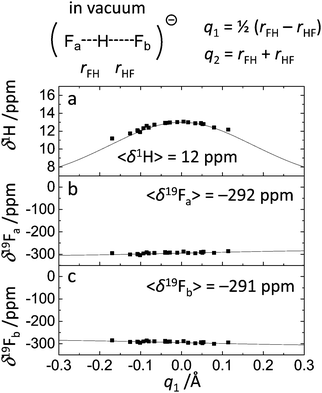
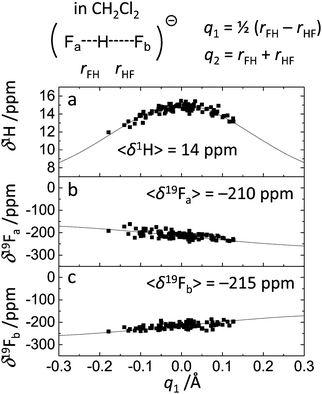
The dependencies of ¹H and ¹⁹F NMR chemical shifts on q₁ values for the studied systems are given in Fig. 4–6. The average values of chemical shifts are added to the figures and also collected in Table 1. The average values for fluorine atoms ¹⁹F_a and ¹⁹F_b coincide within a couple of ppm, indicating that the set of snapshots used to calculate the average is a sufficiently representative one.

Fig. 4 ¹H and ¹⁹F NMR chemical shifts for FHF⁻ in vacuum vs. q₁ for 30 random snapshots of the trajectory. Fitted curves correspond to eqn (3) and (4) with parameters listed in Table 2. 〈δ¹H〉 and 〈δ¹⁹F_a,b〉 stand for the values of chemical shifts averaged over the given set of points.

Fig. 5 ¹H and ¹⁹F NMR chemical shifts for FHF⁻ in CH₂Cl₂vs. q₁ for 100 random snapshots of the trajectory. Fitted curves correspond to eqn (3) and (4) with parameters listed in Table 2. 〈δ¹H〉 and 〈δ¹⁹F_a,b〉 stand for the values of chemical shifts averaged over the given set of points.

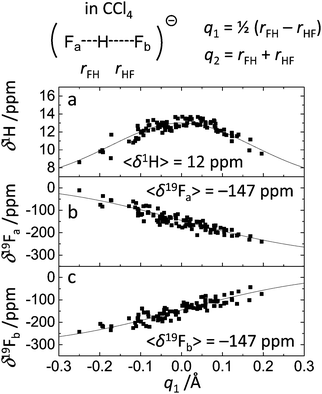Fig. 6 ¹H and ¹⁹F NMR chemical shifts for FHF⁻ in CCl₄vs. q₁ for 100 random snapshots of the trajectory. Fitted curves correspond to eqn (3) and (4) with parameters listed in Table 2. 〈δ¹H〉 and 〈δ¹⁹F_a,b〉 stand for the values of chemical shifts averaged over the given set of points.

Table 1 The values of average ¹H and ¹⁹F NMR chemical shifts for the FHF⁻ anion in vacuum, dissolved in CH₂Cl₂ and dissolved in CCl₄ (see also Fig. 4–6). The labelling of fluorine atoms (a and b) was done arbitrarily and kept consistent during the analysis

System	〈δ^2H〉, ppm	〈δ^19Fa〉, ppm	〈δ^19Fb〉, ppm
FHF^− in vacuum	12	−292	−291
FHF^− in CH2Cl2	14	−210	−215
FHF^− in CCl4	12	−147	−147

---

The δ¹H values for three systems (Fig. 4a, 5a and 6a) behave in a qualitatively similar fashion: a symmetric bell-shaped dependence on q₁ with the maximum corresponding to q₁ = 0 Å, which is typical for formally symmetric hydrogen bonds of various types.^19,67,70 Following the approach outlined in ref. 67, we have attempted to fit these points using the equation

δ¹H = δ(FH̲) + Δ·(4p₁·p₂)², (3)

where p₁ and p₂ are q₁-dependent bond orders from eqn (1), δ(FH̲) is the proton chemical shift of a hypothetical free FH molecule and Δ is the excess chemical shift, which determines the maximum value δ¹H reaches at q₁ = 0 Å. The dependences of δ¹⁹F values on q₁ for two fluorine atoms (Fig. 4b, c, 5b, c and 6b, c) are essentially the same, only the sign of q₁ is reversed. On the first glance, these dependencies look linear. However, they can be fit using an equation similar to the one reported in ref. 67:

δ¹⁹F = δ(F̲H)·p₁ + δ(F̲⁻)·p₂, (4)

where δ(F̲H) and δ(F̲⁻) are fluorine chemical shifts of hypothetical free FH molecule and F⁻ anion, respectively. The fitted curves are depicted in Fig. 4–6 as black traces and the parameters are given in Table 2. The spread of the data points does not allow one to obtain the precise values of the limiting chemical shifts, so the values given in Table 2 serve as rough estimates. Nevertheless, it might be concluded that the sensitivity of the δ(F̲H) to the medium is much larger than that of δ(F̲⁻). It would be interesting to explicitly calculate these values by performing ab initio MD simulations of isolated FH and F⁻ in vacuum and in the medium. However, this task was beyond the scope of this work.

Table 2 The values of the fitted parameters of eqn (3) and (4) used to plot black traces in Fig. 4–6

System	δ(FH̲), ppm	Δ, ppm	δ(F̲H), ppm	δ(F̲^−), ppm
FHF^− in vacuum	6	7	−310	−280
FHF^− in CH2Cl2	6	9	−150	−280
FHF^− in CCl4	6	7	+30	−320

---

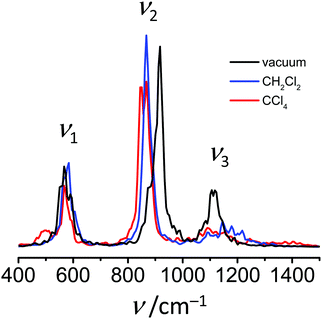
Finally, in Fig. 7 we plot the power spectra, i.e. Fourier transformed velocity autocorrelation function of FHF⁻ atoms. In each case three maxima can be observed at ca. 570 cm⁻¹, around 900 cm⁻¹ and slightly above 1100 cm⁻¹. We remind here that in order to increase the time step of the simulations all hydrogens were simulated with double mass (as deuterons), which affects the vibrational frequencies. The assignment of these maxima to normal modes of the anion can be done either by comparison with the previously reported experimentally measured or computed values of FDF⁻ vibrational frequencies,^26,39 or by performing the normal mode analysis implemented in TRAVIS software package.⁷³ The results of the two approaches coincide and give the following assignment in the order of increasing frequencies: symmetric stretch, bending and asymmetric stretch.

Fig. 7 Power spectra of FHF⁻ in vacuum (black line), in CH₂Cl₂ (blue line) and in CCl₄ (red line).

Discussion

FHF⁻ in vacuum

The structural and spectroscopic featured of FHF⁻ anion are presented in Fig. 1 and 4 and were briefly described in the Results section. The widths of q₁ and q₂ distributions and the width of FHF angle α distribution serve us as a starting point for the discussion of the solvent effects below. Nevertheless, it is interesting to compare our results with the results of PIMD simulation of FHF⁻ and FDF⁻ anions in vacuum (MP2/6-31++G**), published by Suzuki et al.⁴⁸ In ref. 48 authors find that “nuclear quantum effects stretch the FH and FF distances due to potential anharmonicity”. Despite the differences in the level of theory, the average bond lengths and angles agree rather well (for FDF⁻ PIMD and this study, respectively: average F⋯D distances are 1.163 Å and 1.178 Å; average F⋯F distances are 2.324 Å and 2.349 Å; average angles α are 169.6° and 171.4°). Quantum effects also lead to a wider distribution of bond lengths. This effect is more pronounced for hydrogens as compared to deuterons. For example, the root mean square deviation for F⋯D distance in PIMD is 0.097 Å and in our Born–Oppenheimer MD simulation it equals to 0.063 Å. In general, nuclear quantum effects are without a question important for a neat description of strong H-bond parameter distribution,^21–24 however in this paper we focus on solvent–solute interactions and comparisons of different types of specific interactions in condensed phase.

Note, that the distribution of spectroscopic parameters is rather broad even without the influence of fluctuating solvent molecules in the solvation shell. For example, the ¹H NMR chemical shifts cover the range from 9 ppm to 13 ppm (Fig. 4a), while ¹⁹F chemical shift are spread over ca. 20 ppm region (Fig. 4b and c).

FHF⁻ dissolved in CH₂Cl₂

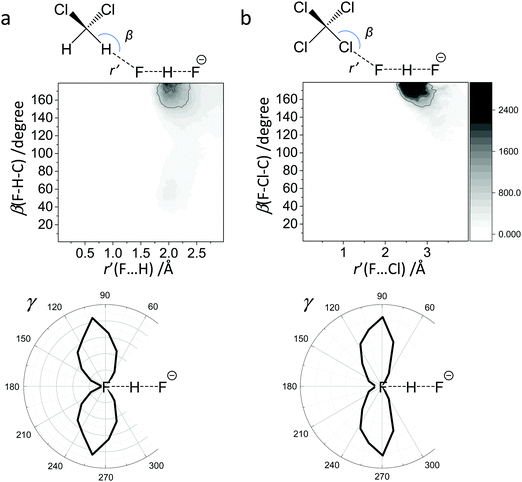
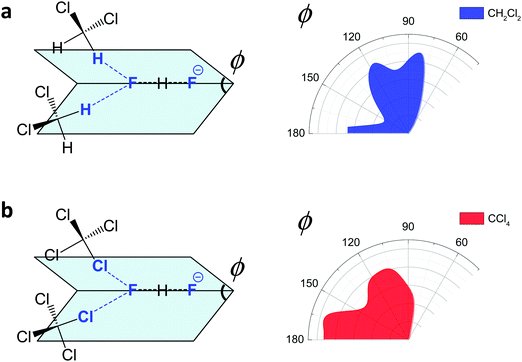
For FHF⁻ in CH₂Cl₂ the solvent–solute interactions lead to the spread of the data points in q₁–q₂ plot (Fig. 2b): the cloud of points starts to “smear” along the solid “equilibrium” curve. The corresponding distribution of q₁ values broadens (σ = 0.07 Å), as compared to FHF⁻ in vacuum, while the average F⋯F distance shortened. It means that the correlation between the proton position and the overall length of the bridge continues to be fulfilled, but there are factors which compress the anion as a whole and also lead to a larger asymmetrization of the anion. The nature of the asymmetrization could be elucidated, considering that along the trajectory, close to each fluorine atom there are one, two, three or even more CH groups of solvent molecules, some of which are forming weak CH⋯F hydrogen bonds. One of such molecules is shown at the top of Fig. 8a (see also the definitions of the distance r′(F⋯H) and the angle β(F–H-C)). These CH⋯F bonds are essentially linear and ca. 2.0 Å in length, as evidenced by the correlation plot of r′ and β. The F–F–H angles γ are distributed around 100° (see Fig. 8a, bottom). This is what one would expect assuming that the interaction occurs with one of the lone pairs of F nucleus. In this case one would expect up to three solvent molecules per fluorine. However, it might be that the maximum number of interacting solvent molecules is dictated primarily by the steric factors.⁷⁴ In order to check this, in Fig. 9a we plot the distribution of F–F–H–H dihedral angles ϕ (four atoms defining the angle are marked blue in the figure) for the cases when there are two and more CH⋯F bonds at the fluorine (r′ < 2.5 Å and 150° < β < 180° criteria were used). In the majority of cases there are two solvent molecules bound to fluorine and these molecules preferentially occupy the positions at ϕ = 90–120°, which is expected if the bonding occurs primarily via the sp³-hybridized lone pairs of fluorine. In case of pure steric repulsion of CH₂Cl₂ molecules the most abundant angle ϕ would be 180°.

Fig. 8 The directionality of the intermolecular solvent–solute interactions: correlations between the intermolecular distance r′ and the bond angle β. (a) FHF⁻ in CH₂Cl₂ (CH⋯F hydrogen bond). (b) FHF⁻ in CCl₄ (CCl⋯F halogen bond).

Fig. 9 The distribution of dihedral angles (see schemes in the left part of the figure; atoms defining the dihedral angle are marked blue) in case of two or more molecules interacting with one fluorine atom of FHF⁻. (a) CH₂Cl₂ solvent; (b) CCl₄ solvent.

The NMR parameters change significantly: firstly, the average δ¹H value grows by 2 ppm: secondly, the scattering of the δ¹⁹F_a,b points dramatically increases and the limiting value, corresponding to the “free” FH molecule, changes from –310 to −150 ppm. (As the other limiting value for “free” F⁻ changes much less, the average δ¹⁹F changes by ca. 80 ppm.) It is difficult to compare directly the absolute values of computed average chemical shifts with the experimental ones, which are collected in Table S1 (ESI†), primarily because in the experiments the conditions are never the same as in our calculations (presence on the counterion, usage of different solvents, in some cases at different temperature). Nevertheless, one can say that admitting a systematic computational error of about 1 ppm, the average δ¹H value of 14 ppm is very close to the experimental value of 16.6 ppm, reported for Bu₄N⁺FHF⁻ dissolved in CDF₃/CDF₂Cl mixture at low temperature.³⁵ This holds even more when comparing with the usual range of proton NMR chemical shifts, e.g. 5 ppm for liquid water and about 1 ppm for isolated water.

FHF⁻ dissolved in CCl₄

The CCl₄ solvent is often viewed as an inert one, influencing the dissolved complexes to a minimal degree. However, this is not the case for FHF⁻ in CCl₄. Here the tendencies described in the previous subsection (FHF⁻ in CH₂Cl₂) continue to develop: the q₁–q₂ dependence is more clearly stretched along the equilibrium line (Fig. 3b), gradually approaching the situation when intermolecular interactions with the solvent would break the symmetry of the complex and lead to formation of an effective double-well potential curve for proton motion. The distribution of q₁ values is also broader (Fig. 3c). This is the evidence for the stronger intermolecular interaction between the solvent and the solute, which in this case is the halogen bonding between the lone pairs of fluorines and the σ-holes of chlorines. From Fig. 8b it is apparent that distributions of the F⋯Cl interatomic distances r′ and of the halogen bond angles β(F–Cl–C) are quite narrow. The r′ distances are shorter than 3 Å, which is smaller than the sum of van der Waals radii of the atoms involved⁷⁵ and the β angle is close to linearity (>160°). The F–F–Cl angles γ (Fig. 8b, bottom) are clustered around 90–110°, quite close to the directions of the lone pairs of fluorines. Note however, that there are occasions when CH approaches FHF⁻ at 90° to its axis, possibly indicating the steric repulsion between the solvent molecules. Interestingly, for CH₂Cl₂ no halogen bonding to the lone pairs of fluorines has been observed in the trajectory (which is linked to the smaller σ-hole in CH₂Cl₂ and its substantial proton-donating ability). The mutual orientation of CCl₄ molecules around the fluorine atom is analysed in Fig. 9b, where the distribution of F–F–Cl–Cl angles is shown. Similar to the results obtained for CH₂Cl₂, for CCl₄ the most abundant configurations have two solvent molecules at fluorine atom (r′ < 3.1 Å; 150° < β < 180°) and these molecules occupy the relative positions at ϕ = 110–130°, fitting to the directions of fluorine lone pairs.

For CCl₄ the limiting values of ¹⁹F chemical shifts have also changed significantly: δ(F̲H) has increased from −150 ppm (for CH₂Cl₂) to +50 ppm (for CCl₄), while δ(F̲⁻) has changed much less (from −280 ppm for CH₂Cl₂ to −320 ppm for CCl₄). The difference between the limiting fluorine chemical shifts is 370 ppm and subsequently, the data points in Fig. 6b and c are noticeably scattered. The exceptionally high sensitivity of ¹⁹F NMR chemical shifts of FHF⁻ anion to the hydrogen bond geometry is not surprizing, as the shieldings are usually extremely sensitive even to sub-picometer fluctuations in bond lengths. However, the overall solvent sensitivity, i.e. the span of the δ¹⁹F values in CH₂Cl₂ and CCl₄, is surprizing and noteworthy in itself, as the experimentally measured ¹⁹F chemical shifts values reported previously in the literature for different environments lie relatively close to each other, covering a narrow range from −141 to −155 ppm (see Table S1 in ESI†). At the moment it is hard to attribute this sensitivity of computed ¹⁹F chemical shifts to any physical or dynamical parameter of the system, though it seems that the δ(F̲H) values are mostly solvent-dependent.

The calculated power spectra (Fig. 7) are not intended to simulate the experimental IR spectra and considered here in a more qualitative way. In the power spectra the difference between the two solvents can be seen (Fig. 7; see also Table S2 in ESI†). Band positions of bending (ν₂) and asymmetric stretching (ν₃) vibrations in liquids are shifted noticeably in comparison to vacuum, while relative differences between CH₂Cl₂ and CCl₄ are somewhat less pronounced. The bending vibration shifts towards lower frequencies upon dissolution, while the frequency of the asymmetric stretching increases. The interpretation of these changes can be done considering that the average F⋯F distance shortens in the condensed medium, but increases again with increasing solvent–solute interaction (2.32 Å in CH₂Cl₂, 2.33 Å in CCl₄ and 2.35 Å in vacuum). The shortening of the F⋯F distance “flattens” the potential energy surface along the bending coordinate,⁴⁰ which decreases the vibrational frequency. In contrast, the asymmetric stretching potential becomes less flat⁴⁶ and the corresponding vibrational frequency increases.

Solvation shell structure. Hydrogen/halogen bond cooperativity

In Fig. 10 we show as an example rather typical snapshots of the solvent structure around the FHF⁻ anion. One can see that in the cases of CH₂Cl₂ and CCl₄ the solvation shell contains a small number of solvent molecules many of which form non-covalent interactions with the fluorine atoms. There is always at least one solvent molecule close to each of the fluorine atoms, as could be seen from Fig. 11, where the joint distribution of the proton position (F⋯H distance within the FHF⁻ anion) and the distance to the closest solvent molecule (F⋯HC or F⋯ClC distances for hydrogen and halogen bond, respectively) are shown. Note, however, that the position of the closest solvent molecule does not determine the bridging proton position in FHF⁻ anion (in both cases the F⋯H distances cover the similar range from 1.05 to 1.25 Å). This is because there could be two, three or even more solvent molecules interacting simultaneously with the lone pairs of each fluorine atom. In Fig. 12 the number of molecules interacting with F_a and F_b is denoted N₁ and N₂, respectively. In order to determine the number of interacting solvent molecules we have chosen the same criteria, as mentioned above: for hydrogen bonds the F⋯HC distance should be shorter than 2.5 Å, for halogen bond the F⋯ClC bond should be shorter than 3.1 Å, while in both cases the angle β (see Fig. 8) should lie within the range 150° < β < 180°. At many occasions N₁ and N₂ values do not match, making the solvation shell asymmetric and causing the asymmetric bridging proton position within the FHF⁻ anion. In other words, it is the balance between the local solvations of one and of the other fluorine atoms that determines the proton position in the FHF⁻ bridge. The diagram showing the number of solvent molecules on either side of FHF⁻ anion is presented in Fig. 13. Clearly, the non-equal numbers of solvent–solute interactions is a quite common occurrence during the simulation. In order to demonstrate that the asymmetry in the solvation shell is linked to the asymmetric proton position, we have introduced the number D = N₁ − N₂. Positive D values mean that F_a is better solvated, while negative D values mean that F_b is better solvated. In Fig. 14 we plot the correlation between D and q₁ values. If there would be no interdependence, the q₁ < 0 Å and q₁ > 0 Å parts of plot would look the same. However, in our case the data is stretched along the diagonal. This correlation is pronounced weaker in case of CH₂Cl₂, which does not break significantly the symmetry of the FHF⁻ anion, and the correlation is pronounced stronger in case of CCl₄. As mentioned before, for us the stronger interaction of FHF⁻ with CCl₄ was an unexpected result. In Fig. 15 we plot the distribution of the solvent–solute bond's lifetimes, confirming that this lifetime for CCl₄ molecules is twice longer than for CH₂Cl₂ molecules.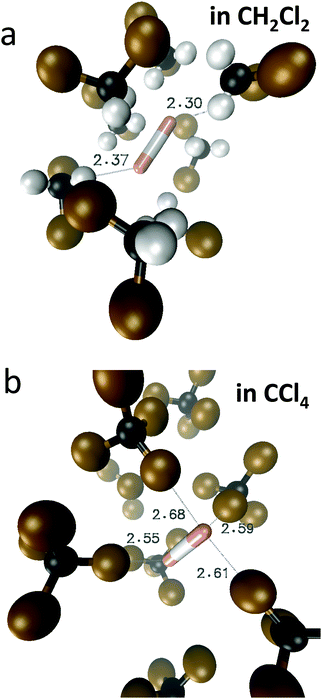

Fig. 10 Typical snapshots of the trajectory, showing the approximate structure of the first solvation shell around FHF⁻ anion. (a) CH₂Cl₂ solvent; (b) CCl₄ solvent.

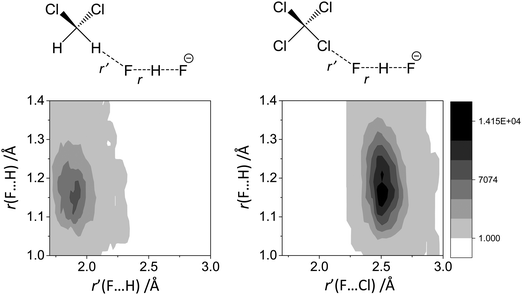Fig. 11 The interdependence between the bridging proton position r(F⋯H distance) and the intermolecular distance r′ to the closest neighbour solvent molecule. (a) FHF⁻ in CH₂Cl₂. (b) FHF⁻ in CCl₄.

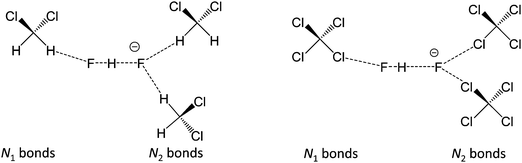Fig. 12 The scheme introducing the numbers N₁ and N₂ of solvent molecules interacting with FHF⁻ anion. Left: FHF⁻ in CH₂Cl₂ (r′ < 2.5 Å; 150° < β < 180°); right: FHF⁻ in CCl₄ (r′ < 3.1 Å; 150° < β < 180°). For the definitions of r′ and β see Fig. 8, top.

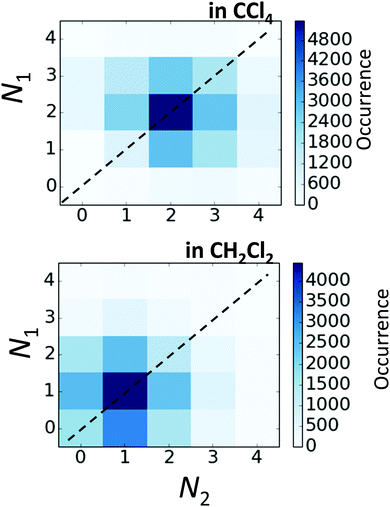Fig. 13 The correlation between N₁ and N₂ values (defined in Fig. 12) for FHF⁻ in CH₂Cl₂ (top) and in CCl₄ (bottom).

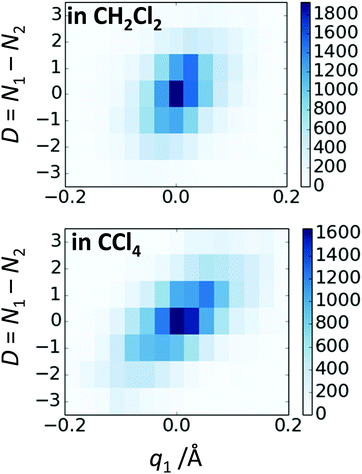Fig. 14 The correlation between D = N₁ − N₂ and q₁ values for FHF⁻ in CH₂Cl₂ (top) and in CCl₄ (bottom).

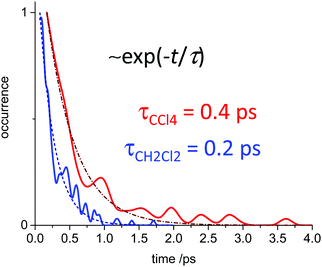Fig. 15 The distribution of solvent–solute interaction lifetimes, i.e. the residence times of solvent molecules fulfilling the criteria for non-covalent interaction. Blue trace: FHF⁻ in CH₂Cl₂ (r′ < 2.5 Å; 150° < β < 180°). Red trace: FHF⁻ in CCl₄ (r′ < 3.1 Å; 150° < β < 180°). For the definitions of r′ and β see Fig. 8, top.

Conclusions

For FHF⁻ in vacuum, dissolved in CH₂Cl₂ or CCl₄ the average D_∞h symmetry is retained, but there are differences in transient symmetry, which depends on the specific intermolecular interaction with the solvent. In case of CH₂Cl₂ is appeared to be CH⋯F hydrogen bonding (no halogen bonds were formed during the simulation), while in case of CCl₄ it is halogen bonding. Both types of intermolecular interactions are preferentially aligned with the lone pairs of fluorine atoms of FHF⁻. The cause of the proton displacement in FHF⁻ seems to be asymmetric solvation, primarily the different number of solvent molecules, non-covalently bonded to fluorine atoms. The stronger the interaction with the solvent, the broader is the q₁ distribution.

It could be speculated that even stronger specific interaction with the solvent would eventually break the symmetry of FHF⁻ completely and led to the situation better described by a two-state proton tautomerism:⁷⁶ elongated F⋯F distance and bimodal distribution of asymmetric proton positions. This transition from a “single-well” to a “double-well” situation could be done in a smooth continuous way (the process previously considered hypothetically for the increased bond length for both symmetric hydrogen⁴⁶ and symmetric halogen bonds⁷⁷).

NMR chemical shift appear to be sensitive markers for the spectral diagnostic of the hydrogen bond geometry, responding sensitively to the bridging proton position and to the medium itself. There is a huge solvent effect on average δ¹⁹F, mainly because the limiting chemical shift of FH is strongly solvent-dependent (the chemical shift of F⁻ anion is much less sensitive). The power spectrum (the autocorrelation function of the atom's velocities), constructed on the basis of computed trajectory, shows the high sensitivity to the average F⋯F distance.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Ab initio MD simulations were performed within the framework of a grant from the Deutsche Forschungsgemeinschaft Se1008/11-1. The analysis of the trajectory, solvent–solute interactions and calculations of the spectroscopic parameters were performed within the framework of the RFBR grant 17-03-00497. We thank Prof. Dr Gleb S. Denisov for valuable discussions of the project and Prof. Dr Hans-Heinrich Limbach for the inspiration of studying hydrogen bond symmetry and the interest in FHF⁻ anion.

References

1. (a) E. Puig, M. Garcia-Viloca, A. González-Lafont and J. M. Lluch, On the ionization state of the substrate in the active site of glutamate racemase. A QM/MM study about the importance of being zwitterionic, J. Phys. Chem. A, 2006, 110, 717–725; (b) P. Deb, T. Haldar, S. M. Kashid, S. Banerjee, S. Chakrabarty and S. Bagchi, Correlating Nitrile IR Frequencies to Local Electrostatics Quantifies Noncovalent Interactions of Peptides and Proteins, J. Phys. Chem. B, 2016, 120, 4034–4046.
2. S. J. Grabowski, [FHF]⁻ – The Strongest Hydrogen Bond under the Influence of External Interactions, Crystals, 2016, 6, 3/1–17.
3. Y. Mori and Y. Masuda, Effect of solvent on proton location and dynamic behavior in short intramolecular hydrogen bonds studied by molecular dynamics simulations and NMR experiments, Chem. Phys., 2015, 458, 18–29.
4. M. Garcia-Viloca, A. Gonzalez-Lafont and J. M. Lluch, Asymmetry of the Hydrogen Bond of Hydrogen Phthalate Anion in Solution. A QM/MM Study, J. Am. Chem. Soc., 1999, 121, 9198–9207.
5. T. Yamashita and K. Takatsuka, Hydrogen-bond assisted enormous broadening of infrared spectra of phenol-water cationic cluster: An ab initio mixed quantum-classical study, J. Chem. Phys., 2007, 126, 074304/1–15.
6. F. Dahms, R. Costard, E. Pines, B. P. Fingerhut, E. T. J. Nibbering and T. Elsaesser, The Hydrated Excess Proton in the Zundel Cation H₅O₂(+): The Role of Ultrafast Solvent Fluctuations, Angew. Chem., Int. Ed., 2016, 55, 10600–10605.
7. C. L. Perrin and J. S. Lau, Hydrogen-Bond Symmetry in Zwitterionic Phthalate Anions:  Symmetry Breaking by Solvation, J. Am. Chem. Soc., 2006, 128, 11820–11824.
8. C. L. Perrin, Are Short, Low-Barrier Hydrogen Bonds Unusually Strong?, Acc. Chem. Res., 2010, 43, 1550–1557.
9. C. L. Perrin and B. K. Ohta, Symmetry of NHN hydrogen bonds in solution, J. Mol. Struct., 2002, 644, 1–12.
10. C. L. Perrin and B. K. Ohta, Symmetry of O–H–O and N–H–N Hydrogen Bonds in 6-Hydroxy-2-formylfulvene and 6-Aminofulvene-2-aldimines, Bioorg. Chem., 2002, 30, 3–15.
11. C. L. Perrin and B. K. Ohta, Symmetry of N–H–N Hydrogen Bonds in 1,8-Bis(dimethylamino)naphthalene·H⁺ and 2,7-Dimethoxy-1,8-bis(dimethylamino)naphthalene·H⁺, J. Am. Chem. Soc., 2001, 123, 6520–6526.
12. P. M. Tolstoy, B. Koeppe, G. S. Denisov and H.-H. Limbach, Combined NMR/UV-Vis Spectroscopy in the Liquid State: Study of the Geometries of Strong OHO Hydrogen Bonds of Phenols with Carboxylic Acids, Angew. Chem., Int. Ed., 2009, 48, 5745–5747.
13. S. Pylaeva, C. Allolio, B. Koeppe, G. S. Denisov, H.-H. Limbach, D. Sebastiani and P. M. Tolstoy, Proton transfer in a short hydrogen bonded complex caused by solvation shell fluctuations: an ab initio MD and NMR/UV study of an (OHO)-bonded system, Phys. Chem. Chem. Phys., 2015, 17, 4634–4644.
14. B. Koeppe, J. Guo, P. M. Tolstoy, G. S. Denisov and H.-H. Limbach, Solvent and H/D Isotope Effects on the Proton Transfer Pathways in Heteroconjugated Hydrogen-Bonded Phenol-Carboxylic Acid Anions Observed by Combined UV-vis and NMR Spectroscopy, J. Am. Chem. Soc., 2013, 135, 7553–7566.
15. B. Koeppe, S. A. Pylaeva, C. Allolio, D. Sebastiani, E. T. J. Nibbering, G. S. Denisov, H.-H. Limbach and P. M. Tolstoy, Polar solvent fluctuations drive proton transfer in hydrogen bonded complexes of carboxylic acid with pyridines: NMR, IR and ab initio MD study, Phys. Chem. Chem. Phys., 2017, 19, 1010–1028.
16. P. M. Tolstoy, S. N. Smirnov, I. G. Shenderovich, N. S. Golubev, G. S. Denisov and H.-H. Limbach, NMR studies of solid state – solvent and H/D isotope effects on hydrogen bond geometries of 1 : 1 complexes of collidine with carboxylic acids, J. Mol. Struct., 2004, 700, 19–27.
17. B. C. K. Ip, I. G. Shenderovich, P. M. Tolstoy, J. Frydel, G. S. Denisov, G. Buntkowsky and H.-H. Limbach, NMR Studies of H/D Isotope and Phase Effects on 4-Methylpyridine-Pentachlorophenol Complexes and Implications for the Shapes of Hydrogen-bonded Protons in the Solid and the Liquid State, J. Phys. Chem. A, 2012, 116, 11370–11387.
18. S. B. Lesnichin, P. M. Tolstoy, H. H. Limbach and I. G. Shenderovich, Counteranion-dependent mechanisms of intramolecular proton transfer in aprotic solution, Phys. Chem. Chem. Phys., 2010, 12, 10373–10379.
19. M. Pietrzak, J. P. Wehling, S. Kong, P. M. Tolstoy, I. G. Shenderovich, C. Lopez, R. M. Claramunt, J. Elguero, G. S. Denisov and H.-H. Limbach, Symmetrization of Cationic Hydrogen Bridges of Protonated Sponges Induced by Solvent and Counteranion Interactions as Revealed by NMR Spectroscopy, Chem. – Eur. J., 2010, 16, 1679–1690.
20. Y. Masuda, Y. Mori and K. Sakurai, Effects of Counterion and Solvent on Proton Location and Proton Transfer Dynamics of N-H⋯N Hydrogen Bond of Monoprotonated 1,8-Bis(dimethylamino)naphthalene, J. Phys. Chem. A, 2013, 117, 10576–10587.
21. P. Durlak and Z. Latajka, Ab initio molecular dynamics study of the very short O–H⋯O hydrogen bonds in the condensed phases, J. Theor. Chem. Comput., 2013, 1, 65–72.
22. P. Durlak, K. Mierzwicki and Z. Latajka, Investigations of the very short hydrogen bond in the crystal of nitromalonamide via Car-Parrinello and path integral molecular dynamics, J. Phys. Chem. B, 2013, 117, 5430–5440.
23. A. Jezierska-Mazzarello, R. Vuilleumier, J. J. Panek and G. Ciccotti, Molecular Property Investigations of an ortho-Hydroxy Schiff Base Type Compound with the First-Principle Molecular Dynamics Approach, J. Phys. Chem. B, 2010, 114(1), 242–253.
24. (a) L. Wang, S. D. Fried, S. G. Boxer and T. E. Markland, Quantum delocalization of protons in the hydrogen-bond network of an enzyme active site, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18454–18459; (b) S. Sappati, A. Hassanali, R. Gebauer and P. Ghosh, Nuclear quantum effects in a HIV/cancer inhibitor: The case of ellipticine, J. Chem. Phys., 2016, 145, 205102.
25. (a) P. G. Wenthold and R. R. Squires, Bond Dissociation Energies of F₂⁻ and HF₂⁻. A Gas-Phase Experimental and G2 Theoretical Study, J. Phys. Chem., 1995, 99, 2002–2005; (b) C. Stein, R. Oswald, P. Sebald, P. Botschwina, H. Stoll and K. A. Peterson, Accurate bond dissociation energies (D-0) for FHF⁻ isotopologues, Mol. Phys., 2013, 111, 2647–2652.
26. K. Kawaguchi and E. Hirota, Infrared diode laser study of the hydrogen bifluoride anion: FHF⁻ and FDF⁻, J. Chem. Phys., 1986, 84, 2953–2960.
27. K. Kawaguchi and E. Hirota, Diode laser spectroscopy of the ν₃ and ν₂ bands of FHF⁻ in 1300 cm⁻¹ region, J. Chem. Phys., 1987, 87, 6838–6841.
28. K. Kawaguchi and E. Hirota, Infrared diode laser spectroscopy of FDF⁻, J. Mol. Struct., 1995, 352-353, 389–394.
29. J. Almlöf, Hydrogen bond studies. 71. Ab initio calculation of the vibrational structure and equilibrium geometry in HF₂⁻ and DF₂⁻, Chem. Phys. Lett., 1972, 17, 49–52.
30. A. R. Ubbelohde, Structure and Thermal Properties Associated with Some Hydrogen Bonds in Crystals. III. Further Examples of the Isotope Effect, Proc. R. Soc. A, 1939, 173, 417–427.
31. X.-Z. Li, B. Walker and A. Michaelides, Quantum nature of the hydrogen bond, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373.
32. (a) R. D. Hunt and L. J. Andrews, FTIR spectra of the HF₂⁻ and H₂F₃⁻ anions isolated in solid argon and neon, J. Chem. Phys., 1987, 87, 6819–6823; (b) S. A. McDonald and L. J. Andrews, Infrared spectrum and structure of the isolated HF₂⁻ ion in solid argon, Chem. Phys., 1979, 70, 3134–3136; (c) B. S. Ault, J. Phys. Chem., 1979, 83, 837–844.
33. P. Dawson, Spectroscopic detection of the hydrogen bond isotope effect in KHF₂, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 1448–1451.
34. P. Schah-Mohammedi, I. G. Shenderovich, C. Detering, H.-H. Limbach, P. M. Tolstoy, S. N. Smirnov, G. S. Denisov and N. S. Golubev, Hydrogen/Deuterium Isotope Effects on NMR Chemical Shifts of Formally Symmetric Complexes with a Strong Intermolecular Hydrogen Bond in Liquid Solutions at 100–150 K, J. Am. Chem. Soc., 2000, 122, 12878–12879.
35. I. Shenderovich, S. Smirnov, G. S. Denisov, V. Gindin, N. S. Golubev, A. Dunger, R. Reibke, S. Kirpekar, O. L. Malkina and H. H. Limbach, Nuclear Magnetic Resonance of Hydrogen Bonded Clusters between F⁻ and (HF)_n: Experiment and Theory, Ber. Bunsenges. Phys. Chem., 1998, 102, 422–428.
36. I. G. Shenderovich, P. M. Tolstoy, N. S. Golubev, S. N. Smirnov, G. S. Denisov and H.-H. Limbach, Low-Temperature NMR Studies of the Structure and Dynamics of a Novel Series of Acid-Base Complexes of HF with Collidine Exhibiting Scalar Couplings Across Hydrogen Bonds, J. Am. Chem. Soc., 2003, 125, 11710–11720.
37. Y. Cornaton and R. Marquardt, A Global Analytical Representation of the Potential Energy Surface of the FHF⁻ Anion, J. Phys. Chem. A, 2016, 120, 5959–5968.
38. P. Sebald, A. Bargholz, R. Oswald, C. Stein and P. Botschwina, FHF⁻ Isotopologues: Highly Anharmonic Hydrogen-Bonded Systems with Strong Coriolis Interaction, J. Phys. Chem. A, 2013, 117, 9695–9703.
39. N. Elghobashi and L. Gonzalez, A theoretical anharmonic study of the infrared absorption spectra of FHF⁻, FDF⁻, OHF⁻, and ODF⁻ anions, J. Chem. Phys., 2006, 124, 174308/1–12.
40. G. Perez-Hernandez, J. Gonzalez-Vazquez and L. Gonzalez, IR Spectrum of FHF⁻ and FDF⁻ Revisited Using a Spectral Method in Four Dimensions, J. Phys. Chem. A, 2012, 116, 11361–11369.
41. S. Hirata, K. Yagi, S. A. Perera, S. Yamazaki and K. Hirao, Anharmonic vibrational frequencies and vibrationally averaged structures and nuclear magnetic resonance parameters of FHF⁻, J. Chem. Phys., 2008, 128, 214305.
42. J. Li, X. Li and S. S. Iyengar, Vibrational Properties of Hydrogen-Bonded Systems Using the Multireference Generalization to the “On-the-Fly” Electronic Structure within Quantum Wavepacket ab Initio Molecular Dynamics (QWAIMD), J. Chem. Theory Comput., 2014, 10, 2265–2280.
43. A. M. Panich, NMR study of the F–H⋯F hydrogen bond. Relation between hydrogen atom position and F–H⋯F bond length, Chem. Phys., 1995, 196, 511–519.
44. J. Guo, P. M. Tolstoy, B. Koeppe, N. S. Golubev, G. S. Denisov, S. N. Smirnov and H.-H. Limbach, Hydrogen Bond Geometries and Proton Tautomerism of Homo-Conjugated Anions of Carboxylic Acids Studied via H/D Isotope Effects on ¹³C NMR Chemical Shifts, J. Phys. Chem. A, 2012, 116, 11180–11188.
45. (a) J. E. Del Bene, I. Alkorta and J. Elguero, A systematic comparison of second-order polarization propagator approximation (SOPPA) and equation-of-motion coupled cluster singles and doubles (EOM-CCSD) spin–spin coupling constants for selected singly bonded molecules, and the Hydrides NH₃, H₂O, and HF and their protonated and deprotonated ions and hydrogen-bonded complexes, J. Chem. Theory Comput., 2008, 4, 967–973; (b) J. E. Del Bene, M. J. T. Jordan, S. A. Perera and R. J. Bartlett, Vibrational effects on the F–F spin–spin coupling constant (^2hJ(F–F)) in FHF⁻ and FDF⁻, J. Phys. Chem. A, 2001, 105, 8399–8402.
46. N. S. Golubev, S. M. Melikova, D. N. Shchepkin, I. G. Shenderovich, P. M. Tolstoy and G. S. Denisov, Interpretation of Hydrogen/Deuterium Isotope Effects on NMR Chemical Shifts of [FHF]⁻ Ion Based on Calculations of Nuclear Magnetic Shielding Tensor Surface, Z. Phys. Chem., 2003, 217, 1549–1563.
47. N. S. Golubev, I. G. Shenderovich, P. M. Tolstoy and D. N. Shchepkin, Solvent induced temperature dependencies of NMR parameters of hydrogen bonded anionic clusters, J. Mol. Struct., 2004, 697, 9–15.
48. K. Suzuki, H. Ishibashi, K. Yagi, M. Shiga and M. Tachikawa, Ab Initio Path Integral Molecular Dynamics Simulations of F₂H⁻ and F₂H₃⁺, in Quantum Systems in Chemistry and Physics, ed. Nishikawaet al., Springer Science, 2012, ch. 10, vol. 26.
49. T. Murakhtina, J. Heuft, E. J. Meijer and D. Sebastiani, First Principles and Experimental ¹H NMR Signatures of Solvated Ions: The Case of HCl_(aq), ChemPhysChem, 2006, 7, 2578–2584.
50. S. O. Kang, D. Powell, V. W. Day and K. Bowman-James, Trapped Bifluoride, Angew. Chem., Int. Ed., 2006, 45, 1921–1925.
51. C. Mundy, F. Mohamed, F. Schiffman, G. Tabacchi, H. Forbert, W. Kuo, J. Hutter, M. Krack, M. Iannuzzi and M. McGrath, http://www.cp2k.org/2000.
52. G. Lippert, M. Parrinello and J. Hutter, A hybrid Gaussian and plane wave density functional scheme, Mol. Phys., 1997, 92, 477–488.
53. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799.
54. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
55. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
56. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
57. S. Goedecker, M. Teter and J. Hutter, Separable dual-space Gaussian pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
58. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126, 014101/1.
59. D. Marx and J. Hutter, in Modern Methods and Algorithms of Quantum Chemistry, ed. J. Grotendorst, NIC Series, 2000, vol. 1, p. 328.
60. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
61. M. Brehm and B. Kirchner, TRAVIS – A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories, J. Chem. Inf. Model., 2011, 51, 2007–2023.
62. M. Thomas, M. Brehm, R. Fligg, P. Voehringer and B. Kirchner, Computing vibrational spectra from ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622.
63. G. Lippert, J. Hutter and M. Parrinello, The Gaussian and augmented-plane-wave density functional method for ab initio molecular dynamics simulations, Theor. Chem. Acc., 1999, 103, 124–140.
64. V. Weber, M. Iannuzzi, S. Giani, J. Hutter, R. Declerck and M. Waroquier, Magnetic linear response properties calculations with the Gaussian and augmented-plane-wave method, J. Chem. Phys., 2009, 131, 014106.
65. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
66. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, Basis Set Exchange: A Community Database for Computational Sciences, J. Chem. Inf. Model., 2007, 47, 1045–1052.
67. D. Feller, The role of databases in support of computational chemistry calculations, J. Comput. Chem., 1996, 17, 1571–1586.
68. W. Kutzelnigg, U. Fleischer and M. Schindler, Deuterium and Shift Calculation, Springer, Berlin, Heidelberg, 1991, vol. 23, p. 165.
69. I. G. Shenderovich, H.-H. Limbach, S. N. Smirnov, P. M. Tolstoy, G. S. Denisov and N. S. Golubev, H/D Isotope Effects on the Low-Temperature NMR Parameters and Hydrogen Bond Geometries of (FH)₂F⁻ and (FH)₃F⁻ dissolved in CDF₃/CDF₂Cl, Phys. Chem. Chem. Phys., 2002, 4, 5488–5497.
70. T. Steiner, Lengthening of the Covalent X-H Bond in Heteronuclear Hydrogen Bonds Quantified from Organic and Organometallic Neutron Crystal Structures, J. Phys. Chem. A, 1998, 102, 7041–7052.
71. H.-H. Limbach, M. Pietrzak, H. Benedict, P. M. Tolstoy, N. S. Golubev and G. S. Denisov, Empirical corrections for anharmonic zero-point vibrations of hydrogen and deuterium in geometric hydrogen bond correlations, J. Mol. Struct., 2004, 706, 115–119.
72. H.-H. Limbach, P. M. Tolstoy, N. Perez-Hernandez, J. Guo, I. G. Shenderovich and G. S. Denisov, OHO Hydrogen Bond Geometries and NMR Chemical Shifts: From Equilibrium Structures to Geometric H/D Isotope Effects with Applications for Water, Protonated Water and Compressed Ice, Israel J. Chem., 2009, 49, 199–216.
73. M. Thomas, M. Brehm, O. Hollóczki, Z. Kelemen, L. Nyulászi, T. Pasinszki and B. Kirchner, Simulating the vibrational spectra of ionic liquid systems: 1-ethyl-3-methylimidazolium acetate and its mixtures, J. Chem. Phys., 2014, 141, 024510.
74. S. Y. Kucherov, S. F. Bureiko and G. S. Denisov, Anticooperativity of FHF hydrogen bonds in clusters of the type F⁻ × (HF)_n, RF × (HF)_n and XF × (HF)_n, R = alkyl and X = H, Br, Cl, F, J. Mol. Struct., 2016, 1105, 246–255.
75. (a) R. S. Rowland and R. Taylor, Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii, J. Phys. Chem., 1996, 100, 7384–7391; (b) A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
76. H.-H. Limbach, G. S. Denisov, I. G. Shenderovich and P. M. Tolstoy, Proton Tautomerism in Systems of Increasing Complexity: Examples from Organic Molecules to Enzymes, in Tautomerism: Concepts and Applications in Science and Technology, ed. L. Antonov, John Wiley and Sons, 2016.
77. S. B. Hakkert and M. Erdelyi, Halogen bond symmetry: the N–X–N bond, J. Phys. Org. Chem., 2015, 28, 226–233.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04493c

---