Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of intermolecular charge delocalization and its dimensionality in efficient band-like electron transport in crystalline 2,5-difluoro-7,7,8,8-tetracyanoquinodimethane (F2-TCNQ)†
Andrey Yu.
Sosorev

Faculty of Physics and International Laser Center, M.V. Lomonosov Moscow State University, Moscow 119991, Russia. E-mail: sosorev@physics.msu.ru
First published on 24th August 2017
Abstract
Theoretical understanding of charge transport in organic semiconductors is exclusively important for organic electronics, but still remains a subject of debate. The recently discovered record-high band-like electron mobility in single crystals of 2,5-difluoro-7,7,8,8-tetracyanoquinodimethane (F2-TCNQ) is challenging from the theoretical viewpoint. First, the very small size of the F2-TCNQ molecule implies high reorganization energy that seems incompatible with efficient charge transport. Second, it is not clear why the crystals of a similar compound, 7,7,8,8-tetracyanoquinodimethane (TCNQ), show an inefficient hopping electron transport mechanism. To address these issues, we apply DFT and QM/MM calculations to the Fn-TCNQ (n = 0,2,4) crystal series. We show that multidimensional intermolecular charge delocalization is of key importance for efficient charge transport in materials consisting of small-sized molecules, and commonly used guidelines for the search for high-mobility organic semiconductors are to be corrected.
Introduction
Organic electronics requires materials with efficient charge transport, i.e. high charge mobility μ. However, only several organic semiconductors (OSCs) with μ > 1 cm2 (V s)−1 have been discovered.1 It is commonly considered that charge transport in OSCs is determined by the interplay of two factors.2–4 The first factor is charge carrier delocalization over several molecules (“sites”) due to the electronic coupling between them; this coupling is commonly described with transfer integrals J. The opposite factor is charge localization at one site due to the electron–phonon coupling. Local contribution to the electron–phonon coupling stems from the site energy change after charge transfer and is associated with the reorganization energy λ. If λ ≫ J, which is typical for OSCs, charge localization occurs, and incoherent hopping charge transport mechanism with low μ takes place. Otherwise, delocalization can enable coherent band-like charge transport with high μ.2,3 In high-mobility OSCs, non-local electron–phonon coupling related to the modulation of J by vibrations plays a significant role.3To improve the charge mobility and reach the efficient band-like charge transport regime, J values are to be increased, and λ is to be decreased. The J values are governed by the crystal structure since they are very sensitive to the relative positions of the molecules.4 The largest J values are typically observed for parallel molecules with strongly overlapping π-conjugated systems (in the so-called π-stacks).5 Reorganization energy λ consists of the intramolecular contribution, λi, related to the changes in molecular geometry after charge transfer, and the outer-sphere one, λo, related to the polarization of the environment. It is commonly assumed that the former contribution dominates in OSCs, i.e. λ ≈ λi.2 The λ value can be reduced via enlarging the molecular conjugated core and increasing its rigidity, that's why most of the developed high-mobility OSCs consist of condensed aromatic molecules with prolonged π-conjugated systems.2,5 Recently, it was noticed that λ in the crystal can be lower than that for the isolated molecule. First, neighboring molecules restrict the geometry reorganization of the given molecule after charge transfer.6,7 Second, charge carrier delocalization over adjacent molecules reduces the excess charge density on each of them and inhibits their geometry relaxation after charge transfer.8 The impact of the crystal environment on λ can be essential for charge transport and should be considered when estimating λ; however, it is usually neglected.
A rigorous theoretical description of the charge transport in OSCs is still missing.3,9 An investigation of the OSC series consisting of structurally close molecules can improve the understanding of this process. A perfect example of such series is the crystals of fluorinated derivatives of 7,7,8,8-tetracyanoquinodimethane (TCNQ). As reported in ref. 10, one of them, 2,5-difluoro-7,7,8,8-tetracyanoquinodimethane (F2-TCNQ), exhibits extremely high electron mobility (μe = 7 cm2 (V s)−1 at room temperature), while the corresponding quantity in its counterparts, TCNQ and F4-TCNQ, is two orders of magnitude lower (μe = 0.1 and 0.2 cm2 (V s)−1, respectively). Moreover, when the temperature decreases, μe in crystalline F2-TCNQ rises up to ca. 15 cm2 (V s)−1 at 200 K and further up to ca. 25 cm2 (V s)−1 at 150 K. In contrast, in TCNQ and F4-TCNQ, μe decreases with cooling, reaching ca. 0.01 and 0.03 cm2 (V s)−1, respectively, at 200 K. Therefore, the charge transport mechanism is qualitatively different in these compounds: it is band-like in F2-TCNQ indicating pronounced electron delocalization, and hopping in TCNQ and F4-TCNQ, indicating localized charges. In ref. 10, record-high electron mobility in F2-TCNQ was attributed to strong electronic coupling between the molecules resulting in a wide conduction band, and low μe in crystalline F4-TCNQ was explained by a narrow conduction band (i.e. low J).10 However, the ca. 70-fold difference in room-temperature μe between F2-TCNQ and TCNQ remained unexplained since the bandwidths were found to be comparable for these materials. Later, in ref. 11, this difference was attributed to strong non-local electron–phonon coupling in crystalline TCNQ, which was deduced from the two-fold decrease in the lowest vibrational frequency ω0 that can affect μe dramatically.3
However, two important issues remain open. First, F2-TCNQ molecules are very small as compared to typical OSCs (e.g. rubrene or pentacene) and are expected to possess strong local electron–phonon interaction (large λ) due to significant changes in molecular geometry after charge transfer.12 A large λ favors charge localization that contradicts the observed efficient band-like transport in F2-TCNQ.3,4 Second, although the different ω0 explains the difference in room-temperature μe between the F2-TCNQ and TCNQ crystals,11 it does not explain the qualitatively different charge transport mechanism for these materials (band-like vs. hopping). In addition, the ω0 difference between F2-TCNQ and TCNQ reduces with cooling (see the ESI† to ref. 11), which should only smoothen out the difference in μe for these materials, in contradiction with the observed increase of the latter up to ca. 1500 times at 200 K.10 Therefore, it appears that non-local electron–phonon interaction is not the source of qualitatively different charge transport in F2-TCNQ and TCNQ.
In this study, we investigate the electron transport in the Fn-TCNQ (n = 0, 2, 4) crystal series using DFT and QM/MM approaches. Two abovementioned issues are addressed: (i) how efficient charge transport can occur in crystalline F2-TCNQ despite the small size of its molecules, and (ii) why electron transport is band-like in crystalline F2-TCNQ but hopping-like in crystalline TCNQ, with three orders of magnitude difference in μe at 200 K. We show that while λ is large in the Fn-TCNQ isolated molecules, in the TCNQ and F2-TCNQ crystals it is strongly reduced due to intermolecular charge delocalization, making efficient charge transport possible. To address the qualitatively different transport mechanism in F2-TCNQ and TCNQ, we analyze J along different directions and find that charge delocalization is three-dimensional in the former material but (quasi) one-dimensional in the latter. Enhanced dimensionality of intermolecular charge delocalization in F2-TCNQ is shown to be more resistant to the electron–phonon coupling and defects, explaining band-like charge transport in this material. Our findings force us to suggest corrections to the current guidelines for the search for high-mobility OSCs.
Computational
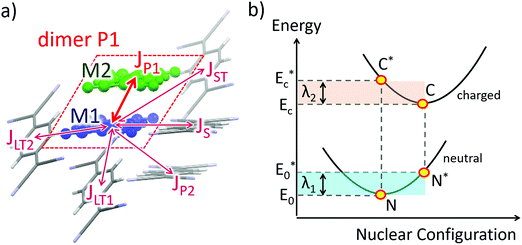
Crystal structures were obtained from the X-ray data.10 One molecule (A) and its selected nearest-neighbors are depicted in Fig. 1a for the TCNQ crystal, and possible charge transfer pathways are shown with arrows and labeled by the dimer types (see below).The transfer integrals, Js, were calculated using a home-written code based on the dimer projection method (DIPRO).13–15 To estimate this quantity for a pair (dimer) of molecules (monomers) A and B depicted in Fig. 1a, JAB, the wavefunctions of these molecules were approximated by their lowest unoccupied molecular orbitals (LUMOs), φA and φB. The latter were written on the basis of the dimer molecular orbitals φi:
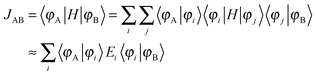 | (1) |
Reorganization energy λ was approximated by λi that is typically considered much larger than λo in OSCs.2 The λ values were calculated according to the 4-point scheme4 illustrated in Fig. 1b. In this approach, the energies of the molecule in 4 states are required: neutral state in its optimized geometry (N state in Fig. 1b), neutral state in the optimized geometry of the charged state (N*), charged state in its optimized geometry (C), and charged state in the geometry of the neutral state (C*). The energy difference between the former two states, λ1 = EN* − EN, describes the energy relaxation of the molecule that has lost the charge carrier, while the energy difference between the latter two states, λ2 = EC* − EC, describes the energy relaxation of the molecule that has accepted the charge. The total reorganization energy is:
| λ = λ1 + λ2 = (EN* − EN) + (EC* − EC) | (2) |
The impact of the crystal environment on λ can be accounted by the calculation of the abovementioned energies for a system containing a given molecule and its frozen-geometry neighbors.6,7 In practice, this task cannot be solved using DFT or other quantum-chemical approaches. Nevertheless, it can be addressed using a combined quantum mechanical/molecular mechanical method (QM/MM) performing quantum mechanical (QM) calculations, e.g. DFT, for the given molecule, and classical molecular mechanics (MM) for its environment.16 To estimate the impact of the charge delocalization, we propose an original approach that is described in the Results section.
For charge mobility estimation within the hopping model, charge transfer rates from a given molecule A to each of its nearest neighbors (e.g. molecule B) were calculated using the Marcus formula:17
 | (3) |
All DFT calculations were performed using the B3LYP functional. For the J calculation, the 6-31g* basis set was used, and λ estimation was conducted using the 6-31+g** basis set for isolated molecules and the 6-31g basis set when considering the crystal environment. The impact of the basis set on λ and J is discussed in ESI,† Section S2. GAMESS package22,23 was used to calculate J and λ for isolated molecules, and NWChem package24 was used for QM/MM estimation of λ in crystals. For QM/MM calculations, mechanic embedding was used, and molecular mechanics was performed using the Amber force field.
Results
Molecular packing and electron transfer integrals
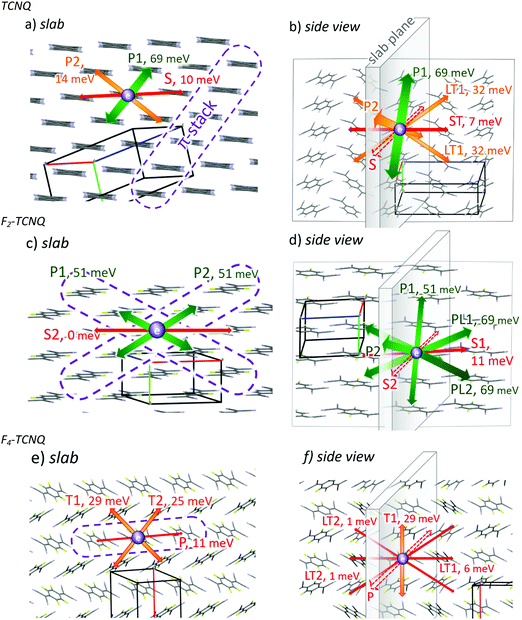
Fig. 2 shows the structures of the investigated crystals according to the X-ray data10 with transport pathways deduced from the calculated J values.The TCNQ crystal can be considered to consist of one-dimensional (1D) π-stacks of parallel and slightly shifted molecules with significant overlapping of their π-conjugated systems (π–π overlapping) providing large J = 69 meV. The dimer configuration in the stack is denominated below as the “parallel” P1-dimer. Stacks with similar orientations of molecular planes form two-dimensional (2D) “slabs” corresponding to the (002) crystal plane. The slab is depicted in Fig. 2a. Within the slab, in addition to P1-dimers, “parallel” P2- and “side” S-dimers are observed (see the corresponding directions in Fig. 2a). In P2-dimers, the molecules are parallel like in P1-dimers, but a large shift along the short molecular axis reduces π–π overlapping resulting in a low J = 14 meV. S-Dimers also show a low J = 10 meV since molecules in them interact via CH⋯N contacts that do not provide considerable π–π overlapping. In adjacent slabs, the molecular planes are tilted with respect to each other (Fig. 2b), like in the herringbone packing motif. Three types of dimers can provide charge transport between the slabs: two “longitudinal, tilted” dimers LT1 and LT2, and “side, tilted” ST-dimers. In the LT1-dimer configuration, the molecules interact via π-electron-rich dicyanomethylidene (DCMI) groups resulting in a moderate J = 32 meV, and for ST and LT2-dimers, negligible J = 7 and 1 meV stem from very weak π–π overlapping.
The F2-TCNQ crystal can be also considered to be formed of 2D slabs of parallel molecules. The slab corresponds to the (001) crystal plane and is shown in Fig. 2c. It is determined by the π-stacking directions P1 and P2, in which the molecules are slightly shifted with respect to each other providing a large J = 50 meV. As in TCNQ crystals, S1-dimers consisting of molecules interacting via side CH⋯N contacts show a low J = 11 meV. Unlike TCNQ, molecular planes in adjacent slabs are not tilted but are parallel (Fig. 2d) due to the specific crystal packing with only one molecule in the reduced cell.10,11 Adjacent molecules from different slabs form “longitudinal” L- and “parallel-longitudinal” PL-dimers, in which the molecules interact via DCMI groups. Interestingly, PL-dimers show a large J = 69 meV despite a significant shift of the molecules; this can be attributed to the proximity of their π-electron-rich DCMI groups resulting in strong π–π overlapping. Negligible J = 4 meV in L-dimers and J = 0 in S2-dimers result from weak π–π overlapping because of a large intermolecular distance.
In crystalline F4-TCNQ, π-stacking takes place along the P direction, but the molecules in the corresponding P-dimers are strongly shifted along both molecular axes resulting in poor π–π overlapping and a low J = 11 meV. Unlike the first two crystals, the molecular planes in any adjacent π-stacks are tilted with respect to each other. The slab definition is therefore arbitrary, and we chose the (002) crystal plane as a slab (Fig. 2e). The dimer types observed within the slab are P-dimers and “transverse” T-dimers (J = 29 and 25 meV). LT-dimers of several types connect different slabs, possessing J = 1 and 6 meV (Fig. 2f).
Fig. 3a collates the J values for various dimer configurations in the considered crystals. The maximal transfer integrals Jmax in TCNQ and F2-TCNQ are equal (69 meV) and rather large (close to ca. 70 meV for pentacene and rubrene1), while in F4-TCNQ Jmax is twice lower (29 meV). In TCNQ and F2-TCNQ, large J values are observed in the dimers of parallel molecules, namely in P1-dimers in TCNQ, and PL-, P1- and P2-dimers in F2-TCNQ. This is in line with the common assumption of the essential role of π-stacking in charge transport.5 The dimers in which the molecular planes are tilted with respect to each other, namely T- and LT-dimers, show J values below 35 meV because of reduced π–π overlapping for non-parallel molecules. Nevertheless, T-dimers contribute significantly to charge transport in crystalline F4-TCNQ since P-dimers in this material possess a low J.
 | ||
| Fig. 3 Electron transfer integrals for various dimer configurations in the Fn-TCNQ crystals (a) and electron mobility estimated within the hopping model based on the Marcus theory (b). | ||
Reorganization energy and electron mobility within the standard hopping model
The calculated intramolecular reorganization energies λ of the isolated TCNQ, F2-TCNQ and F4-TCNQ molecules are very close and equal to 250, 258 and 248 meV, respectively. These values are rather large (compared to λ = 134 meV for rubrene and 91 meV for pentacene1) and stem from the small size of Fn-TCNQ molecules inducing strong changes in molecular geometry after charge transfer,12 in accordance with our concerns mentioned in the Introduction.The electron mobilities μe in the TCNQ, F2-TCNQ and F4-TCNQ crystals estimated within the hopping model based on eqn (3) are 0.25, 0.54, 0.05 cm2 (V s)−1, respectively (Fig. 3b). An order of magnitude lower μ for F4-TCNQ stems from 2.5-fold lower Jmax values (Fig. 3a), in correspondence with experimental data and calculations from ref. 10. However, the calculated μe for F2-TCNQ is 13 times lower than the experimental one. Further, comparable J and λ values for F2-TCNQ and TCNQ resulting in similar μe values do not explain the qualitative experimental difference in charge transport mechanism between the two materials. These are actually the two issues raised in the Introduction: the common model did not resolve them. Therefore, an in-depth analysis is required, which is provided below.
Impact of the crystal environment on reorganization energy
The moderate calculated μe value for F2-TCNQ stems mainly from high λ. To reconcile the contradiction between the calculated λ and observed efficient charge transport in F2-TCNQ, it is natural to suggest that λ in the F2-TCNQ crystal is lower than for the isolated molecule. As mentioned in the Introduction, the crystal environment can reduce λ via two mechanisms: restriction of intramolecular motions (RIM) by surrounding molecules, and intermolecular charge delocalization. To estimate the impact of RIM, we applied a QM/MM-based approach described in ref. 6 and 7. One molecule was calculated at the quantum mechanical (QM) level (DFT, B3LYP/6-31g), while the environment that restricts its motion was described by frozen-geometry nearest neighbors (14 molecules in the considered crystals) using molecular mechanics (MM). The λ value was then calculated according to eqn (2). The obtained λRIM values for TCNQ, F2-TCNQ and F4-TCNQ are 237, 240 and 223 meV, correspondingly. These values are close to those for isolated molecules (237, 230 and 212 meV, respectively, at the same DFT level), and the λ decrease due to RIM is not observed.To estimate the impact of the intermolecular charge delocalization on λ, we propose the following original approach based on QM/MM. We consider systems of several molecules embedded into the crystal environment – dimer, trimer, tetramer, etc. The optimized geometries of these systems are obtained at the QM level considering the crystal environment (frozen-geometry nearest-neighbor molecules) described at the MM level. The reorganization energy considering delocalization, λdel, is estimated using eqn (2), with the only difference that the energies of N, N*, C and C* states are calculated for the dimer (trimer, tetramer, etc.) instead of a single molecule. To the best of our knowledge, QM/MM was not used before to address the impact of the charge delocalization on λ.
Using this approach, we estimated λdel values for the TCNQ and F2-TCNQ crystals, where large J values can promote efficient charge delocalization. The λdel was not calculated for the F4-TCNQ crystal since low J values are not capable of providing substantial charge delocalization. Chart 1 illustrates the considered dimer configurations and their environment for TCNQ (P1, LT and P2 dimers) and F2-TCNQ (PL, P1 and S dimers). Trimers of F2-TCNQ molecules along the P1 and PL directions were regarded, as well as trimers and tetramers of TCNQ molecules along the P1 direction. Fig. 4 collates the calculated λdel for dimers, trimers and tetramers in the crystal environment, as well as λ and λRIM. The λdel values for dimers are about 1.5–2 times lower than the λ and λRIM values. Specifically, in the P1-dimer of F2-TCNQ, the reorganization energy becomes as low as λdel = 130 meV, i.e. its decrease as compared to λ amounts 100 meV. In TCNQ, λdeli = 145 meV for the P1-dimer, which is 90 meV lower than λ. The λdel value decreases further for P1-trimers: it is just 95 meV for F2-TCNQ and 100 meV for TCNQ, which is close to the λ value for the isolated pentacene molecule.1 For the TCNQ tetramer, λdel reaches an extremely low value of ca. 75 meV.
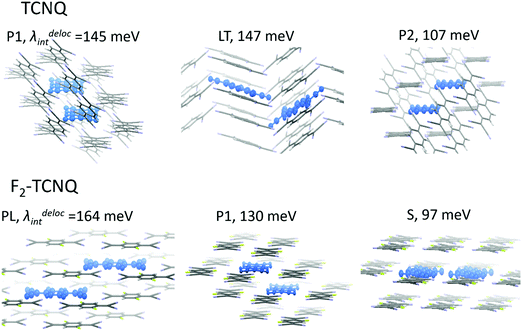 | ||
| Chart 1 TCNQ and F2-TCNQ dimers for which the impact of the intermolecular charge delocalization on the reorganization energy was addressed. | ||
Discussion
The results presented above show that the reorganization energy λ of the Fn-TCNQ molecules is strongly reduced by the crystal environment due to charge delocalization. These results are in line with our recent findings reported in ref. 11, where intermolecular vibrations disrupting the delocalization were suggested to be detrimental for μe. The fact that the second factor, RIM, does not reduce λ can be attributed to the small size of the considered molecules and their internal rigidity. Indeed, a significant λ decrease due to RIM was observed in crystals of large and “soft” molecules.6,7Our method for considering charge delocalization in the λ calculation is a natural combination of the approach suggested in ref. 8 for the same purpose and the approach proposed in ref. 6 and 7 to account for RIM. The advance of our approach as compared to that reported in ref. 8 is in avoiding any artificial geometry constraints for the molecules over which the charge is delocalized. In our method, their geometry is naturally constrained by the interaction with (frozen-geometry) nearest neighbors, while in ref. 8 some of the degrees of freedom were fixed artificially. Although our approach does not provide absolute values of λ in the crystal (since DFT typically overestimates the extent of charge delocalization8), it clearly illustrates a dramatic λ decrease in crystalline Fn-TCNQ due to intermolecular charge delocalization, and provides an opportunity to compare this effect in different materials.
One could suggest that the delocalization-induced decrease of λ is related to J: the larger the J, the more pronounced the delocalization, and probably the lower the λdel. However, this is not observed: for instance, although the P1-dimer in TCNQ has a larger J than in F2-TCNQ, it shows a higher λdel. Moreover, even for different dimers of the same crystal, larger J values do not cause lower λ (cf. P1- and PL-dimers in F2-TCNQ, or P1 and LT-dimers in TCNQ). We suggest that the key factors determining λdel are intermolecular vibrations that can have a large amplitude due to their weak force constant and modulate J significantly thus disrupting the delocalization.3,25 Accordingly, these vibrations affect the energies of the dimers, i.e. contribute to λdel. Parallel sliding along the molecular axis can have a very large amplitude26 and modulate J strongly,27 which explains the larger λdel for the PL-dimer.
Reduction of λ by the crystal environment explains the observed efficient charge transport in F2-TCNQ. Substituting λdel for P1-trimers instead of λ in eqn (3) rises electron mobilities μe in TCNQ and F2-TCNQ up to μdele = 1.7 and 4 cm2 (V s)−1, respectively. The μdele value for F2-TCNQ is much closer to the experimental one (7 cm2 (V s)−1) compared to μe = 0.54 cm2 (V s)−1 without considering delocalization, and the actual intermolecular delocalization length can exceed two molecules resulting in an even higher μdele. We therefore argue that the first issue concerning efficient charge transport in crystalline F2-TCNQ despite the small size of its molecules is reconciled.
However, the second challenge, namely the difference in transport mechanism between F2-TCNQ and TCNQ, remains unsolved. As we have shown above, in these materials λdel and Jmax are similar, with λdel ∼ Jmax that could enable band-like charge transport in both F2-TCNQ and TCNQ.28 Therefore, to explain the experimental data, it is natural to suggest that intermolecular charge delocalization is disrupted in TCNQ, but present in F2-TCNQ. Since delocalization/localization depends on the relationship between J and λ, we analyze below the electron transfer integrals J along different directions.
As can be deduced from Fig. 2a, b and 3a, in the TCNQ crystal, significant J ≥ 2kT (kT = 25 meV at room temperature) are observed in only one direction, namely along the π-stack P1. Transfer integrals connecting the stacks within the slab (P2- and S-dimers) are lower than kT and hence should be strongly modulated by thermal fluctuations, as well as J values between the slabs (LT1) that are comparable to kT. We conclude that in the TCNQ crystal, efficient charge transport can occur only along the π–π stacking direction (P1) at room temperature, i.e. is (quasi)1D. In contrast, in the F2-TCNQ crystal there are 4 directions with J ≥ 2kT (Fig. 2c, d and 3a): two within the slab (P1 and P2), and two between different slabs (PL). These directions cover all the three space dimensions (see Fig. 2c and d). We thus conclude that the dimensionality of charge transport in F2-TCNQ is higher than in TCNQ, namely it is 3D instead of (quasi)1D.
To illustrate the role of charge delocalization dimensionality in charge transport, we use a simple one-electron tight-binding model. Assume a set of N sites arranged in a 1D, 2D or 3D lattice. A charge carrier, e.g. electron, can be either localized at one site or delocalized over several sites. Its wavefunction is  , where φi are the wavefunctions of the electron localized at i-th site and ci are the coefficients. The mechanism of localization is the decrease of the energy for the site occupied by the electron. This decrease corresponds to the polaron binding energy and equals Ep = λ/2; accordingly, larger λ induces stronger localization. Following ref. 29, we assume that if the electron occupies the i-th site partially, the site energy decreases by ci4·λ/2 (proportional to the squared extra charge at the site, which is proportional to ci2). The energy of the state is
, where φi are the wavefunctions of the electron localized at i-th site and ci are the coefficients. The mechanism of localization is the decrease of the energy for the site occupied by the electron. This decrease corresponds to the polaron binding energy and equals Ep = λ/2; accordingly, larger λ induces stronger localization. Following ref. 29, we assume that if the electron occupies the i-th site partially, the site energy decreases by ci4·λ/2 (proportional to the squared extra charge at the site, which is proportional to ci2). The energy of the state is
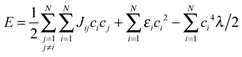 | (4) |
 , and its energy is
, and its energy is| E = mε + Jd(1 − m−1/d) − λ/m, | (5) |
The E(m) dependence described by eqn (5) has a minimum at either m = 1 or m = ∞ depending on the relation between J, λ and d. In the former case, the charge is localized, while in the latter case it is delocalized. Comparison of the E values for these two states yields the charge delocalization criterion: delocalization occurs if
 | (6) |
This criterion is less strict for higher d, i.e. delocalization occurs more readily in the 3D case than in 2D or 1D. Note that in eqn (6), λ denotes the reorganization energy at a single site, i.e. without considering delocalization. From the calculated λ (ca. 250 meV) and J (see Fig. 3a), the delocalization criterion is fulfilled in F2-TCNQ for all the three spatial dimensions (d = 3, Jcr = 43 meV, J = 69 meV for PL-dimer and J = 50 meV for P1- and P2-dimers). Delocalized charge carriers explain the observed efficient band-like charge transport with high μe in this material.10 Disruption of charge delocalization by intermolecular vibrations explains the μe decrease with temperature rise. In contrast, for TCNQ the delocalization criterion is not fulfilled. Assuming d = 1 yields Jcr = 125 meV, while Jmax = 69 meV, i.e. Jmax < Jcr. Even assuming d = 3, we obtain Jcr = 42 meV, but in this case J > Jcr for only one direction (P1), indicating the invalidity of the assumption. Therefore, the charges are localized in TCNQ resulting in hopping charge transport mechanism, which corresponds to the experiment. In addition, lower d results in a stronger impact of static disorder (defects) and dynamic disorder (thermal fluctuations), which are inevitable in OSCs at room temperature and also promote charge localization.3,11 In the case of (quasi)1D transport along the stacks, a single defect in the stack can damage the transport pathway, while in the case of 3D transport, charges can easily circumvent the obstacle.30–32 Summing up, the dimensionality of intermolecular charge delocalization explains the outstanding band-like electron transport in the F2-TCNQ crystal and inefficient hopping transport in TCNQ, which was the second issue addressed in the study.
An improvement in the charge transport with dimensionality for structurally close materials was observed in a number of studies.9,33 In the series of crystalline dinaphtho[2,3-b:2′,3′-d]thiophene derivatives,34 the mobility increased 4 times for materials with an additional transport direction with J > kT. For crystalline 6H-pyrrolo[3,2-b:4,5-b′]bis[1,4]benzothiazine derivatives,35μ was significantly larger in the crystals with several transport directions and moderate J than in the crystals with a single transport direction and large J. Within the series of bulky end-capped [1]benzothieno[3,2-b]benzothiophene (BTBT) crystals, compounds with J > 2kT in several directions exhibited μ about two orders of magnitude larger than the other materials.36 For the crystals of didodecyl-BTBT isomers, an unprecedented μ was observed for the compound with 2D transport and Jmax ∼ 60 meV, while the compound with an extremely large Jmax = 129 meV but 1D transport exhibited a 340-fold lower μ.37 Moreover, the same trend of μ increase with charge transport dimensionality was observed for arrays of nanoparticles.38 Noteworthily, the hopping model was unable to describe the data from ref. 37 even qualitatively, and only the band model considering charge delocalization reproduced the strong positive impact of charge transport dimensionality on μ.
Our results extend far beyond the Fn-TCNQ crystal series. We anticipate that intermolecular charge delocalization is especially important for OSCs consisting of small-sized conjugated molecules (e.g. derivatives of naphthalene-diimide (NDI), tetrathiafulvalene (TTF), etc.). These molecules have large λ, and intermolecular delocalization with high dimensionality is required for efficient charge transport according to our findings. In OSCs consisting of large conjugated molecules like tetracene, rubrene, pentacene, dinaphtho-thieno-thiophene (DNTT), etc., significant charge delocalization occurs already within the molecules, resulting in low λ and making the intermolecular delocalization (especially in the direction of the long axis) less important.
Finally, the obtained results show that the frequently used screening of OSCs based just on single molecule properties, or accounting only the RIM-induced λ decrease in the crystal (e.g. that provided in ref. 21), can overlook OSCs built from molecules of small size. For instance, this approach could not predict high mobility in F2-TCNQ in principle. In order to improve the screening method, intermolecular charge delocalization and the effect of dimensionality should be considered, at least at a very simple level provided by eqn (6).
Conclusions
Electron transport in the Fn-TCNQ (n = 0, 2, 4) crystal family was investigated theoretically using DFT and QM/MM approaches. We have shown that in the TCNQ and F2-TCNQ crystals, intermolecular charge delocalization can reduce dramatically the intramolecular reorganization energy, providing an opportunity for efficient band-like charge transport. However, while in F2-TCNQ large charge transfer integrals promote three-dimensional charge delocalization resistant to vibrations and defects, (quasi)one-dimensional delocalization in TCNQ is readily destroyed by the latter, resulting in inefficient hopping charge transport. We suggest that intermolecular charge delocalization and its high dimensionality are important also for charge transport in other materials consisting of small-sized molecules, and current guidelines for high-mobility organic semiconductors should be corrected by considering these two factors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author would like to thank D. Paraschuk, V. Bruevich, M. Vener and I. Chernyshov for thoughtful critical discussions and ideas. The work was supported by the Russian Foundation for Basic Research (RFBR), projects #16-32-60204 mol_a_dk and #17-02-00841.References
- O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412 CrossRef CAS PubMed.
- G. Schweicher, Y. Olivier, V. Lemaur and Y. H. Geerts, Isr. J. Chem., 2014, 54, 595–620 CrossRef CAS.
- S. Fratini, D. Mayou and S. Ciuchi, Adv. Funct. Mater., 2016, 26, 2292–2315 CrossRef CAS.
- Y. Li, V. Coropceanu and J.-L. Brédas, in The WSPC Reference on Organic Electronics: Organic Semiconductors, ed. J.-L. Brédas and S. R. Marder, World Scientific, Singapore, 2016, ch. 7, pp. 193–230 Search PubMed.
- C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267 CrossRef CAS PubMed.
- H. Li, L. Duan, D. Zhang and Y. Qiu, J. Phys. Chem. C, 2014, 118, 14848–14852 CAS.
- Q. Guo, L. Wang, F. Bai, Y. Jiang, J. Guo, B. Xu and W. Tian, RSC Adv., 2015, 5, 18875–18880 RSC.
- S. T. Bromley, F. Illas and M. Mas-Torrent, Phys. Chem. Chem. Phys., 2008, 10, 121–127 RSC.
- I. Yavuz, B. N. Martin, J. Park and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 2856–2866 CrossRef CAS PubMed.
- Y. Krupskaya, M. Gibertini, N. Marzari and A. F. Morpurgo, Adv. Mater., 2015, 27, 2453–2458 CrossRef CAS PubMed.
- I. Y. Chernyshov, M. V. Vener, E. V. Feldman, D. Y. Paraschuk and A. Y. Sosorev, J. Phys. Chem. Lett., 2017, 8, 2875–2880 CrossRef CAS PubMed.
- T. P. Nguyen, J. H. Shim and J. Y. Lee, J. Phys. Chem. C, 2015, 119, 11301–11310 CAS.
- B. Baumeier, J. Kirkpatrick and D. Andrienko, Phys. Chem. Chem. Phys., 2010, 12, 11103–11113 RSC.
- J. Kirkpatrick, Int. J. Quantum Chem., 2008, 108, 51–56 CrossRef CAS.
- H. Kobayashi, N. Kobayashi, S. Hosoi, N. Koshitani, D. Murakami, R. Shirasawa, Y. Kudo, D. Hobara, Y. Tokita and M. Itabashi, J. Chem. Phys., 2013, 139, 8 CrossRef PubMed.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- W. Q. Deng and W. A. Goddard, J. Phys. Chem. B, 2004, 108, 8614–8621 CrossRef CAS.
- A. N. Sokolov, S. Atahan-Evrenk, R. Mondal, H. B. Akkerman, R. S. Sánchez-Carrera, S. Granados-Focil, J. Schrier, S. C. B. Mannsfeld, A. P. Zoombelt, Z. Bao and A. Aspuru-Guzik, Nat. Commun., 2011, 2, 437 CrossRef PubMed.
- M. V. Basilevsky, A. V. Odinokov and K. G. Komarova, J. Phys. Chem. B, 2015, 119, 7430–7438 CrossRef CAS PubMed.
- C. Schober, K. Reuter and H. Oberhofer, J. Phys. Chem. Lett., 2016, 7, 3973–3977 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry: the First Forty Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, pp. 1167–1189 Search PubMed.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477–1489 CrossRef CAS.
- V. Coropceanu, R. S. Sánchez-Carrera, P. Paramonov, G. M. Day and J.-L. Brédas, J. Phys. Chem. C, 2009, 113, 4679–4686 CAS.
- S. Illig, A. S. Eggeman, A. Troisi, L. Jiang, C. Warwick, M. Nikolka, G. Schweicher, S. G. Yeates, Y. Henri Geerts, J. E. Anthony and H. Sirringhaus, Nat. Commun., 2016, 7, 10736 CrossRef CAS PubMed.
- N. G. Martinelli, Y. Olivier, S. Athanasopoulos, M.-C. Ruiz Delgado, K. R. Pigg, D. A. da Silva Filho, R. S. Sánchez-Carrera, E. Venuti, R. G. Della Valle, J.-L. Brédas, D. Beljonne and J. Cornil, ChemPhysChem, 2009, 10, 2265–2273 CrossRef CAS PubMed.
- Y. Jiang, X. Zhong, W. Shi, Q. Peng, H. Geng, Y. Zhao and Z. Shuai, Nanoscale Horiz., 2016, 1, 53–59 RSC.
- S. Larsson and A. Klimkans, Mol. Cryst. Liq. Cryst., 2001, 355, 217–229 CrossRef CAS.
- P. J. Skabara, J. B. Arlin and Y. H. Geerts, Adv. Mater., 2013, 25, 1948–1954 CrossRef CAS PubMed.
- N. E. Jackson, K. L. Kohlstedt, L. X. Chen and M. A. Ratner, J. Chem. Phys., 2016, 145, 204102 CrossRef PubMed.
- T. Vehoff, B. Baumeier, A. Troisi and D. Andrienko, J. Am. Chem. Soc., 2010, 132, 11702–11708 CrossRef CAS PubMed.
- H. Sirringhaus, T. Sakanoue and J.-F. Chang, Phys. Status Solidi B, 2012, 249, 1655–1676 CrossRef CAS.
- T. Okamoto, C. Mitsui, M. Yamagishi, K. Nakahara, J. Soeda, Y. Hirose, K. Miwa, H. Sato, A. Yamano, T. Matsushita, T. Uemura and J. Takeya, Adv. Mater., 2013, 25, 6392–6397 CrossRef CAS PubMed.
- Z. Wei, W. Hong, H. Geng, C. Wang, Y. Liu, R. Li, W. Xu, Z. Shuai, W. Hu, Q. Wang and D. Zhu, Adv. Mater., 2010, 22, 2458–2462 CrossRef CAS PubMed.
- G. Schweicher, V. Lemaur, C. Niebel, C. Ruzié, Y. Diao, O. Goto, W.-Y. Lee, Y. Kim, J.-B. Arlin, J. Karpinska, A. R. Kennedy, S. R. Parkin, Y. Olivier, S. C. B. Mannsfeld, J. Cornil, Y. H. Geerts and Z. Bao, Adv. Mater., 2015, 27, 3066–3072 CrossRef CAS PubMed.
- Y. Tsutsui, G. Schweicher, B. Chattopadhyay, T. Sakurai, J.-B. Arlin, C. Ruzié, A. Aliev, A. Ciesielski, S. Colella, A. R. Kennedy, V. Lemaur, Y. Olivier, R. Hadji, L. Sanguinet, F. Castet, S. Osella, D. Dudenko, D. Beljonne, J. Cornil, P. Samorì, S. Seki and Y. H. Geerts, Adv. Mater., 2016, 28, 7106–7114 CrossRef CAS PubMed.
- Y. Wang, C. Duan, L. M. Peng and J. H. Liao, Sci. Rep., 2014, 4, 7565 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04357k |
| This journal is © the Owner Societies 2017 |