Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evidence for cooperative Na+ and Cl− binding by strongly hydrated L-proline†
Olga A.
Dmitrieva
a,
Marina V.
Fedotova
 *a and
Richard
Buchner
*a and
Richard
Buchner
 *b
*b
aG.A. Krestov Institute of Solution Chemistry, Russian Academy of Sciences, Akademicheskaya st. 1, 153045 Ivanovo, Russian Federation. E-mail: hebrus@mail.ru
bInstitut für Physikalische und Theoretische Chemie, Universität Regensburg, 93040 Regensburg, Germany. E-mail: Richard.Buchner@chemie.uni-regensburg.de
First published on 19th July 2017
Abstract
In nature the amino acid L-proline (Pro) is a ubiquitous and highly effective osmolyte protecting cells against osmotic stress. To understand this effect knowledge of the hydration of Pro and its interactions with dissolved salts is essential. We studied these properties by combining statistical mechanics and broadband dielectric spectroscopy and found that Pro remains strongly hydrated up to high amino-acid concentrations. This is also the case upon NaCl addition to a 0.6 M Pro solution. Here, additionally a Pro·NaCl aggregate is formed with a stability constant of K° ≈ 0.95…1.25 M−1, where Na+ and Cl− cooperatively bind to adjacent carboxylate-oxygen and ammonium-hydrogen atoms, respectively.
1 Introduction
The compatible osmolyte L-proline (Pro), pyrrolidine-2-carboxylic acid, is a natural amino acid with very high protective activity against protein denaturation evoked by temperature, dehydration, and chemical agents.1–4 In particular, Pro is synthesized and accumulated in cells as a response to osmotic dehydration stress experienced in high-salinity environments.5 Molecular dynamics (MD) simulations suggested that Pro molecules are excluded from direct contact with the protein surface.6 As a consequence, the hydration shell around the protein should be strengthened and thus its native conformation stabilized, suggesting that the protecting effect of Pro is indirect and mediated by the solvent. This contrasts the infrared study of Bruździak et al.7 who claim that Pro directly binds to proteins via its carboxylate group. With regard to freeze protection it is interesting to note that at very high Pro concentrations the solution does not freeze but exhibits a glass transition at 220 K8 similar to water hydrating proteins.9 Proline is a good redox buffer, is capable of maintaining cellular pH and does not perturb regular metabolic reactions even when present at high concentration.10 Pro is also the most soluble of all proteinogenic amino acids11,12 and was found to dramatically enhance the solubility of sparingly soluble proteins in water.13 Due to its isoelectric point of pH = 6.3 the zwitterionic form of Pro, with a positively charged proteinogenic secondary ammonium (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH2+) and a negative carboxylate (–COO−) group, largely predominates in aqueous solution (Fig. 1). In contrast to other proteinogenic amino acids, the nitrogen atom of Pro is part of a pentagonal ring system constraining the rotation angle of the C–N bonds.
NH2+) and a negative carboxylate (–COO−) group, largely predominates in aqueous solution (Fig. 1). In contrast to other proteinogenic amino acids, the nitrogen atom of Pro is part of a pentagonal ring system constraining the rotation angle of the C–N bonds.
 | ||
| Fig. 1 Structure of L-proline14 with atom labeling used in the 1D-RISM calculations. The arrow indicates the direction of the dipole moment. | ||
The claimed6 preferential exclusion of Pro from the protein surface implicates that the ability of this compound to act as a natural bioprotectant should be connected to its hydration. Despite considerable efforts during the last decade to understand Pro–water interactions only a few publications describe its hydration structure.6,7,15–25 Moreover, the available quantitative information is scattered considerably. For instance, hydration numbers range from 20, obtained in a MD simulation,15 to 11–12 from statistical mechanics23 to 8–9, obtained with neutron diffraction.17 Although the importance of hydrogen bonding is well documented, information on the number and strength of the formed Pro⋯H2O H-bonds is contradictory.8,13,16–19,26
Obviously, the current understanding of Pro hydration and thus of its action as a bioprotectant is still insufficient and current knowledge on ion binding is even more patchy. Complementing previous investigations of the Ivanovo group,23–25 the present contribution aims to improve this situation by combining the complementary approaches of broadband dielectric relaxation spectroscopy27,28 (DRS) and statistical mechanics calculations in the framework of the reference interaction site model (RISM) integral equation theory.29 For this purpose the interactions of Pro with water and NaCl were studied over a wide range of L-proline, c(Pro), and salt, c(NaCl), concentrations at room temperature. Dielectric spectroscopy was chosen as it informs on the collective dynamics of the sample and provides quantitative information on solute–solvent and solute–solute interactions in terms of effective hydration numbers and ion-association constants, albeit without direct information on the location of involved interaction sites.28,30 This technique, which probes the response to a harmonic electric field of frequency, ν, in terms of the complex permittivity, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ν) = ε′(ν) − iε′′(ν) (ε′(ν) is the relative permittivity; ε′′(ν) is the dielectric loss),27 has been successfully used to study the hydration of biomolecules.31–33 On the other hand, modern RISM theory accounts for the geometry and partial-charge distribution of solute and solvent molecules and thus provides detailed information on solute–solvent interactions at the molecular level.34–36 RISM calculations cannot provide information on dynamics but are much less computationally demanding than MD simulations at comparable accuracy for structural and thermodynamic data, enabling exploration of the entire phase space covered by the experiments.
(ν) = ε′(ν) − iε′′(ν) (ε′(ν) is the relative permittivity; ε′′(ν) is the dielectric loss),27 has been successfully used to study the hydration of biomolecules.31–33 On the other hand, modern RISM theory accounts for the geometry and partial-charge distribution of solute and solvent molecules and thus provides detailed information on solute–solvent interactions at the molecular level.34–36 RISM calculations cannot provide information on dynamics but are much less computationally demanding than MD simulations at comparable accuracy for structural and thermodynamic data, enabling exploration of the entire phase space covered by the experiments.
2 Methods
2.1 Experimental
Samples were prepared gravimetrically without buoyancy correction, using degassed water (Millipore, specific resistance ≥18 MΩ cm), L-proline (99%, Sigma Aldrich, USA) and NaCl (pro analysi, Merck, Germany). Sample densities, ρ, required to convert solute molalities m (in mol kg−1 solvent) into molar concentrations, c (in M = mol L−1) were determined at (25 ± 0.01) °C with a vibrating tube densimeter (DMA 5000M, Anton Paar, Austria). Taking into account all sources of error we estimate the standard uncertainty of ρ to be 5 × 10−5 kg L−1. Electrical conductivities, κ, were obtained at (25 ± 0.005) °C with a relative uncertainty in κ of 0.005 using the setup and following the procedure described previously.37,38 The obtained data for ρ are included in Tables 1 and 2, and those for κ are given in Table 2.| c(Pro)/M | c(H2O)/M | ρ/kg L−1 | ε | S 1 | τ 1/ps | S 2 | τ 2/ps | S 3 | τ 3/ps | ε ∞ |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.098 | 54.03 | 1.00019 | 79.72 | 2.88 | 51.2 | 0.25 | 17.1 | 70.60 | 8.45 | 5.99 |
| 0.197 | 52.61 | 1.00342 | 81.99 | 5.83 | 52.7 | 1.48 | 17.6 | 68.67 | 8.54 | 6.02 |
| 0.395 | 49.56 | 1.00983 | 85.97 | 12.49 | 56.4 | 2.90 | 19.0 | 64.80 | 8.52 | 5.78 |
| 0.591 | 48.05 | 1.01608 | 90.53 | 17.82 | 61.4 | 4.15 | 19.8 | 62.52 | 8.79 | 6.04 |
| 0.787 | 46.25 | 1.02234 | 94.61 | 23.44 | 65.5 | 5.03 | 21.1 | 59.97 | 9.04 | 6.17 |
| 0.981 | 43.01 | 1.02857 | 98.41 | 30.05 | 67.2 | 6.59 | 21.6 | 55.90 | 8.86 | 5.86 |
| 1.944 | 34.98 | 1.05854 | 117.88 | 55.04 | 92.2 | 11.90 | 30.4 | 44.64 | 9.83 | 6.30 |
| 2.879 | 27.30 | 1.08713 | 136.09 | 77.91 | 126 | 17.64 | 35.0 | 33.97 | 10.8 | 6.56 |
| 3.805 | 22.36 | 1.11472 | 152.30 | 96.43 | 179 | 22.01 | 50.9 | 27.08 | 12.4 | 6.77 |
| 4.700 | 15.39 | 1.14066 | 167.85 | 117.29 | 262 | 26.15 | 57.4 | 17.69 | 12.7 | 6.72 |
| 5.569 | 11.76 | 1.16456 | 182.09 | 134.69 | 418 | 27.91 | 81.8 | 12.79 | 14.4 | 6.69 |
| c(NaCl)/M | c(Pro)/M | ρ/kg L−1 | κ/S m−1 | ε | S 1 | τ 1/ps | S 2 | τ 2/ps | S 3 | τ 3/ps | S 4 | τ 4/ps | ε ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Parameter values followed by the letter F were not adjusted in the fitting procedure. | |||||||||||||
| 0.205 | 0.604 | 1.02595 | 1.74 | 88.46 | 2.19 | 284 | 16.15 | 61F | 4.47 | 19.8F | 59.64 | 8.62 | 6.01 |
| 0.505 | 0.614 | 1.03621 | 4.18 | 85.08 | 4.34 | 213 | 13.98 | 61F | 6.19 | 19.8F | 54.43 | 8.33 | 6.13 |
| 0.999 | 0.605 | 1.05310 | 7.58 | 78.52 | 5.09 | 186 | 11.38 | 61F | 7.40 | 19.8F | 47.96 | 8.03 | 6.69 |
| 1.513 | 0.606 | 1.07483 | 10.58 | 73.41 | 5.92 | 200 | 9.51 | 61F | 9.00 | 19.8F | 42.10 | 7.56 | 6.89 |
| 2.023 | 0.614 | 1.09384 | 13.07 | 68.81 | 6.64 | 213 | 8.09 | 61F | 10.56 | 19.8F | 36.61 | 7.06 | 6.90 |
Broadband spectra of relative permittivity, ε′(ν), and total loss, η′′(ν) = ε′′(ν) + κ/(2πνε0) (ε0 is the electric field constant), were measured at (25 ± 0.05) °C in the frequency range 0.05 ≤ ν/GHz ≤ 89. At 0.05 ≤ ν/GHz ≤ 50 data were determined by reflectometry using an Agilent E8364B vector network analyzer (VNA) with the corresponding E-Cal module. A coaxial-line cut-off cell39 was used for ν ≤ 0.5 GHz whereas two open-ended coaxial-line probes covered 0.2 ≤ ν/GHz ≤ 20 (Agilent 85070E-020) and 1 ≤ ν/GHz ≤ 50 (Agilent 85070E-050).40 Measurements at 60 ≤ ν/GHz ≤ 89 were performed with a waveguide interferometer having a variable-pathlength transmission cell.41 The data obtained with the different instruments were concatenated and, where necessary, η′′(ν) was then corrected for the separately determined DC conductivity, κ, to yield the dielectric loss, ε′′(ν). Examples of the obtained dielectric spectra are shown in Fig. 2, 3 and Fig. S1, S4 (ESI†).
For the formal fit of the obtained ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ν) relaxation models based on the superposition of n ≤ 5 separate modes were tested and scrutinized according to the criteria described in detail previously.42,43 It turned out that the spectra of aqueous L-proline solutions were best fitted with a sum
(ν) relaxation models based on the superposition of n ≤ 5 separate modes were tested and scrutinized according to the criteria described in detail previously.42,43 It turned out that the spectra of aqueous L-proline solutions were best fitted with a sum
 | (1) |
 is the high-frequency permittivity. The static relative permittivity of the sample is given as ε = ε∞ + ∑Sj. The obtained parameters are summarized in Tables 1 and 2.
is the high-frequency permittivity. The static relative permittivity of the sample is given as ε = ε∞ + ∑Sj. The obtained parameters are summarized in Tables 1 and 2.
For dielectric relaxation through dipole rotation, as is the case for all resolved modes of this investigation, the amplitudes, Sj, are linked to the corresponding dipole concentrations, cj, via
 | (2) |
2.2 Calculations
Statistical mechanics calculations using the 1D-RISM approach provide information on solution structure in terms of statistically averaged atom–atom (or site–site, α–β) radial pair distribution functions (PDFs), gαβ(r), for sites α on the reference molecule interacting with sites β on surrounding species, whereas 3D-RISM yields spatial distribution functions (SDFs), gβ(r), for sites β around the reference molecule.29,34,35 For the atom labeling of Pro see Fig. 1; the solvent sites are designated as Ow and Hw. For the present calculations the 1D-RISM Ornstein–Zernike integral equation29 combined with the 1D-Kovalenko–Hirata closure46 and the 3D-RISM integral equation47 coupled with the 3D Kovalenko–Hirata closure48 were used.The calculations were performed using the rism1d and rism3d codes from the AmberTools package49 and the MDIIS (Modifed Direct Inversion in the Iterative Subspace) iterative scheme.48 The 1D-RISM equations were solved on a one-dimensional grid of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 points with a spacing of 2.5 × 10−3 nm and 10 MDIIS vectors. The 3D-RISM equations were solved on a three-dimensional grid of 300 × 288 × 288 points with 5 MDIIS vectors and with a spacing of 0.01 nm. A residual tolerance of 10−6 was chosen. These parameters were large enough to accommodate the solute complex together with sufficient solvation space around so that the obtained results are without significant numerical errors. In the calculations interaction potentials were represented by long-range Coulomb and short-range Lennard-Jones contributions. The atom coordinates of Pro were adopted from the PubChem Structure DataBase,14 whereas partial charges and Lennard-Jones parameters were taken from the General Amber Force Field (GAFF).50 For the solvent the modified SPC/E water model (MSPC/E)51 was used. For further details see the ESI.†
384 points with a spacing of 2.5 × 10−3 nm and 10 MDIIS vectors. The 3D-RISM equations were solved on a three-dimensional grid of 300 × 288 × 288 points with 5 MDIIS vectors and with a spacing of 0.01 nm. A residual tolerance of 10−6 was chosen. These parameters were large enough to accommodate the solute complex together with sufficient solvation space around so that the obtained results are without significant numerical errors. In the calculations interaction potentials were represented by long-range Coulomb and short-range Lennard-Jones contributions. The atom coordinates of Pro were adopted from the PubChem Structure DataBase,14 whereas partial charges and Lennard-Jones parameters were taken from the General Amber Force Field (GAFF).50 For the solvent the modified SPC/E water model (MSPC/E)51 was used. For further details see the ESI.†
3 Results and discussion
3.1 Aqueous L-proline
Qualitatively, the present dielectric spectra of aqueous Pro strongly resemble those of the osmolyte ectoine,31 which is also a zwitterion. The mode at ∼20 GHz, associated with the cooperative relaxation of the H-bond network of—more or less unperturbed—bulk water, strongly decreases in amplitude, S3, with rising solute concentration, c(Pro) (Fig. 2 and Fig. S2, ESI†). At the same time a pronounced solute-related mode rises at low frequencies, shifting from ∼3 GHz at c(Pro) = 0.098 M to ∼0.4 GHz at the highest concentration studied (5.569 M) due to increasing viscosity. Its strongly rising amplitude, S1, largely overcompensates the decrease of S3 (Fig. S3, ESI†), so that the static relative permittivity of the solutions monotonically rises from ε = 78.37 in pure water to 182 close to saturation (Table 1). These findings for the two modes dominating![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) (ν) of aqueous Pro solutions are in qualitative agreement with the previous dielectric study of Rodrguez-Arteche et al.,21 who used a superposition of two Cole–Cole (CC) equations (a CC + CC model) to fit their spectra. Additionally, however, a weak relaxation of amplitude S2, located at ∼8 GHz, could be resolved in our spectra. This weak intermediate-frequency mode, which in ref. 21 is buried under the broad wings of the two CC modes, can be attributed to retarded (slow) water molecules hydrating Pro for reasons explained below and detailed for similar systems elsewhere.28,31–33 No fast water mode at ∼500 GHz31,52 could be resolved for Pro(aq) [and {Pro + NaCl}(aq)] but its presence is obvious from the large values of ε∞ (Tables 1 and 2) and accordingly was taken into account in the calculation of the total amplitude of bulk-like water, Sb = S3 + ε∞(c(Pro)) − ε∞(0), where ε∞(0) = 3.52, (Fig. S3, ESI†).30
(ν) of aqueous Pro solutions are in qualitative agreement with the previous dielectric study of Rodrguez-Arteche et al.,21 who used a superposition of two Cole–Cole (CC) equations (a CC + CC model) to fit their spectra. Additionally, however, a weak relaxation of amplitude S2, located at ∼8 GHz, could be resolved in our spectra. This weak intermediate-frequency mode, which in ref. 21 is buried under the broad wings of the two CC modes, can be attributed to retarded (slow) water molecules hydrating Pro for reasons explained below and detailed for similar systems elsewhere.28,31–33 No fast water mode at ∼500 GHz31,52 could be resolved for Pro(aq) [and {Pro + NaCl}(aq)] but its presence is obvious from the large values of ε∞ (Tables 1 and 2) and accordingly was taken into account in the calculation of the total amplitude of bulk-like water, Sb = S3 + ε∞(c(Pro)) − ε∞(0), where ε∞(0) = 3.52, (Fig. S3, ESI†).30
Fig. 4 shows the effective dipole moment, μeff(Pro), of Pro obtained from S1 with eqn (2), which decreases linearly from 19.3 D at c(Pro) = 0 to 17.2 D at 5.6 M. These data are comparable to the results of Rodrguez-Arteche et al.21 but considerably larger than the value of μeff(Pro) = 12.0 D predicted by DFT calculations (Gaussian at the B3LYP/cc-pVDZ level with the C-PCM solvation model)53,54 for a L-proline molecule embedded in water.55 In analogy to previous osmolyte studies,28,31–33,56 this indicates strong hydration of Pro with parallel alignment of solute and solvent dipoles. Support for this view comes from DFT calculations of Pro·nH2O clusters (Fig. S5, ESI†). Here μeff(Pro) = 20.4 D was obtained for a complex with n = 4 water molecules interacting with the carboxylate moiety of Pro. This value is slightly above the c → 0 limit of the experimental data, whereas n = 3 yielded 16.2 D. Such cluster calculations should not be over-interpreted as they yield a static picture and account only implicitly for the embedding solvent but the present results hint at Pro dehydration as a likely reason for the decrease of experimental μeff(Pro) values with rising c(Pro). A further contribution to this decrease might be the emergence of anti-parallel dipole–dipole correlations amongst neighbouring L-proline molecules. Unfortunately, this cannot be checked as RISM calculations are not sensitive to this effect.
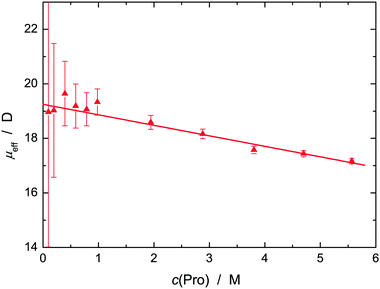 | ||
| Fig. 4 Effective dipole moment, μeff (▲), of L-proline in aqueous solution at 25 °C and solute concentration c(Pro). The straight line represents a weighted fit. | ||
Information on solute hydration was obtained with DRS by evaluating the amplitudes of the solvent-related modes, here S2 (=Ss) and Sb, with eqn (2).30 The quantiy S2 yielded the concentration of retarded (slow) H2O, cs, and thus the corresponding effective hydration number, Zs = cs/c(Pro), of solvent molecules per equivalent of solute that are slowed down compared to more-or-less unperturbed bulk-like water. With increasing solute concentration the retardation factor, r = τ2/τ3, increased from ∼2.0 to ∼5.7, indicating a considerable loss of rotational mobility of these H2O molecules. The concentration of bulk-like water, cb, was calculated from Sb and thus the total effective hydration number, Zt = (c(H2O) − cb)/c(Pro), with c(H2O) as the analytical water concentration. The difference Zib = Zt − Zs indicates the corresponding number of irrotationally bound (ib) solvent molecules (more exactly, a polarization equivalent to Zib solvent dipole moments, μweff57) per mole solute which apparently disappeared from the spectrum. Based on previous results for osmolytes and related compounds28,31–33,56 we argue that these strongly bound H2O molecules contribute to the solute relaxation. Almost certainly, they do not form stiff, long-lived complexes with the solute but adopt the rotational dynamics of Pro which is dominated by the lifetime of the solute–solvent hydrogen bonds.
Fig. 5 shows the thus obtained effective hydration numbers of L-proline. Similar to the hydration numbers reported by Rodrguez-Arteche et al.,21 the present values for Zt exhibit a marked exponential decrease from ∼9 at infinite dilution to ∼3 at the highest concentration studied. The variation of Zs from 5.3 to 3.7 is much weaker and linear. As a consequence, the number of ib water molecules, Zib, rapidly decreases, becoming negligible at c(Pro) ≈ 3.5 M.58 Decreasing Zi (i = t, s, ib) with increasing c(Pro) indicates hydration-shell overlap and thus competition of solute molecules for the same H2O molecules. As a result, the latter become more mobile again. Note that at the highest concentration studied the Pro![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratio has dropped to ∼ 1
H2O ratio has dropped to ∼ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.23. Therefore, all the water present at c(Pro) = 5.57 M is in the first coordination shell of a solute molecule and most of these H2O molecules are slowed in their dynamics. For this reason, it is unlikely for a solvent molecule that was strongly bound (ib) at c(Pro) → 0 to be completely released above 3 M. More likely is the release of water that was weakly bound at low c(Pro), whereas ib H2O molecules gain enough mobility to be detected as slow water with the rather large retardation factor of r ≈ 5.
5.23. Therefore, all the water present at c(Pro) = 5.57 M is in the first coordination shell of a solute molecule and most of these H2O molecules are slowed in their dynamics. For this reason, it is unlikely for a solvent molecule that was strongly bound (ib) at c(Pro) → 0 to be completely released above 3 M. More likely is the release of water that was weakly bound at low c(Pro), whereas ib H2O molecules gain enough mobility to be detected as slow water with the rather large retardation factor of r ≈ 5.
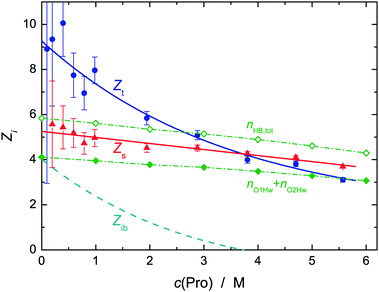 | ||
| Fig. 5 Effective hydration numbers of total bound water, Zt (●), and of slow water, Zs (▲) of L-proline in aqueous solution at 25 °C and solute concentration c(Pro). Solid lines show weighted fits of these data, the broken line gives the number of frozen H2O molecules, Zib = Zt − Zs calculated therefrom.58 Also included are the 1D-RISM results for the total number, nHB,tot (◇), of H2O molecules H-bonded to L-proline and for those binding to the carboxylate group, nO1Hw + nO2Hw (◆, connecting lines are a guide to the eye). | ||
This view is supported by the present statistical mechanics calculations. As expected from a molecule of this size, Pro can accommodate a significant number, nt, of water molecules in it first coordination shell. The 3D-RISM calculations yielded nt = 25.4 at infinite dilution, dropping to 13.2 at c(Pro) = 6 M (Table S1, ESI†), which means that above ∼1 M adjacent Pro molecules will share water molecules. There are water molecules close to the carbon atoms (Table S1, ESI†). However, the large distances and the small peak heights of the associated PDFs, as well as the large distances between the pyrrolidine ring and the H2O located above and below this moiety derived from the CDFs (Fig. S1, ESI†), clearly show that interaction of these solvent molecules with the hydrophobic moieties of Pro is only weak. This is in line with previous investigations.15,17,59 On the other hand, the PDFs gN1Ow(r), gO1Ow(r) and gO2Ow(r) (see Fig. 1 for atom labeling) of water around the hydrophilic sites of Pro exhibit well-defined maxima at r ≈ 0.3 nm indicative of pronounced hydration (Fig. S6 and S7, ESI†). This is also reflected in the spatial distribution function obtained with 3D-RISM (Fig. 6). As expected, the site-specific first-shell coordination numbers obtained from these PDFs (Table S1, ESI†), and thus the resulting sum for all hydrophilic sites, nh = nO1Ow + nO2Ow + nN1Ow, decrease with increasing c(Pro) but with nh varying between 19.5 and 11.2 this value is always significantly larger than the DRS hydration number Zt. Whilst recent MD simulations yielded hydration numbers for the hydrophilic moieties that were similar to the present nh,15 neutron diffraction data gave nh ≈ 8…9, independent of c(Pro).17 The latter value agrees with Zt at vanishing Pro concentration (Fig. 5). In part, this discrepancy between experimental and computational results reflects a deficiency of PDFs as these cannot indicate whether a solvent site at distance r from the chosen reference solute site is not simultaneously at a similar distance to another solute site. In the integration yielding the coordination numbers such shared solvent molecules are counted twice. Most problematic here are the two oxygen atoms of the carboxylate group. The total coordination number of this group at c(Pro) → 0 is almost certainly smaller than the sum of nO1Ow [= 7.95] and nO2Ow [=7.10]. Nevertheless, the RISM data clearly indicate that a large number of H2O molecules experience solute–solvent interactions stronger than solvent–solvent interactions. It is reasonable to assume that these molecules are more-or-less slowed in their rotational dynamics. Confirmation for the strong impact of Pro on water dynamics also comes from the marked distance dependence of the translational diffusion coefficient of water in these solutions, as revealed by quasielastic neutron scattering.22
More specific information on solute–solvent interactions comes from the PDFs gO1Hw(r), gO2Hw(r), gH8Ow(r) and gH9Ow(r) (Fig. S7 and S8, ESI†) as their sharp peaks at ∼0.17 nm indicate hydrogen bonding between the solute and solvent. According to Fig. 5, the sum of carboxylate-H2O H-bonds, nO1Hw + nO2Hw, is somewhat smaller than Zs over the entire concentration range studied, whereas the total number of Pro-H2O H-bonds, nHB,tot = nO1Hw + nO2Hw + nH8Ow + nH9Ow, is slightly larger and all three data sets run practically parallel. Most likely, it is these nHB,tot water molecules hydrogen-bonded to Pro which dominate Zt although it must be noted that according to DRS studies of aqueous sodium n-alkylcarboxylate solutions the carboxylate group in itself already binds ∼5.2 water molecules.60 Of these H2O molecules hydrogen-bonding to Pro, the equivalent of ∼4 × μweff is effectively frozen at c(Pro) → 0 but with increasing L-proline concentration the rotational mobility of this fraction increases57 (contributing thus to the slow-water mode) whereas an equivalent amount of previously slow water becomes indistinguishable in its dynamics from the bulk. Clear support for such a redistribution comes from the observed relaxation times, where that of bulk-like water increases from τ3 = 8.3 ps in pure water to 14.4 ps at 5.6 M, whereas the relaxation time of the slow-water mode simultaneously increases from τ2 = 17.1 ps to 81.8 ps (Fig. S4, ESI†). As a consequence, the retardation factor for slow water increases from r = τ2/τ3 ≈ 2.0 to ∼5.7 and it appears that at c(Pro) ≳ 3 M the water molecules H-bonded to Pro account for Zs.
The above findings allow closing the circle and returning to the solute mode. In line with the cluster calculations (Fig. S5, ESI†) we may conclude that the effective L-proline moment of μeff(Pro) = 19.3 D at c(Pro) = 0 (Fig. 4) is due to the essentially parallel alignment of the solute dipole with Zib ≈ 4 water dipoles. With increasing c(Pro) the latter start to wobble more and more, so that their contribution to μeff(Pro) continuously decreases, reaching 17.2 D at 5.6 M and now caused by Zs ≈ 3.7 rather strongly slowed (r ≈ 5.7) but not frozen H2O molecules.
At very high concentration correlations among L-proline dipoles may also contribute to the reduction of μeff(Pro) but detecting those is outside the reach of RISM calculations. Indeed, based on various experimental techniques and MD simulations Busch et al.59 suggested proline–proline dimerization through electrostatic interactions at high c(Pro). In the postulated aggregate (their Fig. 9) the dipole moments of the two constituting Pro molecules should be practically anti-parallel. Based on results from various techniques Troitzsch et al.16,18,19 also found evidence for dimeric structures at high Pro concentrations, in particular at low temperature. However, they found no evidence for mesoscale aggregation postulated on the basis of spectroscopic and calorimetric data.8 On the other hand, Civera et al.15 did not find any evidence for Pro aggregation in their MD study.
3.2 NaCl addition to 0.6 M aqueous L-proline
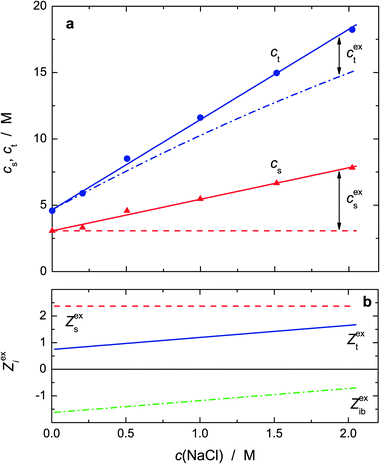
Upon addition of NaCl to a 0.6 M Pro solution an additional weak relaxation (parameters S1 and τ1) emerged at ∼0.7 GHz (Fig. 3 and Fig. S9, ESI†). To some extent, this new mode is almost certainly due to ion-cloud (IC) relaxation of the electrolyte61 but the IC amplitude is small and dies out at high salt concentrations, c(NaCl) (Fig. 7). Since the formation of stable NaCl ion pairs in aqueous solution is negligible,61 this means that a new dipolar species is formed when Pro and NaCl are simultaneously present in aqueous solution. | ||
| Fig. 7 Relaxation amplitudes of slow water, S3 (▲), L-proline, S2 (●), and the lowest frequency mode, S1 (▼), for NaCl solutions of concentration c(NaCl), in 0.6 M aqueous L-proline at 25 °C. Also included is the ion-cloud (IC) amplitude of NaCl(aq) (dash-dotted line; shaded area corresponds to one standard uncertainty)61 and S1 corrected for this contribution (▽). | ||
The modes associated with L-proline (S2 and τ2 in Table 2), slow water (S3, τ3) and bulk-like water (S4, τ4) essentially remained at their positions62 but changed significantly in amplitude. Whilst the decrease of S4—and thus of the associated bulk-water amplitude, Sb = S4 + ε∞(c(NaCl)) − ε∞(0), where ε∞(0) = 3.52 is the pure water value (Fig. S10, ESI†)—was expected because of strong Na+ hydration, the simultaneous increase of the slow-water amplitude, S3 (Fig. 7), was surprising as in the case of aqueous NaCl solutions there is no slow water detected, i.e. Zt(NaCl) = Zt(Na+) = Zib(Na+).61 Also unusual was the strong decrease of the L-proline amplitude, S2. As discussed below, this is due to the formation of a Pro·NaCl aggregate, which mainly causes S1.
With regard to hydration in electrolyte solutions, kinetic depolarization of the bulk solvent by the moving ions has to be taken into account when analyzing DRS data; see the ESI† for details. Accordingly, using the approach of Sega et al.,63 the present Sb values were corrected for this effect to yield the associated equilibrium amplitude, Seqb (Fig. S10, ESI†) and, viaeqn (2), the total concentration of bound water, ct, as a function of salt concentration, c(NaCl) (Fig. 8a). The corresponding concentration of slow water, cs, was directly obtained from S3. Within experimental uncertainty, ct and cs increase linearly with NaCl concentration.
Fig. 8a also shows the values expected for cs and ct on the basis of the effective hydration numbers Zs(Pro), Zt(Pro) and Zt(NaCl) = Zib(Na+),64 assuming additivity of the contributions of 0.6 M Pro (smoothed values from Fig. 5) and the salt61 at c(NaCl). Clearly, the experimental values for cs and ct exceed the predicted concentrations of slow and total bound water, indicating synergistic water binding by Pro and NaCl. Interestingly, the excess of slow water, cexs, exceeds that of total bound water, cext. Expressed in terms of “excess hydration numbers”, Zexs = cexs/c(NaCl), Zext = cext/c(NaCl) and Zexib = Zext − Zexs (Fig. 8b), this means that per formula unit of added NaCl Zext ≈ 0.8 to 1.7H2O dipoles are additionally impeded in their dynamics—presumably by interacting with the formed Pro·NaCl aggregate—but simultaneously about 1.5 to 0.7 initially frozen (ib) dipoles partially regain mobility and are detectable as slow water again.57
The obtained 1D-RISM PDFs and 3D-RISM CDFs, see Fig. S11–S13 (ESI†) for selected examples, and the extracted coordination numbers (Table S2, ESI†) indicate that at least up to c(NaCl) = 2 M added salt has only a marginal effect on the first hydration shell. In that respect, the RISM results do not reflect the additional appearance of ∼2.4 slow H2O dipoles per equivalent of added NaCl suggested by the experiments (Fig. 8b). On the other hand, even when taking into account that with nO1Ow ≈ 7.3 and nO2Ow ≈ 6.6 water molecules interacting with carboxylate may be counted twice in 1D-RISM, these numbers definitely exceed the number of H bonds, nO1Hw ≈ 2.1 and nO2Hw ≈ 1.8 (Table S2, ESI†), involved in the hydration of the anionic residue of Pro. Their sum also clearly exceeds the total hydration number from experiment (Fig. 5); see the discussion for salt-free Pro solutions. For the ammonium group a similar discrepancy between nN1Ow [≈4.2] and the sum of nH8Ow [≈0.85] and nH9Ow [≈0.75] was found. Therefore, it appears likely for the Pro·NaCl aggregate formed in these systems (see below) that some of the H2O molecules which interact with but are not H-bonded to carboxylate or ammonium are reduced in their mobility because now they simultaneously interact with Pro and the attached ions, Na+ or/and Cl−.
Since in the free-running fits of the 0.6 M Pro + NaCl spectra the relaxation time of the L-proline-related relaxation, τ2, was scattering for all samples around the value at c(NaCl) = 0,62 it is reasonable to assume that salt addition does not change the effective radius (defining τ2) and thus the effective dipole moment of this species. Accordingly, the amplitude of this mode, S2, was evaluated with eqn (2) using μeff = 19.3 D. This yielded DRS-detected L-proline concentrations, cDRS(Pro), dropping from the analytical value, 0.6 M, at vanishing salt concentration to 0.27 M at c(NaCl) = 2.023 M in a pattern suggesting an equilibrium of the type
| Pro + X ⇌ Pro·X | (R1) |
 | (3) |
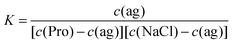 | (4) |
The thus obtained K values decrease initially but then seem to level at ∼0.8 M−1 (Fig. 9). Extrapolation to the equilibrium constant is difficult due to the limited data base and lacking activity coefficients for the involved species but values in the range K° ≈ 0.95…1.25 M−1 can be reasonably assumed. At physiological NaCl concentrations, c(NaCl) ≈ 0.154 M, the concentration ratio is in the range of 0.95…1.15 M (Fig. 9). Obviously, NaCl binding to Pro is weak but certainly it is not negligible. Thus, this equilibrium should impact on the role of this amino acid in physiological processes, ranging from its action as an osmolyte to ion-induced protein folding.
To the best of our knowledge no other numerical data for the binding constant of NaCl to Pro have been published yet so that a direct crosscheck of the present result is not possible. However, Bröhl et al.65 studied anion-binding to L-proline-based peptide models with several sodium salts using NMR and MD simulations. In aqueous solutions they obtained values for the anion binding constant in the range K° ≈ 0.29…0.77 M−1, which are very similar to the present results. Cation binding was found to be negligible for the compounds of that study. However, quantum-chemical calculations66 and gas-phase vibrational spectra67 suggest that for Pro the situation might be different.
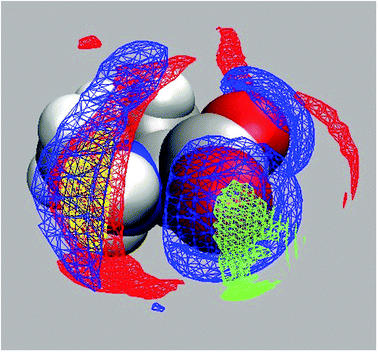
The above determination of the binding constant, eqn (3) and (4), just relies on the concentration of free L-proline calculated from S2. Eqn (R1) is therefore compatible with Pro·Na+, Pro·Cl− and Pro·NaCl as possibly formed complexes. Using the known concentration of this species, c(ag) = c(Pro) − cDRS(Pro), the amplitude of its relaxation, S1, was evaluated with eqn (2) to yield the associated effective dipole moment (Fig. S14, ESI†). Within uncertainty limits μeff decreases linearly from 14.9 D at c(NaCl) → 0 to 13.7 D at c(NaCl) = 2.0 M. Also shown in Fig. S14 (ESI†) are minimum-energy structures of Pro·Na+, Pro·Cl− and Pro·NaCl obtained with Gaussian (B3LYP/cc-pVDZ level with the C-PCM solvation model)53,54 with indicated dipole directions. The corresponding effective dipole moments are (4.7, 10.1 and 19.2) D respectively. These data refer to—so to say—“naked” aggregates embedded in a continuum with the permittivity of water, i.e. the quantum-chemical calculations did not explicitly account for the water molecules hydrating the carboxylate and amino groups of Pro. However, the relevant PDFs (Fig. S12 and Table S2, ESI†) of the 1D-RISM calculations, as well as the 3D-RISM results (Fig. 10) clearly show that also in NaCl solutions Pro remains strongly hydrated. In the hydrated Pro·NaCl complex the dipole vectors of the H2O molecules interacting with carboxylate (respectively ammonium) are oriented roughly anti-parallel to the dipole direction of the bare aggregate. Therefore, its μeff value should be smaller than the 19.2 D of the naked species. Similar considerations apply to Pro·Na+ and Pro·Cl−. Also here the hydrated species should have effective dipole moments that are smaller than the 4.7 D (respectively 10.1 D) of the naked aggregates. For this reason, the latter two species are unlikely candidates for the dipole causing the lowest-frequency mode detected for NaCl-containing solutions of 0.6 M aqueous Pro. On the other hand, Pro·NaCl becomes more likely.
For glycine68 and alanine69 RISM calculations revealed that these two amino acids bind Na+ as well as Cl−. Fedotova and Dmitrieva24 recently showed that also a single L-proline molecule in aqueous NaCl is able to do so and the present 1D-RISM (Table S2 and Fig. S12, ESI†) and 3D-RISM results (Fig. 10) extend this finding to finite (0.6 M) Pro concentrations. In all these calculations Na+ displaces water from the carboxylate group and forms a contact ion pair. According to the potentials of mean force determined for Pro at infinite dilution in NaCl(aq)24 the ammonium group on Pro interacts more strongly with Cl− than with hydrating H2O. In all cases the cation preferably binds to the oxygen atom of the carboxyl group that is closest to the amino group, whereas the anion forms a H bond with the hydrogen atom closest to the carboxylate moiety. For Pro these are O2 and H9 of Fig. 1.
Clearly, all RISM results suggest that Na+ and Cl− are simultaneously bound to the amino acid and that this process involves cooperativity. However, statistical mechanics can only provide equilibrium configurations and thus cannot directly prove that Na+ and Cl− are bound at the same time. Here, the present DRS results can step in. Although the situation is complicated by the overlapping ion cloud relaxation, the data strongly suggest that the lowest-frequency mode detected for aqueous {Pro + NaCl} solutions is due to a single dipolar species and Pro·NaCl is the most likely candidate for that. Of course, probably also Pro·Na+ and Pro·Cl− are formed to some extent. However, within the limitations of the experiment, there are no indications—like peak broadening or systematic deviations in the fit of the spectra—that would hint at the presence of a significant amount of these two species. In view of our combined computational and experimental results we may therefore safely conclude that in aqueous NaCl solutions the amino acid L-proline—and almost certainly also glycine and alanine—binds Na+ and Cl− simultaneously in a cooperative manner. Interestingly, the present data suggest that this cooperative binding even leads to an increased amount of bound water with Zext ≈ 1–1.5 per mole added NaCl (Fig. 8). Whether this is also the case for other amino acids and whether there are possible ion-specific effects for this cooperative binding process have to be elucidated in the future.
4 Concluding remarks
The present results of a combined dielectric and statistical mechanics study of solutions of the amino acid and widespread osmolyte L-proline in water and aqueous NaCl reveal that the hydrophilic moieties of Pro remain strongly hydrated up to high concentrations of Pro (Fig. 5 and Table S1, ESI†). Close to the saturation limit of Pro in water, ∼6 M at room temperature, all H2O molecules are in the first coordination shell of the solute and shared among Pro zwitterions. The majority of these solvent molecules are hydrogen bonded to the –COO− and![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH2+ moieties (Fig. 6) and therefore considerably slowed in its dynamics. The dipole vectors of these H2O are roughly parallel to the dipole direction of Pro, leading to an enhanced effective dipole moment of the solute (Fig. 4).
NH2+ moieties (Fig. 6) and therefore considerably slowed in its dynamics. The dipole vectors of these H2O are roughly parallel to the dipole direction of Pro, leading to an enhanced effective dipole moment of the solute (Fig. 4).
Proline hydration is rather insensitive to NaCl addition (Table S2, ESI†). Most importantly, and this is the key finding of the present investigation, Na+ and Cl− are simultaneously bound to Pro. The close vicinity of the binding sites of anion and cation (Fig. 10) suggests that this ion binding of Pro (and possibly other amino acids) has a cooperative component which also affects hydration (Fig. 8). The binding constant was estimated to be K° ≈ 0.95…1.25 M−1 (Fig. 9).
How do the above findings relate to the well-known protective effect of L-proline against osmotic stress? For unprotected cells high salt content in the environment triggers the flow of water from the cytosol to the extracellular fluid, ultimately leading to dehydration and consequently denaturation of proteins. Due to the strong hydration of Pro molecules, demonstrated by the present investigation, their accumulation in the cell will oppose water drainage under osmotic stress. It is still disputed whether Pro is excluded from the protein surface and thus enforces protein hydration6 or selectively binds via its carboxylate group.7 The present investigation cannot clarify this issue. However, if selective Pro binding to the protein occurs this has apparently no negative effect on protein stability. On the other hand, the cooperative NaCl binding by Pro, demonstrated in this investigation, may prevent direct interactions of Na+ or/and Cl− with proteins and thus help stabilizing them.
Acknowledgements
This work was supported by the Russian Foundation for Basic Research with grant no. 15-43-03004-r_centre_a and by the Deutscher Akademischer Austauschdienst with a research stipend for O. A. D. enabling her stay in Regensburg. The 3D-RISM calculations were performed by means of MVS-100P supercomputer resources of the Joint Supercomputer Center of the Russian Academy of Sciences (Moscow).Notes and references
- C. Rajendrakumar, B. Reddy and A. Reddy, Biochem. Biophys. Res. Commun., 1994, 201, 957–963 CrossRef CAS PubMed.
- D. Samuel, T. K. S. Kumar, G. Jayaraman, P. W. Yang and C. Yu, IUBMB Life, 1997, 41, 235–242 CrossRef CAS.
- D. Samuel, G. Ganesh, P.-W. Yang, M.-M. Chang, S.-L. Wang, K.-C. Hwang, C. Yu, G. Jayaraman, T. K. S. Kumar, V. D. Trivedi and D.-K. Chang, Protein Sci., 2000, 9, 344–352 CrossRef CAS PubMed.
- K. Kar and N. Kishore, Biopolymers, 2007, 87, 339–351 CrossRef CAS PubMed.
- J. C. Measures, Nature, 1975, 257, 398–400 CrossRef CAS PubMed.
- M. R. Bozorgmehr and H. J. Monhemi, J. Solution Chem., 2015, 44, 45–53 CrossRef CAS.
- P. Bruździak, B. Adamczak, E. Kaczkowska, J. Czub and J. Stangret, Phys. Chem. Chem. Phys., 2015, 17, 23155–23164 RSC.
- A. S. Rudolph and J. H. Crowe, Biophys. J., 1986, 50, 423–430 CrossRef CAS PubMed.
- W. Doster, S. Busch, A. M. Gaspar, M.-S. Appavou, J. Wuttke and H. Scheer, Phys. Rev. Lett., 2010, 104, 098101 CrossRef CAS PubMed.
- K. Schwab and D. Gaff, J. Plant Physiol., 1990, 137, 208–215 CrossRef CAS.
- J. P. Greenstein and M. Winitz, Chemistry of the Amino Acids, Wiley, New York, 1961 Search PubMed.
- J. P. Amend and H. C. Helgeson, Pure Appl. Chem., 1997, 69, 935–942 CrossRef CAS.
- B. Schobert and H. Tschesche, Biochim. Biophys. Acta, 1978, 541, 270–277 CrossRef CAS.
- E. E. Bolton, Y. Wang, P. A. Thiessen and S. Bryant, Annu. Rep. Comput. Chem., 2008, 4, 217–241 CAS.
- M. Civera, M. Sironi and S. L. Fornili, Chem. Phys. Lett., 2005, 415, 274–278 CrossRef CAS.
- R. Z. Troitzsch, G. J. Martyna, S. E. McLain, A. K. Soper and J. Crain, J. Phys. Chem. B, 2007, 111, 8210–8222 CrossRef CAS PubMed.
- S. E. McLain, A. K. Soper, A. E. Terry and A. Watts, J. Phys. Chem. B, 2007, 111, 4568–4580 CrossRef CAS PubMed.
- R. Z. Troitzsch, H. Vass, W. J. Hossack, G. J. Martyna and J. Crain, J. Phys. Chem. B, 2008, 112, 4290–4297 CrossRef CAS PubMed.
- R. Z. Troitzsch, P. R. Tulip, J. Crain and G. J. Martyna, Biophys. J., 2008, 95, 5014–5020 CrossRef CAS PubMed.
- P. Zhang, S. Han, Y. Zhang, R. C. Ford and J. Li, Chem. Phys., 2008, 345, 196–199 CrossRef CAS.
- I. Rodrguez-Arteche, S. Cerveny, A. Alegria and J. Colmenero, Phys. Chem. Chem. Phys., 2012, 14, 11352–11362 RSC.
- D. Yu, M. Hennig, R. A. Mole, L. J. Chen, C. Wheeler, T. Strässle and G. J. Kearley, Phys. Chem. Chem. Phys., 2013, 15, 20555–20564 RSC.
- M. V. Fedotova and O. A. Dmitrieva, Russ. J. Phys. Chem. A, 2014, 88, 794–797 CrossRef CAS.
- M. V. Fedotova and O. A. Dmitrieva, New J. Chem., 2015, 39, 8594–8601 RSC.
- M. V. Fedotova and O. A. Dmitrieva, Amino Acids, 2016, 48, 1685–1694 CrossRef CAS PubMed.
- B. Schobert, Naturwissenschaften, 1977, 64, 386 CrossRef CAS PubMed.
- F. Kremer and A. Schönhals, Broadband Dielectric Spectroscopy, Springer, Berlin, 2002 Search PubMed.
- R. Buchner and G. Hefter, Phys. Chem. Chem. Phys., 2009, 11, 8984–8999 RSC.
- D. Chandler and H. C. Andersen, J. Chem. Phys., 1979, 57, 1930–1937 CrossRef.
- A. Eiberweiser, A. Nazet, G. Hefter and R. Buchner, J. Phys. Chem. B, 2015, 119, 5270–5281 CrossRef CAS PubMed.
- A. Eiberweiser, A. Nazet, S. Kruchinin, M. Fedotova and R. Buchner, J. Phys. Chem. B, 2015, 119, 15203–15211 CrossRef CAS PubMed.
- V. Agieienko and R. Buchner, Phys. Chem. Chem. Phys., 2016, 18, 2597–2607 RSC.
- V. Agieienko, D. Horinek and R. Buchner, Phys. Chem. Chem. Phys., 2017, 19, 219–230 RSC.
- Molecular Theory of Solvation, ed. F. Hirata, Kluwer, Dordrecht, 2003 Search PubMed.
- M. V. Fedotova and M. F. Holovko, in The Integral Equation Method in Equilibrium Statistical Theory of Liquids, ed. A. Tsivadze, Prospect, Moscow, 2011, pp. 68–152 Search PubMed.
- J. J. Howard and B. M. Pettitt, J. Stat. Phys., 2011, 145, 441–466 CrossRef CAS PubMed.
- S. Shaukat and R. Buchner, J. Chem. Eng. Data, 2011, 56, 4944–4949 CrossRef CAS.
- A. Nazet, S. Sokolov, T. Sonnleitner, T. Makino, M. Kanakubo and R. Buchner, J. Chem. Eng. Data, 2015, 60, 2400–2411 CrossRef CAS.
- R. Buchner and J. Barthel, Ber. Bunsen-Ges., 1997, 101, 1509–1516 CrossRef CAS.
- T. Sonnleitner, D. A. Turton, S. Waselikowski, J. Hunger, A. Stoppa, M. Walther, K. Wynne and R. Buchner, J. Mol. Liq., 2014, 192, 19–25 CrossRef CAS.
- J. Barthel, R. Buchner, P. N. Eberspächer, M. Münsterer, J. Stauber and B. Wurm, J. Mol. Liq., 1998, 78, 83–109 CrossRef CAS.
- R. Buchner, T. Chen and G. Hefter, J. Phys. Chem. B, 2004, 108, 2365–2375 CrossRef CAS.
- A. Stoppa, A. Nazet, R. Buchner, A. Thoman and M. Walther, J. Mol. Liq., 2015, 212, 963–968 CrossRef CAS.
- J. Barthel, H. Hetzenauer and R. Buchner, Ber. Bunsen-Ges., 1992, 96, 1424–1432 CrossRef CAS.
- R. Buchner, C. Hölzl, J. Stauber and J. Barthel, Phys. Chem. Chem. Phys., 2002, 4, 2169–2179 RSC.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 2000, 113, 2793–2805 CrossRef CAS.
- A. Kovalenko, in Three-dimensional RISM theory for molecular liquids and solid–liquid interfaces, ed. F. Hirata, Kluwer, Dordrecht, 2003, pp. 169–276 Search PubMed.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 1999, 110, 10095–10112 CrossRef CAS.
- D. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. Cheatham III, T. Darden, R. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, R. Luo, S. LeGrand, T. Luchko, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER 14, University of California, San Francisco, 2014 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- L. Lue and D. Blankschtein, J. Phys. Chem., 1992, 92, 8582–8594 CrossRef.
- T. Fukasawa, T. Sato, J. Watanabe, Y. Hama, W. Kunz and R. Buchner, Phys. Rev. Lett., 2005, 95, 197802 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Kiene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- Romano et al.70 reported an effective dipole moment of 10.29 D. This value was obtained from static permittivity measurements under the assumption of ideal behavior of the solvent. However, as discussed in this contribution and in line with ref. 21, the DRS-detected concentration of water is much smaller than its analytical concentration due to strong Pro hydration.
- J. Hunger, K.-J. Tielrooij, R. Buchner, M. Bonn and H. Bakker, J. Phys. Chem. B, 2012, 116, 4783–4795 CrossRef CAS PubMed.
- DRS cannot distinguish between Zib completely immobilized water dipoles (of moment μweff) and Zib′ = Zib/α2 H2O molecules which are restriced in their motion in such a way that the projection α × μweff (0 < α ≤ 1) of their dipole moment is blocked.
- Obviously, the finding of Zt < Zs and thus Zib < 0 for c(Pro) ≳ 3.5 M is unphysical. This is almost certainly due to a change of the effective dipole moment of bulk-like water at these high solute concentrations because of changing dipole–dipole correlations, i.e. a changing Kirkwood factor, for these H2O molecules45.
- S. Busch, C. D. Lorenz, J. Taylor, L. C. Pardo and S. E. McLain, J. Phys. Chem. B, 2014, 118, 14267–14277 CrossRef CAS PubMed.
- H. M. A. Rahman, G. Hefter and R. Buchner, J. Phys. Chem. B, 2013, 117, 2142–2152 CrossRef CAS PubMed.
- A. Eiberweiser and R. Buchner, J. Mol. Liq., 2012, 176, 52–59 CrossRef CAS.
- To reduce the scatter of the amplitudes, the relaxation times τ2 and τ3 were fixed to their values at c(NaCl) = 0 in the final evaluation step leading to the parameter values of Table 2.
- M. Sega, S. Kantorovich and A. Arnold, Phys. Chem. Chem. Phys., 2015, 17, 130–133 RSC.
- For consistency of the present discussion, the data for aqueous NaCl61 were reanalyzed with the approach of Sega et al.63 for kinetic depolarization, yielding slightly larger Zt [=6.06 − 0.453 × c(NaCl)] values for Na+.
- A. Bröhl, B. Albrecht, Y. Zhang, E. Maginn and R. Giernoth, J. Phys. Chem. B, 2017, 121, 2062–2072 CrossRef PubMed.
- T. Marino, N. Russo and M. Toscano, J. Phys. Chem. B, 2003, 107, 2588–2594 CrossRef CAS.
- Y. J. Alahmadi, A. Gholami and T. D. Fridgen, Phys. Chem. Chem. Phys., 2014, 16, 26855–26863 RSC.
- M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2012, 169, 1–7 CrossRef CAS.
- M. V. Fedotova and O. A. Dmitrieva, Amino Acids, 2015, 47, 1015–1023 CrossRef CAS PubMed.
- E. Romano, F. Suvire, M. E. Manzur, S. Wesler, R. D. Enriz and M. A. A. Molina, J. Mol. Liq., 2006, 126, 43–47 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details regarding data processing; tables with RISM coordination numbers; supplementary figures. See DOI: 10.1039/c7cp04335j |
| This journal is © the Owner Societies 2017 |