Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polarization transfer efficiency in PHIP experiments†
M.
Emondts
 a,
J. F. P.
Colell
a,
J. F. P.
Colell
 b,
B.
Blümich
b,
B.
Blümich
 a and
P. P. M.
Schleker
a and
P. P. M.
Schleker
 *acd
*acd
aRWTH Aachen University, Institut für Technische und Makromolekulare Chemie, Worringer Weg 1, 52074 Aachen, Germany. E-mail: philipp.schleker@cec.mpg.de
bDuke University, Department of Chemistry, Durham, North Carolina 27708, USA
cMax-Planck-Institut für Chemische Energiekonversion, Stiftstr. 34-36, 45470 Mülheim an der Ruhr, Germany
dInstitut für Energie und Klimaforschung (IEK-9), Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
First published on 1st August 2017
Abstract
Parahydrogen induced polarization (PHIP) is a hyperpolarization method for NMR signal enhancement with applications in spectroscopy and imaging. Although parahydrogen can be easily enriched up to nearly 95%, the polarization detected on the hydrogenated substrate is substantially lower, where numerous loss mechanisms between the start of the hydrogenation reaction and detection affect polarization levels. The quality of PHIP systems is commonly determined by stating either the polarization degree or the enhancement factor of the product at the time of detection. In this study, we present a method that allows the distinction of polarization loss due to both the catalytic cycle and T1 relaxation of the formed product prior to detection. We determine the influence of homogeneous catalysts and define a rigorous measure of the polarization transfer efficiency (PTE). Our results show that the PTE strongly depends on the concentration of all components and the chemical structure of the catalyst as well as on the magnetic field of detection.
Introduction
The biggest challenge in Nuclear Magnetic Resonance (NMR) originates from low sensitivity as a result of low thermal spin polarization, which can be overcome by hyperpolarization methods. Dynamic Nuclear Polarization (DNP)1,2 and Parahydrogen Induced Polarization (PHIP),3–7 which can be hydrogenative (ALTADENA, PASADENA)5–8 or non-hydrogenative (Signal Amplification By Reversible Exchange, SABRE3,4), increase the NMR signal by many orders of magnitude.In a hydrogenative PHIP experiment the spin order of parahydrogen (p-H2), which can easily be enriched to nearly 95%, corresponding to a hydrogen polarization of >0.9, is transferred to spins in a target molecule by a hydrogenation reaction in the presence of a catalyst. PHIP has become a valuable tool for the analysis of hydrogenation kinetics and reaction mechanisms9,10 and the application for molecular imaging11–13 is emerging.
Despite the high polarization level of the parahydrogen the polarization of the hydrogenated substrate is commonly substantially lower.14,15 The net PHIP efficiency, or absolute polarization of the product compared to the initial H2 polarization, is limited by the kinetics of the catalytic processes as well as by the experimental NMR settings. In order to optimize the polarization retained on a target molecule, the sources and mechanisms of polarization loss have to be identified and quantified.
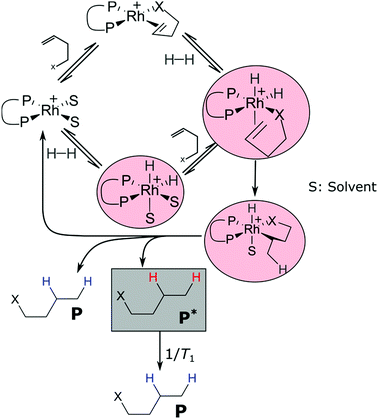
Let us consider a hydrogenation reaction with para enriched hydrogen in the presence of a homogeneous catalyst and in the absence of paramagnetic impurities (e.g. oxygen). Free parahydrogen is protected from polarization loss due to symmetry.16 In a catalytic hydrogenation the first step is the formation of a dihydride (or dihydrogen) transition metal complex as exemplified in Fig. 1.17,18 As soon as the parahydrogen molecule is bound to a catalyst it is no longer protected by symmetry. From this point on polarization is lost by different mechanisms.16,19–21 The hydrogenation reaction proceeds involving several, often undetectable, intermediates in the catalytic cycle.22–25 The product is formed with the effective hydrogenation rate constant khyd. If hyperpolarized (hp) product P* is formed, it is subject to T1 relaxation (Fig. 1) during the delay between product formation and detection. Therefore, the amount of total polarization loss depends on the relaxation rates and lifetimes of catalyst-bound hydrogen and substrate species as well as on the T1 relaxation of the hyperpolarized product before detection.
In the following we will differentiate between polarization loss occurring during the lifetime of catalytic intermediates (Fig. 1, red circles) and T1 relaxation of P* (Fig. 1, grey box). The fraction of the polarization that is transferred from p-H2 to the product, excluding T1 relaxation of P* (or polarization transfer to heteronuclei), quantifies the limit of polarization attainable on one particular type of nucleus in the ensemble of hydrogenated product molecules in a PHIP experiment and is thus a sharply defined measure of the polarization transfer efficiency (PTE). The shortcomings of the polarization degree and the enhancement factor are that neither the kinetics nor T1 relaxation effects are considered, whereas the PTE offers a rigorous measure of the quality of PHIP systems. The advantage over the commonly used enhancement factor and polarization degrees at the time of detection is that polarization loss that can be attributed to the catalytic cycle and loss that originates from T1 relaxation of P* can be distinguished. This distinction allows optimization procedures for the chemical system as well as for the experimental procedure in order to obtain maximal polarization.
In the following we will introduce an easy method for the determination of the PTE. In the Experimental section we investigate the influence of the catalyst concentration and choice of catalysts as well as the effect of the magnetic field under PASADENA8 conditions on the PTE.
Methods
As introduced in the previous section, the PTE is the amount of polarization transferred from para enriched H2 to the product protons. We determine the PTE by comparing the experimental amount of substance of hyperpolarized product molecules P* (nP*,exp) at the time of detection to the idealized case without polarization loss P* (nP*,i), where nP*,i includes correction for longitudinal relaxation of P* between product formation and detection (Fig. 1). Hence, the determination of nP*,i requires knowledge of the T1 constant of P* and of the chemical kinetics to determine the molar amount of hydrogenated substrates at the time of detection. If kinetic studies are performed at a high field under PASADENA8 conditions, the polarization transfer from the hp protons to naturally abundant 13C is negligible, polarization transfer by isotropic mixing is inefficient26 and nP*,exp is determined via line shape analysis of the PASADENA spectrum. The determination of the PTE is a four-step process:(1) Determination of hydrogenation kinetics and T1
(2) Determination of the number of P* for the ideal case (nP*,i) where polarization loss occurs solely due to T1 relaxation of P* (Fig. 1)
(3) Determination of the molar amount of the experimentally observed P* (nP*,exp)
(4) Determination of the PTE by comparing nP*,exp (step 3) to nP*,i (step 2)
Step 1
If the chemical reaction is carried out with a large excess of substrate the kinetics are described by a first order process. By working in a closed vessel the hydrogen amount is limited. The kinetics of the hydrogenation reaction is recorded by applying consecutive 45 degree pulses separated by a time delay Δt (Fig. 2a).9 The time delay Δt is chosen large enough to allow the spins to realign before the next pulse application. The total molar amount of product ntot is the sum of hp molecules P* and thermally polarized (tp) molecules P (ntot(t) = nP*(t) + nP(t)). For a first order process we have: | (1) |
| Δn(t) = ntot(t) − ntot(t − Δt). | (2) |
Step 2
Let us consider an ideal case, where no polarization is lost during the catalytic cycle (PTE = 1) but only due to T1 relaxation between hydrogenation and acquisition.The number of P* at the time of detection will be defined by the initial fraction of hp hydrogen and the reaction rate khyd (as polarization supply rate) as well as by the relaxation rate T1 (as a polarization loss mechanism). The initial fraction x0hp of hp hydrogen can be calculated with the para enrichment factor xpara (see the ESI† for the derivation).
 | (3) |
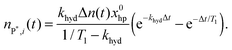 | (4) |
Eqn (4) is equivalent to the kinetics of a first order consecutive reaction;9,27 the hydrogenation reaction with the effective rate constant khyd is followed by T1 relaxation with the rate constant 1/T1 (Fig. 1). nP*,i can be calculated, when khyd, T1 and Δt are known.
Step 3
The determination of the experimentally observed amount of hyperpolarized product molecules nP*,exp includes the analysis of the NMR signal. The NMR signal intensity stp originating from tp molecules is given by their spin density (proportional to the amount of substances ntp) and the magnetic field strength defining their thermal polarization Ptp (stp ∝ nP(t)Ptp). The same applies for the hyperpolarized species (shp ∝ nP*(t)Php). The ratio of the signal intensities shp/stp is equal to their respective signal fractions xs,hp/xs,tp and is given by: | (5) |
In order to determine the individual fractions of hp and tp signals (xs,hp and xs,tp), the quartet of the product peak arising from the methylene-group is analyzed (Fig. 2b). The relative peak intensities I are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the thermally polarized case and 1
1 for the thermally polarized case and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1 for the hyperpolarized one. As exemplified in Fig. 2b, the total NMR signal is a superposition of thermal and hyperpolarized signals. The ratio r12 = r34 of the peak intensities in the quartet allows the calculation of the fraction of hyperpolarized signal xs,hp and thermally polarized signal xs,tp:
−1 for the hyperpolarized one. As exemplified in Fig. 2b, the total NMR signal is a superposition of thermal and hyperpolarized signals. The ratio r12 = r34 of the peak intensities in the quartet allows the calculation of the fraction of hyperpolarized signal xs,hp and thermally polarized signal xs,tp:
 | (6) |
 | (7) |
Step 4
The polarization transfer efficiency (PTE) is simply the ratio of nP*,exp (eqn (7)) to nP*,i (eqn (4)),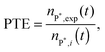 | (8) |
Note that the determination of the PTE requires only the determination of the effective hydrogenation rate khyd and one T1 measurement. The time dependent increase of a tp product peak (or the decrease of the educt peak) allows the determination of the reaction constant khyd. Once T1 and khyd are known, nP*,i can be calculated according to eqn (4). This number is then compared to the experimentally observed value nP*,exp, which can be determined by line shape analysis of the antiphase quartet.
Experimental
In this study the precatalysts [Rh(COD)BINAP]BF4 (BINAP: (2,2′-bis(diphenylphosphino)-1,1′-binaphthyl), COD: cyclooctadiene) and [Rh(COD)DPPB]BF4 (DPPB: (1,4-bis(diphenylphosphino)butane)) were used to investigate the PTE. The complexes were synthesized using published procedures.28 The solvent was d4-MeOH, the substrate butyl acrylate (c = 0.5 M). All samples were prepared in Wilmad medium pressure NMR tubes under inert conditions. The NMR tube was pressurized with 2 bar parahydrogen. After pressurizing, the samples were shaken for five seconds and transferred to the magnetic detection field (Bruker AV III 300, 7.05 T, or Bruker AV II 600, 14.09 T, spectrometer). The kinetics of the hydrogenation reaction (Step 1) was recorded by applying consecutive 45° pulses in time intervals Δt (Fig. 2a). All experiments were conducted at 25 °C.Results
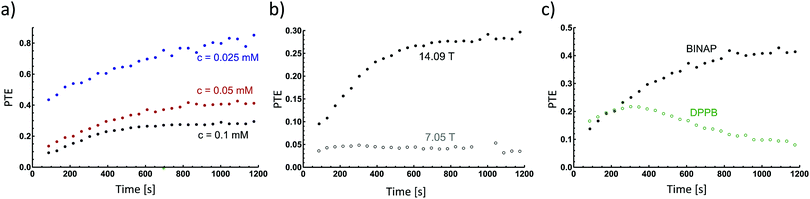
In the experimental study, we investigated the influence of the catalyst concentration, the magnetic field and the chemical structure of the catalyst on the PTE. For each experiment the PTE was determined for the time course of the hydrogenation as described in the Methods section. The kinetic parameters as well as the detailed processing procedure are presented in the ESI.†We recorded the kinetics of hydrogenation reactions at different concentrations of [Rh(COD)BINAP]BF4 and determined the PTE as a function of time (Fig. 3a). The initial efficiency is the highest for the lowest catalyst concentration with about 40% at the beginning, while the other concentrations gain less than 18% at this point. This series shows a tendency of increasing efficiency with decreasing catalyst concentration. Furthermore, the PTE rises with time for all solutions, which can be connected to dropping H2 pressure. Depending on the concentration of the alkene and H2, the former or latter is coordinated longer to the catalytic centre.17,29 The coordination of p-H2 as classical or non-classical hydride opens up the possibility for a relaxation pathway. The dihydrides, in particular the non-classical hydrides, have short T1 relaxation times. T1 is on the order of milliseconds and tends to be longer in higher magnetic fields.23
Hence, changing the magnetic field of detection allows gaining more insight into polarization loss mechanisms. In order to investigate the influence of T1 relaxation of hydride intermediates on the PTE samples of identical composition were analysed in two magnetic fields (7.05 T and 14.09 T). When performing the hydrogenation reaction at 14.09 T the PTE increases from 0.08 to nearly 0.3 as the reaction proceeds (Fig. 3b). At 7.05 T the PTE increases only slightly from 0.04 to 0.06. This clearly shows that T1 relaxation of the intermediates prior to chemical reaction constitutes a highly relevant loss pathway.
To elucidate upon the effect of the catalyst structure on the PTE, we changed the ligand from BINAP to DPPB. The concentration of DPPB was adjusted for the effective hydrogenation rates khyd to match (c([Rh(COD)BINAP]BF4) = 0.05 mM, c([Rh(COD)DPPB]BF4) = 0.01 mM). If we compare the systems the initial PTE is around 0.15 for both (Fig. 3c), showing that the ligand has a significant impact, as one would expect the lower concentrated and faster hydrogenating catalyst to have a higher PTE. Interestingly, the PTE of DPPB increases at first, but declines after approximately 350 s, whereas the PTE of BINAP asymptotically increases from 0.12 to 0.4. The decrease of the PTE over time is attributed to para–ortho (p/o) hydrogen conversion due to its reversible coordination.16 This is also proven by higher o-H2 NMR signal intensity with DPPB (see Fig. S5, ESI†).
Conclusions
In this work we introduced the PTE as a parameter that quantifies the maximal fraction of polarization transferred from p-H2 to the product's protons regardless of subsequent T1 relaxation of the hyperpolarized product prior to detection. We proposed a simple method based on kinetic investigations of the hydrogenation reaction that enables the quantification of the PTE in PHIP experiments. The experimental results show that the PTE is determined by the concentration of all components, the chemical structure of the catalyst as well as the magnetic field.The PTE is a suitable parameter for the characterization of PHIP systems and can not only be used for the investigation of homogeneous, but also for heterogeneous systems. This characterization method is highly important for the fundamental understanding of the established PHIP systems and may also elucidate guidelines for the development of new efficient homogenous and heterogeneous PHIP catalysts and the transfer from batch to continuous flow. We believe this is particularly important in the development for biomedical applications. Future work will involve the investigation of catalysts that have been immobilized in order to analyse the influence of the supporting material on the PTE.
Acknowledgements
The authors would like to thank Jürgen Klankermayer and Ines Bachmann-Remy for support and technical assistance as well as Danila Barskiy for stimulating discussions. We thank S. Lehmkuhl for the provision of the catalyst. This work has been supported by Deutsche Forschungsgemeinschaft (DFG-BL231/47-1). Open Access funding provided by the Max Planck Society.References
- M. Abraham, M. A. H. McCausland and F. N. H. Robinson, Phys. Rev. Lett., 1959, 2, 449–451 CrossRef CAS.
- W. A. Barker, Rev. Mod. Phys., 1962, 34, 173–185 CrossRef CAS.
- R. W. Adams, J. A. Aguilar, K. D. Atkinson, M. J. Cowley, P. I. P. Elliott, S. B. Duckett, G. G. R. Green, I. G. Khazal, J. Lopez-Serrano and D. C. Williamson, Science, 2009, 323, 1708–1711 CrossRef CAS PubMed.
- R. W. Adams, S. B. Duckett, R. A. Green, D. C. Williamson and G. G. R. Green, J. Chem. Phys., 2009, 131, 194505 CrossRef PubMed.
- T. C. Eisenschmid, R. U. Kirss, P. P. Deutsch, S. I. Hommeltoft, R. Eisenberg, J. Bargon, R. G. Lawler and A. L. Balch, J. Am. Chem. Soc., 1987, 109, 8089–8091 CrossRef CAS.
- J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315 CrossRef.
- C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648 CrossRef CAS PubMed.
- C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542 CrossRef CAS.
- P. Hubler, R. Giernoth, G. Kummerle and J. Bargon, J. Am. Chem. Soc., 1999, 121, 5311–5318 CrossRef.
- M. S. Chinn and R. Eisenberg, J. Am. Chem. Soc., 1992, 114, 1908–1909 CrossRef CAS.
- P. Nikolaou, B. M. Goodson and E. Y. Chekmenev, Chem. – Eur. J., 2015, 21, 3156–3166 CrossRef CAS PubMed.
- K. Golman, O. Axelsson, H. Jóhannesson, S. Månsson, C. Olofsson and J. S. Petersson, Magn. Reson. Med., 2001, 46, 1–5 CrossRef CAS PubMed.
- P. Bhattacharya, E. Y. Chekmenev, W. H. Perman, K. C. Harris, A. P. Lin, V. A. Norton, C. T. Tan, B. D. Ross and D. P. Weitekamp, J. Magn. Reson., 2007, 186, 150–155 CrossRef CAS PubMed.
- N. N. Jarenwattananon, S. Glöggler, T. Otto, A. Melkonian, W. Morris, S. R. Burt, O. M. Yaghi and L.-S. Bouchard, Nature, 2013, 502, 537–540 CrossRef CAS PubMed.
- R. V. Shchepin, A. M. Coffey, K. W. Waddell and E. Y. Chekmenev, J. Phys. Chem. Lett., 2012, 3, 3281–3285 CrossRef CAS PubMed.
- J. M. Brown, L. R. Canning, A. J. Downs and A. M. Forster, J. Organomet. Chem., 1983, 255, 103–111 CrossRef CAS.
- I. D. Gridnev and T. Imamoto, Acc. Chem. Res., 2004, 37, 633–644 CrossRef CAS PubMed.
- H. Heinrich, J. Bargon, R. Giernoth and J. M. Brown, Chem. Commun., 2001, 1296–1297 RSC.
- G. Buntkowsky, B. Walaszek, A. Adamczyk, Y. Xu, H. H. Limbach and B. Chaudret, Phys. Chem. Chem. Phys., 2006, 8, 1929–1935 RSC.
- J. Matthes, T. Pery, S. Gründemann, G. Buntkowsky, S. Sabo-Etienne, B. Chaudret and H.-H. Limbach, J. Am. Chem. Soc., 2004, 126, 8366–8367 CrossRef CAS PubMed.
- C. Terenzi, S. Bouguet-Bonnet and D. Canet, J. Phys. Chem. Lett., 2015, 6, 1611–1615 CrossRef CAS PubMed.
- I. D. Gridnev, N. Higashi, K. Asakura and T. Imamoto, J. Am. Chem. Soc., 2000, 122, 7183–7194 CrossRef CAS.
- P. G. Jessop and R. H. Morris, Coord. Chem. Rev., 1992, 121, 155–284 CrossRef CAS.
- J. Halpern, Inorg. Chim. Acta, 1981, 50, 11–19 CrossRef CAS.
- J. Halpern, Science, 1982, 217, 401–407 CAS.
- S. Aime, R. Gobetto, F. Reineri and D. Canet, J. Chem. Phys., 2003, 119, 8890–8896 CrossRef CAS.
- C. T. Jones, Biochem. J., 1970, 118, 810–812 CrossRef CAS PubMed.
- A. Miyashita, A. Yasuda, H. Takaya, K. Toriumi, T. Ito, T. Souchi and R. Noyori, J. Am. Chem. Soc., 1980, 102, 7932–7934 CrossRef CAS.
- O. G. Salnikov, D. A. Barskiy, A. M. Coffey, K. V. Kovtunov, I. V. Koptyug and E. Y. Chekmenev, ChemPhysChem, 2016, 17, 3395–3398 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04296e |
| This journal is © the Owner Societies 2017 |