Open Access Article
Open Access ArticleHelium-3 gas self-diffusion in a nematically ordered aerogel at low temperatures: enhanced role of adsorption
Vyacheslav
Kuzmin
 *a,
Kajum
Safiullin
*a,
Kajum
Safiullin
 *ab,
Andrey
Stanislavovas
a and
Murat
Tagirov
*ab,
Andrey
Stanislavovas
a and
Murat
Tagirov
 ab
ab
aKazan Federal University, Kazan, 420008, Russian Federation. E-mail: slava625@yandex.ru; kajum@inbox.ru; Fax: +7 843 233 7355; Tel: +7 843 233 7306
bInstitute of Perspective Research, Academy of Sciences of the Republic of Tatarstan, Kazan 420111, Russia
First published on 7th August 2017
Abstract
We performed 3He gas diffusion measurements for the first time in a highly porous ordered Al2O3 aerogel sample at a temperature of 4.2 K using a nuclear magnetic resonance field gradient technique. A strong influence of 3He adsorption in the aerogel on self-diffusion is observed. The classical consideration of adsorptive gas diffusion in mesopores leads to anomalously high tortuosity factors. The application of a more sophisticated model than the simple combination of empirical two-phase diffusion and the Knudsen gas diffusion models is required to explain our results. Anisotropic properties of the aerogel are not reflected in the observed gas diffusion even at low gas densities where the anisotropic Knudsen regime of diffusion is expected. The observed gas densification indicates the influence of the aerogel attractive potential on the molecular dynamics, which probably explains the reduced diffusion process. Perhaps this behavior is common for any adsorptive gases in nanopores.
1 Introduction
Diffusion study is a widely used tool for the characterization of porous media.1 The understanding of fluid dynamics in nano and mesoporous materials is required for the correct interpretation of diffusion data. Particularly, gas adsorption/desorption processes play a significant role in gas dynamics.Aerogels with open-space pores present unique model systems for diffusion studies due to a rich variety of available structures. Recently the interest to study superfluids in aerogels also arose due to the observation of polar superfluid phases in nematically ordered aerogels.2,3 The ballistic mean-free path (mfp) in an aerogel λaero is an important parameter for theoretical models of 3He superfluidity and can be determined by diffusion experiments, for instance, via magnetic resonance with pulse gradients. At very low temperatures (<10 mK) the density of quasiparticles in liquid is so small that its mfp is defined by quasiparticle–aerogel collisions4–6 and coincides with the ballistic mean-free path in the aerogel. Under these conditions the self-diffusion of quasiparticles can be considered as Knudsen diffusion. Recently Dmitriev et al.7 have reported the observation of strongly anisotropic Knudsen diffusion of liquid 3He at 1–10 mK in a new type of aerogel (Nafen-90) with almost parallel strands.
Information on the mfp in aerogels may also be obtained from room temperature diffusion experiments with hyperpolarized gases,8 such as 3He or 129Xe. Diffusion measurements with Boltzmann-polarized gases at room temperature are also feasible but require a high gas density or the application of a high magnetic field for a sufficient signal-to-noise ratio. The high density is available, for instance, for strongly adsorbing gases for which a significant fraction of the atoms are in an adsorbed layer with reduced mobility. However in that case the adsorption should be taken into account.9,10 Lee et al.11 reported diffusion experiments of methanol gas significantly adsorbed in slightly anisotropic aerogel samples at room temperature with the aim to characterize the mfp for subsequent studies of superfluid 3He in this aerogel. An empirical model based on “fast exchange”4 that accounts for the adsorbed layer was applied to determine the gas diffusion in the aerogel, which was assumed to be in the Knudsen diffusion regime. On the other hand, Mueller et al.10 applied a similar model to CO2 diffusion in aerogels with additional tortuoisity factors for Knudsen and free gas diffusion. Although such experiments at room temperatures are more feasible in most NMR laboratories, some specific features can make them more problematic to interpret.
The effect of attractive forces from aerogel strands can lead to the formation of adsorbed layers and to a modification of the gas molecule trajectories and therefore to a diffusion suppression of low density gas in nanoscale diameter pores.12 Alternatively, liquid 3He (with surface pre-plating with 4He) at very low temperatures and room temperature hyperpolarized 3He diffusion can be accurately described by the Knudsen model which gives direct information on the mfp. This is due to the absence of the wall attractive potential on quasiparticles in liquid 3He or its small influence in 3He gas at room temperature. Thus the diffusion of free gas in the presence of adsorption cannot be considered as simple Knudsen diffusion even with a low fraction for the adsorbed layer.
A more advanced model for the transport of gases at low density in simple pore geometries named the “oscillator model” was built by Bhatia et al.,12 and considers the atom oscillation movements between walls in the fluid–solid attractive potential of the pore and shows excellent agreement with molecular dynamics simulations. It was shown by the authors of this study that the Knudsen model can significantly overpredict diffusion in the nanoscale diameter pore even at high temperatures.13,14 The “oscillator model” is applicable in the case of negligible particle–particle interaction, which is usual for low gas densities and Henry's adsorption regime, whereas diffusion of high density adsorbing gases still remains poorly studied.
In this article we report low temperature 3He strongly adsorbed gas diffusion experiments in a broad range of gas pressures (and densities) in nematically ordered aerogel (Nafen-90) in which the new superfluid 3He phase was observed.3,7 The aims of our study are to examine empirical diffusion models likewise applied by Lee et al.11 and Mueller et al.10 at various conditions and to assess the ordered aerogel structure. This is the first report on low temperature 3He gas diffusion measurements in nanostructures to our knowledge.
2 Experimental
2.1 Aerogel sample and helium-3 management
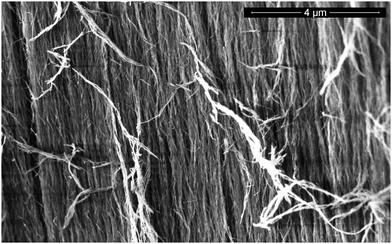
The nematically ordered Nafen aerogel with 90 mg cm−3 density produced by ANF technology was used as a sample. It consists of relatively long (a few centimeters) parallel γ-Al2O3 nano fibers of 8 nm diameter; detailed information on its properties was presented by Asadchikov et al.15 The porosity of this sample is estimated to be 97.8%. The SEM image of the sample (Fig. 1) was obtained by Mikhail Presnyakov on a Titan 80-300 S/TEM (FEI, USA) at Probe and Electron microscopy RC “NANOPROBE”, National Research Center “Kurchatov Institute”, Moscow. The sample length in our experiments is 2.5 cm. It was tightly inserted into a Pyrex glass cell (5 mm i.d.). The sample fibers were oriented along the experimental cell (x) and perpendicular to the external magnetic field (z) as shown in Fig. 2. The experimental cell was sealed to the 3He capillary. The sample and the cell were flushed several times with helium gas and pumped out before experiments. The 4He concentration in the 3He used was less than 0.01%. The gas pressure was measured in a dead volume at room temperature by a Pfeiffer Vacuum RPT-200 Piezo/Pirani pressure gauge with a specially measured calibration curve for 3He gas. The estimated thermomolecular pressure difference between the room temperature dead volume and the low temperature cell volume in our experiments was negligible. | ||
| Fig. 2 The schematic illustration of the relative directions of magnetic field, applied gradients and aerogel fibers in our experiments. | ||
2.2 NMR apparatus and gradient coil
A home-built pulsed NMR spectrometer,16 along with a resistive magnet (up to 0.8 T) and a glass helium cryostat, was used in the NMR diffusion experiments. A BKPrecision XLN-8018 power supply was used to drive the resistive magnet. A single layer solenoidal NMR detection coil was wound on the cell surface with a 0.25 mm copper wire. The resonance circuit was tuned to a frequency of 16.4 MHz and matched to 50 Ω by ceramic capacitors located outside of the helium cryostat, and had a quality factor of Q = 91. A low-noise fast response Miteq AU-1549 rf preamplifier was used for NMR detection. Typical signal-to-noise ratio values in our experiments were in the range of 15 to 140.Anti-Helmholtz gradient coils were wound with a 0.45 mm copper wire on the cylindrical polyester/epoxy shell (5.2 cm i.d., 5.4 cm o.d.) and consisted of 87 turns for every 5 layers. The distance between the coils was set to 5.3 cm in order to fit outside of the glass cryostat used (5.2 cm o.d.). The design of the coil shell allowed us to apply gradients in parallel (x axis) and perpendicular (y axis) directions to the fibers of the sample while the direction of the field B0 was along the z axis (Fig. 2). The pair of coils (1.1 mT cm−1 A−1) produced a constant 90%-homogeneity gradient of magnetic field ∂B0/∂x or ∂B0/∂y over the sample length. The magnetic field gradients and inhomogeneity were deduced from additional H2O NMR experiments at room temperature. The gradient coils were placed on the outside of the glass-made cryostat and were driven by two Aktakom APS-7305 power supplies connected in series. The maximum available current for this configuration is 3 A which induces a magnetic field gradient stronger than the local B0 residual field inhomogeneity by two orders of magnitude. The gradient current was triggered by a combination of Goodsky RW-SH-103D relays which were controlled via TTL pulse during a rf pulse sequence in the NMR experiments. The gradient was turned on for 1 s prior to any rf pulse to avoid the influence of eddy currents generated in the metal shield of the NMR probe on the detected signal.
2.3 NMR diffusion measurements
A standard Hahn echo sequence (4.8 μs–τ–9.6 μs) was used to measure the 3He nuclei transverse magnetization relaxation time T2 in the self-diffusion measurements. Spin echo amplitude decays were obtained at 2.2 mT cm−1 and 3.3 mT cm−1 magnetic field gradient values for two directions: parallel (x) and perpendicular (y) to the sample fibers, but always perpendicular to the external magnetic field (z). The obtained spin echo decay curves were fitted by the following function:17S(2τ) = S0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−2τ/T2)exp(−A(2τ)3), exp(−2τ/T2)exp(−A(2τ)3), | (1) |
| A = γ2DG2/12. | (2) |
3 Results
Fig. 3 (circle symbols) shows the 3He amount in the cell N0 as computed using the measured NMR signal amplitudes versus pressure P in the pure 3He experiments. The signal amplitudes were measured using the spin echo technique with corresponding delays between the π and π/2 pulses of τ = 100 μs, much shorter than T2 (few milliseconds). It is known that 3He forms a monolayer film on the substrate surface at a temperature of 4.2 K, and that the adsorbed 3He amount is almost independent of pressure above 50 mbar and varies within 20% above 1 mbar.19–21 Therefore it was assumed that at high enough pressures the amount of adsorbed 3He is almost constant (after completion of the monolayer) and so the signal amplitude is linear to the amount of 3He in the gas phase. The linear fit gives the slope k which corresponds to the dependence Ngas(P) = kP and capacity of the adsorbed layer (Nads) which corresponds to the extrapolation of a linear fit to zero pressure. Using that, one can estimate the ratio of Ngas to the total 3He amount N0 at any pressure: | (3) |
 | ||
| Fig. 4 Typical 3He spin echo amplitude decay curves with (G = 2.2 mT cm−1 and 3.3 mT cm−1) and without an applied magnetic field gradient obtained in pure 3He experiments at 770 mbar gas pressure and at 4.2 K. The measured 3He transverse magnetization relaxation time T2 = 17.56 ± 0.28 ms is much longer than the probed range of 2τ. Solid lines represent data fits using eqn (1). | ||
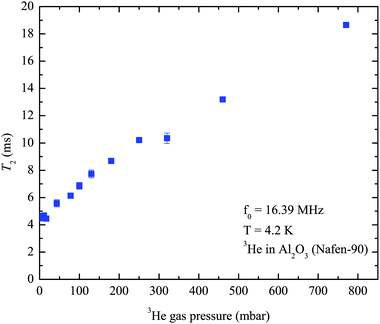 | ||
| Fig. 5 3He transverse relaxation times T2 measured at various 3He gas pressures at 4.2 K in the pure 3He experiment. | ||
The obtained T2 values were used to fit the spin echo amplitude decay curves measured with an applied gradient using eqn (1), with the variable A parameter. Typical measured echo decay curves are presented in Fig. 4 for two gradient values. Application of 2.2 and 3.3 mT cm−1 gradients significantly decreases the echo amplitude decay time. The diffusion coefficient D was then estimated using eqn (2).
The measured 3He diffusion coefficient D dependencies on the 3He gas pressure P at 4.2 K temperature for two different gradient values are shown in Fig. 6. The observed short T2 values allowed us to perform diffusion experiments. The obtained 3He diffusion coefficient D values do not vary with the applied gradient. This is additional evidence that gradient coils create higher magnetic field gradients than that of the resistive magnet in our experiments, therefore the influence of residual gradients on the measured D values is negligible and the obtained values are correct. The measured diffusion coefficients D differ by two orders of magnitude from the one of a free gas at low pressures (see Fig. 6). For the given diffusion coefficients and the measurement durations used the probed range of diffusion lengths ( ) in our experiments varies from 14 μm to 28 μm.
) in our experiments varies from 14 μm to 28 μm.
 | ||
| Fig. 6 Pressure dependence of measured 3He diffusion coefficients D obtained in pure 3He (G = 2.2 mT cm−1 and 3.3 mT cm−1) and in 3He–4He mixture (G = 2.2 mT cm−1 and 3.3 mT cm−1) in Al2O3 aerogel at 4.2 K. The solid line is the expected diffusion (eqn (4)) for 3He gas with a density determined from the linear fit in Fig. 3. | ||
The measured pressure dependence of 3He diffusion is not typical. The anomalous drop in the diffusion coefficient at low pressures is due to the influence of the adsorptive effect of the aerogel whereas at high pressures the measured diffusion coefficient asymptotically converges to the gas diffusion computed for the estimated density. The expected free gas diffusion in the aerogel at a given density was found from the experimentally determined dependence D(ρ) at 4.2 K by Luszczynski24 for a free gas:
| Dρ = 17.5 × 10−6 g s−1 cm−1. | (4) |
Additional experiments with a 4He aerogel coating were performed in order to emphasise the role of the adsorbed 3He layer in apparent diffusion at low pressures (see Fig. 3 and 6). We also observe the increase of the 3He density in the gas phase in the aerogel (by a factor of 1.87 ± 0.03 higher than that of free 3He gas at 4.2 K), but the adsorbed amount of 3He is much smaller compared to that of the pure 3He data (Fig. 3). Precoating the aerogel surface with one layer of 4He significantly increases the diffusion of 3He at low pressures, but at high pressures 3He diffusion converges with the diffusion observed in the pure 3He experiment (Fig. 6).
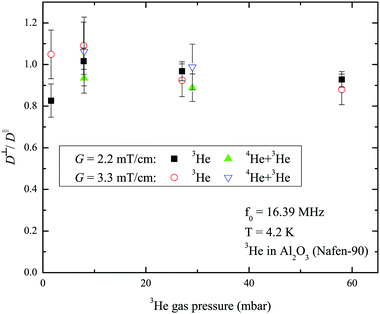
Experiments to probe the diffusion anisotropy were performed for pure 3He and the 3He–4He mixture as well. The ratio of the 3He diffusion coefficients D measured at gradients parallel (D‖) and perpendicular (D⊥) to the aerogel fibers is presented in Fig. 7. Diffusion anisotropy is not observed in these experiments even at low pressures at which the Knudsen regime of diffusion is expected.
4 Discussion
The measured apparent diffusion coefficient of 3He in the aerogel is significantly suppressed by the immobile adsorbed layer of 3He (the estimated diffusion coefficient in the adsorbed layer lies between 10−9 and 10−4 cm2 s−1 depending on the layer coverage25,26). This is demonstrated in Fig. 6, where the diffusion coefficient anomalously drops at low pressures in opposition to that expected for free gas diffusion. It is also confirmed in experiments with the 3He–4He mixture: the covering of the aerogel surface with an approximate monolayer of 4He significantly increases the gaseous 3He diffusion coefficient at low pressures as can be seen from Fig. 6. This occurs due to a preferential adsorption of 4He on the aerogel surface and therefore a high fraction of gas phase 3He in the total 3He amount. Nevertheless the 3He diffusion is much slower than that expected for the bulk 3He free gas which can partly be explained by the presence of a small 3He fraction in the adsorbed layer on the aerogel surface. At high pressures the effect of the 4He adsorbed layer on the 3He diffusion is not significant and therefore D(P) coincides with that of pure 3He in the aerogel. Similarly to our result, Lee et al.11 reported the observation of the “anomalous” diffusion of methanol in aerogels due to the effect of adsorbed layers in the aerogels at room temperatures. Following ref. 9 and 11, the apparent diffusion in this aerogel is just weighted diffusion between that in the adsorbed layer and that in the gas phase. As diffusion in the gas phase is much faster than in the adsorbed layer the apparent diffusion in the aerogel is assumed to be governed by a “fast exchange” process:4 | (5) |
Note that the surface diffusion term which plays an important role1,30 for some gases at high temperatures will be ignored further as being totally negligible even at very low gas fractions compared to the gas diffusion term in our experiment. This is based on the fact that the diffusion coefficient in the 3He surface film is of orders 10−9–10−8 cm2 s−1 for high monolayer coverages at the experimental temperature.26,31,32 According to eqn (5), one can estimate diffusion in the gas phase inside the aerogel (Daerogas), taking into account its fraction. This was done for the apparent diffusion data presented in Fig. 6 using adsorption data from Fig. 3 and applying eqn (3). A similar procedure was applied to the results of the 3He–4He experiments. The obtained results are shown in Fig. 8 where the expected diffusion for free gas is also plotted with density determined from the data of the measured isotherms (Fig. 3) and a known cell volume. It can be seen that in the whole range of P, the computed diffusion is significantly lower than expected especially at low pressures at which the fraction of adsorbed atoms is large. The computed diffusion Daerogas values for the pure 3He experiments and 3He–4He mixtures are close to each other. This validates the correctness of applying the fast-exchange model (eqn (5)) in computing Daerogas. This is also clear and strong evidence that the observed effect is almost independent of the fraction Nads of adsorbed 3He as 4He is known to preferentially occupy the sample surface compared to 3He. The presence of 4He significantly decreases the amount of adsorbed 3He by a factor of ca. 5. Therefore the observed effect of slow diffusion Daerogas cannot be explained by the influence of surface diffusion.
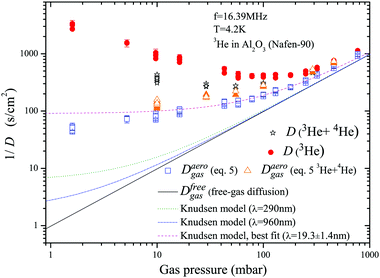 | ||
| Fig. 8 Inverse diffusion gas pressure dependencies and computed Daerogas using data from Fig. 3 and applying eqn (5). The dashed lines show expected free gas diffusion (gas densification is accounted) and the Knudsen gas diffusion in the aerogel with λaero = 290 nm and 960 nm, which correspond to two principal values of lambda obtained for this aerogel7 and λaero = 19.3 ± 1.4 nm which fits the experimental data. | ||
On the other hand, the estimated gas density in the aerogel using eqn (3) and data from Fig. 3 is somewhat 2.03 ± 0.03 times higher than computed for the ideal gas at any given pressure. Reliability of the estimated density by NMR calibration is confirmed by the expected diffusion (for a given density) approaching the experimental diffusion at high pressures (Fig. 6). This occurs when the adsorbed layer fraction becomes negligible, whereas the estimated diffusion of the ideal bulk gas at high pressures is about 3 times higher than measured (not presented). Mueller et al.10 also observed adsorbate densification of CO2 by a factor of ≈2 in an aerogel. They refer this effect to the adsorption of CO2 in micropores. In the case of helium at low temperatures it is known that adsorption in micropores is completed at relatively low pressures of a few mbars.33,34 At higher pressures the excess amount of helium contributes only to the gas phase. Thus the possible source of the observed densification does not involve an additional increase in the adsorbed layer density in our case. The reason for such gas compression could be the modification of gas properties inside the aerogel because the aerogel wall adsorption potential spreads far from the first and the second 3He adsorbed layers on the aerogel surface. Because of that, one can expect a nonuniform gas density depending on the distance from the aerogel strands. Such an effect of gas densification was also found, for instance, in simulations of nitrogen filling nanotubes with diameters of 0.8–6.3 nm at room temperature.35
Another source of reduced apparent diffusion in the aerogel is the 3He atom collisions with the aerogel strands. This is known as the Knudsen diffusion which appears when the mfp in the gas phase, due to atom–atom collisions, is longer or of the order of the geometrical ballistic mfp in an aerogel (λaero). In that case the diffusion coefficient in the gas phase in an aerogel is usually computed as:9–11
 | (6) |
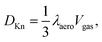 | (7) |
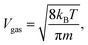 | (8) |
Our diffusion measurements were performed in the gaseous phase far from the Knudsen regime (except for very low pressures) because of sufficiently low temperatures and high gas densities, for which the mfp in the gas phase is much shorter than the expected characteristic length in this aerogel. Dmitriev et al.7 found two principal λaero values for that aerogel: λ⊥aero = 290 nm and λ‖aero = 980 nm. Using these parameters we have plotted the expected 1/Daerogas values in Fig. 8. As it can be seen these plotted curves lie significantly lower than the experimental ones. It was suggested by Tastevin and Nacher8 that in order to explain diffusion data in an aerogel it is necessary to introduce the broad spectrum of λaero which lies within the range of 5–1000 nm. To explain our diffusion-pressure dependence using the Knudsen regime we must introduce very short λaero of the order of 20 nm which seems to be unreasonable taking into account the high porosity of our aerogel (Fig. 8).
Mueller et al.10 suggested using a modified model based on eqn (6) with introduced tortuosity factors for Knudsen diffusion ηK and for free gas in an aerogel ηg:
 | (9) |
In addition, diffusion measurements with parallel and perpendicular gradient orientations to the aerogel fibers show no difference (Fig. 7) even at very low pressures where diffusion is expected to be strongly anisotropic in the Knudsen regime due to anisotropy of the aerogel. Thus we must conclude that the correctness of the simple models application used by Lee et al.11 and Mueller et al.10 is doubtful. The observed diffusion of 3He gas in the aerogel is significantly more suppressed by adsorption than expected. In addition, the Knudsen diffusion seems to be an inppropriate model to describe the diffusion of adsorptive gases. Similar problems of the straightforward application of the Knudsen model are discussed by Bhatia and Nicholson.14
Note that we were able to carefully test the model9,11 for a very broad range of Ngas/N0 ratios (0.01–0.88) focusing on the adsorbed layer effect both far from the Knudsen regime at high pressures and at the Knudsen regime at low pressures, whereas Lee et al. are in the limit of a low gas fraction. The experimental conditions used are also different from those used in the studies of P.-J. Nacher and G. Tastevin8 who measured hyperpolarized gas diffusion in various silica isotropic aerogels for a broad range of pressures and at room temperature with a negligible adsorbed layer effect due to high temperature. Coming back to Lee's article we should say that the described analysis technique11 is very critical to the determination of the gas and the adsorbed layer densities. The described λ anisotropy is highly probable to appear due to the methanol density uncertainty in experiments and is not connected with the properties of the aerogel geometry. The careful absolute gas density determination must be applied in order to exclude an additional free fit parameter of their fitting function. For instance, it seems to be unreasonable that their difference (D‖ − D⊥) changes sign depending on the pressure if one assumes single λ⊥ and λ‖ parameters. Also D‖ and D⊥ are expected to converge at high pressures which is not the case in their fits.
Thus, an appropriate model which takes into account the adsorbing effect of an aerogel instead of a simple atom–wall collision model (which leads to the Knudsen diffusion) should be developed. The developed “oscillator model”12 designed to describe the diffusion of adsorptive gases in simple pore geometries seems to be a good starting point to build such a model. Although it is not applicable in the case of high gas and adsorbed layer densities, it nevertheless shows that in the case of helium gas at low temperatures (<30 K) the error of the Knudsen model can exceed 300% for cylindrical pores with diameters of less than 20 nm.13 It shows that the adsorption potential effect can be very strong at a temperature of 4.2 K even for 100 nm pores and its effect can not be accounted for by an empirical diffusion model of two exchanging phases (adsorbed layer-gas). Perhaps the described above complex adsorption effects in diffusion explain why we do not observe the diffusion anisotropy as Dmitriev et al.7 found at 20 mK in liquid 3He in this aerogel and their λaero values do not describe our data within a combined Knudsen and two-phase fast-exchange model. This occurs due to the fundamental difference between the diffusion processes in adsorptive gases and low temperature quantum liquids confined in pores.
Besides, for a high signal to noise ratio at low temperatures even at a low 3He gas density (unavailable for other gases at this temperature), the usage of 3He to probe porous sample geometries and restricted diffusion provides advantages over other probe gases and allows one to increase the amount of obtained information on samples. Adsorbed layers play a significant role in 3He gas diffusion and its influence can be varied or limited by 4He surface coverage. The effect of adsorbed layers on diffusion can also be removed by H2 and following 4He surface covering.28,36 Moreover, variation of the temperature allows one to change the 3He mfp values in a large range. Therefore aerogels and other porous samples can be studied under a wide range of experimental conditions that are unavailable using gases other than 3He. A high signal to noise ratio for 3He gas NMR also proves 3He as a convincing probe in diffusion experiments. Other gases used in aerogels such as methanol provide poor signal to noise ratios and one has to use adsorbed layers in order to increase the signal magnitude.11
5 Conclusions
We have performed 3He spin echo gas diffusion measurements in a high porosity ordered aerogel sample at a temperature of 4.2 K. This is the first 3He NMR measurement of gas diffusion in a restricted geometry at low temperatures. The strong influence of adsorbed 3He layers on the aerogel is observed. An empirical model for accounting for adsorption by only considering the adsorbed layer9,11 does not correctly describe our data in the full range of pressures, and we have observed much slower diffusion than expected. Moreover, in contrast to the anisotropic diffusion of liquid 3He recently found in this type of aerogel at very low temperatures7 at which quasiparticle–quasiparticle or quasiparticle–aerogel collisions play a dominant role we do not observe anisotropic diffusion at low pressures in our highly ordered aerogel at 4.2 K. This shows the significant effect of the adsorption attractive potential on atom dynamics in the gas phase and that application of the Knudsen diffusion model is incorrect in the case of strongly adsorbing gases at low temperatures. We found additional evidence of the strong influence of attractive potential in 3He gas densification.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Authors are grateful to V. V. Dmitriev for the provided aerogel sample and inspiration for this work. Our thanks to A. V. Klochkov for the interest in this work and helpful discussions. This work was financially supported by the Russian Science Foundation (grant RSF 16-12-10359). The experimental part of this work was partially done on the equipment of the RC of Probe and EM (Kurchatov Complex of NBICS-Technologies, NRC “Kurchatov Institute”).References
- J. Kärger and R. Valiullin, Chem. Soc. Rev., 2013, 42, 4172 RSC
.
- N. Zhelev, M. Reichl, T. S. Abhilash, E. N. Smith, K. Nguyen, E. Mueller and J. M. Parpia, Nat. Commun., 2016, 7, 12975 CrossRef CAS PubMed
.
- V. V. Dmitriev, A. A. Senin, A. A. Soldatov and A. N. Yudin, Phys. Rev. Lett., 2015, 115, 165304 CrossRef CAS PubMed
.
- E. Collin, S. Triqueneaux, Y. M. Bunkov and H. Godfrin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 094422 CrossRef
.
- D. Candela and N. Kalechofsky, J. Low Temp. Phys., 1998, 113, 351 CrossRef CAS
.
- J. A. Sauls, Y. M. Bunkov, E. Collin, H. Godfrin and P. Sharma, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 024507 CrossRef
.
- V. V. Dmitriev, L. A. Melnikovsky, A. A. Senin, A. A. Soldatov and A. N. Yudin, JETP Lett., 2015, 101, 808 CrossRef CAS
.
- G. Tastevin and P.-J. Nacher, J. Chem. Phys., 2005, 123, 064506 CrossRef PubMed
.
- R. Valiullin, P. Kortunov, J. Kärger and V. Timoshenko, J. Phys. Chem. B, 2005, 109, 5746 CrossRef CAS PubMed
.
- R. Mueller, S. Zhang, M. Klink, M. Baumer and S. Vasenkov, Phys. Chem. Chem. Phys., 2015, 17, 27481 RSC
.
- J. A. Lee, A. M. Mounce, S. Oh, A. M. Zimmerman and W. P. Halperin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 174501 CrossRef
.
- S. K. Bhatia, O. Jepps and D. Nicholson, J. Chem. Phys., 2004, 120, 4472 CrossRef CAS PubMed
.
- M. R. Bonilla and S. K. Bhatia, J. Membr. Sci., 2011, 382, 339 CAS
.
- S. K. Bhatia and D. Nicholson, Chem. Eng. Sci., 2011, 66, 284 CrossRef CAS
.
- V. E. Asadchikov, R. S. Askhadullin, V. V. Volkov, V. V. Dmitriev, N. K. Kitaeva, P. N. Martynov, A. A. Osipov, A. A. Senin, A. A. Soldatov, D. I. Chekrygina and A. N. Yudin, JETP Lett., 2015, 101, 556 CrossRef CAS
.
- E. Alakshin, R. Gazizulin, A. Klochkov, V. Kuzmin, A. Sabitova, T. Safin and M. Tagirov, Magn. Reson. Solids, 2013, 15, 13104 Search PubMed
.
-
A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, Oxford, 1961 Search PubMed
.
- E. M. Alakshin, M. Y. Zakharov, A. V. Klochkov, V. V. Kuzmin, K. R. Safiullin, A. A. Stanislavovas and M. S. Tagirov, JETP Lett., 2016, 104, 315 CrossRef CAS
.
- J. G. Daunt and C. Z. Rosen, J. Low Temp. Phys., 1970, 3, 89 CrossRef CAS
.
- M. Bretz, J. G. Dash, D. C. Hickernell, E. O. McLean and O. E. Vilches, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 8, 1589 CrossRef CAS
.
- C. P. Chen, S. Mehta, E. A. Hoefling, S. Zelakiewicz and F. M. Gasparini, J. Low Temp. Phys., 1996, 102, 31 CrossRef CAS
.
-
J. G. Daunt and E. Lerner, Monolayer and Submonolayer helium films, Springer, 1973 Search PubMed
.
- A. V. Klochkov, V. V. Kuz'min, K. R. Safiullin, M. S. Tagirov, D. A. Tayurskii and N. Mulders, JETP Lett., 2008, 88, 823 CrossRef CAS
.
- K. Luszczynski, R. E. Norberg and J. E. Opfer, Phys. Rev., 1962, 128, 186 CrossRef CAS
.
- B. P. Cowan, M. G. Richards, A. L. Thomson and W. J. Mullin, Phys. Rev. Lett., 1977, 38, 165 CrossRef CAS
.
- B. Cowan, M. Fardis, T. Crane and L. Abou-El-Nasr, Phys. B, 1990, 165–166, 707 CrossRef
.
-
R. Kimmich, Principles of Soft-Matter Dynamics: Basic Theories, Non-invasive Methods, Mesoscopic Aspects, Springer, Netherlands, 2012 Search PubMed
.
- C. P. Lusher, M. F. Secca and M. G. Richards, J. Low Temp. Phys., 1988, 72, 25 CrossRef CAS
.
- M. Sinvani, M. W. Cole and D. L. Goodstein, Phys. Rev. Lett., 1983, 51, 188 CrossRef CAS
.
- M. Dvoyashkin, A. Khokhlov, S. Naumov and R. Valiullin, Microporous Mesoporous Mater., 2009, 125, 58 CrossRef CAS
.
- N. S. Sullivan, J. Low Temp. Phys., 1976, 22, 313 CrossRef CAS
.
- D. R. Swanson, D. Candela and D. O. Edwards, J. Low Temp. Phys., 1988, 72, 213 CrossRef CAS
.
- N. Setoyama and K. Kaneko, Adsorption, 1995, 1, 165 CrossRef CAS
.
- N. Setoyama, K. Kaneko and F. Rodriguez-Reinoso, J. Phys. Chem., 1996, 100, 10331 CrossRef CAS
.
- A. W. Thornton, A. Ahmed, S. K. Kannam, B. Todd, M. Majumder and A. J. Hill, J. Membr. Sci., 2015, 485, 1 CrossRef CAS
.
- C. P. Lusher, M. F. Secca and M. G. Richards, J. Low Temp. Phys., 1988, 72, 71 CrossRef CAS
.
Footnote |
| † The lifetime of a 3He atom in the adsorbed layer is determined by eqn (12) of Lusher et al.28 at 4.2 K, a measured aerogel surface of 16.1 m2, a void volume based on an empty cell volume of 0.49 cm3 and aerogel porosity, and a sticking probability of about 1.29 The lifetime of a 3He atom in the gas phase is roughly determined by successive collisions of 3He atoms with aerogel fibers. It is on the scale of λaero2/Daerogas, where λaero is determined by Dmitriev et al.3 |
| This journal is © the Owner Societies 2017 |