Surface chemistry and stability of metastable corundum-type In₂O₃

Abstract

To account for the explanation of an eventual sensing and catalytic behavior of rhombohedral In₂O₃ (rh-In₂O₃) and the dependence of the metastability of the latter on gas atmospheres, in situ electrochemical impedance spectroscopic (EIS), Fourier-transform infrared spectroscopic (FT-IR), in situ X-ray diffraction and in situ thermogravimetric analyses in inert (helium) and reactive gases (hydrogen, carbon monoxide and carbon dioxide) have been conducted to link the gas-dependent electrical conductivity features and the surface chemical properties to its metastability towards cubic In₂O₃. In particular, for highly reducible oxides such as In₂O₃, for which not only the formation of oxygen vacancies, but deep reduction to the metallic state (i.e. metallic indium) also has to be taken into account, this approach is imperative. Temperature-dependent impedance features are strongly dependent on the respective gas composition and are assigned to distinct changes in either surface adsorbates or free charge carrier absorbance, allowing for differentiating and distinguishing between bulk reduction-related features from those directly arising from surface chemical alterations. For the measurements in an inert gas atmosphere, this analysis specifically also included monitoring the fate of differently bonded, and hence, differently reactive, hydroxyl groups. Reduction of rh-In₂O₃ proceeds to a large extent indirectly via rh-In₂O₃ → c-In₂O₃ → In metal. As deduced from the CO and CO₂ adsorption experiments, rhombohedral In₂O₃ exhibits predominantly Lewis acidic surface sites. The basic character is less pronounced, directly explaining the previously observed high (inverse) water–gas shift activity and the low CO₂ selectivity in methanol steam reforming.

---

1. Introduction

Corundum-type rhombohedral In₂O₃ (rh-In₂O₃ hereafter) is the only metastable indium oxide modification accessible for physico-chemical studies.^1,2 The latter, conducted for a direct comparison to the stable cubic bixbyite-type polymorph,³ is of vital importance for the fundamental understanding of the structure–property relationships of In₂O₃-based materials. Considerable effort has therefore been made to establish controllable synthesis routines to various morphologies, such as nano-fibres, nano-sheets or (hollow) nano-spheres, to potentially circumvent high-temperature and high-pressure synthesis pathways.^1,4,5 Most focus was placed on introducing new ambient pressure sol–gel synthesis routines to reproducibly and more easily obtain larger quantities of materials for subsequent physico-chemical characterization.^6,7 Recently, a new water-free solvothermal route was successfully established, allowing for synthesizing large quantities of rh-In₂O₃.⁸ Despite these efforts, only limited information about the physico-chemical properties of metastable In₂O₃ polymorphs is currently available. Characterization is basically restricted to literally single FT-IR or Raman spectra or, in the case of structural characterization, electron microscopy imaging. A systematic characterization approach highlighting the intrinsic properties of rh-In₂O₃ is almost missing, but given the potential technological applications, even more imperative. Besides the experimental electronic structure of rh-In₂O₃,^9,10 only the charge-carrier concentrations and mobilities are available from Hall-effect studies, providing some insight into the gas-sensing properties of corundum-type In₂O₃, assessed previously.¹¹ Recently, the catalytic properties, alongside the stability limits upon reduction, have been successfully elucidated.¹² Also missing are studies on the surface chemistry of rh-In₂O₃, which directly controls its adsorption properties and steers its (surface) reactivity. The studies are also partially fueled by the outstanding reactivity properties of its cubic In₂O₃ counterpart (c-In₂O₃ hereafter), which exhibits extraordinarily high CO₂ selectivities in methanol steam reforming (essentially referenced to the simultaneous largely suppressed inverse water–gas shift reactivity^13,14), as well as the activity in catalytic dehydrogenation of light hydrocarbons¹⁵ and in photocatalytic CO₂ reduction.^16,17 Studies of the surface chemistry of In₂O₃ polymorphs are also needed for understanding the mechanism of gas detection with indium oxide applied as a chemiresistive gas sensor.^18–21 As for the latter, many oxides exhibit excellent sensing properties for various gases. To explain the sensing behavior, a profound knowledge about the interplay between chemistry and conduction properties is required. This is especially true if the conduction is confined to the surface-near regions. In this case, only a concerted approach of operando surface chemical characterization (e.g. by FT-IR spectroscopy) and assessment of the complementary surface conduction properties (e.g. by impedance spectroscopy) yields valuable results. Increasingly, also metastable oxide polymorphs (e.g. rhombohedral In₂O₃)^18–23 are applied as such sensing materials. In this special case, the situation is further complicated by the possible transformation to thermodynamically more stable modifications during sensor operation. As this of course is entangled with the surface chemistry/conduction behavior, a thorough knowledge about the interplay between the latter two and the overall surface and bulk structure stability in various gas atmospheres is necessary. Despite the fact that many such sensing studies are reported, information on this correlation with stability issues, especially as a function of gas composition, is still scarce. This is a particular pity, as the inherent structural metastability will certainly alter the sensing behavior. Exactly such a behavior has been recently monitored in the ZrO₂ polymorphic system, where the surface chemistry and the corresponding conduction properties have been a strong function of the metastability of tetragonal ZrO₂ and the associated transformation to monoclinic ZrO₂ in various gas atmospheres.

The present contribution exemplifies these studies on an archetypical, recently much studied metastable oxide polymorph, namely rh-In₂O₃. As it will turn out, the coincidence and correlation between surface chemical and conduction property changes and stability are outstanding in various gas atmospheres, encompassing reductive (H₂, CO), reactive (CO₂) and basically inert surroundings (He). Hence, the present study is essentially focused on studying the interaction of H₂, CO, He and CO₂ with rh-In₂O₃ in the temperature region up to 673 K, which is of interest for catalytic and gas-sensing studies, and to link the surface chemistry to physical properties such as electrical conductivity. This approach yields not only a particular convenient basis to explore also other (metastable) polymorphic systems, which are yet to be studied, but also data on the catalytically relevant acidity and reactivity of the rh-In₂O₃ surfaces and, therefore, allows highlighting the similarities to and differences from thermodynamically stable c-In₂O₃. Particular emphasis is also given to the structural and chemical stability of rh-In₂O₃ during these treatments.

2. Experimental

2.1. Synthesis of the materials and general experimental features

The synthesis of the materials has been outlined in detail in a recent publication.⁸ High-purity He, H₂, O₂, CO and CO gases were provided by Messer-Griesheim (Germany). Condensable impurities were removed from the gases by cooling traps. For He and H₂, liquid N₂ at 77 K was used; O₂, CO and CO₂ were purified using ethanol/liquid N₂ mixtures at 153 K (O₂ and CO) and 223 K (CO₂). Gas treatments were carried out under flowing conditions (∼1 mL s⁻¹) up to 700 K to avoid triggering the phase transformation to c-In₂O₃ to a large amount.

2.2. In situ electrochemical impedance spectroscopy (EIS)

A heatable in situ impedance cell designed for gas treatments up to 1273 K, situated in a tubular furnace (Linn, Germany) and controlled using a thermocouple located 5 mm downstream of the sample and a Micromega PID temperature controller, was used for analysis. Temperature-dependent impedance measurements were carried out using an IM6e impedance spectrometer with the upper limit of 6 GΩ (Zahner Elektrik, Germany). For all measurements, an excitation frequency of 1 Hz and an amplitude of 20 mV of the superimposed modulation voltage signal at an overall DC potential of 0 V were applied to two circular Pt electrodes (diameter 5 mm) in mechanically enforced contact with the sample (corresponding to a force of 2 N). The latter is a pelletized powder material (several hundred milligrams of the powder are pressed by 2 t into a disk of 5 mm diameter and ∼0.1 mm thickness). The impedance of the pellet is therefore effectively measured in an electrochemically unpolarized state. In all temperature-dependent experiments the impedance modulus value |Z| will be further referred to as “impedance”. To collect the frequency-dependent data, the frequency was varied between 100 mHz and 1 MHz at the same amplitude of the superimposed sinusoidal voltage signal also used for the temperature-dependent impedance measurements. To fit the frequency-dependent data (Nyquist plots), a fit model consisting of grain interior (bulk) and grain boundary contributions of resistances and constant phase elements has been exploited (discussed in detail in Section 3.3). To account for the intrinsic properties of the porous sample, constant phase elements instead of capacitive elements have been used. The intertransition of the latter two is given by the formula:
with α = 1, the phase element behaves like an ideal capacitor and with α = 0, it represents an ideal resistor.

The activation energies (E_A's) of the conductivities for selected temperature regions were calculated from the resistance values obtained from the fit of the Nyquist plots, as well as from the temperature-dependent EIS measurements.

2.3. In situ FT-infrared spectroscopy (FT-IR)

All FT-IR spectra were recorded using a Cary 660 spectrometer (Agilent, Germany) and a home-built high-temperature, high-pressure in situ quartz reactor cell, capable of collecting spectra at temperatures up to 1273 K and pressures up to 1 bar in reactive gases.²⁴ Its dedicated construction allows the use of ultra-dry conditions with a water partial pressure p < 1.0 × 10⁻⁷ mbar. For analysis, the powders are pressed into thin pellets using a hydraulic press at ∼2 t, yielding pellets with a diameter of ∼1.0 cm and a thickness of ∼0.1 mm. Treatments under flowing (exclusively performed in here) and static conditions are equally possible. Both for FT-IR and EIS experiments, the experiments have been repeatedly conducted using several pellets to exclude influences of a different degree of pelletizing. No changes have been observed by repeating the experiments using different pellets.

2.4. In situ X-ray diffraction

The time-resolved in situ synchrotron X-ray powder diffraction (XRPD) studies (angle-dispersive transmission mode, monochromatic 25 keV focussed beam, λ = 0.4959 Å. 30 μm spot size) are conducted at the Advanced Light Source Beamline 12.2.2, Lawrence Berkeley National Labs (California). The rh-In₂O₃ samples in 700 μm quartz capillaries are heated to 700 K with 10 K min⁻¹ heating rate in an IR irradiated tube furnace²⁵ under continuous air, He and pure H₂ flow injected by an open-ended 300 μm capillary. A Perkin Elmer flat panel detector (XRD 1621, dark image and strain correction) is used to record the XRPD patterns every 25 seconds.

2.5. In situ thermogravimetry – mass spectrometry

Simultaneous Thermal Analysis (STA) is conducted in a STA 409 PC LUXX (Netzsch, Germany) device under Air, He and 5% H₂ in Ar using 100 mg sample powder placed in alumina crucibles. The released gaseous species (m/z = 2, 16, 17, 18, 44) are simultanously analysed in an OMNi Star GSD 320 mass spectrometer (Pfeiffer Vacuum, Germany).

3. Results and discussion

3.1. Summary of ex situ determined phase stability and reduction behavior

To simplify the correlated discussion between surface chemistry and surface conduction properties, we will provide a very brief account of the previous findings of the reduction behavior and associated phase stability in H₂ and CO. In both reducing agents, a drastic impedance decrease, leading to metallic conductivity (∼10 Ω) above ∼673 K, has been observed during heating of rh-In₂O₃. Below 673 K, this decrease can be at least in part correlated with the formation of modest amounts of cubic In₂O₃. At temperatures at and especially above 673 K, the formation of different amounts of metallic In sets in, causing metallic conductivity. Annealing to similar temperatures in inert helium does not trigger this phase transformation.¹² The suppression of transformation of large amounts of rh-In₂O₃ into its thermodynamically stable cubic counterpart, being a necessary pre-requisite for studying the intrinsic physico-chemical properties of rh-In₂O₃, can be at least in part controlled by the choice of the reducing agent, annealing temperature and time. At temperatures below ∼623 K, rh-In₂O₃ is stable for days, without transforming into c-In₂O₃ or being reduced to metallic In. In contrast, treatment at 923 K leaves only 30 minutes for successful characterization before the transformation sets in ref. 8 and 12.

3.2. In situ determined phase stability

To understand the relationship between the structure and surface chemistry of In₂O₃, the phase stability of rh-In₂O₃ was examined in He, CO₂ and H₂ atmospheres between room temperature and 700 K by time-resolved in situ synchrotron XRPD experiments. The contour plots in Fig. 1A–C (left panels) show the in situ XRD patterns collected during the heating of rh-In₂O₃ in He, CO₂ and H₂ atmospheres, respectively. The in situ XRPD data reveal that rh-In₂O₃ remains stable upon heating to 700 K in He and CO₂, while it starts to transform into c-In₂O₃ at 640 K in the H₂ atmosphere. The intensities of c-In₂O₃ reflections increase with temperature suggesting the development of the c-In₂O₃ phase. The Rietveld refinement of the sample ex situ heated up to 673 K in H₂ atmosphere indicates the formation of 90 wt% c-In₂O₃ and 10 wt% metallic In.¹² However, no additional reflections related to metallic indium have been observed in the three atmospheres up to 700 K under the chosen experimental conditions, in contrast to the ex situ measurements.

Fig. 1 In situ collected XRD patterns on rh-In₂O₃ during heating in He (A), CO₂ (B) and H₂ (C) up to 700 K. Reference data are shown as ticks below the patterns. The respective right panels show the associated in situ STA (TG, DTA and MS) profiles under comparable experimental conditions.

To confirm the phase stability of rh-In₂O₃, as well as to obtain more precise information about the eventual phase transition observed in XRPD experiments, simultaneous thermal analysis (STA) was performed under He, CO₂, and 5% H₂/Ar (100% H₂ was technically not possible). Fig. 1 (right panels) shows the TG, DTG, and DTA curves of rh-In₂O₃ and the mass spectra collected on-line for H₂ (m/z = 2), O₂ (m/z = 16), H₂O (m/z = 17 and 18) and CO₂ (m/z = 44). The sample exhibits a weight loss of ∼0.5% at 370 K that can be ascribed to the release of some H₂O (m/z = 17 and 18). The exothermic peak observed in the DTA curve at 625 K, which only appears in the H₂ atmosphere, is accompanied by a weight loss of ∼0.5%, the release of H₂O (and, most probably, surface-bound CO₂) and the consumption of H₂ gas (m/z = 2). The in situ XRPD data (Fig. 1C) display the phase transition of rh-In₂O₃ to c-In₂O₃ in the same temperature range. Hence, rh-In₂O₃ becomes destabilised due to the reaction with H₂, which in turn causes the transformation to c-In₂O₃. The release of H₂O as well as the consumption of H₂ gas (m/z = 2) during the phase transition suggests the reaction of H₂ being due to the phase transition of rh-In₂O₃ to c-In₂O₃. This exothermic peak was accompanied by a weight loss of ∼0.5% that is due to the release of some H₂O, and CO₂ gases, as revealed by the MS analysis. The mechanism of the appearance of CO₂ species will be studied in more detail in subsequent work. In He and CO₂ atmospheres rh-In₂O₃ does not display any reaction with the gaseous species and remains stable up to 700 K.

3.3. Surface chemistry in an inert gas atmosphere

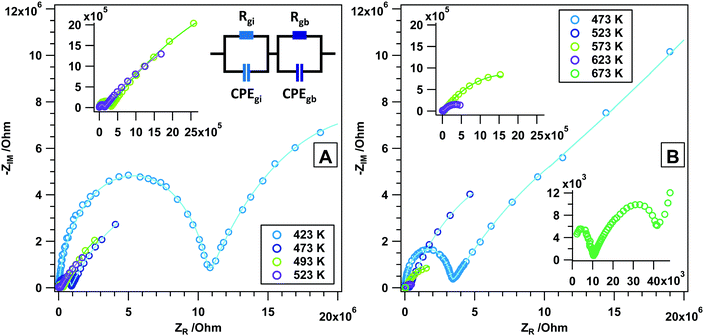
To provide a reference measurement to those in reactive gas atmospheres, Fig. 2A and B discuss the state and changes of the surface chemistry of rh-In₂O₃ as determined by in situ electrochemical impedance and FT-IR spectroscopy. This will in turn help separate direct and indirect (chemical) temperature-induced effects. As such, Fig. 2A shows the impedance change during a heating–cooling cycle from room temperature to 700 K and back. An upper temperature limit (as determined by previous experiments^8,12) has been pre-set to avoid triggering unwanted phase transformations to a large extent. As a general feature, it is noted that heating rh-In₂O₃ slightly above room temperature causes a drastic decrease in the impedance by more than one order of magnitude, being tentatively assigned to effective de-hydroxylation of the surface (similar to c-In₂O₃²⁶). The impedance re-rises between 300 and 330 K, before it smoothly decreases up to 700 K, finally reaching an impedance value of about 1.5 × 10⁴ Ω. In the intermediate temperature region, rh-In₂O₃ shows semiconductive behavior, with a more or less pronounced change in the impedance-temperature slope at around 500 K (note that this is exactly the point between two temperature regions in the Arrhenius plot with different activation energies, see also Table S1, ESI†). In fact, the slope in the temperature region 330–500 K is much smaller compared to between 500 K and 700 K, pointing to a more or less pronounced change in the surface chemistry in that temperature regime. This will subsequently be directly proven by the analysis of the FT-IR spectra shown in Fig. 2B and Fig. S1 (ESI†). The cooling behavior between 700 and 600 K very much resembles the heating routine in this temperature region, with notable differences between 600 K and room temperature, where the surface does not get replenished with hydroxyl groups. Hence, higher final impedance values at room temperature (above the GΩ detection limit of the spectrometer) result. Fig. 2B at the same time reveals the changes in surface chemistry as monitored by in situ FT-IR spectroscopy. Following the results of a recent work,¹² this figure shows the development of particularly water-associated species. In addition, the changes of the total transmittance, being an indication of conduction band electron absorption,²⁶ determined at a specific wavenumber (2000 cm⁻¹), where no overlap with any adsorbed species occurs, are shown. As a general phenomenon, the removal of OH groups starts continuously already at around 330 K up to the highest temperatures and proceeds during the isothermal periods. During cooling, the surface remains essentially in a de-hydroxylated state, corroborating the impedance measurements. More specifically, in the temperature region between 330 and 573 K a continuous removal of specific OH groups at 3640 cm⁻¹ (sharp peak, surface OH groups) takes place, which to some extent between 330 and 410 K proceeds in parallel with the easy removal of bulk OH groups (broad negative feature, incorporated water). Between 410 and 673 K, removal of the latter is more effective. The characteristic change of impedance vs. temperature slope at ∼500 K can be directly related to significant changes in the total transmittance. The latter shows a pronounced maximum exactly at 500 K, which indicates that the electronic state of rh-In₂O₃ changes significantly. Correlating this phenomenon directly with the impedance data, we may assume that thermal removal of reactive lattice oxygen starts with the associated formation of oxygen vacancies, which is also confirmed by previous volumetric adsorption and oxygen re-titration measurements.²⁶ rh-In₂O₃ differs significantly from c-In₂O₃, for which the bulk remains stable and unreactive until ∼770 K.²⁶ As will be shown below, these features are much more pronounced if reducing agents like H₂ or CO are used. The FT-IR data strongly suggest that this particular feature is not related to the removal of surface OH groups, but rather to a bulk-restricted phenomenon, as the maximum of absorbance can be directly correlated with the effective loss of interconnected OH groups. Selected FT-IR spectra during annealing in He are shown in the ESI,† Fig. S1.

Fig. 2 Panel A: in situ impedance spectra on rh-In₂O₃ in flowing He (1 mL s⁻¹). Panel B: in situ FT-IR data of rh-In₂O₃ in flowing He (1 mL s⁻¹). Heating–cooling cycles from room temperature (RT) to 700 K, as well as heating and cooling rates (10 K min⁻¹), are identical in both experiments. h = heating, c = cooling, i.p. = isothermal period.

To obtain more information on the different surface- and bulk-restricted conductivity contributions, we performed associated frequency-dependent impedance measurements and the corresponding Arrhenius activation analysis. Fig. 3 and 4 show these experiments at selected temperatures between 423 K and 673 K. These temperatures were chosen as the first semicircles appear at 423 K, and 673 K was deliberately set as the highest temperature to suppress the eventual phase transformation. From the data it is obvious that for He especially the grain boundary contributions appear separated into two temperature regimes (423–523 K and 473–623 K). These are also the temperatures, where significant changes in the FT-IR experiment were apparent. The inset in Fig. 3 highlights the fit model used to evaluate the frequency-dependent data. Tables S2 and S3 (ESI†) feature the equivalent circuit parameters used to model the impedance spectra. They consist of two grain-related contributions, i.e. grain interior and grain boundary, both of them contributing resistance and constant phase element parts. The general appearance of all data is the presence of at least two depressed semicircles, being directly related to the aforementioned individual contributions. In general, the first semicircle is always fully present, whereas the second one is only partially represented in the chosen frequency range. As for a typical semiconductor, the resistances (especially the grain interior contribution) decrease as the temperature is increased. In line with that, we assume that the conductivity vs. temperature behaviour of rh-In₂O₃ can be either addressed to semiconductive properties (in He) or is (especially in reducing gases, as will be shown below) in some way connected to the formation of oxygen vacancies. An exception concerns the measurement at 673 K, where at low frequencies an additional process is visible, overlapping with the grain boundary contribution. One might also include the possibility of a beginning phase transformation into the cubic polymorph. According to the Arrhenius analysis (Fig. 4), the apparent activation energy of the grain interior contribution is about 82 kJ mol⁻¹ (0.82 eV), which is comparable to YSZ (∼1 eV) for bulk O²⁻ activation, and is significantly smaller than the activation energy (1.5 eV) attributed to the electronic conductivity (above 973 K) associated with the formation of oxygen vacancies in c-In₂O₃.²⁶ In essence, this once again underlines that oxygen vacancies must play a role in explaining the conductivity of rh-In₂O₃. The activation energy values of the grain boundary part, however, are split into two processes: a high-temperature and low-temperature process. At higher temperatures (523–623 K) an activation energy of about 90 kJ mol⁻¹ (0.94 eV) and at lower temperatures (423–523 K) an activation energy of 16 kJ mol⁻¹ (0.16 eV) are determined. This indicates that the latter is essentially a surface-restricted phenomenon, dominating at lower temperatures, but becoming increasingly overwhelmed by the oxygen vacancy-dominated conductivity contribution, once the temperatures starts to exceed 523 K. Note that the dark green square in Fig. 4 was purposely not chosen for the Arrhenius fit since it is part of the low-temperature process and would, hence, falsify the determination of the activation energy for the high-temperature process.

Fig. 3 Nyquist plots (data points) and simulated spectra (continuous lines) of rh-In₂O₃ treated in flowing He (1 mL s⁻¹) at various temperatures between 423 K and 523 K (A) and between 473 K and 673 K (B). The lowest frequency of 100 mHz is at the right side and the highest one of 1 MHz is at the left side of the x-axis. The equivalent circuit model used for fitting the frequency-dependent impedance data of the samples with contributions from the grain interiors (gi) and grain boundaries (gb) is shown as the inset.

Fig. 4 Arrhenius analysis of the grain interior and grain boundary contribution of a rh-In₂O₃ powder pellet sample treated in dry He and CO₂. Based on the data of Fig. 3A (blue traces), Fig. 3B (green traces) and 11 (purple traces). gi contr. = grain interior contribution, gb contr. = grain boundary contribution.

3.4. Surface and bulk reduction in H₂

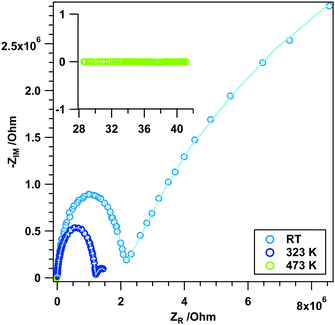
In contrast to the experiments in an inert atmosphere, a direct influence of the reducing agent on the surface chemistry and (surface) conduction properties can be expected. The associated results are highlighted in Fig. 5 and Fig. S2 (ESI†). Note that to provide insight into the kinetics of reduction, different maximum temperatures as well as repeated experiments to identical maximum temperatures have been conducted. For the sake of clarity, in Fig. 5A the measurement in He is also included. As a general remarkable feature, which is observed in almost all experiments displayed in Fig. 5A, the impedance vs. temperature course exhibits two more or less pronounced plateau-like features, where the impedance is almost independent of the annealing temperature. One of these plateaus is observed at lower temperatures (between 310 and 430 K), and the other one between 480 and 550 K. While the latter is present in all experiments, the former is missing for the measurement up to 673 K. However, a slower decrease in the impedance is visible. The reason for this is not entirely clear yet, but given the tremendous influence of the kinetics on the extent of reduction, slight variations in e.g. the heating routine might limit the access to this specific surface reduction state. At temperatures below 310 K (i.e. below the first plateau) and between 430 and 500 K (i.e. between the two plateaus) semiconductive behavior is apparent (cf. Table S1, ESI† for E_A's in these regions for different measurements). A second general feature is the final constant impedance value above ∼570 K (∼15 Ω), which is invariant upon re-cooling. The kinetics of the reduction process is also directly apparent if the two experiments up to a maximum temperature of 523 K (Fig. S2, ESI†) are compared: while the final impedance value reached upon entering the second plateau (∼40 Ω) and the onset temperature of the plateau (∼310 K) appear unaltered, the extent of the plateau in both cases differs by 20 K. Most importantly, these differences can be directly correlated with associated changes in the reduction degree/the amount of states in the conduction band (determined by the transmittance change at 2000 cm⁻¹), but less so with direct changes of the surface chemistry. As shown in Fig. 5B, the OH groups (most likely bulk-related) get only lost rapidly between 593 and 633 K, i.e. at temperatures where the impedance already reached its final metallic value of 15 Ω. In contrast, the relative total intensity at 2000 cm⁻¹, being a direct indicator of the extent of reduction, exactly follows the trends of the impedance vs. temperature course and, also irrespective of the final maximum temperature, exactly copies the plateau-like temperature-invariant impedance features. Also the FT-IR experiments reveal that the extent of reduction is not reversed substantially upon re-cooling, as the relative total intensity hardly changes. One can now directly deduce that all the particular impedance features up to about 600 K without exception arise from a different extent of reduction. This also fits perfectly to previously reported temperature-programmed reduction and -desorption results, which show an increased formation of oxygen vacancies in this temperature region (up to 600 K). More specifically, by correlating the course of the impedance with the volumetric H₂ uptake,¹² it is clear that the first impedance plateau must be associated with predominant surface and the second one with bulk reduction. This follows from a quantification of the oxygen vacancies by oxygen re-titration measurements (cf. Table 2, ref. 12), which shows only modest amounts after reduction at ∼414 K, but a more or less drastic increase particularly at temperatures T > 550 K, i.e. especially in the high-temperature part of the second plateau. Selected FT-IR spectra during annealing in H₂ are shown in the ESI,† Fig. S3. Rietveld analysis of ex situ collected X-ray diffraction data at selected temperatures during the impedance measurements indicated the formation of not more than 10–15 wt% c-In₂O₃ at temperatures of about 473 K, i.e. just before entering the second plateau. This ratio between rh-In₂O₃ and c-In₂O₃ does not change upon heating to ∼570 K, i.e. after the second plateau and when the impedance stays constant even after heating to higher temperatures. Hence, we conclude that the impedance course is not entirely affected by the phase transformation, but reflects the true intrinsic reduction – conduction properties of rh-In₂O₃.

Fig. 5 Panel A: in situ electrochemical impedance measurement on rh-In₂O₃ in flowing H₂ (1 mL s⁻¹). Panel B: in situ FT-IR data of rh-In₂O₃ in flowing H₂ (1 mL s⁻¹). Heating–cooling cycles from room temperature (RT) to 700 K, as well as heating and cooling rates (10 K min⁻¹), are identical in both experiments. h = heating, c = cooling, i.p. = isothermal period.

Frequency-dependent measurements in H₂ also reveal the influence of the reduction agent (Fig. 6). While the experiment at RT exhibits the well-known behavior of grain interior and grain boundary contributions, the Nyquist plots at higher temperatures are clearly different from those in He (fit parameters summarized in Table S4, ESI†). This special frequency-dependent impedance course indicates that the sample changes during the measurement (which is on the time scale of ∼5 minutes for a full measurement cycle). Given the previous experiments on the dependence of the phase transformation on the reduction in the same temperature region, the peculiar impedance course between 323 K and 373 K is related to the phase transformation between rh- and c-In₂O₃ and maybe to some extent also metallic In, as deduced from correlation with previous data. At 523 K, the imaginary part of the impedance is basically zero and a purely ohmic resistance results (for a detailed representation of this NP, see Fig. S4, ESI†). According to previous experiments, this is right on the edge of temperatures, where metallic In appears in the product mixture^12,27 – hence, the ohmic resistance essentially arises from the modest amounts of metallic In.

Fig. 6 Nyquist plots (data points) and simulated spectra (continuous lines) of rh-In₂O₃ treated in dry H₂ at selected temperatures between RT and 523 K.

3.5. Surface and bulk reduction in CO

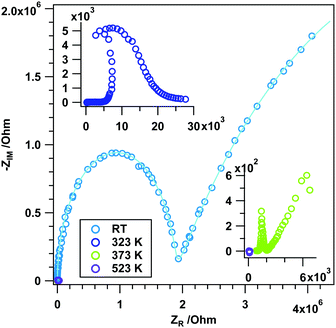
To directly connect to the experiments in flowing H₂ and to previous experiments on the reducibility in CO,¹² we aim in the following at linking the observed impedance behavior to the associated changes in surface chemistry. This is anticipated to be much more complex than in He or H₂ due to the potential formation of surface formates and, via formed and re-adsorbed CO₂, also carbonate species. From previous experiments it is already known that CO at a similar temperature to H₂ causes drastic reduction of rh-In₂O₃, leading to CO₂ formation by the reaction of CO with lattice oxygen.¹² Its effect on surface chemistry is, however, to date unknown.

Fig. 7 now provides the direct link between surface and bulk conduction properties upon annealing in flowing CO (Fig. 7A) and the corresponding FT-IR fingerprint of surface-adsorbed species (Fig. 7B). In Panel A, the inert He measurement is also included. The impedance vs. temperature course in CO shows a very steep impedance decrease between RT and approximately 410 K (depending on the measurement) with a corresponding activation energy of 136 kJ mol⁻¹ (cf. Table S1, ESI†). After this steep decrease a plateau, where the impedance value changes only slightly, is apparent exhibiting a value of ∼60 Ω (light green trace in Fig. 7A) and ∼20 Ω (light purple trace in Fig. 7A), after which the impedance decreases again to adopt a metallic-like value (∼12 Ω) at temperatures above ∼550 K (E_A: 73 kJ mol⁻¹ between 512 and 559 K). The impedance hysteresis between heating and cooling is equally pronounced in CO. Kinetic limitations between two successive experiments (light green/dark green and light purple/dark purple traces) still prevail and manifest themselves as differently extended temperature-independent impedance plateaus. Notable differences from the H₂ measurement concern (i) the missing low-temperature plateaus and (ii) the generally earlier decrease of the impedance (starting already at room temperature) and rapidly accelerating up to ∼410 K. Fig. 7B directly reveals the complex interplay between conduction properties, reduction and surface chemistry. Between 300 K and 500 K, the relative total absorbance increases drastically, with at the same time complete absence of any changes in surface-adsorbed species. This indicates that during the impedance decrease between 300 K and 410 K, but also within the plateau region, the simple reduction of rh-In₂O₃ by CO is the predominant reaction pathway, but without the pronounced formation of CO₂ by the reaction of CO with lattice oxygen. Surface chemistry only starts to play a role at the end of the plateau region, where the impedance suffers a final drop towards metallic conductivity behavior. In due course, the relative total absorbance significantly decreases between 500 K and 600 K and formate signals (as determined from the asymmetric stretching vibration of surface-bound formate species (cf. Fig. S5, ESI†)) start to increase in the same temperature region up to 610 K. The surface of rh-In₂O₃ suffers a reversible poisoning by CO until adsorbed CO predominantly forms formate species, which reverses the reduction to some extent. Formate decomposition is then observed in the temperature region between 633 K and 673 K, which goes along with further massive reduction of surface and probably also bulk regions, finally also yielding gas-phase CO₂. Although it appears that CO₂ is mostly formed by the direct reaction of CO and lattice oxygen (resembling a Mars–van-Krevelen-type reaction mechanism), the decomposition of bulk-like OH groups at and above 650 K (proceeding in parallel with formate decomposition) suggests that in part CO₂ is also formed via the reaction of the latter two. Deep reduction of rh-In₂O₃ beyond 650–670 K is necessarily accompanied by increased formation of In metal.¹² Upon cooling, the state of the surface remains basically unchanged, with the notable exception of CO₂ production upon cooling up to 600 K. As for the already discussed experiments in H₂, an influence of the phase transformation into c-In₂O₃ on the surface conduction and chemistry properties cannot be ruled out, but appears unlikely, as the ratio between rh-In₂O₃ and c-In₂O₃ in the relevant temperature region (before and during the plateau region) remains unchanged (∼90 weight% rh-In₂O₃, 10 weight% c-In₂O₃, no In metal¹²).

Fig. 7 Panel A: in situ electrochemical impedance measurement on rh-In₂O₃ in flowing CO (1 mL s⁻¹). Panel B: in situ FT-IR data of rh-In₂O₃ in flowing CO (1 mL s⁻¹). Heating–cooling cycles from room temperature to different maximum temperatures, as well as applied heating and cooling rates (10 K min⁻¹), are identical in all experiments. h = heating, c = cooling, i.p. = isothermal period.

The frequency-dependent experiments in Fig. 8 at low temperatures (especially at room temperature) resemble that of H₂ at room temperature in terms of the general appearance of the two depressed semicircles (fit parameters Table S5, ESI†). Also at 323 K semicircles are present, albeit with a decreased grain boundary resistance in comparison to room temperature. After heating to 473 K, exclusive ohmic resistance is observed without the imaginary contribution, indicating the formation of metallic In. This temperature-wise matches not only the observations in H₂ (purely ohmic resistance starting at 523 K), but also previous temperature-dependent conductivity measurements in CO.¹²

Fig. 8 Nyquist plots (data points) and simulated spectra (continuous lines) of rh-In₂O₃ treated in dry CO at various temperatures between RT and 473 K. The lowest frequency of 100 mHz is at the right side and the highest one of 1 MHz is at the left side of the x-axis.

3.6. Surface chemistry in CO₂

The reason for including adsorption studies of CO₂ is mainly fueled by its catalytic relevance in terms of explaining the high CO₂ selectivity of its cubic counterpart in methanol steam reforming¹³ and by the fact that it necessarily is a part of the reaction mixture if rh-In₂O₃ is reduced in CO, at least at elevated temperatures. Fig. 9A (EIS) and 9B (FT-IR) reveal that CO₂ only has a comparably small effect on the properties of In₂O₃. The impedance vs. temperature course in certain temperature regions resembles that in He. However, differences in the activation energies are apparent for He and CO₂ (cf. Table S1, ESI†). Expectedly, no metallic conductivity is reached even at the highest temperatures. This blocking effect is also directly reflected in the FT-IR data (Fig. 9B). Most likely bridged carbonate species are predominantly formed upon CO₂ adsorption, but no transformation or even decomposition during the heating–cooling cycle has been observed. This indicates that the surface is essentially blocked for further adsorption. Quantitative analysis of the OH region is severely hampered in the present case due to overlap of the CO₂ overtones, but irreversible removal of bulk OH groups upon heating is observed and directly proven by the vacuum spectra (black trace Fig. 9B) and by the lower impedance values between RT and 310 K (light green trace Fig. 9A). Fig. S6 further elaborates on the development of the discussed carbonate species and proves by plotting the relative absorbance vs. the annealing temperature, that reduction of the surface is essentially absent.

Fig. 9 Panel A: in situ electrochemical impedance measurement on rh-In₂O₃ in flowing CO₂ (1 mL s⁻¹). Panel B: in situ FT-IR spectra of rh-In₂O₃ in flowing CO₂ (1 mL s⁻¹). Heating–cooling cycles from room temperature to different maximum temperatures, as well as applied heating and cooling rates (10 K min⁻¹), are identical in both experiments. h = heating, c = cooling, i.p. = isothermal period.

The general appearance of the Nyquist plots in flowing CO₂ at different temperatures is very similar to the ones obtained in He and H₂ and in CO at lower temperatures pointing out at grain interior and boundary contributions (fit parameters see Table S6, ESI†). At the highest temperatures (673 K), as in He, the potential sample–electrode interaction is visible as a third process (linear increase at the low frequency end, Fig. 10). As also the apparent activation energy of the grain interior contribution at ∼0.86 eV (473–673 K) is very similar to the one obtained for He (0.85 eV between 423–523 K and 0.83 eV between 423–623 K) as shown in Fig. 4.

Fig. 10 Nyquist plots (data points) and simulated spectra (continuous lines) of rh-In₂O₃ treated in dry CO₂ at selected temperatures between 473 and 673 K. The lowest frequency of 100 mHz is at the right side and the highest one of 1 MHz is at the left side of the x-axis.

Hence, one might conclude that CO₂ in fact blocks the surface of the sample and the interaction with the rh-In₂O₃ surface is essentially suppressed. The apparent activation energy derived from the grain boundary resistances (0.3 eV), however, is different than in He (0.17 eV between 423–523 K and 0.94 eV between 423–623 K), indicating that the contribution of the bulk ion conduction is higher. Table S7 (ESI†) summarizes the calculated activation energies determined in all gases.

3.7. Comparative summary about the influence of different gas atmospheres on surface and bulk chemistry of rh-In₂O₃

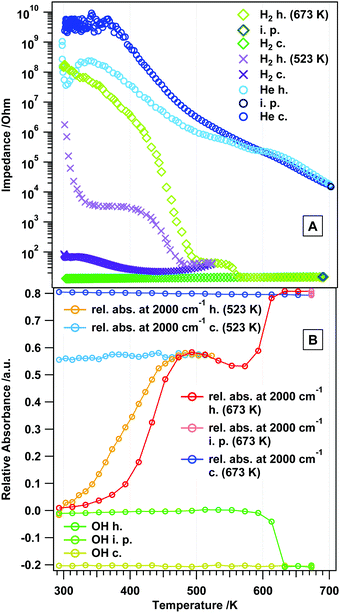
Fig. 11 summarizes the change of the total absorbance at 2000 cm⁻¹ – which is a good measure for the concentration of charge carriers – for all gas treatments in a comparative view. In He, H₂ and CO, the absorbance increase is comparable, but more pronounced in the latter two gases. Above 500 K, the surface chemistry, but also the phase transformation, has a significant influence on the absorbance. In CO₂, the changes are not as pronounced, since the surface is effectively blocked by carbonate species. The observed maximum in the relative absorbance at around 500 K in hydrogen and CO (coinciding with the end of the plateau regions in the impedance graphs), thus, represents the intrinsic conduction properties of rh-In₂O₃, which might be directly associated with the extent of oxygen vacancies formed by reduction. The effect of CO can be understood in terms of reduction and formation of oxygen vacancies. However, the increase in the conductivity of rh-In₂O₃ in H₂ at 523 and 673 K could not be directly correlated with the increase in the total absorbance associated with the conduction band electrons. This indicates that more complex processes take place on the surface/bulk of rh-In₂O₃ in hydrogen (see also the STA analysis in Fig. 1).

Fig. 11 Panel A: temperature-dependent impedance traces comparatively shown for all studied gases. Panel B: comparison of the change of the total absorbance at 2000 cm⁻¹ for all gas treatments.

Directly connected to the vacancy-mediated mechanism is the answer to the question how the reduction of rh-In₂O₃ takes place, i.e. if rh-In₂O₃ is transformed to c-In₂O₃ before metallic In is formed, or if a direct reduction to metallic In takes place. In view of the presented results, a substantial contribution of the latter appears unlikely and the pathway to a large extent most likely is: rh-In₂O₃ → c-In₂O₃ → In metal. The latter would, however, be addressed in more detail in subsequent work.

3.8. Comparative discussion of the surface chemistry of rh-In₂O₃ and c-In₂O₃

The differences in the surface chemistry between the two most abundant In₂O₃ polymorphs, rh-In₂O₃ and c-In₂O₃, are best visualized if discussed in the context of the catalytic applications, as detailed earlier.^12,13 Two different pathways of argumentation are worthwhile in this respect. On the one hand, the FT-IR studies now directly prove the gas–surface interaction of the relevant probe molecules, on the other hand the combination with the impedance data allows some conclusions on the mechanism of the methanol steam reforming reaction on both modifications. Previously only anticipated and indirectly deduced from the catalytic profiles, we are now able to give definite answers to the questions: (1) how does the surface chemistry influence the catalytic properties and (2) does the reaction mechanism of methanol steam reforming take different reaction routes on c-In₂O₃ and rh-In₂O₃.

To introduce question (1), c-In₂O₃ is an outstandingly CO₂-selective methanol steam reforming catalyst,¹³ which can be argued directly on the basis of the acid–base properties of the catalytically relevant oxide surface sites. On the basis of a concept by Tatibouet to account for the selectivity pattern in methanol synthesis,²⁸ also the adsorption and transformation of the intermediates in the reverse reaction, that is, methanol steam reforming, can be directly rationalized. Following dissociative adsorption of methanol, the further fate of the adsorbed methoxy group strongly depends on the acidic strength of the adsorption site of the methoxy group and on the chemical nature of the sites close by. A further reaction of the methoxy group requires C–H bond breaking, which, in the case of heterolytic bond scission, strongly depends on the basic (i.e. nucleophilic) character of the oxygen species. Strong basic sites will help in effectively abstracting the H atoms from the adsorbed methoxy group, thus, favoring the fast onward reaction of the adsorbed formaldehyde intermediate, which is formed by increasing H abstraction from the methoxy group. Weaker basic sites favor the prolonged lifetime of the adsorbed formaldehyde, eventually giving rise to its desorption. In contrast, if the acidic sites are strong, the lifetime of the adsorbed methoxy group is long enough to eventually form condensed products like dimethylether, dioxomethylene or methylal species. Re-addressing the surface chemistry of the In₂O₃ polymorphs under question, the extraordinarily high CO₂ selectivity of c-In₂O₃ directly proves the presence of strong basic, but rather weak acidic sites. Therefore, only CO₂, but no formaldehyde or other condensed reaction products have been observed. In contrast, the intermediate formation of formaldehyde in methanol steam reforming on rh-In₂O₃¹² strongly suggests that neither the basic nor the acidic character of the relevant surface sites is too pronounced. The CO₂ selectivity is accordingly low, but in-parallel also no condensed products are observed.

As for the answer to question (2), we note that the steam reforming reaction can in principle take two different pathways, depending on the partial pressure and temperature: a more oxygen vacancy-dominated route and a more surface-restricted formate-related pathway.¹³ The former is very much pronounced on c-In₂O₃, due to the easy removal of reactive lattice oxygen and at the same time, the associated formate-related mechanism is essentially suppressed. In contrast – although the reduction behavior on rh-In₂O₃ is comparably pronounced (especially in CO) – the formate mechanism does obviously contribute significantly more on rh-In₂O₃. This follows from the correlated impedance and FT-IR data upon treatment in CO. A vital chemistry of formates, especially in the catalytically relevant temperature regime of 500–650 K, is evident. Superimposed on this formate chemistry is the significant contribution of the vacancy reactivity, as reflected in the change of the relative total transmittance.

4. Conclusions

• Particularly important for sensing mechanisms involving redox cycles, by performing reduction experiments in hydrogen and carbon monoxide under identical experimental conditions, it was possible to relate temperature-dependent conductivity features to pronounced changes in surface chemistry, allowing for disentangling purely reduction-related features from those directly arising from surface-chemical alterations. For highly reducible oxides such as rh- or c-In₂O₃, for which not only the formation of oxygen vacancies, but deep reduction to a metallic valence state In⁰ also has to be taken into account, this approach is imperative.

• In the reference inert gas atmosphere, the analysis also included monitoring differently reactive hydroxyl groups (note that the formation of reactant water on particle coarsening or morphology needs to be separately assessed since the latter is continuously removed by performing flowing experiments in the present case).

• Important for catalysis, as deduced from carbon monoxide and carbon dioxide adsorption, rh-In₂O₃ exhibits predominantly Lewis acidic surface sites. The basic character is less pronounced, directly explaining the previously observed high (inverse) water–gas shift activity and the low CO₂ selectivity in methanol steam reforming.

• Necessary for the judgment of the influence of the phase transformation on eventual sensing properties in reductive atmospheres, reduction of rh-In₂O₃ proceeds to a large extent indirectly via rh-In₂O₃ → c-In₂O₃ → In metal and in both CO and H₂ is essentially dominated by the reactivity of the formed oxygen vacancies.

It is worth noting that only via the excellent correlation between in situ – determined electrochemical information and surface chemistry by combining spectroscopic characterization methods performed under identical experimental conditions are such conclusions possible. In due course, it allows not only to gain access to the inherently hard-to-obtain physico-chemical properties of metastable oxide modifications, such as the truly technologically or catalytically important surface reactivity. By performing highly correlated measurements, this information can be related to the surface and bulk conduction properties and to build a bridge to material's-oriented properties, such as the phase stability. The comparison of those features using the In–O, and specifically, the In₂O₃ polymorphic system appears particularly worthwhile given the outstanding technological and catalytic fingerprints of the cubic and rhombohedral modifications. Given the extraordinary coincidence of in situ obtained electrochemical impedance and FT-IR spectra in the present case, we anticipate the extension of these experiments not only to the remaining polymorphs in the In₂O₃ system – provided synthesis routines to access substantial amounts of the material exist – but envision also the establishment of state-of-the-art correlated in situ characterization for oxide or related materials research.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank the FWF (Austrian Science Foundation) for financial support under the SFB project FOXSI F45-03. This work was performed within the framework of the platform “Materials and Nanoscience” at the University of Innsbruck. We thank the Advanced Light Source (which is supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231) where in situ PXRD measurements were conducted at Beamline 12.2.2 within the framework of the AP program ALS-08865. LS appreciates the ALS for supporting his work with a doctoral fellowship. L. S. and A. G. also acknowledge the DFG support (grant GU 992/12-1) within the framework of the priority programme 1415 “Crystalline non-equilibrium phases” (“Kristalline Nichtgleichgewichtsphasen – Präparation, Charakterisierung und in situ Untersuchung der Bildungsmechanismen”). This work was also a part of the Cluster of Excellence “Unifying Concepts in Catalysis” coordinated by the Technische Universität Berlin and supported by the Deutsche Forschungsgemeinschaft.

References

1. M. F. Bekheet, M. R. Schwarz, P. Kroll and A. Gurlo, J. Solid State Chem., 2015, 229, 278–286.
2. M. F. Bekheet, M. R. Schwarz, S. Lauterbach, H. J. Kleebe, P. Knoll, R. Riedel and A. Gurlo, Angew. Chem., Int. Ed., 2013, 52, 6531–6535.
3. L. Pauling and M. D. Shappell, Z. Kristallogr., 1930, 75, 128–133.
4. C. T. Prewitt, R. S. Shannon, D. B. Rogers and A. W. C. Sleight, Inorg. Chem., 1969, 8, 1985–1993.
5. M. F. Bekheet, M. R. Schwarz, S. Lauterbach, H. J. Kleebe, P. Kroll, A. Stewart, U. Kolb, R. Riedel and A. Gurlo, High Pressure Res., 2013, 13, 697–711.
6. M. Epifani, P. Siciliano, A. Gurlo, N. Barsan and U. Weimar, J. Am. Chem. Soc., 2004, 126, 4078–4079 and references therein.
7. C. H. Lee, M. Kim, T. Kim, A. Kim, J. Paek, J. Lee, S. Choi, K. Kim, J. Park and K. Lee, J. Am. Chem. Soc., 2006, 128, 9326–9327.
8. L. Schlicker, M. F. Bekheet and A. Gurlo, Z. Kristallogr., 2017, 232, 129–140.
9. P. D. C. King, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 20511–20518.
10. T. de Boer, M. F. Bekheet, A. Gurlo, R. Riedel and A. Moewes, Phys. Rev. B, 2016, 93, 155205.
11. T. Sahm, A. Gurlo, N. Barsan and U. Weimar, Part. Sci. Technol., 2006, 24, 441–452.
12. E. M. Köck, M. Kogler, C. Zhuo, M. Grünbacher, R. Thalinger, L. Schlicker and A. Gurlo, J. Phys. Chem. C, 2016, 120, 15272–15281.
13. T. Bielz, H. Lorenz, A. Amann, B. Klötzer and S. Penner, J. Phys. Chem. C, 2011, 115, 6622–6628.
14. H. Lorenz, M. Stöger-Pollach, S. Schwarz, K. Pfaller, B. Klötzer and S. Penner, Appl. Catal., A, 2008, 347, 34–42.
15. C. Miao, J. Wu, Y. Liu, Y. Cao, L. Guo, H. He and K. Fan, Appl. Catal., A, 2011, 407, 20–28.
16. B. Hoch, L. He, Q. Qiao, K. Liao, L. Reyes, L. Zhu and G. Ozin, Chem. Mater., 2016, 28, 4160–4168.
17. Y. Pan, Y. You, S. Xin, Y. Li, G. Fu, Z. Cui, Y. Men, F. Cao, A. Yu and J. Goodenough, J. Am. Chem. Soc., 2017, 139, 4123–4129.
18. A. Gurlo, Nanoscale, 2011, 3, 154–165.
19. L. Gao, F. Ren, Z. Cheng, Y. Zhang, Q. Xiang and J. Xu, CrystEngComm, 2015, 17, 3268–3276.
20. L. Gao, Z. Cheng, Q. Xiang, Y. Zhang and J. Xu, Sens. Actuators, B, 2015, 208, 436–443.
21. J. Xu, Y. Chen, Q. Pan, Q. Xiang, Z. Cheng and X. W. Dong, Nanotechnology, 2007, 18, 115615.
22. J. L. Solis, S. Saukko, L. Kish, C. G. Granqvist and V. Lantto, Thin Solid Films, 2001, 391, 255–260.
23. A. K. Prasad, D. J. Kubinski and P. I. Gouma, Sens. Actuators, B, 2003, 93, 25–30.
24. E. M. Köck, M. Kogler, R. Pramsoler, B. Klötzer and S. Penner, Rev. Sci. Instrum., 2014, 85, 084102.
25. A. Doran, L. Schlicker, S. Beavers, S. Bhat and M. F. Bekheet A. Gurlo, Rev. Sci. Instrum., 2016, 88, 1–7.
26. J. H. de Wit, G. Van Unen and M. Lahey, J. Phys. Chem. Solids, 1977, 38, 819–824.
27. T. Bielz, H. Lorenz, W. Jochum, R. Kaindl, F. Klauser, B. Klötzer and S. Penner, J. Phys. Chem. C, 2010, 114, 9022–9028.
28. M. Tatibouet, Appl. Catal., A, 1997, 148, 213–222.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional EIS and FT-IR experiments; collected FT-IR spectra, activation energies and EIS tables. See DOI: 10.1039/c7cp03632a

‡ These authors contributed equally.

---