CO diffusion as a re-orientation mechanism in the NaY zeolite

Abstract

Our work is devoted to DFT calculations of the relative rotational and diffusional barriers for CO motions in zeolite NaY. The diffusion jump of CO adsorbed in NaY from NaII to Na′II has been confirmed as the favored way for CO re-coordination via either the C or the O atom to the Na cations instead of the CO rotation, hence explaining the mechanism which is responsible for the CO exchange between different positions and the changes in the intensities of the vibrational IR spectra. The fine structure of the vibrational C–O bands is explained by the different CO locations of adsorbed mono- and dicarbonyl species. The calculated activation energy of intra-cage CO diffusion from NaII–CO to Na′II–OC matches the respective experimental barrier observed in the NaX zeolite.

---

1. Introduction

Gas separation in zeolites and MOF structures is expected to be one of their main future applications. Verification of their effectiveness in separation requires the estimation of the diffusion coefficients in the intra- and intercrystalline pores for each candidate material. So far, various intra- or intercrystalline diffusion regions have been related to the domination of different molecular properties such as size or weight, respectively.¹ To avoid any influence of intercrystalline diffusion on the measurements, sealing techniques for the intercrystalline pores using silica precursor deposition after CVD-treatment were applied for DDR¹ and MFI² zeolites. For intracrystalline CO diffusion, activation energies of 15.5 kJ mol⁻¹ in DDR¹ and 17.1 kJ mol⁻¹ in NaX³ were, for example, obtained. Within the scope of the translational diffusion model,⁴ activation barriers were also reported in terms of the ratio between kinetic diameters and pore sizes.¹ Nevertheless, comparison between CO and CO₂ is difficult for such classification because of the estimated higher kinetic diameter of CO versus CO₂ (3.76 Å for CO versus 3.30 Å for CO₂¹) due to the evident opposite ratio of their molecular spatial parameters.‡ Theoretical computations of the activation energies required for the migration between the sites^5,6 are rare and most of the data relative to diffusion were obtained experimentally. Hence, a deeper understanding of the relation between the diffusion behavior and molecular properties for CO in zeolites is desirable. The respective jump models over the sites of the NaY zeolite considered as an Ising lattice were already developed even for heavier benzene species.⁵

Another important field wherein the relation between molecular translations and rotations is extremely important is catalysis in zeolites and other solids. As recent theoretical studies, let us cite CO oxidation in the MgPHI zeolite,⁷ CO₂ hydrolysis in the NaX zeolite,⁸ or CH₃OH reaction with CuCO₃Cu carbonate species in the CuMOR zeolite.⁹ In all cases, the orientation of the reagents (CO,⁷ CO₂, H₂O,⁸ CH₃OH⁹) is determined by the media in the pores that can hardly be simulated at the cluster level. The knowledge of all allowed motions for the reagents with definite molecular properties (van der Waals radii, multipole moments, etc.) in a specific zeolite geometry under imposed conditions might be the decisive tip to predict the best position of the reactive center in the zeolite pores. In particular, the case of appropriate CO orientation and subsequent chemisorption in a periodic MgPHI model allowed a significant reduction in the CO oxidation barrier.⁷ Any new data on the restrictions of the CO motions will allow more accurate modeling of the CO dynamics in catalyzed reaction systems and will drastically reduce the number of candidate routes for time consuming modeling of reaction pathways.

Additional landmarks for CO diffusion can be found throughout a large number of IR studies of CO adsorption over alkali and earth alkaline form zeolites.^3,10–15 Two main peaks are most often assigned to MeII–CO and MeII–OC orientations, with Me being the alkali or earth alkaline cation, and alternative interpretations appeared as a consequence of a cationic rearrangement. For NaY, Grey et al.^16,17 and Mellot-Draznieks et al.¹⁸ observed, using XRD data, a decrease of NaI′ occupation and a formation of sites similar to the NaIII′ site in NaX in the presence of adsorbed C₂F₄H₂^16,17 or CFCl₃¹⁸ species. Plant et al. admitted such a possibility of NaI′ migration to the NaIII′ site upon the influence of CO₂ to model the cationic diffusion.¹⁹ An analogous influence of CO on the cationic positions in NaY and CuNaY later led to assigning the origin of the peaks to NaII–OC–NaIII and NaII–CO–NaIII sites²⁰ even if the experimental data did not confirm the possibility of CO diffusion and interaction with NaI′ in sodalite units of NaY.¹⁰ One should note that analogous dual cationic sites for Me⁺–CO–Me⁺ were already confirmed in MeZSM-5²¹ and MeFER,²² Me = Na^21,23 or K,^21,22 zeolites, on the basis of combined DFT modeling and IR experiments to interpret the intermediate bands observed between the monocarbonyl peaks related to either Me–CO or Me-OC orientations. If the NaIII or NaIII′ positions are occupied in NaY, then the NaII–OC (or CO)–NaIII (or NaIII′) dual sites²⁰ should lead to similar intermediate peaks in NaY. Recently, we have modeled the migration of alkali cations between crystallographic positions in MeRHO (Me = Li, Na, K, Cs)²⁴ and MeY (Me = K, Cs)²⁵ upon formation of carbonate or hydrocarbonate anions whose interactions with cations have to be much more effective than the ones of CO and lead to cationic drift. Usually smaller CO interaction energies with cations stimulated us to verify the model of NaIII formation in NaY²⁰ which should have direct consequences for the assignment of IR spectra.

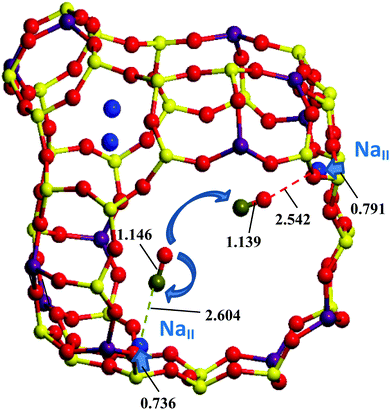
The heats of the respective CO/OC exchanges were determined using van't Hoff dependences of the IR intensities,^13,14,26 but, to our best knowledge, no mechanism of CO redistribution with temperature was proposed. Such a redistribution has been shown to take place for CO adsorbed in H- and any cationic form zeolites.¹⁵ At first glance, the evident idea of CO rotation might resolve the problem of the respective mechanisms. Some attempts to assign the fine structure of CO vibrational peaks in IR spectra in NaA²⁷ and NaY²⁸ to rotational transitions only (in contrast to CaA, NaX, and CaX where no separate peaks were found) were already undertaken many years ago but were not well evidenced. A modeling of the rotational structure of fundamental CO transition was undertaken by Förster et al. by analyzing possible barriers in NaA and NaCaA with a simplified model of a hindered rotator.²⁹ However, the absence of band widening (due to rotational P- and R-branches) for CO/NaZSM-5 at higher temperatures (123–293 K) does not validate the possible CO rotation for all temperatures and for all zeolites because the intensity ratio of the CO vibrational transitions varies between the Me–CO/Me–OC bands within a wide range of temperatures.³⁰ The hindrance of rotation is connected with electrostatic field and/or field gradient variations in the zeolite cages. If these properties decrease from the cation location towards the center of the zeolite Y cage, then almost free CO rotation is allowed far from the cation in monovalent Y forms. The hypothesis that the CO and OC forms can be connected via a diffusion jump between two different Me cations hence deserves attention. As seen from Fig. 1, the CO shift from NaII–CO to Na′II–OC does not require any essential CO axis rotation due to the tetrahedral symmetry of the FAU supercage. Because of the larger electrostatic field and/or field gradient in divalent zeolite forms, this hindrance may be supposed for CO rotation in divalent forms as well and also explain the absence of rotational branches in the vibrational bands of CO adsorbed in zeolites.

Fig. 1 Three-dimensional structure of a NaY cage and possible CO shift from one NaII to the other Na′II site at the PBE/PAW level. The |C–O| and |C/O–Na| distances (in Å) are given. Curved arrows show translational and rotational CO motions. Linear arrows (non-scaled) illustrate the NaII displacements (in Å) from the 6R planes passing through the three nearest O neighbors. Na, O, Si, Al, and C atoms are given in blue, red, yellow, magenta, and olive color, respectively.

Computations of CO adsorption over zeolite clusters showed the necessity of accurate estimation of electrostatic forces³¹ so that Density Functional Theory (DFT) (for example, with VASP^32,33) considering models with periodic boundary conditions (PBC) is needed. The computational scanning of the various Brønsted and Lewis sites in HMOR indeed demonstrated a variety of zeolite properties which can be obtained using a CO probe.³⁴ Recently, various DFT functionals were compared for CO and NO adsorbed in transition metal form zeolites (CuCHA, CoCHA).³⁵

The work presented here is devoted to the calculations of the rotational and diffusional barriers for CO motions in NaY. After the computational details (Section 2), we will discuss the results obtained with different DFT functionals regarding the geometries (Section 3.1), heats (Section 3.2), frequencies (Section 3.3), and barriers of CO rotation and of NaII–CO/Na′II–OC diffusion (Section 3.4) relative to known experimental data.

2. Computational details

Plane wave computations with PBC using the PBE³⁶ and PBEsol³⁷ functionals within the projector augmented wave (PAW) method^38,39 were performed with VASP.^32,33 The energy cut-off was set to 500 eV. The Brillouin zone k-sampling was restricted to the Γ-point. Dispersion energy corrections were considered at the D2⁴⁰ and D3 with Becke–Johnson damping (PBEsol-D3(BJ))^41,42 levels.

Cell parameters were first optimized for the NaY model with the total formula Na₁₂Al₁₂Si₃₆O₉₆. These cell parameters were then used in all further calculations. Full geometry optimizations were performed for each structure (products, reagents) with the fixed cell parameters and switched off symmetry. The climbing image nudged-elastic band method (ciNEB)^43,44 was used to determine the minimum energy path from reagents to products and to locate the transition state structure. Initial images of the intermediate configurations for the NEB calculations were built with the scripts provided by the Transition State Tools for VASP. We assumed that the convergence for geometry optimizations and NEB calculations was reached when the forces on each atom were below 0.05 eV Å⁻¹.

CO vibrational frequencies were calculated using the finite difference method (0.015 Å atomic displacements) as implemented in VASP. Atoms of either one CO or two CO molecules, the closest (one or two) Na cations, and the zeolite O_z atoms coordinated to the Na cations were allowed to move during the vibrational frequency calculations, while all other atoms were kept fixed. The error owing to fixation of the O_z zeolite atoms was estimated to be 1 cm⁻¹. For all reactions, the transition states showed a single imaginary frequency corresponding to the reaction path. Figures of the optimized models were made with MOLDRAW2.0.⁴⁵ Videos of chemical reactions and normal mode animations were made using wxMacMolPlt.⁴⁶

3. Results

3.1 Geometry optimization

The optimized cell volume of each considered NaY structure, including or not either one or two physisorbed CO molecules in various positions, varies most strongly with PBEsol-D3(BJ) (1.71%) and optB86d (0.64%), while minimal changes were obtained with PBE (8 × 10⁻³%) (Table 1 and Fig. 2). PBEsol led to an intermediate variation of 0.26%. In all models, adsorption results in the NaII–O_z elongation, with O_z being the oxygen atom of the zeolite framework.

Table 1 Cell volume of NaY (ų) and its variations ΔV (%) due to CO species (excluding the case with NaIII) adsorbed at the N sites of NaII type (N being the number of Na cations interacting with one or two CO molecules as noted in the first column) in the two different Na–CO or Na–OC orientations (distinguished by the order of C and O labels in the first column) calculated at the different DFT levels

Orientation	N	PBE	PBEsol	PBEsol-D2	OptB86d
a One NaII is replaced by NaIII. b See the geometry in Fig. 2b. c See Fig. 2c.
—	—	3935.6	3889.3	3917.5	3910.2
—^a		3920.7	3876.4	—	3880.3
CO	1	3935.5	3889.3	3858.4	3896.0
OC		3935.3	3879.5	3849.3	3935.5
2CO		3935.6	3888.7^b	3848.2	3892.3
CO, OC		3935.6^c	3880.8	3847.6	3897.6
2CO	2	3935.6	3889.1	—	3909.6
ΔV	—	0.008	0.26	1.79	0.64

---

Fig. 2 Three-dimensional structure of a NaY cage with CO positions (a) between NaII and NaIII, or as (b) OC–NaII–CO or (c) CO–NaII–CO, and (d) NaII–CO optimized at the PBE (a and c), PBEsol (b), and PBEsol-D2 (d) levels. Dashed lines depict the |C–O| and |C/O–Na| distances (in Å) given (a) in Table S2 (ESI†) and (b, c and d) in Table 2. Two degenerate CO positions are shown in (d). The atom color code is the same as in Fig. 1. Linear arrows (non-scaled) illustrate the NaII and NaIII displacements (in Å) from the 6R and 4R planes, respectively, passing through the three nearest O neighbors.

We also analyzed the consequence of Na shift from the NaII to NaIII site^18–20 regarding the total energy (case 5 in Fig. 3), the IR spectra (Section 3.2), and the activation energy (Section S1, ESI†). The cell volumes with NaIII cations are coherently lower by −0.4, −0.3, and −0.8% with PBE, PBEsol, and optB86d, respectively, while the energies are less stable due to poor NaIII coordination by as much as 7.6, 6.1, and 5.8 kcal mol⁻¹, respectively (see Table 2 and Table S2, ESI†). Let us also note that both DFT approaches with dispersion corrections we applied are less consistent relative to the volume perturbation due to CO adsorption. The variations of the volumes while adding either one or two CO molecules do not reveal a systematic trend (Table 1). For example, the cell optimization with one CO molecule for the NaII–CO or NaII–OC configurations led to opposite volume changes by −0.25 or 1.1% with PBEsol and optB86d, respectively. These large distortions look overestimated, while the minor change in the cell volume with one physisorbed molecule is more realistic with PBE, i.e., less than 0.008% in Table 1.

Table 2 Total energy U (eV), energy of adsorption ΔU (kcal mol⁻¹) per CO relative to the non-interacting NaY zeolite and gas phase CO (data in Table S1, ESI), molecular |C–O| bond length and distances towards the Na and O_z zeolite atoms (Å), CO frequencies (ω_HF, ω_LF, cm⁻¹), and their shifts Δω_HF, Δω_LFversus gas phase CO calculated at the different DFT levels. The CO orientation is given in column 2, the first atom of either CO or OC being directed towards NaII. N in the parentheses in column 2 is the number of Na cations interacting with one or two CO molecules if more than 2 molecules are adsorbed. For analogous models with NaIII cations, see Table S2 (ESI)

DFT	Case (N)	−U	−ΔU	|C–O|	|C/O–Na|^a	|Na–Oz|	ω HF, ωLF	ΔωHF, ΔωLF
a The case of an O-connected CO molecule in dicarbonyls at one NaII (N = 1, Fig. 2c) and relevant cases for two NaII (N = 2) are marked by stars. b See Fig. 2c. c See Fig. 2b. d Starting geometry taken from the case with the total energy of −1082.96 eV to reach a more symmetric dicarbonyl structure with energy of −1083.00 eV. e Case shown in Fig. 2d.
PBE	—	1161.21	—	—	—	3 × 2.360	—	—
	CO	1176.22	5.4	1.139	2.604	2.356, 2.378, 2.381	2179.6	44.1
	OC	1176.13	3.3	1.146	2.542	3 × 2.378	2112.8	−22.7
	CO, CO (2)	1191.22	5.3	1.139, 1.139	2.618, 2.617	2.369, 2.372, 2.374, 2.363, 2.370, 2.383	2180.6, 2178.3	45.1, 42.8
	CO, OC (1)^b	1191.05	3.3	1.139, 1.146	2.674, 2.802*	2.406, 2.423, 2.424	2192.3, 2122.3	56.8, −13.2
	2CO (1)	1191.11	4.0	1.140, 1.140	2.682, 2.833*	2.415, 2.440, 2.446	2172.8, 2163.8	37.3, 28.3
	2OC (1)	1190.96	0.3	1.146, 1.146	2.802*, 2.766*	2.407, 2.421, 2.422	2119.8, 2113.9	−15.7, −21.6
PBEsol	—	1129.31	—	—	—	3 × 2.336	—	—
	CO	1144.13	6.2	1.137	2.569	2.333, 2.353, 2.355	2192.6	39.3
	OC	1144.04	4.1	1.145	2.523	2 × 2.363, 2.365	2123.8	−29.5
	CO, CO (2)	1158.92	5.9	1.137, 1.137	2.605, 2.595	2.344, 2.348, 2.358, 2.350, 2.353, 2.355	2193.4, 2189.5	40.1, 36.2
	CO, OC (1)	1158.75	3.9	1.138, 1.145	2.610, 2.705*	2.370, 2.391, 2.394	2191.8, 2124.0	38.5, −29.3
	2CO (1)^c	1158.83	4.8	1.138, 1.138	2.625, 2.761*	2.383, 2.408, 2.417	2185.1, 2175.4	31.8, 22.1
PBEsol-D2	—	1144.90	—	—	—	3 × 2.356	—	—
	CO^e	1159.92	10.8	1.137	2.578	2.324, 2.345, 2.348	2196.2	42.9
	CO^e	1159.92	10.8	1.137	2.615	2 × 2.336, 2.338	2191.1	37.8
	OC	1159.80	8.1	1.144	2.514	2.351, 2.352, 2.356	2127.9	−25.4
	2CO (1)	1174.84	9.6	1.139, 1.138	2.664, 2.687	2.391, 2.401, 2.405	2185.9, 2181.8	32.6, 28.5
	2OC (1)	1174.63	7.2	1.144, 1.144	2.553, 2.562	2.391, 2 × 2.392	2133.6, 2130.6	−19.7, −16.7
	CO, OC (1)	1174.74	8.6	1.138, 1.144	2.655, 2.584	2.380, 2.401, 2.403	2187.0, 2131.7	33.7, −21.6
PBEsol-D3(BJ)	—	1141.12	—	—	—	3 × 2.343	—	—
	CO	1156.03	8.2	1.137	2.620	2.366, 2.364, 2.350	2190.3	37.8
	OC	1155.92	5.8	1.145	2.537*	2.360, 2.360, 2.367	2124.6	−27.9
	CO, CO (2)	1170.93	8.2	1.137, 1.138	2.638, 2.637	2.356, 2.353, 2.352, 2.364, 2.352, 2.356	2190.9, 2186.4	38.4, 33.9
	CO, OC (1)^b	1170.80	6.6	1.138, 1.144	2.691, 2.861*	2.393, 2.392, 2.380	2187.4, 2128.2	34.9, −24.3
	2CO (1)	1170.87	7.5	1.138, 1.139	2.714, 2.909	2.391, 2.410, 2.405	2180.3, 2173.9	27.8, 21.4
	2OC (1)	1170.68	5.4	1.145, 1.144	2.835*, 2.757*	2.392, 2.390, 2.385	2133.6, 2127.0	−18.9, −25.5
OptB86d	—	1056.95	—		—	3 × 2.343	—	—
	CO	1069.97	8.1	1.138	2.607	2.348, 2.350, 2.351	2178.7	49.2
	OC	1069.93	7.0	1.146	2.502	2 × 2.362, 2.364	2111.3	−18.2
	CO, CO (2)	1083.06	8.7	1.138, 1.138	2.604, 2.608	2.343, 2.348, 2.360, 2.350, 2.353, 2.354	2180.7, 2175.8	51.2, 46.3
	CO, OC (1)	1082.96	7.5	1.139, 1.146	2.640, 2.951*	2.362, 2.381, 2.386	2174.3, 2109.3	44.8, −20.5
	CO, OC (1)^d	1083.00	8.0	1.139, 1.146	2.668, 2.628*	2.369, 2.387, 2.388	2173.8, 2113.1	44.3, −16.7
	CO, OC (2)	1082.99	7.8	1.138, 1.145	2.493*, 2.602	2.356, 2.358, 2.359, 2.344, 2.346, 2.348	2181.3, 2115.0	51.8, −14.5
	2CO (1)	1083.03	8.4	1.139, 1.140	2.646, 2.984	2.364, 2.404, 2.407	2171.7, 2160.4	42.2, 30.9

---

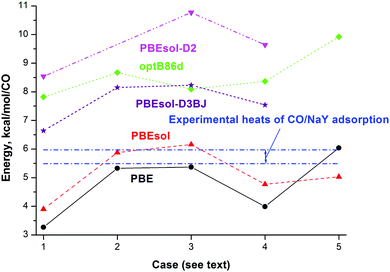Fig. 3 Calculated total energy (kcal mol⁻¹) per CO of each considered NaY model including the various configurations of CO species at the PBE (circles), PBEsol (triangles up), PBEsol-D2 (triangles down), PBEsol-D3BJ (stars), and optB86d (diamonds) levels and experimental heats of adsorption (upper and lower boundaries given via dotted-dashed lines^10,11). Different cases correspond to adsorption of one CO (cases 3 and 5) or two CO (cases 1, 2, and 4) molecules at one NaII site (cases 1, 3, and 4), one NaIII site (case 5) or two NaII sites (case 2) coordinated via the Na–CO orientation (cases 2 and 4) or Na–CO plus Na–OC orientations (case 1).

The local NaII cationic geometry was then analyzed upon CO adsorption (Table 2). Three coinciding NaII–O_z distances of 2.360 Å (Table 2) were obtained at the PBE/PAW level in the 6R window, which are in good agreement with XRD Na–O_z lengths, i.e., 2.337 Å in NaY^16,17 or NaNAT,⁴⁷i.e., as from 2.371 and 2.394 Å towards the O_w atoms of the nearest water molecules to 2.367, 2.395, 2.518, and 2.615 Å towards the zeolite O_z atoms of NaNAT.⁴⁷ The NaII coordination varies between usually lower coordinated NaIII′ cations in the 4R window (with NaIII′–O_z of 2.441, 2.464, 2.519, 2.776 Å) and NaII in the similar FAU cage, i.e., |NaII–O_z| = 2.311, 2.316, and 2.356 Å at the PBE level. We remind that the NaY model with NaIII′ was used herein as proposed in ref. 18–20 (more details in Section S1 of the ESI†). The NaII–O_z value of 2.360 Å at the PBE level slightly shortens to 2.336 and 2.343 Å with PBEsol and optB86d, respectively, also in reasonable agreement with the experimental data.^16,47

The Na–O_z distances elongate due to CO adsorbed at NaII (Table 2) in a less emphasized manner than those measured upon adsorption of 16 or 32 CF₃CFH₂ molecules,^16,17i.e., from 2.337 Å (no physisorbed molecules) to 2.478 Å (16 molecules per unit cell or 2 molecules per NaY supercage) and 2.510 Å (32 molecules per unit cell).^16,17 Other NaII–O_z elongations were computed in the course of carbonate formation in the NaX zeolite.⁴⁸ For comparison, the elongations of the shortest NaII–O_z bonds due to one or two carbonate (or hydrocarbonate) species are given in Fig. 3 of ref. 48. One or two carbonates (or hydrocarbonates) per two NaX supercages are indeed closely connected to the NaII cation/cations, the average elongations being 0.07 and 0.08 Å for one or two carbonates (or hydrocarbonates), respectively, within the most stable configurations and 0.19 and 0.16 Å within the least stable configurations.⁴⁸ These last calculated values are of the same order of value as the ones measured in NaY in the course of CF₃CFH₂ adsorption, 0.141 Å (16 molecules or 2 molecules per supercage) and 0.173 Å (32 molecules) from Table 4 of ref. 16.

3.2 Energy calculations

The molecular properties of CO in the gas phase are required for comparison of the band shifts (BSs) and calculation of adsorption energies of CO in the zeolite framework. The total energies and molecular properties of CO in the gas phase calculated at different DFT levels are given in Table S1 (ESI†). Among the three computational approaches, we note the slightly underestimated and overestimated heats of adsorption with PBE and PBEsol, respectively, relative to experiment^10–12 at small coverage for CO (upper and lower boundaries given by dotted-dashed lines in Fig. 3; data are also presented in Table 3). Values computed with optB86d, PBEsol-D2, and PBEsol-D3BJ are larger than the experimental heat values (to be compared with case 3 in Fig. 3).

Table 3 Heat of CO/OC re-orientation (ΔU, kcal mol⁻¹), activation barrier of CO rotation (E^#_rot, kcal mol⁻¹) and diffusion between NaII sites (E^#_dif, kcal mol⁻¹), isosteric heats of CO adsorption Q_st = −ΔU + RT, where RT was evaluated as the average value between 0.5 and 0.6 kcal mol⁻¹ for the experimental conditions at 250–318 K in ref. 10, ΔU values are from Table 2, splitting of the CO–OC frequencies (Δω = ω_HF − ω_LF, cm⁻¹), and imaginary frequencies −iω, cm⁻¹, at the transition states for CO rotation and diffusion in NaY calculated at the different DFT levels

Parameter	PBE	PBEsol-D3(BJ)	OptB86d	Experiment
a At one NaIII site. b CO rotation along the diffusion trajectory, and it is bonded with NaII with the C atom in the beginning and in the end of migration. c Motion towards the already occupied NaII site. d Migration from the NaII to NaIII site. e Diffusion between NaII sites in neighbor supercages without CO rotation (see the animation file in the ESI). f CO rotation along diffusion between NaII sites in neighbor supercages maintaining the NaII–CO orientation. g For the NaX zeolite.^3 h PBEsol. i PBEsol-D2.
ΔU	2.0, 0.7^a	2.1,^h 1.3,^a^,^h 2.7,^i 1.8	1.1, 0.02^a	0.6^10–12
E ^#rot	5.4	5.3	—	—
−iωrot	107.4	96.6	—	—
E ^#dif	4.1, 5.3,^b 5.5,^c 0.7,^d 4.5,^e 4.9^f	4.7, 6.0,^b 1.0,^d 4.0,^e 4.6^f	—	4.1^g^3
−iωdif	19.1, 71.8,^b 98.5,^c 35.2,^d 72.6,^e 109.9^f	73.7, 71.5,^b 45.4,^d 77.7,^e 80.5^f	—	—
Q st	5.9	6.7,^h 11.3^i	8.7	(5.5–6.1) ± 0.5,^10–12 5.0,^28 5.6^g
Δω	66.8	65.7, 68.8,^h 63.2–68.3^i	67.4	53,^14 49^15

---

Before discussing dicarbonyls, one has to consider the important example of monocarbonyls over NaII which is typical with all DFT methods used herein (Fig. 2d). Two CO molecules corresponding to different monocarbonyls with nearly the same energies of −1156.92 eV (C₁–O₁) and −1156.92 eV (C₂–O₂) at the PBEsol-D2 level (cases (e) in Table 2) were obtained, as shown in Fig. 2d. The C₂–O₂ molecule deviates by around 20° from the C₁–O₁ axis orientation which is perpendicular towards the 6R plane, i.e., O_z–Na–C₂ = 70.28° versus O_z–Na–C₁ = 90.25°. However, it does not lead to a valuable energy variation (0.02 kcal mol⁻¹). The C₁–O₁ → C₂–O₂ motion between two nearly iso-energetic positions is also accompanied by a Na–C shortening (0.037 Å) and a weak Na migration to a less symmetric position relative to the O_z atoms of the 6R window. Comparing the Na–O_z distances at the PBEsol-D2 level with those calculated at the other levels (Table 2), one can guess that the CO position in monocarbonyls corresponds to the C₁–O₁ type (CO is nearly perpendicular to the 6R plane) with optB86d and to the C₂–O₂ type (tilt geometry) with PBE and PBEsol. In dicarbonyls, the C₁–Na–C₂ angle is generally around 70°, i.e., 72.66, 72.44, and 71.83° at the PBE, PBEsol, and optB86d levels, respectively. Hence each CO in dicarbonyls is far from the Na and is outside the abovementioned iso-energetic zone with a steric angle, formed by the C₂–O₂ deviation from the C₁–O₁ axis, around 40°. So, the different CO locations within this steric angle are characterized by the same energy (and slightly different BSs as shown below). An energy advantage of the C₁–O₁ or C₂–O₂ geometry can come from different C₁–O₁ and C₂–O₂ zero point energies (ZPEs). Our estimation at the PBEsol-D2 level leads to a minor value of −0.03 kcal mol⁻¹ (10 cm⁻¹) with a higher ZPE for the C₁–O₁ type. This ZPE estimate corresponds to 9 degrees of freedom for the Na–CO complex versus the other fixed zeolite atoms.

The addition of a second CO molecule at a neighbor NaII site as NaII–CO in the FAU cavity (case 2 in Fig. 3) leads to different energy changes per CO with the different DFT methods, i.e., it slightly decreases with PBE and PBEsol but increases with optB86d. The adsorption of a second CO molecule at the same NaII site as Na–CO (case 4 in Fig. 3) or Na–OC (case 1 in Fig. 3) orientations decreases the energy per CO (in absolute values) in the same manner with both PBE and PBEsol. The average energy per CO changes very little with CO adsorption at the optB86d level, which thus clearly underestimates the role of CO–CO interactions. According to Egerton and Stone, the isosteric heat of CO/NaY adsorption is nearly constant at small coverage, i.e., from 5 × 10⁻⁸ to 10⁻⁷ m³ g⁻¹.¹⁰ The CO/NaX case is characterized by a quick decrease of the heat of adsorption with coverage,⁴⁹ while optB86d demonstrates a rather opposite trend. Based on the narrow interval of the CO coverage and the nearly constant heat of adsorption behavior known for CO/NaY,¹⁰ it is difficult to finally conclude which heat dependence (increase, decrease, or minor dependence) on the CO coverage is closer to the reality. Let us add that the possible modifications of cationic sites at higher CO coverage and the appearance of NaIII sites also complicate the question.

Both PBE and optB86d lead to higher adsorption energies per CO when the NaIII site is occupied (case 5 in Fig. 3). If the less stable NaIII centers with higher adsorption energy are occupied at higher CO coverage, they will moderate the decrease of the adsorption heat with coverage or they will even change the trend to the opposite. The problem is then to determine the coverage at which high CO concentration leads to the migration of CO from NaI′ to NaIII′ sites, but the problem is outside the current study as we focus on small coverage only. We thus compared the adsorption energy gain in the Henry domain (or close to it) at all three PBE, PBEsol, and optB86d levels due to the increase of the single CO interaction with the NaIII cation (6.0, 5.0, and 9.9 kcal mol⁻¹) versus the NaII cation (5.4, 6.2, and 8.1 kcal mol⁻¹) as their differences 0. 7, −1.1,§ and 1.8 kcal mol⁻¹, respectively. The values have to be compared to the destabilization of the NaY zeolite, i.e., the price to move one cation from the NaII to the NaIII site, 7.6, 6.1, and 5.8 kcal mol⁻¹ at the PBE, PBEsol, and optB86d levels, values that cannot be compensated by the higher adsorption energies at the NaIII site instead of NaII, i.e., 0. 7, −1.1, and 1.8 kcal mol⁻¹ at the PBE, PBEsol, and optB86d levels. So, the formation of NaIII¶ cations in NaY cannot be justified thermodynamically if one uses one CO molecule per NaIII. If one would manually construct a NaY model with NaIII cations coming from the NaI positions where they are more tightly connected by three shortest NaI–O distances of 2.251, 2.228, and 2.238 Å instead of the shortest 2.360, 2.336, and 2.343 Å for NaII–O at the PBE, PBEsol, and optB86d levels (Table 2), then the destabilization would be even larger. In relation to this, here we mention that additional restrictions on the formation of NaIII cations can be obtained from spectroscopic interpretations.

The NaII–OC and NaII–CO distance values illustrate the deviations between mono- and dicarbonyl species. When monocarbonyls are observed in the framework, the NaII–CO distance is generally shorter than NaII–OC. When dicarbonyls are formed, it is often the opposite.|| In our opinion, this comes from the non-equivalent CO positions which cannot be achieved at the NaII site of nearly C₃ symmetry, maintaining minimal CO–CO repulsion. As a result, one of the CO molecules, which can be either O-connected, or C-connected, is closer to the 4R windows near NaII. The shift to the 4R oxygens suggests possible multiple minima near the zeolite walls mainly due to dispersion energy. The distances from CO to the 4R O_z are summarized in Table S3 (ESI†). For example, we would like to pinpoint the CO–NaII–OC case (whose optB86d energy is −1082.96 eV in Table 2) with the remote OC location (2.951 Å). At the same optB86d level, one CO is also remote from NaII by as much as 2.984 Å (the “2CO” case whose energy is −1083.03 eV in Table 2). For CO–NaII–OC, we modified the initially optimized position for the O-connected CO and obtained a more stable symmetric geometry (whose optB86d energy is −1083.00 eV), leading to an energy gain of 1.0 kcal mol⁻¹. The |O–Na| = 2.668 Å and |O–Na| = 2.628 Å distances were then shifted to the conventional ratio when |C–Na| > |O–Na| as for single adsorbed CO species (Table 2). The corrected more symmetric geometries, however, do not lead to drastic changes for the ω_HF and ω_LF frequencies as shown in Section 3.3. The displacement towards the 4R window is less emphasized at the PBE level with underestimated dispersion energy, although differences of CO orientations in adsorbed mono- and dicarbonyl species are evident (Table 2). Such a situation was already shown earlier for larger cations like in RbY only using a pair-wise addition scheme,⁵⁰ but the various examples in the current work confirm the role of the NaY cell geometry to explain the differences in CO orientations in mono- and dicarbonyl species. The inequality of the positions of the two CO molecules in the CO–NaII–OC dicarbonyls is one of the reasons for the different CO frequencies without essential coupling between the vibrational CO–CO modes as will be discussed in the next part.

3.3 Band shift calculations

The CO vibration frequencies for species adsorbed at the one NaII (N = 1) or at two different NaII cations (N = 2) are given in Table 2. The DFT frequency splittings Δω = ω_HF − ω_LF between NaII–CO (high frequency or HF branch) and NaII–OC (low frequency or LF branch) are overestimated matching the experimental value of 66 cm⁻¹ for NaZSM-5³⁰ (Table 4). Note that all these values should be compared with characteristic full-width at half-height (FWHH) values of the experimental CO bands and their intensity to evaluate the probability of their registration. The iso-energetic zone for the CO location in monocarbonyls (see Section 3.2) is described by different Δω values at the PBEsol-D2 level (Tables 2 and 4), i.e., from 42.9 cm⁻¹ (C₂–O₂ tilt type in Fig. 2d) to 37.8 cm⁻¹ (C₁–O₁ type being nearly perpendicular to the 6R plane). The change from one position to the other (C₁–O₁ to C₂–O₂ or inversely) upon varying the conditions is the reason for the parallel drift of the NaII–CO band peak. Such a small order of value (4 cm⁻¹) for the NaII–CO BS from 2175 to 2171 cm⁻¹ was already observed with pressure.⁵¹

Table 4 HF and LF frequencies (ω_HF, ω_LF, cm⁻¹) and total splitting (Δω = ω_HF − ω_LF, cm⁻¹) over NaY calculated at the different DFT levels

Type	PBE	PBEsol	PBEsol-D2	PBEsol-D3(BJ)	OptB86d	B3LYP^c	Pair-wise^d	Exper.
a PBE1 periodic model (48T) of NaY with the NaII–CO–NaIII location (Table 2 of ref. 20). b PBE2 periodic model (48T) of NaY with the NaII–CO–NaIII location (Table 2 of ref. 20). c Cluster model (42T) of NaY with the 6-311++G(d,p) (Na–CO–Na)/6-31G(d)(Al, Si, Oz, Na′) basis set, with Na′ being all cations except the two Na in close contact with CO; the case CO and OC correspond to NaII–CO–NaIII and NaII–OC–NaIII, respectively.^20 d Pair-wise addition scheme.^50 e This overestimated absolute value comes from the problem of the approximated repulsive constant for the CO–Oz orientation which has no minimum.^50
ΔωHF	44.1	39.3	42.9, 37.8	37.8	49.2	30.0	30.0	32,^51 28^15
ΔωLF	−22.7, −7,^a −20^b	−29.5	−25.4	−27.9	−18.2	−19.0	−40.5^e	−21^15
Δω	66.8	68.8	68.3, 63.2	65.7	67.4	49.0	70.5	53,^14 49^15

---

One important issue for our computations is the discussion of the dicarbonyl models of two CO–NaII–CO and OC–NaII–CO types. We show below that the ω_HF splitting between mono- and dicarbonyls in NaY is large enough to explain the experimental difference relative to the fine structure of the ω_HF band in NaZSM-5. In NaY, the symmetric shoulders at 2183 cm⁻¹ (red shifted +12 cm⁻¹ relative to the main band at 2171 cm⁻¹) and 2156 cm⁻¹ (blue shifted −15 cm⁻¹) are present within a wide temperature range,¹⁵ while no such shoulders have been observed in NaZSM-5.¹⁵

First, the non-equivalence of CO modes in mono- and dicarbonyl species is not a consequence of vibrational CO–CO coupling in dicarbonyls. A simple verification of their negligible impact can be done when the calculation of the frequencies is performed upon fixed coordinates of the neighbor CO of the same dicarbonyl species. For example, for the OC–NaII–CO dicarbonyl, the alternate freezing of the second CO leads to Δω values of 2172.8 and 2163.1 cm⁻¹ (from two separate frequency computations) instead of 2172.8 and 2163.8 cm⁻¹ (from one single computation with mobile atoms of both CO molecules) at the PBE level (case “2CO (1)” in Table 2). The unique case of interacting CO–CO molecules was obtained in the CO–NaII–OC dicarbonyl at the PBEsol-D2 level.** The respective Cartesian components of the vibrational vectors possess similar orders of values for both C and O atoms for both CO molecules, i.e., x(C1) = −0.638, y(C1) = −0.269, z(C1) = 0.016, and x(C2) = −0.162, y(C2) = 0.249, z(C2) = 0.006. One should, however, emphasize that the existence of CO–NaII–OC dicarbonyl remains in question.

Second, only the PBE/PAW type of calculation allows an interpretation of the red shifted 2183 cm⁻¹ branch¹⁵ due to the Δω_HF increase in CO–NaII–CO dicarbonyl complexes up to 56.8 cm⁻¹ (ω_HF = 2192.3 cm⁻¹ in Table 2). The blue shifted peak (relative to 2179.6 cm⁻¹ for monocarbonyls in Table 2) originates from OC–NaII–CO, i.e., Δω_HF = 37.3 cm⁻¹ (or ω_HF = 2172.8 cm⁻¹ in Table 2). The ω_HF splitting between two CO molecules at two neighbor NaII sites (case “CO, CO (2)”) is smaller, varying between 2.3 cm⁻¹ (PBE) and 4.9 cm⁻¹ (optB86d) that might also be resolved experimentally (Table 2). The dicarbonyls are less energetically favored with all three DFT functionals (Table 2), thus explaining their lower intensities compared to the main peak. The adsorption energy differences for CO–NaII–CO and OC–NaII–CO are rather close, i.e., 2.1 kcal mol⁻¹ (5.4–3.3 = 2.1 kcal mol⁻¹ from Table 2) and 1.4 kcal mol⁻¹ (5.4–4.0 = 1.4 kcal mol⁻¹ from Table 2), respectively, relative to the NaII–CO adsorption energy (5.4 kcal mol⁻¹) at the PBE level. Therefore, these branches will vary nearly simultaneously with the experimental conditions (pressure or temperature). The asymmetry of the main ω_HF peak at any temperature in NaY, i.e., shoulder or shoulders on the blue shifted side, does not contradict the calculated results because all DFT functionals confirm the additional blue shifted peaks relative to the main CO transition in NaII–CO. Concerning NaZSM-5, we unfortunately could not perform the necessary PBC computations using VASP due to its large cell dimensions. As a result, we can only suggest that the dicarbonyl complexes in NaZSM-5 can either be much less stable than in NaY, or present identical locations of both CO molecules, very close to the positions of the monocarbonyl due to the symmetry of the Na sites so that the branches nearly coincide and cannot be observed.

3.4 Activation energies for CO diffusion and rotation

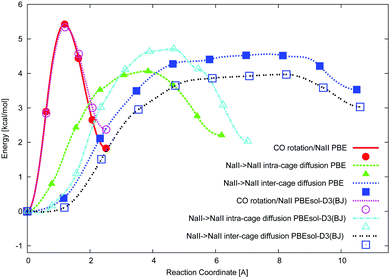
The ciNEB algorithm^43,44 was applied to find transition states (TSs) for both CO rotation at one NaII cation and CO migration between two NaII cations in either one or two neighbor FAU supercages. The closeness of both PBE (activation barrier of 5.4 kcal mol⁻¹) and PBEsol-D3(BJ) (activation barrier of 5.3 kcal mol⁻¹) energy profiles along the rotation trajectory (Fig. 4) shows the minor role of the dispersion energy terms (Table 3). The verification of the calculated TS geometries for CO diffusion did not show a kind of “dual” intermediate, i.e., without imaginary frequencies, like the strong adsorption sites observed between alkali cations separated by around 7 Å in other zeolites.^21–23 The NaY structure leads to much larger NaII⋯Na′II distances ∼10 Å, which can be slightly shortened upon middle coverage due to the cation's deviation from the 6R plane (see the minor growth of |Na–O_z| distances going from one to two CO molecules in Table 2). Na cations cannot move far from SII sites, for example, to stabilize hydrocarbonates in NaY. The latter were found⁵² and interpreted²⁵ only for heavier cations which are less effectively bonded to the zeolite O_z atoms in KY and CsY. Hence, we believe that dual CO sites are less probable for NaY.

Fig. 4 Total energy (kcal mol⁻¹) versus reaction coordinate (in Å) for the CO rotation at the NaII site (circles), CO migration from one NaII to another Na′II site of the same supercage (triangles), and CO migration without rotation from the OC–NaII to CO–NaII′ site of neighboring supercages via the 12R window (squares) at the PBE (closed symbols) and PBEsol-D3(BJ) (open symbols) levels.

Possibilities to change the CO orientation from NaII–CO to Na′II–OC along the reaction coordinate (Fig. 1) or to maintain the NaII–CO orientation were therefore studied. Without CO rotation, the NaII–CO orientation steeply transforms to Na′II–OC, resulting in the lowest TSs (4.1 and 4.7 kcal mol⁻¹ at the PBE and PBEsol-D3(BJ) levels, respectively, in Table 3). The second route (with rotation) requires conserving the most energetically favorable NaII–CO geometry after the migration. It is conditioned by the possibility of CO rotation along the reaction coordinate (Fig. 1) and thus depends on the rotation–translation interaction. Owing to the migration from the initial NaII site, the CO molecule moves far from the cation and hence will be influenced by a weaker electric field. It might decrease the CO rotational barrier along the NaII–Na′II trajectory. Then the molecule might rotate to maintain the energetically favored Na′II–CO orientation after the jump. However, the barrier for the rotation–translation is similar to the barrier of rotation (5.3 instead of 5.4 kcal mol⁻¹ at the PBE level in Table 3), a larger value versus the diffusion barrier. This does not demonstrate a decrease of the electric field gradient value along the trajectory between two NaII cations. It shows that the diffusion jump should be accompanied by a CO re-orientation†† (from NaII–CO to Na′II–OC), avoiding CO rotation (Fig. 4).

The small energy difference per CO for either one or two CO molecules at one single site leads to a natural question, namely, can one CO molecule move to an already occupied NaII site? The PBE activation energy of such migration, 5.5 kcal mol⁻¹, is slightly larger versus the activation energy of pure rotation, 5.4 kcal mol⁻¹, and hence it should also be less feasible compared to CO diffusion to a free NaII site with an activation energy of 4.1 kcal mol⁻¹. The appearance of NaIII′ leads to a much smaller barrier of 0.7 and 1.0 kcal mol⁻¹ at the PBE and PBEsol-D3(BJ) levels, respectively, for the CO migration from NaII to NaIII (Table 3 and Fig. 4). Formally, considerably small barriers allow all possible site configurations producing very complex IR spectra in contrast to the experimental ones. We can thus consider neither NaIII nor NaIII′ cations formed upon CO stimulation as part of a reliable NaY model.

In order to obtain a complete picture of the CO diffusion we also considered the inter-cage diffusion barrier. Passing the 12R window between two NaII sites belonging to neighbor supercages leads to a minimal barrier of 4.5 kcal mol⁻¹ (PBE) when the NaII–CO orientation at the starting point is changed to the NaII–OC orientation at the end point of the trajectory (an animation file of this migration is supplied in the ESI†). The TS geometry corresponds to a CO position in the 12R plane with the C atom separated by close NaII–C distances from both NaII atoms (5.128 and 5.975 Å). Hence, the barriers increase along the series: intra-cage (4.1 kcal mol⁻¹) < inter-cage (4.5 kcal mol⁻¹) < rotation plus translation in intra-cage (5.3 kcal mol⁻¹) < rotation (5.4 kcal mol⁻¹) at the PBE level.

4. Discussion

Grey et al.^16,17 and Mellot-Draznieks et al.¹⁸ showed a possibility of NaI′ shift to the NaIII′ site in the presence of adsorbed C₂F₄H₂^16,17 or CFCl₃¹⁸ species in the NaX type zeolite. Later this idea of NaI′ shift was discussed considering CO spectra in NaY and CuNaY.²⁰ The close positions of the NaIII or NaIII′ sites in NaY²⁰ suggest similar results for the IR spectra and energies using either NaIII or NaIII′ adsorption sites. The authors²⁰ showed that the NaII–CO–NaIII′ configuration (ω_LF = −28 cm⁻¹) is only slightly less stable (by 0.8 kcal mol⁻¹) than the NaII–CO–NaIII one (ω_LF = −19 cm⁻¹) at the B3LYP/6-311++G(d,p)(Na–CO–Na)/6-31G(d)(Al, Si, O_z, Na′) level using a 42T cluster model (Table 4 of ref. 20). The authors also considered a possible Na diffusion together with CO between close SIII and SIII′ sites,²⁰ although the problem of CO-stimulated diffusion of NaI′ to these sites was not resolved as it was experimentally shown for other adsorbates like C₂F₄H₂^16,17 or CFCl₃.¹⁸ Moreover, the experimental data for synthetic Y zeolites did not confirm the CO penetration into sodalite cages to interact with NaI′ and to stimulate its diffusion.¹⁰ Even if no evidence is known for such CO-induced diffusion in NaY at the moment, we considered its transformation to calculate the BS values of CO between NaIII and NaII cations and the respective diffusion coordinate. We did not analyze all possible positions of both NaIII and NaIII′²⁰ sites, limiting our calculations by considering only the NaIII case.

There are two possibilities to occupy the NaIII or NaIII′ site: either to shift the cation from the most stable NaI or NaII site to the NaIII or NaIII′ site (as in ref. 20 and herein), or to find a coverage for which the CO molecules start to stimulate a NaI′ transport without any loss of total stability of the system (which could be considered at the level of Gibbs potential or limited by enthalpy). An appropriate model should lead to stabilization of the system after NaI′ to NaIII diffusion and CO adsorption (or vice versa, CO adsorption and then Na diffusion) and not to the destabilization by 7.6, 6.1, and 5.8 kcal mol⁻¹ at the PBE, PBEsol, and optB86d levels, respectively, as with the model herein without CO adsorption (see column 4 in Table S2 of the ESI†). The orders of the destabilization energy values are close to the decrease of the activation barrier of electric conductivity from NaY (17.7 kcal mol⁻¹) to NaX (12.5 kcal mol⁻¹) in dehydrated states.⁵³ The conductivity is provided by Na jumps between allowed positions. The decrease of the energy barrier by 5.2 kcal mol⁻¹ in NaX is the direct consequence of the presence of the less strongly coordinated NaIII cation in NaX. A compensation of the energy loss by a gain of CO specific adsorption energy (Section 3.2) is not sufficient in alkali forms. One should note that we occupied the NaIII site starting from the NaII cation of the same supercage (just by moving the NaII to the NaIII site and optimizing the fractional coordinates and cell parameters). It led to smaller destabilization of the zeolite as compared to the NaI′ to NaIII′ drift because NaI′ is coordinated more strongly to the framework than NaII is.

The second way, i.e., NaI′ transport at higher CO coverage, requires totally different models. The main problem to apply this scheme with a NaI′ shift is the unknown coverage at which CO starts to stimulate the transport of NaI′ to the NaIII′ sites. We did not consider this case as such a problem is outside the current study wherein we restrict ourselves to a domain of small NaY coverage.

Moreover, CO is an adsorbate molecule with a relatively weak electrostatic interaction which cannot stimulate any ionic transport of alkali and earth alkaline cations.‡‡ The heats of CO interaction with the Na cations (5.5–6.0 kcal mol^{−1 10–12} in NaX or even smaller 5.0 kcal mol⁻¹ in NaY²⁸) are smaller than those of C₂F₄H₂ (16.5 kcal mol^−1 16,17) or CFCl₃ (around 8 kcal mol⁻¹ for similar CF₂Cl₂¹⁸) molecules and hence the time-of-life of the respective Na–CO complex to migrate (Na and CO together) has to be shorter. Within a conventional range of adsorbates from He or H₂ (no transport) to water (there is a cationic drift^54–56), CO is closer to the He or H₂ case.

An important part of our work is the demonstration of larger ω_HF values in dicarbonyls relative to the ones for monocarbonyls, i.e., a Δω_HF value of 56.8 cm⁻¹ for CO–NaII–CO compared to 44.1 cm⁻¹ for NaII–CO at the PBE level (Table 2).§§ The coincidence of CO bands in mono- and dicarbonyls is usually admitted using cluster models. With the cluster approach, the estimation of CO perturbation in either OC–NaII–CO or CO–NaII–CO is hindered. We would like to emphasize that the Δω_HF variation is mainly the result of another CO position in dicarbonyls relative to within monocarbonyls and not the result of a CO–CO coupling (see Section 3.3). Formally, at the NaII site with approximate C₃ symmetry, one cannot find two identical symmetric positions for two CO molecules,¶¶ imposing, morever, the condition of their optimal interaction (at least, minimal CO–CO repulsion, see non-equivalent positions of CO in the upper view of Fig. 2b). An additional difference in the non-equivalence of CO positions in dicarbonyls (not discussed in this work) can come from the various Al distributions in the 6R windows around each NaII site.⁵⁷ The different CO positions for OC–NaII–CO (Fig. 2b) lead to different Δω_HF values irrespective of the strength of CO–CO coupling. As shown in Table 2, the ω_HF value of CO in dicarbonyls can exceed the respective ω_HF in monocarbonyls. As an explanation, it was mentioned that the minor contribution of the μE dipole-field term to the heat of CO adsorption results from the small CO dipole¹² (see also all the energy components in Fig. 4 of ref. 58). Hence, a maximum electric field value at the optimal CO location cannot be a necessary requirement neither in mono- nor in dicarbonyls. The electric field E can vary in any direction (decrease or increase) while going from mono- to dicarbonyls. As the main part of the CO BS (μ(v = 1) − μ(v = 0)) × E depends mainly on the CO dipole change μ(v = 1) − μ(v = 0) upon vibrational transition 0 → 1 and electric field E (Table 4 of ref. 50), a simultaneous increase of ω_HF is not forbidden due to a higher electric field in dicarbonyls.

The simple electrostatic picture of CO adsorption on alkali cationic sites allows some semi-quantitative estimation. Using results of previous empirical calculations,^50,58 one can qualitatively evaluate the possible rotational barrier for adsorbed CO. An accurate electrostatic model for the NaCaA zeolite showed that the CO quadrupole-field gradient is the main contribution to the barrier of CO rotation along the line connecting Ca and the center of the α-cage of NaCaA.⁵⁸ Regarding the higher Ca charge (q(Ca) = 1.2 e for model A of the NaCaA zeolite, see Table 4 of ref. 58) versus the one of Na in NaY (our estimation of Bader charge according to ref. 59 is q(Na) = 0.87 e), the estimations for NaCaA can serve as upper boundaries for the CO location in NaY. The quadrupole-field gradient energy can be crudely evaluated to be 2.6 kcal mol⁻¹ at the minimum of the total CO adsorption energy (R ∼ 5.4 a.u. in Fig. 4 of ref. 58). The barrier of a CO rotation by 90° relative to the axis between the center of mass of CO and the Ca cation corresponds to the double value considering the opposite sign of the “quadrupole-field gradient” contribution after rotation. It is the consequence of the negative sign of the CO quadrupole moment. Hence, the barrier is around 5.2 kcal mol⁻¹. The smaller contribution comes for the change in inductive (or polarization) energy ΔU_ind ∼ ½ × αE² upon CO rotation, with α being the CO polarizability and E, the electric field, i.e., 0.6 kcal mol⁻¹ from Fig. 4 of ref. 58. The U_ind variation after a CO rotation by 90° can be obtained by re-scaling the ratio of the parallel (15.63 a.u. (ref. 30)) to perpendicular (11.97 a.u. (ref. 30)) polarizabilities which are the most important relative to the E field at both orientations 0.63 × (11.97/15.63) = 0.5 kcal mol⁻¹. This value is smaller than U_ind calculated by Dempsey for Ar/NaY (0.9 kcal mol^−1 60) while the polarizability of Ar, i.e., 11.04 a.u.,³ is smaller than that of CO.⁶¹ In total, one gets 5.2 + 0.5 = 5.7 kcal mol⁻¹. The smaller rotational barriers of 5.4 and 5.3 kcal mol⁻¹, calculated at the PBE and PBEsol-D3(BJ) levels, respectively (Table 3), show a qualitative coherence with the simple estimation above. The other electrostatic components (dipole-field etc.) of the energy terms are much smaller (see Fig. 4 of ref. 58). Despite the simple empirical scheme of pair-wise potentials, Fig. 4 from ref. 58 shows a dominant role of the dispersion energy in the cationic zeolite A form. At the PBE0-D level, it was recently demonstrated for all siliceous zeolites that dispersion contributions vary between 70.1 and 94.3% of the total energies.⁶²

5. Conclusions

The NaY zeolite remains a perspective material for separation of gas mixtures. In this work, we tested three selected DFT functionals using PBC and we have found the better agreement with experimental heats of CO adsorption at the PBE and PBEsol levels than with optB86d and PBEsol-D2. In contrast, the difference in the CO energies at the NaII–CO to NaII–OC orientations calculated at the optB86d level is closer to the experimental difference. We obtained smaller activation energy for CO diffusion in the intracrystalline porous space between neighboring NaII sites of one FAU supercage as compared to CO rotation at one NaII center. The presence of nearly symmetric sub-bands was considered as an argument in favor of the CO rotation. Herein, the fine structure of the vibrational C–O bands is explained by the different CO locations of adsorbed mono- and dicarbonyl species instead of CO rotation. This result agrees with the absence of rotational branches in the IR spectra due to hindered CO rotation in other zeolites. The order of the rotational barrier values agrees with the main interaction energy contribution between the electric field gradient and the CO quadrupole in NaCaA obtained in the literature. This barrier is smaller for the NaII–CO to Na′II–OC type jump (changing the CO orientation without rotation) than for the NaII–CO to Na′II–CO route (conserving the CO orientation due to rotation). The CO jump without rotation explains the redistribution of the high frequency (NaII–CO) and low frequency (NaII–OC) intensities with temperature. This illustrates that the electrostatic field gradient does not decrease too steeply from the cation to the center of the zeolite Y cage to allow CO rotation even for monovalent cations. Therefore, such CO behavior in NaY may be extended for divalent zeolite forms with higher field gradients. We did not obtain any confirmation of NaIII formation in NaY with smaller activation energies of both diffusion and rotation regarding the CO/NaY spectra. Hence, the barriers for CO motions in NaY at the PBE level increase as follows: intra-cage diffusion < inter-cage diffusion < rotation. This shows that CO desorption is more probable than its rotation in NaY. Such results can be useful for accurate modeling of restricted CO dynamics in catalyzed reaction systems or adsorption over zeolites as well as in microporous systems in general.

Acknowledgements

The authors thank the Supercomputing Center of Lomonosov Moscow State University⁶³ for computational time. This research used the resources of the “Plateforme Technologique de Calcul Intensif (PTCI)” (http://www.ptci.unamur.be) located at the University of Namur, Belgium, which is supported by the F. R. S.-FNRS under convention no. 2.4520.11. The PTCI is a member of the “Consortium des Équipements de Calcul Intensif (CÉCI)” (http://www.ceci-hpc.be). AAR and AVL thank RFFI for Grant 17-53-18026.

References

1. M. Kanezashi, J. O'Brien-Abraham, Y. S. Lin and K. Suzuki, AIChE J., 2008, 54, 1478–1486.
2. M. Kanezashi and Y. S. Lin, J. Phys. Chem. C, 2009, 113, 3767–3774.
3. J. A. Delgado, V. I. Águeda, M. A. Uguina, J. L. Sotelo, P. Brea and C. A. Grande, Ind. Eng. Chem. Res., 2014, 53, 15414–15426.
4. J. Xiao and J. Wei, Chem. Eng. Sci., 1992, 47, 1123–1141.
5. F. Jousse, S. M. Auerbach and D. P. Vercauteren, J. Phys. Chem. B, 1998, 102, 6507–6514.
6. S. M. Auerbach, Int. Rev. Phys. Chem., 2000, 19, 155–198.
7. A. A. Rybakov, A. V. Larin, G. M. Zhidomirov, D. N. Trubnikov and D. P. Vercauteren, Comput. Theor. Chem., 2011, 964, 108–115.
8. A. A. Rybakov, I. A. Bryukhanov, A. V. Larin and G. M. Zhidomirov, Int. J. Quantum Chem., 2015, 115, 1709–1717.
9. A. A. Rybakov, I. A. Bryukhanov, A. V. Larin and G. M. Zhidomirov, Pet. Chem., 2016, 56, 259–266.
10. T. A. Egerton and F. S. Stone, Trans. Faraday Soc., 1970, 66, 2364–2377.
11. T. A. Egerton and F. S. Stone, J. Colloid Interface Sci., 1972, 38, 195–204.
12. T. A. Egerton and F. S. Stone, J. Chem. Soc., Faraday Trans. 1, 1973, 69, 22–38.
13. C. Otero Areán, G. T. Palomino, A. A. Tsyganenko and E. Garrone, Int. J. Mol. Sci., 2002, 3, 764–776.
14. K. Hadjiivanov, H. Knözinger, E. Ivanova and L. Dimitrov, Phys. Chem. Chem. Phys., 2001, 3, 2531–2536.
15. A. A. Tsyganenko, P. Y. Storozhev and C. Otero Areán, Kinet. Catal., 2004, 45, 530–540.
16. C. P. Grey, F. I. Poshni, A. F. Gualtieri, P. Norby, J. C. Hanson and D. R. Corbin, J. Am. Chem. Soc., 1997, 119, 1981–1989.
17. K. H. Lim and C. P. Grey, J. Am. Chem. Soc., 2000, 122, 9768–9780.
18. C. Mellot-Draznieks, J. Rodriguez-Carvajal, D. E. Cox and A. K. Cheetham, Phys. Chem. Chem. Phys., 2003, 5, 1882–1887.
19. D. F. Plant, G. Maurin, H. Jobic and P. L. Llewellyn, J. Phys. Chem. B, 2006, 110, 14372–14378.
20. Z. Nour, H. Petitjean and D. Berthomieu, J. Phys. Chem. C, 2010, 114, 17802–17811.
21. C. Otero Areán, M. Rodríguez Delgado, K. Frolich, R. Bulánek, A. Pulido, G. Fiol Bibiloni and P. Nachtigall, J. Phys. Chem. C, 2008, 112, 4658–4666.
22. E. Garrone, R. Bulánek, K. Frolich, C. Otero Areán, M. Rodríguez Delgado, G. Turnes Palomino, D. Nachtigallová and P. Nachtigall, J. Phys. Chem. B, 2006, 110, 22542–22550.
23. O. V. Manoilova, M. Peñarroya Mentruit, G. Turnes Palomino, A. A. Tsyganenko and C. Otero Areán, Vib. Spectrosc., 2001, 26, 107–111.
24. A. V. Larin, Microporous Mesoporous Mater., 2014, 200, 35–45.
25. A. V. Larin, Microporous Mesoporous Mater., 2016, 228, 182–195.
26. C. Otero Areán, A. A. Tsyganenko, E. Escalona Platero, E. Garrone and A. Zecchina, Angew. Chem., Int. Ed., 1998, 37, 3161–3163.
27. P. J. Fenelon and H. E. Rubalcava, J. Chem. Phys., 1969, 51, 961–967.
28. E. A. Paukshtis, R. I. Soltanov and E. N. Yurchenko, React. Kinet. Catal. Lett., 1981, 16, 93–96.
29. H. Förster, W. Frede and M. Schuldt, J. Mol. Struct., 1982, 80, 195–198.
30. A. A. Tsyganenko, E. Escalona Platero, C. Otero Areán, E. Garrone and A. Zecchina, Catal. Lett., 1999, 61, 187–192.
31. T. A. Wesołowski, A. Goursot and J. Weber, J. Chem. Phys., 2001, 115, 4791–4797.
32. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
33. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
34. L. Benco, T. Bucko, J. Hafner and H. Toulhoat, J. Phys. Chem. B, 2004, 108, 13656–13666.
35. F. Göltl and J. Hafner, J. Chem. Phys., 2012, 136, 64501.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
38. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
39. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
40. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
41. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
42. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
43. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
44. D. Sheppard, R. Terrell and G. Henkelman, J. Chem. Phys., 2008, 128, 134106.
45. P. Ugliengo, D. Viterbo and G. Chiari, Z. Kristallogr. – Cryst. Mater., 1993, 207, 9–23.
46. B. M. Bode and M. S. Gordon, J. Mol. Graphics Modell., 1998, 16, 133–138.
47. N. E. Ghermani, C. Lecomte and Y. Dusausoy, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 5231–5239.
48. I. A. Bryukhanov, A. A. Rybakov, V. L. Kovalev, A. V. Larin and G. M. Zhidomirov, Dalton Trans., 2015, 44, 2703–2711.
49. D. Saha and S. Deng, J. Chem. Eng. Data, 2009, 54, 2245–2250.
50. A. V. Larin, D. P. Vercauteren, C. Lamberti, S. Bordiga and A. Zecchina, Phys. Chem. Chem. Phys., 2002, 4, 2424–2433.
51. K. Hadjiivanov and H. Knözinger, Chem. Phys. Lett., 1999, 303, 513–520.
52. G. D. Pirngruber, P. Raybaud, Y. Belmabkhout, J. Čejka and A. Zukal, Phys. Chem. Chem. Phys., 2010, 12, 13534–13546.
53. F. J. Jansen and R. A. Schoonheydt, J. Chem. Soc., Faraday Trans. 1, 1973, 69, 1338–1355.
54. T. I. Barry and L. A. Lay, J. Phys. Chem. Solids, 1966, 27, 1821–1831.
55. T. I. Barry and L. A. Lay, J. Phys. Chem. Solids, 1968, 29, 1395–1405.
56. M. Jeffroy, E. Borissenko, A. Boutin, A. Di Lella, F. Porcher, M. Souhassou, C. Lecomte and A. H. Fuchs, Microporous Mesoporous Mater., 2011, 138, 45–50.
57. S. Huber and H. Knözinger, Appl. Catal. A, 1999, 181, 239–244.
58. A. V. Larin, L. Leherte and D. P. Vercauteren, Phys. Chem. Chem. Phys., 2002, 4, 2416–2423.
59. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 84204.
60. E. Dempsey, Proc. Conf. Molecular Sieves 1967, London: Society of Chemical Industry, London, 1968, pp. 293–305.
61. H. B. Levine and G. Birnbaum, J. Chem. Phys., 1971, 55, 2914–2917.
62. E. I. Román-Román and C. M. Zicovich-Wilson, Chem. Phys. Lett., 2015, 619, 109–114.
63. V. Sadovnichy, A. Tikhonravov, V. Voevodin and V. Opanasenko, in Contemporary High Performance Computing From Petascale toward Exascale, ed. J. S. Vetter, CRC Press, Boca Raton, USA, 2013, pp. 283–307.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed discussion of the NaY model containing NaIII cations (Section S1), Table S1 with calculated CO molecular parameters, Table S2 being an analogue of Table 2 for the tentative NaY model containing NaIII cations with additional geometric characterization of adsorbed CO over NaIII (Table S3), and an animation avi-file of CO diffusion between NaII sites in neighbor supercages without CO rotation (case “e” in Table 3). See DOI: 10.1039/c7cp03043f

‡ See footnote in Section 3.2.

§ The negative value with PBEsol-D shows that CO interacts more strongly with NaII than with NaIII; therefore, no gain comes from the adsorption energy at the PBEsol level.

¶ The same estimation is valid for NaIII′ according to ref. 20.

|| It is also important to address the question of the higher kinetic diameter of CO versus CO₂.¹ The same PBE/PAW level of theory gives for |Na–OCO| = 2.300–2.316 Å (Table S9 of SEM in ref. 25) that is slightly shorter than |Na–OC| = 2.542 Å herein (Table 2). But together with two |C–O| bond lengths of 1.178 Å in CO₂, the sum of the distances results in a higher CO₂ diameter.

** In the case of the other DFT methods, the extent of coupling is weaker, i.e., at the PBE level only one component of the second CO presents comparable values, i.e., y(C2) = −0.13, y(O2) = −0.10, while the other x- and z-components of the C2 and O2 atoms are much smaller.

†† We use the word “re-orientation” instead of more frequent “isomerization” because it does not possess a chemical “flavor” which has no place in the current case.

‡‡ Transition metal cations, whose chemical bonding with CO leads to stable carbonyl species, are not included in the discussion.

§§ Slightly larger Δω values are also obtained for two CO molecules adsorbed at two different NaII cations at the PBE, PBEsol-D2, and optB86d levels. This also confirms the possible Δω increases relative to the one for isolated monocarbonyls, even if the difference is smaller than for CO–NaII–CO using PBE.

¶¶ Two nearly symmetric positions for two CO molecules could be found for the OC–NaIII–CO case due to the local C₂ symmetry, but we do not discuss the NaIII case as explained above. The symmetric OC–NaIII–CO location cannot be a favored one.

---