Evidence for coherent mixing of excited and charge-transfer states in the major plant light-harvesting antenna, LHCII

Abstract

LHCII, the major light harvesting antenna from plants, plays a dual role in photosynthesis. In low light it is a light-harvester, while in high light it is a quencher that protects the organism from photodamage. The switching mechanism between these two orthogonal conditions is mediated by protein dynamic disorder and photoprotective energy dissipation. The latter in particular is thought to occur in part via spectroscopically ‘dark’ states. We searched for such states in LHCII trimers from spinach, at both room temperature and at 77 K. Using 2D electronic spectroscopy, we explored coherent interactions between chlorophylls absorbing on the low-energy side of LHCII, which is the region that is responsible for both light-harvesting and photoprotection. 2D beating frequency maps allow us to identify four frequencies with strong excitonic character. In particular, our results show the presence of a low-lying state that is coupled to a low-energy excitonic state. We assign this to a mixed excitonic-charge transfer state involving the state with charge separation within the Chl a603–b609 heterodimer, borrowing some dipole strength from the Chl a602–a603 excited states. Such a state may play a role in photoprotection, in conjunction with specific and environmentally controlled realizations of protein dynamic disorder. Our identification and assignment of the coherences observed in the 2D frequency maps suggests that the structure of exciton states as well as a mixing of the excited and charge-transfer states is affected by coupling of these states to resonant vibrations in LHCII.

---

Introduction

Light-harvesting complex II (LHCII) is the most abundant photosynthetic antenna complex on land, with the primary purpose to harvest solar light and transfer the excitation energy further into the photosynthetic assembly where it can be converted into chemical energy.^1–3 This pigment protein complex manifests as a trimer in the thylakoid membrane (Fig. 1a), with each monomeric unit of native LHCII containing 8 chlorophylls (Chls) a, 6 Chls b, and 4 carotenoids (Cars).^4,5 The relative orientations between these pigments, determined in large part by the protein structure and binding sites, define their mutual resonance interactions and thus the energy landscape of this system. The Chls form strongly excitonically coupled clusters, which are arranged in two layers within the membrane. In a given monomer, the stromal side contains the Chls a602–a603, a–610–a611–a612, and b608–b609–b601′, where the b601′ is from an adjacent monomeric unit. On the lumenal side there are the Chls a613–a614 and a604–b605–b606–b607. (Nomenclature is from Liu, et al.⁴) These excitonic chlorophyll clusters mediate the light-absorption and energy transfer processes that control the function of LHCII.^6,7 Exciton models, based on modified Redfield theory, have been developed to describe these processes in great detail,^8–14 taking into account data from the vast library of experimental work to date.^4,5,15–22 Upon photoexcitation, the energy is funnelled between chlorophyll clusters until it reaches the lowest energy state, assigned to the Chls a610–a611–a612 ‘terminal emitter domain’, from where it can be transferred further into the photosynthetic assembly.^9,16,20,23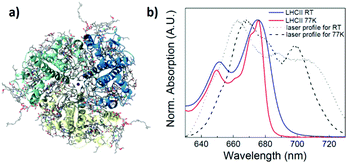

Fig. 1 (a) LHCII trimer from crystal structure obtained at 2.72 Å resolution, image from RCSB PDB (http://www.rcsb.org) of PDI ID 1RWT, published by Liu, et al.⁴ and (b) absorption spectrum of LHCII trimer at RT (blue) and 77 K (red) with laser spectrum for each 2D experiment. The laser was aligned so as to probe features on the low-energy side of the Q_y absorption band.

In addition to light-harvesting, LHCII plays an essential role in protection from excess light energy, which can cause photodamage to the biological assembly.^24,25 This process, called non-photochemical quenching (NPQ), is thought to occur at least in part at the low energy terminal emitter domain.^11,26,27 Low-lying dark states formed by inter-pigment coupling, either Chl–Chl^28–31 or Chl–Car,^26,32–34 are purported to play an essential role in NPQ, acting as trap sites for excess energy. The exact nature of the “quencher” and the mechanism remains a highly debated topic within the field. Identification of such dark states and their coupling to the excitonic manifold is essential to understanding the biophysics of the combined function of light-harvesting and photoprotection in LHCII.³⁵ Conformational (protein) dynamics is also supposed to play a crucial rule in the process of switching between light-harvesting and quenching.^36–39

Previous 2D electronic spectroscopy (2DES) experiments on LHCII have been instrumental to further developing the exciton/energy transfer model of this system. This highly sensitive ultrafast technique returns spectra that correlate photoexcitation and emission frequencies as a function of waiting time, giving not only energy transfer dynamics, but also coherences due to vibrational and/or electronic coupling, which appear as oscillatory features on top of the transient kinetics.^40–42 2DES on LHCII at 77 K helped elucidate energy transfer rates and inter-pigment couplings.^20,21,43,44 Characterization of the energy transfer dynamics have been further refined by recent 2D electronic-vibrational spectroscopy.⁴⁵ 2DES of LHCII was also reported at room temperature, along with a refined model of exciton energy transfer. This work further proposed an excitonic coherence between Chl a and Chl b pools at a 630 cm⁻¹ beating frequency.⁴⁶ 2D experiments on LHCII aggregates, which can approximate the energy dissipating condition,^24,47 showed intermediate Chl a states which were longer lived than in the unaggregated trimer, suggesting that these intermediate states may act as quenchers for excess excitation energy.⁴⁸

In this work, we expand further on the present understanding of LHCII and particularly on the elucidation of possible NPQ states in this ubiquitous pigment–protein complex. We measured 2DES of unaggregated LHCII trimers isolated from spinach, with a particular emphasis on elucidating possible low-lying dark states. We mapped the beating frequencies of these oscillations in LHCII and identified four frequencies with significant contribution from excitonic coherences. We propose that amplitude beating at 99 cm⁻¹ and 221 cm⁻¹ correspond to beating within the Chl a610–a611–a612 trimer and the Chl a602–a603 dimer, respectively. Beating maps at 522 cm⁻¹ and 753 cm⁻¹ identify a low-energy ‘dark’ state, correlated with emission between 700–710 nm. This is assigned to a charge-transfer state in the Chl a603–b609 heterodimer, which demonstrates dynamic coherence with excitonic states of the Chl a602–a603 dimer. Our results give unique insight into the emerging scheme of coherent interactions on the low-energy side of LHCII, the spectral region that controls both light-harvesting and photoprotective quenching.

Results

2DES

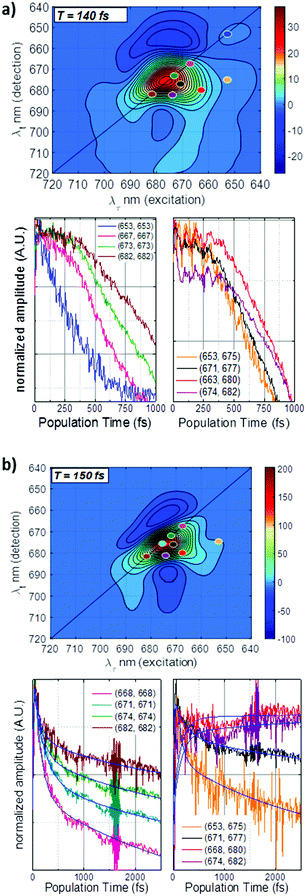
2D electronic spectroscopy of LHCII trimers was measured at room temperature (RT) and at 77 K. Fig. 1b shows the optical absorption of the samples in the spectral region of the measurement, as well as the shape of the laser spectrum for each experiment. The Q_y band of LHCII is characterized by a peak from 640–655 nm, due to Chl b absorption, and a peak from 655–680 nm from Chl a absorption. The laser was aligned so as to probe low energy states on the red side of the Q_y band.

Real total 2D maps correlate the absorption wavelength (λ_τ) with detection (emission) wavelength (λ_t) for a specific population time T (time after photoexcitation). Fig. 2a and b show the real total (phasing plus non-rephasing) 2D spectra at RT and 77 K at population time T = 140 fs for RT and 150 fs for 77 K, along with transient kinetics at selected positions. (2D spectra for a larger selection of population times are shown in Fig. S1, ESI†). The spectra demonstrate a ground state bleaching (GSB) signal from the Chl a pool along the diagonal, between 660–680 nm. In the RT measurements, a second peak is seen along the diagonal at 650 nm, due to GSB from Chl b. A cross-peak at (λ_τ, λ_t) = (653, 675) is due to excitation energy transfer (EET) from the Chl b pool to the Chl a pool. Note that, despite the fact that the Chl b GSB is not revealed along the diagonal in the 77 K measurements, this cross peak still appears, indicating that a population of Chl b is photoexcited in this experiment as well. Another cross-peak at (λ_τ, λ_t) = (660–665, 680–685) is attributed to EET from higher to lower energy Chl a states. Negative features above and below the diagonal are due to excited state absorption (ESA). Transient kinetics taken at selected positions along the diagonal demonstrate the recovery of the GSB features over the population time (Fig. 2). In the 77 K measurements, the feature at ∼1600 fs is an experimental artefact due to the local oscillator. Depopulation of the highest energy Chl features is fastest, and it slows down as the excitonic energy decreases. In the RT measurements, this is also seen in the recovery of the Chl b GSB at (λ_τ, λ_t) = (653, 653). At the end of the measurement window, the traces retain increasing relative population with decreasing excitonic energy, consistent with the current model of LHCII energy transfer. Transient kinetics at the cross-peak positions show how the relative EET rates between excitonic clusters vary. The (λ_τ, λ_t) = (653, 675) Chl b → Chl a kinetics demonstrate the fastest decay. EET in the mid-range Chl a region at (λ_τ, λ_t) = (671, 677) proceeds more slowly, while the cross-peaks associated with transfer to the far-red Chls (λ_τ, λ_t) = (668, 680) and (λ_τ, λ_t) = (674, 682) retain (or gain) more relative population at later times. These trends are also observed in the RT measurements (Fig. 2a).

Fig. 2 Exemplary real total (phasing plus non-rephasing) 2D spectra of LHCII at (a) RT and (b) 77 K and respective transient kinetics at selected on and off-diagonal positions, as indicated by the colored circles. The solid blue lines in the 77 K kinetics are fits derived from global analysis.

In order to gain more insight into the transient dynamics, we isolated selected slices of the 77 K 2D real total maps along the excitation wavelength, λ_τ. Decay-associated spectra (DAS) of the resultant (λ_tT) datasets are shown in Fig. 3 for λ_τ = 653 nm and 668 nm, and in Fig. S2 (ESI†) for λ_τ = 671 nm and 674 nm. The DAS at all three selected λ_τ show a fast component on the order of ∼100 fs, a slower component of ∼3 ps, and a long lived (>10 ps) component, which was not resolved within the experimental conditions. The DAS at λ_τ = 653 nm shows concomitant features at ∼658 nm and 675 nm at early times. This is in agreement with the Chl b → Chl a transfer cross peak at early times identified above in the 2D spectrum. At later times (2.6 ps and >10 ps), the DAS show the decay of excitation at 675 nm and 680 nm, respectively, in agreement with slower decay of excitation energy in the Chl a pool. These last two DAS traces also demonstrate broadening out to 710 nm, which may indicate energy transfer to some low energy red states. The DAS at λ_τ = 668, 671, and 674 nm are very similar to each other, with a decay peak at early times at approximately λ_τ, followed by subsequent energy transfer to the lower energy Chl a pool.

Fig. 3 Decay associated spectra (DAS) from global analysis of 2D spectra along selected excitation wavelengths (λ_τ) as indicated.

Frequency maps

2D spectra mapped at various population times (Fig. S1, ESI†) show that the cross-peaks disappear and reappear with advancing population time T. This manifests as amplitude oscillations in the transient kinetics, both on and off the diagonal (Fig. 2). These oscillations at cross-peak positions correspond to quantum beating resulting from coherently excited delocalized states, providing a visualization of exciton (and exciton–CT) mixing. In order to isolate information regarding coherent interactions, transient kinetics along the entire dataset were fit to a sum of two exponentials, and the resultant residuals were analyzed with a fast Fourier transform (FFT) algorithm. The FFTs were run over a measurement window of 1500 fs, giving a resolution of ≈22 cm⁻¹ along ω_T, and the 10 fs increment of the time delay gives a frequency range out to ω_T ≈ 1600 cm⁻¹. Note that since the FFT is limited to a 1500 fs window, the >10 ps component seen in the global analysis can be neglected.

2D real rephasing Fourier transform (2DFT) maps show the spectral contributions to the amplitude of a particular beating frequency ω_T. These maps allow us to identify and assign different types of coherences in LHCII. Contributions of various types of coherences are superimposed on these maps, resulting in complicated distributions of overlapping features. In photosynthetic antennae, dynamic excitonic coherences are washed out by the disorder (producing many oscillations with different frequencies, thus reducing the amplitude and lifetime of the resulting oscillatory pattern). Conversely, coherent excitation of vibrational satellites associated with each electronic transition produces intense oscillations in the bulk response because vibrational frequencies are not affected by the disorder of electronic energies. These vibrational coherences are furthermore characterized by slower dephasing relative to electronic coherences, giving rise to long-lived oscillations with the frequencies corresponding to the most intense vibrations coupled to electronic transitions. Previous reports have shown that LHCII exhibits 48 vibrational modes in the 90–1700 cm⁻¹ region.²² All of these modes will contribute to the 2D-echo response, masking the signals that stem from exciton coherences.

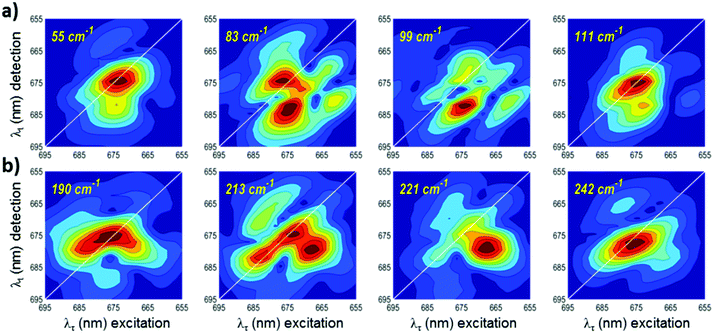
2DFT maps of LHCII at 77 K are shown in Fig. 4, 5 and Fig. S3, S4 (ESI†). In order to assign the coherences observed for LHCII, we have analyzed how the 77 K 2DFT distribution transforms when tuning the frequency around some values. The frequencies chosen for the 2DFT maps are determined by the results of the FFT algorithm as well as the reported vibrational modes observed in LHCII and Chl a (see Tables S1 and S2, ESI†).^22,49,50 An ideal purely vibrational coherence gives a 2DFT map with 5 peaks: the most intense is on the diagonal, 3 weaker peaks below the diagonal, and 1 weak peak above (‘chair-type’ arrangement).^51,52 In the present work, this case is observed in the 2DFT map at 696 cm⁻¹, for example (Fig. S3, ESI†). Such a 2DFT distribution is expected for a real excitonically coupled system if the vibrational frequency exceeds all of the exciton splittings.

Fig. 4 Measured 77 K 2DFT maps for the frequencies from (a) 55–111 cm⁻¹ and (b) 190–242 cm⁻¹. The maps show a development of the exciton off-diagonal peaks, most pronounced at 99 cm⁻¹ and 221 cm⁻¹. In either case, tuning to lower or higher frequencies results in a gradual increase of the diagonal peak, reflecting greater contributions from vibrational coherences.

Fig. 5 Measured 77 K 2DFT maps for frequency regions where we observe the excitonic coherences at λ_t > 700 nm. The two rows show a development of the exciton off-diagonal features when the frequency approaches to 522, and 753 cm⁻¹. Tuning the frequency above and below these values gives the 2DFT distributions with dominant diagonal peaks, corresponding to vibrational coherences.

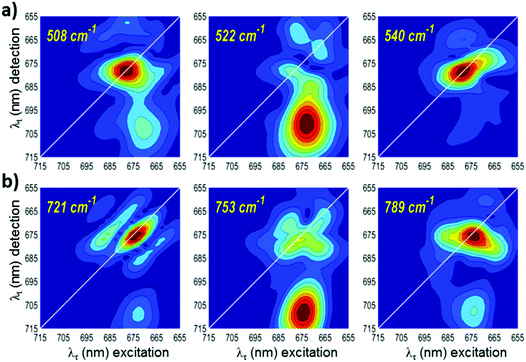
The relative amplitudes of the 5 peaks vary depending on the frequency and system parameters, resulting often in a single diagonal peak dominating the 2DFT map, such as is seen for 55 cm⁻¹, 111 cm⁻¹, 190 cm⁻¹, and 242 cm⁻¹ in Fig. 4.^53,54 But even the ‘pure vibrational coherences’ will contain some degree of the exciton mixing that always exists in excitonically coupled systems. This degree can be calculated for each of the 2DFT peaks, and such calculations have shown that the off-diagonal vibrational peaks contain more excitonic mixing when the vibrational frequency approaches the energy gap between the exciton levels.^51,54 In this case, the observed quantum beats correspond to exciton-vibrational, or vibronic, coherence. In the resonant case, the off-diagonal peak can be dominant, displaying higher amplitude than the diagonal peak. This case is demonstrated in the 2DFT maps at 99, 221, 522, and 753 cm⁻¹ (Fig. 4 and 5). At these four frequencies, the 2DFT maps exhibit pronounced signatures below the diagonal, indicating a stronger degree of excitonic mixing. We explore this further by tuning the frequency above and below these values and observing how the 2DFT map evolves as we approach these frequencies. In Fig. 4a, we show the transformation of the 2DFT maps at 77 K around the frequency value of 99 cm⁻¹, where we observe an intense off-diagonal peak centered at (λ_τ, λ_t) = (674, 682). Similarly, in Fig. 4b, we show a transformation of the 77 K 2DFT maps around 221 cm⁻¹, which demonstrates an off-diagonal peak centered at (λ_τ, λ_t) = (668, 680). Tuning the frequency from 99 cm⁻¹ or 221 cm⁻¹ to lower or higher values reduces the relative amplitude of the off-diagonal exciton peak with simultaneous formation of the diagonal peak determined by vibrational coherences. The maps at 83 cm⁻¹ and 213 cm⁻¹ show contributions both on and off the diagonal. This suggests a co-existence of the vibrational and excitonic coherences and/or exciton-vibrational mixing. The maps at 55 and 111 cm⁻¹ (Fig. 4a) and at 190 cm⁻¹ and 242 cm⁻¹ (Fig. 4b) exhibit features only on the diagonal and indicate purely vibrational coherences.

In Fig. 5, we show a similar transformation of the 77 K 2DFT maps around the values of 522 cm⁻¹ and 753 cm⁻¹. At these frequencies, a strong below diagonal feature dominates the map, appearing at (λ_τ, λ_t) = (673, 700) for 522 cm⁻¹ and (λ_τ, λ_t) = (674, 708) for 753 cm⁻¹. Tuning to higher and lower frequencies results in the disappearance of the below diagonal feature, giving instead 2DFT maps that exhibit mainly vibrational coherences. Therefore, we conclude that the 99 cm⁻¹, 221 cm⁻¹, 522 cm⁻¹, and 753 cm⁻¹ coherences have a significantly higher degree of excitonic-vibrational mixing. Transformations of the 2DFT maps at RT reveal the same increased intensity of the below diagonal features at 520 cm⁻¹ and 755 cm⁻¹ (Fig. S5, ESI†), but with greater vibrational contributions. FFT spectra shown in Fig. 6 demonstrate the increased intensity of the off-diagonal peak relative to the diagonal at the four frequencies identified as excitonic. Power spectral density of the FFTs at the off-diagonal peak positions are also shown in Fig. S6 (ESI†). The remainder of the LHCII 77 K 2DFT maps (Fig. S3 and S4, ESI†) are consistent with purely vibrational coherence. In Fig S4 (ESI†), we show a subset of 2DFT maps that are predominantly vibrational, but also demonstrate significant intensity below the diagonal, suggesting a greater relative degree of excitonic contribution.

Fig. 6 FFT spectra for the off-diagonal peaks (solid lines) compared with the on-diagonal peaks (dashed lines) at 77 K show that the off-diagonal contribution dominates at (a) 99 and 221 cm⁻¹ and (b) 522, and 753 cm⁻¹, indicating a strong contribution from excitonic coherences at these frequencies.

Discussion

2D spectroscopy of LHCII has previously been used to elucidate the excitonic couplings and energy transfer rates within the complex by focusing either on photoexcitation of the entire Q_y absorption band or selectively exciting a sub-population of the Chl pool.^{20,43,44,46,55} Trends observed in the transient kinetics of our experiments agree with earlier 2D measurements as well as, generally, earlier ultrafast work on LHCII. Global analysis of selected slices along λ_τ resulted in lifetimes of ∼100 fs, 3 ps, and >10 ps. In particular, DAS of the 2D spectra at λ_τ = 653 nm demonstrates transfer from Chl b to lower energy Chl a states (675–680 nm), in agreement with earlier work.⁵⁵ These DAS also suggest population of some low energy red states out to 710 nm, which we attribute to incoherent energy transfer at these slower timescales.

A distinguishing focus of this present work is to use 2DES to explore low-energy weakly allowed ‘dark’ states in LHCII by analyzing our 2D results with frequency resolved beating maps. 2DFT maps provide a unique insight into complex multi-pigment systems excited with broadband laser pulses, because the quantum beats reveal electronically and vibrationally coupled states within the excitation/detection range.

Most of the 77 K 2DFT maps demonstrate a single intense peak on the diagonal (Fig. S3, ESI†). As explained briefly above, a purely vibrational coherence gives a 2DFT map with 5 peaks, the most intense on the diagonal, resulting in a ‘chair-type’ arrangement, as has been previously reported at 730 cm⁻¹ for PSII RC.^52,56 The 2DFT map of 77 K LHCII at 696 cm⁻¹ also demonstrates this beating pattern (Fig. S2, ESI†). Relative amplitudes of the 5 peaks will differ, however, depending on frequency and parameters of the complex. In some cases, off-diagonal peaks are hardly discernible while the single diagonal peak dominates, as has been observed previously.⁵⁴ This is the observed case in the majority of the LHCII 77 K 2DFT maps. Tuning to lower frequencies and/or increase in temperature gives maps with overlapping off-diagonal components. In this case, vibrational maps contain two peaks: one intense on-diagonal peak and a weaker off-diagonal peak which is broadened along the diagonal direction.

In the 2DFT maps where the 5 vibrational (vibronic) peaks are well-resolved, the presence of exciton mixing manifests through an increased intensity of one of below-diagonal peaks. Previous work on the B820 dimer has shown that when the vibrational frequency approaches the energy gap between exciton levels, off-diagonal vibrational peaks contain a relatively higher degree of exciton mixing.⁵⁴ We thus classified a number of the LHCII 77 K 2DFT maps as mixed excitonic-vibrational due to the presence of intense off-diagonal features in addition to the strong on-diagonal intensity (Fig. S4, ESI†). Excited- and ground-state vibrational coherences can also give off-diagonal peaks, but these are typically weaker than an on-diagonal vibrational peak.^51,54,57,58

Four of the 2DFT maps are identified as demonstrating a significant degree of exciton mixing. At 99, 221, 522, and 753 cm⁻¹, the 2DFT map demonstrates an intense below diagonal peak. As illustrated in Fig. 4 and 5, outside of these frequencies, the 2DFT maps are dominated by an intense on-diagonal peak, consistent with vibrational coherence. We note that we do not observe any evidence for excitonic coherence between the Chl b and Chl a pools at 630 cm⁻¹.⁴⁶ However this could be due to the suppressed excitation bandwidth at the Chl b region in our experiment.

Due the complexity of LHCII, it is difficult to unambiguously define the origins of the observed coherences, but some tentative assignments can be proposed based on our current model of LHCII. The 99 cm⁻¹ 2DFT map displays a peak centered at (λ_τ, λ_t) = (674, 682). This must originate from a closely energetically spaced coupling associated with the low energy edge of the Q_y absorption band. A splitting at this spectral location and of this order of magnitude can be assigned to a coherent interaction between the two lowest exciton levels of the Chl a610–a611–a612 terminal emitter trimer (Fig. 6).^9,59 This cluster has been identified as comprising the lowest energy state in LHCII and is responsible for transferring energy further into the photosynthetic apparatus.^9,11,16,23 The strong excitonic coupling within this cluster plays a significant role in mediating the energy landscape of LHCII in the presence of energetic disorder.^10,20,38

The peak in the 221 cm⁻¹ 2DFT map is centered at (λ_τ, λ_t) = (668, 680). This most probably reflects an exciton splitting within the Chl a602–a603 dimer (Fig. 6). Similar splitting occurs within the more localized Chl a613–a614 dimer, which may also be giving a significant contribution to the 221 cm⁻¹ exciton coherence (see energy level scheme in Novoderezhkin, et al.⁹). Transient kinetics at the cross-peak positions assigned to these excitonic clusters are seen in Fig. 2b, where the kinetic trace at (674, 682) corresponds to the peak position assigned to the Chl a610–a611–a612 terminal emitter trimer and the trace at (668, 680) corresponds to the peak position assigned to the Chl a602–a603 dimer. Both traces demonstrate increasing population over the time window of the measurement. This agrees with the expected site populations of these clusters from the present LHCII model.^9,13,14

The 522 cm⁻¹ and 753 cm⁻¹ beats are correlated with a far red detection wavelength (λ_t > 700 nm). Recently, time-resolved fluorescence measurements have reported an emissive state at ∼700 nm from LHCII aggregates, which is assigned to mixing between a excitonic and a chlorophyll–chlorophyll charge transfer states.⁶⁰ Previously, single-molecule data for LHCII⁶¹ and the model of exciton–CT mixing in Lhca4⁶² suggest that the a602–a603 dimer is coupled to the CT state corresponding to a charge separation within the a603–b609 heterodimer. Based on these earlier works, we assign the 522 and 753 cm⁻¹ frequency beats to a dynamic coherence between the a603–b609 CT state and the two exciton states of the a602–a603 dimer. Note that the difference between the two values of the exciton–CT splitting, estimated from the 2DFT maps as 522 cm⁻¹ and 753 cm⁻¹, is very close to the intra-dimer splitting, which is 221 cm⁻¹ according to the maps (Fig. 6). Such a CT state has been recently proposed in the peripheral light-harvesting complex Lhca4, which is responsible for the red-most emission in Photosystem 1.^62,63 As noted above, the Chl a603–b609 CT state, red-shifted and fluorescent due to mixing with excitonic states, has also been detected in some conformational realizations of a single LHCII complex.^61,64

The energy level scheme of the red-most clusters of LHCII emerging from our analysis of the 2DFT maps is shown in Fig. 7. According to our assignment, the most pronounced exciton coherences in LHCII occur within the stromal side Chls a clusters, namely the Chl a602–a603 dimer and the Chl a610–a611–a612 trimer. In addition, the data suggests the presence of a CT state mixed with the Chls a602–a603–b609 excited states (at least in some realizations of the disorder). The red-shifted character of the CT state determines a predominant localization of the excitations within the a602–a603–CT mixed states. In realizations without exciton–CT mixing, excitations are localized at the a610–a611–a612 trimer. This response to disorder will play a role in mediating NPQ-related processes. When LHCII is in the light-harvesting condition, excitation energy is funnelled to the Chl a610–a611–a612 terminal emitter trimer, which subsequently transfers energy further into the photosynthetic assembly. However, in some realizations of disorder, excitation energy may instead be transferred to a spectroscopically dark state, such as the assigned a602–a603–CT mixed state. Localization of the energy within such an exciton–CT state could provide an effective pathway for NPQ in LHCII. This supports earlier work regarding NPQ, which have reported a far-red emission at 695–705 nm appearing in samples quenched in vitro.^28–31 This emission has been assigned to a Chl–Chl CT interaction, which is coupled to an excitonic state. NPQ is highly dependent on conformational protein dynamics, giving rise to small reversible changes in pigment coupling.²⁴ Here, 2DES has allowed us to visualize a dynamic coherence that could be tied to such a change in pigment coupling in solubilized LHCII trimers, in agreement with the previous fluorescence measurements on single LHCII complexes.⁶¹ Alternatively, Chl–Car interactions have also been implicated in NPQ, and the Chl a603–b609 site is nearby the carotenoid Lutein 621.^4,26,61 Chmeliov, et al. report that, while an excitonically coupled Chl–Chl CT state is emitting at 700 nm, this state is not directly responsible for NPQ, which in that work is proposed to occur via energy transfer to a carotenoid.^60,65 However, direct evidence of interactions between Chls and Cars is outside the scope of the present measurement. It is also relevant to consider that multiple CT interactions may be present in the densely populated LHCII complex. Our dataset is well described by the assignment of a single CT state, within the context of the present literature and LHCII model. However, further quantitative modeling, as we mention briefly below, would be needed to confirm (or refute) this assignment.

Fig. 7 Energy level scheme within the stromal side low energy excitonic clusters of LHCII, adapted from Novoderezhkin, et al.⁹ Arrows indicate the assignments for exciton (blue) and exciton–CT (red) coherences from this work. (Energy levels are not to scale.)

We now discuss the emerging scheme of coherences within the red-most clusters of LHCII in the context of our results compared to the current exciton model of LHCII.^9,11 Analysis of the 2DFT maps at different frequencies, as shown in Fig. 4, 5 and Fig. S3 and S4 (ESI†), suggests that they are mostly vibrational, but contain some excitonic contributions that are most pronounced within relatively narrow regions near 99 cm⁻¹, 221 cm⁻¹, 522 cm⁻¹, and 753 cm⁻¹. The relationship between these apparent values and the exciton (exciton–CT) splittings in LHCII is complicated due to energetic disorder and exciton-vibrational coupling. For example, in the exciton model,⁹ Chl a602–a603 is an asymmetric dimer with the 130 cm⁻¹ gap between the unperturbed site energies and 38 cm⁻¹ intersite coupling. This gives an exciton splitting of 150 cm⁻¹ without energetic disorder, and a disorder-induced spread of splitting from ≈80–290 cm⁻¹. The question then remains as to why the measured 2DFT maps only display exciton coherences near 221 cm⁻¹, and not across the entire range of 80–290 cm⁻¹. We put forth that all of the exciton splittings do in fact contribute to the disorder-averaged 2D kinetics, but such a superposition of many components oscillating with different frequencies significantly reduces the amplitude of the apparent oscillatory part of the kinetics. In other words, the exciton coherences are washed out by the disorder. Vibrational coherences, which are not affected by the disorder, survive. If any intense vibration falls within a range of exciton splittings, the situation becomes more complicated due to the presence of exciton-vibrational resonance. In this case, contributions from realizations with resonant exciton splitting will be highlighted in the 2D kinetics due to (i) vibration-assisted increase of the degree of exciton mixing in these realizations, and (ii) increase in lifetime of the exciton coherences via continuous re-pumping from the resonant long-lived vibrational coherences.⁶⁶ This is what we observe in LHCII, where the frequencies of the 2DFT maps that are identified as exhibiting excitonic coherences indeed match the reported vibrational frequencies (Tables S1 and S2, ESI†).^22,49,50,67 Coupling to the resonant vibration can significantly change the character of a coherent mixing of pigments within the exciton eigenstates in small and large systems, and can also result in shifting or splitting of some of the exciton levels.^51,54,57 So, the exciton feature appearing near 221 cm⁻¹ and disappearing upon tuning to 190 cm⁻¹ or 242 cm⁻¹ (Fig. 4b) is thus a signature of the exciton coherence enhanced by exciton-vibrational resonance. Similarly, the exciton–CT splittings producing the exciton-type peaks in a relatively narrow range near 99 cm⁻¹, 522 cm⁻¹, and 753 cm⁻¹, are highlighted by resonant vibrations (Tables S1 and S2, ESI†).

This also explains the apparent discrepancy in the spectral signatures of the exciton and exciton–CT coherent interactions. It might appear that if the 522 cm⁻¹ map represents an interaction between a CT state and the lower excitonic state of the a602–a603 dimer, then this spectral feature should absorb at 680 nm, the wavelength assigned to this lower excitonic state from the 221 cm⁻¹ map (and similarly for the 753 cm⁻¹ map and the upper excitonic state, absorbing at 668 nm in the 221 cm⁻¹ map.) However, due to the high degree of disorder in LHCII, the Chls a602 and a603 in fact contribute to the excitonic states ranging from 665–680 nm.⁸ The disorder of the CT transition energy is expected to be several times larger than for usual excited states. The features observed in the 2DFT maps correspond to realizations wherein the a602–CT and a603–CT splittings are resonant with the vibrations at 522 cm⁻¹ and 753 cm⁻¹, respectively. We can identify these contributions only by analysis of the shape of the 2DFT distribution, but it is difficult to identify the exact position of the peaks in the 2DFT map. In other words, the exact excitation wavelength corresponding to the a602–CT coherence can be found in an arbitrary point within the 665–680 nm region.

Resonant coupling between excitonic coherences and vibrational frequencies has been observed before in the B820 dimer,⁵⁴ PSII RC,⁵¹ and in a modified LH2 antenna.⁶⁸ More recently, it was reported that vibronic mixing enhances the energy transfer rates in cryptophyte algae.⁶⁹ From our present work, we cannot as yet draw any similar conclusions regarding interplay between vibronic coupling and energy transfer dynamics in LHCII. The DAS, particularly at λ_τ = 653 nm, (Fig. 3) may be indicative of coherent Chl a602–CT energy transfer in the fastest (90 fs) time component. A similar timescale was reported for vibrationally assisted coherent energy transfer in the PSII RC.⁷⁰ However, the overlapping features and low signal amplitude complicate such an assignment. The slower (2.6, >10 ps) components indicate incoherent transfer to low energy states, which may or may not include the CT state proposed in this work. These questions, along with a more detailed analysis of our assignments for the coherence beating frequencies, will require computational models which can incorporate CT bands as well as vibronic interactions.³⁵

Conclusion

In this work, we have explored coherent interactions in the low-energy region of LHCII trimers with 2DES. We observe the presence of weakly allowed ‘red’ states, possibly charge transfer states, coupled to the exciton manifold of LHCII. Our experimental results suggest that such an optically forbidden state may act as an alternative pathway for excess light energy, via a complex interplay of protein dynamic disorder and exciton-vibrational coupling. We have identified and assigned excitonic coherences at four frequencies based on the existing model and the present understanding of the system. A reliable interpretation of the observed coherences in LHCII will require the development of sophisticated physical models, such as Redfield theory in the exciton-vibrational basis, or non-perturbative approaches.

Experimental

Details regarding preparation of the LHCII trimer samples can be found in the ESI.† Steady-state absorption was done on a Perkin-Elmer Lambda40 spectrophotometer. 2D electronic spectroscopy was carried out on a partially home-built setup⁶⁸ which is modelled after previously established work.^42,71 The coherence time was measured from τ = −75 to 150 fs with 1 fs steps and the population time was measured from T = −100 to 1000 fs with 5 fs steps for the RT and T = −50 to 2500 fs with 10 fs steps for 77 K. Additionally, spectra at some longer population times (T = 5, 7.5, 10, 50, 75, 100 ps) were recorded. The measurements were done at 1 kHz repetition rate, and the spot diameter on the sample was ∼100 μm. The pulse energy was maintained at 6 nJ per pulse. The samples were measured in a quartz cuvette of 200 μm pathlength and the sample O.D. was 0.6 at the maximum of the Q_y absorption peak. The sample was kept stationary during the measurement. An absorption and fluorescence measurement before and after the experiments confirmed that there was minimal degradation over the course of the experiment. For the 77 K measurements, the sample was supplemented with 60% glycerol in order to form an optical glass. The 77 K measurements were done using an LN2 cooled cryostat (Optistat DN2, Oxford Instruments Nanoscience) and temperature controller. Global analysis of 2D slices along λ_τ was done using the open source R package TIMP⁷² and the Java-based graphical user interface Glotaran (v. 1.5.1),⁷³

Acknowledgements

V. I. N. was supported by the Russian Federation for Basic Research (Grant No. 15-04-02136). C. R. and R. v. G. were supported by the VU University Amsterdam, the advanced investigator grant (267333, PHOTPROT) from the European Research Council, and by the EU FP7 projects PAPETS (GA 323901). R. v. G. gratefully acknowledges his Academy Professor grant from the Netherlands Royal Academy of Sciences (KNAW). C. R. and M. F. are also grateful to F. Hendriks and P. Noordeloos of the Fijnmechanische Instrumentatie VU for technical work. The experimental work was carried out at LaserLaB Amsterdam, a part of Laserlab-Europe.

Notes and references

1. R. E. Blankenship, Molecular Mechanisms of Photosynthesis, Wiley-Blackwell, 2002.
2. R. Croce and H. van Amerongen, J. Photochem. Photobiol., B, 2011, 104, 142–153.
3. G. R. Fleming and R. van Grondelle, Phys. Today, 1994, 47, 48–55.
4. Z. Liu, H. Yan, K. Wang, T. Kuang, J. Zhang, L. Gui, X. An and W. Chang, Nature, 2004, 428, 287–292.
5. J. Standfuss, A. C. Terwisscha van Scheltinga, M. Lamborghini and W. Kühlbrandt, EMBO J., 2005, 24, 919–928.
6. H. van Amerongen and R. van Grondelle, J. Phys. Chem. B, 2001, 105, 604–617.
7. V. I. Novoderezhkin and R. van Grondelle, Phys. Chem. Chem. Phys., 2010, 12, 7352–7365.
8. V. I. Novoderezhkin, M. A. Palacios, H. van Amerongen and R. van Grondelle, J. Phys. Chem. B, 2005, 109, 10493–10504.
9. V. I. Novoderezhkin, A. Marin and R. van Grondelle, Phys. Chem. Chem. Phys., 2011, 13, 17093–17103.
10. T. Renger, M. E. Madjet, A. Knorr and F. Müh, J. Plant Physiol., 2011, 168, 1497–1509.
11. F. Muh, M. E. A. Madjet and T. Renger, J. Phys. Chem. B, 2010, 114, 13517–13535.
12. J. Linnanto, J. Martiskainen, V. Lehtovuori, J. Ihalainen, R. Kananavicius, R. Barbato and J. Korppi-Tommola, Photosynth. Res., 2006, 87, 267–279.
13. V. I. Novoderezhkin and R. van Grondelle, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 124003.
14. P. Giorda, S. Garnerone, P. Zanardi and S. Lloyd, 2011, arXiv:1106.1986v1.
15. X. Pan, Z. Liu, M. Li and W. Chang, Curr. Opin. Struct. Biol., 2013, 23, 515–525.
16. H. Rogl, R. Schödel, H. Lokstein, W. Kühlbrandt and A. Schubert, Biochemistry, 2002, 41, 2281–2287.
17. W. Kühlbrandt, Curr. Opin. Struct. Biol., 1994, 4, 519–528.
18. F. J. Kleima, C. C. Gradinaru, F. Calkoen, I. H. M. van Stokkum, R. van Grondelle and H. van Amerongen, Biochemistry, 1997, 36, 15262–15268.
19. J. Pieper, M. Ratsep, K. D. Irrgang and A. Freiberg, J. Phys. Chem. B, 2009, 113, 10870–10880.
20. G. S. Schlau-Cohen, T. R. Calhoun, N. S. Ginsberg, E. L. Read, M. Ballottari, R. Bassi, R. van Grondelle and G. R. Fleming, J. Phys. Chem. B, 2009, 113, 15352–15363.
21. G. S. Schlau-Cohen, T. R. Calhoun, N. S. Ginsberg, M. Ballottari, R. Bassi and G. R. Fleming, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13276–13281.
22. E. J. G. Peterman, T. Pullerits, R. vanGrondelle and H. vanAmerongen, J. Phys. Chem. B, 1997, 101, 4448–4457.
23. R. Remelli, C. Varotto, D. Sandona, R. Croce and R. Bassi, J. Biol. Chem., 1999, 274, 33510–33521.
24. P. Horton, M. Wentworth and A. Ruban, Febs Lett., 2005, 579, 4201–4206.
25. P. Muller, X. P. Li and K. K. Niyogi, Plant Physiol., 2001, 125, 1558–1566.
26. C. D. P. Duffy, J. Chmeliov, M. Macernis, J. Sulskus, L. Valkunas and A. V. Ruban, J. Phys. Chem. B, 2012, 117, 10974–10986.
27. M. Wentworth, A. V. Ruban and P. Horton, J. Biol. Chem., 2003, 278, 21845–21850.
28. Y. Miloslavina, A. Wehner, P. H. Lambrev, E. Wientjes, M. Reus, G. Garab, R. Croce and A. R. Holzwarth, FEBS Lett., 2008, 582, 3625–3631.
29. A. Kell, X. Feng, C. Lin, Y. Yang, J. Li, M. Reus, A. R. Holzwarth and R. Jankowiak, J. Phys. Chem. B, 2014, 118, 6086–6091.
30. M. G. Müller, P. H. Lambrev, M. Reus, E. Wientjes, R. Croce and A. R. Holzwarth, ChemPhysChem, 2010, 11, 1289–1296.
31. M. Wahadoszamen, R. Berera, A. M. Ara, E. Romero and R. van Grondelle, Phys. Chem. Chem. Phys., 2012, 14, 759–766.
32. P. Malý, J. M. Gruber, R. van Grondelle and T. Mančal, Nat. Publ. Gr., 2015, 6, 26230.
33. A. V. Ruban, R. Berera, C. Ilioaia, I. H. M. van Stokkum, J. T. M. Kennis, A. A. Pascal, H. van Amerongen, B. Robert, P. Horton and R. van Grondelle, Nature, 2007, 450, 575–578.
34. B. van Oort, R. van Grondelle and I. H. M. van Stokkum, J. Phys. Chem. B, 2015, 119, 5184–5193.
35. J. R. Reimers, M. Biczysko, D. Bruce, D. F. Coker, T. J. Frankcombe, H. Hashimoto, J. Hauer, R. Jankowiak, T. Kramer, J. Linnanto, F. Mamedov, F. Müh, M. Rätsep, T. Renger, S. Styring, J. Wan, Z. Wang, Z.-Y. Wang-Otomo, Y.-X. Weng, C. Yang, J.-P. Zhang, A. Freiberg and E. Krausz, Biochim. Biophys. Acta, Bioenerg., 2016, 1857, 1627–1640.
36. T. K. Ahn, T. J. Avenson, M. Ballottari, Y.-C. Cheng, K. K. Niyogi, R. Bassi and G. R. Fleming, Science, 2008, 320, 794–797.
37. T. P. J. Krüger, E. Wientjes, R. Croce and R. van Grondelle, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13516–13521.
38. C. Ramanan, J. M. Gruber, P. Malý, M. Negretti, V. I. Novoderezhkin, T. P. J. Krüger, T. Mančal, R. Croce and R. van Grondelle, Biophys. J., 2015, 108, 1047–1056.
39. K. Vrandecic, M. Rätsep, L. Wilk, L. Rusevich, M. Golub, M. Reppert, K.-D. Irrgang, W. Kühlbrandt and J. Pieper, J. Phys. Chem. B, 2015, 119, 3920–3930.
40. D. M. Jonas, Annu. Rev. Phys. Chem., 2003, 54, 425–463.
41. E. Collini, Chem. Soc. Rev., 2013, 42, 4932–4947.
42. T. Brixner, I. V. Stiopkin and G. R. Fleming, Opt. Lett., 2004, 29, 884–886.
43. T. R. Calhoun, N. S. Ginsberg, G. S. Schlau-Cohen, Y.-C. Cheng, M. Ballottari, R. Bassi and G. R. Fleming, J. Phys. Chem. B, 2009, 113, 16291–16295.
44. G. S. Schlau-Cohen, A. Ishizaki, T. R. Calhoun, N. S. Ginsberg, M. Ballottari, R. Bassi and G. R. Fleming, Nat. Chem., 2012, 4, 389–395.
45. N. H. C. Lewis, N. L. Gruenke, T. A. A. Oliver, M. Ballottari, R. Bassi and G. R. Fleming, J. Phys. Chem. Lett., 2016, 7, 4197–4206.
46. H.-G. Duan, A. L. Stevens, P. Nalbach, M. Thorwart, V. I. Prokhorenko and R. J. D. Miller, J. Phys. Chem. B, 2015, 119, 12017–12027.
47. P. Horton, A. V. Ruban, D. Rees, A. A. Pascal, G. Noctor and A. J. Young, Febs Lett., 1991, 292, 1–4.
48. M. M. Enriquez, P. Akhtar, C. Zhang, G. Garab, P. H. Lambrev and H.-S. Tan, J. Chem. Phys., 2015, 142, 212432.
49. D. Kosumi, T. Nishiguchi, M. Sugisaki and H. Hashimoto, J. Photochem. Photobiol., A, 2015, 313, 72–78.
50. M. Rätsep, J. Linnanto and A. Freiberg, J. Chem. Phys., 2009, 130, 194501.
51. V. I. Novoderezhkin, E. Romero and R. van Grondelle, Phys. Chem. Chem. Phys., 2015, 17, 30828–30841.
52. F. D. Fuller, J. Pan, A. Gelzinis, V. Butkus, S. S. Senlik, D. E. Wilcox, C. F. Yocum, L. Valkunas, D. Abramavičius and J. P. Ogilvie, Nat. Chem., 2014, 6, 706.
53. E. Romero, R. Augulis, V. I. Novoderezhkin, M. Ferretti, J. Thieme, D. Zigmantas and R. van Grondelle, Nat. Phys., 2014, 10, 676–682.
54. M. Ferretti, V. I. Novoderezhkin, E. Romero, R. Augulis, A. Pandit, D. Zigmantas and R. van Grondelle, Phys. Chem. Chem. Phys., 2014.
55. K. L. Wells, P. H. Lambrev, Z. Zhang, G. Garab and H.-S. Tan, Phys. Chem. Chem. Phys., 2014, 16, 11640–11646.
56. E. Romero, V. I. Novoderezhkin and R. van Grondelle, Nature, 2017, 543, 355–365.
57. A. Chenu, N. Christensson, H. F. Kauffmann and T. Mančal, Sci. Rep., 2013, 3, 782.
58. V. Tiwari, W. K. Peters and D. M. Jonas, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1203–1208.
59. F. Müh and T. Renger, Biochim. Biophys. Acta, Bioenerg., 2012, 1817, 1446–1460.
60. J. Chmeliov, A. Gelzinis, E. Songaila, R. Augulis, C. D. P. Duffy, A. V. Ruban and L. Valkunas, Nat. Plants, 2016, 2, 16045.
61. T. P. J. Kruger, V. I. Novoderezhkin, C. Ilioaia and R. van Grondelle, Biophys. J., 2010, 98, 3093–3101.
62. V. I. Novoderezhkin, R. Croce, M. Wahadoszamen, I. Polukhina, E. Romero and R. van Grondelle, Phys. Chem. Chem. Phys., 2016, 18, 19368–19377.
63. E. Romero, M. Mozzo, I. H. M. van Stokkum, J. P. Dekker, R. van Grondelle and R. Croce, Biophys. J., 2009, 96, L35–L37.
64. T. P. J. Kruger, C. Ilioaia, M. P. Johnson, A. V. Ruban, E. Papagiannakis, P. Horton and R. Van Grondelle, Biophys. J., 2012, 102, 2669–2676.
65. T. P. J. Krüger, C. Ilioaia, M. P. Johnson, A. V. Ruban and R. van Grondelle, Biochim. Biophys. Acta, 2014, 1837, 1027–1038.
66. M. B. Plenio, J. Almeida and S. F. Huelga, J. Chem. Phys., 2013, 139, 235102.
67. R. A. Avarmaa and K. K. Rebane, Spectrochim. Acta, Part A, 1985, 41, 1365–1380.
68. M. Ferretti, R. Hendrikx, E. Romero, J. Southall, R. J. Cogdell, V. I. Novoderezhkin, G. D. Scholes and R. van Grondelle, Sci. Rep., 2016, 6, 20834.
69. J. C. Dean, T. Mirkovic, Z. S. D. Toa, D. G. Oblinsky and G. D. Scholes, Chemistry, 2016, 1, 858–872.
70. V. I. Novoderezhkin, E. Romero, J. Prior, R. van Grondelle, G. S. Engel, D. Zigmantas, R. van Grondelle, V. A. Nadtochenko, A. Y. Semenov and V. A. Shuvalov, Phys. Chem. Chem. Phys., 2017, 19, 5195–5208.
71. T. Brixner, T. Mancal, I. V. Stiopkin and G. R. Fleming, J. Chem. Phys., 2004, 121, 4221–4236.
72. K. M. Mullen and I. H. M. van Stokkum, J. Stat. Softw., 2007, 18, 1–46.
73. J. J. Snellenburg, S. P. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, J. Stat. Softw., 2012, 49, 1–22.

---

Footnotes

† Electronic supplementary information (ESI) available: Preparation of LHCII trimer samples, additional real total 2D spectra, decay-associated spectra, and 2DFT maps, and tables comparing FFT frequencies found in this study with literature values of vibrational frequencies. See DOI: 10.1039/c7cp03038j

‡ Present address: Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany.

---