On the feasibility of reactions through the fullerene wall: a theoretical study of NH_x@C₆₀

Abstract

We propose a new approach to the synthesis of AH_x@fullerene structures via reactions through the fullerene wall. To investigate the feasibility of the approach, the step-by-step hydrogenation of the template endofullerene N@C₆₀ up to NH₄@C₆₀ has been studied using DFT and MP2 calculations. Protonation of the endohedral guest through the fullerene wall is competitive with escape of the guest, whereas reaction with a hydrogen atom is less favorable. Each protonation step is highly exothermic, so that less active acids can also protonate the guest with less accumulation of energy. The final product, NH₄@C₆₀ is a novel concentric ion pair NH₄⁺@C₆₀˙⁻ in which the charge-centers of the two ions coincide.

---

Introduction

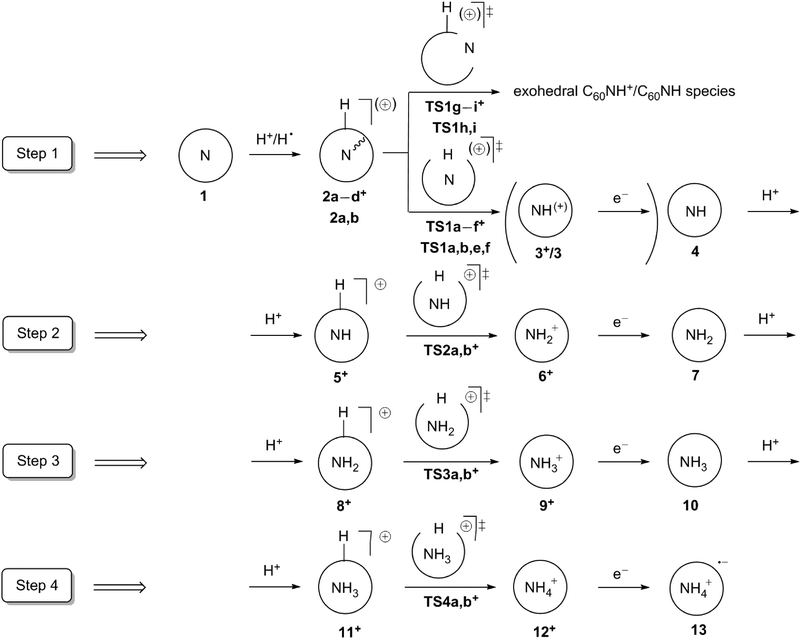
The inner wall of fullerenes is essentially chemically inert because of its concave shape.¹ This inertness allows, for instance, a nitrogen atom in its quartet state to be encapsulated within C₆₀ with a significant barrier to release and without it reacting with the fullerene.^2–4 Before this species was reported, only the cations of electropositive metals^5–7 or noble-gas atoms^8–14 had been observed as endohedral guests within fullerenes. A series of species ranging from hydrogen^15,16 and nitrogen^17,18 molecules, water,¹⁹ carbon monoxide¹⁸ to transition metal atoms and ions (see, for example, reviews^20,21 and references therein), carbides,²⁰ nitrides,²⁰ oxides²⁰ and intermetals^22–24 have since been incorporated into fullerenes to give stable endofullerene derivatives.

Most of the above examples of the endofullerenes were synthesized by constructing or reclosing the fullerene cage in the presence of the moiety to be incorporated. Only the noble gases@C₆₀ were obtained by colliding accelerated charged, closed fullerene with atoms.^8–13 Diatomics were inserted into C₆₀ and C₇₀ under high pressures and temperatures.¹⁸ We have therefore used the examples of NH₃@C₆₀ and NH₄@C₆₀ to conduct a purely theoretical study to investigate the possibility of synthesizing endohedral guests within fullerenes by allowing reagents (in this case protons and atomic hydrogens) to pass through the walls of the fullerene. To our knowledge, the only studies in which atoms or ions have passed through the fullerene cage wall involve escape or insertion of an endohedral guest.^4,25–27

Here we investigate the possibility of synthesizing NH_x@C₆₀ (x = 1–4) starting from N@C₆₀ by insertion of protons or hydrogen atoms through the fullerene wall. NH₃@C₆₀, for instance, has not yet been observed experimentally, although theoretical studies are available.^28–30 In 2008 ammonia was inserted into a chemically opened fullerene.³¹ However, the chemical properties of the host–guest complex obtained must differ greatly from the target endofullerene NH₃@C₆₀, since even at low temperatures (−10 °C) ammonia escapes slowly from this open-cage fullerene.³¹ It is known, however, that NH₃@C₆₀ is thermodynamically stable, while nNH₃@C₆₀ with n = 2–7 represent metastable structures and the cage finally breaks for n = 8.³⁰

Scheme 1 shows a suggested synthetic route to NH₃@C₆₀ and NH₄@C₆₀via consecutive pronation and reduction steps starting from the known^2–4 N@C₆₀, which has been suggested as a possible material for the development of the electron-spin quantum computers.^32,33 We compare this route to the stepwise direct hydrogenation. Since the spin states of nitrogen hydrides vary with the number of hydrogen atoms, we also investigate all the intermediate NH_x@C₆₀ compounds for x = 0–4 as they can be potentially interesting for spintronics applications. In addition, we investigate the electronic properties of NH₄@C₆₀.

Scheme 1 Proposed approach for step-by-step synthesis of NH₄⁺@C₆₀˙⁻ (13). The C₆₀ cage is represented as circles for clarity. Different pathways considered are designated with lower case characters a–i (see Results and discussion).

Computational details

Geometries of all structures were fully optimized at the B3LYP^34–39 level of theory using the 6-31G(d)^40–51 basis set (denoted as “B3LYP” in the following). Stationary points were confirmed to be minima or transition states by calculating the vibrational normal modes within the harmonic approximation. One additional spurious imaginary vibrations (−6.3 cm⁻¹) for TS1b⁺ was ignored. Additional single-point (SP) calculations were performed at the MP2^52–57 level of theory with the same basis set on the DFT-optimized geometries (denoted in the following MP2). All B3LYP/6-31G(d)- and MP2-computed relative energies are corrected for zero-point vibrational energies (ZPEs) calculated at the DFT level. Unrestricted B3LYP calculations were performed for all open-shell systems. However, ROMP2 single points were performed for open-shell systems because of high spin contamination in the unrestricted calculations. All structures were visualised with ChemCraft 1.7.⁵⁸

All Hartree–Fock reference wavefunctions used in RMP2 calculations exhibit RHF/UHF instabilities for the closed-shell systems and the reference UHF wavefunctions have internal instabilities for the open-shell systems. Some, but not all, B3LYP wavefunctions also exhibit instabilities. Wavefunction instabilities cause the large relative energy differences between B3LYP and MP2 calculations in some cases. Thus, the orbital initial guesses for MP2 calculations of the endofullerenes were read from DFT checkpoint files, which lead to the numerically stable and consistent results.

The Gaussian 03⁵⁹ and 09⁶⁰ program packages were used for all calculations. The key reaction pathways along both directions from the transition structures were followed by the IRC method.⁶¹ Natural population analysis^62–68 (NPA) was performed within the Gaussian 03 and 09 packages using the density matrices for the current methods.⁶⁹

Results and discussion

Mechanism of proton penetration and nitrogen escape

Our calculations start from the appropriate exo-protonated NH_x–1@C₆₀ endofullerenes and proceed according to Scheme 1. Any study of these systems is complicated by their many possible spin states. Thus, the first reaction step (step 1 in Scheme 1) begins from N@C₆₀1, which can exist in high- (spin 3/2) and low-spin (spin 1/2) states. It has been shown in previous experimental^2,70–72 and theoretical^4,73,74 studies that the ground state of 1 is high spin. Our current study supports this conclusion, since ⁴1 is more stable than ²1 (see Scheme 2) by 26.0 kcal mol⁻¹ and 79.2 kcal mol⁻¹ at the B3LYP and MP2 levels, respectively. Moreover, although the formation of ⁴1 from a free nitrogen atom and C₆₀ is found to be slightly endothermic (by 1.3 kcal mol⁻¹) at the B3LYP level, earlier UB3LYP/D95*//PM3 calculations,⁴ found it to be exothermic by 0.9 kcal mol⁻¹ and our MP2 calculations predict the formation of ⁴N@C₆₀ to be favorable by −6.8 kcal mol⁻¹. Thus, our further discussion of step 1 (Scheme 1) will be concerned with the quartet potential-energy surface (PES).

Scheme 2 Schematic energy profile for N insertion into C₆₀, relative energies in kcal mol⁻¹ at the B3LYP (black) and MP2 (red) levels.

Several possible pathways exist between the exo-protonated ⁴N@C₆₀H⁺2a⁺ (Fig. 1) and NH⁺@C₆₀3⁺. We will therefore discuss step 1 (Scheme 1) in detail and steps 2–4 more briefly, since they are quite similar. As expected, the exo-protonation step (1 + H⁺ → 2a⁺) is highly exothermic (−211.1 and −196.3 kcal mol⁻¹ at B3LYP and MP2, respectively). The ⁴2a⁺/²2a⁺ gap is only slightly smaller than for ⁴1/²1 (24.9 and 78.2 kcal mol⁻¹ at B3LYP and MP2, respectively).

Fig. 1 Structures and relative energies in kcal mol⁻¹ at the B3LYP (black) and MP2 (red) levels for the quartet minima 2a–d⁺.

Starting from 2a⁺, the proton can reach the nitrogen atom by breaking either a [5,6]- or a [6,6]-bond of C₆₀ (TS1a⁺ and TS1b⁺, respectively, Fig. 2). The more favorable of these two transition states is ⁴TS1a⁺ for migration by breaking a [5,6]-bond, with calculated barriers of 90.0 and 90.1 kcal mol⁻¹ relative to ⁴2a⁺ at the B3LYP and MP2 levels, respectively. No pathways that involve direct passage of the proton through the hexagonal or pentagonal rings were found. An attempted transition-state optimization for the first case without symmetry constraints leads to complex 2a⁺, and in the second case to TS1a⁺.

Fig. 2 Structures and energies relative to 2a⁺ in kcal mol⁻¹ at the B3LYP (black) and MP2 (red) levels for proton migration from 2a–d⁺ to 3⁺via the alternative quartet transition states TS1a–f⁺, and for the N-escape from 2b–d⁺via alternative quartet transition states TS1h⁺ by breaking a [5,6]-bond and TS1i⁺ by breaking a [6,6]-bond. TS1a,e⁺ corresponds to proton migration by breaking a [5,6]-bond; TS1b,f⁺ – by breaking a [6,6]-bond; TS1c⁺ – by breaking two bonds and TS1d⁺ by breaking three bonds. TS1g⁺ corresponds to the formation of 2b⁺ from 2a⁺.

In addition, a previous DFT study of proton migration on the C₆₀ surface,⁷⁵ which should behave very similarly to that on the surface of NH_x@C₆₀H⁺, showed that transition states in which the proton lies above the centers of five- or six-membered rings are those for proton migration over the C₆₀ surface. Nevertheless, transition states for these two processes were computed using symmetry constraints and found to be highly unfavorable relative to proton migration above [5,6]- and [6,6]-bonds.⁷⁵

A mechanism analogous to He-insertion into C₆₀, which occurs through a “window” made by opening two C–C bonds,²⁷ was also considered. However, the transition state for this process, ⁴TS1c⁺ lies much higher in energy than ⁴TS1a,b⁺ (Fig. 2). Another study²⁵ suggested that the most favorable pathway of He-insertion should be to open a window by breaking three-bonds. However, we found that the transition state for this process, ⁴TS1d⁺ is the least favorable of those studied here.

In addition to the pathways discussed above (Fig. 2), we have also considered possible lower-lying ones that occur via the formation of endo-NH_x@C₆₀H⁺ intermediates at [5,6]- and [6,6]-aza bridges. Protonating the C₆₀ cage causes a drastic increase in the number of possible isomeric endofullerenes with aza-bridges. However, due to the stabilizing interaction between the nitrogen lone pair and the positively charged carbon atoms adjacent to the C–H moiety, the three endo-N@C₆₀H⁺ isomers 2b–d⁺ shown in Fig. 2 are expected to be the most favorable. This was confirmed partially by calculating two other endo-N@C₆₀H⁺ isomers in which the nitrogen atom is farthest from the C–H moiety. 2b⁺ is the most stable endo-N@C₆₀H⁺ isomer, but the nitrogen atom does not form an aza-bridge and is rather covalently bound to one carbon atom (denoted “endohedrally bound” below) with a C–N bond length of 1.53 Å. The nitrogen atom has a negative charge of −0.136 e according to an NPA analysis. 2b⁺ can be formed with a relatively low barrier (TS1g⁺, 19.4 and 30.1 kcal mol⁻¹, at the B3LYP and MP2 levels, respectively, Fig. 2) from 2a⁺. This barrier is much lower than that found for N@C₆₀⁴ because of the interaction of the nitrogen lone pair with the protonated C₆₀ cage.

Analogously to TS1a⁺ and TS1b⁺, we found TS1e⁺ and TS1f⁺, which correspond to the transition states for the reaction paths starting from 2b⁺, in which the proton is inserted through the [5,6]- and [6,6]-bonds, respectively. However, they lie too high in energy to play a role in the reaction (Fig. 2). In contrast, N-escape becomes possible from the 2b⁺ intermediate through both the [5,6]- and [6,6]-bonds (TS1h⁺ and TS1i⁺, respectively). The latter is more favorable, as also found for N@C₆₀.⁴TS1i⁺ lies 81.8 kcal mol⁻¹ higher in energy than 2a⁺ on the PES at the B3LYP level and thus lower than TS1a⁺ (90.0 kcal mol⁻¹). However, at the MP2 level, this ordering is reversed: TS1i⁺ lies slightly higher in energy than TS1a⁺ (90.6 vs. 90.1 kcal mol⁻¹). Thus, nitrogen escape and nitrogen protonation can be competitive processes.

We only considered insertion pathways through the [5,6]- and [6,6]-bonds via transition states of the types TS1a⁺ and TS1b⁺, respectively, for the subsequent steps 2–4 (Scheme 1). These pathways are the most favorable for step 1 and the remaining steps appear to be very similar in geometries and barriers heights (see below). The designations a and b used for transition states TS2⁺–TS4⁺ have the same meaning as for the transition states, TS1⁺, for the first step. No stable minima were found for endo-NH@C₆₀ in which NH forms aza-bridges to a nearby C–H moiety. All such starting geometries optimized to NH@C₆₀H⁺ with NH at the center of the C₆₀ cage. We therefore did not investigate pathways for further protonation of the nitrogen-containing moiety via endo-NH_x@C₆₀H⁺ intermediates for steps 2–4.

Energetics of the step-by-step formation of NH₄⁺@C₆₀˙⁻

The energetics of all four steps shown in Scheme 1 are given in Table 1 and in Scheme 3, where energies relative to ⁴2a⁺ and relative energies within a step are shown. All reactions are exothermic, by 7–56 kcal mol⁻¹ at B3LYP and by 18–109 kcal mol⁻¹ at MP2.

Table 1 Energetics of the four-step synthesis of NH₄⁺@C₆₀˙⁻13

Structure	B3LYP		MP2
	Within a step, kcal mol^−1	vs. ^4 2^+, kcal mol^−1	Within a step, kcal mol^−1	vs. ^4 2^+, kcal mol^−1
a Possible change of a multiplicity of the system after the addition of an electron.
Step 1
Quartet PES
^4 2a+	0.0		0.0
^4 2b^+	11.2		8.1
^4 2c^+	18.7		28.7
^4 2d+	24.8		37.7
^4 TS1a^+	90.0		90.1
^4 TS1b^+	112.0		105.9
^4 TS1c^+	172.1		168.1
^4 TS1d^+	211.6		218.4
^4 TS1e^+	130.1		142.5
^4 TS1f^+	149.4		157.1
^4 TS1g^+	19.4		30.1
^4 TS1h^+	96.9		126.9
^4 TS1i^+	81.8		90.6
^4 3^+	−17.8		−25.5
^5 4	−144.7		−158.9
^3 4	−181.6		−179.8
^1 4	−130.3		−122.9
Doublet PES
^2 2a^+	0.0	24.9	0.0	78.2
^2 TS1a^+	90.2	115.1	89.9	168.0
^2 TS1b^+	112.2	137.1	107.7	185.9
^2 3^+	−43.9	−19.0	−46.6	31.5
Step 2 (triplet PES)
^3 5^+	0.0	−393.9	0.0	−376.9
^3 TS2a^+	90.9	−303.0	91.4	−285.5
^3 TS2b^+	112.2	−281.7	109.5	−267.4
^3 6^+	−26.4	−420.3	−37.1	−414.0
^2 7	−188.4	−582.3	−194.2	−571.1
Step 3 (doublet PES)
^2 8^+	0.0	−794.0	0.0	−767.9
^2 TS3a^+	87.5	−706.5	88.3	−679.6
^2 TS3b^+	110.8	−683.2	104.2	−663.7
^2 9^+	−38.0	−832.0	−54.2	−822.1
^1 10	−201.9	−995.9	−212.9	−980.8
Step 4 (singlet PES)
^1 11^+	0.0	−1208.7	0.0	−1178.6
^1 TS4a^+	89.1	−1119.6	90.2	−1088.4
^1 TS4b^+	112.0	−1096.7	108.6	−1070.0
^1 12^+	−6.8	−1215.5	−17.8	−1196.4
^2 13	−135.2	−1343.9	−155.7	−1334.3

---

Scheme 3 Energetics of the four-step synthesis of NH₄⁺@C₆₀˙⁻13via the most favorable transition states and spin states. Energies in kcal mol⁻¹ within a step vs. (/) relative to ⁴2a⁺ at the B3LYP (black) and at the MP2 (red).

The barriers for each type of pathway hardly vary for the different steps and multiplicities. Thus, for step 1 the doublet PES lies almost parallel to the quartet one. Since doublet 2a⁺ lies higher in energy than quartet 2a⁺, and 1 exists in the quartet state (see above) the entire reaction most likely proceeds on the quartet PES. Similarly, the second step should proceed on the triplet, rather than on the singlet or quintet PES, because 4⁺ is by far most stable in the triplet state (Table 1).

The endofullerenes NH_x⁺@C₆₀ all have high electron affinities (from 111 to 164 kcal mol⁻¹ (4.83–7.11 eV) at B3LYP and from 97 to 211 kcal mol⁻¹ (4.23–9.16 eV) at MP2, Table 2) and thus they can be readily reduced to the neutral endofullerenes NH_x@C₆₀, e.g. using gas-phase neutralization as has been demonstrated for other endofullerenes.^11,12

Table 2 Electron affinities of the species NH_x⁺@C₆₀, x = 1–4 (3⁺, 6⁺, 9⁺ and 12⁺, respectively)

Oxidized species	Reduced species	B3LYP		MP2
		kcal mol^−1	eV	kcal mol^−1	eV
Step 1
^4 3^+	^5 4	126.9	5.50	133.4	5.78
	^3 4	163.8	7.10	154.3	6.69
	^1 4	112.6	4.88	97.4	4.23
^2 3^+	^5 4	125.7	5.45	190.4	8.26
	^3 4	162.6	7.05	211.3	9.16
	^1 4	111.3	4.83	154.5	6.70
Step 2
^3 6^+	^2 7	161.9	7.02	157.1	6.81
Step 3
^2 9^+	^1 10	163.9	7.11	158.7	6.88
Step 4
^1 12^+	^2 13	128.4	5.57	137.9	5.98

---

The total energy gain of all transformations starting from 1 and ending with 13 according to eqn (1) is 1555.0 kcal mol⁻¹ at B3LYP and 1530.6 kcal mol⁻¹ at MP2.

N@C₆₀ + 4H⁺ + 4 e⁻ → NH₄⁺@C₆₀˙⁻ (1)

Although the barriers for protonating endohedral nitrogen hydrides through the fullerene cage are too high to be observable in solution, the entire process involves a continuous decrease in energy, so that each step is possible in the gas phase. The calculated proton affinities of NH_x@C₆₀ in the gas phase (Table 3) are very similar to that of C₆₀ itself (211 and 196 kcal mol⁻¹ at the B3LYP and MP2 levels of theory, respectively, compared with the experimental range⁷⁶ of 204 to 207 kcal mol⁻¹ and a further calculated value⁷⁵ of 202 kcal mol⁻¹). The calculated proton affinities for the endohedral nitrogen-containing species lie in the range between 207 and 213 kcal mol⁻¹ with B3LYP and between 194 and 198 kcal mol⁻¹ with MP2.

Table 3 Energetics of protonation of the species NH_x@C₆₀, x = 0–3 (1, 4, 7 and 10, respectively) and of the proton transfer to them from the proton carriers H₃⁺ and CH₅⁺ in kcal mol⁻¹

Reaction	B3LYP		MP2
	Quartet	Doublet	Quartet	Doublet
Step 1
1 + H^+ → 2a^+	−211.1	−212.2	−196.3	−197.4
1 + H3^+ → 2a^+ + H2	−121.8	−122.8	−107.5	−108.5
1 + CH5^+ → 2a^+ + CH4	−85.7	−86.8	−74.9	−75.9
Step 2 (triplet PES)
4 + H^+ → 5^+	−212.3		−197.1
4 + H3^+ → 5^+ + H2	−123.0		−108.2
4 + CH5^+ → 5^+ + CH4	−86.9		−75.6
Step 3 (doublet PES)
7 + H^+ → 8^+	−211.7		−196.8
7 + H3^+ → 8^+ + H2	−122.4		−108.0
7 + CH5^+ → 8^+ + CH4	−86.3		−75.4
Step 4 (singlet PES)
10 + H^+ → 11^+	−212.9		−197.7
10 + H3^+ → 11^+ + H2	−123.5		−108.9
10 + CH5^+ → 11^+ + CH4	−87.5		−76.3

---

Thus, the protonated species NH_x@C₆₀H⁺ possess adequate energy immediately after their formation to cross the calculated barriers for protonation through the C₆₀ cage. Therefore, a protonation-rearrangement cascade from NH_x−1@C₆₀ to NH_x⁺@C₆₀ is possible. However, as the rearrangements to NH_x⁺@C₆₀ are mildly exothermic, the product is even hotter than the protonated fullerene precursor, so that thermal energy would have to be dissipated at the product stage. Using less energy-rich acids such as H₃⁺ and CH₅⁺, which are common protonating agents in ion cyclotron resonance spectrometry,^77–79 would render the initial proton transfer to NH_x@C₆₀ less exothermic. The relevant heats of reaction are shown in Table 3. Generally, the energy gained from protonation by CH₅⁺ is slightly less than the barriers for transferring the proton through the cage to nitrogen. On the other hand, proton transfer from H₃⁺ releases slightly more energy than is necessary to overcome the barrier. Thus, H₃⁺ is a promising candidate for the individual through-cage protonation steps.

Alternative approach using hydrogenation by hydrogen atoms

In addition, we considered the corresponding hydrogenation of nitrogen inside C₆₀1 through the buckminsterfullerene wall by atomic H˙ to compare barriers with those described above for protonation by the bare proton H⁺ (Scheme 1). Three possible spin states (quintet, triplet and singlet) were taken into account. The energetics of the computed pathway are summarized in Table 4. Notations of species are the same as above with the difference that all further discussion will refer to neutral species rather than positively charged ones.

Table 4 Energetics of the formation of NH@C₆₀4

Structure	B3LYP		MP2
	Within a step, kcal mol^−1	vs. ^1 2e, kcal mol^−1	Within a step, kcal mol^−1	vs. ^1 2e, kcal mol^−1
a TS1h optimized to TS1m. b 2b optimized to 2e. c ^1 TS1a optimized to ^1TS1j. d ^1 TS1k was located instead of ^1TS1b.
Quintet PES
^5 2a	0.0	2.2	0	5.9
^5 2b	29.2	31.4	31.7	37.5
^5 TS1a	100.9	103.0	100.8	106.6
^5 TS1b	106.8	108.9	100.1	106.0
^5 TS1e	141.6	143.7	161.4	167.3
^5 TS1f	152.5	154.7	171.9	177.8
^5 TS1m	98.3	100.5	123.1	128.9
^5 TS1i	95.9	98.1	98.8	104.7
^5 4	−0.1	2.1	−16.3	−10.4
Triplet PES
^3 2a	1.6	2.1	76.5	84.7
^3 2b	0.0	0.4	0.0	8.1
^3 TS1a	102.6	103.0	172.6	180.7
^3 TS1b	108.5	108.9	146.9	155.0
^3 TS1e	125.8	126.3	135.2	143.3
^3 TS1f	135.1	108.9	156.0	164.1
^3 TS1m	81.8	82.2	96.6	104.8
^3 TS1i	76.9	77.4	81.0	89.1
^3 4	−35.2	−34.8	−39.5	−31.4
Singlet PES
^1 2a	83.2		111.7
^1 2e	0.0		0.0
^1 TS1j	175.0		137.6
^1 TS1k	126.9		138.3
^1 TS1h	71.1		81.9
^1 TS1i	69.4		80.5
^1 4	16.4		25.5

---

Unlike 2a⁺ with nitrogen located at the center of the protonated C₆₀ cage (Fig. 2), neutral N@C₆₀H 2a is not the most stable isomer. The most favorable one is singlet 2e (Table 4 and Fig. 3). In 2e nitrogen forms covalent bonds with three neighboring carbons of a hexagon and the fourth carbon is saturated with hydrogen atom. Such a structure is so strongly preferred for the singlet state that no 2b can be located: any attempts to find 2b end in 2e.

Fig. 3 Structures and relative energies in kcal mol⁻¹ at the B3LYP (black) and MP2 (red) levels for ⁵2a, ³2b, ¹2e minima, and transition states ¹TS1h–k and ⁵TS1m.

Moreover, ¹2e is closely followed in energy by the most stable triplet isomer of 2 (2b) and by quintet 2a (Fig. 3), which are less favorable by 0.1 and 2.2 kcal mol⁻¹ at DFT and by 8.1 and 5.9 kcal mol⁻¹ at MP2, respectively. Thus, the higher spin state, the lower ability of nitrogen to form covalent bonds with the inner surface of C₆₀ cage. This can be seen clearly from the geometries of ⁵2a, ¹2e and ³2b (Fig. 3): nitrogen is located at the center of the C₆₀ cage for the quintet 2a, it is covalently bound with only one carbon atom in triplet 2b and with three carbon atoms in singlet 2e.

In contrast to the protonation, nitrogen escape appears to be more favorable than hydrogen insertion through the C₆₀ cage for all spin states (Table 4 and Fig. 3). The most favorable transition state is singlet TS1i, i.e. nitrogen escape via breaking the [6,6]-bond (Fig. 3). The barrier to this escape is 69.4 and 80.5 kcal mol⁻¹ at DFT and MP2, respectively. N-escape through a [5,6]-bond breaking via¹TS1h is less than 2 kcal mol⁻¹ higher in energy. Nitrogen escape for the triplet and quintet PESs proceeds via the corresponding TS1i with barriers of 76.9 an 95.9 kcal mol⁻¹ at DFT and of 81.0 and 98.8 kcal mol⁻¹ at MP2, respectively. They are followed up by the TS1m, in which nitrogen displaces the carbon atom (Fig. 3).

Hydrogen penetration through the cage on the singlet PES is highly unfavorable. Moreover, as in the case of minimum ¹2e, nitrogen covalent bonding to carbons is so strong that no ¹TS1a,b were found. ¹TS1j and ¹TS1k (Fig. 3) were located instead and rather than ¹TS1e,f. The TSs for hydrogenation of nitrogen through the fullerene cage for triplet and quintet PESs are similar to those for protonation, i.e.TS1a,b,e,f were found. However, hydrogenation of the N-atom is less favorable than N-escape for the triplet PES by 25.7 and 54.2 kcal mol⁻¹ at DFT and MP2, respectively. Nevertheless, barriers of hydrogenation and N-escape are much closer in energy for the quintet PES: hydrogenation is less favorable by 5.0 and 2.0 kcal mol⁻¹ at DFT and MP2, respectively.

The reaction ¹2e → ¹4 is endothermic by 16.4 and 25.5 kcal mol⁻¹, while ³2b → ³4 is exothermic by 35.2 and 39.5 kcal mol⁻¹ and ⁵2a → ⁵4 is also exothermic by 0.1 and 16.3 kcal mol⁻¹ at DFT and MP2 (Table 4), respectively.

However, hydrogenation of ⁴1 to ¹2e, ³2b and ⁵2a is exothermic by only 44.0, 43.5 and 41.8 kcal mol⁻¹ at DFT and 30.8, 22.7 and 24.9 kcal mol⁻¹ at MP2, respectively. This energy gain is ca. 30–50 kcal mol⁻¹ less than is necessary to overcome the barrier of nitrogen escape through the cage of C₆₀ (for the singlet PES). This is in contrast to the case of protonation through the cage, when initial protonation of NH_x@C₆₀ leads to an energy release larger than that required to overcome the barrier to proton insertion through the C₆₀ cage. Thus, hydrogenation by protonation is expected to be the only way for the synthesis of nitrogen hydrides inside C₆₀.

Electronic properties of NH₄@C₆₀

The formation of NH₄@C₆₀ according to

NH₄⁺ + C₆₀˙⁻ → NH₄@C₆₀ (2)

is calculated to be highly exothermic (−83.9 kcal mol⁻¹ and −156.5 kcal mol⁻¹ at the B3LYP and MP2 levels, respectively). We performed an NPA analysis of the target species NH₄@C₆₀13 at B3LYP both with and without an implicit representation of the solvent (benzene) to study its nature. We used a polarized continuum model (PCM)^80–86 to consider solvent effects. Both calculations confirmed that the NH₄ moiety carries almost a unit positive charge (+0.97 e with and without PCM corrections), while the C₆₀ moiety is correspondingly negatively charged (13). The sum of Coulson charges at the AM1 level⁸⁷ leads to a similar charge of +0.96 e. The total charge of 13 is naturally zero, and the whole species 13 is a radical. Thus, NH₄@C₆₀ is indeed a “concentric ion pair” more properly described as NH₄⁺@C₆₀˙⁻, in agreement with previous theoretical studies for this and related MH₄^±@C₆₀˙⁻ species.⁸⁸

13 has a peculiar electronic structure as its metal-free cation is confined inside the C₆₀ anion and cannot escape from the fullerene cage, although metal containing Ca²⁺@C₆₀²⁻ has been observed experimentally⁸⁹ and M₃N@C_x concentric ion pairs are known for larger fullerenes.^90,9113 is not a classical salt with two counterions held together by electrostatic forces and is also not a zwitterion, because the oppositely charged moieties are not covalently bound. Moreover, charge centers for both the positively charged ammonium ion and the fullerene C₆₀˙⁻ radical anion coincide with the geometrical and mass centers of the C₆₀ cage. The ammonium ion is thus forced to reside at the center of the C₆₀, since otherwise the centers of positive and negative charges would be displaced, and the resulting electrostatic attraction returns NH₄⁺ to the C₆₀˙⁻ origin. Indeed, the dipole moment of NH₄⁺@C₆₀˙⁻ is essentially zero at the B3LYP level of theory. It results in an absence of charge separation and the additional stabilization of the system.

On the other hand, it is known that the naked Rydberg radical [(NH₄⁺)(e⁻)_Rydberg] readily decomposes into (NH₂˙ + H₂) and (NH₃ + H˙),^92–100 which is why we have explored whether these decomposition products are more or less energetically preferable inside C₆₀ than ion pair NH₄⁺@C₆₀˙⁻13. (NH₂˙ + H₂)@C₆₀13a is rather unstable in comparison to 13, since its formation from 13 is highly endothermic (by far more than 50 kcal mol⁻¹) and thus thermodynamically unfavorable (Fig. 4). In addition, optimization of (NH₃ + H˙)@C₆₀ in conformation 13b at the B3LYP level, even starting from the structure with a shortened C–H bond length (1.08 Å) terminated with the structure of NH₄⁺@C₆₀˙⁻13. (NH₃ + H˙)@C₆₀ (or NH₃@C₆₀H˙ as hydrogen is covalently bound to the inner surface of fullerene) in conformation 13c is also highly endothermic and thus very unlikely to exist. Moreover, since ammonia is known to invert readily with a barrier of 5.8 kcal mol⁻¹,¹⁰¹ we have calculated that the barrier to ammonia inversion, which corresponds essentially to the barrier of rearrangement of 13c to 13, is −0.1 and 0.7 kcal mol⁻¹ at the B3LYP and MP2 levels, respectively. Thus, NH₃@C₆₀H 13c obviously transforms directly into NH₄⁺@C₆₀˙⁻13. The electrostatic potential created by the ammonium cation makes the fullerene a much stronger electron acceptor than parent C₆₀. The vertical electron affinity (EA_V) of pure C₆₀ calculated at the B3LYP/6-311+G(d,p)^{44–52,102–104} level on the B3LYP/6-31G(d) geometries is 2.59 eV (close to the experimental value of 2.68 ± 0.02 eV),^105,106 but becomes 3.12 eV larger when NH₄⁺ is placed inside the C₆₀ (Table 5). Moreover, even the second vertical electron affinity of NH₄⁺@C₆₀ (2.71 eV) is higher than the first EA_v of neutral C₆₀, similarly to experimental observations for Ca²⁺@C₆₀²⁻.⁸⁹ Although all further electron affinities are negative for both compounds (Table 5), no electron is transferred to NH₄⁺ from the fullerene. Note that the EAs of NH₄⁺@C₆₀ⁿ⁻ plotted vs. those of C₆₀ⁿ⁻ lie on a straight line (R² = 0.9997) with a slope of 1.0 that intersects the axis at 3.1 eV (Fig. 5). These findings are in agreement with the previous theoretical observation for MH₄⁺@C₆₀ species that their EAs can be described by a simple charged sphere model and particular differences in structures of the endohedral guests has only relatively small effect of 0.1–0.6 eV.⁸⁸

Fig. 4 Relative energies at the B3LYP (first entry) and MP2 levels (second entry) in kcal mol⁻¹ for NH₄⁺@C₆₀˙⁻ (13), (NH₂˙ + H₂)@C₆₀ (13a) and two conformers of NH₃@C₆₀H˙ (13b and 13c).

Table 5 EAs of NH₄⁺@C₆₀ⁿ⁻ and C₆₀ⁿ⁻ in eV at B3LYP/6-311+G(d,p) on B3LYP/6-31G(d) geometries of NH₄⁺@C₆₀ and C₆₀, respectively. The most stable spin states are taken into account

n	EA(NH4^+@C60^n−)	EA(C60^n−)
0	5.71	2.59
1	2.71	−0.54
2	−0.26	−3.16
3	−3.39	−6.38
4	−6.25	−9.14
5	−9.02	−11.79

---

Fig. 5 Plot of EA(NH₄⁺@C₆₀ⁿ⁻) vs. EA(C₆₀ⁿ⁻) in eV at the B3LYP/6-311+G(d,p) level on B3LYP/6-31G(d) geometries of NH₄⁺@C₆₀ and C₆₀, respectively, with the linear regression line and equation.

All these observations are supported by analysis of the local electron affinity (EA_L, RHF-EA_L^107,108 for closed-shell and UHF-EA_L¹⁰⁹ for open-shell species) as calculated from the semiempirical wavefunction obtained using EMPIRE 2013.¹¹⁰ Visualized slices through the EA_L for C₆₀, NH₄⁺@C₆₀, C₆₀˙⁻, and NH₄⁺@C₆₀˙⁻ are given in Fig. 6 and show clearly that NH₄⁺@C₆₀ is by far the strongest electron acceptor, in accordance with the above EAs from DFT calculations. NH₄⁺@C₆₀˙⁻ and C₆₀ are electron acceptors with similar strength, although the former is a stronger electron acceptor. C₆₀˙⁻ is not an acceptor, in accordance with its negative EA.

Fig. 6 Slice through the local electron affinities (EA_L) of NH₄⁺@C₆₀ and NH₄⁺@C₆₀˙⁻vs. C₆₀ and C₆₀˙⁻ at the AM1 level on B3LYP/6-31G(d) geometries. The color scale (kcal mol⁻¹) is shown in the center.

Conclusions

We have demonstrated the possibility in principle of a new approach to the synthesis of endofullerenes via molecular “assembly” from “template” endofullerenes rather than insertion of the whole molecule into the fullerene cage or one-pot formation. N@C₆₀1 was chosen as the “template” for the present study, which was hydrogenated step-by-step up to ammonia inside C₆₀10 and the “concentric ion pair” NH₄⁺@C₆₀˙⁻13 according to Scheme 1. Note that such an approach would allow us to obtain NH@C₆₀ and NH₂@C₆₀, which are open-shell systems and thus potentially interesting for spintronics. NH₄⁺@C₆₀˙⁻ is an end product with electron affinity similar to that of C₆₀.

The rate-determining steps of the approach are proton penetrations through the C₆₀ cage. The most favorable pathways are proton-insertion via [5,6]-bond breaking with barriers about 90 kcal mol⁻¹. The competitive pathway for the first step N@C₆₀H⁺ → NH⁺@C₆₀ is nitrogen escape, the barriers of which are very close in energy. Meanwhile, energy gains during proton transfer to NH_x@C₆₀ from H₃⁺ as proton carrier are about 30 kcal mol⁻¹ larger than the subsequent barriers. Hydrogenation rather than protonation of nitrogen through the C₆₀ wall leads to nitrogen escape from the fullerene cage, rather than to the formation of nitrogen hydrides at C₆₀.

Of course, the proposed approach cannot only be used for the case of N@C₆₀ studied here, but for other endofullerenes too. Interestingly enough, if we start from CO@C₆₀ we can end up with methanol inside buckminsterfullerene CH₃OH@C₆₀ and CH₃OH₂⁺@C₆₀˙⁻.

We note at this point that we use theory to investigate a fascinating possibility for experiments and that we make no attempt at experimental validation, which would be outside our expertise. The levels of theory are adequate that we can be confident of the general features of the calculated energy landscape and can draw conclusions about the feasibility of the approach that we suggest. We can only speculate as to possible experimental realization of the reaction sequence described here. Protonation of the intermediate endohedral species and penetration of the fullerene wall by protons should be achievable under conditions that are well established^77–79,111 for ion–molecule reactions. The subsequent reduction step can be performed either by established gas-phase neutralization techniques^11,12 or after isolating cation intermediates, possibly in a reducing matrix, before proceeding to the next step.

Additional experimental studies are necessary for further investigation of this interesting approach.

Acknowledgements

This work was supported by the Deutsche Forschungsgemeinschaft (DFG) as part of SFB 953 “Synthetic Carbon Allotropes” and by a grant of computer time on HRLB II at the Leibniz Rechenzentrum Munich. The authors thank Andrey A. Fokin, Tatyana E. Shubina and Walter Thiel for fruitful discussions. PD also acknowledges the financial support by the Universität Bayern e.V. via a stipend within the Bavarian Elite Aid Program. Open Access funding provided by the Max Planck Society.

Notes and references

1. H. Mauser, A. Hirsch, N. J. R. V. E. Hommes and T. Clark, J. Mol. Model., 1997, 3, 415–422.
2. T. A. Murphy, T. Pawlik, A. Weidinger, M. Höhne, R. Alcala and J.-M. Spaeth, Phys. Rev. Lett., 1996, 77, 1075–1078.
3. A. Weidinger, M. Waiblinger, B. Pietzerak and T. A. Murphy, Appl. Phys. A: Mater. Sci. Process., 1998, 66, 287–292.
4. H. Mauser, N. J. R. V. E. Hommes, T. Clark, A. Hirsch, B. Pietzak, A. Weidinger and L. Dunsch, Angew. Chem., Int. Ed. Engl., 1997, 36, 2835–2838.
5. D. S. Bethune, R. D. Johnson, J. R. Salem, M. S. D. Vries and C. S. Yannoni, Nature, 1993, 366, 123–128.
6. F. T. Edelmann, Angew. Chem., Int. Ed., 1995, 34, 981–985.
7. R. Tellgmann, N. Krawez, S.-H. Lin, I. V. Hertel and E. E. B. Campbell, Nature, 1996, 382, 407–408.
8. T. Weiske, D. K. Böhme, J. Hruscaronák, W. Krätschmer and H. Schwarz, Angew. Chem., Int. Ed. Engl., 1991, 30, 884–886.
9. T. Weiske, J. Hrusak, D. K. Böhme and H. Schwarz, Chem. Phys. Lett., 1991, 186, 459–462.
10. T. Weiske, D. K. Böhme and H. Schwarz, J. Phys. Chem., 1991, 95, 8451–8452.
11. V. T. Weiske, T. Wong, W. Krätschmer, J. K. Terlouw and H. Schwarz, Angew. Chem., 1992, 104, 242–244.
12. T. Weiske, T. Wong, W. Krätschmer, J. K. Terlouw and H. Schwarz, Angew. Chem., Int. Ed. Engl., 1992, 31, 183–185.
13. T. Weiske, H. Schwarz, A. Hirsch and T. Grösser, Chem. Phys. Lett., 1992, 199, 640–642.
14. M. Saunders, H. A. Jiménez-Vázquez, R. J. Cross and R. J. Poreda, Science, 1993, 259, 1428–1430.
15. K. Komatsu, M. Murata and Y. Murata, Science, 2005, 307, 238–240.
16. Y. Murata, M. Murata and K. Komatsu, J. Am. Chem. Soc., 2003, 125, 7152–7153.
17. T. Suetsuna, N. Dragoe, W. Harneit, A. Weidinger, H. Shimotani, S. Ito, H. Takagi and K. Kitazawa, Chem. – Eur. J., 2002, 8, 5079–5083.
18. T. Peres, B. P. Cao, W. D. Cui, A. Khong, R. J. Cross, M. Saunders and C. Lifshitz, Int. J. Mass Spectrom., 2001, 210, 241–247.
19. K. Kurotobi and Y. Murata, Science, 2011, 333, 613–616.
20. M. N. Chaur, F. Melin, A. L. Ortiz and L. Echegoyen, Angew. Chem., Int. Ed., 2009, 48, 7514–7538.
21. M. Yamada, T. Akasaka and S. Nagase, Acc. Chem. Res., 2010, 43, 92–102.
22. S. R. Plant, T. C. Ng, J. H. Warner, G. Dantelle, A. Ardavan, G. A. D. Briggs and K. Porfyrakis, Chem. Commun., 2009, 4082–4084,  10.1039/B902520k.
23. K. Sakaguchi, R. Fujii, T. Kodama, H. Nishikawa, I. Ikemoto, Y. Achiba and K. Kikuchi, Chem. Lett., 2007, 36, 832–833.
24. K. Kikuchi, K. Akiyama, K. Sakaguchi, T. Kodama, H. Nishikawa, I. Ikemoto, T. Ishigaki, Y. Achiba, K. Sueki and H. Nakahara, Chem. Phys. Lett., 2000, 319, 472–476.
25. D. Zahn and G. Seifert, J. Phys. Chem. B, 2004, 108, 16495–16498.
26. Y. Maruyama, K. Ohno, K. Esfarjani and Y. Kawazoe, Sci. Rep. Res. Inst., Tohoku Univ., Ser. A, 1996, 41, 183–186.
27. S. Patchkovskii and W. Thiel, J. Am. Chem. Soc., 1996, 118, 7164–7172.
28. S. Erkoç and L. Türker, THEOCHEM, 2003, 640, 57–61.
29. Z. Slanina, F. Uhlik, L. Adamowicz and S. Nagase, Mol. Simul., 2005, 31, 801–806.
30. M. D. Ganji, M. Mohseni and O. Goli, THEOCHEM, 2009, 913, 54–57.
31. J. Keith, E. Whitener, M. Frunzi, S.-I. Iwamatsu, S. Murata, R. J. Cross and M. Saunders, J. Am. Chem. Soc., 2008, 130, 13996–13999.
32. D. Suter and K. Lim, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 052309.
33. J. Twamley, Phys. Rev. A: At., Mol., Opt. Phys., 2003, 67, 052318.
34. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
36. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
37. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
38. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
39. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. M. S. Gordon, Chem. Phys. Lett., 1980, 76, 163–168.
41. J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939–947.
42. M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803.
43. J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016–5021.
44. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
45. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, D. J. DeFrees, J. A. Pople and M. S. Gordon, J. Chem. Phys., 1982, 77, 3654–3665.
46. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
47. V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229.
48. R. C. Binning Jr. and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216.
49. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984.
50. P. C. Hariharan and J. A. Pople, Mol. Phys., 1974, 27, 209–214.
51. P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213–222.
52. M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280.
53. M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281–289.
54. M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128.
55. M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 220, 503–506.
56. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
57. S. Sæbø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83–89.
58. G. A. Zhurko and D. A. Zhurko, ChemCraft 1.7, 2013.
59. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision D.02, Gaussian, Inc., Wallingford CT, 2004.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
61. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
62. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
63. A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073.
64. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
65. J. E. Carpenter and F. Weinhold, THEOCHEM, 1988, 46, 41–62.
66. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
67. F. Weinhold and J. E. Carpenter, in The Structure of Small Molecules andIons, ed. R. Naaman and Z. Vager, Plenum, 1988, pp. 227–236.
68. J. E. Carpenter, PhD thesis, University of Wisconsin, 1987.
69. Using the UFF radii as implemented in Gaussian.
70. C. Knapp, K.-P. Dinse, B. Pietzak, M. Waiblinger and A. Weidinger, Chem. Phys. Lett., 1997, 272, 433–437.
71. C. Knapp, N. Weiden and K.-P. Dinse, Magn. Reson. Chem., 2005, 43, S199–S204.
72. M. Waiblinger, K. Lips, W. Harneit, A. Weidinger, E. Dietel and A. Hirsch, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 159901(E).
73. J. C. Greer, Chem. Phys. Lett., 2000, 326, 567–572.
74. J. Lu, X. Zhang and X. Zhao, Chem. Phys. Lett., 1999, 312, 85–90.
75. M. Sala, M. Hodoscek, S. Arulmozhiraja and T. Fujii, J. Phys. Chem. A, 2009, 113, 3223–3226.
76. S. W. McElvany, M. M. Ross and J. H. Callahan, Acc. Chem. Res., 1992, 25, 162–168.
77. M. D. Sefcik, J. M. S. Henis and P. P. Gaspar, J. Chem. Phys., 1974, 61, 4321–4328.
78. T. Su and M. T. Bowers, J. Am. Chem. Soc., 1973, 95, 1370–1373.
79. R. P. Clow and J. H. Futrell, J. Am. Chem. Soc., 1972, 94, 3748–3755.
80. S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117.
81. S. Miertuš and J. Tomasi, Chem. Phys., 1982, 65, 239–245.
82. M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327.
83. M. T. Cances, V. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032.
84. M. Cossi, V. Barone, B. Mennucci and J. Tomasi, Chem. Phys. Lett., 1998, 286, 253.
85. V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404.
86. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995.
87. M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909.
88. O. P. Charkin, N. M. Klimenko, D. O. Charkin and A. M. Mebel, Russ. J. Inorg. Chem., 2004, 49, 868–880.
89. L.-S. Wang, J. M. Alford, Y. Chai, M. Diener and R. E. Smalley, Z. Phys. D: At., Mol. Clusters, 1993, 26, 297–299.
90. J. R. Pinzon, C. M. Cardona, M. A. Herranz, M. E. Plonska-Brzezinska, A. Palkar, A. J. Athans, N. Martin, A. Rodriguez-Fortea, J. M. Poblet, G. Bottari, T. Torres, S. S. Gayathri, D. M. Guldi and L. Echegoyen, Chemistry, 2009, 15, 864–877.
91. M. N. Chaur, F. Melin, A. L. Ortiz and L. Echegoyen, Angew. Chem., Int. Ed., 2009, 48, 7514–7538.
92. H. Cardy, D. Liotard, A. Dargelos and E. Poquet, Chem. Phys., 1983, 77, 287–299.
93. F. Chen and E. R. Davidson, J. Phys. Chem. A, 2001, 105, 10915–10921.
94. E. M. Evleth and E. Kassab, Pure Appl. Chem., 1988, 60, 209–214.
95. J. Kaspar, J. Vedene, H. Smith and B. N. McMaster, Chem. Phys., 1985, 96, 81–95.
96. E. Kassab and E. M. Evleth, J. Am. Chem. Soc., 1987, 109, 1653–1661.
97. J. V. Ortiz, I. Martin, A. M. Velasco and C. Lavin, J. Chem. Phys., 2004, 120, 7949–7954.
98. J. K. Park, J. Chem. Phys., 1998, 109, 9753–9761.
99. J. K. Park, Internet Electron. J. Mol. Des., 2005, 4, 279–308.
100. A. M. Velasco, C. Lavin, I. Martin, J. Melin and J. V. Ortiz, J. Chem. Phys., 2009, 131, 024104.
101. W. Klopper, C. C. M. Samson, G. Tarczay and A. G. Csaszar, J. Comput. Chem., 2001, 22, 1306–1314.
102. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
103. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
104. S. Hashimoto, K. Seki, N. Sato and H. Inokuchi, J. Chem. Phys., 1982, 76, 163–172.
105. C. Brink, L. H. Andersen, P. Hvelplund, D. Mathur and J. D. Voldstad, Chem. Phys. Lett., 1995, 233, 52–56.
106. X.-B. Wang, C.-F. Ding and L.-S. Wang, J. Chem. Phys., 1998, 110, 8217–8220.
107. B. Ehresmann, B. Martin, A. H. C. Horn and T. Clark, J. Mol. Model., 2003, 9, 342–347.
108. T. Clark, J. Mol. Model., 2010, 16, 1231–1238.
109. P. O. Dral, J. Mol. Model., 2014, 20, 2134.
110. T. Clark, M. Hennemann and P. O. Dral, EMPIRE 2013, unreleased version, Universität Erlangen-Nürnberg and Cepos InSilico Ltd, 2013, see also http://www.ceposinsilico.de/products/empire.htm, accessed May 30th, 2017.
111. J. Meyer and R. Wester, Annu. Rev. Phys. Chem., 2017, 68, 333–353.

---

Footnote

† Electronic supplementary information (ESI) available: Gaussian archives of all optimized structures and MS Excel tables with all energies. See DOI: 10.1039/c7cp02865b

---