High cross-plane thermoelectric performance of metallo-porphyrin molecular junctions

Abstract

We investigated the thermoelectric properties of flat-stacked 5,15-diphenylporphyrins containing divalent metal ions Ni, Co, Cu or Zn, which are strongly coordinated with the nitrogens of pyridyl coated gold electrodes. Changing metal atom has little effect on the thermal conductance due to the phonons. The room-temperature Seebeck coefficients of these junctions are rather high, ranging from 90 μV K⁻¹ for Cu, Ni and Zn-porphyrins to −16 μV K⁻¹ for Co-porphyrin. These values could be further increased by lowering molecular energy levels relative to the DFT-predicted Fermi energy. In contrast, the phonon contribution to the thermal conductance of these junctions is rather insensitive to the choice of metal atom. The thermopower, thermal conductance and electrical conductance combined to yield the room-temperature values for the thermoelectric figure of merit ZT ranging from 1.6 for Cu porphyrin to ∼0.02 for Ni-porphyrin.

---

Introduction

Single-molecule thermoelectricity is a rapidly expanding field of fundamental research, which will eventually inform the design and synthesis of high-performance thermoelectric molecular films. Early studies showed that factors governing the sign and magnitude of the Seebeck coefficient S include the length of conjugated molecules and the type of terminal group. For examples thiol-terminated molecules typically exhibit HOMO-dominated transport and a positive S, ranging from 6.8 to 2.4 μV K⁻¹ for n-alkanedithiols, depending on the length n,^1,2 from 7 μV K⁻¹ to 16 μV K⁻¹ for n-benzenedithiols, depending on the number n of phenyl rings, ranging from 7 μV K⁻¹ to 16 μV K⁻¹.^3–9 Positive Seebeck coefficients up to 24 μV K⁻¹ were measured for 1,4-bis((trimethylstannyl)methyl)-n-phenyl (n = 1, 2, 3, 4), up to 10.4 μV K^{−1 1,10,11} for 1,4-n-phenylenediamine (PDA) (n-1, 2, 3) and as high as 14.8 μV K⁻¹ for oligothiophenes on gold.¹² On the other hand pyridyl terminal groups promote LUMO-dominated transport leading to negative Seebeck coefficients as high as −9 μV K⁻¹ and −10 μV K⁻¹ respectively^11,13 4,4′-for bipyridine and 1,2-di(4-pyridyl)ethylene respectively. Fullerenes also exhibit negative Seebeck coefficients, ranging from −10 to −30 μV K⁻¹ for C₆₀¹⁴ to −33 μV K⁻¹ for C₆₀ dimers¹⁵ and up to −31.6 μV K⁻¹ C₈₂ endohedral fullerenes.¹⁶ The sign of the endohedral fullerene Sc3N@C₈₀ was shown to be sensitive to pressure, ranging from −25 μV K⁻¹ to +25 μV K⁻¹, depending on the orientation of the molecule on a gold substrate.¹⁷ Other factors predicted to govern the thermoelectric performance of molecules include the type of electrode. Although most of the above studies used gold electrodes, alternative choices could include graphene,^18,19 silicene,^20,21 platinum,²² palladium,²² iron²³ and nickel,²⁴ which provide a range of Debye frequencies for controlling phonon transport across the electrode–molecule boundary.²⁴

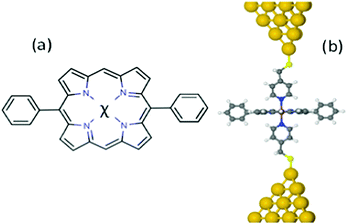
Here, in an effort to further enhance the thermoelectric performance of single-molecule junctions by controlling phonon transport while maintaining good electrical contact, we examine the effect of coating the electrodes with functional units, which form coordination bonds with the molecule of interest. As an example, we examine junctions formed from 5,15-diphenylporphyrins containing divalent metal ions Ni, Co, Cu or Zn, which are strongly coordinated with the nitrogens of pyridyl coated gold electrodes. Porphyrins are attractive as building blocks for molecular-scale devices, because they are conjugated, rigid, chemically stable molecules and their properties could be modified by coordinating a variety of metallic ions (metallo-porphyrins).^25–33 In what follows our aim is to explore the potential of the metallo-porphyrin-based molecular junctions shown in Fig. 1a for high-efficiency thermoelectricity. Since the in-plane electrical conductance of porphyrins is rather low, we consider “cross-plane” junctions in which the current flows perpendicular to the porphyrin plane.³⁴ A shown in Fig. 1b, a porphyrin plane is contacted to gold electrodes via pyridyl groups attached to the gold by thiol anchors, with the plane of the porphyrin stacked perpendicular to the direction of charge transport.

Fig. 1 Diphenylporphyrins-based molecular structures (a) with metallic atom, (b) an example of an optimized configuration of the system containing a single molecule χ-DPP sandwiched between two gold leads which in turn are activated by pyridine-4-yl-methanethiol with different metallic atoms, where χ = Co, Cu, Ni or Zn.

From the point of view of optimising thermoelectric properties, junctions formed from these molecules are of interest, because by varying the metal atom (denoted χ in Fig. 1) residing in the core of the organic porphyrin framework, the molecular energy levels can be tuned relative to the Fermi energy E_F of the electrodes and if energy levels are close enough to E_F, then this should lead to transport resonances, which enhance the thermopower.³⁵ In what follows, we shall demonstrate that this is indeed the case and that large positive and negative thermopowers are achievable. Moreover, our calculations show that although the thermal conductance due to the phonons dominates the total thermal conductance, high values of ZT are obtained.

Recent experiments and theory show that the conductances G of the metallo-porphyrins are enhanced when they are sandwiched between two gold electrodes with pyridine-4-yl-methanethiol anchors (Fig. 1b).^34,36 Since large G is desirable, the 5,15-diphenylporphyrins (χ-DPP) studied in this paper contains metal atoms χ = Co, Cu, Ni or Zn, which are strongly coordinated with the nitrogens of pyridyl coated gold electrodes (Fig. 1a). Our aim in this paper is to investigate the thermoelectric properties of these metallo-porphyrins devices when the metal atom is varied.

Methods

To calculate the electronic and vibrational properties of each metallo-porphyrin, we used the spin density functional (DFT) code SIESTA,³⁷ which employs Troullier–Martins pseudopotentials to represent the potentials of the atomic cores,³⁸ and a local atomic-orbital basis set. We used a double-zeta polarized basis set³⁹ for all atoms and the local density functional approximation (LDA-CA) by Ceperley and Adler.⁴⁰ The Hamiltonian and overlap matrices are calculated on a real-space grid defined by a plane-wave cutoff of 150 Ry. Each molecule was relaxed to the optimum geometry until the forces on the atoms are smaller than 0.02 eV Å⁻¹. The only periodicity is in the electrodes, which are assumed to be composed of a periodic series of principal layers (see Fig. S10, ESI†). In the transverse direction, there is no periodicity and the unit cell is sufficiently large that there is no interaction between the molecule and its image. The mean field Hamiltonian obtained using DFT describes the whole structure including the leads, the interface between the leads and molecule and molecule itself. In this way, all parts of the structure are treated in a holistic manner, at the same level of DFT.

Results and discussion

To obtain the optimized geometry (and the associated mean field Hamiltonian) of χ-DPP we employed the SIESTA³⁷ implementation of spin-polarized density functional theory (DFT) and from the converged mean field DFT Hamiltonian, we used our quantum transport code, Gollum⁴¹ to compute the electronic transmission coefficient T^σ_el(E) for electrons with energy E and spin σ = [↑, ↓] passing from one electrode to the other via the χ-DPP. For each χ-DPP in Fig. 1b and 2a–d shows total electronic transmission coefficients as a function of energy for χ = Co, Cu, Zn or Ni. The corresponding spin-dependent transmissions T^σ_el(E) are shown in the ESI.†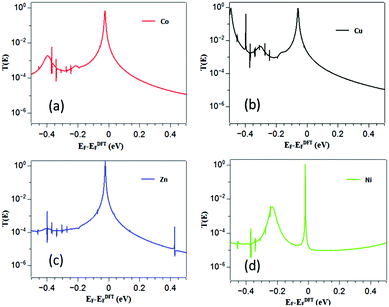

Fig. 2 (a–d) show the electronic transmission coefficients T(E) = T^↑_el(E) + T^↓_el(E) as a function of energy E for χ-DPP with χ = Co, Cu, Zn and Ni.

Due to the presence of thiol anchors, the DFT-predicted Fermi energy is close to the HOMO transmission resonances of each χ-DPP and the slope of T^σ_el(E_F) is negative. Hence from eqn (S5) of the ESI,† one expects the Seebeck coefficient S to be positive. Using the Landauer formula (see ESI†), the electrical conductance was calculated from the transmission coefficient shown in Fig. 2.

The electrical conductances (Fig. S2 of the ESI†) follow the trend G_Zn > G_Cu > G_Co > G_Ni in agreement with the experimental values of Zn-DPP 8.2 × 10⁻², Cu-DPP 4.4 × 10⁻², Co-DPP 2.2 × 10⁻² and Ni-DPP 1.8 × 10⁻².³³

To calculate the vibrational modes of each structure, we use the harmonic approximation to construct the dynamical matrix D and a Green's function approach to calculate the phononic transmission coefficient T_ph(ω) for phonons with energy ℏω passing through the device as explained in ref. 35. Fig. 3 shows the phonon transmission coefficients for each χ-DPP.

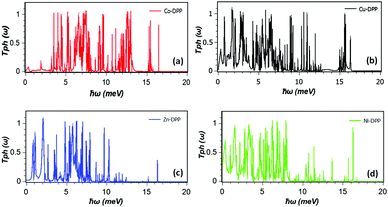Fig. 3 (a–d) Phonon transmission coefficient as a function of ℏω for χ-DPP with χ = Co, Cu, Zn and Ni.

The thermal conductance of the junction (κ = κ_ph + κ_el) is obtained by summing the contributions from both electrons (κ_el) and phonons (κ_ph). The electronic (phononic) thermal conductances are calculated from the electronic (phononic) transmission coefficients (as described in ref. 35).

Comparison between Fig. 4a and b shows that in the vicinity of DFT Fermi energy, the main source of the thermal conductance in these junctions is due to phonons, whose room-temperature contribution is relatively insensitive to the choice of metal atom, varying between 6 and 10 pW K⁻¹ depending on the choice. The inset of Fig. 4b shows the cumulative distribution of eigenvalues (integrated density of states) of each molecule and reveals that the lower frequency modes of the Co porphyrin in the region 0 to 1.5 meV are pushed to higher frequencies, leading to a low-frequency transmission gap below 3 meV. This reflects the higher binding energy of a single pyridyl group to the Co metal atom compared with the other. (These follow the trend Co = −1.2 eV, Zn = −1.2 eV, Cu = −0.4 eV and Ni = −0.17 eV.) (These follow the trend Co = −1.2 eV, Zn = −1.2 eV, Cu = −0.4 eV and Ni = −0.17 eV.)

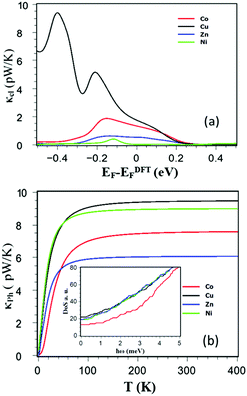Fig. 4 (a) Show electronic contribution of the thermal conductance κ_el and (b) show phononic contribution of the thermal conductance κ_ph for DPP with Co, Cu, Zn and Ni.

Consequently the low-frequency cumulative distribution of Co and the low-temperature thermal conductance initially lies below that of the others and then rises with a steeper slope. Fig. 3c shows that Zn also has a low-frequency transmission gap below 1 meV, which suppresses the low-temperature phonon thermal conductance.

Fig. 5 shows the Seebeck coefficient S and total figure of merit ZT over a range of Fermi energies at room temperature for each metallo-porphyrin. Fig. 5a demonstrates that both the magnitude and sign of S are sensitive to the metal atom at the centre of the DPP, which determine the location of transport resonances relative to the Fermi energy. Since the Fermi energy from DFT is not necessarily reliable, we have presented results for a range of Fermi energies (Fig. 5a).

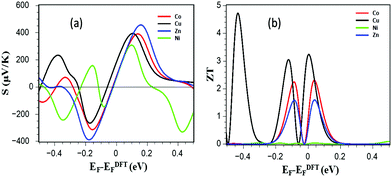Fig. 5 Show (a) Seebeck coefficient S (thermopower) and (b) total figure of merit ZT over a range of Fermi energies at room temperature for each metallo-porphyrin.

For the junctions discussed in this paper, the conductances have been measured experimentally³⁶ so we have estimated the Fermi energy by comparing these measurements with our calculated conductances. This yields a value of E_F = −0.03 eV, compared with the DFT-predicted Fermi energy. Table 1 shows the Seebeck coefficients of porphyrins in the presence of Cu, and then Co, Zn and Ni at E_F = −0.03 eV. The predicted trend is S_Cu > S_Ni > S_Zn > S_Co and when combined with the higher Cu CPP the yield room-temperature values of ZT range from 1.66 for Cu porphyrin to 0.07 for Zn porphyrin, as shown in Fig. 5b.

Table 1 Seebeck coefficient S (thermopower) and total figure of merit ZT at E_F − E^DFT_F = −0.03 eV³³

Metallic	S (μV K^−1)		ZT
	E F = −0.03 eV	E F = 0.0 eV	E F = −0.03 eV	E F = 0.0 eV
Cu	+90	+182	1.66	3.22
Co	−16	+77	0.05	0.92
Zn	−23	+72	0.07	0.56
Ni	−32	+66	0.018	0.05

---

Conclusion

The room-temperature Seebeck coefficients of these junctions are rather high, ranging from 90 μV K⁻¹ for Cu-porphyrin to −16 μV K⁻¹ for Co-porphyrin. The corresponding room-temperature values of ZT range from 1.66 for Cu porphyrin to ∼0.02 for Ni porphyrin. These values could be further increased by shifting molecular energy levels relative to the Fermi, either by doping or gating, which moves the Fermi energy closer to the regions of higher thermopower in Fig. 5. These results demonstrate that metallo-porphyrins are attractive building blocks for molecular-scale thermoelectricity and by passing thermal and charge currents perpendicular to the plane of the porphyrins, large values of the Seebeck coefficient and figure of merit are possible.

Acknowledgements

This work is supported by UK EPSRC grants EP N017188/1, EP/M014452/1, the European Union Marie-Curie Network MOLESCO 606728 and the Ministry of Higher Education and Scientific Research, Thi-Qar University, IRAQ.

References

1. J. A. Malen, et al. , Nano Lett., 2009, 9, 1164.
2. S. Y. Guo, G. Zhou and N. J. Tao, Nano Lett., 2013, 13, 4326.
3. A. Tan, S. Sadat and P. Reddy, Appl. Phys. Lett., 2010, 96, 013110.
4. A. Tan, et al. , J. Am. Chem. Soc., 2011, 133, 8838.
5. S. K. Lee, et al. , Nano Lett., 2014, 14, 5276.
6. Y. Kim, et al. , Appl. Phys. Lett., 2016, 109, 033102.
7. M. Tsutsui, M. Taniguchi and T. Kawai, Nano Lett., 2008, 8, 3293.
8. T. Morikawa, et al. , Nanoscale, 2014, 6, 8235.
9. S. Kaneko, et al. , Appl. Phys. Express, 2015, 8, 095503.
10. D. Kim, P. S. Yoo and T. Kim, J. Korean Phys. Soc., 2015, 66, 602.
11. T. Kim, et al. , Nano Lett., 2014, 14, 794.
12. W. B. Chang, et al. , Chem. Mater., 2014, 26, 7229.
13. J. R. Widawsky, et al. , Nano Lett., 2012, 12, 354.
14. S. K. Yee, et al. , Nano Lett., 2011, 11, 4089.
15. C. Evangeli, et al. , Nano Lett., 2013, 13, 2141.
16. S. K. Lee, et al. , Nanoscale, 2015, 7, 20497.
17. L. Rincon-Garcia, et al. , Nat. Mater., 2016, 15, 289.
18. H. Sadeghi, J. A. Mol, C. S. Lau, G. A. D. Briggs, J. Warner and C. J. Lambert, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2658–2663.
19. C. S. Lau, et al. , Nano Lett., 2016, 16, 170–176.
20. H. Sadeghi, S. Bailey and C. J. Lambert, Appl. Phys. Lett., 2014, 104(10), 103104.
21. H. Sadeghi, S. Sangtarash and C. J. Lambert, Sci. Rep., 2015, 5, 9514.
22. V. M. García-Suárez, A. R. Rocha, S. W. Bailey, C. J. Lambert, S. Sanvito and J. Ferrer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 045437.
23. V. M. García-Suárez, C. M. Newman, C. J. Lambert, J. M. Pruneda and J. Ferrer, J. Phys.: Condens. Matter, 2004, 16, 5453.
24. H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 15, 7467–7472.
25. G. Dorough, J. Miller and F. M. Huennekens, J. Am. Chem. Soc., 1951, 73, 4315–4320.
26. G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott and N. Bennett, Nat. Nanotechnol., 2011, 6, 517–523.
27. D. Gust and J. D. Roberts, J. Am. Chem. Soc., 1977, 99, 3637–3640.
28. Z. Li, M. Smeu, M. A. Ratner and E. Borguet, J. Phys. Chem. C, 2013, 117, 14890–14898.
29. Z. Li and E. Borguet, J. Am. Chem. Soc., 2011, 134, 63–66.
30. Z.-F. Liu, S. Wei, H. Yoon, O. Adak, I. Ponce, Y. Jiang, W.-D. Jang, L. M. Campos, L. Venkataraman and J. B. Neaton, Nano Lett., 2014, 14, 5365–5370.
31. Y. Li, J. Yao, S. Zhong and Z. Zou, Curr. Appl. Phys., 2011, 11, 1349–1353.
32. R. Ferradás, V. M. García-Suárez and J. Ferrer, 2012, arXiv preprint arXiv:1208.3157.
33. I. Beletskaya, V. S. Tyurin, A. Y. Tsivadze, R. Guilard and C. Stern, Chem. Rev., 2009, 109, 1659–1713.
34. A. C. Aragonès, N. Darwish, W. J. Saletra, L. Pérez-García, F. Sanz, J. Puigmartí-Luis, D. B. Amabilino and I. Díez-Pérez, Nano Lett., 2014, 14, 4751–4756.
35. H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 15, 7467–7472.
36. M. Noori, A. C. Aragonès, G. Di Palma, N. Darwish, S. W. Bailey, Q. Al-Galiby, I. Grace, D. B. Amabilino, A. González-Campo and I. Díez-Pérez, Sci. Rep., 2016, 6, 37352.
37. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
38. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993.
39. T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108.
40. D. M. Ceperley and B. Alder, Phys. Rev. Lett., 1980, 45, 566.
41. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. Bailey and K. Gillemot, New J. Phys., 2014, 16, 093029.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp02229h

‡ These author contributed equally to this work.

---