Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Topology of internally constrained polymer chains†
Maziar
Heidari‡
ab,
Vahid
Satarifard‡
ac,
Sander J.
Tans
d,
Mohammad Reza
Ejtehadi
e,
Samaneh
Mashaghi
f and
Alireza
Mashaghi
 *a
*a
aLeiden Academic Centre for Drug Research, Faculty of Mathematics and Natural Sciences, Leiden University, Leiden, The Netherlands
bMax Planck Institute for Polymer Research, Mainz, Germany
cMax Planck Institute of Colloids and Interfaces, Potsdam, Germany
dFOM Institute AMOLF, Amsterdam, The Netherlands
eDepartment of Physics, Sharif University of Technology, Tehran, Iran
fSchool of Engineering and Applied Sciences and Department of Physics, Harvard University, Cambridge, Massachusetts, USA. E-mail: a.mashaghi.tabari@lacdr.leidenuniv.nl
First published on 5th July 2017
Abstract
Linear chains with intra-chain contacts can adopt different topologies and allow transitions between them, but it remains unclear how this process can be controlled. This question is important to systems ranging from proteins to chromosomes, which can adopt different conformations that are key to their function and toxicity. Here, we investigate how the topological dynamics of a simple linear chain is affected by interactions with a binding partner, using Monte Carlo and Molecular Dynamics simulations. We show that two point contacts with a binding partner are sufficient to accelerate or decelerate the formation of particular topologies within linear chains. Computed ‘‘folding-time landscapes” that detail the folding time within the topology space show that such contacts deform these landscapes and hence alter the occupation probability of topological states. The results provide a mechanism by which chain topologies can be controlled externally, which opens up the possibility of regulating topological dynamics and the formation of more complex topologies. The findings may have important implications for understanding the mechanism of chaperone action as well as genome architecture and evolution.
I. Introduction
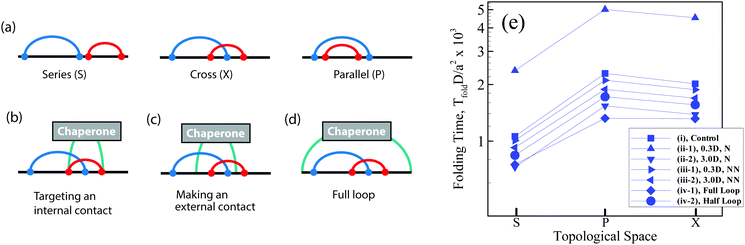
Topology is a generic property of folded biomolecules, independent of their chemical and geometric details, and can determine folding kinetics and mechanisms.1–4 A key topological property of a bimolecular fold is the number and arrangement of intra-molecular interactions (contacts), which can be characterized by pairwise, so-called circuit relations:5–9 series (S), parallel (P), or cross (X) (Fig. 1a). “Circuit topology” is known to be one of the folding rate determinants of biopolymers8 and complements other rate determinants (e.g., contact order and size).10–14 Using the aforementioned fundamental topologies, one can define mathematically a well-defined topological space and categorize the folded chains based on their topologies and then map the corresponding folding time landscape onto the space. However, it is not clear how the folding time landscape of the chain in the topological space would deform in the presence of an external mechanism/molecule which promotes or hinders specific foldimers or pathway. For instance, molecular chaperones recognize and shield exposed hydrophobic residues of folding protein clients and thereby prevent the specific folding pathways of the protein.2 Moreover, chaperones like Trigger Factor form point contacts with the folding clients through finger-like appendages,4 and as such they may influence the stability of the existing intra-molecular contacts. Hence, one may anticipate that the formation of inter-molecular contacts between a chaperone molecule at two or multiple sites on the client chain can affect the formation of further intra-molecular contacts and their arrangements.Here, we investigate how a simple interacting molecule (chaperone) guides folding of client polymer chains toward certain topological states and away from others, and how it modulates the kinetics of folding. We design three simple modeling experiments: (I) an interacting molecule perturbs one of the native intra-chain contacts of the client during folding, by increasing or decreasing the binding affinity of the contact sites (see Fig. 1b); (II) an interacting molecule closes a random loop on its folding substrate which does not exist in the native state (see Fig. 1c); (III) an interacting molecule interferes with client folding by end-to-end cyclization of a linear client polymer chain or by closing a half loop on a partially folded substrate (see Fig. 1d). To this end, we perform Kinetic Monte Carlo (KMC) simulations of a linear Gaussian chain to analyze the folding kinetics and use Molecular Dynamic (MD) simulations for population analysis of topological arrangements in the presence and absence of an interacting molecule. Although the excluded volume interaction is not present in the KMC simulations which makes its outcome difficult to compare with the steric-mediated folding processes of a real biopolymer, such a simple model is able to provide insights into the configurational entropy, topological occupancy, and kinetic pathways of the constrained chain relative to a free chain.15,16 Nonetheless, through integrating these complementary approaches, we endeavor to contextualize the role of an external interacting molecule in modulating the circuit topology of the folding chain and regulating its folding kinetics.
II. Kinetic Monte Carlo
The contact set for a linear ideal polymer chain with m − 1 contacts is defined as C1,…,Cm−1. The association rate constant of a new contact Cm depends on the mean square distance and the diffusion of binding sites:16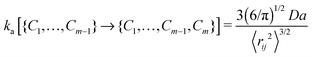 | (1) |
kd[{i,j}] = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(βεij) exp(βεij) | (2) |
To describe the KMC procedure for a polymer whose native state has N native contacts, we consider a polymer chain in a state with m contacts {C1,…,Cm}. To move in the conformer space, any of the N − m contacts could form or each of the m contacts could break; the rate constant of each event is calculated based on eqn (1) and (2). In this step, the total rate constant is defined by
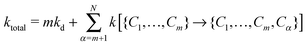 | (3) |
At each stage of folding in KMC, the association (ka) and dissociation rates (kd) of possible new or old contacts are computed. The corresponding probabilities of each move in the conformer space are given by Pi = ki/ktotal, where Pi denotes the probability of the ith possible move in the conformer space. The time when the next event happens is given by tevent = −ln(ξ)/ktotal, where ξ is a random variable with values in [0,1]. We start our KMC simulations from a denatured state of the polymer chain (i.e., initially there is no contact). The chain moves in the conformer space and the simulation ends once the polymer finds its native state. The total times of all the events are summed and called the folding time (Tfold). Since the average value of −〈ln(ξ)〉 is equal to unity, we calculate the time of the next event by tevent = 1.0/ktotal. This protocol generates a random walk through the conformer space and allows one to calculate the folding time of a polymer with a known native state.
Using the procedure explained, we simulate a short and long polymer consisting of 50 and 200 monomers under four sets of conditions:
(i) For the two-contact and four-contact experiments, four and eight monomers are randomly chosen from the polymer respectively and they are mutually connected so as to construct the conformer space. For each experiment, the native state is initially fixed by a set of the defined native contacts. The chain is in its native state and fully folded when all native contacts are formed. The permutation in the connectivity is done using the Heap algorithm17 to ensure all conformations are surveyed and this is done for all 5 × 106 conformations with different topological arrangements. This is verified through obtaining equal values in each topological state. The diffusion constants (D) for all the binding sites are identical and these sets of simulations are named control sets.
(ii) The same number of binding sites as the control sets is selected but the diffusion constant of one of the contacts (which is manipulated by the chaperone and shown in Fig. 1b) is set three times less (i.e. 0.3D) or more (i.e. 3D) than the other contacts; these sets of simulations are named (ii-1) and (ii-2), respectively.
(iii) The number of binding sites (contacts), with respect to case (i), increases by two (one) and then the new binding sites have a diffusion constant three times less (0.3D) or more (3D) than that of the other binding sites (D); these sets are named (iii-1) and (iii-2) respectively. We assume that this extra contact is formed by an external molecule which does not exist in the native state and create a random transient loop along the chain. Sets (ii) and (iii) are designed to investigate the effect of the external molecule on changing the folding times of the control set. In case (iii), the folding time of the external contact is not taken into account when it folds lastly.
(iv) Similar to case (i), additional binding sites close a loop on the polymer chain by attaching the terminal residues of the chain (full loop, (iv-1)) or binding one monomer in the middle of the chain and one terminal monomer (half loop, (iv-2)). In these cases, the external contact is not considered in the calculation of topological fractions. The proposed scenario (iii) gives us a comprehensive view towards the kinetic effect of transient loop formation by interacting an external molecule on the folding substrate.
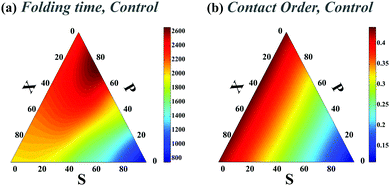
We choose a high unfolding energy barrier in all sets of simulations such that no contact would be able to unfold during the simulations. In all cases, at the beginning of the simulation, the chaperone-induced contact is also introduced in the conformational space of the chain and during the folding process, once it is formed, it is not dissociated during the rest of the simulations. The fraction of three topological relations and their corresponding folding times are calculated. We use a ternary phase diagram to map the topological states and the corresponding folding rates of the polymer chain in the topological fraction space (SPX space). In what follows, we refer to this map simply as the folding time landscape. Due to the scattered points on the ternary plot, we use interpolation techniques to provide a smooth folding time landscape. The corresponding averaged contact orders of each topological set are also calculated. The contact order of two loops with the topology of k is calculated by 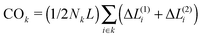 , where Nk is the number of double loops which are categorized in the topological state k, ΔL(1)i and ΔL(2)i are the monomer separation of each loop and L is the total polymer length.
, where Nk is the number of double loops which are categorized in the topological state k, ΔL(1)i and ΔL(2)i are the monomer separation of each loop and L is the total polymer length.
III. Molecular dynamics (MD)
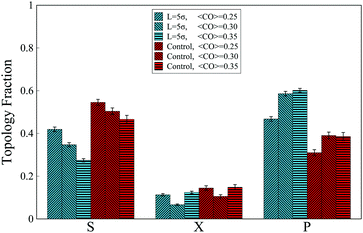
We use a coarse-grained model of a linear self-avoiding polymer chain17,18 to investigate how the topological states of the intra-chain contacts are affected as the external molecule (chaperone) changes the chain's global topology. This is carried out by simulation setups in which the chaperone keeps the chain termini at a certain distance. The contour length of the chain is 200σ where σ denotes the diameter of the chain monomers. The Weeks–Chandler–Andersen (WCA)19 potential with strength ε = kBT is set as the intra-chain interactions. The simulation details of the chain are given in the ESI.† Four monomers on the chain which represent the binding sites in the native state are chosen randomly and then they are sorted in different groups based on the corresponding contact order of their series topological state. Due to the finite size of the chain, loops with the contact order higher than CO ≥ 0.35 are not investigated. The terminal beads of the chain are constrained by a spring whose equilibrium length is set to 5σ. The interaction strength between the binding sites is set to ε0 = 5kBT. The populations of topological states occupancy are analyzed by defining a cut-off radius rc = 1.5σ. Fractions of three distinct topological arrangements, which are named S, P and X, are evaluated based on circuit topology rules.5 For each contact order, 10 distinct groups of binding sites on the chain are chosen and the contact order of each group is calculated by the conformation in which the loops are in series. For each group, the simulation run is performed for 500 × 106 time steps.IV. Results
We first studied the dependency of folding time on contact order and circuit topology for our polymer models. The formation (folding) rates for two contacts on a chain in which the binding sites are separated by contour lengths of l1, l2 and l3 can be estimated based on the shortest distance along the partially folded chain20,21 and it is estimated as rS = 1/(l3/21 + l3/23), rP = 1/(l3/22 + (l1 + l3)3/2) and rX = 1/((l1 + l2)3/2 + (l2 + l3)3/2) for S-, P-, and X-loops respectively. Thus, the folding times of the loops arranged in series are less than those of the loops with cross and parallel arrangements. In this study, we estimated the folding times of a polymer chain (L = 200l) with two (Fig. 1e) and four (Fig. 2a) contacts toward different topologies. The contact order of the chain (〈CO〉) was found to be relatively small when the loops are in series in comparison with when they are in parallel and cross topological relations (〈COS〉 < 〈COX〉 = 〈COP〉), as shown in Fig. 2b (4-contact polymer). This can be readily explained: when the connectivity of the four binding sites which are separated by distances, l1, l2 and l3, is permuted, the overall contact order of the loops in series topology becomes (l1 + l3)/2L while it is (l1 + 2l2 + l3)/2L for both parallel and cross topologies. For parallel and cross topologies with identical contact order, X-loops fold faster than P-loops. This is due to the cooperativity within X-loops which generally increases the folding rate. This can be shown by analyzing the functional dependency of the folding rate, as calculated above, on l1, l2, and l3 variables (see ESI†). To ensure that our results do not depend on polymer length, we carried out a similar analysis for a shorter chain with length L = 50l. We observed that folding times depend on topology in a manner that is qualitatively similar to the observed trends for the longer chain (compare Fig. 1e with Fig. 1 in the ESI†).We next studied how chaperones can affect folding rates by accelerating or decelerating the formation of a native contact or by introducing a transient non-native contact with fast or slow kinetics (compared to native contacts in our control). For doing so, we altered the diffusion constants of binding sites associated with a native contact and asked how that affects the folding time. In the case of decreasing the diffusion constant of a native contact by 0.3D (i.e. case ii-1) (Fig. 3a), as expected, the folding times of all topological states rise. However, when a non-native contact with diffusion constant, 0.3D, is introduced in the contact set of the polymer (i.e. case iii-1) (Fig. 3c), the folding time of the chain decreases with respect to the control set; despite the fact that a non-native contact is formed. Interestingly, although the non-native contact has slower kinetics than the other contacts, overall it expedites the folding process of all the topological states by introducing interfering foldimers in the folding pathway. As is shown in Fig. 3b and d, such a catalyst mechanism reduces the folding time even further when the diffusion constants of the native (ii-1) and non-native (iii-1) contacts are increased three times. Hence, irrespective of whether the interfering contact has slower or faster dynamics with respect to the other contacts, it would enhance the kinetics of the folding process.
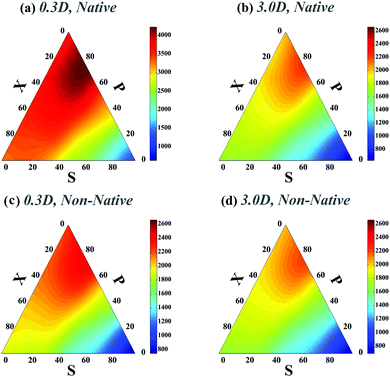 | ||
| Fig. 3 Ternary plots of the rescaled folding time (TfoldD/a2) for a polymer with four contacts in its native state when one native or non-native contact has different diffusion constants with respect to the other polymer contacts. Plots (a)–(d) correspond to cases (ii-1)–(iii-2), respectively. For a better comparison with the control set, the maximum folding time in the colored bars of plots (b)–(d) and the minimum folding time in plot (d) are set to the highest and lowest folding times in Fig. 2a respectively. | ||
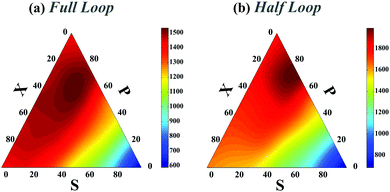
In all preceding analyses, the locations of the non-native binding sites on the chain are random. Thus, the external molecule does not induce any preferential topology on the chain. Subsequently, such inherent randomness in the selection of the binding sites on the chain only changes the overall folding time scales but it does not deform the folding time landscape with respect to the control sets (see Fig. 1e and compare Fig. 2a with Fig. 2 in ESI†) and generally, P-loops are closed slower than X-loops. However, when the external molecule binds both ends of the polymer to form a looped polymer, as discussed in (iv-1), along with global reduction in folding time scales, the folding time landscape deforms such that the maximum peak, which was previously localized near P-loops, moves toward X-loop topologies and it becomes more flattened in the SPX space (Fig. 4a). When a non-native contact connects the middle segment of the chain with one of the chain ends (iv-2) (Fig. 4b), although the global topology of the chain is divided into a half loop and a tail, the loops can randomly form either on the half-loop part or on the tail segment of the chain. Like cases (ii) and (iii), here we observe only a minor change in folding time landscape with respect to the control set; however, the loops in all the topological states fold faster than the loops in the control set (Fig. 4b).
The MD simulations also reveal that in the absence of the interacting molecule and when the chain folds freely in space, for all investigated ranges of contact orders, most of the contacts are arranged in series (Fig. 5). This trend, however, changes when an interacting molecule (chaperone) is present. When the chaperone forces the chain ends to the distance L = 5σ, approximately similar to the full loop case (iv-1), the overall topological fractions change such that the occupancy of series loops is taken over by the parallel loops, due to zipping effects.
V. Conclusion
We used two complementary computational approaches to address how an interacting molecule could change the occupancy of topological states and accordingly the folding kinetics of a polymer chain by reshaping the folding time landscape. This was investigated either through changing the kinetics of one of the native contacts or through the formation of a transient contact within the client during folding. Our results revealed that the loops which are arranged in series have the least folding time and the folding time of parallel loops exceeds that of contact-order-matched cross loops. This can be explained by the change in the chain's configurational entropy after the loops are closed because these events are solely entropy driven in the case of the Gaussian chain. The loops which are closed in series topology restrain local configuration of the chain. Therefore, configurational entropy reduction associated with series loops is milder than the reduction upon formation of globally constraining parallel and cross loops. Additionally, since the zipping mechanism is not an effective pathway in the KMC folding of the Gaussian chain model due to the absence of excluded volume interaction (see ESI†), the parallel loops do not necessarily close faster than cross loops. However, parallel loops are more probable than cross loops in the MD simulation where the excluded volume interaction is present. We also showed that either by perturbing the binding affinity of a native contact during folding or by adding an external loop, chaperones are able to modulate the kinetics of folding. Furthermore, the formation of a transient cyclical loop on the folding client changes the folding time landscape and occupancy of topological states by transferring the peak of the folding time landscape from the parallel to the cross topological state. Our approach can be used for further computational analysis of similar prototypical problems in polymer physics such as folding kinetics of weakly confined semiflexible chains22 and small knotted proteins;23 or chromatin looping in crowded active/passive environments.24,25References
- Y. E. Kim, M. S. Hipp, A. Bracher, M. Hayer-Hartl and F. U. Hartl, Annu. Rev. Biochem., 2013, 82, 323–355 CrossRef CAS PubMed.
- A. Mashaghi, G. Kramer, D. C. Lamb, M. P. Mayer and S. J. Tans, Chem. Rev., 2013, 114, 660–676 CrossRef PubMed.
- A. Mashaghi, G. Kramer, P. Bechtluft, B. Zachmann-Brand, A. J. Driessen, B. Bukau and S. J. Tans, Nature, 2013, 500, 98–101 CrossRef CAS PubMed.
- K. Singhal, J. Vreede, A. Mashaghi, S. J. Tans and P. G. Bolhuis, PLoS Comput. Biol., 2015, 11, e1004444 Search PubMed.
- A. Mashaghi, R. J. van Wijk and S. J. Tans, Structure, 2014, 22, 1227–1237 CrossRef CAS PubMed.
- A. Mashaghi and A. Ramezanpour, RSC Adv., 2015, 5, 51682–51689 RSC.
- N. Nikoofard and A. Mashaghi, Nanoscale, 2016, 8, 4643–4649 RSC.
- A. Mugler, S. J. Tans and A. Mashaghi, Phys. Chem. Chem. Phys., 2014, 16, 22537–22544 RSC.
- A. Mashaghi and A. Ramezanpour, Soft Matter, 2015, 11, 6576–6585 RSC.
- K. W. Plaxco, K. T. Simons and D. Baker, J. Mol. Biochem., 1998, 277, 985–994 CAS.
- A. Šali, E. Shakhnovich and M. Karplus, Nature, 1994, 369, 248–251 CrossRef PubMed.
- J. N. Onuchic, Z. Luthey-Schulten and P. G. Wolynes, Annu. Rev. Phys. Chem., 1997, 48, 545–600 CrossRef CAS PubMed.
- M. R. Ejtehadi, S. P. Avall and S. S. Plotkin, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15088–15093 CrossRef CAS PubMed.
- B. Öztop, M. R. Ejtehadi and S. S. Plotkin, Phys. Rev. Lett., 2004, 93, 208105 CrossRef PubMed.
- D. E. Makarov and G. J. Rodin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011908 CrossRef PubMed.
- D. E. Makarov and H. Metiu, J. Chem. Phys., 2002, 116, 5205–5216 CrossRef CAS.
- O. Mashinchian, S. Bonakdar, H. Taghinejad, V. Satarifard, M. Heidari, M. Majidi, S. Sharifi, A. Peirovi, S. Saffar and M. Taghinejad, et al. , ACS Appl. Mater. Interfaces, 2014, 6, 13280–13292 CAS.
- D. Meluzzi and G. Arya, Nucleic Acids Res., 2012, gks1029 Search PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- A. Szabo, K. Schulten and Z. Schulten, J. Chem. Phys., 1980, 72, 4350–4357 CrossRef CAS.
- T. Guérin, O. Bénichou and R. Voituriez, Nat. Chem., 2012, 4, 568–573 CrossRef PubMed.
- A. Fathizadeh, M. Heidari, B. Eslami-Mossallam and M. R. Ejtehadi, J. Chem. Phys., 2013, 139, 044912 CrossRef CAS PubMed.
- S. Najafi and R. Potestio, J. Chem. Phys., 2015, 143, 12B606_1 Search PubMed.
- N. M. Toan, D. Marenduzzo, P. R. Cook and C. Micheletti, Phys. Rev. Lett., 2006, 97, 178302 CrossRef CAS PubMed.
- J. Smrek and K. Kremer, Phys. Rev. Lett., 2017, 118, 098002 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp02145c |
| ‡ Equal contribution. |
| This journal is © the Owner Societies 2017 |