The effect of Fe on the structure and electrical conductivity of sodium borosilicate glasses

Abstract

We report the synthesis and characterization of iron-bearing sodium borosilicate glasses with an Fe₂O₃ content lower than 10 mol%. Using Mössbauer spectroscopy we demonstrate that Fe ions most probably have a tetrahedral oxygen environment for an iron oxide content higher than 5 mol%. Additionally, the Mössbauer results along with the X-ray diffraction studies indicate the formation of magnetite nanoclusters. The electrical conductivity of iron-containing sodium borosilicate glasses is studied over a wide temperature range. The impact of iron content on the dielectric permittivity and electrical properties is discussed. Finally, ionic conduction is identified in the high temperature region and its physical origin is explained. A similar activation energy of the dc conductivity and the activation energy of the electrical relaxation suggest that both the relaxation and conduction processes can be ascribed to the same type of entities.

---

Introduction

The oxide glasses containing transition metal ions have been widely studied since the 1950s,^1,2 owing to their potential applications in the fields of electrical memory switching, optical fibres, and materials for cathodes.³ This specific interest is primarily due to the possibility of controlling the electron transport properties by embedding iron atoms. This may even result in expansion of the application range. Most of the studies reported in the literature presented the properties of durable single-iron phosphate glasses and mixed-alkali glasses^4–6 with high thermal expansion coefficients and low melting temperatures. An extensive investigation of the structural, thermal and dielectric properties of phosphate glasses containing various amounts of Fe₂O₃ showed a considerable increase in the electronic conductivity caused by iron ions existing in two different valence states, which resulted in either ionic or hopping conductivity mechanisms.^7–9 For such a system, the electronic properties can be widely modified by temperature, iron content, and the average distance between iron ions in glass.^10–12

Sodium borosilicate (SBS) glasses belong to a large glass family with a wide variety of applications. Owing to their low thermal expansion coefficient, low dielectric constant, relatively high electrical resistivity, good chemical stability and high chemical resistance, SBS is used in microelectronics^10,11 and as a host material for porous matrices with controlled porosity.^12,13 Such porous glasses are known to be the basis for many composite materials.^14,15 The structure of SBS glasses can be considered as a three-dimensional network of corner-connected [SiO_4/2] tetrahedra and three- and four-coordinated boron forming the [BO_3/2] and [BO_4/2] boron–oxygen groups.^16,17 It was reported that addition of iron oxide as the network modifier or the glass-former involved the conversion of the [BO_4/2] boron–oxygen tetrahedral group to triangular BO₃ structural units, thus resulting in a decrease in the polymerisation degree of the [SiO_4/2] tetrahedral group.¹⁸ Moreover, Fe²⁺ cations that are predominantly in the sixfold coordination occupy interstitial sites near the trigonal boron–oxygen groups, whereas Fe³⁺ ions are four-coordinated and appear to substitute a silicon. It was observed that the redox equilibrium Fe³⁺ ⇆ Fe²⁺ in the glass melt depended on the melt temperature, its cooling rate, the gas composition in the furnace as well as the melt composition.¹⁸ SBS glass modified in this way is widely used as a nuclear waste form,^19–21 also in medicine for a targeted magnetite crystallization,²² and it is considered as a system for the production of semiconducting fibres²³ as well. Although much effort has been devoted to the study of the structural, dielectric and optical properties of various oxide glasses containing Fe₂O₃ as a glass former,^1–12 insufficient studies have been carried out on SBS glasses doped with Fe₂O₃. In fact, the presented results on the physical properties of sodium borosilicate glasses doped with a low content of Fe₂O₃ have not been reported so far.

Our goal in this work was to investigate the influence of iron ions on the electrical conductivity and dielectric properties of the iron-doped SBS system. The glass structure was studied by X-ray diffraction. In order to infer the redox state of iron and its local environment, we employed ⁵⁷Fe Mössbauer spectroscopy. The main part of the presented investigation of the interesting physical properties is oriented towards future applications in areas of multiferroic elements, optics, nanoelectronics, sensors, biotechnology and medicine. Nanoscale multiferroic elements based on magnetic porous matrices with different shapes and sizes of pores can have totally different magnetic and electric properties. For industrial applications, stable states, well-controlled switching behaviour, and small dependence on size variations are highly desirable. Understanding and controlling these properties of the nanoscale multiferroelectric elements requires thorough investigation of SBS glasses with a low iron content in order to preserve the dielectric properties of porous glass matrices.

Experimental details

Synthesis procedures

The glasses were synthesized with constant Na₂O and SiO₂ contents of 8 and 70 mol%, respectively, and with x (= 3, 4, 6 and 10) mol% of Fe₂O₃ added to each (22 − x) mol% of boron oxide according to the procedure described in ref. 24. The glass charge for each composition was prepared from analytically pure reagents. Na₂CO₃ of ultra-high purity grade and H₃BO₃ and Fe₂O₃ of reagent grade were used. SiO₂ was introduced into the charge as ground quartz glass. The reagents were melted in a platinum crucible at 1500–1520 °C in a silt furnace in air for 2–3 h. After pouring the melts onto a heated metal plate, the obtained glasses were annealed in a muffle furnace at 520 °C for several minutes and then cooled down to room temperature. Pure SBS glass (without Fe₂O₃ addition) was melted under industrial conditions. In order to initiate the phase separation process, the glasses were heat treated at 550 °C for 144 h. According to TEM data, all glasses have interconnected phase-separated structures,²⁴ which means that these compositions can be potentially suitable for making porous glasses.

X-ray diffraction (XRD)

XRD measurements were performed with aid of a two-circle laboratory diffractometer (PANalytical X'Pert PRO) using the standard θ−2θ geometry. The Cu Kα line at 1.54 Å was used and the radiation was converted into a beam by an incident beam optics with 0.5° divergence slit, and 0.04 rad Soller slit collimator. The diffracted beam path was equipped with an anti-scatter slit and 0.04 rad Soller slit collimator. The signal was collected using a solid-state stripe detector with a flat graphite monochromator. All XRD patterns were recorded at 2θ angles ranging from 10 to 140 deg, with an instrumental step of 0.05° and a counting time of 10 minutes for each point.

Mössbauer spectroscopy

⁵⁷Fe Mössbauer measurements were performed in transmission geometry at room temperature using an ∼100 mCi activity ⁵⁷Co/Rh source. The velocity scale was calibrated using an iron foil absorber at room temperature and the isomer shifts are given relative to α-Fe. Spectra were analysed using the Recoil v.1.03a software package with the Rancourt and Ping Voigt-based fitting method.²⁵

Dielectric spectroscopy

The dielectric measurements were carried out using the Novocontrol Alpha Impedance Analyzer. The samples were cut in parallel-flat plate-shaped forms with an average size of 10 × 10 × 0.5 mm. The samples were placed between two copper flat electrodes. The temperature was controlled using the nitrogen gas cryostat with stability higher than 0.1 K. The temperature dependences of the dielectric permittivity and the conductivity were measured between 300 and 600 K with an applied voltage of 1 V. The dielectric spectra were measured in the frequency range of 1 Hz to 10 MHz. Before each measurement, the samples were heated up to 400 K for two hours to remove the residual water adsorbed in the sample.

To obtain two glassy phases, the studied glasses were heat-treated at a temperature above T_g (T = 550 °C) for 144 hours, which is sufficient to reach the phase equilibrium. The T_g values of the studied glasses are in the range 500–504 °C.²⁴ These values correspond to the glass transition interval of the low-melting boron-rich phase. Thus, in the studied glasses, the equilibrium structure, corresponding to the heat treatment temperature (550 °C), is frozen (stabilized). In our experiments, the maximum temperature for measuring the dielectric permittivity and the conductivity did not exceed 600 K (327 °C), that is, it was significantly lower than both the T_g values and the isothermal heat treatment temperature T, which had no effect on the structure of the phase-separated glasses under study.

Results and discussion

XRD results

Table 1 shows the as-analysed glass compositions of 8Na₂O–(22 − x)B₂O₃–70SiO₂–xFe₂O₃, 3 ≤ x ≤ 10 (mol%), while the XRD patterns obtained for the samples containing iron are shown in Fig. 1.

Table 1 Chemical glass compositions of xFe₂O₃–8Na₂O–(22 − x)B₂O₃–70SiO₂. The number following “Fe” in the sample code corresponds to the Fe₂O₃ content in as-analysed mol%. The composition of SBS glass without Fe₂O₃ additives is given according to ref. 26. It should be noted that SBS glass has traces of Al₂O₃ which could be introduced into the glass melt from the refractory at industrial melting

Sample code	Composition (as-analyzed mol%)
	SiO2	B2O3	Na2O	Fe2O3	FeO	Al2O3
SBS	74.93	18.28	6.73	—	—	0.06
SBS-Fe3	71.08	18.38	7.09	2.76	0.69	—
SBS-Fe4	71.26	17.17	7.31	3.23	1.04	—
SBS-Fe6	70.09	15.72	7.13	4.76	2.30	—
SBS-Fe10	68.79	11.83	7.07	7.13	5.18	—

---

Fig. 1 XRD patterns for the xFe₂O₃–8Na₂O–(22 − x)B₂O₃–70SiO₂ glasses. The vertical offsets were used for clarity. The positions of reflections for the bulk magnetite are indicated.

In all cases, the peaks corresponding to the crystalline magnetite phase appear. Additionally, the broad peak at a position of about 23 deg is visible. It originates from the amorphous phase of glass and its intensity is similar to that of all samples. In contrast, the intensities of the peaks arising from the magnetite phase change and increase with increasing amounts of Fe₂O₃ introduced into the glass during the synthesis.

Mössbauer spectroscopy

Mössbauer spectra collected for the samples containing iron are presented in Fig. 2.

Fig. 2 Mössbauer spectra were recorded for the samples containing iron. Different regions on the graphs represent contributions from the different sites.

For the description of the spectra, the best fitting was achieved by using four Mössbauer components: two sextets and two quadrupole doublets. The mean values of the fitted parameters together with the ratio of the integral peak intensities of the electrical quadrupole splitting A⁻/A⁺ and the ratio of the corresponding lines of Zeeman splitting A₂/A₃ are given in Table 2. The ratio of the lines A₁/A₃ was fixed for all magnetic sites and is equal to 3. The isomer shifts, fitted to all spectra, were corrected according to the used source. The main component in all Mössbauer spectra is a strong quadrupole doublet originating from iron atoms in the Fe(1) site. Such a doublet with a similar isomer shift and quadrupole splitting was already reported for sodium borosilicate glasses^27,28 and it corresponded to the high spin Fe³⁺ ions (S = 5/2). The isomer shift for the samples with the highest iron content suggests a tetrahedral oxygen environment of Fe(1) sites,^28–30 while for samples SBS-Fe4 and SBS-Fe3 the mean centre shift decreases which indicates a lower coordination. A high electric quadrupole shift of about 0.9 mm s⁻¹ for this component indicates a significant distortion of the Fe³⁺O_n polyhedra in the glass structure, which induces a large electric field gradient on the ⁵⁷Fe nuclei of spherically symmetric Fe³⁺ cations.²⁷ The low intensity doublet related to Fe(2) sites corresponds to the Fe²⁺ ions (S = 2) with parameters similar to those reported in ref. 27. As in the case of Fe(1), the mean centre shift slightly decreases with decreasing iron content, which suggests an evolution toward lower coordination.²⁸

Table 2 Mössbauer hyperfine parameters for the SBS samples. c is the percentage site fraction, B_hf is the magnetic hyperfine field, and IS is the isomer shift. QS stands for the electric quadrupole shift in the case of magnetic sites or for quadrupole splitting in the case of paramagnetic sites. A⁻/A⁺ is the ratio of the integrated peak intensities for QS, whereas A²/A³ is the ratio of the second (fifth) to the third (fourth) peak intensities for Zeeman splitting. The widths of the hyperfine parameter distributions are shown in square brackets

Sample	Site	c [%]	B hf [T]	IS [mm s^−1]	QS [mm s^−1]	A ^− /A ^+ or A^2/A^3
SBS-Fe10
	Fe(1)	33.1	—	0.22	0.94 [0.48]	1.72
	Fe(2)	5.9	—	2.27	0.76 [0.32]	0.55
	Fe(3)	37.0	45.8 [0.5]	0.68	0.0	2.16
	Fe(4)	24.0	48.7 [0.1]	0.27	0.0	2.29
SBS-Fe6
	Fe(1)	79.8	—	0.21	0.93 [0.55]	2.10
	Fe(2)	20.2	—	2.16	0.91 [0.33]	0.43
SBS-Fe4
	Fe(1)	57.6	—	0.18	0.93 [0.50]	2.09
	Fe(2)	7.9	—	2.16	0.91 [0.33]	0.50
	Fe(3)	23.0	43.1 [0.6]	0.67	0.0	2.0
	Fe(4)	11.5	46.5 [0.2]	0.21	0.0	2.0
SBS-Fe3
	Fe(1)	61.7	—	0.11	0.91 [0.50]	1.72
	Fe(2)	14.7	—	2.05	0.87 [0.34]	0.55
	Fe(3)	12.6	45.2 [0.6]	0.59	0.0	2.0
	Fe(4)	11.0	47.8 [0.2]	0.16	0.0	2.0

---

The presence of two Zeeman sextets for Fe(3) and Fe(4) sites in the Mössbauer spectra (which can be assigned to the magnetite phase) can be well correlated with the magnetite peak widths from the XRD patterns. In the case of the sample with the highest iron content (SBS-Fe10), the magnetite peak widths are the smallest, resulting in sharp and well-defined Zeeman lines with IS, B_hf, and QS being very close to the parameters known for iron ions in the bulk magnetite at room temperature.³¹ The profile of the Zeeman sextets for the samples with a low Fe content (SBS-Fe4 and SBS-Fe3) exhibiting wider XRD peaks and smaller magnetite crystallites indicates the inhomogeneous and disturbed environment of the iron cations. The distribution of the magnetic moment of individual magnetite grains resulted in a decrease in the mean hyperfine fields and in a broadening of the lines. In contrast to these results, the Mössbauer spectrum for the SBS-Fe6 sample did not show magnetic hyperfine interactions. This can be explained by a very small grain size in this sample (approx. 8 nm as calculated using the Scherrer equation^32,33), which entails the continuous fluctuation of the magnetic moments of each magnetite cluster related to superparamagnetic effects. In such a case, if the relaxation time of the superparamagnetic particle is greater than the lifetime of the excited nucleus, it experiences an average zero field only and Zeeman splitting cannot be observed.³⁴

Electrical results

The complex permittivity ε* can be expressed as ε* = ε′ − jε′′, where ε′ and ε′′ denote the real and imaginary parts of the electric permittivity, respectively. In Fig. 3 the frequency dependences of the real part of the electric permittivity of SBS-Fe4 glass at various temperatures are depicted. The real part of the electric permittivity ε′ gradually increases with increasing iron concentration (inset (a) in Fig. 3). Moreover, for all glasses doped with iron ions, the electric permittivity decreases with increasing frequency. It can be noticed that ε′ approaches a constant value at high frequency, most probably due to the polarization process occurring in glasses.^35,36 The rapid increase of ε′ with decreasing frequency is mainly caused by the effect of mobile ion polarization.

Fig. 3 Frequency dependences of the real part of the electric permittivity ε′ at selected temperatures for SBS-Fe4 glass. Inset (a) shows the frequency dependence of the real part of the electric permittivity at 300 K for Na₂O–B₂O₃–SiO₂–Fe₂O₃ glasses (Fe₂O₃ content is indicated). Inset (b) shows the variation in the real part of the electric permittivity at 1 kHz with Fe₂O₃ concentration evaluated at selected temperatures.

The frequency dependences of the dielectric loss tan δ for the SBS-Fe4 sample at various temperatures are shown in Fig. 4. The maximum dielectric loss shifts toward higher frequency with increasing temperature, indicating a thermally activated behaviour.

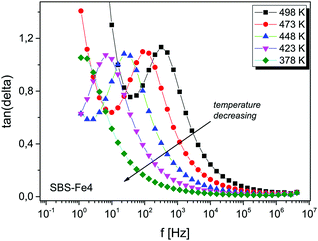Fig. 4 Frequency dependences of the dielectric loss tan δ at selected temperatures for SBS-Fe4 glass. The data are connected as a guide to the eye.

A similar frequency dependence of the electric permittivity and the dielectric loss tan δ was found for all glasses. The increase in ε′ is attributed to an increase in the Fe content, and it is expected to be a result of the conduction and polarization coupling into a single process. The temperature dependence of the real part of the conductivity on the frequency f on a logarithmic scale (where f = ω/2π and ω is the angular frequency) is shown in Fig. 5 for SBS-Fe10 glass.

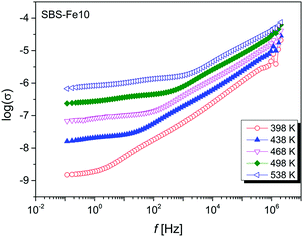Fig. 5 Temperature dependence of the conductivity, σ, at several temperatures for SBS-Fe10 glass. The data are connected as a guide to the eye.

For all investigated samples, the curves have a similar shape which is typical for amorphous materials. For all samples, the conductivity dependence observed for high frequency follows the Jonscher power law. For our glass systems, in order to obtain the dc conductivity, ε′′ (1/ω) data have been fitted.⁹ The temperature dependences of the dc conductivity are shown in Fig. 6 for all samples.

Fig. 6 Temperature dependence of the dc conductivity, σ_DC, for various glass compositions. The solid lines represent the least-square fitting. Inset shows the variation of the σ₀ with the concentration of Fe₂O₃.

The observed dependence obeys a simple Arrhenius formula σ_DC = σ₀ exp(−E_DC/k_BT), where σ₀ is the pre-exponent, E_DC is the activation energy for dc conductivity, T is the temperature and k_B is the Boltzmann constant. For each glass in the present study, the activation energy (E_DC) was determined from the slope of log σ_DCvs. reciprocal temperature (1/T) as shown in Fig. 6. The values of the activation energy E_DC are collected in Table 3 for all samples.

Table 3 Activation energies E_M, E_DC, and E_ac and the relaxation time τ_s at 400 K for the iron–sodium borosilicate glasses

Glass	E ac [eV] f = 10 kHz ±0.5%	E M [eV] ±0.5%	E dc [eV] ±0.5%	τ σ [s]
SBS-Fe10	0.38	0.96	0.97	0.024
SBS-Fe6	0.46	0.94	0.94	0.023
SBS-Fe4	0.54	0.90	0.90	0.016
SBS-Fe3	0.57	0.89	0.88	0.004
SBS	0.60	0.90	0.85	0.003

---

The electrical conductivity in sodium borosilicate glasses is related to the transport of sodium ions through the glass network. It is stated that because of heat treatment of the investigated glasses, the sodium ions are present mainly in the sodium-borate phase. In borate glasses, the Na ions are bound to the BO₄⁻ groups. The results of the chemical durability investigation of these glasses indicate that most of the iron ions are allocated at the sodium-borate phase. It is obvious that both sodium and iron ions contribute to the electrical conductivity in iron-containing alkali borosilicate glasses. The electronic conductivity is considered as the polaron hopping between the iron ions. All the glasses under investigation contain the same concentration of sodium ions; therefore the number of carriers is the same. The increase in the dc conductivity and the activation energy with increasing Fe content is related to the presence of Fe and its influence on the structure of the investigated glasses. The addition of iron ions to the sodium borosilicate network reduced the amount of four-coordinated boron (BO_4/2) and increased the amount of three-coordinated boron (BO_3/2).¹⁸ The structural reorganization of iron-SBS glasses is probably caused by the competition between FeO₄ and BO₄ with a compensation of the negative charge by the Na⁺ ions. At the same time, the number of non-bridging oxygen atoms increases, which produces a weakening of the SBS glass structure. Such structural changes can have an important influence on the mobility of Na⁺. The Na⁺ mobility increases in the presence of non-bridging oxygen atoms.³⁸ These changes can cause an increase in dc conductivity. On the other hand, addition of iron oxide causes the formation of [FeO_4/2]⁻Na⁺ units.³⁹ The increase of the Fe content causes the increase of these units, where the Na⁺ ions are linked stronger than those in the sodium-borate [BO₄]⁻Na⁺ units. In our opinion, this is the most probable reason why the dc activation energy increases. It can be expected that for a constant concentration of Na⁺ in the investigated glasses, the number of [FeO_4/2]⁻Na⁺ units increases with increasing Fe₂O₃/B₂O₃ ratio.

It is known that in ionic conducting glasses, the activation energy is attributed to the Na⁺ ion transport. It is determined by the average height of potential barriers. The main electronic transport in these glasses is hopping through localized states. These localized states can correspond to the gap states which are attributed with structural defects. The value of dc activation energy of 0.88 eV for SBS-Fe3 glasses is similar to that of about 0.85 eV for dc conductivity obtained for iron-free glasses (SBS sample). This suggests that the conduction mechanism in the investigated glasses is ionic, and the dc activation energies are described by the sodium ion transport through the glass network.

The total conductivity is given by the empirical form that is expressed as σ_t(ω) = σ_DC(ω) + σ_AC(ω), where σ_t(ω), σ_DC(ω) and σ_AC(ω) have typical meanings. For the investigated glasses, the values of ac conductivity σ_AC were obtained by subtracting the dc conductivity from the total conductivity. The glass systems presented in this paper, have not been considered till now that occurs more because of very difficult glass network, the full structure of these systems is not accessible now. One of the probable scenarios of reduction of E_ac with increasing Fe concentration is that the doping of Fe in the SBS glass network leads to an increase in the number of glass network defects. As the iron content is increased, the number of defects increases. The reduction of the ac activation energy can be related to the trapping on the defects. As the iron content is increased, the number of defects also increases. The frequency dependence of σ_AC(ω) at various temperatures is shown in Fig. 7 for SBS-Fe10 glass.

Fig. 7 Frequency dependences of the ac conductivity, σ_AC, for the glass containing 10 mol% of Fe₂O₃ (SBS-Fe10) at selected temperatures.

The observed changes are typical for an amorphous material and usually follow the power law relation σ_AC = A·ω^s, where s represents the temperature-dependent degree of an interaction between the mobile ions and generally varies between 0 and 1. The exponent s was calculated for selected temperatures from experimental data by means of linear data fitting.

The fitted value of the exponent s is shown in Fig. 8 for several temperatures. The relative errors are smaller than the given tolerance. It can be seen that s increases with decreasing temperature from approximately 0.51 to approximately 0.68. The temperature behaviour of the s exponent can be useful to clarify the conductivity mechanism in the material. It is known that the decrease of s with increasing temperature is related to the charge transport between the localized states attributed to hopping over the potential barriers.^37–40 For all glasses under study, the s exponent obeys such a temperature-dependent behaviour.

Fig. 8 Temperature dependence of the s parameter for the glasses with various contents of Fe₂O₃.

Electric modulus representation

The relaxation properties of glasses were analysed using the complex electrical modulus formalism and the Kohlrausch–Williams–Watts (KWW) decay function θ(t) = exp(−(t/τ)^β), where t is the time, τ is the electric field relaxation time, and β is the constant (0 < β < 1). The temperature dependence of the imaginary part of the electrical modulus M′′ obtained at various temperatures is shown in Fig. 9 for sodium borosilicate glasses doped with Fe₂O₃.

Fig. 9 Frequency dependences of the electrical modulus M′′ for SBS-Fe3 glass (a), SBS-Fe4 glass (b), SBS-Fe6 glass (c) and SBS-Fe10 glass (d) at selected temperatures. The data are connected as a guide to the eye.

For all glasses, the peaks shift toward higher frequencies with increasing temperature, while the shapes of the curves are asymmetric, exhibiting non-Debye behaviour in the high-frequency region. The broadness of the M′′ curves remains constant for all samples, which may imply the same activation energy for all distribution components. An extra small peak in the glass with the highest content of Fe is observed. As far as we know, in this system it is difficult to enhance the Fe-SBS glasses with higher iron concentrations. Until we obtain glasses with a higher iron content, we can only assume that the extra-smaller peak observed in SBS-Fe10 is related to the Fe content. Fig. 10 shows the temperature dependence of the relaxation frequency obtained from the peak position of M′′.

Fig. 10 Frequency dependences of the M′′ peak on 1000/T for Na₂O–B₂O₃–SiO₂–Fe₂O₃. The data are connected as a guide to the eye.

The relaxation time can be determined as the inverse of the maximum modulus frequency τ_σ = 1/(2·π·f_M). The relative errors are smaller than the given tolerance. For all glasses investigated in the present work the activation energy can be described using the Arrhenius equation f_M = f_M0·exp(−E_M/k_B·T), where E_M is the activation energy of the electrical relaxation, k_B is the Boltzmann constant and f_M0 is the characteristic frequency. The activation energy E_M is almost identical to the activation energy of the conduction process E_DC, and this suggests that both the relaxation and conduction processes may be attributed to the same type of entities. The values of relaxation times τ_σ for the glasses measured at 400 K are shown in Table 3. The relaxation time can be attributed to the time of jumps between two nearest interstitial sites. The values of activation energies E_M, ascribing the motion of Na⁺, calculated from the fitting data, are presented in Fig. 10 and are shown in Table 3.

Conclusions

In summary, we studied the structural and electrical properties of iron-doped SBS glasses as a function of Fe₂O₃ content in the system. We determined by means of X-ray diffraction and Mössbauer spectroscopy that iron atoms occurred in two phases: the magnetite nanocrystalline phase and the amorphous glass matrix with a short-range order. Our dielectric and electrical studies showed that the addition of Fe₂O₃ to SBS increased the electrical conductivity, which was caused by structural changes in the glass network. Additionally, a number of BO_4/2 groups dropped down with increasing Fe₂O₃ content. Simultaneously, the formation of [FeO_4/2]⁻Na⁺ groups was promoted, where Na⁺ ions were linked stronger than those in [BO_4/2]⁻Na⁺. The iron most likely acted as a network modifier, and the conduction mechanism in the investigated range of temperature seemed to be ionic rather than electronic. The value of s parameter obtained for all examined glasses doped with Fe is typical for ionic conducting materials. Our purpose was to create ferromagnetic glasses that exhibit both ferromagnetic and dielectric properties at the same time, which requires a rather low content of iron.

Acknowledgements

The work was carried out under the Polish–Russian joint research project “Ferroelectric, magnetic and optical nanocomposite materials on the basis of porous glasses” (2014/2016). T. V. Antropova acknowledges financial support from the Russian Foundation for Basic Research, Project No. 15-03-06258a.

References

1. E. P. Denton, H. Rawson and J. E. Stanworth, Nature, 1954, 173, 1030.
2. M. Sayer and A. Mansihgh, Phys. Rev. B: Solid State, 1972, 4629.
3. M. Regan and C. F. Drake, Mater. Res. Bull., 1971, 6, 487.
4. A. Santic, et al. , J. Non-Cryst. Solids, 2010, 356, 2699.
5. M. Nagaswa and H. Watanabe, UK Pat., No. 1358930, 1971.
6. R. A. Montani, et al. , J. Non-Cryst. Solids, 1992, 149, 249.
7. L. Murawsky, et al. , J. Non-Cryst. Solids, 1979, 215, 21.
8. N. F. Mott, J. Non-Cryst. Solids, 1968, 1, 1.
9. A. Mogus-Milankovic, D. E. Day and B. Santic, Phys. Chem. Glasses, 1999, 40, 69.
10. H. Jantunen, et al. , J. Eur. Ceram. Soc., 2003, 23, 2541.
11. A. A. El-Khesen and M. F. Zawrah, Ceram. Int., 2003, 29, 251.
12. T. Antropova, Opt. Appl., 2008, 38, 5.
13. E. Rysiakiewicz-Pasek, et al. , Opt. Appl., 2000, 30, 173.
14. A. Cizman, T. Marciniszyn and R. Poprawski, J. Appl. Phys., 2012, 112, 034104.
15. A. Cizman, et al. , J. Nanopart. Res., 2013, 15, 1807.
16. S. P. Zhdanov and G. Shmidel, Fiz. Khim. Stekla, 1975, 1, 452.
17. M. Hubert and A. J. Faber, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2014, 55, 136.
18. O. A. Pshenko, et al. , Glass Phys. Chem., 2016, 42, 33.
19. H. Segawa and N. Hirosaki, Appl. Opt., 2015, 54, 8727.
20. J. S. Jeoung, et al. , J. Am. Ceram. Soc., 2001, 84, 1859.
21. B. Cochain, et al. , J. Am. Ceram. Soc., 2012, 95, 962.
22. C. Worsch, et al. , J. Mater. Sci., 2012, 47, 5886.
23. F. Shun, S. Zhou and F. Chan, J. Non-Cryst. Solids, 1982, 52, 435.
24. M. Yu. Konon, et al. , Glass Phys. Chem., 2015, 41, 116.
25. D. G. Rancourt and J. Y. Ping, Nucl. Instr. And Meth., B, 1991, 58, 85.
26. V. V. Golubkov, et al. , Glass Phys. Chem., 2015, 41, 582.
27. Ya. S. Glazkova, et al. , Glass Phys. Chem., 2015, 41, 367.
28. B. Cochain, et al. , J. Am. Ceram. Soc., 2012, 95, 962.
29. F. Menil, J. Phys. Chem. Solids, 1985, 46, 763.
30. M. D. Dyar, Am. Mineral., 1985, 70, 304.
31. R. E. Vandenberghe and E. Grave, in Mössbauer Spectroscopy Applied to Inorganic Chemistry, ed. G. J. Long and F. Grandjean, New York, Plenum, 1989, vol. 3, p. 59.
32. M. Krupinski, et al. , J. Appl. Phys., 2011, 109, 064306.
33. M. Krupinski, et al. , Nanotechnology, 2015, 26, 425301.
34. E. Murad and J. Cashion, Mössbauer spectroscopy of environmental materials and their industrial utilization, Kluwer Academic Publishers, New York, 2004.
35. C. J. F. Bottcher and P. Bordewijk, Theory of Electrical Polarization, Elsevier, Amsterdam, 1978.
36. P. Ishai, M. Talary, A. Caduff, E. Levy and Y. Feldman, Meas. Sci. Technol., 2013, 24, 102001.
37. I. G. Austin and E. S. Gebert, Electronic and Structural Properties of Amorphous Semiconductor, Academic Press, New York, 1973, p. 393.
38. R. Vaish and K. B. R. Varma, Ionics, 2011, 17, 727.
39. A. Al-Shahrani, A. Al-Hajry and M. M. El-Desoky, Physica B, 2005, 364, 248.
40. A. Gosh, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1388.

---