Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cross-impact of surface and interaction anisotropy in the self-assembly of organic adsorption monolayers: a Monte Carlo and transfer-matrix study†
V. A.
Gorbunov
 *a,
S. S.
Akimenko
*a,
S. S.
Akimenko
 a and
A. V.
Myshlyavtsev
a and
A. V.
Myshlyavtsev
 ab
ab
aOmsk State Technical University, pr. Mira, 11, Omsk, Russian Federation. E-mail: vitalygorbunov@mail.ru
bInstitute of Hydrocarbon Processing SB RAS, 56 Neftezavodskaya Str., Omsk, Russian Federation
First published on 12th June 2017
Abstract
Using a simple lattice gas model we study the features of self-assembly in adsorption layers where both “molecule–surface” and “molecule–molecule” interactions are anisotropic. Based on the example of adsorption layers of mono-functional organic molecules on the heterogeneous surface with strip-like topography, we have revealed plenty of possible self-assembled structures in this simple system, such as discrete, linear, zigzag, chess board-like, two-dimensional porous and close-packed patterns. However, the phase behavior of the adsorption layer is much richer, if the interactions between functional and non-functional parts of adjacent adsorbed molecules have comparable strength and opposite signs. It is demonstrated that filling of the strips composed of relatively “strong” adsorption sites with the increase of chemical potential can be non-monotonic. This effect is associated with surface anisotropy and results from the changing of the driving force of the self-assembly process – interactions between the adsorbed molecule and the surface dominate at low surface coverages, but intermolecular forces prevail at higher ones. Additionally, when the width of the strip composed of “strong” adsorption sites is two or more times greater than that of the adsorbed molecule, a local assembly of the ordered phases on the “strong” adsorption sites is observed. Our results suggest strategies for controlling the self-assembly in experiments involving mono-functional organic molecules on a strip-like heterogeneous surface.
Introduction
Adsorption and self-assembly of functional organic molecules on metal and graphite surfaces is the most promising approach to create large-scale functional nanostructures.1–6 The self-assembly of molecules at surfaces can be caused by a range of physical mechanisms. In the simplest case, self-assembly can be driven by intermolecular forces or/and interaction between the adsorbed molecule and the surface.7–9 In turn, the chemical structure of the molecule – size, shape, the set of functional groups and symmetry of their arrangement – determines the types of interactions between the molecules in the adsorption overlayer.1,3,10–15 As a rule, the molecules are coupled via highly directional forces, such as hydrogen bonding. Through its high selectivity and directionality, hydrogen bonding enables equilibrium structures of the adsorption layer to be achieved at relatively low temperatures. In some cases, when the interaction anisotropy results from the molecule geometry (e.g. bulky substituent), less directional forces like van der Waals can trigger a self-assembly of adsorption layers.11,16,17 On the other hand, we should not neglect the role of the surface in the self-assembly of organic adsorption layers. It is usually believed that weak non-covalent interactions between a molecule and a relatively inert surface (such as van der Waals or dispersion forces) determine only the conformation of the adsorbed molecules, whereas intermolecular interactions only affect the structure of the self-assembling adsorption layer.8,18 The situation changes significantly when the solid surface is heterogeneous.3,7,8,19 Surface heterogeneity can be represented as steps and terraces on the vicinal surfaces of metal single crystals, surface reconstructions,20–23 for example “herringbone” reconstruction at the Au(111) surface, and chemically modified surfaces (surface oxides, nitrides and alloys).24–26 In all these cases, there are “strong” and “weak” adsorption sites regularly distributed on the surface. Consequently, the interaction between the adsorbed molecules and the solid surface is anisotropic. When the molecule–surface interaction is strong enough the structure of the adsorbed phase usually reflects the topography of the underlying surface.Following on from the above, to date, a large amount of experimental data on the self-assembly of functional organic molecules on heterogeneous surfaces with various topographies have been collected. On the other hand, there is no theory or model that allows us to summarize the data and formulate the general patterns of phase behavior for such systems. Usually, the statistical methods combined with the lattice-gas model are used for such purposes. This is the most appropriate approach taking into account the length and time scales of the self-assembly processes in organic adsorption layers.
The so-called patchwise model is widely used for modeling adsorption on a heterogeneous surface with a regular distribution of several types of adsorption sites.27–30 In this model, the surface is assumed to be composed of isotropic domains consisting of the same adsorption sites. Using the patchwise model, the adsorption of monomers, dimers and linear k-mers on a square lattice with “square-patches” and “strip” topographies has been studied.28–41 It is shown that the surface topography and the characteristic size of patches significantly affect the phase behavior of the adsorption layers. In particular, it is established that the presence or absence of long-range order and the type of phase transition are determined by the ratio between the absorption energy and size of the patches and strips. In summary, the influence of the “adsorbate–adsorbent” interaction anisotropy on the phase behavior of the adsorption layer has been studied in detail, but only for the case of isotropic intermolecular interactions.
Statistical modeling of the self-assembly in adsorbed layers characterized by the high directionality of intermolecular interactions is only just beginning, despite an obvious practical importance. To date the statistical models with paired directional interactions between the adsorbed molecules of a simple shape and chemical structure (mostly the molecules with C3 and C4 symmetry) have been studied extensively. The adsorption of organic molecules with different amounts of functional groups and the symmetry of their arrangement were investigated.17,42–52 Phase transitions, their order and universality class have been analyzed for the simplest models.53–57
In this work, using a simple lattice gas model we study the features of the self-assembly in adsorption layers where both “adsorbate–adsorbate” and “adsorbate–adsorbent” interactions are anisotropic. To that end we examine the self-assembly of mono-functional organic molecules on the heterogeneous surface with the “strip” topography that is typical for vicinal, reconstructed and chemically modified surfaces of metallic single crystals.
Model and simulation techniques
In this study, we investigate the simplest case of adsorption of rigid planar molecules having a single functional group capable of forming a hydrogen bond (e.g. –COOH). The rigid core of the molecule is supposed to comprise one or more aromatic rings. Alternatively, it may be a short aliphatic chain (C2–C4, or hetero-substituted analogs). Except the functional group, the adsorbed molecule is assumed to have side substituents. The size of the functional groups and side substituents of the adsorbed molecule is either smaller than or commensurate with the size of their cores. Examples of such systems include the adsorption layers of amino acids,7,23,58 alkoxybenzoic acids,59 functional derivatives of benzene,23 naphthalene and other bicyclic and more complicated organic molecules22,23,60 such as anthracene,61 porphyrin and phthalocyanine.12,19,20,62–65 It is important to stress that all the above mentioned molecules have a single functional group capable of forming a hydrogen bond. From the viewpoint of the intermolecular interactions in the adsorption layer, the only difference between them is the set of side substituents.In the present model, the molecule is assumed to adsorb on a single site of a square lattice. The size of the adsorption site is assumed to be large enough and commensurate with the size of the adsorbed molecule. It is important to stress that the adsorption site can represent not one, but a number of atoms on the surface (for example, hollow sites or few atop sites on a crystalline surface). Therefore, the symmetry of the lattice is mainly determined by the symmetry of the molecule and does not reflect the actual arrangement of atoms on the solid surface. The only feature of the surface taken into account is the anisotropy of the adsorption site distribution.
Due to the symmetry of the lattice, the adsorbed molecule has four distinct orientations related to directions of the functional group (Fig. 1). The energy of the pair interactions between the molecules depends on their relative position and orientation. The molecules are allowed to attract via the functional groups of the nearest neighbor molecules with the energy w < 0. Additionally, the model includes a repulsive interaction ε > 0 that takes into account bulky side substituents in the chemical structure of the molecule and/or arises from the interactions with the substrate. Thus, the ratio ε/|w| depends on the chemical structure of the molecule and it is defined by the set of functional groups. If the adsorbed molecules have bulky side substituents (similar to the size of their cores), we consider only geometric factors, the case of ε/|w| = ∞. When ε/|w| = 0, the interactions between the non-functional parts of the molecules are weak. In this case, the side substituents are either absent (for example, benzoic acid and other functional derivatives of benzene and naphthalene) or short, e.g. C1–C4 alkyl substituents with different structures.
The heterogeneous surface with anisotropic distribution of the adsorption sites was modeled as a square lattice composed of two types of adsorption sites, “w” (“weak”) and “s” (“strong”), that are arranged in strips. The lattice topography is specified by the widths of the strips, Ls for the strong adsorption sites and Lw for the weak ones. The difference between the energies of adsorption on the weak and strong centers is Δ > 0. The linear size of the lattice L = 60 was chosen to be comparable with periods of all the possible ordered structures and the lattice size was chosen so as to be commensurate with the periods of all possible ordered structures and large enough to reduce the statistical fluctuations. Periodic boundary conditions in both planar directions were imposed.
Considering the open system, a thermodynamic Hamiltonian of the constructed model can be written as follows:51
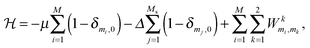 | (1) |
μ is the chemical potential of the molecule in the gas phase, i – the sequence number of the adsorption site, δ – the Kronecker delta, and mi – the occupation variable which is equal to 1, 2, 3 or 4 (depending on the molecular orientation), if the i adsorption site is occupied, and 0, if the i site is empty. Δ is the binding energy at the strong adsorption site j (binding energy at the weak adsorption site is supposed to be zero). M and Ms are the total number of adsorption sites and the number of strong adsorption sites in the lattice. The first term in the Hamiltonian describes the interaction with the gas phase and the sum is over all possible lattice sites. The second sum is over all strong adsorption sites and gives the binding energy impact on the potential energy of the adsorption layer. Finally, the third sum is over all distinct pairs of nearest neighbor lattice sites and takes into account the interaction energy between the adsorbed molecules. The variable k in the third term of the thermodynamic Hamiltonian is the nearest neighbor indicator (1 – right nn of the i site, 2 – bottom nn of the i site). W(k) are the interaction matrices. Elements of these matrices are the energy of the pairwise interaction of two molecules adsorbed on nearest neighbor sites mi and mk along the k direction on the underlying lattice. Thus, the matrices W(1) and W(2) describe the interactions between a molecule adsorbed on the central site i and a molecule adsorbed on the right and bottom neighboring sites, respectively. All energy values, temperature and the chemical potential are rescaled to a dimensionless form by |w|. The model has been investigated in a wide interval of parameters: μ/|w| = {−5, −4.9, −4.8,…, 8} и Δ/|w| = {0, 0.4, 0.6, 0.8,…, 4}. The temperature was fixed during the simulations at a value of RT/|w| = 0.1662. That was low enough to yield well-defined ordered structures and high enough to avoid long-lived metastable states.
The model has been investigated using two substantially different methods – the Monte Carlo method and the transfer-matrix technique. In this paper we focused on the equilibrium characteristics of the adsorption layer. In particular, we studied the dependence of its equilibrium structure on the external parameters and surface coverage, not on the kinetics of phase transitions in the adsorption layer. In this regard, we preferred to use the standard Monte Carlo method to the Kinetic Monte Carlo method.
On the other hand, we did not utilize the quantum chemistry methods because of the high computational cost and subsequent limitations on the system size. It is a critical limitation for our aim, since unit cells of the ordered phase in the adsorption layer usually contain a large number of molecules of large size (more than 10 atoms). However, the quantum chemistry calculations can be effectively used for the parameterization of statistical models, namely, for calculating the adsorption energies and pair interaction energies for specific molecules and surfaces,66–70e.g. ε, w and Δ parameters for the model under consideration.
We performed conventional grand canonical ensemble Monte Carlo calculations with Metropolis sampling. The adsorbed layer was equilibrated by the adsorption–desorption and diffusion dynamics, simultaneously. Additionally, the Monte Carlo algorithm involves the in-plane rotation of the molecule around its center by a multiple of 90°. To decide whether the new state of the system should be accepted or rejected we used the standard Metropolis acceptance scheme p = min{1, exp(ΔE/RT)}, where ΔE is the difference between the total energies of the system in the new and old states. Once all sites of the lattice have been given a chance to change their state one Monte Carlo step (MCS) has been made. At each value of the chemical potential, 107 MCSs were taken to equilibrate the adsorption layer and next 107 MCSs were used to compute ensemble averages. We calculated the partial coverage of weak θW(μ) and strong θS(μ) adsorption sites, total surface coverage θ(μ), and internal energy of the adsorption layer U and the differential heat of adsorption71qd = 〈θ·U〉 − 〈θ〉·〈U〉/〈θ2〉 − 〈θ〉2.
The model was independently studied with the transfer-matrix technique, whose main feature is the consideration of a lattice on an infinite length cylinder that is infinite in one direction and has a finite width M in the other.
It is noteworthy that periodic boundary conditions in the M direction were imposed to eliminate the influence of boundary effects. The transfer-matrix method is a deterministic approach, which allows obtaining the grand partition function of the lattice gas model through the calculation of the largest absolute eigenvalue of a transfer-matrix.41,50,72–79 The elements of the transfer-matrix are calculated as Ti,j = exp(0.5ui + 0.5uj + vi,j), where i and j are the numbers of one-dimensional rings of sites 1 ≤ i, j ≤ 5M on the infinite length cylinder. The states of the sites vary from ring to ring in such a way that each ring is unique. Thus, the amount of different rings in the model under consideration is equal to 5M. The operator uj gives the interaction energy along the i ring and vi,j describes the interaction energy between the i and j rings. The largest eigenvalue of the resulting transfer-matrix λmax is the model partition function. It makes it possible to calculate the grand thermodynamic potential (Ω), entropy (S) and surface coverage (θ) using the following equations: Ω = −(RT/M)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λmax, S = −(∂Ω/∂T)μ, ρ = −(∂Ω/∂μ)T. All transfer-matrix calculations were carried out using an in-house code. In this paper, the transfer-matrix calculations were performed for the semi-infinite lattice with M = 6. The choice of size is conditioned by the computational complexity of the problem and the structure of ordered phases formed in the adsorption layer on the surfaces of different topographies (various Ls and Lw values). In particular, the size M should be comparable to the linear sizes of unit cells of all ordered structures found in the ground state of the adsorption layer. A further increase in the system size leads to the exponentially increasing size of the transfer-matrix and, as a consequence, the computational complexity of the problem. Therefore, we did not perform the calculations at higher values of M. However, a comparison between the transfer-matrix and Monte Carlo data allows us to evaluate the statistical error and influence of the size effects.
λmax, S = −(∂Ω/∂T)μ, ρ = −(∂Ω/∂μ)T. All transfer-matrix calculations were carried out using an in-house code. In this paper, the transfer-matrix calculations were performed for the semi-infinite lattice with M = 6. The choice of size is conditioned by the computational complexity of the problem and the structure of ordered phases formed in the adsorption layer on the surfaces of different topographies (various Ls and Lw values). In particular, the size M should be comparable to the linear sizes of unit cells of all ordered structures found in the ground state of the adsorption layer. A further increase in the system size leads to the exponentially increasing size of the transfer-matrix and, as a consequence, the computational complexity of the problem. Therefore, we did not perform the calculations at higher values of M. However, a comparison between the transfer-matrix and Monte Carlo data allows us to evaluate the statistical error and influence of the size effects.
Results and discussion
Effect of the chemical structure of the adsorbing molecule
To evaluate the effect of the chemical structure of the adsorbed molecule on the phase behavior of the adsorption layer, we have examined two extreme cases of the model described above that differ in the value of the interaction parameter ε/|w|. This value is defined by the set of functional groups in the chemical structure of the adsorbed molecule, e.g. the presence or absence of bulky substituents.In the first case, the interaction between the non-functional parts of the adjacent adsorbed molecules was assumed to be non-repulsive. The interactions are either absent or short having a weak attractive character, such that |ε| ≪ |w|. It is nearly identical to the condition ε/|w| = 0. Therefore, there are no steric restrictions when filling the neighboring adsorption sites. This situation can occur in the adsorption layers of simple amino acids,7,23,58 benzoic acid and other mono-functional derivatives of benzene,23 naphthalene and other bicyclic and more complicated organic molecules.22,23,60
We performed the ground state analysis of such a model which relied on two thermodynamic principles: (i) the minimum of grand thermodynamic potential for open systems; (ii) the number of molecules on the surface is a never-decreasing function of the chemical potential. The structures of the possible ordered phases were determined from the Monte Carlo simulations. The results of the ground state analysis and the presence of two horizontal plateaus on the adsorption isotherms calculated using Monte Carlo and transfer-matrix methods indicate that only two stable phases are formed in the equilibrium adsorption layer on the surface with simple Ls = 1 and Lw = 1 topography (Fig. 2). The first phase that assembled at a relatively low surface coverage is linear and follows the surface topography. The second one corresponds to a close-packed monolayer. Obviously, the same self-assembly mechanism is true for a surface with any Ls/Lw topography. Firstly, the strips composed of strong adsorption sites are locally filled with the dimers of the adsorbed molecules stabilized with hydrogen bonding. Subsequently, the weak sites are occupied and the close-packed monolayer is achieved. It is worth noting that on the surfaces with low energetic heterogeneity Δ/|w| < 0.4 at non-zero temperatures the formation of the close-packed monolayer with an increase in the chemical potential occurs, passing a phase replicating the topography of the heterogeneous surface.
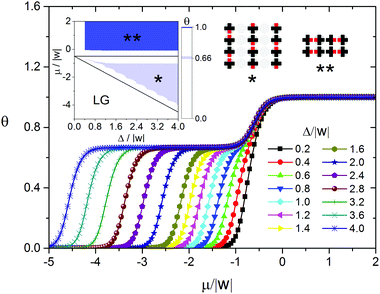
Another extreme case of the model is the adsorption of mono-functional molecules with bulky side substituents with the size similar to that of their cores, when |ε| → ∞. As a first approximation, we took into account only geometric constraints – the prohibition of adsorption on the nearest neighboring sites. If the distance between the adsorbed molecules is greater than the nearest neighbor one, the molecules either do not interact, or weakly attract each other. This attractive interaction is negligible compared to the interaction between the functional groups. Examples of such systems include adsorption layers of alkoxybenzoic acids,59 mono-functional derivatives of anthracene,61 porphyrin and phthalocyanine.12,19,20,62–65 As seen in Fig. 3, the phase behavior of the adsorption layer in this case is more complicated. When Δ/|w| < 0.4 and RT/|w| > 0, the only ordered phase appearing in the adsorption layer is a chess board-like pattern Ψ2.1, which is also formed on the homogeneous surface. In general, the self-assembly process of the adsorption layer depends on the energetic heterogeneity of the surface Δ/|w|. When Δ/|w| > 0.4, the increasing chemical potential results in the assembly of the Ψ1 phase. This phase consists of the dimers of the adsorbed molecules and, taking into account the presence of bulky side substituents, has a linear structure reproducing the surface topography. Further growth of the chemical potential leads to dense monolayers (Ψ2.1 and Ψ2.2 structures). When 0.4 < Δ/|w| < 1, the close-packed monolayer has the chess board-like structure Ψ2.1 mentioned above (Fig. 3). This clearly indicates a change in the driving force of the self-assembly process when undergoing the transition from the Ψ1 to Ψ2.1 phase. In particular, the predominance of the interaction between the molecule and the surface is replaced by the intermolecular repulsion, which is infinitely strong in this case and, as a first approximation, takes into account the shape of the molecule. A close-packed monolayer comprising the molecules with bulky side substituents on the surfaces with a strong energetic heterogeneity Δ/|w| > 1 has the Ψ2.2 structure (Fig. 3), which is largely determined by the surface topography.
The described scenarios of the self-assembly process qualitatively coincide with the scanning tunneling microscopy data for the self-assembled monolayers consisting of the above mentioned molecules on the heterogeneous surfaces with a strip-like topography.7,12,19,22,23,58,60–62,65
It is reasonable to suppose that in real adsorption layers on such surfaces the interactions between the functional and non-functional parts of adjacent adsorbed molecules can be comparable in strength, but not the extreme ones as is considered above. In the following part of the paper we discuss in detail the surface anisotropy effects in the organic adsorption layers using the model with ε/|w| = 2.
Effect of surface heterogeneity/anisotropy
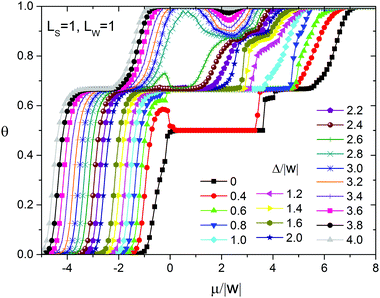
To assess the effect of surface heterogeneity on the self-assembly in the adsorption layer of the molecules with ε/|w| = 2, we used the strip-like surface with the simplest topography. Fig. 4 shows the adsorption isotherms and the differential heat of adsorption vs. surface coverage obtained with the Monte Carlo method at Ls = 1, Lw = 1 and different values of the energetic heterogeneity parameter Δ/w. As can be seen, in addition to the lattice gas (LG) characterized by the surface coverage θ close to zero, there are six distinct surface coverages which remain constant in the particular ranges of the chemical potential (pressure in the gas phase). This indicates the formation of six stable phases of the adsorption layer. Each phase is characterized by a specific adsorption energy corresponding to the horizontal plateaus on the differential heat of adsorption curves (Fig. 4b). It is important to stress that on the homogeneous surface and on the surface with a random distribution of the strong and weak sites at a similar set of intermolecular interactions only three ordered phases appear in the adsorption layer.49,80 Namely, they are chess board-like, zigzag and close-packed phases, consisting of dimers of the adsorbed molecules stabilized with hydrogen bonding. Thus, an anisotropic distribution of the strong and weak adsorption sites leads to a considerable complication of the phase behavior.Partial adsorption isotherms on the strong sites (Fig. 5) reveal that filling of the adsorption layer occurs via different mechanisms depending on the energetic heterogeneity of the surface Δ/w. In particular, the filling of the strong adsorption sites with the increase of the chemical potential can be monotonic or non-monotonic. Non-monotonic changing of the strong site coverage versus the chemical potential is observed only on the surfaces characterized by weak or moderate energetic heterogeneity, when Δ/|w| < 0.6 and 2.6 < Δ/|w| < 4, respectively. This effect is associated with the surface anisotropy, because it is not observed on the surface with a random distribution of the strong and weak adsorption sites. In the latter case, non-monotonic changing of the strong site coverage with respect to the chemical potential takes place only on the surfaces with weak energetic heterogeneity Δ/w.80
We have also calculated the entropy of the adsorption layer as a function of surface coverage using the transfer-matrix method Fig. 6. It is important to observe several different minima of the entropy in the same range of the chemical potential depending on the energetic heterogeneity of the surface. This means that in the same range of the chemical potential, on the surfaces with the same topography, but different energetic heterogeneities, there are ordered phases of the adsorption layer having various structures.
Structure of thermodynamically stable phases and phase diagrams
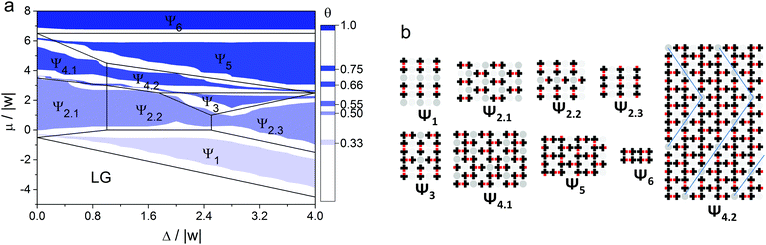
Using the Monte Carlo method, we identified all ordered structures that appear in the adsorption layer at different {Ls, Lw} sets. We combined all the adsorption isotherms calculated at RT/|w| = 0.1662 into phase diagrams in (Δ/|w|, μ/|w|) coordinates. In Fig. 7 an example of the phase diagram at Ls = 1 and Lw = 1 and the structures of the corresponding ordered phases are shown. The color on the diagram shows the areas, where these ordered structures were found at non-zero temperatures. The ground state phase diagram is presented in Fig. 7 in the form of black lines.As can be seen in Fig. 7, several types of ordered structures are formed in the adsorption layer such as discrete (Ψ1), linear (Ψ2.3), zigzag (Ψ4.1), chess board-like (Ψ2.1 and Ψ2.2), two-dimensional porous networks (Ψ5), and close-packed phases (Ψ6). Regions of existence of the ordered phases obtained at the finite temperature coincide with those determined in the ground state of the model, taking into account the obvious influence of the entropy factor, which leads to a marked shift of the phase coexistence lines. This allows us to conclude that the identified phases of the adsorption layer are stable over a relatively wide range of temperature. The analysis of the phase diagram and structures of the ordered phases shown in Fig. 7 enabled us to make some conclusions about the cause of the non-monotonic changing of the strong site coverage with an increase in the chemical potential. In the case of adsorption on a surface with low energetic heterogeneity, such as Δ/|w| = 0.4, initially the phase Ψ1 appears. The structure of this phase is completely determined by the “adsorbate–adsorbent” interactions and the topography of the surface. A further increase in the surface coverage leads to the formation of the Ψ2.1 phase, which has the chess board-like structure comprising the dimers of the adsorbed molecules. But the self-assembly of the Ψ2.1 phase is obviously determined by the repulsive interaction between the “non-functional” parts of the adsorbed molecules. And the above mentioned drop in the strong site coverage is precisely observed near the transition between Ψ1 and Ψ2.1 phases. A similar switch of the driving force is also observed on the surface with a high energetic heterogeneity. The difference lies in the fact that it occurs at higher surface coverage. Thus, the effect of non-monotonic filling of the strong sites with the increase of the chemical potential of the molecules (pressure in the gas phase) results from the changing of the driving force of the self-assembly process.
When Δ/|w| < 0.4 the phase behaviors of the adsorption layer on the heterogeneous and uniform surfaces are qualitatively the same at finite temperature. In this case, the structures of the ordered phases are determined only by the intermolecular interactions. As a result, the hierarchical nature of the self-assembly process inherent for the adsorption layer of mono-functional organic molecules on a homogeneous surface is preserved.49 This means that paired forms of the adsorbed molecules stabilized with an attractive interaction between their functional groups appear at low surface coverages. Further, they act as building blocks for more complicated structures appearing at higher surface coverages. On the other hand, when Δ/|w| > 4, the self-assembly mechanism and structure of the adsorption layer are driven only by the heterogeneous surface topography. It is worth noting that the partial adsorption isotherms on the strong sites are monotonic in both mentioned cases (Δ/|w| < 0.4 and Δ/|w| > 4).
Next, we have evaluated the effect of the surface topography (Ls/Lw ratio) on the phase behavior of the adsorption layer. As seen in Fig. 7 and 8, there are a large number of ordered phases in each case. Therefore, to preserve a general character of the discussion, we do not distinguish the ordered phases by the structure, but only by their types. There are discrete (D) phases, such as Ψ1, chess board-like (Ch) ones – Ψ2.1 и Ψ2.2, linear (L) – Ψ2.3, zigzag (Z) – Ψ4.1, two-dimensional porous networks (2DPN) – Ψ5, and close-packed structures (CP) – Ψ6. Furthermore, some mixed phases are formed in the adsorption layer, e.g. L–Ch, L–D, D–Ch and L–Z–Ch. The mixed-type phases usually appear on the surfaces with Ls > 1, when the ordered structure of one type appears on the strong adsorption sites and the other type of structure is observed on the weak sites. The exact structures of the ordered phases for each surface topography and related thermodynamic functions are presented in the ESI.†
 | ||
| Fig. 8 Phase diagrams of the adsorption layer calculated for different Ls/Lw ratios: (a) Ls = 1 and Lw = 2, (b) Ls = 1 and Lw = 3, (c) Ls = 2 and Lw = 1, and (d) Ls = 3 and Lw = 1. Black lines represent the diagrams in the ground states of the systems (RT/|w| = 0), and color shows the areas, where the corresponding ordered structures were found using the Monte Carlo method at ε/|w| = 2, RT/|w| = 0.1662. The structures of the phases are shown in the ESI.† | ||
As observed from the phase diagrams in Fig. 7 and 8, when Δ/|w| < 2, chess board-like (Ch) and zigzag (Z) phases assemble in the adsorption layers of mono-functional organic molecules on strip-like heterogeneous surfaces with any topography (Ls/Lw). The range of the chemical potential, where these phases are stable, is determined by the topography and energetic heterogeneity of the surface. In some cases, the chess board-like structure is more stable, in others – the zigzag one. A phase is more stable in terms of the changing chemical potential, when the unit cell of its structure is commensurate with the periodicity of the strong site arrangement.
A markedly different situation was encountered in the case when the width of the strip composed of strong adsorption sites Ls is two or more times greater than the size of the adsorbed molecule. Namely, a local assembly of the ordered phases on the strong adsorption sites is observed at Δ/|w| > 4. In this case, adsorption on the weak sites begins only after all the strong sites have been occupied. It is interesting that ordered structures formed on the strips of strong adsorption sites are similar to those formed on the homogeneous surface – Ch, Z and CP phases. This is reflected in the phase diagrams as the occurrence of the mixed linear structures L–x (where x – Ch, Z or CP) that reproduce the surface topography. For example, the following sequence of ordered structures occurs on the surface with Ls = 2 and Lw = 1 topography and Δ/|w| = 5 when the chemical potential increases: L–Ch, L–Z, L–CP, L–2DPN и CP (Fig. 8C and 9). The local assembly of the ordered phases on the surface with a strong energetic heterogeneity Δ/|w| > 4 results in the monotonic partial isotherms. This finding harmonizes with our previous statement that the non-monotonic filling of the strong adsorption sites is observed only on the surfaces with low and moderate energetic heterogeneity Δ/|w|.
 | ||
| Fig. 9 Ordered structures of the adsorption layer of mono-functional organic molecules observed on the heterogeneous surface with Ls = 2 and Lw = 1 topography at Δ/|w| = 5. | ||
One important remark which has to be made here is that the formation of the close-packed monolayers on the homogeneous and heterogeneous surfaces at non-zero temperatures occurs at practically the same values of the chemical potential μ/|w|. This value is determined by the ε/|w| ratio, which is defined by the chemical structure of the adsorbed molecule.
Thus, the obtained findings show that the phase behavior of the adsorption layer of mono-functional organic molecules on the heterogeneous surfaces with a strip-like topography is much richer, if the interaction between the functional and non-functional parts of adjacent adsorbed molecules is comparable as in the case of ε/|w| = 2, which has been discussed above in detail. In this case of the model, only a few ordered structures were experimentally established. These phases are stable in a wide range of chemical potential (gas phase pressure) and weakly depend on the energetic heterogeneity parameter (Δ/|w|). Other ordered phases are either not formed in the real adsorption layers or it is difficult to identify them experimentally, unless specifically looked for. The self-assembly of these phases is sufficiently dependent on the gas phase pressure and energetic heterogeneity of the surface. In addition to linear (L and L–X) and close-packed phases observed both in the extreme cases of our model and in the published STM images, the existence of discrete structures (isolated dimers of the adsorbed molecules),7,22,23 Z and Z–X structures21,22 is also confirmed experimentally. Therefore, the formation of other ordered phases in the adsorption layer is a prediction and should encourage further experimental studies.
Conclusions
In this paper, we have used a simple lattice gas model to study the features of the self-assembly in organic adsorption layers where, in addition to the anisotropy of the interaction between adsorbed molecules caused by the presence of functional groups in the chemical structure of the molecule, there is an anisotropy of interaction between the molecule and the solid surface. In particular, we examined the self-assembly of mono-functional organic molecules on the heterogeneous surface with the strip-like topography that is typical for vicinal, reconstructed and chemically modified surfaces of metallic single crystals. The surface is implied to be composed of “weak” and “strong” adsorption sites that are arranged in strips. Using a combination of the Monte Carlo and transfer-matrix methods within the grand canonical ensemble, we have calculated and analyzed the thermodynamic properties of the adsorption layer, which is summarized in the set of phase diagrams.We have shown that the structure of organic adsorption layers can be controlled not only by selecting a molecule with an appropriate chemical structure (arrangement of the functional groups). The organic adsorption layer of the desired structure can be obtained through the self-assembly of relatively simple molecules on a heterogeneous solid surface with simple topography.
We have demonstrated that adsorption layers of simple mono-functional organic molecules on solid surfaces with strip-like topography can self-assemble into various types of structures, such as discrete, linear, zigzag, chess board-like, two-dimensional porous and close-packed phases. And, the phase behavior of the adsorption layer is much richer, if the interactions between the functional and non-functional parts of adjacent adsorbed molecules have comparable strength and opposite signs.
When the width of the strip composed of the strong adsorption sites is two or more times greater than the adsorbed molecule, a local assembly of the ordered phases on the strong adsorption sites is observed at Δ/|w| > 4.
It was also revealed that filling of the strong adsorption sites with increasing chemical potential can be non-monotonic. This effect is associated with the surface anisotropy and results from the changing of the driving force of the self-assembly process with increasing surface coverage. In particular, the predominance of the interaction between the molecule and the surface is replaced by the repulsive interaction between the bulky side substituents (if any) in the chemical structure of the adsorbed molecules.
Acknowledgements
This study was supported by the Ministry of Education and Science of the Russian Federation through Project No. 16.2413.2014/K.References
- J. V. Barth, Annu. Rev. Phys. Chem., 2007, 58, 375–407 CrossRef CAS PubMed
.
- J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671–679 CrossRef CAS PubMed
.
- L. Bartels, Nat. Chem., 2010, 2, 87–95 CrossRef CAS PubMed
.
- A.-M. Andringa, M.-J. Spijkman, E. C. P. Smits, S. G. J. Mathijssen, P. A. van Hal, S. Setayesh, N. P. Willard, O. V. Borshchev, S. A. Ponomarenko, P. W. M. Blom and D. M. de Leeuw, Org. Electron., 2010, 11, 895–898 CrossRef CAS
.
- S. T. Marshall, M. O’Brien, B. Oetter, A. Corpuz, R. M. Richards, D. K. Schwartz and J. W. Medlin, Nat. Mater., 2010, 9, 853–858 CrossRef CAS PubMed
.
- W. Yao and Y. S. Zhao, Nanoscale, 2014, 6, 3467 RSC
.
- A. Kühnle, Curr. Opin. Colloid Interface Sci., 2009, 14, 157–168 CrossRef
.
- R. Otero, J. M. Gallego, A. L. V. de Parga, N. Martín and R. Miranda, Adv. Mater., 2011, 23, 5148–5176 CrossRef CAS PubMed
.
- S. Whitelam, Adv. Mater., 2015, 27, 5720–5725 CrossRef CAS PubMed
.
- H.-Y. Gao, H. Wagner, P. A. Held, S. Du, H.-J. Gao, A. Studer and H. Fuchs, Appl. Phys. Lett., 2015, 106, 081606 CrossRef
.
- R. Gutzler, L. Cardenas and F. Rosei, Chem. Sci., 2011, 2, 2290 RSC
.
- D. Heim, K. Seufert, W. Auwärter, C. Aurisicchio, C. Fabbro, D. Bonifazi and J. V. Barth, Nano Lett., 2010, 10, 122–128 CrossRef CAS PubMed
.
- N. Martsinovich and A. Troisi, J. Phys. Chem. C, 2010, 114, 4376–4388 CAS
.
-
F. Cicoira, C. Santato and F. Rosei, in STM and AFM Studies on (Bio)molecular Systems: Unravelling the Nanoworld, ed. P. Samorì, Springer Berlin Heidelberg, 2008, pp. 203–267 Search PubMed
.
- H. Liang, Y. He, Y. Ye, X. Xu, F. Cheng, W. Sun, X. Shao, Y. Wang, J. Li and K. Wu, Coord. Chem. Rev., 2009, 253, 2959–2979 CrossRef CAS
.
- K. Tahara, S. Furukawa, H. Uji-i, T. Uchino, T. Ichikawa, J. Zhang, W. Mamdouh, M. Sonoda, F. C. De Schryver, S. De Feyter and Y. Tobe, J. Am. Chem. Soc., 2006, 128, 16613–16625 CrossRef CAS PubMed
.
- A. Kasperski and P. Szabelski, Adsorption, 2012, 19, 283–289 CrossRef
.
- S. D. Feyter and F. C. D. Schryver, Chem. Soc. Rev., 2003, 32, 139–150 RSC
.
- M. Koepf, F. Chérioux, J. A. Wytko and J. Weiss, Coord. Chem. Rev., 2012, 256, 2872–2892 CrossRef CAS
.
- J. Kröger, H. Jensen, N. Néel and R. Berndt, Surf. Sci., 2007, 601, 4180–4184 CrossRef
.
- J. Kröger, N. Néel, H. Jensen, R. Berndt, R. Rurali and N. Lorente, J. Phys.: Condens. Matter, 2006, 18, S51–S66 CrossRef
.
- D. Écija, R. Otero, L. Sánchez, J. M. Gallego, Y. Wang, M. Alcamí, F. Martín, N. Martín and R. Miranda, Angew. Chem., Int. Ed., 2007, 46, 7874–7877 CrossRef PubMed
.
- S. M. Barlow and R. Raval, Surf. Sci. Rep., 2003, 50, 201–341 CrossRef CAS
.
- D. Écija, M. Trelka, C. Urban, P. de Mendoza, A. Echavarren, R. Otero, J. M. Gallego and R. Miranda, Appl. Phys. Lett., 2008, 92, 223117 CrossRef
.
- R. Otero, Y. Naitoh, F. Rosei, P. Jiang, P. Thostrup, A. Gourdon, E. Lægsgaard, I. Stensgaard, C. Joachim and F. Besenbacher, Angew. Chem., Int. Ed., 2004, 43, 2092–2095 CrossRef CAS PubMed
.
- M. S. Baviloliaei and L. Diekhöner, Phys. Chem. Chem. Phys., 2014, 16, 11265 RSC
.
-
W. Rudzinski and D. H. Everett, Adsorption of Gases on Heterogeneous Surfaces, Academic Press, London, 1992 Search PubMed
.
- L. B. Harris, Surf. Sci., 1968, 10, 129–145 CrossRef
.
- L. B. Harris, Surf. Sci., 1969, 13, 377–392 CrossRef CAS
.
- M. Jaroniec and W. Rudziński, Thin Solid Films, 1976, 37, L43–L47 CrossRef CAS
.
- F. A. Putnam and T. Fort, J. Phys. Chem., 1975, 79, 459–467 CrossRef CAS
.
- A. Patrykiejew, Thin Solid Films, 1993, 223, 39–50 CrossRef CAS
.
- T. Nitta and A. Yamaguchi, Langmuir, 1993, 9, 2618–2623 CrossRef CAS
.
- A. J. Ramirez-Pastor, M. S. Nazzarro, J. L. Riccardo and G. Zgrablich, Surf. Sci., 1995, 341, 249–261 CrossRef CAS
.
- A. J. Ramirez-Pastor, J. L. Riccardo and V. Pereyra, Langmuir, 2000, 16, 682–689 CrossRef CAS
.
- F. Bulnes, A. J. Ramirez-Pastor and G. Zgrablich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031603 CrossRef CAS PubMed
.
- F. Romá, F. Bulnes, A. J. Ramirez-Pastor and G. Zgrablich, Phys. Chem. Chem. Phys., 2003, 5, 3694–3699 RSC
.
- W. Rżysko and M. Borówko, Thin Solid Films, 2003, 425, 304–311 CrossRef
.
- F. Bulnes, A. J. Ramirez-Pastor and G. Zgrablich, Langmuir, 2007, 23, 1264–1269 CrossRef CAS PubMed
.
- M. Borówko and W. Rżysko, J. Colloid Interface Sci., 1996, 182, 268–274 CrossRef
.
- A. V. Myshlyavtsev and M. D. Myshlyavtseva, Appl. Surf. Sci., 2007, 253, 5591–5595 CrossRef CAS
.
- P. Szabelski, W. Rżysko, T. Pańczyk, E. Ghijsens, K. Tahara, Y. Tobe and S. De Feyter, RSC Adv., 2013, 3, 25159 RSC
.
- A. Kasperski and P. Szabelski, Surf. Sci., 2014, 629, 57–64 CrossRef CAS
.
- M. Šimėnas and E. E. Tornau, J. Chem. Phys., 2014, 141, 054701 CrossRef PubMed
.
- T. Misiūnas and E. E. Tornau, J. Phys. Chem. B, 2012, 116, 2472–2482 CrossRef PubMed
.
- A. Ibenskas, M. Šimėnas and E. E. Tornau, J. Phys. Chem. C, 2016, 120, 6669–6680 CAS
.
- N. Batina, A. Huerta, O. Pizio, S. Sokolowski and A. Trokhymchuk, J. Electroanal. Chem., 1998, 450, 213–223 CrossRef CAS
.
- C. Buzano, E. De Stefanis, A. Pelizzola and M. Pretti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 061502 CrossRef CAS PubMed
.
- S. S. Akimenko, V. A. Gorbunov, A. V. Myshlyavtsev and V. F. Fefelov, Surf. Sci., 2015, 639, 89–95 CrossRef CAS
.
- V. A. Gorbunov, S. S. Akimenko, A. V. Myshlyavtsev, V. F. Fefelov and M. D. Myshlyavtseva, Adsorption, 2013, 19, 571–580 CrossRef CAS
.
- S. S. Akimenko, V. A. Gorbunov, A. V. Myshlyavtsev and P. V. Stishenko, Phys. Rev. E, 2016, 93, 062804 CrossRef CAS PubMed
.
- T. J. Roussel and L. F. Vega, J. Chem. Theory Comput., 2013, 9, 2161–2169 CrossRef CAS PubMed
.
- A. Patrykiejew, O. Pizio and S. Soko\lowski, Phys. Rev. Lett., 1999, 83, 3442 CrossRef CAS
.
- M. A. A. Barbosa and V. B. Henriques, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051204 CrossRef PubMed
.
- C. E. Fiore, M. M. Szortyka, M. C. Barbosa and V. B. Henriques, J. Chem. Phys., 2009, 131, 164506 CrossRef PubMed
.
- M. Šimėnas, A. Ibenskas and E. E. Tornau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042124 CrossRef PubMed
.
- A. Ibenskas and E. E. Tornau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 051118 CrossRef CAS PubMed
.
- A. Schiffrin, A. Riemann, W. Auwärter, Y. Pennec, A. Weber-Bargioni, D. Cvetko, A. Cossaro, A. Morgante and J. V. Barth, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 5279–5284 CrossRef CAS PubMed
.
- K. S. Mali, K. Lava, K. Binnemans and S. De Feyter, Chem. – Eur. J., 2010, 16, 14447–14458 CrossRef CAS PubMed
.
- F. De Marchi, D. Cui, J. Lipton-Duffin, C. Santato, J. M. MacLeod and F. Rosei, J. Chem. Phys., 2015, 142, 101923 CrossRef PubMed
.
- C. Lu, Y. Wei, E. Zhu, J. E. Reutt-Robey and B. Xu, Int. J. Mol. Sci., 2012, 13, 6836–6848 CrossRef CAS PubMed
.
- S. Yoshimoto, N. Yokoo, T. Fukuda, N. Kobayashi and K. Itaya, Chem. Commun., 2006, 500–502 RSC
.
-
Functional Phthalocyanine Molecular Materials, ed. J. Jiang, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, vol. 135 Search PubMed
.
- J. Otsuki, Coord. Chem. Rev., 2010, 254, 2311–2341 CrossRef CAS
.
- C. Iacovita, P. Fesser, S. Vijayaraghavan, M. Enache, M. Stöhr, F. Diederich and T. A. Jung, Chem. – Eur. J., 2012, 18, 14610–14613 CrossRef CAS PubMed
.
- M. Seydou, J. Teyssandier, N. Battaglini, G. T. Kenfack, P. Lang, F. Tielens, F. Maurel and B. Diawara, RSC Adv., 2014, 4, 25698 RSC
.
- C. Li, N. Li, L. Liu, Y. Zhang, C. Yuan, L. Peng, S. Hou and Y. Wang, Chem. Commun., 2017, 53, 2252–2255 RSC
.
- A. I. Livshits and L. Kantorovich, J. Phys. Chem. C, 2013, 117, 5684–5692 CAS
.
- M. Mura and F. Silly, J. Phys. Chem. C, 2015, 119, 27125–27130 CAS
.
- M. Sicot, D. Tristant, I. C. Gerber, B. Kierren, F. Chérioux, Y. Fagot-Revurat, L. Moreau, J. Granet and D. Malterre, J. Phys. Chem. C, 2017, 121, 2201–2210 CAS
.
- J. E. González, A. J. Ramirez-Pastor and V. D. Pereyra, Langmuir, 2001, 17, 6974–6980 CrossRef
.
- W. Kinzel and M. Schick, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 324 CrossRef CAS
.
- P. A. Rikvold, J. B. Collins, G. D. Hansen and J. D. Gunton, Surf. Sci., 1988, 203, 500–524 CrossRef CAS
.
- A. V. Myshlyavtsev and V. P. Zhdanov, Chem. Phys. Lett., 1989, 162, 43–46 CrossRef CAS
.
- A. J. Phares, F. J. Wunderlich, J. D. Curley and D. W. Grumbine Jr, J. Phys. A: Math. Gen., 1993, 26, 6847 CrossRef
.
- A. J. Phares and D. W. Grumbine, Langmuir, 2014, 30, 6831–6840 CrossRef CAS PubMed
.
- H. A. Kramers and G. H. Wannier, Phys. Rev., 1941, 60, 252 CrossRef
.
- H. A. Kramers and G. H. Wannier, Phys. Rev., 1941, 60, 263–276 CrossRef
.
-
R. J. Baxter, Exactly solved models in statistical mechanics, Elsevier, 1982 Search PubMed
.
- V. A. Gorbunov, S. S. Akimenko and A. V. Myshlyavtsev, Adsorption, 2016, 22, 621–630 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional adsorption isotherms, differential heat of adsorption and internal energy vs. coverage curves, and detailed structures of ordered phases for different surface topographies. See DOI: 10.1039/c7cp01863k |
| This journal is © the Owner Societies 2017 |