On the structure of prilocaine in aqueous and amphiphilic solutions

Abstract

The solvation of prilocaine has been investigated in pure water and in an amphiphilic methanol/water solution using a combination of neutron diffraction with isotopic substitution augmented by Empirical Potential Structure Refinement (EPSR) simulations. This combination of techniques allows for details of the solvation structure on the atomic scale to be unravelled. The hydration of prilocaine is significantly altered relative to when this molecule is in pure water (as a hydrochloride salt) or in an amphiphilic environment (as a freebase compound). Interestingly, there is not a significant change in hydration around the amine group on prilocaine hydrochloride compared with prilocaine as a freebase. Despite this group being an ammonium group in water and an amine group in methanol/water solutions, the hydration of this motif remains largely intact. The changes in hydration between prilocaine as a free base and prilocaine·HCl instead appears to arise from a change in hydration around the aromatic ring and the amide group in the prilocaine molecule.

---

Introduction

Even though it is generally agreed that local anaesthetics (LA) function by disrupting the transfer of ions across membranes,¹ the precise mechanism of action of local anaesthetics remains largely unknown.² For instance, it is not clear as to whether these molecules interact solely with channel proteins or at the interface between the protein and surrounding lipids of the membrane bilayer given that LAs have a wide range of physiological affects which cannot be attributed to a single binding site.³ It has been further suggested that LAs amphiphilically interact with membranes, ordering the hydrophilic head groups of lipids while disordering the hydrophobic inner region,^1,4,5 where these modifications to the membranes have been hypothesized to affect the transport of ions through nerve membranes.^2,5

Prilocaine ((RS)-N-(2-methylphenyl)-N2-propylalaninamide; C₁₃H₂₀N₂O), is an aminoamide LA, which, can be applied in its freebase form as a eutectic mixture of prilocaine and lidocaine (EMLA®) as a topical preparation for dermal anaesthesia. Interestingly, the addition of water to this mixture results in an greater stability of this topical compound under ambient conditions,⁶ where the underlying causes of this enhanced stability from hydration are unknown. Prilocaine freebase is poorly water soluble and as a result is injected, as a water soluble salt (as the active ingredient in CITANEST®).⁷ Commercial products of prilocaine are racemic and the enantiomers appear to have a similar effectiveness in vitro, although in vivo the S(+) isomer is more active than the R(−) form.⁸ With respect to membrane–prilocaine interactions, it is thought that while uncharged prilocaine is preferentially located in the hydrophobic regions of the lipid bilayer,⁹ charged prilocaine is thought to be more effective in ordering the hydrophilic groups in lipid bilayers.⁵

In addition to acting as a LA, prilocaine is a drug which can also enter the blood stream and can be transported across the blood–brain barrier (BBB) in vivo, where currently there is no consensus as to how small molecules pass through this membrane via lipid mediated diffusion.¹⁰ A full understanding of the underlying mechanisms of this phenomenon is crucial as a substantial number of drugs fail due to inadequate BBB permeability.^11–13 Given that biological and physiological processes mostly take place in an aqueous or partly aqueous amphiphilic environment such as membranes,¹⁴ understanding how pharmaceuticals behave in solutions of similar characteristics is of utter importance for drug development.

In the present work, the structure of prilocaine has been investigated in solution in order to deduce how the solvation of this molecule is related to molecular mechanisms associated with its function in vivo. Specifically, the atomic scale hydration of prilocaine as a salt (hPLC) and as a freebase (PLC) has been assessed by using a combination of neutron diffraction with isotopic substitution augmented by Empirical Potential Structure Refinement (EPSR) computer simulations. hPLC has been measured in pure water solutions, while PLC in methanol/water solution both because it is insufficiently soluble in pure water to be measured using neutron diffraction and also to understand how the hydration of this molecule changes in amphiphilic solution. The use of the methanol/water solutions is advantageous as it provides a solution where hydrophobic and hydrophilic molecular motifs are in relatively close proximity to one another, allowing for details of prilocaine interactions with these motifs to be directly assessed.¹⁵

Materials and methods

Sample preparation

D₂O and all isotopomers of methanol (CD₃OD, CD₃OH, CH₃OD and CH₃OH) were obtained from Sigma-Aldrich. Each of the methanol isotopomers were refluxed over Mg metal, which was activated by I₂, for 24–48 hours and subsequently cryogenically distilled onto pre-dried 4 Å molecular sieves in order to remove any impurities. The samples were checked for purity using ¹H NMR. Prilocaine·HCl (hPLC; CAS:1786-81-8; Fig. 1) was also obtained from Sigma-Aldrich and its purity verified using NMR (see ESI†). All manipulations of methanol were performed under an N₂ atmosphere or using a high vacuum line (10⁻⁵ mbar).

Fig. 1 Axes and labels for prilocaine·HCl (hPLC; top), methanol and water (bottom). Freebase prilocaine PLC, where the N2 amonium group is deprotonated to an amine group (with only one H_N2) has the same axes and labelling scheme as hPLC.

Freebase prilocaine (PLC) was synthesized from hPLC as previously described.¹⁶ hPLC was dissolved in an excess of H₂O and excess NaOH was added to the solution in a 2 : 1 NaOH : PLC molar ratio. After precipitation in the aqueous solution, PLC was subsequently extracted in CH₂Cl₂. In order to remove all water from PLC, appropriate quantities of Na₂SO₄, until the phase-separated aqueous droplets were no longer visible by eye, was added to the solution, which was subsequently filtered and dried under vacuum, leaving PLC as an oil. The oil was subsequently stored at −20 °C for 24–48 hours, after which a powder is obtained. The purity of the prilocaine was verified using ¹H NMR (see ESI†), which shows that the ammonium nitrogen has been deprotonated to form an amine group and the yield of this process was ∼40–50%.

Deuterated-hPLC, where the exchangeable N–H hydrogens were substituted with deuterium was prepared by dissolving hPLC in excess D₂O, 99.8%-D. The solution was subsequently freeze-dried and this process was repeated three times in order to ensure adequate deuteration, verified by NMR, for the neutron diffraction measurements. All neutron samples (see below) were prepared by weight under an N₂ atmosphere, for hPLC in water at a ratio of 1 : 150 HLPC : H₂O and for PLC in methanol/water at a ratio of 1 : 75 : 75 PLC : CH₃OH : H₂O.

Neutron diffraction measurements

Neutron diffraction with isotopic substitution (NDIS) is a technique by which the structure of hydrogen containing liquids and solutions can be measured directly.^{10,15,17–29} The use of neutrons as a probe for hydrogen containing solutions exploits the different neutron scattering intensities for H versus D.³⁰

Neutron diffraction measurements give the average structure in solution in reciprocal space as a structure factor F(Q), where

and Q is the vector between the incident and scattered radiation ((Q = 4π sin θ/λ); λ is the incident wavelength and 2θ is the scattering angle), c and b are the concentrations and the coherent scattering lengths, respectively, of atom types, α and β and δ_αβ is the Kronecker delta. F(Q) is the weighted sum of the partial structure factors, S_αβ(Q) which are related to the atomic distances in real space, the radial distribution functions (RDFs; g_αβ(r)), via Fourier transformation:where ρ is the atomic number density (atoms per ų).

Measurement of a range of isotopomers at the same molar ratio, which differ only with respect to their scattering length (eqn (1)), gives rise to a series of diffraction patterns where different atomic correlations are more well represented in some patterns relative to others. While for simple systems these data can be combined to extract individual S_αβ(Q) for each unique atom in the sample,^18,19 for more complex systems which measure a large number of different atomic correlations this is not possible and computer simulations must be employed in order to extract a full set of correlations.

In the present work, the seven different isotopomeric samples of PLC in water/methanol and five different isotopomeric samples of hPLC in water (Table 1), contained in SiO₂ cells with a 1 mm wall thickness and 1 mm wall thickness were measured using the SANDALS instrument at the ISIS Neutron Facility (STFC, UK). Data for each sample were collected for between 8–9.5 hours per sample as well as for the empty cells, the empty instrument and a vanadium standard for background subtraction and normalization. The data for samples, cells, empty instrument and vanadium were corrected for absorption, multiple scattering and inelasticity effects and converted to F(Q) using the GUDRUN program.³¹

Table 1 Samples measured by neutron diffraction

	hPLC/H2O		PLC/H2O/CH3OH
		VI	CH3OH : H2O
I	H2O	VII	CD3OH : H2O
II	0.64 H2O/0.36 D2O	VIII	CH3OD : D2O
III	0.5 H2O/0.5 D2O	IX	CD3OD/CH3OH : H2O/D2O
IV	0.36 H2O/0.64 D2O	X	CD3OD/CD3OH : H2O/D2O
V	D2O	XI	CD3OD : D2O

---

Empirical potential structure refinement (EPSR)

Empirical potential structure refinement is a Monte Carlo based simulation specifically designed to model the structure of liquids and other disordered materials.³² EPSR is a technique which has been used in combination with NDIS measurements to determine the local structure of a variety of molecules in solution,^{10,15,20–24,26–28,33} and is unique as it uses a set of measured diffraction data as a constraint for resultant computational model. By beginning with a set of starting potentials, Lennard-Jones and appropriate charges in the present work, these potentials are iteratively refined until the molecular structure is consistent with the measured F(Q) data. Details of the EPSR technique are presented elsewhere.^32,34,35

The individual site–site RDFs can be extracted from EPSR and the coordination numbers (n^β_α(r)) of these functions can be determined from integration via

Two EPSR simulations were performed at the same molecular ratios as the measurements, where each simulation contained a racemic mixture of 26 prilocaine molecules (hPLC or PLC), with 3900 water molecules for the hPLC in water or 1950 water and 1950 methanol molecules for PLC in methanol/water at a density of ρ = 0.091 atoms per ų and ρ = 0.100 atoms per ų, respectively. PLC and hPLC were generated using Avogadro, and Lennard-Jones potentials and charges using ANTECHAMBER,³⁶ methanol potentials were taken from the OPLS-AA force field³⁷ and the SPC/E water model was used.³⁸ The seed potentials are listed in the ESI.† After an appropriate fit to the experimental data was reached, the simulation was accumulated for ∼30 000 iterations, and the molecular coordinates were saved every 10th configuration for the ANGULA analysis, to ensure a reasonable average sampling of the simulation box.

ANGULA analysis

Spatial arrangements of molecules relative to one another can be extracted from the EPSR simulation using ANGULA.^39,40 Cartesian axes were assigned to different fragments of hPLC and PLC and the methanol and water molecules as shown in Fig. 1. The distribution of the origin of nearest neighbour solvent molecules around different portions of PLC or hPLC can then be plotted as a three-dimensional Spatial Density Map (SDM).^40,41 For the SDMs presented here, analysis was performed for ∼3000 snapshots for each simulation. The angles between the sets of axes for the molecules were also used to find the most probable orientation of the solvent molecules relative to different sites on PLC or hPLC as has been previously described.^10,40 Whole molecule analysis (WMA) was also performed using ANGULA, where for this the centre of mass of any molecule within a chosen distance range from any atom on hPLC or PLC can be extracted.

Results and discussion

Fig. 2 shows the measured NDIS data compared with the EPSR fits to these data. For both hPLC in water and PLC in methanol/water solutions, the comparison between data and fit is good, with the major discrepancies between data and fit at lower values of Q, the region in which the background effects are most difficult to correct for in neutron diffraction measurements of solutions containing light atoms such as hydrogen and deuterium.⁴²

Fig. 2 F(Q) for hPLC in water (left) and PLC in methanol/water solutions (right). The circles are the experimental data, the solid lines are EPSR fits to this data and the grey lines are the difference between the fit and the experimental data.

Amide group solvation

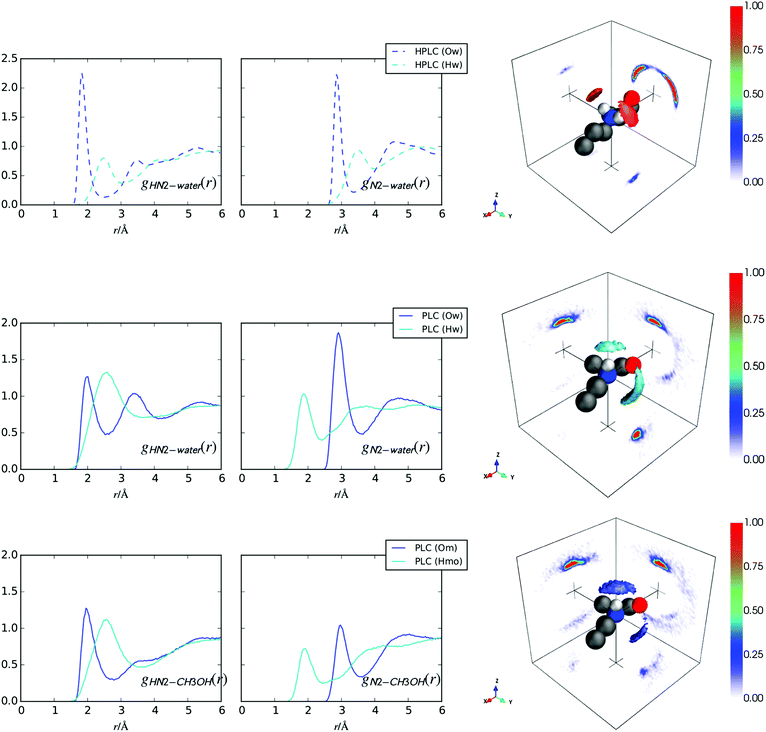
In water, the hPLC amide group (Fig. 1) donates a hydrogen bond to the surrounding water solvent as evidenced by the sharp peaks present in both the g_HN1Ow(r) and g_HN1Hw(r) functions at distances of 1.8 Å and 2.5 Å, respectively, in Fig. 3. Somewhat surprisingly, the same H_N1–Ow hydrogen bonding does not occur for PCL in methanol/water solutions, as the RDFs in Fig. 3 show an absence of peaks at low values of r. For hPLC, the SDM shows that the nearest neighbour water molecules are highly localised in the +z-direction pointed slightly away from (in the −x-direction) the methylphenyl ring. For PLC, the water molecules in the nearest neighbour shell have been depleted around the –NH group, where the highest density in this SDM is closer to the C=O oxygen rather than above the NH group despite N1 being at the origin of axes used in the SDM analysis.

Fig. 3 RDFs (top) and SDMs (bottom) for N1 and H_N1–water interactions for hPLC in water and PLC in methanol/water solution. The SDMs show 50% of the surrounding solvent molecules plotted in the surrounding density clouds and the cut throughs show the absolute density and are displaced from the central axis for clarity.

Fig. 4 shows the methanol –OH–amide interactions for PLC. Similar to the hydration of this group in PLC, the first peaks in the RDFs for the methanol –OH atoms show an absence of strong-hydrogen bonding interactions, with only a small, broad peak at ∼2.3 Å in the g_HN1Om(r) function. The SDM for the nearest neighbour –NH–hydroxyl interactions shows slightly higher association above H_N1 in the +z-direction, yet in general the nearest neighbour methanol molecules are highly diffuse around this group on PLC, similar to the water SDMs for PLC in Fig. 3.

Fig. 4 RDFs (top) for methanol –OH–amide interactions for PLC in methanol/water solution. SDMs (bottom) for methanol Om interactions around N1, where 50% of the surrounding solvent molecules are plotted in the surrounding density clouds and the cut throughs show the absolute density and are displaced from the central axis for clarity.

Table 2 shows the coordination numbers for amide H_N1–solvent hydrogen bonding RDFs in Fig. 3 and 4. A comparison of these numbers, clarifies that hydrogen bonding to the amide group from the solvent is considerably lower for PLC in the methanol/water solution compared with hPLC in water. Specifically, , representing around a 75% loss in hydration from this group upon transferring prilocaine to an amphiphilic solution.

Table 2 Coordination numbers (n^β_α) for H_N1–Ow/Om at 2.73 Å from Fig. 3 and 4

	hPLC	PLC
HN1–Ow	1.00	0.11
HN1–Om	—	0.14

---

In contrast, Fig. 5 shows that the prilocaine C=O oxygen accepts hydrogen bonds from water in both solutions as evidenced by the sharp peaks present in both the g_OOw(r) and g_OHw(r) functions. The double peak in g_OOw(r) for hPLC in pure water is likely an effect of water–NH bonding as shown in Fig. 3, given the absence of this peak in the same function for PLC in methanol/water solutions. On the average, in both hPLC and PLC the carbonyl oxygen accepts more than one hydrogen bond from the surrounding water solvent (Table 3). It should be noted that the difference in peak height for PLC versus hPLC in the functions in Fig. 5 is not due to a greater coordination of water but are larger likely due to density effects, that is the g(r)s are normalized to the bulk density of the solution which may in fact differ from the local coordination density at a specific hydration site. The nearest neighbour water coordination around this C=O group in the SDMs in Fig. 5 for PLC in methanol/water is more diffuse compared with the same for pure water, where the density is more localised directly above the C=O oxygen in the +z-direction.

Fig. 5 RDFs (top) and SDMs (bottom) for carbonyl C=O water interaction for hPLC and PLC in solution. SDMs for water Ow atoms around O, where 50% of the surrounding solvent molecules are plotted in the surrounding density clouds and the cut throughs show the absolute density and are displaced from the central axis for clarity.

Table 3 Coordination numbers (n^β_α) for the O–Hw/Hmo RDFs (at the r_min indicated) in Fig. 5 and 6

	hPLC	PLC	r min
O–Hw	1.36	1.23	2.40
O–Hmo	—	0.58	2.40
O–Ow	1.33	1.10	3.00
O–Om	—	0.64	3.2

---

Fig. 6 shows the methanol–OH interactions with the C=O oxygen on PLC, where the nearest neighbour solvation is more diffuse compared with hydration of this group in either solution (Fig. 5). The average coordination is also lower; with the methanol –OH forming ∼0.6 hydrogen bonds with the PLC amide oxygen. Interestingly, for PLC this oxygen forms more hydrogen bonds in total compared to hPLC as ^PLCn^O_Hw + ^PLCn^O_Hmo = 1.82 > ^hPLCn^O_Hw = 1.36 (Table 3). This increased electrostatic solvation of the –C=O group (near saturation) in contrast to the decreased hydration of the amide –NH group, suggests a local shift in hydration of the amide group from N1 to O and, perhaps, to other coordination centres in the molecule, upon the increase in hydrophobicity of the solution.

Fig. 6 RDFs (left) and SDM (right) for the methanol –OH–PLC carbonyl oxygen interactions for PLC in methanol/water solutions. SDMs for water Ow atoms around O, where 50% of the surrounding solvent molecules are plotted in the surrounding density clouds and the cut throughs show the absolute density and are displaced from the central axis for clarity.

Ammonium/amine solvation

Fig. 7 (top row) shows the hydration of the –NH₂⁺ group for hPLC (Fig. 1) in water. Compared with the –NH hydration in hPLC (Fig. 3), both N2 and H_N2 show more well defined hydrogen bonding peaks with the surrounding water solvent. The H_N2–Ow coordination numbers in Table 4 confirm that the solvation of this group is fully saturated by water as each H_N2 forms ∼1 hydrogen bond to the surrounding water solvent. This is further consistent with the hydration SDM in Fig. 7 which shows highly localised water density directly above each of the ammonium hydrogens.

Fig. 7 RDFs and SDMs for ammonium–water (top row) interactions for hPLC in water and amine–water (middle row) and amine–methanol hydroxyl (bottom row) interactions for PLC in methanol/water solutions. The SDMs show the surrounding nearest neighbour solvent molecules around N2, where 50% of these molecules are plotted in the surrounding density clouds and the cut throughs show the absolute density and are displaced from the central axis for clarity.

Table 4 Coordination numbers ((n^β_α)) for the H_N2–Ow/Om RDFs (at the r_min indicated) in Fig. 7

	hPLC	PLC	r min/Å
HN2–Ow	1.07	0.40	2.60
HN2–Hw	2.98	—	3.10
HN2–Hw	—	3.29	3.70
HN2–Om	—	0.41	2.80

---

In the methanol/water system, the PLC amine group hydrogen bonds with both water and methanol as evidenced by the fairly sharp peaks in the RDFs and the highly localised nearest neighbour SDMs for both water and methanol in Fig. 7 (bottom 2 rows). Compared to hPLC, the first peak in the g_HN2Ow(r) (Fig. 7) for PLC is slightly broader and shows a lower coordination with water (Table 4), which is not merely due to a replacement with H_N2–Om hydrogen bonds as the total hydrogen bonding is ∼0.8 hydrogen bonds per H_N2 atom compared to in hPLC = 1.07. In addition, both SDMs for the solvation around this group in PLC show the presence of solvation in front of N2 in the +y direction slightly displaced below the xy-plane, where this density is higher in the nearest neighbour water SDM. In both cases, this solvation suggests the presence of some hydrogen bonding donation to N2 from the surrounding solvent molecules.

Methylphenyl solvation

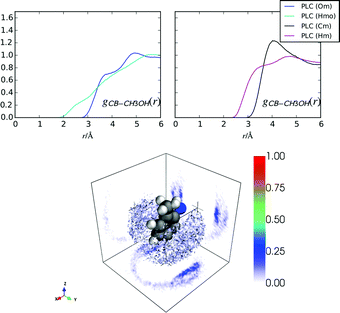
Fig. 8 shows the hydration around the methylphenyl ring for hPLC and PLC. In both cases, the most probable nearest neighbour water density around this group is located either above or below the plane of the methylphenyl ring, similar to what occurs for cocaine and indole in solution.^10,22,43 That there is more water present in the absence of methanol is also consistent with investigations on indole, where methanol was found to displace some of the hydration density from around the phenyl ring.⁴³ The correlation at shorter distances for g_CBHw(r) compared to g_CBOw(r) is indicative of an electrostatic π–H interaction. However, the absence of a clearly defined peak in the g_CBHw(r), suggests that there is no highly-directed hydrogen bonding (Fig. 8) between the methylphenyl ring and the surrounding water molecules beyond nearest neighbour investigations, similar to cocaine in solution.¹⁰

Fig. 8 RDFs (top) and SDMs (bottom) for the methylphenyl–water interactions for hPLC in water and PLC in methanol/water solutions. In the SDMs 50% of the surrounding water molecules are plotted in the surrounding density clouds and the cut throughs show the absolute density and are displaced from the central axis for clarity. It should be noted that for the SDMs the nearest neighbours are calculated from the centre of the methylphenyl ring to water oxygen, whereas the RDFs are a weighted average of all of the methylphenyl carbon–water RDFs.

Comparing the nearest distances in the RDFs for methanol around the methylphenyl ring in PLC (Fig. 9), it is clear that the nearest neighbour methanol coordination is mostly due to electrostatic–π interactions between the methanol –OH and the methylphenyl ring, as the g_CBHmo(r) has density at lower values of r than g_CBHm(r). However, g_CBCm(r)s shows a slightly more well defined peak than g_CBOw(r) at about 4 Å, implying that the –CH₃ groups may be more localised around the methylphenyl ring compared with the –OH groups. In general, the methylphenyl group on prilocaine has more tightly packed nearest-neighbours in hPLC (Table 5) as ^hPLCn^Ow_CB = 3.46, whereas ^PLCn^Ow_CB + ^PLCn^Om_CB = 1.53 within 4 Å of the methylphenyl ring atoms.

Fig. 9 RDFs (top) and SDMs (bottom) for the methylphenyl–methanol interactions for PLC in methanol/water solution. It should be noted that for the SDMs the nearest neighbours are calculated from the centre of the methylphenyl ring to the –OH oxygen, whereas the RDFs are a weighted average of all the methylphenyl carbon–methanol RDFs.

Table 5 Coordination numbers for the CB–water and methanol correlations for the RDFs shown in Fig. 8 and 9

	hPLC	PLC	r min/Å
CB–Ow	3.46	0.87	4.0
CB–Om	—	0.66	4.0
CB–Cm	—	0.88	4.0

---

From the methylphenyl–methanol RDFs in Fig. 9 it is not clear how the methanol molecules are oriented with respect to the ring. The orientational analysis in Fig. 10 shows the 2D Euler angle probability density maps for the orientations of these nearest neighbour methanol molecules in PLC (the Euler definitions are shown in more detail in the ESI†). These figures show that the preferred orientation of –OH group on methanol (θ_or, ϕ_or) is pointing towards the methylphenyl ring, while the orientation around this bond of the –CH₃ group (ψ_or) is not as clearly defined. The bottom panel of Fig. 10 shows a distribution of methanol molecules which span the range of orientations shown for the Euler angles in the top plane as well as underneath this ring (the orientational maps for these are shown in the ESI†). It is clear that while the methanol oxygen is closer to the methylphenyl group, the –CH₃ groups are oriented such that they are relatively flat relative to the plane of the ring.

Fig. 10 Euler angle probability density maps for nearest neighbour methanol molecules around the methylphenyl ring (top). Left: (cos θ_or, ϕ_or), right: (cos θ_or, ψ_or). Bottom: Representative PLC molecule depicting methanol molecules in a superposition of several probable orientations, on both sides of the methylphenyl ring depicted in the 2D Euler angle plots above. The Euler definitions are shown in more detail in the ESI.†

Whole molecule analysis

Whole molecule analyses (WMA), used to identify the most relevant solvation sites from 0–4 Å for both PLC and hPLC, are shown in Fig. 11. This distance range was chosen so that the nearest neighbour solvation for all the atomic sites could be encompassed in the WMA. Consistent with the site-specific hydration SDMs for hPLC, the most favourable hydration sites are mostly located around the three H_Nx sites as well as around the C=O oxygen where there is also a relatively large density of water molecules between C=O and –NH₂⁺ group. For PLC, water is preferentially located where it can act as a hydrogen bond donor to the amine group, whereas methanol tends to be preferentially located both near H_N2 where it can accept a hydrogen bond from PLC (Fig. 11, bottom) or between the amide N1 and the alkyl methyl and C=O groups displacing the water molecules in this region seen in hPLC.

Fig. 11 WMA for hPLC (left) and PLC (right), depicting the most preferential solvation sites on the prilocaine molecule in both solutions. The isocontour levels depict 50% of surrounding solvent molecules with the nearest neighbour water density in blue and the nearest neighbour methanol density in magenta. The prilocaine molecules are displayed as superposition of several possible conformations.

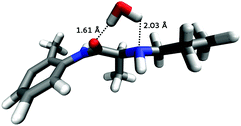
For PLC, most of the nearest neighbour water density seen in hPLC has been replaced by methanol molecules, apart from the amide group which, similar to hPLC, remains hydrated above N2. As this is the only region where hydration was persistent between prilocaine in the two solutions, further orientational analysis was performed to identify the most probable orientations of molecules around this region around PLC. Fig. 12 shows the most likely water orientation, where it appears that water is oriented such that it bridges from O to N2 forming two hydrogen bonds with both sites on PLC. The Euler angle maps used to generate this most probable orientation are shown in the ESI.†

Fig. 12 Plot depicting a single water molecule forming two hydrogen bonds, as donor to both –C=O oxygen and N2 amine nitrogen. (bottom) The distribution of orientations indicate that although the preferential orientation is somewhat broad, it is highly likely that a single water molecule will form two hydrogen bonds on prilocaine.

Conclusions

It is clear that the hydration of prilocaine changes relative to when this molecule is in only water or in aqueous amphiphilic environment. Interestingly, this appears not to be solely a result of the change from ammonium to amine group on prilocaine as the hydration of the amine nitrogen (N2; Fig. 1) remains largely intact in both solutions. Rather, it is the other motifs on prilocaine which are less hydrated in the presence of methanol, namely the amide –NH and methylphenyl groups which are desolvated in PLC relative to hPLC. The C=O group is somewhat more solvated for PLC relative to hPLC, but the solvation is much more diffuse around this group (Fig. 5 and 6) for PLC in methanol water solution.

The somewhat similar hydration of the amine motif in PLC and the ammonium motif in hPLC is consistent with Monte Carlo simulations of these groups in pure water,⁴⁴ however here it might be expected that this hydration would be more significantly altered, perhaps being more reduced, given that PLC is highly insoluble in pure water and that there are relatively fewer water molecules present in the methanol/water solution. While it may be that the water molecules that donate hydrogen bonds to the amine group in PLC are less tightly bound compared with amine or ammonium H⋯Ow hydrogen bonds, as was observed in MD simulations for methylamine in aqueous solution,⁴⁵ this does not account for the relatively low solubility of PLC in water given that methylamine is highly water soluble. This also helps to emphasize that it is rather the dehydration of the other sites around PLC which are responsible for its low solubility in water and, perhaps, for its ability to shed water as it crosses the BBB in vivo.

Overall, hPLC is relatively more solvated compared with PLC. For the nearest neighbour direct hydrogen bonding interactions, the more polar motifs on hPLC form ∼4.4 hydrogen bonds with the surrounding solvent , as opposed ∼3.8 for PLC in solution. For both, this is consistent with the theory that small molecules which cross the blood–brain barrier (BBB) must form no greater than eight hydrogen bonds in solution.¹³ For PLC, methanol displaces the water solvent from around both amide (H_N1) and amine (H_N2) hydrogens while water molecules in the nearest neighbour shell around PLC, tend to hydrogen bond to both the C=O group and the amine –N₂. Further, there is a relatively high probability of single water molecule binding to both groups simultaneously (as depicted in Fig. 11). The bridging hydration interaction could confer lipophilicity to PLC, as this bridging water may shield the hydrophilic groups on the molecule allowing it to more easily cross through membranes;¹ a similar mechanism has been proposed for cocaine.¹⁰

The largest ‘hydrophobic surface’ in prilocaine is the methylphenyl ring, however in PLC this ring is preferentially solvated by electrostatic interactions as has been observed for similar aromatic rings using a variety of techniques.^{10,22,43,46–48} Interestingly, for hPLC the nearest neighbour water molecules are more highly localised in this purely polar environment, while in the presence of methanol, the nearest neighbour hydration is disrupted by the presence of methanol and the overall solvation of this group is decreased for PLC in methanol/water solutions.

The difference in solvation between PLC and hPLC in solution may also be related to how LAs affect the order in the internal hydrocarbon region of a lipid bilayer.¹ PLC is more likely to penetrate into the hydrocarbon interior of a phospholipid membrane than its charged counterpart, hPLC.^1,9 This may be due, in part, to the ability of PLC to shed water molecules from around its methylphenyl ring in an amphiphilic environment as water appears to be weakly bound to this motif in the present solutions. This coupled with a highly constrained bridging water which ‘shields’ the charges of both the C=O and amine groups on PLC, may confer lipophilicity onto prilocaine in its deprotonated form, allowing it to more effectively penetrate the hydrophobic portions of a membrane. LAs are also thought to bind to the hydrophilic phosphate and carbonyl groups in phospholipids;⁴ in the case of prilocaine, the hydration observed here suggests that these electrostatic interactions would occur by virtue of both nitrogen motifs on the prilocaine molecule. hPLC appears to bind more strongly to its nearest neighbour water molecules, which, may correlate to how charged LAs affect the ordering of hydrophilic head groups to a greater extent than LAs which do not carry a formal charge.¹

This study emphasises that the hydration of molecules can be quite variable depending on the polarity of the solution. While some of the most probable hydration remains intact for hPLC in water compared with PLC in an amphiphilic solution, much of the nearest neighbour solvation is significantly altered between the two solutions. While a greater hydration of the –NH₂⁺ group is entirely expected for hPLC compared with PLC, the decrease in solvation around both the methylphenyl ring and the amide –NH group is not as obvious. The work here suggests that investigations of the hydration of pharmaceuticals should be performed in amphiphilic solutions, which afford a somewhat more physiologically relevant environment, as the hydration of molecules in these solutions may be vastly different to what occurs in a pure water solvent.

Acknowledgements

We thank the ISIS Facility (Rutherford Appleton Laboratories, STFC, UK) for the allocation of neutron beam time (RB-1600049), the UK Engineering and Physical Sciences Research Council (EP/J002615/1), Spanish MINECO (grants no. FIS2014a-54734-P and FIS2012-39443-C02-01) and the Government of Catalonia (grants no. 2009SGR-1003 and 2014SGR-00581) for funding.

References

1. I. C. P. Smith, M. Auger and H. C. Jarrell, Ann. N. Y. Acad. Sci., 1991, 625, 668–684.
2. H. Tsuchiya and M. Mizogami, Anesthesiol. Res. Pract., 2013, 2013, 1–18.
3. W. Kopeć, J. Telenius and H. Khandelia, FEBS J., 2013, 280, 2785–2805.
4. A. Shibata, K. Ikawa and H. Terada, Biophys. J., 1995, 69, 470–477.
5. I. Yun, E.-S. Cho, H.-O. Jang, U.-K. Kim, C.-H. Choi, I.-K. Chung, I.-S. Kim and W. Wood, Biochim. Biophys. Acta, 2002, 1564, 123–132.
6. A. A. Nyqvist-Mayer, A. F. Brodin and S. G. Frank, J. Pharm. Sci., 1986, 75, 365–373.
7. P. Bromage, Acta Anaesthesiol. Scand., Suppl., 1965, 9, 55.
8. B. Åkerman, H. Persson and C. Tegnér, Acta Pharmacol. Toxicol., 2009, 25, 233–241.
9. M. Pickholz, L. F. Fraceto and E. de Paula, Synth. Met., 2009, 159, 2157–2158.
10. A. J. Johnston, S. Busch, L. C. Pardo, S. K. Callear, P. C. Biggin and S. E. McLain, Phys. Chem. Chem. Phys., 2016, 18, 991–999.
11. W. J. Geldenhuys, D. D. Allen and J. R. Bloomquist, Expert Opin. Drug Metab. Toxicol., 2012, 8, 647–653.
12. A. B. Haberman, Genet. Eng. Biotechnol. News, 2009, 29, 48–49.
13. W. M. Pardridge, J. Cereb. Blood Flow Metab., 2012, 32, 1959–1972.
14. G. M. Cooper, The Cell, Sinauer Associates, 2nd edn, 2000.
15. S. Dixit, J. Crain, W. C. K. Poon, J. L. Finney and A. K. Soper, Nature, 2002, 416, 829–832.
16. D. B. Larsen, H. Parshad, K. Fredholt and C. Larsen, Int. J. Pharm., 2002, 232, 107–117.
17. S. E. McLain, C. J. Benmore and J. F. C. Turner, J. Phys. Chem., 2002, 117, 3816.
18. S. E. McLain, C. J. Benmore, J. E. Siewenie, J. Urquidi and J. F. C. Turner, Angew. Chem., Int. Ed., 2004, 43, 1952–1955.
19. A. K. Soper and R. N. Silver, Phys. Rev. Lett., 1982, 49, 471–474.
20. J. J. Shephard, S. K. Callear, S. Imberti, J. S. O. Evans and C. G. Salzmann, Phys. Chem. Chem. Phys., 2016, 18, 19227–19235.
21. J. J. Shephard, A. K. Soper, S. K. Callear, S. Imberti, J. S. O. Evans and C. G. Salzmann, Chem. Commun., 2015, 51, 4770–4773.
22. A. J. Johnston, Y. R. Zhang, S. Busch, L. C. Pardo, S. Imberti and S. E. McLain, J. Phys. Chem. B, 2015, 119, 5979–5987.
23. A. Sridhar, A. J. Johnston, L. Varathan, S. E. McLain and P. C. Biggin, Phys. Chem. Chem. Phys., 2016, 18, 22416–22425.
24. N. H. Rhys, A. K. Soper and L. Dougan, J. Phys. Chem. B, 2012, 116, 13308–13319.
25. J. Hladílková, H. E. Fischer, P. Jungwirth and P. Mason, J. Phys. Chem. B, 2015, 119, 6357–6365.
26. S. E. Norman, A. H. Turner, J. D. Holbrey and T. G. A. Youngs, ChemPhysChem, 2016, 17, 3923–3931.
27. E. Scoppola, A. Sodo, S. E. McLain, M. A. Ricci and F. Bruni, Biophys. J., 2014, 106, 1701–1709.
28. S. Soffientini, L. Bernasconi and S. Imberti, J. Mol. Liq., 2015, 205, 85–92.
29. Y. M. Delavoux, M. Gilmore, M. P. Atkins, M. Swadzba-Kwasny and J. D. Holbrey, Phys. Chem. Chem. Phys., 2017, 19, 2867–2876.
30. V. F. Sears, Neutron News, 1992, 3, 29.
31. A. K. Soper, GudrunN and GudrunX: programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section; RAL Technical Report (RAL-TR-2011-013), Rutherford Appleton Laboratory, STFC, UK, 2011.
32. A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204.
33. N. H. Rhys, R. J. Gillams, L. E. Collins, S. J. Callear, M. J. Lawrence and S. E. McLain, J. Chem. Phys., 2016, 145, 224504.
34. A. K. Soper, Mol. Simul., 2012, 38, 1171–1185.
35. A. K. Soper, ISRN Phys. Chem., 2013, 2013, 1–67.
36. J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260.
37. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
38. P. Mark and L. Nilsson, J. Phys. Chem. B, 2002, 106, 9440–9445.
39. http://https://gcm.upc.edu/en/members/luis-carlos/angula/ANGULA .
40. S. Busch, C. D. Lorenz, J. Taylor, L. C. Pardo and S. E. McLain, J. Phys. Chem. B, 2014, 118, 14267–14277.
41. L. C. Pardo, M. Rovira-Esteva, J. L. Tamarit, N. Veglio, J. F. Bermejo and G. J. Cuello, in Metastable Systems under Pressure, ed. R. Sylwester, D. Aleksandra and M. Victor, Springer, Netherlands, 2010, pp. 79–91.
42. A. Soper, Mol. Phys., 2009, 107, 1667–1684.
43. A. Henao, A. J. Johnston, E. Guàrdia, S. E. McLain and L. C. Pardo, Phys. Chem. Chem. Phys., 2016, 18, 23006–23016.
44. W. L. Jorgensen and J. Gao, J. Phys. Chem., 1986, 90, 2174–2182.
45. P. G. Kusalik, D. Bergman and A. Laaksonen, J. Chem. Phys., 2000, 113, 8036–8046.
46. D. Sharma and M. J. Paterson, Photochem. Photobiol. Sci., 2014, 13, 1549–1560.
47. S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard and G. A. Blake, Science, 1992, 257, 942–945.
48. W. Zhang, B. N. Markiewicz, R. S. Doerksen, A. B. Smith, III and F. Gai, Phys. Chem. Chem. Phys., 2016, 18, 7027–7034.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp01723e

---