Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Establishing the link between fibril formation and Raman optical activity spectra of insulin†
Jiří
Kessler
ab,
Shigeki
Yamamoto
c and
Petr
Bouř
 *a
*a
aInstitute of Organic Chemistry and Biochemistry, Academy of Sciences, Flemingovo náměstí 2, 16610 Prague, Czech Republic. E-mail: bour@uochb.cas.cz
bDepartment of Physical and Macromolecular Chemistry, Faculty of Science, Charles University, Hlavova 8, 12840 Prague, Czech Republic
cDepartment of Chemistry, Graduate School of Science, Osaka University, Osaka 560-0043, Japan
First published on 11th May 2017
Abstract
Folding of proteins into insoluble amyloidal fibrils is implicated in a number of biological processes. Optical spectroscopy represents a convenient tool to monitor such structural variations. Recently, characteristic changes in Raman optical activity (ROA) spectra of insulin during a pre-fibrillar stage were reported but not supported by a theoretical model. In the present study, molecular dynamics and the density functional theory are used to simulate the spectra and understand the connection between the structure, and ROA and Raman spectral intensities. Theoretical results are consistent with the observations and only confirm exceptional ROA sensitivity to the protein tertiary structure. Surprisingly, this sensitivity reflects local conformational changes in the peptide main and side chains, rather than a direct through-space interaction of the protein components. Side chains providing strong ROA signals, such as tyrosine, can additionally report on local conformational features. Theoretical modeling helps in explaining the observed spectral changes and is likely to enable future applications of ROA spectroscopy in protein structural studies.
1. Introduction
Amyloidal protein aggregates and fibrils are involved in a wide variety of biological processes including serious medical conditions such as neurodegenerative disorders.1 Insulin itself, a peptide hormone essential for the regulation of carbohydrate metabolism,2 adopts several fibril forms participating in various metabolic pathways.3Insoluble protein precipitates are difficult to study by standard high-resolution techniques; the structure is not regular enough for standard X-ray diffraction and provides a mediocre signal for nuclear magnetic resonance spectroscopy.4 Vibrational optical activity (VOA), including spectroscopies of vibrational circular dichroism (VCD) and Raman optical activity (ROA), has been suggested as an alternative technique that is extremely sensitive to protein structural variations.5,6 Indeed, VCD spectroscopy could detect not only the formation of insulin fibrils, but also subtle changes in their macroscopic helical twist caused by pH variation.7
The ROA technique, although in principle capable of capturing a wider range of molecular vibrations than VCD, has not been extensively used yet for fibrils due to experimental artifacts8 inherent to inhomogeneous samples. The problem was recently overcome for a pre-fibrillar state of insulin, where ROA spectra could be recorded on an incident circularly polarized (ICP) ROA spectrometer.9 Amyloidal clear or milky gels were incubated from a solution of bovine insulin and 0.1 M hydrochloric acid at 82 °C. After several hours at 22 °C the amyloid/fibrils refolded to their native form, and the whole process could be monitored spectroscopically.10 In the future, ROA spectroscopy is thus expected to provide a more detailed insight into the fibrils' world. However, rather minute changes in the spectra have been interpreted predominantly empirically or only on simplified systems.
In the present study we develop a theoretical basis to interpret these experimental results, by comparing them to density functional theory simulations of Raman and ROA intensities. This is a challenging task because the amyloid insulin structure is unknown at atomic resolution. In the past, the Cartesian coordinate transfer (CCT)11,12 technique enabled us to model spectral intensities of the native insulin form13 or even of larger globular proteins14 with unprecedented precision. In these cases, however, the geometries in solutions were supposed to be rather rigid and close to the published X-ray structures.
Fortunately, earlier studies indicate the most likely insulin secondary and tertiary structure in the fibrils as well. On a simplified insulin peptide sequence, a parallel β-sheet structure has been identified by X-ray as the basis of fibril conformation.15 The parallel β-sheets are also formed by proteins of similar size and sequences to insulin.16,17 Finally, ROA and Raman spectra of fibrous insulin resemble those of other proteins forming parallel β-sheets.10 In the present study, β-sheet structures derived from X-ray geometries of other proteins and molecular dynamics (MD) simulations are jointly used to model the insulin structure.
Quantum-mechanical simulations of ROA spectral intensities stimulated this kind of spectroscopy, making it a reliable tool to determine the absolute configuration18,19 and conformation20 of biomolecules. In particular, spectral computations within the density functional theory (DFT) provide sufficient precision at acceptable computational cost.21,22 They are based on a perturbation treatment of the interactions of molecules with circularly polarized light;23,24 the origin-independence of results obtained at approximate computational levels is typically ensured by field-dependent atomic orbitals.25 Normally, a harmonic approximation26,27 is used for vibrational frequencies, although anharmonic extensions are possible as well.28
Nevertheless, in spite of efficient implementations22,29 the direct “ab initio” simulations (including DFT) become very lengthy indeed for larger molecules.30 Therefore, various simplifications were suggested in the past, such as the intensity-carrying normal mode algorithm31 and the molecules-in-molecules (MIM) fragment-based approach.32 We use the CCT methodology11,12 allowing one to efficiently simulate large-molecule spectra14 as well as to average a large number of MD snapshots with a minimal loss of DFT accuracy.13
As we show in the present study, the method enabled us to link the observed spectral features to the protein structure and the native → fibril conformational change. By several computational experiments we could also test the sensitivity of ROA spectra to finer structural variations, investigate the role of contact (non-covalent) interactions of peptide chains, identify aromatic marker bands sampling the local geometry, and test other details of the computational methodology. Although primarily aimed at the insulin fibril experiment, the results confirm the potential of ROA spectroscopy to sense protein structural variations, including subtle conformational changes.
2. Methods
Measurement of Raman and ROA spectra
The spectra of native and fibrous insulin have been measured according to the protocol detailed elsewhere.9 Briefly, after condensation at elevated temperature and sonification, a metastable fibril state was obtained and its Raman and ICP ROA spectra were recorded simultaneously. The formation of the fibrils was confirmed by electronic circular dichroism and fluorescence of the thioflavin T dye. The sample was kept in a 30 μl fused silica cell and after about 3 hours the conformation changed back to the native one and its spectra were measured as well.Geometry models
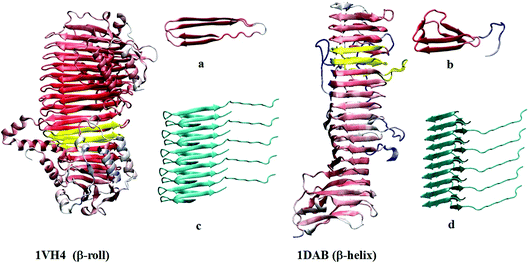
Two similar structural models of the amyloid were considered in the theoretical modeling, β-roll and β-helix. The β-roll insulin conformation was based on the β-roll protein (1VH4 in the structural database, http://www.rcsb.org/), i.e. the torsion angles of insulin were set to those in the A256-A306 residues of the protein. As for native insulin13 polar groups were protonated to correspond to the experimental pH of 2.5–3.1. An analogous procedure was used for the β-helix, where the torsion angles matched those in the A113 to A163 residues in the β-helix protein (item 1DAB in the database). The terminal part of the insulin B chain (B22–B30) was kept in its native β-sheet-like conformation. The 1VH4 and 1DAB proteins, and the derived insulin pentamer models are plotted in Fig. 1. An alternate view is provided in Fig. S1 in the ESI.† The β-helix geometry differs from β-roll by an additional loop separating two β-sheet parts, making the structure triangular (Fig. 1, part b). However, the two amyloidal models provided very similar spectra (Fig. S2, ESI†), and only the β-roll-like geometry was used for extensive modeling and analysis.Molecular dynamics
To account for protein flexibility and temperature fluctuations, molecular dynamics simulations were performed within the Amber10 environment.33 Monomeric insulin and the insulin trimer based on the β-roll geometry were placed in rectangular boxes (40 Å × 40 Å × 40 Å and 80 Å × 30 Å × 50 Å, respectively) filled with water molecules. In the trimer model only the middle molecule could move. The Amber03 force field,34 the NTV thermodynamic ensemble, temperature of 300 K, 1 fs integration step and periodic boundary conditions were used. The systems were equilibrated for 1 ns; during a production run (8.65 ns) 865 snapshot geometries were taken (i.e., each 10 ps). An average nuclear density was generated and for the best matching snapshot35 spectral parameters were calculated as described below, transferred to the other snapshots, and the resultant spectra were averaged.Other MD runs were performed within the Tinker program36 modified to simulate the macroscopic twist.37 The X-ray derived insulin geometry was placed in a rectangular box (12 Å × 110 Å × 110 Å) filled with water molecules. Helical periodic boundary conditions37 were applied to allow for a minor (0°–6°) twist between neighboring insulin units. The Amber99 force field38 was used in the NVT run with 1 fs integration time. During a 0.1 ns production run 100 snapshots were selected each ps and the spectra were generated as in the previous case.
Computation of vibrational spectra
The force field and tensor derivatives23,24,39 needed to generate vibrational Raman and ROA spectra for the native and X-ray mimicking fibrous insulin forms were generated from smaller molecular fragments via the CCT method.11,12 Following the automatic procedure described elsewhere14 the insulin molecule was divided into overlapping “covalent” fragments containing four amino acid residues, complemented by “contact” fragments accounting for interactions between close side chains. However, test computations confirmed that non-covalent through-space interactions influence the resultant Raman and ROA spectra only in a minor way (Fig. S3, ESI†); thus the contact fragments were not considered further. This is consistent with previous results on other proteins14 and benchmark numerical tests.12,40 The omission of the non-covalent interactions led to significant saving of computer time.The fragments were capped by methyl groups and subjected to partial optimization in vibrational normal mode coordinates,41 fixing the limiting normal frequency42 to 100 cm−1. This lower value allowed for a more extensive relaxation of the geometries and provided slightly better spectra (Fig. S4, ESI†) than the limit of 300 cm−1 used as default in the past.13 Program Qgrad41 was used for the normal mode optimization; the program is interfaced with the Gaussian43 software. All quantum chemical computations on the fragments were carried out using the B3PW9144 functional providing excellent results for protein ROA,45 the standard 6-31++G** basis set and the conductor-like polarizable continuum solvent model (CPCM)46,47 with water parameters accounting for both protein and aqueous environments.
For the optimized fragments, the harmonic force field (second energy derivatives) and derivatives of the α, G′ and A polarizability tensors23,24 were calculated using the Gaussian and transferred to the insulin molecule, and then back-scattered Raman and ICP24 ROA intensities were generated as usual.24,39 From the intensities, spectral curves were generated by a convolution with Lorentzian bands; full width at half maximum was set to 10 cm−1.
3. Results and discussion
Computation versus experiment
Simulated and experimental spectra of the native and fibrous/amyloidal insulin are compared in Fig. 2. Details of the experimental spectral shapes (upper panels in the figure) were discussed elsewhere.10 In the Raman spectra, formation of the fibrils is associated with minor spectral changes, such as the shift of the principal amide I band (mostly C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching), from 1659 to 1674 cm−1, and small intensity variations elsewhere. The ROA spectrum changes more; the fibril form gives a more compact “−/+” amide I “couplet” at 1660/1674 cm−1 instead of a broader one at 1640/1668 cm−1 of native insulin. The native −/+ 1240/1313 cm−1 band intensities become smaller and a positive 1271 cm−1 signal appears in this region for the fibril. The ROA signal around 1313 cm−1 has been previously identified as an important marker band for the α-helix,10,14,48–50 forming approximately 43% of native insulin, and the 1271 cm−1 band for the β-turn.10 Negative bands at 282, 993 and 1447 cm−1 in the ROA spectrum of native insulin disappear for the fibril, or are at least much less prominent due to experimental noise.
O stretching), from 1659 to 1674 cm−1, and small intensity variations elsewhere. The ROA spectrum changes more; the fibril form gives a more compact “−/+” amide I “couplet” at 1660/1674 cm−1 instead of a broader one at 1640/1668 cm−1 of native insulin. The native −/+ 1240/1313 cm−1 band intensities become smaller and a positive 1271 cm−1 signal appears in this region for the fibril. The ROA signal around 1313 cm−1 has been previously identified as an important marker band for the α-helix,10,14,48–50 forming approximately 43% of native insulin, and the 1271 cm−1 band for the β-turn.10 Negative bands at 282, 993 and 1447 cm−1 in the ROA spectrum of native insulin disappear for the fibril, or are at least much less prominent due to experimental noise.
The simulation (lower part of Fig. 2) reproduces many of these observations, sometimes in surprising details. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching frequencies of amide I and carboxyl (experimentally within 1659–1728 cm−1) are calculated to be very high, which is common for modeling at this level and has been identified as an error inherent to the dielectric solvent model.51,52 In the Raman spectra, the observed shift in an average amide I frequency (1659 → 1674 cm−1 for native → fibril transition) is reproduced reasonably well, as 1730 → 1742 cm−1. In ROA, the fibril form exhibits a sharp 1660(−)/1674(+) “couplet” in the experiment, which is well reproduced by the theory at 1728/1740 cm−1. This seems to be a typical feature of β-sheet structures also observed in globular proteins rich in β-sheets (e.g. concanavalin A),53 although model simulations indicate a significant dependence on detailed geometry, such as the β-sheet twist.20 In the native form, the amide I ROA signal is broader and mostly positive. The experimental Raman 1617 cm−1 band (calculated at 1669 cm−1, cf.Table 1) belongs to C
O stretching frequencies of amide I and carboxyl (experimentally within 1659–1728 cm−1) are calculated to be very high, which is common for modeling at this level and has been identified as an error inherent to the dielectric solvent model.51,52 In the Raman spectra, the observed shift in an average amide I frequency (1659 → 1674 cm−1 for native → fibril transition) is reproduced reasonably well, as 1730 → 1742 cm−1. In ROA, the fibril form exhibits a sharp 1660(−)/1674(+) “couplet” in the experiment, which is well reproduced by the theory at 1728/1740 cm−1. This seems to be a typical feature of β-sheet structures also observed in globular proteins rich in β-sheets (e.g. concanavalin A),53 although model simulations indicate a significant dependence on detailed geometry, such as the β-sheet twist.20 In the native form, the amide I ROA signal is broader and mostly positive. The experimental Raman 1617 cm−1 band (calculated at 1669 cm−1, cf.Table 1) belongs to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations in aromatic tyrosine residues, and is accompanied by a close band (“shoulder”, experimentally at ∼1608 cm−1) due to analogous phenylalanine vibrations. These “aromatic” vibrations generate a fairly strong negative ROA signal at 1620 cm−1 for the amyloid, reproduced by the simulation at 1657 cm−1.
C stretching vibrations in aromatic tyrosine residues, and is accompanied by a close band (“shoulder”, experimentally at ∼1608 cm−1) due to analogous phenylalanine vibrations. These “aromatic” vibrations generate a fairly strong negative ROA signal at 1620 cm−1 for the amyloid, reproduced by the simulation at 1657 cm−1.
| Calculated | Experimental | Assignmenta | |
|---|---|---|---|
| Native | Fibril | ||
| a ν and δ denote stretching and bending modes, respectively, “s” in the band frequency denotes a shoulder, oop – out of plane bending. b Approximate local symmetry with respect to the benzene (D6h) ring. | |||
| 1790 | 1728s | 1728s |
ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (COO−) O) (COO−) |
| 1742 | 1659 | 1674 |
ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) (amide I) O) (amide I) |
| 1669 | 1617 | 1617 | Tyr ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
| 1662s | 1608 | 1609s | Phe ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
| 1557 | 1537 | — |
ν(N–CO) + δ(N–H) (amide II), ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) His C) His |
| 1522 | 1460s | 1460s | His def. |
| 1477 | 1446 | 1446 | δ(C–H), sciss. |
| 1408 | — | 1395 | Amide III, δ(C–H) |
| 1352 | 1345 | 1345 | Tyr/Phe δ(C–H) |
| 1336 | 1345 | 1345 | δ(αC–H) |
| 1306 | — | 1271 | δ(αC–H) |
| 1290 | 1264 | 1247 | Tyr δ(C–H), ν(C–O) |
| 1239 | 1240 | 1233 | Amide III |
| 1230 | 1205 | 1205 | Tyr δ(C–H) |
| 1140 | 1123 | 1123 | δ(αC–N) |
| 1052 | 1032 | 1032 | Phe def. (E1ub) |
| 1012 | 1002 | 1002 | Phe def. (B2ub) |
| 995 | 993 | — | ν(C–C) |
| 866 | 852 | 855 | Tyr breathing def. |
| 846 | 830 | 828 | Tyr, Phe, oop(C–H) |
| 757 | 741 | 741 | oop(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
| 670 | 640 | 640 | oop(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,N–H,C–H) O,N–H,C–H) |
| 503 | 508 | 508 | ν(S–S) |
| 263 | 282 | — | Backbone |
The amide II band (C–N stretching and NH bending, around 1540 cm−1) is weak, which is usual in non-resonance Raman peptide spectroscopy. Only in resonance does its Raman intensity become comparable to that of amide I.54 In native insulin, however, there is a weak negative ROA signal (1537 cm−1, computed at 1557 cm−1), disappearing for the amyloid, both in theory and experiment.
The histidine C–H bending vibration (calculated 1522 cm−1, experimentally 1446 cm−1) gives strong Raman bands but generates a very weak ROA signal, at spectrometer detection limits. In the extended “amide III” region (∼1200–1400 cm−1) the simulation confirms that ROA is relatively strong and changes with the conformation. The 1313/1339 cm−1 (exp./calc.) ROA positive band of native insulin loses intensity and a new 1271/1306 cm−1 positive band appears in the fibril. The simulated spectrum changes even more, and predicts a 1343 cm−1 negative ROA band for the amyloid, undetected experimentally. Previously, vibrational modes in this region were identified as vibration of the main peptide chain coupled with αC–H bending and side chain vibrations,9,14,48–50 lending them exceptional sensitivity to fine geometry changes.
The negative 1240 cm−1 (exp.) ROA band of native insulin slightly shifts to 1233 cm−1 for the fibril, in accord with the simulations (1239 → 1213 cm−1), although here the observed intensity also changes less than that in theory. Partially, this can be explained by the incomplete conversion of the native state into the fibrillar one in the experiment.10 The negative 993 cm−1 experimental ROA band of native insulin is not well predicted theoretically either.
What is truly remarkable is the intense ROA signal in the lowest-wavenumber region (200–300 cm−1), comparable with the strongest bands of the extended amide III region. This region was largely ignored in previous protein studies, mostly for experimental reasons (unavailability of narrow filters) and due to difficult interpretation. The +/− native insulin bands at 224/282 cm−1 transform into a positive signal for the fibril, which seems qualitatively reproduced by the theory, although the simulated intensity is lower. Visualization of the dynamic displacement of vibrational normal modes revealed that the negative (282 cm−1) ROA bands largely arise from α-helical like segments of insulin. Previously, a similar +/− pattern was observed at 229/302 cm−1 for highly-helical human serum albumin,14 thus confirming the potential of the low-energy vibrations for probing the protein structure.
Signal of the aromatic residues
Insulin aromatic residues comprise one histidine, three phenylalanine and four tyrosine groups. Even though the aromatic rings themselves are not chiral, a strong ROA signal can be induced by coupling of their vibrations with neighboring covalent bonds and other peptide parts.14,55,56 In turn, they can locally sample the protein conformation. Indeed, according to the molecular dynamic modeling, phenylalanine and tyrosine conformer ratios (χ1 and χ2 side chain torsion angles) significantly change when insulin adopts the fibril/amyloidal form (Table S1, ESI†).To understand how the Phe and Tyr residues may contribute to insulin ROA spectra, we simulated Raman and ROA spectra of NH2-Phe-COH and NH2-Tyr-COH model aldehydes (Fig. S5, ESI†). The simulations revealed significant changes in spectral shapes of aromatic bands at 1005, 1330 and 1650 cm−1 due to the conformation of the aromatic side chain. For NH2-Phe-COH, the conformers were averaged using MD populations; Raman and ROA spectra were generated for the native and fibrillar insulin and are plotted in Fig. 3 (spectra of individual conformers are shown in Fig. S6, ESI†). For the fibril, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching band (number III in Fig. 3) generates a relatively strong negative ROA signal, corresponding to the observed band at 1620 cm−1 (Fig. 2). A similar intensity change occurs for the aromatic hydrogen bending (∼1350 cm−1, number II) and out of plane motion (∼1000 cm−1, number I), where, however, correspondence to the experiment is not so obvious due to overlap with other vibrations.
C stretching band (number III in Fig. 3) generates a relatively strong negative ROA signal, corresponding to the observed band at 1620 cm−1 (Fig. 2). A similar intensity change occurs for the aromatic hydrogen bending (∼1350 cm−1, number II) and out of plane motion (∼1000 cm−1, number I), where, however, correspondence to the experiment is not so obvious due to overlap with other vibrations.
Effect of fibril twist on the spectra
As pointed out above, Raman and ROA insulin spectra simulated with and without the fragments accounting for non-bonding inter-chain interactions were almost identical (Fig. S3, ESI†). Earlier studies also suggest that the through-space mutual polarization and other effects contribute to the resultant intensities only marginally.12 However, this does not mean that the ROA technique is insensitive to the tertiary protein structure. It does reflect the fine twist of fibril threads because the twist itself causes local changes in insulin conformation. This is documented in Fig. 4 where the spectra are simulated for three values of the twist (0°, −3° and −6°). The Tinker program was used to simulate the helical periodic boundary conditions,37 so that the spectra for the 0° twist do not completely coincide with those simulated by the Amber program; the shapes are fairly similar nonetheless. The twist variation approximately corresponds to that found in the model X-ray protein structures (Fig. 1). | ||
| Fig. 4 ROA and Raman spectra of an insulin fibril simulated for three values of the twist (τ) between neighboring insulin units (average from 100 MD snapshots). | ||
While the Raman spectra (bottom of Fig. 4) are more or less insensitive to the twist, the opposite is the case for ROA shapes (top). The ROA intensity variations are less pronounced above 1500 cm−1, e.g., the amide “W” shape is conserved for the three twist values. On the other hand, the extended amide III region 1200–1400 cm−1 undergoes more profound changes. All intensity variations are not monotonic, e.g., for the −3° twist a positive ROA signal appears around 1275 cm−1, with the intensity being smaller both for 0° and −6°. In the lower-wavenumber region (below ∼1000 cm−1) the spectra are less sensitive to the twist and depend on it in a more monotonic way. At the current level of experimental noise and computational precision it would be too speculative to deduce the twist of insulin fibrils merely by comparing the theoretical and experimental spectra; this “computational experiment” nevertheless documents the potential of ROA spectroscopy for future fibril structural studies.
Because the spectra for different fibril twist were generated from a limited number of MD snapshots, we had to ensure that the error of averaging is smaller than the effect of the twist itself. This is documented in Fig. S7 (ESI†): the small differences in Raman and ROA intensities obtained for the 50 and 100 snapshot simulations indicate that the twist-induced changes in the spectra are realistic indeed, i.e. they are mostly caused by structural changes, such as variation of the distribution of torsional angles, rather than by incomplete MD averaging. Examples of the angular distributions are given in Fig. 5, for the main chain φ and ψ torsion angles, and histidine and tyrosine χ1 side chain angle. Note, for example, that the (φ, ψ) values are close to (−145°, 150°), i.e., corresponding to the canonical β-sheet conformation,57 and that some twist-induced changes are not monotonic in the row 0 → −3° → −6°, as is the case for the ROA spectra. As may be expected, the individual side chain angle χ1 distributions react more sensitively to the twist than the averaged φ and ψ ones.
 | ||
| Fig. 5 Distribution of selected torsion angles for the three twist values (cf. τFig. 4): average φ and ψ main chain angles, and the χ1 angle of the histidine and tyrosine side chains. | ||
ROA versus VCD
From a more practical point of view it may be useful to summarize some specific features of fibril ROA as compared to another form of the vibrational optical activity, vibrational circular dichroism. As mentioned already in the introduction, one needs to be aware that inhomogeneous anisotropic samples, such as the fibrils, may for both techniques cause instrumental artifacts.8,24,58 This problem seems to be less serious for VCD, where sample rotation or measurement in different orientations usually eliminates the problem.59 For ROA, depolarization and reflection effects destroy the signal more and many researchers including us look for ways to stabilize it. Therefore, in the present work, we restrict the discussion to the “immature” fibril experiment, assuring sample homogeneity. Preliminary data nevertheless suggest that the observed spectral features will also apply to “mature” fibrils consisting of larger insoluble aggregates.Based on the results shown above, we can also conclude that the formation of the fibrils causes specific changes in ROA spectra. They are less spectacular than those for VCD; in particular insulin fibrils provided 10–100 fold VCD enhancement if compared to the native form.7,60 The enhancement seems to stem from a long-range synchronization of amide I (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching) vibrations.61 Such an enhancement is to some extent possible also for ROA,62 but has not been observed for the insulin fibrils. Here, the amide I signal “only” changes the shape (Fig. 2). As indicated by the simulations incorporating the macroscopic twist (Fig. 4), the longer-range order is reflected in the ROA spectra, too, but it is mediated by local conformational changes.
O stretching) vibrations.61 Such an enhancement is to some extent possible also for ROA,62 but has not been observed for the insulin fibrils. Here, the amide I signal “only” changes the shape (Fig. 2). As indicated by the simulations incorporating the macroscopic twist (Fig. 4), the longer-range order is reflected in the ROA spectra, too, but it is mediated by local conformational changes.
Finally, as a big advantage of ROA and Raman techniques in general, a wider range of wavenumbers is accessible than for VCD. For the insulin fibrils, secondary structure change visible in the amide I region could be confirmed by the αC–H bending (around 1310 cm−1) and low-frequency modes (<300 cm−1). Obviously, a combination of multiple techniques, such as ROA and VCD, is desirable for obtaining complete information on protein conformational behavior.
4. Conclusions
By combining molecular dynamics and density functional theory we simulated Raman and ROA spectra of the fibrillar conformation of insulin. Based on the modeling we could interpret most of the experimentally observed spectral changes, in particular the dependence of the ROA peak signs and intensities on the structure. The geometries derived from the β-roll and β-helix proteins provided similar spectra. Roughly speaking, most spectral changes could be interpreted as an α-helix → β-sheet secondary structure transition. Most significant changes comprised the amide I, extended amide III and the lowest-wavenumber (<300 cm−1) spectral regions.The aromatic residues not only had a strong Raman signal, but also an ROA signal that may locally probe the structure. One has also to admit that many spectral features potentially useful for structure determination are obscured due to limited accuracy of the simulations, band overlaps and experimental noise.
Rather surprising and potentially useful for future fibril studies was the sensitively responding amide III ROA signal to the fine changes of the conformation simulated for different macroscopic twists. The modeling showed that this does not reflect any direct non-covalent interaction of peptide chains, but is mediated by subtle changes in the local protein conformation. All the results confirm that the ROA technique is indeed very sensitive to protein conformational changes including the fibrillation, and that the complex simulations help extract additional details about the molecular structure and dynamics.
Acknowledgements
This work was supported by the Grant Agency of the Czech Republic (16-05935S and 15-09072S), the COST EU program (CA15214), and JSPS KAKENHI (JP26708017 and JP26246037) to S. Y.Notes and references
- S. Crunkhorn, Nat. Rev. Drug Discovery, 2012, 11, 105 CAS.
- E. Arbid and M. Kidron, J. Diabetes Sci. Technol., 2009, 3, 562–567 CrossRef PubMed.
- W. C. Duckworth and A. E. Kitabchi, Endocr. Rev., 2008, 2, 210–233 CrossRef PubMed.
- D. Reichert, O. Pascui, E. R. deAzevedo, T. J. Bonagamba, K. Arnold and D. Huster, Magn. Reson. Chem., 2004, 42, 276–284 CrossRef CAS PubMed.
- F. Zhu, J. Kapitán, G. E. Tranter, P. D. A. Pudney, N. W. Isaacs, L. Hecht and L. D. Barron, Proteins, 2008, 70, 823–833 CrossRef CAS PubMed.
- T. A. Keiderling, Curr. Opin. Chem. Biol., 2002, 6, 682–688 CrossRef CAS PubMed.
- D. Kurouski, R. A. Lombardi, R. K. Dukor, I. K. Lednev and L. A. Nafie, Chem. Commun., 2010, 46, 7154–7156 RSC.
- W. Hug, Appl. Spectrosc., 2003, 57, 1–13 CrossRef CAS PubMed.
- S. Yamamoto and H. Watarai, J. Raman Spectrosc., 2010, 41, 1664–1669 CrossRef.
- S. Yamamoto and H. Watarai, Chirality, 2012, 24, 97–103 CrossRef CAS PubMed.
- P. Bouř, J. Sopková, L. Bednárová, P. Maloň and T. A. Keiderling, J. Comput. Chem., 1997, 18, 646–659 CrossRef.
- S. Yamamoto, X. Li, K. Ruud and P. Bouř, J. Chem. Theory Comput., 2012, 8, 977–985 CrossRef CAS PubMed.
- S. Yamamoto, J. Kaminský and P. Bouř, Anal. Chem., 2012, 84, 2440–2451 CrossRef CAS PubMed.
- J. Kessler, J. Kapitán and P. Bouř, J. Phys. Chem. Lett., 2015, 6, 3314–3319 CrossRef CAS.
- M. I. Ivanova, S. A. Sievers, M. R. Sawaya, J. S. Wall and D. Eisenberga, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18990–18995 CrossRef CAS PubMed.
- P. Emsley, I. G. Charles, N. F. Fairweather and N. W. Isaacs, Nature, 1996, 381, 90–92 CrossRef CAS PubMed.
- J. Badger, J. M. Sauder, J. M. Adams, S. Antonysamy, K. Bain, M. G. Bergseid, S. G. Buchanan, M. D. Buchanan, Y. Batiyenko, J. A. Christopher, S. Emtage, A. Eroshkina, I. Feil, E. B. Furlong, K. S. Gajiwala, X. Gao, D. He, J. Hendle, A. Huber, K. Hoda, P. Kearins, C. Kissinger, B. Laubert, H. A. Lewis, J. Lin, K. Loomis, D. Lorimer, G. Louie, M. Maletic, C. D. Marsh, I. Miller, J. Molinari, H. J. Muller-Dieckmann, J. M. Newman, B. W. Noland, B. Pagarigan, F. Park, T. S. Peat, K. W. Post, S. Radojicic, A. Ramos, R. Romero, M. E. Rutter, W. E. Sanderson, K. D. Schwinn, J. Tresser, J. Winhoven, T. A. Wright, L. Wu, J. Xu and T. J. R. Harris, Proteins, 2005, 60, 787–796 CrossRef CAS PubMed.
- J. Costante, L. Hecht, P. L. Polavarapu, A. Collet and L. D. Barron, Angew. Chem., Int. Ed., 1997, 36, 885–887 CrossRef CAS.
- J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526–529 CrossRef CAS PubMed.
- T. Weymuth and M. Reiher, J. Phys. Chem. B, 2013, 117, 11943–11953 CrossRef CAS PubMed.
- K. Ruud, T. Helgaker and P. Bouř, J. Phys. Chem. A, 2002, 106, 7448–7455 CrossRef CAS.
- K. Ruud and J. Thorvaldsen, Chirality, 2009, 21, E54–E67 CrossRef CAS PubMed.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, UK, 2004 Search PubMed.
- L. Nafie, Vibrational optical activity: Principles and applications, Wiley, Chichester, 2011 Search PubMed.
- T. Helgaker, K. Ruud, K. L. Bak, P. Joergensen and J. Olsen, Faraday Discuss., 1994, 99, 165–180 RSC.
- E. B. Wilson, J. Chem. Phys., 1939, 7, 1047–1052 CrossRef CAS.
- D. Papoušek and M. R. Aliev, Molecular Vibrational/Rotational Spectra, Academia, Prague, 1982 Search PubMed.
- J. Hudecová, V. Profant, P. Novotná, V. Baumruk, M. Urbanová and P. Bouř, J. Chem. Theory Comput., 2013, 9, 3096–3108 CrossRef PubMed.
- J. R. Cheeseman, M. S. Shaik, P. L. A. Popelier and E. W. Blanch, J. Am. Chem. Soc., 2011, 133, 4991–4997 CrossRef CAS PubMed.
- S. Luber and M. Reiher, J. Phys. Chem. B, 2010, 114, 1057–1063 CrossRef CAS PubMed.
- S. Luber and M. Reiher, ChemPhysChem, 2009, 10, 2049–2057 CrossRef CAS PubMed.
- K. V. Jose and K. Raghavachari, J. Chem. Theory Comput., 2016, 12, 585–594 CrossRef PubMed.
- D. A. Case, I. T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, J. K. M. Merz, A. Onufriev, C. Simmerling, B. Wang and R. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- R. B. Best and G. Hummer, J. Phys. Chem. B, 2009, 113, 9004–9015 CrossRef CAS PubMed.
- J. Kessler, M. Dračínský and P. Bouř, J. Comput. Chem., 2013, 34, 366–371 CrossRef CAS PubMed.
- J. W. Ponder, Tinker, Software Tools for Molecular Design, Washington University School of Medicine, Saint Louis, 2000 Search PubMed.
- J. Kessler and P. Bouř, J. Comput. Chem., 2014, 35, 1552–1559 CAS.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins, 2006, 65, 712–725 CrossRef CAS PubMed.
- P. L. Polavarapu, Vibrational spectra: principles and applications with emphasis on optical activity, Elsevier, Amsterdam, 1998 Search PubMed.
- S. Yamamoto and P. Bouř, Collect. Czech. Chem. Commun., 2011, 76, 567–583 CrossRef CAS.
- P. Bouř and T. A. Keiderling, J. Chem. Phys., 2002, 117, 4126–4132 CrossRef.
- J. Hudecová, K. H. Hopmann and P. Bouř, J. Phys. Chem. B, 2012, 116, 336–342 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, USA, 2009 Search PubMed.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS.
- S. Yamamoto, H. Watarai and P. Bouř, ChemPhysChem, 2011, 12, 1509–1518 CrossRef CAS PubMed.
- A. Klamt, in The Encyclopedia of Computational Chemistry, ed. P. R. Schleyer, N. L. Allinger, T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schaefer III and P. R. Schreiner, John Wiley & Sons, Chichester, 1998, vol. 1, pp. 604–615 Search PubMed.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- E. W. Blanch, L. A. Morozova-Roche, D. A. E. Cochran, A. J. Doig, L. Hecht and L. D. Barron, J. Mol. Biol., 2000, 301, 553–563 CrossRef CAS PubMed.
- I. H. McColl, E. W. Blanch, L. Hecht and L. D. Barron, J. Am. Chem. Soc., 2004, 126, 8181–8188 CrossRef CAS PubMed.
- L. D. Barron, L. Hecht, E. W. Blanch and A. F. Bell, Prog. Biophys. Mol. Biol., 2000, 73, 1–49 CrossRef CAS PubMed.
- J. Kubelka and T. A. Keiderling, J. Phys. Chem. A, 2001, 105, 10922–10928 CrossRef CAS.
- P. Bouř, D. Michalík and J. Kapitán, J. Chem. Phys., 2005, 122, 144501 CrossRef PubMed.
- Z. Q. Wen, L. Hecht and L. D. Barron, Protein Sci., 1994, 3, 435–439 CrossRef CAS PubMed.
- S. A. Oladepo, K. Xiong, Z. Hong and S. A. Asher, J. Phys. Chem. Lett., 2011, 2, 334–344 CrossRef CAS PubMed.
- C. R. Jacob, S. Luber and M. Reiher, ChemPhysChem, 2008, 9, 2177–2180 CrossRef CAS PubMed.
- J. Hudecová, J. Horníček, M. Buděšínský, J. Šebestík, M. Šafařík, G. Zhang, T. A. Keiderling and P. Bouř, ChemPhysChem, 2012, 13, 2748–2760 CrossRef PubMed.
- G. D. Fasman, Prediction of Protein Structure and the Principles of Protein Conformation, Plenum, New York, 1989 Search PubMed.
- W. Hug and G. Hangartner, J. Raman Spectrosc., 1999, 30, 841–852 CrossRef CAS.
- F. Tobias and T. A. Keiderling, Langmuir, 2016, 32, 4653–4661 CrossRef CAS PubMed.
- D. Kurouski, R. K. Dukor, X. Lu, L. A. Nafie and I. K. Lednev, Chem. Commun., 2012, 48, 2837–2839 RSC.
- V. Andrushchenko and P. Bouř, J. Comput. Chem., 2008, 29, 2693–2703 CrossRef CAS PubMed.
- V. Profant, M. Šafařík, P. Bouř and V. Baumruk, Spectroscopy, 2010, 24, 213–217 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Computational tests and details of spectra simulation. See DOI: 10.1039/c7cp01556a |
| This journal is © the Owner Societies 2017 |